模式识别实验
实验1 图像的贝叶斯分类1.1 实验目的将模式识别方法与图像处理技术相结合，掌握利用最小错分概率贝叶斯分类器进行图像分类的基本方法，通过实验加深对基本概念的理解。
1.2 实验仪器设备及软件HP D538、MATLAB1.3 实验原理1.3.1 基本原理阈值化分割算法是计算机视觉中的常用算法，对灰度图象的阈值分割就是先确定一个处于图像灰度取值范围内的灰度阈值，然后将图像中每个像素的灰度值与这个阈值相比较。
并根据比较的结果将对应的像素划分为两类，灰度值大于阈值的像素划分为一类，小于阈值的划分为另一类，等于阈值的可任意划分到两类中的任何一类。
此过程中，确定阈值是分割的关键。
对一般的图像进行分割处理通常对图像的灰度分布有一定的假设，或者说是基于一定的图像模型。
最常用的模型可描述如下：假设图像由具有单峰灰度分布的目标和背景组成，处于目标和背景内部相邻像素间的灰度值是高度相关的，但处于目标和背景交界处两边的像素灰度值有较大差别，此时，图像的灰度直方图基本上可看作是由分别对应于目标和背景的两个单峰直方图混合构成。
而且这两个分布应大小接近，且均值足够远，方差足够小，这种情况下直方图呈现较明显的双峰。
类似地，如果图像中包含多个单峰灰度目标，则直方图可能呈现较明显的多峰。
上述图像模型只是理想情况，有时图像中目标和背景的灰度值有部分交错。
这时如用全局阈值进行分割必然会产生一定的误差。
分割误差包括将目标分为背景和将背景分为目标两大类。
实际应用中应尽量减小错误分割的概率，常用的一种方法为选取最优阈值。
这里所谓的最优阈值，就是指能使误分割概率最小的分割阈值。
图像的直方图可以看成是对灰度值概率分布密度函数的一种近似。
如一幅图像中只包含目标和背景两类灰度区域，那么直方图所代表的灰度值概率密度函数可以表示为目标和背景两类灰度值概率密度函数的加权和。
如果概率密度函数形式已知，就有可能计算出使目标和背景两类误分割概率最小的最优阈值。
假设目标与背景两类像素值均服从正态分布且混有加性高斯噪声，上述分类问题可以使用模式识别中的最小错分概率贝叶斯分类器来解决。
以1p 与2p 分别表示目标与背景的灰度分布概率密度函数，1P 与2P 分别表示两类的先验概率，则图像的混合概率密度函数可用下式表示1122()()()p x P p x P p x =+式中1p 和2p 分别为2121()21()x p x μσ--=222()22()x p x μσ--=121P P +=1σ、2σ是针对背景和目标两类区域灰度均值1μ与2μ的标准差。
若假定目标的灰度较亮，其灰度均值为2μ，背景的灰度较暗，其灰度均值为1μ，因此有12μμ<现若规定一门限值T 对图像进行分割，势必会产生将目标划分为背景和将背景划分为目标这两类错误。
通过适当选择阈值T ，可令这两类错误概率为最小，则该阈值T 即为最佳阈值。
把目标错分为背景的概率可表示为12()()TE T p x dx -∞=⎰把背景错分为目标的概率可表示为21()()TE T p x dx +∞=⎰总的误差概率为2112()()()E T P E T PE T =+为求得使误差概率最小的阈值T ，可将()E T 对T 求导并令导数为零，可得1122()()P p T P p T =代换后，可得221212222111()()ln 22P T T P σμμσσσ---=-此时，若设12σσσ==，则有2122121ln 2P T P μμσμμ⎛⎫+=+ ⎪-⎝⎭若还有12P P =的条件，则122T μμ+=这时的最优阈值就是两类区域灰度均值1μ与2μ的平均值。
上面的推导是针对图像灰度值服从正态分布时的情况，如果灰度值服从其它分布，依理也可求出最优阈值来。
一般情况下，在不清楚灰度值分布时，通常可假定灰度值服从正态分布。
因此，本课题中亦可使用此方法来求得最优阈值，来对实验图像进行分割。
1.3.2 最优阈值的迭代算法在实际使用最优阈值进行分割的过程中，需要利用迭代算法来求得最优阈值。
设有一幅数字图像(,)f x y ，混有加性高斯噪声，可表示为(,)(,)(,)g x y f x y n x y =+此处假设图像上各点的噪声相互独立，且具有零均值，如果通过阈值分割将图像分为目标与背景两部分，则每一部分仍然有噪声点随机作用于其上，于是，目标1(,)g x y 和2(,)g x y 可表示为11(,)(,)(,)g x y f x y n x y =+ 22(,)(,)(,)g x y f x y n x y =+迭代过程中，会多次地对1(,)g x y 和2(,)g x y 求均值，则111{(,)}{(,)(,)}{(,)}E g x y E f x y n x y E f x y =+= 222{(,)}{(,)(,)}{(,)}E g x y E f x y n x y E f x y =+= 可见，随着迭代次数的增加，目标和背景的平均灰度都趋向于真实值。
因此，用迭代算法求得的最佳阈值不受噪声干扰的影响。
利用最优阈值对实验图像进行分割的迭代步骤为： （1）确定一个初始阈值0T ，0T 可取为m i n m a x02S ST +=式中，min S 和max S 为图像灰度的最小值和最大值。
（2）利用第k 次迭代得到的阈值将图像分为目标1R 和背景2R 两大区域，其中1{(,)|(,)}k R f x y f x y T =≥ 2{(,)|0(,)}k R f x y f x y T=<< （3）计算区域1R 和2R 的灰度均值1S 和2S 。
（4）计算新的阈值1k T +，其中1212k S S T ++=（5）如果1||k k T T +-小于允许的误差，则结束，否则1k k =+，转步骤（2）。
利用迭代法求得最优阈值后，仍需进行一些人工调整才能将此阈值用于实验图像的分割，这是因为，这种最优阈值仍然属于全局阈值，它利用了图像中所有像素点的信息，但当光照不均匀时，图像中部分区域的灰度值可能差距较大，造成计算出的最优阈值分割效果不理想，此时，可设一人工经验因子进行校正。
四、实验步骤程序按照试验的要求结果，设计算法并用matlab实现。
a=imread('e:/shiyan/peppers.bmp');figure(1)imshow(a)b=a(:);Smax=max(b);Smin=min(b);T0=(Smax+Smin)/2;delta=1;while delta>=0.01clear R1R2m=1;l=1;for n=1:65536;if b(n)<=T0R1(m)=b(n);m=m+1;elseR2(l)=b(n);l=l+1;endendTnext=0.5*(mean(R1)+mean(R2));delta=abs(Tnext-T0);T0=Tnext;endfor n=1:256for m=1:256if a(n,m)>=T0c(n,m)=1;elsec(n,m)=0;endendendfigure(2)imshow(c)五、实验结果与分析阈值T。
=99. 24由两图对比可以看出，经过阈值分割后，高于阈值的点令其等于1，图中的黑色，低于阈值的点令其等于0，图中的白色，可见可以将其中的尖椒分出来，但是这种做法也有一种缺点，就是将像素都高于阈值的菜椒和背景没有分割开，将三类像素分成了两类。
如果要改进则需要进行重新分类，利用聚类的方法进行图像像素的归类和处理。
实验2 K均值聚类算法2.1 实验目的将模式识别方法与图像处理技术相结合，掌握利用K均值聚类算法进行图像分类的基本方法，通过实验加深对基本概念的理解。
2.2 实验仪器设备及软件HP D538、MATLAB、WIT2.3 实验原理K均值聚类法分为如下几个步骤：一、初始化聚类中心1、凭经验选择。
根据具体问题，凭经验从样本集中选出K个比较合适的样本作为初始聚类中心。
2、用前K个样本作为初始聚类中心。
3、将全部样本随机地分成K类，计算每类的样本均值，将样本均值作为初始聚类中心。
4、密度法。
以每个样本为球心，用某个正数为半径作一个球形邻域，落在邻域内的样本数为该点密度，选密度最大点为第一初始聚类中心。
在离开第一点规定距离范围外确定次大密度点，以避免初始聚类中心聚集。
K 个聚类划分的解中产生K个聚类划分的初始聚类中心。
先把全部5、从1样本看作一个聚类，其聚类中心为样本的总均值；然后确定两聚类问题的聚类中心是一聚类问题的总均值和离它最远的点；以此类推。
二、初始聚类1、按就近原则将样本归入各聚类中心所代表的类中。
2、取一样本，将其归入与其最近的聚类中心的那一类中，重新计算样本均值，更新聚类中心。
然后取下一样本，重复操作，直至所有样本归入相应类中。
三、判断聚类是否合理采用误差平方和准则函数判断聚类是否合理，不合理则修改分类。
循环进行判断、修改直至达到算法终止条件。
2.4 实验步骤及程序ticimg= imread ('e:/shiyan/peppers.bmp');[m,n]=size(img);subplot(2,2,1),imshow(img);title('原始图')subplot(2,2,2),imhist(img);title('灰度直方图')hold off;img=double(img);for i=1:200c1(1)=25;c2(1)=125;c3(1)=200;r=abs(img-c1(i));g=abs(img-c2(i));b=abs(img-c3(i));r_g=r-g;g_b=g-b;r_b=r-b;n_r=find(r_g<=0&r_b<=0);n_g=find(r_g>0&g_b<=0);n_b=find(g_b>0&r_b>0);i=i+1;c1(i)=sum(img(n_r))/length(n_r);c2(i)=sum(img(n_g))/length(n_g); c3(i)=sum(img(n_b))/length(n_b); d1(i)=(c1(i)-c1(i-1))^2;d2(i)=(c2(i)-c2(i-1))^2;d3(i)=(c3(i)-c3(i-1))^2;if d1(i)<=0.001&&d2(i)<=0.001&&d3(i)<=0.001R=c1(i);G=c2(i);B=c3(i);k=i;break;endendRGBimg=uint8(img);img(find(img<R))=0;img(find(img>R&img<G))=128;img(find(img>G))=255;tocsubplot(2,2,3),imshow(img);title('聚类后图像') subplot(2,2,4),imhist(img);title('聚类后灰度直方图')2.5 实验结果与分析聚类类别数为3类，聚类中心R =46.2688 G =120.5350 B =169.6114，迭代次数为12次，运行时间为0.363067 seconds。
模式识别 实验报告一
402
132
识别正确率
73.36
84.87
99.71
70.31
82.89
86.84
结果分析：
实验中图像3的识别率最高，图像1和图像2的识别率次之。图像1和图像2的分辨率相对图像3更低，同时图像2有折痕影响而图像1则有大量噪声。通过阈值处理能较好的处理掉图像1的噪声和图像2的折痕，从而使得图像1的识别率有所提升，而图像2的识别率变化不大。从而可以得出结论，图像3和图像2识别率不同的原因主要在于图像分辨率，而图像2和图像1识别率的不同则在于噪声干扰。
实验报告
题目
模式识别系列实验——实验一字符识别实验
内容：
1．利用OCR软件对文字图像进行识别，了解图像处理与模式识别的关系。
2．利用OCR软件对文字图像进行识别，理解正确率的概念。
实验要求：
1．利用photoshop等软件对效果不佳的图像进行预处理，以提高OCR识别的正确率。
2．用OCR软件对未经预处理和经过预处理的简体和繁体中文字符图像进行识别并比较正确率。
图像4内容既有简体又有繁体，从识别结果中可了解到错误基本处在繁体字。
遇到的问题及解决方案：
实验中自动旋转几乎没效果，所以都是采用手动旋转；在对图像4进行识别时若采用系统自己的版面分析，则几乎识别不出什么，所以实验中使用手动画框将诗的内容和标题及作者分开识别。
主要实验方法：
1．使用汉王OCR软件对所给简体和繁体测试文件进行识别；
2．理，再次识别；
实验结果：
不经过图像预处理
经过图像预处理
实验图像
图像1
图像2
图像3
图像4
图像1
图像2
字符总数
458
《模式识别》实验报告-贝叶斯分类
《模式识别》实验报告---最小错误率贝叶斯决策分类一、实验原理对于具有多个特征参数的样本（如本实验的iris 数据样本有4d =个参数），其正态分布的概率密度函数可定义为112211()exp ()()2(2)T d p π-⎧⎫=--∑-⎨⎬⎩⎭∑x x μx μ 式中，12,,,d x x x ⎡⎤⎣⎦=x 是d 维行向量，12,,,d μμμ⎡⎤⎣⎦=μ是d 维行向量，∑是d d ⨯维协方差矩阵，1-∑是∑的逆矩阵，∑是∑的行列式。
本实验我们采用最小错误率的贝叶斯决策，使用如下的函数作为判别函数()(|)(),1,2,3i i i g p P i ωω==x x （3个类别）其中()i P ω为类别i ω发生的先验概率，(|)i p ωx 为类别i ω的类条件概率密度函数。
由其判决规则，如果使()()i j g g >x x 对一切j i ≠成立，则将x 归为i ω类。
我们根据假设：类别i ω，i=1,2,……,N 的类条件概率密度函数(|)i p ωx ，i=1,2,……,N 服从正态分布，即有(|)i p ωx ~(,)i i N ∑μ，那么上式就可以写为1122()1()exp ()(),1,2,32(2)T i i dP g i ωπ-⎧⎫=-∑=⎨⎬⎩⎭∑x x -μx -μ对上式右端取对数，可得111()()()ln ()ln ln(2)222T i i i i dg P ωπ-=-∑+-∑-i i x x -μx -μ上式中的第二项与样本所属类别无关，将其从判别函数中消去，不会改变分类结果。
则判别函数()i g x 可简化为以下形式111()()()ln ()ln 22T i i i i g P ω-=-∑+-∑i i x x -μx -μ二、实验步骤（1）从Iris.txt 文件中读取估计参数用的样本，每一类样本抽出前40个，分别求其均值，公式如下11,2,3ii iii N ωωω∈==∑x μxclear% 原始数据导入iris = load('C:\MATLAB7\work\模式识别\iris.txt'); N=40;%每组取N=40个样本%求第一类样本均值 for i = 1:N for j = 1:4w1(i,j) = iris(i,j+1); end endsumx1 = sum(w1,1); for i=1:4meanx1(1,i)=sumx1(1,i)/N; end%求第二类样本均值 for i = 1:N for j = 1:4 w2(i,j) = iris(i+50,j+1);end endsumx2 = sum(w2,1); for i=1:4meanx2(1,i)=sumx2(1,i)/N; end%求第三类样本均值 for i = 1:N for j = 1:4w3(i,j) = iris(i+100,j+1); end endsumx3 = sum(w3,1); for i=1:4meanx3(1,i)=sumx3(1,i)/N; end（2）求每一类样本的协方差矩阵、逆矩阵1i -∑以及协方差矩阵的行列式i ∑， 协方差矩阵计算公式如下11()(),1,2,3,41i ii N i jklj j lk k l i x x j k N ωωσμμ==--=-∑其中lj x 代表i ω类的第l 个样本，第j 个特征值；ij ωμ代表i ω类的i N 个样品第j 个特征的平均值lk x 代表i ω类的第l 个样品，第k 个特征值；iw k μ代表i ω类的i N 个样品第k 个特征的平均值。
实验七基于神经网络的模式识别实验
实验七基于神经网络的模式识别实验一、实验目的利用神经网络实现模式识别，并验证其性能。
掌握基于神经网络的模式识别方法。
二、实验原理1.神经网络神经网络是一种模仿生物神经系统的计算模型，它由大量的神经元节点相互连接而成。
在模式识别中，我们一般采用多层前向神经网络进行模式的训练和识别。
2.神经网络的训练过程神经网络的训练过程可以分为两步：前向传播和反向传播。
前向传播是指将输入样本通过网络的各个层传递到输出层，并计算输出结果。
反向传播是指根据输出结果和目标结果之间的误差，将误差反向传播到网络的各个层，并根据误差调整网络中的权值。
3.模式识别对于模式识别问题，我们首先需要将输入模式转化为特征向量，然后通过神经网络来训练这些特征向量，并将其与已知类别的模式进行比较，从而进行模式的识别。
三、实验步骤1.数据准备选择适当的模式识别数据集，例如手写数字识别的MNIST数据集，将其分为训练集和测试集。
2.特征提取对于每个输入模式，我们需要将其转化为一个特征向量。
可以使用各种特征提取方法，例如像素值，轮廓等。
3.神经网络设计设计合适的神经网络结构，包括输入层、隐藏层和输出层，并确定各层的神经元数目。
4.神经网络训练使用训练集对神经网络进行训练，包括前向传播和反向传播过程。
可以使用各种优化算法，例如梯度下降法。
5.模式识别使用测试集对训练好的神经网络进行测试和验证，计算识别的准确率和性能指标。
6.性能评估根据得到的结果，评估神经网络的性能，并分析可能的改进方法。
四、实验结果通过实验我们可以得到神经网络模式识别的准确率和性能指标，例如精确度、召回率和F1-score等。
五、实验总结在本次实验中，我们利用神经网络实现了模式识别，并验证了其性能。
通过实验，我们可以掌握基于神经网络的模式识别方法，了解神经网络的训练和识别过程，以及模式识别中的特征提取方法。
实验结果表明，神经网络在模式识别问题中具有较好的性能，并且可以根据需要进行改进和优化。
《模式识别》实验报告K-L变换特征提取
《模式识别》实验报告K-L变换特征提取基于K-L 变换的iris 数据分类⼀、实验原理K-L 变换是⼀种基于⽬标统计特性的最佳正交变换。
它具有⼀些优良的性质：即变换后产⽣的新的分量正交或者不相关；以部分新的分量表⽰原⽮量均⽅误差最⼩；变换后的⽮量更趋确定，能量更集中。
这⼀⽅法的⽬的是寻找任意统计分布的数据集合之主要分量的⼦集。
设n 维⽮量12,,,Tn x x x =x ，其均值⽮量E=µx ，协⽅差阵()T x E=--C x u)(x u ，此协⽅差阵为对称正定阵，则经过正交分解克表⽰为x =TC U ΛU ,其中12,,,[]n diag λλλ=Λ，12,,,n u u u =U 为对应特征值的特征向量组成的变换阵，且满⾜1T-=UU。
变换阵TU 为旋转矩阵，再此变换阵下x 变换为()T -=x u y U ,在新的正交基空间中，相应的协⽅差阵12[,,,]xn diag λλλ==x U C U C。
通过略去对应于若⼲较⼩特征值的特征向量来给y 降维然后进⾏处理。
通常情况下特征值幅度差别很⼤，忽略⼀些较⼩的值并不会引起⼤的误差。
对经过K-L 变换后的特征向量按最⼩错误率bayes 决策和BP 神经⽹络⽅法进⾏分类。
⼆、实验步骤（1）计算样本向量的均值E =µx 和协⽅差阵()T xE ??=--C x u)(x u5.8433 3.0573 3.7580 1.1993??=µ，0.68570.0424 1.27430.51630.04240.189980.32970.12161.27430.3297 3.1163 1.29560.51630.12161.29560.5810x----=--C （2）计算协⽅差阵xC 的特征值和特征向量，则4.2282 , 0.24267 , 0.07821 , 0.023835[]diag =Λ-0.3614 -0.6566 0.5820 0.3155 0.0845 -0.7302 -0.5979 -0.3197 -0.8567 0.1734 -0.0762 -0.4798 -0.3583 0.0755 -0.5458 0.7537??=U从上⾯的计算可以看到协⽅差阵特征值0.023835和0.07821相对于0.24267和4.2282很⼩，并经计算个特征值对误差影响所占⽐重分别为92.462%、5.3066%、1.7103%和0.52122%，因此可以去掉k=1~2个最⼩的特征值，得到新的变换阵12,,,newn k u u u -=U。
实验七基于神经网络的模式识别实验
实验七基于神经网络的模式识别实验
一、实验背景
模式识别是机器学习领域中的一项重要研究领域，它可以被应用于多个领域，包括计算机视觉，图像处理，智能交通，自然语言处理和生物信息学等。
模式识别的目的是从观察到的数据中检测，理解和预测结果。
其中，神经网络（应用模式识别）是人工智能的关键部分，它模拟人类的神经元的工作方式，并且可以被用来识别，分类，计算和获取模式。
二、实验目标
本次实验的目的是，探讨神经网络在模式识别中的应用，并使用一个基于神经网络的模式识别系统来识别模式。
三、实验内容
（一）数据预处理
在进行本次实验之前，需要进行数据预处理，以便能够更好地使用神经网络。
数据预处理的目的是通过将原始数据处理成神经网络可以处理的格式，以便更好地提取特征。
（二）神经网络模型设计
（三）神经网络模型训练
在训练神经网络模型时，首先需要准备一组被识别的模式。
《模式识别》线性分类器设计实验报告
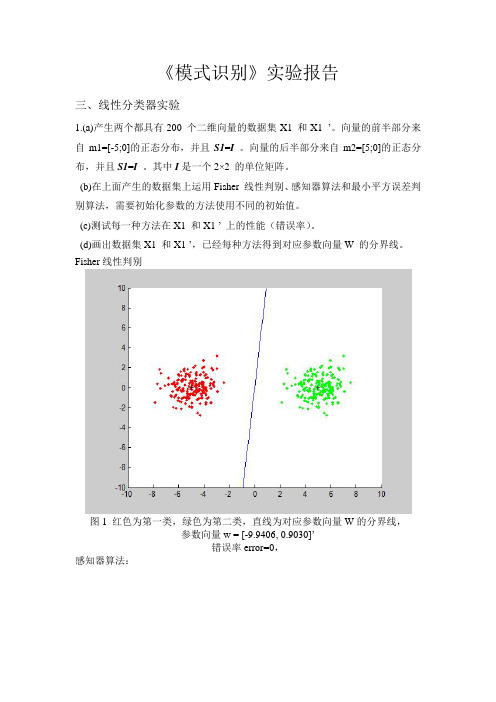
《模式识别》实验报告三、线性分类器实验1.(a)产生两个都具有200 个二维向量的数据集X1 和X1 ’。
向量的前半部分来自m1=[-5;0]的正态分布，并且S1=I 。
向量的后半部分来自m2=[5;0]的正态分布，并且S1=I。
其中I是一个2×2 的单位矩阵。
(b)在上面产生的数据集上运用Fisher 线性判别、感知器算法和最小平方误差判别算法，需要初始化参数的方法使用不同的初始值。
(c)测试每一种方法在X1 和X1 ’ 上的性能（错误率）。
(d)画出数据集X1 和X1 ’，已经每种方法得到对应参数向量W 的分界线。
Fisher线性判别图1 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数向量w = [-9.9406, 0.9030]’错误率error=0，感知器算法：图2 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[0.1;0.1]；迭代次数iter=2参数向量w = [-4.8925, 0.0920]’错误率error=0图3 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[1; 1]；迭代次数iter=2参数向量w = [-3.9925, 0.9920]’错误率error=0图4 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[10; 10]；迭代次数iter=122参数向量w = [-5.6569, 7.8096]’错误率error=0图5 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[50; 50]；迭代次数iter=600参数向量w = [-27.0945, 37.4194]’错误率error=0图6 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[50; 100]；迭代次数iter=1190参数向量w = [-54.0048, 74.5875]’错误率error=0最小平方误差判别算法：图7 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[0.1; 0.1]；参数向量w = [-0.1908, -0.0001]’错误率error=0图8 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[0.5; 0.5]；参数向量w = [-0.1924, 0.1492]’错误率error=0图9 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[1; 0.5]；参数向量w = [-0.1914, 0.0564]’错误率error=0图10 红色为第一类，绿色为第二类，直线为对应参数向量W的分界线，参数的初始值为[1; 1]；参数向量w = [-0.1943, 0.3359]’错误率error= 0.00502.重复1.中的实验内容，数据集为X2 和X2 ’。
实验课程-091042-模式识别
模式识别实验教学大纲(实验课程)◆课程编号：091042◆课程英文名称：Pattern Recognition◆课程类型：☐通识通修☐通识通选☐学科必修☐学科选修☐跨学科选修☐专业核心 专业选修（学术研究）☐专业选修（就业创业）◆适用年级专业（学科类）：计算机科学与技术、网络工程、软件工程四年级◆先修课程：高等数学、线性代数、概率与数理统计、程序设计语言◆总学分：1◆总学时：32一、课程简介与教学目标《模式识别实验》是配合计算机科学与技术、网络工程和软件工程专业课程《模式识别》开设的实验课程。
要求学生在理解模式识别理论及方法的基础上，应具有设计、实现、分析和维护模式识别等方面的能力。
通过本实验课程的训练，使学生熟练掌握模式识别的基本原理和方法，加深对各方法涉及的基础知识的认识，强化编程技能，培养创新能力。
二、教学方式与方法教学方式：学生动手实验为主，辅以适当的提问、小组讨论及实验点评等。
教学方法：探讨式教学、启发式教学、实验教学相结合；尝试包括实验设计、研究设计、答辩、总结等环节的教学。
三、教学重点与难点（一）教学重点理解模式识别系统的基本原理，掌握模式识别中Bayes分类器、Parzen窗估计与K N近邻估计、最近邻方法和C均值聚类算法等，学会使用相应工具进行模式识别方法的设计与实现，从而进一步理解模式识别课程中所讲授的理论知识。
（二）教学难点H-K算法、基于K-L变换的实现。
四、学时分配计划五、教材与教学参考书（一）教材1.《模式识别（第2版）》，边肇祺，张学工等，清华大学出版社，2000。
（二）教学参考书1．《模式识别导论》，齐敏、李大健、郝重阳，清华大学出版社，2009；2．《模式识别原理》，孙亮，北京工业大学出版社，2009；3．《模式识别（第3版）》，张学工，清华大学出版社，2010；4．《模式识别(英文版·第3版)(经典原版书库)》，(希腊)西奥多里迪斯等著，机械工业出版社，2006。
模式识别试验(基于Fisher准则线性分类器设计)
模式识别实验（三）一、实验名称基于Fisher准则线性分类器设计二、实验目的：本实验旨在让同学进一步了解分类器的设计概念，能够根据自己的设计对线性分类器有更深刻地认识，理解Fisher准则方法确定最佳线性分界面方法的原理，以及Lagrange乘子求解的原理。
三、实验原理：线性判别函数的一般形式可表示成其中根据Fisher选择投影方向W的原则，即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开，类内样本投影尽可能密集的要求，用以评价投影方向W的函数为：上面的公式是使用Fisher准则求最佳法线向量的解，该式比较重要。
另外，该式这种形式的运算，我们称为线性变换，其中(m1-m2)式一个向量，Sw-1是Sw的逆矩阵，如(m1-m2)是d维，Sw和Sw-1都是d×d维，得到的也是一个d维的向量。
向量就是使Fisher准则函数达极大值的解，也就是按Fisher准则将d维X 空间投影到一维Y空间的最佳投影方向，该向量的各分量值是对原d维特征向量求加权和的权值。
以上讨论了线性判别函数加权向量W 的确定方法，并讨论了使Fisher 准则函数极大的d 维向量 的计算方法，但是判别函数中的另一项w0尚未确定，一般可采用以下几种方法确定w0如或者或当与已知时可用……当W 0确定之后，则可按以下规则分类，使用Fisher 准则方法确定最佳线性分界面的方法是一个著名的方法，尽管提出该方法的时间比较早，仍见有人使用。
四、实验内容：已知有两类数据1ω和2ω二者的概率已知=0.6，=0.4。
1ω中数据点的坐标对应一一如下：数据：x =0.2331 1.5207 0.6499 0.7757 1.0524 1.19740.2908 0.2518 0.6682 0.5622 0.9023 0.1333-0.5431 0.9407 -0.2126 0.0507 -0.0810 0.73150.3345 1.0650 -0.0247 0.1043 0.3122 0.6655 0.5838 1.1653 1.2653 0.8137 -0.3399 0.5152 0.7226 -0.2015 0.4070 -0.1717 -1.0573 -0.2099 y =2.3385 2.1946 1.6730 1.6365 1.7844 2.0155 2.0681 2.1213 2.4797 1.5118 1.9692 1.83401.87042.2948 1.7714 2.3939 1.5648 1.93292.2027 2.4568 1.7523 1.6991 2.4883 1.7259 2.0466 2.0226 2.3757 1.7987 2.0828 2.0798 1.9449 2.3801 2.2373 2.1614 1.9235 2.2604 z =0.5338 0.8514 1.0831 0.4164 1.1176 0.55360.6071 0.4439 0.4928 0.5901 1.0927 1.07561.0072 0.4272 0.4353 0.9869 0.4841 1.0992 1.0299 0.7127 1.0124 0.4576 0.8544 1.1275 0.7705 0.4129 1.0085 0.7676 0.8418 0.8784 0.9751 0.7840 0.4158 1.0315 0.7533 0.9548 数据点的对应的三维坐标为2x2 =1.4010 1.23012.0814 1.1655 1.3740 1.1829 1.7632 1.9739 2.4152 2.5890 2.8472 1.9539 1.2500 1.2864 1.2614 2.0071 2.1831 1.79091.3322 1.1466 1.7087 1.59202.9353 1.46642.9313 1.8349 1.8340 2.5096 2.7198 2.3148 2.0353 2.6030 1.2327 2.1465 1.5673 2.9414y2 =1.0298 0.9611 0.9154 1.4901 0.8200 0.93991.1405 1.0678 0.8050 1.2889 1.4601 1.43340.7091 1.2942 1.3744 0.9387 1.2266 1.18330.8798 0.5592 0.5150 0.9983 0.9120 0.71261.2833 1.1029 1.2680 0.7140 1.2446 1.33921.1808 0.5503 1.4708 1.1435 0.7679 1.1288z2 =0.6210 1.3656 0.5498 0.6708 0.8932 1.43420.9508 0.7324 0.5784 1.4943 1.0915 0.76441.2159 1.3049 1.1408 0.9398 0.6197 0.66031.3928 1.4084 0.6909 0.8400 0.5381 1.37290.7731 0.7319 1.3439 0.8142 0.9586 0.73790.7548 0.7393 0.6739 0.8651 1.3699 1.1458数据的样本点分布如下图：0.511.522.5五、实验要求：1. 可以选择二维的数据，或者选择三维的数据作为样本。
模式识别实验报告
模式识别实验报告关键信息项：1、实验目的2、实验方法3、实验数据4、实验结果5、结果分析6、误差分析7、改进措施8、结论1、实验目的11 阐述进行模式识别实验的总体目标和期望达成的结果。
111 明确实验旨在解决的具体问题或挑战。
112 说明实验对于相关领域研究或实际应用的意义。
2、实验方法21 描述所采用的模式识别算法和技术。
211 解释选择这些方法的原因和依据。
212 详细说明实验的设计和流程，包括数据采集、预处理、特征提取、模型训练和测试等环节。
3、实验数据31 介绍实验所使用的数据来源和类型。
311 说明数据的规模和特征。
312 阐述对数据进行的预处理操作，如清洗、归一化等。
4、实验结果41 呈现实验得到的主要结果，包括准确率、召回率、F1 值等性能指标。
411 展示模型在不同数据集或测试条件下的表现。
412 提供可视化的结果，如图表、图像等，以便更直观地理解实验效果。
5、结果分析51 对实验结果进行深入分析和讨论。
511 比较不同实验条件下的结果差异，并解释其原因。
512 分析模型的优点和局限性，探讨可能的改进方向。
6、误差分析61 研究实验中出现的误差和错误分类情况。
611 分析误差产生的原因，如数据噪声、特征不充分、模型复杂度不足等。
612 提出减少误差的方法和建议。
7、改进措施71 根据实验结果和分析，提出针对模型和实验方法的改进措施。
711 描述如何优化特征提取、调整模型参数、增加训练数据等。
712 预测改进后的可能效果和潜在影响。
8、结论81 总结实验的主要发现和成果。
811 强调实验对于模式识别领域的贡献和价值。
812 对未来的研究方向和进一步工作提出展望。
在整个实验报告协议中，应确保各项内容的准确性、完整性和逻辑性，以便为模式识别研究提供有价值的参考和借鉴。
《模式识别》课程实验 线性分类器设计实验
《模式识别》课程实验线性分类器设计实验一、实验目的：1、掌握Fisher 线性分类器设计方法；2、掌握感知准则函数分类器设计方法。
二、实验内容：1、对下列两种情况，求采用Fisher 判决准则时的投影向量和分类界面，并做图。
12{(2,0),(2,2),(2,4),(3,3)}{(0,3),(2,2),(1,1),(1,2),(3,1)}T T T T T T T T T ωω⎧=⎪⎨=-----⎪⎩ 12{(1,1),(2,0),(2,1),(0,2),(1,3)}{(1,2),(0,0),(1,0),(1,1),(0,2)}T T T T T T T T T T ωω⎧=⎪⎨=-----⎪⎩ 2、对下面的两类分类问题，采用感知准则函数，利用迭代修正求权向量的方法求两类的线性判决函数及线性识别界面，并画出识别界面将训练样本区分的结果图。
12{(1,1),(2,0),(2,1),(0,2),(1,3)}{(1,2),(0,0),(1,0),(1,1),(0,2)}T T T T T T T T T T ωω⎧=⎪⎨=-----⎪⎩ 三、实验原理：（1）Fisher 判决准则投影方向：*112()w w S μμ-=-（2）感知准则函数：()()kT p z Z J v v z ==-∑当k Z为空时，即()0J v ，*v即为所求p四、解题思路:1、fisher线性判决器：A.用mean函数求两类样本的均值B.求两类样本的均值的类内离散矩阵SiC.利用类内离散矩阵求总类内离散矩阵SwD.求最佳投影方向WoE.定义阈值，并求得分界面2、感知准则函数分类器：A.获得增广样本向量和初始增广权向量B.对样本进行规范化处理C.获得解区，并用权向量迭代修正错分样本集，得到最终解区五、实验结果：1、fisher线性判决分类器：条件：取pw1=pw2=0.5,阈值系数为0.5A．第一种情况B.第二种情况2、感知准则函数判决：条件：取步长row为1判决结果：六、结果分析：1、fisher线性判决器中，调整阈值系数时，分界面会随之平行上下移动，通过调整阈值系数的大小，就能比较合理的得到分界面。