金山银山的折叠方法(详细图解)
半成品的金山银山组装方法

半成品的金山银山组装方法
嘿,朋友们!今天咱就来讲讲这半成品的金山银山组装方法。
这可真是个神奇又有趣的事儿啊!
你看,这就好比搭积木一样,咱得有耐心,还得有巧思。
先得找到那些关键的“积木块”,这就像是挖掘宝藏的过程,充满了惊喜和期待呢!每一块都有着它独特的价值和作用。
半成品的金山银山,那可不是随随便便就能拼凑起来的呀!这需要我们细心地去挑选那些有潜力的部分,就像挑选最甜的果子一样。
然后呢,把它们巧妙地组合在一起,让它们相互作用,产生奇妙的化学反应。
这不就跟做菜似的嘛,各种食材搭配好了,才能做出美味佳肴。
我们要把那些看似普通的元素,通过我们的智慧和努力,变成闪闪发光的财富。
有人可能会问了,这真的能做到吗?嘿,为啥不行呢!只要我们有决心,有毅力,就没有办不成的事儿!想想看,那些成功的人,不都是从一点一滴积累起来的嘛。
咱们不能小瞧了这些半成品,它们就像是未被完全发掘的宝藏。
只要我们用心去打磨,去雕琢,它们就能绽放出耀眼的光芒。
而且啊,这过程中可不能怕失败。
失败算啥呀,那就是成功的垫脚石!每次失败都是一次学习的机会,让我们能更好地改进方法,找到更合适的途径。
你说,要是我们都能掌握这半成品的金山银山组装方法,那生活得变得多精彩呀!那可真是让人兴奋不已啊!我们可以创造属于自己的财富王国,让梦想照进现实。
所以啊,别犹豫,别观望,赶紧行动起来吧!去寻找那些半成品的宝藏,用我们的双手和智慧,组装出属于我们自己的金山银山!让我们的生活充满无限可能!。
叠元宝的24种方法

叠元宝的24种方法叠元宝是一种古老的手工艺品,它不仅具有收藏价值,还可以用来装饰家居环境。
在中国传统文化中,元宝象征着财富和好运,因此叠元宝也被视为一种吉祥物。
如果你对叠元宝感兴趣,那么接下来我将为你介绍24种叠元宝的方法,希望能够帮助你更好地了解这项手工艺品。
1. 传统叠法,传统的叠元宝方法是将金属元宝叠成塔状或圆锥状,这种方法最为经典,也是最为常见的叠法之一。
2. 编织叠法,利用绳子或者线将元宝编织成各种形状,比如花朵、动物等,这种方法需要一定的手工技巧。
3. 粘贴叠法,使用胶水或者双面胶将元宝粘贴在一起,可以制作成各种图案,比如心形、星形等。
4. 悬挂叠法,将叠好的元宝挂在绳子或者链条上,可以做成吊坠、挂件等装饰品。
5. 拼接叠法,利用不同形状的元宝进行拼接,可以制作成各种立体的图案,比如立体动物、建筑等。
6. 穿线叠法,将元宝穿在细线或者金属线上,可以做成手链、项链等饰品。
7. 摆放叠法,将叠好的元宝摆放在特定的位置,比如书桌、茶几等,起到装饰作用。
8. 嵌入叠法,将元宝嵌入到其他材料中,比如木头、玻璃等,可以做成各种工艺品。
9. 组合叠法,将不同材质、颜色的元宝组合在一起,形成丰富多彩的图案。
10. 立体叠法,利用多层次的叠法,将元宝叠成立体的形状,比如立体花、立体动物等。
11. 织网叠法,将元宝编织成网状的结构,可以做成各种器皿、饰品等。
12. 镶嵌叠法,将元宝镶嵌在其他物品上,比如首饰盒、摆件等。
13. 摺叠叠法,利用摺纸的原理,将元宝叠成各种几何形状,比如三角形、正方形等。
14. 悬浮叠法,利用透明材料将元宝悬浮在空中,形成立体的效果。
15. 沙盘叠法,将元宝铺设在沙盘中,可以做成各种风景、建筑等。
16. 点缀叠法,将元宝点缀在其他物品上,比如画作、雕塑等。
17. 拼贴叠法,将元宝拼贴在画布或者纸张上,可以做成各种艺术作品。
18. 空间叠法,利用元宝的空间感,进行各种立体构图,比如城市景观、宇宙飞船等。
金山的折叠方法

金山的折叠方法
金山的折叠方法是一种非常实用的技巧,可用于折叠各种不同类型的纸张,如纸巾、信封、文件夹等。
以下是金山的折叠方法的步骤:
1. 将纸张放在桌子上,确保它是平的。
2. 折叠纸张的一端,使其与另一端对齐。
3. 将折叠的一端再次折叠,使其与另一端再次对齐。
这将折叠的一端分成两部分。
4. 从折叠的一端的底部开始,将纸张向上折叠,直到折叠线与另一端对齐。
5. 将折叠的一端向下弯曲,使其形成一个V形。
6. 将V形折叠起来,使其对齐。
7. 将纸张的底部向上折叠,使其与V形对齐。
8. 最后,将V形向下折叠,使其与折叠线对齐。
这样就完成了金山的折叠方法。
使用金山的折叠方法可以使纸张更容易保存和携带,同时还能使其更加整洁和美观。
- 1 -。
折纸金斗的叠法

折纸金斗的叠法
折纸金斗是一种常见的折纸手工艺品。
以下是折纸金斗的叠法步骤:
1. 准备一个正方形的折纸,颜色可以根据个人喜好选择。
2. 将折纸对角线对折,然后展开。
3. 将折纸上下两边对折,然后展开。
4. 将折纸左右两边对折,然后展开。
5. 将折纸四个角对准交点,将纸折叠成一条长方形,然后展开。
6. 将纸水平翻转,将左右两边对折,然后展开。
7. 将纸左右两边对折,然后展开。
8. 将纸两个角位对准,对折成一个小三角形。
9. 对纸进行一系列对折,按照步骤6和7的方式,再按照步骤
1至5的方式。
完成叠法。
完成以上步骤后,可以折出一个金斗形状的手工艺品。
根据个人喜好,可以使用不同颜色的折纸进行叠法,使金斗更加丰富多彩。
金鱼折纸简单步骤

金鱼折纸简单步骤
第1步:找到一张正方形折纸。
第2步:上下两边,沿中心线对折。
第3步:左右两边,沿边对折。
第4步:展开纸张,从右往左折。
第5步:从左至右,对准中心线折。
第6步:从下往上,沿边线折。
第7步:从左往右,沿边折。
第8步:从右至左,沿边折。
第9步:从下往上,沿边线折。
第10步:从下往上,沿边线折。
第11步:用剪刀从两边剪开。
第12步:向背面折。
第13步:内侧按压的同时往前折。
第14步:从左往右,沿边折。
最后:用黑色水性笔画出眼睛的形状。
金鱼的制作教程结束,大家学会了吗?是不是很简单,赶快自己动手试着做一个出来吧。
1。
纸活金山银山制作方法

纸活金山银山制作方法
要制作纸活金山银山,您需要准备以下材料和工具:
1. 纸张(可以选用彩色、质地较硬的纸张)
2. 剪刀
3. 胶水
4. 大石头(用来作为山的基座)
制作步骤:
1. 使用剪刀将纸张剪成不同大小的三角形,这些三角形将被用来构建山体的外形。
2. 将纸张三角形依次从大到小贴在大石头上,使用胶水将它们粘贴在一起,使其形成类似金字塔形状的山体。
3. 在每个纸张三角形的底部,使用剪刀将它们剪成波浪形,以模拟山脉的形状。
4. 添加额外的纸张三角形以填补山体上没有覆盖到的区域,并创造出更多的起伏和山脉的细节。
5. 在山体上使用颜料或铅笔添加阴影和细节,使其看起来更逼真。
6. 在山的底部使用胶水将大石头固定在纸板或其他平面的基座上,以保持稳定。
7. 可以进一步装饰山体,例如添加一些植物、草地等,以增加山体的逼真感。
制作完毕后,您就可以欣赏到自己的纸活金山银山了。
金刚元宝折法

金刚元宝折法
金刚元宝折法的步骤如下:
1. 准备一张方形的纸,将其对折成一个长方形。
2. 将长方形的一边向内折,使其与对角线重合。
另一边也向内折,使其与对角线重合。
3. 打开折好的长方形,将一边的两个角向内折,使其与对角线重合。
另一边也进行同样的操作。
4. 将折好的图形翻转过来,将上下两个边沿中线向内折。
5. 将左右两个边也向内折,使其与中线重合。
6. 将上下两个边再次向外折,使其与中线重合。
7. 将左右两个边也向外折,使其与中线重合。
8. 将折好的图形翻转过来,用手将其压平,这样一个金刚元宝就折好了。
你可以根据以上步骤进行尝试,如果遇到问题可以再次向我提问。
金山银山的折叠方法

金山银山的折叠方法
金山银山的折叠方法是一种将大面积金纸折叠成小且有规律的图案的技巧。
以下是一个简单的金山银山折叠方法:
1. 准备一张方形的金纸。
2. 将金纸对角线折叠,对折线要折得尽量准确。
3. 展开金纸,将左右两边的对折线与中心对齐,再将上下两边的对折线与中心对齐。
4. 将纸的四个角向中心折叠,形成一个小方块。
5. 将小方块的四个边向中心折叠,形成一个更小的正方形。
6. 重复以上步骤,将金纸不断折叠,直到折叠的图案达到满意程度。
请注意,金山银山的折叠方法可以根据个人的创意和想法进行改变和调整,上述方法只是一个简单的参考。
贵州省贵阳市名校2024-2025学年九上数学开学检测试题【含答案】
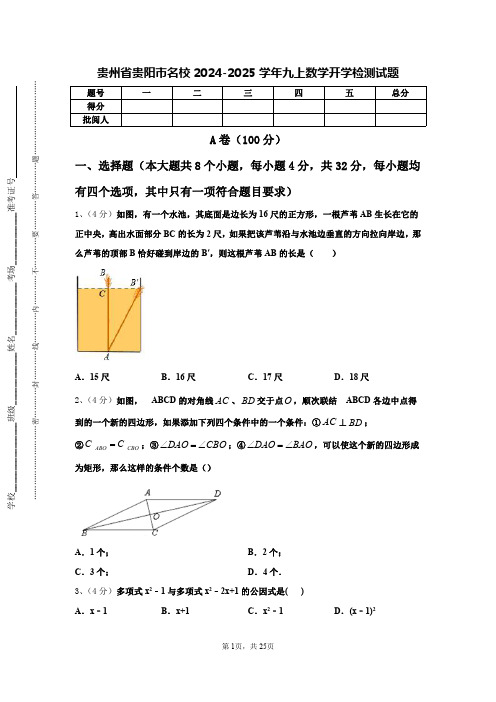
贵州省贵阳市名校2024-2025学年九上数学开学检测试题题号一二三四五总分得分批阅人A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB 生长在它的正中央,高出水面部分BC 的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B 恰好碰到岸边的B′,则这根芦苇AB 的长是()A .15尺B .16尺C .17尺D .18尺2、(4分)如图,ABCD 的对角线AC 、BD 交于点O ,顺次联结ABCD 各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①AC ⊥BD ;②ABO CBO C C =;③DAO CBO ∠=∠;④DAO BAO ∠=∠,可以使这个新的四边形成为矩形,那么这样的条件个数是()A .1个;B .2个;C .3个;D .4个.3、(4分)多项式x 2﹣1与多项式x 2﹣2x+1的公因式是()A .x ﹣1B .x+1C .x 2﹣1D .(x ﹣1)24、(4分)若实数m 、n 满足02m +=-,且m 、n 恰好是等腰△ABC 的两条边的边长,则△ABC 的周长是()A .12B .10C .8或10D .65、(4分)如图,矩形ABCD 的两条对角线相交于点O ,∠AOD=60°,AD=2,则AC 的长是()A .2B .4C .D .6、(4分)能判定四边形ABCD 是平行四边形的是()A .AD //BC ,AB =CD B .∠A =∠B ,∠C =∠D C .∠A =∠C ,∠B =∠D D .AB =AD ,CB =CD7、(4分)化简222x y x xy -+的结果为()A .﹣y x B .﹣y C .x y x +D .x y x -8、(4分)已知一次函数y=(m+1)x+n-2的图象经过一.三.四象限,则m ,n 的取值范围是()A .m >-1,n >2B .m <-1,n >2C .m >-1,n <2D .m <-1,n <2二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)如图,矩形纸片ABCD 中,已知4=AD ,3AB =,点E 在BC 边上,沿AE 折叠纸片,使点B 落在点'B 处,连结'CB ,当'CEB ∆为直角三角形时,BE 的长为______.10、(4分)分解因式:222m -=_________________________.11、(4分)如图,一张三角形纸片ABC ,其中90C =∠,4AC =,3BC =,现小林将纸片做三次折叠:第一次使点A 落在C 处;将纸片展平做第二次折叠,使点B 若在C 处;再将纸片展平做第三次折叠,使点A 落在B 处,这三次折叠的折痕长依次记为,,a b c ,则,,a b c 的大小关系是(从大到小)__________.12、(4分)若菱形的周长为14cm ,一个内角为60°,则菱形的面积为_____cm 1.13、(4分)如图,在平行四边形ABCD 中,连接AC ,按以下步骤作图:分别以点A ,C 为圆心,以大于12AC 的长为半径画弧,两弧分别相交于点M ,N ,作直线MN 交CD 于点E ,交AB 于点F .若AB =5,BC =3,则△ADE 的周长为__________.三、解答题(本大题共5个小题,共48分)14、(12分)如图所示,AC 是▱ABCD 的一条对角线,过AC 中点O 的直线EF 分别交AD ,BC 于点E ,F .(1)求证:△AOE ≌△COF ;(2)连接AF 和CE ,当EF ⊥AC 时,判断四边形AFCE 的形状,并说明理由15、(8分)菱形ABCD 在平面直角坐标系中的位置如图所示,对角线AC 与BD 的交点E 恰好在y 轴上,过点D 和BC 的中点H 的直线交AC 于点F,线段DE,CD 的长是方程x 2﹣9x+18=0的两根,请解答下列问题:(1)求点D 的坐标;(2)若反比例函数y=k x (k≠0)的图象经过点H,则k=;(3)点Q 在直线BD 上,在直线DH 上是否存在点P,使以点F,C,P,Q 为顶点的四边形是平行四边形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.16、(8分)某学校抽查了某班级某月5天的用电量,数据如下表(单位:度):度数91011天数311(1)求这5天的用电量的平均数;(2)求这5天用电量的众数、中位数;(3)学校共有36个班级,若该月按22天计,试估计该校该月的总用电量.17、(10分)解方程(1)()6511x x x x +=++(2)28142xx x =---18、(10分)如图,在方格纸中(小正方形的边长为1),△ABC 的三个顶点均为格点,将△ABC 沿x 轴向左平移5个单位长度,根据所给的直角坐标系(O 是坐标原点),解答下列问题:(1)画出平移后的△A ′B ′C ′,并直接写出点A ′、B ′、C ′的坐标;(2)求在平移过程中线段AB 扫过的面积.B 卷(50分)一、填空题(本大题共5个小题,每小题4分,共20分)19、(4分)如图,在△ABC 中,AB =3cm ,BC =5cm ,将△ABC 折叠,使点C 与A 重合,得折痕DE ,则△ABE 的周长等于_______cm .20、(4分)“绿水青山就是金山银山”.为了山更绿、水更清,某县大力实施生态修复工程,发展林业产业,确保到2021年实现全县森林覆盖率达到72.75%的目标.已知该县2019年全县森林覆盖率为69.05%,设从2019年起该县森林覆盖率年平均增长率为x ,则可列方程___.21、(4分)在菱形ABCD 中,M 是BC 边上的点(不与B ,C 两点重合),AB=AM ,点B 关于直线AM 对称的点是N ,连接DN ,设∠ABC ,∠CDN 的度数分别为x ,y ,则y 关于x 的函数解析式是_______________________________.22、(4分)若关于x 的分式方程当311x a x -=-的解为正数,那么字母a 的取值范围是_____.23、(4分)将正比例函数6y x =-的图象向右平移2个单位,则平移后所得到图象对应的函数解析式是__________.二、解答题(本大题共3个小题,共30分)24、(8分)为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:分组/分频数频率50≤x <6060.1260≤x <70a 0.2870≤x <80160.3280≤x <90100.2090≤x ≤100c b 合计50 1.00(1)表中的a=______,b=______,c=______;(2)把上面的频数分布直方图补充完整,并画出频数分布折线图;(3)如果成绩达到90及90分以上者为优秀,可推荐参加进入决赛,那么请你估计该校进入决赛的学生大约有多少人.25、(10分)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,5×5正方形方格纸图中,点A ,B 都在格点处.(1)请在图中作等腰△ABC ,使其底边AC =,且点C 为格点;(2)在(1)的条件下,作出平行四边形ABDC ,且D 为格点,并直接写出平行四边形ABDC的面积.26、(12分)先化简再求值:(x+y)2﹣x(x+y),其中x=2,﹣1.参考答案与详细解析一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、C【解析】我们可以将其转化为数学几何图形,如图所示,根据题意,可知EB'的长为16尺,则B'C=8尺,设出AB=AB'=x尺,表示出水深AC,根据勾股定理建立方程,求出的方程的解即可得到芦苇的长.【详解】解:依题意画出图形,设芦苇长AB=AB′=x尺,则水深AC=(x-2)尺,因为B'E=16尺,所以B'C=8尺在Rt△AB'C中,82+(x-2)2=x2,解之得:x=17,即芦苇长17尺.故选C.本题主要考查勾股定理的应用,熟悉数形结合的解题思想是解题关键.2、C【解析】根据顺次连接四边形的中点,得到的四边形形状和四边形的对角线位置、数量关系有关,利用三角形中位线性质可得:当对角线垂直时,所得新四边形是矩形.逐一对四个条件进行判断.【详解】解:顺次连接四边形的中点,得到的四边形形状和四边形的对角线位置、数量关系有关,利用三角形中位线性质可得:当对角线垂直时,所得新四边形是矩形.①∵AC⊥BD,∴新的四边形成为矩形,符合条件;②∵四边形ABCD是平行四边形,∴AO=OC,BO=DO.=C△CBO,∴AB=BC.∵C△ABO根据等腰三角形的性质可知BO⊥AC,∴BD⊥AC.所以新的四边形成为矩形,符合条件;③∵四边形ABCD是平行四边形,∴∠CBO=∠ADO.∵∠DAO=∠CBO,∴∠ADO=∠DAO.∴AO=OD.∴AC=BD,∴四边形ABCD是矩形,连接各边中点得到的新四边形是菱形,不符合条件;④∵∠DAO=∠BAO,BO=DO,∴AO⊥BD,即平行四边形ABCD的对角线互相垂直,∴新四边形是矩形.符合条件.所以①②④符合条件.故选:C.本题主要考查矩形的判定、平行四边形的性质、三角形中位线的性质.3、A【解析】x2-1=(x+1)(x-1),x2-2x+1=(x-1)2,所以公因式是:x-1,故选A.本题考查多项式的公因式,解题的关键是把每一个多项式都因式分解.4、B【解析】根据绝对值和二次根式的非负性得m、n的值,再分情况讨论:①若腰为2,底为4,由三角形两边之和大于第三边,舍去;②若腰为4,底为2,再由三角形周长公式计算即可.【详解】由题意得:m-2=0,n-4=0,∴m=2,n=4,又∵m、n恰好是等腰△ABC的两条边的边长,①若腰为2,底为4,此时不能构成三角形,舍去,②若腰为4,底为2,则周长为:4+4+2=10,故选B.本题考查了非负数的性质以及等腰三角形的性质,根据非负数的性质求出m 、n 的值是解题的关键.5、B 【解析】解:在矩形ABCD 中,OA=OC ,OB=OD ,AC=BD ,∴OA=OC .∵∠AOD=60°,∴△OAB 是等边三角形.∴OA=AD=1.∴AC=1OA=1×1=2.故选B .6、C 【解析】根据平行四边形的判定定理依次确定即可.【详解】A.AD//BC ,AB=CD ,不能判定四边形ABCD 是平行四边形,故不符合题意;B.∠A=∠B ,∠C=∠D ,不能判定四边形ABCD 是平行四边形,故不符合题意;C.∠A=∠C ,∠B=∠D ,能判定四边形ABCD 是平行四边形,故符合题意;D.AB=AD ,CB=CD ,不能判定四边形ABCD 是平行四边形,故不符合题意;故选:C.此题考查平行四边形的判定定理,熟记定理内容即可正确解答.7、D 【解析】先因式分解,再约分即可得.【详解】()()()222x y x y x y x yx xy x x y x+---==++故选D .本题主要考查约分,由约分的概念可知,要首先将分子、分母转化为乘积的形式,再找出分子、分母的最大公因式并约去,注意不要忽视数字系数的约分.8、C 【解析】根据一次函数的图象和性质得出m+1>0,n-2<0,解不等式即可.【详解】解:∵一次函数y=(m+1)x+n-2的图象经过一.三.四象限∴m+1>0,n-2<0∴m >-1,n <2,故选:C .本题主要考查了一次函数图象与系数的关系,关键是掌握数形结合思想.二、填空题(本大题共5个小题,每小题4分,共20分)9、3或32【解析】分两种情况:①当∠EFC=90°,先判断出点F 在对角线AC 上,利用勾股定理求出AC ,设BE=x,表示出CE ,根据翻折变换的性质得到AF=AB,EF=BE ,再根据Rt △CEF 利用勾股定理列式求解;②当∠CEF=90°,判断四边形ABEF 是正方形,根据正方形的性质即可求解.【详解】分两种情况:①当∠EFC=90°,如图1,∵∠AFE=∠B=90°,∠EFC=90°,∴点A 、F 、C 共线,∵矩形ABCD 的边AD=4,∴BC=AD=4,在Rt △ABC 中,5==设BE=x ,则CE=BC-BE=4-x ,由翻折的性质得AF=AB=3,EF=BE=x ,∴CF=AC-AF=5-3=2在Rt △CEF 中,EF 2+CF 2=CE 2,即x 2+22=(4-x)2,解得x=32;学校________________班级____________姓名____________考场____________准考证号…………………………密…………封…………线…………内…………不…………要…………答…………题…………………………②当∠CEF=90°,如图2由翻折的性质可知∠AEB=∠AEF=45°,∴四边形ABEF 是正方形,∴BE=AB=3,故BE 的长为3或32此题主要考查矩形的折叠问题,解题的关键是根据图形进行分类讨论.10、2(1)(1)m m +-.【解析】试题分析:222m -=22(1)m -=2(1)(1)m m +-.故答案为2(1)(1)m m +-.考点:提公因式法与公式法的综合运用.11、b >c >a.【解析】由图1,根据折叠得DE 是△ABC 的中位线,可得出DE 的长,即a 的长;由图2,同理可得MN 是△ABC 的中位线,得出MN 的长,即b 的长;由图3,根据折叠得:GH 是线段AB 的垂直平分线,得出AG 的长,再利用两角对应相等证△ACB ∽△AGH ,利用比例式可求GH 的长,即c 的长.【详解】解:第一次折叠如图1,折痕为DE ,由折叠得:AE =EC =12AC =12×4=2,DE ⊥AC ∵∠ACB =90°∴DE ∥BC ∴a =DE =12BC =12×3=32,第二次折叠如图2,折痕为MN ,由折叠得:BN =NC =12BC =12×3=32,MN ⊥BC ∵∠ACB =90°∴MN ∥AC ∴b =MN =12AC =12×4=2,第三次折叠如图3,折痕为GH ,由勾股定理得:AB =5由折叠得:AG =BG =12AB =52,GH ⊥AB ∴∠AGH =90°∵∠A =∠A ,∠AGH =∠ACB ,∴△ACB ∽△AGH ∴AC BC AG GH =,即4352GH =,∴GH =158,即c =158,∵2>158>32,∴b >c >a ,故答案为:b >c >a.本题考查了折叠的问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.本题的关键是明确折痕是所折线段的垂直平分线,准确找出中位线,利用中位线的性质得出对应折痕的长,没有中位线的可以考虑用三角形相似来解决.12、【解析】根据已知可求得菱形的边长,再根据直角三角形的性质求得菱形的高,从而根据菱形的面积公式计算得到其面积【详解】解:菱形的周长为14cm ,则边长为6cm ,可求得60°所对的高为32×6=,则菱形的面积为=1.故答案为.此题主要考查菱形的面积公式:边长乘以高,综合利用菱形的性质和勾股定理13、8【解析】解:由做法可知MN 是AC 的垂直平分线,∴AE =CE .∵四边形ABCD 是平行四边形∴CD =AB =5,AD =BC =3.∴AD +DE +AE =AD +DE +CE =AD +CD =5+3=8,∴△ADE 的周长为8.三、解答题(本大题共5个小题,共48分)14、(1)详见解析;(2)是菱形;【解析】根据菱形判定定理:对角线互相垂直且平分的四边形是菱形【详解】(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠EAO=∠FCO ,∵O 是OA 的中点,∴OA=OC ,在△AOE 和△COF 中,∠EAO=∠FCO OA=OC ∠AOE=∠COF ,∴△AOE ≌△COF (ASA );(2)EF ⊥AC 时,四边形AFCE 是菱形;由(1)中△AOE ≌△COF ,得AE=CF ,OE=OF ,又∵OA=OC ,EF ⊥AC ∴四边形AFCE 是菱形.此题主要考查全等三角形的判定和菱形判定定理,熟练能掌握即可轻松解题.15、(1)(﹣32,(2)2(3)(92)或(﹣152,)或(212)【解析】(1)由线段DE,CD 的长是方程x 2﹣9x+18=0的两根,且CD >DE ,可求出CD、DE 的长,由四边形ABCD 是菱形,利用菱形的性质可求得D 点的坐标.(2)由(1)可得OB 、CM ,可得B、C 坐标,进而求得H 点坐标,由反比例函数y=k x (k≠0)的图象经过点H,可求的k 的值;(3)分别以CF 为平行四边形的一边或者为对角线的情形进行讨论即可.【详解】(1)x 2﹣9x+18=0,(x ﹣3)(x ﹣6)=0,x=3或6,∵CD >DE ,∴CD=6,DE=3,∵四边形ABCD 是菱形,∴AC ⊥BD ,AE=EC==3,∴∠DCA=30°,∠EDC=60°,Rt △DEM 中,∠DEM=30°,∴DM=DE=,∵OM ⊥AB ,∴S 菱形ABCD =AC•BD=CD•OM ,∴=6OM ,OM=3,∴D (﹣,3);(2)∵OB=DM=,CM=6﹣=,∴B (,0),C (,3),∵H 是BC 的中点,∴H (3,),∴k=3×=;故答案为;(3)①∵DC=BC ,∠DCB=60°,∴△DCB 是等边三角形,∵H 是BC 的中点,∴DH ⊥BC ,∴当Q 与B 重合时,如图1,四边形CFQP 是平行四边形,∵FC=FB ,∴∠FCB=∠FBC=30°,∴∠ABF=∠ABC ﹣∠CBF=120°﹣30°=90°,∴AB ⊥BF ,CP ⊥AB ,Rt △ABF 中,∠FAB=30°,AB=6,∴FB=2=CP ,∴P (,);②如图2,∵四边形QPFC 是平行四边形,∴CQ ∥PH ,由①知:PH⊥BC ,∴CQ ⊥BC ,Rt △QBC 中,BC=6,∠QBC=60°,∴∠BQC=30°,∴CQ=6,连接QA,∵AE=EC ,QE ⊥AC ,∴QA=QC=6,∴∠QAC=∠QCA=60°,∠CAB=30°,∴∠QAB=90°,∴Q (﹣,6),由①知:F(,2),由F 到C 的平移规律可得P 到Q 的平移规律,则P(﹣﹣3,6﹣),即P(﹣,5);③如图3,四边形CQFP 是平行四边形,同理知:Q(﹣,6),F (,2),C (,3),∴P (,﹣);综上所述,点P 的坐标为:(,)或(﹣,5)或(,﹣).本题主要考查平行四边形、菱形的图像和性质,反比例函数的图像与性质等,综合性较大,需综合运用所学知识充分利用已知条件求解.16、(1)1.6度;(2)1度;1度;(3)2.2度.【解析】(1)用加权平均数的计算方法计算平均用电量即可;(2)分别利用众数、中位数及极差的定义求解即可;(3)用班级数乘以日平均用电量乘以天数即可求得总用电量.【详解】(1)平均用电量为:(1×3+10×1+11×1)÷5=1.6度;(2)1度出现了3次,最多,故众数为1度;第3天的用电量是1度,故中位数为1度;(3)总用电量为22×1.6×36=2.2度.17、(1)1x =;(2)无解【解析】(1)将分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解;(2)将分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.【详解】解:(1)()6511x x x x +=++方程两边同乘()1x x +,得65x x =+解得:1x =经检验:1x =是原方程的解所以原分式方程的解为1x =(2)28142xx x =---方程两边同乘24x -,得2(2)(4)8x x x +--=22+248x x x -+=解得:2x =当2x =时,24=0x -∴2x =是原方程的增根所以原分式方程无解.此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.18、(1)图见解析,'''(1,5),(4,0),(1,0)A B C ---;(2)25【解析】(1)由题意直接根据图形平移的性质画出△A ′B ′C ′,并写出各点坐标即可;(2)由题意可知AB 扫过的部分是平行四边形,根据平行四边形的面积公式即可得出结论.【详解】解:(1)平移后的△A′B′C′如图所示,观察图象可知点A′、B′、C′的坐标分别为:'''(1,5),(4,0),(1,0)A B C ---.(2)由图象以及平移的性质可知线段AB 扫过部分形状为平行四边形,且底为5,高为5,故线段AB 扫过的面积为:5525⨯=.本题考查的是作图-平移变换,熟练掌握图形平移不变性的性质是解答此题的关键.一、填空题(本大题共5个小题,每小题4分,共20分)19、8【解析】由折叠的性质知,AE=CE ,∴△ABE 的周长=AB+BE+AE=AB+BE+CE=AB+BC=3+5=8cm .20、69.05%(1+x )2=72.75%【解析】此题根据从2019年起每年的森林覆盖率年平均增长率为x,分别列出2020年以及2021年得森林覆盖面积,即可得出方程.【详解】∵设从2019年起每年的森林覆盖率年平均增长率为x,∴根据题意得:2020年覆盖率为:69.05%(1+x),2021年为:69.05%(1+x)²=72.75%,故答案为:69.05%(1+x)²=72.75%此题考查一元二次方程的应用,解题关键在于列出方程21、5180,607225180,72902x xyx x⎧︒-︒<≤︒⎪⎪=⎨⎪-︒︒<≤︒⎪⎩【解析】首先根据菱形的性质得出∠ABC=∠ADC=x,AB=BC=CD=AD,AD∥BC,进而得出∠BAM,然后根据对称性得出∠AND=∠AND=1802DAN︒-∠=180°-32x,分情况求解即可.【详解】∵菱形ABCD中,AB=AM,∴∠ABC=∠ADC=x,AB=BC=CD=AD,AD∥BC ∴∠ABC+∠BAD=180°,∴∠BAD=180°-x∵AB=AM,∴∠AMB=∠ABC=x∴∠BAM=180°-∠ABC-∠AMB=180°-2x连接BN、AN,如图:∵点B 关于直线AM 对称的点是N ,∴AN=AB ,∠MAN=∠BAM=180°-2x ,即∠BAN=2∠BAM=360°-4x ∴AN=AD ,∠DAN=∠BAD-∠BAN=180°-x -(360°-4x )=3x -180°∴∠AND=∠AND=1802DAN ︒-∠=180°-32x ∵M 是BC 边上的点(不与B ,C 两点重合),∴6090x ︒︒<<∴451803902x ︒︒-︒<<若32180x x ≥︒-,即7290x ︒≤︒<时,∠CDN=∠ADC-∠AND=52180x -︒,即80521y x =-︒;若32180x x ︒-<即6072x ︒︒<<时,∠CDN=∠AND-∠ADC =18052x ︒-,即52180y x =︒-∴y 关于x 的函数解析式是5180,607225180,72902x x y x x ⎧︒-︒<≤︒⎪⎪=⎨⎪-︒︒<≤︒⎪⎩故答案为:5180,607225180,72902x xy x x ⎧︒-︒<≤︒⎪⎪=⎨⎪-︒︒<≤︒⎪⎩.此题主要考查菱形的性质与一次函数的综合运用,熟练掌握,即可解题.22、a >1且a ≠3【解析】首先根据题意求解x 的值,再根据题意可得分式方程的解大于0,注意分式方程的增根问题.【详解】解:去分母得:3x ﹣a =x ﹣1,解得:x =12a -,由分式方程的解为正数,得到12a ->0,12a -≠1,解得:a >1且a ≠3,故答案为:a >1且a ≠3本题主要考查分式方程的解参数问题,这类题目特步要注意分式方程的增根问题.23、612y x =-+【解析】根据“左加右减”的法则求解即可.【详解】解:将正比例函数6y x =-的图象向右平移2个单位,得()6-2y x =-=612x -+,故答案为:612y x =-+.本题考查的是一次函数的图象与几何变换,熟知函数图象变换的法则是解答此题的关键.二、解答题(本大题共3个小题,共30分)24、(1)14;0.08;4;(2)详见解析;(3)80.【解析】(1)根据频率分布表确定出总人数,进而求出a ,b ,c 的值即可;(2)把上面的频数分布直方图补充完整,并画出频数分布折线图,如图所示;(3)根据样本中90分及90分以上的百分比,乘以1000即可得到结果.【详解】解:(1)根据题意得:a=6÷0.12×0.28=14,b=1﹣(0.12+0.28+0.32+0.20)=0.08,c=6÷0.12×0.08=4;故答案为:14;0.08;4;(2)频数分布直方图、折线图如图,(3)根据题意得:1000×(4÷50)=80(人),则你估计该校进入决赛的学生大约有80人.此题考查了频数(率)分布折线图,用样本估计总体,频数(率)分布表,以及频数(率)分布直方图,弄清题中的数据是解本题的关键.25、(1)见解析;(2)画图见解析;其面积为8.【解析】(1)根据每个正方形的边长为1,利用勾股定理确定C 点的位置(使),再连接AB,AC 即可.(2)根据平行四边形的性质确定点D 连接BD,CD 即可得到所求四边形;再根据平行四边形面积公式即可求出.【详解】(1)如图,△ABC 即为所求.(2)如图,平行四边形ABDC 即为所求,其面积为8.本题考查了等腰三角形的性质以及平行四边形的性质,熟练掌握性质定理是解题的关键.26、2.【解析】根据整式乘法法则将式子化简,再代入求值,要注意二次根式的运算法则的应用.【详解】解:原式2222x xy y x xy =++--2 xy y =+x 2,y 1==-当时))2211=+原式 231=+-=2本题考核知识点:二次根式化简求值.解题关键点:掌握乘法公式.。
2023-2024学年浙江省湖州市长兴县龙山中学共同体七年级(下)第三次独立作业数学试卷+答案解析

2023-2024学年浙江省湖州市长兴县龙山中学共同体七年级(下)第三次独立作业数学试卷一、选择题:本题共10小题,每小题3分,共30分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列方程是二元一次方程的是()A. B. C. D.2.如图,和不是同位角的是()A. B.C. D.3.为了解我校1200名学生的身高,从中抽取了200名学生对其身高进行统计分析,则下列说法正确的是()A.1200名学生是总体B.每个学生是个体C.200名学生是抽取的一个样本D.每个学生的身高是个体4.下列计算正确的是()A. B. C. D.5.下列等式,从左到右的变形是因式分解的是()A. B.C. D.6.如图,将沿BC方向平移1cm得到对应的若,则的长是()A.2cmB.3cmC.4cmD.5cm7.当时,下列分式没有意义的是()A. B. C. D.8.绿水青山就是金山银山.某工程队承接了100万平方米的荒山绿化工程,由于情况有变……设原计划每天绿化的面积为x万平方米,列方程为,根据方程可知省略的部分是()A.实际工作时每天的工作效率比原计划提高了,结果提前20天完成了这一任务B.实际工作时每天的工作效率比原计划提高了,结果延误20天完成了这一任务C.实际工作时每天的工作效率比原计划降低了,结果延误20天完成了这一任务D.实际工作时每天的工作效率比原计划降低了,结果提前20天完成了这一任务9.一个长方体模型的长、宽、高分别是,,,某种油漆每千克可漆面积为,则漆这个模型表面需要的油漆是千克.A.76aB.38aC.D.10.如图,正方形ABCD和长方形DEFG的面积相等,且四边形AEFH也为正方形,欧几里得在《几何原本》中利用该图得到了:设,若,则图中阴影部分的周长为()A.40B.45C.50D.60二、填空题:本题共6小题,每小题3分,共18分。
11.因式分解:______.12.空气的密度为,这个数用科学记数法可表示为______.13.从100名学生中随机抽查了40名学生的数学成绩,按成绩共分六组,第一组至第四组的人数分别是10,5,7,6,第五组所占的百分比为,则第六组所占的百分比为______.14.照相机成像应用了一个重要原理,用公式表示,其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示胶片像到镜头的距离.已知f,v,则______.15.如图,ABCD为一长条形纸带,,将纸带沿EF折叠,,两点分别与C,D对应,若比大,则的度数为______.16.已知关于x,y的方程组,给出下列结论:①无论a取何值,x,y的值都不可能互为相反数.②当时,方程组的解也是方程的解.③若,则④无论a取何值,的值始终不变.其中正确的有______填写序号三、解答题:本题共8小题,共72分。
东南西北手工折纸方法

东南西北手工折纸方法
1. 东方鹤折纸:步骤如下:
a. 折方形纸为对角线。
b. 将上角折到下角。
c. 再将左角和右角向中心折叠。
d. 打开纸后,将两侧向中心折叠,形成鹤的双翼。
e. 将上下两侧对折,形成鹤的脖子和头。
f. 使用折叠技巧将纸张压出折痕,形成鹤的身体和尾巴。
g. 最后将翅膀翘起,鹤就完成了。
2. 南瓜灯折纸:步骤如下:
a. 将方形纸沿对角线对折成三角形。
b. 将左右两角向中心折叠,形成一个菱形。
c. 将上下两侧对折,形成正方形。
d. 两侧对折后,将下侧向上翻折,形成口袋。
e. 将口袋两侧向中心对折,形成南瓜的棱角。
f. 最后将上侧向内翻折,形成南瓜的顶部。
3. 西流湖折纸:步骤如下:
a. 折一张方形纸沿对角线成三角形。
b. 将左右两角向中心折叠,形成一个菱形。
c. 将上下两侧对折,形成正方形。
d. 将两侧对折后,用手指压出四个折痕,并将每侧向内翻折。
e. 用手指将两侧翘起,形成帆船的双桅。
f. 最后将双桅的顶端向内折叠,形成帆船的桅杆。
4. 北方兔子折纸:步骤如下:
a. 折一张正方形纸沿对角线成三角形。
b. 将左右两角向中心折叠,形成一个菱形。
c. 将上下两侧对折,形成正方形。
d. 将两侧向中心对折,形成一个小正方形。
e. 将纸张翻转,将上侧向内折叠,形成兔子的耳朵。
f. 用手指压出兔子的脸部轮廓,并将下侧向内折叠。
注:以上步骤仅为基础步骤,具体操作可参考相关手工书籍或视频教程。
2024年四川省南充市数学九年级第一学期开学统考试题【含答案】

2024年四川省南充市数学九年级第一学期开学统考试题题号一二三四五总分得分A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)如图,在平行四边形ABCD 中,对角线相交于点O ,AC=AB ,E 是AB 边的中点,G 、F 为BC 上的点,连接OG 和EF ,若AB =13,BC =10,GF =5,则图中阴影部分的面积为()A .48B .36C .30D .242、(4分)要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是()A .调查九年级全体学生B .调查七、八、九年级各30名学生C .调查全体女生D .调查全体男生3、(4分)在平面直角坐标系中,点P(2,-3)关于原点对称的点的坐标是()A .(2,3)B .(-2,3)C .(-2,-3)D .(-3,2)4、(4分)如图,折叠菱形纸片ABCD ,使得A ′D ′对应边过点C ,若∠B =60°,AB =2,当A ′E ⊥AB 时,AE 的长是()A .B .2-CD .15、(4分)的积为有理数的是()A .B .C .D .2-6、(4分)为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产并进行治污改造,其月利润(万元)与月份之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是()A .4月份的利润为万元B .污改造完成后每月利润比前一个月增加万元C .治污改造完成前后共有个月的利润低于万元D .9月份该厂利润达到万元7、(4分)矩形的对角线长为20,两邻边之比为3:4,则矩形的面积为()A .56B .192C .20D .以上答案都不对8、(4分)甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A 地到B 地,乙驾车从B 地到A 地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y (千米)与甲出发的时间x (分)之间的关系如图所示,乙从B 地到A 地需要()分钟A .12B .14C .18D .20二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)如图,菱形的周长为20,对角线的长为6,则对角线的长为______.学校________________班级____________姓名____________考场____________准考证号…………………………密…………封…………线…………内…………不…………要…………答…………题…………………………10、(4分)图1是一个地铁站人口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A 与B 之间的距离为10cm ,双翼的边缘56AC BD cm ==,且与闸机侧立面夹角30PCB BDQ ︒∠=∠=.当双翼收起时,可以通过闸机的物体的最大宽度PQ 为______cm 11、(4分)如果关于x 的一元二次方程x 2﹣6x+c=0(c 是常数)没有实根,那么c 的取值范围是.12、(4分)若直线y =ax +7经过一次函数y =4﹣3x 和y =2x ﹣1的交点,则a 的值是_____.13、(4分)若对于()1x x ≠-的任何值,等式32311x m x x -=+++恒成立,则m =__________.三、解答题(本大题共5个小题,共48分)14、(12分)某高速公路要对承建的工程进行招标,现在甲、乙两个工程队前来投标,根据两队的申报材料估计:若甲、乙两队合作,24天可以完成;若由甲队单独做20天后,余下的工程由乙队做,还需40天完成,求甲、乙两队单独完成这项工程各需多少天?15、(8分)如图所示,在△ABC 中,点D 为BC 边上的一点,AD =12,BD =16,AB =20,CD =1.(1)试说明AD ⊥BC .(2)求AC 的长及△ABC 的面积.(3)判断△ABC 是否是直角三角形,并说明理由.16、(8分)已知4x y -=,5xy =,求下列代数式的值.(1)(x 2)(y 2)-+(2)32232x y x y xy -+17、(10分)如图,ABCD 的对角线相交于点O ,直线EF 过点O 分别交BC ,AD 于点E 、F ,G 、H 分别为OB 、OD 的中点,求证:四边形GEHF 是平行四边形.18、(10分)已知:如图,在ABC ∆中,AD BC ⊥于点D ,E 为AC 上一点,连结BE 交AD 于F ,且AC BF =,DC DF =,求证:BE AC ⊥.B 卷(50分)一、填空题(本大题共5个小题,每小题4分,共20分)19、(4分)如图,在平面直角坐标系中,点A 的坐标为(0,6),将△OAB 沿x 轴向左平移得到△O′A′B′,点A 的对应点A′落在直线y=﹣x 上,则点B 与其对应点B′间的距离为.20、(4分)如图,在ABC ∆中,o o 9030C B AD ∠=∠=,,是ABC ∆的角平分线,DE AB ⊥,垂足为E ,1DE =,则ABC ∆的周长为________.21、(4分)如图,在R t △ABC 中,∠ACB =90°,∠A =60°,AB =6,△BCD 为等边三角形,点E 为△BCD 围成的区域(包括各边)内的一点,过点E 作EM ∥AB ,交直线AC 于点M ,作EN ∥AC ,交直线AB 于点N ,则12+AN AM 的最大值为_____.22、(4分)如图,点D 是Rt △ABC 斜边AB 的中点,AC =1,CD =1.5,那么BC =_____.23、(4分)直线y kx b =+与51y x =-+平行,且经过(2,1),则k +b =____________.二、解答题(本大题共3个小题,共30分)24、(8分)如图,直线y =12x +b 分别交x 轴、y 轴于点A 、C ,点P 是直线AC 与双曲线y =k x 在第一象限内的交点,PB ⊥x 轴,垂足为点B ,且OB =2,PB =1.(1)求反比例函数的解析式;(2)求△APB 的面积;(3)求在第一象限内,当x 取何值时一次函数的值小于反比例函数的值?25、(10分)已知关于x 的一元二次方程x 2﹣2tx +t 2﹣2t +4=1.(1)当t =3时,解这个方程;(2)若m ,n 是方程的两个实数根,设Q =(m ﹣2)(n ﹣2),试求Q 的最小值.26、(12分)如图,在菱形ABCD 中,对角线AC ,相交于点O ,4AC =cm ,2BD =cm ,E ,F 分别是AB ,BC 的中点,点P 是对角线AC 上的一个动点,设AP x =cm ,1PE y =cm ,2PF y =cm 小明根据学习函数的经验,分别对这两种函数随自变量的变化而变化的情况进行了探究,下面是小明探究过程,请补充完整:(1)画函数1y 的图象①按下表自变量的值进行取点、画图、测量,得到了1y 与x 的几组对应值:x /cm 00.51 1.52 2.53 3.541y /cm 1.120.50.71 1.12 1.58 2.06 2.55 3.04②在所给坐标系中描出补全后的表中的各对应值为坐标的点,画出函数1y 的图象;(2)画函数2y 的图象在同一坐标系中,画出函数2y 的图象;(3)根据画出的函数1y 的图象、函数2y 的图象,解决问题①函数1y 的最小值是________________;②函数1y 的图象与函数2y 的图象的交点表示的含义是________________;③若PE PC ,AP 的长约为________________cm参考答案与详细解析一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、C 【解析】连接EO ,设EF ,GO 交于点H ,过点H 作NM ⊥BC 与M ,交EO 于N ,过点A 作AP ⊥BC ,将阴影部分分割为△AEO ,△EHO ,△GHF ,分别求三个三角形的面积再相加即可.【详解】解:如图连接EO ,设EF ,GO 交于点H ,过点H 作NM ⊥BC 与M ,交EO 于N ,∵四边形ABCD 为平行四边形,O 为对角线交点,∴O 为AC 中点,又∵E 为AB 中点,∴EO 为三角形ABC 的中位线,∴EO ∥BC ,∴MN ⊥EO 且MN =12AP 即EO =5,∵AC =AB ,∴BP =PC 12BC =5,在Rt △APB 中,12AP ==,∴三角形AEO 的以EO 为底的高为12AP =6,MN =12AP =6∴16152AEO S EO =⨯=,11115551522222EHO GHF S S EO NH GF MH NH MH MN +=⨯+=⨯⨯+⨯⨯==,∴=30AEO EHO GHF S S S S ++=阴影,故选:C2、B【解析】【分析】如果抽取的样本得当,就能很好地反映总体的情况,否则抽样调查的结果会偏离总体情况.要抽出具有代表性的调查样本.【详解】A.只调查九年级全体学生,没有代表性;B.调查七、八、九年级各30名学生,属于分层抽样,有代表性;C.只调查全体女生,没有代表性;D.只调查全体男生,没有代表性.故选B.【点睛】本题考核知识点:抽样调查.解题关键点:要了解全校学生的课外作业负担情况,抽取的样本一定要具有代表性.3、B【解析】根据“平面直角坐标系中任意一点P(x,y),关于原点的对称点是(-x,-y)”解答.【详解】根据中心对称的性质,得点P(2,-3)关于原点对称的点的坐标是(-2,3).故选B.关于原点对称的点坐标的关系,是需要识记的基本问题.记忆方法是结合平面直角坐标系的图形记忆.4、B【解析】先延长AB,D'A'交于点G,根据三角形外角性质以及等腰三角形的判定,即可得到BC=BG=BA,设AE=x=A'E,则BE=2−x,GE=4−x,A'G=2x,在Rt△A'GE中,依据勾股定理可得A'E2+GE2=A'G2,进而得出方程,解方程即可.【详解】解:如图所示,延长AB,D'A'交于点G,∵A'E⊥AB,∠EA'C=∠A=120°,∴∠BGC =120°﹣90°=30°,又∵∠ABC =60°,∴∠BCG =60°﹣30°=30°,∴∠BGC =∠BCG =30°,∴BC =BG =BA ,设AE =x =A'E ,则BE =AB ﹣AE =2﹣x ,A'G =2x ,∴GE =BG+BE =2+2﹣x =4﹣x ,∵Rt △A'GE 中,A'E 2+GE 2=A'G 2,∴x 2+(4﹣x )2=(2x )2,解得:x =﹣2+2,(负值已舍去)∴AE =﹣2,故选B .本题主要考查了折叠问题,等腰三角形的判定,菱形的性质,解一元二次方程以及勾股定理的运用;解决问题的关键是作辅助线构造直角三角形,依据勾股定理列方程求解.5、C 【解析】根据实数运算的法则对各选项进行逐一计算作出判断.【详解】解:A =,是无理数,故本选项错误;B 、=C 、6=,是有理数,故本选项正确;D (23-=,是无理数,故本选项错误.故选C .6、C 【解析】首先设反比例函数和一次函数的解析式,根据图像信息,即可得出解析式,然后即可判断正误.【详解】设反比例函数解析式为根据题意,图像过点(1,200),则可得出当时,,即4月份的利润为万元,A 选项正确;设一次函数解析式为根据题意,图像过点(4,50)和(6,110)则有解得∴一次函数解析式为,其斜率为30,即污改造完成后每月利润比前一个月增加万元,B 选项正确;治污改造完成前后,1-6月份的利润分别为200万元、100万元、万元、50万元、110万元,共有3个月的利润低于万元,C 选项错误;9月份的利润为万元,D 选项正确;故答案为C .此题主要考查一次函数和反比例函数的实际应用,熟练掌握,即可解题.7、B【解析】首先设矩形的两邻边长分别为:3x,4x,可得(3x)2+(4x)2=202,继而求得矩形的两邻边长,则可求得答案.【详解】解:∵矩形的两邻边之比为3:4,∴设矩形的两邻边长分别为:3x,4x,∵对角线长为20,∴(3x)2+(4x)2=202,解得:x=4,∴矩形的两邻边长分别为:12,16;∴矩形的面积为:12×16=1.故选B.8、A【解析】根据题意,得到路程和甲的速度,然后根据相遇问题,设乙的速度为x,列出方程求解,然后即可求出乙需要的时间.【详解】解:由纵坐标看出甲先行驶了1千米,由横坐标看出甲行驶1千米用了6分钟,∴甲的速度是:1÷6=16千米/分钟,由纵坐标看出AB两地的距离是16千米,设乙的速度是x千米/分钟,由题意,得:10x+16×16=16,解得:x=4 3,∴乙从B地到A地需要的时间为:416=123 (分钟);故选:A.本题考查了一次函数的应用,利用同路程与时间的关系得出甲乙的速度是解题关键.二、填空题(本大题共5个小题,每小题4分,共20分)9、8【解析】利用菱形的性质根据勾股定理求得AO 的长,然后求得AC 的长即可.【详解】如图,∵四边形ABCD 是菱形,∴AC ⊥BD ,AO=CO ,BO=DO ∵BD=6,∴BO=3,∵周长为20,∴AB=5,由勾股定理得:AO==4,∴AC=8,故答案为:8本题主要考查了菱形的性质,解题的关键是菱形问题转化为直角三角形问题求解.10、66【解析】过点A 作AE ⊥PC 于点E ,过点B 作BF ⊥QD 于点F ,根据含30度角的直角三角形的性质即可求出AE 与BF 的长度,然后求出EF 的长度即可得出答案.【详解】解:过点A 作AE ⊥PC 于点E ,过点B 作BF ⊥QD 于点F ,∵AC=56,∠PCA=30°,1282AE AC ∴==由对称性可知:BF=AE ,∴通过闸机的物体最大宽度为2AE+AB=56+10=66;故答案为:66cm .本题考查解直角三角形,解题的关键是熟练运用含30度的直角直角三角形的性质,本题属于基础题型.11、c >1【解析】根据关于x 的一元二次方程没有实数根时△<0,得出△=(-6)2-4c <0,再解不等式即可.【详解】∵关于x 的一元二次方程x 2-6x+c=0(c 是常数)没有实根,∴△=(-6)2-4c <0,即36-4c <0,解得:c >1.故答案为c >1.12、-2【解析】根据题意,得4﹣3x=2x ﹣1,解得x=1,∴y=1.把(1,1)代入y=ax +7,得a +7=1,解得a=﹣2.故答案为﹣2.13、5-【解析】先通分,使等式两边分母一样,然后是使分子相等,可以求出结果。
折纸金元宝的三种折法

折纸金元宝的三种折法
一. 小正八角金元宝折法
1. 将纸平放,从中央折叠半,然后把上半部分再折成左右两半。
2. 把两半各折叠成斜角,交叉放在中间,得到四个小正八角形,然后
将每一个小正八角形折叠成金元宝。
3. 如需将金元宝变大,可在其两侧各拉出一半,继续折叠,在原基础
上重复步骤2的折法,不断拉伸、折叠,即可完成折制。
二. 金字塔金元宝折法
1. 将纸放平,从中央把纸剪下三分之一,即可得到六角形。
2. 将六角形朝上,将两个指角折向中间,再将其内外两侧折向中间,
最后将金字塔折叠成金元宝。
3. 如需再大,可将金元宝中间拉伸,继续重复步骤2,进行反复拉伸、折叠,即可完成折纸金元宝折制。
三. 六边形金元宝折法
1. 将纸放平,从中央折叠半,从底部向两侧拉伸。
2. 从中心向上将纸折叠,使得上半部分弯曲,在中部重叠形成六边形,将迤反夹折成月牙形,拉伸折叠以形成扇形。
3. 再将金元宝向上翻转,把两腰部的三角形,展开进行拉伸折叠,进
行多次重复,使金元宝边缘一圈一圈叠加就可成功折制。
金银山的折法

金山是金小宝塔。
银山是金小宝塔。
1、首先将正方形彩纸沿中线对折;
2、将其竖放,然后,沿中线对折;
3、展开,将折痕两侧的正方形压折;
4、取右侧一角向上折,与中线对齐,同理,完成正反两面的;
5、取右侧一角压折成正方形,同理,完成正反两面的;
6、沿正方形对角线对折;
7、沿右侧边向内折,与中线对齐;
8、将其展开,沿折痕将其反折向背面,同理,完成其余3处;
9、将两侧拉开,然后压平,同理,完成背面的。
10、到此,小宝塔就完成了。
扩展资料:
折纸大约起源于公元1世纪或者2世纪时的中国,6世纪时传入日本,再经由日本传到全世界。
也有说法认为折纸起源于日本和西班牙。
折纸与自然科学结合在一起,不仅成为建筑学院的教具,还发展出了折纸几何学成为现代几何学的一个分支。
折纸既是一种玩具,也是一项思维活动;是一个和平与纪念的象征手段,也是一种消遣方式。
烧纸用的金山银山的叠法步骤__概述说明以及解释

烧纸用的金山银山的叠法步骤概述说明以及解释1. 引言1.1 概述:本文将探讨烧纸时使用的金山银山的叠法步骤,并详细解释其背后的原理和技术。
烧纸是一种古老的传统活动,广泛用于祭祀、拜神和纪念逝者等场合。
而金山银山的叠法是一种手艺精湛、工序复杂的独特技术,在烧纸过程中起到制作华丽造型和增加视觉效果的作用。
本文旨在向读者介绍金山银山的叠法步骤,帮助他们更好地了解和学习这一传统工艺。
1.2 文章结构:本文分为引言、正文、叠法步骤解释、结论以及参考资料和来源(可选)五个部分。
在引言部分,我们将介绍文章的主题和目标,并依次概述文章结构。
1.3 目的:本文旨在提供对金山银山的叠法步骤进行全面而清晰地说明,通过详细解释每个步骤的操作方法、特点和注意事项,帮助读者正确理解并学会金山银山的叠法技巧。
同时,通过展望未来发展可能性,鼓励读者挖掘和创新这一传统手艺,推动其在现代社会中的传承与发展。
通过本文的阅读,读者可以更深入地了解金山银山的叠法步骤,并对其在烧纸活动中的重要性有一个全面而清晰的认识。
2. 正文烧纸用的金山银山是一种传统的祭祀仪式中常见的叠法,具有浓厚的民俗文化色彩。
金山银山叠法主要通过将纸张叠成不同形状来象征财富和福气的到来。
下面我们将详细介绍金山银山叠法的步骤以及其背后的意义。
首先,在进行金山银山叠法之前,需要准备一定数量和不同大小的纸张。
常见的选择是黄色纸张代表金山,而白色纸张则代表银山。
接下来,我们将开始进行烧纸用的金山银山叠法:第一步,取一个较大的黄色正方形纸张作为基层,代表主体部分的“金山”。
将该黄色纸张对折成一个三角形,并确保对齐边缘。
然后再次对折这个三角形,让边缘还是对齐。
第二步,将这个三角形翻过来,使得折痕处向上。
然后将左侧角折向右侧,在接着将右侧角再次折向左侧。
此时你将会看到中间部分出现了两个小三角形。
接下来,只需将这两个小三角形的上一层纸张逐渐叠降下来,最后固定好。
第三步,我们需要准备一个较小的白色正方形纸张作为“银山”。
