几种典型带电体的场强和电势公式
大学物理下知识点总结

电流分布 直 无限长 电 流 半无限长
导线所在直线上
圆 圆心处 电 流 弧电流圆心 长直载流密绕螺线管 载流密绕细螺绕环
磁场分布
B μ0 I 2πa
B 0I 4 a
B0
BO
0 I
2R
BO
0 I
2R
2
B内 0nI B内 0nI
B外 0 B外 0
1、B 、H 关系:
磁介质概要
对各向同性磁介质: B H
L L
di dt
(1)自感磁能:Wm
1 2
LI 2
(2)磁能密度:wm
1 2
B2
1 H 2
2
1 BH 2
磁能:Wm wmdV V
6、Maxwell位移电流假说: 实质:变化电场→ 磁场
平板电容器中总位移电流:
Jd
D t
Id
C dU dt
0 S板
dE dt
全电流定律:
H dl
L
Ic Id
n
点电荷系场: u ui 无连限续大带或电无体限场长: 带ui电1 体q du不能q 使4d用q0r该(方u法 0)
计算量
q
E
4
r2
0
r0
E
i
qi
40ri2
r0i
dq
E 40r 2 r0
1
S
E dS
0
qi
s内
Up
U0 E dl p
q U
4 0r
U
i
qi
4
0
ri
U
dq
40r
Q1 ,R1 Q2 ,R2 R1 R2
场强分布
E 2 0a
静电场中几种典型电场的场强及电势的描述(共37张PPT)

8k
Q R2
cos3
可知中垂线上O向两侧场强大小一直
减小,各点场强方向一直,平行于AB连
线指向负电荷。
相距为R的等量异种点电荷连线、中垂线上电势分布情 况:
Q Q
1,连线任取一点P:
o
A
B
k
Q r
k
Q (R r)
θ pO
A
A至B电势一直减小,中点O点电势最小
-
B
EQ Q
- θ Ep p
o
A
-
p' B
Q'
连线间及中垂线上各点场强大小分布 与等量正点电荷分布同,各场点方向与等 量正电荷相反。
相距为R的等量同种负点电荷连线、中垂线上电势分布 情况:取无穷远电势为0
Q Q
-
θ
p
p
o
A
-
p' B
Q'
连线上由A至B,电势先增后减,中点O 处电势最大。中垂线上向两侧电势增大,O 点最小,对称点电势相等,均为负值。
示,电场方向竖直向下,若不计空气阻力,则带电油
滴从a运动到b的过程中:
A,动能减小
B,电势能增加
C,动能和电势能之和减小
b
D,重力势能与电势能之和增加
F合
θ
a
v
E
四、北京市高考近十年相关问题回顾
(一)、对电场线和等势面基本功能的考察
(2009年)16.某静电场的电场线分布如图所示,图
中P、Q两点的电场强度的大小分别为EP和EQ,电势分
16 9
3
K
Q R2
可知中垂线上O处场强为0。由O向Q
电场

同 种 正 电 荷
等量异种电荷的等势面
连线上从正电荷向负电荷 电势降低
等量同种电荷的等势面 连线上电势先降低后升高, 中点最低 中垂线上由中点向两边降 低,中点最高
中垂线为等势面且电势为零
(4)、等势面的特点 ①同一等势面上的任意两点间移动电荷电场力不做功 ②等势面一定跟电场线垂直 ③电场线总是从电势较高的等势面指向电势较低的等势面 ④等势面密的地方电场强
x
例6、如图所示,AC、BD为圆的两条互相垂直的直径,圆心 为O,半径为R,将等电量的正、负点电荷放在圆周上,它们 的位置关于AC对称,+q与O点的连线和OC间夹角为30°,下 列说法正确的是 A.A、C两点的电势关系是ΦA=ΦC B.B、D两点的电势关系是ΦB=ΦD C.O点的场强大小为Kq/r2 D. O点的场强大小为31/2Kq/r2
带电粒子在电场中运动 平衡 直线加速 偏转
电场中的导体 静电感应 静电平衡 电容器 电容:C=Q/U
一:电荷 库仑定律
一、电荷
1、两种电荷 丝绸摩擦玻璃棒 2、元电荷 玻璃棒 正电 丝绸 负电 毛皮摩擦橡胶棒 橡胶棒 负电 毛皮 正电
最早由密立根用实验测得
带电体所带电荷量为元电荷的整数倍 带电体所带电荷量与其质量之比 q/m ① 摩擦起电 ② 感应起电 ③ 接触起电(电荷中和) 电子的转移
d.电场线和带电粒子的运动轨迹是两回事.
(3)几种常见的电场中电场线的分布及特点
匀强电场
等量异种点电荷的电场
等量同种点电荷的电场
二、等势面
形象描述电场中各点电势的情况
(1)、概念: 电场中电势相等的点构成的面
(2)、意义:等势面来表示电势的高低 (3)、典型电场的等势面
静电场公式集锦

静电场公式集锦
1、元电荷: e =×10-19C (元电荷是个数值)
2、电场力:
1、定义式:F =qE
2、点电荷:2
21r q q k F = 3、电场强度: 1、定义式:E =F/q
2、点电荷:2r
Q k E = 3、匀强电场:d U E AB =
4、电势差: 1、定义:U AB =φA -φB
2、电势差与电场强度关系:U AB =Ed (d 为沿电场线方向的距离)
3、电场力做功与电势差关系:q W U AB
AB =
5、电场力做功:
1、电场力做功与电势能关系:W AB =Ep A -Ep B
2、电场力做功与电势差关系:W AB =qU AB (与路径无关)
6、电势能和电势: Ep A =q φA
7、电容
1、定义式:C =Q/U (C 与Q 、U 无关)
2、平行板电容器决定式:kd
S C r πε4=(C 与S 成正比、与d 成反比) 8、粒子在电场中加速: 动能定理:22
1mv qU =-0 9、粒子在电场中偏转: 1、时间:0
v L t = 2、加速度: md
Uq m Eq m F a === 3、竖直偏转位移:221at y =
4、偏转角度(速度与水平夹角):0
0tan v at v v y ==θ 电场线从正电荷出发终止于负电荷,电场线不相交,切线方向为场强方向,电场线密处场强大,顺着电场线电势越来越低,电场线与等势线垂直;
电场强度与电势均由电场本身决定,电场力与电势能还与带电体的电量多少和电荷正负有关; 处于静电平衡导体是个等势体,表面是个等势面,导体外表面附近的电场线垂直于导体表面,导体内部合场强为零,净电荷只分布于导体外表面。
几种典型带电体的场强和电势公式

几种典型带电体的场强和电势公式
本文介绍了几种电荷分布所产生的场强和电势。
首先是均匀分布的球面电荷,对于球面外的情况,电场强度矢量为
1/4πεr*q/r^2,对于球面内的情况,电场强度矢量为q/4πεR^3.电势分布方程为q/4πεr(球外)和q/4πεR(球内)。
其次是均匀分布的球体电荷,对于球体内的情况,电场强度矢量为1/4πεR*q/r^2,对于球体外的情况,电场强度矢量为1/4πεr*q/r^2.电势分布方程为q/8πεR(r R)。
第三种情况是均匀分布的无限大平面电荷,电场强度矢量为σ/2ε(±i),电势分布方程为σ(r-r0)/2ε。
如果以带电平面为零电势参考点,则电势表达式为-Ux(x≥0)和Ux(x≤0),其中Ux=σx/2ε。
第四种情况是均匀分布的无限长圆柱柱面电荷,对于柱面外的情况,电场强度矢量为λ/2πεr,对于柱面内的情况,电场强度矢量为λ/2πεR。
电势分布方程为ln(r/a)*λ/2πε(r>a)和
ln(R/a)*λ/2πε(r<a),其中a为零电势参考点。
最后一种情况是均匀分布的无限长带电圆柱体,对于圆柱体内的情况,电场强度矢量为ρr/2ε,对于圆柱体外的情况,电场强度矢量为ρR^2/r/2ε。
电势分布方程为-ρr^2/4ε(r≤R)和-ρR^2/2εln(r/R)(r>R)。
大学物理知识点(静电学)

" 0" A
E dl
2)电势
3)电势差(电压)
" 0" WA UA E dl A q0
3)电势叠加原理
U AB
n
rB rA
E dl
1 qi 点电荷系: U U1 U 2 U n i 1 4π 0 ri 连续带电体: U
真空中 介质中
2、电极化强度: P 0 (r 1)E 0 r E
3、极化电荷面密度:
Pn
E 0
4、电场与电荷面密度的关系:
0 E0 0
5、 有电介质时的高斯定理
如果电荷和介质的分布具有一定对称性: 球对称、柱对称、镜面对称 可利用介质中的高斯定理求场强。 思路: 先根据自由电荷的分布利用介质中的高斯定理 求出电位移矢量的分布;
1场强叠加原理2均匀带电圆盘的场强2几个典型带电体的场强公式1均匀带电圆环的场强无限大3均匀带电球壳的电场分布均匀带电总电量为q若球壳无限薄则不需考虑壳内电场得均匀带电球面内外的场强4无限长带电圆柱体的电场分布均匀带电体密度为对无限长带电圆筒面因筒内无电荷故有柱面其中
第一章主要内容总结
一、两个基本物理量
对于连续带电体:
方法Ⅰ
i 1
4πε0 ri
典型带电体的电势
电势叠加原理
常用方法:化“整”为“零”;补偿法;叠加法。
方法Ⅱ
UA
场强积分法(沿电力线积分)
"0" A
E dl
U AB
B A
E dl
W AB qU AB
熟记均匀带电圆环/ 圆盘、均匀带电球面/ 球体,无限长均匀 带电圆柱面/ 柱体、无限大带电平面的E、U分布。
高中物理电场公式

高中物理电场公式1.两种电荷、电荷守恒定律、元电荷:(e=1.60×10-19C);带电体电荷量等于元电荷的整数倍2.库仑定律:F=kQ1Q2/r2(在真空中){F:点电荷间的作用力(N),k:静电力常量k=9.0×109Nm2/C2,Q1、Q2:两点电荷的电量(C),r:两点电荷间的距离(m),方向在它们的连线上,作用力与反作用力,同种电荷互相排斥,异种电荷互相吸引}3.电场强度:E=F/q(定义式、计算式){E:电场强度(N/C),是矢量(电场的叠加原理),q:检验电荷的电量(C)}4.真空点(源)电荷形成的电场E=kQ/r2 {r:源电荷到该位置的距离(m),Q:源电荷的电量}5.匀强电场的场强E=UAB/d {UAB:AB两点间的电压(V),d:AB两点在场强方向的距离(m)}6.电场力:F=qE {F:电场力(N),q:受到电场力的电荷的电量(C),E:电场强度(N/C)}7.电势与电势差:UAB=φA-φB,UAB=WAB/q=-ΔEAB/q8.电场力做功:WAB=qUAB=Eqd{WAB:带电体由A到B时电场力所做的功(J),q:带电量(C),UAB:电场中A、B两点间的电势差(V)(电场力做功与路径无关),E:匀强电场强度,d:两点沿场强方向的距离(m)}9.电势能:EA=qφA {EA:带电体在A点的电势能(J),q:电量(C),φA:A点的电势(V)}10.电势能的变化ΔEAB=EB-EA {带电体在电场中从A位置到B位置时电势能的差值}11.电场力做功与电势能变化ΔEAB=-WAB=-QuAb (电势能的增量等于电场力做功的负值)12.电容C=Q/U(定义式,计算式) {C:电容(F),Q:电量(C),U:电压(两极板电势差)(V)}13.平行板电容器的电容C=εS/4πkd(S:两极板正对面积,d:两极板间的垂直距离,ε:介电常数)14.带电粒子在电场中的加速(V0=0):W=ΔEK或qU=mVt2/2,Vt=(2qU/m)1/215.带电粒子沿垂直电场方向以速度V0进入匀强电场时的偏转(不考虑重力作用的情况下)类平抛运动;垂直电场方向:匀速直线运动L=V0t,平行电场方向:初速度为零的匀加速直线运动d=at2/2,a=F/m=qE/m高中物理恒定电流公式1.电流强度:I=q/t{I:电流强度(A),q:在时间t内通过导体横载面的电量(C),t:时间(s)}2.欧姆定律:I=U/R {I:导体电流强度(A),U:导体两端电压(V),R:导体阻值(Ω)}3.电阻、电阻定律:R=ρL/S{ρ:电阻率(Ω?m),L:导体的长度(m),S:导体横截面积(m2)}4.闭合电路欧姆定律:I=E/(r+R)或E=Ir+IR也可以是E=U内+U外{I:电路中的总电流(A),E:电源电动势(V),R:外电路电阻(Ω),r:电源内阻(Ω)};5.电功与电功率:W=UIt,P=UI{W:电功(J),U:电压(V),I:电流(A),t:时间(s),P:电功率(W)};6.焦耳定律:Q=I2Rt{Q:电热(J),I:通过导体的电流(A),R:导体的电阻值(Ω),t:通电时间(s)};7.纯电阻电路中:由于I=U/R,W=Q,因三此W=Q=UIt=I2Rt=U2t/R;8.电源总动率、电源输出功率、电源效率:P总=IE,P出=IU,η=P出/P总{I:电路总电流(A),E:电源电动势(V),U:路端电压(V),η:电源效率}9.电路的串/并联串联电路(P、U与R成正比) 并联电路(P、I与R成反比)电阻关系(串同并反) R串=R1+R2+R3+ 1/R并=1/R1+1/R2+1/R3+电流关系 I总=I1=I2=I3 I并=I1+I2+I3+电压关系 U总=U1+U2+U3+ U总=U1=U2=U3功率分配 P总=P1+P2+P3+ P总=P1+P2+P3+10.欧姆表测电阻:(1)电路组成 (2)测量原理两表笔短接后,调节R0使电表指针满偏,得Ig=E/(r+Rg+R0);接入被测电阻Rx 后通过电表的电流为Ix=E/(r+Rg+R0+Rx)=E/(R中+Rx);由于Ix与Rx对应,因此可指示被测电阻大小(3)使用方法:机械调零、选择量程、欧姆调零、测量读数{注意挡位(倍率)}、拨off挡。
高中物理电学基本公式有哪些

⾼中物理电学基本公式有哪些 对于⾼中物理电学知识的学习,应该以电学实验为基础,通过切实的实际操作从⽽更加直观的观察到相应的电学原理,下⾯是店铺给⼤家带来的⾼中物理电学基本公式,希望对你有帮助。
⾼中物理电学公式 ⾼中物理电场公式 1.两种电荷、电荷守恒定律、元电荷:(e=1.60×10-19C);带电体电荷量等于元电荷的整数倍 2.库仑定律:F=kQ1Q2/r2(在真空中){F:点电荷间的作⽤⼒(N),k:静电⼒常量k=9.0×109Nm2/C2,Q1、Q2:两点电荷的电量(C),r:两点电荷间的距离(m),⽅向在它们的连线上,作⽤⼒与反作⽤⼒,同种电荷互相排斥,异种电荷互相吸引} 3.电场强度:E=F/q(定义式、计算式){E:电场强度(N/C),是⽮量(电场的叠加原理),q:检验电荷的电量(C)} 4.真空点(源)电荷形成的电场E=kQ/r2 {r:源电荷到该位置的距离(m),Q:源电荷的电量} 5.匀强电场的场强E=UAB/d {UAB:AB两点间的电压(V),d:AB两点在场强⽅向的距离(m)} 6.电场⼒:F=qE {F:电场⼒(N),q:受到电场⼒的电荷的电量(C),E:电场强度(N/C)} 7.电势与电势差:UAB=φA-φB,UAB=WAB/q=-ΔEAB/q 8.电场⼒做功:WAB=qUAB=Eqd{WAB:带电体由A到B时电场⼒所做的功(J),q:带电量(C),UAB:电场中A、B两点间的电势差(V)(电场⼒做功与路径⽆关),E:匀强电场强度,d:两点沿场强⽅向的距离(m)} 9.电势能:EA=qφA {EA:带电体在A点的电势能(J),q:电量(C),φA:A点的电势(V)} 10.电势能的变化ΔEAB=EB-EA {带电体在电场中从A位置到B位置时电势能的差值} 11.电场⼒做功与电势能变化ΔEAB=-WAB=-QuAb (电势能的增量等于电场⼒做功的负值) 12.电容C=Q/U(定义式,计算式) {C:电容(F),Q:电量(C),U:电压(两极板电势差)(V)} 13.平⾏板电容器的电容C=εS/4πkd(S:两极板正对⾯积,d:两极板间的垂直距离,ε:介电常数) 14.带电粒⼦在电场中的加速(V0=0):W=ΔEK或qU=mVt2/2,Vt=(2qU/m)1/2 15.带电粒⼦沿垂直电场⽅向以速度V0进⼊匀强电场时的偏转(不考虑重⼒作⽤的情况下)类平抛运动;垂直电场⽅向:匀速直线运动L=V0t,平⾏电场⽅向:初速度为零的匀加速直线运动d=at2/2,a=F/m=qE/m ⾼中物理恒定电流公式 1.电流强度:I=q/t{I:电流强度(A),q:在时间t内通过导体横载⾯的电量(C),t:时间(s)} 2.欧姆定律:I=U/R {I:导体电流强度(A),U:导体两端电压(V),R:导体阻值(Ω)} 3.电阻、电阻定律:R=ρL/S{ρ:电阻率(Ω?m),L:导体的长度(m),S:导体横截⾯积(m2)} 4.闭合电路欧姆定律:I=E/(r+R)或E=Ir+IR也可以是E=U内+U外{I:电路中的总电流(A),E:电源电动势(V),R:外电路电阻(Ω),r:电源内阻(Ω)}; 5.电功与电功率:W=UIt,P=UI{W:电功(J),U:电压(V),I:电流(A),t:时间(s),P:电功率(W)};6.焦⽿定律:Q=I2Rt{Q:电热(J),I:通过导体的电流(A),R:导体的电阻值(Ω),t:通电时间(s)};7.纯电阻电路中:由于I=U/R,W=Q,因三此W=Q=UIt=I2Rt=U2t/R;8.电源总动率、电源输出功率、电源效率:P总=IE,P出=IU,η=P出/P总{I:电路总电流(A),E:电源电动势(V),U:路端电压(V),η:电源效率} 9.电路的串/并联串联电路(P、U与R成正⽐) 并联电路(P、I与R成反⽐) 电阻关系(串同并反) R串=R1+R2+R3+ 1/R并=1/R1+1/R2+1/R3+ 电流关系 I总=I1=I2=I3 I并=I1+I2+I3+ 电压关系 U总=U1+U2+U3+ U总=U1=U2=U3 功率分配 P总=P1+P2+P3+ P总=P1+P2+P3+ 10.欧姆表测电阻:(1)电路组成 (2)测量原理 两表笔短接后,调节R0使电表指针满偏,得Ig=E/(r+Rg+R0);接⼊被测电阻Rx后通过电表的电流为 Ix=E/(r+Rg+R0+Rx)=E/(R中+Rx);由于Ix与Rx对应,因此可指⽰被测电阻⼤⼩ (3)使⽤⽅法:机械调零、选择量程、欧姆调零、测量读数{注意挡位(倍率)}、拨off挡。
几种典型电场线分布示意图及场强电势特点
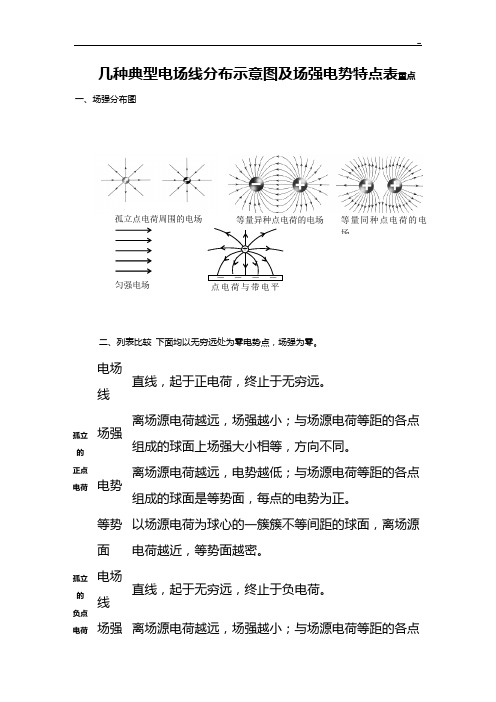
匀强电场 等量异种点电荷的电场 等量同种点电荷的电场- - - - 点电荷与带电平+孤立点电荷周围的电场几种典型电场线分布示意图及场强电势特点表重点一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的 正点电荷电场线直线,起于正电荷,终止于无穷远。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的 负点电荷电场线直线,起于无穷远,终止于负电荷。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
几种典型电场线分布示意图及场强电势特点

匀强电场等量异种点电荷的电场等量同种点电荷的电场点电荷与带电平孤立点电荷周围的电场 几种典型电场线分布示意图及场强电势特点表重点一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的正点电荷 电场线直线,起于正电荷,终止于无穷远。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的 负点电荷电场线直线,起于无穷远,终止于负电荷。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量电场大部分是曲线,起于正电荷,终止于无穷远;有两条同种正点电荷线电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
22-场强环路定理、电势

2012年4月26日
∞
∞
q 4πε 0 r
2
dr =
q 4πε 0 r
11 11
r
大连理工大学 秦 颖
大连理 工大学
例 5 :长为 l 的均匀带电直线,电荷线密度为 λ 。 求:图中 p 点的电势。 解:如图选取坐标系,
dU = dq 4π ε 0 r
l
dq = λd x
x
o
r
l
dx
dU
a
p
x
=
作功与检验电荷的电量和电场强度的线积分成正比。 ① 单位正电荷放在a点处, 系统的电势能。 ② 把单位正电荷从 a 点移 到0电势(无限远)处,电场 力所做的功。
2. 电势差:在电场中移动单位正电荷时电场作的功。
Ua − Ub =
∫
∞ a
E ⋅ dr −
∫
∞ b
E ⋅ dr =
∫
b a
E ⋅ dr 电 压
4πε 0 R 球面内 q U= 4πε 0 r 球面外
a
q
均匀带电 λ ln r 无限长直线 U =
2π ε 0
均匀带电 无限长直线
方向垂直于直线
λ E= 2πε 0 r
均匀带电 无限大平面
σ ⋅d U = Ed = 2ε 0
σ 均匀带电 E= 无限大平面 2ε 0
方向垂直于平面
秦 颖
17 17
2012年4月26日
∫
∞
r
qr ⋅ d r = 3 4π ε 0 r
∫
∞
r
dr
4π ε 0 r 4π ε 0 r r 例2 :求一对正、负电荷连线中垂线上的电势。
O
第五部分真空中的静电场,电势

第五部分 真空中的静电场,电势,静电平衡班级 ____________ 班内学号 ___________ 姓名 ____________知识点:1. 场强(1) 电场强度的定义0F E q = (2) 场强叠加原理 i i E E =∑(矢量叠加)(3) 点电荷的场强公式0204q E r r πε= (4) 用叠加法求电荷系的电场强度 0204dq E r rπε=⎰2. 高斯定理真空中 01sE dS qε⋅=∑⎰ 内电介质中 sD dS q ⋅=∑⎰ 内,自由 0r DE E εεε==3. 电势(1) 电势的定义 ppV E dl =⋅⎰零势点对有限大小的带电体,取无穷远处为零势点,则 p pV E dl ∞=⋅⎰(2 电势差 bab aV V E dl -=⋅⎰(3) 电势叠加原理 i iV V =∑ (标量叠加)(4) 点电荷的电势 04q Vrπε=(取无穷远处为零势点)电荷连续分布的带电体的电势 04dq V rπε=⎰(取无穷远处为零势点)4. 电荷q 在外电场中的电势能 aa w aV =5. 移动电荷时电场力的功()ab a b A q V V =-6. 场强与电势的关系 E V =-∇7..导体的静电平衡条件(1)0E 内= (2) E表面垂直导体表面8. 静电平衡导体上的电荷分布导体内部处处静电荷为零.电荷只能分布在导体的表面上. 0E σε表面=重点:1. 掌握电场强度和电势的概念以及相应的叠加原理。
掌握电与势电场强的积分关系,了解场强与电势的微分关系。
能用微积分计算一些简单问题中的场强和电势。
2. 确切理解高斯定理,掌握用高斯定理求场强的方法。
3. 理解导体的静电平衡条件。
掌握有导体存在时的电场和导体上电荷分布的计算。
难点:1. 用微积分计算电荷连续分布的带电体的场强和电势。
2.场强与电势的微分关系。
3.有导体存在时的电场和导体上电荷分布的计算。
解题要点:A 电场部分:(根据静止的场源电荷分布求静电场分布)1) 叠加法:基于点电荷的场强分布利用叠加原理求解。
几种典型电场线分布示意图以及场强电势特点

几种典型电场线散布表示图及场强电势特色表一、场强散布图孤立点电荷四周的电场等量异种点电荷的电场等量同种点电荷的电场+匀强电场----点电荷与带电平二、列表比较下边均以无量远处为零电势点,场强为零。
电场线直线,起于正电荷,停止于无量远。
孤立离场源电荷越远,场强越小;与场源电荷等距的各点构成的球面上场强盛小相等,方向不场强的同。
正点离场源电荷越远,电势越低;与场源电荷等距的各点构成的球面是等势面,每点的电势为电势电荷正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
电场线直线,起于无量远,停止于负电荷。
孤立离场源电荷越远,场强越小;与场源电荷等距的各点构成的球面上场强盛小相等,方向不场强的同。
负点离场源电荷越远,电势越高;与场源电荷等距的各点构成的球面是等势面,每点的电势为电势电荷负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
电场线大多数是曲线,起于无量远,停止于负电荷;有两条电场线是直线。
等量电势每点电势为负值。
同种连以中点最小为零;对于中点对称的随意两点场强盛小相等,方向相反,都是背叛中负点场强线点;由连线的一端到另一端,先减小再增大。
电荷上电势由连线的一端到另一端先高升再降低,中点电势最高不为零。
中以中点最小为零;对于中点对称的随意两点场强盛小相等,方向相反,都沿着中垂场强垂线指向中点;由中点至无量远处,先增大再减小至零,必有一个地点场强最大。
线中点电势最低,由中点至无量远处渐渐高升至零。
电势上电场线大多数是曲线,起于正电荷,停止于无量远;有两条电场线是直线。
电势每点电势为正当。
连以中点最小为零;对于中点对称的随意两点场强盛小相等,方向相反,都是指向中等量场强线点;由连线的一端到另一端,先减小再增大。
同种上电势由连线的一端到另一端先降低再高升,中点电势最低不为零。
正点中以中点最小为零;对于中点对称的随意两点场强盛小相等,方向相反,都沿着中垂电荷场强垂线指向无量远处;由中点至无量远处,先增大再减小至零,必有一个地点场强最大。
高中物理电场公式

高中物理电场公式1.两种电荷、电荷守恒定律、元电荷:(e=1.60×10-19C);带电体电荷量等于元电荷的整数倍2.库仑定律:F=kQ1Q2/r2(在真空中){F:点电荷间的作用力(N),k:静电力常量k=9.0×109Nm2/C2,Q1、Q2:两点电荷的电量(C),r:两点电荷间的距离(m),方向在它们的连线上,作用力与反作用力,同种电荷互相排斥,异种电荷互相吸引}3.电场强度:E=F/q(定义式、计算式){E:电场强度(N/C),是矢量(电场的叠加原理),q:检验电荷的电量(C)}真空点(源)电荷形成的电场E=kQ/r2{r:源电荷到该位置的距离(m),Q:源电荷的电量}匀强电场的场强E=UAB/d{UAB:AB两点间的电压(V),d:AB两点在场强方向的距离(m)}电场力:F=qE{F:电场力(N),q:受到电场力的电荷的电量(C),E:电场强度(N/C)}电势与电势差:UAB=φA-φB,UAB=WAB/q=-ΔEAB/q电场力做功:WAB=qUAB=Eqd{WAB:带电体由A到B时电场力所做的功(J),q:带电量(C),UAB:电场中A、B两点间的电势差(V)(电场力做功与路径无关),E:匀强电场强度,d:两点沿场强方向的距离(m)}电势能:EA=qφA{EA:带电体在A点的电势能(J),q:电量(C),φA:A点的电势(V)}电势能的变化ΔEAB=EB-EA{带电体在电场中从A位置到B位置时电势能的差值}电场力做功与电势能变化ΔEAB=-WAB=-QuAb(电势能的增量等于电场力做功的负值)电容C=Q/U(定义式,计算式){C:电容(F),Q:电量(C),U:电压(两极板电势差)(V)}平行板电容器的电容C=εS/4πkd(S:两极板正对面积,d:两极板间的垂直距离,ε:介电常数)14.带电粒子在电场中的加速(V0=0):W=ΔEK或qU=mVt2/2,Vt=(2qU/m)1/215.带电粒子沿垂直电场方向以速度V0进入匀强电场时的偏转(不考虑重力作用的情况下)类平抛运动;垂直电场方向:匀速直线运动L=V0t,平行电场方向:初速度为零的匀加速直线运动d=at2/2,a=F/m=qE/m高中物理恒定电流公式1.电流强度:I=q/t{I:电流强度(A),q:在时间t内通过导体横载面的电量(C),t:时间(s)}2.欧姆定律:I=U/R{I:导体电流强度(A),U:导体两端电压(V),R:导体阻值(Ω)}3.电阻、电阻定律:R=ρL/S{ρ:电阻率(Ω?m),L:导体的长度(m),S:导体横截面积(m2)}4.闭合电路欧姆定律:I=E/(r+R)或E=Ir+IR也可以是E=U内+U外{I:电路中的总电流(A),E:电源电动势(V),R:外电路电阻(Ω),r:电源内阻(Ω)};5.电功与电功率:W=UIt,P=UI{W:电功(J),U:电压(V),I:电流(A),t:时间(s),P:电功率(W)};6.焦耳定律:Q=I2Rt{Q:电热(J),I:通过导体的电流(A),R:导体的电阻值(Ω),t:通电时间(s)};7.纯电阻电路中:由于I=U/R,W=Q,因三此W=Q=UIt=I2Rt=U2t/R;8.电源总动率、电源输出功率、电源效率:P总=IE,P出=IU,η=P出/P总{I:电路总电流(A),E:电源电动势(V),U:路端电压(V),η:电源效率}9.电路的串/并联串联电路(P、U与R成正比)并联电路(P、I与R成反比)电阻关系(串同并反)R串=R1+R2+R3+1/R并=1/R1+1/R2+1/R3+电流关系I总=I1=I2=I3I并=I1+I2+I3+电压关系U总=U1+U2+U3+U总=U1=U2=U3功率分配P总=P1+P2+P3+P总=P1+P2+P3+10.欧姆表测电阻:(1)电路组成(2)测量原理两表笔短接后,调节R0使电表指针满偏,得Ig=E/(r+Rg+R0);接入被测电阻Rx后通过电表的电流为Ix=E/(r+Rg+R0+Rx)=E/(R中+Rx);由于Ix与Rx对应,因此可指示被测电阻大小(3)使用:机械调零、选择量程、欧姆调零、测量读数{注意挡位(倍率)}、拨off挡。
4.大学物理场强电势求法

E1
直圆柱为高斯面 .
由高斯定理:
h
E2
E dS E2S E1S
s
1
0
q内
1
0
hS
0 (E2
h
E1 )
8.85 1012 1.5 103
(100 25)
4.431013(C m3 )
〈2〉作高斯面如图
由高斯定理:
3. 非均匀带电,线密度为 0sin
y dq
d o
x
R
dE
思路:叠加法
dq dE E
解:1)
dq Rd
dE dq ;沿径向
4 R2 0
y
dq
dE
d o
x
用分量叠加,由对称性:
E y
dEy
0
R
dE
Ex dEx dE sin
挖去空腔 —— 失去球对称性,
R1
a o1
r1E2R2Pro22
E1
能否恢复对称性?补偿法!
半径 R 1均匀带电实心球体在P点的场强:E1 所半求径场R强2均E匀P 带E电1 实 E心2 球而体E在1、P点E2的均场可强由:高E斯2 定理求出。
(2) 作高斯面 S1 , S2 求 E1 , E2 .
1 2
UP
L
dU L
qdx
q ln L
8 0 L( x 2
a2
)
1 2
4 0 L
a2 L2 a
(2) 求细棒延长线上距细棒中心 b处 P点的电势
高中物理U=φ比t

高中物理U=φ比t高中物理电场公式1、两种电荷、电荷守恒定律、元电荷:(e=×10-19c);带电体电荷量等于元电荷的整数倍2、库仑定律:f=kq1q2/r2(在真空中){f:点电荷间的作用力(n),k:静电力常量k=×109nm2/c2,q1、q2:两点电荷的电量(c),r:两点电荷间的距离(m),方向在它们的连线上,作用力与反作用力,同种电荷互相排斥,异种电荷互相吸引}3、电场强度:e=f/q(定义式、计算式){e:电场强度(n/c),是矢量(电场的叠加原理),q:检验电荷的电量(c)}4、真空点(源)电荷形成的电场e=kq/r2 {r:源电荷到该位置的距离(m),q:源电荷的电量}5、匀强电场的场强e=uab/d {uab:ab两点间的电压(v),d:ab 两点在场强方向的距离(m)}6、电场力:f=qe {f:电场力(n),q:受到电场力的电荷的电量(c),e:电场强度(n/c)}7、电势与电势差:uab=φa-φb,uab=wab/q=-δeab/q8、电场力做功:wab=quab=eqd{wab:带电体由a到b时电场力所做的功(j),q:带电量(c),uab:电场中a、b两点间的电势差(v)(电场力做功与路径无关),e:匀强电场强度,d:两点沿场强方向的距离(m)}9、电势能:ea=qφa {ea:带电体在a点的电势能(j),q:电量(c),φa:a点的电势(v)}10、电势能的变化δeab=eb-ea {带电体在电场中从a位置到b 位置时电势能的差值}11、电场力做功与电势能变化δeab=-wab=-quab (电势能的增量等于电场力做功的负值)12、电容c=q/u(定义式,计算式) {c:电容(f),q:电量(c),u:电压(两极板电势差)(v)}13、平行板电容器的电容c=εs/4πkd(s:两极板正对面积,d:两极板间的垂直距离,ε:介电常数)14、带电粒子在电场中的加速(v0=0):w=δek或qu=mvt2/2,vt=(2qu/m)1/215、带电粒子沿垂直电场方向以速度v0进入匀强电场时的偏转(不考虑重力作用的情况下)类平抛运动;垂直电场方向:匀速直线运动l=v0t,平行电场方向:初速度为零的匀加速直线运动d=at2/2,a=f/m=qe/m高中物理恒定电流公式1、电流强度:i=q/t{i:电流强度(a),q:在时间t内通过导体横载面的电量(c),t:时间(s)}2、欧姆定律:i=u/r {i:导体电流强度(a),u:导体两端电压(v),r:导体阻值(ω)}3、电阻、电阻定律:r=ρl/s{ρ:电阻率(ω?m),l:导体的长度(m),s:导体横截面积(m2)}4、闭合电路欧姆定律:i=e/(r+r)或e=ir+ir也可以是e=u内+u 外{i:电路中的总电流(a),e:电源电动势(v),r:外电路电阻(ω),r:电源内阻(ω)};5、电功与电功率:w=uit,p=ui{w:电功(j),u:电压(v),i:电流(a),t:时间(s),p:电功率(w)};6、焦耳定律:q=i2rt{q:电热(j),i:通过导体的电流(a),r:导体的电阻值(ω),t:通电时间(s)};7、纯电阻电路中:由于i=u/r,w=q,因三此w=q=uit=i2rt=u2t/r;8、电源总动率、电源输出功率、电源效率:p总=ie,p出=iu,η=p出/p总{i:电路总电流(a),e:电源电动势(v),u:路端电压(v),η:电源效率}9、电路的串/并联串联电路(p、u与r成正比) 并联电路(p、i 与r成反比)电阻关系(串同并反) r串=r1+r2+r3+ 1/r并=1/r1+1/r2+1/r3+ 电流关系 i总=i1=i2=i3 i并=i1+i2+i3+电压关系 u总=u1+u2+u3+ u总=u1=u2=u3功率分配 p总=p1+p2+p3+ p总=p1+p2+p3+10、欧姆表测电阻:(1)电路组成 (2)测量原理两表笔短接后,调节r0使电表指针满偏,得ig=e/(r+rg+r0);接入被测电阻rx后通过电表的电流为ix=e/(r+rg+r0+rx)=e/(r中+rx);由于ix与rx对应,因此可指示被测电阻大小(3)使用方法:机械调零、选择量程、欧姆调零、测量读数{注意挡位(倍率)}、拨off挡。
大学物理电磁学公式全集

连续带电体场强、电场强度、场强迭加原理M n点电荷系场强・dq| _ 2 J Q 4 昭 r四、静电场高斯定理五、几种典型电荷分布的电场强度静电场小结 、库仑定律均匀带电球体均匀带电球面 r>R r <R (f) (r<R)均匀带电长直圆柱体无限大均匀带电平面'(0)E drva均匀带电长直圆柱面 六、静电场的环流定理七、电势八、电势迭加原理点电荷电势 w九、几种典型电场的电势r>R 均匀带电球面(r<R) (r>R)r<R点电荷系电势连续带电体电势V = -- Inr+C均匀带电直线‘恋十、导体静电平衡条件(1)导体内电场强度为零';导体表面附近场强与表面垂直卜“(2)导体是一个等势体,表面是一个等势面。
推论一电荷只分布于导体表面推论二导体表面附近场强与表面电荷密度关系“.十、静电屏蔽导体空腔能屏蔽空腔内、外电荷的相互影响。
即空腔外(包括外表面)的电荷在空腔内的场强为零,空腔内(包括内表面)的电荷在空腔外的场强为零。
十二、电容器的电容u一C=£-平行板电容器圆柱形电容器球形电容器心「孤立导体球此一:十三、电容器的联接并联电容器"二电场的能量密度丄汀丄串联电容器.十四、电场的能量 电容器的能量电场的能量稳恒电流磁场小结一、 磁场运动电荷的磁场毕奥一一萨伐尔定律r 2二、 磁场高斯定理押込0三、 安培环路定理四、 几种典型磁场B = —(cosA -cosft 有限长载流直导线的磁场 4疗' 1 'B =^L无限长载流直导线的磁场 2苏三一朋圆电流轴线上的磁场%川+ "严B_ N圆电流中心的磁场J.长直载流螺线管内的磁场g=卩昶载流密绕螺绕环内的磁场y五、载流平面线圈的磁矩m和S沿电流的右手螺旋方向六、洛伦兹力F = qvxB七、安培力公式八、载流平面线圈在均匀磁场中受到的合磁力抡=0载流平面线圈在均匀磁场中受到的磁力矩电磁感应小结电动势非静电性场强g电源电动势一段电路的电动势s- -<A闭合电路的电动势■当一•」时,电动势沿电路(或回路)I的正方向,「:时沿反方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几种电荷分布所产生的场强和电势1、均匀分布的球面电荷(球面半径为R ,带电量为q )电场强度矢量:⎪⎩⎪⎨⎧<=>=)(球面内,即。
)(球面外,即R r r E R r rr q r E 0)( , 41)( 3επ电势分布为:()()⎪⎪⎩⎪⎪⎨⎧==(球内)。
(球外), 41 41 0 0R qr U r q r U επεπ2、均匀分布的球体电荷(球体的半径为R,带电量为q )电场强度矢量:⎪⎪⎩⎪⎪⎨⎧>=<=)(球体外,即。
)(球体内,即,R r rr q r E R r R r q r E 41)( 41)( 3030επεπ 电势分布为:()()()⎪⎪⎩⎪⎪⎨⎧<-=>=即球内)(。
即球外)(, 3 81 41 3220 0R r R r R q r U R r r q r U επεπ 3、均匀分布的无限大平面电荷(电荷面密度为σ)电场强度矢量:离无关。
)(平板两侧的场强与距 ) (2)(0i x E ±=εσ电势分布为:()()r r r U -=002εσ其中假设0r 处为零电势参考点。
若选取原点(即带电平面)为零电势参考点。
即00=U 。
那么其余处的电势表达式为:()()⎪⎪⎩⎪⎪⎨⎧≤=≥-=0 2 0 2 00x x x U x x x U εσεσ 4、均匀分布的无限长圆柱柱面电荷(圆柱面的半径为R ,单位长度的带电量为λ。
)电场强度矢量 ⎪⎩⎪⎨⎧<=>=,即在柱面内)(。
即在柱面外)(,R r r E R r r r r E 0)( , 2 )( 2επλ 电势分布为:()()⎪⎪⎩⎪⎪⎨⎧<=>=即柱体内)(。
即柱体外)( ln 2 , ln 2 00R r R r r U R r r r r U a a επλεπλ其中假设a r 处为零电势参考点。
且a r 处位于圆柱柱面外部。
(即a r >R )。
若选取带电圆柱柱面处为零电势参考点。
(即()0=R U )。
那么,其余各处的电势表达式为:()()()()⎪⎩⎪⎨⎧≥-=≤≤=即在圆柱面外即在圆柱面内 ln 2 0 0 0R r R r r U R r r U επλ 5、均匀分布的无限长带电圆柱体(体电荷密度为ρ、半径为R 。
)电场强度矢量: ()()()()⎪⎪⎩⎪⎪⎨⎧≥=≤≤=圆柱体外圆柱体内2 0 2 2020R r r r R r E R r r r Eερερ电势: ()()()()⎪⎪⎩⎪⎪⎨⎧≥+-=≤≤-=圆柱体外圆柱体内ln 2 4 0 4020202R r r R R R r U R r r r U ερερερ 其中假设圆柱体轴线处为零电势参考点。
即()00==r U 。
6、均匀分布的带电圆环(带电量为q ;圆环的半径为R 。
)在其轴线上x 处的电场强度和电势电场强度矢量: ()()0232241x Rxqxx E+=επ。
其中0x 为轴线方向的单位矢量。
讨论: (a )当 20 4 )( x iq x E x R x p επ ≅∞→>>时或。
此时带电圆环可视为点电荷进行处理。
(b )当0)0( 0 =→<<p E x R x 时或 。
即,带电圆环在其圆心处的电场强度为零。
电势: ()()21220 41R x qx U +=επ 。
其中电势的零参考点位于无穷远处。
带电圆环在其圆心处的电势为: Rq x U x 004)(πε== 。
7、均匀分布的带电直线(其中,线电荷密度λ,直线长为l ) (1)在直线的延长线上,与直线的端点距离为d 的P 点处:电场强度矢量: ()()i d l d i d l d l d E p ⎪⎭⎫ ⎝⎛+-=+=114 400επλεπλ 。
()ddl d U p +=ln 40επλ 。
(2)在直线的中垂线上,与直线的距离为d 的Q 点处:电场强度矢量为:()j d l d lj d l d l d E Q 2202242 42 4+=+⎪⎭⎫⎝⎛=επλεπλ。
电势:()222202222044ln 42222ln4dl l d l l d l l d l l d U Q ++-++=+⎪⎭⎫⎝⎛+-+⎪⎭⎫⎝⎛+=επλεπλ。
(3)在直线外的空间中任意点处:电场强度矢量: ()j E i E r E y x+= 。
其中:()()⎪⎪⎩⎪⎪⎨⎧-=-=210120 4 4 θθεπλθθεπλCos Cos E Sin Sin E y x 。
或者改写为另一种表示式:即: k E r E z r E z r p+=0),( 。
其中:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++--+=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++++--++-+-=22220222222220)2(1)2(1 4 )2()2()2(1)2()2()2(1 4 l z r l z r E l z r l z r l z l z r l z r l z r E z r επλεπλ电势: 22220)2(2)2(2ln 4lz r l z lz r l z U p -++-++++=επλ 。
(4)若带电直线为无限长时,那么,与无限长带电直线的距离为d 的P 点处: 电场强度矢量: ()()r rr E d d d E p p 2000 2 2επλεπλ==或 。
电势: ()()rr r U d d d U p p 0000ln 2 ln 2επλεπλ==或 。
其中假设d 0或(r 0)为电势的零参考点。
(5)半无限长带电直线在其端点处:(端点与带电直线的垂直距离为d )电场强度矢量:dE E j E i E E y x y x 0 4 επλ==+=其中。
8、电偶极子P的电场强度和电势(1)在电偶极子的延长线上x 处:其中(X >>l )电场强度矢量:()()30302 41 2 41r Pr E x P x Eεπεπ==或 。
电势: ()()2020 41r U 41r Px P x U επεπ==或 。
(2)在电偶极子的中垂线上y 处:其中(Y >>l )电场强度矢量: ()30 41yPy Eεπ-= 。
电势: ()0 410=⎪⎭⎫⎝⎛-+=r q r q y U επ 。
(3)在空间中任意点r 处:其中(r >>l )电场强度矢量:(采用平面极坐标系)()13 4 2 4122003030+=⎪⎭⎫ ⎝⎛+=θεπθθθεπCos r PE r PSin r r pCos r E 其大小为,方向为⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛==--θϕθθtg tg E E tg E E arctgrr 2111。
其中ϕ为E 与0r 之间的夹角。
电势:()302 41 41rrP r Cos P r U o•==επθεπ 。
电场强度矢量的另一种表达式为:上式电场强度矢量的表达式就是将电场强度E 矢量分解在电偶极矩e P 和矢径r的方向上。
可以证明:该表达式与电场强度的平面极坐标表达式是相等的。
()[]r p r p rE e e ˆˆ3413⋅+-=επ方向的单位矢量。
为矢径式中:r r rˆ=若采用二维笛卡尔坐标系(平面直角坐标系):因为各物理量之间的关系为:。
, rxCos 22222yx x y x r +==+=θ 所以电势的表达式为: ()()23220 41y x Pxr U +=επ 。
而电场强度的表达式为: j E i E E y x+= 。
其中:()()()。
, 3 41 2 41252202522220y x Pxy y U E y x y x P x U E yx +=∂∂-=+-=∂∂-=επεπ其大小为:()222220224 41yx yx P E E E yx++=+=επ 。
若采用三维笛卡尔坐标系(即三维直角坐标系)则有如下关系式:。
, 2222222zy x z rzCos z y x r ++==++=θ 那么,电势的表达式为: ()()232220 41z y x zP r U ++=επ 。
而电场强度的表达式为: k E j E i E E z y x++= 。
其中:()(); z x 3 4 3 4252220252220++=∂∂-=++=∂∂-=y zy P y U E z y x z x P x U E y x επεπ; ()()。
2 4252222220z y x y x z P z U E z ++--=∂∂-=επ9、带电圆盘在其轴线上距离圆心为x 点处:电场强度矢量: i R x xx E p⎪⎪⎭⎫ ⎝⎛+-=22012)(εσ。
对上式结果进行讨论:(a )当 02020 4)( 4)( x r rq r E i x q x E R x p p επεπ≅≅∞→>>或时或 此时带电圆盘可视为点电荷进行处理。
(b )当。
则,时或 2)( 0 0i x E x R x pεσ≅→<<即此时带电圆盘可视为无限大带电平板进行处理。
电势: ()x x Rx U p -+=222)(εσ 。
带电圆盘在其圆心处附近处的电势为: 。
02)(εσR x U x == 10、均匀分布的带电半球面在其球心处:(球面的面电荷密度为σ,球面的半径为R 。
)电场强度矢量: i E004εσ= 。
电势: 。
42 )(00RQR x U p επεσ==此时电势并不是⎰∞•=0)(r d E x U o p ,因为04)()(εσ=≠x E x E o 。
