常用傅里叶变换表

合集下载

常用傅立叶变换表

时域信号
弧频率表示的
傅里叶变换
注t)+b・h(t)
iGV) + b・H(f)
线性
2
g(f —q)
「如叮G(f)
时域平移
3
广勺(t)
W)
频域平移，变换2的频域对应
4
g(at)
如果hl值较大，则g(m)会收缩到原点附近，而间丿会扩
散并变得扁平.当丨$丨趋向无穷时，成为Delta函数。
2
由变换1和25得到，应用了：cos （at）=（尹 +e F）/2.
22
sin(at)
灯-刼-幻+知
21
由变换1和25得到
23
tn
（2；）网⑺
这里，n是一个.6®（3）是狄拉克5函数分布的力阶微分。这个变换是根据变换7和24得到的。将此变换与1结合使用，我们可以变换所有。
24
1
1
一沏•sgn(/)
Mrec,(0
变换10的频域对应。矩形函数是理想的低通滤波器，是这类滤波器对冲击的响应。
11
sine2(at)
右'trl(0
tri是
12
tri (at)
变换12的频域对应
13
e~°^
/7T(“2
低•…
exp(-a r)的傅里叶变换是他本身.只有当Re(a)> 0时，这是可积的。
14
cos(al2)
W)
15
sin (at2)
卜(卓)
16
e-a|t|
2a
3>0
a2H-47T2/2
17
1丽
1
丽
变换本身就是一个公式
18

常用傅里叶_拉普拉斯_Z变换表

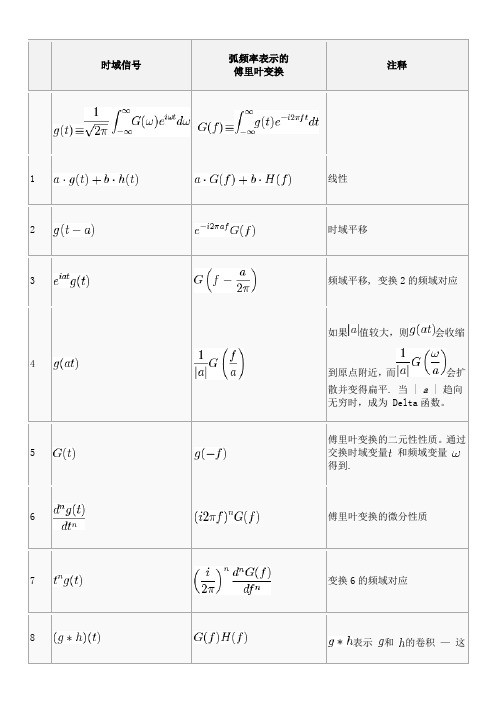
时域信号弧频率表示的傅里叶变换注释1 线性2 时域平移3 频域平移, 变换2的频域对应4 如果值较大，则会收缩到原点附近，而会扩散并变得扁平. 当 | a | 趋向无穷时，成为 Delta函数。

5 傅里叶变换的二元性性质。

通过交换时域变量和频域变量得到.6 傅里叶变换的微分性质7 变换6的频域对应8表示和的卷积—这就是卷积定理9 矩形脉冲和归一化的sinc函数10 变换10的频域对应。

矩形函数是理想的低通滤波器，sinc函数是这类滤波器对反因果冲击的响应。

11 tri是三角形函数12 变换12的频域对应13 高斯函数 exp( −αt2) 的傅里叶变换是他本身. 只有当Re(α) > 0时，这是可积的。

141516 a>018 δ(ω) 代表狄拉克δ函数分布. 这个变换展示了狄拉克δ函数的重要性：该函数是常函数的傅立叶变换19 变换23的频域对应20 由变换3和24得到.21 由变换1和25得到，应用了欧拉公式: cos(at) = (e iat + e−iat) / 2.22 由变换1和25得到23 这里, n是一个自然数. δ(n)(ω) 是狄拉克δ函数分布的n阶微分。

这个变换是根据变换7和24得到的。

将此变换与1结合使用，我们可以变换所有多项式。

24 此处sgn(ω)为符号函数；注意此变换与变换7和24是一致的.25 变换29的推广.26 变换29的频域对应.17 变换本身就是一个公式27 此处u(t)是单位阶跃函数; 此变换根据变换1和31得到.28 u(t)是单位阶跃函数，且a > 0.34 狄拉克梳状函数——有助于解释或理解从连续到离散时间的转变.附录A 拉普拉斯变换及反变换1.拉氏变换的基本性质附表A-1 拉氏变换的基本性质1()1()([n n k F s f t dt s s-+=+∑⎰个[f L 2．常用函数的拉氏变换和z 变换表3．用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。

常用傅里叶变换表

G ⑴ 1 2 3 g(M) 4 a a 5 6 7 2T T dt n 注释 5(0=| 盘・g ⑴+ b ・h(t\ 线性 QT 如吋G(f) 曲一。

）时域平移频域平移，变换2的频域对应如果Ml 值较大，则ggt ）会收缩到原会扩散并变得 b (-f) 阳刀切傅里叶变换的微分性质变换6的频域对应弧频率表示的傅里叶变换傅里叶变换的二元性性质。

通过交换时域变量f 和频域变量 3得到. '用 G(f) 时域信号「gg 叫才 J _8 点附近，而kl 扁平.当| a |趋向无穷时，成为 Delta 函数。

18 S ( 3 )代表狄拉克S函数分布• 这个变换展示了狄拉克S函数的重要性：该函数是常函数的傅立叶变换19 变换23的频域对应20 由变换3和24得到.21 cos(at)2223242526 sgn(t)27 u(f) 咐-卸+刃十知由变换1和25得到，应用了欧拉公式：cos( at) = ( e iat + e - iat) / 2.卩(于一薛)一d"十盏) 2i-仙*Sgll：/)一卅黑；'唧(f)"(刀由变换1和25得到这里,n是一个自然数.S (n)( 3 ) 是狄拉克S函数分布的n阶微分。

这个变换是根据变换7和24得到的。

将此变换与1结合使用，我们可以变换所有多项式。

此处sgn( 3)为符号函数；注意此变换与变换7和24是一致的.变换29的推广.变换29的频域对应.此处u(t)是单位阶跃函数；此变换根据变换1和31得到.。

常用傅里叶变换表

时域信号弧频率表示的傅里叶变换注释1线性2时域平移3频域平移, 变换2的频域对应4如果值较大，则会收缩到原点附近，而会扩散并变得扁平. 当| a | 趋向无穷时，成为Delta函数。

5傅里叶变换的二元性性质。

通过交换时域变量和频域变量得到.6傅里叶变换的微分性质7变换6的频域对应8表示和的卷积—这就是卷积定理9矩形脉冲和归一化的sinc函数10变换10的频域对应。

矩形函数是理想的低通滤波器，sinc函数是这类滤波器对反因果冲击的响应。

11tri是三角形函数12变换12的频域对应13高斯函数exp( − αt2) 的傅里叶变换是他本身. 只有当Re(α) > 0时，这是可积的。

14 1518δ(ω) 代表狄拉克δ函数分布. 这个变换展示了狄拉克δ函数的重要性：该函数是常函数的傅立叶变换19变换23的频域对应20由变换3和24得到.21由变换1和25得到，应用了欧拉公式: cos(at) = (e iat + e−iat) / 2.22由变换1和25得到23这里, n是一个自然数. δ(n)(ω) 是狄拉克δ函数分布的n阶微分。

这个变换是根据变换7和24得到的。

将此变换与1结合使用，我们可以变换所16a>017变换本身就是一个公式有多项式。

此处sgn(ω)为符号函数；注意此变换24与变换7和24是一致的.25变换29的推广.26变换29的频域对应.此处u(t)是单位阶跃函数; 此变换根27据变换1和31得到.28u(t)是单位阶跃函数，且a > 0.狄拉克梳状函数——有助于解释或34理解从连续到离散时间的转变.。

常用傅里叶变换表

时域信号
弧频率表示的
傅里叶变换
注释
1
线性
2
时域平移
3
频域平移, 变换2的频域对应
4
如果
值较大，则会收缩到原
点附近，而会扩散并变得
扁平. 当 | a | 趋向无穷时，成为
Delta 函数。

5
傅里叶变换的二元性性质。

通过交换时域变量和频域变量得到.
6
傅里叶变换的微分性质
7
变换6的频域对应
表示和的卷积—这就是卷积定理
矩形脉冲和归一化的
变换
想的低通滤波器，
滤波器对反因果冲击的响应。

tri
变换
高斯函数
换是他本身
这是可积的。

a>0
变换本身就是一个公式δ
这个变换展示了狄拉克要性：
变换
由变换
由变换
式
由变换
这里
是狄拉克
这个变换是根据变换将此变换与
换所有多项式。

此处
换与变换
变换
变换
此处
根据变换
u
狄拉克梳状函数
理解从连续到离散时间的转变
Welcome !!! 欢迎您的下载，资料仅供参考！。

常用傅立叶变换表

18
δ(ω) 代表分布. 这个变换展示了狄拉克δ函数的重要性：该
时域信号
弧频率表示的
傅里叶变换
注释
1
线性
2
时域平移
3 频域平移, 变换2的频域对应 4
如果
值较大，则
会收缩
到原点附近，而会扩散并变得扁平. 当 | a | 趋向无穷时，成为 Delta 函数。

5 傅里叶变换的二元性性质。

通过交换时域变量和频域变量得到.
6 傅里叶变换的微分性质 7
变换6的频域对应
8
表示和的卷积 — 这
就是
9 和归一化的 10 变换10的频域对应。

矩形函数是理想的低通滤波器，是这类滤波器对冲击的响应。

11 tri 是
12
变换12的频域对应 13 exp( αt 2) 的傅里叶变换是
他本身. 只有当 Re(α) > 0时，这是可积的。

14
15 16 a>0
17 变换本身就是一个公式。

傅里叶变换简表

傅里叶变换简表
傅里叶变换（Fourier Transform）是一种将信号从时域（时间域）转换到频域（频率域）的数学方法。

傅里叶变换在信号处理、图像处理、通信等领域都有广泛的应用。

下面是傅里叶变换的简表：
傅里叶变换函数：
傅里叶变换F(k) = ∫[f(x) * e^(-2πikx)] dx
反变换函数：
反傅里叶变换f(x) = ∫[F(k) * e^(2πikx)] dk
常见信号的傅里叶变换：
1. 矩形函数（方波）的傅里叶变换：
F(k) = T * sin(πkT) / (πk)
2. 三角波的傅里叶变换：
F(k) = 2AT * sinc(2πATk)
3. 周期函数的傅里叶级数展开：
f(x) = a0 + Σ(an * cos(nωt) + bn * sin(nωt))
4. 高斯函数的傅里叶变换：
F(k) = σ * sqrt(2π) * e^(-π^2σ^2k^2)
5. 常见频率域运算的傅里叶变换：
a. 时移：f(x - x0) 的傅里叶变换F(k) * e^(2πikx0)
b. 频移：e^(2πik0x) 的傅里叶变换 F(k - k0)
c. 放大：f(ax) 的傅里叶变换 F(k/a) / a
d. 缩小：f(bx) 的傅里叶变换 F(k/b) * b
这只是一些傅里叶变换的简单例子，实际上傅里叶变换的应用十分广泛，还有很多复杂的数学关系和公式。

需要根据具体的问题和需求来进行深入研究和学习。

常用傅里叶变换表

弧频率表示的时域信号注释傅里叶变换线性1时域平移2频域平移3, 变换2的频域对应会收缩值较大，则如果4会扩而到原点附近，a趋向 | | . 散并变得扁平当无穷时，成为函数。

Delta 通过傅里叶变换的二元性性质。

5交换时域变量和频域变量.得到6傅里叶变换的微分性质变换76的频域对应表示和的卷积—这8就卷积定9矩形脉冲和归一化的sinc函数变换10的频域对应。

矩形函数是理想的低通滤波器，sinc函数是这类10 滤波器对反因果冲击的响应。

tri是三角形函数 1112变换12的频域对应2t) ?α的傅里叶变 exp( 高斯函数换是他本身. 只有当 Re(α) 13> 0时，这是可积的。

1415a>0 1617变换本身就是一个公式δ(ω) 代表狄拉克δ函数分布.这个变换展示了狄拉克18δ函数的重要性：该函数是常函数的傅立叶变换19变换23的频域对应20由变换3和24得到.由变换1和25得到，应用了欧拉公21iat?iat eeat) / 2.式: cos() = ( +22由变换1和25得到n)(n(ω) . δ这里, 自然数是一个n阶微分。

函数分布的是狄拉克δ这个变换是根据变换237和24得到的。

将此变换与1结合使用，我们可以变换所有多项式。

此处sgn(ω)为符号函数；注意此变24换与变换7和24是一致的.25变换29的推广.26变换29的频域对应.ut)是单位阶跃函数此处(; 此变换27根据变换1和31得到.uta > 0.，且()是单位阶跃函数28狄拉克梳状函数——有助于解释或34 理解从连续到离散时间的转变.。

常用傅里叶变换表

时域信号
弧频率表示的
傅里叶变换
注释
1
线性
2
时域平移
3
频域平移, 变换2的频域对应
4
如果
值较大，则会收缩到原
点附近，而会扩散并变得
扁平. 当 | a | 趋向无穷时，成为
Delta 函数。

5
傅里叶变换的二元性性质。

tri
变换
高斯函数
换是他本身
这是可积的。

此处
换与变换
变换
变换
此处
根据变换
u
狄拉克梳状函数
理解从连续到离散时间的转变
Welcome !!! 欢迎您的下载，资料仅供参考！。

常用傅里叶变换表

咼斯函数exp(-at2)的傅里叶变换是他本身•只有当Re(a) > 0时，这是可积的。
14
cos(af2)
V2/27r\
、也-2丿
15
sill (tzf2ຫໍສະໝຸດ 162a~|a2+47T2/3
a>0
17
1
1 1
J/||
变换本身就是一个公式
S(3)代表狄拉克S函数分布•
这个变换展示了狄拉克S函数的重
要性：该函数是常函数的傅立叶变换
24
1
一加-sgn(H
此处sgn(3)为符号函数：注意此变
换与变换7和24是一致的.
时域信号
弧频率表示的
傅里叶变换
注释
1/oo .
——I血
©(£)^\/2^J_w
日(/)』＞忙叫1
1
a・5(i)+b•h(t.)
“GV) + b・H⑴
线性
2
g(£-a)
e一伽可GJ)
时域平移
3
宀(t)
F(V)
频域平移，变换2的频域对应
4
—
Iff(at)
|a|G(J
如也皿值较大，则畑会收缩
LLg?^]_
1忆
…sine
a
矩形脉冲和归一化的sine函数
10
sinc(at)
1
…rcct
(9
变换10的频域对应。矩形函数是理想的低通滤波器，sine函数是这类滤波器对反因果冲击的响应。
11
sine2(<zt)
1
「(
i]
tri是三角形函数
12
tri(at)
1
严(£
变换12的频域对应

常用傅里叶变换表

常用傅里叶变换表在数学和工程领域，傅里叶变换是一种极其重要的工具，它能够将复杂的时域信号转换为频域表示，从而帮助我们更好地理解和处理各种信号。

而了解常用的傅里叶变换表，则能让我们在解决实际问题时更加得心应手。

傅里叶变换的基本概念可以简单地理解为：任何一个周期函数都可以表示为一系列正弦和余弦函数的叠加。

而傅里叶变换就是找到这些正弦和余弦函数的频率、振幅和相位的过程。

下面我们来看看一些常见的函数及其对应的傅里叶变换：1、单位冲激函数（狄拉克δ函数）单位冲激函数在时域中只在一个瞬间有值，其他时间为 0。

其傅里叶变换是常数 1。

这意味着单位冲激函数包含了所有频率的成分，且各个频率成分的幅度相同。

2、单位阶跃函数单位阶跃函数在 t ＜ 0 时为 0，在t ≥ 0 时为 1。

它的傅里叶变换是1 ／（jω) ＋πδ(ω) ，其中 j 是虚数单位，ω 是角频率，δ(ω) 是狄拉克δ函数。

3、正弦函数对于正弦函数sin(ω₀t) ，其傅里叶变换是π δ(ω ω₀) δ(ω ＋ω₀) 。

这表明正弦函数在频域中只在正负ω₀处有值。

4、余弦函数余弦函数cos(ω₀t) 的傅里叶变换是π δ(ω ω₀) ＋δ(ω ＋ω₀) 。

5、矩形脉冲函数矩形脉冲函数在一个有限的时间区间内有值，其他时间为 0。

其傅里叶变换是一个 sinc 函数，即Sa(ω) ，其中Sa(ω) ＝sin(ω) ／ω 。

6、指数函数指数函数 e^（at) （a ＞ 0）的傅里叶变换是 1 ／（a ＋jω) 。

这些只是常见傅里叶变换中的一部分，掌握它们对于解决信号处理、通信、控制等领域的问题非常有帮助。

在实际应用中，傅里叶变换有着广泛的用途。

例如，在通信系统中，我们需要对信号进行调制和解调，傅里叶变换可以帮助我们理解信号在频域的特性，从而设计更有效的调制方式和滤波器。

在图像处理中，傅里叶变换可以用于图像的滤波、增强和压缩等操作。

通过对傅里叶变换表的熟悉和运用，我们能够从不同的角度分析和处理问题，揭示隐藏在复杂信号背后的规律和特征。

常用傅立叶变换表

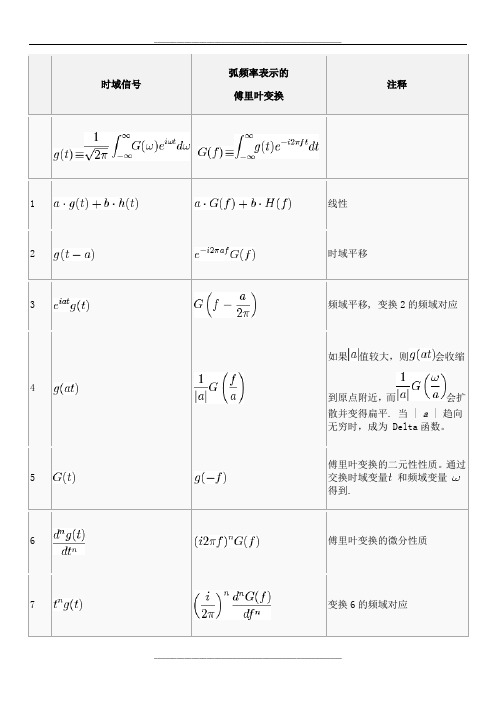
时域信号弧频率表示的傅里叶变换注释1 线性2 时域平移3 频域平移, 变换2的频域对应4如果值较大，则会收缩到原点附近，而会扩散并变得扁平. 当 | a | 趋向无穷时，成为 Delta函数。

5傅里叶变换的二元性性质。

通过交换时域变量和频域变量得到.6 傅里叶变换的微分性质7 变换6的频域对应8表示和的卷积—这就是9 和归一化的10 变换10的频域对应。

矩形函数是理想的低通滤波器，是这类滤波器对冲击的响应。

11 tri是12 变换12的频域对应13 exp( −αt2) 的傅里叶变换是他本身. 只有当 Re(α) > 0时，这是可积的。

141516 a>018 δ(ω) 代表分布. 这个变换展示了狄拉克δ函数的重要性：该函数是常函数的傅立叶变换19 变换23的频域对应20 由变换3和24得到.21 由变换1和25得到，应用了: cos(at) = (e iat + e−iat) / 2.22 由变换1和25得到23 这里, n是一个. δ(n)(ω) 是狄拉克δ函数分布的n阶微分。

这个变换是根据变换7和24得到的。

将此变换与1结合使用，我们可以变换所有。

24 此处sgn(ω)为；注意此变换与变换7和24是一致的.25 变换29的推广.17 变换本身就是一个公式26 变换29的频域对应.27 此处u(t)是; 此变换根据变换1和31得到.28 u(t)是，且a > 0.34 ——有助于解释或理解从连续到的转变.。

傅里叶变换 - 维基百科,自由的百科全书

代表狄拉克δ函数分布.这个变换展示了狄拉克δ函数的重要性：该函数是常函数的傅立叶变换
变换23的频域对应
由变换3和24得到.
由变换1和25得到，应用了欧拉公式:
由变换1和25得到
这里, 是一个自然数. 是狄拉克δ函数分布的
阶微分。这个变换是根据变换7 和24得到的。将此变换与1结合使用，我们可以变换所有多项式。
7/8
三元函数
时域信号
角频率表示的
傅里叶变换
参见
正交变换傅里叶级数连续傅里叶变换离散时间傅里叶变换离散傅里叶变换傅里叶分析拉普拉斯变换小波变换
参考资料
弧频率表示的傅里叶变换
注释
此球有单位半径；fr是频率矢量的量值 {fx,fy,fz}.
1. ^ 林家翘、西格尔著《自然科学中确定性问题的应用数学》，科学出版社，北京。原版书名为C. C. Lin & L. A. Segel, Mathematics Applied to Deterministic Problems in the Natural Sciences, Macmillan Inc., New York, 1974
时频分析变换
小波变换，chirplet转换和分数傅里叶变换试图得到时间信号的频率信息。同时解析频率和时间的能力在数学上受不确定性原理的限制。
傅里叶变换家族
下表列出了傅里叶变换家族的成员。容易发现，函数在时（频）域的离散对应于其像函数在频（时）域的周期性.反之连续则意味着在对应域的信号的非周期性.
来自“/w/index.php?title=傅里叶变换&oldid=24462958”
其中an和bn是实频率分量的振幅。
傅里叶分析最初是研究周期性现象，即傅里叶级数的，后来通过傅里叶变换将其推广到了非周期性现象。理解这种推广过程的一种方式是将非周期性现象视为周期性现象的一个特例，即其周期为无限长。