2016年《电磁场与电磁波》仿真实验.
电磁仿真软件在《电磁场与波》教学中的应用

电磁仿真软件在《电磁场与波》教学中的应用作者:张华美徐立勤来源:《软件导刊》2016年第11期摘要:《电磁场与波》课程理论性强、概念抽象。
通过对典型实例的仿真研究,利用电磁仿真软件设计出适合该课程的实践教学环节,形象演示了电磁波在空间的传播和分布,学生加深了对电磁波传播特性的理解,提高了教学质量。
关键词:教学改革;电磁仿真;XFDTD;MatlabDOIDOI:10.11907/rjdk.161934中图分类号:G434文献标识码:A 文章编号文章编号:16727800(2016)0110212040 引言1873年麦克斯韦尔提出了著名的Maxwell方程组,并预示了电磁波的存在。
1888年,赫兹通过实验测量证明了电磁波的存在。
20世纪初,意大利发明家兼商人马尔可尼用简单的无线电收、发装置实现了跨大西洋的简单电报传输,开辟了无线通信广阔的应用前景。
随着电磁场与波在雷达、通信、导航、遥感、医学、空间等领域应用的不断深入,电磁场与波技术在高等院校电子信息类学科发展和学生培养中的作用日趋重要[1]。
《电磁场与波》课程是电子信息类专业必修的专业基础课,更是后续课程《微波技术》、《天线与电波传播》、《移动通信技术》的基础课 [2]。
《电磁场与波》的前修课程是《大学物理》和《高等数学》,其课程特点是概念抽象、理论深奥、计算复杂、公式繁多,具有“学生难学、教师难教”的特点[3]。
由于电磁场与波看不见摸不着,传统的教学模式又是学生被动接受知识,从而使学生更加难以理解和掌握电磁场与波理论。
为了使学生直观、生动理解电磁场模型,很多高校加入了实验教学环节。
但就“场”类的硬件测量实验来说,实验配套设备昂贵、仪器操作复杂,使用不当可能造成较大的经济损失[4],且“场”类实验需要专门的测试场地,如微波暗室。
有些高校不具备这样的实验条件,即使有微波暗室,也很难在微波暗室中给本科生开设实验课。
因而,“场”类硬件测量实验在很多高校中要么不开设,即使开设的也是一些非常简单的实验,很难满足学生对电磁场与波的深刻理解要求。
2016年《电磁场与电磁波》仿真实验

2016年《电磁场与电磁波》仿真实验D《电磁场与电磁波》仿真实验介绍《电磁场与电磁波》课程属于电子信息工程专业基础课之一,仿真实验主要目的在于使学生更加深刻的理解电磁场理论的基本数学分析过程,通过仿真环节将课程中所学习到的理论加以应用。
受目前实验室设备条件的限制,目前主要利用 MATLAB 仿真软件进行,通过仿真将理论分析与实际编程仿真相结合,以理论指导实践,提高学生的分析问题、解决问题等能力以及通过有目的的选择完成实验或示教项目,使学生进一步巩固理论基本知识,建立电磁场与电磁波理论完整的概念。
本课程仿真实验包含五个内容:一、电磁场仿真软件——Matlab的使用入门二、单电荷的场分布三、点电荷电场线的图像四、线电荷产生的电位五、有限差分法处理电磁场问题目录一、电磁场仿真软件——Matlab的使用入门 (4)二、单电荷的场分布 (10)三、点电荷电场线的图像………………………………………………………………………………………12四、线电荷产生的电位 (14)五、有限差分法处理电磁场问题 (17)实验一电磁场仿真软件——Matlab的使用入门一、实验目的1. 掌握Matlab仿真的基本流程与步骤;2. 掌握Matlab中帮助命令的使用。
二、实验原理(一)MATLAB运算1.算术运算(1).基本算术运算MATLAB的基本算术运算有:+(加)、-(减)、*(乘)、/(右除)、\(左除)、^(乘方)。
注意,运算是在矩阵意义下进行的,单个数据的算术运算只是一种特例。
(2).点运算在MATLAB中,有一种特殊的运算,因为其运算符是在有关算术运算符前面加点,所以叫点运算。
点运算符有.*、./、.\和.^。
两矩阵进行点运算是指它们的对应元素进行相关运算,要求两矩阵的维参数相同。
例1:用简短命令计算并绘制在0≤x≦6范围内的sin(2x)、sinx2、sin2x。
程序:x=linspace(0,6)y1=sin(2*x),y2=sin(x.^2),y3=(sin(x)).^2;plot(x,y1,x, y2,x, y3)(二)几个绘图命令1. doc命令:显示在线帮助主题调用格式:doc 函数名例如:doc plot,则调用在线帮助,显示plot函数的使用方法。
辽工大电磁场与电磁波平板电容器实验报告_实验一

电磁场与电磁波实验报告实验一班级:姓名:学号:日期:实验一静电场问题实例:平板电容器电容计算仿真1.实验目的1.学习Ansoftmaxwell软件的使用方法。
2.复习电磁学相关的基本理论。
3.通过软件的学习掌握运用Ansoft Maxwell运行电磁场仿真的流程。
4.通过对对平板电容器电容计算仿真实验进一步熟悉Ansoft Maxwell软件的应用。
2.实验内容1.学习Ansoftmaxwell有限元分析步骤2.会用Ansoftmaxwell后处理器和计算器对仿真结果分析3.对圆柱体电容器电容仿真计算结果与理论结果值进行比较3.实验步骤平板电容器模型描述:上下两极板尺寸:25mm×25mm×2mm,材料:pec(理想导体)介质尺寸:25mm×25mm×1mm,材料:mica(云母介质)激励:电压源,上极板电压:5V,下极板电压:0V。
要求计算该电容器的电容值1.建模(Model)Project > Insert Maxwell3D DesignFile>Save as>Planar Cap(工程命名为“Planar Cap”)选择求解器类型:Maxwell > Solution Type>Electric>Electrostatic(静电的)创建下极板六面体Draw > Box(创建下极板六面体)下极板起点:(X,Y,Z)>(0,0,0)坐标偏置:(dX,dY,dZ)(25,25,0)坐标偏置:(dX,dY,dZ)>(0, 0, 2)将六面体重命名为DownPlateAssign Material>pec(设置材料为理想导体perfect conductor)创建上极板六面体Draw > Box(创建下极板六面体)上极板起点:(X,Y,Z)>(0, 0, 3)坐标偏置:(dX,dY,dZ)>(25, 25,0)坐标偏置:(dX,dY,dZ)>(0, 0, 2)将六面体重命名为UpPlateAssign Material >pec(设置材料为理想导体perfect conductor)创建中间的介质六面体Draw > Box(创建下极板六面体)介质板起点:(X,Y,Z)>(0, 0, 2)坐标偏置:(dX,dY,dZ)>(25, 25,0)坐标偏置:(dX,dY,dZ)>(0, 0,1)将六面体重命名为mediumAssign Material > mica(设置材料为云母mica,)图3-12.创建计算区域(Region)Padding Percentage:0%图3-2电容器中电场分布的边缘效应忽略电场的边缘效应(fringing effect)3.设置激励(Assign Excitation)选中上极板UpPlate,Maxwell3D> Excitations > Assign(计划,分配)>Voltage> 5V选中下极板DownPlate,Maxwell3D> Excitations > Assign >Voltage> 0V4.设置计算参数(AssignExecutive Parameter)Maxwell 3D> Parameters > Assign >Matrix(矩阵)> Voltage1,Voltage25.设置自适应计算参数(Create Analysis Setup)Maxwell3D> Analysis Setup > Add Solution Setup最大迭代次数:Maximum number of passes > 10误差要求:Percent Error>1%每次迭代加密剖分单元比例:Refinement per Pass>50%图3-36. Check & Run7.查看结果Maxwell3D>Reselts>Solution data > Matrix 电容值: -31.543pF图3-4图3-54.实验结果由实验数据可得电容为-31.543PF平板式电容计算公式:C=ε *ε0* S/d;ε0真空介电常数8.86×10(-12方)单位F/m;5.心得体会在实验之前我以为这个实验一定十分简单。
《电磁场与电磁波》仿真实验

年《电磁场与电磁波》仿真实验————————————————————————————————作者:————————————————————————————————日期:《电磁场与电磁波》仿真实验2016年11月《电磁场与电磁波》仿真实验介绍《电磁场与电磁波》课程属于电子信息工程专业基础课之一,仿真实验主要目的在于使学生更加深刻的理解电磁场理论的基本数学分析过程,通过仿真环节将课程中所学习到的理论加以应用。
受目前实验室设备条件的限制,目前主要利用MATLAB 仿真软件进行,通过仿真将理论分析与实际编程仿真相结合,以理论指导实践,提高学生的分析问题、解决问题等能力以及通过有目的的选择完成实验或示教项目,使学生进一步巩固理论基本知识,建立电磁场与电磁波理论完整的概念。
本课程仿真实验包含五个内容:一、电磁场仿真软件——Matlab的使用入门二、单电荷的场分布三、点电荷电场线的图像四、线电荷产生的电位五、有限差分法处理电磁场问题目录一、电磁场仿真软件——Matlab的使用入门 (4)二、单电荷的场分布 (10)三、点电荷电场线的图像 (12)四、线电荷产生的电位 (14)五、有限差分法处理电磁场问题 (17)实验一电磁场仿真软件——Matlab的使用入门一、实验目的1. 掌握Matlab仿真的基本流程与步骤;2. 掌握Matlab中帮助命令的使用。
二、实验原理(一)MATLAB运算1.算术运算(1).基本算术运算MATLAB的基本算术运算有:+(加)、-(减)、*(乘)、/(右除)、\(左除)、^(乘方)。
注意,运算是在矩阵意义下进行的,单个数据的算术运算只是一种特例。
(2).点运算在MATLAB中,有一种特殊的运算,因为其运算符是在有关算术运算符前面加点,所以叫点运算。
点运算符有.*、./、.\和.^。
两矩阵进行点运算是指它们的对应元素进行相关运算,要求两矩阵的维参数相同。
例1:用简短命令计算并绘制在0≤x≦6范围内的sin(2x)、sinx2、sin2x。
电磁场与电磁波虚拟仿真实验系统的设计与开发

第42卷 第5期2020年10月电气电子教学学报JOURNALOFEEEVol.42 No.5Oct.2020收稿日期:2019 03 21;修回日期:2019 10 27基金项目:中国民航大学通信工程专业“双语/全英文”试点班,2016年获批校级示范建设课程“电磁场与电磁波”(CAUC-2016-B1-25)作者简介:万棣(1968 ),女,学士,副教授,主要研究图像处理方向,E mail:dwan@cauc.edu.cn电磁场与电磁波虚拟仿真实验系统的设计与开发万 棣,范 懿(中国民航大学电子信息与自动化学院,天津300300)摘要:电磁场与电磁波虚拟仿真实验系统的设计,采用三维可视化技术,运用3dmax进行实体建模、Unity3d编辑动画及控制GUI界面,实现实验操作步骤。
该系统打破时间、空间的局限,可以通过网络本地下载,方便的利用手持式设备(平板电脑和手机等)进行移动式、开放学习,从而达到让学生真正成为能动性高的学习主体,激发学生的主动学习兴趣。
关键词:电磁场与电磁波实验;虚拟仿真;网络共享中图分类号:G642.423;O441.4 文献标识码:B 文章编号:1008 0686(2020)05 0130 04DesignandDevelopmentoftheVirtualSimulationExperimentalSgsremforElectomagneticFieldElectromagneticWavesWANDi,FANYi(CollegeofElectronicInformationandAutomation,CivilAviationUniversityOfChina,Tianjin300300,China)Abstract:Forthevirtualsimulationsystemfortheelectromagneticfieldandelectromagneticwavesexperimentsys tem,3Dvisualizationtechnology?isadoptedin?solidmodeling,editinganimationandGUIinterfacecontrol,inordertorealizeexperimentaloperationsteps.Thesystembreaksthelimitationoftimeandspace.Itcanbedown loadedlocallythroughthenetwork,andcanmakeuseofhand helddevices(tabletcomputersandmobilephones)forMobileopenlearning,soastoenablestudentstotrulybecomeactivelearningsubjects,andstimulatestudents'interestinactivelearning.Keywords:electromagneticfieldandelectromagneticwavesexperiment;virtualsimulation;networksharing0 引言“电磁场与电磁波”课程理论性强,十分抽象,所以实验教学的作用十分重要,即使学生在实验室做实验,由于很难感官上感受到电磁波的存在,不易了解和掌握电磁场和电磁波的现象和基本规律[1~2]。
电磁场与电磁波实验报告.

电磁场与电磁波实验报告.中南⼤学信息科学与⼯程学院课题名称:电磁场与电磁波实验报告信息科学与⼯程学院通信⼯程1201 学班学姓院:级:号:名:0909120927 苏⽂强指导⽼师:陈宁实验⼀电磁波反射实验⼀实验⽬的1. 掌握微波分光仪的基本使⽤⽅法;2. 了解3cm 信号源的产⽣、传输及基本特性;3. 验证电磁波反射定律。
⼆预习内容电磁波的反射定律三实验原理微波与其它波段的⽆线电波相⽐具有:波长极短,频率很⾼,振荡周期极短的特点。
微波传输具有似光特性,其传播为直线传播。
电磁波在传播过程中如遇到障碍物,必定要发⽣反射。
本实验以⼀块⼤的⾦属板作为障碍物来研究当电磁波以某⼀⼊射⾓投射到此⾦属板上所遵循的反射定律,即:反射电磁波位于⼊射电磁波和通过⼊射点的法线所决定的平⾯上反射电磁波和⼊射电磁波分别位于法线两侧;反射⾓θr 等于⼊射⾓θi。
原理如图1.1所⽰。
图1.1四实验内容与步骤1. 调整微波分光仪的两喇叭⼝⾯使其互相正对,它们各⾃的轴线应在⼀条直线上,指⽰两喇叭位置的指针分别指于⼯作平台的0-180 刻度处。
将⽀座放在⼯作平台上,并利⽤平台上的定位销和刻线对正⽀座,拉起平台上四个压紧螺钉旋转⼀个⾓度后放下,即可压紧⽀座。
2. 将反射全属板放到⽀座上,应使⾦属板平⾯与⽀座下⾯的⼩圆盘上的90-90 这对刻线⼀致,这时⼩平台上的0 刻度就与⾦属板的法线⽅向⼀致。
将⾦属板与发射、接收喇叭锁定,以保证实验稳定可靠。
3. 打开信号源开关,将三厘⽶固态信号源设置在:“电压”和“等幅”档。
4. 调节可变衰减器,使得活动臂上微安表的读数为满量程的80%左右。
5. 转动微波分光仪的⼩平台,使固定臂指针指在刻度为30 度处,这个⾓度数就是⼊射⾓度数,然后转动活动臂,使得表头指⽰最⼤,此时活动臂上指针所指的刻度就是反射⾓度数,记下该⾓度读数。
如果此时表头指⽰太⼤或太⼩,应调整微波分光仪中的可变衰减器或晶体检波器,使表头指⽰接近满量程的80%做此项实验。
电磁场仿真实验报告

电磁场仿真实验报告第一篇:电磁场仿真实验报告电磁场仿真实验报告电气工程学院 2011级2班 2011302540056 黄涛实验题目:有一极长的方形金属槽,边宽为1m,除顶盖电位为100sin(pi*x)V外,其它三面的电位均为零,试用差分法求槽内点位的分布。
1、有限差分法的原理它的基本思想是将场域划分成网格,用网格节点的差分方程近似代替场域内的偏微分方程,然后解这些差分方程求出离散节点上位函数的值。
一般来说,只要划分得充分细,其结果就可达到足够的精确度。
差分网格的划分有多种不同的方式,这里将讨论二维拉普拉斯方程的正方形网格划分法。
如下图1所示,用分别平行与x,y轴的两组直线把场域D划分成许多正方行网格,网格线的交点称为节点,两相邻平行网格线间的距离h称为步距。
用表示节点处的电位值。
利用二元函数泰勒公式,可将与节点(xi,yi)直接相邻的节点上的电位值表示为上述公式经整理可得差分方程这就是二维拉普拉斯方程的差分格式,它将场域内任意一点的位函数值表示为周围直接相邻的四个位函数值的平均值。
这一关系式对场域内的每一节点都成立,也就是说,对场域的每一个节点都可以列出一个上式形式的差分方程,所有节点的差分方程构成联立差分方程组。
已知的边界条件经离散化后成为边界点上已知数值。
若场域的边界正好落在网格点上,则将这些点赋予边界上的位函数值。
一般情况下,场域的边界不一定正好落在网格节点上,最简单的近似处理就是将最靠近边界点的节点作为边界节点,并将位函数的边界值赋予这些节点。
2、差分方程的求解方法:简单迭代法先对静电场内的节点赋予迭代初值,其上标(0)表示初始近似值。
然后再按下面的公式:进行多次迭代(k=0,1,2,3…)。
当两次邻近的迭代值差足够小时,就认为得到了电位函数的近似数值解。
实验程序: a=zeros(135,135);for i=1:135 a(i,i)=1;end;for i=1:7 a(15*i+1,15*i+2)=-0.25;a(15*i+1,15*i+16)=-0.25;a(15*i+1,15*i-14)=-0.25;end for i=1:7 a(15*i+15,15*i+14)=-0.25;a(15*i+15,15*i+30)=-0.25;a(15*i+15,15*i)=-0.25;enda(1,2)=-0.25;a(1,16)=-0.25;a(121,122)=-0.25;a(121,106)=-0.25;a(135,134)=-0.25;a(135,120)=-0.25;a(15,14)=-0.25;a(15,30)=-0.25;for i=2:14 a(i,i-1)=-0.25;a(i,i+1)=-0.25;a(i,i+15)=-0.25;end for i=122:134 a(i,i-1)=-0.25;a(i,i+1)=-0.25;a(i,i-15)=-0.25;end for i=1:7 for j=2:14;a(15*i+j,15*i+j-1)=-0.25;a(15*i+j,15*i+j+1)=-0.25;a(15*i+j,15*i+j+15)=-0.25;a(15*i+j,15*i+j-15)=-0.25;end end b=a^(-1);c=zeros(135,1);for i=121:135 c(i,1)=25;end d=b*c;s=zeros(11,17);for i=2:16 s(11,j)=100*sin(pi.*i);end for i=1:9 for j=1:15 s(i+1,j+1)=d(15*(i-1)+j,1);end end subplot(1,2,1),mesh(s)axis([0,17,0,11,0,100])subplot(1,2,2),contour(s,32)实验结果如下:***010***65432151015以上是划分为135*135个网格的过程,同理可有如下数据:(1)将题干场域划分为16个网格,共有25各节点,其中16个边界的节点的电位值是已知,现在要解的是经典场域内的9个内节点的电位值。
中南大学电磁场与电磁波实验报告

。
三、实验步骤
1、连接仪器 按下图连接仪器。
2、校正仪器 使两喇叭口面互成 90 度。
3、固定半透射板 半透射板与两喇叭轴线互成 45 度。
4、固定反射板 将读数机构通过它本身上带有的两个螺钉旋入底座上,使其固定在底座上, 再插上反射扳,使固定反射板的法线与接受喇叭的轴线一致,可移反射板的 法钱与发射喇叭轴线一致。
二 实验原理
待测介质板
A(固定反射板)
发射喇叭
半透射板
接收喇叭
B(可移反射板)
图 4.1 介质参数测量原理图 在上一个实验的基础上,在固定反射板前放一块待测介质板,其相对介电
常数为 r ,厚度为 d,这样固定反射板的电磁波的波程差将会增加,为了得到新
的极小点位置,必需将可移动反射板向右移 l ,待测介质板的相对介电常数 r 与
(2)引起误差的主要原因,除了客观因素(实验器材本身)和人为 因素(读数不准确)外,还包括 1.实验开始时喇叭口校准不到位 2.实验过程中不小心造成的已校准过的喇叭口的偏移 3.来自其他实验组的干扰
(3)实验过程中测量所得的角度是反射光最强的处对应的角度,角 度的偏差是由(3)中所述的误差原因造成的。
(4)实验过程中测量所得的电流表读数是在反射光一侧的电流最大 值,代表反射光的强度。反射光在传播过程中会有损耗,所以 反射光强度不严格等于入射光的情况是合理存在的。若反射光 强度大于入射光强度,极可能是其他实验组产生干扰而造成的。
实验二 单缝衍射实验
一、实验目的
1.了解微波分光仪的结构,学会调整它并能用它进行实验; 2.进一步认识电磁波的波动性,测量并验证单缝衍射现象的规律。
5、调节衰减器 按信号源操作规程接通电源,调节衰减器使信号电平读数指示合适值。
华中科技大学《电磁场与电磁波》课程仿真实验报告

华中科技⼤学《电磁场与电磁波》课程仿真实验报告.《电磁场与电磁波》课程仿真实验报告学号*********姓名Crainax专业光学与电⼦信息学院院(系)******2016 年11⽉27⽇1.实验⽬的1)理解均匀波导中电磁波的分析⽅法,TEM/TE/TM 模式的传输特性;2)了解HFSS 仿真的基本原理、操作步骤;3)会⽤HFSS 对⾦属波导的导波特性进⾏仿真;4)画出波导主模的电磁场分布;5)理解波导中的模式、单模传输、⾊散与截⽌频率等概念。
2.实验原理2.1导波原理如图1,z轴与⾦属波导管的轴线重合。
假设:1)波导管内填充的介质是均匀、线性、各向同性的;2)波导管内⽆⾃由电荷和传导电流;3)波导管内的场是时谐场。
图1 矩形波导以电场为例⼦,将上式代⼊亥姆霍兹⽅程?2E+k2E=0,并在直⾓坐标内展开,即有:其中?k c表⽰电磁波在与传播⽅向相垂直的平⾯上的波数。
如果导波沿z⽅向传播,则对波导中传播的电磁波进⾏分析可知:1)场的横向分量可由纵向分量表⽰;2)既满⾜亥姆霍兹⽅程有满⾜边界条件的解很多,每个解对应⼀个波形(或称之为模式)3)k c是在特定边界条件下的特征值,当相移常数β=0 时,意味着波导系统不在传播,此时k c=k,k c称为截⽌波数。
2.2 矩形波导中传输模式的纵向传输特性波导中的电磁波在传输⽅向的波数β由下式给出:式中k为⾃由空间中同频率的电磁波的波数。
要使波导中存在导波,则β必须为实数,即>或<>如上式不满⾜,则电磁波不能在波导内传输,即截⽌。
矩形波导中TE10模的截⽌波长最长,故称它为最低模式,其余模式均称为⾼次模。
由于TE10模的截⽌波长最长且等于2a,⽤它来传输可以保证单模传输。
当波导尺⼨给定且有a>2b时,则要求电磁波的⼯作波长满⾜a<λ<2a λ>2b当⼯作波长给定时,则波导尺⼨必须满⾜<<<3.实验内容在HFSS中完成圆波导的设计与仿真,要求画出电场分布,获得⾊散曲线。
电磁场与电磁波实验报告

电磁场与电磁波实验报告班级:学号:姓名:实验一:验证电磁波的反射和折射定律1学时1、实验目的验证电磁波在媒质中传播遵循反射定理及折射定律;1研究电磁波在良好导体表面上的全反射;2研究电磁波在良好介质表面上的反射和折射;3研究电磁波全反射和全折射的条件;2、实验原理电磁波在传播过程中如遇到障碍物,必定要发生反射,本处以一块大的金属板作为障碍物来研究当电磁波以某一入射角投射到此金属板上所遵循的反射定律,即反射线在入射线和通过入射点的法线所决定的平面上,反射线和入射线分居在法线两侧,反射角等于入射角;3、实验结果:图1.1 电磁波在介质板上的折射图1.2 电磁波在良导体板上的反射实验二:电磁波的单缝衍射实验、双缝干涉实验;1、实验目的1研究当一平面波入射到一宽度和波长可比拟的狭缝时,就要发生衍射的现象;在缝后面出现的衍射波强度不是均匀的,中央最强;2研究当一平面波垂直入射到一金属板的两条狭线上,则每一条狭缝就是次级波波源;由两缝发出的次级波是相干波,因此在金属板的背后面空间中,将产生干涉现象;2、实验原理单缝衍射实验原理见下图 5:当一平面波入射到一宽度和波长可比拟的狭缝时,就要发生衍射的现象;在缝后面将出现的衍射波强度不是均匀的,中央最强,同时也最宽,在中央的两侧衍射波强度迅速减小,直至出现衍射波强度的最小值,即一级极小,此时衍射角为,其中λ是波长,λ是狭缝宽度;两者取同一长度单位,然后,随着衍射角增大,衍射波强度又逐渐增大,直至一级极大值,角度为:图 5 单缝衍射实验原理图如图 8:当一平面波垂直入射到一金属板的两条狭缝上时,则每一条狭缝就是次级波波源,由于两缝发出的次级波是相干波,因此在金属板的背后面空间中,将产生干涉现象;当然电磁波通过每个缝也有狭缝现象;因此实验将是衍射和干涉两者结合的结果;为了只研究主要是由于来自双缝的两束中央衍射波相互干涉的结果,令双缝的缝宽α接近入,例如:,这时单缝的一级极小接近53°;因此取较大的b,则干涉强受单缝衍射影响大;干涉加强的角度为:干涉减弱的角度为:3、实验结果图2.1 单缝衍射的I-α曲线图2.2双缝干涉的I-α曲线实验三:布朗格衍射的实验1、实验目的本实验是仿造X射线入射真实晶体发生衍射的基本原理,人为的制作了一个方形点阵的模拟晶体,以微波代替X射线,使微波向模拟晶体入射,观察从不同晶面上点阵的反射波产生干涉应符合的条件;这个条件就是布拉格方程;1掌握100面,110面点阵的反射波产生干涉的条件,得出布拉格方程;2了解直线极化和圆极化波特性参数的测试方法;2、实验原理任何的真实晶体,都具有自然外形和各向异性的性质,这和晶体的离子、原子或分子在空间按一定的几何规律排列密切相关;晶体内的离子、原子或分子占据着点阵的结构, 两相邻结点的距离叫晶体的晶格常数;真实晶体的晶格常数约在10−8厘米的数量级,X 射线的波长与晶体的常数属于同一数量级,实际上晶体是起着衍射光栅的作用,因此可以利用 X 射线在晶体点阵上的衍射现象来研究晶体点阵的间距和相互位置的排列,以达到对晶体结构得了解;本实验是仿造 X 射线入射真实晶体发生衍射的基本原理,人为的制作了一个方形点阵的模拟晶体,以微波代替 X 射线,使微波向模拟晶体入射,观察从不同晶面上点阵的反射波产生干涉应符合的条件,这个条件就是布拉格方程;它是这样说的,当波长为入的平面波射到间距为α的晶面上,入射角为Θ°,当满足条件时n为整数发生衍射;衍射线在所考虑的晶面反射线方向;在布拉格衍射实验中采用入射线与晶面的夹角即通称的入射角,是为了在实验时方便,因为当被研究晶面的法线与分光仪上度盘的 0 度刻度一致时,入射线与反射线的方向在度盘上有相同的示数,不容易搞错,操作方便;3、实验结果图3.1 布拉格衍射I-θ关系曲线由实验数据可得,两侧发生衍射的角度大约在34°和65°附近;根据布拉格方程nλ=2aCOSθ,将λ=32mm,a=40mm代入得:当n=1时,θ=66.42°;当n=2时,θ=36.87°.实验测得数据与理论计算值比较接近,可验证布拉格方程;69°附近产生的峰值可能是由其他实验组影响造成的,不计入考虑;实验四:均匀无损耗媒质参量的测量2学时1、实验目的了解电磁波在真空中传播特性和相干原理;1在学习均匀平面电磁波的基础上,观察电磁波传播特性,E、H、S互相垂直;2推导相干波理论数学模型,自行调节测量仪器,测量基本参量;3测定自由空间内电磁波波长λ、频率f,并确定电磁波的相位常数β和波速υη的测量;4了解电磁波的其他参量,如波阻抗5利用相干波接点位移法推导测量均匀无损耗媒质参量的ε和μ的数学模型6了解均匀无损耗媒质参量λ、β、的差别7熟悉均匀无损耗媒质分界面对电磁波的反射和折射的特性;2、实验原理迈克尔逊干涉试验的基本原理见下图 13 所示:在平面波前进的方向上放置一个成45°的半透射板,由于该板的作用,将入射波分成两束波:一束由于反射向 A 方向传播;另一束透过半透射板向B 方向传播;由于A﹑B 处全反射板的作用,两列波就再次回到半透射板并到达接收喇叭处,于是接收喇叭收到两束同频率且振动方向一致的两个波;如果这两个波的位相差为2π的整数倍,则干涉加强;当相位差为π的奇数倍则干涉减弱;因此在 A 处放一固定板,让 B 处的反射板移动,当表头指示从一次极小变到又一次极小时,则 B 处的反射板就移动λ⁄2的距离,因此有这个距离就可求得平面波的波长;3、实验结果()()mm 32.341-443.5-91.5621n 0L -3L 2=⨯=-⨯=λ实验五:利用微波衰减测量湿度、厚度2学时1、实验目的学习介质特性参量:相移常数和衰减常数的测量方法,自行推导出介质厚度和湿度的数学模型,设计实验方法;1了解被测量的物质所用波为TEM 波,TEM 波产生的条件; 2相移常数和衰减常数测量方法; 3湿度、厚度测量方法 4信号处理方法 2、实验原理同迈克尔干涉实验原理 3、实验结果491.5602.5592.4067.4172.2357.2643.532.13-+-+-+-=91.2=n33221100L L L L L L L L L -'+-'+-'+-'=∆()()mm80.271-432.13-2.05521n 0-32ˊ=⨯=-''⨯'L L λ()d L /1/∆+= λλ()d /91.21/32.3480.27+=mmd 6.12≈。
电磁场与电磁波Matlab仿真
2-28.两无限大平行导体平面,相距为 a,上下极板电位均为 0.它们之间有一与
z 轴平行的线电荷 (C/m) ,位于(0,d)处。求板间电位分布。
解:得到最后得电位解为:
0
取 a= =10;
n | x| 1 n n sin( d )sin( y )e a a a n 1 n
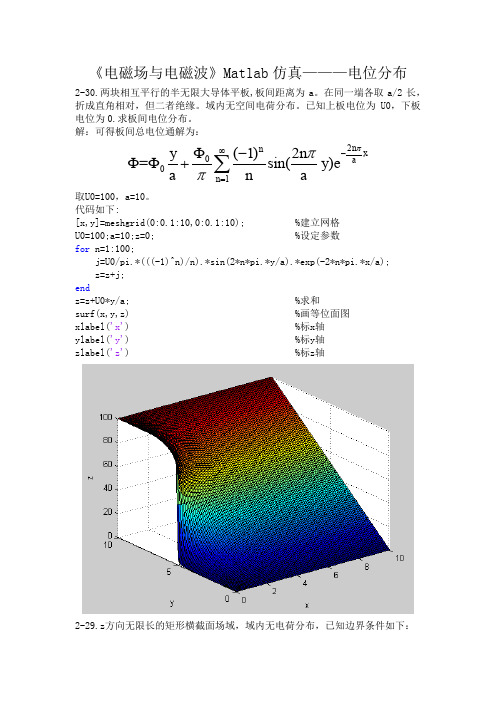
《电磁场与电磁波》Matlab 仿真———电位分布
2-30.两块相互平行的半无限大导体平板,板间距离为 a。在同一端各取 a/2 长, 折成直角相对,但二者绝缘。域内无空间电荷分布。已知上板电位为 U0,下板 电位为 0.求板间电位分布。 解:可得板间总电位通解为:
2 n x y 0 (1) n 2n a = 0 sin( y ) e a n1 n a
cosh(
n n x)sin( y) b b
取U0=100,a=10,b=10。 代码如下: [x,y]=meshgrid(0:0.1:10,0:0.1:10); %建立网格 U0=100;a=10;b=10;z=0; %设定参数 for i=1:100; n=2*i-1; j=4*U0/pi*(1/(n*cosh(n*pi*a/b)).*(cosh(n*pi*x/b)).*(sin(n*pi*y/b))); z=z+j; end %求和 surf(x,y,z) %画等位面图 xlabel('x') %标x坐标 ylabel('y') %标y坐标 zlabel('z') %标z坐标
2-29.z方向无限长的矩形横截面场域,域内无电荷分布,已知边界条件如下:
| y 0 | y b 0 ,
|x 0 0 , |x a :
电磁场与电磁波实验报告

电磁场与电磁波实验报告
实验目的:通过实验探究电磁场和电磁波的相关性质,加深对电磁
学原理的理解,掌握相关实验操作技巧。
一、实验仪器与材料
本次实验所用仪器设备包括:
1. 电磁场产生装置;
2. 电场仪表;
3. 磁场仪表;
4. 信号发生器;
5. 示波器等。
二、实验步骤
1. 观察并记录电磁场产生装置的工作原理,了解电磁场的形成过程;
2. 利用电场仪表和磁场仪表分别测量电磁场的电场分量和磁场分量,并记录实验数据;
3. 通过调节信号发生器的频率和幅度,产生不同频率的电磁波,并
利用示波器观察并记录波形;
4. 将电磁场和电磁波的实验数据整理,形成图表和曲线。
三、实验结果与分析
根据实验数据,我们可以观察到电磁场和电磁波在不同频率下的表现。
电磁场的电场分量和磁场分量呈现出明显的变化规律,频率越高,波动频率越密集;而电磁波的波形随着频率的增加呈现出不同的特征,频率在一定范围内变化会引起频率响应的变化。
四、结论与思考
通过本次实验,我们深入了解了电磁场和电磁波的相关特性,了解
到电磁场和电磁波在不同频率下的表现差异。
同时,我们也发现了实
验过程中需要注意的细节问题,如仪器的校准和操作注意事项等。
通
过实验,我们不仅加深了对电磁学理论知识的理解,也提高了实验操
作的技巧和分析能力。
综上所述,电磁场与电磁波实验为我们提供了一个直观、具体的实
践平台,促进了电磁学知识的学习与应用,为我们日后的研究与工作
打下了坚实的基础。
电磁场与电磁波静电场物理模拟实验报告

电磁场与电磁波实验报告实验项目:__ 静电场物理模拟_____________________一、实验目的要求1. 理解物理模拟法的实验原理和应用条件。
2. 学习用物理模拟法研究静电场。
3. 加深对静电场场强和电位的理解。
二、实验内容1. 了解装置电路及实验原理。
2. 描绘矩形水槽薄水层中两个点电极产生的二维静电场。
三、实验仪器与软件矩形水槽、坐标纸两张、稳压电源和电压表,模拟电极、导线、固定支架。
四、实验原理理论上讲,如果知道了电荷的分布,就可以确定静电场的分布。
电场既可以用电场强度0E(电力线)来描述,又可以用电势U (等势面、线)来描述。
由于标量的测量和计算比矢量简便,因此,人们更愿意用电势来描述电场。
在给定条件下,确定系统静电场分布的方法,一般有解析法﹑数值模拟法和物理模拟法。
解析法只能求解一些简单的问题;数值模拟法,也就是数值计算方法,它能解决一些复杂的问题,虽计算量很大,但在计算机的帮助下,目前已经得到长足的发展,应用很广,数值模拟也有不足之处,对于一些形状比较复杂的带电体或电极周围静电场的分布,求解也非常困难。
模拟法作为一种重要的实验研究方法,它本质上是用一种易于实现﹑便于测量的物理状态或过程来模拟另一种不易实现﹑不便测量的物理状态或过程。
其条件是两种状态或过程有两组一一对应的物理量,并且满足相同形式的数学规律。
由于静电场中不存在电流,一般磁电式仪表,在有电流时才会有反应,因此难以确定静电场的等势线。
由于在一定条件下电介质中的稳恒电流场与静电场服从相同的数学规律,可以用恒定电流的电场模拟静电场。
如接到直流电源两端的小圆柱形电极之间形成的恒定电场,可以用来模拟等量异种电荷之间的静电场。
静电场与稳恒电流场的对应关系为导体上的电荷 ±Q电场强度 E介电常数极间电流±I 电场强度E电导率电位移 D=E无电荷区0E dS ε⋅=⎰电位满足 02=∇U电流密度 J=E无源区0E dS σ⋅=⎰电位满足 02=∇U根据上表中的对应关系可知,要想在实验上用稳恒电流场来模拟静电场,需要满足下面三个条件:⑴电极系统与导体几何形状相同或相似; ⑵导电质与电介质分布规律相同或相似;⑶电极的电导率远大于导电质的电导率,以保证电极表面为等势面。
2016年《电磁场与电磁波》仿真实验

《电磁场与电磁波》仿真实验2016年11月《电磁场与电磁波》仿真实验介绍《电磁场与电磁波》课程属于电子信息工程专业基础课之一,仿真实验主要目的在于使学生更加深刻的理解电磁场理论的基本数学分析过程,通过仿真环节将课程中所学习到的理论加以应用。
受目前实验室设备条件的限制,目前主要利用MATLAB 仿真软件进行,通过仿真将理论分析与实际编程仿真相结合,以理论指导实践,提高学生的分析问题、解决问题等能力以及通过有目的的选择完成实验或示教项目,使学生进一步巩固理论基本知识,建立电磁场与电磁波理论完整的概念。
本课程仿真实验包含五个内容:一、电磁场仿真软件——Matlab的使用入门二、单电荷的场分布三、点电荷电场线的图像四、线电荷产生的电位五、有限差分法处理电磁场问题目录一、电磁场仿真软件——Matlab的使用入门 (4)二、单电荷的场分布 (10)三、点电荷电场线的图像 (12)四、线电荷产生的电位 (14)五、有限差分法处理电磁场问题 (17)实验一电磁场仿真软件——Matlab的使用入门一、实验目的1. 掌握Matlab仿真的基本流程与步骤;2. 掌握Matlab中帮助命令的使用。
二、实验原理(一)MATLAB运算1.算术运算(1).基本算术运算MATLAB的基本算术运算有:+(加)、-(减)、*(乘)、/(右除)、\(左除)、^(乘方)。
注意,运算是在矩阵意义下进行的,单个数据的算术运算只是一种特例。
(2).点运算在MATLAB中,有一种特殊的运算,因为其运算符是在有关算术运算符前面加点,所以叫点运算。
点运算符有.*、./、.\和.^。
两矩阵进行点运算是指它们的对应元素进行相关运算,要求两矩阵的维参数相同。
例1:用简短命令计算并绘制在0≤x≦6范围内的sin(2x)、sinx2、sin2x。
程序:x=linspace(0,6)y1=sin(2*x),y2=sin(x.^2),y3=(sin(x)).^2;plot(x,y1,x, y2,x, y3)(二)几个绘图命令1. doc命令:显示在线帮助主题调用格式:doc 函数名例如:doc plot,则调用在线帮助,显示plot函数的使用方法。
电磁场与电磁波实验6分布交指型微带滤波器设计

电磁场与电磁波实验实验报告姓名:学号:班级:上课时间:周二10-12节实验名称:分布交指型微带滤波器设计一、实验目的1.了解微波交指滤波器的概念2、掌握MWO EM structure仿真方法3、掌握在原理图添加EM Structure方法二、实验内容与要求内容:根据样例微波交指滤波器 EM仿真设计。
观察EM仿真的三维动画输出,观察勾选显示电流(电场)方向后仿真图形差别学会在原理图引入EM结构(子电路一种)利用Emsight可以对多种场进行分析,例如微波天线,大家可以探索下。
实验报告列出主要步骤及最后写出对这段MWO软件微波仿真的心得体会。
包括学到什么,这个软件还有哪些不足。
要求:1.熟悉利用MWO软件进行EM仿真。
2.熟悉交指滤波器特性3.了解WMO原理图引入EM 结构方法。
4.熟悉EM结构中求解电流分布和电场分布的方法三、实验程序与结果主要步骤:1.创建EM structure2.建立an enclosure3.创建层4.过孔建模观察三维结构5.定义端口配置计算网格6.观察电流密度和电场强度7.执行频率扫描(AFS) 将EM structure添加到原理图并仿真需要注意的问题:选择color时最好选择不一样的color,不然颜色混合在一起,没办法看清楚内部结构。
侧边边界条件软件上只有一个完美导体,要想和教材一致就需要自己手动插入金导体,并设置好参数。
在选择时要记得之前在添加过孔时我们将属性调到了via,在后面完成滤波器布线时我们一定要记住将属性调回conductor,不然会导致实验失败。
四、实验结果分析实验结果与教材基本一致,达到了预期的结果,从实验中可以发现如何通过观察仿真结果来逐渐逼近频率范围。
最终添加子电路图得到的仿真结果似乎和添加EM结构仿真得到的结果没有不同。
五、实验问题解答与体会体会:本次使用MWO软件进行微波仿真我体会到该软件是一款功能十分强大的软件,能够完成通信领域电磁场与微波方面的许多实验,并且不需要许多昂贵的设备,只需要一台计算机即可。
电磁场与电磁波实验报告之令狐文艳创作

电磁场与电磁波实验报告令狐文艳班级:学号:姓名:实验一:验证电磁波的反射和折射定律(1学时)1、实验目的验证电磁波在媒质中传播遵循反射定理及折射定律。
(1)研究电磁波在良好导体表面上的全反射。
(2)研究电磁波在良好介质表面上的反射和折射。
(3)研究电磁波全反射和全折射的条件。
2、实验原理电磁波在传播过程中如遇到障碍物,必定要发生反射,本处以一块大的金属板作为障碍物来研究当电磁波以某一入射角投射到此金属板上所遵循的反射定律,即反射线在入射线和通过入射点的法线所决定的平面上,反射线和入射线分居在法线两侧,反射角等于入射角。
3、实验结果:图1.1 电磁波在介质板上的折射反射角32°34°36°44°47°52°37°61°图1.2 电磁波在良导体板上的反射实验二:电磁波的单缝衍射实验、双缝干涉实验。
1、实验目的(1)研究当一平面波入射到一宽度和波长可比拟的狭缝时,就要发生衍射的现象。
在缝后面出现的衍射波强度不是均匀的,中央最强;(2)研究当一平面波垂直入射到一金属板的两条狭线上,则每一条狭缝就是次级波波源。
由两缝发出的次级波是相干波,因此在金属板的背后面空间中,将产生干涉现象。
2、实验原理单缝衍射实验原理见下图 5:当一平面波入射到一宽度和波长可比拟的狭缝时,就要发生衍射的现象。
在缝后面将出现的衍射波强度不是均匀的,中央最强,同时也最宽,在中央的两侧衍射波强度迅速减小,直至出现衍射波强度的最小值,即一级极小,此时衍射角为,其中λ是波长,λ是狭缝宽度。
两者取同一长度单位,然后,随着衍射角增大,衍射波强度又逐渐增大,直至一级极大值,角度为:图 5 单缝衍射实验原理图如图 8:当一平面波垂直入射到一金属板的两条狭缝上时,则每一条狭缝就是次级波波源,由于两缝发出的次级波是相干波,因此在金属板的背后面空间中,将产生干涉现象。
当然电磁波通过每个缝也有狭缝现象。
电磁场与电磁波实验报告

实验一 静电场仿真1.实验目的建立静电场中电场及电位空间分布的直观概念。
2.实验仪器计算机一台3.基本原理当电荷的电荷量及其位置均不随时间变化时,电场也就不随时间变化,这种电场称为静电场。
点电荷q 在无限大真空中产生的电场强度E 的数学表达式为(1-1)真空中点电荷产生的电位为(1-2)其中,电场强度是矢量,电位是标量,所以,无数点电荷产生的电场强度和电位是不一样的,电场强度为4= (1-3) 电位为4= (1-4) 本章模拟的就是基本的电位图形。
4.实验内容及步骤(1)点电荷静电场仿真题目:真空中有一个点电荷-q,求其电场分布图。
程序1:负点电荷电场示意图clear[x,y]=meshgrid(-10:1.2:10);E0=8.85e-12;q=1.6*10^(-19);r=[];r=sqrt(x.^2+y.^2+1.0*10^(-10))m=4*pi*E0*r;m1=4*pi*E0*r.^2;E=(-q./m1).*r;surfc(x,y,E);负点电荷电势示意图clear[x,y]=meshgrid(-10:1.2:10); E0=8.85e-12;q=1.6*10^(-19);r=[];r=sqrt(x.^2+y.^2+1.0*10^(-10))m=4*pi*E0*r;m1=4*pi*E0*r.^2;z=-q./m1surfc(x,y,z);xlabel('x','fontsize',16)ylabel('y','fontsize',16)title('负点电荷电势示意图','fontsize',10)程序2clearq=2e-6;k=9e9;a=1.0;b=0;x=-4:0.16:4;y=x; [X,Y]=meshgrid(x,y);R1=sqrt((X+1).^2+Y.^2+1.0*10^(-10)); R2=sqrt((X-1).^2+Y.^2+1.0*10^(-10));Z=q*k*(1./R2-1./R1);[ex,ey]=gradient(-Z);ae=sqrt(ex.^2+ey.^2);ex=ex./ae;ey=ey./ae; cv=linspace(min(min(Z)),max(max(Z)),40); contour(X,Y,Z,cv,'k-');hold onquiver(X,Y,ex,ey,0.7);clearq=2e-6;k=9e9;a=1.0;b=0;x=-4:0.15:4;y=x; [X,Y]=meshgrid(x,y);R1=sqrt((X+1).^2+Y.^2+1.0*10^(-10));R2=sqrt((X-1).^2+Y.^2+1.0*10^(-10));U=q*k*(1./R2-1./R1);[ex,ey]=gradient(-U);ae=sqrt(ex.^2+ey.^2);ex=ex./ae;ey=ey./ae; cv=linspace(min(min(U)),max(max(U)),40); surfc(x,y,U);实验二恒定电场的仿真1.实验目的建立恒定电场中电场及电位空间分布的直观概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电磁场与电磁波》仿真实验2016年11月《电磁场与电磁波》仿真实验介绍《电磁场与电磁波》课程属于电子信息工程专业基础课之一,仿真实验主要目的在于使学生更加深刻的理解电磁场理论的基本数学分析过程,通过仿真环节将课程中所学习到的理论加以应用。
受目前实验室设备条件的限制,目前主要利用MATLAB 仿真软件进行,通过仿真将理论分析与实际编程仿真相结合,以理论指导实践,提高学生的分析问题、解决问题等能力以及通过有目的的选择完成实验或示教项目,使学生进一步巩固理论基本知识,建立电磁场与电磁波理论完整的概念。
本课程仿真实验包含五个内容:一、电磁场仿真软件——Matlab 的使用入门二、单电荷的场分布三、点电荷电场线的图像四、线电荷产生的电位五、有限差分法处理电磁场问题目录一、电磁场仿真软件——Matlab 的使用入门⋯⋯⋯⋯..⋯ (4)二、单电荷的场分布⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1⋯0三、点电荷电场线的图像⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12⋯四、线电荷产生的电位⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯.⋯⋯⋯⋯⋯⋯1⋯4⋯五、有限差分法处理电磁场问题⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯17⋯实验一电磁场仿真软件——Matlab 的使用入门一、实验目的1.掌握Matlab 仿真的基本流程与步骤;2.掌握Matlab 中帮助命令的使用。
二、实验原理(一) MATLAB运算1.算术运算(1).基本算术运算MATLAB的基本算术运算有:+(加)、-(减)、*( 乘)、/( 右除)、\( 左除)、^(乘方)。
注意,运算是在矩阵意义下进行的,单个数据的算术运算只是一种特例。
(2).点运算在MATLAB中,有一种特殊的运算,因为其运算符是在有关算术运算符前面加点,所以叫点运算。
点运算符有.* 、./ 、和.^。
两矩阵进行点运算是指它们的对应元素进行相关运算,要求两矩阵的维参数相同。
例1:用简短命令计算并绘制在0≤x≦6 范围内的sin(2x) 、sinx 2、sin 2x。
程序:x=linspace(0,6)y1=sin(2*x),y2=sin(x.^2),y3=(sin(x)).^2;plot(x,y1,x, y2,x, y3)(二)几个绘图命令1.doc 命令:显示在线帮助主题调用格式:doc 函数名例如:doc plot ,则调用在线帮助,显示plot 函数的使用方法。
2.plot 函数:用来绘制线形图形plot(y),当y是实向量时,以该向量元素的下标为横坐标,元素值为纵坐标画出一条连续曲线,这实际上是绘制折线图。
plot(x,y),其中x 和y为长度相同的向量,分别用于存储x 坐标和y坐标数据。
plot(x,y,s)contour 函数:用来绘制等高线图形ezplot 函数:对于显式函数f=f(x),在默认范围[-2π<x<2π]上绘制函数f(x)的图形;对于隐式函数f=f(x,y),在默认的平面区域[-2π<x<2π , -2π<y<2π]上绘制函数f(x,y) 的图形。
3.具有两个纵坐标标度的图形在MATLAB中,如果需要绘制出具有不同纵坐标标度的两个图形,可以使用plotyy 绘图函数。
调用格式为:plotyy(x1,y1,x2,y2)其中x1,y1对应一条曲线,x2,y2对应另一条曲线。
横坐标的标度相同,纵坐标有两个,左纵坐标用于x1,y1 数据对,右纵坐标用于x2,y2数据对。
4.三维曲线plot3 函数与plot 函数用法十分相似,其调用格式为:plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,⋯,xn,yn,zn,选项n) 其中每一组x,y,z组成一组曲线的坐标参数,选项的定义和plot 函数相同。
当x,y,z 是同维向量时,则x,y,z 对应元素构成一条三维曲线。
当x,y,z是同维矩阵时,则以x,y,z 对应列元素绘制三维曲线,曲线条数等于矩阵列数。
5.legend 命令:为绘制的图形加上图例调用格式:legend('string1','string2',...) 例如:legend('电信161班','学号:05401111','张三','Location','best');6. xlabel 命令:给X 轴加标题调用格式:xlabel('string') 例如:xlabel('x');三、实验内容1.在命令窗口中运行一个加法程序;2.在命令窗口中练习帮助命令( doc 命令)的使用。
3.建立第一个M 文件,并运行,观察并保存运行结果。
四、实验步骤1. 在命令窗口中运行一个加法程序 (1)点击桌面上matlab7.0 快捷方式图标,如图 1.1 所示,启动该软件。
图 1.1 matlab7.0 快捷方式图标(2)在打开的界面右方,是命令窗口(Command Windows),如图 1.2 所示,在闪动光标处可以写入命令;图 1.2 Matlab 的命令窗口3)在光标处写入如图 1.3 所示的命令(注意:前两个语句后面有分号,最后一个语句没有分号);按回车键,则得到运行结果为50,如图 1.4所示图 1.3 在命令窗口输入命令图 1.4 按回车键执行命令得到正确运行结果2.在命令窗口中练习帮助命令(doc 命令)的使用在命令窗口光标处输入命令:doc plot ;回车,则进入在线帮助文件,显示plot 命令的使用方法页面,如图 1.5 所示图 1.5 plot 命令的在线帮助页面3.建立第一个M 文件,并运行,观察并保存运行结果。
(1)点击图标,如图 1.6 中红色圆圈所示,即创建了一个新的M 文件,如图 1.7 所示。
图 1.6 红色圆圈的图标用于创建新的M 文要求:在 E 盘建立新文件夹,命名为Fiele_Wave_simulation_2012_10_27;将M 文件保存在Fiele_Wave_simulation_2012_10_27目录下,命名为Exp_1.m;特别说明两点: a. M 文件名及保存的路径名均应为英文,否则运行出错;b.程序中的所有字符均应为英文状态下输入,特别注意单引号,逗号,空格,这些细节会导致运行报错,又极难发现。
五、实验工具1.计算机2.MATLAB 仿真软件 六、实验报告要求 1.写出仿真程序源代码。
2.在同一窗口用不同的线性绘制 y=sinx ,y=cosx 在[0,2*pi] 上的图像, 并加标 注。
3. 在同一窗口用不同的线性绘制 y=sin2x ,y=cos2x 在[-2*pi,2*pi] 上的图1台 1套图 M 文件的保存、运行按键及运行结果像,并加标注。
(要在图中绘制出姓名与学号)实验二单电荷的场分布、实验目的1.掌握MATLAB 仿真的基本流程与步骤;2.学会绘制单电荷的等位线和电力线分布图、实验原理1.基本原理单电荷的外部电位计算公式:等位线就是连接距离电荷等距离的点,在图上表示就是一圈一圈的圆,而电力线就是由点向外辐射的线,比较简单,这里就不再赘述2.参考程序创建向量theta ,确定theta 的范围为0 到2*pi ,半径分别为r=0,1,2,...,10绘制10 个圆x=linspace(-5,5,100);% 创建线性空间向量x, 从-5 到5,等间距分为100个点for theta=[-pi/4 0 pi/4]y=x*tan(theta); % 分别绘制y=x*tan(theta) 的三条直线,其中theta 分别取-pi/4 ,0,pi/4hold on;%Hold 住绘制的图形plot(x,y); % 绘制y=x*tan(theta) 的三条直线endgrid on% axis tight%l egend(' 电信本162 班',' 学号:16401111',' 张三','Location','best'); legend('boxoff');% 加上图例% xlabel('x');% 加上横坐标标题% ylabel('y');;% 加上纵坐标标题theta=[0:0.01:2*pi]';% 步距为0.01r=0:10; %x=sin(theta)*r;y=cos(theta)*r;plot(x,y,'b') %% hold on;3.程序参考运行结果运行程序,获得图像大致如图 2.1 所示108642-2-4-6-8图 2.1 单电荷的等位线和电力线分布图三、实验内容绘制单电荷的等位线和电力线分布图。
四、实验步骤1.在 E 盘建立新文件夹,命名为Fiele_Wave_simulation_2012_10_27;2. 打开Matlab 软件,新建一个空白的M 文件,保存在Fiele_Wave_simulation_2012_10_27目录下,命名为Exp_2.m;3.将源程序拷贝到M 文件中,保存;4.点击运行按钮,观察程序运行结果。
五、实验工具1.计算机 1 台2.MATLAB 仿真软件 1 套六、实验报告要求1.写出仿真程序源代码。
2.绘制单电荷的等位线和电力线分布图。
(要在图中绘制出姓名与学号)实验三点电荷电场线的图像、实验目的学会由解析表达式进行数值求解的方法。
、实验原理1.基本原理考虑一个三点电荷系所构成的系统。
如图所示,其中一个点电荷-q 位于坐标原点,另一个-q 位于y 轴上的点,最后一个+2q 位于y 轴的-点,则在xoy 平面内,电场强度应满足任意条电场线应该满足方程:1)求解( 1)式可得:这就是电场线满足的方程,常数 C 取不同值将得到不同的电场线。
2.参考程序解出y=f(x) 的表达式再作图是不可能的。
用Matlab 语言即能轻松的做到这一点。
其语句是:syms x y % 设置x,y 变量;for C=0:0.1:3.0ezplot(2*(y+1)/sqrt((y+1)^2+x^2)-y/sqrt(y^2+x^2)-(y-1)/sqrt((y-1)^2+x^2)-C, [- 5,5,0.1]); %其中取了a=1,C=0,0.1,0.2,⋯⋯,3.0 hold on;2)3.程序参考运行结果运行程序,获得图像大致如图 3.1 所示x图 3.1 点电荷电场线的图像三、实验内容根据给出的三点电荷系所构成的系统电场线满足的方程,绘制其图像。
四、实验步骤1.在 E 盘建立新文件夹,命名为Fiele_Wave_simulation_2012_10_27;2. 打开Matlab 软件,新建一个空白的M 文件,保存在Fiele_Wave_simulation_2012_10_27目录下,命名为Exp_3.m; 3.将源程序拷贝到M 文件中,保存;4.点击运行按钮,观察程序运行结果。
