第10章 3#导流洞施工方法及附图——【水利水电工程 精】
机械制图(第四版)第10章第三节 圆柱管制件的展开
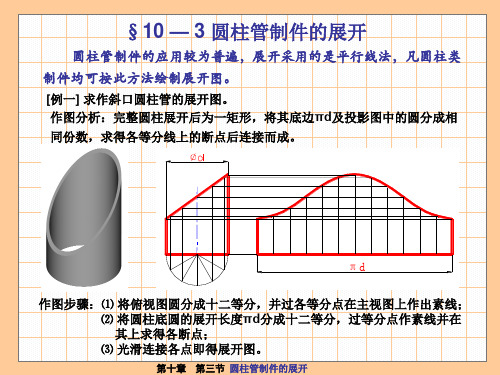
[例二] 作出五节直角弯管的展开图。 作图分析:多节圆柱弯管常用于通风、除尘的管道中。图示为一五节等径直 角弯管。其中中间的三节为整节(两面带斜口),端部的两节为半节(一面 带斜口)。 图中所示的半节斜面的倾斜角=11.25°。若将各节一顺一倒排列恰可构成
一圆管。因此如有现成的直圆管即可按图示位置切成五节,
第十章 第三节 圆柱管制件的展开
定准各节的相对位置后焊成直角弯管。也可按右图所示方法展开后,分别剪切 出各节用料再焊接成型,此法不但节约用料,而且可提高工效。
第十章 第三 圆柱管制件的展开
作业:按图中给定尺寸作出圆柱管接头模型。
偏交圆柱管接头
斜交料圆柱管接头
带补料圆柱管接头
§10 — 3 圆柱管制件的展开
圆柱管制件的应用较为普遍,展开采用的是平行线法,凡圆柱类 制件均可按此方法绘制展开图。
[例一] 求作斜口圆柱管的展开图。 作图分析:完整圆柱展开后为一矩形,将其底边πd及投影图中的圆分成相 同份数,求得各等分线上的断点后连接而成。
πd
作图步骤:⑴ 将俯视图圆分成十二等分,并过各等分点在主视图上作出素线; ⑵ 将圆柱底圆的展开长度πd分成十二等分,过等分点作素线并在 其上求得各断点; ⑶ 光滑连接各点即得展开图。
2020高中数学第十章 3《二项式定理》复习学案+检测

2020高中数学复习学案第10章 计数原理、概率、随机变量及其分布3 二项式定理【要点梳理·夯实知识基础】1.二项式定理(a +b )n =C 0n a n +C 1n a n -1b 1+…+C r n an -r b r +…+C n n b n(n ∈N +). 这个公式所表示的规律叫做二项式定理,等式右边的多项式叫做(a +b )n 的二项展开式,其中的系数C r n (r =0,1,2,…,n )叫做 二项式系数 .式中的 C r n an -rb r 叫做二项展开式的 通项 ,用T r +1表示,通项是展开式的第 r +1 项,即T r +1=C r n an -r b r (其中0≤r ≤n ,r ∈N ,n ∈N +). 2.二项展开式形式上的特点 (1)项数为 n +1 .(2)各项的次数都等于二项式的幂指数n ,即a 与b 的指数的和为 n . (3)字母a 按 降幂 排列,从第一项开始,次数由n 逐项减1直到零;字母b 按 升幂 排列,从第一项起,次数由零逐项增1直到n .(4)二项式的系数从C 0n ,C 1n ,一直到 C n -1n ,C nn .3.二项式系数的性质(1)对称性:与首末两端“ 等距离 ”的两个二项式系数相等,即C m n =C n -m n .(2)增减性与最大值:二项式系数C r n,当r <n +12时,二项式系数是递增的;当r >n +12时,二项式系数是递减的.当n 是偶数时,那么其展开式中间两项T n2+1的二项式系数最大. 当n 是奇数时,那么其展开式中间两项T n +12和T n +12+1的二项式系数相等且最大.(3)各二项式系数的和(a +b )n 的展开式的各个二项式系数的和等于2n ,即C 0n +C 1n +C 2n +…+C r n +…+C n n =2n.二项展开式中,偶数项的二项式系数的和等于奇数项的二项式系数的和,即C 1n +C 3n +C 5n +…=C 0n +C 2n +C 4n +…=2n -1 . 【学练结合】[思考辨析]判断下列说法是否正确,正确的在它后面的括号里打“√”,错误的打“×”.(1)C k n an -k b k是(a +b )n 的展开式中的第k 项.( ) (2)二项展开式中,系数最大的项为中间一项或中间两项.( ) (3)(a +b )n 的展开式中某一项的二项式系数与a ,b 无关.( )(4)若(3x -1)7=a 7x 7+a 6x 6+…+a 1x +a 0,则a 7+a 6+…+a 1的值为128.( )答案:(1)× (2)× (3)√ (4)× [小题查验]1.若(x -1)4=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4,则a 0+a 2+a 4的值为( ) A .9 B .8 C .7D .6解析:B [令x =1,则a 0+a 1+a 2+a 3+a 4=0,令x =-1,则a 0-a 1+a 2-a 3+a 4=16,两式相加得a 0+a 2+a 4=8.]2.(教材改编)若⎝ ⎛⎭⎪⎫x +1x n 展开式的二项式系数之和为64,则展开式的常数项为( )A .10B .20C .30D .120解析:B [二项式系数之和2n =64,所以n =6,T k +1=C k 6·x 6-k ·⎝ ⎛⎭⎪⎫1x k =C k 6x 6-2k,当6-2k =0,即当k =3时为常数项,T 4=C 36=20.]3.(2018·全国Ⅲ卷)⎝ ⎛⎭⎪⎫x 2+2x 5的展开式中x 4的系数为( )A .10B .20C .40D .80解析:C [T r +1=C r 5(x 2)5-r ⎝ ⎛⎭⎪⎫2x r =C r 52r x 10-3r ,由10-3r =4,得r =2,所以x 4的系数为C 25×22=40.]4.若⎝ ⎛⎭⎪⎫x 2-1x n 展开式的二项式系数之和为128,则展开式中x 2的系数为( )A .-21B .-35C .35D .21解析:C [由已知得2n =128,n =7,所以T r +1=C r 7x 2(7-r )·⎝ ⎛⎭⎪⎫-1x r =C r 7(-1)r x 14-3r,令14-3r =2,得r =4,所以展开式中x 2的系数为C 47(-1)4=35.故选C.]5.⎝ ⎛⎭⎪⎫1x +x n 的展开式中,第3项与第7项的二项式系数相等,则展开式中的第4项为 ________ .解析:由题意得C 2n =C 6n ,所以n =8.所以⎝ ⎛⎭⎪⎫1x +x 8展开式的第4项为T 4=C 38⎝ ⎛⎭⎪⎫1x 3x 5=56x 2. 答案:56x 2【考点探究·突破重点难点】考点一 二项展开式的特定项或系数问题(多维探究)[命题角度1] 求展开式中的某一项1.⎝ ⎛⎭⎪⎫x 3-2x 4+⎝ ⎛⎭⎪⎫x +1x 8的展开式中x 4的常数项为( ) A .32 B .34 C .36D .38解析:D [⎝ ⎛⎭⎪⎫x 3-2x 4的展开式的通项为T k +1=C k 4·(x 3)4-k ·⎝ ⎛⎭⎪⎫-2x k =C k 4(-2)k x 12-4k,令12-4k =0,解得k =3, ⎝ ⎛⎭⎪⎫x +1x 8的展开式的通项为 T r +1=C r 8·x 8-r ·⎝ ⎛⎭⎪⎫1x r =C r 8·x 8-2r , 令8-2r =0,得r =4,所以所求常数项为C 34(-2)3+C 48=38.][命题角度2] 求展开式中的系数或二项式系数2.(1+x )(1-x )5的展开式中x 4的系数是( ) A .-35 B .-5 C .5D .35解析:B [(1-x )5展开式的通项是T r +1=C r 5(-x )r =(-1)r C r 5x r ,所以(1-x )5展开式中x 4的系数是(-1)4C 45=5,x 3项的系数是(-1)3C 35=-10,所以(1+x )(1-x )5的展开式中x 4项的系数是1×5+1×(-10)=-5,故选B.][命题角度3] 由已知条件求n 的值或参数的值3.若⎝⎛⎭⎪⎫ax 2+1x 5的展开式中x 5的系数是-80,则实数a = ________ .解析:⎝⎛⎭⎪⎫ax 2+1x 5的展开式的通项T r +1=C r 5(ax 2)5-r ·x -r 2=C r 5a 5-r ·x 10-5r 2,令10-52r =5,得r =2,所以C 25a 3=-80,解得a =-2.答案:-2 【解题规律方法】与二项展开式有关问题的解题策略(1)求展开式中的第n 项,可依据二项式的通项直接求出第n 项.(2)求展开式中的特定项,可依据条件写出第r +1项,再由特定项的特点求出r 值即可.(3)已知展开式的某项,求特定项的系数,可由某项得出参数项,再由通项写出第r +1项,由特定项得出r 值,最后求出其参数.[跟踪训练](1)(x +y )(2x -y )5的展开式中x 3y 3的系数为( ) A .-80 B .-40 C .40D .80解析:C [因为x 3y 3=x ·(x 2y 3),其系数为-C 35·22=-40,x 3y 3=y ·(x 3y 2),其系数为C 25·23=80.所以x 3y 3的系数为80-40=40.故选C.] (2)若⎝ ⎛⎭⎪⎪⎫x -23x n (n ∈N +)展开式的二项式系数和为32,则其展开式的常数项为( )A .80B .-80C .160D .-160解析:B [根据二项式系数和的性质,可知2n =32,解得n =5,所以⎝⎛⎭⎪⎪⎫x -23x n的展开式的通项为T r +1=C r 5·(x )5-r⎝⎛⎭⎪⎪⎫-23x r =(-2)r C r 5x 5-r 2-r 3,令5-r 2-r 3=0,解得r =3,所以其展开式的常数项为(-2)3C 35=-80,故选B.]考点二 二项式系数的性质或各项系数的和(师生共研)[典例] (1)在二项式⎝ ⎛⎭⎪⎫x 2-1x 11的展开式中,系数最大的项为第 ________项.(2)若(x +2+m )9=a 0+a 1(x +1)+a 2(x +1)2+…+a 9(x +1)9,且(a 0+a 2+…+a 8)2-(a 1+a 3+…+a 9)2=39,则实数m 的值为 ________ .[解析] (1)依题意可知T r +1=C r 11(-1)r x 22-3r,0≤r ≤11,r ∈Z ,二项式系数最大的是C 511与C 611.当r =6时,T 7=C 611x 4,故系数最大的项是第七项.(2)令x =0,得到a 0+a 1+a 2+…+a 9=(2+m )9,令x =-2,得到a 0-a 1+a 2-a 3+…-a 9=m 9,所以有(2+m )9m 9=39,即m 2+2m =3,解得m =1或-3.[答案] (1)七 (2)1或-3 [互动探究]本例(2)变为:若(x +2+m )9=a 0+a 1(x -1)+a 2(x -1)2+…+a 9(x -1)9,且(a 0+a 2+…+a 8)2-(a 1+a 3+…+a 9)2=39,则实数m 的值为 ________ .解析:令x =2,得到a 0+a 1+a 2+…+a 9=(4+m )9,令x =0,得到a 0-a 1+a 2-a 3+…-a 9=(m +2)9,所以有(4+m )9(m +2)9=39,即m 2+6m +5=0,解得m =-1或-5.答案:-1或-5 【解题方法指导】(1)“赋值法”普遍适用于恒等式,对形如(ax +b )n ,(ax 2+bx +c )m (a ,b ,c ∈R )的式子求其展开式的各项系数之和,常用赋值法.(2)若f (x )=a 0+a 1x +a 2x 2+…+a n x n ,则f (x )展开式中各项系数之和为f (1),奇数项系数之和为a 0+a 2+a 4+…=f (1)+f (-1)2,偶数项系数之和为a 1+a 3+a 5+…=f (1)-f (-1)2.[跟踪训练](1)已知(2x -1)10=a 0+a 1x +a 2x 2+…+a 9x 9+a 10x 10,则a 2+a 3+…+a 9+a 10的值为( )A .-20B .0C .1D .20解析:D [令x =1,得a 0+a 1+a 2+…+a 9+a 10=1,再令x =0,得a 0=1,所以a 1+a 2+…+a 9+a 10=0,又易知a 1=C 910×21×(-1)9=-20,所以a 2+a 3+…+a 9+a 10=20.](2)在二项式⎝ ⎛⎭⎪⎫x +3x n 的展开式中,各项系数之和为A ,各项二项式系数之和为B ,且A +B =72,则展开式中常数项的值为 ________ .解析:令x =1,得各项系数的和为4n ,而各项的二项式系数的和等于2n ,根据已知,得方程4n +2n =72,解得n =3.所以二项展开式的通项T r +1=C r 3(x )3-r⎝ ⎛⎭⎪⎫3x r =3r C r 3x 32-32r ,显然当r =1时,T r +1是常数项,值为3C 13=9. 答案:92020高中数学复习学案第10章 计数原理、概率、随机变量及其分布3 二项式定理检测一、选择题1.C 1n +2C 2n +4C 3n +…+2n -1C n n 等于( D ) A .3n B .2·3n C.3n2-1D.3n -12解析:因为C 0n +2(C 1n +2C 2n +4C 3n +…+2n -1C n n )=(1+2)n ,所以C 1n +2C 2n +4C 3n +…+2n -1C n n =3n -12.2.在⎝ ⎛⎭⎪⎫x 2+1x 5的展开式中x 的系数为( B )A .5B .10C .20D .40解析:∵T r +1=C r 5(x 2)5-r ⎝ ⎛⎭⎪⎫1x r=C r 5x 10-3r,令10-3r =1,得r =3,∴x 的系数为C 35=10.3.已知⎝ ⎛⎭⎪⎫x 3+2x n的展开式的各项系数和为243,则展开式中x 7的系数为( B )A .5B .40C .20D .10解析:由题意,二项式⎝ ⎛⎭⎪⎫x 3+2x n 的展开式中各项的系数和为243,令x =1,则3n=243,解得n =5,所以二项式⎝ ⎛⎭⎪⎫x 3+2x 5的展开式的通项公式为T r +1=C r 5(x 3)5-r⎝ ⎛⎭⎪⎫2x r =2r C r 5x 15-4r ,令15-4r =7,得r =2,则T 3=22C 25x 15-4×2=40x 7,即x 7的系数为40,故选B.4.1+(1+x )+(1+x )2+…+(1+x )n 的展开式的各项系数之和为( C )A .2n -1B .2n -1C .2n +1-1D .2n解析:令x =1,得1+2+22+ (2)=1×(2n +1-1)2-1=2n +1-1.5.(3-2x -x 4)(2x -1)6的展开式中,含x 3项的系数为( C )A .600B .360C .-600D .-360解析:由二项展开式的通项公式可知,展开式中含x 3项的系数为3×C 3623(-1)3-2×C 2622(-1)4=-600.6.已知(2x -1)5=a 5x 5+a 4x 4+a 3x 3+a 2x 2+a 1x +a 0,则|a 0|+|a 1|+…+|a 5|=( B )A .1B .243C .121D .122解析:令x =1,得a 5+a 4+a 3+a 2+a 1+a 0=1,① 令x =-1,得-a 5+a 4-a 3+a 2-a 1+a 0=-243,② ①+②,得2(a 4+a 2+a 0)=-242, 即a 4+a 2+a 0=-121.①-②,得2(a 5+a 3+a 1)=244, 即a 5+a 3+a 1=122.所以|a 0|+|a 1|+…+|a 5|=122+121=243.故选B. 7.在⎝ ⎛⎭⎪⎫1+x +1x 2 01510的展开式中,x 2的系数为( C )A .10B .30C .45D .120解析:因为⎝ ⎛⎭⎪⎫1+x +1x 2 01510=⎣⎢⎡⎦⎥⎤(1+x )+1x 2 01510=(1+x )10+C 110(1+x )91x 2 015+…+C 1010⎝ ⎛⎭⎪⎫1x2 01510,所以x 2只出现在(1+x )10的展开式中,所以含x 2的项为C 210x 2,系数为C 210=45.故选C. 二、填空题8.(x 2-1x )8的展开式中x 7的系数为-56.(用数字作答)解析:二项展开式的通项T r +1=C r 8(x 2)8-r ·(-1x )r =(-1)r C r 8x 16-3r,令16-3r =7,得r =3,故x 7的系数为-C 38=-56. 9.若二项式(x -23x)n 的展开式中仅有第6项的二项式系数最大,则其常数项是13_440.解析:∵二项式(x -23x)n 的展开式中仅有第6项的二项式系数最大,∴n=10,∴T r +1=C r 10(x )10-r(-23x )r =(-2)r C r 10·x 30-5r6 ,令30-5r 6=0,解得r =6,∴常数项是(-2)6C 610=13 440.10.若(x +a )(1+2x )5的展开式中x 3的系数为20,则a =-14.解析:(x +a )(1+2x )5的展开式中x 3的系数为C 25·22+a ·C 35·23=20,∴40+80a =20,解得a =-14.11.在(x +4x -4)5的展开式中,x 3的系数是180.解析:(x +4x -4)5=(-4+x +4x )5的展开式的通项T r +1=C r 5(-4)5-r·(x +4x )r ,r =0,1,2,3,4,5,(x +4x )r 的展开式的通项T k +1=C k r x r -k (4x )k =4k C k r xr -2k ,k =0,1,…,r .令r -2k =3,当k =0时,r =3;当k =1时,r =5.∴x 3的系数为40×C 03×(-4)5-3×C 35+4×C 15×(-4)0×C 55=180.12.在(x +x )6⎝ ⎛⎭⎪⎫1+1y 5的展开式中,x 4y 2项的系数为( C )A .200B .180C .150D .120解析:(x +x )6展开式的通项公式为T r +1=C r 6(x )6-r x r=C r 6,令6+r2=4,得r =2,则T 3=C 26=15x 4.⎝ ⎛⎭⎪⎫1+1y 5展开式的通项公式为T r +1=C r 5⎝ ⎛⎭⎪⎫1y r =C r 5y -r ,令r =2可得T 3=C 25y -2=10y -2.故x 4y 2项的系数为15×10=150.13.已知(2x -1)4=a 0+a 1(x -1)+a 2(x -1)2+a 3(x -1)3+a 4(x -1)4,则a 2=( B )A .18B .24C .36D .56解析:∵(2x -1)4=[(2x -2)+1]4=[1+(2x -2)]4=a 0+a 1(x -1)+a 2(x -1)2+a 3(x -1)3+a 4(x -1)4,∴a 2=C 24·22=24,故选B.14.⎝ ⎛⎭⎪⎫x -a x ⎝ ⎛⎭⎪⎫2x -1x 5的展开式中各项系数的和为2,则该展开式中含x 4项的系数为-48.解析:令x =1,可得⎝ ⎛⎭⎪⎫x -a x ⎝ ⎛⎭⎪⎫2x -1x 5的展开式中各项系数的和为1-a =2,得a =-1,则⎝ ⎛⎭⎪⎫x +1x ⎝ ⎛⎭⎪⎫2x -1x 5展开式中x 4项的系数即是⎝ ⎛⎭⎪⎫2x -1x 5展开式中的x 3项与x 5项系数的和.又⎝ ⎛⎭⎪⎫2x -1x 5展开式的通项为T r +1=C r 5(-1)r ·25-r ·x 5-2r,令5-2r =3,得r =1,令5-2r =5,得r =0,将r =1与r =0分别代入通项,可得x 3项与x 5项的系数分别为-80与32,故原展开式中x 4项的系数为-80+32=-48.尖子生小题库——供重点班学生使用,普通班学生慎用15.已知(1+ax +by )5(a ,b 为常数,a ∈N *,b ∈N *)的展开式中不含字母x 的项的系数和为243,则函数f (x )=sin2x +b 2sin (x +π4),x ∈[0,π2]的最小值为2.解析:令x =0,y =1,得(1+b )5=243,解得b =2.因为x ∈[0,π2],所以x+π4∈[π4,3π4],则sin x +cos x =2sin(x +π4)∈[1,2],所以f (x )=sin2x +b 2sin (x +π4)=sin2x +2sin x +cos x =2sin x ·cos x +2sin x +cos x=sin x+cos x+1sin x +cos x≥2(sin x +cos x )·1sin x +cos x=2,当且仅当sin x +cos x =1时取“=”,所以f (x )的最小值为2.。
第十章 生物碱3

根据生物碱的碱性强弱、酚羟基的有无及溶解性能,将生物碱初步分成弱碱性、中强碱性、强碱性、水溶性、酚性、非酚性生物碱五类。
(二)单体生物碱的分离
1、利用生物碱碱性的差异进行分离
一般采用PH梯度萃取法
1)将总碱溶于酸水,调PH7、8、9、10,每调一次PH值,用氯仿等亲脂性有机溶剂萃取一次;(弱碱先萃取出)
授课
对象
系别药学系讨论□
示教□
其他□
课程
类型
理论课
实验课□
见习课□
其他□
题目
生物碱的检识、提取与分离方法
课时安排
2学时
教学
目的
要求
1、掌握生物碱检识方法。
2、掌握生物碱的提取方法。
3、熟悉生物碱的分离原理与方法。
4、掌握生物碱的单体分离。
教学内容
重点(*)
难点(#)
疑点(?)
3、利用生物碱特殊功能基不同进行分离
如:吗啡与可待因的分离
吗啡为酚性生物碱,可溶于NaOH溶液中,而可待因属于非酚性生物碱不溶于NaOH溶液,因此可用NaOH溶液进行分离。
4、利用色谱法进行分离
漳州卫生职业学院教案纸
第15页
5、水溶性生物碱的分离
包括季铵碱及含有较多极性基团的小分子生物碱。可采用下列方法除去水溶性杂质。
课程名称:中药化学编号:3
漳州卫生职业学院教案纸
第10页
(三)两性生物碱
具有酚羟基、羧基、内酯或内酰胺结构的生物碱类。
五、沉淀反应
生物碱在酸水中(苦味酸除外)或稀醇中与某些试剂生成难溶于水的复盐或配合物的反应,称为生物碱的沉淀反应。与生物碱形成沉淀的化学试剂称为生物碱沉淀试剂。利用该反应可预测中药是否存在生物碱;也可用于提取与分离。
第十章 电磁感应3

我们现将研究随时间变化的磁场,电场, 我们现将研究随时间变化的磁场,电场,以进 一步揭示电与磁的联系。 一步揭示电与磁的联系。
稳恒-- 不随时间变化, 稳恒-- 不随时间变化, 注意区分 均匀-- 不随位置变化, 均匀-- 不随位置变化,
非稳恒 − 场量是时间的函数 非均匀- 非均匀-场量是位置的 函数
5 首 页 上 页 下 页退 出
②式中的负号是楞次定律的数学表示 ③若为N 匝线圈,则 若为 匝线圈,
称作磁通匝链数,简称磁链。 式中 Ψ = N Φ 称作磁通匝链数,简称磁链。
(3)磁通计 (3) 如果闭合回路为纯电阻R 如果闭合回路为纯电阻 时,则回路中的感应电流为
1 dΦ I = =− R R dt
那么t 那么 1 ~ t2 时间内通过导线上任一截面的感应电量大 小为
ε
q=∫
t2
t1
1 Φ2 1 Idt = − ∫ dΦ = (Φ1 − Φ 2 ) R Φ1 R
时刻回路中的磁通。 式中 Φ1,Φ 2 是t1 , t2 时刻回路中的磁通。
6 首 页 上 页 下 页退 出
上式说明,在一段时间内, 上式说明,在一段时间内,通过导线截面的电量 与这段时间内导线所围磁通的增量成正比。 与这段时间内导线所围磁通的增量成正比。 *:如果能测出导线中的感应电量, *:如果能测出导线中的感应电量,且回路中的电 如果能测出导线中的感应电量 阻为已知时,那么由上面公式, 阻为已知时,那么由上面公式,即可算出回路所围 面积内的磁通的变化量——磁通计就是根据这个原 面积内的磁通的变化量 磁通计就是根据这个原 理设计的。 理设计的。
12 首 页 上 页 下 页退 出
一是磁场不变, 一是磁场不变,回路的一部分相对磁场运动或回 路面积发生变化致使回路中磁通量变化而产生的感 应电动势,谓之动生电动势 动生电动势。 应电动势,谓之动生电动势。 另一种情况是回路面积不变, 另一种情况是回路面积不变,因磁场变化使回路 中磁通量变化而产生的感应电动势,谓之感生电动势。 中磁通量变化而产生的感应电动势,谓之感生电动势。 感生电动势
第10章---第3节
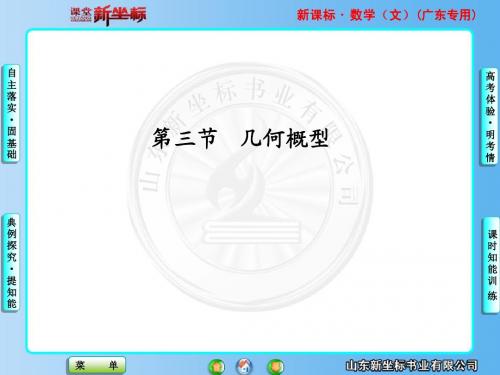
2-1 2 故所求概率为 P= = . 1 3 2- 2
【答案】 2 3
课 时 知 能 训 练
菜
单
新课标 ·数学(文)(广东专用)
自 主 落 实 · 固 基 础
πx 1 在区间[-1,1]上随机取一个数 x, cos 的值介于 0 到 之间的概 2 2 率为( A. 1 3 ) B. 2 π C. 1 2 D. 2 3
高 考 体 验 · 明 考 情
典 例 探 究 · 提 知 能
π 【思路点拨】 先判断 x 的范围,然后根据 y=cos x 的图象寻找 2 π π 1 x 满足的条件,从而确定使 cos x 的值介于 0 到 的 x 的取值范围. 2 2 2
课 时 知 能 训 练
菜
单
新课标 ·数学(文)(广东专用)
3. (2012· 广州质检)一只小蜜蜂在一个棱长为 3 的正方体内自由飞
自 主 落 实 · 固 基 础
行,若蜜蜂在飞行过程中始终保持与正方体 6 个面的距离均大于 1, 称其为“安全飞行”,则蜜蜂“安全飞行”的概率为( 1 A.8 1 B.16 1 C.27 3 D.8 )
高 考 体 验 · 明 考 情
x+y- 2≤0 在区域x-y+ 2≥0 内任取一点 P,则点 P 落在单位 y≥0
圆 x2+y2=1 内的概率为( A. π 2 B. π 8 C. π 6 ) D. π 4
高 考 体 验 · 明 考 情
典 例 探 究 · 提 知 能
x+y- 2≤0 【解析】 如图所示,不等式x-y+ 2≥0 y≥0
高 考 体 验 · 明 考 情
典 例 探 究 · 提 知 能
【思路点拨】 由于随机往单位圆内掷一点,落在任何一处是等可
第十章 3 热力学第一定律 能量守恒定律

人教版物理·选修3-3
返回导航 上页 下页
应用热力学第一定律解题的一般步骤 (1)根据符号法则写出各已知量(W、Q、ΔU)的正、负. (2)根据方程ΔU=W+Q求出未知量. (3)再根据未知量结果的正、负来确定吸热、放热情况或做功情况.
人教版物理·选修3-3
返回导航 上页 下页
1.一定量的气体在某一过程中,外界对气体做了8×104 J的功,气体的内能减少 了1.2×105 J,则下列各式正确的是( ) A.W=8×104 J,ΔU=1.2×105 J,Q=4×104 J B.W=8×104 J,ΔU=-1.2×105 J,Q=-2×105 J C.W=-8×104 J,ΔU=1.2×105 J,Q=2×105 J D.W=-8×104 J,ΔU=-1.2×105 J,Q=-4×104 J
人教版物理·选修3-3
返回导航 上页 下页
2.与某种运动形式对应的能是否守恒是有条件的.例如,物体的机械能守恒,必须 是只有重力或系统内的弹力做功;而能量守恒定律是没有条件的,它是一切自然现 象都遵守的基本规律. 3.第一类永动机失败的原因分析 如果没有外界热源供给热量,则有U2-U1=W,就是说,如果系统内能减少,即 U2<U1,则W<0,系统对外做功是要以内能减少为代价的.若想源源不断地做功, 就必须使系统不断回到初始状态,在无外界能量供给的情况下是不可能的.
2.气体膨胀对外做功100 J,同时从外界吸收了120 J的热量,它的内能的变化是
()
A.减少20 J
B.增大20 J
C.减少220 J
D.增大220 J
解析:研究对象为气体,依符号规则,对外做功W=-100 J,吸收热量Q=+120 J. 由热力学第一定律有 ΔU=W+Q=-100 J+120 J=20 J, ΔU>0,说明气体的内能增加,故选项B正确.
(课件):高三数学第10章第三节

思考感悟
几何概型与古典概型的区别是什么?
提示:几何概型中的基本事件是无限多个,而
古典概型中的基本事件是有限个.
课前热身 1.(2010年高考湖南卷)在区间[-1,2]上随机取 一个数x,则|x|≤1的概率为________.
2 答案: 3
2.如图,矩形长为6,宽为4,在矩形内随机
地撒300颗黄豆,数得落在椭圆外的黄豆数为96
【解】 (1)如图,点 P 所在的区域为正方形 ABCD 的内部(含边界), 满足(x-2)2+(y-2)2≤4 的点的区域为以(2,2)为圆心, 为半径的圆面(含 2 边界). 1 π×22 4 π ∴所求的概率 P1= = . 4× 4 16
(2)满足 x,y∈Z,且|x|≤2,|y|≤2 的点(x,y) 有 25 个, 满足 x, y∈Z, 且(x-2) +(y-2)≤4 的点(x,y)有 6 个, 6 ∴所求的概率 P2= . 25
2 解析:由几何概型的知识知 P= =0.004. 500
答案:0.004
4.如图所示,在直角坐标系内,射线OT落在 30°角的终边上,任作一条射线OA,则射线 OA落在∠yOT内的概率为________.
1 答案: 6
考点探究·挑战高考
考点突破
与长度有关的几何概型 如果一次试验中所有可能结果和某个事件A包含 的结果(基本事件)都对应一个长度,如线段长、 时间区间、距离路程等,那么只需求出各自对 应的长度,然后运用几何概型的概率计算公式 求事件A发生的概率.
会面问题中的概率
本类问题常涉及与面积有关的几何概型,难点
在于怎样构造出面积,或者建立怎样的变量间
的联系.
例3
两人约定在20∶00到21∶00之间相见,并
高中物理必修三 练透试卷 第10章 3 电势差与电场强度的关系

3 电势差与电场强度的关系考点一 公式U AB =Ed 或E =U ABd 的理解及简单应用1.(多选)下列说法正确的是( )A .由公式E =U ABd 得,电场强度E 与电势差U AB 成正比,与两点间距离d 成反比B .由公式E =U ABd 得,在匀强电场中沿电场线方向上两点间距离越大,电场强度就越小C .在匀强电场中,任意两点间电势差等于电场强度和这两点沿电场方向的距离的乘积D .公式E =U ABd只适用于匀强电场2.(2023·无锡市立人高中高二学业考试)如图为某匀强电场的等势面分布图(等势面竖直分布),已知每两个相邻等势面相距2 cm ,则该匀强电场的电场强度大小和方向分别为( )A .E =1 V/m ,水平向左B .E =1 V/m ,竖直向上C .E =100 V/m ,水平向左D .E =100 V/m ,竖直向上3.(2023·台山市第一中学高二期中)正常情况下空气是不导电的,但如果空气中的电场很强,空气也可以被击穿,空气被击穿时会看到电火花或闪电。
若观察到某次闪电的火花长约 1 000 m ,且已知空气的击穿电场强度大小为3×106 V/m ,那么发生此次闪电的电势差约为( ) A .3×109 V B .3×108 V C .3×105 VD .3×104 V4.如图所示,点A 位于沿x 轴正方向的匀强电场中,电场强度大小为E ,OA 的连线与x 轴正方向(E 的方向)成θ角(θ<π2),则以O 为圆心、以r =OA 为半径的圆周上各点与A 点间最大的电势差为( )A.Er B.Er(sin θ+1)C.Er(cos θ+1) D.2Er5.如图所示,两平行金属板A、B间为一匀强电场,A、B相距6 cm,C、D为电场中的两点(其中C点在金属板上),且CD=4 cm,CD连线和电场强度方向成60°角。
大学精品课件:第10章 三羧酸循环

三羧酸循环
Tricarboxylic Acid Cycle
的发现
Discovery of the Citric Acid Cycle
2
一、三羧酸循环是三类营养物质氧化分解的 (共同)第二阶段
* 营养物在生物体内氧化的一般过程 糖原 三酯酰甘油 蛋白质
5
1937 年, Hans Krebs 利用鸽子胸肌(这块肌
肉在飞行中有相当高的呼吸频率,因此特别适合
于氧化过程的研究)的组织悬液,测定了在不同 的有机酸作用下,丙酮酸氧化过程中的耗氧率, 首次提出在动物组织中丙酮酸氧化途径的假说。
6
Albert Szent-Gyorgyi等已经发现动物肌肉组
葡萄糖 脂酸 + 甘油 氨基酸
乙酰CoA
TCA 循环
CO2 2H
3
ADP+Pi
ATP
H2O
呼吸链
在真核生物,TCA循环在线粒体中进行, 与呼吸链在功能和结构上相偶联。
4
二、Krebs发现三羧酸循环
三羧酸循环亦称柠檬酸循环
(citric acid cycle),这是因 为循环反应中的第一个中间产物是 一个含三个羧基的柠檬酸 。由于 Krebs 正式提出了三羧酸循环的 学说,故此循环又称为 Krebs 循 环。
GDP
ADP
ATP
(六)琥珀酸脱氢生成延胡索酸
• 由琥珀酸脱氢酶催化,其辅酶是FAD,是三羧酸 循环中唯一与内膜结合的酶。
20
(七)延胡索酸加水生成苹果酸
• 延胡索酸酶催化此步反应
21
(八)苹果酸脱氢生成草酰乙酸
苹果酸脱氢酶催化,辅酶是NAD+。
高三数学第十章第3课时好课件

考点探究•讲练互动
考点突破
考点1 例1 与长度、角度有关的几何概型
点 A 为周长等于 3 的圆周上的一个定点. 若在该圆
周上随机取一点 B,则劣弧 AB 的长度小于 1 的概率为 __________.
目录
【解析】
如图所示,可设 AM=1,AN=1,根据题意只要点 B 在优 弧 MAN 上,劣弧 AB 的长度就小于 1,故这个概率是优弧 2 MAN 的长度与圆的周长之比,即这个概率是 . 3
目录
跟踪训练
3.在铸铁过程中,经常出现铸件里面混入气泡的情况,但 是如果在加工过程中气泡不暴露在表面,对产品就不会造 成影响,否则产品就会不合格.在一个棱长为 4 cm 的正方 体铸件中不小心混入一个半径为 0.1 cm 的球形气泡,在加 工这个铸件的过程中,如果将铸件去掉 0.5 cm 的厚度后产 品外皮没有麻眼(即没有露出气泡),产品就合格,问产品合 格的概率是多少?
1 答案: 3
目录
5.
如图,在平面直角坐标系 xOy 中,设 D 是横坐标与纵坐标 的绝对值均不大于 2 的点构成的区域, 是到原点的距离不 E 大于 1 的点构成的区域,向 D 中随机投一点,则落入 E 中 的概率为________.
解析: 如题图所示, 区域 D 表示边长为 4 的正方形的内部(含 π×12 π 边界),区域 E 表示单位圆及其内部,因此 P= = . 4×4 16 π 答案: 16
2 2
π 2 π 以输出的有序实数对(x,y)的概率 P= = . 2 4
目录
考点3 与体积有关的几何概型 例3 有一个底面圆的半径为 1,高为 2 的圆柱,点 O 为这
个圆柱底面圆的圆心,在这个圆柱内随机取一点 P,则点 P 到点 O 的距离大于 1 的概率为________.
第十章3 三相空间电压矢量控制方式原理实验

实验10-3三相空间电压矢量变频原理实验
一、实验目的
(1)通过实验,掌握空间电压矢量控制方式的原理及其实现方法。
(2)熟悉与空间电压矢量控制方式有关的信号波形。
二、实验所需挂件及附件
三、实验方法
(1)接通挂件电源,关闭电机开关,并将调制方式设定在空间电压矢量方式下(将控制部分S、V两端用导线短接,P端悬空),然后打开电源开关。
(2)点动“增速”按键,将频率设定在0.5Hz,用示波器观测SVPWM 部分的三相矢量信号(在测试点“10、11、12”),三角载波信号(在测试点“14”), PWM信号(在测试点“13”),三相SVPWM调制信号(在测试点“15、16、17”);再点动“转向”按键,改变转动方向,再观测上述各信号的相位关系的变化。
(3)逐步升高频率,直至50Hz处,重复以上的步骤。
(4)将频率设置为0.5Hz~60Hz的范围内改变,在测试点“13”中观
160
测占空比与频率的关系(在V/F函数不变的情况下)。
四、实验报告
(1)简述空间电压矢量控制变频调速的原理。
(2)画出在试验中观测到的所有波形。
(3)简述注入“零矢量”的作用。
161。
第十章 电泳-3

电泳
6.2.3 进样系统
进样方式与常规电泳不同: 进样方式与常规电泳不同: 1、流体力学进样: 、流体力学进样:
电泳
♦进样体积: V inj 进样体积:
π ⋅ ∆ p ⋅ α 4 ⋅ t inj = 8η L
μeffi:电泳速度 μeo:电渗速度
E:电压 :
α:内半径
Ci: Ci:浓度
电泳
6.2.4 检测器
紫外吸收法:灵敏度达 ; ♦紫外吸收法:灵敏度达10-17g; ;(在 激光诱导荧光检测法:灵敏度 ;( 中插入 ♦激光诱导荧光检测法:灵敏度10-19g;(在DNA中插入 荧光试剂) 荧光试剂) ♦质谱检测法:10-21g; 质谱检测法: ; ♦核磁共振检测法: 10-21g。 核磁共振检测法: 。
1、毛细管区带电泳: 、毛细管区带电泳:
又称毛细管自由溶液电泳,最简单的一种毛细管电泳。 又称毛细管自由溶液电泳,最简单的一种毛细管电泳。 自由溶液电泳 分离机理: 分离机理: 被分离物质荷比的差异 质量与净电荷之比) 质荷比的差异( 被分离物质荷比的差异(质量与净电荷之比)
电泳
2、毛细管凝胶电泳(CGE) 、毛细管凝胶电泳( )
第六节 高效毛细血管电泳
• HPCE:高效毛细血管电泳 : (high performance capillary electrophoresis) ) 在极细的管内实现具有高效、快速( )、灵敏度高 在极细的管内实现具有高效、快速(0.5h)、灵敏度高 )、 的一大类电泳分析技术
电泳
6.1 基本原理
6.1.1 常用术语 电泳淌度( 电泳淌度(electric field mobility,µef)(泳动度) , )(泳动度) 泳动度 带电粒子在毛细管中,电泳速度与所在电场强度之比。 带电粒子在毛细管中,电泳速度与所在电场强度之比。
第10章3沙门菌属

二、主要生物学特性
• (一)形态染色
– 多具有周身鞭毛, 能运动,有时也会 出现无鞭毛的突变 型。
2020/9/18
(二)培养
2020/9/18
猪霍乱沙门菌SS
2020/9/18
伤寒沙门菌菌落特征(SS)
2020/9/18
伤寒沙门菌菌落特征(血平板)
伤寒、副伤寒沙门氏菌与 大肠杆菌菌落形态鉴别
• 分离菌株可排除沙门菌:
– 乳糖+ 、吲哚+ :可排除沙门菌 – 脲酶+:可排除沙门菌
• 属间鉴别
2020/9/18
• 2、最后鉴定(属内鉴定)
– (1)生化鉴定: – (2)血清学分型:
2020/9/18
位相诱导
• 1. Gard氏半固体琼脂平板传代法 • 2. Gard氏位相诱导法 • 3.软琼脂斜面位相诱导法 • 4.毛细管法
• 对动物致病
– 如鸡沙门菌、都柏林沙门菌(牛)。
• 对人和动物都能致病
– 如鼠伤寒沙门菌、猪霍乱沙门菌和肠炎沙门菌等。
• 沙门菌可致多种感染
– 轻者为自愈性胃肠炎,重可引起致死性伤寒等。
2020/9/18
所致疾病
• 伤寒和副伤寒 • 急性胃肠炎或食物中毒 • 菌血症(或败血症)
2020/9/18
沙门菌属
大肠杆菌
MAC平板 不发酵乳糖(无色)的光 发酵乳糖(粉色)的光滑
滑型菌落
型菌落
SS平板
不发酵乳糖、产H2S (中 心黑色的无色菌落) 或不 产H2S
发酵乳糖(粉色)菌落
2020/9/18
(三)生化反应
• 具有肠杆菌一般特征
– 如氧化酶-,触酶+,还原硝酸盐
• 不发酵乳糖和蔗糖 • 发酵葡萄糖、麦芽糖和甘露醇发酵,产酸、产
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章3#导流洞工程施工方法说明及附图
10.1 概述
10.1.1 工程概况
3#导流洞由引渠段、闸室段、无压洞段和出口挑流鼻坎组成,设计最大流量3700m3/s,最大流速41.63m/s。
进口引渠段长65.0m,底板高程2745.00m,建基面高程2742.00m,引渠底板及边坡均采用混凝土保护。
进口闸室段采用岸塔式,进口采用短有压接无压的型式,闸室建基面高程2740.00m,底板高程2745.00m,闸室顶高程2793.00m。
闸室尺寸为47.0m×22.0m×53.0m(长×宽×高),设一弧形闸门承担蓄水时调节下泄流量和下闸封堵的任务,闸室闸门孔口尺寸为12.0m×14.0m(宽×高)。
无压洞段长1209.99m(出口洞段与竖井泄洪洞完全结合段长940.52m),底板纵坡采用变坡设计,分别为i=0.06和i=0.09655,洞身为城门洞型,随着洞身水面线变化断面尺寸分别为12.0m×15.5~22.0m(宽×高)。
非结合洞段设1道掺气坎,洞身采用钢筋混凝土衬砌,衬砌厚度分别为1.2m、1.0m。
3#导流洞工程特性见表10-1-1。
表10-1-1 3#导流洞工程特性表
10.1.2 地质条件
进水塔地基为弱风化、弱卸荷砂板岩,岩石较坚硬,中厚层状—镶嵌结构为主,岩体完整性总体较差,但嵌合较紧密,工程岩体分类为Ⅳ2类,地基强度较低,基础内砂板岩变形差异较大,尤其是基础内挤压破碎带等软弱带(Ⅴ2类),其承载和抗变形能力较低,基础岩体均一性差。
沿洞线最大埋深约360m,出露的地层为T3lh1(2)、T3lh1(4)、T3lh1(5)层及T3lh2(1)—T3lh2(5)层,f1、f8系列、f9、f10、f11、f13等断层与泄洪洞轴线大角度相交。
0+000~0+004m为T3lh1(2)层变质粉砂岩夹板岩,岩体弱风化、弱卸荷,岩石中等坚硬—软弱,块裂—镶嵌结构为主,岩体完整性差,卸荷松弛,透水性较强,围岩类别为Ⅳ类围岩,围岩自稳时间短,可能产生较大规模的变形破坏。
0+261~0+281m、0+281~0+430m、0+444~0+603m,微风化—新鲜T3lh1(5)、T3lh2(2)-①变质砂岩、变质粉砂岩及T3lh2(1)、T3lh2(3)砂板岩,岩石坚硬,中厚层—互层状结构为主,岩体较完整,嵌合紧密,透水性微弱,以Ⅲ1类为主,围岩基本稳定;0+000~0+261m、0+430~0+440m、0+603~1+116m,微风化—新鲜T3lh1(2)、T3lh1(4)、T3lh2(2)-②、T3lh2(4)、T3lh2(5)砂板岩,岩石较坚硬,中厚层状—镶嵌结构为主,岩体完整性总体较差,但嵌合较紧密,透水性弱,围岩类别以Ⅲ2类为主,围岩局部稳定性较差。
Ⅲ类围岩局部稳定性主要受结构面不利组合影响,其中①组或⑨组裂隙与④、⑥、②组裂隙构成不利的楔形体,其交棱线中陡倾墙外且与边墙呈。
