伯努利方程实验(二)
伯努利方程实验
实验二伯努利方程实验一.实验目的1.观察恒定流情况下,水流所具的位置势能、压强势能和动能,以及在各种边界条件下能量的守恒和转换规律,加深对能量方程物理意义的理解。
2.观察测压管水头线和总水头线沿程变化的规律,以及水头损失现象。
3.验证测速管〔毕托管〕原理。
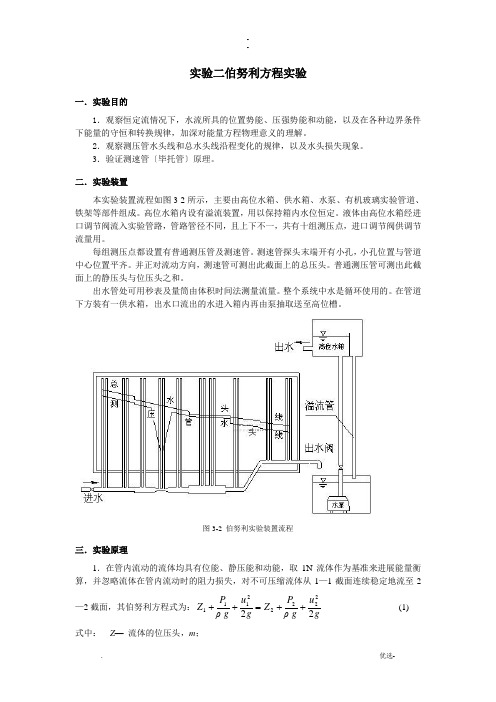
二.实验装置本实验装置流程如图3-2所示,主要由高位水箱、供水箱、水泵、有机玻璃实验管道、铁架等部件组成。
高位水箱内设有溢流装置,用以保持箱内水位恒定。
液体由高位水箱经进口调节阀流入实验管路,管路管径不同,且上下不一,共有十组测压点,进口调节阀供调节流量用。
每组测压点都设置有普通测压管及测速管。
测速管探头末端开有小孔,小孔位置与管道中心位置平齐。
并正对流动方向,测速管可测出此截面上的总压头。
普通测压管可测出此截面上的静压头与位压头之和。
出水管处可用秒表及量筒由体积时间法测量流量。
整个系统中水是循环使用的。
在管道下方装有一供水箱,出水口流出的水进入箱内再由泵抽取送至高位槽。
图3-2 伯努利实验装置流程三.实验原理1.在管内流动的流体均具有位能、静压能和动能,取1N 流体作为基准来进展能量衡算,并忽略流体在管内流动时的阻力损失,对不可压缩流体从1—1截面连续稳定地流至2—2截面,其伯努利方程式为:gu g ρP Z g u g ρP Z 2222222111++=++ (1)式中: Z — 流体的位压头,m ;gPρ— 流体的静压头,m ; gu 22— 流体的动压头,m ; 下标1和2分别为系统的进口和出口两个截面。
同样,取1N 流体作为基准来进展能量衡算,而流体在管内流动时的阻力损失能量不可忽略时,对不可压缩流体从1—1截面连续稳定地流至2—2截面,其柏努利方程式为:f h gu g ρP Z g u g ρP Z +++=++2222222111(2)式中:f h —1N 流体从1—1截面流至2—2截面时损失的能量,称损失压头,m 。
2.在管内稳定连续流动的不可压缩流体,忽略流体流动的阻力损失能量时,在管路上任意截面的总压头均相等。
伯努利方程实验

实验一 伯努利方程实验一、实验目的观察流体在管道中流动时能量的相互转化现象,加深对柏努利方程的理解。
原理二、实验原理流体在流动时,具有3种机械能:位能、静压能和动能,这3种机械能是可以相互转化的。
在没有摩擦损失的自流管路中,任意两截面处的机械能总和是相等的。
在有摩擦损失的自流管路中,任意两截面处的总机械能之差为摩擦损失。
2.对理想流体,在系统中任一截面处,尽管三种机械能彼此不一定相等,但这三种机械能的总和是不变的。
对于实际流体,由于在内摩擦,流体在流动过程中总有一局部机械能随摩擦转化为热能而损耗了,故对于实际流体,任意两截面上的机械能的总和并不相等,两者的差值即为能量损失。
3流体流经管路某截面处的各种机械能大小均可以用测压管中的一 段液柱高度来表示,在流体力学中,用以表示各种机械能大小的流体柱高度称之为“压头’。
分别称为位压头、动压头、静压头、损失压头。
机械能可用测压管中液柱的高度来表示。
当测压管口平行于流动方向时,液柱的高度表示静压能;当测压管口正对流体流动方向时,液柱的高度表示动能与静压能之和,两者之差就是动能。
实验中通过测定流体在不同管径、不同位置测压管中液面高度,反映出摩擦损失的存在及动能、静压能之间的相互转化。
〔4〕流体的机械能衡算,以单位质量〔1kg 〕流体为衡算基准,当流体在两截面之间稳定流动且无外功参加时,伯努利方程的表达形式为 式中z —— 位压头〔m 流体柱〕; —— 静压头〔m 流体柱〕; —— 动压头〔m 流体柱〕。
三、实验设备及流程 1. 实验装置流程C gv g p z =++22ρg Pρ22v如图3-1所示,实验设备由玻璃管、测压管、活动测压头、水槽、循环水泵等组成。
水槽中的水通过循环水泵将水送到高位槽,并由溢流口保持一定水位,然后流经玻璃管中的各测点,再通过出口阀A流回水箱,由此利用循环水在管路中流动观察流体流动时发生能量转化及产生能量损失。
活动测压头的小管端部封闭,管身开有小孔,小孔位置与玻璃管中心线平齐,小管又与测压管相通,转动活动测压头就可以测量动、静压头。
实验一伯努利方程实验报告 2

液压传动实验报告姓名:陈国庆学号:0806110902班级:机械1107班实验一 伯努利方程实验一、实验目的要求1.验证流体恒定流动时的总流伯努利方程; 2.进一步掌握有压管流中,流动液体能量转换特性;3.掌握流速、流量、压强等动水力学水流要素的实际量测技能。
二、实验原理实际流体在做稳定管流时的总流伯努利方程为:2211122212f12p p z z h g 2g g 2g-αυαυ++=+++ρρ选测压点⑴~⒁,从相应各测压管的水面读数测得z+p/r 值,并分别计算各测点速度水头,并将各过流断面处速度水头与z+p/r 相加,据此,可在管流轴线图上方绘制出测压管水头线P-P 和总水头线E-E (见图2-1)。
液体流动时的机械能,以位能、压力能和动能三种形式出现,这三种形式的能量可以互相转换,在无流动能量损失的理想情况下,它们三者总和是一定的。
伯努利方程表明了流动液体的能量守恒定律。
对不可压缩流体恒定流动的理想情况,总流伯努利方程可表示为:2211122212p P z z C g 2g g 2gαυαυ++=++=ρρ (C 为常数)对实际液体要考虑流动时水头损失,此时方程变为:2211122212f12p p z z h g 2g g 2g-αυαυ++=+++ρρ2f1h -为1、2两个过流断面间单位重量流体的水头损失。
三、实验方法和步骤:1.选择实验管B 上的⑴~⒁十四个过流断面,每个过流断面对应有一根测压管。
2.开启水泵。
使恒压水箱溢流杯溢流,关闭节流阀31后,检查所有测压管水面是否平齐(以工作台面为基准)。
如不平,则应仔细检查,找出故障原因(连通管受阻、漏气、有气泡) ,并加以排除,直至所有测压管水面平齐。
3.打开节流阀31,观察测压管○1~○14的水位变化趋势,观察流量增大或减小时测压管水位如何变化。
4.当节流阀31的开度固定后,记测各测压管液位高度(即pz g+ρ的值),同时测量出实验管B 中的流量。
伯努利方程实验
实验二柏努利方程实验一、实验目的1、熟悉流体流动中各种能量和压头的概念及其相互转换关系,在此基础上,掌握柏努利方程;2、观察流速变化的规律;3、观察各项压头变化的规律。
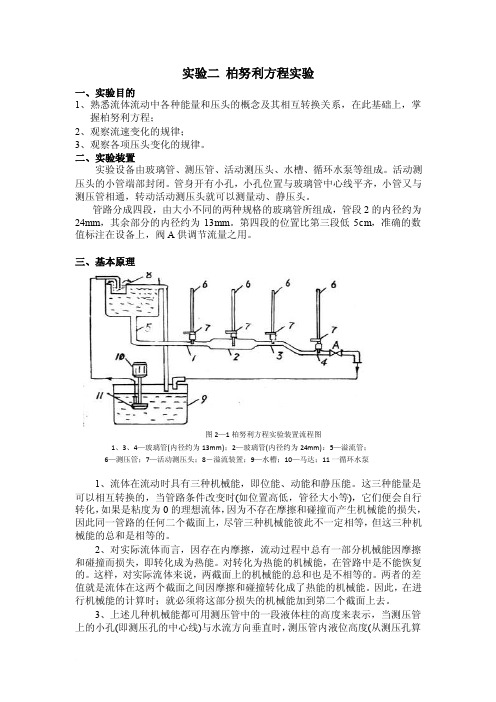
二、实验装置实验设备由玻璃管、测压管、活动测压头、水槽、循环水泵等组成。
活动测压头的小管端部封闭。
管身开有小孔,小孔位置与玻璃管中心线平齐,小管又与测压管相通,转动活动测压头就可以测量动、静压头。
管路分成四段,由大小不同的两种规格的玻璃管所组成,管段2的内径约为24mm,其余部分的内径约为13mm。
第四段的位置比第三段低5cm,准确的数值标注在设备上,阀A供调节流量之用。
三、基本原理图2—1柏努利方程实验装置流程图1、3、4—玻璃管(内径约为13mm);2—玻璃管(内径约为24mm):5—溢流管;6—测压管;7—活动测压头;8-溢流装置;9—水槽;10—马达;11一循环水泵1、流体在流动时具有三种机械能,即位能、动能和静压能。
这三种能量是可以相互转换的,当管路条件改变时(如位置高低,管径大小等),它们便会自行转化,如果是粘度为0的理想流体,因为不存在摩擦和碰撞而产生机械能的损失,因此同一管路的任何二个截面上,尽管三种机械能彼此不一定相等,但这三种机械能的总和是相等的。
2、对实际流体而言,因存在内摩擦,流动过程中总有一部分机械能因摩擦和碰撞而损失,即转化成为热能。
对转化为热能的机械能,在管路中是不能恢复的。
这样,对实际流体来说,两截面上的机械能的总和也是不相等的。
两者的差值就是流体在这两个截面之间因摩擦和碰撞转化成了热能的机械能。
因此,在进行机械能的计算时;就必须将这部分损失的机械能加到第二个截面上去。
3、上述几种机械能都可用测压管中的一段液体柱的高度来表示,当测压管上的小孔(即测压孔的中心线)与水流方向垂直时,测压管内液位高度(从测压孔算起)即为静压头,它反映测压点处液体压强大小。
当测压孔由与水流方向垂直方位转为正对水流方向时,测压管内液位将因此上升,所增加的液位高度即为测压孔处液体的动压头,它反映出该点水流动能的大小。
最新伯努利方程实验实验报告

伯努利方程实验实验目的:1、 熟悉流体流动中各种能量和压头的概念及其相互转化关系,加深对伯努利方程的理解。
2、 观察各项能量(或压头)随流速的变化规律。
基本原理:不可压缩流体在管内作稳定流动时,由于管路条件的变化,会引起流动过程中三种机械能――位能、动能、静压能的相应改变及相互转换,对于理想流体,在系统内任一截面处,虽然三种能量不一定相等,但是能量之和是守恒的。
而对于实际流体,由于存在内摩擦,流体在流动中总有一部分机械能随摩擦和碰撞转化为热能而损耗了。
所以对于实际流体,任意两截面上机械能总和并不相等,两者的差值即为机械能损失。
f H gu g p Z g u g p Z ∑+++=++2222222111ρρ 以上几种机械能均可用测压管中的液贮高度来表示,分别称为位压头、动压头、静压头。
当测压直管中的小孔与水流方向垂直时,测压管内液柱高度即为静压头;当测压孔正对水流方向时,测压管内液柱高度则为静压头和动压头之和。
测压孔处流体的位压头由测压孔的几何高度确定。
任意两截面间位压头、静压头、动压头总和的差值,则为损失压头。
1为高位水槽; 2为玻璃管; 3为测压管; 4为循环水槽; 5为阀门;6为循环水泵; 操作步骤:1、 关闭阀5,启动循环泵6,旋转测压孔,观察并记录各测压管中液柱高度h ;2、 将阀5开启到一定大小,观察并记录测压孔正对和垂直于水流方向时,测压管中心的液柱高度h ’和h ’’。
3、 继续开大阀5,测压孔正对水流方向,观察并记录测压管中液柱高度h ’’;4、 在阀5开到一定时,用量筒、秒表测定液体的体积流量。
问题讨论:1、 关闭阀5时,各测压管内液位高度是否相同,为什么?答:相同。
因为流体静止时,u =0,ΣH f =0。
所以有Z +h =常数。
根据上面的流程图,设ABC 的高度为Z ,其液体高度分别为h A 、h B 、h C ,则有h A +Z = h B +Z = h C +Z =常数,所以h A =h B =h C =h 。
流体力学-伯努利方程实验报告

中国石油大学(华东)工程流体力学实验报告实验日期:2014.12.11 成绩:班级:石工12-09学号:12021409姓名:陈相君教师:李成华同组者:魏晓彤,刘海飞实验二、能量方程(伯诺利方程)实验一、实验目的1.验证实际流体稳定流的能量方程;2.通过对诸多动水水力现象的实验分析,理解能量转换特性;3.掌握流速、流量、压强等水力要素的实验量测技能。
二、实验装置本实验的装置如图2-1所示。
图2-1 自循环伯诺利方程实验装置1. 自循环供水器;2.实验台;3. 可控硅无极调速器; 4 溢流板; 5. 稳水孔板;6. 恒压水箱;7. 测压机;8滑动测量尺;9. 测压管;10. 试验管道;11.测压点;12 皮托管;13. 试验流量调节阀说明本仪器测压管有两种:(1)皮托管测压管(表2-1中标﹡的测压管),用以测读皮托管探头对准点的总水头;(2)普通测压管(表2-1未标﹡者),用以定量量测测压管水头。
实验流量用阀13调节,流量由 调节阀13 测量。
三、实验原理在实验管路中沿管内水流方向取n 个过水断面。
可以列出进口断面(1)至另一断面(i )的能量方程式(i =2,3,…,n )i w i i ii h gv p z gp z -+++=++122221111αγυαγ取12n 1a a a ==⋅⋅⋅==,选好基准面,从已设置的各断面的测压管中读出 z+p/r 值,测出 透过管路的流量 ,即可计算出 断面平均流速 ,从而即可得到 各断面测压管水头和总水头 。
四、实验要求1.记录有关常数 实验装置编号 No._4____均匀段1d = 1.40 -210m ⨯;缩管段2d = 1.01-210m ⨯;扩管段3d =2.00-210m ⨯;水箱液面高程0∇= 47.6 -210m ⨯; 上管道轴线高程z ∇= 19 -210m ⨯ (基准面选在标尺的零点上)2.量测(pz γ+)并记入表2-2。
注:ii i p h z γ=+为测压管水头,单位:-210m ,i 为测点编号。
伯努利方程实验实验报告

伯努利方程实验实验报告实验名称:伯努利方程实验实验目的:1.验证伯努利方程的有效性;2.学习使用伯努利方程进行流体力学分析;3.掌握测量流体压力和流速的实验技巧。
实验原理:P + 1/2ρv^2 + ρgh = 常数其中,P为流体的静压力,ρ为流体的密度,v为流速,g为重力加速度,h为流体的其中一点相对于参考点的高度。
伯努利方程表明了流体流动过程中的能量守恒。
实验器材:1.伯努利装置(包括水槽、水泵、流量调节阀、压力计等材料)2.压力计3.流速计实验步骤:1.构建伯努利装置,包括水泵接通电源,调节流量阀使水槽中的水量保持稳定。
2.选取三个高度不同的位置,在各个位置上分别测量对应的静压力、流速和高度。
3.使用压力计分别测量各个位置的静压力,并记录下来。
4.使用流速计分别测量各个位置的流速,并记录下来。
5.使用尺子测量各个位置处相对于参考点的高度,并记录下来。
实验数据记录:位置1:静压力:P1=20Pa流速:v1=1m/s相对高度:h1=0m位置2:静压力:P2=30Pa流速:v2=1.5m/s相对高度:h2=1m位置3:静压力:P3=40Pa流速:v3=2m/s相对高度:h3=2m实验结果计算:根据伯努利方程,我们可以得到以下等式:P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2 = P3 +1/2ρv3^2 + ρgh3代入实验数据:20+1/2×ρ×1^2+ρ×0×9.8=30+1/2×ρ×1.5^2+ρ×1×9.8=40+1 /2×ρ×2^2+ρ×2×9.8化简等式,解方程组,求解出流体密度ρ。
实验讨论:通过实验测量的数据进行计算,我们可以得到流体密度的数值。
对于实验结果的误差分析和原因探究,可以从测量仪器的精度、实验操作的误差以及系统误差等方面进行分析。
伯努利方程实验

柏努利方程实验(一)实验目的1、了解流体以恒定流流经特定管路(柏努利方程实验管)时一些(四个)特定截面上的总压头⎪⎪⎭⎫ ⎝⎛++g u p Z 22ρ、测压管压头⎪⎪⎭⎫ ⎝⎛+ρp Z ,并计量出相应截面的静压头ρp 和动压(g u 22),再绘制出近似的压头线,从而加深对柏利方程的理解和认识。
2、学会各种压头的测试和计量方法。
3、了解一种测量流体流速方法—皮托管测速方法的原理。
(二)实验装置及其工作原理实验装置的结构示意图如图1所示。
柏努利方程实验装置主要由恒水位水箱6、柏努利方程实验管4、测压管5、蓄水箱7、离心泵供水系统(自循环)和电测流量装置等组成。
恒水位水箱6靠溢流来维持其恒定水位,在水箱左下部装接水平放置的柏努利方和实验管4,恒水位水箱中的水可经柏努利方程实验管以恒定流流出,并可通过出水阀门2调节其出流量。
恒定流以一定流量流经实验管道时,通过布设在实验管4个截面上的测压孔及其测压管(8根)5,可以观察到相应截面上的各各压头的高低,从而可以分析管道中稳定液流的各种能量形式、大小及其相互转化关系。
图4-2 柏努利方程实验装置结构示意图1-电测流量装置及其计量水箱 2-出水阀门 3-流量显示仪 4-柏努利方程实验管 5-测压管 6-恒水位水箱 7-储水箱 8-水泵 9-进水阀门 10-实验台桌 11-集水槽实验时,还需要测定液流的流量。
在阀门2的下面,装有回水箱和计量水箱,计量水箱里装有电测流量装置1(由浮子、光栅计量尺光电传感器组成),可以在电测流量仪3上直接数显出实验时的流体流量(数显出流体积W[立升]和相应的出流时间τ [秒]从而可以计算出流量Vs 来)。
回水箱和计量水箱中的水可以通过集水槽12,回流到储水箱7中。
柏努利方程实验管4上每个测量截面上的一组测压管都相当于一个皮托管,所以,通过实验,也可以了解一种测量流量的原理和方法。
(三)实验操作1、实验前的准备 1)关闭出水阀门22)打开进水阀门9后,按下流量显示仪3上的水泵开关,启动水泵8,向恒水位水箱6上水。
伯努利方程实验实验报告

伯努利方程实验实验报告伯努利方程实验报告实验一伯努利方程一、实验目的1.理解液体的静压原理2.验证伯努利方程3.验证液体在流动状态下压力损失与速度的关系二、实验仪器伯努利方程实验装置三、实验原理伯努利方程是流体动力学中一个重要的基本规律,是能量守恒定律在流体力学中的具体应用。
主要反映液体在恒定流动时压力能、位能和动能三者之间的关系,即在任一截面上这三种能量形式之间可以互相转换,但三者之和为一定值,即能量守恒。
22p1u1p2u2?z1z2?理想液体的伯努利方程为:?g2g?g2g2p1?u12p2?u2z1z2hw实际液体的伯努利方程为:g2gg2g当液体处于静止状态时,液体内任一点处的压力为:p?p0??gh这是液体静力学基本方程式。
四、实验装置伯努利试验仪主要由实验导管、稳压溢流槽和四对测压管所组成。
实验导管为一水平装置的变径圆管,沿程分四处设置测压管。
每处测压管由一对并列的测压管组成,分别测量该截面处的静压头(压力能)和冲压头(压力能、位能和动能三者之和)。
实验装置的流程如图1所示。
液体由稳压槽流入实验导管,途径A点、B点、C点、D点直径分别为15mm、34mm、15mm、15mm的管子,最后排出设备。
液体流量由出口调节阀调节。
流量由流量计读出。
五、实验步骤实验前,先缓慢开启进水阀,将水充满稳压溢流水槽,并保持有适量溢流水流出,使槽内液面平稳不变。
最后,设法排尽设备内的空气泡,否则会干扰实验现象和测量的准确性。
1.关闭实验导管出口调节阀,观察和测量液体处于静止状态下各测试点(A、B、C和D四点)的压力,验证液体的静压原理。
并设定此处的水位高度为基准面。
2.开启实验导管出口调节阀,保持稳压溢流水槽有适量溢流水流出,观察比较液体在流动情况下的各测试点的压头变化。
3.缓慢调节实验导管的出口调节阀,测量液体在不同流量下的各测试点的静压头、动压头和损失压头,并记录下各项数据。
4.实验结束后,应先关闭进水的总阀门,然后再开大出口调节阀,排尽稳压溢流水槽内的水。
伯努利方程实验
注意:一是阀门开启中,要保证测压管液面不要降到标尺零点以下。二是随时观察上水箱、计量水箱水位高度,要使水位保持一个合理水位,防止水溢出水箱和水箱见底。
五、实验结果及要求
1、流量调整稳定后,基准面选在标尺的零点,将各测点的测压管水头( ),以及计量水箱流入水的水位高度差 和流入时间一并记入表1,并计算出每次实验时的平均流量。
2、根据连续性方程,利用体积法,计算出不同断面的流速,以及相应的速度水头,将计算结果记
表1测压管水头表(单位:mm)
测点编号
A
A’
B
B’
C
C’
D
D’
H
(mm)
T
(s)
Q
实验
次数
1
2
3
*计量水箱底面积为240*365mm2
表2各断面速度与速度水头(体积法)
断面编号
(计算项目)
A
B
C
D
直径
(mm)
流速
速度水头(mm)
4、打开并逐步调整流量调节阀11,观察流量增加或减少时,各测点测压管水头(径向测点)和各测点总水头(轴向测点)的变化趋势,以及它们与位置水头、压强水头之间的相互关系。
5、调整流量调节阀11适当开度,并待流量稳定后,记录各测压管液面读数。与此同时,观察计量水箱13中水位的高度,用直尺和秒表分别记录计量水箱13中水位的高度差以及所用时间,并计算出流入水箱的体积和相应的平均流量。
1
2
3
入表2。
3、根据各测点测压管高度,以及计算的各断面的流速水头和总水头,记入表3中,沿管路绘制出的测压管水头线和总水头线,并分析测压管水头线和总水头线的变化规律。
化工原理伯努利试验

三、实验装置
整个装置由高位槽、透明测量管和测压管三部分组成。 透明测量管由小透明管、大透明管和弯管三段组成。在测量管的适当位置安装了四根测压管10,测压 管与透明管的连接采用活动测头12,活动测头一端伸入透明测量管,端部的取压小孔中心线与透明管的 中心线处于同一水平面,其另一端与测压管相连接,活动测头可以旋转,使取压孔可以在水平面上旋转 360度,以便测取同一截面上的静压头和动压头。 § 小管内径d1=16mm,大管内径d2=22mm,弯管内径d3=16mm。 第4个取压点位置比第3个低70mm。
3、阀门开度不变,将取压孔旋至与水流方向垂直,观察并记录各测压管液位Hc。 § 思考题: (1)阀门开度未变,为什么各测压管液位下降?
(Hb-Hc)代表什么压头? (2)比较各点的(Hb-Hc),可以说明什么问题? (3)H2c可能大于H1c,如何解释?
4、将调节阀开至最大,取压孔正对水流方向,观察并记录测压管液位Hd,并测量此时水的体积流量 (方法同2)。
五、实验结果分析
1、在直角坐标纸上,以纵坐标表示压头,横坐标表示测点距离,把各点在不同流量下的位能、势能 (位能+静压能)和总能(位能+静压能+动能)以及能量损失以压头形式表示出来。
2、运用Bernoulli方程分析各项能量变化情况。 3、阻力损失与流速的关系 以第2号测点在不同流量下的数据,分析压头损失与流速的关系。
谢谢大家!
g1zp1u212 g2zp2u222Wf
式中各项能量均以单位质量流体为衡算基准,单位为J/kg
§ 如果以单位重量流体为衡算基准
z1pg 12 u1 g 2 z2pg 22 ug 2 2Hf
式中z称为位压头,
p g 称为静压头,
化工原理 伯努利方程

伯努利方程流体宏观运动机械能守恒原理的数学表达式。
1738年瑞士数学家D.伯努利在《水动力学──关于流体中力和运动的说明》中提出了这一方程。
它可由理想流体运动方程(即欧拉方程)在定态流动条件下沿流线积分得出;也可由热力学第一定律导出。
它是一维流动问题中的一个主要关系式,在分析不可压缩流体的定态流动时十分重要,常用于确定流动过程中速度和压力之间的相互关系。
方程的形式 对于不可压缩的理想流体,密度不随压力而变化,可得:Zg+22u P +ρ=常数式中Z 为距离基准面的高度;P 为静压力;u 为流体速度;ρ为流体密度;g 为重力加速度。
方程中的每一项均为单位质量流体所具有的机械能,其单位为N ·m/kg ,式中左侧三项,依次称为位能项、静压能项和动能项。
方程表明三种能量可以相互转换,但总和不变。
当流体在水平管道中流动时Z 不变,上式可简化为:ρPu +22=常数 此式表述了流速与压力之间的关系:流速大处压力小,流速小处压力大。
对于单位重量流体,取管道的1、2两截面为基准,则方程的形式成为:gu g P Z g u g P Z 2222222111++=++ρρ 式中每一项均为单位重量流体的能量,具有长度的因次,三项依次称为位头、静压头和动压头(速度头)。
对于可压缩理想流体,密度随压力而变化。
若这一变化是可逆等温过程,则方程可写成下式:1211222211ln 22P PP u gZ u gZ ρ++=+若为可逆绝热过程,方程可写为:1211222211ln 22P PP u gZ u gZ ρ++=+式中γ为定压比热容Cp 和定容比热容Cv 之比,即比热容比,也称为绝热指数。
对于粘性流体,流动截面上存在着速度分布,如用平均流速u 表达动能项,应对其乘以动能校正系数d ο。
此外,还需考虑因粘性引起的流动阻力,即造成单位质量流体的机械能损失h f ,若在流体流动过程中,单位质量流体又接受了流体输送机械所做的功W ,在这些条件下,若取处于均匀流段的两截面1和2为基准,则方程可扩充为:α值可由速度分布计算而得, 流体在圆管内作层流流动时α=2;作湍流流动时,α≈1.06。
实验二 伯努利实验报告

gZ1 +
p1 ρ
+
1 2
u12
=
gZ2
+
p2 ρ
+
1 2
u22
+ Σhf
J ⋅ kg−1
(1)
若以单位重量流体 为横算基准时差,则又可表达为:
Z1
+
p1 gρ
+
1 2g
u12
伯努利实验装置,温度计,500ml 量筒(或容器与台秤),秒表一个。 【实验注意事项】
1、实验前一定要将试验导管和测压管中的空气泡排出干净,否则会干扰实验现象和测 量的准确性。
2、开启进水阀向稳压水槽注水,或开关试验导管出口调节阀时,一定要缓慢地调节开 启程度,并随时注意设备内的变化。
3、试验过程中需根据测压管量程范围,确定最大和最小流量。 4、为了便于观察测压管的液柱高度,可在临实验测定前,向各测压管滴入几滴红墨水。 【实验目的】
=
Z2
+
p2 ρg
+
1 2
u22
+
ΣH
f
m液柱
(2)
式中: Z 是流体的位压头,单位是 m 为液柱; p 是液体的压强,单位是 Pa ; u 是流体的
平均流速,单位是 m ⋅ s−2 ; ρ 为流体的密度,单位是 kg ⋅ m3; Σhf 是系统内因阻力造成的能
量损失,单位是 J ⋅ kg −1 ; ΣH f 是流动系统内因阻力造成的压头损失,单位是 m液柱 。下
实验序号
温度
密度
A
伯努利方程能量实验报告

一、实验目的1. 通过实验,加深对伯努利方程式及能量之间转换的了解。
2. 观察水流沿程的能量变化,并了解其几何意义。
3. 了解压头损失大小的影响因素。
二、实验原理伯努利方程是描述流体在稳态流动过程中能量守恒的方程。
对于不可压缩流体,伯努利方程可表示为:P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2其中,P1、P2分别为流体在截面1和截面2处的压强;ρ为流体密度;v1、v2分别为流体在截面1和截面2处的流速;g为重力加速度;h1、h2分别为流体在截面1和截面2处的位能。
在实验过程中,通过测量不同截面处的压强、流速和位能,可以验证伯努利方程的正确性,并观察能量在流动过程中的变化。
三、实验仪器与设备1. 实验装置:水槽、实验管道、阀门、测压管、计时器等。
2. 测量工具:压力表、流速计、尺子等。
四、实验步骤1. 将实验装置组装完毕,确保各连接部位密封良好。
2. 将水注入实验管道,调整水位,确保管道内水流稳定。
3. 在管道上设置多个测点,分别测量各点的压强、流速和位能。
4. 记录各测点的数据,包括压强、流速、位能等。
5. 根据伯努利方程,计算各测点处的总能量,并分析能量变化规律。
五、实验结果与分析1. 实验数据记录如下:测点 | 压强P (Pa) | 流速v (m/s) | 位能h (m) | 总能量E (J/kg)----|----------|----------|--------|---------1 | 1000 | 1.5 | 0.5 | 15002 | 950 | 2.0 | 0.6 | 15503 | 900 | 2.5 | 0.7 | 16004 | 850 | 3.0 | 0.8 | 16502. 根据伯努利方程,计算各测点处的总能量:E1 = P1 + 1/2ρv1^2 + ρgh1 = 1000 + 1/2 × 1000 × 1.5^2 + 1000 × 9.8 × 0.5 = 1500 J/kgE2 = P2 + 1/2ρv2^2 + ρgh2 = 950 + 1/2 × 1000 × 2.0^2 + 1000 × 9.8 × 0.6 = 1550 J/kgE3 = P3 + 1/2ρv3^2 + ρgh3 = 900 + 1/2 × 1000 × 2.5^2 + 1000 × 9.8 × 0.7 = 1600 J/kgE4 = P4 + 1/2ρv4^2 + ρgh4 = 850 + 1/2 × 1000 × 3.0^2 + 1000 × 9.8 × 0.8 = 1650 J/kg3. 分析实验结果:(1)从实验数据可以看出,随着流速的增加,总能量呈线性增加。
(二)流体机械能转换

实验名称:流体机械能转换学院:环境与化学工程学院专业:化学工程与工艺班级: 14化工02班姓名:胡海明学号: 21404070217指导教师:赵亚梅日期: 2016年11月16日 化工原理实验报告流体机械能转换一.实验目的1.研究流体各种形式能之间的关系及转化,加深对能量转化概念的理解。
2.深入了解伯努利方程的意义。
二.实验原理利用伯努利方程进行测量和计算三.实验装置及流程实验前,先关闭试验管出口调节阀,并将水灌满流水槽,然后开启调节阀,水由进水管流入流水槽,流经水平安装的实验导管后,实验导管排出水和溢流出来的水直接排入下水管道。
流体流量由试验导管出口阀控制。
进水管调节阀控制溢流水槽内的溢流量,以保持槽内液面稳定,保证流动系统在整个实验过程中维持稳定流动。
实验装置图四.实验步骤(一)演示1.静止流体机械能的分布及转换将实验导管出口阀全部关闭,与便于观察(也可在测压管内滴入几滴红墨水),观察A、B、C、D点处测压管内液压柱高低。
2、一定流量下流体的机械能分布及转换缓慢调节进水管内调节阀,调节流量使流水槽中有足够的水溢出,在缓慢开启试验管出口调节阀,使导管内水流动,当观察到实验管中部的两支测压水柱略有差别,将流量固定不变,当各测压管的水柱高度稳定不变时,说明导管内流动状态稳定。
可开始观察实验现象。
3.不同流量下稳定流体机械能分布及装机转换连续缓慢的开启试验管的出口阀,调节出口阀使流量不断加大,观察A、B、C、D处测压管内液柱变化(二)实验改变流体流量进行两次实验,记录数据五.实验记录及数据处理1.实验基本参数D=2.5㎝d=1.5㎝2.实验数据记录及整理由伯努利方程计算可得各组机械能如下表伯努利方程Z1g+ += Z2g+ +由实验结果可得:Z1g+ +> Z3g+ +Z5g+ +> Z7g+ +Z2g+ +> Z4g+ +Z6g+ +> Z8g+ +由于实际流体在流动时存在阻力损失,因此Z1g+ += Z3g+ ++理想流体在管内稳态流动,若无外加能量和损失,则可得Z1g+ += Z3g+ +六.实验结果与讨论1.管内的空气泡会干扰实验现象,请问如何排除?答:减小流量,使测压管内的水溢出以排除气泡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
伯努利方程实验
—、实验设备的特点
1.实验装置体积小,重量轻,使用方便,移动方便。
2.实验测试导管、测压管均用玻璃制成便于观测。
3.所有设备采用了耐腐蚀材料制成管中不会生锈。
二、实验装置的基本情况(流程图见图一)
不锈钢离心泵 WB50/025 型
低位槽 880×370×550 材料不锈钢
高位槽 445×445×550 材料有机玻璃
实验测试导管的结构尺寸见图二中标绘
三、实验的操作方法:
1.将低位槽灌有一定数量的蒸馏水,关闭离心泵出口上水阀及实验测试导管
出口流量调节阀和排气阀、排水阀,打开回水阀和循环水阀而后启动离心泵。
2.逐步开大离心泵出口上水阀当高位槽溢流管有液体溢流后,利用流量调节
阀出水的流量。
3.流体稳定后读取并记录各点数据。
4.关小流量调节阀重复步骤。
5.分析讨论流体流过不同位置处的能量转换关系并得出结果。
6.关闭离心泵,实验结束。
四、使用设备时应注意的事项:
1.不要将离心泵出口上水阀开得过大以免使水流冲击到高位槽外面,同时导致高位槽液面不稳定。
2.流量调节阀开大时,应检查一下高位槽内的水面是否稳定,当水面下降时应适当开大泵上水阀。
3.流量调节阀须缓慢地关小以免造成流量突然下降测压管中的水溢出管外。
4.注意排除实验导管内的空气泡。
5.离心泵不要空转和出口阀门全关的条件下工作。
五.观察结果:(举例计算)
实验结果分析:
A截面的直径14mm;B截面的直径28mm;C截面、D截面的直径14mm;以D
截面中心线为零基准面(即标尺为125毫米)Z
D =0。
A、B、C截面Z
A
=Z
B
=Z
C
=125mm
A截面和D截面的距离为110mm。
由以上实验数据可以分析到
1.A 、D 截面间静压头的分析:
出口阀全开时,A 处和D 处的静压头分别为811和558mmH 2O 柱,从A 到D 静压头降低了70mmH 2O 柱。
这是因为,在A 、D 间列柏努利方程。
由于D 、A 截面积相等即动能相同。
f D
D
H z
g
p -
=
)
((
ρ 从A 到D 的减小值,决定于(Z A -Z D )和H f ,A-D 。
当(Z A -Z D )小于H f ,A-D 时,静压头的增值为负,反之,静压头的增值为正。
2.压头损失的计算:。
以出口阀全开时从A 到D 的压头损失和H f ,A-D 为例。
因为在A 、D 两截面间列柏努利方程。
f D D
D H Z g
u g p +++=++2
2ρ
所以,压头损失的算法之一是用冲压头来计算: )()2(2
D D D Z g u g p H +⎥⎦⎤⎢⎣⎡+-+=ρ
=(882-637)+(235-125)=245(mmH 2O 柱)
压头损失的算法之二是用静压头来计算:(u A =u D ) )()D D
Z g
p H +=ρ =(811-558)+(235-125)=253(mmH 2O 柱) 两种计算方法所得结果基本一致,说明所得实验数据是正确的
思考题:
1.为什么小流量时所观察到的读数比大流量时大?。
