2019年朝阳区理科一模及答案
2019届北京市朝阳区高三一模理综化学试卷【含答案及解析】
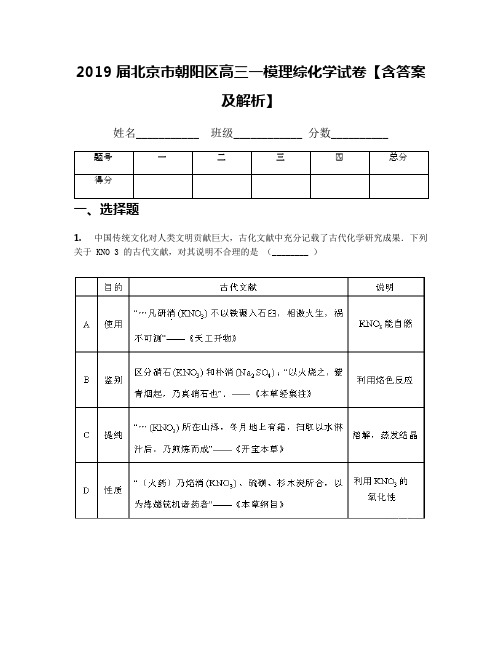
2019届北京市朝阳区高三一模理综化学试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 中国传统文化对人类文明贡献巨大,古化文献中充分记载了古代化学研究成果.下列关于 KNO 3 的古代文献,对其说明不合理的是(________ )2. N 2 (g) 与 H 2 (g) 在铁催化剂表面经历如下过程生成 NH 3 (g) :下列说法正确的是(________ )A .Ⅰ中破坏的均为极性键B .Ⅳ中 NH 3 与 H 2 生成 NH 3C .Ⅱ、Ⅲ、Ⅳ均为放热过程D .3. 下列检测方法不合理的是(________ )4. 某厂用 Na 除掉苯中的水分。
某次生产误将甲苯当做苯投进反应釜中,由于甲苯中含水量少,最后反应釜还残留大量的 Na 。
下列处理方法更合理、更安全的是(________ )A .打开反应釜,将 Na 暴露在空气中与氧气反应B .向反应釜通入 Cl 2 , Na 在 Cl 2 中燃烧生成 NaClC .向反应釜加大量 H 2 O ,通过化学反应“ 除掉” 金属钠D .向反应釜滴加 C 2 H 5 OH ,并设置放气管,排出氢气和热量5. 《常用危险化学用品贮存通则》规定:“ 遇火、遇热、遇潮能引起燃烧、爆炸或发生化学反应,产生有毒气体的化学危险品不得在露天或在潮湿、积水的建筑物中贮存” 。
下列解释事实的方程式中,不合理的是(________ )A .贮存液氮的钢瓶防止阳光直射:B .硝酸铵遇热爆炸:C .干燥的 AlCl 3 遇水产生气体:D .火灾现场存有电石,禁用水灭火:6. 下列“ 试剂” 和“ 试管中的物质” 不能完成“ 实验目的” 的是(________ )7. 某同学做如下实验:下列说法正确的是(________ )A .“ 电流计指针未发生偏转” ,说明铁片Ⅰ、铁片Ⅱ均未被腐蚀B .用 K 3 [Fe(CN) 3 ] 溶液检验铁片Ⅲ、Ⅳ附近溶液,可判断电池的正、负极C .铁片Ⅰ、Ⅲ所处的电解质溶液浓度相同,二者的腐蚀速率相等D .铁片Ⅳ的电极反应式为 Fe-3e - =Fe 3+二、推断题8. 有机物 A 为缓释阿司匹林的主要成分。
北京市朝阳区2019届高三一模数学(理)试题及答案

北京市朝阳区高三年级第一次综合练习数学(理) 2019.3本试卷共4页。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知集合A={x︳x>1},集合B={ x︳x²<4},则A∩B=A. {x︳x>-2}B. {x︳1<x<2}C. {x︳1≤x<2}D. R2. 在复平面内,复数z=对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. ()的展开式中的常数项为A. -12B. -6C. 6D. 124. 若函数f(x)=则函数f(x)的值域是A. (-∞,2)B. (-∞,2]C. [0,+ ∞)D. (-∞,0)∪(0,2)5. 如图,函数f(x)的图像是由正弦曲线或余弦曲线经过变换得到的,则f(x)的解析式可以是A. f(x)=sin(2x+)B. f(x)=sin(4x+)C. f(x)=cos(2x+)D. f(x)=cos(4x+)6. 记不等式组,所表示的平面区域为D,“点(-1,1)∈D”是“k”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件7. 某三棱锥的三视图如图所示(网格纸上小正方形的边长为1),则该三棱锥的体积为A. 4B. 2C.D.8. 某单位周一、周二、周三开车上班的职工人数分别是14、10、8,若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是A. 5B. 6C. 7D. 8第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分。
9. 双曲线-=1的右焦点到其一条渐近线的距离是10. 执行如图所示的程序框图,输出的x值为11.在极坐标系中,直线cosθ=1与圆cosθ交于A,B两点,则=12.能说明“函数f(x)的图像在区间[0,2]上是一条连续不断的曲线,若f(0), f(2)>0则f(x)在(0,2)内无零点”为假命题的一个函数是13.天坛公园是明、清两代皇帝“祭天”“祈谷”的场所,天坛公园中的圜丘台共有三层(如下页本题图1所示)上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石铺成(如下页本题图2所示),上层从第一环至第九还共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是;上、中、下三层坛所有的扇面形石块数是14.在平面内,点A是定点,动点B,C满足==1,·=0,则集合=+,1≤≤2|所表示的区域面积是三、解答题共6小题,共80分,解答应写出文字说明,演算步骤或证明过程15.(本小题满分13分)在△ABC中,a=,∠A=120°,△ABC的面积等于,且b<c,(I)求b的值;(II)求cos2B的值16.(本小题满分13分)某部门在同一上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客。
朝阳一模
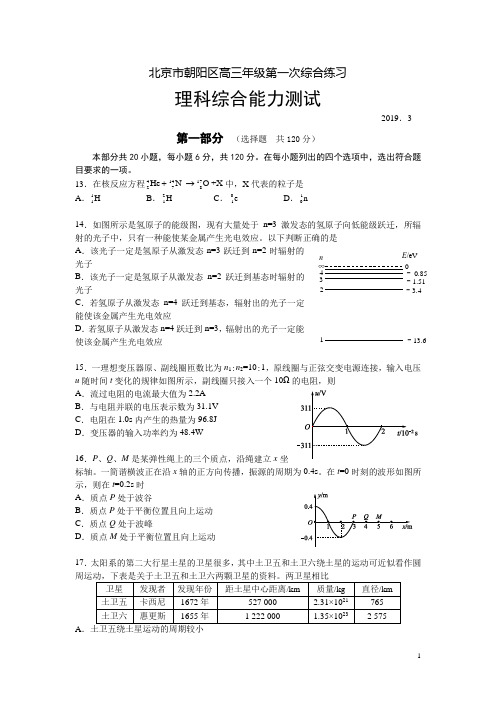
北京市朝阳区高三年级第一次综合练习理科综合能力测试2019.3第一部分 (选择题 共120分)本部分共20小题,每小题6分,共120分。
在每小题列出的四个选项中,选出符合题目要求的一项。
13.在核反应方程41417278He N O +X +→中,X 代表的粒子是 A .11H B .21H C .0-1e D .10n14.如图所示是氢原子的能级图,现有大量处于n=3激发态的氢原子向低能级跃迁,所辐射的光子中,只有一种能使某金属产生光电效应。
以下判断正确的是 A .该光子一定是氢原子从激发态n=3跃迁到n=2时辐射的光子 B .该光子一定是氢原子从激发态n=2跃迁到基态时辐射的光子 C .若氢原子从激发态n=4跃迁到基态,辐射出的光子一定能使该金属产生光电效应 D .若氢原子从激发态n=4跃迁到n=3,辐射出的光子一定能使该金属产生光电效应15.一理想变压器原、副线圈匝数比为n 1:n 2=10:1,原线圈与正弦交变电源连接,输入电压u 随时间t 变化的规律如图所示,副线圈只接入一个10Ω的电阻,则 A .流过电阻的电流最大值为2.2A B .与电阻并联的电压表示数为31.1V C .电阻在1.0s 内产生的热量为96.8J D .变压器的输入功率约为48.4W16.P 、Q 、M 是某弹性绳上的三个质点,沿绳建立x 坐标轴。
一简谐横波正在沿x 轴的正方向传播,振源的周期为0.4s 。
在t =0时刻的波形如图所示,则在t =0.2s 时 A .质点P 处于波谷B .质点P 处于平衡位置且向上运动C .质点Q 处于波峰D .质点M 处于平衡位置且向上运动 17.太阳系的第二大行星土星的卫星很多,其中土卫五和土卫六绕土星的运动可近似看作圆周运动,下表是关于土卫五和土卫六两颗卫星的资料。
两卫星相比A .土卫五绕土星运动的周期较小 1 2 3 4 ∞n- 13.6 - 3.4- 1.51 - 0.85 0 E/eVB .土卫五绕土星运动的线速度较小C .土卫六绕土星运动的角速度较大D .土卫六绕土星运动的向心加速度较大18.插有铁芯的线圈(电阻不能忽略)直立在水平桌面上,铁芯上套一铝环,线圈与电源、开关相连。
北京市朝阳区2019届高三一模数学(理)(解析版)

北京市朝阳区高三年级第一次综合练习数 学(理)2019.3本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知集合A ={x ︳x >1},集合B ={ x ︳x²<4},则A∩B = A. {x ︳x >-2} B. {x ︳1<x<2}C. {x ︳1≤x<2}D. R答案:B考点:集合的运算,一元二次不等式。
解析:集合B ={ x ︳-2<x <2},所以,A∩B ={ x ︳1<x <2},选B 。
2. 在复平面内,复数z =12ii+对应的点位于 A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案:D考点:复数的运算,复数几何意义。
解析:z =212(12)2i i ii i i ++==-,对应的点为(2,-1),在第四象限。
3. 41)x x-(的展开式中的常数项为 A. -12 B. -6 C. 6 D. 12答案:C考点:二项式定理。
解析:4241441()()(1)r r r r r r r T C x C x x--+=⨯-=-,令2r-4=0,得r =2,x 的系数为:24C =6 4. 若函数f(x)=则函数f(x)的值域是A. (-∞,2)B. (-∞,2]C. [0,+ ∞)D. (-∞,0)∪(0,2)答案:A考点:对数函数和指数函数的图象及其性质。
解析:分别画出2(1)xy x =<和2log (1)y x x =-≥的图象,如下图: 由图象可知,函数的值域为:(-∞,2)5. 如图,函数f(x)的图像是由正弦曲线或余弦曲线经过变换得到的,则f(x)的解析式可以是A. f(x)=sin(2x +3π)B. f(x)=sin(4x +6π)C. f(x)=cos(2x +3π)D. f(x)=cos(4x +6π) 答案:A考点:正弦函数的图象解析:设()sin()f x x ωϕ=+,由图可知:T =722()1212ππππω-==,所以,2ω=, ()sin(2)11212f ππϕ=⨯+=,则262k ππϕπ+=+,23k πϕπ=+,令k =0,得:3πϕ=,所以,()sin(2)3f x x π=+,经检验图象上其它2个点,所以,选A 。
2019年北京市朝阳一模理科答案终稿

北京市朝阳区高三年级第一次综合练习2019. 3三、解答题:(本题满分80 分)因为b c c ,所以b =1 .ab(n)由正弦定理二—=上-sin A sin B即 sin B =—^ =—.V 21 14所以 cos2B=1 -2sin 2 B =1 —2(0)2 二1314 1416. (本小题满分13分)解:(I )设M 表示事件“乘客 A 乘车等待时间小于 20分钟”,N 表示事件“乘客 B 乘车等待时间小于20分钟”,C 表示事件“乘客 A,B 乘车等待时间都小于 20分钟”.由题意知,乘客 A 乘车等待时间小于20分钟的频率为15.(本小题满分 13分)解:(I )由已知得 1 S=1bcsi nA=^, { 2[(妬)2二b 2 +c 2 -2bccos120。
整理得I bc=4, 'b 2 +C 2=17.解得【;=4,或 P=4, .c=1..8分.13分(0.012 +0.040 +0.048)咒5 =0.5,故 P(M)的估计值为 0.5 . 乘客B 乘车等待时间小于 20分钟的频率为(0.016 +0.028 +0.036)x5 =0.4,故 P(N)的估计值为 0.4 . 又 P(C) =P(MN ) = P(M ) P(N)=丄咒2 =12 5 51故事件C 的概率为- .... ...........5(n )由(I )可知,乙站乘客乘车等待时间小于所以乙站乘客乘车等待时间小于20分钟的概率为2显然,X 的可能取值为0,1,2,3且X ~B (3,2).517. (本小题满分14分)解:(I )证明:因为 ADEF 为正方形, 所以AF 丄AD .又因为平面 ADEF 丄平面ABCD , 且平面ADEF ("1平面ABCD = AD , 所以AF 丄平面ABCD . 所以AF 丄CD .(n )由(I )可知, AF 丄平面ABCD ,所以AF 丄AD , AF 丄AB .因为N BAD =90°,所以AB, AD,AF 两两垂直.分别以AB, AD, AF 为x 轴,y 轴,z 轴建立空间直角坐标系(如图) 因为 AB =AD =1 , BC =3,所以 A(0,0,0), B(1,0,0), C(1,3,0), D(0,1,0), E(0,1,1), F (0,0,1), 所以 BF =(—1,0,1), DC =(1,2,0), DE =(0,0,1) •所以 P(X =0) =c3\3)5 2^2 P(X =2)=C3M5Q-7;p (x =1)=c 33 5故随机变量X 的分布列为2'(3)2125 ' ‘ 飞 5 3632 3芮 P(X =32C 3(5)54 "125 8一.6分20分钟的频率为0.4 ,.13分(川)设罟“.仃r ,i]),设 M (N ,y i ,Z i ),则(N —1, y i ,Z i )=几(―1,1,0), 所以 Xr =1 —几,yr = k , Z 1 = 0 ,所以 M (1 — L A ,0 ), 所以 AM = (1 -L A ,0 )•设平面AFM 的一个法向量为 m= (x 0,y 0,z 0),则=0,[m ”AF =0.因为 AF =(0,0,1),所以!(j )X 0+心 770 =0.令 X 0 = A ,贝y y 。
2018-2019朝阳区一模数学理科答案

北京市朝阳区高三年级第一次综合练习数学(理)答案2019.3二、填空题:(本题满分30分)三、解答题:(本题满分80分) 15. (本小题满分13分)解:(Ⅰ)由已知得2221=sin 2=2cos120.S bc A b c bc ⎧⎪⎨⎪+-︒⎩整理得22=4,=17.bc b c ⎧⎨+⎩解得=1,=4b c ⎧⎨⎩,或=4,=1.b c ⎧⎨⎩ 因为b c <,所以1b =.………………………………………………….8分(Ⅱ)由正弦定理sin sin a bA B=, 即sin 14B =.所以2213cos 2=12sin 114B B -=-= ……………………………….13分16.(本小题满分13分)解:(Ⅰ)设M 表示事件“乘客A 乘车等待时间小于20分钟”,N 表示事件“乘客B 乘车等待时间小于20分钟”,C 表示事件“乘客A,B 乘车等待时间都小于20分钟”.由题意知,乘客A 乘车等待时间小于20分钟的频率为0.0120.0400.048)50.5(++⨯=,故()P M 的估计值为0.5.乘客B 乘车等待时间小于20分钟的频率为0.0160.0280.036)50.4(++⨯=,故()P N 的估计值为0.4.又121()()()()255P C P MN P M P N ==⋅=⨯=. 故事件C 的概率为15.………………………………………………………….6分 (Ⅱ)由(Ⅰ)可知,乙站乘客乘车等待时间小于20分钟的频率为0.4,所以乙站乘客乘车等待时间小于20分钟的概率为25. 显然,X 的可能取值为0,1,2,3且2(3,)5~X B .所以033327(0)()5125P X C ===;1232354(1)()55125P X C ==⋅=; 2232336(2)()55125P X C ==⋅=;33328(3)()5125P X C ===.故随机变量X 的分布列为2355EX =⨯= .……………….13分 17.(本小题满分14分)解:(Ⅰ)证明:因为ADEF 为正方形,所以AF AD ⊥.又因为平面ADEF ⊥平面ABCD ,且平面ADEF I 平面ABCD AD =, 所以AF ⊥平面ABCD . 所以AF CD ⊥.………………4分(Ⅱ)由(Ⅰ)可知,AF ⊥平面ABCD ,所以AF AD ⊥,AF AB ⊥. 因为90BAD ∠=︒,所以,,AB AD AF 两两垂直.分别以,,AB AD AF 为x 轴,y 轴,z 轴建立空间直角坐标系(如图). 因为1AB AD ==,3BC =,所以(0,0,0),(1,0,0),(1,3,0),(0,1,0),(0,1,1),(0,0,1)A B C D E F ,所以(1,0,1),(1,2,0),(0,0,1)BF DC DE =-==u u u r u u u r u u u r.设平面CDE 的一个法向量为(,,x y =n 则0,0.DC DE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u rn n 即20,0. x y z +=⎧⎨=⎩ 令2x =,则1y =-, 所以(2,1,0)=-n .设直线BF 与平面CDE 所成角为θ,则sin |cos ,|5BF θ=〈〉==u u u r n .……………….9分 (Ⅲ)设( (01])BMBDλλ=∈,, 设()111,,M x y z ,则()1111,,(1,1,0)x y z λ-=-, 所以1111,,0x y z λλ=-==,所以()1,,0M λλ-,所以()1,,0AM λλ=-u u u u r.设平面AFM 的一个法向量为000(,,)x y z =m ,则0,0.AM AF ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u rm m 因为()0,0,1AF =u u u r ,所以000(1)0,0.x y z λλ-+=⎧⎨=⎩令0x λ=,则01y λ=-,所以(,1,0)λλ=-m .在线段BD 上存在点M ,使得//CE 平面AFM 等价于存在[0,1]λ∈,使得0CE ⋅=u u u rm . 因为()1,2,1CE =--u u u r,由0CE ⋅=u u u r m ,所以2(1)0λλ---=, 解得2[0,1]3λ=∈, 所以线段BD 上存在点M ,使得//CE 平面AFM ,且23BM BD =.……………….14分18. (本小题满分13分) 解:(Ⅰ)当1a =时,ln ()x f x x =.所以21ln ()xf x x-'=. 因为(1)1,(1)0f f '==,所以曲线()y f x =在(1,(1))f 处的切线方程为1y x =-.……………….3分(Ⅱ)当1a =-时,ln()()x f x x-=. 函数()f x 的定义域为(,0)-∞. 不等式()1f x x ≥+成立⇔ln()1x x x-≥+成立⇔2ln()0x x x ---≤成立. 设2()ln()g x x x x =---((,0))x ∈-∞,则2121(21)(1)()21x x x x g x x x x x--+-++'=--==.当x 变化时,()g x ',()g x 变化情况如下表:所以()(1)g x g ≤-.因为(1)0g -=,所以()0g x ≤,所以ln()1x x x-≥+.………………………………………………………………….8分 (Ⅲ)求导得21ln()()ax f x x -'=. 令()0f x '=,因为0a ≠可得ex a=. 当0a >时,()f x 的定义域为()0,+∞.当x 变化时,()f x ',()f x 变化情况如下表:此时()f x 有极大值e ()eaf a =,无极小值. 当0a <时,()f x 的定义域为(),0-∞,当x 变化时,()f x ',()f x 变化情况如下表:此时()f x 有极小值e ()ef a =,无极大值.……………………………………………….13分19. (本小题满分14分)解:(Ⅰ)由题意a =1b =,1c =所以离心率c e a ==,左焦点(1,0)F -.………………………………………….4分(Ⅱ)当00y =时直线l 方程为x =x =l 与椭圆C 相切.当00y ≠时,由22001,222x y x x y y ⎧+=⎪⎨⎪+=⎩得2222000(2)4440y x x x x y +-+-=, 由题知,220012x y +=,即220022x y +=, 所以 22220000(4)4(2)(44)x y x y ∆=-+- 220016[2(1)]x y =-- =22016(22)0x y +-=. 故直线l 与椭圆C 相切.………………………………………………………….8分(Ⅲ)设11(,)A x y ,22(,)B x y ,当00y =时,12x x =,12y y =-,1x =2211(1)FA FB x y ⋅=+-u u u r u u u r 2211(1)6(1)x x =+-+-21240x =-=,所以FA FB ⊥u u u r u u u r,即90AFB ∠=o .当00y ≠时,由2200(1)6,22x y x x y y ⎧-+=⎪⎨+=⎪⎩ 得2222000(1)2(2)2100y x y x x y +-++-=, 则20012202(2)1y x x x y ++=+,21222101y x x y -=+, 2001212122220001()42x x y y x x x x y y y =-++200254422x x y --+=+. 因为1122(1,)(1,)FA FB x y x y ⋅=+⋅+u u u r u u u r1212121x x x x y y =++++2222000000220042084225442222y y x y x x y y -++++--+=+++ 220025(2)10022x y y -++==+. 所以FA FB ⊥u u u r u u u r,即90AFB ∠=o .故AFB ∠为定值90o . ………………………………………………………….14分20. (本小题满分13分)解:(I)9101000,1,1a a a ===..………………………………………………………….3分 (II)反证法:假设i ∀,0.i a ≠由于21n n n a a a ++=-, 记1,2max{}M a a =.则12,a M a M ≤≤.则32101a a a M <=-≤-,43201a a a M <=-≤-,54302a a a M <=-≤-,65402a a a M <=-≤-,L ,依次递推,有76503a a a M <=-≤-,87603a a a M <=-≤-…,则由数学归纳法易得21,.k a M k k *+≤-∈N当k M >时,210,k a +<与210k a +>矛盾. 故存在i ,使=0.i a所以,数列{}n a 必在有限项后出现值为0的项.………………………………………….8分 (III)首先证明:数列{}n a 中必有“1”项.用反证法,假设数列{}n a 中没有“1”项,由(II)知,数列{}n a 中必有“0”项,设第一个“0”项是m a (3)m ≥,令1m a p -=,1,p p >∈N *,则必有2m a p -=,于是,由1233||||m m m m p a a a p a ----==-=-,则32m a p -=,因此p 是3m a -的因数, 由2344|||2|m m m m p a a a p a ----==-=-,则4m a p -=或3p ,因此p 是4m a -的因数. 依次递推,可得p 是12,a a 的因数,因为1p >,所以这与12,a a 互质矛盾.所以,数列{}n a 中必有“1”项.其次证明数列{}n a 中必有无穷多项为“1”.假设数列{}n a 中的第一个“1”项是k a ,令1k a q -=,1,q q >∈N *, 则111k k k a a a q +-=-=-,若1k a +=11q -=,则数列中的项从k a 开始,依次为“1,1,0”的无限循环, 故有无穷多项为1;若111k a q +=->,则213212,1k k k k k k a a a q a a a +++++=-=-=-=, 若221k a q +=-=,则进入“1,1,0”的无限循环,有无穷多项为1;若221k a q +=->,则从k a 开始的项依次为1,1,2,1,3,4,1q q q q ----,……, 必出现连续两个“1”项,从而进入“1,1,0”的无限循环,故必有无穷多项为1.……13分。
2019年北京市朝阳一模理科终稿

北京市朝阳区高三年级第一次综合练习数学(理)A . {X|XA-2} B. {X|1 <x c2} C. {X|1 <xc2}1 +2iA .第一象限B.第二象限C.第三象限 D •第四象限1(--X)4的展开式中的常数项为X若函数f(x)=1 2,X ^1 2则函数l-log2 X, x>1,A.(二,2) B .(二,2]对应的点位于22019. 3本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上, 在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40 分)、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中, 选出符合题目要求的一项.1 .Q已知集合A={X|X>1},集合B={X|X <4},则AnB =A . -12 B. -6 D . 12如图,函数f(x)的图象是由正弦曲线或余弦曲线经过变换得到的,则f(X)=sin(2 X拧)B. f(X)=si n(4x+^6f(X)=cos(2x +寸)JIf(X)=cos(4x+-)6y 30,f(X)的解析式可以是记不等式组知<x+3,所表示的平面区域为 D .“点(—1,1)忘D ”是“ k<—1 ”的l y <kx2. 在复平面内,复数3.f (X)的值域是C . [0,均(r0)UA .充分而不必要条件B .必要而不充分条件7.某三棱锥的三视图如图所示(网格纸上小正方形的边长为&某单位周一、周二、周三开车上班的职工人数分别是14, 10, 8.若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是C . 7第二部分(非选择题 共110分)二、填空题:本大题共 6小题,每小题5分,共30分•把答案填在答题卡上 2X «9•双曲线 ——y 2 =1的右焦点到其一条渐近线的距离是411 .在极坐标系中,直线 P COS0 =1与圆12.能说明“函数f (X )的图象在区间0,2 ]上是一条连续不断的曲线•若 f (0)讦(2) >0,则f (x )在(0,2)内无零点”为假命题的一个函数是C .正(主)视图 侧(左)视图1),则该三棱锥的体积为10.执行如图所示的程序框图,则输出的13•天坛公园是明、清两代皇帝“祭天”“祈谷”的场所•天坛公园中的圜丘台共有三层(如图1所示),上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石(如图2所示)•上层坛从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有三层坛所有的扇面形石块数是14.在平面内,点A 是定点,动点B,C 满足I ABRAC 1=1 , AB -AC =0,则集合{ P |AP = A AB所表示的区域的面积是 三、解答题:本大题共 6小题,共80分•解答应写出文字说明,演算步骤或证明过程. 15. (本小题满分13分)在^ ABC 中,a =721 , N A =120。
2019年北京朝阳高三一模理综试题及答案共15页文档

2019年北京朝阳高三一模理综试题及答案北京市朝阳区高三年级第一次综合练习理科综合生物试卷2019.4第一部分1.下列关于细胞的叙述,正确的是A.都进行有氧呼吸B.蛋白质的合成场所均相同C.都具有细胞周期D.均可表现出接触抑制现象2.萌发的种子中酶有两个来源,一是由干燥种子中的酶活化而来,二是萌发时重新合成。
研究发现种子萌发时,新的RNA在吸水后12h开始合成,而蛋白质合成在种子吸水后15 ~ 20min便可开始。
以下叙述不.正确的是A.有些酶、RNA可以在干种子中长期保存B.干燥种子中自由水与结合水的比例低于萌发种子C.萌发时消耗的有机物根本上来源于母体的光合作用D.种子吸水后12h内新蛋白的合成不需要RNA参与3.下图表示高等动物细胞间信息交流方式。
据图推断错误的是A.图1、2中的细胞b、d可以是同一种细胞B.图1、3所示的方式不能同时发生在免疫调节中C.图1、2、3所示方式的实现均需要受体参与D.图1、2、3所示方式利于实现细胞间功能的协调4.下列有关生物多样性和进化的叙述,正确的是A.基因突变和自然选择均定向改变种群的基因频率B.群落演替过程中生物多样性增加,生物不发生进化C.共生关系的两种生物在进化过程中可形成适应对方的特征D.生态系统保持相对稳定,体现了生物多样性的直接价值5.下列实验做法不.能达到实验预期的是A.用兔成熟红细胞制备细胞膜和粗提取DNAB.制作泡菜时向坛盖边沿的水槽中注满清水C.制作果酒时适时拧松瓶盖,制作果醋时持续供氧D.用稀释涂布平板法估测某土壤浸出液中活菌数目29.(18分)油菜素内酯是植物体内一种重要的激素.为探究油菜素内酯(BL)对生长素(IAA)生理作用的影响,研究人员做了如下实验.⑴实验一:利用不同浓度的BL和IAA处理油菜萌发的种子,观察其对主根伸长的影响.结果如图所示.由图可知,单独IAA处理,对主根伸长的影响是;BL与IAA同时处理,在IAA浓度为nM时,BL对主根伸长的抑制作用逐渐增强;当IAA浓度继续增加时,BL对主根伸长的影响是.⑵实验二:用放射性碳标记的IAA处理主根,检测油菜素内酯对于生长素运输的影响.实验方法及结果如下.上图表明标记的生长素在根部的运输方向为,BL可以(促进/抑制)生长素运输,且对(运输方向)的作用更显著.⑶实验三:PIN蛋白与生长素的运输有关.研究人员测定了PIN蛋白基因表达的相关指标.测定方法:从植物特定组织中提取RNA,利用RNA为模板经得cDNA;以该cDNA为模板进行PCR,向反应体系中加入dNTP、Taq酶及不同的得到不同的DNA片段.根据扩增出的不同DNA片段的量不同,反映相关基因在特定组织中的水平,用以代表相应基因的表达水平.检测BL处理的根部组织中PIN蛋白基因的表达水平,结果如表所示.⑷上述系列实验结果表明,油菜素内酯通过影响根细胞中,从而影响生长素在根部的和分布,进而影响了生长素的生理作用.30.(18分)金鱼草(二倍体)辐射对称花型(c650)基因与两侧对称花型(c)基因是一对等位基因;自交亲和(Sc)基因与自交不亲和(S)基因是一对等位基因。
北京市朝阳区2019届高三第一次(3月)综合练习(一模)数学理试题-4bc21495a00e4b619347986777f886f1

○…………外………○…………内………绝密★启用前 【区级联考】北京市朝阳区2019届高三第一次(3月)综合练习(一模)数学理试题 试卷副标题 注意事项: 1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 第I 卷(选择题) 请点击修改第I 卷的文字说明 一、单选题 1.已知集合 ,集合 ,则 ( ) A . B . C . D . 2.在复平面内,复数 对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 3. 的展开式中的常数项为( ) A . B . C . D . 4.若函数 则函数 的值域是( ) A . B . C . D .5.如图,函数 的图象是由正弦曲线或余弦曲线经过变换得到的,则 的解析式可以是( )………订…………○…※※线※※内※※答※※题※※ ………订…………○…C . D . 6.记不等式组 所表示的平面区域为 .“点 ”是“ ”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件 7.某三棱锥的三视图如图所示(网格纸上小正方形的边长为 ),则该三棱锥的体积为( )A .B .C .D .8.某单位周一、周二、周三开车上班的职工人数分别是14,10,8.若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是( ) A .5 B .6 C .7 D .8…○…………订…………○………_____班级:___________考号:___________ …○…………订…………○………第II 卷(非选择题) 请点击修改第II 卷的文字说明 二、填空题 9.双曲线 的右焦点到其一条渐近线的距离是_____. 10.执行如图所示的程序框图,则输出的 值为_____.11.在极坐标系中,直线 与圆 相交于 两点,则 ___. 12.能说明“函数 的图象在区间 上是一条连续不断的曲线.若 ,则 在 内无零点”为假命题的一个函数是_________. 13.天坛公园是明、清两代皇帝“祭天”“祈谷”的场所.天坛公园中的圜丘台共有三层(如图1所示),上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石(如图2所示).上层坛从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是______;上、中、下三层坛所有的扇面形石块数是_______.○…………装……………线…………○……※※请※※不※※要※※在※※○…………装……………线…………○…… 14.在平面内,点 是定点,动点 满足 , ,则集合 所表示的区域的面积是_______.三、解答题15.在 中, , , 的面积等于 ,且 .(1)求 的值;(2)求 的值.16.某部门在同一上班高峰时段对甲、乙两地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟).将统计数据按 分组,制成频率分布直方图:假设乘客乘车等待时间相互独立.(1)在上班高峰时段,从甲站的乘客中随机抽取1人,记为 ;从乙站的乘客中随机抽取1人,记为 .用频率估计概率,求“乘客 , 乘车等待时间都小于20分钟”的概率;(2)从上班高峰时段,从乙站乘车的乘客中随机抽取3人, 表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量 的分布列与数学期望.17.如图,在多面体 中,平面 平面 .四边形 为正方形,四边形 为梯形,且 , , , .…………○………………○…… (1)求证: ; (2)求直线 与平面 所成角的正弦值; (3)线段 上是否存在点 ,使得直线 平面 若存在,求 的值;若不存在,请说明理由. 18.已知函数 且 . (1)当 时,求曲线 在点 处的切线方程; (2)当 时,求证: ; (3)讨论函数 的极值. 19.已知点 为椭圆 上任意一点,直线 与圆 交于 两点,点 为椭圆 的左焦点. (1)求椭圆 的离心率及左焦点 的坐标; (2)求证:直线 与椭圆 相切; (3)判断 是否为定值,并说明理由. 20.在无穷数列 中, 是给定的正整数, , . (1)若 ,写出 的值; (2)证明:数列 中存在值为 的项; (3)证明:若 互质,则数列 中必有无穷多项为 .参考答案1.B【解析】【分析】解一元二次不等式求得集合,由此求得两个集合的交集.【详解】由解得,故,故选B.【点睛】本小题主要考查集合的交集,考查一元二次不等式的解法,属于基础题.2.D【解析】【分析】由题意可得:,据此确定复数所在的象限即可.【详解】由题意可得:,则复数z对应的点为,位于第四象限.本题选择D选项.【点睛】本题主要考查复数的运算法则,各个象限内复数的特征等知识,意在考查学生的转化能力和计算求解能力.3.C【解析】【分析】化简二项式的展开式,令的指数为零,求得常数项.【详解】二项式展开式的通项为,令,故常数项为,故选C.【点睛】本小题主要考查二项式展开式的通项公式,考查二项式展开式中的常数项,属于基础题. 4.A【解析】【分析】画出函数的图像,由此确定函数的值域.【详解】画出函数的图像如下图所示,由图可知,函数的值域为,故选A.【点睛】本小题主要考查指数函数和对数函数的图像,考查分段函数的值域,考查数形结合的数学思想方法,属于基础题.5.A【解析】【分析】将图像上特殊点的坐标代入选项进行排除,由此得出正确选项.【详解】对于B选项,由于,不正确;对于C选项,由于,不正确;对于D选项,由于,不正确.故本题选A.【点睛】本小题主要考查已知三角函数图像判断函数的解析式,利用特殊值排除法,可快速得出正确选项,属于基础题6.C【解析】【分析】画出可行域和点,将旋转到点的位置,求得的值,由此求得的取值范围,进而判断出充分、必要性.【详解】画出可行域和点如下图所示,将旋转到点的位置,得,当时,;当时,.故“点”是“”的充分必要条件.故选C.【点睛】本小题主要考查线性规划可行域的画法,考查充分、必要条件的判断,属于基础题.7.D【解析】【分析】首先由三视图还原几何体,然后由几何体的空间结构特征求解三棱锥的体积即可.【详解】由三视图可知,在棱长为2的正方体中,其对应的几何体为棱锥,该棱锥的体积:.本题选择D选项.【点睛】(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.8.B【解析】【分析】将原问题转化为Venn的问题,然后结合题意确定这三天都开车上班的职工人数至多几人即可.【详解】如图所示,(a+b+c+x)表示周一开车上班的人数,(b+d+e+x)表示周二开车上班人数,(c+e+f+x)表示周三开车上班人数,x表示三天都开车上班的人数,则有:, 即,即 ,当b =c =e =0时,x 的最大值为6, 即三天都开车上班的职工人数至多是6. 【点睛】本题主要考查Venn 图的应用,数形结合的数学思想等知识,意在考查学生的转化能力和计算求解能力. 9.1 【解析】 【分析】由题意可知,双曲线的右焦点坐标为 ,渐近线方程为 ,结合点到直线距离公式求解距离即可. 【详解】由题意可知,双曲线的右焦点坐标为 ,渐近线方程为:,即 , 则焦点到渐近线的距离为:.故答案为: .【点睛】本题主要考查双曲线渐近线方程的求解,点到直线距离公式的应用等知识,意在考查学生的转化能力和计算求解能力.10.【解析】【分析】运行程序,当时退出循环,计算得输出的值.【详解】运行程序,,判断是,,判断是,,判断否,输出. 【点睛】本小题主要考查程序框图,考查计算程序框图输出的结果,属于基础题.11.【解析】【分析】将极坐标方程转化为直角坐标方程,将直线方程代入圆的方程,求得的坐标,由此求得..【详解】直线即.圆两边乘以得,即,令,解得,故,所以.【点睛】本小题主要考查极坐标方程化为直角坐标方程,考查直线和圆的交点坐标的求法,属于基础题.12.【解析】【分析】由题意给出一个满足题意的函数解析式,然后绘制函数图像说明命题为假命题即可.【详解】考查函数,绘制函数图像如图所示,该函数的图像在区间上是一条连续不断的曲线,,但是函数在内存在零点,故该函数使得原命题为假命题.【点睛】本题主要考查函数零点存在定理应用的条件,注意所有的条件都满足时才能利用函数零点存在定理,否则可能会出现错误.13.【解析】【分析】由题意可知每环的扇面形石块数是一个以9为首项,9为公差的等差数列,据此确定第二十七环的扇面形石块数和上、中、下三层坛所有的扇面形石块数即可.【详解】第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则依题意得:每环的扇面形石块数是一个以9为首项,9为公差的等差数列,所以,a n=9+(n-1)×9=9n,所以,a27=9×27=243,前27项和为:=3402.【点睛】本题主要考查等差数列的通项公式,等差数列的前n项和及其应用等知识,意在考查学生的转化能力和计算求解能力.14.【解析】以为原点建立平面直角坐标系,根据设出两点的坐标,利用向量运算求得点的坐标,化简后可求得点的轨迹也即表示的区域,由此计算出区域的面积.【详解】以为原点建立平面直角坐标系,由于,,即,故设,即,设,由得,即,则,故表示的是原点在圆心,半径为的圆,由于,故点所表示的区域是圆心在原点,半径为的两个圆之间的扇环,故面积为.【点睛】本小题主要考查数形结合的数学思想方法,考查向量的坐标运算,考查化归与转化的数学思想方法,考查分析求解能力,属于中档题.15.(Ⅰ)1;(Ⅱ).【解析】【分析】(I)利用三角形的面积公式和余弦定理列方程组,解方程组求得的值.(II)利用正弦定理求得的的值,利用二倍角公式求得的值.解:(Ⅰ)由已知得整理得解得,或因为,所以.(Ⅱ)由正弦定理,即.所以【点睛】本小题主要考查三角形的面积公式,考查余弦定理解三角形,考查正弦定理解三角形,考查二倍角公式,属于中档题.16.(Ⅰ);(Ⅱ)详见解析.【解析】【分析】(I)根据频率分布直方图分别计算出两个乘客等待时间小于分钟的频率,按照相互独立事件概率计算公式,计算出“乘客,乘车等待时间都小于20分钟”的概率.(II)根据二项分布概率计算公式以及数学期望计算公式,求得的分布列和数学期望.【详解】解:(Ⅰ)设表示事件“乘客乘车等待时间小于20分钟”,表示事件“乘客乘车等待时间小于20分钟”,表示事件“乘客乘车等待时间都小于20分钟”.由题意知,乘客乘车等待时间小于20分钟的频率为,故的估计值为.乘客乘车等待时间小于20分钟的频率为,故的估计值为.又.故事件的概率为.(Ⅱ)由(Ⅰ)可知,乙站乘客乘车等待时间小于20分钟的频率为,所以乙站乘客乘车等待时间小于20分钟的概率为.显然,的可能取值为且.所以;;;.故随机变量的分布列为【点睛】本小题主要考查相互独立事件概率计算,考查二项分布分布列和数学期望的计算,还考查了由频率分布直方图求频率的方法,属于中档题.17.(Ⅰ)详见解析;(Ⅱ);(Ⅲ)线段上存在点,使得平面,且.【解析】【分析】(I)根据面面垂直的性质定理,证得平面,由此证得.(II)以为轴,轴,轴建立空间直角坐标系,通过计算直线的方向向量和平面的法向量,由此计算出线面角的正弦值.(III)设,,用表示出点的坐标,利用直线的方向向量和平面的法向量垂直列方程,解方程求得的值,由此判断存在符合题意的点.【详解】解:(Ⅰ)证明:因为为正方形,所以.又因为平面平面,且平面平面,所以平面.所以.(Ⅱ)由(Ⅰ)可知,平面,所以,.因为,所以两两垂直.分别以为轴,轴,轴建立空间直角坐标系(如图).因为,,所以,所以.设平面的一个法向量为,则即令,则,所以.设直线与平面所成角为,则.(Ⅲ)设,,设,则,所以,所以,所以.设平面的一个法向量为,则因为,所以令,则,所以.在线段上存在点,使得平面等价于存在,使得.因为,由,所以,解得,所以线段上存在点,使得平面,且.【点睛】本小题主要考查面面垂直的性质定理,考查利用空间向量法求解线面所成角的正弦值,考查线面平行的向量表示,考查空间想象能力和逻辑推理能力,属于中档题.18.(Ⅰ);(Ⅱ)详见解析;(Ⅲ)详见解析.【解析】【分析】(I)求得切点坐标和斜率,由此求得切线方程.(II)将原不等式转化为成立,构造函数,利用导数求得的最大值为零,由此证得不等式成立.(III)对求导后,对分成两类,结合函数的单调区间,讨论得出函数的极值.【详解】解:(Ⅰ)当时,.所以.因为,所以曲线在处的切线方程为.(Ⅱ)当时,.函数的定义域为.不等式成立成立成立.设,则.当变化时,,变化情况如下表:所以.因为,所以,所以.(Ⅲ)求导得. 令,因为可得.当时,的定义域为.当变化时,,变化情况如下表:此时有极大值,无极小值.当时,的定义域为,当变化时,,变化情况如下表:此时有极小值,无极大值.【点睛】本小题主要考查利用导数求曲线的切线方程,考查利用导数证明不等式,考查利用导数研究函数的极值,考查化归与转化的数学思想方法,综合性较强,属于中档题.19.(1);(2)证明见解析;(3)答案见解析.【解析】【分析】(1)由题意可得,,据此确定离心率即可;(2)由题意可得.分类讨论和两种情况证明直线与椭圆相切即可;(3)设,,当时,易得.当时,联立直线方程与椭圆方程可得,结合韦达定理和平面向量的数量积运算法则计算可得.据此即可证得为定值.【详解】(1)由题意,,所以离心率,左焦点.(2)由题知,,即.当时直线方程为或,直线与椭圆相切.当时,由得,即所以故直线与椭圆相切.(3)设,,当时,,,,,所以,即.当时,由得,则,,.因为.所以,即.故为定值.【点睛】(1)解答直线与椭圆的题目时,时常把两个曲线的方程联立,消去x(或y)建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系.(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形.20.(Ⅰ);(Ⅱ)详见解析;(Ⅲ)详见解析.【解析】【分析】(I)根据以及的值,由此求得的值,找出规律,求得的值.(II)利用反证法,先假设,利用递推关系找出规律,推出矛盾,由此证明原命题成立.(III)首先利用反证法证明数列中必有“1”项,其次证明数列中必有无穷多项为“1”,由此证得原命题成立.【详解】解:(I)由,以及,可知,,,从开始,规律为两个和一个,周期为,重复出现,故.(II)反证法:假设,由于,记.则.则,,,,,依次递推,有,…,则当时,与矛盾.故存在,使所以,数列必在有限项后出现值为的项.(III)首先证明:数列中必有“1”项.用反证法,假设数列中没有“1”项,由(II)知,数列中必有“0”项,设第一个“0”项是,令,,则必有,于是,由,则,因此是的因数,由,则或,因此是的因数.依次递推,可得是的因数,因为,所以这与互质矛盾.所以,数列中必有“1”项.其次证明数列中必有无穷多项为“1”.假设数列中的第一个“1”项是,令,,则,若,则数列中的项从开始,依次为“1,1,0”的无限循环,故有无穷多项为1;若,则,若,则进入“1,1,0”的无限循环,有无穷多项为1;若,则从开始的项依次为,必出现连续两个“1”项,从而进入“1,1,0”的无限循环,故必有无穷多项为1.【点睛】本小题主要考查递推数列,考查合情推理,考查与数列有关的证明,考查分析问题与解决问题的能力,综合性很强,属于难题.。
北京市朝阳区2019届高三第一次(3月一模)理科综合试卷(含答案)

北京市朝阳区高三年级第一次综合练习理科综合能力测试2019.3 可能用到的相对原子质量:H 1 N 14 O 16 S 32 Cl 35.5本试卷共16页,共300分。
考试时长120:分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
1.人体内环境中的蛋白质不具有的功能是A.调节机体生命活动B.作为氧运输的载体C.抗击入侵的病原体D.维持内环境渗透压2.非洲爪蟾卵母细胞对水的通透性极低。
科学家将细胞膜蛋白CHIP28的mRNA注人到非洲爪蟾卵母细胞内,72h后将其放人低渗溶液中,与未注入此mRNA的细胞做比较,结果如下图。
下列说法不合理的是A.注入的mRNA在细胞中可作为翻译的模板B.推侧CHIP28蛋白借助囊泡定位到细胞膜上C.水分子自由扩散进入卵母细饱导致其涨破D. CHIP28蛋白增大了卵母细胞对水的通透性3.磷酸破转运器是叶绿体膜上的重要结构.可将暗反应过程中产生的磷酸丙糖运出,同时将释放的Pi运回。
Pi和磷酸丙通过磷酸转运器的运输,严格按照1:1的反向交换方式进行,如下图所示。
下列叙述正确的是A.光合色素吸收、传递和转换光能后激发A的进入直接被光反应产生的【H】还原B.叶绿体基质中的C02C.磷酸转运器运输Pi会造成叶绿体基质中的Pi堆积D.磷酸转运器可协调蔗糖合成速率与C02固定速率4.为研究赤霉索(GA)和脱落酸(ABA)在种子萌发中的作用,科学家利用拟南芥突变体进行系列实脸,实脸处理及结果如下表。
据实班结果推测,错误的是A. 突变体1是GA受体异常突变体B. 突变体2是ABA受体异常突变体C. 野生型种子萌发时内源ABA含量很低D. GA与ABA在此过程中有拮抗作用5.以下关于生物学实验和技术的叙述,正确的是①检测生物组织中的还原糖②用高倍显徽镜观察叶绿体③肺炎双球菌的体外转化④果酒和果醋的制作作⑤DNA的粗提取与鉴定⑥单克隆杭体的制备A.①⑤均需使用酒精溶液B.②⑥均可体现细胞膜流动性C.③④均制备固体培养基D.③⑥均需利用无菌操作技术6.我国科技创新成果斐然,下列成果与电化学无关..的是A B C D有机金属材料吸附与转化CO2研发出水溶液锂离子电池研发出“可呼吸”Na—CO2电池常温常压下用电解法制备高纯H27.下列实验中的颜色变化,与氧化还原反应无关..的是A B C DFeCl3溶液滴入Mg(OH)2浊液中AgNO3溶液滴入氯水中Na块放在坩埚里并加热H2C2O4溶液滴入KMnO4酸性溶液中白色浑浊转化为红褐色沉淀产生白色沉淀,随后淡黄绿色褪去发出黄色火焰,生成淡黄色固体产生气泡,随后紫色褪去8.某科研人员提出HCHO与O2在羟基磷灰石(HAP)表面催化氧化生成CO2、H2O 的历程,该历程示意图如下(图中只画出了HAP的部分结构)。
北京市朝阳区2019年高三年级第一次综合练习理科综合试题(含答案,pdf版)
25.(17分)(1)取代反应(2)浓硫酸、浓硝酸(3)+ 2NH 3NO 2Cl NO 2NH 2+ 2NH 4Cl(4)NH 2NH 2(5)碳碳双键、酯基(6)CH 2CHCOCH 3n +n H 2O H +CH 2CH n +n CH 3COOH (7)H NHCH 2C OOH n(8)NH 2NHCO CH 2NH 2NHNH COH CH 2NH 2 26.(13分)(1)①1783 kJ mol --⋅② 变小(2)()()222222Cl 2Ca OH CaCl Ca ClO 2H O +==++(3)AC(4)① pH 降低,ClO - + H + = HClO ,溶液中()HClO c 增大② HClO + Cl + + H + = Cl 2↑+ H 2O (或22ClO Cl 2H Cl H O --+++=↑+)③ HClO 受热分解,()HClO c 浓度减小;气体溶解度降低;反应b 平衡逆向移动;反应ⅲ平衡逆向移动等(合理即可)27.(13分)(1)()2224MnO OH O 4MnO 2H O +==+(2)①42NH H O ++⇌32NH H O H +⋅+(或4NH +水解产生H +)②蒸发浓缩,冷却结晶,过滤③加热4NH Cl 粗品至340℃左右,NH 4Cl = NH 3 + HCl ;收集产物并冷却,NH 3 + HCl=NH 4Cl ,得到纯净NH 4Cl 。
(3)KSCN 溶液,不变红(4)①22224422MnO H O H SO MnSO 2H O O ++==++↑②i 中2MnO 作催化剂,反应快,2MnO 只催化分解22H O ;ii 中2MnO 作氧化剂,加入稀24H SO 后,2MnO 的氧化性增强,被22H O 还原为4MnSO 。
28.(15分)(1)还原(2)i .大 ii .222324I SO H O 2I SO 2H ---+++=++(3)少量23Na SO (4)①生成白色沉淀②I -③此时,a 极区发生反应IO 3- + 5I - + 6H + = 3I 2 + 3H 2O ,IO 3-不再与SO 32-发生反应,外电路无电流通过(5)A C。
2019年北京市朝阳区高三年级一模数学(理)试题和答案

北京市朝阳区高三年级第一次综合练习数 学(理)2019.3本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知集合A ={x ︳x >1},集合B ={ x ︳x²<4},则A∩B = A. {x ︳x >-2}B. {x ︳1<x<2}C. {x ︳1≤x<2}D. R2. 在复平面内,复数z =12ii+对应的点位于 A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 41)x x-(的展开式中的常数项为 A. -12B. -6C. 6D. 124. 若函数f(x)=则函数f(x)的值域是 A. (-∞,2)B. (-∞,2]C. [0,+ ∞)D. (-∞,0)∪(0,2)5. 如图,函数f(x)的图像是由正弦曲线或余弦曲线经过变换得到的,则f(x)的解析式可以是A. f(x)=sin(2x +3π) B. f(x)=sin(4x +6π) C. f(x)=cos(2x +3π) D. f(x)=cos(4x +6π) 6. 记不等式组,所表示的平面区域为D ,“点(-1,1)∈D”是“k”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件7. 某三棱锥的三视图如图所示(网格纸上小正方形的边长为1),则该三棱锥的体积为A. 4B. 2C.83 D. 438. 某单位周一、周二、周三开车上班的职工人数分别是14、10、8,若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是 A. 5B. 6C. 7D. 8第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分。
9. 双曲线2214xy-=的右焦点到其一条渐近线的距离是10. 执行如图所示的程序框图,输出的x值为11. 在极坐标系中,直线cosθ=1与圆cosθ交于A,B两点,则=12.能说明“函数f(x)的图像在区间[0,2]上是一条连续不断的曲线,若f(0)•f(2)>0,则f(x)在(0,2)内无零点”为假命题的一个函数是13.天坛公园是明、清两代皇帝“祭天”“祈谷”的场所,天坛公园中的圜丘台共有三层(如下页本题图1所示)上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石铺成(如下页本题图2所示),上层从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是;上、中、下三层坛所有的扇面形石块数是14.在平面内,点A 是定点,动点B ,C 满足==1,·=0,则集合{P |AP u u u r =+AC u u u r,1≤≤2}所表示的区域面积是三、解答题共6小题,共80分,解答应写出文字说明,演算步骤或证明过程 15.(本小题满分13分)在△ABC 中,a =,∠A =120°,△ABC 的面积等于,且b<c ,(I )求b 的值;(II )求cos2B 的值16.(本小题满分13分)某部门在同一上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019北京市朝阳区高三一模数 学(理)2019.3本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知集合{|1}A x x =>,集合2{|4}B x x =<,则AB =A .{|2}x x >-B .{|12}x x <<C .{|12}x x ≤<D .R2.在复平面内,复数12iiz +=对应的点位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限3.41()x x-的展开式中的常数项为A .12-B .6-C .6D . 124.若函数22,1,()log ,1x x f x x x ⎧<=⎨-≥⎩,则函数()f x 的值域是A .(,2)-∞B .(,2]-∞C .[0,)+∞D .(,0)(0,2)-∞5.如图,函数()f x 的图象是由正弦曲线或余弦曲线经过变换得到的,则()f x 的解析式可以是A .()sin(2)3f x x π=+π1y7πC .()cos(2)3f x x π=+D .()cos(4)6f x x π=+6.记不等式组0,3,y y x y kx ≥⎧⎪≤+⎨⎪≤⎩所表示的平面区域为D .“点(1,1)D -∈”是“1k ≤-”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件7.某三棱锥的三视图如图所示(网格纸上小正方形的边长为1),则该三棱锥的体积为 A .4B .2C .83D .438.某单位周一、周二、周三开车上班的职工人数分别是14,10,8.若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是A .5B .6C .7D .8第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.9.双曲线2214x y -=的右焦点到其一条渐近线的距离是 .10.执行如图所示的程序框图,则输出的x 值为正(主)视图俯视图侧(左)视图11.在极坐标系中,直线cos 1ρθ=与圆4cos ρθ=相交于,A B 两点,则AB =___.12.能说明“函数()f x 的图象在区间[]0,2上是一条连续不断的曲线.若(0)(2)0f f ⋅>,则()f x 在(0,2)内无零点”为假命题的一个函数是 .13.天坛公园是明、清两代皇帝“祭天”“祈谷”的场所.天坛公园中的圜丘台共有三层(如图1所示),上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石(如图2所示).上层坛从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是______;上、中、下三层坛所有的扇面形石块数是 .14.在平面内,点A 是定点,动点C B ,满足||||1AB AC ==,0AB AC ⋅=,则集合{=+,12}|P AP AB AC λλ≤≤所表示的区域的面积是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)在ABC △中,a 120A ∠=︒,ABC △b c <. (Ⅰ)求b 的值; (Ⅱ)求cos2B 的值. 图1图2某部门在同一上班高峰时段对甲、乙两地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟).将统计数据按[5,10),[10,15),[15,20),,[35,40]分组,制成频率分布直方图:假设乘客乘车等待时间相互独立.(Ⅰ)在上班高峰时段,从甲站的乘客中随机抽取1人,记为A ;从乙站的乘客中随机抽取1人,记为B .用频率估计概率,求“乘客A ,B 乘车等待时间都小于20分钟”的概率;(Ⅱ)从上班高峰时段,从乙站乘车的乘客中随机抽取3人,X 表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量X 的分布列与数学期望.时间(分钟)乙站甲站时间(分钟)如图,在多面体ABCDEF 中,平面ADEF ⊥平面ABCD .四边形ADEF 为正方形,四边形ABCD 为梯形,且//AD BC ,90BAD ∠=︒,1AB AD ==,3BC =. (Ⅰ)求证:AF CD ⊥;(Ⅱ)求直线BF 与平面CDE 所成角的正弦值;(Ⅲ)线段BD 上是否存在点M ,使得直线//CE 平面AFM ? 若存在,求BMBD的值;若不存在,请说明理由.EDCBA F已知函数ln()()ax f x x=(R a ∈且0)a ≠. (Ⅰ)当1a =时,求曲线()y f x =在点(1,(1))f 处的切线方程; (Ⅱ)当1a =-时,求证:()1f x x ≥+; (Ⅲ)讨论函数()f x 的极值.已知点00(,)M x y 为椭圆22:12x C y +=上任意一点,直线00:22l x x y y +=与圆22(1)6x y -+=交于,A B 两点,点F 为椭圆C 的左焦点.(Ⅰ)求椭圆C 的离心率及左焦点F 的坐标; (Ⅱ)求证:直线l 与椭圆C 相切;(Ⅲ)判断AFB ∠是否为定值,并说明理由.在无穷数列{}n a 中,12,a a 是给定的正整数,21n n n a a a ++=-,N n ∈*. (Ⅰ)若123,1a a ==,写出910100,,a a a 的值; (Ⅱ)证明:数列{}n a 中存在值为0的项;(Ⅲ)证明:若12,a a 互质,则数列{}n a 中必有无穷多项为1.数学试题答案一、选择题:(本题满分40分)二、填空题:(本题满分30分)三、解答题:(本题满分80分) 15.(本小题满分13分)解:(Ⅰ)由已知得2221=sin 2=2cos120.S bc A b c bc ⎧⎪⎨⎪+-︒⎩整理得22=4,=17.bc b c ⎧⎨+⎩ 解得=1,=4b c ⎧⎨⎩,或=4,=1.b c ⎧⎨⎩ 因为b c <,所以1b =.………………………………………………….8分(Ⅱ)由正弦定理sin sin a bA B=, 即sin B =.所以2213cos 2=12sin 12()1414B B -=-= ……………………………….13分 16.(本小题满分13分)解:(Ⅰ)设M 表示事件“乘客A 乘车等待时间小于20分钟”,N 表示事件“乘客B 乘车等待时间小于20分钟”,C 表示事件“乘客A,B 乘车等待时间都小于20分钟”.由题意知,乘客A 乘车等待时间小于20分钟的频率为0.0120.0400.048)50.5(++⨯=,故()P M 的估计值为0.5.乘客B 乘车等待时间小于20分钟的频率为0.0160.0280.036)50.4(++⨯=,故()P N 的估计值为0.4.又121()()()()255P C P MN P M P N ==⋅=⨯=. 故事件C 的概率为15.………………………………………………………….6分 (Ⅱ)由(Ⅰ)可知,乙站乘客乘车等待时间小于20分钟的频率为0.4,所以乙站乘客乘车等待时间小于20分钟的概率为25. 显然,X 的可能取值为0,1,2,3且2(3,)5~X B .所以033327(0)()5125P X C ===;1232354(1)()55125P X C ==⋅=; 2232336(2)()55125P X C ==⋅=;33328(3)()5125P X C ===. 故随机变量X 的分布列为26355EX =⨯= .……………….13分 17.(本小题满分14分)解:(Ⅰ)证明:因为ADEF 为正方形,所以AF AD ⊥.且平面ADEF 平面ABCD AD =,所以AF ⊥平面ABCD .所以AF CD ⊥.………………4分(Ⅱ)由(Ⅰ)可知,AF ⊥平面ABCD ,所以AF AD ⊥,AF AB ⊥. 因为90BAD ∠=︒,所以,,AB AD AF 两两垂直.分别以,,AB AD AF 为x 轴,y 轴,z 轴建立空间直角坐标系(如图). 因为1AB AD ==,3BC =,所以(0,0,0),(1,0,0),(1,3,0),(0,1,0),(0,1,1),(0,0,1)A B C D E F , 所以(1,0,1),(1,2,0),(0,0,1)BF DC DE =-==. 设平面CDE 的一个法向量为(,x =n 则0,0.DC DE ⎧⋅=⎪⎨⋅=⎪⎩n n 即20,0. x y z +=⎧⎨=⎩令2x =,则1y =-, 所以(2,1,0)=-n .设直线BF 与平面CDE 所成角为θ则sin |cos ,|BF θ=〈〉==n (Ⅲ)设( (01])BMBDλλ=∈,, 设()111,,M x y z ,则()1111,,(1,1,0)x y z λ-=-, 所以1111,,0x y z λλ=-==,所以()1,,0M λλ-, 所以()1,,0AM λλ=-.设平面AFM 的一个法向量为000(,,)x y z =m ,则0,0.AM AF ⎧⋅=⎪⎨⋅=⎪⎩m m因为()0,0,1AF =,所以000(1)0,0. x y z λλ-+=⎧⎨=⎩令0x λ=,则01y λ=-,所以(,1,0)λλ=-m .在线段BD 上存在点M ,使得//CE 平面AFM 等价于存在[0,1]λ∈,使得0CE ⋅=m . 因为()1,2,1CE =--,由0CE ⋅=m , 所以2(1)0λλ---=, 解得2[0,1]3λ=∈, 所以线段BD 上存在点M ,使得//CE 平面AFM ,且23BM BD =.……………….14分 18. (本小题满分13分) 解:(Ⅰ)当1a =时,ln ()x f x x =.所以21ln ()xf x x-'=. 因为(1)1,(1)0f f '==,所以曲线()y f x =在(1,(1))f 处的切线方程为1y x =-.……………….3分(Ⅱ)当1a =-时,ln()()x f x x-=. 函数()f x 的定义域为(,0)-∞.不等式()1f x x ≥+成立⇔ln()1x x x-≥+成立⇔2ln()0x x x ---≤成立. 设2()ln()g x x x x =---((,0))x ∈-∞,则2121(21)(1)()21x x x x g x x x x x--+-++'=--==.当x 变化时,()g x ',()g x 变化情况如下表:所以()(1)g x g ≤-.因为(1)0g -=,所以()0g x ≤,所以ln()1x x x-≥+.………………………………………………………………….8分 (Ⅲ)求导得21ln()()ax f x x -'=. 令()0f x '=,因为0a ≠可得ex a=. 当0a >时,()f x 的定义域为()0,+∞.当x 变化时,()f x ',()f x 变化情况如下表:此时()f x 有极大值e ()eaf a =,无极小值. 当0a <时,()f x 的定义域为(),0-∞,当x 变化时,()f x ',()f x 变化情况如下表:此时()f x有极小值e ()eaf a =,无极大值.……………………………………………….13分 19. (本小题满分14分)解:(Ⅰ)由题意a =1b =,1c ==所以离心率c e a ==,左焦点(1,0)F -.………………………………………….4分 (Ⅱ)当00y =时直线l 方程为x x =l 与椭圆C 相切.当00y ≠时,由22001,222x y x x y y ⎧+=⎪⎨⎪+=⎩得2222000(2)4440y x x x x y +-+-=, 由题知,220012x y +=,即220022x y +=, 所以 22220000(4)4(2)(44)x y x y ∆=-+-220016[2(1)]x y =-- =22016(22)0x y +-=. 故直线l 与椭圆C 相切.………………………………………………………….8分(Ⅲ)设11(,)A x y ,22(,)B x y ,当00y =时,12x x =,12y y =-,1x =2211(1)FA FB x y ⋅=+-2211(1)6(1)x x =+-+-21240x =-=, 所以FA FB ⊥,即90AFB ∠=.当00y ≠时,由2200(1)6,22x y x x y y ⎧-+=⎪⎨+=⎪⎩ 得2222000(1)2(2)2100y x y x x y +-++-=, 则20012202(2)1y x x x y ++=+,2012202101y x x y -=+, 2001212122220001()42x x y y x x x x y y y =-++200254422x x y --+=+. 因为1122(1,)(1,)FA FB x y x y ⋅=+⋅+ 1212121x x x x y y =++++2222000000220042084225442222y y x y x x y y -++++--+=+++ 220025(2)10022x y y -++==+. 所以FA FB ⊥,即90AFB ∠=.故AFB ∠为定值90. ………………………………………………………….14分20. (本小题满分13分)解:(I)9101000,1,1a a a ===..………………………………………………………….3分 (II)反证法:假设i ∀,0.i a ≠由于21n n n a a a ++=-, 记1,2max{}M a a =.则12,a M a M ≤≤.则32101a a a M <=-≤-,43201a a a M <=-≤-,54302a a a M <=-≤-,65402a a a M <=-≤-,,依次递推,有76503a a a M <=-≤-,87603a a a M <=-≤-…,则由数学归纳法易得21,.k a M k k *+≤-∈N 当k M >时,210,k a +<与210k a +>矛盾. 故存在i ,使=0.i a所以,数列{}n a 必在有限项后出现值为0的项.………………………………………….8分 (III)首先证明:数列{}n a 中必有“1”项.用反证法,假设数列{}n a 中没有“1”项,由(II)知,数列{}n a 中必有“0”项,设第一个“0”项是m a (3)m ≥,令1m a p -=,1,p p >∈N *,则必有2m a p -=,于是,由1233||||m m m m p a a a p a ----==-=-,则32m a p -=,因此p 是3m a -的因数, 由2344|||2|m m m m p a a a p a ----==-=-,则4m a p -=或3p ,因此p 是4m a -的因数.依次递推,可得p 是12,a a 的因数,因为1p >,所以这与12,a a 互质矛盾.所以,数列{}n a 中必有“1”项. 其次证明数列{}n a 中必有无穷多项为“1”.假设数列{}n a 中的第一个“1”项是k a ,令1k a q -=,1,q q >∈N *, 则111k k k a a a q +-=-=-,若1k a +=11q -=,则数列中的项从k a 开始,依次为“1,1,0”的无限循环, 故有无穷多项为1;若111k a q +=->,则213212,1k k k k k k a a a q a a a +++++=-=-=-=, 若221k a q +=-=,则进入“1,1,0”的无限循环,有无穷多项为1;若221k a q +=->,则从k a 开始的项依次为1,1,2,1,3,4,1q q q q ----,……, 必出现连续两个“1”项,从而进入“1,1,0”的无限循环,故必有无穷多项为1.……13分。
