三角函数化简题
高中数学三角函数的恒等变换及化简求值精选题

三角函数的恒等变换及化简求值精选题一.选择题(共7小题) 1.若3ta n 4α=,则2c o s 2s in 2(αα+=)A .6425B .4825C .1D .16252.若3c o s ()45πα-=,则sin 2(α=)A .725B .15C .15-D .725-3.已知向量(sin ,2),(1,c o s )ab θθ=-=,且ab⊥,则2sin 2c o s θθ+的值为( )A .1B .2C .12D .34.若1ta n 3θ=,则c o s 2(θ=)A .45-B .15- C .15D .455.已知角α的终边经过点(2,1)P -,则sin c o s (sin c o s αααα-=+ )A .3B .13C .13-D .3- 6.已知函数()s in (2)6f x x π=-,若方程3()5f x =的解为1x ,212(0)x x x π<<<,则12sin ()(x x -=)A .45-B .35-C .3-D .3-7.已知1ta n 4ta n θθ+=,则2c o s ()(4πθ+=)A .12B .13C .14D .15二.填空题(共15小题)9.设当x θ=时,函数()s in o s f x x x=+取得最大值,则ta n ()4πθ+=.10.求值:s in 50(1n 10)︒+︒=.11.1s in 10c o s 10-=︒︒.12.已知s in 10c o s 102c o s 140m ︒+︒=︒,则m=.13.4c o s 50ta n 40︒-︒=.14.2c o s 10s in 20s in 70︒-︒=︒.15.已知1ta n 31ta n αα+=-,则2sin 2sin co s 1ααα-+=.16.若1s in ()43πα-=,则c o s ()4πα+=.17.若o s 2in 2c o s ()4θθπθ=+,则s in 2θ=.18.若ta n 3α=,则s in 2ta n ()4απα+的值为 .19.若ta n 3,(0,)2παα=∈,则c o s ()4πα-=.20.公元前6世纪,古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图,发现了黄金分割值约为0.618,这一数值也可以表示为2s in 18m =︒,若24m n +=,si n 63=︒.21.公元前6世纪,古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,发现0.618就是黄金分割,这是一个伟大的发现,这一数值也表示为2s in 18a=︒,若24a b +=,则2=.22.函数2()ta n 60s in 2inf x x x=︒+在[,]2ππ上的值域为 .三.解答题(共3小题) 23.设函数()s in ()s in ()62f x x x ππωω=-+-,其中03ω<<,已知()06f π=.(Ⅰ)求ω; (Ⅱ)将函数()yf x =的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移4π个单位,得到函数()y g x =的图象,求()g x 在[4π-,3]4π上的最小值.24.已知α,β为锐角,4ta n 3α=,c o s ()5αβ+=-(1)求c o s 2α的值; (2)求tan ()αβ-的值.25.已知函数22()s inc o s in f x x x x =--co s ()x x R ∈.(Ⅰ)求2()3f π的值.(Ⅱ)求()f x 的最小正周期及单调递增区间.三角函数的恒等变换及化简求值精选题25道参考答案与试题解析一.选择题(共7小题) 1.若3ta n 4α=,则2c o s 2s in 2(αα+=)A .6425B .4825C .1D .1625【分析】将所求的关系式的分母“1”化为22(c o s sin )αα+,再将“弦”化“切”即可得到答案. 【解答】解:3ta n 4α=,22222314c o s 4s in c o s 14ta n 644c o s 2s in 29s in c o s ta n 125116ααααααααα+⨯++∴+====+++.故选:A .【点评】本题考查三角函数的化简求值,“弦”化“切”是关键,是基础题. 2.若3c o s ()45πα-=,则sin 2(α=)A .725B .15C .15-D .725-【分析】法1︒:利用诱导公式化s in 2c o s (2)2παα=-,再利用二倍角的余弦可得答案.法︒:利用余弦二倍角公式将左边展开,可以得s in c o s αα+的值,再平方,即得s in2α的值【解答】解:法31:c o s ()45πα︒-=,297s in 2c o s (2)c o s 2()2c o s ()1212442525πππαααα∴=-=-=--=⨯-=-,法32:c o s ()in c o s )425πααα︒-=+=,∴19(1s in 2)225α+=,97s in 2212525α∴=⨯-=-,故选:D .【点评】本题考查三角函数的恒等变换及化简求值,熟练掌握诱导公式化与二倍角的余弦是关键,属于中档题.3.已知向量(sin ,2),(1,c o s )ab θθ=-=,且ab⊥,则2sin 2c o s θθ+的值为( )A .1B .2C .12D .3【分析】由题意可得a b ⋅=,即解得ta n 2θ=,再由222222s in c o s c o s 2ta n 1s in 2c o s c o s s in 1ta n θθθθθθθθθ+++==++,运算求得结果.【解答】解:由题意可得sin 2co s 0ab θθ⋅=-=,即ta n 2θ=.222222s in c o s c o s 2ta n 1s in 2c o s 1c o s s in 1ta n θθθθθθθθθ++∴+===++,故选:A .【点评】本题主要考查两个向量数量积公式的应用,两个向量垂直的性质;同角三角函数的基本关系的应用,属于基础题. 4.若1ta n 3θ=,则c o s 2(θ=)A .45-B .15- C .15D .45【分析】原式利用二倍角的余弦函数公式变形,再利用同角三角函数间的基本关系化简,将ta n θ的值代入计算即可求出值.【解答】解:1ta n 3θ=,22224c o s 22c o s 11111519ta n θθθ∴=-=-=-=++.故选:D .【点评】此题考查了二倍角的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.5.已知角α的终边经过点(2,1)P -,则sin c o s (sin c o s αααα-=+ )A .3B .13C .13-D .3-【分析】先根据已知条件得到ta n α,再化简s in c o s s in c o s αααα-+代入即可得到结果.【解答】解:因为角α的终边经过点(2,1)P -,所以1ta n 2α=-,则11s in c o s ta n 1231s in c o s ta n 112αααααα----===-++-+,故选:D .【点评】本题考查三角函数的化简求值,着重考查同角三角函数的基本关系式,考查任意角的三角函数的定义,属于中档题. 6.已知函数()s in (2)6f x x π=-,若方程3()5f x =的解为1x ,212(0)x x x π<<<,则12sin ()(x x -=)A .45- B .35-C.3-D.3-【分析】由已知可得2123x x π=-,结合12x x <求出1x 的范围,再由12112s i n ()s i n (2)c o s (2)36x xx x ππ-=-=--求解即可. 【解答】解:因为0x π<<,∴112(,)666x πππ-∈-,又因为方程3()5f x =的解为1x ,212(0)x x x π<<<,∴1223x x π+=,∴2123x x π=-,∴12112s in ()s in (2)c o s (2)36x x x x ππ-=-=--,因为12212,3x x x x π<=-,103x π∴<<,∴12(,)662x πππ-∈-,∴由113()s in (2)65f x x π=-=,得14c o s (2)65x π-=,∴124s in ()5x x -=-,故选:A .【点评】本题考查了三角函数的恒等变换及化简求值和三角函数的图象与性质,属中档题. 7.已知1ta n 4ta n θθ+=,则2c o s ()(4πθ+=)A .12B .13C .14D .15【分析】由已知求得s in c o s θθ的值,再由二倍角的余弦及诱导公式求解2c o s ()4πθ+的值.【解答】解:由1ta n 4ta n θθ+=,得s in c o s 4c o s s in θθθθ+=,即224s in c o s s in c o s θθθθ+=,1s in c o s 4θθ∴=,∴21c o s (2)1s in 22c o s ()422πθπθθ++-+==11212s in c o s 14224θθ-⨯-===.故选:C .【点评】本题考查三角函数的化简求值,考查了同角三角函数基本关系式及诱导公式的应用,是基础题.二.填空题(共15小题) 9.设当xθ=时,函数()s in o s f x x x=+取得最大值,则ta n ()4πθ+=2+【分析】()f x 解析式提取,利用两角和与差的正弦公式化为一个角的正弦函数,由x θ=时函数()f x 取得最大值,得到θ的取值,后代入正切公式中计算求值.【解答】解:()sin o s 2sin ()3f x x x x π=+=+;当xθ=时,函数()f x 取得最大值2,32k k zππθπ∴+=+∈;26k πθπ∴=+,kz∈;∴1ta n ()ta n (2)ta n ()2464463k πππππθπ++=++=+==+故答案为:2+.【点评】本题考查了两角和与差的正弦函数公式,同角三角函数间的基本关系,熟练掌握公式是解本题的关键.10.求值:s in 50(1n 10)︒+︒=1 .【分析】先把原式中切转化成弦,利用两角和公式和整理后,运用诱导公式和二倍角公式化简整理求得答案.【解答】解:原式2s in 40s in 80c o s 10s in 50c o s 401c o s 10c o s 10c o s 10c o s 10︒︒︒=︒⋅=︒===︒︒︒︒故答案为:1【点评】本题主要考查了三角函数的恒等变换及其化简求值,以及两角和公式,诱导公式和二倍角公式的化简求值.考查了学生对三角函数基础知识的综合运用. 11.1s in 10c o s 10-=︒︒4 .【分析】s in 10c o s 10得结果.【解答】解:12(c o s 10in 10)1221s in 10c o s 10s in 10c o s 10s in 202︒-︒-==︒︒︒︒︒4s in 20420S in ==故答案为:4【点评】本题主要基础知识的考查,考查了在三角函数的化简与求值中,综合运用二倍角正弦公式、两角和的正弦公式,要求考生熟练运用公式对三角函数化简. 12.已知s in 10c o s 102c o s 140m ︒+︒=︒,则m=【分析】由题意可得2c o s 140s in 10c o s 10m ︒-︒=︒,再利用三角恒等变换求得它的值. 【解答】解:由题意可得2c o s 140s in 102c o s 40s in 102c o s (3010)s in 10c o s 10c o s 10c o s 10m ︒-︒-︒-︒-︒+︒-︒===︒︒︒2c o s 10s in 10s in 102c o s 10-︒+︒-︒==︒故答案为:【点评】本题主要考查三角恒等变换,属于中档题. 13.4c o s 50ta n 40︒-︒=【分析】表达式第一项利用诱导公式化简,第二项利用同角三角函数间的基本关系切化弦,通分后利用同分母分式的减法法则计算,再利用诱导公式及两角和与差的正弦函数公式化简,整理后利用两角和与差的余弦函数公式化为一个角的余弦函数,约分即可得到结果. 【解答】解:4c o s 50ta n 404s in 40ta n 40︒-︒=︒-︒4s in 40c o s 40s in 40c o s 40︒︒-︒=︒2s in 80s in (3010)c o s 40︒-︒+︒=︒12c o s 10c o s 10in 1022c o s 40︒-︒-︒=︒3c o s 10in 1022c o s 40︒-︒=︒==.【点评】本题考查了两角和与差的正弦、余弦函数公式,同角三角函数间的基本关系,以及诱导公式的作用,熟练掌握公式是解本题的关键. 14.2c o s 10s in 20s in 70︒-︒=︒【分析】利用两角和差的余弦公式,进行化简即可.【解答】解:原式12o s 20s in 20)s in 202c o s (3020)s in 2022c o s 20c o s 20︒+︒-︒︒-︒-︒==︒︒o s 20s in 20s in 20o s 20c o s 20c o s 20︒+︒-︒︒===︒︒【点评】本题主要考查三角函数值的化简,利用两角和差的余弦公式是解决本题的关键. 15.已知1ta n 31ta n αα+=-,则2sin 2sin co s 1ααα-+=25.【分析】由1ta n 31ta n αα+=-,我们可计算出ta n α的值,由于2sin α2c o s +α1=,所以将所求的代收式变形为222222s in c o s s in s in c o s s in c o s ααααααα-+++,然后化弦为切,代入求值.【解答】解:1ta n 31ta n αα+=-,1ta n 2α∴=.22222222222112()212s in c o s 2ta n 1222s in 2s in c o s 1115()12s in s in c o s ta n ta n s in c o s ta n αααααααααααααα⨯-⨯+-++-++∴-+====+++. 故答案是:25.【点评】本题考查的知识点是三角函数的恒等变换及化简求值,同角三角函数间的基本关系,解题的关键是将角的弦化切,属于中档题. 16.若1s in ()43πα-=,则c o s ()4πα+=13.【分析】由已知利用诱导公式化简所求即可得解. 【解答】解:1sin ()43πα-=,∴1c o s ()s in (())s in ()42443a ππππαα+=--=-=.故答案为:13.【点评】本题主要考查了诱导公式在三角函数化简求值中的应用,考查了转化思想,属于基础题. 17.若o s 2in 2c o s ()4θθπθ=+,则s in 2θ=23-.【分析】由已知利用三角函数恒等变换的应用可得:2(c o s s in )in 2θθθ+=,平方后整理可得:23sin 24sin 240θθ--=,进而解得s in 2θ的值. 【解答】解:o s 22c o s()4θθπθ=+,∴2(c o s s in )in 22θθθ=+=,∴平方可得:24(1sin 2)3sin 2θθ+=,整理可得:23sin 24sin 240θθ--=,∴解得:2s in 23θ=-,或2(舍去).故答案为:23-.【点评】本题主要考查了三角函数恒等变换的应用,考查了计算能力和转化思想,属于中档题. 18.若ta n 3α=,则s in 2ta n ()4απα+的值为310-.【分析】直接利用三角函数关系式的变换和倍角公式的应用求出结果.【解答】解:由于ta n 3α=,所以22ta n 3s in 21ta n 5ααα==+,1ta n 4ta n ()241ta n 2πααα++===---所以3s in 235210ta n ()4απα==--+.故答案为:310-【点评】本题考查的知识要点:三角函数关系式的恒等变换,倍角公式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型. 19.若ta n 3,(0,)2παα=∈,则c o s ()4πα-=5.【分析】由已知结合同角三角函数基本关系式求解s in α、c o s α的值,然后展开两角差的余弦求解.【解答】解:由ta n 3α=,得s in 3c o s αα=,即s in 3c o s αα=.又22sin c o s 1αα+=,且(0,)2πα∈,解得:s in 10α=,c o s 10α=.∴c o s ()c o s c o s s in s in4441021025πππααα-=+=+=.故答案为:5.【点评】本题考查三角函数的化简求值,考查了同角三角函数基本关系式及两角差的余弦,是基础题.20.公元前6世纪,古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图,发现了黄金分割值约为0.618,这一数值也可以表示为2s in 18m=︒,若24m n +=,则s i n 63m +=︒【分析】根据三角函数同角三角函数关系表示n ,利用辅助角公式结合两角和差的正弦公式进行化简即可. 【解答】解:2s in 18m =︒,∴由24m n +=,得222444sin 184co s 18nm =-=-︒=︒,则2s in 182c o s 18in (4518)in 63s in 63s in 63s in 63s in 63m +︒+︒︒+︒︒====︒︒︒︒故答案为:【点评】本题主要考查三角函数值的化简和求解,利用辅助角公式以及两角和差的正弦公式进行化简是解决本题的关键.21.公元前6世纪,古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图,发现0.618就是黄金分割,这是一个伟大的发现,这一数值也表示为2s in 18a=︒,若24a b +=,则2=12-.【分析】由已知利用同角三角函数基本关系式可求24co s 18b =︒,然后利用降幂公式,诱导公式,二倍角的正弦函数公式化简得答案. 【解答】解:2s in 18a =︒,若24a b +=,2222444sin 184(1sin 18)4c o s 18b a∴=-=-︒=-︒=︒,∴22c o s 54sin 3614sin 18c o s 182sin 362-︒-︒====-︒︒︒,故答案为:12-.【点评】本题主要考查了同角三角函数基本关系式,降幂公式,诱导公式,二倍角的正弦函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.22.函数2()ta n 60s in 2inf x x x=︒+在[,]2ππ上的值域为.【分析】由已知利用三角函数恒等变换的应用可求()in (2)4f x x π=-+[,]2x ππ∈,可得:32[44x ππ-∈,7]4π,进而利用正弦函数的性质即可得解.【解答】解:2()tan 60sin 22f x x x=︒+1c o s 2in 22xx -=+2o s 2x x=+-in (2)4x π=-+又[,]2x ππ∈,可得:32[44xππ-∈,7]4π,s in (2)[14x π∴-∈-,2,可得()in (2)4f x x π=-+-,.故答案为:.【点评】本题主要考查了三角函数恒等变换的应用及正弦函数的性质,考查了转化思想和函数思想,属于基础题. 三.解答题(共3小题) 23.设函数()s in ()s in ()62f x x x ππωω=-+-,其中03ω<<,已知()06f π=.(Ⅰ)求ω; (Ⅱ)将函数()yf x =的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移4π个单位,得到函数()y g x =的图象,求()g x 在[4π-,3]4π上的最小值.【分析】(Ⅰ)利用三角恒等变换化函数()f x 为正弦型函数,根据()06f π=求出ω的值;(Ⅱ)写出()f x 解析式,利用平移法则写出()g x 的解析式,求出[4x π∈-,3]4π时()g x 的最小值.【解答】解:(Ⅰ)函数()s in ()s in ()62f x x x ππωω=-+-s in c o sc o s s ins in ()662x x x πππωωω=---3in c o s 22x xωω=-in ()3x πω=-,又()in ()0663f πππω=-=,∴63k ππωπ-=,k Z∈,解得62k ω=+,又03ω<<,2ω∴=;(Ⅱ)由(Ⅰ)知,()in (2)3f x x π=-,将函数()y f x =的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得到函数in ()3y x π=-的图象;再将得到的图象向左平移4π个单位,得到in ()43yx ππ=+-的图象,∴函数()in ()12yg x x π==-;当[4x π∈-,3]4π时,[123xππ-∈-,2]3π,s in ()[122x π∴-∈-,1],∴当4xπ=-时,()g x取得最小值是322-=-.【点评】本题考查了三角恒等变换与正弦型函数在闭区间上的最值问题,是中档题. 24.已知α,β为锐角,4ta n 3α=,c o s ()5αβ+=-(1)求c o s 2α的值; (2)求tan ()αβ-的值.【分析】(1)由已知结合平方关系求得s in α,c o s α的值,再由倍角公式得c o s 2α的值; (2)由(1)求得t a n 2α,再由c o s ()5αβ+=-求得t a n (αβ+,利用tan ()tan [2()]αβααβ-=-+,展开两角差的正切求解.【解答】解:(1)由22431s in c o s s in c o s ααααα⎧=⎪⎪+=⎨⎪⎪⎩为锐角,解得4s in 53c o s 5αα⎧=⎪⎪⎨⎪=⎪⎩,227c o s 225c o s s in ααα∴=-=-;(2)由(1)得,24s in 22s in c o s 25ααα==,则s in 224ta n 2c o s 27ααα==-.α,(0,)2πβ∈,(0,)αβπ∴+∈,s in ()5αβ∴+==.则s in ()ta n ()2c o s ()αβαβαβ++==-+.ta n 2ta n ()2ta n ()ta n [2()]1ta n 2ta n ()11ααβαβααβααβ-+∴-=-+==-++.【点评】本题考查三角函数的恒等变换及化简求值,考查同角三角函数基本关系式的应用,是中档题. 25.已知函数22()s inc o s in f x x x x =--co s ()x x R ∈.(Ⅰ)求2()3f π的值.(Ⅱ)求()f x 的最小正周期及单调递增区间.【分析】利用二倍角公式及辅助角公式化简函数的解析式,(Ⅰ)代入可得:2()3f π的值.(Ⅱ)根据正弦型函数的图象和性质,可得()f x 的最小正周期及单调递增区间【解答】解:函数22()s inc o s in f x x x x =--7c o s in 2c o s 22s in (2)6x x x x π=-=+(Ⅰ)2275()2s in (2)2s in 23362f ππππ=⨯+==,(Ⅱ)2ω=,故Tπ=,即()f x 的最小正周期为π,由72[262xk πππ+∈-+,2]2k ππ+,k Z∈得:5[6x k ππ∈-+,]3k ππ-+,kZ∈,故()f x 的单调递增区间为5[6k ππ-+,]3k ππ-+或写成[6k ππ+,2]3k ππ+,kZ∈.【点评】本题考查的知识点是三角函数的化简求值,三角函数的周期性,三角函数的单调区间,难度中档。
三角函数化简题

三角函数的化简、求值与证明 日期:2009年 月 日星期式进行三角函数式的化简与恒等式的证明.用.(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③ 三角公式的逆用等。
(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如2(),()()ααββααβαβ=+-=++-等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。
3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分.三角函数的求值: 2.正确灵活地运用公式,通过三角变换消去或约去一些非特殊角的三角函数值; 3.一些常规技巧:“1”的代换、切割化弦、和积互化、异角化同角等. 1.三角函数式的化简: 三角函数式的化简常用方法是:异名函数化为同名三角函数,异角化为同角,异次化为同次,切割化弦,特殊值与特殊角的三角函数互化. 2.三角恒等式的证明: 三角恒等式包括有条件的恒等式和无条件的恒等式.①无条件的等式证明的基本方法是化繁为简、左右归一、变更命题等,使等式两端的“异”化为“同”;②有条件的等式常用方法有:代入法、消去法、综合法、分析法等.1、已知θ是第三象限角,且4459sin cos θθ+=,那么2sin θ等于 ( A )A B 、 C 、23 D 、23-2、函数22y sin x x =-的最小正周期 ( B )A 、2πB 、πC 、3πD 、4π3、tan 70cos10(3tan 201)-等于 ( D )A 、1B 、2C 、-1D 、-24、已知46sin (4)4m m m αα-=≠-,则实数m 的取值范围是__[-1,73]___。
(完整版)三角函数化简求值证明技巧
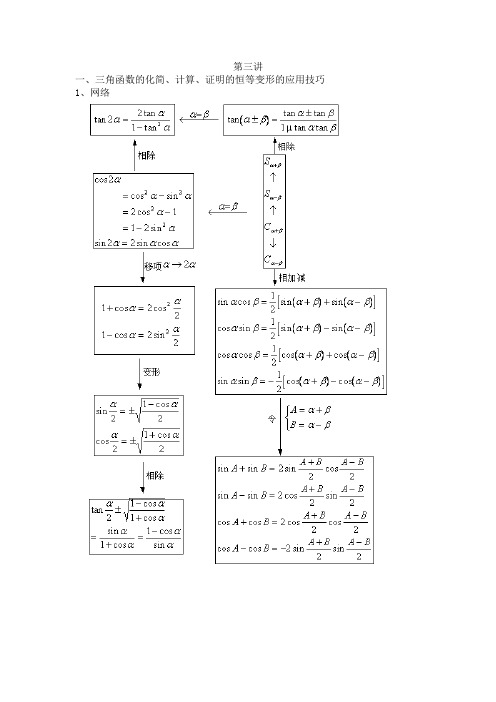
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。
三角函数化简求值每日一练

三角函数化简求值每日一练1、的值为____________2、计算:=____________3、化简=____________4、sin15°+sin75°的值是____________5、求值:sin10°tan70°﹣2cos40°=____________6、sin315°sin(﹣1260°)+cos390°sin(﹣1020°)=____________7、=____________8、sin2230°+sin110°•cos80°=____________9、=____________10、=____________11、求值sin17°cos47°﹣sin73°cos43°=____________12、=____________13、﹣的值是____________14、(1+tan21°)(1+tan24°)的值为____________15、=____________16、计算3tan10°+4 =____________17、化简:=____________18、=____________19、sin40°(tan190°﹣)=____________20、计算:=____________21、求值:=____________22、计算:=____________答案解析部分一、单选题1、【答案】B【考点】三角函数的化简求值【解析】【解答】解:= = = ,故选:B.【分析】利用三角恒等变换化简所给的式子,可得结果.二、填空题2、【答案】1【考点】三角函数的化简求值,两角和与差的正切函数【解析】【解答】解:∵tan60°= ,∴==tan(60°﹣15°)=tan45°=1.故答案为:1.【分析】由tan60°= ,利用两角差的正切公式,即可求出答案来.3、【答案】﹣8【考点】三角函数的化简求值【解析】【解答】解:∵tan12°﹣= = = =﹣8sin12°cos24°,∴= =﹣8.故答案为:﹣8.【分析】由同角函数的三角函数关系以及两角和差的正弦公式转化原式可得tan12°﹣=﹣8sin12°cos24°,整理化简可得结果。
考点15 三角函数式的化简与求值(答案)

,故选 B.
3.【2017
届广西玉林市、贵港市高中毕业班质量检测】若
cos
−
3sin
=
0
,则
tan
−
4
=
(
)
−1
1
A. 2
B.-2
C. 2
D.2
【答案】A
【解析】由 cos
− 3sin
=
0
tan
,知
=
1 3
,则
tan
− 4
=
tan −1 1+ tan
=
−
1 2
,故选 A
.
4.【山西省孝义市 2017 届高三下学期高考考前质量检测三(5 月)】已有角 的顶点与坐标原点重合,
+ cos2
sin ”;(3)化正弦、余弦为正切,即 cos
=
tan
;
tan = sin
(4)化正切为正弦、余弦,即
cos ;( 5 ) 正 弦 、 余 弦 和 ( 差 ) 与 积 的 互 化 , 即
(sin cos )2 =1 2sin cos .
tan = 3
1− sin 2 =
【变式 1】【例题中的条件不改变,所求三角函数式改变】若
【解析】
16 8 ,选 D.
【方法技巧归纳】二倍角公式的正用、逆用、变形用是公式的种主要应用手段,特别是二倍角的余弦 公式,其变形公式在求值与化简中有广泛的应用,在综合使用两角和与差、二倍角公式化简求值时,要注 意以下几点:(1)熟练掌握公式的正用、逆用和变形使用;(2)擅于拆角、配角;(3)注意二倍角的相对性; (4)注意角的范围;(5)熟悉常用的方法和技巧,如切化弦、异名化同名、异角化同角等.
数学基础训练15 三角函数化简、求值及证明

数学基础训练15 三角函数化简、求值及证明●训练指要灵活运用公式进行三角恒等变形,掌握三角函数的“给角求值”“给值求值”及“给值求角”的基本方法.一、选择题1.sin15°sin30°sin 75°的值等于 A.43 B.83 C.81 D.41 2.若cot θ=3,则cos 2θ+21sin2θ的值是 A.-56 B.-54 C.54 D. 56 3.若角α的终边落在直线y =3x 上,那么sin α,cos α,tan α的值分别为 A.3,1010,10103 B.1010,10103±-,±3 C.±10103,±1010,±3 D.±10103,±1010,3 二、填空题4.求值:︒︒-︒︒︒+︒7sin 75sin 68cos 7sin 75cos 68sin =_________. 5.(2002年北京春季高考题)如果cos θ=-1312,θ∈(π,23π),那么cos(θ+4π)的值等于_________.三、解答题6.(2002年全国高考题)已知sin 22α+sin2αcos α-cos2α=1,α∈(0,2π).求sin α,tan α的值.7.已知cos(α-2,32)2sin(,91)2πβαβ且=--=<α<π,0<β<2π,求cos(α+β)的值. 8.若α、β均为锐角,且tan α=101sin ,71=β,求α+2β的值.数学基础训练15答案一、1.C提示:原式=sin15°sin30°cos15°=21sin 230°=81. 2.D 提示:原式=56cot 1cot cot cos sin cos sin cos 22222=++=++θθθθθθθθ. 3.D二、4.2+3提示:变角:68°=75°-7°.5.-2627 三、6.sin α=21 tan α=33 提示:已知等式化为2cos 2α(2sin α-1)(sin α+1)=0∵α∈(0,2π),∴仅2sin α-1=0,sin α=21,tan α=33 7.-729239 提示:变角:(α-2)2()2βαβαβ+=--. 8.4π 提示:求得tan β=31,tan2β=43,tan(α+2β)=1. 又0<α<2π,求得0<β<4π. ∴0<α+2β<π,故α+2β=4π.。
三角函数化简题

例3.已知,求的值.
解:由题意,,
∴原式.
例4.已知,求的值.
解:∵,,
∴,
得,若,则,
若,无意义.
说明:角的和、差、倍、半具有相对性,如,,等,解题过程中应充分利用这种变形.
例5.已知关于的方程的两根为,
求:(1)的值;(2)的值;(3)方程的两根及此时的值.
①
②
解:(1)由根与系数的关系,得,
3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明。
主要方法1.三角函数的求值:
1.寻求角与角之间的关系,化非特殊角为特殊角;
给出某些角的三角函数式的值求另外一些角的三角函数值解题的关键在于变角如等把所求角用含已知角的式子表示求解时要注意角的范围的讨论
本资料为word版本,可以直接编辑和打印,感谢您的下载
三角函数化简题
地点:__________________
时间:__________________
说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容
2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。
三角函数的化简与求值2

三角函数的化简与求值 (2)一、小题训练1.(A )已知tan α=4,tan β=3,那么tan(α+β)= .2.(A )计算:sin 75°·cos 30°-sin 15°·sin 150°= .3.(A )已知tan -6πα⎛⎫ ⎪⎝⎭=37,tan +6πβ⎛⎫ ⎪⎝⎭=25,那么tan(α+β)= . 4.(B )已知sin α=35,那么cos 2α= .5.(B )已知α为第二象限角,且sin α+cos α=3,则cos 2α= . 6.(B )已知sin(α+β) =21,sin(α-β) =101,则βαtan tan 的值为 .二、例题选讲例1.(A)目标角与已知角之间的变换已知α,β均为锐角,且sin α=35,tan(α-β)= 1-3.(1)求sin(α-β)的值;(2)求cos β的值.3 5,cos(α+β)=5-13,求sin β的值.变式(B)已知α,β均为锐角,且sin α=例2.(B)二倍角的三角函数公式的简单应用已知sin α=1213,且α∈2ππ⎛⎫⎪⎝⎭,,求sin 2α,cos 2α,tan 2α的值.变式(A ) (1)已知sin 2 cos α= . (2)设α为第二象限角,sin α=35,则sin2α= .例3.(B ) 二倍角的化简与求值(1sin cos )sin -cos θθθθ⎛⎫++ ⎪0<θ<π.变式 (B ) (1)化简:0205-cos203-cos 10= .(2)求证:= 21sin4cos41-tan θθθ++1sin4-cos42tan θθθ+例4 .(C )二倍角公式的简单应用已知函数f (x )2x cos 2x 22x . (1)求f (x )的最小正周期;(2)求f (x )在区间[-π,0]上的最小值.变式 (C )已知函数f (x )=sin 2x-sin 26x π⎛⎫- ⎪⎝⎭,x ∈R .(1)求f (x )的最小正周期;(2)求f (x )在区间,34ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值.例5.与三角函数的图象与性质综合运用已知函数f(x)=A sin(ωx+φ)的部分图象如图所示.(1) 求函数f(x)的解析式;(2) 若f(α)=32,求sin26πα⎛⎫+⎪⎝⎭的值.ππ0022A Aωϕωϕ⎛⎫>>-<<⎪⎝⎭其中,,为常数,且,,变式 已知函数f (x )=12sin 2x 2x . (1) 求f (x )的最小正周期和最小值;(2) 将函数f (x )的图象上每一点的横坐标伸长到原来的两倍,纵坐标不变, 得到函数g (x )的图象,当x ∈2ππ⎡⎤⎢⎥⎣⎦,时,求g (x )的值域.四、巩固练习1.(A )计算:sin 20°cos 10°-cos 160°sin 10°= .2.(A )若α,β为锐角,cos α=17,cos(α+β)=-1114,则β= .3.(A )已知α,β均为锐角,且tan β=cos -sin cos sin αααα+,则tan(α+β)= .4.(A )已知sin2θ=45,cos 2θ =3-5,那么角θ在第 象限. 5.(A )已知sin α+2cos α=0,则sin 2α+cos 2α= .6.(B )已知sin -6πα⎛⎫ ⎪⎝⎭=13,那么cos 2+23πα⎛⎫⎪⎝⎭= .7.(B )在平面直角坐标系xOy 中,角α的终边经过点P (3,4).(1)求sin +4πα⎛⎫ ⎪⎝⎭的值;(2)若点P 关于x 轴的对称点为点Q ,求OP ·OQ 的值.8.(B )设α为锐角,若cos +6πα⎛⎫⎪⎝⎭=45,求sin 2+12πα⎛⎫ ⎪⎝⎭的值.9.(B )已知sin α∈0,2π⎛⎫⎪⎝⎭,tan β=13.(1)求tan α的值; (2)求tan(α+2β)的值.10.(C )设函数f (x )=A cos 46x π⎛⎫+⎪⎝⎭,x ∈R ,且f 3π⎛⎫⎪⎝⎭(1)求A 的值;(2)已知α,β∈0,2π⎡⎤⎢⎥⎣⎦,且f443πα⎛⎫+⎪⎝⎭=3017-,f 243πβ⎛⎫-⎪⎝⎭=85, 求cos(α+β)的值.参考答案一、小题训练1.7-11 2 3.1 4.725 5.6.23 二、例题选讲 例1.【解析】(1)因为α,β∈02π⎛⎫⎪⎝⎭,,所以-2π<α-β<2π,又tan(α-β)= 1-3<0,所以-2π<α-β<0,所以sin(α-β)=-10.(2)由(1)可得cos(α-β).因为α为锐角,sin α=35,所以cos α=45,所以cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β). 变式.【解析】因为sin α=35,α为锐角,所以cos α=45, 又α,β均为锐角,cos(α+β)=5-13,所以0<α+β<π,所以sin(α+β)=1213,所以sin β=sin[(α+β)-α]=sin(α+β)cos α-cos(α+β)sin α=6365. 例2.【解析】 【思维引导】直接使用二倍角公式即可.因为α∈2ππ⎛⎫⎪⎝⎭,,sin α=1213,所以cos α=5-13, 所以sin 2α=2sin αcos α=120-169, cos 2α=cos 2α-sin 2α=119-169, tan 2α=sin2cos2αα=120119.【精要点评】求cos α的值时,要注意正负的判断.变式【解析】(1)13 (2)2425- (1)cos α=1-2sin 22α=13.(2)直接求得cos α=45-,代入正弦的二倍角公式即可.例3.【解析】 【思维引导】考虑通过把角θ统一化为2θ,同时去掉根号.因为0<θ<π,所以0<2θ<2π,所以cos2θ>0,原式22cos 2sin cos sin -cos θθθθθ⎛⎫⎛⎫+ ⎪⎪=2cos sin cos sin -cos 222222cos2θθθθθθ⎛⎫⎛⎫+ ⎪⎪⎝⎭⎝⎭=sin 22θ-cos 22θ=-cos θ.变式.【解析】 (1) 2【解析】0205-cos203-cos 10=005-cos201cos203-2+=002(5-cos20)5-cos20=2例4.【解析】(1)因为f (x )=2sinx-2(1-cos x )=sin 4x π⎛⎫+ ⎪⎝⎭-2,所以f (x )的最小正周期为2π. (2)因为-π≤x ≤0,所以34π-≤x+4π≤4π. 当x+4π=-2π,即x=-34π时,f (x )取得最小值,所以f (x )在区间[-π,0]上的最小值为f 34π⎛⎫⎪⎝⎭=-1-2. 变式【解析】(1)由题意得f (x )=1cos 2x 2--1cos 232x π⎛⎫-- ⎪⎝⎭=11cos 2222x x ⎛⎫+ ⎪ ⎪⎝⎭1cos 22x -=1sin 226x π⎛⎫- ⎪⎝⎭,所以f (x )的最小正周期T=2π2=π.(2)当2k π-π2<2x-π6<2k π+π2,k ∈Z ,即k π-π6<x<k π+π3(k ∈Z )时,f (x )单调递增;当2k π+π2<2x-π6<2k π+3π2,k ∈Z ,即k π+π3<x<k π+5π6(k ∈Z )时,f (x )单调递减,所以f (x )在区间π,36π⎡⎤--⎢⎥⎣⎦上是减函数,在区间ππ64⎡⎤-⎢⎥⎣⎦,上是增函数,f -3π⎛⎫ ⎪⎝⎭=1-4,f -6π⎛⎫ ⎪⎝⎭=12-,f 4π⎛⎫ ⎪⎝⎭=4,所以f (x )在区间,34ππ⎡⎤-⎢⎥⎣⎦上的最大值为4,最小值为12-.例5.【解析】(1) 由图可知,A=2,T=2π,故ω=1,所以f (x )=2sin (x +φ).又f 2π3⎛⎫ ⎪⎝⎭=2sin 2π3ϕ⎛⎫+ ⎪⎝⎭=2,且-π2<φ<π2,故φ=-π6,于是f (x ) =2sin π-6x ⎛⎫ ⎪⎝⎭. (2) 由f (α)=32,得sin π-6α⎛⎫ ⎪⎝⎭=34,所以sin π26α⎛⎫+ ⎪⎝⎭=sin π2-62πα⎡⎤⎛⎫+ ⎪⎢⎥⎝⎭⎣⎦ =cos π26α⎡⎤⎛⎫- ⎪⎢⎥⎝⎭⎣⎦ =1-2sin 2π-6α⎛⎫ ⎪⎝⎭=1-2×234⎛⎫ ⎪⎝⎭=-18.变式:【解答】(1) f (x )=12sin 2x2x =12sin 2x-(1+cos 2x )=12sin 2x-cos 2x-=sinπ2-3x ⎛⎫ ⎪⎝⎭-, 故f (x )的最小正周期为π,最小值为-.(2) 由条件可知g (x )=sin π-3x ⎛⎫ ⎪⎝⎭-2.当x ∈ππ2⎡⎤⎢⎥⎣⎦,时,有x -π3∈π2π63⎡⎤⎢⎥⎣⎦,, 从而sin π1-132x ⎛⎫⎡⎤⎪⎢⎥⎝⎭⎣⎦的值域为,,所以g (x )=sin π-3x ⎛⎫ ⎪⎝⎭-的值域为⎣⎦. 巩固练习 1.122.3π 3.1 4.θ是第三象限角 5.7-5 6.7-97.(1)因为角α的终边经过点P (3,4),所以sin α=45,cos α=35,所以sin +4πα⎛⎫ ⎪⎝⎭=sinαcos4π+cos αsin 4π. (2)因为P (3,4)关于x 轴的对称点为Q ,所以Q (3,-4).所以OP =(3,4),OQ =(3,-4),所以OP ·OQ =3×3+4×(-4)=-7. 8.由cos +6πα⎛⎫⎪⎝⎭=45,得cos 2+3πα⎛⎫ ⎪⎝⎭=2cos 2+6πα⎛⎫ ⎪⎝⎭-1=725. 因为cos 2+3πα⎛⎫ ⎪⎝⎭>0,α为锐角,所以2α+3π∈0,2π⎛⎫ ⎪⎝⎭,所以sin 2+3πα⎛⎫ ⎪⎝⎭=2425,所以sin 2+12πα⎛⎫ ⎪⎝⎭=sin π234πα⎡⎤⎛⎫+- ⎪⎢⎥⎝⎭⎣⎦=50.9.(1)因为sinα∈0,2π⎛⎫⎪⎝⎭,所以cosα=tan α=sin cos αα=12.(2)因为tan β=13,所以tan 2β=22tan 1-tan ββ=212311-3⨯⎛⎫ ⎪⎝⎭=34,所以tan(α+2β)=tan tan21-tan tan2αβαβ+=1324131-24+⨯=2.10.(1)fπ3⎛⎫⎪⎝⎭=A cosππ126⎛⎫+⎪⎝⎭=A cosπ4=A=2.(2)f4π43α⎛⎫+⎪⎝⎭=2cosππ36α⎛⎫++⎪⎝⎭=2cosπ2α⎛⎫+⎪⎝⎭=-2sin α=-3017,即sin α=15 17.f2π4-3β⎛⎫⎪⎝⎭=2cosππ-66β⎛⎫+⎪⎝⎭=2cos β=85,即cos β=45.因为α,β∈π2⎡⎤⎢⎥⎣⎦,,所以cosα=817,sin35,所以cos(α+β)=cos αcos β-sin αsinβ=817×45-1517×35=-1385.。
高中数学三角函数专题:三角函数化简(一)

高中数学三角函数专题:三角函数化简第一部分:三角函数化简基本原理知识点一:余弦的两角和差公式。
关系式一:βαβαβαsin sin cos cos )cos(-=+。
关系式二:βαβαβαsin sin cos cos )cos(+=-。
推理方法:向量积。
第一种向量积的计算方法:非坐标的向量积计算。
θcos ||||⋅⋅=⋅b a b a 。
第二种向量积的计算方法:坐标的向量积计算。
),(11y x a =,212122),(y y x x b a y x b +=⋅⇒=。
证明:βαβαβαsin sin cos cos )cos(+=-。
如下图所示:图甲图乙如图乙所示:过点A 作x 轴垂线,垂足为C 。
在OAC Rt ∆中:1||==r OA ,α=∠AOC 。
ααααsin sin 1sin ||||||||sin =⋅=⋅=⇒=OA AC OA AC ;ααααcos cos 1cos ||||||||cos =⋅=⋅=⇒=OA OC OA OC 。
αsin ||=AC ,)sin ,(cos cos ||αααA OC ⇒=。
如图甲所示:同理可以得到:)sin ,(cos ββB 。
)sin ,(cos )0,0()sin ,(cos αααα=-=OA ;)sin ,(cos )0,0()sin ,(cos ββββ=-=OB ;根据向量积的非坐标运算得到:βαβαsin sin cos cos +=⋅OB OA 。
1||||===r OB OA ,向量OA 与OB 的夹角为βα-=∠AOB 。
根据向量积的坐标运算得到:)cos()cos(11cos ||||βαβα-=-⋅⋅=∠⋅⋅=⋅AOB OB OA OB OA 。
βαβαsin sin cos cos +=⋅OB OA ,)cos(βα-=⋅OB OA βαβαβαsin sin cos cos )cos(+=-⇒。
三角函数的奇偶性:①函数x x f sin )(=是奇函数x x sin )sin(-=-⇒。
三角函数化简求值练习题(超级好)

三⾓函数化简求值练习题(超级好)三⾓化简求值测试题1.若sin α=35,α∈(-π2,π2),则cos(α+5π4)=________.2.已知π<θ<32π,则 12+12 12+12cos θ=________.3.计算:cos10°+3sin10°1-cos80°=________.4.函数y =2cos 2x +sin2x 的最⼩值是__________________.5.函数f (x )=(sin 2x +12010sin 2x )(cos 2x +12010cos 2x)的最⼩值是________. 6.若tan(α+β)=25,tan(β-π4)=14,则tan(α+π4)=_____.7.若3sin α+cos α=0,则1cos 2α+sin2α的值为________.8.2+2cos8+21-sin8的化简结果是________.9.若tan α+1tan α=103,α∈(π4,π2),则sin(2α+π4)的值为_________.10.若函数f (x )=sin2x -2sin 2x ·sin2x (x ∈R ),则f (x )的最⼩正周期为________.11. 2cos5°-sin25°cos25°的值为________.12.向量a =(cos10°,sin10°),b =(cos70°,sin70°),|a -2b |=________________.13.已知1-cos2αsin αcos α=1,tan(β-α)=-13,则tan(β-2α)=________.14.设a =sin14°+cos14°,b =sin16°+cos16°,c =62,则a 、b 、c 的⼤⼩关系是________.15.已知⾓α∈(π4,π2),且(4cos α-3sin α)(2cos α-3sin α)=0.(1)求tan(α+π4)的值;(2)求cos(π3-2α)的值.16. 已知tan α=2.求(1)tan(α+π4)的值;(2)sin2α+cos 2(π-α)1+cos2α的值.17.如图,点A ,B 是单位圆上的两点,A ,B 两点分别在第⼀、⼆象限,点C 是圆与x 轴正半轴的交点,△AOB 是正三⾓形,若点A 的坐标为(35,45),记∠COA =α. (1)求1+sin2α1+cos2α的值;(2)求|BC |2的值.18.△ABC 中,A ,B ,C 所对的边分别为a ,b ,c ,tan C =sin A +sin Bcos A +cos B,sin(B -A )=cos C .,,求⾓A 。
高中数学三角函数式的化简与求值

三角函数三角函数式的化简和求值是高考考查的重点内容之一.通过本节的学习使考生掌握化简和求值问题的解题规律和途径,特别是要掌握化简和求值的一些常规技巧,以优化我们的解题效果,做到事半功倍.●难点磁场(★★★★★)已知2π<β<α<43π,cos(α-β)=1312,sin(α+β)=-53,求sin2α的值_________.●案例探究[例1]不查表求sin 220°+cos 280°+3cos20°cos80°的值.命题意图:本题主要考查两角和、二倍角公式及降幂求值的方法,对计算能力的要求较高.属于★★★★级题目.知识依托:熟知三角公式并能灵活应用. 错解分析:公式不熟,计算易出错.技巧与方法:解法一利用三角公式进行等价变形;解法二转化为函数问题,使解法更简单更精妙,需认真体会.解法一:sin 220°+cos 280°+3sin 220°cos80°=21 (1-cos40°)+21(1+cos160°)+ 3sin20°cos80° =1-21cos40°+21cos160°+3sin20°cos(60°+20°)=1-21cos40°+21(cos120°cos40°-sin120°sin40°)+3sin20°(cos60°cos20°-sin60°sin20°)=1-21cos40°-41cos40°-43sin40°+43sin40°-23sin 220°=1-43cos40°-43(1-cos40°)= 41解法二:设x =sin 220°+cos 280°+3sin20°cos80° y =cos 220°+sin 280°-3cos20°sin80°,则 x +y =1+1-3sin60°=21,x -y =-cos40°+cos160°+3sin100° =-2sin100°sin60°+3sin100°=0 ∴x =y =41,即x =sin 220°+cos 280°+3sin20°cos80°=41. [例2]设关于x 的函数y =2cos 2x -2a cos x -(2a +1)的最小值为f (a ),试确定满足f (a )=21的a 值,并对此时的a 值求y 的最大值.命题意图:本题主要考查最值问题、三角函数的有界性、计算能力以及较强的逻辑思维能力.属★★★★★级题目知识依托:二次函数在给定区间上的最值问题.错解分析:考生不易考查三角函数的有界性,对区间的分类易出错.技巧与方法:利用等价转化把问题化归为二次函数问题,还要用到配方法、数形结合、分类讲座等.解:由y =2(cos x -2a )2-2242+-a a 及cos x ∈[-1,1]得:f (a )⎪⎪⎩⎪⎪⎨⎧≥-<<-----≤)2( 41)22( 122)2( 12a a a a a a∵f (a )=21,∴1-4a =21⇒a =81∉[2,+∞) 故-22a -2a -1=21,解得:a =-1,此时,y =2(cos x +21)2+21,当cos x =1时,即x =2k π,k ∈Z ,y max =5.[例3]已知函数f (x )=2cos x sin(x +3π)-3sin 2x +sin x cos x (1)求函数f (x )的最小正周期;(2)求f (x )的最小值及取得最小值时相应的x 的值; (3)若当x ∈[12π,127π]时,f (x )的反函数为f -1(x ),求f --1(1)的值. 命题意图:本题主要考查三角公式、周期、最值、反函数等知识,还考查计算变形能力,综合运用知识的能力,属★★★★★级题目.知识依托:熟知三角函数公式以及三角函数的性质、反函数等知识.错解分析:在求f --1(1)的值时易走弯路. 技巧与方法:等价转化,逆向思维.解:(1)f (x )=2cos x sin(x +3π)-3sin 2x +sin x cos x =2cos x (sin x cos 3π+cos x sin 3π)-3sin 2x +sin x cos x=2sin x cos x +3cos2x =2sin(2x +3π)∴f (x )的最小正周期T =π(2)当2x +3π=2k π-2π,即x =k π-125π(k ∈Z )时,f (x )取得最小值-2.(3)令2sin(2x +3π)=1,又x ∈[27,2ππ],∴2x +3π∈[3π,23π],∴2x +3π=65π,则 x =4π,故f --1(1)= 4π. ●锦囊妙计本难点所涉及的问题以及解决的方法主要有:1.求值问题的基本类型:1°给角求值,2°给值求值,3°给式求值,4°求函数式的最值或值域,5°化简求值.2.技巧与方法:1°要寻求角与角关系的特殊性,化非特角为特殊角,熟练准确地应用公式. 2°注意切割化弦、异角化同角、异名化同名、角的变换等常规技巧的运用.3°对于条件求值问题,要认真寻找条件和结论的关系,寻找解题的突破口,很难入手的问题,可利用分析法.4°求最值问题,常用配方法、换元法来解决. ●歼灭难点训练 一、选择题1.(★★★★★)已知方程x 2+4ax +3a +1=0(a >1)的两根均tan α、tan β,且α,β∈ (-2,2ππ),则tan2βα+的值是( ) A.21 B.-2C.34 D.21或-2 二、填空题2.(★★★★)已知sin α=53,α∈(2π,π),tan(π-β)= 21,则tan(α-2β)=_________.3.(★★★★★)设α∈(43,4ππ),β∈(0,4π),cos(α-4π)=53,sin(43π+β)=135,则sin(α+β)=_________.三、解答题4.不查表求值:.10cos 1)370tan 31(100sin 130sin 2︒+︒+︒+︒5.已知cos(4π+x )=53,(1217π<x <47π),求x x x tan 1sin 22sin 2-+的值.6.(★★★★★)已知α-β=38π,且α≠k π(k ∈Z ).求)44(sin 42sin2csc )cos(12βπαααπ-----的最大值及最大值时的条件.7.(★★★★★)如右图,扇形OAB 的半径为1,中心角60°,四边形PQRS 是扇形的内接矩形,当其面积最大时,求点P 的位置,并求此最大面积.8.(★★★★★)已知cos α+sin β=3,sin α+cos β的取值范围是D ,x ∈D ,求函数y =10432log 21++x x 的最小值,并求取得最小值时x的值.参考答案难点磁场解法一:∵2π<β<α<43π,∴0<α-β<4π.π<α+β<43π, ∴sin(α-β)=.54)(sin 1)cos(,135)(cos 122-=+--=+=--βαβαβα∴sin2α=sin [(α-β)+(α+β)]=sin(α-β)cos(α+β)+cos(α-β)sin(α+β) .6556)53(1312)54(135-=-⨯+-⨯= 解法二:∵sin(α-β)=135,cos(α+β)=-54,∴sin2α+sin2β=2sin(α+β)cos(α-β)=-6572sin2α-sin2β=2cos(α+β)sin(α-β)=-6540∴sin2α=6556)65406572(21-=--歼灭难点训练一、1.解析:∵a >1,tan α+tan β=-4a <0.tan α+tan β=3a +1>0,又α、β∈(-2π,2π)∴α、β∈(-2π,θ),则2βα+∈(-2π,0),又tan(α+β)=342tan 12tan2)tan(,34)13(14tan tan 1tan tan 2=β+α-β+α=β+α=+--=βα-β+α又a a , 整理得2tan 222tan 32-β+α+β+α=0.解得tan 2β+α=-2. 答案:B2.解析:∵sin α=53,α∈(2π,π),∴cos α=-54则tan α=-43,又tan(π-β)=21可得tan β=-21,247)34()43(1)34(432tan tan 1tan tan )2tan(.34)21(1)21(2tan 1tan 22tan 222=-⨯-+---=β⋅α+β-α=β-α-=---⨯=β-β=β答案:2473.解析:α∈(43,4ππ),α-4π∈(0, 2π),又cos(α-4π)=53. 6556)sin(.655613554)1312(53)43sin()4sin()43cos()4cos()]43()4cos[(]2)43()4sin[()sin(.1312)43cos(,135)43sin().,43(43).4,0(,54)4sin(=β+α=⨯+-⨯-=β+π⋅π-α+β+π⋅π-α-=β+π+π-α-=π-β+π+π-α=β+α∴-=β+π∴=β+πππ∈β+π∴π∈β=π-α∴即 答案:6556 三、4.答案:2752853)54(257)4cos()4sin(2sin sin cos cos )cos (sin sin 2cos sin 1sin 2cos sin 2tan 1sin 22sin 54)4sin(,2435,471217.257)4(2cos 2sin ,53)4cos(:.522=-⨯=++=-+=-+=-+-=+∴<+<∴<<=+-=∴=+x x x xx xx x x x x x x x x x x x x x x x x ππππππππππ又解2)322sin(22)21()322sin(4.32243824,3822cos 2sin 42)2sin 2(sin 2)2sin 2121(42cos 2cos 22sin 2)22cos(142sin 1)cos 1(2sin )44(sin 42sin 2csc )cos(1:.62222-π-α-=--⨯π-α=∴π-α=π-α=β-α∴π=β-α-β-αβ+α=-β+α=β--αα⋅α=β-π--α-α+α=β-π-α-αα-π-=t t 令解 π≠αk (k ∈Z ),322322π-π≠π-α∴k (k ∈Z ) ∴当,22322π-π=π-αk 即34π+π=αk (k ∈Z )时,)322sin(π-α的最小值为-1.7.解:以OA 为x 轴.O 为原点,建立平面直角坐标系,并设P 的坐标为(cos θ,sin θ),则|PS |=sin θ.直线OB 的方程为y =3x ,直线PQ 的方程为y =sin θ.联立解之得Q (33sin θ;sin θ),所以|PQ |=cos θ-33sin θ. 于是S PQRS =sin θ(cos θ-33sin θ)=33(3sin θcos θ-sin 2θ)=33(23sin2θ-22cos 1θ-)=33(23sin2θ+21cos2θ-21)= 33sin(2θ+6π)-63.∵0<θ<3π,∴6π<2θ+6π<65π.∴21<sin(2θ+6π)≤1.∴sin(2θ+6π)=1时,PQRS 面积最大,且最大面积是63,此时,θ=6π,点P 为的中点,P (21,23). 8.解:设u =sin α+cos β.则u 2+(3)2=(sin α+cos β)2+(cos α+sin β)2=2+2sin(α+β)≤4.∴u 2≤1,-1≤u ≤1.即D =[-1,1],设t =32+x ,∵-1≤x ≤1,∴1≤t ≤5.x =232-t ..21,232,2,258log 2log 82log ,0log .82,2,42.8224142142104325.05.05.0min 5.0max 2-==+==-==∴>=====≤+=+=++=∴x x t y M M y M t t t tt t t x x M 此时时时是减函数在时即当且仅当第四章 三角函数§4-1 任意角的三角函数 一、选择题:1.使得函数 有意义的角在( )(A)第一,四象限 (B)第一,三象限 (C)第一、二象限 (D)第二、四象限2.角α、β的终边关于У轴对称,(κ∈Ζ)。
三角函数化简例题大全

三角函数化简例题大全三角函数化简是高中数学中的重要内容,也是学生们容易混淆和困惑的部分。
在学习三角函数化简时,掌握一些常见的例题可以帮助我们更好地理解和掌握相关知识。
下面,我将为大家整理一些三角函数化简的例题,希望能够帮助大家更好地理解和掌握这一部分知识。
1. 化简sin²x + cos²x的值。
解,根据三角恒等式sin²x + cos²x = 1,所以sin²x + cos²x的值为1。
2. 化简tanx + cotx的值。
解,根据tanx = 1/cotx,所以tanx + cotx = cotx + cotx = 2cotx。
3. 化简sinx/cosx的值。
解,sinx/cosx = tanx。
4. 化简1 cos²x的值。
解,1 cos²x = sin²x。
5. 化简(1 + sinx)² cos²x的值。
解,(1 + sinx)² cos²x = 1 + 2sinx + sin²x cos²x = 1 + 2sinx + sin²x (1 sin²x) =2sinx + 2sin²x = 2sinx(1 + sinx)。
6. 化简sinx/cosx + cosx/sinx的值。
解,sinx/cosx + cosx/sinx = (sin²x + cos²x) / (sinxcosx) = 1/(sinxcosx)。
7. 化简sinx sinxcos²x的值。
解,sinx sinxcos²x = sinx(1 cos²x) = sinxsin²x = sin³x。
通过以上例题的化简过程,我们可以看到,三角函数化简实际上就是利用三角恒等式和基本的三角函数关系,将复杂的三角函数表达式化简成更简单的形式。
专题07 帮你做好带有根号的三角函数式化简(解析版)

帮你做好带有根号的三角函数式化简在三角函数式的化简中常遇到带有根号的化简,带有根号的化简我们一般首先想到将根号去掉,去掉a =,关键是将被开方数变为平方形式,变为平方形式的方法主要有以下几种。
现结合实例说明如下:一、利用同角三角函数关系式中的平方关系例1.cos 1sin αα-=成立,求α的取值范围。
分析:可以将已知等式的左端化简,将根号去掉。
解1cos 1cos cos 1sin sin sin αααααα---=====, ()sin sin ,sin 0,2,2,k k k Z ααααπππ∴=-<∴∈-+∈。
点评:本题是利用同角三角函数关系式中的平方关系将被开方数变为平方形式,还用到了余弦函数的最值。
变式。
α为第二象限角。
解:∵α为第二象限角,cos 0α∴<。
===1+sin 1sin 2sin 2tan cos cos cos ααααααα-=-==----。
二、利用二倍角公式例2.若322παπ<<分析:可以由内向外,利用二倍角的余弦公式将被开方数变为平方形式。
解:∵322παπ<<,342αππ∴<<,cos 0,cos 02αα∴><.原式===cos 2α===-. 点评:本题两次用了二倍角的余弦公式,将被开方数变为平方形式。
变式.4cos 2sin 22+-的值等于( ).A .2sinB .2cos -C .2cos 3D .2cos 3-答案:D 解析:22222sin 2cos4(1sin 2)(cos41)cos 22cos 2-+=-++=+ 3|cos 2|3cos 2==-.三、利用完全平方公式例3.化简1sin101sin10++-分析:利用二倍角公式和完全平方公式将被开方数变为平方形式。
解:375,sin 5cos50,sin 5cos5024ππ<<∴+<-<。
三角函数化简练习题及答案

三角函数化简练习题及答案1.能正确运用三角公式,进行简单三角函数式的化简和恒等式证明2.掌握三角函数式的化简和证明的方法及步骤。
1.cosαcosβ=sinαcosβ=2.sinθ+sinφ= ;sinθ-sinφ= ;cosθ+cosφ= ; cosθ-cosφ=1cos2a1.已知tan ? ? ,则sin2a?2的值是4cos2a-4sin2a5A.B.?22C. 1D.?114142.?sin22?cos4等于A.C. sin B.D.4?cos?3coscos. 1 a等于 cosa-sina?sin2asinA.C. cosa sina B. cos2aD sin2a4.化简2?sin4?2?2cos4的结果是sin? sin?]可化简为. ? ?)cosa ?[sin?sin?B. ?sinC. sin?D. 0?)??)等于.化简4北京一对一上门家教品牌家教电话:010—6256125 xx??x2xx A. tanx B.tanxtan2tan222cos100-sin200的值是 D.1 A. C.2. tan700?cos100等于化简 ??a?cos?a-cos?a10. cos sina a?sin???11.如果tana,tna?是方程x2?3x?3?0两根,则。
cossin12.2cos2a?1化简2?a)sin24413.求证: sinsin??2cos?sina sina1214.讨论函数f?cos?cos??2coscosxcos?的值域、周期性、2奇偶性及单调性北京一对一上门家教品牌家教电话:010—6256125515.设sin??msin?2?????m?0?,????k??k?z?,求证:tan??????无论是化简还是证明都要注意:角度的特点函数名的特点化切为弦是常用手段升降幂公式的灵活应用1?mtan? 1?m3.2.2三角函数化简及证明111.[cos+cos];[sin+sin];22.2sin3.2cos???2coscos???22;2cos;-2sin???22sinsin???22; ???2?????????1.C2.D3.B4.2sin25.C.6.B北京一对一上门家教品牌家教电话:010—62561255 7.C8.C9.-210.cos?11.?12.cos2a?1-a)??cos2=2cosa?113. ?a)?-a)442cos2a-1cos2a? ? 1 cos2acos2a2证明∵sin?2cossina=sin[?a]?2cossina=sincosa?cossina?2cossina=sincosa?cossina=sin[-a]=sin?.sinsin?两边同除以sina?2cos=.sinasina12214.解:f?[2cos?1]?cos??2coscosxcos?12 =cos??2coscosxcos??cos?12=cos[cos?2cosxcos?]?cos??12=cos[sinxsin??cosxcos?]?cos??11=cos[?cos]?cos2? ??cos2x211∴f的值域为[?,],周期为π,是偶函数,2??当x?[k?,k??]时f是增函数,当x?[k??,k?]时f是减函22北京一对一上门家教品牌家教电话:010—62561255 数。
三角函数的化简模拟试题

三角函数的化简模拟试题考虑以下三角函数的化简问题,试解答以下模拟试题。
1. 化简以下表达式:a) $\sin(\frac{\pi}{2} - x)$b) $\cos(\frac{\pi}{2} + x)$c) $\tan(\pi - x)$2. 将下列表达式化简为同角三角函数的形式:a) $\sin(-x)$b) $\cos(\pi + x)$c) $\tan(\frac{\pi}{2} - x)$3. 根据倍角公式,化简以下表达式,其中 $0 \leq x \leq\frac{\pi}{2}$:a) $\sin(2x)$b) $\cos(2x)$c) $\tan(2x)$4. 根据半角公式,将下列表达式化简为三角函数的形式:a) $\sin^2\frac{x}{2}$b) $\cos^2\frac{x}{2}$c) $\tan^2\frac{x}{2}$5. 根据和差公式,化简以下表达式:a) $\sin(x + \frac{\pi}{3})$b) $\cos(x - \frac{\pi}{4})$c) $\tan(x + \frac{\pi}{6})$6. 化简以下复合角三角函数表达式:a) $\sin[2(\frac{\pi}{4} - x)]$b) $\cos[2(\frac{\pi}{6} + x)]$c) $\tan[2(\pi - x)]$7. 结合以上知识,化简以下复合角三角函数表达式:a) $\sin[2(\frac{\pi}{4} - x)] + \cos[2(\frac{\pi}{6} + x)]$b) $\cos[2(\frac{\pi}{6} + x)] - \sin[2(\frac{\pi}{4} - x)]$8. 进一步化简以下复合角三角函数表达式:a) $2\sin(\pi - \frac{x}{2})\cos(\pi + \frac{x}{2})$b) $2\cos^2(\frac{\pi}{4} - x) - 1$试题解答如下:1.a) $\sin(\frac{\pi}{2} - x)= \cos(x)$b) $\cos(\frac{\pi}{2} + x) = -\sin(x)$c) $\tan(\pi - x)= \tan(x)$2.a) $\sin(-x) = -\sin(x)$b) $\cos(\pi + x) = -\cos(x)$c) $\tan(\frac{\pi}{2} - x) = \cot(x)$3.a) $\sin(2x) = 2\sin(x)\cos(x)$b) $\cos(2x) = \cos^2(x) - \sin^2(x)$c) $\tan(2x) = \frac{2\tan(x)}{1-\tan^2(x)}$4.a) $\sin^2\frac{x}{2} = \frac{1 - \cos(x)}{2}$b) $\cos^2\frac{x}{2} = \frac{1 + \cos(x)}{2}$c) $\tan^2\frac{x}{2} = \frac{1 - \cos(x)}{1 + \cos(x)}$5.a) $\sin(x + \frac{\pi}{3}) = \frac{\sqrt{3}}{2}\sin(x) +\frac{1}{2}\cos(x)$b) $\cos(x - \frac{\pi}{4}) = \frac{\sqrt{2}}{2}\cos(x) +\frac{\sqrt{2}}{2}\sin(x)$c) $\tan(x + \frac{\pi}{6}) = \frac{\sqrt{3}+1}{\sqrt{3}-1}\tan(x)$6.a) $\sin[2(\frac{\pi}{4} - x)] = 2\sin(\frac{\pi}{4} - x)\cos(\frac{\pi}{4} - x)$b) $\cos[2(\frac{\pi}{6} + x)] = \cos^2(\frac{\pi}{6} + x) -\sin^2(\frac{\pi}{6} + x)$c) $\tan[2(\pi - x)] = \frac{2\tan(\pi - x)}{1-\tan^2(\pi - x)}$7.a) $\sin[2(\frac{\pi}{4} - x)] + \cos[2(\frac{\pi}{6} + x)] =2\sin(\frac{\pi}{4} - x)\cos(\frac{\pi}{4} - x) + \cos^2(\frac{\pi}{6} + x) -\sin^2(\frac{\pi}{6} + x)$b) $\cos[2(\frac{\pi}{6} + x)] - \sin[2(\frac{\pi}{4} - x)] =\cos^2(\frac{\pi}{6} + x) - \sin^2(\frac{\pi}{6} + x) - 2\sin(\frac{\pi}{4} - x)\cos(\frac{\pi}{4} - x)$8.a) $2\sin(\pi - \frac{x}{2})\cos(\pi + \frac{x}{2}) = \sin(\pi - x) =\sin(x)$b) $2\cos^2(\frac{\pi}{4} - x) - 1 = 2(\frac{1}{2}\cos(x) +\frac{\sqrt{2}}{2}\sin(x))^2 - 1 = \cos^2(x) - \sin^2(x)$通过上述题目的解答,我们学习了三角函数的化简方法,包括基础的化简公式,倍角公式,半角公式以及和差公式等。
三角函数辅助角公式化简

三角函数辅助角公式化简一、解答题1.已知函数f x sin 2 x cos2x , x R3( 1)求 f x 的对称中心;( 2)讨论f x 在区间, 上的单调性 .3 42.已知函数f x 4sinxcos x 3 .3( 1)将 f x 化简为 f x Asin x 的形式,并求f x 最小正周期;( 2)求 f x 在区间, 上的最大值和最小值及取得最值时x 的值 .4 63.已知函数f x 4tanxsin x cos x 3 .2 3( 1)求 f x 的最小正周期;( 2)求 f x 在区间, 上的单调递增区间及最大值与最小值.4 4 4.设函数 f x3cos2 x sinxcosx 3 .2(1)求函数 f x 的最小正周期 T 及最大值;(2)求函数 f x 的单调递增区间 .πππ5.已知函数f x cos 2x 2sin x sin x3 4 4 (Ⅰ)求函数 f x 的最小正周期和图象的对称轴方程;π π(Ⅱ)求函数 f x 在区间, 上的值域 .12 26.已知函数 f x 3sinxcosx cos2 x 1 .2( Ⅰ) 求函数f x 的对称中心;( Ⅱ) 求 f x 在 0, 上的单调区间 .第1页共8页◎第2页共8页7.已知函数 f x4cosxsin x 1,求6(1)求 f x 的最小正周期;(2)求函数 f x 的单调递增区间(3)求 f x 在区间, 上的最大值和最小值.6 4sinx3cosx ?cos x8.设函数 f x2. tanx(1)求 f x 的最小正周期;(2)讨论f x 在区间0, 上的单调性 .29.已知函数f x 2 3sinxcosx 2cos2x 1 ,(I )求 f x 的最大值和对称中心坐标;( Ⅱ) 讨论f x 在 0, 上的单调性。
10.已知函数.(1) 求的最小正周期;(2) 若关于的方程在上有两个不同的实根,求实数的取值范围 . 11.设 f x sinxcosx cos2x .4(1)求 f x 的单调递增区间;(2)锐角ABC 中,角 A, B, C 的对边分别为 a, b,c ,若fA0 ,a 1, bc 3 ,求212.已知函数.( 1)求函数的单调增区间;第3页共8页◎第4页共8页( 2) 的内角 , , 所对的边分别是 , , ,若, ,且 的面积为 ,求 的值 .13.设函数. 16.已知向量 a =( 2cosx , 3 sin x ), b =( cos x ,2cos x)0),( x )2 2 2 2( 1)求 的最大值,并写出使 取最大值时的集合;且 f ( x )的最小正周期为 π .( 1)求函数 f ( x )的表达式;( 2)已知中, 角的边分别为,若 ,求 的最小值 .( 2)求 f ( x )的单调递增区间.117.已知函数f x Asin x( A 0,0, ) 的部分图象如图14.已知 f x3sin xcos x cos x 0 ,若 f x 的最小正周期为 4 . 2 ,其中2( 1) 求函数 f x 的解析式;( 1)求函数 f x 的单调递增区间;( 2) 如何由函数 y 2sinx 的通过适当图象的变换得到函数 f x 的图象,换过程 ;( 2)锐角三角形 ABC 中, 2a c cosB bcosC ,求 f A 的取值范围 .( 3) 若 f1,求 sin的值 .42615. 已知 =sinx ,), b =cos φ, sin φ )( | φ| < ).函数18. 已知函数a ((cosxf (x)= a ?b 且 f (-x)=f( x).(1)求函数在上的单调递增区间;3(2)若(Ⅰ)求 f (x)的解析式及单调递增区间;且,求的值。
三角函数的化简与求值
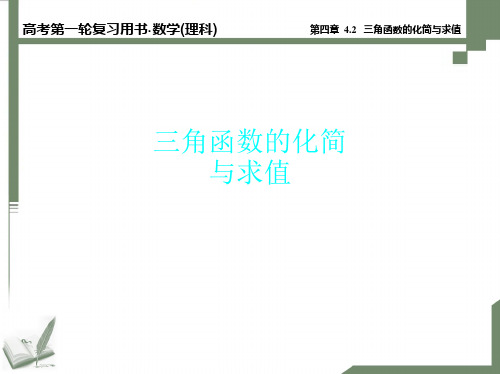
φ=
2
a
2
a b
,sin φ=
b
2
a b2
).
二、二倍角公式
sin 2α=2sin αcos α;
高考第一轮复习用书· 数学(理科)
第四章 4.2 三角函数的化简与求值
cos 2α=cos α-sin α=1-2sin α=2cos α-1; tan 2α=
7 2 = sin( -x).
第四章 4.2 三角函数的化简与求值
题型1 三角函数式的化简
例1 (1)化简sin(3x+ )cos(x- )+cos(3x+ )cos(x+ );
3
6
3
3
(2)化简
tan α tan2α tan2α tan α
+ 3 (sin α-cos α).
2
2
高考第一轮复习用书· 数学(理科)
第四章 4.2 三角函数的化简与求值
三、半角公式 sin =±
2 θ
1 cos θ , 2
cos =±
2
θ
1 cos θ , 2
tan =±
2
θ
1 cos θ , 1 cos θ
θ 其中符号“±”的选取由 角的范围确定. 2
用正余弦来表示正切的半角公式: tan =
α 2
s in α 1 cos α = 1 cos α s in α
= 1 m2
m
2 ,tan 5 = 1 ta n 2 5
2 ta n 5
=
1 m m 2 1 1 m
2
m
2
三角函数化简求值练习题(超级好)

三角化简求值测试题1.若sin α=35,α∈(-π2,π2),则cos(α+5π4)=________.2.已知π<θ<32π,则 12+12 12+12cos θ=________.3.计算:cos10°+3sin10°1-cos80°=________.4.函数y =2cos 2x +sin2x 的最小值是__________________.5.函数f (x )=(sin 2x +12010sin 2x )(cos 2x +12010cos 2x)的最小值是________. 6.若tan(α+β)=25,tan(β-π4)=14,则tan(α+π4)=_____.7.若3sin α+cos α=0,则1cos 2α+sin2α的值为________.8.2+2cos8+21-sin8的化简结果是________.9.若tan α+1tan α=103,α∈(π4,π2),则sin(2α+π4)的值为_________.10.若函数f (x )=sin2x -2sin 2x ·sin2x (x ∈R ),则f (x )的最小正周期为________.11. 2cos5°-sin25°cos25°的值为________.12.向量a =(cos10°,sin10°),b =(cos70°,sin70°),|a -2b |=________________.13.已知1-cos2αsin αcos α=1,tan(β-α)=-13,则tan(β-2α)=________.14.设a =sin14°+cos14°,b =sin16°+cos16°,c =62,则a 、b 、c 的大小关系是________.15.已知角α∈(π4,π2),且(4cos α-3sin α)(2cos α-3sin α)=0.(1)求tan(α+π4)的值;(2)求cos(π3-2α)的值.16. 已知tan α=2.求(1)tan(α+π4)的值;(2)sin2α+cos 2(π-α)1+cos2α的值.17.如图,点A ,B 是单位圆上的两点,A ,B 两点分别在第一、二象限,点C 是圆与x 轴正半轴的交点,△AOB 是正三角形,若点A 的坐标为(35,45),记∠COA =α. (1)求1+sin2α1+cos2α的值;(2)求|BC |2的值.18.△ABC 中,A ,B ,C 所对的边分别为a ,b ,c ,tan C =sin A +sin Bcos A +cos B,sin(B -A )=cos C .,,求角A 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:∵………………………………………………2分
…………………………………………………4分
…………6分
…………………………8分
…………………………………………10分
又 ∴………………………12分
9.(05浙江卷)已知函数f(x)=-sin2x+sinxcosx.
∴原式.
(2)由①平方得:,,即,故.
(3)当,解得,
∴或,
∵,∴或.
例1.化简:
(1);
(2);
(3).
解:(1)原式
.
(2)原式
.
(3)原式
∵,∴,∴,
∴原式.
例3.证明:(1);(2).
证:(1)左边
右边,∴得证.
说明:由等式两边的差异知:若选择“从左证到右”,必定要“切化弦”;若“从右证到左”,必定要用倍角公式.
3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明。
主要方法1.三角函数的求值:
1.寻求角与角之间的关系,化非特殊角为特殊角;
三角恒等式包括有条件的恒等式和无条件的恒等式.①无条件的等式证明的基本方法是化繁为简、左右归一、变更命题等,使等式两端的“异”化为“同”;②有条件的等式常用方法有:代入法、消去法、综合法、分析法等.
基本训练
1、已知是第三象限角,且,那么等于 ( A )
A、 B、 C、 D、
2、函数的最小正周期 ( B )
本资料为word版本,可以直接编辑和打印,感谢您的下载
三角函数化简题
地点:__________________
时间:__________________
说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容
2.正确灵活地运用公式,通过三角变换消去或约去一些非特殊角的三角函数值;
3.一些常规技巧:“1”的代换、切割化弦、和积互化、异角化同角等.
1.三角函数式的化简:
三角函数式的化简常用方法是:异名函数化为同名三角函数,异角化为同角,异次化为同次,切割化弦,特殊值与特殊角的三角函数互化.
2.三角恒等式的证明:
(Ⅰ) 求f()的值; (Ⅱ) 设∈(0,),f()=-,求sin的值.
解:(Ⅰ)
(Ⅱ)
解得
1.( )
2.已知,当时,式子可化简为( )
3. 1 .
课后作业
课题:§4.04三角函数的化简、求值与证明 日期:2009年 月 日星期
一、选择题
1、已知,则的值等于 ( D )
A、 B、 C、 D、
2、已知、是方程的两根,且,则等于 (B)
2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。
∴原式.
例3.已知,求的值.
解:由题意,,
∴原式.
例4.已知,求的值.
解பைடு நூலகம்∵,,
∴,
得,若,则,
若,无意义.
说明:角的和、差、倍、半具有相对性,如,,等,解题过程中应充分利用这种变形.
例5.已知关于的方程的两根为,
求:(1)的值;(2)的值;(3)方程的两根及此时的值.
①
②
解:(1)由根与系数的关系,得,
(2)左边
右边,∴得证.
课堂练习
1.若,则( )
2.( )
24816
3.化简: 答案:
4.设,求的值。答案:
6.已知,求的值。答案:
7.(05北京卷)已知=2,求(I)的值;( = 2 \* ROMAN II)的值.
解:(I)∵ tan=2, ∴ ;
所以=;
( = 2 \* ROMAN II)由( = 1 \* ROMAN I), tanα=-, 所以==.
A、 B、 C、 D、
3、等于 ( D )
A、1 B、2 C、-1 D、-2
4、已知,则实数的取值范围是__[-1,]___。
5、设,则=_____。
例题分析:
例1.已知,(),则( )
或
略解:由得或(舍),∴,∴.
例2.已知,是第三象限角,求的值.
解:∵是第三象限角,∴(),
∵,∴是第四象限角,∴,
7、(北京卷)已知tan =2,则tanα的值为-,tan的值为 -
8、已知,则的值为_______。
9、已知A、B为锐角,且满足,则=__.
三、解答题
10、求证:
11、已知,试用表示的值。
答案:
12、求值:
答案:
13、已知,求的值。答案:3
【备用题】
【参考资料】
A、 B、 C、或 D、或
3、化简为 ( B )
A、 B、 C、 D、
4、(全国卷Ⅲ) ( B )
(A) (B) (C) 1 (D)
5、(山东卷)函数,若,则的所有可能值为( B )
(A)1 (B) (C) (D)
班级 姓名
二、填空题
6、(全国卷Ⅱ)设a为第四象限的角,若 ,则tan 2a =______________.
课题:§4.04三角函数的化简、求值与证明 日期:2009年 月 日星期
高考目标能正确地运用三角函数的有关公式进行三角函数式的求值,能正确地运用三角公式进行三角函数式的化简与恒等式的证明.
教学重点熟练地运用三角公式进行化简与证明.有关公式的灵活应用及一些常规技巧的运用.
知识回顾
1、三角函数式的化简:(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③ 三角公式的逆用等。(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数
