射频与微波基础知识
射频与微波的基本概念

射频与微波的基本概念
射频(RF)和微波(Microwave)是电磁波的一部分,它们在频率上分别处于3 kHz 至300 GHz和300 MHz至300 GHz之间。
射频和微波是广泛应用于通信、雷达、卫星、无线电调制解调器、无线电发射和接收设备等领域的电磁波。
射频和微波是无线电波的特殊类型,具有以下特征:
1. 高频:射频和微波的频率非常高,通常比较可见光的频率高数百万倍甚至更高。
2. 高速:射频和微波在空气和真空中的传输速度几乎达到光速。
3. 无线传输:射频和微波可以在不依赖传输媒介的情况下在空气、真空和其他透明材料中传输。
4. 强穿透能力:射频和微波可以穿透某些材料和物体,这使得它们在通信和雷达等领域中得到广泛应用。
射频和微波的应用非常广泛,例如在移动通信领域中,射频和微波被用于发送和接收无线信号。
在卫星通信中,射频和微波作为数据传输和信号接收的媒介。
在
雷达中,利用射频和微波来探测目标物体的距离和速度。
射频与微波原理及应用介绍

射频与微波原理及应⽤介绍射频与微波技术原理及应⽤培训教材华东师范⼤学微波研究所⼀、Maxwell(麦克斯韦)⽅程Maxwell ⽅程是经典电磁理论的基本⽅程,是解决所有电磁问题的基础,它⽤数学形式概括了宏观电磁场的基本性质。
其微分形式为0B E t DH J tD B ρ=-=+??=?=(1.1)对于各向同性介质,有D E B H J E εµσ===(1.2)其中D 为电位移⽮量、B为磁感应强度、J 为电流密度⽮量。
电磁场的问题就是通过边界条件求解Maxwell ⽅程,得到空间任何位置的电场、磁场分布。
对于规则边界条件,Maxwell ⽅程有严格的解析解。
但对于任意形状的边界条件,Maxwell ⽅程只有近似解,此时应采⽤数值分析⽅法求解,如矩量法、有限元法、时域有限差分法等等。
⽬前对应这些数值⽅法,有很多商业的电磁场仿真软件,如Ansoft 公司的Ensemble 和HFSS 、Agilent 公司的Momentum 和ADS 、CST 公司的Microwave Studio 以及Remcom 公司的XFDTD 等。
由⽮量亥姆霍兹⽅程联⽴Maxwell ⽅程就得到⽮量波动⽅程。
当0,0J ρ==时,有 22220E k E H k H ?+=?+= (1.3) 其中k 为传播波数,22k ωµε=。
⼆、传输线理论传输线理论⼜称⼀维分布参数电路理论,是射频、微波电路设计和计算的理论基础。
传输线理论在电路理论与场的理论之间起着桥梁作⽤,在微波⽹络分析中也相当重要。
1、微波等效电路法低频时是利⽤路的概念和⽅法,各点有确切的电压、电流概念,以及明确的电阻、电感、电容等,这是集总参数电路。
在集总参数电路中,基本电路参数为L、C、R。
由于频率低,波长长,电路尺⼨与波长相⽐很⼩,电磁场随时间变化⽽不随长度变化,⽽且电感、电阻、线间电容和电导的作⽤都可忽略,因此整个电路的电能仅集中于电容中,磁能集中于电感线圈中,损耗集中于电阻中。
射频与微波基础知识

¾ 回波损耗(Return Loss) :传输线上任一点入射功率和反射功率之比
RL( dB
)
= 10 lg⎜⎜⎝⎛
Pi Po
⎟⎟⎠⎞
=
10
lg
⎜⎛ቤተ መጻሕፍቲ ባይዱ⎜
⎝
1 Γ2
⎟⎞ ⎟ ⎠
=
−20 lg
Γ
第二章
Z. Q. LI
16
传输线阻抗变换
¾ 基本原理-传输线对阻抗的改变
第二章
Z. Q. LI
17
传输线阻抗变换
= − d V(x) dx
) = − d I( x ) dx
⎧ ⎪⎪ ⎨ ⎪ ⎪⎩
jωLI( x ) jωCV ( x
= +
− V ( x + Δx ) −V ( x ) Δx
Δx ) = − I( x + Δx ) − Δx
I(
x
)
⎧ ⎪⎪ ⎨ ⎪ ⎪⎩
d2 dx2 d2 dx2
V (x) + I(x) +
传输线无损耗 γ = α + jβ = jβ
(( )) (( )) Z(d) =
Zin (− d ) =
Z0
1 + ΓLe−2γd 1 − ΓLe−2γd
= Z0
1 + ΓLe−2 jβd 1 − ΓLe−2 jβd
=
Z0
(Z L (Z0
+ +
jZ 0 jZ L
tan tan
βd βd
) )
¾ (电压)驻波比
I ( x)
R1
L1
I (x + Δx)
V (x) R2
x
射频与微波技术

射频与微波技术:让我们的世界更连通近年来,的发展和应用越来越受到关注。
从无线通讯到医疗设备,从航空航天到军事领域,这项技术已经渗透到了我们生活的各个方面。
那么,什么是射频和微波技术呢?它有哪些优点和应用呢?本文将探讨这些问题,为大家揭秘的奥秘。
一、的基本概念简单来说,射频就是指频率在几个千赫兹至几个千兆赫兹之间的无线电波。
而微波则是频率在1千兆赫兹至300千兆赫兹之间的电磁波。
与低频和中频相比,射频和微波的频率高,波长短,传输速度快,能量密度大,能够穿透障碍物并传输较远的距离。
这些特点使得射频和微波技术成为了一种重要的通信手段。
二、的优点1.高速传输:射频和微波技术的传输速度非常快,比起传统的有线传输方式,能够提高数据传输的效率。
2.节省空间:相对于有线传输方式而言,射频和微波技术的设备和器件体积小巧,节省了空间,适用于各种紧凑的应用场景。
3.维护成本低:无需担心线缆老化和损坏问题,也无需担心设备移动或更改位置带来的麻烦。
这样,射频和微波技术能够降低系统部署和维护的成本。
4.无干扰:射频和微波技术的传输方式可以减少噪音和干扰的影响,避免信息的损失和干扰。
三、的应用1.通讯领域:射频和微波技术在通讯领域的应用非常广泛,如手机、对讲机、卫星通讯等。
除此之外,无线电台、微波通道、通讯系统的天线等也都使用了这项技术。
2.医疗设备:射频和微波技术在医疗设备领域也有着广泛的应用,如磁共振成像、医疗诊断、治疗设备等。
3.航空航天:射频和微波技术在航空航天领域也有着广泛的应用,如雷达、导航设备等。
4.军事领域:射频和微波技术在军事领域的应用非常广泛,如合成孔径雷达、电子对抗等。
四、未来展望随着科技的不断发展,也将得到进一步的发展和应用。
例如,5G通讯技术的使用已经慢慢普及,机器人、智能家居等智能设备的开发也需要大量依赖射频和微波技术,这将为的发展提供更广阔的应用空间。
总之,的不断发展和应用,不仅让我们的生活更加便捷、舒适,而且也为人类社会的进步和发展作出了巨大的贡献。
《射频技术基础》课件

军事领域:雷达、电子对抗、通信等
射频技术的发展历程
19世纪末,无线 电技术的诞生
20世纪初,无线 电技术的快速发展
20世纪中叶,射 频技术的广泛应用
21世纪初,射频 技术的创新与突破
03 射频技术基础知识
电磁波基础知识
电磁波:由电场和磁场相互激发产生的波
无线传感器网络中的射频技术
射频技术在无线传感器网 络中的应用
射频技术的特点和优势
射频技术的应用场景和案 例
射频技术在无线传感器网 络中的挑战和问题
物联网中的射频技术
射频识别 (RFID): 用于物品识别
和追踪
无线传感器网 络(WSN): 用于环境监测
和数据采集
近场通信 (NFC): 用于移动支付 和身份验证
射频技术在无线通信系统中的应用 实例
添加标题
添加题
添加标题
射频技术在无线通信系统中的发展 趋势
雷达系统中的射频技术
雷达系统:用于探测、跟踪和识别目标 射频技术:在雷达系统中用于发射和接收电磁波 应用实例:雷达系统中的射频技术用于探测、跟踪和识别目标 特点:射频技术在雷达系统中具有高精度、远距离、全天候等优点
调制:将信息信号转换为射 频信号的过程
解调方式:幅度解调、频率 解调、相位解调等
调制解调器的作用:实现射 频信号的调制和解调
射频信号的传输与接收:通 过天线进行传输和接收
射频信号的发射与接收
射频信号的发射:通过天线 将信号发射到空气中
射频信号的产生:通过振荡 器产生高频信号
射频信号的接收:通过天线 接收信号,并通过滤波器、
滤波器的类型:包括低通滤 波器、高通滤波器、带通滤 波器等
射频微波基础知识

射频微波基础知识射频简称RF射频就是射频电流,它是一种高频交流变化电磁波的简称。
每秒变化小于1000次的交流电称为低频电流,大于10000次的称为高频电流,而射频就是这样一种高频电流。
有线电视系统就是采用射频传输方式的。
在电子学理论中,电流流过导体,导体周围会形成磁场;交变电流通过导体,导体周围会形成交变的电磁场,称为电磁波。
在电磁波频率低于100khz时,电磁波会被地表吸收,不能形成有效的传输,但电磁波频率高于100khz时,电磁波可以在空气中传播,并经大气层外缘的电离层反射,形成远距离传输能力,我们把具有远距离传输能力的高频电磁波成为射频,英文缩写:RF一、射频和微波技术基础知识1、什么是射频?射频(RF)是指无线通信系统中使用的电磁频率范围。
它涵盖了广泛的频率范围,通常从3kHz(千赫)到300GHz(千兆赫)。
射频信号的特点是能够长距离传播并穿过障碍物,这使其成为各种通信应用的理想选择。
2、微波频率微波是射频频率的一个子集,频率范围为300MHz(兆赫)到300GHz。
虽然微波仍然是像射频一样的电磁波,但它们具有更短的波长,这在特定应用中提供了某些优势,例如高数据传输速率和精确成像能力。
二、射频和微波技术的应用1、无线通信射频和微波技术最突出的应用之一是在无线通信系统中。
从简单的无线电传输到复杂的蜂窝网络,射频技术使移动设备上的语音通话、短信、互联网浏览和视频流成为可能。
此外,Wi-Fi网络、蓝牙连接和其他无线协议依赖RF信号进行无缝数据交换。
2、卫星通信卫星通信严重依赖微波频率。
地球静止轨道或近地轨道卫星利用微波远距离传输电视信号、互联网数据和电话,确保在传统通信基础设施有限,或无法使用的偏远地区实现全球连接。
3、雷达系统微波雷达系统对各种应用至关重要,包括空中交通管制、天气监测和军事防御。
雷达使用微波脉冲来探测物体的存在、距离和速度,从而进行精确的跟踪和分析。
4、医疗应用射频和微波技术在医学领域有着重要的应用,例如磁共振成像(MRI)和微波消融。
射频与微波知识点总结

射频与微波知识点总结一、引言射频(Radio Frequency, RF)与微波(Microwave)技术在现代通信、雷达、无线电频谱、天线设计等领域发挥着重要作用。
射频与微波技术涉及到电磁波的传播、调制解调、射频功率放大、频率变换、天线设计等方面的知识。
本文将从射频与微波的基本原理、传输线理论、射频放大器、射频调制解调、天线设计等方面进行知识点总结。
二、射频与微波的基本原理1. 电磁波的基本概念电磁波是一种由电场和磁场相互作用而产生的波动现象。
根据波长的不同,电磁波可以分为射频、微波、红外线、可见光、紫外线、X射线和γ射线等不同频段的电磁波。
射频与微波技术主要涉及射频和微波频段的电磁波。
2. 电磁波的特性电磁波具有波长、频率、速度、传播特性等基本特性。
其中,波长和频率之间的关系由光速公式c=λf(c为光速,λ为波长,f为频率)决定。
在射频与微波领域,常用的频率单位有千兆赫兹(GHz)、兆赫兹(MHz)和千赫兹(kHz)等,波长单位常用的是米(m)。
根据电磁波在介质中传播的特性,常见的介质波速和传播常数也会影响射频微波在介质中的传播特性。
3. 电磁波在空间中的传播电磁波在自由空间中传播的特性是由麦克斯韦方程组决定的,其中包括麦克斯韦方程组的电场和磁场分布规律、电磁波的波动性等。
了解电磁波在不同介质中的传播特性有利于射频与微波技术在不同环境中的应用。
4. 电磁波的天线辐射和接收天线是电磁波的辐射和接收装置,根据天线的结构和工作原理,天线可以分为定向天线和非定向天线。
定向天线主要用于定向传输和接收电磁波;非定向天线主要用于对全向的电磁波进行辐射和接收。
天线的辐射和接收特性与天线的形状和尺寸、频率、方向性等因素有关。
三、传输线理论1. 传输线的基本概念传输线是用于传输电磁波的导线或介质,主要包括同轴电缆、微带线、矩形波导和圆柱波导等。
传输线具有阻抗匹配、功率传输和信号传输等功能。
根据传输线的不同特性和应用场景,可以选择不同类型的传输线。
射频微波(知识点)

一、射频/微波技术及其基础1、射频/微波技术的基础 ✓ 什么是微波技术研究微波的产生、放大、传输、辐射、接收和测量的科学。
射频/微波技术是研究射频/微波信号的产生、调制、混频、驱动放大、功率放大、发射、空间传输、接收、低噪声放大、中频放大、解调、检测、滤波、衰减、移相、开关等各个电路及器件模块的设计和生产的技术,利用不同的电路和器件可以组合成相应的射频/微波设备。
微波技术主要是指通信设备和系统的研究、设计、生产和应用。
✓ 微波技术的基本理论是以麦克斯韦方程为核心的场与波的理论2、射频/微波的基本特性✓ 频率高、穿透性、量子性、分析方法的独特性射频频段为30 ~ 300MHz ,微波频段为300MHz ~ 3000GHz ,相对应波长为1m ~0.1mm ,照射于介质物体时能深入到该物质的内部。
根据量子理论,电磁辐射能量不是连续的,而是由一个个的“光量子”组成,单个量子的能量与其频率的关系为e = h ·f式中,h = 4×10-15电子伏·秒 (eV ·S) 成为普朗克常数3、射频/微波技术在工程里的应用✓ 无线通信的工作方式1、单向通信方式通信双方中的一方只能接收信号,另一方只能发送信号,不能互逆,收信方不能对发信方直接进行信息反馈2、双向单工通信方式3、双向半双工通信方式通信双方中的一方使用双频双工方式,可同时收发;另一方则使用双频单工方式,发信时要按下“送话”开关。
4、双向全双工通信方式通信双方可以通信进行发信和收信,这时收信与发信一般采用不同的工作频率,通-讲 开关按-讲 按-讲 受话器受话器二、电磁波频谱12、射频/✓GSM900系统的频道配置GSM-900系统采用等间隔方式,频道间隔为200KHz,同一信道的收发频率间隔为45MHz, 频道序号和频道标称中心频率的关系为F上行(n)= 890.2 +(n-1)×0.2 MHzF下行(n)= F上行(n)+ 45 MHz式中:频道序号 n = 1 ~ 124在我国的GSM900网络中,1~94号载频分配给中国移动使用,96~124号载频分配给中国联通使用,95号载频作为保护隔离,不用于业务。
射频基础知识资料(最新整理)

第一部分射频基本概念第一章常用概念一、特性阻抗特征阻抗是微波传输线的固有特性,它等于模式电压与模式电流之比。
对于TEM波传输线,特征阻抗又等于单位长度分布电抗与导纳之比。
无耗传输线的特征阻抗为实数,有耗传输线的特征阻抗为复数。
在做射频PCB板设计时,一定要考虑匹配问题,考虑信号线的特征阻抗是否等于所连接前后级部件的阻抗。
当不相等时则会产生反射,造成失真和功率损失。
反射系数(此处指电压反射系数)可以由下式计算得出:z1二、驻波系数驻波系数式衡量负载匹配程度的一个指标,它在数值上等于:由反射系数的定义我们知道,反射系数的取值范围是0~1,而驻波系数的取值范围是1~正无穷大。
射频很多接口的驻波系数指标规定小于1.5。
三、信号的峰值功率解释:很多信号从时域观测并不是恒定包络,而是如下面图形所示。
峰值功率即是指以某种概率出现的尖峰的瞬态功率。
通常概率取为0.1%。
四、功率的dB 表示射频信号的功率常用dBm 、dBW 表示,它与mW 、W 的换算关系如下:dBm=10logmWdBW=10logW例如信号功率为x W ,利用dBm 表示时其大小为五、噪声噪声是指在信号处理过程中遇到的无法确切预测的干扰信号(各类点频干扰不是算噪声)。
常见的噪声有来自外部的天电噪声,汽车的点火噪声,来自系统内部的热噪声,晶体管等在工作时产生的散粒噪声,信号与噪声的互调产物。
六、相位噪声相位噪声是用来衡量本振等单音信号频谱纯度的一个指标,在时域表现为信号过零点的抖动。
理想的单音信号,在频域应为一脉冲,而实际的单音总有一定的频谱宽度,如下页所示。
一般的本振信号可以认为是随机过程对单音调相的过程,因此信号所具有的边带信号被称为相位噪声。
相位噪声在频域的可以这样定量描述:偏离中心频率多少Hz处,单位带宽内的功率与总信号功率相比。
例如晶体的相位噪声可以这样描述:噪声系数是用来衡量射频部件对小信号的处理能力,通常这样定义:单元输入信噪比除输出信噪比,如下图:对于线性单元,不会产生信号与噪声的互调产物及信号的失真,这时噪声系数可以用下式表示:Pno 表示输出噪声功率,Pni 表示输入噪声功率,G 为单元增益。
电子信息工程中的射频与微波技术

电子信息工程中的射频与微波技术射频(Radio Frequency)和微波(Microwave)技术是电子信息工程中不可或缺的两个分支。
这两种技术都涉及到无线传输和通信,尤其是在无线电设备的制造和应用领域,但它们又各具特色,有着各自的应用范围和优劣势。
本文将就射频和微波技术,它们的定义、发展历程、应用领域以及未来的前景进行探讨。
一、射频技术射频技术是指在高频和超高频范围内(约从3kHz到300GHz)传输和处理无线电信号的技术。
射频技术在电视、手机、广播、无线网络、卫星通信、雷达和导航等领域得到广泛应用。
它的来源可追溯到19世纪末,当时马克士威提出了电磁场的统一理论,开启了电磁波研究的新时代。
随着技术的不断发展,射频技术也得到了进一步的提高和完善,目前已经成为现代通信领域的关键技术。
射频技术的应用非常广泛,在无线电器材、导航系统、广告媒体等方面都有广泛的应用。
其中最为重要的莫过于无线电通信了。
我国在无线电通信方面的应用非常广泛,除了现在很多人都能接触到的无线局域网和蜂窝移动通信,还有新兴的物联网、车联网、以及无人机领域都是射频技术的重要应用。
无论是哪个行业,都必须依靠射频技术才能实现远距离通信,这也是射频技术的最大优势。
二、微波技术微波技术是指在高频(3GHz~30GHz)甚至极高频(30GHz~300GHz)范围内传输和处理无线电信号的技术。
微波技术在雷达、卫星通信、无线电和电视广播等领域得到广泛应用。
它的产生时间比较晚,大部分应用都集中在二战以后的60年代左右。
随着技术的不断发展,微波技术也得到了很大的提高和发展,被广泛应用于航空航天、国防军工、通信和广播等领域。
和射频技术相比,微波技术的传输距离更远、频率更高、传输速度更快、噪声更小,因此其实用性更为广泛。
在卫星通信和雷达领域,微波技术的应用尤其重要。
卫星通信可以实现全球通信,让人们无论在哪里都可以通过卫芯地的链接完成信息交流。
而雷达技术,则可以检测和跟踪任何物体的运动,是空军、海军等军事行业的必要设备。
射频微波

射频微波隔离器、环形器、同轴负载、同轴终端、同轴衰减器、放大器、滤波器、功分器、双工器、合路器定义:波的波长微波是指频率为300MHz-300GHz的电磁波,是无线电波中一个有限频带的简称,即波长在1米(不含1米)到1 毫米之间的电磁波,是分米波,厘米波,毫米波的统称。
微波频率比一般的无线电波频率高。
微波的波长微波是指频率为300MHz-300GHz的电磁波,是无线电波中一个有限频带的简称,即波长在1米(不含1米)到1毫米之间的电磁波,是分米波、厘米波、毫米波的统称。
微波频率比一般的无线电波频率高,通常也称为“超高频电磁波”。
微波作为一种电磁波也具有波粒二象性,微波量子的能量为9×l0 -25~ 1.99×10-22j.微波的性质:微波的基本性质通常呈现为穿透,反射,吸收三个特性。
对于玻璃、塑料和瓷器,微波几乎是穿越而不被吸收。
对于水和食物等就会吸收微波而使自身发热。
而对金属类东西,则会反射微波。
一、穿透性微波比其它用于辐射加热的电磁波,如红外线,远红外线等波长更长,因此具有更好的穿透性。
微波透入介质时,由于介质损耗引起的介质温度的升高,使介质材料内部、外部几乎同时加热升温,形成体热源状态,大大缩短了常规加热中的热传导时间,且在条件为介质损耗因数与介质温度呈负相关关系时,物料内外加热均匀一致。
二、选择性加热物质吸收微波的能力,主要由其介质损耗因数来决定。
介质损耗因数大的物质对吸收能力就强,相反,介质损耗因数小的物质吸收微波的能力弱。
由于各物质的损耗因数存在差异,微波加热就表现出选择性加热的特点。
物质不同,产生的热效果不同,水分子属极性分子,介电常数较大,其介质损耗因素也很大,对微波具有强吸收能力。
而蛋白质,碳水化合物等的介电常数相对较小,其对微波的吸收能力比水小得多。
因此,对于食品来说,含水量的多少对微波加热效果影响很大。
三、热惯性小微波对介质材料是瞬时加热升温,能耗也很低。
西电-射频微波教程课件

THANKS
感谢您的观看
设计实例
雷达系统的设计实例包括气象雷达、军事雷达、航空雷达 等。在设计过程中,需要考虑目标的探测精度、跟踪速度 、抗干扰能力等因素,同时还需要考虑设备的可靠性、可 维护性和成本等因素。
卫星通信系统设计实例
要点一
卫星通信系统概述
卫星通信是一种利用人造地球卫星作 为中继站实现地球站之间通信的方式 。它具有覆盖范围广、传输容量大、 可靠性高等优点,广泛应用于国际通 信、远程教育、电视广播等领域。
网络分析应用
在微波器件测试、电路 设计、天线测量等领域 有广泛应用,用于网络 性能评估、故障诊断和 优化设计。
信号分析
信号分析概述
信号分析是研究信号的时域和频域特性的方法,用于信号处理、 通信和雷达等领域。
信号分析原理
基于傅里叶变换、小波变换等数学工具,将信号从时域转换到频域, 分析信号的频率成分、调制方式和动态特性。
无线通信系统主要由发射机、接收机、天线和传输媒介等部分组成。发射机负责将信号转换为电磁波并发送出去,接 收机则负责接收电磁波并将其还原为信号。天线的作用是发射和接收电磁波,传输媒介则负责传输电磁波。
设计实例
无线通信系统的设计实例包括移动通信基站、无线局域网路由器、广播发射机等。在设计过程中,需要 考虑信号的覆盖范围、系统容量、传输速率、抗干扰能力等因素,同时还需要考虑设备的可靠性、可维 护性和成本等因素。
挑战
混频器的性能受到非线性效应、噪声 和失真等因素的影响,需要精心设计 和优化。
振荡器
种类
原理
振荡器可分为LC振荡器、 晶体振荡器和负阻振荡
器等。
振荡器通过正反馈和选频网 络,使电路产生自激振荡,
输出一定频率的信号。
射频微波常用知识
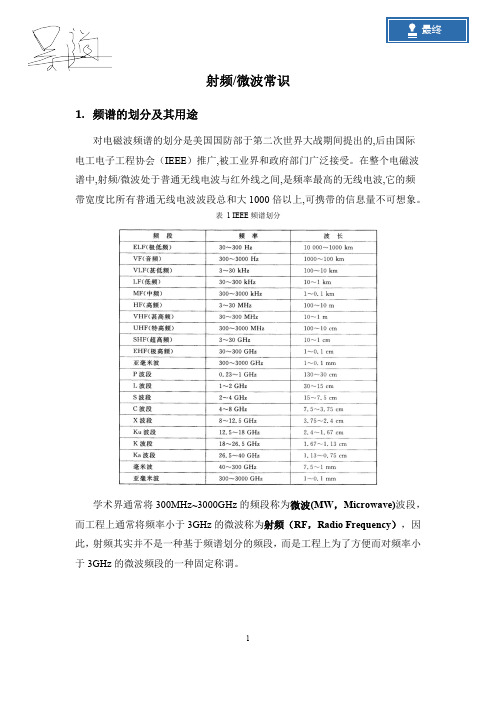
由于射频/微波本身的特点, 也会带来一些局限性。 主要体现在如下几个方面: (1) 元器件成本高。 (2) 辐射损耗大。 (3) 大量使用砷化镓器件,而不是通常的硅器件。 (4) 电路中元件损耗大,输出功率小。 (5) 设计工具精度低,成熟技术少。 这些问题都是我们必须面对的,在工程中应合理设计电路,取得一个比较好 的折中方案。
射频/微波的应用
微波的应用包括作为信息载体的应用和作为微波能的应用两个方面。
7
微波的经典用途是通信和雷达系统。这是微波作为信息载体的应用。 近年来发展最为迅猛的当数个人通信系统,当然,导航、遥感、科学研究、 生物医学和微波能的应用也占有很大的市场份额。 在通信应用方面,由于微波具有频率高、频带、信息量大的特点,所以被广 泛应用于各种通信业务,包括微波多路通信、微波中继通信、散射通信、移动通 信和卫星通信。利用微波波长短的特点可作特殊用途的通信,例如从 S 到 Ku 波 段的微波适用作以地面为基地的通信;毫米波适用于空间与空间的通信;毫米波 段的 60GHz 频段的电波大气衰减较大,适于作近距离保密通信;而 90GHz 频段 的电波在大气中的衰减却很小,是个窗口频段,适于作地空和远距离通信;对于 很长距离的通信,则 L 波段更适合,因为在此波段容易获得较大的功率。 微波作为能源的应用始于 20 世纪 50 年代后期,至 60 年代末,微波能应用 随着微波炉的商品化进入家庭而得到大力发展。 微波能应用包括微波的强功率应用和弱功率应用两个方面。强功率应用是微 波加热; 弱功率应用是用于各种电量和非电量 (包括长度、 速度、 湿度、 温度等) 的测量。 微波加热可以深入物体内部,热量产生于物体内部,不依靠热传导,里外同 时加热,具有热效率高、节省能源、加热速度快、加热均匀等特点,便于自动化 连续生产。用于食品加工时,还有消毒作用,清洁卫生,既不污染食品,也不污 染环境, 而且不破坏食品的营养成份。 微波加热现在已被广泛应用于食品、 橡胶、 塑料、化学、木材加工、造纸、印刷、卷烟等工业中;在农业上,微波加热可用 于灭虫、育种、干燥谷物等。 弱功率应用的电量和非电量的测量,其显著特点是不需要和被测量物体接触, 因而使非接触式的无损测量,特别适宜于生产线测量或进行生产的自动控制。现 在应用最多的是测量湿度,即测量物质(如煤、原油等)中的含水量。 微波的生物医学应用,也属于微波能的加热应用。利用微波对生物体的热效 应,选择性局部加热,是一种有效的热疗方法,临床上可用来治疗人体的各种疾 病。微波的医学应用包括微波诊断、微波治疗、微波解冻、微波解毒和微波杀菌 等。用微波对生物体作局部照射,可提高局部组织的新陈代谢,并诱导产生一系 列的物理化学变化,从而达到解痉镇痛、抗炎脱敏、促进生长等作用,广泛用于
射频微波基础知识:基本概念和术语

射频微波基础知识:基本概念和术语•波器技术第一群(新5G群)全面开放十天射频微波基础知识射频基础知识1、功率/电平(dBm):放大器的输出能力,一般单位为w、mw、dBm注:dBm是取1mw作基准值,以分贝表示的绝对功率电平。
换算公式:电平(dBm)=10lgw5W → 10lg5000=37dBm10W → 10lg10000=40dBm20W → 10lg20000=43dBm从上不难看出,功率每增加一倍,电平值增加3dBm2、增益(dB):即放大倍数,单位可表示为分贝(dB)。
即:dB=10lgA(A为功率放大倍数)3、插损:当某一器件或部件接入传输电路后所增加的衰减,单位用dB表示。
4、选择性:衡量工作频带内的增益及带外辐射的抑制能力。
-3dB带宽即增益下降3dB时的带宽,-40dB、-60dB同理。
5、驻波比(回波损耗):行驻波状态时,波腹电压与波节电压之比(VSWR)附:驻波比——回波损耗对照表:SWR 1.2 1.25 1.30 1.35 1.40 1.50回波损耗(dB) 21 19 17.6 16.6 15.6 14.06、三阶交调:若存在两个正弦信号ω1和ω2 由于非线性作用将产生许多互调分量,其中的2ω1-ω2和2ω2-ω1两个频率分量称为三阶交调分量,其功率P3和信号ω1或ω2的功率之比称三阶交调系数M3。
即M3 =10lg P3/P1 (dBc)7、噪声系数:一般定义为输出信噪比与输入信噪比的比值,实际使用中化为分贝来计算。
单位用dB。
8、耦合度:耦合端口与输入端口的功率比, 单位用dB。
9、隔离度:本振或信号泄露到其他端口的功率与原有功率之比,单位dB。
10、天线增益(dB):指天线将发射功率往某一指定方向集中辐射的能力。
一般把天线的最大辐射方向上的场强E与理想各向同性天线均匀辐射场场强E0相比,以功率密度增加的倍数定义为增益。
Ga=E2/ E0211、天线方向图:是天线辐射出的电磁波在自由空间存在的范围。
射频微波工程基础介绍课件

不同雷达系统中天线的设计和应用,如阵列天线 、相控阵天线等。
电子对抗系统中的射频微波技术
通信对抗
射频微波技术在通信对抗中的应用,包括通信干扰、通信侦察等 。
雷达对抗
射频微波技术在雷达对抗中的应用,包括雷达干扰、雷达侦察与 反侦察等。
电子支援措施
射频微波技术在电子支援措施中的应用,如电磁频谱监测、信号 分析等。
射频微波工程基础介绍课件
目录
CONTENTS
• 射频微波工程概述 • 射频微波基础知识 • 射频微波工程关键技术 • 射频微波工程应用实例 • 射频微波工程测试与仿真 • 射频微波工程发展趋势与挑战
01 射频微波工程概述
CHAPTER
射频微波工程定义
01
射频微波工程是一门研究射频和 微波频段内电磁波的产生、传输 、控制和应用的学科。
避免频谱冲突是射频微波工程需要解决的重要问题。
射频微波工程未来发展展望
5G/6G移动通信技术
随着5G/6G移动通信技术的不断发展,射频微波工程将在其 中发挥重要作用,如毫米波通信、大规模天线阵列等技术的 研究和应用。
物联网与智能家居
物联网和智能家居的快速发展为射频微波工程提供了新的应 用场景和需求,如无线传感器网络、智能家居控制系统等的 研究和开发。
射频微波在其他领域的应用
医学影像
射频微波技术在医学影像中的应用,如核磁共振成像(MRI)中的 射频脉冲发生器和接收器。
微波炉
射频微波技术在微波炉中的应用,利用微波加热食物。
工业加热与干燥
射频微波技术在工业加热与干燥中的应用,如高频感应加热、微波干 燥等。
05 射频微波工程测试与仿真
CHAPTER
射频微波信号特点与传播
射频与微波技术知识点总结

射频/微波的特点: 1.频率高 2.波长短 3.大气窗口 4.分子谐振 微波频率:300MHz-3000GHz 波长:0.1mm-1m独特的特点:RF/MW 的波长与自然界物体尺寸相比拟在RF/MW 波段,由于导体的趋肤效应、介质损耗效应、电磁感应等影响,期间区域不再是单纯能量的集中区,而呈现分布特性。
长线概念:通常把RF/MW 导线(传输线)称为长线,传统的电路理论已不适合长线! RF/MW 系统的组成:传输线:传输RF/MW 信号微波元器件:完成微波信号的产生、放大、变换等和功率的分配、控制及滤波 天线:辐射或接收电磁波微波、天线与电波传播的关系:(简答) 微波: 对象:如何导引电磁波在微波传输系统中的有效传输目的:希望电磁波按一定要求沿微波传输系统无辐射的传输; 天线任务:将导行波变换为向空间定向辐射的电磁波,或将在空间传播的电磁波变为微波设备中的导行波 作用:1.有效辐射或接收电磁波;2.把无线电波能量转换为导行波能量 电波传播分析和研究电波在空间的传播方式和特点常用传输线机构:矩形波导 共面波导 同轴线 带状线微带线 槽线分析方法称为传输线的特性阻抗特性阻抗Z0通常是个复数, 且与工作频率有关。
它由传输线自身分布参数决定而与负载及信源无关, 故称为特性阻抗 对于均匀无耗传输线, R=G=0, 传输线的特性阻抗为 此时, 特性阻抗Z0为实数, 且与频率无关。
常用的平行双导线传输线的特性阻抗有250Ω, 400Ω和600Ω三种。
常用的同轴线的特性阻抗有50 Ω 和75Ω两种。
均匀无耗传输线上任意一点的输入阻抗与观察点的位置、传输线的特性阻抗、终端负载阻抗及工作频率有关, 且一般为复数, 故不宜直接测量。
无耗传输线上任意相距λ /2处的阻抗相同, 一般称之为λ /2重复性。
传输线上电压和电流以波的形式传播, 在任一点的电压或电流均由沿-z 方向传播的行波(称为入射波)和沿+z 方向传播的行波(称为反射波)叠加而成。
第1章-射频微波工程基础介绍

第1章 射频/微波工程介绍 表1-1
第1章 射频/微波工程介绍
以上这些波段的划分并不是惟一的,还有其他许多 不同的划分方法,它们分别由不同的学术组织和政府机 构提出,甚至还在相同的名称代号下有不同的范围,因 此波段代号只是大致的频谱范围。其次,以上这些波段 的分界也并不严格,工作于分界线两边临近频率的系统 并没有质和量上的跃变,这些划分完全是人为的,仅是 一种助记符号。
电路,取得一个比较好的折中方案。
第1章 射频/微波工程介绍
1.3 射频/
1.3.1 由于频率、 阻抗和功率是贯穿射频/微波工程的
三大核心指标,故将其称为射频铁三角。它能够形象地 反映射频/微波工程的基本内容。这三方面既有独立特 性,又相互影响。三者的关系可以用图1-2表示。
第1章 射频/微波工程介绍
第1章 射频/微波工程介绍
1.2.2 射频/ 由上述基本特性可归纳出射频/微波与普通无线电相
比有以下优点: (1) 频带宽。可传输的信息量大。 (2) 分辨率高。连续波多普勒雷达的频偏大,成像更
清晰,反应更灵敏。 (3) 尺寸小。电路元件和天线体积小。 (4) 干扰小。不同设备相互干扰小。 (5) 速度快。数字系统的数据传输和信号处理速度
第1章 射频/微波工程介绍
(3) 导航系统: 微波着陆系统(MLS),GPS,无线信标,防撞系统, 航空、 航海自动驾驶等。 (4) 遥感: 地球监测,污染监测,森林、 农田、 鱼汛监测,矿 藏、 沙漠、 海洋、 水资源监测,风、 雪、 冰、 凌监 测,城市发展和规划等。
第1章 射频/微波工程介绍
4. 射频/微波频带比普通的中波、 短波和超短波的 频带要宽几千倍以上,这就意味着射频/微波可以携带 的信息量要比普通无线电波可能携带的信息量大的多。 因此,现代生活中的移动通信、 多路通信、 图像传输、 卫星通信等设备全都使用射频/微波作为传送手段。 射频/微波信号还可提供相位信息、 极化信息、 多普勒频移信息等。这些特性可以被广泛应用于目标 探测、 目标特征分析、 遥测遥控、 遥感等领域。
第2章_射频与微波基础知识V2013

51
阻抗匹配技术
阻抗匹配的类型 集中参数阻抗匹配器; 分布参数阻抗匹配器;
宽带阻抗匹配器;
窄带阻抗匹配器----阻抗匹配和滤波性能。
微波单片集成电路
52
复数阻抗间的功率传输
微波单片集成电路
53
复数阻抗间的功率传输
输入功率的表达式为:
当Pin最大的时候,表示最大的功率传输。 并令其偏导数都为0。
微波单片集成电路
第二章:射频与微波基础知识
注明:该课件内容来自于李智群等编著的《射频集成 电路与系统》书籍,东南大学射频与光电集成电路研 究所,复旦大学,香港城市大学以及网络上等相关的 课程讲义。 微波单片集成电路 1
本章内容
传输线理论; 二端口网络基础; S参数分析; Smith圆图; 阻抗匹配技术。
微波单片集成电路
62
L型匹配网络
由两个电抗元件组成; 窄带网络,带有滤波特性; 两种情况分析:
微波单片集成电路
63
L型匹配Hale Waihona Puke 络微波单片集成电路64
L型匹配网络
微波单片集成电路
65
L型匹配网络举例
微波单片集成电路
66
L型匹配网络举例
微波单片集成电路
67
L型匹配问题
问题2:采用L型结构匹配负载阻抗 ZL=RL+jXL到Zs=Rs+jXs。求解参数解 析方法以及适用范围。
Pi型匹配网络举例
微波单片集成电路
72
Pi型匹配网络举例
微波单片集成电路
73
Pi型匹配网络举例
微波单片集成电路
74
T型匹配网络
微波单片集成电路
75
射频与微波手册

射频与微波手册
射频与微波是无线通信领域中的重要概念。
它们在许多领域都有广泛的应用,如无线通信、雷达、导航、电子对抗等。
射频是指频率在100KHz到300GHz之间的电磁波。
而微波则是指频率在
300MHz到300GHz之间的电磁波。
它们在电磁波谱中处于较高的位置,因此具有很高的频率和波长。
在无线通信中,射频与微波技术被广泛应用于信号的传输和处理。
例如,在移动通信中,射频信号被用来传输语音和数据信息。
在雷达和导航系统中,微波信号被用来检测目标并确定其位置。
为了实现这些应用,需要设计和制造各种射频与微波器件,如滤波器、放大器、混频器、振荡器等。
这些器件的性能对整个系统的性能有着重要的影响。
此外,射频与微波技术还涉及到许多复杂的问题,如信号的传输、衰减、干扰、噪声等。
为了解决这些问题,需要深入了解电磁波的传播特性、材料的电磁性质以及信号处理技术等。
总的来说,射频与微波手册是一本介绍射频与微波技术的重要参考书。
它包含了射频与微波的基本概念、原理、应用和发展趋势等方面的内容。
通过阅读这本手册,读者可以深入了解射频与微波技术的各个方面,并掌握相关的知识和技能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z
Output V
5.0
2.5
z
Input V
5.0
2.5
z T=l/vp 2T
Z. Q. LI
Open
t t
13
传输线(Transmission Lines)
第二章
Z. Q. LI
14
传输线(Transmission Lines)
¾ 反射系数
传输线在x处的反射系数用Γ(x)表示,坐标原点定义在负载处
= − d V(x) dx
) = − d I( x ) dx
⎧ ⎪⎪ ⎨ ⎪ ⎪⎩
jωLI( x ) jωCV ( x
= +
− V ( x + Δx ) −V ( x ) Δx
Δx ) = − I( x + Δx ) − Δx
I(
x
)
⎧ ⎪⎪ ⎨ ⎪ ⎪⎩
d2 dx2 d2 dx2
V (x) + I(x) +
第二章
Z. Q. LI
4
传输线(Transmission Lines)
¾传输线电路模型:L、C、R、G分布系统
x x + Δx
R——两根导线每单位长度具有的电阻, 其单位为Ω/m。
L——两根导线每单位长度具有的电感, 其单位为H/m。
G——每单位长度导线之间具有的电导, 其单位为S/m。
C——每单位长度导线之间具有的电容, 其单位为F/m。
─ 但是当信号频率很高时,由于寄生元件的存在,理想的开路和短路很难 实现,尤其在宽频范围内实现理想的短路和开路会更加困难。
─ 即使可以做到接近理想的开路和短路,电路也很有可能因此而不稳定。
─ 由于信号以波的形式传播,在不同测量点上幅度和相位都可能不同。
─ 这些问题使得基于电压和电流的测量方法难以应用。 ─ 因此,人们提出了散射参数(Scattering Parameters)的概念
Z. Q. LI
9
传输线(Transmission Lines)
─ 特征阻抗计算:
对于同轴电缆,
Z0 =
μ / ε0 ln⎜⎛ b ⎟⎞ = 377 ln⎜⎛ b ⎟⎞ 2π εr ⎝ a ⎠ 2π εr ⎝ a ⎠
对于微带线, Z0 =
μ / ε0 h = 377 h εr w εr w
(忽略边缘效应)
─ 不同传输线的特征阻抗和应用范围
第二章
Z. Q. LI
10
传输线(Transmission Lines)
¾ 有损耗的传输线
由于导体的电导率和介质的电阻率都是有限的,损耗不可避免
─ 经过同样的推导过程,可以得到
( ) ( ) ( ) ( ) ⎧V
⎪
x
= V0+e−γ x + V0−eγ x = V +
ωt
+
βx
)
第二章
Z. Q. LI
8
传输线(Transmission Lines)
¾ 相速和特征阻抗
─ 相速:定义为行波上某一相位点的传播速度(Phase velocity),对于一个正
弦波 cos(ωt-βx),一定相位可表示为ωt-βx=constant,于是相位速度
vp
=
dx dt
=ω β
= ω
x
+V−
x
= V0+
e−γ x + ΓLeγ x
( ) ( ) ( ) ( ) ( ) ⎨
⎪I ⎩
x
=1 Z0
V0+e−γ x − V0−eγ x
= I+
x
− I−
x
= V0+ Z0
e−γ x − ΓLeγ x
γ = (R + jωL)(G + jωC ) = α + jβ 称为传输常数(propagation constant)
─ 对应的时间函数表示为
v(x, t) = Re[V (x)e jωt ] = Re[V0+e−α xe− j(β x−ωt) + V0−eα xe j(β x+ωt) ]
i(x, t) = Re[I (x)e jωt ] = Re[V0+ e e −α x − j(β x−ωt) − V0− eα xe j(β x+ωt) ]
传输线无损耗 γ = α + jβ = jβ
(( )) (( )) Z(d) =
Zin (− d ) =
Z0
1 + ΓLe−2γd 1 − ΓLe−2γd
= Z0
1 + ΓLe−2 jβd 1 − ΓLe−2 jβd
=
Z0
(Z L (Z0
+ +
jZ 0 jZ L
tan tan
βd βd
) )
¾ (电压)驻波比
第二章 射频与微波基础知识
¾ 传输线 ¾ 传输线阻抗变换 ¾ 二端口网络与S参数 ¾ Smith圆图 ¾ 阻抗匹配
第二章
Z. Q. LI
1
传输线(Transmission Lines)
¾ 分布(distributed)系统与集总(lumped)系统
─ 环路电压和节点电流定律在任何时候都成立吗? 当然,如果模型正确的话。
ω LC
=
1 LC
但是我们知道, v p = λf 因而
β = 2π λ
─ 传输线特征阻抗(Z0):定义为入射电压和入射电流的比值
Z0
=
V +(x) I +(x)
=
ωL β
=
L C
在没有反射波的情况下,传输线上任意一点的输入阻抗为特征阻抗。 由于无限长传输线没有反射波,因此其输入阻抗等于特征阻抗。
第二章
第二章
Z. Q. LI
19
二端口网络与S参数
¾ z-参数
¾ y-参数
¾ h-参数和ABCD-参数(级联参数)
第二章
Z. Q. LI
20
二端口网络与S参数
¾ z、y和级联参数的应用情况
第二章
Z. Q. LI
21
二端口网络与S参数
¾ 高频网络参数测量遇到的问题
─ 这些二端口参数必须在某个端口开路或短路的条件下,通过测量端口电 压电流的方法获得。
β即为相位常数;α称为衰减常数,表示传输线的衰减特性,单位为(Np/m),
Np与dB的关系为1dB=8.686Np
ΓL = V0− V0+ 表示传输线在负载端(x=0)的反射系数
第二章
Z. Q. LI
11
传输线(Transmission Lines)
─ 特征阻抗不再是一个实数
─ 当R<<ωL, G<<ωC时,β 和Z0近似于无损耗的情况
+ v(x + Δx,t) Δx,t) + i(x + Δx,
t
)
⎪⎪⎧− ⎨ ⎪⎪⎩−
v( x + Δx,t ) − v( x ,t ) = L ∂ i(
Δx
∂t
i( x + Δx,t ) − i( x,t ) = C ∂ v(
Δx
∂t
x,t x+
) Δx,t
)
⎧ ⎪⎪
L
⎨
⎪⎪⎩c
∂i( x,t ∂t
¾ 抽象的传输线
─ 一根信号线和地(线或面)就组成了传输线 ─ 电磁波将沿信号线传输并被限制在信号线和地之间
第二章
Z. Q. LI
3
传输线(Transmission Lines)
¾ 具体的传输线
─ 同轴线或同轴电缆(coaxial cable),平行双线(twin-lead, two wire) ─ 微带线 (microstrip),共面波导(co-planar wave guide, CPW)
ωL
对它们进行相量域到时间域的反变换可得电压和电流的时域表达式:
[ ] ⎧
⎪
v
(
x ,t
)
=
Re
V
(
x
)e
jω t
=
V
+ 0
cos(
ωt
−
βx
)
+
V
− 0
cos(
ωt
+
βx )
[ ] [ ] ⎨
⎪⎩i( x ,t ) =
Re
I ( x )e jωt
=β ωL
V
+ 0
cos(
ωt
−
βx
)
−
V
− 0
cos(
Γ (x ) =
V V
− (x ) + (x )
=
V
− 0
e
γ
x
V
+ 0
e
−
γ
x
= ΓL e 2γx
其中
ΓL
=
V
− 0
V
+ 0
= Γ (0 )
¾ 输入阻抗
(( )) Z in
(x ) =
V (x ) I (x )
=
Z0
e −γx + ΓL eγx e −γx − ΓL eγx
Zin
(0)
=
Z0
(1+ (1−
¾ S-参数(散射参数)
— 入射波和反射波 (a和b 的平方即为入射和反射波的功率)
─ 任何电路、元器件、连接线本质上都是分布系统,在某些条件下它们 的分布特性可以被忽略,正如在某些条件下微积分可以简化为四则运算 ─ 对于一条长度为l的低损耗连接线和波长为λ的信号
