基于RBF网络的机械手Matlab仿真实验
利用matlab的机器人试验仿真
选择MATLAB2016a版,高版本不能安装。
安装好按照下面的操作做出来,然后截图做成Word文档发给我。
MATLAB2016a版同学们网上下载安装,安装方法网上随便可找到。
机器人工具箱我发给你们。
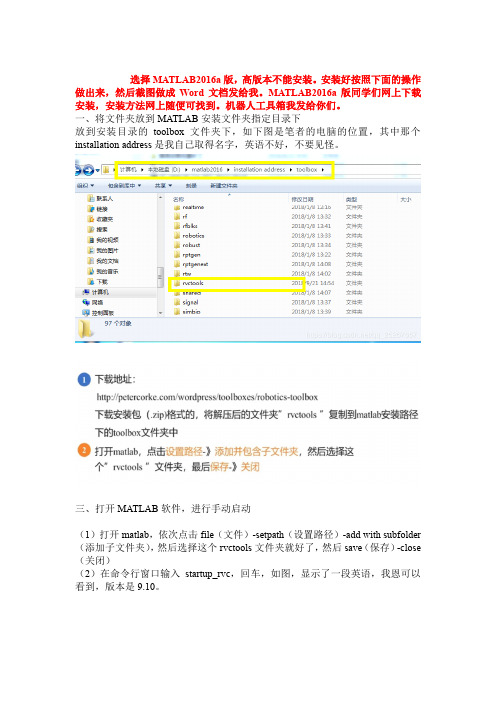
一、将文件夹放到MATLAB安装文件夹指定目录下放到安装目录的toolbox文件夹下,如下图是笔者的电脑的位置,其中那个installation address是我自己取得名字,英语不好,不要见怪。
三、打开MATLAB软件,进行手动启动(1)打开matlab,依次点击file(文件)-setpath(设置路径)-add with subfolder (添加子文件夹),然后选择这个rvctools文件夹就好了,然后save(保存)-close (关闭)(2)在命令行窗口输入startup_rvc,回车,如图,显示了一段英语,我恩可以看到,版本是9.10。
本文主要是给大家一个系统的概念,如何用Matlab实现六轴机器人的建模和实现轨迹规划。
以后将会给大家讲解如何手写正逆解以及轨迹插补的程序。
程序是基于Matlab2016a,工具箱版本为Robotic Toolbox 9.10。
1.D-H建模三个两两相互垂直的XYZ轴构成欧几里得空间,存在六个自由度:沿XYZ 平移的三个自由度,绕XYZ旋转的三个自由度。
在欧几里得空间中任意线性变换都可以通过这六个自由度完成。
Denavit-Hartenberg提出的D-H参数模型能满足机器人学中的最小线性表示约定,用4个参数就能描述坐标变换:绕X轴平移距离a;绕X轴旋转角度alpha;绕Z轴平移距离d;绕Z轴旋转角度theta。
2.标准D-H模型和改进D-H模型对比来看参数并没有改变,标准的D-H 模型是将连杆的坐标系固定在该连杆的输出端(下一关节),也即坐标系i-1与关节i对齐;改进的D-H模型则是将坐标系固定在该连杆的输入端(上一关节),也即坐标系i-1与关节对齐i-1。
RBF神经网络:原理详解和MATLAB实现

RBF神经⽹络:原理详解和MATLAB实现RBF神经⽹络:原理详解和MATLAB实现——2020年2⽉2⽇⽬录RBF神经⽹络:原理详解和MATLAB实现 (1)⼀、径向基函数RBF (2)定义(Radial basis function——⼀种距离) (2)如何理解径向基函数与神经⽹络? (2)应⽤ (3)⼆、RBF神经⽹络的基本思想(从函数到函数的映射) (3)三、RBF神经⽹络模型 (3)(⼀)RBF神经⽹络神经元结构 (3)(⼆)⾼斯核函数 (6)四、基于⾼斯核的RBF神经⽹络拓扑结构 (7)五、RBF⽹络的学习算法 (9)(⼀)算法需要求解的参数 (9)0.确定输⼊向量 (9)1.径向基函数的中⼼(隐含层中⼼点) (9)2.⽅差(sigma) (10)3.初始化隐含层⾄输出层的连接权值 (10)4.初始化宽度向量 (12)(⼆)计算隐含层第j 个神经元的输出值zj (12)(三)计算输出层神经元的输出 (13)(四)权重参数的迭代计算 (13)六、RBF神经⽹络算法的MATLAB实现 (14)七、RBF神经⽹络学习算法的范例 (15)(⼀)简例 (15)(⼆)预测汽油⾟烷值 (15)⼋、参考资料 (19)⼀、径向基函数RBF定义(Radial basis function——⼀种距离)径向基函数是⼀个取值仅仅依赖于离原点距离的实值函数,也就是Φ(x)=Φ(‖x‖),或者还可以是到任意⼀点c的距离,c点称为中⼼点,也就是Φ(x,c)=Φ(‖x-c‖)。
任意⼀个满⾜Φ(x)=Φ(‖x‖)特性的函数Φ都叫做径向基函数。
标准的⼀般使⽤欧⽒距离(也叫做欧式径向基函数),尽管其他距离函数也是可以的。
在神经⽹络结构中,可以作为全连接层和ReLU层的主要函数。
⼀些径向函数代表性的⽤到近似给定的函数,这种近似可以被解释成⼀个简单的神经⽹络。
径向基函数在⽀持向量机中也被⽤做核函数。
常见的径向基函数有:⾼斯函数,⼆次函数,逆⼆次函数等。
MATLAB机器人仿真程序

附录MATLAB 机器人工具箱仿真程序:1)运动学仿真模型程序(Rob1.m)L1=link([pi/2 150 0 0])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})=’MOTOMAN-UP6’ % 模型的名称>>drivebot(r)2)正运动学仿真程序(Rob2.m)L1=link([pi/2 150 0 0])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})=’MOTOMAN-UP6’t=[0:0.01:10];%产生时间向量qA=[0 0 0 0 0 0 ]; %机械手初始关节角度qAB=[-pi/2 -pi/3 0 pi/6 pi/3 pi/2 ];%机械手终止关节角度figure('Name','up6机器人正运动学仿真演示');%给仿真图像命名q=jtraj(qA,qAB,t);%生成关节运动轨迹T=fkine(r,q);%正向运动学仿真函数plot(r,q);%生成机器人的运动figure('Name','up6机器人末端位移图')subplot(3,1,1);plot(t, squeeze(T(1,4,:)));xlabel('Time (s)');ylabel('X (m)');subplot(3,1,2);plot(t, squeeze(T(2,4,:)));xlabel('Time (s)');ylabel('Y (m)');subplot(3,1,3);plot(t, squeeze(T(3,4,:)));xlabel('Time (s)');ylabel('Z (m)');x=squeeze(T(1,4,:));y=squeeze(T(2,4,:));z=squeeze(T(3,4,:));figure('Name','up6机器人末端轨迹图'); plot3(x,y,z);3)机器人各关节转动角度仿真程序:(Rob3.m)L1=link([pi/2 150 0 0 ])L2=link([0 570 0 0])L3=link([pi/2 130 0 0])L4=link([-pi/2 0 0 640])L5=link([pi/2 0 0 0 ])L6=link([0 0 0 95])r=robot({L1 L2 L3 L4 L5 L6})='motoman-up6't=[0:0.01:10];qA=[0 0 0 0 0 0 ];qAB=[ pi/6 pi/6 pi/6 pi/6 pi/6 pi/6]; q=jtraj(qA,qAB,t);Plot(r,q);subplot(6,1,1);plot(t,q(:,1));title('转动关节1');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,2);plot(t,q(:,2));title('转动关节2');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,3);plot(t,q(:,3));title('转动关节3');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,4);plot(t,q(:,4));title('转动关节4');xlabel('时间/s');ylabel('角度/rad' );subplot(6,1,5);plot(t,q(:,5));title('转动关节5');xlabel('时间/s');ylabel('角度/rad');subplot(6,1,6);plot(t,q(:,6));title('转动关节6');xlabel('时间/s');ylabel('角度/rad');4)机器人各关节转动角速度仿真程序:(Rob4.m)t=[0:0.01:10];qA=[0 0 0 0 0 0 ];%机械手初始关节量qAB=[ 1.5709 -0.8902 -0.0481 -0.5178 1.0645 -1.0201]; [q,qd,qdd]=jtraj(qA,qAB,t);Plot(r,q);subplot(6,1,1);plot(t,qd(:,1));title('转动关节1');xlabel('时间/s');ylabel('rad/s');subplot(6,1,2);plot(t,qd(:,2));title('转动关节2');xlabel('时间/s');ylabel('rad/s');subplot(6,1,3);plot(t,qd(:,3));title('转动关节3');xlabel('时间/s');ylabel('rad/s');subplot(6,1,4);plot(t,qd(:,4));title('转动关节4');xlabel('时间/s');ylabel('rad/s' );subplot(6,1,5);plot(t,qd(:,5));title('转动关节5');xlabel('时间/s');ylabel('rad/s');subplot(6,1,6);plot(t,qd(:,6));title('转动关节6');xlabel('时间/s');ylabel('rad/s');5)机器人各关节转动角加速度仿真程序:(Rob5.m)t=[0:0.01:10];%产生时间向量qA=[0 0 0 0 0 0]qAB =[1.5709 -0.8902 -0.0481 -0.5178 1.0645 -1.0201]; [q,qd,qdd]=jtraj(qA,qAB,t);figure('name','up6机器人机械手各关节加速度曲线');subplot(6,1,1);plot(t,qdd(:,1));title('关节1');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)');subplot(6,1,2);plot(t,qdd(:,2));title('关节2');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)');subplot(6,1,3);plot(t,qdd(:,3));title('关节3');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)')subplot(6,1,4);plot(t,qdd(:,4));title('关节4');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)')subplot(6,1,5);plot(t,qdd(:,5));title('关节5');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)')subplot(6,1,6);plot(t,qdd(:,6));title('关节6');xlabel('时间 (s)');ylabel('加速度 (rad/s^2)')如有侵权请联系告知删除,感谢你们的配合!。
MATLAB在RBF神经网络模型中的应用

MATLAB 在RBF 神经网络模型中的应用高宁1,张建中2(1.安徽农业大学信息与计算机学院,安徽合肥230036;2.安徽建筑工业学院电子与信息工程学院,安徽合肥230022)摘要:本文介绍了RBF 神经网络的基本原理及主要特点,并举例说明了基于MATLAB 神经网络工具箱建立RBF 神经网络模型及实现仿真的方法。
关键词:仿真;MATLAB 神经网络工具箱;RBF 神经网络中图分类号:TP399文献标识码:A文章编码:1672-6251(2009)02-0110-02Application of RBF neural network model based on MATLABGAO Ning 1,ZHANG Jan-zhong 2(1.College of Information and computer,Anhui Agriculture University,Hefei 230036,China;2.College of Electronics and Information Enginner,Anhui Architecture University,Hefei 230022,China)Abstract:In this paper,the principle and characteristic of RBF neural network are explained,and the method of building and simulating RBF neural network model is introduced.Key words:Simulation;MATLAB neural network toolbox;RBF neural network人工神经网络具有大规模并行处理能力、分布式存储能力、自适应(学习)能力等特征,神经网络特有的非线性适应性信息处理能力,克服了传统人工智能方法的缺陷,已广泛应用于模式识别、信号处理等各种应用领域。
基于MATLAB五自由度机械手运动学仿真分析

基于MATLAB五自由度机械手运动学仿真分析五自由度机械手是一种具有五个独立自由度的机械装置,可以实现复杂的姿态和路径规划。
为了研究其运动学特性,可以使用MATLAB进行仿真分析。
本文将基于MATLAB对五自由度机械手的运动学进行仿真分析,包括直接运动学和逆运动学。
首先,我们需要定义机械手的结构和参数。
五自由度机械手通常由五个关节连接而成,每个关节的旋转角度可以通过电机控制。
我们可以使用DH参数建立机械手的运动学模型,在MATLAB中定义每个关节的DH参数。
DH参数包括关节的长度、偏移、旋转角度和连接方式等。
在定义了机械手的结构和参数之后,我们可以进行直接运动学分析。
直接运动学是指根据机械手的关节角度计算末端执行器的位置和姿态。
在MATLAB中,可以使用正运动学算法根据给定的关节角度计算末端执行器的位置和姿态。
这个过程可以通过建立运动学模型和坐标变换矩阵实现,在MATLAB中可以使用符号计算工具箱对模型进行符号计算,得到末端执行器的位置和姿态的闭式解。
接下来,我们可以进行逆运动学分析。
逆运动学是指根据机械手的末端执行器位置和姿态计算关节角度。
在MATLAB中,可以使用逆运动学算法根据给定的末端执行器的位置和姿态计算关节角度。
这个过程通常需要使用数值方法进行迭代求解,MATLAB提供了多种数值求解方法,如牛顿法和Levenberg-Marquardt算法等。
我们可以使用这些算法对逆运动学进行求解,得到关节角度的解。
在进行仿真分析之前,我们还需要定义机械手的工作空间。
工作空间是机械手可以达到的位置和姿态的集合。
对于五自由度机械手,可以使用三维空间中的一个区域表示其工作空间。
在MATLAB中,可以定义一个三维空间的体积,在此体积内的点被认为是机械手的工作空间。
在MATLAB中进行仿真分析时,可以使用图形界面工具进行交互式仿真分析。
MATLAB提供了多种可视化和动画功能,可以实时显示机械手的运动过程和工作空间。
基于MATLAB的机器人柔性手臂控制系统设计与仿真【毕业作品】

任务书设计题目:基于MATLAB的机器人柔性手臂控制系统设计与仿真1.设计的主要任务及目标学生应通过本次毕业设计,综合运用所学过的基础理论知识,在深入了解反馈控制系统工作原理的基础上,掌握机械系统建模、分析及校正环节设计的基本过程;初步掌握运用MATLAB/Simulink相关模块进行控制系统设计与仿真的方法,为学生在毕业后从事机械控制系统设计工作打好基础。
2.设计的基本要求和内容(1)根据已有的机器人柔性手臂系统相关资料,对其结构特点及工作原理进行分析;(2)建立柔性手臂系统的数学模型;(3)应用极点配置对系统进行状态反馈设计;(4)运用MATLAB/SIMULINK对系统进行仿真计算;(5)通过动态仿真设计优化系统参数,对反馈系数K进行确定;3.主要参考文献[1] 刘白燕等编,机电系统动态仿真-基于MATLAB/SIMULINK[M].北京:机械工业出版社,2005.7[2] 王积伟,吴振顺等著,控制工程基础[M].北京:高等教育出版社2001.8[3] (日)末松良一. 机械控制入门[M].北京:科学出版社,2000[4] 徐昕等著. MATLAB工具箱应用指南.北京:电子工业出版社,2000 4.进度安排基于MATLAB的机器人柔性手臂控制系统设计与仿真摘要:机械臂未来的发展趋势是高速、高精度和轻型化、操作灵活的柔性机械臂。
柔性机械臂系统的动力学特点是大范围刚体运动的同时,伴随着柔性臂杆的小幅弹性运动。
柔性臂杆的弹性振动将极大地影响机械臂末端的定位精度。
本设计结合机器人柔性手臂的结构特点,对机器人柔性手臂进行了受力分析,建立了柔性手臂系统的集中参数模型。
对柔性手臂系统的特性、系统的可控制性和可观测性进行了分析,用极点配置求取状态反馈系数K对系统进行反馈。
使柔性手臂系统的振动快速达到稳态,用MATLAB仿真确认控制效果。
关键词:柔性机械臂,控制系统,MATLAB仿真Design and simulation system for flexible manipulator control basedon MATLABAbstract:The trend of the development of mechanical arm is high speed, high precision and light-duty, flexible operation of the flexible manipulator. The dynamics of flexible manipulator system is characterized by a wide range of rigid motion at the same time, with flexible arm slightly elastic movement. The elastic vibration of flexible arm will greatly influence the mechanical arm at the ends of the positioning accuracy. This design with the structure characteristics of a flexible robot arm, has carried on the stress analysis of flexible robot arms, established the lumped parameter model of the flexible arm system. Characteristics of the flexible arm system, system controllability and observability are analyzed, using pole assignment for state feedback coefficient K to feedback system. To make the vibration of the flexible arm system to reach steady state quickly, MATLAB simulation confirm the control effect.Key words:Flexible manipulator, Control system, MATLAB simulation目录1概述 (1)1.1引言 (1)1.2研究目的及意义 (2)1.3国内外柔性机械臂的研究现状 (3)1.3.1柔性臂动力学建模的研究现状 (3)1.3.2柔性机械臂的主动控制 (4)2柔性手臂的建模过程 (5)2.1柔性手臂对机器人的重要性 (5)2.2柔性手臂的试验模型 (6)2.3状态方程的建立 (8)2.3.1集中参数模型 (8)2.3.2系统参数和变量的定义 (8)2.3.3数学模型 (10)3系统的特性分析 (13)3.1实验参数 (13)3.2比例变换 (14)3.3系统矩阵的特征值和手臂的振型 (15)3.4可控制性和可观测性 (20)4用极点配置法进行设计和仿真 (22)4.1状态反馈设计 (22)4.2控制系统设计方法选择 (22)4.3利用仿真确认控制效果 (24)5控制系统的实现 (26)总结 (27)参考文献 (29)致谢 (30)附录 (31)1 概述1.1 引言随着人类科技水平的不断进步,机器人的应用越来越广泛。
6.3 基于RBF神经网络的辨识 [系统辨识理论及Matlab仿真]
![6.3 基于RBF神经网络的辨识 [系统辨识理论及Matlab仿真]](https://img.taocdn.com/s3/m/41e3af4aa216147916112830.png)
RBF网络特点
(1) RBF网络的作用函数为高斯函数,是局部 的,BP网络的作用函数为S函数,是全局的;
(2) 如何确定RBF网络隐层节点的中心及基宽 度参数是一个困难的问题;
(3) 已证明RBF网络具有唯一最佳逼近的特性, 且无局部极小[1]。
RBF网络结构 RBF网络是一种三层前向网络,由于输入
到输出的映射是非线性的,而隐含层空间到 输出空间的映射是线性的,从而可以大大加 快学习速度并避免局部极小问题。
RBF网络结构图1所示。
图1 RBF网络结构
2、RBF网络的逼近
采用RBF网络逼近一对象的结构如图2所 示。
图2 RBF神经网络逼近
在RBF网络结构中,X x1,x2,....xnT 为网络的输入
m
wjhj
j 1
c1 j x1 b2j
其中取 x1 u(k) 。
3、RBF网络逼近仿真实例
使用RBF网络逼近下列对象:
y(k)
u(k
)3
1
y(k 1) y(k 1)2
• RBF网络逼近程序见chap6_4.m
参考文献
[1] J.Park, I.W.Sandberg, Universal approximation
6.3 基于RBF神经网络的辨识
1、RBF神经网络 径向基函数(RBF-Radial Basis Function)神经 网络是由J.Moody和C.Darken在80年代末提出的 一种神经网络,它是具有单隐层的三层前馈网络 。由于它模拟了人脑中局部调整、相互覆盖接收 域(或称感受野-Receptive Field)的神经网络结 构,因此,RBF网络是一种局部逼近网络,已证 明它能任意精度逼近任意连续函数[1]。
采摘机械臂的PSO-RBF神经网络自适应控制

1 机械臂系统问题描述
由于机械臂的每个关节就是一个输入ꎬ也是一个输
出ꎬ而且关节与关节之间又存在着扰动ꎬ耦合关系复杂ꎮ
由于径向基神经网络结构简单ꎬ具有较强的泛化性
能ꎬ近年来ꎬ很多人对 RBF 神经网络在机械臂控制的方
向进行了研究ꎬ极大地推动了机械臂的 RBF 神经网络控
制发展的进程ꎮ 一些研究人员运用 RBF 神经网络的特
子规模ꎮ
来决定下一步运动速度和位置ꎮ 基本 PSO 算法的粒子位
τ = M 0( q) ( q-k v e-k p e) +C0( qꎬq ) q +G0( q) -f( ) (3)
其中:k p = êê
法ꎬ第 t1 次迭代时ꎬ粒子将根据自身的经验和同伴的经验
(7)
(8)
其中 f ∗( )= w ∗ T h( x) ꎬw ∗ 表示 f( ) 的最佳逼近权值
( 期望) 的角度、角速度、角加速度指令ꎮ
在实际工程中ꎬf( ) 通常是未知的ꎬ需要估计 f( )
并对其补偿ꎮ 利用 RBF 神经网络逼近任意非线性函数的
特性逼近 f( ) ꎬ并对其进行补偿ꎬ就可以达到想要的控
制效果ꎮ
2 PSO -RBF 神经网络
采用 RBF 网络逼近 f( ) ꎬ其算法为
adaptive control method is designedꎬ with which a radial basis function neural network is used to approximate and compensate for
system model errorsꎬ and particle swarm optimization is applied to optimize RBF weight parameters to ensure better PSO - RBF
实验四、RBF神经网络实验报告

如果对于输入空间的某个局部区域只有少数几个连接权值影响输出,则该网络称为局部逼近网络。常见的局部逼近网络有RBF网络、小脑模型(CMAC)网络、B样条网络等。
广义RBF网络
Cover定理指出:将复杂的模式分类问题非线性地映射到高维空间将比投影到低维空间更可能线性可分。
广义RBF网络:从输入层到隐藏层相当于是把低维空间的数据映射到高维空间,输入层细胞个数为样本的维度,所以隐藏层细胞个数一定要比输入层细胞个数多。从隐藏层到输出层是对高维空间的数据进行线性分类的过程,可以采用单层感知器常用的那些学习规则,参见神经网络基础和感知器。
寻找逼近函数F(x)通过最小化下面的目标函数来实现:
加式的第一项好理解,这是均方误差,寻找最优的逼近函数,自然要使均方误差最小。第二项是用来控制逼近函数光滑程度的,称为正则化项,λ是正则化参数,D是一个线性微分算子,代表了对F(x)的先验知识。曲率过大(光滑度过低)的F(x)通常具有较大的||DF||值,因此将受到较大的惩罚。
3)Inverse multiquadrics(拟多二次)函数
σ称为径向基函数的扩展常数,它反应了函数图像的宽度,σ越小,宽度越窄,函数越具有选择性。
完全内插存在一些问题:
1)插值曲面必须经过所有样本点,当样本中包含噪声时,神经网络将拟合出一个错误的曲面,从而使泛化能力下降。K,K<P,从样本中选取K个(假设不包含噪声)作为Φ函数的中心。
隐藏层的作用是把向量从低维m映射到高维P,低维线性不可分的情况到高维就线性可分了。
Matlab的RBF神经网络程序

求助,Matlab的RBF神经网络程序为什么测试均方误差很大?clcclearclose all%-------------------------------------------------%产生训练样本与测试样本A=0.086207 0.262772 0.1269570.113793 0.261712 0.1464890.113793 0.261176 0.1855530 0.253351 0.1757870.006897 0.239692 0.1269570 0.233549 0.1269570 0.232297 0.1025420 0.231777 0.1123080 0.231585 0.1660210 0.231511 0.0439470 0.231155 0.1562550 0.230674 0.1513720 0.230357 0.0781270 0.229985 0.1855530 0.2295 0.126957 0 0.229246 0.1562550 0.229015 0.0585960 0.228854 0.0585960 0.228858 0.1513720 0.228995 0.131840 0.229027 0.1025420 0.229285 0.1562550 0.2297 0.136723 0 0.230721 0.1171910.034483 0.230721 0.1709040.006897 0.237376 0.1269570.086207 0.245976 0.1562550.062069 0.289381 0.1562550.086207 0.351242 0.1855530.062069 0.491243 0.1123080.086207 0.605574 0.1123080.034483 0.674478 0.1562550.062069 0.733842 0.1709040.196552 0.768613 0.1123080.086207 0.792452 0.1709040.034483 0.807965 0.1171910.086207 0.826889 0.131840.168966 0.844617 0.1660210.168966 0.859543 0.1367230.196552 0.879376 0.1367230.196552 0.894525 0.2246160.196552 0.911278 0.1464890.141379 0.922284 0.0585960.196552 0.927073 0.1367230.113793 0.930332 0.1464890.168966 0.932973 0.1464890.168966 0.938881 0.0634780.168966 0.94669 0.1025420.196552 0.952802 0.0976590 0.958737 0.1513720.006897 0.960443 0.1025420 0.96324 0.117191 0.113793 0.965827 0.0781270.034483 0.966464 0.2392650.113793 0.969583 0.1709040.086207 0.971601 0.1855530.141379 0.973354 0.131840.034483 0.974763 0.1367230.062069 0.975569 0.1171910.034483 0.976746 0.1367230.006897 0.977846 0.131840.062069 0.978429 0.1757870.086207 0.979458 0.1562550.062069 0.9806 0.1171910.006897 0.980925 0.1367230.141379 0.981492 0.1269570.086207 0.982099 0.1269570.113793 0.982412 0.1269570.141379 0.982897 0.1367230.141379 0.983022 0.1660210.141379 0.983042 0.1269570.168966 0.982819 0.1025420.113793 0.98267 0.1123080.034483 0.982283 0.1269570.062069 0.981973 0.1269570.034483 0.981375 0.1269570.034483 0.98087 0.097659 0.062069 0.980189 0.1367230.006897 0.979309 0.0927760.062069 0.97864 0.156255 0.034483 0.978171 0.1123080.086207 0.976915 0.1513720.034483 0.97639 0.092776 0.141379 0.974982 0.1367230.113793 0.97389 0.117191 0.141379 0.972857 0.1269570.006897 0.971918 0.1367230.034483 0.971257 0.1855530.034483 0.970788 0.1464890.141379 0.946456 0.1562550.141379 0.946006 0.1123080.196552 0.945368 0.1513720.196552 0.944625 0.1367230.168966 0.944014 00.168966 0.94322 00.168966 0.942578 00.086207 0.942183 0.1367230.168966 0.941189 0.6152530.168966 0.940438 00.113793 0.939679 0.2783290.168966 0.93903 00.113793 0.938545 0.7861570.141379 0.938212 00.113793 0.937371 0.8398690.141379 0.936737 0.1025420.196552 0.936103 00.141379 0.935489 00.196552 0.935199 00.168966 0.934507 0.1464890.168966 0.934213 0.2099670.168966 0.933709 0.1562550.168966 0.933075 0.1171910.168966 0.932586 0.0976590.196552 0.932183 0.0927760.196552 0.931936 0.1513720.141379 0.931326 0.131840.168966 0.931087 0.0781270.196552 0.92881 0.2246160.086207 0.928482 0.1660210.141379 0.927965 0.1123080.113793 0.927402 0.13184 0.113793 0.926866 0.13184 0.141379 0.926568 0.126957 0.141379 0.926392 0.097659 0.196552 0.926079 0.112308 0.141379 0.923708 0.097659 0.141379 0.923188 0.146489 0.113793 0.922887 0.097659 0.168966 0.922503 0.126957 0.141379 0.922053 0.102542 0.086207 0.921791 0.136723 0.086207 0.921463 0.151372 0.062069 0.921247 0.117191 0.086207 0.920946 0.078127 0.062069 0.920747 0.126957 0.113793 0.920484 0.136723 0.141379 0.920359 0.078127 0.034483 0.920121 0.063478 0.113793 0.918869 0.200201 0.062069 0.918626 0.327158 0.086207 0.918477 0.156255 0.141379 0.918254 0.327158 0.034483 0.918078 0.117191 0.034483 0.917879 0.078127 0.086207 0.917714 0.146489 0.006897 0.917589 0.063478 0.113793 0.917425 0.136723 0.086207 0.917167 0.136723 0.034483 0.917006 0.136723 0.062069 0.916232 0.073244 0.086207 0.916118 0.200201 0.113793 0.916056 0.092776 0.062069 0.915922 0.126957 0.086207 0.915762 0.058596 0.113793 0.915696 0.126957 0.168966 0.914048 0.185553 0.113793 0.913199 0.117191 0.113793 0.912487 0.185553 0.086207 0.912014 0.009766 0.168966 0.911642 0.078127 0.034483 0.911087 0.166021 0.168966 0.910637 0.200201 0.113793 0.910472 0.166021 0.196552 0.910324 0.1367230.141379 0.90978 0.131840.113793 0.907644 0.1660210.224138 0.907569 0.1464890.196552 0.907468 0.1464890.196552 0.907444 0.1367230.196552 0.907338 0.1171910.168966 0.907237 0.1269570.196552 0.907202 0.2050840.196552 0.907123 0.1269570.196552 0.907045 0.0781270.168966 0.906767 0.1660210.196552 0.906724 0.1513720.196552 0.906716 0.1123080.141379 0.906615 0.1513720.168966 0.906509 0.1855530.196552 0.906458 0.1562550.196552 0.906043 0.1123080.168966 0.905938 0.1709040.168966 0.905691 0.131840.168966 0.905394 0.126957; %训练样本,共三百组A=A';A1=A(1,:);A2=A(2,:);A3=A(3,:);B=3.1:.0458:16.8; %训练目标C=0.168966 0.905394 0.1269570.168966 0.905277 0.1025420.196552 0.905155 0.1367230.168966 0.905171 0.131840.141379 0.90519 0.1464890.141379 0.905194 0.048830.196552 0.905198 0.1171910.141379 0.905167 0.1269570.113793 0.905163 0.1123080.168966 0.905155 0.1123080.168966 0.905124 0.1513720.196552 0.905065 0.1171910.168966 0.905069 0.1367230.196552 0.905026 0.2002010.141379 0.905011 0.0781270.113793 0.904971 0.1709040.196552 0.904905 0.146489 0.141379 0.904881 0.151372 0.113793 0.904838 0.146489 0.168966 0.904799 0.156255 0.141379 0.904748 0.058596 0.168966 0.904717 0.112308 0.196552 0.904635 0.102542 0.141379 0.904627 0.126957 0.086207 0.904568 0.097659 0.196552 0.904545 0.097659 0.196552 0.904431 0.136723 0.196552 0.90442 0.117191 0.141379 0.904381 0.117191 0.168966 0.904353 0.136723 0.141379 0.904326 0.156255 0.168966 0.904259 0.13184 0.168966 0.904228 0.151372 0.168966 0.904224 0.063478 0.141379 0.904204 0.112308 0.141379 0.904212 0.126957 0.168966 0.904177 0.151372 0.141379 0.904146 0.151372 0.086207 0.90413 0.151372 0.141379 0.904099 0.078127 0.113793 0.904099 0.126957 0.086207 0.904079 0.146489 0.141379 0.904044 0.112308 0.168966 0.904025 0.092776 0.141379 0.903989 0.073244 0.113793 0.903985 0.092776 0.196552 0.90397 0.112308 0.196552 0.903954 0.097659 0.141379 0.903923 0.170904 0.113793 0.903888 0.112308 0.141379 0.903856 0.097659 0.168966 0.903817 0.13184 0.141379 0.903817 0.102542 0.141379 0.90379 0.073244 0.141379 0.903778 0.13184 0.141379 0.903762 0.073244 0.113793 0.903755 0.136723 0.062069 0.903719 0.175787 0.168966 0.903708 0.1513720.141379 0.903708 0.1123080.168966 0.903657 0.1855530.113793 0.903653 0.1171910.113793 0.903637 0.1367230.168966 0.90361 0.1709040.168966 0.903575 0.1269570.141379 0.903551 0.1025420.141379 0.903532 0.1367230.141379 0.903512 0.1367230.141379 0.903481 0.1513720.141379 0.903473 0.1269570.113793 0.903434 0.1367230.141379 0.903457 0.1171910.168966 0.903473 0.1757870.141379 0.903418 0.1171910.168966 0.903406 0.1562550.086207 0.903383 0.1562550.141379 0.903363 0.1464890.141379 0.903359 0.1367230.141379 0.903328 0.1123080.141379 0.903297 0.131840.141379 0.90325 0.1464890.168966 0.902917 0.1269570.168966 0.902851 0.131840.113793 0.902816 0.1855530.141379 0.902816 0.0732440.141379 0.902792 0.0781270.086207 0.902792 0.1464890.141379 0.902745 0.1660210.168966 0.902675 0.1171910.141379 0.902632 0.1562550.086207 0.902612 0.1367230.113793 0.902612 0.126957;%测试样本,共一百组C=C';C1=C(1,:);C2=C(2,:);C3=C(3,:);D=3.1:.1383:16.8; %测试目标%--------------------------------------------------%归一化[PN1,mina1,maxa1,TN,minb,maxb] = premnmx(A1,B);[PN2,mina2,maxa2,TN,minb,maxb] = premnmx(A2,B);[PN3,mina3,maxa3,TN,minb,maxb] = premnmx(A3,B);PN4 = tramnmx(C1,mina1,maxa1);PN5 = tramnmx(C2,mina2,maxa2);PN6 = tramnmx(C3,mina3,maxa3);TN2 = tramnmx(D,minb,maxb);A=[PN1;PN2;PN3];C=[PN4;PN5;PN6];%---------------------------------------------------% 训练switch 2case 1spread = 0.2;net = newrbe(A,TN,spread);case 2goal =0;spread =0.2;MN = size(A,2);DF = 25;net = newrb(A,TN,goal,spread,MN,DF);case 3spread = 0.2;net = newgrnn(A,TN,spread);end%--------------------------------------------------% 测试YN1 = sim(net,A); % 训练样本实际输出YN2 = sim(net,C); % 测试样本实际输出MSE1 = mean((TN-YN1).^2) % 训练均方误差MSE2 = mean((TN2-YN2).^2) % 测试均方误差%--------------------------------------------------% 反归一化Y2 = postmnmx(YN2,minb,maxb);%--------------------------------------------------% 结果作图plot(1:length(D),D,'r:',1:length(Y2),Y2,'b-');clear; >> xdata=xlsread('2011.xls'); >> x1=xdata(1:12,1:3); >> P1=x1'; >> T1 = [repmat([1;0;0],1,4),repmat([0;1;0],1,4),repmat([0;0;1],1,4)]; >> x2=xdata(13:44,1:3); >> P2=x2'; >> T2 = [repmat([1;0;0],1,9),repmat([0;1;0],1,10),repmat([0;0;1],1,13)]d=t123'; %ÇóתÖÃdp=[0.3 30000 0.001];B = int8(d);sizeofp=size(91);sizeft=size(1);[pn,meanp,stdp,tn,meant,stdt]=prestd(91,1);[ptrans,transMat]=prepca(pn,0.001);iitr1=6:3:1;iitr2=[9:3:1 9:3:1 6:3:1 6:3:1 4:3:1];P1=tranbr(:iitr1)P2=tranbr(:iitr2)。
基于Matlab的RBF神经网络设计与仿真试验

青年与社会 2014年6月上 第16期总第562期人工神经网络(ANN-Artificial Neural Network)是一种与传统计算机系统不同的信息处理工具,具有人脑的某些功能特征,可用来解决模式识别与人工智能中用传统方法难以解决的问题。
神经网络具有高度的自学习、自组织和自适应能力,通过学习和训练网络模型的输入、输出数据就可以获得网络的权值和结构,从而得出隐含在输入、输出数据中的关系。
这种关系隐含在神经网络内部,它不需要知道具体的精确模型,只需用神经网络就能逼近输入和输出之间的多维非线性特性,从而建立输入与输出之间的关系,这种非线性映射能力在人工智能、模式识别、信息处理等工程领域得到了广泛的应用。
随着神经网络理论研究和实际应用的不断深入,《人工神经网络》课程逐渐受到较多高校的重视,并将其列入教学计划,成为电气信息类学科的一门专业选修课。
但《人工神经网络》课程的理论性非常强,对本科生的教学具有一定的难度。
作为入门课程,本科生的教学重点应放对各种网络模型的结构和特点的理解,并结合应用实例,使学生能够获取一些初步设计经验的基础上,掌握有关模型的用法和性能。
因此,笔者以RBF神经网络为例设计仿真试验,通过实例增强学生的对神经网络模型的设计和仿真的认识,加深学生神经网络理论的理解。
一、RBF神经网络RBF网络可以根据问题确定相应的网络拓扑结构,学习速度快,不存在局部最小问题。
RBF网络的优良特性使得它基于Matlab的RBF神经网络设计与仿真试验石 岩(重庆科技学院 电气工程系,重庆 401331)【摘 要】人工神经网络是一门理论性很强而又应用广泛的课程,将神经网络应用于本科毕业设计能促进高校培养出工程应用型人才。
文章利用MATLAB平台将实验仿真教学与理论学习相结合,以RBF神经网络为例设计仿真试验,通过实例增强学生的对神经网络模型的设计和仿真的认识,加深学生神经网络理论的理解和应用设计能力。
【关键词】Matlab;RBF神经网络;仿真试验经济等原因所迫,不得已把子女留于家乡,而自己在外打工。
基于RBF网络的机械手Matlab仿真实验

(2.1)
������2 = ������1������������������������1 + ������2������������������(������1 + ������2)
(2.2)
将(2.1)的平方加上式(2.2)的平方,可得:
������21 + ������22 = ������21+������22 + 2������1������2������������������������2
想的速度和加速度。
定义
������(������) = ������������(������) ‒ ������(������)
(2.8)
������������(������) = ������������(������) + ⋀������(������)
(2.9)
������(������) = ������������(������) ‒ ������(������) = ������(������) + ⋀������(������)
X Cj 2 bi3
bi (k) bi (k 1) bi (bi (k 1) bi (k 2))
cij (k )
(y(k)
ym (k))i
xi cij bi 2
cij (k) cij (k 1) cij (k) (cij (k 1) cij (k 2))
工作空间中机械手的 神经网络自适应控制
学院:自动化信息与工程学院 班级:研 1509 姓名:陈维多 学号:2150321271
工作空间中机械手的神经网络自适应控制
摘要
本设计为一个基于神经网络自适应控制的机械手运动模型的 MATLAB 仿真实 验。以平面二关节机械手为控制对象,以一圆为目标轨迹。先得到机械手的运 动方程的形式,用 RBF 径向基神经网络对方程式中的系统的各个参数进行建模, 利用每个时刻的估计状态和理想状态的误差,通过梯度下降法对网络参数进行 修正,在若干次修正后,神经网络模型所得的状态跟踪到理想状态。
RBF网络的matlab实现

RBF⽹络的matlab实现⼀、⽤⼯具箱实现函数拟合参考:(1)newrb()该函数可以⽤来设计⼀个近似径向基⽹络(approximate RBF)。
调⽤格式为:[net,tr]=newrb(P,T,GOAL,SPREAD,MN,DF)其中P为Q组输⼊向量组成的R*Q位矩阵,T为Q组⽬标分类向量组成的S*Q维矩阵。
GOAL为均⽅误差⽬标(Mean Squard Error Goal),默认为0.0;SPREAD为径向基函数的扩展速度,默认为1;MN为神经元的最⼤数⽬,默认为Q;DF维两次显⽰之间所添加的神经元数⽬,默认为25;ner为返回值,⼀个RBF⽹络,tr为返回值,训练记录。
⽤newrb()创建RBF⽹络是⼀个不断尝试的过程(从程序的运⾏可以看出来),在创建过程中,需要不断增加中间层神经元的和个数,知道⽹络的输出误差满⾜预先设定的值为⽌。
(2)newrbe()该函数⽤于设计⼀个精确径向基⽹络(exact RBF),调⽤格式为:net=newrbe(P,T,SPREAD)其中P为Q组输⼊向量组成的R*Q维矩阵,T为Q组⽬标分类向量组成的S*Q维矩阵;SPREAD为径向基函数的扩展速度,默认为1和newrb()不同的是,newrbe()能够基于设计向量快速,⽆误差地设计⼀个径向基⽹络。
(3)radbas()该函数为径向基传递函数,调⽤格式为A=radbas(N)info=radbas(code)其中N为输⼊(列)向量的S*Q维矩阵,A为函数返回矩阵,与N⼀⼀对应,即N的每个元素通过径向基函数得到A;info=radbas(code)表⽰根据code值的不同返回有关函数的不同信息。
包括derive——返回导函数的名称name——返回函数全称output——返回输⼊范围active——返回可⽤输⼊范围使⽤exact径向基⽹络来实现⾮线性的函数回归:%%清空环境变量clcclear%%产⽣输⼊输出数据%设置步长interval=0.01;%产⽣x1,x2x1=-1.5:interval:1.5;x2=-1.5:interval:1.5;%按照函数先求的响应的函数值,作为⽹络的输出F=20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2);%%⽹络建⽴和训练%⽹络建⽴,输⼊为[x1;x2],输出为F。
基于Matlab的RBF神经网络设计与仿真试验

基于Matlab的RBF神经网络设计与仿真试验作者:石岩来源:《青年与社会》2014年第16期【摘要】人工神经网络是一门理论性很强而又应用广泛的课程,将神经网络应用于本科毕业设计能促进高校培养出工程应用型人才。
文章利用MATLAB平台将实验仿真教学与理论学习相结合,以RBF神经网络为例设计仿真试验,通过实例增强学生的对神经网络模型的设计和仿真的认识,加深学生神经网络理论的理解和应用设计能力。
【关键词】Matlab;RBF神经网络;仿真试验人工神经网络(ANN-Artificial Neural Network)是一种与传统计算机系统不同的信息处理工具,具有人脑的某些功能特征,可用来解决模式识别与人工智能中用传统方法难以解决的问题。
神经网络具有高度的自学习、自组织和自适应能力,通过学习和训练网络模型的输入、输出数据就可以获得网络的权值和结构,从而得出隐含在输入、输出数据中的关系。
这种关系隐含在神经网络内部,它不需要知道具体的精确模型,只需用神经网络就能逼近输入和输出之间的多维非线性特性,从而建立输入与输出之间的关系,这种非线性映射能力在人工智能、模式识别、信息处理等工程领域得到了广泛的应用。
随着神经网络理论研究和实际应用的不断深入,《人工神经网络》课程逐渐受到较多高校的重视,并将其列入教学计划,成为电气信息类学科的一门专业选修课。
但《人工神经网络》课程的理论性非常强,对本科生的教学具有一定的难度。
作为入门课程,本科生的教学重点应放对各种网络模型的结构和特点的理解,并结合应用实例,使学生能够获取一些初步设计经验的基础上,掌握有关模型的用法和性能。
因此,笔者以RBF神经网络为例设计仿真试验,通过实例增强学生的对神经网络模型的设计和仿真的认识,加深学生神经网络理论的理解。
一、RBF神经网络RBF网络可以根据问题确定相应的网络拓扑结构,学习速度快,不存在局部最小问题。
RBF网络的优良特性使得它正显示出比BP网络更强的生命力,正在越来越多的领域替代了BP网络。
基于RBF网络的机械手Matlab仿真实验

工作空间中机械手的神经网络自适应控制学院:自动化信息与工程学院班级:研1509姓名:***学号:**********工作空间中机械手的神经网络自适应控制摘要本设计为一个基于神经网络自适应控制的机械手运动模型的MATLAB仿真实验。
以平面二关节机械手为控制对象,以一圆为目标轨迹。
先得到机械手的运动方程的形式,用RBF径向基神经网络对方程式中的系统的各个参数进行建模,利用每个时刻的估计状态和理想状态的误差,通过梯度下降法对网络参数进行修正,在若干次修正后,神经网络模型所得的状态跟踪到理想状态。
关键词:二关节机械手;神经网络;RBF一、概述1.1研究背景经过几十年的努力,工业机器人(机械手)的控制领域出现了很多成果,控制方法也多种多样,例如最经典成熟的PID控制在一些简单系统中仍然广泛应用,但对于复杂系统显示出了不太好的动态性能;还有计算力矩控制,鲁棒控制等,在调节时间、超调量方面都有非常不错的品质,共性缺点是对机械手数学模型方面的参数有依赖性。
他们都需要一个精确的机械手的数学模型,或系统边界的不确定性是给出的。
然而现实是,机械手在操作过程中伴随着不完整的信息和不精确定义的参数,以及外部因素干扰等,这些控制方法对缺少的传感器信息、未规划的偶然事件的发生非常敏感,这就导致了常规的基于模型的机器人控制方法不能保证系统在实际不可预知环境下的鲁棒性。
为此,有必要采用新的混合控制方法来解决类似问题。
神经网络自适应算法在机械手控制中的应用是非常广泛的,尤其是在机械手实时轨迹跟踪方面,此种算法有很强的自学习特性、并行处理能力、非线性映射能力以及容错性,可以非常好的满足机械手在轨迹跟踪方面要求。
1.2 神经网络特点(1)神经网络可利用少量先验知识,进行自我学习,具备自学习能力。
这种特质对繁复的数学计算来说是一种解放,在涉及到理论计算的控制领域,可发挥其强大的作用。
一般的控制算法需要大量的模型先验信息来设计控制方案,例如需要建立被控对象的数学模型。
基于RBF神经网络的多自由度机械臂控制方法和仿真分析

research and solve related equations. Of course, these traditional methods have certain limitations. At the same time, due to the large amount
of calculation,there will be many difficulties in the process, especially when there are multiple solutions, singularities and other problems, it
is difficult to achieve the desired goal. This article mainly summarizes the latest research findings based on the RBF neural network-based
multi-degree-of-freedom manipulator control method and simulation analysis, in order to provide ideas and methods for the related multi-
Variable Parameter Manipulator [J]. Journal of Physics: Conference
Series, 2020, 1670(1): 012002-012003. [5]刘福才,刘林,郭根旺.柔性关节空间漂浮机械臂奇异摄动
械臂控制的要求。当然自适应控制也存在一定的局限性, 在学习过程中可以根据问题来确定网络的拓扑结构,使
尤其是在结构不稳定或者是结构不确定的情况下,机械臂 网络权系数计算的复杂性得到降低,学习过程得到加速。
RBF神经网络:原理详解和MATLAB实现

RBF神经网络:原理详解和MATLAB实现——2020年2月2日目录RBF神经网络:原理详解和MATLAB实现 (1)一、径向基函数RBF (2)定义(Radial basis function——一种距离) (2)如何理解径向基函数与神经网络? (2)应用 (3)二、RBF神经网络的基本思想(从函数到函数的映射) (3)三、RBF神经网络模型 (3)(一)RBF神经网络神经元结构 (3)(二)高斯核函数 (6)四、基于高斯核的RBF神经网络拓扑结构 (7)五、RBF网络的学习算法 (9)(一)算法需要求解的参数 (9)0.确定输入向量 (9)1.径向基函数的中心(隐含层中心点) (9)2.方差(sigma) (10)3.初始化隐含层至输出层的连接权值 (10)4.初始化宽度向量 (12)(二)计算隐含层第j 个神经元的输出值zj (12)(三)计算输出层神经元的输出 (13)(四)权重参数的迭代计算 (13)六、RBF神经网络算法的MATLAB实现 (14)七、RBF神经网络学习算法的范例 (15)(一)简例 (15)(二)预测汽油辛烷值 (15)八、参考资料 (19)一、径向基函数RBF定义(Radial basis function——一种距离)径向基函数是一个取值仅仅依赖于离原点距离的实值函数,也就是Φ(x)=Φ(‖x‖),或者还可以是到任意一点c的距离,c点称为中心点,也就是Φ(x,c)=Φ(‖x-c‖)。
任意一个满足Φ(x)=Φ(‖x‖)特性的函数Φ都叫做径向基函数。
标准的一般使用欧氏距离(也叫做欧式径向基函数),尽管其他距离函数也是可以的。
在神经网络结构中,可以作为全连接层和ReLU层的主要函数。
如何理解径向基函数与神经网络?一些径向函数代表性的用到近似给定的函数,这种近似可以被解释成一个简单的神经网络。
径向基函数在支持向量机中也被用做核函数。
常见的径向基函数有:高斯函数,二次函数,逆二次函数等。
MATLAB机器人仿真程序

MATLAB机器人仿真程序随着机器人技术的不断发展,机器人仿真技术变得越来越重要。
MATLAB是一款强大的数学计算软件,也被广泛应用于机器人仿真领域。
本文将介绍MATLAB在机器人仿真程序中的应用。
一、MATLAB简介MATLAB是MathWorks公司开发的一款商业数学软件,主要用于算法开发、数据可视化、数据分析以及数值计算等。
MATLAB具有丰富的工具箱,包括信号处理、控制系统、神经网络、图像处理等,可以方便地实现各种复杂的计算和分析。
二、MATLAB机器人仿真程序在机器人仿真领域,MATLAB可以通过Robotics System Toolbox实现各种机器人的仿真。
该工具箱包含了机器人运动学、动力学、控制等方面的函数库,可以方便地实现机器人的建模、控制和可视化。
下面是一个简单的MATLAB机器人仿真程序示例:1、建立机器人模型首先需要定义机器人的几何参数、连杆长度、质量等参数,并使用Robotics System Toolbox中的函数建立机器人的运动学模型。
例如,可以使用robotics.RigidBodyTree函数来建立机器人的刚体模型。
2、机器人运动学仿真在建立机器人模型后,可以使用Robotics System Toolbox中的函数进行机器人的运动学仿真。
例如,可以使用robotics.Kinematics函数计算机器人的位姿,并使用robotics.Plot函数将机器人的运动轨迹可视化。
3、机器人动力学仿真除了运动学仿真外,还可以使用Robotics System Toolbox中的函数进行机器人的动力学仿真。
例如,可以使用robotics.Dynamic函数计算机器人在给定速度下的加速度和力矩,并使用robotics.Plot函数将机器人的运动轨迹可视化。
4、机器人控制仿真可以使用Robotics System Toolbox中的函数进行机器人的控制仿真。
例如,可以使用robotics.Controller函数设计机器人的控制器,并使用robotics.Plot函数将机器人的运动轨迹可视化。
基于MATLAB的六轴工业机械手运动学分析与仿真研究

基于MATLAB的六轴工业机械手运动学分析与仿真研究以六轴工业机械手为研究对象,应用标准的参数法建立机器人各杆件坐标系,并根据坐标系之间的齐次变换关系建立运动学方程,从而得出正解。
该机械手后3个关节为旋转关节,且在腕中心点解耦,故用代数法计算得出逆解。
基于MATLAB Robotics Toolbox工具箱,构建该机械手的三维模型图,依据关节空间、笛卡尔空间的转换关系,应用FKINE、IKINE函数对该机械手进行正、逆运动学问题进行仿真。
仿真结果验证了所开发的正逆运动学算法的正确性且所建模型能快速地进行正逆解求解,有效地获得机器人的关节角、位姿等运动参数,这对于进一步系统研究该六轴工业机器人的轨迹规划提供了数据保障和理论分析依据。
标签:六轴工业机械手MATLAB 运动学机器人工具箱0.引言工业机器人是一种自动的、位置可控的、具有编程能力的多功能、多自由度机械手,可用来搬运、码垛等[1]。
随着“中国制造”向“中国智造”升级,六轴工业机器人逐渐取代产线工人被应用到生产中,解决劳动力短缺和劳动力成本增长问题,尤其是在珠三角制造行业中大规模应用,诸如家电、汽配、电子信息、食品等诸多行业。
但与此同时,为了满足更加复杂的产线作业和更加快速的生产节奏,对其性能指标的要求也越来越高,因此,对机器人的运动学进行深入研究从而提高精度等关键指标,在生产实践中有极其重大的意义[2]。
针对六自由度串联工业机器人,本文分析其运动学正逆解问题,实质是实现关节空间下的关节角和笛卡尔空间下的位姿转换。
在MATLAB Robotics toolbox 中,先用Drivebot()函数构建机器人模型,再应用FKINE、IKINE函数对该机械手进行正、逆运动学问题仿真分析,从而对开发的正逆运动学算法进行仿真验证[3]。
1.运动学模型本文研究的六轴工业机械手,共有6个旋转关节,主要用于搬运和码垛。
参数法是用一系列坐标系来描述一个串联的链式机械臂的方法,具体为用扭角、杆长、偏距和转角这四个参数来唯一确定各相邻杆件的位置和姿态,从而描述此刻机械手的位形[4]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工作空间中机械手的神经网络自适应控制学院:自动化信息与工程学院班级:研1509姓名:陈维多学号:2150321271工作空间中机械手的神经网络自适应控制摘要本设计为一个基于神经网络自适应控制的机械手运动模型的MATLAB仿真实验。
以平面二关节机械手为控制对象,以一圆为目标轨迹。
先得到机械手的运动方程的形式,用RBF径向基神经网络对方程式中的系统的各个参数进行建模,利用每个时刻的估计状态和理想状态的误差,通过梯度下降法对网络参数进行修正,在若干次修正后,神经网络模型所得的状态跟踪到理想状态。
关键词:二关节机械手;神经网络;RBF一、概述1.1研究背景经过几十年的努力,工业机器人(机械手)的控制领域出现了很多成果,控制方法也多种多样,例如最经典成熟的PID控制在一些简单系统中仍然广泛应用,但对于复杂系统显示出了不太好的动态性能;还有计算力矩控制,鲁棒控制等,在调节时间、超调量方面都有非常不错的品质,共性缺点是对机械手数学模型方面的参数有依赖性。
他们都需要一个精确的机械手的数学模型,或系统边界的不确定性是给出的。
然而现实是,机械手在操作过程中伴随着不完整的信息和不精确定义的参数,以及外部因素干扰等,这些控制方法对缺少的传感器信息、未规划的偶然事件的发生非常敏感,这就导致了常规的基于模型的机器人控制方法不能保证系统在实际不可预知环境下的鲁棒性。
为此,有必要采用新的混合控制方法来解决类似问题。
神经网络自适应算法在机械手控制中的应用是非常广泛的,尤其是在机械手实时轨迹跟踪方面,此种算法有很强的自学习特性、并行处理能力、非线性映射能力以及容错性,可以非常好的满足机械手在轨迹跟踪方面要求。
1.2神经网络特点(1)神经网络可利用少量先验知识,进行自我学习,具备自学习能力。
这种特质对繁复的数学计算来说是一种解放,在涉及到理论计算的控制领域,可发挥其强大的作用。
一般的控制算法需要大量的模型先验信息来设计控制方案,例如需要建立被控对象的数学模型。
而利用自学习特性,控制器不需要太多系统的模型和参数信息,因此,神经网络控制可以广泛用于解决具有不确定模型的控制问题。
(2)由于某些单一控制方法对非线性系统束手无策,而神经网络隐含层传递函数的设计形式有很多,可采用非线性函数达到非线性映射功能,所以结合神经网络为解决非线性控制问题提供了有效的途径。
(3)神经网络的分布式结构,以及并行的计算方法使其具有容错性的优点,某些少量的连接错误对整个系统的影响不是很大,甚至没有影响。
1.3RBF径向基神经网络本文用到的算法是径向基函数神经网络(RBFNN)算法。
模式识别技术带动了RBF网络的发展,RBF网络在各个领域正在得到愈来愈广泛的应用,并成为多层前向网络的主要竞争者。
与多层前馈网络(MFN)相比,RBF神经网络具有更好的泛化能力,而且网络结构相对简单,避免了不必要和冗长的计算。
关于RBF网络的研究表明了此种网络能够在一个紧凑集合下,逼近任何非线性函数。
RBFNN是一种三层前向网络。
RBF网络的拓扑结构如下图所示。
图1.1径向基网络图中,,为输出层权向量,y=f(X)为RBF网络的输出,表示隐含层的第i个径向基函数,表达式为2exp i i i X c h ⎛⎫-= -⎪ ⎪⎝⎭(1.1)其中为第i 个隐节点的置信域中心点向量,为置信域的宽度。
在图3-4中,网络的输入层是由实际系统已知的参数组成的。
中间层为隐含层,其神经元个数的确定也是根据实际模型的需要而定。
最后一层是输出层,主要是根据输入量,通过中间层的映射,得出所需要的量。
此网络结构具有这样的特性,即输入空间至隐含层空间的信息传递为非线性的,而隐含层到输出层的传递方式为线性。
RBF 网络是基于BP 神经网络改进二来的,它的指标函数以及权值矫正算法和BP 网络基本一致。
RBF 网络性能指标函数为21(()())2m J y k y k =-(1.2)根据梯度下降法,输出权值、置信域中心点以及置信域宽度的迭代算法如下()(()())j m i k y k y k h ωλ∆=-(1.3)22()(1)()((1)(2))()(()())()(1)((1)(2))()(()())()(1)()((1)(2))i i i i i j i m i i i i i i i i i ijij m i i ij ij ij ij ij k k k k k X C b k y k y k h b k b k b b k b k x c c k y k y k b c k c k c k c k c k ωωωαωωλωαλωα=-+∆+----∆=-=-+∆+----∆=-=-+∆+---(1.4)式中,λ为学习速率,α为动量因子。
RBF 神经网络的工作方式,先给输出权值、置信域中心点以及置信域赋宽度给初值,计算网络输出,判断性能指标函数的值是否符合要求,如不符合,择用上述公式对输出权值、置信域中心点以及置信域宽度进行矫正,在计算下一次的网络输出;若能指标函数的值符合要求,则停止工作。
二、机械手的神经网络建模2.1工作空间直角坐标与关节角位置的转换将工作空间中的关节末端节点直角坐标()转为二关节关节角位置()的问题,即机器人的逆向运动学问题。
根据图2.1可得:图2-1二自由度机械手(2.1)(2.2)将(2.1)的平方加上式(2.2)的平方,可得:+(2.3)从而可以得到:(2.4)取,,则(2.5)2.2被控对象神经网络建模考虑一个刚性n 关节机械手,其动态特性为:(2.6)其中是表示关节变量的向量,是执行机构施加的关节扭矩向量,为对称正定惯性矩阵,为哥氏力和离心力向量,为重力向量。
机械手动态方程具有下面特性:特性1惯性矩阵对称正定;特性2矩阵是斜对称的采用神经网络建模,则机械手在工作空间中的动态方程可写为:()(,)()D q q C q q q G q τ++=(2.7)其中其中,,为矩阵Dx ,Cx ,Gx 中的元素。
写成矩阵形式()[{}{()}]T x D q q =Θ⋅Ξ(,)[{}{()}]T x C q qZ z =A ⋅ ()[{}{()}]T x G q B H q =⋅三、控制器的设计设是在工作空间中的理想轨迹,则和分别是理想的速度和加速度。
定义(2.8)(2.9)(2.10)其中是一个正定矩阵。
根据式(2.7)控制器取:[{}{()}][{}{()}][{}{()}]T T T x r r F q x Z z xB H q Kr =Θ⋅Ξ+A ⋅+⋅+ 如图2-2神经网络控制的过程。
将控制对象初值赋给运动方程,每经过时间t 神经网络模型就会得到一个新的状态。
将该状态和理想状态作比较,按照(2.8)(2.9)(2.10)所示误差模型计算误差,用误差对网路的权值进行矫正,得到新的系统参数Dx ,Cx ,Gx ,再带入神经网络模型,计算下一次的状态。
如此循环,达到控制目的。
图2-2神经网络控制过程四、仿真实例使用平面二关节机械臂模型进行仿真,机械臂动力学方程为()(,)()D q q C q q q G q τ++= (4.1)123223223222cos cos ()cos m m m q m m q D q m m q m +++⎡⎤=⎢⎥+⎣⎦3223122312sin ()sin (,)sin 0.0m q q m q q q C q q m q q --+⎡⎤=⎢⎥⎣⎦41512512cos cos()()cos()m g q m g q q G q m g q q ++⎡⎤=⎢⎥+⎣⎦上式中i m 值由式l M P p L =+给出,有[]12345T M m m m m m =[]12345T P p p p p p =22121212T L l l l l l l ⎡⎤=⎣⎦其中l p 为负载,1l 和2l 分别为关节1和关节2的长度,p 是机器人自身的参数向量。
机械臂实际的参数为[]121.660.420.63 3.75 1.25,1TP l l ===。
为了测试控制器对载荷扰动的抑制能力,在t=4.0时载荷l p 的值从0变道0.5。
在笛卡尔空间中的理想跟踪轨迹取12() 1.00.2cos()() 1.00.2sin()d d x t t x t t ππ=+=+(4.2)该轨迹为一个半径为0.2,圆心在(1.0 1.0)的圆。
初始条件时,机械臂末端的执行器在圆的中心(1.0 1.0)。
由于跟踪轨迹为工作空间中的直角坐标系,而不是关节空间的角位置,应按照第一部分的式子将工作空间中的关节末端直角坐标转()12x x 为二关节空间中关节角的角位置()12q q 。
对应于机械臂动力学方程,雅各比矩阵为1121221211212212sin()sin()sin()()cos()cos()cos()l q l q q l q q J q l q l q q l q q --+-+⎡⎤=⎢⎥+++⎣⎦(4.5)则112122121112122122122122212212cos()cos()cos()()sin()sin()sin()cos()cos()sin()sin()l q l q q l q q J q q l q l q q l q q l q q l q q q l q q l q q --+-+⎡⎤=⎢⎥--+-+⎣⎦-+-+⎡⎤+⎢⎥-+-+⎣⎦ (4.6)控制器取式()(,)()x x x x D q x C q q x G q F ++=,针对Dx ,Cx 和Gx 的每一个元素的逼近,公设计10个RBF 网络。
对Dx 和Gx ,网络输入为q ,分别使用7个隐含层节点的静态RBF 神经网络,而对Cx 中的元素,网络输入为()q q ,分别使用7个隐含层节点的动态RBF神经网络。
所有RBF 网络的隐含层节点的高斯参数中心适量值分别按照输入值的有效范围来取,即针对输入为q 时,取值范围为[0.25,1.75],针对输入为q 的导数时,取值范围为[-1.5,1.5],基宽向量取10。
控制器的增益选为3030K ⎡⎤=⎢⎥⎣⎦,k=0.5,1515⎡⎤Λ=⎢⎥⎣⎦。
仿真结果如图所示:图4-1末关节节点的位置跟踪图4-2末关节节点的速度跟踪图4-3系统参数DCG的2范数如图4-1为末关节节点的位置跟踪,图中红线为理想位置,蓝线为神经网络模型下得到的位置,可以看出,在不到2s的时间内,神经网络模型就很好地跟踪到理想轨迹上;如图4-2为末关节节点的速度跟踪,图中红线为理想速度,蓝线为神经网络模型下得到的速度,同样在不到2s的时间内,神经网络模型就很好地跟踪到理想速度;图4-3为系统参数D、C、G的对比,红色线为由模型(4-1)得到的系统参数,蓝色为由神经网络模型得到的系统参数,网络在经过5s左右时间的矫正,和理想的系统参数基本保持一致。
