高级生物统计万能模板3因素二次回归正交旋转组合设计
三元二次回归旋转组合设计例题

三元二次回归旋转组合设计例题在日常生活中,数据分析与处理是一项重要的技能,尤其在科学研究、产品研发等领域。
为了更好地研究多个变量之间的关系,一种常用的方法就是运用三元二次回归旋转组合设计。
下面,我们就来详细了解一下这种设计方法。
一、三元二次回归旋转组合设计的概念三元二次回归旋转组合设计是一种试验设计方法,它通过对多个变量进行组合,构建出一个旋转矩阵,从而达到降维、简化数据的目的。
在这种设计中,每个变量都有两个水平,可以表示为(-1, 1)。
通过这种设计,我们可以得到较少的试验次数,同时还能保证试验结果的有效性。
二、三元二次回归旋转组合设计的优点1.试验次数较少:与全因子设计相比,三元二次回归旋转组合设计的试验次数较少,可以节省人力、物力和时间成本。
2.保持变量间的相关性:在旋转组合设计中,各个变量之间的相关性得以保持,便于我们研究变量之间的相互作用。
3.易于分析:通过旋转矩阵的构建,可以将多个变量之间的关系简化为少数几个线性关系,便于我们进行后续的数据分析。
三、实例题目解析下面,我们通过一个具体的实例来详细讲解三元二次回归旋转组合设计的应用。
例题:某研究者想要研究三个变量X、Y、Z之间的关系,可以采用三元二次回归旋转组合设计。
设定每个变量的两个水平分别为(-1, 1),构建旋转矩阵。
解:根据三元二次回归旋转组合设计的构建方法,我们可以得到如下的旋转矩阵:X:[1 0 0][0 1 0]Y:[0 1 0][0 0 1]Z:[0 0 1][1 0 0]通过这个旋转矩阵,我们可以将三个变量之间的关系简化为以下形式:X = a0 + a1*Y + a2*ZY = b0 + b1*X + b2*ZZ = c0 + c1*X + c2*Y研究者可以根据这个简化后的模型,进行后续的数据分析,从而研究变量之间的相互关系。
总之,三元二次回归旋转组合设计是一种实用且高效的数据处理方法,通过简化变量关系、降低试验次数,为我们研究多个变量之间的相互作用提供了便利。
二次回归正交旋转组合设计优化大肥蘑菇液体培养基

二次回归正交旋转组合设计优化大肥蘑菇液体培养基杨琴;张桂香;杨建杰;王英利【摘要】为优化大肥蘑菇液体培养基,通过单因子试验确定大肥蘑菇最佳碳源(葡萄糖)、最佳氮源(蛋白胨)及矿物质的适宜浓度(用量)范围,采用二次回归旋转组合设计研究3个参数对大肥蘑菇菌丝生物量的影响,建立数学模型,以获得适宜的配方组合.结果表明,葡萄糖浓度、蛋白胨浓度对大肥蘑菇菌丝体生物量的影响达极显著水平,矿物质添加剂用量达显著水平.最优培养基参数为葡萄糖浓度33.26 g/L、蛋白胨浓度4.24 g/L、矿物质添加剂1.82 mL/L,在该参数组合下,28℃振荡培养8 d,菌丝干重可达16.44 g/L,且经反复试验验证可行.【期刊名称】《甘肃农业科技》【年(卷),期】2017(000)011【总页数】6页(P12-17)【关键词】大肥蘑菇;培养基;二次回归旋转组合;优化【作者】杨琴;张桂香;杨建杰;王英利【作者单位】甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070;甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070;甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070;甘肃省农业科学院蔬菜研究所, 甘肃兰州 730070【正文语种】中文【中图分类】S646.9博斯腾湖位于巴音郭楞蒙古自治州焉耆盆地的博湖县境内,总面积1 228 km2,蓄水量8.0×109m3,是开都河的归宿,孔雀河的源头,更是一座天然的大型调节水库,也是新疆最大的内陆淡水湖。
大肥蘑菇(经ITS序列分析确定[1])是在新疆博斯腾湖特殊环境条件下形成的极为珍贵的野生食用菌,在分类上隶属于担子菌纲(Basidiomycetes)伞菌目(Agaricales)蘑菇科(Agaricaceae)蘑菇属(Agaricua),其子实体硕大、菌肉肥厚细嫩,通过营养成分、氨基酸组成、矿物质、脂肪酸营养成分的测定[2-3],发现大肥蘑菇具有极高的风味物质、营养价值和保健作用。
冬小麦三因子二水平通用旋转组合设计方案
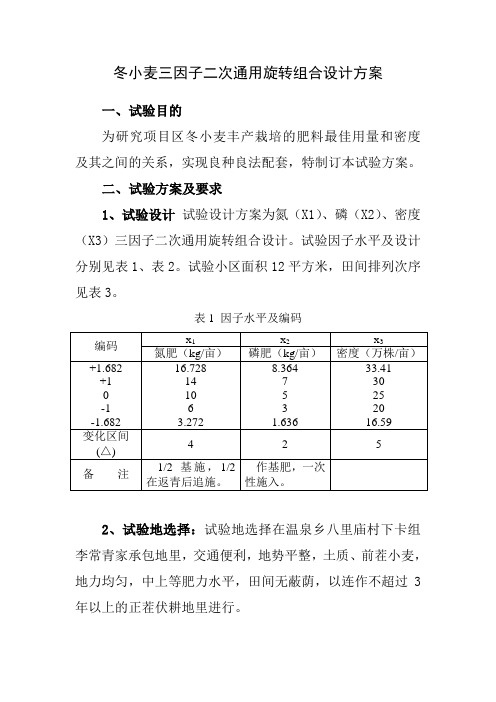
冬小麦三因子二次通用旋转组合设计方案一、试验目的为研究项目区冬小麦丰产栽培的肥料最佳用量和密度及其之间的关系,实现良种良法配套,特制订本试验方案。
二、试验方案及要求1、试验设计试验设计方案为氮(X1)、磷(X2)、密度(X3)三因子二次通用旋转组合设计。
试验因子水平及设计分别见表1、表2。
试验小区面积12平方米,田间排列次序见表3。
表1 因子水平及编码2、试验地选择:试验地选择在温泉乡八里庙村下卡组李常青家承包地里,交通便利,地势平整,土质、前茬小麦,地力均匀,中上等肥力水平,田间无蔽荫,以连作不超过3年以上的正茬伏耕地里进行。
表2 二次通用旋转组合设计表3、施肥及密度:要求亩施优质农家肥5000公斤,化肥施用量和密度严格按照方案要求进行。
化肥必须使用单质肥料,氮肥要求用尿素,磷肥要求用过磷酸钙。
每小区化肥施用量及密度见表3,实物用量按下式计算:尿素(g)=X1÷46%(1/2用于基肥,1/2用于追肥);过磷酸钙(g)= X2÷P2O5%(用于基肥);播量(g)= 千粒重×X3÷1000。
播前要求各承试单位计算出每小区的过磷酸钙和种子实物用量,并填写表4,以便于播种和田间管理时参考。
表3 各小区化肥施用量(g)及密度(株)4、播期及品种:9月中旬适时播种,试验排列方式按各地情况具体确定,尽量减少误差。
小区基肥用量按方案要求,每小区严格称量基施;小区播量根据品种千粒重和各小区处理计算,播种要求人工开沟溜种,行距15cm,每小区按行分种溜播,播深5~6cm,应做到行直下籽均匀,小区地头两端要种到;为减少不同处理之间肥料的相互影响,保护行至少在80cm以上;试验应在同一天完成,播后进行镇耱。
表4 各小区化肥实物用量及种子播量(g)5、田间管理:田间管理应高于当地生产水平,要求及时、准确,同一项田间管理或测定应在同一天内完成,如遇特殊天气,至少同一重复必须在同一天内完成。
二次回归正交组合设计及其统计分析

二次回归正交组合设计及其统计分析一、组合设计(一)组合设计的概念组合设计:在自变量(因素,也称因子)空间中选择几种类型的点,组合成的试验计划。
(P.31)由于组合设计可选择多种类型的点,而且有些类型的点的数目(试验处理数)又可适当调节,因此组合设计在调节试验处理数N(从而在调节剩余自由度)方面,要比全面试验灵活得多。
(二)组合设计的组成二次回归正交组合设计试验方案由三种类型的点组成,即:式中:N为处理组合数;为二水平析因点,(p为因素个数);为轴点,;为中心区(或原点)。
①二水平析因点():这些点的每一个坐标(自变量)都各自分别只取1或-1;这些试验点的数目记为。
当这些点组成二水平全面试验时,。
而若这些点是根据正交表配制的二水平部分实施(1/2或1/4等)的试验点时,。
调节了这个,就相应地调节了剩余自由度。
②轴点():这些点都在坐标轴上,且与坐标原点(中心点)的距离都为。
也就是说,这些点只有一个坐标(自变量)取或,而其余坐标都取零。
这些点在坐标图上通常用星号标出,故又称星号点。
其中称为轴臂或星号臂,是待定参数,可根据下述正交性或旋转性要求而确定。
这些点的数目显然为2P,记为。
③原点():又称中心点,即各自变量都取零水平的点,该试验点可作1次,也可重复多次,其次数记为。
调节,显然也能相应地调节剩余自由度。
(三)试验点(处理)的分布情况1、P=2(二因素)的分布情况(1)处理组合数:若=1,处理组合数为9,即(2)处理组合表2.2.1。
(P.32)(3)处理组合分布图2.2.1。
(P.31)二因素(X1、X2)二次回归组合设计的结构矩阵如表2.2.2。
(P.32)2、P=3(三因素)的分布情况(1)处理组合数:若=1,处理组合数为15,即(2)处理组合表:P=3(X1、X2、X3)二次回归正交组合设计,由15个试验点组成。
如表2.2.3所示。
(P.33)(3)处理组合分布图2.2.2。
(P.32)三因素(X1、X2、X3)二次回归组合设计的结构矩阵如表2.2.4。
三元二次正交回归旋转通用设计

三元二次正交回归旋转通用设计引言:在现代科学与技术领域,研究人员经常需要对大量数据进行分析和处理。
其中,回归分析是一种常用的数据分析方法,用于研究变量之间的关系。
然而,传统的回归分析方法在处理高维数据时存在一些问题,例如维度灾难和多重共线性。
因此,三元二次正交回归旋转通用设计被提出,旨在解决这些问题,提高回归分析的准确性和可解释性。
一、维度灾难与多重共线性的问题在传统的回归分析中,当自变量维度较高时,会出现维度灾难的问题。
维度灾难指的是随着自变量维度的增加,样本空间的体积迅速膨胀,导致所需的样本数量呈指数增长。
这使得回归分析在高维数据中变得困难且不可靠。
多重共线性是指自变量之间存在较高的相关性,这会导致回归分析结果不稳定且难以解释。
在传统的回归模型中,多重共线性会导致回归系数的估计不准确,增加了模型的不确定性。
二、三元二次正交回归旋转通用设计的原理为了解决维度灾难和多重共线性的问题,三元二次正交回归旋转通用设计被提出。
该方法的核心思想是通过正交设计和回归旋转的方式来提高回归分析的效果。
通过正交设计的方法,可以使自变量之间的相关性尽可能小。
正交设计是一种特殊的实验设计方法,它通过合理安排实验因素的水平组合,降低了自变量之间的相关性。
这样一来,回归分析中的多重共线性问题就能够得到缓解,提高了模型的稳定性。
通过回归旋转的方式,可以将高维数据转化为低维数据,从而降低了维度灾难的影响。
回归旋转是一种将原始自变量进行线性或非线性变换的方法,使得新的自变量能够更好地解释因变量的变化。
通过回归旋转,可以使自变量的数量减少,同时保留了原始数据的信息。
三、三元二次正交回归旋转通用设计的应用三元二次正交回归旋转通用设计在实际应用中具有广泛的应用价值。
它可以用于多个领域的数据分析,如经济学、医学、环境科学等。
在经济学中,三元二次正交回归旋转通用设计可以用于预测和解释经济变量之间的关系。
通过分析各种经济指标的数据,可以帮助经济学家预测未来的经济发展趋势,为政策制定者提供决策依据。
二次正交回归试验设计

二次正交回归试验设计二次正交回归试验设计,这个名字听起来挺复杂对吧?感觉像是数学课上的一堆公式堆积在一起,听得人一头雾水。
别急,咱们慢慢聊,搞清楚这玩意儿到底是个啥。
简单来说,二次正交回归试验设计就是一种聪明的实验方法,用来找出那些对结果有最大影响的因素。
你想呀,咱们做实验不就是想知道:到底什么东西能帮我们搞出最好的结果?这就像你做饭,想知道是盐多点好,还是油多点好。
然后,你一开始根本不知道哪个因素最重要,所以你就得试试看,试了几次后,你就能总结出哪几个东西一变,结果就差得远,哪几个因素是关键。
好啦,接下来咱们说说正交回归的“正交”俩字。
它其实很简单,就是把几个因素按特定的组合方式安排,让实验的结果能最有效地帮助你找出最佳的操作方式。
就像打麻将,四个玩家各有不同的牌,正交设计就像把这些牌按特定规则摆开,保证每个人的牌都有机会碰到关键的“胡牌点”,从而找到最合适的做法。
你可能会问:为什么不直接搞个试验,把所有可能的组合都做一遍?那样不就得了嘛!但问题来了,如果你尝试所有的组合,得花多少钱啊!时间也得浪费,精力也得花费。
比如,你要搞个烤面包的实验,试试不同的温度、时间、酵母量,这得试多少次?估计都能烤出一整车的面包来。
正交回归的聪明之处就在于它帮你减少了不必要的试验次数,给你最有效的提示,告诉你哪个因素最关键,哪个因素影响不大,直接省事儿。
那具体咋做呢?我们先选几个可能的影响因素,然后通过一定的设计方式安排它们的组合。
比如说,你在研究做面包时,可能考虑的因素就有面粉的种类、发酵的时间、温度和湿度等等。
然后你就按照正交设计的规律,安排这些因素的组合,反复试几次,你就能得出一个最佳方案,不至于迷失在海量的数据中。
说到这里,大家是不是觉得挺神奇的?对!正交回归就是这么有趣,简洁高效地帮你减少试验次数,节省时间、金钱和脑细胞。
不过,有人可能会说了:“这不就是实验吗?试试、改改,然后结果出来了呗。
”但它更像是一个聪明的助手,总能在你试探的过程中,给你一些深刻的见解。
三元二次正交回归旋转通用设计

三元二次正交回归旋转通用设计在统计学和机器学习领域中,回归分析是一种重要的建模方法,用于探究自变量与因变量之间的关系。
而正交回归是一种特殊的回归方法,它可以解决自变量之间共线性的问题,提高模型的稳定性和可解释性。
本文将介绍三元二次正交回归旋转通用设计方法,以及其在实际应用中的意义和优势。
一、三元二次正交回归在传统的回归分析中,如果自变量之间存在较强的相关性,会导致模型的方差变大,降低模型的预测能力。
而正交回归通过将自变量进行正交化处理,消除它们之间的相关性,从而提高模型的稳定性。
在三元二次正交回归中,通常会将自变量进行二次展开,以更好地捕捉自变量之间的非线性关系。
二、回归旋转回归旋转是一种将原始自变量进行旋转变换的技术,旨在提高模型的解释能力和预测准确性。
通过回归旋转,可以将原始的自变量空间转换为一个新的正交空间,从而使模型更容易解释和理解。
在三元二次正交回归中,回归旋转可以进一步优化模型的设计,提高模型的拟合效果和泛化能力。
三、通用设计三元二次正交回归旋转通用设计是一种灵活而有效的建模方法,适用于各种类型的数据分析和预测问题。
通过将正交回归和回归旋转相结合,可以充分挖掘数据中隐藏的非线性关系,提高模型的拟合效果和预测准确性。
同时,通用设计的特点使得模型具有较强的适应能力,可以应用于不同领域和不同类型的数据集。
四、应用意义三元二次正交回归旋转通用设计在实际应用中具有重要的意义和应用价值。
首先,它可以帮助研究人员更好地理解数据中的复杂关系,揭示隐藏在数据背后的规律和模式。
其次,通过建立高效稳健的模型,可以为决策者提供可靠的决策支持,帮助他们更好地制定策略和规划。
最后,三元二次正交回归旋转通用设计还可以为学术研究和工程实践提供有力的工具和方法,推动科学技术的发展和创新。
三元二次正交回归旋转通用设计是一种强大而灵活的建模方法,具有广泛的应用前景和深远的意义。
通过合理运用这一方法,可以更好地理解和利用数据,为决策和创新提供有力支持,推动社会经济的持续发展。
一次回归正交设计、二次回归正交设计、二次回归旋转设计说明
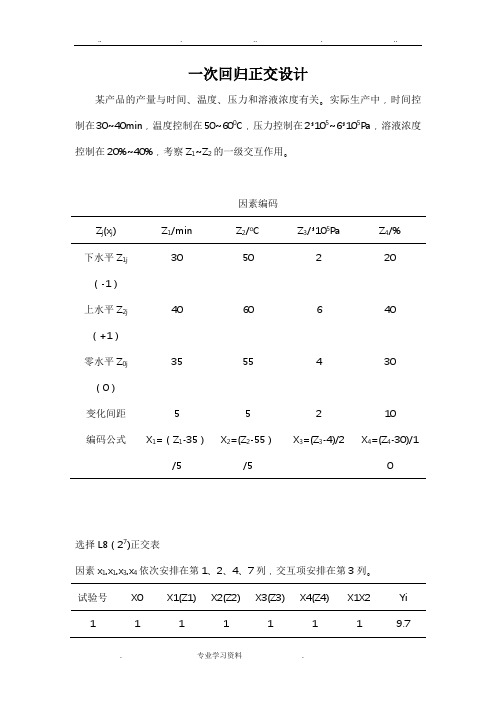
一次回归正交设计某产品的产量与时间、温度、压力和溶液浓度有关。
实际生产中,时间控制在30~40min,温度控制在50~600C,压力控制在2*105~6*105Pa,溶液浓度控制在20%~40%,考察Z1~Z2的一级交互作用。
因素编码Z j(x j) Z1/min Z2/o C Z3/*105Pa Z4/%下水平Z1j(-1)30 50 2 20上水平Z2j(+1)40 60 6 40零水平Z0j(0)35 55 4 30变化间距 5 5 2 10编码公式X1=(Z1-35)/5 X2=(Z2-55)/5X3=(Z3-4)/2 X4=(Z4-30)/1选择L8(27)正交表因素x1,x1,x3,x4依次安排在第1、2、4、7列,交互项安排在第3列。
试验号X0 X1(Z1) X2(Z2) X3(Z3) X4(Z4) X1X2 Yi1 1 1 1 1 1 1 9.72 1 1 1 -1 -1 1 4.63 1 1 -1 1 -1 -1 10.04 1 1 -1 -1 1 -1 11.05 1 -1 1 1 -1 -1 9.06 1 -1 1 -1 1 -1 10.07 1 -1 -1 1 1 1 7.38 1 -1 -1 -1 -1 1 2.49 1 0 0 0 0 0 7.910 1 0 0 0 0 0 8.111 1 0 0 0 0 0 7.4 Bj=∑xjy 87.4 6.6 2.6 8.0 12.0 -16.0aj=∑xj2 11 8 8 8 8 8bj = Bj7.945 0.825 0.325 1.000 1.500 -2.00/aj393 5.445 0.845 8.000 18.000 32.000Qj =Bj2 /aj可建立如下的回归方程。
Y=7.945+0.825x1+0.325x2+x3+1.5x4-2x1x2显著性检验:1、回归系数检验回归关系的方差分析表变异来源SS平方和Df自由度MS均方F显著水平x1 5.4451 5.44576.250.01 x20.84510.84511.830.05 x38.00018.000112.040.01 x4 18.000118.000252.100.01 x1x2 32.000132.000448.180.01 回归64.29 5 12.858180.080.01 剩余0.357 5 0.0714失拟0.097 3 0.0323 0.25 <1 误差e 0.2620.13总和64.64710经F检验不显著的因素或交互作用直接从回归方程中剔掉,不必再重新进行回归分析。
