(完整word版)MATLAB实训实验讲解
matlab实验指导2019-11-12

实验1 熟悉软件环境和基本的操作一、实验目的熟悉MATLAB运行环境和了解基本操作。
二、实验内容MATLAB的启动、操作界面组成1.熟悉MATLAB图形界面打开MATLAB,单击命令窗口菜单栏中的各个下拉菜单按钮,试使用各个按钮引出的选项;把光标移动到工具栏中各个图标上(不要按下),查看它们与菜单选项的对应情况。
2.熟悉MATLAB的基本命令。
在命令窗口中分别键入以下内容,以建立若干变量:A=[1 2;3 4;5 6]B=[7,8,9;10,11,12]C=[5 6 7;1 8 3];D=B+C问题1:如何输入一个矩阵变量的行元素和列元素?问题2:观察每行命令后是否加“;”,对显示执行结果有什么区别?键入以下命令或执行操作,查看效果,并体会命令功能:(1)工作空间管理。
whowhosclear A(2)路径编辑。
试用菜单File/Set Path将D盘根目录及其下的所有子目录和文件夹包含进来,设为搜索路径。
问题3:当前路径是什么?问题4:搜索路径是什么意思?(3)联机帮助help pausehelpwin(4)窗口清理。
先画出正弦函数在0-2π之间的图形,再用以下各种窗口清理命令,看每项命令都清除了什么。
figureplot(sin(0:0.1:6.28))claclfclose注意:figure为打开一幅图形图像窗口close为关闭当前图形图像窗口,而close all为关闭所有已打开的图形图像窗口。
(5)MATLAB基本矩阵操作演示playshow intro(6)MATLAB图形绘制演示playshow buckydem(7)MATLAB数学功能演示(快速傅氏变换)playshow fftdemo(8)MATLAB三维造型演示(茶壶演)playshow teapotdemo3.打开MATLAB命令窗口,键入demos,观看演示程序。
三、思考题1.将pi分别用15位数字格式、分数格式、十六进制格式、5位数字的科学计数法显示。
(完整版)MATLAB)课后实验[1]
![(完整版)MATLAB)课后实验[1]](https://img.taocdn.com/s3/m/88685371e53a580217fcfe63.png)
实验一 MATLAB 运算基础1. 先求以下表达式的值,尔后显示 MATLAB 工作空间的使用情况并保存全部变量。
(1)2sin 85 z1 21 e(2) 12z ln( x 1 x ) ,其中22 x2 1 2i5(3)ae e az sin( a 0.3) ln , a 3.0, 2.9, L , 2.9, 32 22t 0 t 1(4) 2z t 1 1 t 242t 2t 1 2 t 3,其中解:M 文件:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5];z2=1/2*log(x+sqrt(1+x^2))a=-3.0:0.1:3.0;z3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2)t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1)4. 完成以下操作:(1) 求[100,999] 之间能被 21 整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:m=100:999;n=find(mod(m,21)==0);length(n)ans =43(2). 建立一个字符串向量比方:ch='ABC123d4e56Fg9'; 那么要求结果是:ch='ABC123d4e56Fg9';k=find(ch>='A'&ch<='Z');ch(k)=[]ch =123d4e56g9实验二 MATLAB矩阵解析与办理1. 设有分块矩阵 A E R3 3 3 2O S2 3 2 2,其中 E、R、O、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试经过数值计算考据 2A E R RS2O S。
(完整word版)MATLAB实训实验讲解

2015/2016学年下学期《信号与系统》实验报告班级:学号:学生姓名:指导教师:2016年3月8 日实验一 基本函数仿真实验项目: 基本函数仿真实验时间: 2016年 3 月 8 日 星期 二 第 34 节课 实验地点: 1501实验室 实验目的:1、 学习使用MATLAB 软件2、 学习MATLAB 中各种函数,并应用函数分析3、 对MATALB 的进一步的学习了解,熟练掌握MATALB 的各种操纵,学会使用MATALB 解决复杂的运算并学会用MATALB 解决平时学习4、 了解MATALB 的数值运算5、 了解MATALB 的基本函数和命令6、 学习掌握MATALB 有关命令 实验内容: 1、(1) 题目:应用MA TLAB 方法实现单位阶跃信号和矩形脉冲。
(2) 程序清单(源程序)解:对于阶跃函数,MATLAB 中有专门的stairs 绘图命令。
例如,实现)(t 和矩形脉冲的程序如下:t=-1:2; % 定义时间范围向量t x=(t>=0);subplot(1,2,1),stairs(t,x);axis([-1,2,-0.1,1.2]); grid on % 绘制单位阶跃信号波形 t=-1:0.001:1; % 定义时间范围向量t g=(t>=(-1/2))-(t>=(1/2));subplot(1,2,2),stairs(t,g);axis([-1,1,-0.1,1.2]); grid on % 绘制矩形脉冲波形(3) 运行结果(截图)00.20.40.60.8100.20.40.60.81图1 例1图(4)函数解析Subplot:使用方法:subplot (m,n,p )或者subplot (m n p )。
是将多个图画到一个平面上的工具。
其中,m 表示是图排成m 行,n 表示图排成n 列,也就是整个figure 中有n 个图是排成一行的,一共m 行,如果m=2就是表示2行图。
(完整word版)使用matlab绘制眼图.docx

使用 matlab 绘制数字基带信号的眼图实验一、实验目的1、掌握无码间干扰传输的基本条件和原理,掌握基带升余弦滚降系统的实现方法;2、通过观察眼图来分析码间干扰对系统性能的影响,并观察在输入相同码率的NRZ 基带信号下,不同滤波器带宽对输出信号码间干扰大小的影响程度;3、熟悉 MATLAB语言编程。
二、实验原理和电路说明1、基带传输特性基带系统的分析模型如图3-1 所示,要获得良好的基带传输系统,就应该a n t nT s基带传输a n h t nT sn n抽样判决H ( )图 3-1基带系统的分析模型抑制码间干扰。
设输入的基带信号为a n t nT s, T s为基带信号的码元周期,则经过n基带传输系统后的输出码元为a n h t nT s。
其中nh(t )1H ()e j t d(3-1 )2理论上要达到无码间干扰,依照奈奎斯特第一准则,基带传输系统在时域应满足:,k 0h( kT s)(3-2)0,k为其他整数频域应满足:T s,T s(3-3)H ( )0,其他H ( )T sT sT s图 3-2 理想基带传输特性此时频带利用率为2Baud / Hz , 这是在抽样值无失真条件下,所能达到的最高频率利用率。
由于理想的低通滤波器不容易实现,而且时域波形的拖尾衰减太慢,因此在得不到严格定时时,码间干扰就可能较大。
在一般情况下,只要满足:2 i H2 2 ,(3-4)HH ( ) HT s iT sT sT sT s基带信号就可实现无码间干扰传输。
这种滤波器克服了拖尾太慢的问题。
从实际的滤波器的实现来考虑,采用具有升余弦频谱特性H ( ) 时是适宜的。
1 sinT s ( ) , (1 ) (1 )2T sT sT sH ( )1, (1 ) 0(3-5)T s0,(1 )T s这里称为滚降系数,1。
所对应的其冲激响应为:sin tcos( t T s )h(t )T s (3-6)t 1 4 2t 2 T s 2T s此时频带利用率降为 2 / (1 ) Baud/ Hz ,这同样是在抽样值无失真条件下,所能达到的最高频率利用率。
(完整word版)含答案《MATLAB实用教程》

第二章 MATLAB 语言及应用实验项目实验一 MATLAB 数值计算三、实验内容与步骤1.创建矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a(1(2)用(3)用(42.矩阵的运算(1)利用矩阵除法解线性方程组。
⎪⎪⎩⎪⎪⎨⎧=+++=-+-=+++=+-12224732258232432143214321421x x x x x x x x x x x x x x x 将方程表示为AX=B ,计算X=A\B 。
(2)利用矩阵的基本运算求解矩阵方程。
已知矩阵A 和B 满足关系式A -1BA=6A+BA ,计算矩阵B 。
其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=7/10004/10003/1A ,Ps: format rata=[1/3 0 0;0 1/4 0;0 0 1/7];b=inv(a)*inv(inv(a)-eye(3))*6*a(3)计算矩阵的特征值和特征向量。
已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=1104152021X ,计算其特征值和特征向量。
(4)Page:322利用数学函数进行矩阵运算。
已知传递函数G(s)=1/(2s+1),计算幅频特性Lw=-20lg(1)2(2w )和相频特性Fw=-arctan(2w),w 的范围为[0.01,10],按对数均匀分布。
3.多项式的运算(1)多项式的运算。
已知表达式G(x)=(x-4)(x+5)(x 2-6x+9),展开多项式形式,并计算当x 在[0,20]内变化时G(x)的值,计算出G(x)=0的根。
Page 324(2)多项式的拟合与插值。
将多项式G(x)=x 4-5x 3-17x 2+129x-180,当x 在[0,20]多项式的值上下加上随机数的偏差构成y1,对y1进行拟合。
对G(x)和y1分别进行插值,计算在5.5处的值。
Page 325 四、思考练习题1.使用logspace 函数创建0~4π的行向量,有20个元素,查看其元素分布情况。
Ps: logspace(log10(0),log10(4*pi),20) (2) sort(c,2) %顺序排列 3.1多项式1)f(x)=2x 2+3x+5x+8用向量表示该多项式,并计算f(10)值. 2)根据多项式的根[-0.5 -3+4i -3-4i]创建多项式。
MATLAB实验指导书(DOC)

MATLAB实验指导书(DOC)MATLAB实验指导书前⾔MATLAB程序设计语⾔是⼀种⾼性能的、⽤于科学和技术计算的计算机语⾔。
它是⼀种集数学计算、分析、可视化、算法开发与发布等于⼀体的软件平台。
⾃1984年MathWorks公司推出以来,MATLAB以惊⼈的速度应⽤于⾃动化、汽车、电⼦、仪器仪表和通讯等领域与⾏业。
MATLAB有助于我们快速⾼效地解决问题。
MATLAB相关实验课程的学习能加强学⽣对MATLAB程序设计语⾔理解及动⼿能⼒的训练,以便深⼊掌握和领会MATLAB应⽤技术。
⽬录基础型实验............................................................................................ - 1 - 实验⼀MATLAB集成环境使⽤与基本操作命令练习............. - 1 - 实验⼆MATLAB中的数值计算与程序设计 ............................. - 7 - 实验三MATLAB图形系统......................................................... - 9 -基础型实验实验⼀ MATLAB 集成环境使⽤与基本操作命令练习⼀实验⽬的熟悉MATLAB 语⾔编程环境;熟悉MATLAB 语⾔命令⼆实验仪器和设备装有MATLAB7.0以上计算机⼀台三实验原理MATLAB 是以复杂矩阵作为基本编程单元的⼀种程序设计语⾔。
它提供了各种矩阵的运算与操作,并有较强的绘图功能。
1.1基本规则1.1.1 ⼀般MATLAB 命令格式为[输出参数1,输出参数2,……]=(命令名)(输⼊参数1,输⼊参数2,……)输出参数⽤⽅括号,输⼊参数⽤圆括号如果输出参数只有⼀个可不使⽤括号。
1.1.2 %后⾯的任意内容都将被忽略,⽽不作为命令执⾏,⼀般⽤于为代码加注释。
(完整word版)Gauss消去法Matlab

实验一 用列主元Gauss 消去法求解线性方程组实验目的会使用Matlab 语言编程使用列主元Gauss 消去法求解线性方程组.实验原理1、 列主元Gauss 消去法记线性方程组1112111212222212n n n n nn n n a a a x b a a a x b a a a x b ⎛⎫⎛⎫⎛⎫⎪⎪ ⎪ ⎪⎪ ⎪=⎪⎪ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭ 为Ax=b, 其中A =111212122212n n n n nn a a a a a a a a a ⎛⎫ ⎪ ⎪ ⎪⎪⎝⎭,x=12n x x x ⎛⎫⎪ ⎪ ⎪⎪⎝⎭, b=12n b b b ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭, 记其增广矩阵为()(1)(1)(1)1111(1)(1)(1)(1)(1)2122(1)(1)(1)1n nn nnn a a b aa b Ab a a b ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭。
设主元(1)11a 0≠,记(1)11(1)11(2,3,,)i i a l i n a =-=,用1i l 乘增广矩阵()(1)(1)A b 的第1行,再分别与第i 行相加,得()(1)(1)(1)(1)111211(1)(1)(2)(2)(2)2222(2)(2)(2)2b 00n nn nnn a a a a a b Ab a a b ⎛⎫ ⎪⎪= ⎪ ⎪ ⎪⎝⎭, 其中(2)(1)(1)1,ij ij i ij a a l a =+ i ,j=2,3,,n(2)(1)(1)11,i i i b b l b =+ i=2,3,,n又设主元(2)(2)i222i2(2)22a 0,l =-a a≠用乘矩阵()(2)(2)A b 的第二行,再与第i 行相加(i=3,4,,n ),得()(1)(1)(1)(1)(1)1112131n 1(2)(2)(2)(2)22232n 2(3)(3)(3)(3)(3)333n3(3)(3)(3)n3nnn b 0b Ab =0b 00b a a a a a a a a a a a ⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭. 经过n-1步消去后,增广矩阵最终变为()=)()( n n b A实验程序function x=gaussc(A ,b ) [n,m ]=size(A); A=[A ,b]; for k=1:n —1for p=k+1:nif abs(A (p ,k))>abs(A(k ,k )) for j=k :n+1 t=A(k,j );A (k,j)=A(p,j ); A(p,j)=t; end endend %搜索主元并交换 for i=k+1:nl=-A(i ,k )/A(k,k); for j=k+1:n+1A (i,j )=A(i ,j )+l*A(k,j); end endend %消去过程结束 x(n)=A (n,n+1)/A (n ,n); for i=n —1:-1:1 s=0;for j=i+1:ns=s+A (i,j)*x(j ); endx (i)=(A (i,n+1)-s )/A (i,i); end实验结果设A=[2,5;4,6],b=[3;4],求解线形方程组Ax=b.实验步骤:1) 先在matlab 里输入上面的程序;2) 然后输入A=[2,5;4,6] b=[3;4]3)再输入x=gaussc(A,b)命令即得出结果.由以上程序可求解得到x=( 0.2500 0。
(完整word)用matlab分析曲柄摇杆机构

机械原理第一次作业(matlab7。
0):求:r1旋转360°时,θ2,θ3,ω2,ω3,α2,α3和C点的加速度。
设r1=400,r2=1000,r3=700,r4=12001、角位移的M函数:function y=jweiyi(x)% Input parameters% x(1)=theta—1% x(2)=theta—2 guess value% x(3)=theta-3 guess value% x(4)=r1% x(5)=r2% x(6)=r3% x(7)=r4% Output parameters% y(1)=theta-2% y(2)=theta—3theta2=x(2);theta3=x(3);%epsilon=1.0E—6;%f=[x(4)*cos(x(1))+x(5)*cos(theta2)—x(7)—x(6)*cos(theta3);x(4)*sin(x(1))+x(5)*sin(theta2)—x(6)*sin(theta3)];%while norm(f)〉epsilonJ=[—x(5)*sin(theta2) x(6)*sin(theta3);x(5)*cos(theta2) —x(6)*cos(theta3)]; dth=inv(J)*(-1.0*f);theta2=theta2+dth(1);theta3=theta3+dth(2);f=[x(4)*cos(x(1))+x(5)*cos(theta2)-x(7)—x(6)*cos(theta3);x(4)*sin(x(1))+x(5)*sin(theta2)—x(6)*sin(theta3)];norm(f);end;y(1)=theta2;y(2)=theta3;r1旋转360°时,θ2,θ3的M文件程序:r(1)=400;r(2)=1000;r(3)=700;r(4)=1200;dr=pi/180;th(1)=0;th(2)=44。
(完整word版)Matlab数学实验报告

Matlab 数学实验报告一、实验目的通过以下四组实验,熟悉MATLAB的编程技巧,学会运用MATLAB的一些主要功能、命令,通过建立数学模型解决理论或实际问题。
了解诸如分岔、混沌等概念、学会建立Malthu模型和Logistic 模型、懂得最小二乘法、线性规划等基本思想。
二、实验内容2.1实验题目一2.1.1实验问题Feigenbaum曾对超越函数y=λsin(πx)(λ为非负实数)进行了分岔与混沌的研究,试进行迭代格式x k+1=λsin(πx k),做出相应的Feigenbaum图2.1.2程序设计clear;clf;axis([0,4,0,4]);hold onfor r=0:0.3:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.5)for i=101:150plot(r,x(i),'k.');endtext(r-0.1,max(x(101:150))+0.05,['\it{r}=',num2str(r)]) end加密迭代后clear;clf;axis([0,4,0,4]);hold onfor r=0:0.005:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.1)for i=101:150plot(r,x(i),'k.');endend运行后得到Feigenbaum图2.2实验题目二2.2.1实验问题某农夫有一个半径10米的圆形牛栏,长满了草。
他要将一头牛拴在牛栏边界的桩栏上,但只让牛吃到一半草,问拴牛鼻子的绳子应为多长?2.2.2问题分析如图所示,E为圆ABD的圆心,AB为拴牛的绳子,圆ABD为草场,区域ABCD为牛能到达的区域。
问题要求区域ABCD等于圆ABC的一半,可以设BC等于x,只要求出∠a和∠b就能求出所求面积。
(word完整版)高斯白噪声的matlab实现

通信系统建模与仿真实验一、高斯白噪声的matlab 实现要求:样本点:100 1000标准差:0.2 2 10均值: 0 0.2白噪声如果噪声的功率谱密度在所有的频率上均为一常数,即)/(),(,)(0Hz W f n f P n +∞<<-∞=式中:0n 为常数,责成该噪声为白噪声,用)(t n 表示。
高斯白噪声的matlab实现1.样本点为1000、均值为0、标准差为0.2时,高斯白噪声分布为下图所示:程序如下所示:% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (0.2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i));endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft));plot(ti,realx2)程序如下所示:% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示:% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (10) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示:% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (0.2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示:% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示:% White background noisclear allf = 1:1:1000;for i = 1:length(f)K = (10) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示:% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (0.2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示:% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (2) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示:% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (10) * randn(1,1) - 0;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示:% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (0.2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示:% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (2) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)程序如下所示:% White background noisclear allf = 1:1:100;for i = 1:length(f)K = (10) * randn(1,1) - 10;P(i) = 10.^(K - 3.95*(10^-5)*f(i));A(i) = sqrt(2*P(i)); endxifft = ifft(A);realx = real(xifft);ti = [1:length(xifft)-1]/1000;realx2(1:length(xifft)-1) = realx(2:length(xifft)); plot(ti,realx2)。
(完整word版)Matlab解决电路问题

如下图所示的电桥电路, 其中I1是16V 的电压源, I2是1A 的电流源,R1为8 , 电桥的四个臂分别为R2, R3, R4, R5电阻值如图所示, 求流过R4的电流I 的大小?解法一: 利用戴维南定理进行求解:解题思路:将A.B 两点断开, 求A.B 两点之间的等效电阻与等效电压, 等效之后的图形 如下图所示:I=? ABAB其中R6是等效电阻, I3是等效电压。
①求解等效电阻:求解等效电阻时把所有的电流源开路, 电压源短路, 得到如下所示的电路:AB则AB两端的电阻值即等效电阻R6=(R2+R3)//R1+R5②求解等效电压可以利用叠加法求解AB 两端的电压值, 先不看电压源(即电压源相当于短路), 计算电流源对AB 两端的电压值, 再不看电流源(即电流源相当于断路), 再计算AB 两端的电压值, 然后将俩种情况下的电压值叠加即得到AB 两端的等效电压。
不看电压源的电路图如下:则UCB+I2*R5+I2*(R1+R2)//R3=0 可以得到:UCB =-[I2*R5+I2*(R1+R2)//R3]U AB1 =-I2*R5-I2*3213)21(R R R R R R ++•++I2*R2*3213R R R R ++不看电流源的电路图如下:ABC很容易的知道AB 两端的电压值为:U AB2=321)32(*1R R R R R I +++所以UAB=UAB1+UAB2则经过戴维南等效之后的电路图如下:可以很简单的求解出II=64R R U AB+ABMatlab求解程序如下:(程序代码如下)R1=8;R2=4;R3=20;R4=3;R5=3;I1=16;I2=1;R6=R5+(R2+R3)*R1/(R1+R2+R3);UAB1=-I2*R5-I2*(R1+R2)*R3/(R1+R2+R3)+I2*R2*R3/(R1+R2+R3); UAB2=I1*(R2+R3)/(R1+R2+R3);UAB=UAB1+UAB2;I=UAB/(R4+R6);解法二: 运用叠加定理直接求解①先考虑电压源对AB两点的电流影响, 此时不看电流源, 电流源相当于断路, 电路图如下:根据电路图, 容易知道: AB 之间的电流I1 为I 1=543232)54//()32(11R R R R R R R R R R R I ++++•+++②再考虑电流源对AB 端电流源的影响, 此时不看电压源, 即将电压源短路, 电路图如下所示:根据电路图, 分析容易知道: 可以根据三角形与Y 形电路之间的转换, 将三角形电阻ACD 转换为Y 形电阻, 公式为:ABI 1BCD形电阻之和相邻电阻的乘积形电阻∆∆Y转换之后的电路图如下:可以得到:R12=32121R R R R R ++•R13=32131R R R R R ++•由于是电流源, 电流一定, 可以忽略与电流源串联的电阻R23 所以I 2=-I2*541312513R R R R R R ++++综上知道:I=I 1+I 2Matlab 求解程序如下: (程序代码如下) R1=8 R2=4;I 2R3=20; R4=3; R5=3; I1=16; I2=1;i1=[(R2+R3)/(R2+R3+R4+R5)]*I1/[R1+(R2+R3)*(R4+R5)/(R2+R3+R4+R5)];R12=R1*R2/(R1+R2+R3); R13=R1*R3/(R1+R2+R3);i2=-I2*(R13+R5)/(R12+R13+R4+R5); I=i1+i2解法三: 利用回路电流法进行求解 实验电路图如下:将无伴电流源的支路作为一个回路电流, 可以有电路图结合回路电i1i2流法列出如下方程:i1=I2I*(R2+R3+R4+R5)+i1*(R3+R5)-i2*(R2+R3)=0 -I*(R2+R3)-i1*R3+i2*(R1+R2+R3)=I1解方程可以很容易解的I 的值。
matlab实验指导答案详解(非常详细正确)

实验一MATLAB 工作环境熟悉及简单命令的执行一、实验目的:熟悉MATLAB 的工作环境,学会使用MATLAB 进行一些简单的运算。
二、实验内容:MATLAB 的启动和退出,熟悉MATLAB 的桌面(Desktop ),包括菜单(Menu )、工具条(Toolbar )、命令窗口(Command Window)、历史命令窗口、工作空间(Workspace)等;完成一些基本的矩阵操作;学习使用在线帮助系统。
三、实验步骤:1、启动MATLAB ,熟悉MATLAB 的桌面。
2、在命令窗口执行命令完成以下运算,观察workspace 的变化,记录运算结果。
(1)(365-52⨯2-70)÷3 >>(365-52*2-70)/3 ans = 63.6667(2)>>area=pi*2.5^2 area = 19.6350(3)已知x=3,y=4,在MATLAB 中求z :()232y x y x z -= >>x=3 >>y=4>>z = x ^2 * y ^3 / (x - y) ^2 z = 576(4)将下面的矩阵赋值给变量m1,在workspace 中察看m1在内存中占用的字节数。
m1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11514412679810115133216 执行以下命令>>m1 =[16 2 3 13 ; 5 11 10 8 ; 9 7 6 12 ; 4 14 15 1 ] >>m1( 2 , 3 ) ans = 10 >>m1( 11 ) ans = 6>>m1( : , 3 ) ans =3 10 6 15>>m1( 2 : 3 , 1 : 3 ) ans =5 11 10 9 7 6>>m1( 1 ,4 ) + m1( 2 ,3 ) + m1( 3 ,2 ) + m1( 4 ,1) ans = 34(5)执行命令>>help abs查看函数abs 的用法及用途,计算abs( 3 + 4i ) (6)执行命令>>x=0:0.1:6*pi; >>y=5*sin(x); >>plot(x,y)(6)运行MATLAB 的演示程序,>>demo ,以便对MATLAB 有一个总体了解。
MATLAB实训实验讲解

2015/2016学年下学期《信号与系统》实验报告班级:学号:学生姓名:指导教师:2016年3月8 日实验一 基本函数仿真实验项目: 基本函数仿真实验时间: 2016年 3 月 8 日 星期 二 第 34 节课 实验地点: 1501实验室 实验目的:1、 学习使用MATLAB 软件2、 学习MATLAB 中各种函数,并应用函数分析3、 对MATALB 的进一步的学习了解,熟练掌握MATALB 的各种操纵,学会使用MATALB 解决复杂的运算并学会用MATALB 解决平时学习中的实际问题 。
4、 了解MATALB 的数值运算 5、 了解MATALB 的基本函数和命令 6、 学习掌握MATALB 有关命令 实验内容: 1、(1) 题目:应用MA TLAB 方法实现单位阶跃信号和矩形脉冲。
(2) 程序清单(源程序)解:对于阶跃函数,MATLAB 中有专门的stairs 绘图命令。
例如,实现)(t 和矩形脉冲的程序如下:t=-1:2; % 定义时间范围向量t x=(t>=0);subplot(1,2,1),stairs(t,x);axis([-1,2,-0.1,1.2]); grid on % 绘制单位阶跃信号波形 t=-1:0.001:1; % 定义时间范围向量t g=(t>=(-1/2))-(t>=(1/2));subplot(1,2,2),stairs(t,g);axis([-1,1,-0.1,1.2]); grid on % 绘制矩形脉冲波形(3) 运行结果(截图)-11200.20.40.60.81-1-0.50.5100.20.40.60.81图1 例1图(4)函数解析Subplot:使用方法:subplot (m,n,p )或者subplot (m n p )。
是将多个图画到一个平面上的工具。
其中,m 表示是图排成m 行,n 表示图排成n 列,也就是整个figure 中有n 个图是排成一行的,一共m 行,如果m=2就是表示2行图。
(完整word)Matlab实验报告
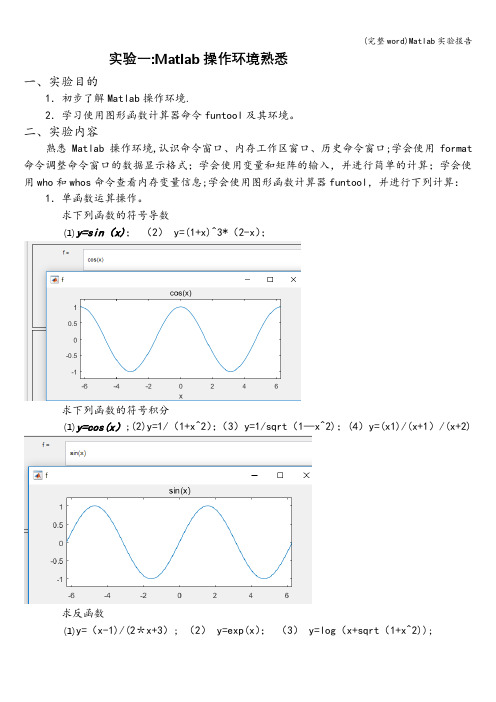
实验一:Matlab操作环境熟悉一、实验目的1.初步了解Matlab操作环境.2.学习使用图形函数计算器命令funtool及其环境。
二、实验内容熟悉Matlab操作环境,认识命令窗口、内存工作区窗口、历史命令窗口;学会使用format 命令调整命令窗口的数据显示格式;学会使用变量和矩阵的输入,并进行简单的计算;学会使用who和whos命令查看内存变量信息;学会使用图形函数计算器funtool,并进行下列计算:1.单函数运算操作。
求下列函数的符号导数(1)y=sin(x);(2) y=(1+x)^3*(2-x);求下列函数的符号积分(1)y=cos(x);(2)y=1/(1+x^2);(3)y=1/sqrt(1—x^2);(4)y=(x1)/(x+1)/(x+2)求反函数(1)y=(x-1)/(2*x+3); (2) y=exp(x);(3) y=log(x+sqrt(1+x^2));代数式的化简(1)(x+1)*(x-1)*(x-2)/(x-3)/(x—4);(2)sin(x)^2+cos(x)^2;(3)x+sin(x)+2*x—3*cos(x)+4*x*sin(x);2.函数与参数的运算操作。
从y=x^2通过参数的选择去观察下列函数的图形变化(1)y1=(x+1)^2(2)y2=(x+2)^2(3) y3=2*x^2 (4) y4=x^2+2 (5) y5=x^4 (6) y6=x^2/2 3.两个函数之间的操作求和(1)sin(x)+cos(x) (2) 1+x+x^2+x^3+x^4+x^5乘积(1)exp(—x)*sin(x) (2) sin(x)*x商(1)sin(x)/cos(x); (2) x/(1+x^2); (3) 1/(x—1)/(x—2); 求复合函数(1)y=exp(u) u=sin(x) (2) y=sqrt(u) u=1+exp(x^2)(3) y=sin(u) u=asin(x) (4) y=sinh(u) u=-x实验二:MATLAB基本操作与用法一、实验目的1.掌握用MATLAB命令窗口进行简单数学运算。
MATLAB实验报告(word文档良心出品)

《MATLAB/Simulink与控制系统仿真》实验报告专业:班级:学号:姓名:指导教师:实验1、MATLAB/Simulink 仿真基础及控制系统模型的建立一、实验目的1、掌握MATLAB/Simulink 仿真的基本知识;2、熟练应用MATLAB 软件建立控制系统模型。
二、实验设备电脑一台;MATLAB 仿真软件一个 三、实验内容1、熟悉MATLAB/Smulink 仿真软件。
2、一个单位负反馈二阶系统,其开环传递函数为210()3G s s s=+。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MATLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
图 1系统结构图图 2示波器输出结果图3、某控制系统的传递函数为()()()1()Y s G s X s G s =+,其中250()23s G s s s+=+。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MA TLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
图 3系统结构图 图 4 示波器输出结果图图 5 工作空间中仿真结果图形化输出4、一闭环系统结构如图所示,其中系统前向通道的传递函数为320.520()0.11220s G s s s s s+=+++g ,而且前向通道有一个[-0.2,0.5]的限幅环节,图中用N 表示,反馈通道的增益为1.5,系统为负反馈,阶跃输入经1.5倍的增益作用到系统。
用Simulink 建立该控制系统模型,用示波器观察模型的阶跃响应曲线,并将阶跃响应曲线导入到MATLAB 的工作空间中,在命令窗口绘制该模型的阶跃响应曲线。
图 6 系统结构图图 7 示波器输出结果实验2 MATLAB/Simulink 在控制系统建模中的应用一、实验目的1、掌握MATLAB/Simulink 在控制系统建模中的应用; 二、实验设备电脑一台;MA TLAB 仿真软件一个 三、实验内容1、给定RLC 网络如图所示。
MATLAB实验讲义

MATLAB实验讲义目录实验大纲 (2)实验一/二 MATLAB的基础操作 (3)实验三 MATLAB运算基础(一) (3)实验四 MATLAB运算基础(二) (4)实验五循环结构程序设计(一) (5)实验六循环结构程序设计(二) (5)实验七 MATLAB的绘图操作(一) (6)实验八 MATLAB的绘图操作(二) (7)实验九函数和文件(一) (7)实验十函数和文件(二) (7)实验十一线性代数中的数值计算问题 (8)实验十二 MATLAB函数库的运用(一) (9)实验十三 MATLAB函数库的运用(二) (10)《MATLAB》课程实验教学大纲课程名称:MATLAB(MATLAB)课程编号:16072327课程性质:选修实验总学时:27实验室名称:电子设计自动化一、课程简介:本课程是电气工程及其自动化、自动化、电力工程与管理专业本科生的学科基础选修课,它在线性代数、信号分析和处理、控制系统设计和仿真等方面有着广泛的应用。
主要是学习MATLAB的语法规则、基本命令和使用环境,使学生掌握MATLAB的基本命令和基本程序设计方法,提高使用该语言的应用能力,具有使用MATLAB语言编程和调试的能力,以便为后续多门课程使用该语言奠定必要的基础。
二、课程实验目的与要求:1.基本掌握MATLAB在线帮助功能的使用、熟悉MATLAB运行环境和MATLAB语言的主要特点,掌握MATLAB语言的基本语法规则及基本操作命令的使用,学会M文件的建立和使用方法以及应用MATLAB实现二维和三维图形的绘制方法,具有使用MATLAB语言编程和调试的能力。
2.初步掌握MATLAB在电路和信号与系统中的应用。
3.能根据需要选学参考书,查阅手册,通过独立思考,深入钻研有关问题,学会自己独立分析问题、解决问题,具有一定的创新能力。
三、主要仪器设备及台(套)数:计算机50台、MATLAB软件五、主要参考书目:1.《MATLAB及在电子信息课程中的应用》陈怀琛、杨吉斌编著,电子工业出版社,2002年1版2.《MATLAB7.0编程基础》王家文、王皓、刘海等;机械工业出版社,2005年7月3.《MATLAB教程——基于6.x版本》张志涌、徐彦琴等;北京航空航天大学出版,2001年4月出版实验一/二 MATLAB的基础操作一、实验目的1、掌握MATLAB的启动和退出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015/2016学年下学期《信号与系统》实验报告班级:学号:学生姓名:指导教师:2016年3月8 日实验一 基本函数仿真实验项目: 基本函数仿真实验时间: 2016年 3 月 8 日 星期 二 第 34 节课 实验地点: 1501实验室 实验目的:1、 学习使用MATLAB 软件2、 学习MATLAB 中各种函数,并应用函数分析3、 对MATALB 的进一步的学习了解,熟练掌握MATALB 的各种操纵,学会使用MATALB 解决复杂的运算并学会用MATALB 解决平时学习4、 了解MATALB 的数值运算5、 了解MATALB 的基本函数和命令6、 学习掌握MATALB 有关命令 实验内容: 1、(1) 题目:应用MA TLAB 方法实现单位阶跃信号和矩形脉冲。
(2) 程序清单(源程序)解:对于阶跃函数,MATLAB 中有专门的stairs 绘图命令。
例如,实现)(t 和矩形脉冲的程序如下:t=-1:2; % 定义时间范围向量t x=(t>=0);subplot(1,2,1),stairs(t,x);axis([-1,2,-0.1,1.2]); grid on % 绘制单位阶跃信号波形 t=-1:0.001:1; % 定义时间范围向量t g=(t>=(-1/2))-(t>=(1/2));subplot(1,2,2),stairs(t,g);axis([-1,1,-0.1,1.2]); grid on % 绘制矩形脉冲波形(3) 运行结果(截图)00.20.40.60.8100.20.40.60.81图1 例1图(4)函数解析Subplot:使用方法:subplot (m,n,p )或者subplot (m n p )。
是将多个图画到一个平面上的工具。
其中,m 表示是图排成m 行,n 表示图排成n 列,也就是整个figure 中有n 个图是排成一行的,一共m 行,如果m=2就是表示2行图。
p 表示图所在的位置,p=1表示从左到右从上到下的第一个位置。
Stairs: stairs 函数用于绘制阶梯状图 axis 函数通常在绘图中用于设置坐标值范围2、(1)题目例2 应用MA TLAB 方法生成信号)(sin )(t c t f =和)()(t S t f a =的波形。
(2)程序清单解:为生成函数ttt c ππsin )(sin =可直接调用MA TLAB 中的专门命令,程序如下:t=-5:0.01:5; % 定义时间范围向量t f=sinc(t); % 计算Sa(t)函数 plot(t,f); grid on % 绘制Sa(t)的波形(3)运行结果-0.4-0.20.20.40.60.81图2 例2程序运行结果一)(t S a 和)(sin t c 的关系如下:)(sin )sin()sin(sin )()(t c t t t tttt S t f a '=''====ππππππ生成信号)()(t S t f a =波形的MA TLAB 程序如下:t=-3*pi:0.01*pi:3*pi; % 定义时间范围向量t f=sinc(t/pi); % 计算Sa(t)函数 plot(t,f); grid on % 绘制Sa(t)的波形(3)运行结果图3 例2程序运行结果二(4)函数解析Plot :函数命令 plot 是 MA TLAB 二维曲线绘图中最简单、最重要、使用最广泛的一个线性绘图函数。
它可以生成线段、曲线和参数方程曲线的函数图形。
grid on 是matlab 中的一种函数,表示在画图的时候添加网格线3、(1)题目应用MA TLAB方法生成相加信号t t t f ππ20cos 18cos )(+=和相乘信号)20cos()(sin )(t t c t f π⋅=的波形。
(课本上没有) (2)程序清单解:对相加信号t t t f ππ20cos 18cos )(+=,程序如下:syms t; % 定义符号变量tf=cos(18*pi*t)+cos(20*pi*t); % 计算符号函数f(t)=cos(18*pi*t)+cos(20*pi*t) ezplot(f,[0 pi]); grid on % 绘制f(t)的波形(3)运行结果图4 例3程序运行结果一对相乘信号)20cos()(sin )(t t c t f π⋅=,程序如下:t=-5:0.01:5; % 定义时间范围向量f=sinc(t).*cos(20*pi*t); % 计算函数f(t)=sinc(t)*cos(20*pi*t) plot(t,f); % 绘制f(t)的波形 title('sinc(t)*cos(20*pi*t)'); grid on % 加注波形标题运行结果如图5所示。
图5 例3程序运行结果二(4)函数解析syms 函数用于创建符号对象ezplot 即:Easy to use function plotter 。
它是一个易用的一元函数绘图函数 。
特别是在绘制含有符号变量的函数的图像时,ezplot 要比plot 更方便。
因为plot 绘制图形时要指定自变量的范围,而ezplot 无需数据准备,直接绘出图形。
4、(1)题目应用MA TLAB 方法生成调制信号t t f ππ50cos )4sin 22()(⋅+=的波形。
(2)程序清单解:对调制信号t t f ππ50cos )4sin 22()(⋅+=,程序如下:syms t; % 定义符号变量tf=(2+2*sin(4*pi*t))*cos(50*pi*t); % 计算符号函数f(t)=(2+2*sin(4*pi*t))*cos(50*pi*t) ezplot(f,[0 pi]); grid on % 绘制f(t)的波形(3)运行结果如图6所示。
图6 例4图(4)函数解析grid on 是matlab 中的一种函数,表示在画图的时候添加网格线实验二 连续系统时域响应仿真实验项目: 连续系统时域响应仿真实验时间: 2016年 3 月 22 日 星期 二 第 34 节课 实验地点: 1501实验室 实验目的:1、 对MATALB 的进一步的学习了解,熟练掌握MATALB 的各种操纵,学会使用MATALB 解决复杂的运算并学会用MATALB 解决平时学习中的实际问题。
2、 了解MATALB 的数值运算3、 了解MATALB 的基本函数和命令4、 学习掌握MATALB 有关命令 实验内容:任务1(1) 题目例5设方程 )(2)(6)(5)(t e t y t y t y tε-=+'+'',试求零状态响应)(t y 。
(2) 程序清单(源程序) 解:程序如下:yzs=dsolve('D2y+5*Dy+6*y=2*exp(-t)','y(0)=0,Dy(0)=0') % 利用dslove 命令求解零状态响应 ezplot(yzs,[0 8]); grid on % 绘制零状态响应曲线运行结果:yzs =exp(-t)+exp(-3*t)-2*exp(-2*t)即:)()2()(32t e e e t y t t t ε---+-=(3)运行结果(截图图7 例5图(4)函数解析solve(f,v):求方程关于指定自变量的解,f 可以是用字符串表示的方程、符号表达式或符号方程 dsolve:微分方程任务2(1) 题目 已知二阶系统方程)(1)(1)()(t LCt u LC t u L R t u c c cδ=+'+''对下列情况分别求)(t h ,并画出其波形。
(课本上没有)a. F C H L R 3/1,1,4==Ω=b. F C H L R 1,1,2==Ω=c. F C H L R 1,1,1==Ω=d. F C H L R 1,1,0==Ω= (2)程序清单 解:程序如下:R=input('电阻R='); % 以交互方式输入电阻R 的值 L=input('电感L='); % 以交互方式输入电阻L 的值 C=input('电容C='); % 以交互方式输入电阻C 的值 b=[1/(L*C)]; a=[1 R/L 1/(L*C)];impulse(b,a); % 绘制脉冲响应h(t)的波形(3)运行结果(截图)a. 电阻R=4 电感L=1 电容C=1/3图8 例6程序运行结果一b. 电阻R=2 电感L=1 电容C=1图9 例6程序运行结果二c. 电阻R=1 电感L=1 电容C=1图10 例6程序运行结果三d. 电阻R=0 电感L=1 电容C=1图11 例6程序运行结果四(4)函数解析(例如题1-2中,解释sinc ()函数的作用)7、(1)题目 实现卷积)(*)(t h t f ,其中:)2()()()],1()([2)(--=--=t t t h t t t f εεεε。
(课本上没有)(2)程序清单 解:主程序如下:p=0.01; % 取样时间间隔 nf=0:p:1; % f(t)对应的时间向量 f=2*((nf>=0)-(nf>=1)); % 序列f(n)的值 nh=0:p:2; % h(t)对应的时间向量 h=(nh>=0)-(nh>=2); % 序列h(n)的值 [y,k]=sconv(f,h,nf,nh,p); % 计算y(t)=f(t)*h(t) subplot(3,1,1),stairs(nf,f); grid on % 绘制f(t)的波形 title('f(t)');axis([0 3 0 2.1]);subplot(3,1,2),stairs(nh,h); grid on % 绘制h(t)的波形 title('h(t)');axis([0 3 0 2.1]);subplot(3,1,3),plot(k,y); grid on % 绘制y(t)=f(t)*h(t)的波形 title('y(t)=f(t)*h(t)');axis([0 3 0 2.1]);子程序sconv 如下:% 此函数用于计算连续信号的卷积y(t)=f(t)*h(t) function [y,k]=sconv(f,h,nf,nh,p) % y:卷积积分y(t)对应的非零样值向量 % k:y(t)对应的时间向量 % f:f(t)对应的非零样值向量 % nf:f(t)对应的时间向量 % h:h(t)对应的非零样值向量 % nh:h(t)对应的时间向量 % p:取样时间间隔y=conv(f,h); % 计算序列f(n)与h(n)的卷积和y(n) y=y*p; % y(n)变成y(t)left=nf(1)+nh(1); % 计算序列y(n)非零样值的起点位置 right=length(nf)+length(nh)-2; % 计算序列y(n)非零样值的终点位置 k=p*(left:right); % 确定卷积和y(n)非零样值的时间向量(3)运行结果图12 例7图(4)函数解析 Function 函数调用8、(1)题目 实现卷积)(*)(t h t f ,其中:)()()],2()([2)(t e t h t t t f tεεε-=--=。
