大连理工大学自动控制原理考研试题
大连理工研究报告生考试自动控制真题

大连理工大学二o0五年硕士生入学考试《自动控制原理 <含20%现代)》试卷、<15分)试求图1所示电路的传递函数U c (s> / U r (S>。
、<25分)已知负反馈系统的开环传递函数为K1.试绘制以K 为参量的根轨迹图;2. 试求系统处于临界稳定状态时的闭环极点。
四、<15分)已知负反馈系统的开环传递函数为 G(s>H(s>=三!1 ,试绘制开环幅相特性曲 线,并应用奈奎斯特判据判断系统的稳定性。
五、<15分)已知负反馈系统的开环传递函数为 G(s>H(s>= ,并绘制开环频率特性对数坐标曲线,并计算相角裕度。
六、<15分)给定系统微分方程为 v-厂丿“,试确定奇点位置及类型,并绘制相平面草图。
七、<15分)设系统结构如图3所示。
试求C(z>,并判断K=1时系统的稳定性。
、<20分)给定系统结构如图2所示1. 设r(t>=n i (t>=n 2(t>=1(t>,试求系统的稳态误差e ss 。
2. 在r(t>=n i (t>=n 2(t>=1(t>情况下,如何使稳态误差八、<10分)已知离散系统的状态方程为0 IX(k+1)= °00 2aa>0,试用李雅普诺夫第二方法确定使平衡点渐进稳定的01X(k)a 取值范1"s+F1.试建立系统的状态空间描述;2 •试设计状态反馈阵,使系统闭环极点位于-2, -2处;3.K是否可以取为0.5,为什么?大连理工大学二OO四年硕士生入学考试《自动控制原理<含30%现代)》试卷、<15分)试求图1所示电路的结构图和传递函数。
/?/ 出、<10分)已知系统的特征方程为:4 3 2s4+2.5s3+2.5s2+10s -6 = 试求特征根在S平面上的分布。
的=3三、<10分)试求系统"小八—的单位脉冲响应。
大连理工1999研究生考试自动控制原理真题

大连理工大学二O O 五年硕士生入学考试《自动控制原理(含20%现代)》试题一、(15分)试求图1所示电路的传递函数U c (s) / U r (s) 。
二、(20分)给定系统结构如图2所示。
1.设r(t)=n 1(t)=n 2(t)=1(t), 试求系统的稳态误差e ss ;2.在r(t)=n 1(t)=n 2(t)=1(t)情况下,如何使稳态误差e ss =0。
三、(25分)已知负反馈系统的开环传递函数为1.试绘制以K 为参量的根轨迹图;2.试求系统处于临界稳定状态时的闭环极点。
四、(15分)已知负反馈系统的开环传递函数为G(s)H(s)=)1)(5()1(10-++s s s ,试绘制开环幅相特性曲线,并应用奈奎斯特判据判断系统的稳定性。
五、(15分)已知负反馈系统的开环传递函数为G(s)H(s)=)50)(5(2500++s s s ,并绘制开环频率特性对数坐标曲线,并计算相角裕度。
六、(15分)给定系统微分方程为,试确定奇点位置及类型,并绘制相平面草图。
七、(15分)设系统结构如图3所示。
试求C(z),并判断K=1时系统的稳定性。
八、(10分)已知离散系统的状态方程为a>0,试用李雅普诺夫第二方法确定使平衡点渐进稳定的a取值范围。
九、(20分)给定系统结构如图4所示。
1.试建立系统的状态空间描述;2.试设计状态反馈阵,使系统闭环极点位于-2,-2处;3.K是否可以取为0.5,为什么?大连理工大学二O O 四年硕士生入学考试《自动控制原理(含30%现代)》试题一、(15分)试求图1所示电路的结构图和传递函数。
二、(10分)已知系统的特征方程为: s 4+2.5s 3+2.5s 2+10s -6 = 0 试求特征根在S 平面上的分布。
三、(10分)试求系统的单位脉冲响应。
四、(20分)设系统的开环传递函数为:1. 试绘制根轨迹图(可能的分离点为:-1.2、-1.6、-2.6、-2.9、-3.5);2. 试求出分离点处的K 值。
大连理工大学854自动控制原理历年考研真题专业课考试试题

四、G(s)H(s)=
,求
的关系及各自意义。
五、
,求极坐标的稳定性。
六、非线性二阶系统
七、离散系统 稳定性和ess的影响。
求奇点附近的相轨迹。 ,求稳定时T的范围。讨论T对
八、系统运动方程为
,
表达式,并将其化为对角标准型。
1.求闭环脉冲传递函数C(z)/R(z)。 2.求闭环系统稳定时的K值范围。 八、如图所示,状态空间描述
1.判断系统的能控性,能观性。
2.采用状态反馈使得配置极点为a,b(a,b值略),求出反馈阵k。
3.已知
,求出闭环传递函数Y(S)/V(s),求出稳态
输出及闭环稳态增益。
4.如何使系统的闭环稳态增益为1?
四、根轨迹方程为 震荡时的K值范围。
,求出根轨迹,求出系统衰减
五、
(a,b值略)
1.画出极坐标图,并写出系统稳定的K值范围。
2.当K=1时,画出系统的Bode图,并在图中标出相角裕量和幅值 裕量。
六、非线性系统方程 相平面草图。
,求出系统的奇点,并画出
七、闭环离散系统如图所示,其中u(k)=u(k1)+e(k),G(s)= ,T=1
1999年大连理工大学自动控制原理考研真题
2014年大连理工大学854自动控制原理考研 真题(回忆版)
2013年大连理工大学854自动控制原理考研 真题(回忆版)
大连理工大学2013年硕士生入学考试 《自动控制原理(含20%现代)》试题
一、简答 1.分析单位闭环反馈系统常用什么分析系统的性能? 2.超前反馈校正环节与滞后反馈校正环节的优缺点? 3.对于受控系统采用状态反馈能镇定的充要条件是什么? 4.采取哪种措施可以减少系统稳态误差? 5.在系统设计时是否要使系统闭环稳定增益为1或者接近于1?
大连理工研究报告生考试自动控制真题

大连理工大学二O O五年硕士生入学考试《自动控制原理<含20%现代)》试卷一、<15分)试求图1所示电路的传递函数U c(s> / U r(s> 。
二、<20分)给定系统结构如图2所示。
1.设r(t>=n1(t>=n2(t>=1(t>, 试求系统的稳态误差e ss。
2.在r(t>=n1(t>=n2(t>=1(t>情况下,如何使稳态误差e ss=0。
三、<25分)已知负反馈系统的开环传递函数为1.试绘制以K为参量的根轨迹图;2.试求系统处于临界稳定状态时的闭环极点。
四、<15分)已知负反馈系统的开环传递函数为G(s>H(s>=,试绘制开环幅相特性曲线,并应用奈奎斯特判据判断系统的稳定性。
五、<15分)已知负反馈系统的开环传递函数为G(s>H(s>=,并绘制开环频率特性对数坐标曲线,并计算相角裕度。
六、<15分)给定系统微分方程为,试确定奇点位置及类型,并绘制相平面草图。
七、<15分)设系统结构如图3所示。
试求C(z>,并判断K=1时系统的稳定性。
八、<10分)已知离散系统的状态方程为a>0,试用李雅普诺夫第二方法确定使平衡点渐进稳定的a取值范围。
九、<20分)给定系统结构如图4所示。
1.试建立系统的状态空间描述;2.试设计状态反馈阵,使系统闭环极点位于-2,-2处;3.K是否可以取为0.5,为什么?大连理工大学二O O四年硕士生入学考试《自动控制原理<含30%现代)》试卷一、<15分)试求图1所示电路的结构图和传递函数。
二、<10分)已知系统的特征方程为:s4+2.5s3+2.5s2+10s -6 = 0试求特征根在S平面上的分布。
三、<10分)试求系统的单位脉冲响应。
四、<20分)设系统的开环传递函数为:1.试绘制根轨迹图<可能的分离点为:-1.2、-1.6、-2.6、-2.9、-3.5);2.试求出分离点处的K值。
12年真题
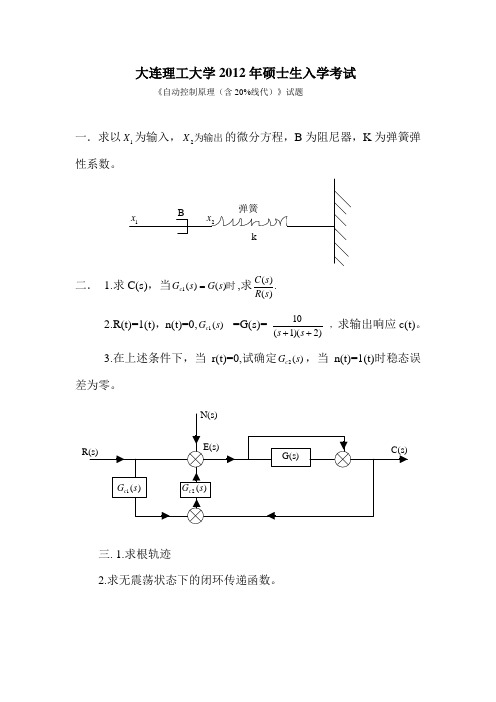
大连理工大学2012年硕士生入学考试《自动控制原理(含20%线代)》试题一.求以1X 为输入,为输出2X 的微分方程,B 为阻尼器,K 为弹簧弹性系数。
弹簧1x B2x k二. 1.求C(s),当时)()(1s G s G c =,求.)()(s R s C 2.R(t)=1(t),n(t)=0,)(1s G c =G)2)(1(10++s s ,求输出响应c(t)。
3.在上述条件下,当r(t)=0,试确定)(2s G c ,当n(t)=1(t)时稳态误差为零。
G(s))(2s G c )(1s G c R(s)N(s)E(s)C(s)三. 1.求根轨迹2.求无震荡状态下的闭环传递函数。
)22)(2(2+++s s s s kR(s)E(s)四.1.求开环传递函数的极坐标图2.用奈氏判据判断系统稳定时的K 值范围)3(102+s s ——C(s)R(s))2(+s K五.1.求两系统传递函数。
2.比较两系统在阶跃输入下的动态性能指标。
w)(w L 250.120六.1.求闭环临界放大系数K2.若r(t)=t ,求系统的稳态误差。
se Ts--1)1(+s s k T=1R(s)C(s)七.1.N(A)=24++A A ,求系统稳定,不稳定,做周期运动时的K 取值范围。
2.求出系统做周期运动的A 和wN(A)2)1(+s s K八.1.画出系统的状态变量图,并求出系统状态描述2.求出a 取什么值系统是可控的,可观的?32+s as +11x 2x y九.已知u t x t X ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-=10)(00)(ππ ,x y )21(=,离散周期T=1s 时,写出离散系统的表达式。
将此定常连续系统离散化后的系统模型。
大工自控2005
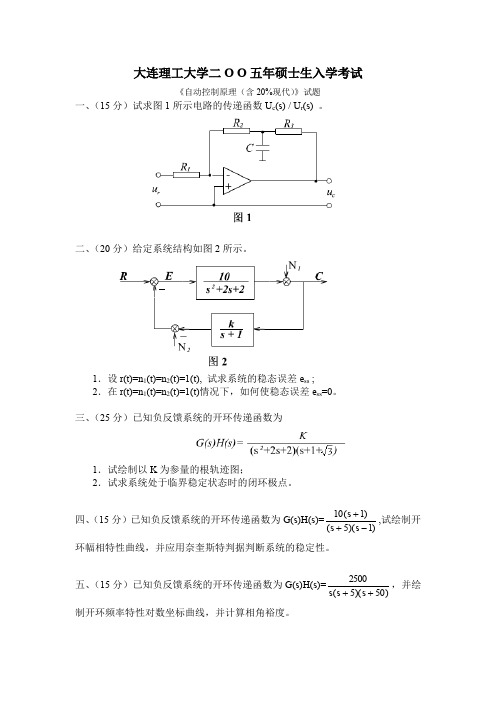
大连理工大学二O O 五年硕士生入学考试
《自动控制原理(含20%现代)》试题
一、(15分)试求图1所示电路的传递函数U c (s) / U r (s) 。
二、(20分)给定系统结构如图2所示。
1.设r(t)=n 1(t)=n 2(t)=1(t), 试求系统的稳态误差e ss ;
2.在r(t)=n 1(t)=n 2(t)=1(t)情况下,如何使稳态误差e ss =0。
三、(25分)已知负反馈系统的开环传递函数为
1.试绘制以K 为参量的根轨迹图;
2.试求系统处于临界稳定状态时的闭环极点。
四、(15分)已知负反馈系统的开环传递函数为G(s)H(s)=)1)(5()1(10-++s s s ,试绘制开环幅相特性曲线,并应用奈奎斯特判据判断系统的稳定性。
五、(15分)已知负反馈系统的开环传递函数为G(s)H(s)=
)50)(5(2500++s s s ,并绘制开环频率特性对数坐标曲线,并计算相角裕度。
大连理工854 自动控制原理考研真题
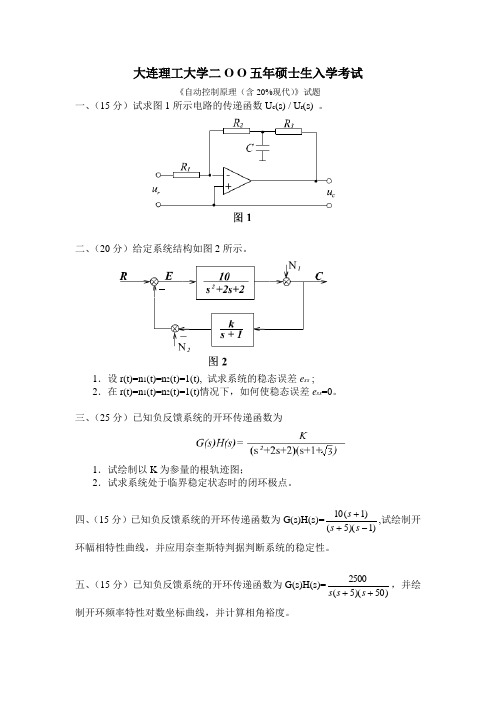
大连理工大学二O O 五年硕士生入学考试《自动控制原理(含20%现代)》试题一、(15分)试求图1所示电路的传递函数U c (s) / U r (s) 。
二、(20分)给定系统结构如图2所示。
1.设r(t)=n 1(t)=n 2(t)=1(t), 试求系统的稳态误差e ss ;2.在r(t)=n 1(t)=n 2(t)=1(t)情况下,如何使稳态误差e ss =0。
三、(25分)已知负反馈系统的开环传递函数为1.试绘制以K 为参量的根轨迹图;2.试求系统处于临界稳定状态时的闭环极点。
四、(15分)已知负反馈系统的开环传递函数为G(s)H(s)=)1)(5()1(10-++s s s ,试绘制开环幅相特性曲线,并应用奈奎斯特判据判断系统的稳定性。
五、(15分)已知负反馈系统的开环传递函数为G(s)H(s)=)50)(5(2500++s s s ,并绘制开环频率特性对数坐标曲线,并计算相角裕度。
六、(15分)给定系统微分方程为,试确定奇点位置及类型,并绘制相平面草图。
七、(15分)设系统结构如图3所示。
试求C(z),并判断K=1时系统的稳定性。
八、(10分)已知离散系统的状态方程为a>0,试用李雅普诺夫第二方法确定使平衡点渐进稳定的a取值范围。
九、(20分)给定系统结构如图4所示。
1.试建立系统的状态空间描述;2.试设计状态反馈阵,使系统闭环极点位于-2,-2处;3.K是否可以取为0.5,为什么?《自动控制原理》教学大纲(学分 4 ,学时64 )一、课程的性质与任务二、本课程是自动化类专业的理论基础课之一。
本课程的任务是使学生掌握反馈控制系统的构成、控制系统数学模型的建立方法及系统时域、频域分析和校正方法;学习掌握非线性系统和离散控制系统的分析方法。
二、课程内容、基本要求与学时分配本人有自动控制原理教材及较全的考研真题(及复印版一份,及赠送回忆版照片形式),如需要请联系扣扣238七93 2654另外有华中科技大学传热学真题,全部是复印版(学生出售,值得信赖)(一)自动控制的基本概念2学时1.了解反馈控制系统的基本工作原理。
大连理工1999-2005研究生考试自动控制原理真题

大连理工大学二O O 五年硕士生入学考试《自动控制原理(含20%现代)》试题一、(15分)试求图1所示电路的传递函数U c (s) / U r (s) 。
二、(20分)给定系统结构如图2所示。
1.设r(t)=n 1(t)=n 2(t)=1(t), 试求系统的稳态误差e ss ;2.在r(t)=n 1(t)=n 2(t)=1(t)情况下,如何使稳态误差e ss =0。
三、(25分)已知负反馈系统的开环传递函数为1.试绘制以K 为参量的根轨迹图;2.试求系统处于临界稳定状态时的闭环极点。
四、(15分)已知负反馈系统的开环传递函数为G(s)H(s)=)1)(5()1(10-++s s s ,试绘制开环幅相特性曲线,并应用奈奎斯特判据判断系统的稳定性。
五、(15分)已知负反馈系统的开环传递函数为G(s)H(s)=)50)(5(2500++s s s ,并绘制开环频率特性对数坐标曲线,并计算相角裕度。
六、(15分)给定系统微分方程为,试确定奇点位置及类型,并绘制相平面草图。
七、(15分)设系统结构如图3所示。
试求C(z),并判断K=1时系统的稳定性。
八、(10分)已知离散系统的状态方程为a>0,试用李雅普诺夫第二方法确定使平衡点渐进稳定的a取值范围。
九、(20分)给定系统结构如图4所示。
1.试建立系统的状态空间描述;2.试设计状态反馈阵,使系统闭环极点位于-2,-2处;3.K是否可以取为0.5,为什么?大连理工大学二O O 四年硕士生入学考试《自动控制原理(含30%现代)》试题一、(15分)试求图1所示电路的结构图和传递函数。
二、(10分)已知系统的特征方程为: s 4+2.5s 3+2.5s 2+10s -6 = 0 试求特征根在S 平面上的分布。
三、(10分)试求系统的单位脉冲响应。
四、(20分)设系统的开环传递函数为:1. 试绘制根轨迹图(可能的分离点为:-1.2、-1.6、-2.6、-2.9、-3.5);2. 试求出分离点处的K 值。
2006—2007年大连理工大学562自动控制原理考研真题【圣才出品】

2007年大连理工大学562自动控制原理考研真题大连理工大学2007年硕士生入学考试《自动控制原理(含20%现代)》试题一、(10分)简单回答下列问题1.某闭环系统在给定的输入下,稳态误差为无穷大,是否说明该系统不稳定?2.线性系统能否维持稳定的自激震荡?为什么?3.什么样的系统是最小相位系统?4.请给出求X(t+3T)的z变换。
5.为甚麽要研究控制系统状态的可控性和可观测性?二、(12分)试求图中所示系统的传递函数G(s)=C(s)/ R(s)。
.三、(18分)已知系统结构图如图所示。
1.试求K=0,r (t )=1(t ),初始条件为0时的响应c (t ),超调量,峰值时间tp ; 2.K ≠0,r (t )=t 时,试问可否通过改变K 值使ess=0.05,为什么?C四、(20分)某负反馈系统的开环传递函数G (s )H (s )=)3)(2)(1(+++s s s K;1.试绘制以K 为参量的根轨迹,并确定系统处于过阻尼状态时K 的范围? 2.试判断-1+j 是否在根轨迹上?五、(15)某负反馈系统的开环传递函数为G (s )H (s )=)1()1(10+-s s s 。
试绘制系统的对数坐标曲线,并求相角裕度。
六、(15分)某负反馈系统的开环传递函数为)1()10()()(2++=s s s s H s G 。
1.试绘制完整的开环频率特性的幅相特性曲线以及相应的S 平面上的封闭曲线。
2.使用奈奎斯特判据判断系统的稳定性。
七、给定系统的微分方程为02=-++x x x x,试确定奇点的位置和类型,并绘制相平面草图。
八、(15分)离散系统如图3所示。
图中Gh (S )为零阶保持器,采样周期T=1秒,当输入r (t )=1(t )时,要求输入C (t )=1(t-T ),试确定D (z ),并求稳态误差(e=r-c )。
九、(12分) 系统微分方程为:1.试建立系统状态空间的约当标准型; 2.试绘制系统的状态变量图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∠G0(jω) -100o -115o -130o -140o -145o -150o -160o 180o
1. 求系统的相位裕量和幅值裕量; 2. 欲使系统具有 20db 的幅值裕量,系统的开环增益应变化多少? 3. 欲使系统具有 40o 的相位裕量,系统的开环增益应变化多少?
五、(15 分)试求图四所示系统的闭环 Z 传递函数 C(z)/R(z)。T 为采样周期。
2003 年大连理工大学自动控制原理考研试题 一、(14 分)系统如图一所示。其中 K1,K2 为弹簧的弹性系数,B 为阻尼器的粘 性摩擦系数。试写出以 yi 为输入,y0 为输出的传递函数。
二、(15 分)系统如图二所示,假设输入是斜坡信号,即 r(t)=at ,式中 a 是 一个任意非零常数。试通过适当地调节 Ki 的值,使系统对斜坡输入响应的稳态 误差达到零。
三、(20 分)设系统如图三所示。 (1)为了使闭环极点为 s=-1±j 3 ,试确定增益 K 和速度反馈 Ki 的数值; (2)利用求出的 Ki 画出根开环频率响应特性如下:
ω
2
3
|G0(jω)| 10
8.5
4
5
6
7
8
10
6
4.18 2.7 1.5 1.0 0.6
六、(15 分)试用奈氏判据分析具有下列开环传递函数的闭环系统的稳定性。 G(s)H(s)= K (s + 3) s(s −1)
七、(14 分)试用相平面法分析如下系统的稳定性。
八、(25 分)给线性系统:
(1) 判断系统的状态能控性与状态能观测性; (2) 如该系统状态是能控的,试写出系统的能控标准型;如状态是不能控的,
请指出对应于系统哪个极点的状态是不能控的。
九、(20 分)设系统的状态方程和输入方程为 中
。其
试(1)确定状态反馈矩阵 K,使闭环系统的极点配置在-1±j2 ; (2)画出闭环系统的状态变量图。
