完整版初中数学面积公式总结.doc
面积公式大全及口诀

面积公式大全及口诀三角形的面积=底×高÷2。
公式 S= a×h÷2正方形的面积=边长×边长公式 S= a×a长方形的面积=长×宽公式 S= a×b平行四边形的面积=底×高公式 S= a×h梯形的面积=(上底+下底)×高÷2 公式 S=(a+b)h÷2内角和:三角形的内角和=180度。
长方体的体积=长×宽×高公式:V=abh长方体(或正方体)的体积=底面积×高公式:V=abh正方体的体积=棱长×棱长×棱长公式:V=aaa圆的周长=直径×π公式:L=πd=2πr圆的面积=半径×半径×π公式:S=πr2圆柱的表(侧)面积:圆柱的表(侧)面积等于底面的周长乘高。
公式:S=ch=πdh=2πrh圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。
公式:S=ch+2s=ch+2πr2圆柱的体积:圆柱的体积等于底面积乘高。
公式:V=Sh圆锥的体积=1/3底面×积高。
公式:V=1/3Sh分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变。
异分母的分数相加减,先通分,然后再加减。
分数的乘法则:用分子的积做分子,用分母的积做分母。
分数的除法则:除以一个数等于乘以这个数的倒数。
读懂理解会应用以下定义定理性质公式一、算术方面1、加法交换律:两数相加交换加数的位置,和不变。
2、加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,再同第三个数相加,和不变。
3、乘法交换律:两数相乘,交换因数的位置,积不变。
4、乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变。
5、乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变。
《面积》知识点总结

《面积》知识点总结面积是几何学中的一个重要概念,它描述了一个平面图形所占据的区域大小。
在现实生活和学习中,我们经常需要计算图形的面积,以求解各种问题。
面积的概念和计算方法有很多重要的知识点,下面将对这些知识进行总结。
一、基本概念1.面积的定义:面积是指平面上其中一个面或者图形所占据的区域大小。
2. 面积的单位:常用的面积单位有平方米(m²)、平方厘米(cm²)、平方毫米(mm²)等。
3.面积的符号:表示面积通常使用大写字母A表示。
二、常见平面图形的面积计算1.矩形:矩形的面积计算公式是A=长×宽。
2.正方形:正方形的面积计算公式是A=边长×边长。
3.三角形:三角形的面积计算公式是A=底×高÷24.平行四边形:平行四边形的面积计算公式是A=底×高。
5.梯形:梯形的面积计算公式是A=(上底+下底)×高÷26.圆:圆的面积计算公式是A=π×半径²(π取近似值3.14或3.1415)。
7.扇形:扇形的面积计算公式是A=弧长×半径÷2或A=半径²×弧度÷2(其中,弧度等于圆心角的度数除以360度再乘以2π)。
三、复杂图形的面积计算1.复杂图形的分解法:将复杂的图形分解成多个简单的图形,计算出各个简单图形的面积,再将各个简单图形的面积相加,即可得到复杂图形的面积。
这种方法适用于不规则图形、多边形等复杂图形的面积计算。
2.高度法:对于有高度的梯形、三角形等图形,可以利用垂直高度计算面积。
通过画高线,将图形分成上下两个部分,分别计算上下两部分图形的面积,再将两部分面积相加,即可得到整个图形的面积。
3.面积差法:对于有相似图形或同心图形的给定面积的图形,可以通过面积差法计算图形的面积。
将给定面积的图形与另一规定图形进行重合,计算重合图形的面积,再用给定面积减去重合图形的面积,即可得到所求图形的面积。
初中数学全套公式大全

初中数学全套公式大全1.代数公式- 分配律:a(b+c) = ab + ac-结合律:(a+b)+c=a+(b+c)- 因式分解:ab+ac = a(b+c)-二次方差:(a+b)(a-b)=a^2-b^2- 三次方差:a^3 + b^3 = (a+b)(a^2-ab+b^2)- 一次方程求解:ax + b = 0 => x = -b/a- 二次方程求解:ax^2 + bx + c = 0 => x = (-b±√(b^2-4ac))/(2a)- 三次方程求解:ax^3 + bx^2 + cx + d = 0 => 需用牛顿法等等2.几何公式-周长:正方形周长=4×边长矩形周长=2×(长+宽)圆周长=π×直径-面积:正方形面积=边长×边长矩形面积=长×宽三角形面积=底×高/2圆面积=π×半径^2-体积:长方体体积=长×宽×高圆柱体积=圆面积×高圆锥体积=圆面积×高/3-相似三角形面积比:AB/CD=BC/EF=AC/DE-圆的性质:正切与切线垂直相等弧所对的圆心角是相等的相等弧的扇形所对的弧长和扇形的面积也相等3.概率公式-事件的概率:P(A)=事件A发生的次数/总的样本空间次数-对立事件:P(A')=1-P(A)-全概率公式:事件B在事件A发生的条件下发生的概率为P(A)×P(B,A),而总概率为P(A)-乘法公式:两个同时发生的独立事件A和B的概率为P(A∩B)=P(A)×P(B)-加法公式:两个互不相容(即不能同时发生)的事件A和B的概率为P(A∪B)=P(A)+P(B)4.超越函数的公式- e^x、e^(-x)、ln(x)、log(x)等函数的展开公式-三角函数的和差化积公式和倍角公式-反三角函数的公式-指数函数、对数函数的性质及展开公式5.统计学公式-平均值:平均值=总和/总数-中位数:将数据从小到大排列,如果总数是奇数,则中位数为中间的那个数;如果总数是偶数,则中位数为中间两个数的平均值-众数:出现次数最多的数-极差:最大值-最小值-方差:各数据与平均数的差的平方和的均值-标准差:方差的平方根-相关系数:相关系数范围为-1到1,接近1表示正相关,接近-1表示负相关,接近0表示无关。
所有的面积公式

所有的面积公式数学中,面积公式可以让我们计算出它的具体面积。
下面是店铺给大家整理的所有的面积公式,供大家参阅!梯形面积公式S=(a+b)×h÷2{梯形面积=(上底+下底)×高÷2}球体(正球)表面积公式S=4πr^2{球体(正球)表面积=圆周率×半径×半径×4}坐标公式1:△ABC,三顶点的坐标分别为 A(a1,a2),B(b1,b2)C(c1,c2),S△ABC=∣a1b2+b1c2+c1a2-a1c2-c1b2-b1a2∣/2.2:空间△ABC,三顶点的坐标分别为A(a1,a2,a3),B(b1,b2,b3)C(c1,c2c3),面积为S,则S^2=(a1b2+b1c2+c1a2-a1c2-c1b2-b1a2)^2+(a2b3+b2c3+c2a3-a2c3-c2b3-b2a3)^2+(a1b3+b1c3+c1a3-a1c3-c1b3-b1a3)^2.圆公式/面积公式设圆半径为:r, 面积为:S .则面积S= π·r^2 ; π 表示圆周率即圆面积等于圆周率乘以圆半径的平方扇形面积公式在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积S=πR^2,所以圆心角为n°的扇形面积:比如:半径为1cm的圆,那么所对圆心角为135°的扇形的周长:C=2R+nπR÷180=2×1+135×3.14×1÷180=2+2.355=4.355(cm)=43.55(mm)扇形的面积:S=nπR^2÷360=135×3.14×1×1÷360=1.1775(cm^2)=117.75(mm^2)扇形还有另一个面积公式面积公式其中l为弧长,R为半径扇环面积公式面积公式图册圆环周长:外圆的周长+内圆的周长(圆周率X(大直径+小直径))圆环面积:外圆面积-内圆面积(圆周率X大半径的平方-圆周率X小半径的平方\圆周率X(大半径的平方-小半径的平方)用字母表示:S内+S外(πR方)S外—S内=∏(R方-r方)还有第二种方法:S=π[(R-r)×(R+r)]R=大圆半径r=圆环宽度=大圆半径-小圆半径还有一种方法:已知圆环的外直径为D,圆环厚度(即外内半径之差)为d。
初中数学面积问题总结归纳

初中数学面积问题总结归纳
在初中数学中,面积问题主要涉及到平面图形的面积计算。
以下是在初中数学中常见的面积问题总结归纳:
1. 矩形的面积计算:矩形的面积可以通过长度和宽度的乘积来计算,即面积 = 长 ×宽。
2. 正方形的面积计算:正方形的边长相等,所以正方形的面积可以通过边长的平方来计算,即面积 = 边长 ×边长。
3. 三角形的面积计算:三角形的面积可以通过底边长和高的乘积再除以2来计算,即面积 = 底边长度 ×高 ÷ 2。
4. 平行四边形的面积计算:平行四边形的面积可以通过底边长和高的乘积来计算,即面积 = 底边长度 ×高。
5. 梯形的面积计算:梯形的面积可以通过上底与下底之和的一半再乘以高来计算,即面积 = (上底 + 下底) ×高 ÷ 2。
6. 圆的面积计算:圆的面积可以通过半径的平方再乘以π(pi)来计算,即面积 = 半径 ×半径× π。
在解决这些面积问题时,需要注意图形的参数,如边长、底边长、高、半径等,并且对于复杂图形,可能需要将其分解为多个基本图形来计算面积。
此外,也要注意单位的转换和精确计算的问题。
面积总结归纳

面积总结归纳在日常生活中,面积是一种用来描述物体表面大小的计量单位。
它在各个领域都有着广泛的应用,无论是在建筑设计、农业生产还是科学研究中,都需要准确地计算和比较不同物体的面积。
本文将对面积的概念进行简要介绍,并总结归纳面积的计算方法和应用场景。
一、什么是面积面积是平面几何中一种用来描述物体表面大小的量度。
它通常以平方单位(如平方米、平方厘米)表示。
在二维平面中,一个物体的面积等于其所占据的平面区域的大小。
二、常见物体的面积计算方法1. 矩形的面积计算:对于一个矩形,其面积可以通过将其宽度与长度相乘得到。
公式为:面积 = 宽度 ×长度。
2. 正方形的面积计算:对于一个正方形,其面积可以通过将其边长的平方得到。
公式为:面积 = 边长 ×边长。
3. 圆的面积计算:对于一个圆,其面积可以通过将其半径的平方乘以π(圆周率)得到。
公式为:面积 = 半径 ×半径× π。
4. 三角形的面积计算:对于一个三角形,其面积可以通过将其底边长度与高的乘积再除以2得到。
公式为:面积= (底边长度×高)/ 2。
三、面积的应用场景1. 建筑设计中的面积计算:在建筑设计过程中,需要计算各个房间、楼层、建筑物的面积,以便进行合理的空间规划和材料使用。
面积计算还有助于评估建筑的使用效率和设计质量。
2. 农业生产中的面积计算:在农业生产中,面积计算是农田规划、种植布局和农作物产量评估的重要依据。
通过计算田地面积,农民可以准确地安排种植区域,合理使用肥料和水资源,提高农作物的产量和质量。
3. 科学研究中的面积计算:在科学研究中,面积计算在各个学科领域都有广泛的应用。
例如,在地理学中,需要计算陆地和海洋的面积以研究地球表面的特征和分布;在生物学中,需要计算生物群落的面积以评估生态系统的健康状况。
4. 商业活动中的面积计算:在商业活动中,面积计算是商场、仓库和办公室管理的重要环节。
通过准确计算商业场所的面积,可以合理配置商品陈列、库存管理和工作空间,提高经营效率和顾客体验。
面积计算公式大全

面积计算公式大全面积是物体或图形所占据的平面的大小,通常用来衡量物体或图形的大小或面积。
在几何学中,我们可以根据不同的物体或图形的特征使用不同的公式来计算其面积。
以下是一些常见的面积计算公式。
一、平行四边形的面积计算公式:平行四边形是一种具有两对平行边的四边形。
其面积可以通过底边与高之积来计算。
公式为:面积=底边×高二、矩形的面积计算公式:矩形是一种特殊的平行四边形,其所有角都是直角。
其面积可以通过宽度与长度之积来计算。
公式为:面积=宽度×长度三、三角形的面积计算公式:三角形是一种具有三个边和三个角的多边形。
根据不同的已知条件,可以使用以下几种公式来计算三角形的面积:1.根据底边和高计算:面积=1/2×底边×高2. 根据两边和夹角计算:面积= 1/2 × 边1 × 边2 × sin(夹角)3.根据三条边的长度计算(海伦公式):面积=√[s(s-边1)(s-边2)(s-边3)],其中s为半周长四、梯形的面积计算公式:梯形是一种具有两条平行边的四边形。
其面积可以通过上底和下底之和的一半乘以高来计算。
公式为:面积=1/2×(上底+下底)×高五、圆的面积计算公式:圆是具有相同半径的一组点的集合,其中半径是从圆心到圆周上的任何点的距离。
圆的面积可以通过半径的平方乘以π来计算。
公式为:面积=半径²×π六、正方形的面积计算公式:正方形是一种具有相等边长和直角的矩形,也是一种具有四个直角的等边矩形。
其面积可以通过边长的平方来计算。
公式为:面积=边长²七、菱形的面积计算公式:菱形是一种具有相等对角线和直角的平行四边形。
其面积可以通过对角线之积除以2来计算。
公式为:面积=(对角线1×对角线2)/2八、五边形的面积计算公式:没有通用的五边形面积计算公式,因为五边形的形状和属性各不相同。
可以通过将五边形划分为更小的图形,然后使用各个图形的面积公式进行计算。
面积公式大全

面积公式大全在数学中,面积是描述一个平面图形所占据的空间大小的概念。
计算面积是数学中的一个重要问题,不同的图形有不同的计算方法。
下面我们将介绍一些常见图形的面积公式,希望对大家有所帮助。
1. 矩形的面积公式。
矩形是最简单的图形之一,其面积可以通过长度和宽度相乘来计算,即。
面积 = 长×宽。
2. 正方形的面积公式。
正方形是一种特殊的矩形,其四边相等。
因此,正方形的面积可以用边长的平方来表示,即。
面积 = 边长×边长。
3. 三角形的面积公式。
对于任意三角形,可以利用其底和高来计算面积,即。
面积 = 底×高÷ 2。
4. 圆的面积公式。
圆的面积公式是数学中的经典问题,其面积可以通过半径的平方乘以π来计算,即。
面积 = π×半径×半径。
5. 梯形的面积公式。
梯形是一个有两个平行边的四边形,其面积可以通过上底和下底的平均值乘以高来计算,即。
面积 = (上底 + 下底)×高÷ 2。
6. 平行四边形的面积公式。
平行四边形的面积可以通过底和高来计算,即。
面积 = 底×高。
7. 椭圆的面积公式。
椭圆的面积公式是一个复杂的问题,其面积可以通过长轴和短轴的乘积再乘以π来计算,即。
面积 = π×长轴×短轴。
8. 正多边形的面积公式。
对于正多边形,可以利用边长和周长来计算面积,即。
面积 = 周长×边长÷ 2。
以上就是一些常见图形的面积公式,希望能对大家有所帮助。
在实际问题中,计算面积是一个常见的数学运算,掌握好面积公式对于解决实际问题非常重要。
希望大家能够通过实际练习加深对面积公式的理解,提高数学水平。
面积公式大全

面积公式大全面积是数学中一个基础的概念,广泛应用于几何学和物理学等领域。
在解决问题和计算物体表面或图形面积时,掌握各种不同形状的面积公式是非常重要的。
本文将为你介绍一些常见的面积公式及其应用。
1. 矩形面积公式矩形是最简单的几何图形之一,其面积公式非常直观和简单。
对于矩形而言,其面积公式为:面积 = 长 ×宽。
例如,如果矩形的长为5个单位,宽为3个单位,则其面积为15个单位。
2. 正方形面积公式正方形是一种特殊的矩形,它的四条边相等且四个角都为直角。
正方形的面积公式为:面积 = 边长 ×边长,也可以写作面积 = 边长²。
假设一个正方形的边长为4个单位,则其面积为16个单位。
3. 三角形面积公式三角形是几何学中最重要的形状之一,有多种计算面积的公式,其中最常用的是“底乘高除以二”的公式。
假设三角形的底为b,高为h,则其面积可以表示为:面积 = (底 ×高) / 2。
举例而言,如果一个三角形的底长是6个单位,高度为3个单位,则它的面积为9个单位。
另外,还有一个常用的三角形面积公式叫做海伦公式,用于计算任意三角形的面积。
根据海伦公式,三角形的面积可以表示为:面积 =√[s(s-a)(s-b)(s-c)],其中a、b、c为三角形的三边长度,s为三边长度的一半。
4. 圆的面积公式圆是平面上距离圆心相等的一组点的集合,其面积公式由著名的数学常数π(pi)决定。
圆的面积公式为:面积= π × 半径²。
假设一个圆的半径为r个单位,则其面积为πr²。
5. 椭圆的面积公式椭圆是另一种重要的几何图形,其形状介于圆和矩形之间。
椭圆的面积公式为:面积= π × 长半轴 ×短半轴。
假设一个椭圆的长半轴为a,短半轴为b,则它的面积为πab。
6. 梯形的面积公式梯形是一个有四边的几何图形,其中两边平行而另外两边不平行。
梯形的面积公式为:面积 = (上底 + 下底) ×高度 / 2。
面积公式大全

面积公式大全
以下是一些常见的面积公式,其中涉及到圆的、长方形、正方形、平行四边形、三角形和梯形的面积计算。
这些公式可以帮助你在计算几何图形面积时,更加便捷、高效地解决问题。
1. 圆的面积公式:S = πr²,其中S代表面积,r代表半径。
2. 长方形的面积公式:S = l×w,其中S代表面积,l代表长,w代表宽。
3. 正方形的面积公式:S = a²,其中S代表面积,a代表边长。
4. 平行四边形的面积公式:S = a×h,其中S代表面积,a代表底边长度,h代表高。
5. 三角形的面积公式:S = 1/2×a×b,其中S代表面积,a代表底边长度,b代表高。
6. 梯形的面积公式:S = (上底+下底)×高÷2,其中S代表面积,a 和b分别代表上底和下底的长度,h代表高。
7. 圆环的面积公式:S = π×R² - π×r²,其中S代表面积,R和r分别代表大圆和小圆的半径。
8. 扇形的面积公式:S = 1/2×π×r²,其中S代表面积,r代表半径,θ代表弧度。
这些公式不仅仅适用于平面图形的面积计算,也同样适用于立体图形的体积计算,比如圆柱、长方体和正方体等的体积计算,只需将公式中的面积换成体积就可以了。
希望这些公式能帮助你在学习中更加轻松和自信!。
初中的面积公式归纳

图形的面积计算公式 1、长方形的周长=(长+宽)×2 C=(a+b)×2 2、正方形的周长=边长×4 C=4a 3、长方形的面积=长×宽 S=ab 4、正方形的面积=边长×边长 S=a.a 5、三角形的面积=底×高÷2 S=ah÷2 6、平行四边形的面积=底×高 S=ah 7、梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷2 8、圆形直径=半径×2 圆形半径=直径÷2 d=2r r= d÷2 9、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr 10、圆的面积=圆周率×半径×半径 S=πr ^2 11、长方体的表面积=(长×宽+长×高+宽×高)×2 S=(ab+bc+ca)×2 12、长方体的体积 =长×宽×高 V =abh 13、正方体的表面积=棱长×棱长×6 S =6a 14、正方体的体积=棱长×棱长×棱长 V=a.a.a 15、圆柱的侧面积=底面圆的周长×高 S=ch 16、圆柱的表面积=上下底面面积+侧面积 S=2πr +2πrh=2π(d÷2)+2π(d÷2)h=2π(C÷2÷π) +Ch 17、圆柱的体积=底面积×高 V=Sh V=πrh=π(d÷2)h=π(C÷2÷π)h 18、圆锥的体积=底面积×高÷3 V=Sh÷3 =πr h÷3 =π(d÷2)h÷3=π(C÷2÷π)h÷3 19、长方体(正方体、圆柱体)的体积=底面积×高 V=Sh。
初中数学的公式总结(通用12篇)

初中数学的公式总结(通用12篇)篇1:初中数学公式总结参考三角形的面积=底×高÷2。
公式S=a×h÷2正方形的面积=边长×边长公式S=a×a长方形的面积=长×宽公式S=a×b平行四边形的面积=底×高公式S=a×h梯形的面积=(上底+下底)×高÷2公式S=(a+b)h÷2内角和:三角形的内角和=180度。
长方体的体积=长×宽×高公式:V=abh长方体(或正方体)的体积=底面积×高公式:V=abh正方体的体积=棱长×棱长×棱长公式:V=aaa圆的周长=直径×π公式:L=πd=2πr圆的面积=半径×半径×π公式:S=πr2圆柱的表(侧)面积:圆柱的表(侧)面积等于底面的周长乘高。
公式:S=ch=πdh=2πrh圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积。
公式:S=ch+2s=ch+2πr2圆柱的体积:圆柱的体积等于底面积乘高。
公式:V=Sh圆锥的体积=1/3底面×积高。
公式:V=1/3Sh分数加减定律:分母相同的分数加减,只加减分子,分母不变。
不同分母的分数相加和相减,首先相除,然后相加和相减。
分数的乘法是:用分子的乘积做分子,分母的乘积做分母。
分数的除法法则:除以一个数等于乘以这个数的倒数。
阅读理解会应用以下定义定理、性质、公式。
1.算术1.加法交换律:两个数相加并交换加数,和不变的位置。
2.加法组合定律:三个数相加时,先加前两个数,或先加后两个数,再加第三个数,和不变。
3.乘法交换定律:两个数相乘,交换因子的位置不变。
4.乘法结合律:三个数相乘时,前两个数相乘,或者后两个数先相乘,再相乘第三个数,它们的乘积不变。
5、乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变。
面积公式大全

面积公式大全在数学中,面积是指一个平面图形所覆盖的表面大小。
不同的图形有不同的计算面积的公式,下面将为大家介绍一些常见图形的面积公式。
1. 矩形的面积公式。
矩形是最简单的图形之一,其面积公式为,面积=长×宽。
其中,长和宽分别代表矩形的长和宽。
2. 正方形的面积公式。
正方形是一种特殊的矩形,其面积公式与矩形相同,也是面积=边长×边长。
正方形的特点是四条边长度相等。
3. 三角形的面积公式。
对于任意三角形,其面积公式为,面积=底边长度×高÷2。
其中,底边长度为三角形底边的长度,高为从顶点到底边的垂直距离。
4. 圆的面积公式。
圆的面积公式为,面积=π×半径的平方。
其中,π是一个数学常数,约为3.14159,半径为圆的半径长度。
5. 梯形的面积公式。
梯形是一种四边形,其面积公式为,面积=(上底+下底)×高÷2。
其中,上底和下底分别代表梯形的上底和下底的长度,高为梯形的高度。
6. 平行四边形的面积公式。
平行四边形的面积公式为,面积=底边长度×高。
其中,底边长度为平行四边形的底边长度,高为从底边到对边的垂直距离。
7. 椭圆的面积公式。
椭圆的面积公式为,面积=π×长轴长度×短轴长度。
其中,长轴和短轴分别代表椭圆的长轴和短轴的长度。
8. 正多边形的面积公式。
正多边形是指所有边和角均相等的多边形,其面积公式为,面积=(边长×边长)×边数÷(4×tan(π/边数))。
其中,边长为正多边形的边长,边数为正多边形的边数,tan为正切函数。
以上就是一些常见图形的面积公式,希望对大家有所帮助。
在实际应用中,熟练掌握这些公式可以帮助我们更快、更准确地计算各种图形的面积。
如果你还有其他图形的面积公式想要了解,可以继续深入学习,探索更多数学的奥秘。
面积公式大全

面积公式大全1、长方形的周长=(长+宽)×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽S=ab4、正方形的面积=边长×边长S=a.a= a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高S=ah7、梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷28、直径=半径×2 d=2r 半径=直径÷2 r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr10、圆的面积=圆周率×半径×半径?=πr11、长方体的表面积=(长×宽+长×高+宽×高)×212、长方体的体积=长×宽×高V =abh13、正方体的表面积=棱长×棱长×6 S =6a14、正方体的体积=棱长×棱长×棱长V=a.a.a= a15、圆柱的侧面积=底面圆的周长×高S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr +2πrh=2π(d÷2) +2π(d÷2)h=2π(C÷2÷π) +Ch17、圆柱的体积=底面积×高V=ShV=πr h=π(d÷2) h=π(C÷2÷π) h18、圆锥的体积=底面积×高÷3V=Sh÷3=πr h÷3=π(d÷2) h÷3=π(C÷2÷π) h÷319、长方体(正方体、圆柱体)的体积=底面积×高V=Sh表面积S=π*r^2+πrl (l为母线长)把圆锥体的侧面积打开是扇形,扇形的半径就是母线坐标几何一对垂直相交于平面的轴线,可以让平面上的任意一点用一组实数来表示。
面积公式大全及口诀

7、么叫等式?等号左边的数值与等号右边的数值相等的式子 叫做等式。
等式的基本性质:等式两边同时乘以(或除以)一个相同的数,
等式仍然成立。
8、什么叫方程式?答:含有未知数的等式叫方程式。
9、 什么叫一元一次方程式?答:含有一个未知数,并且未知数的次 数是一次的等式叫做一元一次方程式。
学会一元一次方程式的例法及计算。即例出代有X的算式并计算。
9、比例的基本性质:在比例里,两外项之积等于两内项之积。
10、 解比例:求比例中的未知项,叫做解比例。女口3:x^9:18
11、正比如果这两种量中相对应的的比值(也就是商k)一定,这两种量就叫 做成正比例的量,它们的关系就叫做正比例关系。如:y/x=k( k一
面积公式大全及口诀
二角形的面积=底乂咼—2。公式S= a xh —2
正方形的面积=边长x边长 公式S= axa
长方形的面积=长乂宽公式S= a xb
平行四边形的面积=底乂高 公式S= a xh
梯形的面积=(上底+下底)x高—2公式S=(a+b)h—2
内角和:三角形的内角和=180度。
长方体的体积=长乂宽x高 公式:V=abh
10、分数:把单位“1”平均分成若干份,表示这样的一份或几分的 数,叫做分数。
11、分数的加减法则:同分母的分数相加减,只把分子相加减,分 母不变。异分母的分数相加减,先通分,然后再加减。
12、分数大小的比较:同分母的分数相比较,分子大的大,分子小 的小。异分母的分数相比较,先通分然后再比较;若分子相同,分母 大的反而小。
初一数学平方公式大全
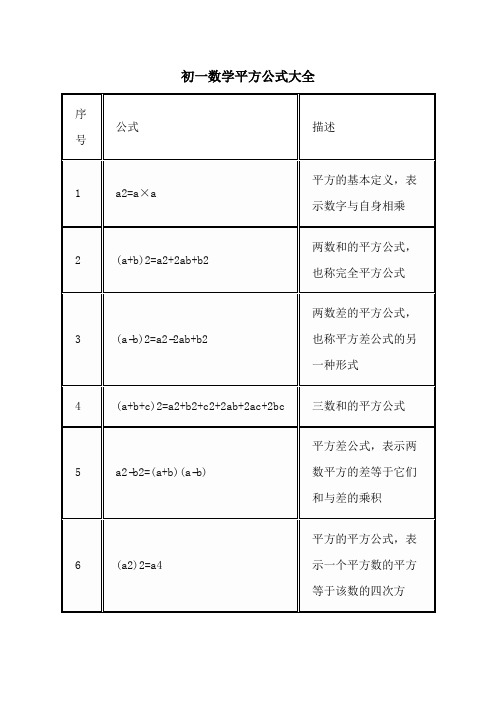
序号
公式
描述
1
a2=a×a
平方的基本定义,表示数字与自身相乘
2
(a+b)2=a2+2ab+b2
两数和的平方公式,也称完全平方公式
3
(a−b)2=a2−2ab+b2
两数差的平方公式,也称平方差公式的另一种形式
4
(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
三数和的平方公式
5
a2−b2=(a+b)(a−b)
平方差公式,表示两数平方的差等于它们和与差的乘积
6
(a2)2=a4
平方的平方公式,表示一个平方数的平方等于该数的四次方
7
(a )2=a
平方根的平方公式,表示一个数的平方根的平方等于该数(a≥0)
8
(\sqrt{a^2} =
a
9
(ab)2=a2b2
平方的乘积公式,表示两数乘积的平方等于,表示一个数与它的相反数的平方相等
11
(a1 )2=a21
平方的倒数公式,表示一个数的倒数的平方等于该数平方的倒数
12
(a21 )2=a41
平方的倒数的平方公式,表示一个数的平方的倒数的平方等于该数四次方的倒数
初中数学面积函数公式

乘法与因式分a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2)a3-b3=(a-b(a2+ab+b2)三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-√(b2-4ac)/2a根与系数的关系X1+X2=-b/a X1*X2=c/a 注:韦达定理判别式b2-4ac=0 注:方程有两个相等的实根b2-4ac>0 注:方程有两个不等的实根b2-4ac<0 注:方程没有实根,有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R 注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB 注:角B是边a和边c的夹角圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h 斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h' 正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l 球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h 圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*r a是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H 圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L 注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h 圆柱体V=pi*r2h计算方法:a5*a5=(a*(a+1))(5*5=25)比如:15*15=(1*2)(5*5=25)=225 25*25=(2*3)(5*5)=625希望对你有用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四边形的面积公式
长方形:S=ab{长方形面积=长×宽}
正方形:S=a^2{正方形面积=边长×边长}
平行四边形:S=ah{平行四边形面积=底×高}
梯形:S=(a+b)×h÷2{梯形面积=(上底+下底)×高÷2}
三角形的面积公式
三角形:S=ah÷2{三角形面积=底×高÷2}
圆的面积公式
圆形(正圆):S=πr^2{圆形(正圆)面积=圆周率×半径×半径}
圆环:S=(R^2-r^2)×π{圆形(外环)面积={圆周率×(外环半径^2-内环半径^2)}
扇形:S=πr^2×n/360{圆形(扇形)面积=圆周率×半径×半径×扇形角度/360}
椭圆S=π(圆周率)×a×b(其中a,b分别是椭圆的长半轴,短半轴的长).
半圆半圆形的面积公式=圆周率×半径的平方÷2
用字母公式表示是:S半=Πr^2÷2
立方体的面积公式
长方体表面积:S=2(ab+ac+bc){长方体表面积=(长×宽+长×高+宽×高)×2}
正方体表面积:S=6a^2{正方体表面积=棱长×棱长×6}
球体(正球)表面积:S=4πr^2{球体(正球)表面积=圆周率×半径×半径×4}
2018中考数学复习快速记忆的6个技巧
日期:2018-06-27 来源:中考网责编:樊亚蕾
1、归类记忆法
就是根据识记材料的性质、特征及其内在联系,进行归纳分类,以便帮助学生记忆大量的知识。
比如,学完计量单位后,可以把学过的所有内容归纳为五类:长度单位;面积单位;体积和容积单位;重量单位;时间单位。
这样归类,能够把纷纭复杂的事物系统化、条理化,易于记忆。
2、歌诀记忆法
就是把要记忆的数学知识编成歌谣、口诀或顺口溜,从而便于记忆。
比如,量角的方法,就可编出这样几句歌诀:“量角器放角上,中心对准顶点,零线对着一边,另一边看度数。
”再如,小数点位置移动引起数的大小变化,“小数点请你跟我走,走路先要找准‘左’和‘右’;横撇带口是个you,扩大向you走走走;横撇加个zuo,缩小向zuo走走走;十倍走一步百倍两步走,数位不够找‘0’拉拉钩。
”采用这种方法来记忆,学生不仅喜欢记,而且记得牢。
3、规律记忆法
即根据事物的内在联系,找出规律性的东西来进行记忆。
比如,识记长度单位、面积单位、体积单位的化法和聚法。
化法和聚法是互逆联系,即高级单位的数值×进率=低级单位的数值,低级单位的数值÷进率=高级单位的数值。
掌握了这两条规律,化聚问题就迎刃而解了。
规律记忆,需要学生开动脑筋对所学的有关材料进行加工和组织,因而记忆牢固。
4、列表记忆法
就是把某些容易混淆的识记材料列成表格,达到记忆之目的。
这种方法具有明显性、直观性和对比性。
比如,要识记质数、质因数、互质数这三个概念的区别,就可列成表来帮助学生记忆。
5、重点记忆法
随着年龄的增长,所学的数学知识也越来越多,学生要想全面记住,既浪费时间且记忆效果不佳。
因此,要让学生学会记忆重点内容,学生在记住了重点内容的基础上,再通过推导、联想等方法便可记住其他内容了。
比如,学习常见的数量关系:工作效率×工作时间=工作量。
工作量÷工作效率=工作时间;工作量+工作时间=工作效率。
这三者关系中只要记住了第一个数量关系,后面两个数量关系就可根据乘法和除法的关系推导出来。
这样去记,减轻了学生记忆的负担,提高了记忆的效率。
6、联想记忆法
就是通过一件熟悉的事物想到与它有联系的另一件事物来进行记忆。
