自动控制原理MATLAB仿真实验报告
北工大自控matlab实验报告

自动控制原理实验报告一、试验设计构造一个二阶闭环系统,使得该系统的%30≥p M对于任意二阶系统,其闭环传递函数为2222)(G nn nc s s s ωξωω++=,其中ξ为二阶系统的阻尼比,n ω为二阶系统的无阻尼振荡频率,该系统的超调量为πξξ21--=e M p 。
若要%30≥p M ,则0.36≤ξ。
取0.3=ξ,又n ω任意,所以取20=n ω,则要求设计的闭环传递函数为40012400)(2++=s s s G c 。
二、实验内容及步骤1.以MATLAB 命令行的方式,进行系统仿真,确定系统时域性能指标 num=[400]; den=[1 12 400]; step(num,den)由图可知,该系统的超调量为%30%37>=p M ,满足要求,上升时间为0985.0=r t ,峰值时间为164.0=p t ,调节时间为0.472=s t 。
2.通过改变系统的开环放大倍数K (分增大和减小两种情况)和系统的阻尼比系数(分增大和减小两种情况),进行系统仿真分析,确定新的性能指标,并与原构造系统的进行比较,根据响应曲线分析并说明出现的现象 (1)增大开环放大倍数num=[500]; den=[1 12 500]; step(num,den)由图可知,该系统的超调量为%30%42>=p M ,上升时间为0858.0=r t ,峰值时间146.0=p t ,调节时间0.48=s t 。
(2)减小开环放大倍数 num=[300]; den=[1 12 300]; step(num,den)由图可知,该系统的超调量为%30%31>=p M ,上升时间为119.0=r t ,峰值时间为0.1921=p t ,调节时间为0.455=s t 。
(3)增大阻尼比 num=[400];den=[1 12.4 400]; step(num,den)由图可知,该系统的超调量为%30%36>=p M ,上升时间为0995.0=r t ,峰值时间为0.163=p t ,调节时间为0.486=s t 。
自控仿真实验报告

一、实验目的1. 熟悉MATLAB/Simulink仿真软件的基本操作。
2. 学习控制系统模型的建立与仿真方法。
3. 通过仿真分析,验证理论知识,加深对自动控制原理的理解。
4. 掌握控制系统性能指标的计算方法。
二、实验内容本次实验主要分为两个部分:线性连续控制系统仿真和非线性环节控制系统仿真。
1. 线性连续控制系统仿真(1)系统模型建立根据题目要求,我们建立了两个线性连续控制系统的模型。
第一个系统为典型的二阶系统,其开环传递函数为:\[ G(s) = \frac{1}{(s+1)(s+2)} \]第二个系统为具有迟滞环节的系统,其开环传递函数为:\[ G(s) = \frac{1}{(s+1)(s+2)(s+3)} \](2)仿真与分析(a)阶跃响应仿真我们对两个系统分别进行了阶跃响应仿真,并记录了仿真结果。
(b)频率响应仿真我们对两个系统分别进行了频率响应仿真,并记录了仿真结果。
(3)性能指标计算根据仿真结果,我们计算了两个系统的性能指标,包括上升时间、超调量、调节时间等。
2. 非线性环节控制系统仿真(1)系统模型建立根据题目要求,我们建立了一个具有饱和死区特性的非线性环节控制系统模型。
其传递函数为:\[ W_k(s) = \begin{cases}1 & |s| < 1 \\0 & |s| \geq 1\end{cases} \](2)仿真与分析(a)阶跃响应仿真我们对非线性环节控制系统进行了阶跃响应仿真,并记录了仿真结果。
(b)相轨迹曲线绘制根据仿真结果,我们绘制了四条相轨迹曲线,以分析非线性环节对系统性能的影响。
三、实验结果与分析1. 线性连续控制系统仿真(a)阶跃响应仿真结果表明,两个系统的性能指标均满足设计要求。
(b)频率响应仿真结果表明,两个系统的幅频特性和相频特性均符合预期。
2. 非线性环节控制系统仿真(a)阶跃响应仿真结果表明,非线性环节对系统的性能产生了一定的影响,导致系统响应时间延长。
自控MATLAB实验一

《自动控制原理》课程实验报告实验名称初步认识MATLAB和系统仿真专业班级过程自动化03班学号2011500169姓名鲁雅洁指导教师李离学院名称电气信息学院2013 年10 月22 日实验一初步认识MATLAB和控制系统仿真一、实验目的(1)了解并掌握MATLAB仿真软件的使用方法;(2)掌握控制系统数学模型的多种描述方法及其仿真实现和互相转换; (3)熟悉控制系统仿真常用的MATLAB函数。
二、实验设备(1)硬件:个人计算机;(2)软件:MATLAB仿真软件(版本6.5或以上)。
三、实验内容和步骤1.质量—弹簧—阻尼器系统的零输入响应修改并运行程序lab1_1.m以求取下列情形的零输入响应曲线并存盘:Lab1_1_1.m程序:y0=0.15;wn=sqrt(2);zeta=1/(2*sqrt(2));t=[0:0.1:10];c=(y0/sqrt(1-zeta^2));y=c*exp(-zeta*wn*t).*sin(wn*sqrt(1-zeta^2)*t+acos(zeta));bu=c*exp(-zeta*wn*t);bl=-bu;plot(t,y,t,bu,'k--',t,bl,'k--'),gridxlabel('Time (sec)'),ylabel('y(t) (meters)')legend(['\omega_n=',num2str(wn),' \zeta=',num2str(zeta)]) 仿真结果:(1)零输入响应曲线Lab1_1_2.m程序:y0=0.15;wn=sqrt(2);zeta=1;t=[0:0.1:10];y=y0*(exp(-wn*t)+wn*t.*exp(-wn*t));plot(t,y),gridxlabel('Time (sec)'),ylabel('y(t) (meters)')legend(['\omega_n=',num2str(wn),' \zeta=',num2str(zeta)]) 仿真结果:(2)零输入响应曲线Lab1_1_3.m程序:y0=0.15;wn=sqrt(2);zeta=sqrt(2);t=[0:0.1:10];s1=-wn*(zeta+sqrt(zeta^2-1));s2=-wn*(zeta-sqrt(zeta^2-1));k1=(1-zeta/sqrt(zeta^2-1))/2;k2=(1+zeta/sqrt(zeta^2-1))/2;y=y0*(k1*exp(s1*t)+k2*exp(s2*t));plot(t,y),gridxlabel('Time (sec)'),ylabel('y(t) (meters)')legend(['\omega_n=',num2str(wn),' \zeta=',num2str(zeta)]) 仿真结果:(3)零输入响应曲线2.系统传递函数的MATLAB实现及零极点分布(1)多项式的表示及求值:系数按降幂顺序构成行向量;求值函数polyval;(2)多项式的根:由函数roots求得;函数poly(roots())的功能;(3)多项式的积:由函数conv实现;(4)系统传递函数:由函数tf实现;(5)传递函数的零极点表示:函数pole,zero和pzmap的运用。
(最新版)自动控制原理MATLAB仿真实验报告

实验一 MATLAB及仿真实验(控制系统的时域分析)一、实验目的学习利用MATLAB进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性;二、预习要点1、系统的典型响应有哪些?2、如何判断系统稳定性?3、系统的动态性能指标有哪些?三、实验方法(一)四种典型响应1、阶跃响应:阶跃响应常用格式:1、;其中可以为连续系统,也可为离散系统。
2、;表示时间范围0---Tn。
3、;表示时间范围向量T指定。
4、;可详细了解某段时间的输入、输出情况。
2、脉冲响应:脉冲函数在数学上的精确定义:其拉氏变换为:所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式:①;②③(二)分析系统稳定性有以下三种方法:1、利用pzmap绘制连续系统的零极点图;2、 利用tf2zp 求出系统零极点;3、 利用roots 求分母多项式的根来确定系统的极点 (三) 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1. 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ,试判断其稳定性2. 用Matlab 求出的极点。
%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den) 运行结果: p =-1.7680 + 1.2673i -1.7680 - 1.2673i 0.4176 + 1.1130i 0.4176 - 1.1130i -0.2991P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.5-1-0.500.5-1.5-1-0.50.511.5图1-1 零极点分布图由计算结果可知,该系统的2个极点具有正实部,故系统不稳定。
自动控制原理 matlab实验报告

自动控制原理实验(二)一、实验名称:基于MATLAB的控制系统频域及根轨迹分析二、实验目的:(1)、了解频率特性的测试原理及方法;(2)、理解如何用MATLAB对根轨迹和频率特性进行仿真和分析;(3)、掌握控制系统的根轨迹和频率特性两大分析和设计方法。
三、实验要求:(1)、观察给定传递函数的根轨迹图和频率特性曲线;(2)、分析同一传递函数形式,当K值不同时,系统闭环极点和单位阶跃响应的变化情况;(3)、K值的大小对系统的稳定性和稳态误差的影响;(4)、分析增加系统开环零点或极点对系统的根轨迹和性能的影响。
四、实验内容及步骤(1)、实验指导书:实验四(1)、“rlocus”命令来计算及绘制根轨迹。
会出根轨迹后,可以交互地使用“rlocfind”命令来确定点击鼠标所选择的根轨迹上任意点所对应的K值,K值所对应的所有闭环极点值也可以使用形如“[K, PCL] = rlocfind(G1)”命令来显示。
(2)、波特图:bode(G1, omga)另外,bode图还可以通过下列指令得出相位和裕角:[mag,phase,w] = bode(sys)(3)、奈奎斯特图:nuquist(G, omega)(2)课本:例4-1、4-2、4-7五实验报告要求(1)、实验指导书:实验四思考题请绘制下述传递函数的bode图和nyquist图。
1. 根据实验所测数据分别作出相应的幅频和相频特性曲线;2. 将思考题的解题过程(含源程序)写在实验报告中。
幅频特性曲线相频特性曲线Gs = zpk([10], [-5; -16; 9], 200)subplot(1, 2, 1)bode(Gs)gridsubplot(1, 2, 2)nyquist(Gs)grid(2)课本:例4-1、4-2、4-7图像结果:程序:Gs = zpk([-1], [0; -2; -3],1) rlocus(Gs)图像结果:程序:Gs = zpk([-2], [-1-j; -1+j],1) rlocus(Gs)程序:K=[0.5 1 2]for i=1:1:3num=[1,1,0,0]; den=[1,1,K(i)]; sys=tf(num,den); rlocus(sys); hold ongrid onend图像结果:目标:改变增益K和转折频率依次调节源程序:k1=[4.44,10,20];num=[1,2];den=conv([1,1],[1,2,4]);%一阶转折频率 1/T(wn1=2,wn2=1)二阶转折频率 wn3=wn'=2,伊布西塔=1/2 num1=[1,1];den1=conv([1,2],[1,2,4]);%一阶转折频率 1/T(wn1=1,wn2=2)二阶转折频率 wn3=wn'=2,伊布西塔=1/2 t=[0:0.1:7]; %for i=1:3g0=tf(k1(i)*num,den);g=feedback(g0,1);[y,x]=step(g,t);c(:,i)=y;g1=tf(k1(i)*num1,den1);g(1)=feedback(g1,1);[y1,x]=step(g(1),t);c1(:,i)=y1;endplot(t,c(:,1),'-',t,c(:,2),'-',t,c(:,3),'-',t,c1(:,1),'-',t,c1(:,2), '-',t,c1(:,3),'-');gridxlabel('Time/sec'),ylabel('out')结果分析:在本题中(1)改变k值:k值越大,超调量越大,调节时间越长,峰值时间越短,稳态误差越小(2)改变转折频率:超调量,调节时间,峰值时间,稳态误差同样有相应的变化。
自动控制原理MATLAB实验报告
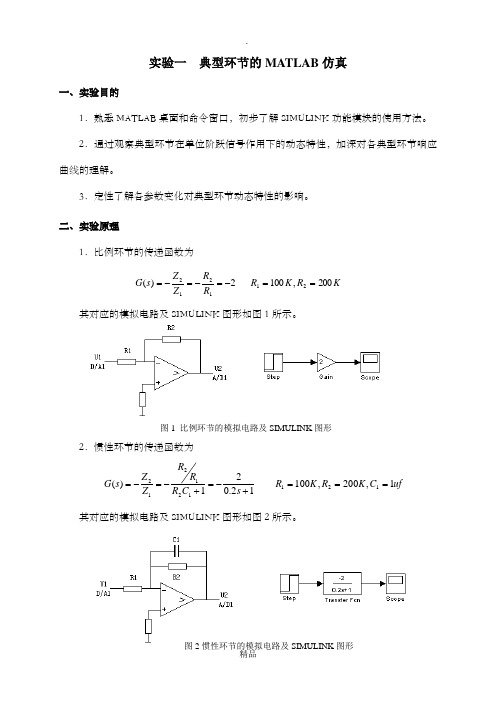
实验一 典型环节的MATLAB 仿真一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验原理1.比例环节的传递函数为 K R K R R R Z ZsG 200,1002)(211212==-=-=-=其对应的模拟电路及SIMULINK 图形如图1所示。
2.惯性环节的传递函数为uf C K R K R s C R R R Z Z s G 1,200,10012.021)(121121212===+-=+-=-=其对应的模拟电路及SIMULINK 图形如图2所示。
图1 比例环节的模拟电路及SIMULINK 图形3.积分环节(I)的传递函数为uf C K R s s CR Z Z s G 1,1001.011)(111112==-=-=-=其对应的模拟电路及SIMULINK 图形如图3所示。
4.微分环节(D)的传递函数为uf C K R s s C R Z Z s G 10,100)(111112==-=-=-= uf C C 01.012=<<其对应的模拟电路及SIMULINK 图形如图4所示。
5.比例+微分环节(PD )的传递函数为)11.0()1()(111212+-=+-=-=s s C R R R Z Z s G uf C C uf C K R R 01.010,10012121=<<===其对应的模拟电路及SIMULINK 图形如图5所示。
图3 积分环节的模拟电路及及SIMULINK 图形图4 微分环节的模拟电路及及SIMULINK 图形6.比例+积分环节(PI )的传递函数为 )11(1)(11212sR s C R Z Z s G +-=+-=-= uf C K R R 10,100121=== 其对应的模拟电路及SIMULINK 图形如图6所示。
自动控制原理MATLAB仿真实验报告

实验一 MATLAB 及仿真实验(控制系统的时域分析)一、实验目的学习利用MATLAB 进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性; 二、预习要点1、 系统的典型响应有哪些2、 如何判断系统稳定性3、 系统的动态性能指标有哪些 三、实验方法(一) 四种典型响应1、 阶跃响应:阶跃响应常用格式:1、)(sys step ;其中sys 可以为连续系统,也可为离散系统。
2、),(Tn sys step ;表示时间范围0---Tn 。
3、),(T sys step ;表示时间范围向量T 指定。
4、),(T sys step Y =;可详细了解某段时间的输入、输出情况。
2、 脉冲响应:脉冲函数在数学上的精确定义:0,0)(1)(0〉==⎰∞t x f dx x f其拉氏变换为:)()()()(1)(s G s f s G s Y s f ===所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式: ① )(sys impulse ; ②);,();,(T sys impulse Tn sys impulse③ ),(T sys impulse Y =(二) 分析系统稳定性 有以下三种方法:1、 利用pzmap 绘制连续系统的零极点图;2、 利用tf2zp 求出系统零极点;3、 利用roots 求分母多项式的根来确定系统的极点 (三) 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容 (一) 稳定性1. 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ,试判断其稳定性2. 用Matlab 求出253722)(2342++++++=s s s s s s s G 的极点。
%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den)运行结果: p =+ - + -P ole-Zero MapReal AxisI m a g i n a r y A x i s-2-1.5-1-0.500.5-1.5-1-0.50.511.5图1-1 零极点分布图由计算结果可知,该系统的2个极点具有正实部,故系统不稳定。
自动控制原理MATLAB仿真实验报告

实验一MATLAB 及仿真实验(控制系统的时域分析)一、实验目的学习利用MATLAB进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性;二、预习要点1、系统的典型响应有哪些?2、如何判断系统稳定性?3、系统的动态性能指标有哪些?三、实验方法(一)四种典型响应1、阶跃响应:阶跃响应常用格式:1 、step ( sys ) ;其中 sys 可以为连续系统,也可为离散系统。
2 、step ( sys ,Tn ) ;表示时间范围0---Tn 。
3 、step ( sys ,T ) ;表示时间范围向量T 指定。
4 、Y step ( sys , T ) ;可详细了解某段时间的输入、输出情况。
2、脉冲响应:f (x)dx 1脉冲函数在数学上的精确定义:f ( x) 0, t 0f ( s) 1其拉氏变换为:Y ( s) G (s) f (s) G ( s)所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式:①impulse ( sys ) ;impulse ( sys , Tn );②impulse ( sys , T );③Y impulse ( sys ,T )(二)分析系统稳定性有以下三种方法:1、利用 pzmap绘制连续系统的零极点图;2、利用 tf2zp 求出系统零极点;3、利用 roots 求分母多项式的根来确定系统的极点(三)系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容(一) 稳定性1.系统传函为4 3 23s 2s 5s 4s 6G s ,试判断其稳定性5 4 3 2s 3s 4 s 2s 7s 22.用 Matlab 求出2s 2 s 2G 的极点。
( s)4 3 2s 7 s 3s 5 s 2%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den)运行结果:p =-1.7680 + 1.2673i-1.7680 - 1.2673i0.4176 + 1.1130i0.4176 - 1.1130i-0.2991Pole-Zero Map 1.510.5sixAyranigamI-0.5-1-1.5-2 -1.5 -1 -0.5 0 0.5Real Axis图 1-1 零极点分布图由计算结果可知,该系统的 2 个极点具有正实部,故系统不稳定。
《自动控制原理》仿真实验报告

中国地质大学江城学院《自动控制原理》仿真实验报告姓名吴丽芳班级数控(2)班学号2520110228指导教师祁锋2013年12月9 日目录实验一 MATLAB软件的安装与认知实验二使用软件进行数值运算和绘图实验三采用SIMULINK仿真模块进行系统性能分析实验一 MATLAB软件的认识一、实验目的MATLAB软件是具有数值分析、矩阵运算、复杂的信息处理和完美的图形显示等多种功能的软件包,它具有许多专门用途的工具箱,进一步扩展了MATLAB 的应用领域,使其在自动控制系统的分析和设计方面获得广泛的应用。
1、熟悉启动和退出MATLAB软件的方法;2、熟悉MATLAB软件的运行环境;3、熟悉MATLAB软件的基本操作;4、掌握建立矩阵的方法;5、掌握熟悉MATLAB软件各种表达式的书写规则以及常用函数的使用;6、能够进行基本的数组、矩阵运算。
二、实验内容熟悉MATLAB软件的各个工具箱、指令及常用工具,掌握数值的表示方法、运算符的使用规则及运算表达式的写法。
三、分析讨论题1、MATLAB软件有哪些常用指令?有哪些专用工具箱?help elfun %列出所有基本函数。
lookfor image 查找有关图像的函数和命令。
几个常用的通用命令。
quit 关闭MATLABexit 关闭MATLABclc 清除MATLAB命令窗口中的所有显示内容clear 清除工作空间中保存的所有变量Matlab Main Toolbox——matlab主工具箱Control System Toolbox——控制系统工具箱Communication Toolbox——通讯工具箱Financial Toolbox——财政金融工具箱System Identification Toolbox——系统辨识工具箱Fuzzy Logic Toolbox——模糊逻辑工具箱Neural Network Toolbox——神经网络工具箱Optimization Toolbox——优化工具箱Partial Differential Toolbox——偏微分方程工具箱Robust Control Toolbox——鲁棒控制工具箱Signal Processing Toolbox——信号处理工具箱Spline Toolbox——样条工具箱Statistics Toolbox——统计工具箱Symbolic Math Toolbox——符号数学工具箱Simulink Toolbox——动态仿真工具箱Wavele Toolbox——小波工具箱2、用举例的方法说明数值的表示方法是怎样的?MATLAB的数值采用十进制,可以带小数点或负号。
自动控制原理MATLAB分析与设计仿真实验报告(最终版)

兰州理工大学《自动控制原理》MATLAB分析与设计仿真实验报告学院:电气工程与信息工程学院专业班级: 13级自动化3班姓名:学号:时间: 2015年12月Step ResponseTime (seconds)A m p l i t u d e1234567891000.511.5System: sys1Rise time (seconds): 1.17System: sys1P eak amplitude: 1.41Overshoot (%): 40.6At time (seconds): 2.86System: sys1Final value: 1第三章 线性系统的时域分析法一、教材第三章习题3.5设单位反馈系统的开环传递函数为G(s)=0.41(0.6)s s s ++(1)试求系统在单位阶跃输入下的动态性能。
(2)忽略闭环零点的系统在单位阶跃输入下的动态性能。
(3)对(1) 和(2)的动态性能进行比较并分析仿真结果。
(1)A :程序如下。
B :系统响应曲线如下图。
Step Response Time (seconds)A m p l i t u d e01234567891000.20.40.60.811.21.4System: sys1Final value: 1System: sys1Settling time (seconds): 8.08System: sys1P eak amplitude: 1.16Overshoot (%): 16.3At time (seconds): 3.63System: sys1Rise time (seconds): 1.64(2)A :程序如下。
B :系统响应曲线如下图。
(3) A :程序如下。
B 响应曲线如下图。
阶跃响应t (sec)c (t )0123456789100.20.40.60.811.21.4System: sysRise Time (sec): 1.46System: sys1Rise Time (sec): 1.64System: sys1P eak amplitude: 1.16Overshoot (%): 16.3At time (sec): 3.63System: sys P eak amplitude: 1.18Overshoot (%): 18At time (sec): 3.16System: sys1Final Value: 1System: sys1Settling Time (sec): 8.08System: sysSettling Time (sec): 7.74120,0.1ττ==120.1,0ττ==分析:忽略闭环零点时,系统的峰值时间,调节时间,上升时间均为增大的,而超调量减小。
自动控制原理MATLAB仿真实验报告

实验一 典型环节的MATLAB 仿真 一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验内容① 比例环节1)(1=s G 和2)(1=s G ;Simulink 图形实现:示波器显示结果:② 惯性环节11)(1+=s s G 和15.01)(2+=s s GSimulink 图形实现:示波器显示结果:③ 积分环节s s G 1)(1Simulink 图形实现:示波器显示结果:④ 微分环节s s G )(1Simulink 图形实现:波器显示结果:⑤ 比例+微分环节(PD )2)(1+=s s G 和1)(2+=s s G1)、G1(s )=s+2Simulink 图形实现:示波器显示结果:2)、G2(s)=s+1 Simulink图形实现:示波器显示结果:⑥ 比例+积分环节(PI )s s G 11)(1+=和s s G 211)(2+=1)、G1(1)=1+1/sSimulink 图形实现:示波器显示结果:2)G2(s)=1+1/2s Simulink图形实现:示波器显示结果:三、心得体会通过这次实验我学到了很多,对课本内容加深了理解,熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法,加深对各典型环节响应曲线的理解,这为对课程的学习打下了一定基础。
实验二线性系统时域响应分析一、实验目的1.熟练掌握step( )函数和impulse( )函数的使用方法,研究线性系统在单位阶跃、单位脉冲及单位斜坡函数作用下的响应。
2.通过响应曲线观测特征参量ζ和nω对二阶系统性能的影响。
3.熟练掌握系统的稳定性的判断方法。
二、实验内容1.观察函数step( )的调用格式,假设系统的传递函数模型为243237()4641s s G s s s s s ++=++++绘制出系统的阶跃响应曲线?2.对典型二阶系统222()2n n n G s s s ωζωω=++1)分别绘出2(/)n rad s ω=,ζ分别取0,0.25,0.5,1.0和2.0时的单位阶跃响应曲线,分析参数ζ对系统的影响,并计算ζ=0.25时的时域性能指标,,,,p r p s ss t t t e σ。
Matlab仿真实验-自动控制原理

实验一 典型环节的MATLAB 仿真一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK 的使用MATLAB 中SIMULINK 是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK 功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB 软件,在命令窗口栏“>>”提示符下键入simulink 命令,按Enter 键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK 仿真环境下。
2.选择File 菜单下New 下的Model 命令,新建一个simulink 仿真环境常规模板。
3.在simulink 仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:图1-1 SIMULINK 仿真界面 图1-2 系统方框图1)进入线性系统模块库,构建传递函数。
点击simulink 下的“Continuous ”,再将右边窗口中“Transfer Fen ”的图标用左键拖至新建的“untitled ”窗口。
2)改变模块参数。
在simulink 仿真环境“untitled ”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK ,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的simulink 的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math ”右边窗口“Gain ”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink 下的“Source ”,将右边窗口中“Step ”图标用左键拖至新建的“untitled ”窗口,形成一个阶跃函数输入模块。
自动控制原理实验报告MATHLAB建模.doc

自动控制原理实验报告学院:机电工程学院班级:姓名:学号:指导老师:实验一:在MATLAB中创建系统模型一、实验目的:1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
二、实验过程:1.传递函数模型的建立1)多项式形式的传递函数①课本例2.23上机操作过程如下:②课本P62,习题2-3上机操作过程如下:2)零、极点形式的传递函数课本例2.24上机操作过程如下:3)分子、分母为因式乘积形式的传递函数课本例2.25上机操作过程如下:2.Simulink 建模①课本例题上机操作如下:设单位反馈系统的开环传递函数为:)1(1)(+=s s s G将其转换成Simulink 框图,输入为阶跃信号,它的Simulink 框图如下所示:② 比例环节1)(1=s G 和2)(1=s G 的SIMULINK 图形建模操作如下;比例环节1)(1=s G 的SIMULINK 图形如下图所示:比例环节2)(1=s G 的SIMULINK 图形3.课后练习用matlab求下列函数的拉氏变换(习题2-1),上机操作过程如图所示:实验二:在MATLAB中算特征根及绘制根轨迹图一、实验目的:1.掌握MATLAB下的根轨迹绘制方法;2.学会利用根轨迹进行系统分析。
二、实验过程:1)例3-21 试利用MATLAB函数求例3.1中k=2.k=20时系统的特征根,并分别判定稳定性。
上机操作过程如下:>> num=[2];den=conv([1 0],conv([0.1 1],[0.25 1]));g=tf(num,den);sys=feedback(g,1);>> pzmap(sys)p=pole(sys)p =-11.0314-1.4843 + 2.2470i-1.4843 - 2.2470i2)例3-22 二阶系统如图3.13所示,设Wn=1,试研究系统的单位阶跃响应与参数ξ的关系。
自动控制原理matlab实验报告
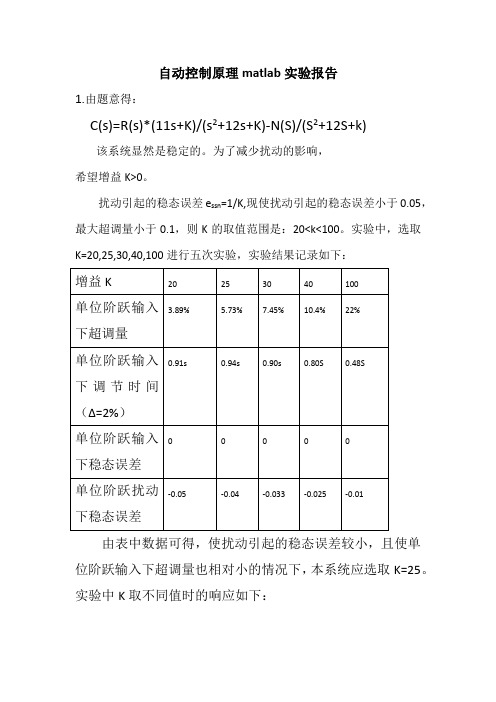
自动控制原理matlab实验报告1.由题意得:C(s)=R(s)*(11s+K)/(s2+12s+K)-N(S)/(S2+12S+k)该系统显然是稳定的。
为了减少扰动的影响,希望增益K>0。
扰动引起的稳态误差e ssn=1/K,现使扰动引起的稳态误差小于0.05,最大超调量小于0.1,则K的取值范围是:20<k<100。
实验中,选取K=20,25,30,40,100进行五次实验,实验结果记录如下:由表中数据可得,使扰动引起的稳态误差较小,且使单位阶跃输入下超调量也相对小的情况下,本系统应选取K=25。
实验中K取不同值时的响应如下:K=20 K=25K=30 K=40K=1002.C(s)=R(s)*Ka/(s2+k1s+Ka)-N(S)/(S2+k1S+ka)(1)在阶跃指令r(t)作用下,系统输出的超调量小于或等于10%; 由解得:代入σ=0.1,求出 ζ=0.59,取ζ=0.6。
因而,在满足σ%≤10%指标要求下,应选(2)在斜坡输入作用下,稳态误差达到最小; 令斜坡输入为r(t)=Bt,可得斜坡输入作用下的稳态误差:结合要求(1)可得此式表明K a 应取尽可能大(3)减小单位阶跃扰动的影响。
阶跃扰动作用下的稳态误差22)(ln 11σπ+=ζaa 1K 2.1K 2K =ζ=a 1ssrK BK K B e ==assrK B 2.1e =)s (sC )s (sEe n 0s ns ssn l i m l i m →→-==aa 12s 00s K 1s1K s K s 1s)s (N )s (G 1)s (G s l i m l i m -=++-=+-=→→%e100%21 / ζ- πζ - =σ可见,增大K a可以同时减小e ssn及e ssr。
在实际系统中,K a的选取必须受到限制,以使系统工作在线性区。
实验中选取以下几组数据进行仿真。
KA=100,K1=12 KA=576,K1=30KA=625,K1=30 KA=900,K1=40KA=1000,K1=45由上表及仿真图分析可知应取K a =1000,K 1=45.3. 此系统的特征方程为:s 4+8s 3+17s 2+(10+K 1)s+aK 1=0 由题目要求可得: 斜坡输入下的稳态误差:K K )a 64116(12600aK 126K 21111>--+><令斜坡输入为r(t)=At令稳态误差等于输入指令幅度的24%。
自动控制原理Matlab实验1(初步认识MATLAB和系统仿真)

《自动控制原理》课程实验报告实验名称初步认识MATLAB和系统仿真专业班级 ********* 学************号姓名**指导教师李离学院名称电气信息学院2012 年 11 月 5 日Lab1_1_1.m程序:y0=0.15;wn=sqrt(2);zeta=1/(2*sqrt(2));t=[0:0.1:10];c=(y0/sqrt(1-zeta^2));y=c*exp(-zeta*wn*t).*sin(wn*sqrt(1-zeta^2)*t+acos(zeta)); bu=c*exp(-zeta*wn*t);bl=-bu;plot(t,y,t,bu,'k--',t,bl,'k--'),gridxlabel('Time (sec)'),ylabel('y(t) (meters)')legend(['\omega_n=',num2str(wn),' \zeta=',num2str(zeta)])仿真结果:(1)零输入响应曲线理论分析:0<ζ<1,对于二阶响应,其瞬态响应应该是一个按照指数衰减的振荡过程,ζ越小,衰减越慢,该系统是欠阻尼系统。
从图中也可以看出,系统是零输入响应,是个震荡衰减的过程,符合理论判断。
Lab1_1_2.m程序:y0=0.15;wn=sqrt(2);zeta=1;t=[0:0.1:10];y=y0*(exp(-wn*t)+wn*t.*exp(-wn*t));plot(t,y),gridxlabel('Time (sec)'),ylabel('y(t) (meters)')legend(['\omega_n=',num2str(wn),' \zeta=',num2str(zeta)])仿真结果:(2)零输入响应曲线理论分析:在图中可以看到,随着时间的增加,响应在逐渐减小。
《自动控制原理》MATLAB的使用分析与设计研究 仿真实验报告

兰州理工大学《自动控制原理》MATLAB分析与设计仿真实验报告院系:电信学院班级:姓名:学号:时间:2010年11月30日电气工程与信息工程学院《自动控制原理》MATLAB分析与设计仿真实验任务书(2009)一.仿真实验内容及要求:1.MATLAB软件要求学生通过课余时间自学掌握MATLAB软件的基本数值运算、基本符号运算、基本程序设计方法及常用的图形命令操作;熟悉MATLAB仿真集成环境Simulink的使用。
2.各章节实验内容及要求1)第三章线性系统的时域分析法• 对教材P136.3-5系统进行动态性能仿真,并与忽略闭环零点的系统动态性能进行比较,分析仿真结果;• 对教材P136.3-9系统的动态性能及稳态性能通过的仿真进行分析,说明不同控制器的作用;• 在MATLAB 环境下完成英文讲义P153.E3.3。
• 对英文讲义中的循序渐进实例“Disk Drive Read System ”,在100=a K 时,试采用微分反馈使系统的性能满足给定的设计指标。
2)第四章 线性系统的根轨迹法• 在MATLAB 环境下完成英文讲义P157.E4.5; • 利用MATLAB 绘制教材P181.4-5-(3);• 在MATLAB 环境下选择完成教材第四章习题4-10或4-18,并对结果进行分析。
3)第五章 线性系统的频域分析法利用MATLAB 绘制本章作业中任意2个习题的频域特性曲线; 4)第六章 线性系统的校正利用MATLAB 选择设计本章作业中至少2个习题的控制器,并利用系统的单位阶跃响应说明所设计控制器的功能。
5)第七章 线性离散系统的分析与校正• 利用MATLAB 完成教材P383.7-20的最小拍系统设计及验证。
• 利用MATLAB 完成教材P385.7-25的控制器的设计及验证。
二.仿真实验时间安排及相关事宜1.依据课程教学大纲要求,仿真实验共6学时,教师可随课程进度安排上机时间,学生须在实验之前做好相应的准备,以确保在有限的机时内完成仿真实验要求的内容; 2.实验完成后按规定完成相关的仿真实验报告; 3.仿真实验报告请参照有关样本制作并打印装订;4.仿真实验报告必须在本学期第15学周结束之前上交授课教师。
自动控制原理Matlab实验2(基于MATLAB仿真的系统时域分析)

⾃动控制原理Matlab实验2(基于MATLAB仿真的系统时域分析)《⾃动控制原理》课程实验报告实验名称基于MATLAB仿真的系统时域分析专业班级 ********************学号姓名**指导教师李离学院名称电⽓信息学院2012 年 11 ⽉ 20 ⽇Lab3_1.m程序:t=[0:0.1:12]; num=[1];zeta1=0.1; den1=[1 2*zeta1 1]; sys1=tf(num,den1); zeta2=0.2; den2=[1 2*zeta2 1]; sys2=tf(num,den2); zeta3=0.4; den3=[1 2*zeta3 1]; sys3=tf(num,den3); zeta4=0.7; den4=[1 2*zeta4 1]; sys4=tf(num,den4); zeta5=1.0; den5=[1 2*zeta5 1];sys5=tf(num,den5); zeta6=2.0; den6=[1 2*zeta6 1]; sys6=tf(num,den6); [y1,T1]=step(sys1,t); [y2,T2]=step(sys2,t);[y3,T3]=step(sys3,t); [y4,T4]=step(sys4,t);[y5,T5]=step(sys5,t); [y6,T6]=step(sys6,t);plot(T1,y1,T2,y2,T3,y3,T4,y4,T5,y5,T6,y6)xlabel('\omega_n t'), ylabel('y(t)')title('\zeta = 0.1, 0.2, 0.4, 0.7, 1.0, 2.0'), grid仿真结果:理论分析:从上图可以看出,保持)/(1s rad n=ω不变,依次取值0.1,0.2,0.4,0.7,1.0和2.0时,系统逐渐从⽋阻尼系统过渡到临界阻尼系统再到过阻尼系统,系统的超调量随ζ的增⼤⽽减⼩,上升时间随ζ的增⼤⽽变长,系统的响应速度随ζ的增⼤⽽变慢,系统的稳定性随ζ的增⼤⽽增强。
自动控制原理Matlab仿真实验实验

源程序: numg=[1];deng=[500,0,0]; numc=[1,1];denc=[1,2]; [num1,den1]=series(numg,deng,numc,denc); [num,den]=cloop(num,den,-1); printsys(num,den) 运行结果: num/den = s + 1 ---------------------------500 s^3 + 1000 s^2 + 4 s + 4 3、 传递函数零、极点的求取 在命令窗口依次运行下面命令,并记录各命令运行后结果
示波器显示仿真结果:
(2)G2(s)= 1+1/2s Simulink 图形:
示波器显示仿真结果:
实验三 控制系统的时域分析
一、实验目的 学习利用 MATLAB 进行控制系统时域分析,包括典型响应、判断系统稳定性和分 析系统的动态特性。 二、实验内容 (一) 稳定性 1、系统传函为 G(s) =
4
源程序: roots([1 7 3 5 2]) 运行结果: ans = - 6.6553 0.0327 + 0.8555i 0.0327 - 0.8555i - 0.4100 结论: 特征方程根具有正实部,因而系统是不稳定的 (二)阶跃响应 1. 二阶系统 G (s ) =
10 s + 2 s + 10
示波器显示仿真结果如下:
②惯性环节 G1(s)=1/s+1 和 G2(s)=1/0.5s+1。 Simulink 图形:
示波器显示仿真结果如下:
③积分环节 G1(s)=1/s。
Simulink 图形:
示波器显示仿真结果如下:
④微分环节 G1(s)= s。 Simulink 图形:
《自动控制原理》实验报告-MATLAB分析与设计仿真

兰州理工大学《自动控制原理》MATLAB分析与设计仿真实验报告院系:电信学院班级:姓名:学号:时间:2010 年11 月22 日电气工程与信息工程学院《自动控制原理》MATLAB分析与设计仿真实验任务书(2010)一.仿真实验内容及要求:1.MATLAB软件要求学生通过课余时间自学掌握MATLAB软件的基本数值运算、基本符号运算、基本程序设计方法及常用的图形命令操作;熟悉MATLAB仿真集成环境Simulink的使用。
2.各章节实验内容及要求1)第三章线性系统的时域分析法•对教材P136.3-5系统进行动态性能仿真,并与忽略闭环零点的系统动态性能进行比较,分析仿真结果;•对教材P136.3-9系统的动态性能及稳态性能通过的仿真进行分析,说明不同控制器的作用;•在MATLAB环境下完成英文讲义P153.E3.3。
•对英文讲义中的循序渐进实例“Disk Drive Read System”,在100=K时,试采a用微分反馈使系统的性能满足给定的设计指标。
2)第四章线性系统的根轨迹法•在MATLAB环境下完成英文讲义P157.E4.5;•利用MATLAB绘制教材P181.4-5-(3);•在MATLAB环境下选择完成教材第四章习题4-10或4-18,并对结果进行分析。
3)第五章线性系统的频域分析法利用MATLAB绘制本章作业中任意2个习题的频域特性曲线;4)第六章线性系统的校正利用MATLAB选择设计本章作业中至少2个习题的控制器,并利用系统的单位阶跃响应说明所设计控制器的功能。
5)第七章线性离散系统的分析与校正•利用MATLAB完成教材P383.7-20的最小拍系统设计及验证。
•利用MATLAB完成教材P385.7-25的控制器的设计及验证。
二.仿真实验时间安排及相关事宜1.依据课程教学大纲要求,仿真实验共6学时,教师可随课程进度安排上机时间,学生须在实验之前做好相应的准备,以确保在有限的机时内完成仿真实验要求的内容;2.实验完成后按规定完成相关的仿真实验报告;3.仿真实验报告请参照有关样本制作并打印装订;4.仿真实验报告必须在本学期第15学周结束之前上交授课教师。
自动控制原理MATLAB仿真实验指导书(4个实验)

自动控制原理MATLAB仿真实验实验指导书电子信息工程教研室实验一典型环节的MA TLAB仿真一、实验目的1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MA TLAB软件,在命令窗口栏“>>”提示符下键入simulink命令,按Enter键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK仿真环境下。
2.选择File菜单下New下的Model命令,新建一个simulink仿真环境常规模板。
图1-1 SIMULINK仿真界面图1-2 系统方框图3.在simulink仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击simulink下的“Continuous”,再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。
2)改变模块参数。
在simulink仿真环境“untitled”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的simulink的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math”右边窗口“Gain”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink下的“Source”,将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口,形成一个阶跃函数输入模块。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制原理实验报告学 院 电子信息与电气工程学院实验一 MATLAB 及仿真实验(控制系统的时域分析)一、实验目的学习利用MATLAB 进行控制系统时域分析,包括典型响应、判断系统稳定性和分析系统的动态特性;二、预习要点1、 系统的典型响应有哪些?2、 如何判断系统稳定性?3、 系统的动态性能指标有哪些?三、实验方法(一) 四种典型响应1、 阶跃响应:阶跃响应常用格式:1、)(sys step ;其中sys 可以为连续系统,也可为离散系统。
2、),(Tn sys step ;表示时间范围0---Tn 。
3、),(T sys step ;表示时间范围向量T 指定。
4、),(T sys step Y =;可详细了解某段时间的输入、输出情况。
2、 脉冲响应:脉冲函数在数学上的精确定义:0,0)(1)(0〉==⎰∞t x f dx x f 其拉氏变换为:)()()()(1)(s G s f s G s Y s f === 所以脉冲响应即为传函的反拉氏变换。
脉冲响应函数常用格式: ① )(sys impulse ;② );,();,(T sys impulse Tn sys impulse ③ ),(T sys impulse Y =(二) 分析系统稳定性有以下三种方法:1、 利用pzmap 绘制连续系统的零极点图;2、 利用tf2zp 求出系统零极点;3、 利用roots 求分母多项式的根来确定系统的极点(三) 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容(一) 稳定性1. 系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ,试判断其稳定性2. 用Matlab 求出253722)(2342++++++=s s s s s s s G 的极点。
%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den)运行结果:p =-1.7680 + 1.2673i-1.7680 - 1.2673i0.4176 + 1.1130i0.4176 - 1.1130i-0.2991图1-1 零极点分布图由计算结果可知,该系统的2个极点具有正实部,故系统不稳定。
%求取极点num=[1 2 2];den=[1 7 3 5 2];p=roots(den)运行结果:p =-6.65530.0327 + 0.8555i0.0327 - 0.8555i-0.4100 故253722)(2342++++++=s s s s s s s G 的极点s1=-6.6553 , s2=0.0327 + 0.8555i ,s3= 0.0327 - 0.8555i , s4=-0.41(二)阶跃响应1. 二阶系统()102102++=s s s G1)键入程序,观察并记录单位阶跃响应曲线2)计算系统的闭环根、阻尼比、无阻尼振荡频率,并记录3)记录实际测取的峰值大小、峰值时间及过渡过程时间,并填表:由图1-3及其相关理论知识可填下表:3//πωπ==d p t =1.0472 实际值 理论值峰值C max 1.35 1.3509峰值时间t p 1.09 1.0472 过渡时间 t s 3.5 4.5 4)修改参数,分别实现1=ζ和2=ζ的响应曲线,并记录 4.52%(00.9)3.55%ns nt ζωζζω⎧∆=⎪⎪=<<⎨⎪∆=⎪⎩5)修改参数,分别写出程序实现0121w w n =和022w w n =的响应曲线,并记录 %单位阶跃响应曲线num=[10];den=[1 2 10];step(num,den);title('Step Response of G(s)=10/(s^2+2s+10)'); 图1-2 二阶系统()102102++=s s s G 单位阶跃响应曲线%计算系统的闭环根、阻尼比、无阻尼振荡频率num=[10];den=[1 2 10];G=tf(num,den);[wn,z,p]=damp(G)运行结果:wn =3.16233.1623z =0.31620.3162p =-1.0000 + 3.0000i-1.0000 - 3.0000i 由上面的计算结果得系统的闭环根s= -1±3i ,阻尼比=ς3162.0、无阻尼振荡频率1623.3=n ω实验二 MATLAB 及仿真实验(控制系统的根轨迹分析)一 实验目的1.利用计算机完成控制系统的根轨迹作图2.了解控制系统根轨迹图的一般规律3.利用根轨迹图进行系统分析二 预习要点1. 预习什么是系统根轨迹?2. 闭环系统根轨迹绘制规则。
三 实验方法(一) 方法:当系统中的开环增益k 从0到变化时,闭环特征方程的根在复平面上的一组曲线为根轨迹。
设系统的开环传函为:)()()(0s Q s N k s G =,则系统的闭环特征方程为:0)()(1)(10=+=+s Q s N k s G 根轨迹即是描述上面方程的根,随k 变化在复平面的分布。
(二) MATLAB 画根轨迹的函数常用格式:利用Matlab 绘制控制系统的根轨迹主要用pzmap ,rlocus ,rlocfind ,sgrid 函数。
1、零极点图绘制❑ [p,z]=pzmap(a,b,c,d):返回状态空间描述系统的极点矢量和零点矢量,而不在屏幕上绘制出零极点图。
❑ [p,z]=pzmap(num,den):返回传递函数描述系统的极点矢量和零点矢量,而不在屏幕上绘制出零极点图。
❑ pzmap(a,b,c,d)或pzmap(num,den):不带输出参数项,则直接在s 复平面上绘制出系统对应的零极点位置,极点用×表示,零点用o 表示。
❑ pzmap(p,z):根据系统已知的零极点列向量或行向量直接在s 复平面上绘制出对应的零极点位置,极点用×表示,零点用o 表示。
2、根轨迹图绘制❑ rlocus(a,b,c,d)或者rlocus(num,den):根据SISO 开环系统的状态空间描述模型和传递函数模型,直接在屏幕上绘制出系统的根轨迹图。
开环增益的值从零到无穷大变化。
❑ rlocus(a,b,c,d,k)或rlocus(num,den,k): 通过指定开环增益k 的变化范围来绘制系统的根轨迹图。
❑ r=rlocus(num,den,k) 或者[r,k]=rlocus(num,den) :不在屏幕上直接绘出系统的根轨迹图,而根据开环增益变化矢量k ,返回闭环系统特征方程1+k*num(s)/den(s)=0的根r ,它有length(k)行,length(den)-1列,每行对应某个k 值时的所有闭环极点。
或者同时返回k 与r 。
❑ 若给出传递函数描述系统的分子项num 为负,则利用rlocus 函数绘制的是系统的零度根轨迹。
(正反馈系统或非最小相位系统)3、rlocfind()函数❑ [k,p]=rlocfind(a,b,c,d)或者[k,p]=rlocfind(num,den)它要求在屏幕上先已经绘制好有关的根轨迹图。
然后,此命令将产生一个光标以用来选择希望的闭环极点。
命令执行结果:k 为对应选择点处根轨迹开环增益;p 为此点处的系统闭环特征根。
❑ 不带输出参数项[k,p]时,同样可以执行,只是此时只将k 的值返回到缺省变量ans 中。
4、sgrid()函数❑ sgrid :在现存的屏幕根轨迹或零极点图上绘制出自然振荡频率wn 、阻尼比矢量z 对应的格线。
❑ sgrid(‘new’):是先清屏,再画格线。
❑ sgrid(z,wn):则绘制由用户指定的阻尼比矢量z 、自然振荡频率wn 的格线。
四 实验内容1.()()()21++=s s s k s G g 要求: 二、记录根轨迹的起点、终点与根轨迹的条数; 三、确定根轨迹的分离点与相应的根轨迹增益; 四、 确定临界稳定时的根轨迹增益gL k%Matlab 计算程序z=[];p=[0 -1 -2];k=1;G=zpk(z,p,k);figure(1);pzmap(G)figure(2);rlocus(G)title('实验2.1所作曲线');(a )由图2-2知,起点分别为0,-1,-2,终点为无穷远处,共三条根轨迹.(b) 结合图2-3和图2-5得分离点d=-0.4226,相应的根轨迹增益k=-0.3849.(c) 结合图2-3和图2-4得临界稳定时的根轨迹增益gL k =6.01图2-1 零、极点分布图图2-2 根轨迹图图2-3 根轨迹图(2)%求临界稳定时的根轨迹增益Kglz=[];p=[0 -1 -2];k=1;G=zpk(z,p,k);rlocus(G)title('实验2.1 临界稳定时的根轨迹增益Kgl');[k,p]=rlocfind(G)运行结果:Select a point in the graphics windowselected_point =0.0059 + 1.4130ik =6.0139p =-3.00130.0006 + 1.4155i0.0006 - 1.4155i图2-4 根轨迹图(3)实验三 MATLAB 及仿真实验(控制系统的频域分析)一 实验目的1. 利用计算机作出开环系统的波特图2. 观察记录控制系统的开环频率特性3. 控制系统的开环频率特性分析二 预习要点1. 预习Bode 图和Nyquist 图的画法;2. 映射定理的内容;3. Nyquist 稳定性判据内容。
三 实验方法1、奈奎斯特图(幅相频率特性图)❑ 对于频率特性函数G(jw),给出w 从负无穷到正无穷的一系列数值,分别求出Im(G(jw))和Re(G(jw))。
以Re(G(jw)) 为横坐标, Im(G(jw)) 为纵坐标绘制成为极坐标频率特性图。
MATLAB 提供了函数nyquist()来绘制系统的极坐标图,其用法如下:❑ nyquist(a,b,c,d):绘制出系统的一组Nyquist 曲线,每条曲线相应于连续状态空间系统[a,b,c,d]的输入/输出组合对。
其中频率范围由函数自动选取,而且在响应快速变化的位置会自动采用更多取样点。
❑ nyquist(a,b,c,d,iu):可得到从系统第iu 个输入到所有输出的极坐标图。
❑ nyquist(num,den):可绘制出以连续时间多项式传递函数表示的系统的极坐标图。
