梁格法截面特性计算知识讲解
谈谈梁格法

谈谈梁格法目前解决曲线桥梁计算方法有以下几种:1、空间梁元模型法2、空间薄壁箱梁元模型法3、空间梁格模型法4、实体、板壳元模型法第一种方法,是不能考虑桥梁的横向效应的,使用时要求桥梁的宽跨比不易太大。
第二种方法,是第一种方法的改进,主要区别是采用了不同的单元模型,考虑了横向作用如翘曲和畸变。
第四种方法,是解决问题最有效的方法,能够考虑各种结构受力问题。
第三种方法,是目前设计及科研中常采用的方法,其特点是容易掌握,且对设计能保证足够的精度,其中采用比较多的方法是剪力-柔性梁格法,能充分考虑弯桥横向的受力特性。
剪力-柔性梁格法的原理是当梁格节点与结构重合的点承受相同挠度和转角时,由梁格产生的内力局部静力等效与结构的内力。
其实质是将传统的一维杆单元计算模式推进到二维计算模型,用一个二维的空间网格来模拟结构的受力特性。
对于梁格法的讨论这里也有不少帖子进行了讨论,实际与梁格之间的等效关系,主要表现在梁格各个构件的刚度计算上,理论上,原型和等效梁格承受相等的外荷载时,必须具有恒等的挠曲和扭转,等效梁格中每一构件的内力也必须等于该构件所代表的原型截面的,事实上这种理想状况是达不到的,模拟也是近似的,但事实是按梁格计算能把握住结构的总体性能,对于设计来说应该是能满足精度的。
梁格也是近似的模拟,只要计算者能够和好的模拟了横向纵向的特性,应该是可以作为设计依据的。
你在这里说的横向的切分使得预应力产生的次内力问题我不太清楚你指的什么,但是只要横向的刚度业等效了原型,对于计算应该不会出现逆所说的结构内力失真,这条可以通过结果验证。
当然任何结构,只要不怕麻烦都可以用实体单元来分析,只要正确模拟,实体分析也是最精确的,但是对于这种模型要准确模拟可不是一件容易的事,并且预应力的损失计算,施加等等都非常麻烦,还有最后结果的查看也不方便,因此除了结构局部的分析,一般是没有拿实体来进行全桥的整体分析的,至于说单梁我也说了,有些时候精度是可以的,但是对于这种结构相对于梁格来说单梁的精度是不如梁格的。
截面几何特性怎么计算公式

截面几何特性怎么计算公式截面几何特性的计算公式。
截面几何特性是指在工程学和物理学中,用来描述截面形状和尺寸的一些参数,这些参数对于材料的强度、刚度和形变等性能具有重要的影响。
在工程设计和分析中,我们经常需要计算截面的一些特性,比如面积、惯性矩、截面模量等。
下面我们将介绍一些常见的截面几何特性的计算公式。
1. 面积。
截面的面积是描述截面大小的一个重要参数,通常用A表示,其计算公式为:A = ∫y dA。
其中y是截面某一点到参考轴的距离,dA表示微元面积。
对于简单几何形状的截面,可以直接通过几何关系计算出面积,比如矩形的面积为长乘以宽,圆形的面积为πr^2。
2. 惯性矩。
截面的惯性矩描述了截面对于转动的惯性,通常用I表示,其计算公式为:I = ∫y^2 dA。
对于简单几何形状的截面,可以通过几何关系计算出惯性矩,比如矩形的惯性矩为bh^3/12,圆形的惯性矩为πr^4/4。
3. 截面模量。
截面模量描述了截面对拉伸和压缩的抵抗能力,通常用S表示,其计算公式为:S = I/c。
其中c为截面到参考轴的距离。
对于简单几何形状的截面,可以通过几何关系计算出截面模量,比如矩形的截面模量为bh^2/6,圆形的截面模量为πr^3/4。
4. 弯曲模量。
截面的弯曲模量描述了截面对弯曲的抵抗能力,通常用W表示,其计算公式为:W = S/y_max。
其中y_max为截面到参考轴的最大距离。
对于简单几何形状的截面,可以通过几何关系计算出弯曲模量,比如矩形的弯曲模量为bh^2/4,圆形的弯曲模量为πr^3/2。
5. 截面形心。
截面的形心描述了截面的几何中心,通常用x_bar和y_bar表示,其计算公式为:x_bar = ∫x dA / A。
y_bar = ∫y dA / A。
对于简单几何形状的截面,可以通过几何关系计算出形心的坐标,比如矩形的形心坐标为(b/2, h/2),圆形的形心坐标为(0, 0)。
以上是一些常见的截面几何特性的计算公式,这些参数对于工程设计和分析具有重要的意义。
梁的截面尺寸计算公式

梁的截面尺寸计算通常涉及到多种参数,如荷载、材料特性、梁的长度等。
下面是一些常见的梁截面尺寸计算公式:
1.弯曲应力计算:
弯曲应力是梁截面上由于弯曲而引起的应力。
弯曲应力的计算公式为:σ= M * c / S
其中,
σ是弯曲应力(单位:Pa),
M 是梁上的弯矩(单位:Nm),
c 是梁截面上离中性轴最远点的距离(也称为最大截面偏心距,单位:m),
S 是梁截面的抵抗矩(单位:m^3)。
2.剪切应力计算:
剪切应力是梁截面上由于剪力而引起的应力。
剪切应力的计算公式为:τ= V * Q / (I * b)
其中,
τ是剪切应力(单位:Pa),
V 是梁上的剪力(单位:N),
Q 是梁截面的截面模量(单位:m^3),
I 是梁截面的惯性矩(单位:m^4),
b 是梁截面的宽度(单位:m)。
3.拉伸应力计算:
拉伸应力是梁截面上由于拉伸力而引起的应力。
拉伸应力的计算公式为:
σ= F / A
其中,
σ是拉伸应力(单位:Pa),
F 是梁上的拉伸力(单位:N),
A 是梁截面的面积(单位:m^2)。
此外,还需要考虑梁的材料特性,如弹性模量(E)和抗拉强度(σ_yield)。
这些参数用于验证梁的强度和稳定性。
对于具体的工程设计,还需要根据梁的加载情况、支承条件、设计要求等进行进一步的计算和分析。
通常会参考结构设计规范和使用专业的结构分析软件进行详细的截面尺寸计算。
第6讲 曲线梁桥空间有限元分析方法—梁格法

id 2 h t1t 2 t1 t 2
2
(2-4)
式中: t 1 、 t 2 分别为顶板、底板的厚度,主要纵向构件的有效剪切面积等于腹板面积。
10
湖南大学土木工程学院桥梁工程系
1/ 4 , 箱形桥横向梁格构件的间距至少应接近于纵向弯曲的反弯点之间的间距的 采用太稀的横向构件 将使结果不精确。当有横隔板时,横隔板位置处一般也应设置横向构件。悬臂板部分横向构件的截面特性 按所代表的悬臂宽度进行计算;箱室部分横向构件(如无横隔板)的抗弯惯矩应按绕顶、底板的共同重心 处的水平中心轴进行计算,每单位宽度抗弯惯性矩的计算公式:
)
18
湖南大学土木工程学院桥梁工程系
3.3 横向梁格构件刚度确定
1)横向梁格构件的弯曲刚度
EIx=E· (横向梁格所代表的截面对X中性轴惯性矩),如果横梁内包
截面特性计算表
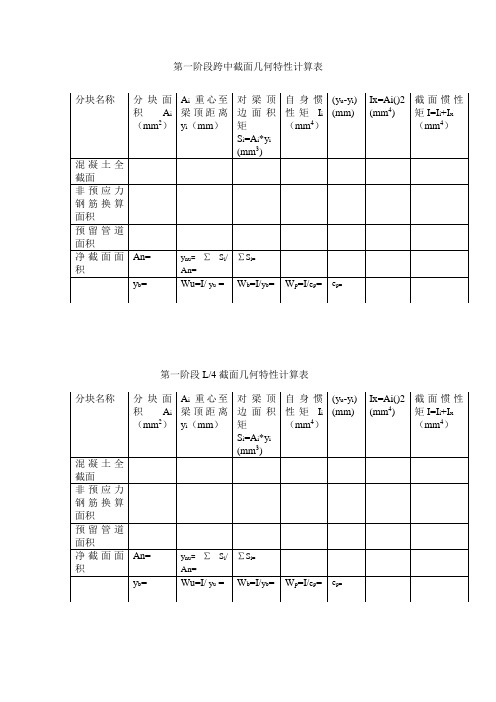
分块名称
分块面积Ai(mm2)
Ai重心至梁顶距离yi(mm)
对梁顶边面积矩Si=Ai*yi
(mm3)
自身惯性矩Iiቤተ መጻሕፍቲ ባይዱmm4)
(yu-yi)
(mm)
Ix=Ai()2
(mm4)
截面惯性矩I=Ii+Ix
(mm4)
混凝土全截面
非预应力钢筋换算面积
预留管道面积
净截面面积
An=
ynu=∑Si/ An=
∑Si=
yb=
Wu=I/yu=
Wb=I/yb=
Wp=I/ep=
ep=
分块名称
分块面积Ai(mm2)
Ai重心至梁顶距离yi(mm)
对梁顶边面积矩Si=Ai*yi
(mm3)
自身惯性矩Ii(mm4)
(yu-yi)
(mm)
Ix=Ai()2
(mm4)
截面惯性矩I=Ii+Ix
(mm4)
混凝土全截面
非预应力钢筋换算面积
(mm3)
自身惯性矩Ii(mm4)
(yu-yi)
(mm)
Ix=Ai()2
(mm4)
截面惯性矩I=Ii+Ix
(mm4)
混凝土全截面
非预应力钢筋换算面积
预留管道面积
净截面面积
An=
ynu=∑Si/ An=
∑Si=
yb=
Wu=I/yu=
Wb=I/yb=
Wp=I/ep=
ep=
第一阶段支点截面几何特性计算表
(yu-yi)
(mm)
Ix=Ai()2
(mm4)
截面惯性矩I=Ii+Ix
梁格法

当桥梁上部结构宽度和跨度之比较大时,荷载作用时不仅使 上部构造产生纵向弯曲、整体扭转,同时还使截面产生横向 变形——此时,不能采用空间直梁、曲线梁简化模型,而必 须考虑具有弹性刚度横向构件的结构体系 ——自然也需要采 用其它方法如实体单元、梁格法等。
方法二:空间实体单元(块体、板壳)
属于通用方法,可作精确分析、适用范围广 ; 存在应力集中现象 某些情况下模拟存在问题——横梁(尺寸大) 给出的是应力状态与桥规按内力配筋不匹配。 数据量大、烦琐,不便于结构设计与验算,也 无法正确评价结构受力特征。 移动活载作用效应的计算较为麻烦。 桥梁结构计算方法及应用
大量的研究和分析表明 对于大部分桥梁结构形式 使用梁格法具有足够的精度 大量的研究和分析表明:对于大部分桥梁结构形式,使用梁格法具有足够的精度。
桥梁结构计算方法及应用
梁格法的应用
四种典型结构
板式 肋板式 箱形梁 铰接板、梁
方向规定(右手螺旋法则)
x x—— 纵桥向 y——横桥向 z——竖桥向
横梁水平轴、竖向轴抗弯惯性矩按矩形板截面绕其自身形心 横梁水平轴 竖向轴抗弯惯性矩按矩形板截面绕其自身形心 主轴计算。扭转惯性矩仍按矩形板公式: bd 3
IT
6
桥梁结构计算方法及应用
二、肋板式上部结构空间构架分析
肋板式上部结构是一薄板贯通多根纵横梁顶面连接成一个整体(图10)。
(a)小跨径、纵梁密布、只在端部设置横隔板
方法一:空间梁单元
采用一维梁单元,能给出结构整体意义上的内力 和变形。 根据受载后截面是否保持平面,可分为自由扭转 理论和翘曲扭转理论。一般混凝土梁可用前者分 析 钢箱梁则必须用后者分析 析。钢箱梁则必须用后者分析。 对于宽箱梁分析,本方法计算有问题——不能得 到横梁内力
梁格法在城市立交桥异型箱梁设计中应用

梁格法在城市立交桥异型箱梁设计中的应用摘要:梁格法是城市立交桥梁上部异型结构计算分析中的一种有效方法。
本文以某立交工程上部异型结构为例,介绍了梁格法,指出分析时应注意的问题。
关键词:城市立交异型箱梁梁格法中图分类号:f291.1 文献标识码:a 文章编号:随着城市的迅速增长,互通立交的兴建越来越多。
在城市立交桥主线与匝道的相接部分,其上部结构形成了结构和受力都很复杂的异型梁桥,梁格法是一种空间分析方法,其概念清晰,易于理解、适用,在异型梁桥的设计中大量得到采用,在各种曲线和异型桥梁中应用越来越广泛。
1梁格法的优点目前桥梁空间分析的主要方法有梁单元法、板壳元法、实体分析法及梁格法。
梁单元直接给出内力和变形,但在宽梁计算中误差较大,板壳元法及实体分析法输出的是应力结果,不能直接用于强度计算,且模型复杂,数据处理繁琐、计算成本高,用于结构设计并不适用。
梁格法是唯一即有相当精度又比较容易实行的方法,可以直接输出各主梁的内力,便于根据规范进行条文验算,整体精度能够满足设计要求。
2 空间梁格法的分析步骤梁格等效模拟包括三方面,划分结构网格、模拟梁格截面特性及施加荷载。
2.1划分网格梁格法计算的准确依赖于模型网格划分的准确,在建立梁格模型时,应力学概念清晰,明确结构的传力方式,使得模型的建立尽量和结构的实际传力路径一致。
(1)纵向网格的模拟。
将多室箱梁分割为梁格时,各纵梁的中性轴应与原截面中性轴位置一致。
纵向构件的位置与纵向腹板相重合,这种布置可使腹板剪力直接由横截面上同一点的梁格剪力来表示。
(2)横向梁格设置应视结构的实际情况确定。
若横隔板较多,这时横向构件应与横隔板重心重合。
若横隔板的间距较大,则必须增加横向虚拟粱格,每跨内的虚拟的横向联系梁数量不应过分少,在连续梁结构中纵向的一个反弯点范围内要设置4~5个单元。
虚拟的横向联系梁的重量应设为零。
(3)当虚拟的横向联系梁悬挑出边梁外时,为自振周期的准确计算和分配荷载,应设置虚拟的边纵梁。
梁格法

梁格法
对于单箱单室或者双室的截面可以将顶底板均分,基本上中性轴是一致的。
对于单箱多室截面,建议参考《桥梁上部构造性能》相关部分的讲解。
一定要注意不论怎么划分要保证截面特性的一致性,抗弯惯性距是按照原来的中性轴来计算的。
箱梁在纵向弯曲时应符合平截面假定,而箱梁的纵向弯曲由各纵向单元的弯曲来模拟,因此各纵向单元顶底板的纵向划分位置应尽量使各单元截面的中性轴在同一水平面,并和原箱梁整体截面的中性轴在同一位置。
梁格法划分完的结果最好是“各单元截面的中性轴在同一水平面,并和原箱梁整体截面的中性轴在同一位置”,请问大家是怎么做到的,是cad中一遍一遍试,还是有自己的方法或经验,希望大家不啬赐教!
midas应该还做不到将每个截面划分梁格的中性轴和整体中性轴一样,都是通过移轴来实现的,不过midas划分截面貌似是保证在顺桥向,每个纵梁的各个截面的质心大致在一条直线上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梁格法截面特性计算梁格法截面特性计算读书报告目录第一章梁格法简介 (1)1.1梁格法基本思想 (1)1.2梁格网格的划分 (1)1.2.1 纵梁的划分 (2)1.2.2 虚拟横梁的设置间距 (2)第二章梁格分析板式上部结构 (3)2.1 结构类型 (3)2.2 梁格网格 (3)2.3 截面特性计算 (4)2.3.1 惯性矩 (4)2.3.2 扭转 (4)第三章梁格法分析梁板式上部结构 (5)3.1 结构类型 (5)3.2 梁格网格 (5)3.3 截面特性计算 (6)3.3.1 纵向梁格截面特性 (6)3.3.2 横向梁格截面特性 (7)第四章梁格法分析分格式上部结构 (8)4.1 结构形式 (8)4.2 梁格网格 (8)4.3 截面特性计算 (9)4.3.1 纵向梁格截面特性 (9)4.3.2 横向梁格截面特性 (12)第五章箱型截面截面特性计算算例 (15)第一章梁格法简介1.1梁格法基本思想梁格法主要思路是将上部结构用一个等效梁格来模拟,如图1.1示,将分散在板式或箱梁每一段内弯曲刚度和抗扭刚度集中于最邻近的等效梁格内,实际结构的纵向刚度集中于纵向梁格内,而横向刚度则集中于横向梁格构件内。
从理论上讲,梁格必须满足一个等效原则:当原型实际结构和对应的等效梁格承受相同荷载时,两者的挠曲应是恒等的,而且在任一梁格内的弯矩、剪力和扭矩应等于该梁格所代表的实际结构的部分内力。
图1.1 (a)原型上部结构(b)等效梁格1.2梁格网格的划分采用梁格法对桥梁结构进行分析时,首先考虑的是如何对梁格单元的合理划分。
网格划分的枢密程度是保证比拟梁格与实际结构受力等效的必要条件之一。
合理的网格划分,不仅能准确反映结构的受力特征,还能提高工作效率。
1.2.1纵梁的划分纵梁的划分是梁格划分的关键,其划分原则有:1.纵梁划分后,每片纵梁的形心高度大概一致,也就是要保证箱梁截面在纵梁划分之后,每片纵梁的中性轴与箱梁整体截面的中性轴保持一致,这样才能使梁格模型与实际结构在纵向弯曲上等效。
2.梁格的纵向构件间距和横向构件间距必须接近,从而使荷载在桥梁结构上的静力分布比较敏感。
遵循这种原则划分可以使梁格的受力线或中心线与设计时的重合,也就是根据实际结构的受力情形来划分网格。
3.对于实际结构中应力变化较为复杂的区域,要想得到构件中较为精确的应力分布,必须在相应区域细化网格。
1.2.2 虚拟横梁的设置间距建立梁格模型时,在把结构离散为多片纵梁后,纵梁与纵梁之间必须通过虚拟横梁来连接,才能保证所有纵梁共同作用并承担外力荷载。
虚拟横梁的划分根据上部结构横向刚度的大小来确定,当实际结构的横向有多个横隔板连接时,只在对应的横隔板位置处设置虚拟横梁;当实际结构的横隔板间距稀疏时,为使梁格模型模拟实际结构具有连续性,可适度加密,其设置间隔大概是反弯点距离的1/4且不大于纵梁的设置间隔。
在建立梁格模型时,桥梁的纵桥向每跨至少划分4~6个单元,其中虚拟横梁必须设置在截面突变处、支撑条件改变处、控制截面(如跨中、四分点)处,一般每跨划分为8个单元或更多,即可保证足够的精确度。
经大量研究和实践表明,对于跨径为20m的桥梁,每跨在纵向上划分6~8个单元即能满足工程精度要求。
对于连续曲线弯梁桥,由于弯曲曲率的影响导致中间支座区域的应力变化较为复杂,故应考虑在此区域加密网格。
综上所述,在设置虚拟横梁时应综合考虑桥梁跨径、腹板间距等因素,选择合适的跨径划分单元数,并尽量满足以上提到的各种要求。
第二章梁格分析板式上部结构2.1 结构类型板式上部结构,在二维平面板内结构上是连续的,因此作用荷载由剪力、弯矩和扭矩的二维分布来支撑。
其结构形式如图2.1。
板式上部结构可分为:①各向同性,即纵向和横向上具有相同刚度;②正交导性,即刚度在两个方向上不同,如图3.1c、3.1d。
图2.1 板式上部结构(a)实体的(b)空心的(c)混合实体的(d)混合空心的2.2 梁格网格某一空心板两个模型如图2.2示:图2.2 空心板上部结构纵向梁格布置2.3 截面特性计算对于各向同性板,纵向和横向梁格截面特性计算相同,以下只介绍个性同性板截面特性计算方法。
2.3.1 惯性矩惯性矩计算考虑每根构件代表至相邻平行构件间对中划分的桥面板的宽度来计算,如图2.3。
应按板的中性轴计算惯性矩。
图2.3 板式上部结构对于纵向梁格杆件的划分 312bd I = (2.1) 2.3.2 扭转一块板每单位宽度的抗扭常数为: 36d c =每单位宽度 (2.2) 对于板宽为b 的梁格,抗扭常数为: 36bd C = (2.3)第三章梁格法分析梁板式上部结构3.1 结构类型大多数梁板式上部结构,在桥台之间设置多根纵梁,而在横向上用一薄板横盖其顶面,如图4.1示。
对于小跨径,纵梁通常密排,如图4.1a示。
对较大跨径,设置如图4.2b、c,并在支点上设置称为“横隔板”的横梁。
弯桥通常用板的边宽来调节成合适的弯度,但支承在每跨为直线的梁上;有时也把纵梁做成曲线的。
图3.1 梁板式上部结构(a)密排式(b)稀排式工字梁(c)稀排式箱梁(d)格梁3.2 梁格网格1、在图3.2a中,结构形式:纵梁和横梁的梁格,因为平均的纵向和横向弯曲刚度相差不大。
梁格采用:与原型梁中心线相重合的构件近似模拟。
2、在图3.2b中,结构形式:上部结构纵梁比行车道略窄。
梁格采用: 将原型梁中心线作为纵向梁格。
对于没有跨中横隔板的横向梁格,其间距可以任意选择,一般取有效跨径的1/4~1/8。
如原型支点上有横隔板,则必须设置一根梁格与它重合。
3、在图3.2c中,结构形式:中心密排的梁式上部结构。
梁格采用: 用一根梁格去代替一根以上的纵梁。
注意,梁格间距不超过1/10跨径。
4、在图3.2d中,结构形式:上部结构具有纵向大梁。
梁格采用: 每根纵梁用两根梁格的板式上部结构来处理,但必须作为一块板来计算抗扭参数。
图3.2 梁格的网格3.3 截面特性计算3.3.1 纵向梁格截面特性1、每一梁格惯性矩按截面形心计算。
2、若上部结构的梁间距大于有效跨径的1/6,或若边缘悬臂超过有效跨径的1/12,剪力滞后使梁的翼缘有效板宽度明显减小,梁格惯性矩必须用折减的板宽计算。
3、有时为改进作用荷载的模拟效果,纵向需设置虚拟刚度的梁格。
4、板梁式上部结构承受扭转时,梁部分如同梁单独承受纵向扭转一样,而板部分如同在两个方向上承受扭转。
故梁格的抗扭常数C 为梁的抗扭常数的总和见式3.1,板的抗扭常数同式2.3。
24s A C d t=⎰Ñ (3.1) 其中:A-壁的中心线围成的面积 s d t ⎰Ñ-壁的中心线长度除以壁厚沿周壁的积分3.3.2 横向梁格截面特性可用一块板表示惯性矩 312bd I = 抗扭常数 36bd C = (3.2)当梁格有横隔板时,必须把板视为翼缘计算。
若横隔板的中心线不远,则翼缘可以假定延伸到两横隔板间的中点。
若翼缘宽度超过横向弯矩零点之间的有效横向跨度的1/12时,考虑剪力滞影响。
如事先不知道横向弯矩,为安全起见通常假定有效翼缘为纵向构件间距的0.3。
第四章梁格法分析分格式上部结构4.1 结构形式分格式上部结构有图4.1a-薄板封闭式、矩形宽的多格式上部结构,仅有一个或少数几个格室的上部结构,图4.1c-具有斜腹板的上部结构。
图4.1 分格式上部结构4.2 梁格网格离散箱梁截面的基本原则:①保证被切开的每片τ型梁及工字梁的中性轴与原整体箱梁结构的纵向弯曲中性轴重合,全部纵向构件均与纵向腹板重合。
②虚拟横梁的刚度依据箱梁顶底板的横向刚度来模拟,实用计算中可以将每跨横向的抗弯(扭)刚度平均分配于该跨虚拟横梁中;不管横隔板设置在何处,其纵向间距要接近于反弯点之间的1/4,但在中支点上间隔较小。
注意:若横向构件间隔稀疏,由于在节点处弯矩过渡的不连续性,结果不精确;若间隔较密,虽对力提供较详力的细节,但不能使梁格的特征性能接近于分格式上部结构。
图4.2 分格式上部结构的梁格网格4.3 截面特性计算4.3.1 纵向梁格截面特性4.3.1.1 纵向抗弯刚度通常将箱梁上部结构在腹板之间沿纵向切开成许多工字梁,如图4.3示。
根据梁格等效的基本原理,当发生纵向弯曲时梁格模型与实际上部结构具有相同的曲率,因此纵梁的弯曲应力与简单梁理论的结果相似,如图4.4示的正应力和剪应力分布。
图4.3 箱梁截面纵梁划分形式(a)中性轴不等高(b)中性轴等高图4.4 纵向弯曲时箱梁截面应力分布结论:无论划分的纵梁截面中性轴是否等高,构件的截面模量和惯性矩都取上部结构的主轴计算,即纵梁的抗弯刚度为:EI y=E·每片纵梁截面对箱梁整体截面中性轴的惯性矩(4.1)应用:箱梁截面典型的梁格划分,如图4.5示。
图4.5 箱梁的典型梁格划分纵向“结构”构件2、3和4与箱梁腹板重合,两根“虚拟”构件1和5则沿悬臂边缘设置。
对于此种对称型的箱型截面,纵向“结构”构件2、3和4的纵向弯曲惯性矩可“实用”的计入1/3顶板和1/3底板,其惯性矩是整体箱梁总惯性矩的1/3;虚拟”边构件1和5的惯性矩则取为悬臂截面惯性矩的一半。
4.3.1.2 扭转刚度这里的扭转仅指箱梁的刚性扭转,而不考虑箱梁截面的畸变的影响,即箱梁虽然发生扭转但其截面周边不发生变形。
当截面发生刚性扭转时,如图4.6示,剪应力沿顶板、底板和腹板呈网图4.6 箱梁受扭时剪力流分布和梁格内力状剪力流分布,大部分剪力流环绕顶板、底板、边腹板流动,只有少数通过中腹板。
由图4.6可知梁格的扭矩T代表顶板、底板内相反的剪力流在上部结构内形成的扭矩;剪力S T代表腹板内的剪力流。
把箱梁比拟上、下两层薄实体板组成的正交同性板,不计腹板及箱梁外侧悬臂板的影响,如图4.7图4.7 箱梁抗扭计算简化模型不计上、下板本身的惯性矩,则有:22221122111222i A h A h b d h b d h=+=+因箱梁顶板和底板的中性轴位置与板厚成反比,故有121211d h h hd h h-==由以上二式推导可得,格室每单位宽度的惯性矩为:22212112212ih d dh d h dd d=+=+(4.2)格室每单位宽度的抗扭常数为:2121222h d dc id d==+(4.3)4.3.1.3 剪切刚度箱梁截面在纵向弯曲和刚性扭转时,其腹板处分别产生剪力,并共同组成腹板剪力。
从所受剪力的方向来讲,箱梁截面顶板和底板面积抵抗纵向梁格的横向剪力,腹板面积抵抗对应的竖向剪力;同时,轴向的拉压面积则应取纵向梁格的整个截面积。
结论:由于箱梁发生剪切变形时,大部分剪力由腹板承受,故纵梁的抗剪面积等于腹板面积。
4.3.2 横向梁格截面特性4.3.2.1 横向弯曲刚度如图4.8所示的横向弯曲,是顶板和底板一致地绕他们的共同重心的水平中性轴而弯曲,如同有一剪力刚性腹板将他们连接一样。
