《半导体器件》习题及参考答案模板
第六章 习题及参考答案

第六章习题及参考答案
1. 某半导体存储器容量16K ×8位,可选芯片容量为4K×4/片。
地址总线A15-A0(低),双向数据线D7-D0(低),由R
W/线控制读写。
请设计并画出该存储器逻辑图,注明地址分配、片选逻辑式及片选信号极性。
参考答案:
(1) 芯片选取与存储空间分配:
共需8片“4K×4/片”的芯片,存储空间分配如下图所示:
(2).地址分配与片选逻辑如下图所示:
(3).存储器逻辑图如下图所示:
2. 某半导体存储器总容量15k ×8位,其中固化区8k ×8,选用EPROM芯片4K ×8/片,可随机读写区7K ×8,可选用SRAM芯片有:4K ×4/片、2K ×4/片、1K ×4/片。
地址总线A15∼A0,双向数据总线D7∼D0,由R
W/线控制读写,MREQ为低电平时允许存储器工作。
请设计并画出该存储器逻辑图,注明地址分配、片选逻辑式及片选信号极性。
参考答案:
(1)芯片选取与存储空间分配如下图所示:
(2)地址信号与片选逻辑如下图所示:
(4)存储器逻辑图如下图所示:。
电子电路基础习题册参考答案第一章

电⼦电路基础习题册参考答案第⼀章电⼦电路基础习题册参考答案(第三版)全国中等职业技术第⼀章常⽤半导体器件§1-1 晶体⼆极管⼀、填空题1、物质按导电能⼒的强弱可分为导体、绝缘体和半导体三⼤类,最常⽤的半导体材料是硅和锗。
2、根据在纯净的半导体中掺⼊的杂质元素不同,可形成N 型半导体和P 型半导体。
3、纯净半导体⼜称本征半导体,其内部空⽳和⾃由电⼦数相等。
N型半导体⼜称电⼦型半导体,其内部少数载流⼦是空⽳;P 型半导体⼜称空⽳型半导体,其内部少数载流⼦是电⼦。
4、晶体⼆极管具有单向导电性,即加正向电压时,⼆极管导通,加反向电压时,⼆极管截⽌。
⼀般硅⼆极管的开启电压约为0.5 V,锗⼆极管的开启电压约为0.1 V;⼆极管导通后,⼀般硅⼆极管的正向压降约为0.7 V,锗⼆极管的正向压降约为0.3 V。
5.锗⼆极管开启电压⼩,通常⽤于检波电路,硅⼆极管反向电流⼩,在整流电路及电⼯设备中常使⽤硅⼆极管。
6.稳压⼆极管⼯作于反向击穿区,稳压⼆极管的动态电阻越⼩,其稳压性能好。
7在稳压电路中,必须串接限流电阻,防⽌反向击穿电流超过极限值⽽发⽣热击穿损坏稳压管。
8⼆极管按制造⼯艺不同,分为点接触型、⾯接触型和平⾯型。
9、⼆极管按⽤途不同可分为普通⼆极管、整流⼆极管、稳压⼆极管、开关、热敏、发光和光电⼆极管等⼆极管。
10、⼆极管的主要参数有最⼤整流电流、最⾼反向⼯作电压、反向饱和电流和最⾼⼯作频率。
11、稳压⼆极管的主要参数有稳定电压、稳定电流和动态电阻。
12、图1-1-1所⽰电路中,⼆极管V1、V2均为硅管,当开关S与M 相接时,A点的电位为⽆法确定V,当开关S与N相接时,A点的电位为0 V.13图1-1-2所⽰电路中,⼆极管均为理想⼆极管,当开关S打开时,A点的电位为10V 、流过电阻的电流是4mA ;当开关S闭合时,A点的电位为0 V,流过电阻的电流为2mA 。
14、图1-1-3所⽰电路中,⼆极管是理想器件,则流过⼆极管V1的电流为0.25mA ,流过V2的电流为0.25mA ,输出电压U0为+5V。
参考答案-《电工与电子技术基础(第三版)习题册》-A06-3760

第一章直流电路一、填空题1.电源、负载、导线和控制装置2.通路、断路、和短路短路3.定向移动 I A mA μA4.某点参考点有无5. 20V -50V -30V6. b指向a a指向b 1.5 V7.阻碍 R 欧姆(Ω)8.正比反比 I=U/R9.5A10.0.4A11.电能其他电功 W 焦耳12.213.单位时间14.115.导体发热电烙铁电吹风电熨斗16.0.4548417.50Ω 2Ω18.1:2 1:1 1:1 2:119.4 6 7 320.6A21.短路二、判断题1.√ 2. √ 3. √ 4. × 5. √ 6. × 7. ×8. ×9. √ 10. × 11. √ 12. ×三、选择题1.C 2.C 3.C 4. C 5. A 6. B 7. D 8. B9. C 10. C 11.A 12. A四、问答题1.答:电流热效应的利:利用电流热效应可以制成很多电器设备,如:电烙铁、电饭煲、电熨斗等。
电流热效应的弊:元器件和电气设备发热过多,不仅消耗电能,而且会加速绝缘材料的老化,严重时还会引起电气火灾。
2. “220V ”表示这个灯泡的额定电压“40W ”表示这个灯泡的额定功率3.答:(1)对交、直流电流应分别使用交流电流表和直流电流表测量。
(2)电流表必须串接到被测量的电路中。
(3)电流必须从电流表的正端流入负端流出。
(4)选择合适的量程。
五、计算题1.解:(1)C 为参考点,则 U A =-3V-5V=-8VU B =-5VU C =0VU AB = U A - U B =-8V-(-5V)=-3VU BC = U B - U C =-5VU AC = U A - U C =-8V(2)以B 为参考点,则U A =-3V=-3VU B =0VU C =5VU AB = U A - U B =-3VU BC = U B - U C =0-(5)=-5VU AC = U A - U C =-3-(5)=-8V(3)从上面的结果可知:电位随着参考点的改变而改变;电压不随参考点的改变而改变。
课后习题答案

项目一任务一一.判断题(下列判断正确的话打“√”,错误的打“×”)1.P型半导体中的多数载流子是电子。
(×)2.PN结具有单向导电性,其导通方向为N区指向P区。
(×)3.二极管反向击穿就说明管子已经损坏。
(×)4.小电流硅二极管的死区电压约为0.5V,正向压降约为0.7V。
(√ )5.发光二极管发光时处于正向导通状态,光敏二极管工作时应加上反向电压。
(√)二.填空题1.半导体中的载流子有_____________和___________。
(自由电子、空穴)2.晶体三极管内部的PN结有___________个。
(2)3.晶体管型号2CZ50表示___________。
(50 A的硅整流二极管)4..PN结的反向漏电流是由___________产生的。
(少数载流子)三.简答题1.常用片状元件有哪些?和普通电气元件相比,有什么优点?答:片状元器件属于无引线或短引线的新型微型电子元件,是表面组装技术SMT(Surface Mounted Technology)的专用元器件。
可分为片状无源器件、片状有源器件和片状组件等三类。
片状无源器件包括片状电阻器、片状网络电阻器、片状热敏电阻器、片状电位器、片状电容器、片状微调电容器和片状电感器等。
片状有源器件包括片状二极管、片状开关二极管、片状快恢复二极管、片状稳压二极管、片状三极管和片状场效应管等。
片状元器件的主要特点是其外形结构不同于传统的插装式产品,其体积小,重量轻,无引线或引线短,可靠性高,耐振动冲击,抗干扰性好,易于实现半自动化和自动化的低成本、高密度组装,其焊点失效率达到百万分之十以下;利用片状元器件贴装可使电子线路的工作频率提高到3000MHz(通孔插装的为500MHz),而且能够有效地降低寄生参数,有利于提高设备的高频特性和工作速度;片状元器件产品的器件形状、尺寸精度和一致性高。
大部分可编带包装,有利于提高生产装配效率,且能够从根本上解决元器件与整机间的共存可靠性问题。
半导体器件物理施敏答案

半导体器件物理施敏答案【篇一:施敏院士北京交通大学讲学】t>——《半导体器件物理》施敏 s.m.sze,男,美国籍,1936年出生。
台湾交通大学电子工程学系毫微米元件实验室教授,美国工程院院士,台湾中研院院士,中国工程院外籍院士,三次获诺贝尔奖提名。
学历:美国史坦福大学电机系博士(1963),美国华盛顿大学电机系硕士(1960),台湾大学电机系学士(1957)。
经历:美国贝尔实验室研究(1963-1989),交通大学电子工程系教授(1990-),交通大学电子与资讯研究中心主任(1990-1996),国科会国家毫微米元件实验室主任(1998-),中山学术奖(1969),ieee j.j.ebers奖(1993),美国国家工程院院士(1995), 中国工程院外籍院士 (1998)。
现崩溃电压与能隙的关系,建立了微电子元件最高电场的指标等。
施敏院士在微电子科学技术方面的著作举世闻名,对半导体元件的发展和人才培养方面作出了重要贡献。
他的三本专著已在我国翻译出版,其中《physics of semiconductor devices》已翻译成六国文字,发行量逾百万册;他的著作广泛用作教科书与参考书。
由于他在微电子器件及在人才培养方面的杰出成就,1991年他得到了ieee 电子器件的最高荣誉奖(ebers奖),称他在电子元件领域做出了基础性及前瞻性贡献。
施敏院士多次来国内讲学,参加我国微电子器件研讨会;他对台湾微电子产业的发展,曾提出过有份量的建议。
主要论著:1. physics of semiconductor devices, 812 pages, wiley interscience, new york, 1969.2. physics of semiconductor devices, 2nd ed., 868 pages, wiley interscience, new york,1981.3. semiconductor devices: physics and technology, 523 pages, wiley, new york, 1985.4. semiconductor devices: physics and technology, 2nd ed., 564 pages, wiley, new york,2002.5. fundamentals of semiconductor fabrication, with g. may,305 pages, wiley, new york,20036. semiconductor devices: pioneering papers, 1003 pages, world scientific, singapore,1991.7. semiconductor sensors, 550 pages, wiley interscience, new york, 1994.8. ulsi technology, with c.y. chang,726 pages, mcgraw hill, new york, 1996.9. modern semiconductor device physics, 555 pages, wiley interscience, new york, 1998. 10. ulsi devices, with c.y. chang, 729 pages, wiley interscience, new york, 2000.课程内容及参考书:施敏教授此次来北京交通大学讲学的主要内容为《physics ofsemiconductor device》中的一、四、六章内容,具体内容如下:chapter 1: physics and properties of semiconductors1.1 introduction 1.2 crystal structure1.3 energy bands and energy gap1.4 carrier concentration at thermal equilibrium 1.5 carrier-transport phenomena1.6 phonon, optical, and thermal properties 1.7 heterojunctions and nanostructures 1.8 basic equations and exampleschapter 4: metal-insulator-semiconductor capacitors4.1 introduction4.2 ideal mis capacitor 4.3 silicon mos capacitorchapter 6: mosfets6.1 introduction6.2 basic device characteristics6.3 nonuniform doping and buried-channel device 6.4 device scaling and short-channel effects 6.5 mosfet structures 6.6 circuit applications6.7 nonvolatile memory devices 6.8 single-electron transistor iedm,iscc, symp. vlsi tech.等学术会议和期刊上的关于器件方面的最新文章教材:? s.m.sze, kwok k.ng《physics of semiconductordevice》,third edition参考书:? 半导体器件物理(第3版)(国外名校最新教材精选)(physics of semiconductordevices) 作者:(美国)(s.m.sze)施敏 (美国)(kwok k.ng)伍国珏译者:耿莉张瑞智施敏老师半导体器件物理课程时间安排半导体器件物理课程为期三周,每周六学时,上课时间和安排见课程表:北京交通大学联系人:李修函手机:138******** 邮件:lixiuhan@案2013~2014学年第一学期院系名称:电子信息工程学院课程名称:微电子器件基础教学时数: 48授课班级: 111092a,111092b主讲教师:徐荣辉三江学院教案编写规范教案是教师在钻研教材、了解学生、设计教学法等前期工作的基础上,经过周密策划而编制的关于课程教学活动的具体实施方案。
半导体物理 习题练习2参考答案

y E
C
Ei EF E
V
x
Nd= Ne-ax,则电子为主要载流子 n(x)=ni+Nd=ni+ Ne-ax
y E EF Ei
C
Eห้องสมุดไป่ตู้
V
x
• 4. 某半导体硅样品中含磷浓度为1016/cm3, 含硼的浓度为2X1015/cm3,已知在T=260K时, 本征载流子浓度为ni = 2X109/cm3, 且费米 能级EF与ED重合,试求: • (1)未电离的施主浓度; • (2)多子浓度和少子浓度 • (3)设un= 1300cm2/(v.s),up = • 500cm2/(v.s), 求此样品电导率
练习二(参考答案)
1。Zn在Si中是一双重受主,即每一个Zn原子 可在EA1(EA1-EV=0.31eV),能级接受1个电 子,在较高能级EA2(EA2-Ev=0.55eV)上接受 第2个电子。为了完全补偿1个Nd=1016cm-3的 n-Si样品,需要掺入Zn的密度是多少?(设 Eg=1.12eV)。
Ec
EA2-Ev=0.55ev
1.12ev
EF=Ei
EA1-Ev=0.31ev
Ev
1。如图所示的硅样品,尺寸为h=1.0mm, W=4.0mm, L=8.0mm.在霍尔效应实验中, I=1mA, B=4000 (0.4T), 实验中测出在77K~ 400K的温度范围内霍尔电势差不变,其数值 为Vac= Va-Vc =-5.0mV。在300K测得Vx= 200mV 200mV。
半导体物理综合练习题(3)参考答案

1、晶格常数2.5?的一维晶格,当外加102V/m 和107V/m 电场时,试分别计算电子自能带底运动到能带顶所需时间。
(1?=10nm=10 -10m ) 解:设电场强度为E.因为代入数据得6, 62 X 10 创2 X 1, 6 X IO -19 X 2. 5 X IO -10 X E 当:E=10s V/m 时昇=&3X10_s (s);E^107V/m 时"=8. 3X10J 13(S )S2、指出下图中各表示的是什么半导体E.r所以—吐?(取绝对值d/Ci击=I I II II II '3- E------ E.If& 3 X IO -6 ( s)4、若费米能E F =5eV ,利用费米分布函数计算在什么温度下电子占据 计算在该温度下电子分布概率 0.9~0.1所对应的能量区间。
解:由费卷分布函数 吕) E —E F&叫 7^5 "1) 其中 t ieV=l. 602XlQ-12erg^Q = L 38 X 10~1G erg/K = 8. 63X1O _S eV/K w 代人有关数 摘得f 5 — 5 H = -- ---------- - -------------- \ --------- '8. 63 X 10Y % 叫厂厉一1)由费米雷数可得当f = 0. 9时吊=+ & 63 X IO -5 X 1251 X In=— 24 (eV)= B E -t- 8. 63 X 1O _& X 1261 X In5、两块n 型硅材料,在某一温度T 时,第一块与第二块的电子密度之比为n i /n 2=e (e 是自然对数的底)(1) 如果第一块材料的费米能级在导带底之下3 k o T ,试求出第二块材料中费米能级的位置;(2) 求出两块材料中空穴密度之比p i /p 2。
E=5.5eV 能级的概率为1%。
并/(£:)= -------------- 1 + cxpj 可得=1261 CK) A -1)'解:设第 块和第二块材料的费农能级分別为巴:和E F —利用式(饥1)可得 t 一 Epj 、^T)--爲丁已知E FL =E 「3怂T,所以E 昭=耳一4為0即第二块材料的费米能级在导带底之下 4Ao K (2〉珥P\='吃=怔6、硼的密度分别为 N A1和N A2(N A1>N A2)的两个硅样品,在室温条件下(1)哪个样品的少子密度低 ?(2)哪个样品的 E F 离价带顶近?(3) 如果再掺入少量的磷 (磷的密度N'D < N A 2),它们的E F 如何变化?解;为了使问题简单明确(半然也足实际一匸作中常遇到的悄况儿我们假定“AI 和为皿 郁远大于室温下的本征载流子密度•即讨论杂质饱和电离的悄况。
电子电路基础习题册参考答案-第一章讲解

电子电路基础习题册参考答案(第三版)全国中等职业技术第一章常用半导体器件§1-1 晶体二极管一、填空题1、物质按导电能力的强弱可分为导体、绝缘体和半导体三大类,最常用的半导体材料是硅和锗。
2、根据在纯净的半导体中掺入的杂质元素不同,可形成N 型半导体和P 型半导体。
3、纯净半导体又称本征半导体,其内部空穴和自由电子数相等。
N型半导体又称电子型半导体,其内部少数载流子是空穴;P型半导体又称空穴型半导体,其内部少数载流子是电子。
4、晶体二极管具有单向导电性,即加正向电压时,二极管导通,加反向电压时,二极管截止。
一般硅二极管的开启电压约为0.5 V,锗二极管的开启电压约为0.1 V;二极管导通后,一般硅二极管的正向压降约为0.7 V,锗二极管的正向压降约为0.3 V。
5.锗二极管开启电压小,通常用于检波电路,硅二极管反向电流小,在整流电路及电工设备中常使用硅二极管。
6.稳压二极管工作于反向击穿区,稳压二极管的动态电阻越小,其稳压性能好。
7在稳压电路中,必须串接限流电阻,防止反向击穿电流超过极限值而发生热击穿损坏稳压管。
8二极管按制造工艺不同,分为点接触型、面接触型和平面型。
9、二极管按用途不同可分为普通二极管、整流二极管、稳压二极管、开关、热敏、发光和光电二极管等二极管。
10、二极管的主要参数有最大整流电流、最高反向工作电压、反向饱和电流和最高工作频率。
11、稳压二极管的主要参数有稳定电压、稳定电流和动态电阻。
12、图1-1-1所示电路中,二极管V1、V2均为硅管,当开关S与M 相接时,A点的电位为无法确定V,当开关S与N相接时,A点的电位为0 V.13图1-1-2所示电路中,二极管均为理想二极管,当开关S打开时,A点的电位为10V 、流过电阻的电流是4mA ;当开关S闭合时,A点的电位为0 V,流过电阻的电流为2mA 。
14、图1-1-3所示电路中,二极管是理想器件,则流过二极管V1的电流为0.25mA ,流过V2的电流为0.25mA ,输出电压U0为+5V。
(整理)电子电路基础习题册参考答案

电子电路基础习题册参考答案免费提供(第三版)全国中等职业技术第一章常用半导体器件§1-1 晶体二极管一、填空题1、物质按导电能力的强弱可分为导体、绝缘体和半导体三大类,最常用的半导体材料是硅和锗。
2、根据在纯净的半导体中掺入的杂质元素不同,可形成N 型半导体和P 型半导体。
3、纯净半导体又称本征半导体,其内部空穴和自由电子数相等。
N型半导体又称电子型半导体,其内部少数载流子是空穴;P型半导体又称空穴型半导体,其内部少数载流子是电子。
4、晶体二极管具有单向导电性,即加正向电压时,二极管导通,加反向电压时,二极管截止。
一般硅二极管的开启电压约为0.5 V,锗二极管的开启电压约为0.1 V;二极管导通后,一般硅二极管的正向压降约为0.7 V,锗二极管的正向压降约为0.3 V。
5.锗二极管开启电压小,通常用于检波电路,硅二极管反向电流小,在整流电路及电工设备中常使用硅二极管。
6.稳压二极管工作于反向击穿区,稳压二极管的动态电阻越小,其稳压性能好。
7在稳压电路中,必须串接限流电阻,防止反向击穿电流超过极限值而发生热击穿损坏稳压管。
8二极管按制造工艺不同,分为点接触型、面接触型和平面型。
9、二极管按用途不同可分为普通二极管、整流二极管、稳压二极管、开关、热敏、发光和光电二极管等二极管。
10、二极管的主要参数有最大整流电流、最高反向工作电压、反向饱和电流和最高工作频率。
11、稳压二极管的主要参数有稳定电压、稳定电流和动态电阻。
12、图1-1-1所示电路中,二极管V1、V2均为硅管,当开关S与M 相接时,A点的电位为无法确定V,当开关S与N相接时,A点的电位为0 V.13图1-1-2所示电路中,二极管均为理想二极管,当开关S打开时,A点的电位为10V 、流过电阻的电流是4mA ;当开关S闭合时,A点的电位为0 V,流过电阻的电流为2mA 。
14、图1-1-3所示电路中,二极管是理想器件,则流过二极管V1的电流为0.25mA ,流过V2的电流为0.25mA ,输出电压U0为+5V。
半导体物理课后习题(保密)

解: 须先求出本征载流子浓度ni,即
代入数据得,ni=1.86 ×1013cm-3 根据电中性条件有 p0+ND+=n0+NA-
ni
q( n p )
i
1 i ( n p )
联立 载流子浓度公式
n0p0=ni2
可求解得 n0=3.89 ×1013cm-3, p0=8.89 ×1012cm-3 所以样品的电导率为:
解: 由图3-7查得T=500k时,Si的本征载流子浓度ni=3.5×1014cm-3 联立方程
p0=ni2/n0
解得, ND=3.5×1014cm-3时,n0≈4.3×1014cm-3, p0=2.8×1014cm-3 —— n0,p0差别不显著,杂质导电特性不很明显 ND=1012cm-3时,n0≈ni=3.5×1014cm-3, p0=3.5×1014cm-3,即n0=p0. —— 进入本征 半导体材料在某一温度下所处的区域与杂质浓度相关 或 杂质浓度不同,材料进入同一区域所需要的温度不一样。
m0为电子惯性质量,k1=1/2a; a=0.314nm。试求: (1)禁带宽度; (2)导带底电子有效质量; (3)价带顶电子有效质量; (4)价带顶电子跃迁到导带底时准动量的变化。
练习2-课后习题2
第一章 半导体中的电子状态
2.晶格常数为0.25nm的一维晶格,当外加102V/m和107V/m 的电 场时,试分别计算电子自能带底运动到能带顶所需的时间。
作业-课后习题14
第三章 半导体中载流子的统计分布
计算含有施主杂质浓度ND=9×1015cm-3与受主杂质浓度为1.1×1016cm-3 的硅在室温时的电子和空穴浓度以及费米能级的位置。
半导体物理与器件第四版课后习题答案(供参考).doc

Chapter 44.1n i 2E gN c N expkTT 3E gexpN cO N O300kTwhere N cO and N Oare the values at 300 K.(a) SiliconT (K) kT (eV) n i (cm 3) 200 0.01727 7.68 104 400 0.03453 2.38 1210 6000.05189.74 1014(c) GaAs(b) GermaniumT (K)n i (cm 3 ) n i (cm 3 ) 200 2.16 10101.38 4008.60 1014 3.28 109 6003.82 10165.72 1012_______________________________________ 4.2Plot_______________________________________4.3(a) n i 2 N c NexpE gkT31121919T5 2.8 1.04 101010300exp1.120.0259 T 300T 32.5 10 232.912 10 38300exp1.12 3000.0259 TBy trial and error, T 367.5 K(b)n i25 10 1222.5 10 2532.912 10 38T exp 1.12 300300 0.0259 TBy trial and error,T 417.5 K _______________________________________4.4At T200 K, kT0.02592003000. 017267eVAt T400 K, kT0.02594003000. 034533eVn i 2400 7.70 101023.025 10 17n i 2 2001.40 10 2 23400expE g3000.0345333200Egexp300 0.017267E gE g8 exp0.0345330.0172673.025 10178 exp E g 57 .9139 28.9578orE g 28.9561ln 3.025 1017 38.17148 or E g 1.318 eVNow7.70 1010N co N o340023001.318 exp0.03453321N co N o 2.370 175.929 10 2.658 10so N co N o 9.41 10 37 cm 6_______________________________________4.5exp 1.10n i kT 0.20Bexpn i A 0.90 kTexp kTFor T 200 K, kT 0.017267 eVFor T 300 K, kT 0.0259 eVFor T 400 K, kT 0.034533 eV(a) For T 200K,n i B exp 0.20 9.325 10 6n i A 0.017267(b) For T 300K,n i Bexp 0.204.43 10 4n i A 0.0259 (c) For T 400K,n i Bexp 0.203.05 10 3n i A 0.034533_______________________________________ 4.6(a) g c f FE E FE E c expkTThen g c f F x expxkTTo find the maximum value:d g c f F 1 x1 / 2 exp xdx 2 kT1 x1 /2 exp x 0kT kTwhich yields1/ 21 x kT2x1/ 2 x 2kTThe maximum value occurs atEkTE c2(b)g 1 f FE F EE E expkTE EE E expkTexpE F EkTLet E E xThen g 1 f F x expxkTTo find the maximum valued g 1 f F d xdx dxx expkTSame as part (a). Maximum occurs atxkT2E E c exp E E ckTorkTE E2E c EF expkTLet E E c x _______________________________________ 4.7E1 E c exp E1 E cn E1 kTn E2E2 E c exp E2 E c kTwhereE1 E c 4kT and E 2 E c kT 2Thenn E1 4kTexp E1 E2n E2 kT kT22 2 exp 4 12 exp 3.522orn E10.0854n E 2_______________________________________ 4.8Plot_______________________________________4.9Plot_______________________________________ 4.10E Fi E midgap 3kT ln m*pm n* 4Silicon: m*p 0.56 m o , m n* 1.08m oE Fi E midgap 0.0128 eVGermanium: m*p 0. 37m o ,*0.55m om nE Fi E midgap 0 .0077 eVGallium Arsenide: m*p 0.48m o ,m n* 0.067m oE Fi E midgap 0 .0382 eV_______________________________________ 4.11E Fi E midgap 1 kT ln N2 N c1kT ln 1.04 1019 0.4952 kT2 2.8 1019T (K) kT (eV) ( E Fi E midgap )(eV) 200 0.01727 0.0086 400 0.03453 0.0171 600 0.0518 0.0257_______________________________________4.12(a) E Fi E midgapm*p3 kT ln4 m n*3 0.0259 ln0.704 1.2110.63 meV(b) E Fi E midgap 3 0.0259 ln0.754 0.08043.47 meV_______________________________________4.13Let g c E K constantThenn o g c E f F E dEE cK1dEE E FEc 1 expkTK expE E FdEkTE cLetE E cso that dE kT dkTWe can writeE EF E c E F E E cso thatE E Fexp E c E FexpexpkTkTThe integral can then be written asn o K kT exp E c E Fexp d kTwhich becomesn o K kTE c EF expkT_______________________________________4.14Let g c E C1E E c for E E cThenn o g c E f F E dEE cC1 E E cdEE c 1exp E EF kTC1 EE E FdE E C expE ckTLetE E cdE kT dso thatkTWe can writeE EF E E c E c E FThenE c E Fn o C1 expkTE E cE E cdE expE ckT orn oE c EF C1 expkTkT exp kT d 0We find thatexp d exp 1 1So2 E c E Fn o C1 kT expkT_______________________________________4.15r1 m oWe have rm*a oFor germanium, r 16 , m* 0.55m oThenr1 16 1 a o 29 0.530.55oror1 15.4 AThe ionization energy can be written asm*2E o 13.6 eVm o s0.552 13.6 E 0.029 eV16_______________________________________ 4.16We have r1 m orm*a oFor gallium arsenide, r 13.1 , *m0.067 m o1or1 13.1 104 A0.530.067The ionization energy ism*20.067E o 13.6 13.6m o s 13.1 2orE0.0053 eV_______________________________________4.17Nc(a) E c E F kT ln2.8 10190.0259 ln 157 100.2148 eV(b) E F E E g E c E F1.12 0.2148 0.90518eV(c) p o NE F E expkT1.04 19 0.9051810 exp0.02596.90 103cm 3(d) Holesn o(e) E F E Fi kT lnn i710 150.0259 ln1.5 10100.338 eV_______________________________________4.18N(a) E F E kT lnp o190.0259 ln 1.0410210160.162 eV(b) E c E F E g E F E1.12 0.162 0.958 eV(c) n o 2.8 19 0.95810 exp0.02592.41 103cm3p o(d) E Fi E F kT lnn i2 10 160.0259 ln 101.5 100.365eV_______________________________________4.19Nc(a) E c E F kT ln0.0259 ln 2.810192 1050.8436 eVE F E E g E c E F1.12 0.8436E F E 0.2764 eV(b) p o 1.04 1019 exp 0.276370.02592.414 1014cm3(c)p-type_______________________________________4.20(a) kT3750.032375 eV0.02593003 / 2n o 4.7 10 17 375 exp 0.28300 0.0323751.15 1014cm3E F E E g E c E F 1.42 0.281.14 eV375 3 / 2 1.14 p o 7 18 exp10300 0.0323754.99 103cm 3(b) E c E F 0.0259 ln 4.7 10171.15 10 140.2154 eVE F E E g E c E F 1.42 0.21541.2046 eVp o 7 10 18 exp 1.20460.02594.42 10 2cm 3_______________________________________ 4.21(a) kT 0.0259 3750.032375 eV 300375 3 / 2 0.28n o 2.8 19 exp10300 0.0323756.86 1015cm 3E F E E g E c E F 1.12 0.280.840 eV375 3 / 20.840p o 1.04 1019 exp300 0.0323757.84 107cm 3(b) E c E F kT ln N cn o0.0259 ln2.8 10196.862 10 150.2153 eVE F E 1.12 0.2153 0.9047 eVp o 1.04 10 19 exp 0.9046680.02597.04 103 cm 3_______________________________________4.22(a) p-typeE g(b) E F E1.124 0.28 eV4p o N exp E F EkT1.04 10 19 exp 0.280.02592.10 1014cm 3E c EF E g E F E1.12 0.28 0.84 eVn o N c exp E c E FkT2.8 1019exp0.840.02592.30 105cm 3_______________________________________4.23(a) n o n iE F E FiexpkT1.5 1010 exp 0.220.02597.3313cm310p oE Fi E Fn i expkT1.5 1010 exp 0.220.02593.07 106cm 3(b) n o n iE F E FiexpkT1.8 10 6 exp 0.220.02598.80 109cm 3p o n i expE Fi E FkT1.8 106 exp 0.220.02593.68 102cm 3_______________________________________4.24(a) E F ENkT lnp o0.0259 ln1.04 10 195 10 150.1979 eV(b) E c E F E g E F E1.12 0.19788 0.92212 eV(c) n o 2.8 1019 exp 0.922120.02599.66 103cm 3(d) Holesp o(e) E Fi E F kT lnn i510 150.0259 ln1.5 10100.3294 eV _______________________________________4.25kT 0.0259 4000.034533 eV 3003 / 2N 1.04 10 19400300 1.601 1019cm 33 / 2N c 2.8 1019400300 4.3109 1019cm 30.2642 eV _______________________________________4.26(a) p o 7 1018 exp 0.250.02594.50 1014cm 3E c EF 1.42 0.25 1.17 eVn o 4.7 10 17 exp 1.170.02591.13 10 2cm 3(b)kT 0.034533eV3 / 2N 7 10184003001.078 1019cm 33 / 217 400N c 4.7 103007.236 1017cm3expn i 2 4.3109 10 19 1.601 10191.12NE F E kT lnp o19 0.0345335.67022410n i 2.381 1012 cm 3(a) E F ENkT lnp o0.034533 ln 1.601 10195 1015 0.2787 eV(b) E c E F 1.12 0.27873 0.84127 eV(c) n o 4.3109 10 19 exp 0.841270.0345331.134 109cm3(d) Holes(e) E Fi E F kT ln p on i510150.034533 ln2.381 10120.034533 ln1.078104.50 10 140.3482 eVE c EF 1.42 0.3482 1.072 eVn o 7.236 1017 exp 1 .071770. 0345332.40 104cm 3_____________________________________4.27(a) p o 1.04 1019 exp 0.250.02596.68 1014cm 3E c EF 1.12 0.25 0.870 eVn o 2.8 10 19 exp 0.8700.0259n o7.2310 4 cm 3(b)kT0.034533 eV3 / 2N 1.04 10194003001.601 1019cm 33 / 2N c 2.8 1019 4003004.311 1019cm 3NE F E kT lnp o1.60110 190.034533ln6.6810140.3482 eVE c EF 1.12 0.34820.7718 eVn o 4.311 1019 exp 0.771750.0345338.49 109cm 3_______________________________________4.282(a) n o N c F1 / 2 FFor E F E c kT 2 ,E F E c kT 2 FkT 0.5kTThen F1/ 2 F 1.0n o 2 2.8 1019 1.03.16 1019cm 3(b) n o 2 N c F1 / 2 F24.7 1017 1.05.30 1017cm 3_______________________________________ 4.29p o 2 N F1/2 F5 1019 2 1.04 1019 F1/2 FSo F1/ 2 F 4.26We find F 3.0E E FkTE EF 3.0 0.0259 0.0777 eV_______________________________________4.30E F E c 4kT(a) F 4kT kTThen F1 / 2 F 6.02N c F1 / 2n o F2 2.8 1019 6.01.90 10 20 cm 3(b) n o 2 4.7 1017 6.03.18 1018cm 3_______________________________________ 4.31For the electron concentrationn E g c E f F EThe Boltzmann approximation applies, so4 * 3 / 22m nE E cn Eh3E E FexpkTor4 2m n* 3 / 2 E c E Fexpn E h3kTE E c E E ckT expkTkTDefinexEE ckTThenn E n x K x exp xTo find maximumn E n x , setdn x 0 K 1 x 1 / 2 exp xdx 2x 1 / 21 expxorKx 1 / 2 expx1 x2which yieldsx1 E E cE E c12kTkT2For the hole concentrationp Eg E 1f F EUsing the Boltzmann approximation4 2m p * 3 / 2p EEEh 3E F EexpkT or3 / 242m *p E F Ep Eh 3expkTE E E EkTexpkTkTDefinexE EkTThenp xK x exp xTo find maximum value ofp Ep x ,setdp xUsing the results from0 dxabove,we find the maximum at1E E kT2_______________________________________4.32 (a) Silicon:We haven oN c expE cE FkTWe can writeE c E FE c E d E d E FForE c E d 0.045 eV andE dE F3kT eVwe can writen o2.8 1019 exp 0.04530.02592.8 1019exp 4.737or10 17 cm3n o2.45 We also havep oN expE F EkTAgain, we can writeE FEE FE aE aEForE FE a3kTandE aE0.045eVThenp o1.04 1019 exp 3 0.0450.02591.04 1019 exp4.737orp o9.12 10 16 cm 3(b) GaAs: assume E c E d0.0058eVThenn o4.7 1017 exp0.0058 30.025917exp 3.2244.7 10orn o1.87 1016 cm3Assume E a E 0.0345 eVThenp o71018 exp0.0345 30.02597 1018 exp 4.332orp o9.20 1016 cm 3_______________________________________ 4.33Plot_______________________________________4.34 10 151015 cm 3(a)p o415 31.5 10 10 2n o7.5 10 4 cm33 10153(b) n oN d316cm1010 2p o1.5 107.5 10 3cm 33 1016 (c)n op on i 1.5 10 10cm33(d) n i 22.8 10 19 1.041019 375300 exp1.12 3000.0259 375n i7.334 1011 cm3p o N a4 10 15 cm 37.334 10 11 2n o1.34 10 8 cm34 10 153(e) n i 22.8 10 19 1.04 10 19 4503001.12 300exp0.0259 450133n i1.722 10 cm14142n o1.722 10 1310102221.029 1014 cm 31.722 1013 2p o2.88 1012 cm 31.029 1014_______________________________________(a) p oN aN d4 101510153 1015 cm 3n i 2 1.8 10 6 2n o1.08 10 3cm 3p o3 1015(b) n oN d 3 10 16 cm 3p o1.8 10 6 2 1.08 10 4 cm33 10163(c) n o p on i1.8 10 6cm375 3(d) n i 24.7 1017 7.0 10 18300 exp1.42 3000.0259 375n i 7.580 10 8 cm 3p o N a4 1015 cm 38 2n o7.580 10 1.44 10 2 cm 34 10 153 (e) 2 4.7 10 17 7.0 18450 n i 10 300 exp1.42 3000.0259 450n i 3.853 1010 cm3n oN d10 14 cm 33.853 1010 2p o1.48 10 7 cm 310 14_______________________________________4.3610 13 cm 3(a) Ge: n i2.42(i) n oN dN dn i 22 22 10152 210152.4 13 22210or2 1015 cm 3n oN d4.35n i 2 2.4 1013 2p o2 1015n o2.88 1011 cm 3(ii) p o N a N d 10167 10153 1015 cm 32n i22.4 10 13n op o310 151.92 1011cm3(b) GaAs: n i 1.8 10 6cm3(i) n o N d2 1015 cm62p o1.8 10 1.62 10 3cm32 10 15(ii) p oN aN d3 10 15 cm 362n o1.8 101.08 10 3cm 33 1015 (c) The result implies that there is only one 33minority carrier in a volume of 10 cm ._______________________________________4.37(a) For the donor leveln d 1N d1 1exp EdE F2kT11 1 exp 0.2020.0259orn d8.85 10 4N d (b) We havef F E1E E F1expkTNowE E FE E cE c E ForE EF kT 0.245Thenf F E10.2451 exp 1 0.0259orf F E 2.87 10 5_______________________________________4.38N aN d(a) p-type(b) Silicon:10131013p oN aN d 2.5 1 or1013 cm 3p o1.5Thenn i 21.5 10 10 210 7cm 3n o1.5p o 1.5 1013 Germanium:N aN d N a N d 2p o2n i 221.5131.5 10 1322.4 101310222or3.26 10 13 cm 3p oThen2n i 22.4 10 13n o1.76 10 13p o3.264 1013cm 3Gallium Arsenide:p oN a N d1.5 10 13 cm 3and2n i 21.8 10 6n o0.216 cm 3p o1.5 1013_______________________________________4.39 (a) N d N an-type(b) n oN d N a 2 10151.2 10158 1014 cm 3n i 21.5 101022.81 10 5cm 3p o8 14n o10(c)p o N aN a N d4 1015N a 1.2 10 152 1015N a 4.8 10 15 cm31.5 10 102n o5.625 10 4cm 3 4 1015_______________________________________4.40n i21.5 101021. 153n o2 10 5 125 10cmp on o p on-type_______________________________________4.413n i 21.04 10196.0 10 18 250300 exp0.660.0259250 3001.8936 102412n i 1.376cm310 n on i 2 n i 2n o 21n i 2p o4n o 4n o1n i2Son o 6.88 1011 cm 3 ,Then p o2.75 1012cm3N a N a 2p on i 222N a22.752 10122N a21.8936 10 24227.5735 10 242.752 10 12 N aN a2N a 21.8936 10 242so that N a 2.064 1012cm 3_______________________________________4.42Plot_______________________________________4.43Plot_______________________________________4.44Plot_______________________________________ 4.45N d N aN dN a 2n o2n i 2214141.1 1014 2 10 1.2 102 2 10141.2 1014 2n i 221.1 10144 10 1324 10132n i 24.9 10 271.6 10 27n i2so n i5.74 10 13 cm 3p on i 23.3 10 273 133n o 1.1 10 1410 cm_______________________________________4.46(a)N a N d p-typeMajority carriers are holesp o N a N d16163 101.5 101.5 1016 cm 3Minority carriers are electrons210 10 2n on i 1.5 1.5 10 4 cm 3p o 1.5 1016(b) Boron atoms must be addedp o N a N aN d5 1016N a 3 10161.5 1016So N a3.5 10 16 cm 31.5 10 102n o4.5 10 3cm 35 10 16_______________________________________4.47p on i (a)n-type(b) p on i 2 n on i 2n op o1.5 10 1021016 cm3n o4 1.125 2 10electrons are majoritycarriersp o2 10 4cm3holes are minority carriers(c) n oN d N a1.125 101615N d 7 10so N d1.825 1016 cm3_______________________________________4.48E Fi E FkT lnp on iFor GermaniumT (K)kT (eV)n i (cm 3)200 0.01727 2.16 1010400 0.03453 8.60 1410 6000.05183.82 1016N aN a 2p o n i 2and22N a10 15 cm 3T (K)p o (cm3)E Fi EF (eV)200 1.0 1015 0.1855 4001.49 1015 0.01898 6003.87 10160.000674_______________________________________4.49(a) E c E FkT lnN cN d0.0259 ln 2.8 1019N dFor 1014cm 3 , E cE F 0.3249eV15 cm 3 ,E cE F0.2652eV1016cm 3, E c E F 0.2056eV 101017 cm 3 , E c E F0.1459eV(b) E F E FikT lnN dn i0.0259 lnN d1.51010For 1014cm 3 , E FE Fi 0.2280 eV15cm 3, E F E Fi 0.2877 eV10 1016 cm 3 , E F E Fi 0.3473 eV 1017 cm 3 ,E F E Fi0.4070 eV_______________________________________ 4.50N d N d 2(a) n on i 222n o1.05N d1.05 10 15 cm 31.05 10150.5 10 1520.5 10152n i2son i 25.25 10 28Now3n i 22.8 1019 1.04 1019T300exp1.120.0259 T 30035.25 10 28 2.912 10 38 T300exp 12972.973TBy trial and error, T 536.5K(b) At T 300 K,E c EF kT ln N cn oE c EF 0.0259 ln 2.8 1019 1015T 536.5 K, 0.2652 eVAt536.5kT0.02590.046318 eV3003 / 2N c 2.8 1019 536.53006.696 1019cm 3E c E FN c kT lnn oE c E F6.696 10 19 0.046318 ln10151.050.5124 eVthen E c E F 0.2472 eV(c)Closer to the intrinsic energy level._______________________________________4.51p oE Fi EF kT lnn iAt T 200K, kT 0.017267 eVT 400 K, kT 0.034533 eVT 600 K, kT 0.0518 eV At T 200K,22.8 10191019 200n i 1.04300exp1.120.017267n i 7.638 10 4 cm 3At T 400 K,3n i 2 2.8 1019 1.04 10 19 4003001.12exp0.034533n i 2.381 1012 cm 3At T 600 K,322.8 1019 19 600n i 1.04 10300exp 1.120.0518n i 9.740 1014 cm 3At T 200 K and T 400 K,p o N a 3 1015 cm 3At T 600 K,N a N a2p o n i22 23 15 3 10 15 2 9.740 10 1410 22 23.288 1015cm3Then, T 200K, E Fi E F 0.4212eVT 400K,E Fi EF 0.2465 eVT600K,E Fi EF 0.0630 eV_______________________________________4.52(a)N a N aE Fi EF kT ln 0.0259 ln6n i 1.8 10For N a10 14 cm 3 ,E FiE F0.4619 eVN a 10 15 cm 3,E FiE F0.5215 eV163,N a 10 cmE FiE F0.5811 eVN a 10 17cm 3,E FiE F 0.6408 eV(b)E FEN7.0 1018kT ln0.0259 lnN aN aFor N a10 14 cm 3 ,E F E0.2889 eVN a 10 15 cm 3 ,E FE0.2293 eV163,N a 10 cmE F E0.1697 eVN a 10 17 cm3,E F E 0.1100 eV_______________________________________ 4.53(a) E Fi3 m *p E midgapkT ln4m n *3 0.0259 ln 104 orE Fi E midgap 0.0447 eV(b) Impurity atoms to be added soE midgap EF 0.45 eV(i) p-type, so add acceptor atoms(ii)E Fi EF 0.0447 0.45 0.4947 eVThenp oE FiE Fn i expkT10 5exp 0.49470.0259 or10 13 cm3p o N a1.97_______________________________________4.54n oN d N aN c expE c E FkTsoN d 5 10 15 2.8 10 19 exp0.2150.025951015 6.95 1015orcm 3N d 1.2 1016_______________________________________4.55(a) Silicon(i) E cE F N ckT lnN d0.0259 ln 2.8 10 190.2188 eV6 1015(ii) E cE F0.2188 0.0259 0.1929 eVN dN c expE c E FkT2.8 10 19 exp0.19290.0259N d1.631 1016 cm3N d 6 1015N d1.031 10 16 cm 3Additional donor atoms(b) GaAs(i) E c E F0.0259 ln4.7101710150.15936eV(ii) E cE F0.15936 0.0259 0.13346 eVN d4.7 1017 exp0.133460.02592.718 1015 cm 3N d 1015N d1.718 10 15 cm3Additionaldonor atoms_______________________________________ 4.56(a) E Fi E FN kT lnN a0.0259 ln 1.04 10190.1620 eV2 1016(b) E F E Fi kT ln N c N d0.0259 ln 2.8 1019 0.1876 eV2 10 16(c) For part (a);p o 2 1016 cm 3n i2 1.5 1010 2n op o 2 10161.125 104cm3For part (b):3n o 2 1016 cmn i 2 1.5 1010 2p on o 2 10 161.125 104cm3_______________________________________ 4.57n oE F E Fin i expkT1.8 10 6 exp 0.550.02593.0 1015cm 3Add additional acceptor impuritiesn o N d N a3 10 15 7 10 15 N aN a 4 10 15 cm 3_______________________________________(a) E Fi E F kT lnpon i0.02593 10 150.3161 eVln10 101.5(b) E F E Fin okT lnn i0.02593 10160.3758 eVln10 101.5(c) E F E Fi(d) E Fi E Fp okT lnn i0.0259 375 ln 4 1015300 7.334 10 110.2786 eV(e) E F E Fi kT lnnon i140.0259 450 ln 1.029 10300 1.722 10 130.06945eV_______________________________________4.59(a) E F ENkT lnp o0.0259 ln7.0 10180.2009 eV3 1015(b) E F E 0.0259 l n7.0 10 181.08 10 41.360 eV(c) E F E 0.0259 l n 7.0 10181.8 10 60.7508 eV4.58(d) E F E 0.0259 375300ln 7.0 10 18 375 300 3 / 24 10 150.2526 eV(e) E F E 0.0259 450 300ln 7.0 10 18 450 300 3/ 21.48 10 71.068 eV_______________________________________4.60n-typeE F E Fi kT ln n o n i0.02591.125 10 16ln100.3504 eV1.5 10______________________________________ 4.61N a N a 2 p o 22 2 n i5.08 1015 5 101525 10 15 2n i225.08 10 15 2.5 10 15 22.5 1015 2n i26.6564 10 30 6.25 10 30 n i2n i 2 4.064 10 29n i2 N c N expE gkTkT 0.02593500.030217 eV3003502N c 1.2 10 19 1.633 1019 cm 33003502N 1.8 1019 2.45 10 19 cm 3300Now4.064 10 29 1.633 1019 2.45 1019E gexp0.030217SoE g 0.030217 ln 1.633 10 19 2.45 10 194.064 10 29E g 0.6257 eV_______________________________________4.62(a) Replace Ga atoms Silicon acts as adonorN d0.05 7 1015 3.5 10 14 cm 3Replace As atoms Silicon acts asanacceptorN a 0.95 7 1015 6.65 10 15 cm 3(b) N a N d p-type(c) p o N a N d 6.65 1015 3.5 10146.3 1015cm 3n i 2 1. 810 6 2n o 5.14 10 4 cm 3 p o 6 .3 1015(d) E Fi E F kT ln p o n i0.0259 ln 6.3 10 150.5692 eV1.8 10 6_______________________________________。
半导体物理第五章习题参考答案pn 结

ln
Nd Na ni 2
1.381023 300 1.6 1019
ln
1015 1017 (1.51010 )2
V
0.694V
(2) 当 ni=2.31013/cm3 时:
i
kT q
ln
Nd Na ni 2
1.381023 300 1.6 1019
ln
1015 1017 (2.3 1013 )
掺杂浓度 Nd 和 Na 越高,耗尽电容越大。 4) 由自建势公式:
i
kT q
ln
Nd Na ni 2
0.7V
从而:
0.73m V 0.3V
W
20 Si q
1 Na
1 Nd
i
V
1.341104 i V m V 1 2 0.97m
3.79m
V 0 V 10V
1.4610-4 F m2
答:t<0 时,pn 结正向导通,p 区的空穴,n 区的电子不断向对方区域扩散,并 在对方区域内形成相当数量的存储积累,正向电流越大,存储载流子的数目也越 多,在 t=0 时,外加电压突然由Va 变为 Va 时,上述存储的电荷基本不变,但电
场出现反向,因此会出现电流反向,大小保持不变的现象。在反向电压作用下, 此前注入基区的积累电荷逐渐被反向电压抽走,积累电荷浓度逐渐减小,反向电 流也随之减小,逐渐减小到反向饱和电流,pn 结转为截止状态。
qN
0
a
qNd
xp x 0 x xp , 0 x d, x xn
d x xn
结合 E d ,以及边界条件: dx
d 2
dx 2
Si
E xp E xn 0 E 0 E 0 Ed Ed
第1章课后习题参考答案
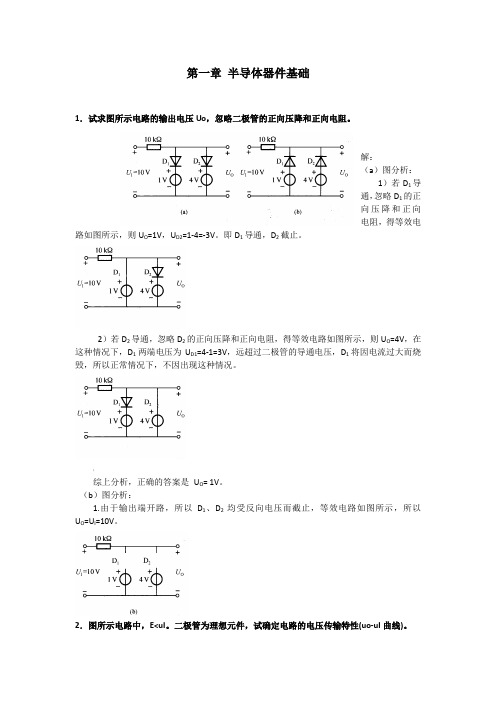
第一章半导体器件基础1.试求图所示电路的输出电压Uo,忽略二极管的正向压降和正向电阻。
解:(a)图分析:1)若D1导通,忽略D1的正向压降和正向电阻,得等效电路如图所示,则U O=1V,U D2=1-4=-3V。
即D1导通,D2截止。
2)若D2导通,忽略D2的正向压降和正向电阻,得等效电路如图所示,则U O=4V,在这种情况下,D1两端电压为U D1=4-1=3V,远超过二极管的导通电压,D1将因电流过大而烧毁,所以正常情况下,不因出现这种情况。
;综上分析,正确的答案是U O= 1V。
(b)图分析:1.由于输出端开路,所以D1、D2均受反向电压而截止,等效电路如图所示,所以U O=U I=10V。
2.图所示电路中,E<uI。
二极管为理想元件,试确定电路的电压传输特性(uo-uI曲线)。
解:由于E<u I,所以D1截止、D2导通,因此有u O=u I –E。
其电压传输特性如图所示。
E uiu o3.选择正确的答案填空在图所示电路中,电阻R为6Ω,二极管视为理想元件。
当普通指针式万用表置于R×1Ω挡时,用黑表笔(通常带正电)接A点,红表笔(通常带负电)接B点,则万用表的指示值为( a )。
Ω,Ω,Ω,Ω,Ω。
解:由于A端接电源的正极,B端接电源的负极,所以两只二极管都截止,相当于断开,等效电路如图,正确答案是18Ω。
4.在图所示电路中,uI =10sinωt V,E = 5V,二极管的正向压降可忽略不计,试分别画出输出电压uo的波形。
解:(a)图当u I<E时,D截止,u O=E=5V;当u I≥E时,D导通,u O=u Iu O波形如图所示。
u Iωt5V10Vuoωt5V10V~(b)图当u I<-E=-5V时,D1导通D2截止,uo=E=5V;当-E<u I<E时,D1导通D2截止,uo=E=5V;当u I≥E=5V时,uo=u I所以输出电压u o的波形与(a)图波形相同。
《半导体器件》习题与参考答案

第二章1 一个硅p -n 扩散结在p 型一侧为线性缓变结,a=1019cm -4,n 型一侧为均匀掺杂,杂质浓度为3×1014cm -3,在零偏压下p 型一侧的耗尽层宽度为0.8μm ,求零偏压下的总耗尽层宽度、建电势和最大电场强度。
解:)0(,22≤≤-=x x qax dxd p S εψ)0(,22n SD x x qN dx d ≤≤-=εψ 0),(2)(22≤≤--=-=E x x x x qa dx d x p p Sεψ n n SDx x x x qN dx d x ≤≤-=-=E 0),()(εψ x =0处E 连续得x n =1.07µm x 总=x n +x p =1.87µm⎰⎰=--=-npx x bi V dx x E dx x E V 0516.0)()(m V x qa E p S/1082.4)(252max ⨯-=-=ε,负号表示方向为n 型一侧指向p 型一侧。
2 一个理想的p-n 结,N D =1018cm -3,N A =1016cm -3,τp =τn =10-6s ,器件的面积为1.2×10-5cm -2,计算300K 下饱和电流的理论值,±0.7V 时的正向和反向电流。
解:D p =9cm 2/s ,D n =6cm 2/scm D L p p p 3103-⨯==τ,cm D L n n n 31045.2-⨯==τnp n pn p S L n qD L p qD J 0+=I S =A*J S =1.0*10-16A 。
+0.7V 时,I =49.3µA , -0.7V 时,I =1.0*10-16A3 对于理想的硅p +-n 突变结,N D =1016cm -3,在1V 正向偏压下,求n 型中性区存贮的少数载流子总量。
设n 型中性区的长度为1μm ,空穴扩散长度为5μm 。
解:P +>>n ,正向注入:0)(20202=---pn n n n L p p dx p p d ,得:)sinh()sinh()1(/00pnn pn kTqV n n n L x W L xW e p p p ---=- ⎰⨯=-=nnW x n n A dx p p qA Q 20010289.5)(4一个硅p +-n 单边突变结,N D =1015cm -3,求击穿时的耗尽层宽度,若n 区减小到5μm ,计算此时击穿电压。
(完整版)电子电路基础习题册参考答案-第一章

电子电路基础习题册参考答案(第三版)全国中等职业技术第一章常用半导体器件§1-1 晶体二极管一、填空题1、物质按导电能力的强弱可分为导体、绝缘体和半导体三大类,最常用的半导体材料是硅和锗。
2、根据在纯净的半导体中掺入的杂质元素不同,可形成N 型半导体和P 型半导体。
3、纯净半导体又称本征半导体,其内部空穴和自由电子数相等。
N型半导体又称电子型半导体,其内部少数载流子是空穴;P型半导体又称空穴型半导体,其内部少数载流子是电子。
4、晶体二极管具有单向导电性,即加正向电压时,二极管导通,加反向电压时,二极管截止。
一般硅二极管的开启电压约为0.5 V,锗二极管的开启电压约为0.1 V;二极管导通后,一般硅二极管的正向压降约为0.7 V,锗二极管的正向压降约为0.3 V。
5.锗二极管开启电压小,通常用于检波电路,硅二极管反向电流小,在整流电路及电工设备中常使用硅二极管。
6.稳压二极管工作于反向击穿区,稳压二极管的动态电阻越小,其稳压性能好。
7在稳压电路中,必须串接限流电阻,防止反向击穿电流超过极限值而发生热击穿损坏稳压管。
8二极管按制造工艺不同,分为点接触型、面接触型和平面型。
9、二极管按用途不同可分为普通二极管、整流二极管、稳压二极管、开关、热敏、发光和光电二极管等二极管。
10、二极管的主要参数有最大整流电流、最高反向工作电压、反向饱和电流和最高工作频率。
11、稳压二极管的主要参数有稳定电压、稳定电流和动态电阻。
12、图1-1-1所示电路中,二极管V1、V2均为硅管,当开关S与M相接时,A点的电位为无法确定V,当开关S与N相接时,A点的电位为0 V.13图1-1-2所示电路中,二极管均为理想二极管,当开关S打开时,A点的电位为10V 、流过电阻的电流是4mA ;当开关S闭合时,A点的电位为0 V,流过电阻的电流为2mA 。
14、图1-1-3所示电路中,二极管是理想器件,则流过二极管V1的电流为0.25mA ,流过V2的电流为0.25mA ,输出电压U0为+5V。
(完整版)半导体芯片制造中级复习题A

半导体芯片制造中级工复习题一判断题:1.单晶是原子或离子沿着三个不同的方向按一定的周期有规则的排列,并沿一致的晶体学取向所堆垛起来的远程有序的晶体。
( √)2.迁移率是反映半导体中载流子导电能力的重要参数。
掺杂半导体的电导率一方面取决于掺杂的浓度,另一方面取决于迁移率的大小。
同样的掺杂浓度,载流子的迁移率越大,材料的电导率就越高。
(√)3.点缺陷,如空位、间隙原子、反位缺陷、替位缺陷,和由它们构成的复合体。
(√)4.位错就是由范性形变造成的,它可以使晶体内的一原子或离子脱离规则的周期排列而位移一段距离,位移区与非位移区交界处必有原子的错位,这样产生线缺陷称为位错。
(√)5.抛光片的电学参数包括电阻率,载流子浓度,迁移率,直径、厚度、主参考面等。
(×)6.液相外延的原理是饱和溶液随着温度的降低产生过饱和结晶。
( √)7.离子源是产生离子的装置。
(√)8.半导体芯片制造工艺对水质的要求一般. (×)9.光致抗蚀剂在曝光前对某些溶剂是可溶的,曝光后硬化成不可溶解的物质,这一类抗蚀剂称为负性光致抗蚀剂,由此组成的光刻胶称为负性胶。
(√)10.设备、试剂、气瓶等所有物品不需经严格清洁处理,可直接进入净化区。
(×)11.干法腐蚀清洁、干净、无脱胶现象、图形精度和分辨率高。
(√)12.光刻工艺要求掩膜版图形黑白区域之间的反差要低。
(×)13.在半导体集成电路中,各元器件都是制作在同一晶片内。
因此要使它们起着预定的作用而不互相影响,就必须使它们在电性能上相互绝缘。
(√)14.金属剥离工艺是以具有一定图形的光致抗蚀剂膜为掩膜,带胶蒸发或溅射所需的金属,然后在去除光致抗蚀剂膜的同时,把胶膜上的金属一起去除干净。
(√)15.表面钝化工艺是在半导体芯片表面复盖一层保护膜,使器件的表面与周围气氛隔离。
(√)二选择题1.下列材料属于N型半导体是AC 。
A 硅中掺有元素杂质磷(P)、砷(As) B.硅中掺有元素杂质硼(B)、铝(Al)C 砷化镓掺有元素杂质硅(Si)、碲(Te) D.砷化镓中掺元素杂质锌、镉、镁2.属于绝缘体的正确答案是 B 。
半导体物理第三章习题参考答案

NA
解得:
p
NA 2
1
1
4ni2
N
2 A
1
2
1 叶良修,半导体物理学(第二版),上册,129 页。
(1) T 300K 时,硼原子全部电离,此时本征载流子浓度 ni 1.51010cm-3 有:
NA ,
p
NA
1014 cm-3 , n
ni2 p
2.3106 cm-3 ;
(2) T 400K 时,此时本征载流子浓度23 ni 1.31014 cm-3 NA ,本征激发已不 能忽略,有:
答:当T 300K 时,有:
3
3
NC
2
2 mnkT h2
2
2.509 1019
mn m0
2
cm-3
3
3
NV
2
2
mp h2
kT
2
2.509
1019
mp m0
2
cm-3
ni
NC NV
1
2
exp
Eg 2kT
代入数据得到:
Si GaAs
NC cm-3 2.7581019 4.351017
由波尔兹曼分布近似:
n NA ND nD
n
NC
exp
EC EF kT
以及施主能级上的电子的分布规律:
有:
nD
ND
1 gD
exp
EF ED kT
1
1 gD
exp
EF ED kT
n NA n n ND nD
ND NA n
nD
n
ND nD
1
n
1 gD
exp
半导体物理第四章习题参考答案

9. 由于光的照射在半导体中产生了非平衡载流子 n p 1012 cm-3 ,分别计算
施主掺杂浓度为 ND 1016 cm-3 的 N 型硅和本征硅在这种情况下的准费米能 级的位置,并与原来的费米能级的位置做比较,画出相应的能带图。 答:有:
n
ni
exp
E fn kT
Ei
,
n
E fn
答:(1) 电离杂质散射是由电离的杂质对载流子的库仑相互作用引起的,其特点 为:掺杂浓度越高,电离杂质散射越显著;温度越高,载流子的动能越大,受库 仑相互作用力的影响相对减弱,因此,电离杂质散射在低温时起主要作用,其 、
与温度的关系为:
3
3
I T 2 , I T 2
(2) 声学波散射是晶格振动对载流子散射中作用大的一种,属于晶格自身的特
10. 设空穴浓度是线性分布,在 3μm 内浓度分布差 1015cm-3,μp=400cm2·V-1·s-1, 试计算空穴扩散电流密度。
答:由爱因斯坦关系:
Dp
kT q
p
有:
jp
qDp
p x
kT p
p x
5.52 A
cm2
11. 考虑平衡情形,证明:
en
Vthn nni
exp
Et Ei kT
i niqn piqp 4.45106 Ω cm
(2)
当掺入百万分之一的
As
时,施主浓度为:
ND
5 1022 106
cm-3
51016 cm-3
(其中 N 51022 cm-3 为 Si 的原子密度)。
由于杂质全部电离,从而: n
ND
51016 cm-3,
p
半导体器件原理简明教程习题答案(供参考)

文档来源为:从网络收集整理.word 版本可编辑.欢迎下载支持.半导体器件原理简明教程习题答案傅兴华1.1 简述单晶、多晶、非晶体材料结构的基本特点.解整块固体材料中原子或分子的排列呈现严格一致周期性的称为单晶材料;原子或分子的排列只在小范围呈现周期性而在大范围不具备周期性的是多晶材料; 原子或分子没有任何周期性的是非晶体材料.1.6 什么是有效质量,根据E(k)平面上的的能带图定性判断硅鍺和砷化镓导带电子的迁移率的相对大小.解有效质量指的是对加速度的阻力.kE h m k ∂∂=21*1由能带图可知由能带图可知,Ge ,Ge 与Si 为间接带隙半导体为间接带隙半导体,Si ,Si 的Eg 比Ge 的Rg 大,所以Ge μ>Si μ.GaAs 为直接带隙半导体直接带隙半导体,,它的跃迁不与晶格交换能量它的跃迁不与晶格交换能量,,所以相对来说GaAs μ>Ge μ>Si μ.1.10 假定两种半导体除禁带宽度以外的其他性质相同假定两种半导体除禁带宽度以外的其他性质相同,,材料1的禁带宽度为1.1eV,1.1eV,材料材料2的禁带宽度为 3.0eV,3.0eV,计算两种半导体材料的本征载流子浓度比值计算两种半导体材料的本征载流子浓度比值计算两种半导体材料的本征载流子浓度比值,,哪一种半导体材料更适合制作高温环境下工作的器件合制作高温环境下工作的器件? ? 解本征载流子浓度本征载流子浓度::)exp()(1082.42015Tdp dn ik Eg m m m n ⨯=Θ两种半导体除禁带以外的其他性质相同∴)9.1exp()exp()exp(0.31.121T k k k n n T T ==--ΘTk 9.1>0 ∴21n n >∴在高温环境下2n 更合适1.11在300K 下硅中电子浓度330102-⨯=cm n ,计算硅中空穴浓度0p ,画出半导体能带图,判断该半导体是n 型还是p 型半导体. 解31732100220010125.1102)105.1(p -⨯=⨯⨯==→=cm n n n p n i i ∴>00n p Θ是p 型半导体1.16硅中受主杂质浓度为31710-cm ,计算在300K 下的载流子浓度0n 和0p ,计算费米能级相对于本征费米能级的位置,画出能带图. 解317010-==cm N p A 200i n p n =T=300K →310105.1-⨯=cm n i 330201025.2-⨯==∴cm p n n i00n p >Θ∴该半导体是p 型半导体1.27砷化镓中施主杂质浓度为31610-cm ,分别计算T=300K 、400K 的电阻率和电导率。
半导体器件基础习题答案(完美版)

半导体器件习题答案
片的电阻率较大?说明理由。 A:
1 , n型半导体 q n N D 1 , p型半导体 q p N A
两片晶片的掺杂浓度相同,而电子的迁移率大于空穴的迁移率,因此 p 型半导体即晶片 2 的电阻率较大。 Q: (e) 在室温下硅样品中测得电子的迁移率 cm2/V .s 。求电子的扩散系数。 A:
第二章 2.2 使用价键模型,形象而简要地说明半导体 (a) 失去原子 (b) 电子 (c) 空穴 (d) 施主 (e) 受主
2.3 Q: 使用能带模型,形象而简要地说明半导体: (a) 电子 (b) 空穴 (c) 施主
(d) 受主
(e) 温度趋向于 0 K 时,施主对多数载流子电子的冻结
(f) 温度趋向于 0 K 时,受主对多数载流子空穴的冻结 (g) 在不同能带上载流子的能量分布 (h) 本征半导体
说明:当材料内存在电场时,能带能量变成位置的函数,称为“能带弯曲” Q: (b) 电子的动能为零,即 K.E.=0 A: 说明:
Q: (c) 空穴的动能 K.E.=EG/4 A: 说明:
Q: (d) 光产生 A:
说明:从外部输入的光被吸收,电子被激发后,直接从价带进入导带 Q: (e) 直接热产生
1062109053 杨旭一整理 (仅供参考)
* m* p 2 m p ( Ev E )
g v ( E )[1 f ( E )] ( Ev E ) e
1/ 2
2
3
e ( E EF ) / kT
( E E F ) / kT
...
* m* p 2m p
d g c ( E ) f ( E ) dE e ( E EF ) / kT ( Ev E )1/ 2 e ( E EF ) / kT 1/ 2 2( Ev E ) kT 0 EE
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章1 一个硅p -n 扩散结在p 型一侧为线性缓变结,a=1019cm -4,n 型一侧为均匀掺杂,杂质浓度为3×1014cm -3,在零偏压下p 型一侧的耗尽层宽度为0.8μm ,求零偏压下的总耗尽层宽度、内建电势和最大电场强度。
解:)0(,22≤≤-=x x qax dxd p S εψ)0(,22n SD x x qN dx d ≤≤-=εψ 0),(2)(22≤≤--=-=E x x x x qa dx d x p p Sεψ n n SDx x x x qN dx d x ≤≤-=-=E 0),()(εψ x =0处E 连续得x n =1.07µm x 总=x n +x p =1.87µm⎰⎰=--=-npx x bi V dx x E dx x E V 0516.0)()(m V x qa E p S/1082.4)(252max ⨯-=-=ε,负号表示方向为n 型一侧指向p 型一侧。
2 一个理想的p-n 结,N D =1018cm -3,N A =1016cm -3,τp =τn =10-6s ,器件的面积为1.2×10-5cm -2,计算300K 下饱和电流的理论值,±0.7V 时的正向和反向电流。
解:D p =9cm 2/s ,D n =6cm 2/scm D L p p p 3103-⨯==τ,cm D L n n n 31045.2-⨯==τnp n pn p S L n qD L p qD J 0+=I S =A*J S =1.0*10-16A 。
+0.7V 时,I =49.3µA , -0.7V 时,I =1.0*10-16A3 对于理想的硅p +-n 突变结,N D =1016cm -3,在1V 正向偏压下,求n 型中性区内存贮的少数载流子总量。
设n 型中性区的长度为1μm ,空穴扩散长度为5μm 。
解:P +>>n ,正向注入:0)(20202=---pn n n n L p p dx p p d ,得:)sinh()sinh()1(/00pnn pn kTqV n n n L x W L xW e p p p ---=- ⎰⨯=-=nnW x n n A dx p p qA Q 20010289.5)(4一个硅p +-n 单边突变结,N D =1015cm -3,求击穿时的耗尽层宽度,若n 区减小到5μm ,计算此时击穿电压。
解:m V N E B g c /1025.3)1.1E )q(101.14814321S7⨯=⨯=(εV qN E V BCS B 35022==εm qN V x BBS mB με5.212==n 区减少到5µm 时,V V x W x V B mBmB B9.143])(1[22/=--= 第三章1 一个p +-n-p 晶体管,其发射区、基区、集电区的杂质浓度分别是5×1018,1016,1015cm -3,基区宽度W B 为1.0μm ,器件截面积为3mm 2。
当发射区-基区结上的正向偏压为0.5V ,集电区-基区结上反向偏压为5V 时,计算(a)中性基区宽度,(b)发射区-基区结的少数载流子浓度,(c)基区内的少数载流子电荷。
解:(a )热平衡下,内建电势2ln iDA bi n N N q kT V =EB 结,V bi =0.857V ;m V V N N N N q x eb bi BB E ES neb με217.0)()(2=-+=CB 结,V bi =0.636V ;m V V N N N N q x cb bi BB E CS ncb με261.0)()(2=-+=W =W B -x neb -x ncb =0.522µm(b )312/01073.4)0(-⨯==cm e p p kT qV n n BE(c )C qAWp Q n B 131093.52)0(-⨯==2 推导基区杂质浓度为l x B B e N x N /)0()(-=时的基区内建电场公式及基区少子浓度分布表达式。
解:不妨设为NPN 晶体管,由于基区中杂质存在浓度梯度,其多数载流子(空穴)的分布也存在浓度梯度,它使空穴作扩散运动,这一运动的产生破坏了基区中的电中性,为维持电中性,基区中就产生一电场来阻止基区中空穴的扩散运动。
电场的大小是恰好使电场产生的空穴漂移流与因杂质浓度梯度所引起的扩散流相抵消,这一电场就称为缓变基区内建电场。
考虑基区中自建电场对电流的贡献,热平衡时,净空穴电流为零。
即0)()()(00=-=dxx dp qD x x p q J B pBB B pB pB εμ 由此求得εB 为 dxx dp x p D x B B pBpBB )()(1)(00⋅=με平衡时基区中的空穴浓度P B0等于基区的杂质浓度N B ,于是上式写为dx x dN x N q kT x B B B )()(1)(=ε,代入lx B B e N x N /)0()(-= 则有lq kT B 1⋅-=ε 考虑电子电流密度:dxx dn qD x x n q J B nBB B nB nB )()()(+⋅⋅=εμ 将εB (x )代入上式,可得 ))()()()((dxx dn dx x dN x N x n qD J B B B B nB nB +⋅= 若忽略基区中空穴的复合,即J nB 为常数,我们可以用N B (x )乘上式两端,并从x 到W B 积分,得⎰⎰=BBW xB B W xB nBnB dx dxx n x N d dx x N qD J ))()(()(近似认为在x=W B 处,n B =0,有⎰-=B W x B B nB nBB dx x N x N qD J x n )()()( 积分之得到 {}]/)(ex p[1)(l x W l qD J x n B nBnBB ----=若忽略发射极电子电流在发射结势垒区中的复合,即用J nE 代替上式中的J nB ,有 {}]/)(ex p[1)(l x W l qD J x n B nBnEB ----= 3 一个硅n +-p-n 晶体管的发射区和集电区两侧的掺杂是突变的。
其发射区、基区、集电区的杂质浓度分别为1019,3×1016,5×1015cm -3,(a)求集电区-基区电压的上限,在该电压下,发射结偏置电压已不再能控制集电极电流,设基区宽度为0.5μm 。
(b)若截止频率主要受少子穿过基区的渡越时间限制,求在零偏压下共基极和共发射级的电流截止频率(晶体管的发射效率为0.999,基区传输因子为0.99)。
解:(a )热平衡下,V n N N q T k V iBC B biCB 707.0ln 2==当B bc bi BB E CS p W V V N N N N q x =-+=)()(2ε时穿通,可得:V V V PT BC 5.39==(b )s D W nB 1121068.32-⨯==τ而f T 主要受B τ限制,GHz f BT 32.421==πτ9010=-=T T γαγαβ,MHz ff T 1.480==ββ,GHz f f T 38.4)1(0=+=βα4 一个开关晶体管,基区宽度为0.5μm ,扩散系数为10cm 2/s ,基区内的少数载流子寿命为10-7s ,晶体管加偏压V CC =5V ,负载电阻为10KΩ,若在基极上加2μA 的脉冲电流,持续时间为1μs ,求基区的存贮电荷和存贮延迟时间。
解:不妨设为N +PN 管,)1()(/n t n B B e I t Q ττ--=在t 1时刻达到饱和,相应集电极电流为mA R V V I CCECC CS 5.0=-=s D W nB 1021025.12-⨯==τC I Q B CS S 141025.6-⨯==τs Q I t SnB n S 71016.1ln-⨯==ττ 存储电荷为C e I s Q n t n B B 13/102)1()1(--⨯=-=ττμ5. 一理想的PNP 晶体管,其发射区、基区、集电区的杂质浓度分别为1019、1017、5×1015cm-3,而少数载流子的寿命分别为10-8、10-7和10-6s ,假设器件有效横截面积A 为0.05mm 2,且射基结上正向偏压为0.6V ,请求出晶体管的共基极电流增益。
晶体管的其他参数为:D E =1cm 2/s , Dp=10cm 2/s , D C =2cm 2/s , W =0.5μm 。
解:0γααT =6. 欲设计一双极型硅晶体管,其截止频率f T 为5GHz ,请问中性基区宽度W 需为多少?假设Dp 为10cm 2/s ,并可忽略发射极和集电极延迟。
解:PNP 管,f T 忽略E τ和C τ,主要受B τ限制,GHz f BT 521==πτpB D W 22=τ=3.2*10-11s 则:B p D W τ2==2.53*10-5cm=0.253μm第四章1、求势垒高度为0.8V 的Au -Si 肖特基二极管的空穴电流和电子电流的比值。
硅为n 型,电阻率为1Ωcm ,寿命τp =100μs ,μp =400cm 2/(Vs)。
解:电阻率为1Ωcm ,查n -Si 的电阻率和浓度的关系图可得N D =4.5×1015cm -3。
s cm qkTD p p /4.102==μ,m D L p p p μτ2.32==,空穴电流密度为Dp i p p N L n qD J 20==2.41×10-12A/cm 2,电子电流密度为kTq S Bn eT A J φ-=2*=4.29×10-7A/cm 2,其中A *=110A/K 2cm 2。
401062.5-⨯=Sp J J2、一个欧姆接触的面积为10-5cm 2,比接触电阻为10-6Ωcm 2,这个欧姆接触是在一个n 型硅上形成的。
若N D =5×1019cm -3,ФBn =0.8V ,电子有效质量为0.26m 0,求有1A 正向电流通过时,欧姆接触上的电压降。
解:比接触电阻为10-6Ωcm 2, N D =5×1019cm -3,是高掺杂,因此隧道电流起主要支配作用,))(2exp(DBn S n N V m AK I --=φε,1)])(2exp(2[--=DBn S n DS n C N m K N m φεερ,其中K 是常数。
由此得到)2exp(21V N m N A m I DS n DS n Cεερ-=,计算得,V =3.53mV 。
