Buck直流变换器的工作原理及动态建模
Buck-Boost电路建模及分析

题目:Buck-Boost电路建模及分析摘要:作为研究开关电源的基础,DC-DC开关变换器的建模分析对优化开关电源的性能和提高设计效率具有重要意义。
而Buck-Boost电路作为DC-DC开关变换器的其中一种电路拓扑形式,因其输出电压极性与输入电压相反,而幅度既可比输入电压高,也可比输入电压低,且电路结构简单而流行。
为了达到全面而深入的研究效果,本文对Buck-Boost电路进行了稳态分析和小信号分析。
稳态分析中,首先介绍了电路工作原理,得出了两种工作模式下的电压转换关系式,并同时可知基于占空比怎样计算其输出电压以及最小最大电感电流和输出纹波电压计算公式;接着推导了状态空间模型,以在MATLAB中进行仿真;而最后仿真得到的电感电流、输出电压的变化规律符合理论分析。
小信号分析中,首先推导了输出与输入间的传递函数表达式,以了解低频交流小信号分量在电路中的传递过程;接着分析其零极点,且仿真绘制波特图进行了验证。
经过推导与研究,稳态分析和小信号分析下仿真得到的变化规律均与理论上的推导一致。
关键词:Buck-Boost;稳态分析;小信号分析;MATLAB仿真1.概论现代开关电源有两种:直流开关电源、交流开关电源。
本课题主要介绍直流开关电源,其功能是将电能质量较差的原生态电源,如市电电源或蓄电池电源,转换为满足设备要求的质量较高的直流电源,即将“粗电”转换为“精电”。
直流开关电源的核心是DC-DC变换器。
作为研究开关电源的基础,DC-DC开关变换器的建模分析对开关电源的分析和设计具有重要意义。
DC-DC开关变换器最常见的三种电路拓扑形式为:降压(Buck)、升压(Boost)和降压-升压(Buck-Boost) [1],如图1-1所示。
其中Buck-Boost变换器因其输出电压极性与输入电压相反,而幅度既可比输入电压高,也可比输入电压低,且电路结构简单而流行。
(a) Buck型电路结构(b) Boost型电路结构(c) Buck-Boost型电路结构图1-1 DC-DC变换器的三种电路结构本课题针对Buck-Boost变换器的建模分析进行深入研究,以优化开关电源的性能和提高设计效率。
buck-boost变换器工作原理

buck-boost变换器工作原理
Buck-boost变换器是一种电力转换装置,它可以将直流电压转换为不同的电压水平,从而实现电源的调整和控制。
它工作的原理基于开关电源的工作原理和能量储存原理。
Buck-boost变换器的基本结构包括开关管、电感、电容和控制电路。
工作原理如下:
1. 当输入电压高于输出电压时,开关管K1关闭,开关管K2打开。
此时,电感L和电容C组成的LC滤波回路开始储存能量。
电感L的磁场储存了电流的能量,电容C储存了电压的能量。
2. 在上述状态下,当开关管K1关闭时,由于电感的特性,电流不会突变。
电感L会释放储存的能量,电流会从电感流向负载。
3. 当电感释放能量时,负载上的电压会高于输入电压。
这样就实现了电压升高的功能。
4. 当输入电压低于输出电压时,开关管K1打开,开关管K2关闭。
此时,电容C充满了能量,而电感L则储存能量。
5. 在上述状态下,当开关管K1打开时,电感的磁场会继续储存能量。
电感释放能量,电流从电感流向负载。
6. 当电感释放能量时,负载上的电压会低于输入电压。
这样就实现了电压降低的功能。
通过不断地开关开关管K1和K2,Buck-boost变换器可以实现输入电压到输出电压的转换。
控制电路会根据输出电压的变化来控制开关管的状态,以实现稳定的输出电压。
总结起来,Buck-boost变换器通过周期性地储存和释放能量来实现对输入电压的调节,从而实现对输出电压的升高或降低。
这种转换过程是通过改变开关管的状态来控制的,通过控制电路实现对输出电压的稳定性控制。
Buck变换器建模和仿真
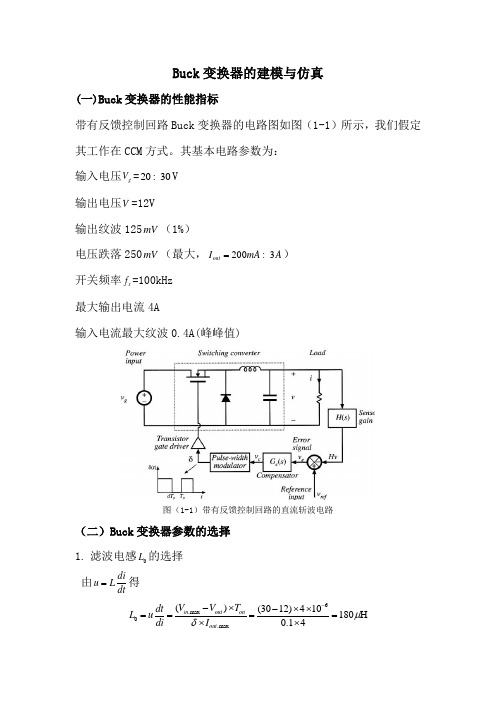
Buck 变换器的建模与仿真(一)Buck 变换器的性能指标带有反馈控制回路Buck 变换器的电路图如图(1-1)所示,我们假定其工作在CCM 方式。
其基本电路参数为: 输入电压g V =2030V 输出电压V =12V 输出纹波125mV (1%)电压跌落250mV (最大,2003out I mA A =) 开关频率s f =100kHz 最大输出电流4A输入电流最大纹波0.4A(峰峰值)图(1-1)带有反馈控制回路的直流斩波电路(二)Buck 变换器参数的选择 1. 滤波电感0L 的选择 由diu Ldt=得 6.max 0.max ()(3012)410180H 0.14in out on out V V T dt L u di I μδ--⨯-⨯⨯====⨯⨯这里我们取0L 为180H μ 最大负载时的峰值电流为.max .max 40.054 4.22peak out out I I I A δ=+=+⨯=2. 滤波电容0C 的选择 由dui cdt=得 其向量形式为I j cU ω=I jcUω=所以需要穿越频率的带宽为2outc out outI f C V π∆=∆如果假定穿越频率为10kHz250892.8out c out V mZ m I ∆===Ω∆ 原则上为了留有设计裕量,电阻的阻抗按13计算阻抗选取 根据上面计算结果,我们可以在Rubycon 公司的ZL 系列,16V 中选取以下规格:C=330F μ,760C rms I mA =@105A C =︒ ,72ESR low R m =Ω@20A T C =︒ ,220ESR low R m =Ω@10A T C =-︒电容ESR 的阻抗应小于输出电容在穿越频率处的阻抗11482 6.2810330c out m f C k π==Ω⨯⨯86c Z m ≤==Ω设计余量不足,我们重新选ZL 系列中C=1000F μ,同样的过程,我们可以得出满足条件。
Buck降压式变换器基本结构及原理

Buck降压式变换器基本结构及原理一、Buck变换器:也称降压式变换器,是一种输出电压小丁输入电压的单管不隔离直流变换器。
图中,Q为开关管,其驱动电压一般为PWM(Pulse width modulation脉宽调制)信号,信号周期为Ts ,则信号频率为f=1/Ts ,导通时间为Ton,关断时间为Toff,则周期Ts=Ton+Toff ,占空比Dy= Ton/Ts。
Buck变换器有两种基本工作方式:CCM(Continuous current mode) :电感电流连续模式,输出滤波电感Lf的电流总是大丁零DCM(Discontinuous current mode) :电感电流断续模式,在开关管关断期间有一段时间Lf的电流为零1.1 CCM时的基本关系:0.5 1-0 g 050 L0V tlt= corist V0 = const1.3.11.2 DCM 时的基本关系:% %输出电压与输人电反间的关系:曜== 七一 4劣十口 其中:AD <(1 一心)为美断后电感电流下降到零的时问J =气;% 乙狄011 1,小,V 七 输出平均曲克:二〒七+ T0二司土~ W 〔气*& £ 顷心 J在电勰喽时,%附不但与占空比Dy 有关』而且与或载电流卜大小有关,若1口=0,则%=甲血 DCM 可分为两种典型情况:输入电压Vin 不变,输出电压Vo 变化,常用作电动机速度控 制或充电器对蓄电池的包流充电输入电压Vin 变化,输出电压Vo 包定,即普通开关稳压电源1.3 电感电流临界连续的边界:用f g 表示临界电流通彼阿的负更电疏】Q ,则:; 鱼w 吃眼w (D* 头h ' 头L 叫史输入电压包定不变时:Vin=const临界负载电流是大值在Dy=0 5时出现: 皿】如=4—球(1-巳)劣电添临界连续时前输出电压:争= ------------ \ --------顷 一 - + 140; ^O (?HMX可画出Buck 变换器在Vin=const 时的外特性曲线:输出走压与情人电压间的关策:竺=一-—。
同步Buck变换器动态解析

同步Buck变换器动态解析1 概述相对于传统的线性电源,开关电源具有转换效率高、输入电压范围大、输出电压稳定等优点,广泛应用于工业控制、电力系统等领域。
开关电源的拓扑形式多种多样,其中Buck变换器是最为简单且具代表的一种,已应用于光伏并网、LED和电池充电等领域。
虽然Buck变换器应用广泛,但其分析过程大部分是基于微分方程的,分析过程欠直观,难于工程应用。
相平面法是分析非线性系统的一种常用方法,通过相平面图直观清晰地反映系统的动态过程及性能,其计算简单、概念清晰,非常适合于工程应用。
本文利用相平面法对同步Buck变换器的动态过程进行分析,选取具体的物理量为相平面坐标轴,通过相平面得到Buck变换器中变量的变化趋势,为后续的分析设计提供依据。
2 同步Buck变换器模型Buck变换器的原理图如下:当开关S1、S2处于不同状态时,该电路有不同的动态特性,该系统属于切换系统,其数学模型如下:当S1闭合、S2断开时,Buck变换器的状态空间模型如下:当S1断开、S2闭合时,Buck变换器的状态空间模型如下:式(1)、式(2)中:L表示电感感量;C表示输出电容容量;R表示负载电阻阻值;iL表示电感电流;vi表示输入电压;vo表示输出电压。
当电路正常工作时,以上两种状态不停切换,其整体呈现出来的动态特性就是以上两种特性的叠加。
3 Buck变换器的相平面模型及其动态分析若对同步Buck变换器直接套用传统的相平面法,则获得输出电压及其导数构成的相平面,与实际物理量不存在直接对应的关系。
为了获得物理意义明确的相平面图,这里选择实际物理量作为相平面坐标,使相平面更加直观清晰。
对上述的同步Buck模型,选取vo为横坐标、iL为纵坐标,则相平面中的曲线斜率如下:当S1闭合、S2断开时,相平面中的斜率为:当S1断开、S2闭合时,相平面中的斜率为:根据以上式(3)和式(4),对vi=12V、L=5uH、C=22uF,R=1Ω的同步Buck变换器进行计算,得到以下相平面曲线:当S1闭合、S2断开时,vo和iL会沿着图2中“o-”的方向顺时针变化,其运动轨迹如图3实线所示;当S1断开、S2闭合时,vo和iL会沿着图2中“*-”的方向顺时针变化,其运动轨迹如图3虚线所示。
Buck变换器的结构及工作原理

Buck变换器的结构及工作原理高压水射流清洗技术是近年来在国际上兴起的一门高科技清洗技术,具有清洗速度快、效率高、成本低、清洁环保、不腐蚀损伤基体、适用范围广、易于实现自动化和智能化控制等优点,可清洗形状结构复杂的零部件[1]。
近年来,随着自动控制技术的不断发展,工业自动化水平日益提高。
为了提高高压水射流设备的清洗效率和清洗效果,有研究人员将自动控制技术运用到射流清洗过程中。
其清洗效果和清洗效率相对于传统的人工清洗有了很大的提升,但该过程对于控制系统的实时性、稳定性具有较高的要求。
因而作为控制系统的驱动部分,直流电源输出的快速性、稳定性也有较高的要求。
传统的驱动电源多以线性直流稳压电源为主,由于电压调整功能的器件始终工作于线性放大区,因而在应用过程中存在着功耗大、能量转换效率低、输出响应速度慢等问题。
这为线性直流电源的应用带来了很大的局限性。
近年来,随着电力电子功率器件的不断发展,开关电源得到了越来越广泛的应用,其相关的技术及发展现状如文献[2]所述。
开关电源具有较多的优点。
如内部功率损耗小、转换效率高。
随着超高频功率变换技术[3]的不断发展与应用,开关电源的转换效率可以大幅度提高,其转换效率可高达90%以上,即达到文献[4]所述合理使用能源、减少能量损耗的目的。
而且开关电源由于没有传统的工频变压器,散热器相对较小,因而具有体积小、重量轻的特点。
开关电源不仅具有以上所说的优点,与其相应的电路的控制方法也比较多,如循环控制方法[5]、滞环控制方法[6]、移相控制方法[7]等。
设计人员可以根据实际应用的要求和需要,灵活地选用各种类型的开关电源电路和控制方法。
本文针对传统线性直流稳压电源与开关直流电源的以上特点,结合射流清洗设备的触摸屏驱动电源输入输出响应要求。
设计了一种基于传统线性直流电源电路的开关电源电路结构,文中首先给出了相应的电路结构,并对相应的工作原理做了简要说明,其次给出了仿真结构图的搭建方法及结果分析,最后给出了所得结论。
Buck直流变换器的工作原理及动态建模

2 Buck 直流变换器的工作原理及动态建模DC/DC 变换器的概念7【】15【】19【】将一个固定的直流电压变换成可变的直流电压称之为DC/DC 变换,亦称为直流斩波。
用斩波器斩切直流的基本思想是:如果改变开关的动作频率,或者改变直流电流通和断的时间比例,就可以改变加到负载上的电压、电流的平均值。
Buck 变换器又称降压变换器、串连开关稳压电源、三端开关型降压稳压器。
基本的DC/DC 变换器按输入输出之间是否有电气隔离可分为两类:隔离型DC/DC 变换器和非隔离型DC/DC 变换器。
非隔离型DC/DC 变换器中存在四种基本的变换器拓扑,它们是降压式(Buck )型,升压式(Boost)型,升降压式(Buck-boost)型,Cuk 型,此外还有Sepic 型和Zeta 型变换器。
二电平Buck 直流变换器的工作原理及主电路图2【】13【】25【】26【】1 主电路拓扑Buck 变换器是一种输出电压等于或小于输入电压的单管非隔离直流变换器。
它的拓扑为电压源、串联开关和电流负载组合而成。
如图所示:图 Buck 电路主电路拓扑为了分析稳态特性,简化推导公式的过程,特作如下假定。
(1) 开关晶体管、二极管均是理想元件。
也就是可以瞬间的导通和截至,而且导通时降压为零,截至时漏电流为零。
(2) 电感、电容是理想元件。
电感工作在线性区而未饱和,寄生电阻为零,电容的等效串联电阻为零。
(3) 输出电压中的纹波电压与输出电压的比值小到允许忽略。
Buck 变换器的工作原理:当开关管S 导通时,电容开始充电,i U 通过向负载传递能量,此时,L i 增加,电感内的电流逐渐增加,储存的磁场能量也逐渐增加,而续流二极管因反向偏置而截至;当S 关断时,由于电感电流L i 不能突变,故L i 通过二极管VD 续流,电感电流逐渐减小,由于二极管VD 的单向导电性,L i 不可能为负,即总有L 0i ,从而可在负载上获得单极性的输出电压。
开关电源 之BUCK变换器工作原理及Multisim实例仿真
D1 1N5824
A PR1
PR3
V
3
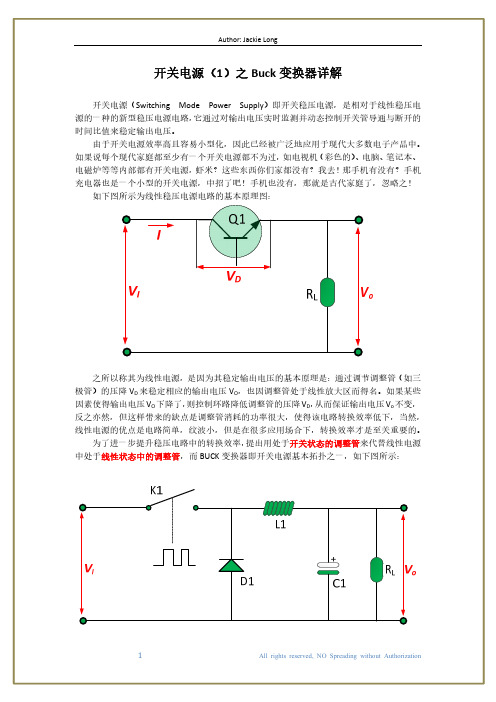
V: 5.71 V V(p-p): 29.3 mV V(rms): 5.73 V V(dc): 5.70 V V(f req): 22.3 kHz
C1
R1
22பைடு நூலகம்µF
5Ω
根据上图仿真结果,则有:
1.14 5.7 0.58 12
93.36%
其中,开关 K1 代表三极管或 MOS 管之类的开关管(本文以 MOS 管为例),通过矩形波 控制开关 K1 只工作于截止状态(开关断开)或导通状态(开关闭合),理想情况下,这两种 状态下开关管都不会有功率损耗,因此,相对于线性电源的转换效率有很大的提升。
开关电源调压的基本原理即面积等效原理,亦即冲量相等而形状不同的脉冲加在具有惯 性环节上时其效果基本相同,如下图所示:
理想的 MOS 管在工作时(即导通或截止)的压降及流过其中的电流应如下图所示:
9
All rights reserved, NO Spreading without Authorization
DS
Author: Jackie Long
D
其中,VDS 表示 MOS 管两端的压降,而 ID 表示流经 MOS 管的电流,在任意时刻,VDS 与 ID 都会有一个参数为 0,因此消耗的功率 P=U×I 也应当是 0,但是实际 MOS 管的开关与 闭合都是需要过渡时间的,真实的开/关状态如下图所示:
同样是从输入电源 10V 中获取 5V 的输出电压,线性稳压电源的有效面积为 5×T,而对 应在开关稳压电源的单个有效周期内,其有效面积为 10×T×50%(占空比)=5×T,这样只要 在后面加一级滤波电路,两者的输出电压有效值(平均值)是相似的。
BUCK变换器设计

BUCK变换器设计报告一、BUCK变换器原理降压变换器(Buck Converter)就是将直流输入电压变换成相对低的平均直流输出电压。
它的特点是输出电压比输入的电压低,但输出电流比输入电流高。
它主要用于直流稳压电源。
二、BUCK主电路参数计算及器件选择1、BUCK变换器的设计方法利用MATLAB和PSPICE对设计电路进行设计,根据设计指标选取合适的主电路及主电路元件参数,建立仿真模型,并进行变换器开环性能的仿真,再选取合适的闭环控制器进行闭环控制系统的设计,比较开环闭环仿真模型的超调量、调节时间等,选取性能优良的模型进行电路搭建。
2、主电路的设计指标输入电压:标称直流48V,范围43~53V输出电压:直流24V,5A输出电压纹波:100mV电流纹波:0.25A开关频率:250kHz相位裕量:60°幅值裕量:10dB3、BUCK 主电路主电路的相关参数:开关周期:T S =s f 1=4×10-6s占空比:当输入电压为43V 时,D max =0.55814当输入电压为53V 时,D min =0.45283输出电压:V O =24V 输出电流I O =5A纹波电流:Δi L =0.25A纹波电压:ΔV L =100mV电感量计算:由Δi L =2Lv -V o max -in DT S 得: L=L o max -in i 2v -V ΔD min T S=25.022453⨯-×0.4528×4×10-6=1.05×10-4H 电容量计算:由ΔV L =Ci L 8ΔT S 得: C=L L V 8i ΔΔT S =1.0825.0⨯×4×10-6=1.25×10-6F 而实际中,考虑到能量存储以及输入和负载变化的影响,C 的取值一般要大于该计算值,故取值为120μF 。
实际中,电解电容一般都具有等效串联电阻,因此在选择的过程中要注意此电阻的大小对系统性能的影响。
开关电源(1)之BUCK变换器工作原理及Multisim实例仿真

Author: Jackie Long
纹波峰峰值为 2.25mV,还是比较低的(实际的电路很有可能没这么低,特别是接上开 关之类负载之后) 还有一个效率问题,与线性电源不同的是,BUCK 变换器的输入电流与输出电流是不一 样的, 因此, 不能简单地用输出电压与输入电压的比值来表征, 我们只有用最原始的方法了, 就是计算输出功率与输入功率的比值,如下式:
0
Vo
原来 来的纹波 波峰峰值
平 平均值
新的 的纹波峰峰 峰峰值
t
0
对于具体的 的 BUCK 拓扑降 降压芯片,厂 厂家都会提供 供典型的应用 用电路及相关 关的参数值,如下 所示为 TI 公司 司的集成降压 压芯片 LM259 96 典型应用电路图: 图所
我们也可以 以通过提高开 开关的频率来 降低纹波,这 这样,在同样 样的电感量与 与电容量条件 件下, 每次 次充放电的时 时间缩短了,这样纹波的 峰峰值就下降 降了,如下图 图所示:
A
PR1
V
PR3
1
I: -1.55 A I(p-p): 15.9 A I(rms): 892 mA I(dc): 580 mA I(f req): 150 kHz
3
V: 5.71 V V(p-p): 29.3 mV V(rms): 5.73 V V(dc): 5.70 V V(f req): 22.3 kHz
同样是从输入电源 10V 中获取 5V 的输出电压,线性稳压电源的有效面积为 5×T,而对 应在开关稳压电源的单个有效周期内,其有效面积为 10×T×50%(占空比)=5×T,这样只要 在后面加一级滤波电路,两者的输出电压有效值(平均值)是相似的。 下面我们来看看 BUCK 转换电路的工作原理 (假设高电平开关闭合, 低电平开关断开) 。
Buck变换器工作原理分析和总结

题目: Buck变换器工作原理分析与总结目录一、关于Buck变换器的简单介绍 (2)1、Buck变换器另外三种叫法 (2)2、Buck变换器工作原理结构图 (2)二、Buck变换器工作原理分析 (3)1、Buck变换器工作过程分析 (3)2、Buck变换器反馈环路分析 (4)3、Buck变换器的两种工作模式 (4)1)Buck变换器的CCM工作模式 (5)2)Buck变换器的DCM工作模式 (6)3)Buck变换器CCM模式和DCM模式的临界条件 (7)4)两种模式的特点 (8)4、Buck变换器电感的选择 (8)5、Buck变换器输出电容的选择和纹波电压 (9)三、Buck变换器工作原理总结 (10)Buck 变换器工作原理分析与总结一、关于Buck 变换器的简单介绍1、Buck 变换器另外三种叫法1. 降压变换器:输出电压小于输入电压。
2. 串联开关稳压电源:单刀双掷开关(晶体管)串联于输入与输出之间。
3. 三端开关型降压稳压电源:1) 输入与输出的一根线是公用的。
2) 输出电压小于输入电压。
2、Buck 变换器工作原理结构图GabcWMV Gd图1. Buck 变换器的基本原理图由上图可知,Buck 变换器主要包括:开关元件M1,二极管D1,电感L1,电容C1和反馈环路。
而一般的反馈环路由四部分组成:采样网络,误差放大器(Error Amplifier ,E/A ),脉宽调制器(Pulse Width Modulation ,PWM )和驱动电路。
二、Buck 变换器工作原理分析1、Buck 变换器工作过程分析图2. Buck 变换器的工作过程为了便于对Buck 变换器基本工作原理的分析,我们首先作以下几点合理的假设:1) 开关元件M1和二极管D1都是理想元件。
它们可以快速的导通和关断,且导通时压降为零,关断时漏电流为零;2) 电容和电感同样是理想元件。
电感工作在线性区而未饱和时,寄生电阻等于零。
Buck变换器工作原理分析和总结

题目: Buck变换器工作原理分析与总结目录一、关于Buck变换器的简单介绍 (2)1、Buck变换器另外三种叫法 (2)2、Buck变换器工作原理结构图 (2)二、Buck变换器工作原理分析 (3)1、Buck变换器工作过程分析 (3)2、Buck变换器反馈环路分析 (4)3、Buck变换器的两种工作模式 (4)1)Buck变换器的CCM工作模式 (5)2)Buck变换器的DCM工作模式 (6)3)Buck变换器CCM模式和DCM模式的临界条件 (7)4)两种模式的特点 (8)4、Buck变换器电感的选择 (8)5、Buck变换器输出电容的选择和纹波电压 (9)三、Buck变换器工作原理总结 (10)Buck 变换器工作原理分析与总结一、关于Buck 变换器的简单介绍1、Buck 变换器另外三种叫法1. 降压变换器:输出电压小于输入电压。
2. 串联开关稳压电源:单刀双掷开关(晶体管)串联于输入与输出之间。
3. 三端开关型降压稳压电源:1) 输入与输出的一根线是公用的。
2) 输出电压小于输入电压。
2、Buck 变换器工作原理结构图GabcWMV Gd图1. Buck 变换器的基本原理图由上图可知,Buck 变换器主要包括:开关元件M1,二极管D1,电感L1,电容C1和反馈环路。
而一般的反馈环路由四部分组成:采样网络,误差放大器(Error Amplifier ,E/A ),脉宽调制器(Pulse Width Modulation ,PWM )和驱动电路。
二、Buck 变换器工作原理分析1、Buck 变换器工作过程分析图2. Buck 变换器的工作过程为了便于对Buck 变换器基本工作原理的分析,我们首先作以下几点合理的假设:1) 开关元件M1和二极管D1都是理想元件。
它们可以快速的导通和关断,且导通时压降为零,关断时漏电流为零;2) 电容和电感同样是理想元件。
电感工作在线性区而未饱和时,寄生电阻等于零。
DC_DC BUCK功率变换器的动力学建模及其动力学行为研究

DC2DC BUCK功率变换器的动力学建模及其动力学行为研究戎小戈1 李小玲2 罗晓曙1 梁宗经3 汪秉宏4(1.广西师范大学物理与电子科学系,广西桂林 541004; 2.广西师范大学学报编辑部;3.广西师范大学科研处;4.中国科技大学近代物理系,安徽合肥 230026)摘 要:首先利用K C L和K V L定律导出了三阶DC2DC BUCK功率变换器的分段光滑的动力学方程,然后用数值方法研究了误差放大器的放大倍数与这种变换器的非线性动力学行为的关系.研究结果表明:随着放大倍数的增加,该变换器的输出电压变量呈现混沌、周期运动,且其电压转换效率在负载电容较大时,随电阻R1(即放大倍数)增加而增加,在负载电容取较小值时,随R1增加而减小.关键词:电子技术;功率变换器;动力学建模;动力学行为中图分类号:T M132 文献标识码:A 文章编号:1001-7119(2003)05-0365-04Dynamics Modeling for DC2DC Buck Converter and Studyof Its Dynamics B ehaviorRONG Xiao2ge1 LI Xiao2ling2 LUO Xiao2shu1 LIANG Zong2jing3 WANG Bing2hong4(1.Department of Physics and E lectronic Science,G uangxi N ormal University,G uilin541004,China;2.Editorial Department of Journal of G uangxi N ormal University;3.G uangxi N ormal University Science Research M anagement O ffice;4.Department of M odern Physics,University of Science and T echnology of China,Hefei230026,China)Abstract:A piece wise sm ooth dynamics equations for third order buck DC2DC power is setup by K C L and K V L law at first.T hen, the relationship between am plification ratio of error am plifier and dynamics behavior of this converter is investigated by numerical meth od.T he research results sh ow that this circuit system behaviors chaos and period m otion with increasing of am plification ratio of error am plifier.And its v oltage converter efficiency while load capcitor big,increase with the electric resistance R1(namely am plifi2 cation ratio)but increase,at load capcitor to take small,v oltage converter efficiency is reduce with the R1but increase.K ey w ords:electronics technology;power converter;dynamics m odeling;dynamics behavior DC2DC开关功率变换器是一种强非线性系统[1],它在电力电子工业、军工系统中有着十分广泛的应用,因此研究这种直流功率变换器新的理论分析和设计方法,对于提高其各种性能如工作范围、稳定性、效率及减少电磁污染等[2,3]具有十分重要的实用价值.对于直流功率变换器,目前工程界采用的主要分析与设计方法是R.D.Middlebrook和Slobodan Cuk在1976年提出的状态空间平均法[4].该法根据小信号线性化模型,较好地解决了PW M型DC2DC 开关功率变换器的稳态和动态低频小信号的分析和设计问题.但由于直流功率变换器的强非线性,使得Middlebrook等人的状态空间平均法在大信号条件下,系统易失去稳定性.而且这种小信号线性 第19卷第5期2003年9月 科技通报BU LLETI N OF SCIE NCE AND TECH NO LOGYV ol.19 N o.5 Sep.2003收稿日期:2003-05-14基金项目:国家重点基础研究发展规划(973计划专项经费)项目“非线性科学中的前沿问题研究”;国家自然科学基金(10247005, 19974039);the China2Canada University Industry Partnership Program(CCUIPP2NSFC70142005)资助项目;广西自然科学基金(0135063)资助项目作者简介:戎小戈,男,1967年生,浙江萧山人,讲师.化模型难以真实地反映系统的物理特性,因而就很难进一步提高系统的各种性能.为了克服这种分析和设计方法的缺陷,科学工作者近来提出和发展了一些新的分析和控制设计方法,主要有双线性理论[5]、自适应控制[6]、滑动模控制[7]等.这些新的分析与控制方法虽然对系统的性能有一定的改善,但仍存在算法复杂、实时性差等许多不足.近30年来,随着非线性动力学理论的发展和完善,为DC 2DC 开关功率变换器这种强非线性系统的分析与设计开创了新的途径.国际上一些科学家相继发现了PW M 型DC 2DC 开关功率变换器中具有十分丰富的动力学行为如倍周期分岔、H opf 分岔和混沌运动[5~7].这些研究成果解决了一些长期困扰电子工程师设计和调试中面临的问题,例如DC 2DC 开关功率变换器在一定的参数范围内出现幅度很高的噪声和不稳定行为,上述现象现在已被证实是系统出现了混沌行为.要研究直流开关功率变换器的非线性动力学行为,关键问题是采用适当的方法对其建立相应的动力学模型.目前主要采用两种方法:一是对电路系统进行简化和近似,导出其离散映射模型;另一种方法是直接根据系统的拓扑结构用K C L 定律和K V L 定律导出其状态变量的微分方程.本文采用后一种方法,为DC 2DC BUCK 开关功率变换器建立了一个3维分段光滑的微分方程.然后研究了误差放大器的放大倍数对系统动力学性质的影响,得到了一些有实际应用价值的结果.1 三阶DC 2DC BUCK 开关功率变换 器的动力学方程建立 三阶DC 2DC BUCK 开关功率变换器的电路原理图如图1所示.图1 DC 2DC BUCK 开关功率变换器原理图F ig.1 S chem atic d iagram o f the D C 2D C B U CK s w itch pow er c onv erter 当三极管T 饱和导通时,状态方程推导如下:令i L =x 1,v co =x 2,v 1=x 3,则由K CL 定律、K VL 定律、欧姆定律及理想运放的特性,得到下列方程式: E =L d x 1d t+(R L +R r )i 1(1a ) i 1+i 2=x 1(1b ) i 1=x 2R L +R r(1c ) i 2=Cod x 2d t(1d ) i ′=i 3+i 4(2a ) i ′=v R 2R 2(2b ) v R 2=i 1R r (2c ) i 4=x 3-v R 2R 1(2d ) i 3=Cd (x 3-v R 2)d t(2e )对1(a )~1(d )和2(a )~2(e )式进行整理得:x 1=EL -x 2L(3a )x 2=1C ox 1-1C o (R L +R r )x 2(3b )x 3=R rC o (R L +R r )x 1+R r (R 1+R 2)C 1R 1R 2(R L +R r )-R rC o (R L +R r )2x 2-1C 1R 1x 3(3c )同理可得当三极管T 截止时,系统的状态方程为:x 1=-1Lx 2(4a ) x 2=-1C ox 1-1C o (R L +R r )x 2(4b )x 3=R rC o (R L +R r )x 1+R r (R 1+R 2)C 1R 1R 2(R L +R r )-R rC o (R L +R r )2x 2-1C 1R 1x 3(4c )在上述状态方程3(a )~3(c ),4(a )~4(c )中,三极管T 的导通与截止时间由状态变量x 1、x 2、x 3和外部输入三角波电压v ref 共同决定,且是x 1、x 2、x 3和v ref 的非线性函数,故一般不能用解析方法导出,只能用数值方法得到.图2是其典型的开关逻辑演化图.其中三角波的表达式为: 366 科 技 通 报第19卷v ref (t )=v 1+(v 2-v 1)(t m od T )(5)式中T 为三角波的周期.图2 BUCK 变换器典型的开关逻辑Fig.2 The diagram of a typical switchlogic of BUCK converter2 误差放大器A 1的放大倍数对 BUCK 变换器动力学的影响研究 在图(1)所示BUCK 变换器电路中,R r 对输出电压进行取样后,输入到误差放大器A 1进行积分、放大,得到反馈电压v 1(t )(即x 3),v 1(t )与外部输入信号v ref (t )送入比较放大器A 2进行比较放大,当v 1(t )>v ref (t )时,A 2输出低电平,三极管T 截止;当v 1(t )<v ref (t )时,A 2输出高电平,三极管T 饱和导通.A 2的输出电压控制三极管T 的导通和截止,从而达到对输出电压v co 的调整和稳定.由于外部输入信号v ref (t )是周期性的三角波信号,故图1所示BUCK 变换器属于非自治非线性系统.因此,本文用闪频采样[8]方法来研究BUCK 变换器的动力学性质.文献[9]研究了二阶BUCK 变换器(省掉负载电容C o )随入输入电压E in 、负载电阻R L 变化时的动力学性质.由于负载电容在该电路中是一个十分重要元件,对系统的各种性能如谐波辐射、输出电压稳定性有重要的影响,故省掉该元件得到的动力学性质与其实际物理特性有重大差别.为了全面、准确地揭示该电路系统的动力学性质,本文首先为这种直流功率变换器建立了一个三阶分段光滑动力学方程,如式3(a )~3(c ),4(a )~4(c )所示,然后研究误差放大器A 1的放大倍数对该系统动力学性质的影响.图1所示BUCK 变换器中误差放大器A 1的电压放大倍数的表达式为:| A v |=1+1R 2ω2C 21+1R 21(6)显然,误差放大器的放大倍数A v 与R 1有关.在下面的研究工作中,改变电阻R 1,其余元件取下列参数值:R 2=220Ω,T =392μs ,R L =20Ω,R r =1Ω,C 1=20NF ,L =11.6mH ,v 1=1.0(V ),v 2=4.0(V ),在负载电容C o 取两种不同数值的条件下,改变R 1,用闪频采样方法得到BUCK 变换器中变量x 2的分岔图及相应的电压转换效率图,分别如图3~图4所示. 第5期戎小戈等.DC 2DC BUCK 功率变换器的动力学建模及其动力学行为研究367 以上各图中,电压转换效率η=v C0E in ,v C0为负载电容C 0的输出电压的平均值,数值计算中取30万个数据的平均.由上述数值计算结果可见,在一定输入电压E in 的条件下,随着参数R 1的变化,图1所示的BUCK 变换器表现出十分丰富的非线性动力学行为.当负载电容C o 取较大值时(C 0=47μF ),系统变量x 2在参数R 1的整个变化范围内,出现混沌运动的参数范围很小,如图3(a )所示,当负载电容C 0取较小值时(C 0=10μF ),系统出现混沌运动的参数范围较大,这表明负载电容的大小对该电路系统的动力学性质有重要影响,因而文献[9]忽略负载电容得到的结果与实际情况相差是很大的.此外,从图3(b )、图4(b )可以看出,负载电容的大小对电压转换效率也有重要影响.一方面,在总体上,负载电容大时,电压转换效率就高;另一方面,负载电容C 0取较大值时,电压转换效率随R 1增大而增加,而负载电容C 0取较小值时,电压转换效率随R 1增大而减小.但在上述两种情况下,电压转换效率随电阻R 1变化时,均存在不连续跳跃现象,如图3(b )、图4(b )所示.这说明对电压转换效率这一性能指标而言,R 1存在一些临界参数值,使电压转换效率这一性能指标达到局部最优化设计.3 结 论本文首先对三阶BUCK 直流开关功率变换器建立了一个完整的分段光滑动力学方程,然后用数值方法研究了在取不同负载电容C 0的条件下,改变电阻R 1(即改变误差放大器A 1的放大倍数)时系统的动力学性质变化情况.全面描绘了分岔图.通过分岔图,使人们能完整、准确地掌握这种直流开关功率变换器在不同参数条件下状态变量的运动形态,从而掌握其物理特性,以利于电路系统的分析和设计.本文的工作对于设计者选择最佳参数值,从而达到最佳的产品技术要求有一定的应用价值.参考文献:[1] M arion di Bernardo.Discrete 2time maps for the analysis of bifurcationand chaos in DC 2DC converters[J ].IEEE T rans on Circuit System I ,2000,47(2):130~142.[2] T im oor A ,Sakharu K.E ffects of finite switching frequency and delayon PW M controlled system [J ].IEEE T rans on Circuit System I ,2000,42(4):555~567.[3] 曾 嵘,肖如泉,盛新富.高压串级DC 2DC 开关电源的研制[J ].电力电子技术,1998,32(2):5~7.[4] M iddlebrook R D ,Cuk S.A general unified approach to m oddingswitching 2converter power stages [R ].IEEE P ower E lectron S pec C on f Rec ,1976,13~34.[5] Andreas M ,S oumitro B.Bifurcation and chaos in the tolerance bandPW M technique[J ].IEEE T rans on Circuit and System I ,2000,47(2):254~259.[6] Tse C K,Lai Y M ,Ln H H.H opf bifurcation and chaos in a free 2running current controlled cuk switching regulator[J ].IEEE T rans on Circuit and System.I ,2000,47(4):448~456.[7] T etsuya M ,T akashi N ,Nachiko Inabs.Chaotic attractor with a char 2acteristic of T orus[J ].IEEE T rans on Circuit and System I ,2000,47(6):994~948.[8] 王光瑞,陈光旨.非线性常微方程的混沌运动[M].广西:广西科学技术出版社,1995.89~92.[9] K rishnendu Chakrabarty ,G outam P oddar ,S oumitro Banerjee.Bifur 2cation behavior of the Buck converter [J ]IEEE T rans P ower E lec 2tronics ,1996,11(3):439~447. 368 科 技 通 报第19卷。
BUCK电路的建模

系统建模作业——BUCK电路的建模一.BUCK 电路简介BUCK 电路是一种降压式变换电路,降压变换器输出电压平均值U 0总是小于输出电压U D 通常电感中的电流是否连续,取决于开关频率、滤波电感L 和电容C 的数值。
二.BUCK 电路建模1. BUCK 电路基本结构Va)VVb) c)图1. BUCK 电路基本结构a) Buck 变换器 b)开关处于通态[t ,t+DTs] c)开关处于断态[t+DTs ,t+Ts]2.符号说明1、 输入直流电压(Vg):2、 输出电压(Vo):3、 输入电流(Ig):4、 输出电流(Io):5、 电感电压(VL):6、 电感电流(IL):7、 电容电流(IC):3. Buck 变换器达到稳态时的电压电流关系当Buck 变换器达到稳态时,电感电压为()()()ss L s0L L T I t T I t V t LT +-==(1)并且()()()()sss ss L L L L ss 11d d d t T t DT t T g o T tt t DT v t V t t V t t V t t V D V T T ++++⎡⎤==+=-⎢⎥⎣⎦⎰⎰⎰ (2) 则结合(1)和(2),其稳态电压传输比为:goV D V = (3)若略去开关损耗,则Buck 变换器的输入输出功率平衡有:g g o o V I V I =,得o g DI I =。
4.大信号模型在开关管处于通态时,即时间在[t ,t+DT s ]区间时,电感两段电压为:()()()()L g d d L o I t V t LV t V t t==- (4)通过电容的电流为:()()()()C d d o og V t V t I t CI t t R==- (5)当开关管处于断态时,即时间[t+DT s ,t+T s ]区间时,电感两端电压为:()()()L d d L o I t V t LV t t==- (6)通过电容的电流为:。
Buck变换器的发展与工作原理

从一个电压(高)得到自己想要的电压值(低)的最简单的方法是通过电阻分压实现,如图1.1 所示。
图1.1 电阻分压电路这种方式最方便快捷,现在普通的电压采样基本采用这种方式,但是如果功率稍微大一点,由于R1 和R2 是串联的,所以在R1 上的损耗不可忽视,如果所要的电压值远低于输入电压,那末该电路的效率就会极其低下。
对该电路尝试进行变形,将R2 更换为三极管,也就是现在的LDO 模型,如图1.2 所示。
图1.2 LDO 模型通过变型,那末原来在电阻R2 上的损耗转移至分析三极管Q1 的损耗,由于Q1 承受输入和输出的压差,导致该电路的效率也比较低下。
为了提升效率,之前三极管是工作在线性状态,若将其更改为开关状态,使三极管惟独开关损耗和导通损耗,大大的降低其总损耗。
更改后的电路如图1.3 所示。
图1.3 开关电路图1.4 占空比和电压比的关系由图 1.4 可知,该电路工作周期时间为Ts,导通时间为Ton,占空比为D=Ton/Ts,输出电压与开关状态高度关联,S1 导通时有输出电压,S1 关断时没有输出电压。
可以看出输出负载总是需要连续的能量供给,开关S1 的导通与关断在图1.3 所示的电路中产生的断续能量波动对于输出端负载是不可接受的。
因此需要需要进行解耦,在变换器一定位置引入储能元器件电容,使输入端在S1 断开的情况下,输出端电容也可以进行持续的能量输出,保证输出电压的稳定。
图1.5 初步解耦电路由图1.5 所示的电路,根据电容两端的电压不能突变的原理,当S1 闭合的时候,路线中会产生一个非常大的冲击电流,它不仅导致噪声和EMI 问题,也可能会损坏S1 。
所以需要对其采取限流措施。
图1.6 电阻R2 限流的解耦电路如图1.6 所示,加入R2 限流电阻后,在S1 闭合瞬间就没有那末大的冲击电流了,但是由于R2 是串联在主功率回路中,电阻就会消耗功率,那末在开关上减小的功耗最终可能又消耗在所加的电阻上。
Buck变换器工作原理分析和总结

Buck变换器工作原理分析和总结一、简述首先简单地说,Buck变换器就像是一个电力的“翻译官”。
它接收一种电压,然后转换成另一种电压输出。
你可能会问,为什么需要转换电压呢?别着急我们慢慢说,在现代电子设备中,不同的部件需要不同的电压来运行。
而Buck变换器,就是帮助我们调整电压,确保每个部件都能得到合适的能量。
Buck变换器就像一个电力调节器,确保我们的电子设备在不同电压条件下都能稳定运行。
那么它是如何实现这一功能的呢?接下来我们会深入探讨它的工作原理。
1. 介绍Buck变换器的基本概念及其在电源管理领域的重要性好的让我为你介绍一下关于《Buck变换器工作原理分析和总结》中的第一部分内容:介绍Buck变换器的基本概念及其在电源管理领域的重要性。
想必大家对电子设备中的各种电源管理技术都颇感兴趣吧,作为其中的重要一员,Buck变换器可以说是电源管理领域的明星角色。
那究竟什么是Buck变换器呢?简单来说它就像一个灵活的电力调整器,负责把输入的高电压转换成我们设备需要的低电压。
Buck变换器是电源管理领域不可或缺的一部分。
它的基本概念就是把高电压转换成我们设备需要的低电压,确保设备的稳定运行。
而它在电源管理领域的重要性,就像一位优秀的管家,确保电力供应的稳定和高效。
2. 简述文章目的和内容概述接下来让我们简要谈谈本文的目的和内容概述,写这篇文章的目的,是为了帮助大家更好地理解Buck变换器的工作原理,并通过分析和总结,使大家对这一技术有更深入的认识。
毕竟技术虽专业,但也需要我们能接地气地理解和运用。
这篇文章中,首先会介绍一下什么是Buck变换器,以便大家有个初步的了解。
接着我们会深入浅出地讲述它的工作原理,通过简单易懂的语言和生动的比喻让大家更容易明白。
然后我们会深入分析它的实际应用场景以及在实际操作中可能遇到的问题。
当然还会包括如何进行优化和调整的实用技巧,在文章的最后部分,我们会对整个Buck变换器的工作原理进行综合性的总结,帮助大家形成一个清晰的思路和体系。
DCM Buck 变换器CPM控制的动态模型
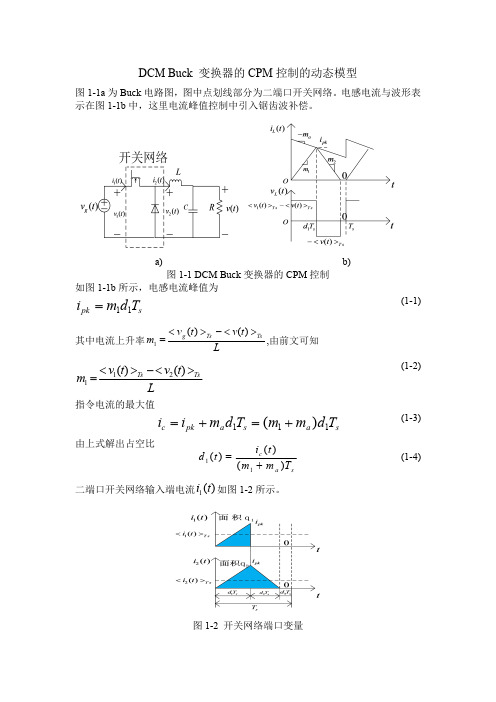
1 i pk (t )d1 (t ) 2 1 2 m1d1 (t )Ts 2
将式(1-2)和式(1-4)带入上式,化简得到 1 2 Lic (t ) f s 2 i (t )
1 Ts
[ v1 (t )Ts v2 (t ) Ts ](1
ma 2 ) m1
(1-6)
由上式得到二端口开关网络输入平均功率为
i1 (t ) Ts v1 (t ) Ts
1 m1d12Ts v1 (t ) Ts p(t ) Ts m [ v1 (t ) Ts v2 (t ) Ts ](1 a )2 2 m1
(1-7)
1 2 Lic f s v1 (t ) Ts 2
在阶段 1,能量通过主开关存储至电感中,输入能量为
1 2 Lic f s 2
f1 ( v1 (t ) Ts , v2 (t ) Ts , ic (t ) Ts )
将上式在静态工作点附近作泰勒级数展开得到
I1 i1 (t ) f1 (V1 , V2 , I c ) v1 (t ) i c (t )
^
^
^
df1 (v1 , V2 , I c ) dv1
ma 2 ) m1
交流项 式中,
i1 (t ) v1 (t )
^
^
^ 1 ^ v 2 (t ) g1 i c (t ) f1 r1
1 df1 (v1 , V2 , Id ( I c2 f s ) 2 (m1 ma ) 2 dm1 dm1 dv1 m1 ma 1 1 I c2 f s 2 L (m1 ma ) 2 (m1 ma ) I1 (V1 V2 )(1 L I1 (V1 V2 ) m1 ma L2 m12 m1 ma ma 2 ) m1 m1 ma 1 L (m1 ma ) 2 (m1 ma )
buck电路的基本原理

buck电路的基本原理Buck电路的基本原理Buck电路是一种常见的直流-直流降压转换电路,它具有简单、高效的特点,被广泛应用于各种电子设备中。
本文将介绍Buck电路的基本原理,包括其工作原理、关键组成部分和应用范围等。
一、工作原理Buck电路通过控制开关管的导通时间来实现电压的降低。
其基本原理是利用电感储能和电容滤波的方式,将输入电压转换为所需的输出电压。
当开关管导通时,电感储能,此时电感上的电流增大,而输出电压维持在正常范围。
当开关管关闭时,电感释放储能,通过二极管向负载提供电能,同时电容器对电流进行滤波,使输出电压保持稳定。
二、关键组成部分1.开关管:Buck电路中常用的开关管为MOSFET,它具有低导通电阻和快速开关速度的特点,能够有效地控制电流的流动。
2.电感:电感是Buck电路中的能量储存元件,通过电感的储能和释能来实现电压降低。
3.二极管:二极管在Buck电路中起到了反向电流的导通作用,它能够保证电压的平稳输出。
4.电容:电容用于对电流进行滤波和储能,使输出电压更加稳定。
5.控制电路:控制电路负责监测输出电压,并根据需要调整开关管的导通时间,以保持输出电压的稳定性。
三、应用范围Buck电路具有高效、简单、稳定的特点,因此被广泛应用于各种电子设备中:1.电源适配器:Buck电路常被用于电源适配器中,将市电的高电压转换为设备所需的低电压,以满足电子设备对电压的要求。
2.电动车充电器:电动车充电器需要将市电的交流电转换为直流电进行充电,Buck电路可以有效地降低电压,保证电动车电池的安全充电。
3.太阳能充电器:Buck电路可以将太阳能电池板输出的低电压升高至所需的充电电压,实现对电池的高效充电。
4.LED驱动器:LED灯需要稳定的电流来保证其正常工作,Buck电路可以将输入电压降低为LED所需的电压,同时保持恒定的电流输出。
总结:Buck电路作为一种常见的直流-直流降压转换电路,通过控制开关管的导通时间来实现电压的降低。
buck工作原理

buck工作原理
Buck转换器是一种直流-直流(DC-DC)转换器,它可以将一个直流
电压转换为另一个不同的直流电压。
Buck转换器也被称为降压转换器,因为它可以将输入电压降低到输出电压。
Buck转换器的工作原理如下:
1. 输入电源将直流电压输入到Buck转换器中。
2. 输入电源通过一个开关管(MOSFET)控制输入电压的通断,从而
控制输出电压的大小。
3. 当开关管处于导通状态时,输入电源通过一个电感(L)充电,并将能量存储在磁场中。
在此期间,输出负载通过一个二极管(D)获得能量,并维持输出电压。
4. 当开关管处于关闭状态时,磁场中的能量被释放,并通过二极管传
递到输出负载。
这样就保证了输出负载始终有稳定的能量供应。
5. 控制开关管导通时间和关闭时间的频率和占空比可以控制输出电压
大小和稳定性。
6. Buck转换器还配备了一个滤波网络来抑制任何噪声或干扰信号,并确保输出电压平稳无波动。
总之,Buck转换器是一种高效的DC-DC转换器,可以将输入电压降低到输出电压,并且可以通过控制开关管的导通时间和关闭时间来控制输出电压大小和稳定性。
它在许多应用中都得到了广泛的应用,例如电源适配器,LED驱动器等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 Buck 直流变换器的工作原理及动态建模DC/DC 变换器的概念7【】15【】19【】将一个固定的直流电压变换成可变的直流电压称之为DC/DC 变换,亦称为直流斩波。
用斩波器斩切直流的基本思想是:如果改变开关的动作频率,或者改变直流电流通和断的时间比例,就可以改变加到负载上的电压、电流的平均值。
Buck 变换器又称降压变换器、串连开关稳压电源、三端开关型降压稳压器。
基本的DC/DC 变换器按输入输出之间是否有电气隔离可分为两类:隔离型DC/DC 变换器和非隔离型DC/DC 变换器。
非隔离型DC/DC 变换器中存在四种基本的变换器拓扑,它们是降压式(Buck )型,升压式(Boost)型,升降压式(Buck-boost)型,Cuk 型,此外还有Sepic 型和Zeta 型变换器。
二电平Buck 直流变换器的工作原理及主电路图2【】13【】25【】26【】1 主电路拓扑Buck 变换器是一种输出电压等于或小于输入电压的单管非隔离直流变换器。
它的拓扑为电压源、串联开关和电流负载组合而成。
如图所示:图 Buck 电路主电路拓扑 为了分析稳态特性,简化推导公式的过程,特作如下假定。
(1) 开关晶体管、二极管均是理想元件。
也就是可以瞬间的导通和截至,而且导通时降压为零,截至时漏电流为零。
(2) 电感、电容是理想元件。
电感工作在线性区而未饱和,寄生电阻为零,电容的等效串联电阻为零。
(3) 输出电压中的纹波电压与输出电压的比值小到允许忽略。
Buck 变换器的工作原理:当开关管S 导通时,电容开始充电,i U 通过向负载传递能量,此时,L i 增加,电感内的电流逐渐增加,储存的磁场能量也逐渐增加,而续流二极管因反向偏置而截至;当S 关断时,由于电感电流L i 不能突变,故L i 通过二极管VD 续流,电感电流逐渐减小,由于二极管VD 的单向导电性,L i 不可能为负,即总有L 0i ,从而可在负载上获得单极性的输出电压。
根据晶体管的开关特性,在管子的基极加入开关信号,就能控制它的导通和截至,对于NPN 晶体管,当基极加入正向信号时,将产生积极电流b i ,基极正向电压电压升高,b i 也随之升高,b i 达到一定数值后,集电极电流c i 达到最大值,其后继续增加b i ,b i 基本上保持不变,这种现象称为饱和。
在饱和状态下,晶体管的集射极电压很小,可以忽略不计。
因此晶体管的饱和状态相当于开关的接通状态。
当基极加入反向偏压时,晶体管截至,集电极电流c i 接近于零,而晶体管的集射极电压接近于电源电压。
晶体管的这种状态相当于开关的断开状态,通常称为截至状态,或称为关断状态。
Buck 变换器的工作模式5【】8【】27【】29【】由Buck 变换器的工作原理可以看出,电感可以工作在电流连续的方式下,也可能工作在电流不连续的工作状态。
以此为标准将Buck 变换器的工作模式分为两种:电感电流连续工作模式(continuous current mode, CCM)和电感电流断续模式(discontinuous current mode, DCM)。
电感电流连续是指输出滤波电感的电流总大于零,电感电流断续是指在快关管段期间有一段时间输出滤波的电流为零。
在这种工作方式之间有一个工作边界,称为电感电流临界连续状态,即在开关管关断末期,滤波电感的电流刚好降为零。
下面分别讨论电感电流处于不同模式时的变换器工作原理。
(1) 电感电流连续模式如图所示为电流连续导电模式下的相关波形:图 电流连续模式下电路波形在[]10t 区间,开关管S 处于导通状态,电源电压通过S 到二极管VD 两端,故二极管VD 截至。
电流流过电感,由于输出滤波电容保持不变,则电感两端呈现正电压L i 0U U U =-,由于i 0U U >所以,在该电压作用下输出滤波电感中电流L i 线性增长,知道1t 时刻,L i 达到最大值L1I 。
在S 导通期间,电感电流的增量及开关管的占空比D 分别为21000L()s 1s ()(1)t t U U U i dt T t D T L L L-∆=-=-=-⎰ 其中1s t D T =( 0D 1<<) (2-1)在[]1s t t 区间,S 关断,由于电感的储能作用,L i 经二极管VD 继续流通,此时加在输出滤波电感上的电压L 0U U =-,呈现负值,电感中电流L i 线性衰减,直到s T 时刻,L i 达到最小值L2I 。
在S 截至期间,电感电流的减小量为s 1000L()s 1s ()(1)T t U U U i dt T t D T L L L -∆=--=-=-⎰(2-2)由于稳态工作下的电感电流L i 波形必然周期性重复,因此S 导通期间L i 的增量必然等于S 截至期间的减小量,即L(+)L(-)i i ∆=∆,所以i 00s s (1)U U U DT D T L L-=-(2-3)整理得0iU D U =(2-4) 由式(2-4)可知,输出电压与开关管的占空比D 成正比,所以通过改变开关管的占空比可以控制输出平均电压的大小。
由于占空比总是小于1,所以输出电压总是小于输入电压,故常称为降压式变换器。
改变占空比就可以改变输出电压值。
(2)电感电流断续模式当电感较小,负载电阻较大或s T 较大时,将出现电感电流已下降到0,但新的周期却尚未开始的情况。
如图为电流断续模式下Buck 电路的相关波形图 电流断续模式下电路波形在[]10t 区间,开关管S 处于导通状态,与电感电流连续模式下的工作情况相同,此时()L L1i I +∆=。
在1T 时刻,S 关断,电感中电流L i 线性衰减,直到dis t 时刻下降到0,即(2-5) 式中,dis 1s(),(1)t t D D D T -∆=∆<-且。
由于L()L()=i i +-∆∆得 0(1)i U D D D U D D =∆<-+∆ ,其中(2-6)此时,变换器输出电流0I 任等于电感电流平均值,即2i 0L1dis i S S 011(1)22U D I I t U T Lf U =⨯=- (2-7) 上式表明。
电感电流断续时0i U U 不仅与占空比D 有关,而且与负载电流0I 有关。
若00I =,则D 多大,输出电压0U 必等于输入电压i U 。
(3)电感电流临界连续模式在有关电流断续工作模式的数学关系中,首先需要推导的是电感电流连续与断续的临界条件,其推导过程如下。
降压型电路电感电流处于连续与断续的临界状态时,在每个开关周期开始和结束的时刻,电感电流正好为零,如图2-4所示。
图 降压型电路电流临界连续工作时的波形稳态条件下,由于电容C 的开关周期平均电流为零,因此电感电流L i 在一个开关周期内的平均值等于负载电流为o o U I R =(2-8) 而电感电流L i 的开关周期平均值可以按下式计算:S L L 0()T I i t dt =⎰(2-9)0L I I ≥,即得到电感电流连续的临界条件。
这种计算方法需要导出()L I t 的表达式,还要计算定积分,比较繁琐。
我们采用一种简单的方法。
根据图2-4,电感电流在一个开关周期中的波形正好是一个三角形,它的高L I ∆,底边长为s T ,面积为I L S 12S I T =∆(2-10) 在几何意义上,电感电流的开关周期平均值等于和该三角形同底的矩形的高,因此电感电流开关周期平均值等于三角形面积除以s T ,即L L 12I I =∆(2-11) L I ∆的计算方法如下:电感电流在零时刻从零开始线性上升,在s DT 时刻达到L I ∆,上升的斜率为L i o di LU U dt =-(2-12) 有: i o L S U U I DT L-∆=(2-13)此时电感电流仍为连续,故有 o iU D U = 将其代入式(2-13),有L o S 1D I U T L -∆=(2-14)则可得电感电流开关平均值的表达式为 L o S 12D I U T L -=(2-15)电感电流连续的临界条件为 0L I I ≥将式(2-8)和式(2-9)带入上式有00s 12U D U T R L-≥ (2-16)整理得 S 12L D RT -≥(2-17)这就是用于判断降压型电路电感电流连续与否的临界条件。
随后需要推导的是电感电流断续条件下输出与出入电压的比例。
首先设开关S 关断后电感的续流时间为s aT ,如图3-7所示,其中()01a D ≤≤-。
图 电感电流断续工作时的波形 根据稳态条件下电感电压开关平均值为零的原理,有i o S o S ()U U DT U T α-= (2-18) 电感电流开关周期平均值为L L 1()2I I D α=∆+ (2-19) 而负载电流为 o o U I R=(2-20) 稳态条件下,电容C 的开关周期平均电流为零,故电感电流开关周期平均值等于 负载电流,即oL 1()2U I D Rα∆+= (2-21)从式(2-18)中,解出α的表达式,与式(2-15)一起代入式(2-21)中得i o o i S o ()12U U U U DT D L U R-= (2-22)整理得 2i i 2o o S 2()0U U L U U D T R --= (2-23) 令2S 2L K D T R=解方程,并略去负根,得o i 12U U K= (2-24) 值得注意的是,式(2-24)在电路工作在电感电流断续条件下成立,而电路工作在电感电流连续条件下不成立。
特别是,当电感电流处于临界连续状态时,S ()2L/RT =1-D /,代入式(2-17)得时0i U U D =。
从式(2-17)可以看出,电流断续时电压比与占空比D 和负载R 相关,也与电路参数L 和s T 有关。
主回路电感、电容参数整定3【】22【】33【】根据对二电平Buck 型直流变换器工作原理的分析以及电感电流连续和断续的临界条件的推导,可以计算出二电平Buck 型直流变换器滤波电感和滤波电容的参数。
稳态时,电感电流连续的临界条件为:o L I I ≥ (2-25)利用上节内容提到的三角形面积法我们得到电感电流的临界条件为:S 12L D RT -≥ 整理得s 12D L RT -≥(2-26) 在本次的设计中,给定工作电压i U 为40V ,输出电压0U 为20V ,负载电阻R 为50Ω,开关周期s f 为40kHz ,带入式2-26中得到电感电流临界值:s 3111500.00031H 244010D L RT -≥=⨯⨯=⨯(2-27) 即当主电路电感大于0.31mH 时, 电路工作在电感电流连续工作模式,当主电路电感小于0.31mH 时,则为电感电流断续工作模式。
