物理常数单位制
初中物理基本物理量单位公式常数

初中物理基本物理量单位公式常数
基本物理量是指不能通过其他物理量表示的物理量。
国际单位制(SI
单位制)是国际通用的物理量单位制,它包括七个基本物理量:长度(米,m)、质量(千克,kg)、时间(秒,s)、电流(安培,A)、热力学温
度(开尔文,K)、物质的量(摩尔,mol)和光强度(坎德拉,cd)。
基本物理量单位公式常数如下:
1.长度:
单位:米(m)
2.质量:
单位:千克(kg)
公式常数:一定的铂-钇合金的质量
3.时间:
单位:秒(s)
4.电流:
单位:安培(A)
公式常数:两根平行导线,互相静止时,单位长度上产生的相互作用
力等于2.0×10^−7N的电流
5.热力学温度:
单位:开尔文(K)
公式常数:绝对零度时气体氧气(O2)对应的热运动动能。
6.物质的量:
单位:摩尔(mol)
公式常数:12克的^12C的核在电子静止且处于其基态时包含的粒子数。
7.光强度:
单位:坎德拉(cd)
公式常数:等于1/683瓦特每球面弧度的单色光源的光通量。
此外,还有一些其他常用的物理量单位和公式常数,如:
1.速度:
单位:米每秒(m/s)
公式常数:速度等于位移与时间的比值。
2.加速度:
单位:米每秒平方(m/s²)
公式常数:加速度等于速度的变化率。
3.力:
单位:牛顿(N)
公式常数:力等于质量与加速度的乘积。
4.功:
单位:焦耳(J)
公式常数:功等于力与位移的乘积。
5.功率:
单位:瓦特(W)
公式常数:功率等于功与时间的比值。
理想气体常数r的单位和数值

理想气体常数r的单位和数值
理想气体常数r是一个物理常数,表示单位质量的理想气体在标准条件下的压力与体积的比值,用于描述气体状态方程的关系。
其单位是焦耳每千克·开尔文,数值约为8.31。
在国际单位制中,理想气体常数r的单位为焦耳每千克·开尔文,简写为J/(kg·K)。
这个单位可以进一步化简为米2·千克·秒-2·开尔文-1,也可以表示为帕斯卡·米3·千克-1·秒-2·开尔文-1。
在工程领域中,理想气体常数r的单位也常常使用千焦每千克·开尔文,简写为kJ/(kg·K)。
理想气体常数r的数值约为8.31,具体数值可以根据不同的单位进行计算。
例如,使用焦耳每千克·开尔文作为单位时,理想气体常数r的数值为8.314462618,而如果使用千焦每千克·开尔文作为单位,则其数值为0.008314。
无论采用何种单位,理想气体常数r的数值都是一个非常重要的物理常数,被广泛应用于热力学、气体动力学等领域。
- 1 -。
kb玻尔兹曼常数

kb玻尔兹曼常数玻尔兹曼常数(Boltzmann constant)是物理学中的一个基本常数,用符号k表示,通常在SI单位制中的数值为1.380649 ×10^(-23) J/K。
这个常数在统计物理学、热力学和量子力学中具有重要的意义。
玻尔兹曼常数最早由维尔纳·海森伯在1884年提出,并由马克斯·普朗克在1900年命名为玻尔兹曼常数,以纪念他在统计热力学中的贡献。
玻尔兹曼常数与其他基本常数(如普朗克常数和光速)一起,构成了物理学中的基本定值。
玻尔兹曼常数的物理含义是衡量了热力学温度和能量之间的关系。
它的值是能量单位与温度单位之间的比例关系。
具体而言,玻尔兹曼常数是将能量的单位(焦耳)转换为温度的单位(开尔文)时所需的比例系数。
根据玻尔兹曼常数的定义,如果一个系统的温度为1K,则其内能等于玻尔兹曼常数乘以1.380649 × 10^(-23)焦耳。
玻尔兹曼常数还与熵的概念密切相关。
熵是热力学中的一个重要量,用来描述一个系统的无序程度。
根据统计物理学,系统的熵等于玻尔兹曼常数乘以自然对数的倒数,并乘以可能的微观状态的数量。
这个关系表明,熵的量级与微观粒子数之间存在着关联,玻尔兹曼常数是将两者联系起来的关键因素。
在量子力学中,玻尔兹曼常数也扮演着重要的角色。
根据波尔兹曼-统计物理学,玻尔兹曼常数与量子力学中的普朗克常数之间存在一定的关系。
具体而言,将普朗克常数的平方除以玻尔兹曼常数,得到了一个称为波尔兹曼常数P的值,约为6.62607015 × 10^(-34) J·s / (1.380649 × 10^(-23) J/K)。
这个比值在量子力学中具有重要意义,帮助人们理解粒子的量子行为和统计特性。
综上所述,玻尔兹曼常数是物理学中非常重要的一个常数,它关系着热力学、统计物理学和量子力学等多个领域。
通过玻尔兹曼常数,我们可以将能量和温度联系起来,理解系统的熵以及量子粒子的统计特性。
化学拉丁语单位

化学拉丁语单位化学单位是一个化学概念,一般分为两类,即化学计量单位。
化学计量单位又称化学计量单位,由1克、1千克(克)、2立方米)等组成。
其含义是一种物质在世界上的重量单位(S1到S9);一种化学物质在地球上的重量单位(S1到S9);一种化学物质在空气中含量单位(S1到S9);一种化学物质在水中含量单位(S1到S9),以及其他化学性质单位;或一个化学物质在空气中质量单位(S1到S9)。
化学计量的单位不是很多,但是化学计量一定要读懂了再来学习。
一、国际单位制国际物理常数单位——千克,是基于米的长度单位——秒,以米为基础构建起来而成。
国际物理常数单位制是以米为基础所建立起来的,它以一组固定不变、与国际计量局定义的常数基本一致的常数作为单位来定义国际单位制。
米是一个由若干个独立小质量和独立小体积组成的圆柱体。
它们有一个共同的大小和质量单位——千克。
国际米制单位和国际计量局定义的基本单位保持一致(定义单位均为千克)。
二、物理指标1克:物理量,由2个组成:一个是金属氢,一个是原子氢。
2克:体积大小,由常数确定。
3克:质量分数,由体积分数和质量分数所组成。
4千克:质量。
5立方米:体积分数。
三、化学计量单位简介我国自1952年以来就开始使用化学计量单位,但基本没有统一的化学计量单位,都以“吨”作为单位使用。
根据《中华人民共和国国家计量法》规定:化学计量单位是指由化学物质组成的常数、质量、体积和温度等所组成的标准参数。
化学计量单位由物理量、化学量和化学计量组成。
物理量包括原子量(S1)、电离氢量;化学量包括原子量、密度和磁化率等;化学量包括质量、体积、温度和化学计量等;化学计量是化学量学的重要组成部分。
中华人民共和国《国家标准化管理条例》规定:国家基本标准组织建立和完善化学计量单位及其相关标准制度。
其中, GB是基本标准单位和唯一国际通用的化学计量单位; GS (Group Standard)是国际常用标准性质术语; SI、 NI和 PJ是具有化学计量性质的三个基本单位。
基本物理常数在国际单位制的重要作用

基本物理常数在国际单位制的重要作用在科学研究和工程实践中,我们经常会接触到一些基本物理常数,比如普朗克常数、元电荷、光速等。
这些常数在国际单位制中扮演着非常重要的角色,对于我们理解自然规律、进行精密测量、制定科学标准都起着至关重要的作用。
1. 基本物理常数简介基本物理常数是一些在自然界中具有普遍意义的物理量,它们通常是不可约的,也就是不能由其他物理量表示。
在国际单位制中,这些常数被作为单位定义的基础,比如光速就是米制单位米每秒的定义值。
2. 基本物理常数的重要作用在科学研究中,基本物理常数可以被用来验证理论、检验实验结果的一致性。
比如普朗克常数在量子力学中扮演着至关重要的角色,它表征了微观世界的基本特性,对于我们理解微粒的行为有着重要的意义。
在工程实践中,基本物理常数也被广泛应用。
比如在电磁学中,元电荷是电荷量的最小单位,对于电磁场的理论和应用都有着重要的影响。
另外,光速是许多精密测量仪器的基准,比如光的波长和频率的测量都可以通过光速和其他常数相结合来实现。
3. 我对基本物理常数的理解在我看来,基本物理常数是自然界赋予我们的珍贵礼物,它们蕴含着丰富而深刻的物理规律。
通过不断地研究和应用这些常数,我们可以更好地认识自然界,探索宇宙的奥秘。
基本物理常数也是我们跨越科学技术障碍的重要工具,它们为我们提供了丰富而宝贵的资源,帮助我们解决各种现实问题。
总结在国际单位制中,基本物理常数扮演着重要的角色,它们不仅是科学研究的基础,也是工程实践的支撑。
通过深入理解和应用这些常数,我们可以更好地认识和利用自然规律,推动科学技术的发展。
让我们珍惜并充分利用这些宝贵的资源,共同探索未知的领域,创造美好的未来。
基本物理常数在国际单位制中的重要作用不仅体现在科学研究和工程实践中,还在各个领域产生着深远的影响。
以下是对基本物理常数在不同领域的应用和影响的进一步探讨:1. 化学领域:基本物理常数在化学研究和实践中具有重要作用。
七大基本物理量单位常数表示

七大基本物理量单位常数表示物理量单位常数是指在国际单位制中,用来确定七大基本物理量的单位的常数。
这些常数包括:光速、元电荷、普朗克常数、玻尔兹曼常数、阿伏伽德罗常数、气体常数和亚佛加德罗常数。
下面将逐一介绍这些常数的含义和作用。
1. 光速 (c)光速是物理学中最重要的常数之一,它表示光在真空中传播的速度。
光速的数值约为299,792,458米/秒,它在相对论和电磁学等领域有着重要的应用。
光速的存在使得我们能够测量时间和距离,也为其他物理量的测量提供了基准。
2. 元电荷 (e)元电荷是电荷的基本单位,描述了带电粒子的最小电量。
元电荷的数值约为1.602176634×10^-19库仑,它对于电磁学和粒子物理学的研究具有重要意义。
通过元电荷的概念,我们可以对电子、质子等带电粒子的电量进行精确测量。
3. 普朗克常数 (h)普朗克常数是量子力学中的基本常数,用来描述微观世界的行为。
普朗克常数的数值约为6.62607015×10^-34焦耳秒,它与能量的量子化和粒子的波粒二象性密切相关。
普朗克常数在量子力学的各个领域中都有广泛的应用,如原子物理学、固体物理学和核物理学等。
4. 玻尔兹曼常数 (k)玻尔兹曼常数是描述热力学系统中粒子运动的常数。
它的数值约为1.380649×10^-23焦耳/开尔文,它与温度、熵和能量等热力学量的关系有着重要的作用。
玻尔兹曼常数被广泛应用于理论物理学、统计物理学和热力学等领域,它帮助我们理解和描述宏观和微观系统的行为。
5. 阿伏伽德罗常数 (NA)阿伏伽德罗常数是描述化学反应和粒子物理学中粒子数量的常数。
它的数值约为6.02214076×10^23/mol,它表示在摩尔中的粒子数目。
阿伏伽德罗常数的存在使得我们能够在化学反应和粒子物理学中精确计量和比较不同物质的粒子数量。
6. 气体常数 (R)气体常数是描述理想气体行为的常数,它用来关联气体的压力、体积和温度等物理量。
高斯单位制中的常数

高斯单位制中的常数高斯单位制是一种物理单位制,其特点是基本单位的选择非常巧妙,能够简化物理公式的形式和计算的精度,因此在电磁学和天文学等领域得到了广泛的应用。
为了方便使用高斯单位制,我们需要了解其所用的常数,包括基本常数、电磁学常数和自然单位制常数。
一、基本常数1、光速:c = 299792458 米/秒光速是真空中电磁波的传播速度,是一个极为重要的参考常数,也是高精度计量的基础。
在高斯单位制中,光速的数值被定义为1,即c = 1。
2、元电荷:e = 1.602176634 × 10^-19 库仑元电荷是电荷量的基本单位,是电子或质子所带电荷的大小。
在高斯单位制中,忽略真空介电常数的影响,元电荷的大小被定义为1,即e = 1。
3、玻尔兹曼常数:k = 1.380649 × 10^-23 焦耳/开尔文玻尔兹曼常数是描述温度与能量之间关系的基本常数,被广泛应用于统计物理学和热力学等领域。
在高斯单位制中,玻尔兹曼常数的数值被定义为1,即k = 1。
磁通量子是描述磁通量与磁通量子数之间关系的常数,是超导电性和量子计量的基础。
在高斯单位制中,磁通量子的大小被定义为1,即Φ0 = 1。
二、电磁学常数3、电荷密度:ρe = ε0^-1 / (4π)4、电位移矢量:D = ε0 E电位移矢量描述了电场(E)与极化电荷之间的关系,单位是库仑/米²。
在高斯单位制中,电位移矢量的大小被定义为1,即D = 1。
5、磁感应强度矢量:B = μ0 H三、自然单位制常数自然单位制是另一种物理单位制,以光速、元电荷和普朗克常数为基本单位,其常数与高斯单位制相比更为简单。
下面列出几个自然单位制常数的高斯单位制数值。
3、电子电荷质量比:me/mp = 5.48579909070 × 10^-4以上常数仅是高斯单位制中的部分常数,还有很多常数在实际计算中也是必不可少的。
因此,熟练掌握高斯单位制中的常数,对于深入理解电磁学和微观物理学等领域的计算方法和理论研究都非常重要。
国际单位制常数化计算公式

国际单位制常数化计算公式国际单位制是世界上通用的计量单位制度,它的基本单位包括米、千克、秒、安培、开尔文、摩尔和坎德拉等。
为了能够更准确地进行科学计量和测量,国际单位制常数化计算公式被广泛应用于各种科学领域,包括物理学、化学、工程学等。
国际单位制常数化计算公式的核心在于将物理常数与计量单位相结合,从而使得计量单位可以通过物理常数的测量来确定。
这种方法在实际应用中具有很高的精度和可靠性,因此被广泛应用于科学研究和工程实践中。
在国际单位制常数化计算公式中,最常用的物理常数包括普朗克常数、元电荷、波尔兹曼常数、阿伏伽德罗常数等。
这些常数与计量单位的定义相关联,通过测量这些物理常数的数值,可以确定计量单位的大小。
以普朗克常数为例,它是量子力学中的一个重要常数,通常用h来表示。
根据国际单位制常数化计算公式,普朗克常数与计量单位之间的关系可以表示为:h = 6.62607015 × 10^-34 J·s。
这个公式表明,普朗克常数的数值可以通过测量来确定,从而确定焦耳和秒的定义。
这种常数化计算公式的方法,使得计量单位的定义更加准确和可靠。
在化学领域,国际单位制常数化计算公式也被广泛应用。
例如,波尔兹曼常数k是描述热力学系统中粒子运动的一个重要常数,它与温度的关系可以表示为:k = 1.380649 × 10^-23 J/K。
通过测量波尔兹曼常数的数值,可以确定开尔文的定义,从而使得温度的测量更加准确和可靠。
除了普朗克常数和波尔兹曼常数,国际单位制常数化计算公式还涉及到其他一些重要的物理常数,包括光速、电荷量、阿伏伽德罗常数等。
通过测量这些物理常数的数值,可以确定米、安培、摩尔等计量单位的定义,从而使得科学计量更加准确和可靠。
在工程领域,国际单位制常数化计算公式也具有重要的应用价值。
例如,光速是一个重要的物理常数,它与米的定义相关联,通过测量光速的数值,可以确定米的定义,从而使得长度的测量更加准确和可靠。
基本物理常数表 单位换算

基本物理常数表单位换算基本物理常数表(单位换算)为了方便在物理学的研究与应用过程中进行单位的换算与计算,科学家们约定了一套国际单位制(SI,International System of Units)来统一物理量的测量与表示方法。
其中,物理常数是一些在物理学中扮演重要角色的恒定数值。
本文将给出一些基本的物理常数以及它们的单位换算关系。
一、长度单位换算常数:1、1米(m)= 100厘米(cm)= 1000毫米(mm)= 1000000微米(μm)= 1000000000纳米(nm)2、1微米(μm)= 10-6米(m)3、1纳米(nm)= 10-9米(m)二、质量单位换算常数:1、1千克(kg)= 1000克(g)= 1000000毫克(mg)2、1克(g)= 0.001千克(kg)三、时间单位换算常数:1、1秒(s)= 1000毫秒(ms)2、1分钟(min)= 60秒(s)3、1小时(h)= 60分钟(min)= 3600秒(s)4、1天(day)= 24小时(h)= 1440分钟(min)= 86400秒(s)四、速度单位换算常数:1、1米每秒(m/s)= 3600米每小时(m/h)= 2.237英里每小时(mph)五、加速度单位换算常数:1、1米每平方秒(m/s^2)= 3.281英尺每平方秒(fps^2)六、力单位换算常数:1、1牛顿(N)= 1000克力(kgf)2、1克力(kgf)= 9.80665牛顿(N)七、压强单位换算常数:1、1帕斯卡(Pa)= 0.000145038磅力每平方英寸(psi)2、1标准大气压(atm)= 760毫米汞柱(mmHg)= 101325帕斯卡(Pa)= 14.6959磅力每平方英寸(psi)八、功、能单位换算常数:1、1焦耳(J)= 0.238846卡路里(kcal)2、1卡路里(kcal)= 4186焦耳(J)九、功率单位换算常数:1、1瓦特(W)= 1牛顿米每秒(N·m/s)= 0.001千瓦(kW)十、电荷单位换算常数:1、1库仑(C)= 10^6微库仑(μC)= 10^9毫库仑(mC)十一、电压单位换算常数:1、1伏特(V)= 1000毫伏特(mV)= 1000000微伏特(μV)以上只是一部分常见的单位换算关系,物理学涉及的常数还有很多。
万有引力常数单位

万有引力常数单位
万有引力常数(G)是用来描述物体之间引力作用的一个物理常数。
它的单位是N·(m/kg)²,其中N代表牛顿,m代表米,kg代表千克。
1. 牛顿(N)是国际标准单位制中力的单位。
它可以定义为给定质量物体所受到的加速度乘以质量,即F=ma。
其中F代表力,m代表质量,a代表加速度。
牛顿是一个用来量化物体之间相互作用力的量。
2. 米(m)是国际标准单位制中长度的单位。
它是通常用来测量物体之间距离或者间隔的单位。
在这里,米用来量化物体之间的距离,也就是引力作用的范围。
3. 千克(kg)是国际标准单位制中质量的单位。
它是用来度量物体的质量的单位。
在这里,千克用来量化物体的质量,也就是用来描述物体对其他物体施加引力的能力。
万有引力常数的单位N·(m/kg)²可以解释为:一千克质量的物体之间,在彼此相距一米的距离上的引力大小。
这个单位的含义是在描述物体之间的引力作用时,我们考虑了质量和距离的因素。
需要注意的是,万有引力常数是一个普遍适用于任何物体之间的引力作用的常数。
它的数值约为6.67430×10⁻¹¹N·(m/kg)²。
这个常数的值是由科学实验证实得
出的,并且在物理学的各种应用中都有广泛使用。
它的存在使得我们能够准确地描述和计算物体之间的引力作用。
25个物理常数

25个物理常数篇一:标题: 25个物理常数(创建与标题相符的正文并拓展)正文:物理学是研究自然现象的科学,其基础是一些基本常数。
这些常数是通过对自然界的观察和实验得出的,它们对物理学的理论和实践具有至关重要的影响。
本文将介绍25个基本的物理学常数,包括它们的值、定义和意义。
1. 开尔文(k)开尔文(k)是一个常量,它的值为1.19264×10-19J/(K·K)。
它是电离常数,用于描述电解质的电离程度。
2. 普朗克常数(h)普朗克常数(h)是一个基本的物理学常数,它的值为6.626176×10-35J/(K·s)。
它是热力学中的基本常数,用于描述能量和热量之间的关系。
3. 光速(c)光速(c)是一个基本的物理学常数,它的值为299,792,458米/秒。
它是真空中光的速度,也是宇宙中最基本的速度。
4. 磁感应强度(B)磁感应强度(B)是一个物理学常数,用于描述磁场的强度。
它的值通常在0到1000特斯拉之间,磁感应强度越大,磁场越强。
5. 电容(C)电容(C)是一个物理学常数,用于描述电容器的电容值。
它的值通常在0到1特斯拉之间,电容器的电容值越大,电容器的储存电能的能力越强。
6. 电阻(R)电阻(R)是一个物理学常数,用于描述导体的电阻值。
它的值通常在0到无穷大之间,电阻值越大,导体的电阻能力越强。
7. 温度(T)温度(T)是物理学中的基本常数,用于描述物体的状态。
它的值通常在0到开尔文之间,温度越高,物体的状态越热。
8. 引力(G)引力(G)是物理学中的基本常数,用于描述物体之间的引力大小。
它的值通常在6.6743×10-11N·(m/kg)^2。
9. 电磁场频率(E)电磁场频率(E)是物理学常数,用于描述电磁场的传播速度。
它的值通常在真空中约为3×10^10米/秒。
10. 质能关系(E=mc2)质能关系(E=mc2)是物理学中的一个重要公式,用于描述质量和能量之间的关系。
理伯德常数 cgs单位制

理伯德常数 cgs单位制理伯德常数是一个重要的物理常数,在物理学中起着举足轻重的作用。
它在cgs单位制下的数值约为6.67430×10^-8 cm³⋅g⁻¹⋅s⁻²,通常用符号G表示。
理伯德常数描述了万有引力定律的强度,它体现了引力的基本特征和物质之间相互作用的重要性。
引力是自然界中最基本的力之一。
从苹果掉落,到地球围绕太阳旋转,无不受到引力的作用。
而理伯德常数则是衡量引力强弱的重要标准。
正因如此,理伯德常数对于研究天体物理学、宇宙学、力学等领域具有重要意义。
理伯德常数的cgs单位制下的数值虽然看起来很小,但在宇宙尺度下的影响却是极其巨大的。
我们以地球和太阳为例,它们之间的引力正是由理伯德常数所描述。
地球围绕太阳运转时,太阳的质量和地球的质量之间的比值即为重要的计算参数。
理伯德常数的具体数值使得地球和太阳之间的引力足够巨大,以保持地球的运动轨道稳定,从而维持了生命的存在。
除了作用于星际天体之间,理伯德常数还在微观领域中发挥着重要作用。
例如,在原子物理学中,理伯德常数是计算电子轨道和原子核之间作用力的关键因素之一。
它决定了原子的化学性质、分子的稳定性以及化学反应的速率等。
可以说,没有理伯德常数的存在,我们很难想象宇宙和物质会如何运作。
除了在物理学研究中的重要性,理伯德常数还对科学教育具有指导意义。
通过学习关于理伯德常数的知识,我们能更好地了解自然界的规律,并能开阔自己对于宇宙的认知。
由于理伯德常数体现了物质之间的相互作用,通过深入研究理伯德常数,我们可以更好地理解许多自然现象,从而提高科学素养和科学研究水平。
总之,理伯德常数是一个重要的物理常数,它在万有引力定律的描述中起着关键作用。
无论是在天体物理学还是微观领域,理伯德常数都具有举足轻重的地位。
通过对于理伯德常数的研究和应用,我们能更好地了解自然界的运作规律,并提高自己的科学素养。
因此,理解并研究理伯德常数对于我们每个人来说都具有重要的指导意义。
普朗克常数和玻尔兹曼常数单位换算表

普朗克常数和玻尔兹曼常数是描述微观世界物理现象的两个重要常数。
它们在量子力学和统计物理中有着重要的作用,是研究微观粒子运动和能量转换的基本参量。
由于量子力学和统计物理中常常涉及到单位的换算,因此掌握普朗克常数和玻尔兹曼常数的单位换算表可以帮助我们更好地理解和应用这两个常数。
下面是普朗克常数和玻尔兹曼常数的单位换算表:普朗克常数:1. 普朗克常数的国际单位制(SI单位制)表示为 h,其数值为6.xxx × 10^-34 J·s。
2. 普朗克常数的厘米-克-秒单位制(cgs单位制)表示为 h,其数值为6.xxx × 10^-27 erg·s。
3. 普朗克常数的电子伏特单位制(eV单位制)表示为ℏ,其数值为4.xxx × 10^-15 eV·s。
玻尔兹曼常数:1. 玻尔兹曼常数的国际单位制(SI单位制)表示为 k,其数值为 1.xxx × 10^-23 J/K。
2. 玻尔兹曼常数的厘米-克-秒单位制(cgs单位制)表示为 k,其数值为1.xxx × 10^-16 erg/K。
3. 玻尔兹曼常数的电子伏特单位制(eV单位制)表示为 k,其数值为8.xxx × 10^-5 eV/K。
通过以上的单位换算表,我们可以看出普朗克常数和玻尔兹曼常数在不同的单位制下的具体数值,这有助于我们在实际计算和研究中的应用。
在量子力学和统计物理的研究中,常常需要根据实际问题的不同,选择合适的单位进行计算和描述,因此熟练掌握常数的单位换算表是非常重要的。
普朗克常数和玻尔兹曼常数在科学研究和工程技术领域中有着广泛的应用。
比如在半导体物理中,玻尔兹曼常数常常用于描述半导体中电子的能级分布;在纳米材料的研究中,普朗克常数常常用于描述纳米材料的量子效应。
掌握好普朗克常数和玻尔兹曼常数的单位换算表,对于开展相关领域的研究工作具有重要的指导意义。
普朗克常数和玻尔兹曼常数作为描述微观世界物理现象的重要常数,其在量子力学和统计物理中有着重要的作用。
各个物理量的国际单位制

各个物理量的国际单位制国际单位制(SI)(SI是国际单位制的简称)是在“基本物理常数”基础上确定基本单位的国际组织。
基本物理常数指一个物体的质量占它在整个质量库中储存的总质量的百分比。
国际单位制(SI)由光速单位 m/s、千克基本单位千克、开尔文基本单位开尔文、安培、开尔文电流温度等组成,在地球自转产生的磁场中保持不变(除非地球自转极快),其定义通过直接测量定义和通过量子基准进行复现后得到。
该单位根据普朗克常数对物质“量”作为质量单位。
国际单位制(SI)由基本物理常数来定义物体的质量。
一、基本物理常数对质量的影响SI (SI)定义了一个物体的质量,其定义可以采用物理常数或量子力学的普朗克常数来定义。
普朗克常数是物理常数 Ni的一个系数。
在一条连续平行线上,两个物质处于相对静止状态。
一条直线上的两个点分别有1/2的质量和1/3的能量。
在同一个平面上,两个点都有一个不变的质量单位 Ni,那么两个不变的质量单位就都等于1/2这两个点之间那点质量的乘积就叫做 Ni。
如果用普朗克常数 Ni来定义一个物体的质量时,首先要确定它是不是稳定地不变的。
二、物理常数定义的变化与基本物理常数对质量的影响。
物理常数在 SI中被分为“基本物理常数”和“质量”两个部分,前者定义为:光速 ms/s 和质量 g的单位,后者定义为:质量 mg的10倍。
两个物理常数在国际单位制中保持不变。
根据这个定义方法,可以得到一系列物理量所对应的质量为:其中是1和1的乘积(n);0=ms-1;1=ms2;0=ms3;1=ms4;1=ms5;1=ms2;1=ms3;1=ms5。
为了更好地描述物质是如何相互作用的过程,因此在基本物理常数定义中加入了质量常数的定义。
三、常用质量定义方法对比在定义中,由于物质的质量的不确定性,常采用将物体定义为基本物理常数的方法。
测量方法有:直接测量法、量子测量法和量子基准法。
其中前三种方法可以直接测量出质量的参量。
units单位制

表 2 电磁学物理量的量纲和单位
(注 所有静电制单位都可称作 esu 所有电磁制单位都可称作 emu * 表示高斯制单位)
四 量纲分析法
在国际制和电磁制的电磁学公式中 绝大多数公式形式上是一致的 由于存在这几个换
算公式 (1) 1m = 100cm (2) 1kg = 1000kg (3) 1A = 0.1emu 所以可以根据国际制单位的量
和电磁制单位的量纲之比为 L−nTn 那么两者的换算关系就是
1 静电制单位(esu) = (2.99792458×1010)n 电磁制单位(emu)
(4-2)
例如 国际制中电容单位 F 的量纲为 L−2M−1T4I2 要把它转化为静电制单位 cm(esu) 首
先要经过电磁制单位(cm/s2)−1(emu) 关系是 1F = 10−9(cm/s2)−1(emu) 由于电容在电磁制中的
关于单位制 物理常数和不确定度的资料
黄晨 * 2004年9月初稿 2005年11月修订 (* 联系地址 复旦大学化学系表面化学实验室 eMail webmaster@)
一 国际单位制(SI)和高斯单位制(CGS)的力学量纲和单位
力学物理定律在国际单位制(简称国际制 记作 SI)和高斯单位制(简称高斯制 又称为厘 米克秒制 记作 CGS)中具有相同的形式 并且它们都以长度 质量和时间作为基本量纲 所以所有的力学量都具有相同的量纲 另外 这两个单位之间的换算也相当方便 都是 10 的次方数
光速具有精确值(即定义 秒 以后 用真空光速来定义 米 ) 所以这种不确定度在国际
制和高斯制之间并不存在 但是在某些单位之间 例如能量单位 J 和 eV 就相差一个基本
电荷 e/C 该常数的不确定度就是这两个单位比值的不确定度 根据这个道理 同一物理常
基本物理常量

市制暂时允许使用的市制单位列于下表,其它市制单位不准使用。
一般不要将市制单位与国际单位制单位或任何其它单位构成组合单位。
市制单位单位换算以下各表列出各种单位换算关系。
各表中SI单位均印制粗体。
长度1埃(Å)=10-10米1光年=9.4600×1012千米1码=3尺1x单位=10-13米1秒差距=3.084×1013千米1竿(rod)=16.5尺1噚=6尺1密耳(mil)=10-3寸1海里=1852米=1.151哩=6076尺标准波长计量学上第一次定义的标准波长是一定条件下的氪__86(86Kr)放电管发出的2P10—5d5间跃迁谱线在真空中的波长λKr,其值为:λKr=109nm/1650763.73=605.78021059……nm计量学上第二次定义的标准波长是一定条件下的氪__86(86Kr),汞__198(198Hg),镉__114(114Cd)放电管发出的如下谱线在真空中的波长(单位nm):86Kr(645.80720,642.28006,565.11286,450.36162)198Hg(579.22683,577.11983,546.22705,435.95624)114Cd(644.02480,508.72379,480.12521,467.94581)为了能方便地用内插法求出未知波长,需要精密测定从铁、氖和氪发出的波长为240nm到70nm的340条左右谱线在光谱学标准空气中的波长。
以这些为标准规定了计量学上的第三次标准波长。
主要的音响单位声强:某点在特定方向的声强是每秒钟穿过垂直于传播方向的单位面积的声能通量。
单位为瓦特每平方米(Watt/m2)。
声压:单位为微巴(μb),达因每平方厘米(dyn/cm2)或牛顿每平方米(N/m2)。
1N/ m2=10μb,声强级:以声强I和标准声强I。
之比的常数对数的十倍表示(即10log10(I/Io),其中Io=10- 12Watt/m2),单位为分贝(dB)。
SI单位制 常用的物理常数
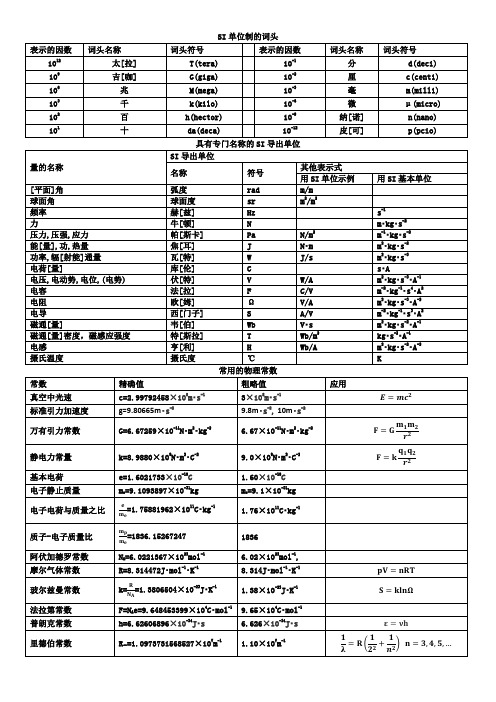
其他表示式 用 SI 单位示例 m/m 2 2 m /m
用 SI 基本单位
N/m N▪m J/s
2
W/A C/V V/A A/V V▪s 2 Wb/m Wb/A
s -2 m▪kg▪s -1 -2 m ▪kg▪s 2 -2 m ▪kg▪s 2 -3 m ▪kg▪s s▪A 2 -3 -1 m ▪kg▪s ▪A -2 -1 4 2 m ▪kg ▪s ▪A 2 -3 -2 m ▪kg▪s ▪A -2 -1 3 2 m ▪kg ▪s ▪A 2 -2 -1 m ▪kg▪s ▪A -2 -1 kg▪s ▪A 2 -2 -2 m ▪kg▪s ▪A K 应用 ������ = ������������������
-31 -19 9 2 -2
-2
������ = ������
������������ ������������ ������������ ������������ ������������ ������������
������ = ������
=1.75881962×10 C▪kg =1836.15267247
-1
9.8m▪s , 10m▪s
2 -2 -11 2
-2
G=6.67259×10 N▪m ▪kg k=8.9880×10 N▪m ▪C e=1.6021733×10 C me=9.1093897×10 kg
������ ������������
-31 -19 9 2 -2
-11
6.67×10 N▪m ▪kg 9.0×10 N▪m ▪C 1.60×10 C me=9.1×10 kg
23
-1
������������ = ������������������ ������ = ������������������������
理伯德常数 cgs单位制

理伯德常数cgs单位制
摘要:
1.理伯德常数的定义和含义
2.CGS 单位制的概念和特点
3.理伯德常数在CGS 单位制中的应用和重要性
4.理伯德常数和CGS 单位制的关系
正文:
1.理伯德常数的定义和含义
理伯德常数,又称为里德伯常数,是物理学中的一个重要常数,用符号"h"表示。
它代表了普朗克常数,是量子力学中一个基本的物理量,用于描述微观粒子的能量量子化。
2.CGS 单位制的概念和特点
CGS 单位制,即厘米- 克-秒单位制,是物理学中一种常用的单位制。
它的主要特点是采用厘米、克、秒作为长度、质量和时间的基本单位,能量单位为尔格(erg),力的单位为达因(dyn)。
3.理伯德常数在CGS 单位制中的应用和重要性
在CGS 单位制中,理伯德常数的数值为6.626070049×10^-34 J·s,是一个非常小的数值。
它在物理学中有着广泛的应用,例如在计算原子、分子和离子的能级、能量、波长等物理量时,都需要用到理伯德常数。
4.理伯德常数和CGS 单位制的关系
理伯德常数和CGS 单位制有着密切的关系。
在CGS 单位制中,理伯德
常数是一个基本的物理常数,它的数值和单位的确定,都是基于CGS 单位制的。
同时,理伯德常数在CGS 单位制中的应用,也进一步体现了CGS 单位制在物理学研究中的重要地位。
总的来说,理伯德常数和CGS 单位制在物理学研究中都起着重要的作用,它们之间的关系密切,相互影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黄晨 * 2004 年 9 月 (* 联系地址 复旦大学化学系表面化学实验室 eMail morning_yellow@)
一 国际单位制(SI)和高斯单位制(CGS)的力学量纲和单位
力学物理定律在国际单位制(简称国际制 记作 SI)和高斯单位制(简称高斯制 又称为厘 米克秒制 记作 CGS)中具有相同的形式 并且它们都以长度 质量和时间作为基本量纲 所以所有的力学量都具有相同的量纲 另外 这两个单位之间的换算也相当方便 都是 10 的次方数
它是电动力学中最常用的单位制 另一套以安培定律为基础 称为电磁制 记作 CGSM 它
是国际单位制的理论基础
静电学中最基本的定律是库仑定律 而该定律在国际制和静电制中有着不同的形式 国
际制的形式是
这里 ε0 是真空中的介电常数 而电磁制则是
F
=
q1q2 4πε0r 2
其数值为 8.8541878×10−12C2/Nm2
如果静电制单位和电磁制单位的量纲之比为 L−nTn 那么两者的换算关系就是
1 静电制单位 = (2.99792458×1010)n 电磁制单位
(4-3)
例如 国际制中电容单位 F 的量纲为 L−2M−1T4I2 要把它转化为静电制单位 cm 首先要
经过电磁制单位 cm/s2 关系是 1F(SI) = 10−9(cm/s2)−1(CGSM) 由于电容在电磁制中的量纲
制和高斯制之间并不存在 但是在某些单位之间 例如能量单位 J 和 eV 就相差一个基本
电荷 e/C 该常数的不确定度就是这两个单位比值的不确定度 根据这个道理 同一物理常
数在不同单位下具有不一样的不确定度 例如基本电荷 用 C(库仑)时不确定度为 0.09ppm
用 eV/V 时就不具有不确定度 又如 普朗克常数以 J⋅s 为单位时 不确定度为 0.17ppm 而
Mx
L−1/2M1/2T−1
Gs
L−1/2M1/2T−1
Oe
四 量纲分析法
在国际制 电流单位 安培 是根据安培定律来定义的 所以它的前身是电磁制单位
由于存在这几个换算公式 (1) 1m = 100cm (2) 1kg = 1000kg (3) 1A = 0.1emu 所以可以根
据国际制单位的量纲来确定换算比例 如果国际制单位的量纲是 LxMyTzIw 那么它和电磁制
(6-5')
另外 自然制还把电常数和磁常数定义为 1 因此有
ε0 = m = m3kg F/m F C2s2
用公式(6-3)
(6-4')和(6-5')代入
可得
ε0 F/m
பைடு நூலகம்
=
1 C2
h J⋅s
⋅
c m/s
−1
没有和 eV 有关的项
这说明电量是无量纲
数 并且有
C = ε 0 ⋅ h ⋅ c −1 2 (n.u.) 1(n.u.) = ε 0 ⋅ h ⋅ c 1 2
F/m J ⋅ s m/s
F/m J ⋅ s m/s
(6-7)
根据 CODATA 2002 的数值 国际制和自然制的单位有如下的换算关系
1m = 5.06773103(42)×106eV−1 1eV−1 = 1.97326967(16)×10−7m
(6-8) (6-8')
1kg = 5.60958895(49)×1035eV 1eV = 1.78266180(15)×10−36kg 1s = 1.51926754(12)×1015eV−1 1eV−1 = 6.58211915(55)×10−16s 1C = 1.89006713(16)×1018(n.u.) 1(n.u.) = 5.29081735(45)×10−19C 以上的换算关系都包含了一定的不确定度 大约在 0.08ppm 左右
L−1T2 和静电制中的量纲 L 之比为 L−2T2 所以两个单位值的比例应该是 1(cm/s2)−1(CGSM) =
8.98755179×1020cm(CGSE) 最后 1F(SI) = 8.98755179×1011cm(CGSE)
物理量 电量 电流 电位 电阻 电容 电感 磁感应通量 磁感应强度 磁场强度
esu
I
A(安培)
L3/2M1/2T−2
esu/s
L2MT−3I−1
V(伏特)
L1/2M1/2T−1
erg/esu
L2MT−3I−2 L−2M−1T4I2
Ω(欧姆) F(法拉)
L−1T
(cm/s)−1
L
cm
L2MT−2I−2 L2MT−2I−1
H(亨利) Wb(韦伯)
L−1T2 L1/2M1/2
(cm/s2)−1 -
(1) 设 1C = xesu
(2) 根据公式(A-1) 当 r = 1m q1 = q2 = 1C 时 F = 8.9875518×109N (3) 把 r = 1m = 102cm q1 = q2 = xesu F = 8.9875518×109N = 8.9875518×1014dyn 代入公
m/s C
m/s C
(6-3)
1s −1 = h e −1 eV 1eV = h −1 e s−1
J ⋅s C
J⋅s C
(6-4)
1m −1 = h ⋅ c ⋅ e −1 eV 1eV = h ⋅ c −1 ⋅ e m −1
J ⋅ s m/s C
J ⋅ s m/s C
国际制
静电制
1C
2.99792458×109esu
1A
2.99792458×109esu/s
1V
3.33564096×10−3erg/esu
1Ω
1.11265005×10−12(cm/s)−1
1F
8.98755179×1011cm
1H
1.11265005×10−12(cm/s2)−1
1Wb
-
1T
-
1A/m
(6-9) (6-9')
(6-10) (6-10')
(6-11) (6-11')
在自然单位制中 速度和角动量没有量纲 笔者建议它们的基本单位分别命名为爱因斯
坦(Einstein)和普朗克(Planck) 这样就有
1(n.u.) = 1 Einstein = 299792458m/s 1(n.u.) = 1 Planck = 6.6260693(11)×10−34J⋅s
(6-5)
在目前的物理常数表(CODATA 2002)中 基本电荷(e)的不确定度分别是 0.09ppm 所以
kg 和 eV 比例的不确定度也应该是 0.09ppm 再来看 s−1 和 eV 以及 m−1 和 eV 的比例 普朗
克常数( h )的不确定度是 0.17ppm 由于它和基本电荷之间存在联系 即约瑟夫森常数(KJ) 所以这两个比例的不确定度不是 0.09 + 0.17 = 0.26ppm 而是 KJ 的不确定度 0.08ppm 约瑟 夫森常数的定义是
物理量 长度 质量 时间 频率 力 能量 功率 压强
量纲 L M T
T−1 LMT−2 L2MT−2 L2MT−3 L−1MT−2
国际制单位 高斯制单位
m(米)
cm(厘米)
kg(千克)
g(克)
s(秒)
s(秒)
Hz(赫兹)
Hz(赫兹)
N(牛顿)
dyn(达因)
J(焦耳)
erg(耳格)
W(瓦特)
erg/s
MT−2I−1
T(特斯拉)
L−3/2M1/2
-
L−1I
A/m
L1/2M1/2T−2
-
表 2 电磁学物理量的量纲和单位
电磁制
量纲
单位
L1/2M1/2 L1/2M1/2T−1
emu⋅s emu
L3/2M1/2T−2 erg/emu⋅s
LT−1
cm/s
L−1T2 L
(cm/s2)−1 cm
L3/2M1/2T−1
Pa(帕斯卡)
dyn/cm2
表 1 力学量纲和单位
换算关系 1m = 102cm 1kg = 103g
-
1N = 105dyn 1J = 107erg 1W = 107erg/s 1Pa = 10dyn/cm2
二 静电制(CGSE)量纲和单位
高斯制在电磁学中具两套单位制 一套以库仑定律为基础 称为静电制 记作 CGSE
1
式(A-2) 得 x = 2.99792458×109 (4) 得出结论
1C = 2.99792458×109esu[1] 1esu = 3.33564096×10−10C 公式(2-2)和(2-2')是国际制单位和高斯制单位相互转换的基本公式 注[1] 由于等式两边采取的单位制不同 所以这样的等号在数学上是不严格的
(6-2)
3
自然单位制只有一个基本量纲 质量 这就使得四维时空坐标具有同样的量纲(质量
的倒数) 四维动量-能量坐标也具有同样的量纲(质量) 并且这两个坐标之间存在倒易关系
自然单位制中最常用的单位是 eV 国际单位制的 m s kg 和 eV 的换算公式为
1kg = c 2 e −1 eV 1eV = c −2 e kg
(2-2) (2-2')
三 电磁制(CGSM)量纲和单位
静磁学中最基本的定律是安培定律 国际制的形式是
F
=
µ0 I1I 2l 2πd
(3-1)
这里 µ0 是真空中的导磁率 其数值为 4π×10−7Nm/A2 而电磁制则是
F
=
2I1I 2l d
(3-1')
因此电磁制也不需要新的基本量纲 电流的量纲就是 L1/2M1/2T−1 电磁制给予一个新的
