大学物理A1简谐振动
大学物理规范作业A(本一)振动解答

( D)
根据
1 2 E kA , 2
15 Ek E E P E 16
Ek 15 所以 : E 16
3
3.已知一简谐振动x1=4cos(10t+3π /5),另有一个 同方向简谐振动x2=6cos(10t+φ );若令两振动合成 的振幅最小,则φ 的取值应为:
( A)
3
,
7 ( B) , 5
7
三、计算题
1.作简谐振动的小球,速度最大值vm=3cm/s,振幅A=2cm , 若令速度具有正最大值的时刻为t=0,求(1)振动周期; (2)加速度最大值;(3)振动表达式。
x A cos(t ) 解:设振动方程为:
dx ⑴速度为 v A sin(t ) dt
x2 y2 1 2 。 2 A1 A2
由振动方程得 1 4 ,
2
4
所以 2 1 2 将其代入合振动轨迹方程:
x 2 y 2 2 xy 2 2 1 cos sin 2 1 2 2 A1 A2 A1 A2 x2 y2 质点的轨迹方程: 2 2 1 A1 A2
大学物理规范作业
总(07) 振 动
1
一、选择题 1.一质点作简谐振动,周期为T。当它由平衡位置 向x轴正向运动时,从二分之一最大位移到最大位 移处,这段路程所需要的时间为:
( A) T / 4 , ( B) T / 6, ( C) T / 8 , ( D) T / 12
(B)
分析: 当质点从二分之一最大位移处运动到最大 位移处时,旋转矢量转过的角度为:
vm 0.03 1.5rad / s A 0.02
大学物理简谐振动

A2
A
A2 sin 2
2 -1
2
O
1 A1 x2
A1 sin 1
x2 x
x1x1
x2
x
A1 cos1 A2 cos2
合振动振幅:A A12 A22 2A1A2 cos(2 1)
1. 两个分振动的相位相同(同相)
5 (或 3 )
4
4
第六章
机械波
mechanical wave
6.1 机械波的产生、传播和描述 波动: 振动在空间中的传播过程.
机械波: 机械振动在弹性介质中的传播过程. 波动
电磁波: 交变电磁场在空间中的传播过程. 6.1.1 机械波的产生
当弹性介质中的一部分发生振动时,由于介质各个 部分之间的弹性力作用,振动就由近及远地传播出去. (1) 机械波实质上是介质中大量质点参与的集体振动;
20 0.47
(2) 30为何值时, x1+x3 的振幅为最大; 30为何值时, x2+x3的振幅为最小.
x1 0.05cos10t 3 4
x2 0.06cos10t 4
x3 0.07 cos10t 30
30
10
0 时,x1+x3 振幅最大:30
10
3
4
30 20 时,x2+x3 振幅最小:30 20
t 时刻点 P 的振动状态
P点在
t
时刻的位移
y P ,t
yO ,t x
u
A c os [ (t
x) u
0 ]
波函数 (波方程)
y( x, t )
A cos[ (t
大学物理振动

4.1 简谐振动
一.简谐振动
一物理量随时间的变 化规律遵从余弦函数 关系,则称该物理量 作简谐振动。
表达式 x(t)=Acos( t+)
特点 (1)等幅振动 (2)周期振动 x(t)=x(t+T )
-A 0 A
X
表达式 x(t)=Acos( t+)
二. 描述简谐振动的特征量 1. 振幅 A: 即最大位移:x=±A 2. 角频率 (圆频率)ω (弧度/秒:rad/s) 3. 周期T 和频率 v ∵ ωT=2π ∴ T=2π/ω (s) (完成一次全振动所需的时间) 而 v = 1/T =ω/2π (Hz)
a
d2x d t2
2 Acos(
t
0)
2 Acos(
t
0
)
x、 v 、a
2A
A v
A
x
0
-A
- A
- 2A v > 0
<0
a<0 减速
<0 加速
<0 >0 减速
a
T t
>0 >0 加速
解题方法
由初始条件求解振幅和初位相:
设 t =0 时,振动位移:x = x0
振动速度:v = v0
x Acos( t ) xo Acos
谐振系统的总机械能:
E Ek Ep
1 m 2 A2 sin 2 ( t ) 1 kA2 cos2 ( t )
2
2
E
1 2
kA2
1 2m2 A2来自1 2mvm 2
x Acos t
X
Ep
Ek
E 1 kA2
2
X
结论:
大学物理A第九章 简谐振动

第九章 简谐振动一、填空题(每空3分)9-1 质点作简谐振动,当位移等于振幅一半时,动能与势能的比值为 ,位移等于 时,动能与势能相等。
(3:1,22A ±)9-2两个谐振动方程为()120.03cos (),0.04cos 2()x t m x t m ωωπ==+则它们的合振幅为 。
(0.05m )9-3两个同方向同频率的简谐振动的表达式分别为X 1=6.0×10-2cos(T π2t+4π) (SI) , X 2=4.0×10-2cos(T π2t -43π) (SI) ,则其合振动的表达式为______(SI).( X=2.0×10-2cos(T π2t+4π) (SI)) 9-4一质点作周期为T 、振幅为A 的简谐振动,质点由平衡位置运动到2A处所需要的最短时间为_________。
(12T) 9-5 有两个同方向同频率的简谐振动,其表达式分别为 )4cos(1πω+=t A x m 、)43cos(32πω+=t A x m ,则合振动的振幅为 。
(2 A)9-6 已知一质点作周期为T 、振幅为A 的简谐振动,质点由正向最大位移处运动到2A处所需要的最短时间为_________。
(6T) 9-7有两个同方向同频率的简谐振动,其表达式分别为 )75.010cos(03.01π+=t x m 、)25.010cos(04.02π-=t x m ,则合振动的振幅为 。
(0.01m )9-8 质量0.10m kg =的物体,以振幅21.010m -⨯作简谐振动,其最大加速度为24.0m s -⋅,通过平衡位置时的动能为 ;振动周期是 。
(-32.010,10s J π⨯) 9-9一物体作简谐振动,当它处于正向位移一半处,且向平衡位置运动,则在该位置时的相位为 ;在该位置,势能和动能的比值为 。
(3,1:3π)9-10质量为0.1kg 的物体,以振幅21.010m -⨯作谐振动,其最大加速度为14.0m s -⋅,则通过最大位移处的势能为 。
大学物理第九章振动

⼤学物理第九章振动第9章振动本章要点:1. 简谐振动的定义及描述⽅法.2. 简谐振动的能量3. 简谐振动的合成物体在⼀定位置附近作周期性的往返运动,如钟摆的摆动,⼼脏的跳动,⽓缸活塞的往复运动,以及微风中树枝的摇曳等,这些都是振动。
振动是⼀种普遍⽽⼜特殊的运动形式,它的特殊性表现在作振动的物体总在某个位置附近,局限在⼀定的空间范围内往返运动,故这种振动⼜被称为机械振动。
除机械振动外,⾃然界中还存在着各式各样的振动。
今⽇的物理学中,振动已不再局限于机械运动的范畴,如交流电中电流和电压的周期性变化,电磁波通过的空间内,任意点电场强度和磁场强度的周期性变化,⽆线电接收天线中,电流强度的受迫振荡等,都属于振动的范畴。
⼴义地说,凡描述物质运动状态的物理量,在某个数值附近作周期性变化,都叫振动。
9.1 简谐振动9.1.1 简谐振动实例在振动中,最简单最基本的是简谐振动,⼀切复杂的振动都可以看作是由若⼲个简谐振动合成的结果。
在忽略阻⼒的情况下,弹簧振⼦的⼩幅度振动以及单摆的⼩⾓度振动都是简谐振动。
1. 弹簧振⼦质量为m的物体系于⼀端固定的轻弹簧(弹簧的质量相对于物体来说可以忽略不计)的⾃由端,这样的弹簧和物体系统就称为弹簧振⼦。
如将弹簧振⼦⽔平放置,如图9-1所⽰,当弹簧为原长时,物体所受的合⼒为零,处于平衡状态,此时物体所在的位置O就是其平衡位置。
在弹簧的弹性限度内,如果把物体从平衡位置向右拉开后释放,这时由于弹簧被拉长,产⽣了指向平衡位置的弹性⼒,在弹性⼒的作⽤下,物体便向左运动。
当通过平衡位置时,物体所受到的弹性⼒减⼩到零,由于物体的惯性,它将继续向左运动,致使弹簧被压缩。
弹簧因被压缩⽽出现向右的指向平衡位置的弹性⼒,该弹性⼒将阻碍物体向左运动,使物体的运动速度减⼩直到为零。
之后物体⼜将在弹性⼒的作⽤下向右运动。
在忽略⼀切阻⼒的情况下,物体便会以平衡位置O为中⼼,在与O点等距离的两边作往复运动。
图中,取物体的平衡位置O为坐标原点,物体的运动轨迹为x轴,向右为正⽅向。
大学物理 第9章 简谐振动

9.2 简谐振动的规律 9.3 简谐振动的合成
9.1 简谐振动的定义
9.1.1 弹簧振子的振动
9.1.2 简谐振动的定义
9.1.3 单摆的运动规律
9.1.4 LC振荡回路中电容器 上电量的变化规律
振动是与人类生活和科学技术密切相关的一种 基本运动形式。
广义的振动 一物理量在某一定值附近周期性变化的现象称振动。
下面我们重点对合振动的振幅进行讨论
A A1 A2 2 A1 A2 cos( 2 1 )
2 2
t 2 t 1 2 1
讨论:两种特殊情况
(1) 21=2k (k=0,1,2,…) 两分振动同相
A A1 A 2
o
考虑方向 F mg 简谐振动!
mg
0
F ma mg
t 0
l
又 a
l d
2
dv dt
l
d
2
dt
2
T
F
O
dt
2
g
即
d 2 g 0 2 l dt
d (v l ) dt
mg
g l
2 T 2
2
x
A x A y cos t
2 2
(2)相位差 y x ,轨迹方程为
x Ax y Ay 0
x
2 2
y
2 2
2
xy Ax Ay
cos(
Ax
Ay
y
x ) sin (
2
y
大学物理简谐振动知识点及试题带答案

简谐振动一、基本要求1、掌握简谐振动的定义,描述简谐振动的各物理量及其相互关系,会根据定义来判断一各物体的运动是不是简谐振动。
2、掌握简谐振动的旋转矢量表示法。
3、掌握简谐振动的基本特征,能根据一定的初始条件写出简谐振动的运动方程。
4、掌握同方向频率的两个简谐振动的合成,了解相互垂直同频率的简谐振动的合成。
二、主要内容1、简谐振动的表达式(运动方程) cos()x A t ωϕ=+三个特征量:振幅A ,决定与振动的能量;角频率ω,决定于振动系统的固有属性; 初相位ϕ,决定于振动系统初始时刻的状态。
简谐运动可以用旋转矢量来表示。
2、振动的相位:()t ωϕ+两个振动的相差:同相2k ϕπ∆=,反相(21)k ϕπ∆=+3、简谐振动的运动微粉方程:2220d x x dtω+=4、简谐振动的实例弹簧振子:220,2d x k x T dt m π+==单摆小角度振动:220,2d g T dt l θθ+==LC振荡:2210,2d q q T dt LCπ+== 5、简谐振动的能量:222111()222k P dx E E E m kx kA dt =+=+= 6、两个简谐振动的能量(1)同方向同频率的简谐振动的合成合振动是简谐振动,合振动的振幅和初相位由下式决定A =11221122sin sin tan cos cos A A A A ϕϕϕϕϕ+=+(2)相互垂直的两个同频率的简谐振动的合成合运动的轨迹一般为椭圆,其具体形状决定于两个分振动的相差和振幅。
当2k ϕπ∆=或(21)k π+时,合运动的轨迹为直线,这时质点在做简谐振动。
三、习题与解答1、两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为)cos(1ϕω+=t A x 。
某时刻当第一个质点正在平衡位置向负方向运动时,第二个质点正在最大位移处。
则第二个质点的振动方程为:( B )(A ))2cos(2πϕω++=t A x (B ))2cos(2πϕω-+=t A x(C ))23cos(2πϕω-+=t A x (D ))cos(2πϕω++=t A x 2、一物体做简谐振动,振幅为A ,在起始时刻质点的位移为2A-且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为:( D )3、一质点作简谐振动,振动方程)cos(ϕω+=t A x ,当时间 t =T/4 时,质点的速度为:( C )(A ) ϕωsin A - (B) ϕωsin A (C )ϕωcos A - (D )ϕωcos A4、一质点作谐振动,周期为T ,当它由平衡位置向 x 轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的时间为( A )(A )T /6(B )T /12 (C)T /4 (D )T /85、有两个沿x 轴做简谐运动的质点,其频率、振幅皆相同,当第一个质点自平衡位置向负方向运动时,第二个质点在处(A 为振幅)也向负方向运动,则两者的相位差(12ϕϕ-)为:( C )2Ax -=(A )2π (B )32π (C )6π (D )65π6、质量为10×10-3 kg 的小球与轻弹簧组成的系统,按20.1cos(8)3x t ππ=+(SI)的规律做谐振动,求:(1)振动的周期、振幅、初位相及速度与加速度的最大值;(2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等? (3)t 2=5 s 与t 1=1 s 两个时刻的位相差. 解:(1)设谐振动的标准方程为)cos(0φω+=t A x ,则知:3/2,s 412,8,m 1.00πφωππω===∴==T A 又 πω8.0==A v m 1s m -⋅ 51.2=1s m -⋅2.632==A a m ω2s m -⋅(2) N 63.0==ma F mJ 1016.32122-⨯==m mv E J 1058.1212-⨯===E E E k p当p k E E =时,有p E E 2=, 即)21(212122kA kx ⋅= ∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=-=-=∆t t7、一个沿x 轴做简谐振动的弹簧振子,振幅为A ,周期为T ,其振动方程用余弦函数表出.如果t =0时质点的状态分别是:(1)x 0=-A ;(2)过平衡位置向正向运动;(3)过2Ax =处向负向运动; (4)过x =处向正向运动.试求出相应的初位相,并写出振动方程.解:因为 ⎩⎨⎧-==000sin cos ϕωϕA v A x将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有)2cos(1πππϕ+==t T A x)232cos(232πππϕ+==t T A x)32cos(33πππϕ+==t T A x)452cos(454πππϕ+==t T A x8、一质量为10×10-3 kg 的物体做谐振动,振幅为24 cm ,周期为4.0 s ,当t =0时位移为+24 cm.求:(1)t =0.5 s 时,物体所在的位置及此时所受力的大小和方向; (2)由起始位置运动到x =12 cm 处所需的最短时间; (3)在x =12 cm 处物体的总能量. 解:由题已知 s 0.4,m 10242=⨯=-T A ∴ 1s rad 5.02-⋅==ππωT又,0=t 时,0,00=∴+=ϕA x 故振动方程为m )5.0cos(10242t x π-⨯=(1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=-t x πN102.417.0)2(10103232--⨯-=⨯⨯⨯-=-=-=πωxm ma F方向指向坐标原点,即沿x 轴负向. (2)由题知,0=t 时,00=ϕ,t t =时 3,0,20πϕ=<+=t v A x 故且 ∴ s 322/3==∆=ππωϕt (3)由于谐振动中能量守恒,故在任一位置处或任一时刻的系统的总能量均为J101.7)24.0()2(10102121214223222--⨯=⨯⨯⨯===πωA m kA E9、有一轻弹簧,下面悬挂质量为1.0 g 的物体时,伸长为4.9 cm.用这个弹簧和一个质量为8.0 g 的小球构成弹簧振子,将小球由平衡位置向下拉开1.0 cm 后,给予向上的初速度v 0=5.0 cm·s -1,求振动周期和振动表达式. 解:由题知12311m N 2.0109.48.9100.1---⋅=⨯⨯⨯==x g m k 而0=t 时,-12020s m 100.5m,100.1⋅⨯=⨯-=--v x ( 设向上为正)又 s 26.12,51082.03===⨯==-ωπωT m k 即 m102)5100.5()100.1()(22222220---⨯=⨯+⨯=+=∴ωv x A45,15100.1100.5tan 022000πφωϕ==⨯⨯⨯=-=--即x v ∴ m )455cos(1022π+⨯=-t x10、图为两个谐振动的x -t 曲线,试分别写出其谐振动方程.题10图解:由题10图(a),∵0=t 时,s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ 即 1s rad 2-⋅==ππωT故 m )23cos(1.0ππ+=t x a 由题10图(b)∵0=t 时,35,0,2000πϕ=∴>=v A x 01=t 时,35,0,2000πϕ=∴>=v A x又 ππωϕ253511=+⨯=∴ πω65=故 m t x b )3565cos(1.0ππ+=11、有两个同方向、同频率的简谐振动,其合成振动的振幅为0.20 m ,位相与第一振动的位相差为6π,已知第一振动的振幅为0.173 m ,求第二个振动的振幅以及第一、第二两振动的位相差.解:由题意可做出旋转矢量图如下. 由图知01.02/32.0173.02)2.0()173.0(30cos 222122122=⨯⨯⨯-+=︒-+=A A A A A ∴ m 1.02=A 设角θ为O AA 1,则θcos 22122212A A A A A -+=即 01.0173.02)02.0()1.0()173.0(2cos 2222122221=⨯⨯-+=-+=A A A A A θ 即2πθ=,这说明,1A 与2A 间夹角为2π,即二振动的位相差为2π.12、试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅:(1)125cos(3),375cos(3);3x t cm x t cm ππ⎧=+⎪⎪⎨⎪=+⎪⎩(2)125cos(3),345cos(3).3x t cm x t cm ππ⎧=+⎪⎪⎨⎪=+⎪⎩解: (1)∵ ,233712πππϕϕϕ=-=-=∆ ∴合振幅 cm 1021=+=A A A (2)∵ ,334πππϕ=-=∆∴合振幅 0=A13、一质点同时参与两个在同一直线上的简谐振动,振动方程为120.4cos(2),650.3cos(2).6x t m x t m ππ⎧=+⎪⎪⎨⎪=-⎪⎩试分别用旋转矢量法和振动合成法求合振动的振幅和初相,并写出谐振动方程. 解:∵ πππϕ=--=∆)65(6 ∴ m 1.021=-=A A A 合3365cos 3.06cos 4.065sin3.06sin4.0cos cos sin sin tan 22122211=+-⨯=++=ππππϕϕϕϕφA A A A ∴ 6πϕ=其振动方程为m )62cos(1.0π+=t x14、若简谐运动方程为0.10cos(200.25)()x t m ππ=+,求:(1)振幅、频率、角频率、周期和初相;(2)2t s =时的位移、速度和加速度。
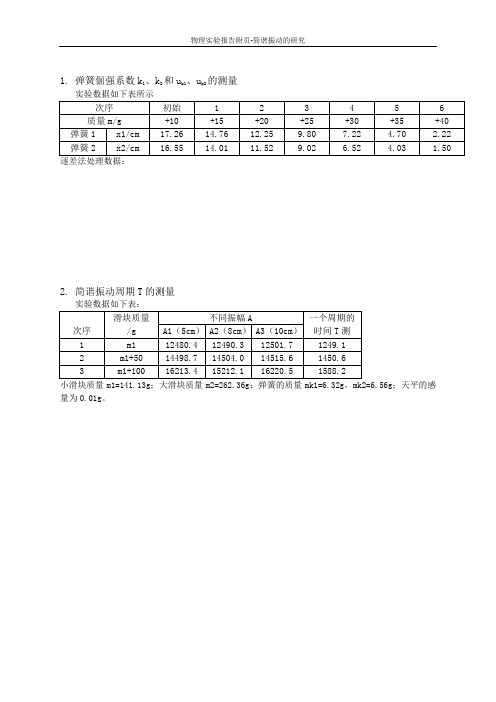
实验报告-大学物理-简谐振动的研究
物理实验报告附页-简谐振Hale Waihona Puke 的研究3. 动量守恒的验证
实验数据记录如下表
次序
1 2 3
m1 碰撞 前速度 v1(单 位) 147.86 153.37 65.60
m1 碰撞 后速度 v1'(单 位) 38.47 33.33 57.19
m2 碰撞 后速度 v2(单 位) 99.17 106.95 67.90
4 +30 7.22 6.52
5 +35 4.70 4.03
6 +40 2.22 1.50
2. 简谐振动周期 T 的测量
实验数据如下表:
不同振幅 A 滑块质量 一个周期的 次序 /g A1(5cm) A2(8cm) A3(10cm) 时间 T 测 1 m1 12480.4 12490.3 12501.7 1249.1 2 m1+50 14498.7 14504.0 14515.6 1450.6 3 m1+100 16213.4 15212.1 16220.5 1588.2 小滑块质量 m1=141.13g;大滑块质量 m2=262.36g;弹簧的质量 mk1=6.32g,mk2=6.56g;天平的感 量为 0.01g。
碰撞前总动 量 P 前(kg* 速度单位) 20.87 21.65 9.26
碰撞后总 动量 P 后 (kg*速度 单位) 20.59 23.36 9.74
其中,碰撞前的动量 P 前 = 碰撞后的动量 P 后=
物理实验报告附页-简谐振动的研究
1. 弹簧倔强系数 k1、k2 和 uk1、uk2 的测量
实验数据如下表所示
次序 质量 m/g 弹簧 1 x1/cm 弹簧 2 x2/cm 逐差法处理数据:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简谐运动
1、简谐振动的运动方程和动力学方程
2、振幅、周期、频率、相位、初相位
3、通过已知条件求物体的振动方程
第八章 简谐运动 一 简谐运动
1 机械振动
物体或物体的某一部分在一定位置 附近来回往复的运动 平衡位置 实例:
心脏的跳动, 钟摆,乐器, 地震等
2 简谐振动 简谐运动 简谐运动 谐振子 最简单、最基本的振动 合成 复杂振动
情况同动能。
机械能
1 2 E E k E p kA 2
简谐振动系统机械能守恒
简谐运动的合成和分解
简谐运动的合成
1. 两个同方向、同频率的简谐运动的合成 某一质点在直线上同时参与两个独立的同频 率的简谐运动,其振动表达式分别表示为:
x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
dv π 2 2 a t 0.5 0.12π cos( π t ) t 0.5 0.103 m s dt t 0.5 3
设在某一时刻 t1, x = - 0.06 m 代入振动方程:
0.06 0.12 cos (π t1 π 3 )
1 cos ( π t1 π 3 ) 2
解:设振动方程
x A cos(t 0 )
t 0, x0 A cos 0 7.5cm
v0 A sin 0 75cm
解得:
A 10.6cm, 0
4
x 10.6 10 2 cos(10t
4
)m
14
例3:通过振动曲线求振动方程
振动方程为: 5 2 x 0.02 cos( t ) m 6 3
简谐运动的旋转矢量表示法
旋转矢量A在 x 轴上 的投影点 M 的运动规律: y
P
x A cos( t )
结论:
A
t 0
0
M
x
投影点M的运动 为简谐振动。
• 旋转矢量的模A:振幅
• 旋转矢量A的角速度: 角频率 • 旋转矢量A与 x 轴的 夹角( t+ ): 相位 • t = 0 时, A与x 轴 的夹角 :初相位。 • 旋转矢量A旋转一周, M点完成一次全振动。
x A cos ( t )
v A sin ( t )
x0 A cos
v0 A sin
x0 A cos
x
2 0
2 2
v0
A sin
2 2
v
2 0 2
A (sin cos ) A
A
2
x0
v0
拍的频率:
从解析式来分析:
x1 A cos(1t )
2 1
2
x2 A cos(2t )
2 1
2
x x1 x2 A cos(1t ) A cos( 2 t ) 2 A cos t cos( t )
当 2 1 2 1
x(m)
解:由振动曲线 可知:
0.02 0.01 0 0.01 0.02
A 0.02m
1
t (s )
t 0时,x0 0.01 0; v0沿x轴负方向,v0 0
2 3
2 由t=1s时,x1=0得, 0 0.02 cos( 1 ) 3 2 3 1 3 2
相位的意义: 表征任意时刻(t)物体振 动状态. 物体经一周期的振动,相位改变 2 .
例1 一轻弹簧一端固定,另一端连一定质量的物体。 整个振动系统位于水平面内。今将物体沿平面向右拉 长到 x0 = 0.04 m 处释放,试求: 简谐振动方程。
解:x0 0.04m
, v0 0
x0
2
, 6.0 rad s
分解
作简谐运动的物体
弹簧振子的振动
l0 k
m
x
A
o
A
x0 F 0
振动的成因: 回复力+惯性
3 弹簧振子的运动分析
F
o
m
x
2
x
F kx ma
2
d x 2 x 得 a 2 x 即 2 dt 简谐运动的特征:加速度 a 与位移的大小x 成正比,方向相反
k 令 m
2
) t cos(
2 1
2
t )
合振动不是简谐振动
当21时, 2 1 2 1 则:x
2 1 ) t 随t 缓变 式中 A( t ) 2 A cos( 2 2 1 cos( t ) cos[( )t ] 随t 快变 2
A A1 A2
A2
2
x2
A
1
x x1 x2
A1
x
x A cos( t )
结论:
x1
x
一个质点参与两个在同一直线上频率相同的 简谐运动,其合成运动仍为简谐运动。
A
A1 A2 2 A1 A2 cos( 2 1)
2 2
A1 sin 1 A2 sin 2 arctan A1 cos 1 A2 cos 2
简谐振动的动能和势能是时间的周期性函数
动 E 1 mv 2 k 2 能
1 2 Ek max kA 2
Ek min 0
1 2 2 kA sin ( t 0 ) 2
势 能
1 2 E p kx 2
1 2 kA cos 2 ( t 0 ) 2
E p max , E p min
某一时刻,谐振子速度为v,位移为x
v A sin( t 0 ) x A cos( t 0 )
1 E k mv 2 2 1 2 kA sin2 ( t 0 ) 2
1 2 E p kx 2
1 2 kA cos 2 ( t 0 ) 2
2
vo tan xo
v A sin(t ) π A cos(t ) 2 2 a A cos( t )
A cos( t π)
2
x A cos(t ) 2π T 取 0
A A
x
π 2π π t1 3 3
4π 或 3
y
2π 3
π 2π π t1 3 3
t1 1s
4π 3
x
π 3π π t2 3 2
11 t2 s 6
11 5 t t 2 t1 1 s 6 6
简谐振动的能量
以弹簧振子为例:
谐振动系统的能量=系统的动能Ek+系统的势能Ep
周期 T
2π
1 频率 T 2π
圆频率
A
x
x t 图
T
T 2
2π 2 π T
o
A
t
周期和频率仅与振动系统本身的 物理性质有关
四 相位 t
x A cos(t )
相 位 初相位
(t) t
t 0时,(t )
时
x 2 A cos
2 1
2
2 1 t cos t 2
二、同方向不同频率简谐振动的合成 分振动 合振动
x1 A cos( 1t ) x2 A cos( 2 t )
x x1 x2
x 2 A cos(
2 1
π 3 π 3
1 π cos 2 3
x
v0 A sin 0
sin 0
振动方程:
π 3
π x 0.12 cos( π t ) 3
dx π 1 v t 0.5 0.12π sin( π t ) t 0.5 0.189 m s dt t 0.5 3
解方程
d2 x 2 x 2 dt 设初始条件为:
简谐运动的微分方程
t 0 时,x x0 ,v=v0
解得 x A cos(t )
简谐运动方程
积分常数,根据初始条件确定
解题方法
由初始条件求解振幅和初相位: 设 t = 0时,振动位移:x = x0
振动速度:v = v0
x A cos ( t ) 2π 1 已知:A =12 cm , T = 2 s , πs T x 0.12 cost
解: 设简谐振动表达式为 初始条件: t = 0 时, x0 = 0.06 m , v0 > 0
0.06 =0.12 cos
y
x0 0.04 m
1
振幅: A
v0
2 2
0
v0 arctan 0 x0
得
x 0.04 cos (6.0t )
例2、一质点沿x轴作简谐振动,其圆频率w = 10 rad/s.试写出以下初始 状态时的振动方程: 其初始位移x0 = 7.5 cm,初始速度v0 = 75.0 cm/s;
合振动可看作振幅缓变的简谐振动
A(t )cos( t )
内容小结:
1、简谐振动的运动方程和动力学方程
d2 x x A cos(t ) 2 x 2 dt 2、振幅、周期、频率、圆频率、相位、 初相位
3、通过已知条件求物体的振动方程
t 0 时,x x0 ,v=v0
y
P
A
t 0
M
x
周期:
T
