ABAQUS中动力有效应力分析方法的实现
Abaqus-中显示动力学分析步骤

Abaqus-中显示动力学分析步骤准静态分析——ABAQUS/Explicit准静态过程(guasi-static process)在过程进行的每一瞬间,系统都接近于平衡状态,以致在任意选取的短时间dt内,状态参量在整个系统的各部分都有确定的值,整个过程可以看成是由一系列极接近平衡的状态所构成,这种过程称为准静态过程。
无限缓慢地压缩和无限缓慢地膨胀过程可近似看作为准静态过程。
准静态过程是一种理想过程,实际上是办不到的。
准静态原为一个热力学概念,在这里引用主要是指模型在加载的过程中任意时刻所经历的中间状态都可近似地视为静力状态,因此当加载过程进行得无限缓慢时,在各个时刻模型所处的状态就可近似地看作是静态,该过程便是准静态过程。
准静态啮合过程仿真主要考虑的是弧齿锥齿轮副在加载时的接触状态,以及齿面和齿根的应力变化规律,其前提是不考虑齿轮副惯性的影响。
ABAQUS/Explicit准静态分析显式求解方法是一种真正的动态求解过程,它的最初发展是为了模拟高速冲击问题,在这类问题的求解中惯性发挥了主导性作用。
当求解动力平衡的状态时,非平衡力以应力波的形式在相邻的单元之间传播。
由于最小稳定时间增量一般地是非常小的值,所以大多少问题需要大量的时间增量步。
在求解准静态问题上,显式求解方法已经证明是有价值的,另外ABAQUS/Explicit在求解某些类型的静态问题方面比ABAQUS/Standard更容易。
在求解复杂的接触问题时,显式过程相对于隐式过程的一个优势是更加容易。
此外,当模型很大时,显式过程比隐式过程需要较少的系统资源。
将显式动态过程应用于准静态问题需要一些特殊的考虑。
根据定义,由于一个静态求解是一个长时间的求解过程,所以在其固有的时间尺度上分析模拟常常在计算上是不切合实际的,它将需要大量的小的时间增量。
因此,为了获得较经济的解答,必须采取一些方式来加速问题的模拟。
但是带来的问题是随着问题的加速,静态平衡的状态卷入了动态平衡的状态,在这里惯性力成为更加起主导作用的力。
abaqus动力学分析

目 录第一章ABAQUS动力学问题概述 (1)§1-1 动力学问题 (1)§1-2 结构动力学研究的内容 (3)§1-3 振动的分类 (4)§1-4 结构动力学的研究方法 (5)§1-5 动力学问题的基本方程 (5)小结 (6)§1-6第2章结构特征值的提取 (7)§2-1 问题的产生 (7)§2-2 特征值的求解方法 (7)§2-3 特征值求解器的比较 (8)§2-4 重复的特征频率 (9)§2-5 征值频率的提取 (9)§2-6 频率输出 (12)§2-7 有预载结构的频率 (16)§2-8 复特征频率和刹车的啸声分析 (17)第3章模态叠加法 (22)§3-1 模态叠加法的基本概念 (22)§3-2 模态叠加法的应用 (24)第4章阻尼 (26)§4-1 引言 (26)§4-2 阻尼 (26)§4-3在ABAQUS中定义阻尼 (27)1§4-4 阻尼选择 (31)第5章稳态动力学分析 (33)§5-1 稳态动力学简介 (33)§5-2 分析方法 (35)§5-3 激励和输出 (36)§5-4 算例—轮胎的谐波激励稳态响应 (42)第6章瞬态动力学分析 (49)§6-1 引言 (49)§6-2 模态瞬态动力学简介 (49)§6-3 分析方法 (54)§6-4 载荷和输出 (55)§6-5 算例—货物吊车 (58)第7章基础运动 (64)§7-1 基础运动形式 (64)§7-2 初级基础运动 (65)§7-3 次级基础运动 (66)§7-4 在ABAQUS中定义基础运动 (66)§7-5 算例 (70)第8章加速度运动的基线校准 (73)§8-1 加速度基线调整和校准简介 (73)§8-2 基线校准方法 (74)§8-3 加速度基线校准步骤 (76)§8-4 考虑基线校准的悬臂梁算例分析 (77)234第1章ABAQUS 动力学问题概述§1-1 动力学问题的产生在现代结构和机械设计中,通常需要考虑两类荷载的作用——静力荷载(static loading)和动力荷载(dynamic loading),因此结构的设计也经常分为静力设计和动力设计两部分。
浅谈Abaqus稳态动力学分析的几种方法
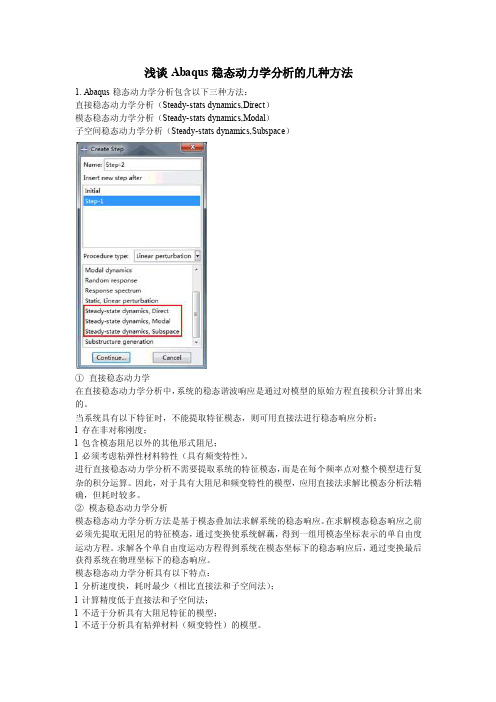
浅谈Abaqus稳态动力学分析的几种方法1. Abaqus稳态动力学分析包含以下三种方法:直接稳态动力学分析(Steady-stats dynamics,Direct)模态稳态动力学分析(Steady-stats dynamics,Modal)子空间稳态动力学分析(Steady-stats dynamics,Subspace)①直接稳态动力学在直接稳态动力学分析中,系统的稳态谐波响应是通过对模型的原始方程直接积分计算出来的。
当系统具有以下特征时,不能提取特征模态,则可用直接法进行稳态响应分析:l 存在非对称刚度;l 包含模态阻尼以外的其他形式阻尼;l 必须考虑粘弹性材料特性(具有频变特性)。
进行直接稳态动力学分析不需要提取系统的特征模态,而是在每个频率点对整个模型进行复杂的积分运算。
因此,对于具有大阻尼和频变特性的模型,应用直接法求解比模态分析法精确,但耗时较多。
②模态稳态动力学分析模态稳态动力学分析方法是基于模态叠加法求解系统的稳态响应。
在求解模态稳态响应之前必须先提取无阻尼的特征模态,通过变换使系统解藕,得到一组用模态坐标表示的单自由度运动方程。
求解各个单自由度运动方程得到系统在模态坐标下的稳态响应后,通过变换最后获得系统在物理坐标下的稳态响应。
模态稳态动力学分析具有以下特点:l 分析速度快,耗时最少(相比直接法和子空间法);l 计算精度低于直接法和子空间法;l 不适于分析具有大阻尼特征的模型;l 不适于分析具有粘弹材料(频变特性)的模型。
另外需要注意,使用基于模态的分析方法时,用户必须确定需要保留的特征模态,以确保用这些模态能够精确描述系统的动力学特征。
③子空间稳态动力学分析与模态动力学分析不同,子空间稳态动力学分析是将运动方程投影到一组特征模态上再进行求解。
子空间稳态动力学分析的基本思想是:首先提取无阻尼、对称系统的特征模态,并选取适当的特征向量组成特征模态子空间,然后将稳态动力学方程组投影到特征模态子空间上,通过直接法求解子空间下的稳态动力学方程。
abaqus接触动力学分析

部件模态综合法随着科学和生产的发展,特别是航空、航天事业的发展,越来越多的大型复杂结构被采用,这使得建模和求解都比较困难。
一方面,一个复杂结构势必引入较多的自由度,形成高维的动力学方程,使一般的计算机在内存和求解速度方面都难以胜任,更何况一般的工程问题主要关心的是较低阶的模态。
仅为了获取少数的几个模态,必须为求解高维方程付出巨大的代价也是不合适的。
另一方面,正是由于结构的庞大和复杂,一个完整的结构往往不是在同一地区生产完成的,可能一个结构的各个主要零部件不得不由不同的地区、不同的厂家生产。
而且由于试验条件的限制只能进行部件的模态实验,而无法对整体结构进行模态实验。
针对这些主要的问题,为了获得大型、复杂结构的整体模态参数,于是发展了部件模态综合法。
部件模态综合法又叫子结构耦合法。
它的基本思想是按工程观点或结构的几何轮廓,并遵循某些原则要求,把完整的结构进行人为抽象肢解成若干个子结构(或部件);首先对子结构(或部件)进行模态分析,然后经由各种方案,把它们的主要模态信息(常为低阶主模态信息)予以保留,并借以综合完整结构的主要模态特征。
它的主要有点是,可以通过求解若干小尺寸结构的特征问题来代替直接求解大型特征值问题。
同时对各个子结构可分别使用各种适宜的数学模型和计算程序,也可以借助试验的方法来获得他们的主要模态信息。
对于自由振动方程在数学上讲就是固有(特征)值方程。
特征值方程的解不仅给出了特征值,即结构的自振频率和特征矢量——振兴或模态,而且还能使结构在动力载荷作用下的运动方程解耦,即所谓的振型分解法或叫振型叠加法。
因此,特征值问题的求解技术,对于解决结构振动问题来说吧,是非常重要的。
考虑阻尼的振型叠加法振型叠加法的定义:将结构各阶振型作为广义坐标系,求出对应于各阶振动的结构内力和位移,经叠加后确定结构总响应的方法。
振型叠加法的使用条件:∙(1)系统应该是线性的:线性材料特性,无接触条件,无非线性几何效应。
ABAQUS热应力分析实例详解[整理]
![ABAQUS热应力分析实例详解[整理]](https://img.taocdn.com/s3/m/6d04c637182e453610661ed9ad51f01dc2815769.png)
学习要点通过实例分析,学习如何进行热应力分析,并掌握ABAQUS/CAE 的以下功能:1)在Material 功能模块中,定义线胀系数;2)在Load 功能模块中,使用预定义场(predefined field)来定义温度场;定义材料属性——Property Property——Material——Edit——steelMechanical——Elastic, 输入弹性模量和泊松比定义材料属性——Property Property——Material——Edit——steelMechanical——Expansion, 输入线胀系数定义边界条件——Load定义边界条件——Load定义边界条件——Load固支边界条件使用预定义场定义初始温度Load——PredefinedField Manager使用预定义场使模型温度升高至120℃网格划分——Mesh结果分析——Visualization小结在ABAQUS中进行热应力分析的基本步骤:⏹定义线胀系数⏹定义初始温度场⏹定义分析步中的温度场实例2:法兰盘感应淬火的残余应力场模拟问题描述:◆表面感应淬火是一种工程中常用的热处理工艺,其原理是使用感应器来对工件的局部进行加热,然后迅速冷却,从而使工件表面产生残余压应力,抵消工作载荷所产生的一部分拉应力。
◆表面感应淬火可显著提高工件弯曲疲劳抗力和扭转疲劳抗力,工件表面产生的马氏体具有良好的耐磨性。
实例2:法兰盘感应淬火的残余应力场模拟 本例中的法兰盘经淬火后,由试验测得法拉盘的内圆角表面残余压应力约为-420MPa。
法拉盘的一端固定,另一端的整个端面受向下的面载荷p=100MPa,法拉盘内孔直径为24mm,材料的弹性模量为210000MPa,泊松比为0.3,线胀系数为1.35e-5/ ℃。
要求:模拟分析感应淬火所产生的残余应力场,并分析此残余应力场在缓和应力集中方面所起的作用。
建模要点说明☐使用ABAQUS可以模拟感应淬火的完整过程,即通过分析工件与感应器之间以及工件和冷却液之间的传热过程来确定工件的温度场,从而得到相应的塑性应变场和冷却后的残余应力场。
ABAQUS动力分析

ABAQUS动力分析1. 简介ABAQUS是由达索系统有限公司(Dassault Systemes SA)开发和销售的一款用于有限元分析(FEA)的商业软件。
它提供了完整的解决方案,包括建模、求解和后处理功能,广泛应用于工程和科学领域。
动力分析是ABAQUS中的一个重要应用领域,它用于研究结构或材料在受到外部载荷作用下的动态响应。
ABAQUS动力分析可以帮助工程师预测和评估结构的动态行为,以及优化设计,提高结构的可靠性和性能。
2. 动力分析的基本原理动力分析的基本原理是通过求解结构或材料的运动方程来研究动态响应。
在ABAQUS中,动力分析是基于有限元方法的,它将结构的连续域离散化为有限数量的子域,然后通过求解离散化系统的运动方程得到结构的运动情况。
动力分析的过程可以简要概括为以下几个步骤:2.1 建立几何模型在进行动力分析之前,需要准备好结构的几何模型。
ABAQUS提供了丰富的建模工具和操作,可帮助用户创建复杂的几何模型。
2.2 定义材料特性在进行动力分析之前,需要定义结构中所用材料的特性。
ABAQUS支持多种材料模型,如线性弹性模型、非线性弹性模型和塑性模型等。
用户可以根据实际需求选择适当的材料模型,并设置材料的参数。
2.3 网格生成在进行动力分析之前,需要将结构的几何模型离散化为有限元网格。
ABAQUS 提供了强大的网格生成工具,可以根据用户的需求自动生成合适的网格。
2.4 定义边界条件和加载在进行动力分析之前,需要定义结构的边界条件和加载。
边界条件包括约束条件和初始条件,加载包括外部载荷和初始速度等。
ABAQUS提供了灵活的边界条件和加载设置,用户可以根据需求自定义。
2.5 求解动力分析问题在完成前面的准备工作后,就可以使用ABAQUS进行动力分析了。
ABAQUS使用显式或隐式求解器来求解动力分析问题。
显式求解器适用于短时间内的动力响应,而隐式求解器适用于长时间内的动力响应。
2.6 后处理结果在求解动力分析问题后,还需要对结果进行后处理。
abaqus中的有效应力和总应力

abaqus中的有效应力和总应力在Abaqus中,有效应力(Equivalent Stress)和总应力(Total Stress)是两个非常重要的概念。
有效应力是指在材料内部的应力状态,它是根据von Mises屈服准则计算得出的一个标量。
有效应力表示了材料的应力状态,能够更好地预测材料的破坏行为。
在Abaqus中,有效应力可以通过后处理模块进行计算和输出。
总应力是指在材料中所有应力分量的总和。
总应力包括正应力和剪应力。
在Abaqus中,总应力可以通过Abaqus分析的结果输出进行计算和查看。
需要注意的是,在一些情况下,有效应力和总应力可能是相等的,比如在没有外力加载的情况下,或者在完全塑性的情况下。
但在大多数情况下,材料中的有效应力和总应力是有区别的,并且有效应力比总应力更能够反映材料的应力状态。
abaqus动力边界地应力平衡

abaqus动力边界地应力平衡1. 介绍在工程结构分析中,地应力是一个重要的影响因素,特别是对于地下工程和岩土工程来说。
abaqus是一款常用的有限元分析软件,可以用于分析各种工程结构的热、力学和动力学问题。
在abaqus中,通过设置动力边界条件来模拟地应力的作用,保证结构在地应力的作用下可以达到平衡状态。
2. 地应力的作用地应力是指在地下岩土中由地球自身重力和地球内部物质的重力所产生的应力。
它对地下工程结构的稳定性、变形和破坏具有重要的影响。
在地下工程中,结构体受到地应力的约束,必须在地应力的作用下达到平衡状态,因此需要进行地应力平衡的分析。
3. abaqus中动力边界条件的设置在abaqus中,可以通过设置动力边界条件来模拟地应力的作用。
首先需要建立模型,并对模型进行网格划分。
然后可以通过创建荷载来模拟地应力的作用,通常使用压力荷载来表示地应力的作用。
在abaqus中,可以选择不同的压力类型,比如静态压力、动态压力或者地震荷载等,根据实际情况选择合适的压力类型。
在设置动力边界条件时,需要考虑地应力的方向和大小,以及结构的几何形状和材料特性等因素。
4. 地应力平衡的分析方法在abaqus中,可以通过施加地应力荷载和设置动力边界条件来进行地应力平衡的分析。
首先需要对结构进行静力分析,确定结构的初始受力状态。
然后根据地应力的方向和大小,在结构表面施加相应的地应力荷载。
接着设置动力边界条件,对结构进行动力分析,通过迭代计算使结构达到地应力平衡状态。
最终得到结构在地应力作用下的平衡位移和应力分布情况。
5. 地应力平衡分析的应用地应力平衡分析在地下工程和岩土工程中具有广泛的应用。
比如在隧道、地铁、水坝、地下管道等工程中,地应力的影响必须得到合理的分析和处理。
通过使用abaqus软件进行地应力平衡分析,可以更准确地预测结构的受力状态,提高工程设计的安全性和可靠性。
6. 结论abaqus是一款强大的有限元分析软件,可以用于地应力平衡分析。
abaqus中应力和等效应力的区别

abaqus是一款常用的有限元分析软件,它可以用于求解复杂的结构力学问题。
在abaqus中,应力和等效应力是两个重要的概念,它们在工程分析中起着非常重要的作用。
本文将介绍abaqus中应力和等效应力的区别,帮助读者更好地理解这两个概念。
1. 应力的定义在力学中,应力是描述单位面积上的力的概念。
在abaqus中,应力通常用一个3x3的矩阵来表示,这个矩阵称为应力张量。
应力张量的各个分量代表了不同方向上的应力值,包括正向拉伸应力、剪切应力等。
在有限元分析中,可以通过求解力学方程或直接读取计算结果来获得每个节点的应力值。
2. 等效应力的定义等效应力是一种将多个方向上的应力值综合为一个单一值的概念。
在实际工程中,由于工程材料的强度通常是以单一值来标定的,因此需要将多个方向上的应力值合并为一个单一值,这个单一值即为等效应力。
在abaqus中,等效应力通常使用von Mises应力来表示,它是一种将拉伸应力和剪切应力综合考虑的等效应力定义方式。
3. 区别与通联应力和等效应力是两个不同的概念,但它们之间有着密切的通联。
应力是描述力的作用效果的物理量,而等效应力则是将多个方向上的应力综合为一个单一值的结果。
在工程分析中,我们通常关注的是材料的强度,因此更关心等效应力的大小,以确定结构是否会发生破坏。
而应力值则更多地用于分析结构的受力情况和变形情况。
4. 在abaqus中的应用在abaqus中,通常会通过计算得到每个节点的应力值,然后可以根据这些应力值计算出每个节点的等效应力。
等效应力的分布图常常被用来判断结构的稳定性和破坏情况,从而指导工程设计和材料选取。
也可以通过对应力值和等效应力的分析来优化结构设计,以提高结构的安全性和性能。
abaqus中的应力和等效应力是两个在工程分析中非常重要的概念。
它们分别描述了材料的受力情况和强度情况,对于工程设计和分析具有重要的指导意义。
通过对应力和等效应力的分析,可以更好地理解结构的受力情况,帮助工程师进行合理优化设计。
ABAQUS应力与应变

ABAQUS应力与应变简介ABAQUS是一种有限元分析软件,可以用来进行复杂结构的力学分析,包括应力分析和应变分析。
本文将介绍如何在ABAQUS中进行应力和应变分析。
应力分析ABAQUS中应力分析可以在几何结构的基础上,给定材料特性、载荷和边界条件,计算出结构中的应力分布。
下面是ABAQUS中进行应力分析的步骤:创建几何模型在ABAQUS中,几何模型可以通过使用ABAQUS/CAE创建。
ABAQUS/CAE是可视化的用户界面,包括几何建模、前置处理、后置处理、分析、结果查看等功能。
定义材料和热力学特性结构分析中,物理特性是非常重要的参数。
ABAQUS中定义材料特性和热力学特性的方式有很多种,如使用材料库、用户定义材料参数等。
定义载荷和边界条件在ABAQUS中,载荷是指施加在结构上的外力或力矩。
边界条件是指结构自身的约束情况。
这些都是透过使用约束和载荷来完成的。
各种载荷和边界条件的定义,在ABAQUS中都是很灵活的。
进行建模建模部分是ABAQUS应力分析中的核心。
各种建模方法都可以在ABAQUS中实现,包括曲面细分、自由形变、等效拉伸和均匀图元等。
运行ABAQUS求解器和查看结果完成建模之后,就可以进行ABAQUS求解器的运行等操作。
求解器的运行时间取决于模型的大小、复杂程度以及计算机性能等因素。
运行完毕后,可以通过后置处理程序查看模型的应力分布和其他结果。
应变分析ABAQUS中的应变分析可以计算出材料中产生的应变分布。
下面是ABAQUS中进行应变分析的步骤:定义几何特征和材料特性和应力分析一样,应变分析也需要进行几何特征和材料特性的定义。
建立加载模型建立一个正确的加载模型非常重要。
ABAQUS中可以通过使用动力学模拟或者静力学模拟等方式来实现。
定义弯曲、拉伸和切削等载荷对材料进行弯曲、拉伸和切削等,是通过制定载荷来完成的。
运行ABAQUS求解器和查看结果完成建模之后,就可以运行ABAQUS求解器。
abaqus动力学分析

目 录第一章ABAQUS动力学问题概述 (1)§1-1 动力学问题 (1)§1-2 结构动力学研究的内容 (3)§1-3 振动的分类 (4)§1-4 结构动力学的研究方法 (5)§1-5 动力学问题的基本方程 (5)小结 (6)§1-6第2章结构特征值的提取 (7)§2-1 问题的产生 (7)§2-2 特征值的求解方法 (7)§2-3 特征值求解器的比较 (8)§2-4 重复的特征频率 (9)§2-5 征值频率的提取 (9)§2-6 频率输出 (12)§2-7 有预载结构的频率 (16)§2-8 复特征频率和刹车的啸声分析 (17)第3章模态叠加法 (22)§3-1 模态叠加法的基本概念 (22)§3-2 模态叠加法的应用 (24)第4章阻尼 (26)§4-1 引言 (26)§4-2 阻尼 (26)§4-3在ABAQUS中定义阻尼 (27)1§4-4 阻尼选择 (31)第5章稳态动力学分析 (33)§5-1 稳态动力学简介 (33)§5-2 分析方法 (35)§5-3 激励和输出 (36)§5-4 算例—轮胎的谐波激励稳态响应 (42)第6章瞬态动力学分析 (49)§6-1 引言 (49)§6-2 模态瞬态动力学简介 (49)§6-3 分析方法 (54)§6-4 载荷和输出 (55)§6-5 算例—货物吊车 (58)第7章基础运动 (64)§7-1 基础运动形式 (64)§7-2 初级基础运动 (65)§7-3 次级基础运动 (66)§7-4 在ABAQUS中定义基础运动 (66)§7-5 算例 (70)第8章加速度运动的基线校准 (73)§8-1 加速度基线调整和校准简介 (73)§8-2 基线校准方法 (74)§8-3 加速度基线校准步骤 (76)§8-4 考虑基线校准的悬臂梁算例分析 (77)234第1章ABAQUS 动力学问题概述§1-1 动力学问题的产生在现代结构和机械设计中,通常需要考虑两类荷载的作用——静力荷载(static loading)和动力荷载(dynamic loading),因此结构的设计也经常分为静力设计和动力设计两部分。
Abaqus 中显现动力学分析步骤

准静态分析——ABAQUS/Explicit准静态过程(guasi-static process)在过程进行的每一瞬间,系统都接近于平衡状态,以致在任意选取的短时间dt内,状态参量在整个系统的各部分都有确定的值,整个过程可以看成是由一系列极接近平衡的状态所构成,这种过程称为准静态过程。
无限缓慢地压缩和无限缓慢地膨胀过程可近似看作为准静态过程。
准静态过程是一种理想过程,实际上是办不到的。
准静态原为一个热力学概念,在这里引用主要是指模型在加载的过程中任意时刻所经历的中间状态都可近似地视为静力状态,因此当加载过程进行得无限缓慢时,在各个时刻模型所处的状态就可近似地看作是静态,该过程便是准静态过程。
准静态啮合过程仿真主要考虑的是弧齿锥齿轮副在加载时的接触状态,以及齿面和齿根的应力变化规律,其前提是不考虑齿轮副惯性的影响。
ABAQUS/Explicit准静态分析显式求解方法是一种真正的动态求解过程,它的最初发展是为了模拟高速冲击问题,在这类问题的求解中惯性发挥了主导性作用。
当求解动力平衡的状态时,非平衡力以应力波的形式在相邻的单元之间传播。
由于最小稳定时间增量一般地是非常小的值,所以大多少问题需要大量的时间增量步。
在求解准静态问题上,显式求解方法已经证明是有价值的,另外ABAQUS/Explicit在求解某些类型的静态问题方面比ABAQUS/Standard更容易。
在求解复杂的接触问题时,显式过程相对于隐式过程的一个优势是更加容易。
此外,当模型很大时,显式过程比隐式过程需要较少的系统资源。
将显式动态过程应用于准静态问题需要一些特殊的考虑。
根据定义,由于一个静态求解是一个长时间的求解过程,所以在其固有的时间尺度上分析模拟常常在计算上是不切合实际的,它将需要大量的小的时间增量。
因此,为了获得较经济的解答,必须采取一些方式来加速问题的模拟。
但是带来的问题是随着问题的加速,静态平衡的状态卷入了动态平衡的状态,在这里惯性力成为更加起主导作用的力。
abaqus中简支梁利用平面应力法

abaqus中简支梁利用平面应力法【Abaqus中简支梁利用平面应力法】1. 引言简支梁是结构力学中最基本的结构形式之一。
为了研究简支梁在不同工况下的力学性能,ABAQUS是一种常用的有限元分析软件,可以模拟不同的边界条件和荷载情况。
本文将详细介绍如何使用ABAQUS中的平面应力法来分析简支梁的应力和变形。
2. 简支梁的基本概念与力学模型简支梁是一种在两端支承的梁,其边界条件为端点的弯矩和剪力均为零。
可以将简支梁建模为一个二维平面结构,假设材料为线弹性材料,具有均匀的横截面积、弹性模量和泊松比。
3. ABAQUS建模步骤a) 创建新模型:在ABAQUS中新建一个模型,选择平面应力作为分析类型,并设置合适的尺寸和材料属性。
b) 定义几何形状:使用节点、线和面等几何实体定义梁的几何形状。
可以通过绘制节点和连接线来创建梁的模型。
c) 设置材料属性:定义材料的弹性模量和泊松比等材料属性。
根据实际情况选择合适的材料模型。
d) 定义边界条件:设置梁的边界条件,包括约束和加载。
对于简支梁,需要定义两端的约束条件,使其在端点无法旋转和平移。
e) 定义荷载:定义梁上施加的荷载,可以是集中力、均布荷载或者边界条件,根据具体问题进行选择。
f) 设置分析类型:选择平面应力分析类型,设置合适的分析选项和求解器设置。
g) 进行分析:运行ABAQUS求解器对模型进行分析,得到应力和变形结果。
4. 分析结果的后处理a) 结果显示:根据分析的要求,选择合适的结果显示方式,例如应力云图、剪力图或位移图等。
通过这些图形可以直观地了解梁的应力和变形情况。
b) 结果提取:在关注的位置提取应力和变形数据,例如节点处的最大应力或变形。
这些数据可以用于后续的结构评估和设计。
c) 结果对比:根据分析结果,可以对不同的边界条件和荷载进行对比,评估不同工况下梁的性能差异。
5. 结论通过使用ABAQUS中的平面应力法,可以对简支梁的应力和变形进行准确的分析。
基于ABAQUS的热应力分析

基于ABAQUS的热应力分析热应力分析是一种用于研究物体在温度变化下产生的应力变化的方法。
在工程设计中,热应力分析可以用于评估零件或结构在温度变化下的稳定性和可靠性。
ABAQUS是一种常用的有限元分析软件,可以用于进行热应力分析。
在ABAQUS中进行热应力分析的基本步骤如下:1.定义几何模型:首先需要根据实际情况创建一个几何模型。
可以通过ABAQUS中的几何建模工具创建几何体,也可以导入已有的CAD模型。
2.定义材料特性:接下来需要定义材料的热物性参数。
ABAQUS提供了多种材料模型,可以根据实际情况选择合适的模型。
在热应力分析中,需要定义材料的热导率和热膨胀系数等参数。
3.定义温度加载:在热应力分析中,温度加载是一个非常重要的因素。
可以通过定义恒定温度、温度梯度或温度函数等方式对模型进行加热或冷却。
ABAQUS提供了丰富的温度加载选项,可以根据具体需求进行配置。
4.定义边界条件:根据实际情况,在模型中定义边界条件。
这些边界条件可以包括约束条件、固定支撑点和力加载等。
在热应力分析中,边界条件可以用于约束模型的自由度,以及模拟外部力的作用。
5.网格划分:在进行有限元分析之前,需要对几何模型进行网格划分。
网格划分的精度和质量将直接影响到分析结果的准确性。
ABAQUS提供了多种网格划分工具,可以根据具体需求选择合适的方法。
6.定义分析步:根据实际情况,定义热应力分析的时间步长和总时长。
ABAQUS提供了多种分析步选项,可以根据具体需求进行配置。
在热应力分析中,需要考虑热传导和热膨胀的时间尺度。
7.运行分析:完成模型设置后,可以运行热应力分析。
ABAQUS将根据设定的边界条件、材料特性和加载条件对模型进行求解,得到温度分布和应力分布等结果。
8.结果分析:分析完成后,可以使用ABAQUS提供的后处理工具对结果进行可视化和分析。
可以绘制温度云图、应力云图、应变云图等等,以便更好地理解模型的行为。
总结:通过上述步骤,可以使用ABAQUS进行热应力分析。
abaqus应力释放模拟方法

abaqus应力释放模拟方法
在Abaqus中进行应力释放模拟,可以按照以下步骤进行:
1. 导入几何模型:使用Abaqus的几何建模工具或从其他CAD
软件中导入几何模型。
2. 设置材料属性:选择合适的材料模型,输入材料的弹性模量、泊松比等相关参数。
3. 定义约束条件:设置边界条件,包括固定边界条件和荷载边界条件。
4. 创建加载步:确定加载步的类型,如静态加载、动态加载等,并设置加载步的参数。
5. 设置应力释放区域:选择需要进行应力释放的区域,可以使用局部坐标系或全局坐标系进行定义。
6. 定义应力释放方法:选择适当的释放方法,如固定应力释放或固定位移释放,并输入相应的释放参数。
7. 运行模拟:运行模拟并等待计算结果。
8. 分析结果:分析模拟结果,根据需要进行后续处理和分析。
需要注意的是,在进行应力释放模拟时,应根据实际情况合理选择模型和参数,并进行验证和验证。
abaqus 节点应力 单元应力

Abaqus节点应力和单元应力分析在工程和科学领域中,节点应力和单元应力分析是非常重要的任务,它们可以帮助我们了解材料的行为和结构的稳定性。
Abaqus是一种常用的有限元分析软件,可以用于进行节点应力和单元应力分析。
节点应力分析节点应力是指在有限元模型中每个节点处的应力值。
通过节点应力分析,我们可以确定结构中各个位置的最大、最小以及平均应力值,并且可以对结构进行强度评估。
Abaqus使用有限元方法来计算节点应力。
有限元方法将结构离散化为许多小型单元,然后通过求解线性方程组来估计每个节点处的位移和变形。
根据位移和变形信息,可以计算出每个节点处的应力。
要进行节点应力分析,在Abaqus中需要完成以下步骤:1.创建几何模型:使用Abaqus提供的几何建模工具来创建你想要分析的结构模型。
2.定义材料属性:根据所选材料的特性,在Abaqus中定义材料属性。
这些属性包括弹性模量、泊松比等。
3.设置边界条件:定义结构上的边界条件,例如固定支撑、施加的力或位移等。
4.网格划分:将结构离散化为小型单元,并生成网格。
可以根据需要调整网格密度。
5.定义分析步骤:通过定义加载步骤和分析类型来设置节点应力分析。
6.运行分析:在Abaqus中运行节点应力分析,并获得每个节点处的应力结果。
单元应力分析单元应力是指在有限元模型中每个单元内部的应力值。
通过单元应力分析,我们可以了解结构中不同单元的受力情况,从而评估结构的稳定性和强度。
Abaqus使用有限元方法计算单元应力。
在有限元模型中,结构被划分为许多小型单元,每个单元都有自己的材料属性和几何特性。
通过求解线性方程组,可以得到每个单元内部的位移和变形信息,并根据这些信息计算出每个单元内部的应力。
要进行单元应力分析,在Abaqus中需要完成以下步骤:1.创建几何模型:使用Abaqus提供的几何建模工具来创建你想要分析的结构模型。
2.定义材料属性:根据所选材料的特性,在Abaqus中定义材料属性。
ABAQUS热应力分析实例详解

ABAQUS热应力分析实例详解热应力分析是指在材料受到热载荷的作用下,由于温度和热应力的非均匀分布而产生的应力状态。
ABAQUS是一种常用的有限元分析软件,可以用于进行热应力分析。
下面将以一个实例来详细介绍ABAQUS热应力分析的流程和步骤。
假设我们有一个具有热源的方形材料板,需要分析其热应力分布情况。
首先,我们需要确定仿真模型的几何尺寸和材料属性。
假设板材的尺寸为10cm x 10cm,材料为铝,具有线膨胀系数α=23.1×10^-6/°C和热导率λ=237W/m·K。
1. 创建模型:打开ABAQUS软件,创建一个新模型,并在模型中创建一个二维平面应变比例等效热应力分析。
选择“3D”模型,然后在“Parts”面板中点击右键,选择“Create”->“Part”,设置尺寸为10cm x 10cm。
2. 材料属性定义:在“Model”面板中选择“Materials”->“Create”->“Isotropic”来定义材料的力学性能。
输入铝的杨氏模量E=71 GPa和泊松比ν=0.333. 模型网格划分:在“Model”面板中选择“Mesh”->“Create”->“Part”,选择要进行网格划分的实体和面,然后定义网格大小。
可以根据需要设置不同大小的网格。
4. 网格单元类型选择:在“Mesh”面板中选择网格划分的网格单元类型。
可以选择线性三角形元、线性四边形元或其他类型的单元。
5. 温度加载:在“Model”面板中选择“Loads”->“Create”->“Temperature”来定义温度加载。
选择加载的表面或体实体,并设置温度大小和类型(恒定温度或温度曲线)。
6. 边界条件定义:在“Model”面板中选择“Bounadry Conditions”->“Create”->“Encastre”来定义边界条件。
选择边界条件所在的边或节点,并设置边界条件类型(固支、自由度约束等)。
abaqus中显示动力学分析步骤

准静态分析——ABAQUS/Explicit准静态过程(guasi-static process )在过程进行的每一瞬间,系统都接近于平衡状态,以致在任意选取的短时间dt 内,状态参量在整个系统的各部分都有确定的值,整个过程可以看成是由一系列极接近平衡的状态所构成,这种过程称为准静态过程。
无限缓慢地压缩和无限缓慢地膨胀过程可近似看作为准静态过程。
准静态过程是一种理想过程,实际上是办不到的。
准静态原为一个热力学概念,在这里引用主要是指模型在加载的过程中任意时刻所经历的中间状态都可近似地视为静力状态,因此当加载过程进行得无限缓慢时,在各个时刻模型所处的状态就可近似地看作是静态,该过程便是准静态过程。
准静态啮合过程仿真主要考虑的是弧齿锥齿轮副在加载时的接触状态,以及齿面和齿根的应力变化规律,其前提是不考虑齿轮副惯性的影响。
ABAQUS/Explicit 准静态分析显式求解方法是一种真正的动态求解过程,它的最初发展是为了模拟高速冲击问题在这类问题的求解中惯性发挥了主导性作用。
当求解动力平衡的状态时,非平衡力以应力波的形式在相邻的单元之间传播。
由于最小稳定时间增量一般地是非常小的值,所以大多少问题需要大量的时间增量步。
在求解准静态问题上,显式求解方法已经证明是有价值的,另外ABAQUS/Explicit求解某些类型的静态问题方面比ABAQUS/Standard更容易。
在求解复杂的接触问题时,显式过程相对于隐式过程的一个优势是更加容易。
此外,当模型很大时,显式过程比隐式过程需要较少的系统资源。
将显式动态过程应用于准静态问题需要一些特殊的考虑。
根据定义,由于一个静态求解是一个长时间的求解过程,所以在其固有的时间尺度上分析模拟常常在计算上是不切合实际的,它将需要大量的小的时间增量。
因此,为了获得较经济的解答,必须采取一些方式来加速问题的模拟。
但是带来的问题是随着问题的加速,静态平衡的状态卷入了动态平衡的状态,在这里惯性力成为更加起主导作用的力。
ABAQUS中动力有效应力分析方法的实现

动力有效应力本构模型介绍
• 砂土材料模量与有效固结应力的关系
Gmax
σ v' 0 =KP(
1 a
Pa
)n
G0,sec
' G0,max = 6920 K 2 (σ m )0.5
σ v' 0 − u n = G0,max ( ) ' σ v0
每一次荷载循环内:G = G0,secγ [1 − H (γ )]
动力有效应力本构模型介绍读入模型参数判断使用静力或动力模块计算进入静力计算进入动力计算计算oct0sec采用滞回曲线公式计算g计算应力并获取判断是否卸载计算各应力分量判断内外力是否平衡结束yes初始加载更新octc判断动力加载阶段采用初始加载曲线公式计算g获取清零计算u及u计算体变增量及回弹模量yesyes判断终止条件是否满足孔压计算终止yes程序计算流程分析方法验证模型分析方法验证模型有限元验证模型分析方法流程及验证计算结果分析计算结果分析0102030405060708091015202530深度4m深度8m01020304050607080910152025300075g正弦波作用下深度4m位置孔压比时程曲线martinfinn模型byrne简化模型0102030405060708091015202530byrne简化模型martinfinn模型03gnj03波下深度5m位置孔压比时程曲线101520253035401015202530深度5m深度10m0075g正弦波作用下土体模量软化曲线分析方法流程及验证321004002002004v0023kpa10755257510050050100150200250v010kpa正弦波作用下土单元滞回曲线图计算结果分析计算结果分析分析方法流程及验证1
2011.10 ABAQUS中动力有效应力分析方法 ABAQUS中动力有效应力分析方法 的实现
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• Byrne利用相同的实验资料,提出以下简化公式
∆ε v ,d
γa
ε v,d =C1 exp C2 () γa
(7)
模型特点: 1.以动剪应变幅值为指标的应变模型 2.振动孔压计算既考虑加载历史的影响,又与当前时刻荷载作用直接相关 3.对于非等幅荷载具有良好的适用性
有效应力方法与总应力方法的比较
NJ10波下场地位移矢量
NJ10波下场地位移矢量图(有效应力算法)
有效应力方法与总应力方法的比较
地面竖向位移比较
△U=0.021m
地面竖向位 位移/m
△U=0.016m
有效应力方法与总应力方法的比较
侧墙剪应力时程比较
1.2 1
剪应力/M Mpa
0.8 0.6 总应力算法 0.4 有效应力算法 0.2 0 0 5 10 15 20 25 30
程序计算流程
分析方法流程及验证
分析方法验证模型 • 有限元验证模型
分析方法流程及验证
计算结果分析
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 5 10 15 20
G0,sec/MPa u/σ´v0 vc
u/σ´v0 v
深度4m 深度8m
25
30
t/s
0.075g正弦波作用下孔压比时程曲线
∆ε v , f = 0
– 假定饱和砂土的回弹模量为Er ,则有
∆ε v ,d = −∆ε v ,r
(2)
∆ε v ,r
∆σ ∆u = =− Er Er
(3) (4)
∆u = Er ∆ε v ,d
动力有效应力本构模型介绍
Martin和Finn的振动孔隙水压力模型及Byrne的相关简化模型 Martin和Finn的振动孔隙水压力模型及Byrne的相关简化模型 的振动孔隙水压力模型及Byrne
动力有效应力本构模型介绍
• 砂土材料模量与有效固结应力的关系
Gmax
σ v' 0 =KP(
1 a
Pa
)n
G0,sec
' G0,max = 6920 K 2 (σ m )0.5
σ v' 0 − u n = G0,max ( ) ' σ v0
每一次荷载循环内:G = G0,secγ [1 − H (γ )]
2011.10 ABAQUS中动力有效应力分析方法 ABAQUS中动力有效应力分析方法 的实现
龙慧
南京工业大学交通学院
汇报提纲
• 动力有效应力分析方法及采用本构模型介绍 • 分析方法流程及验证
• 有效应力方法与总应力方法的比较
动力有效应力分析方法
何谓动力有效应力分析方法? 何谓动力有效应力分析方法?
基于有效应力原理,考虑振动孔隙水压力变化对砂性土动 力特性的影响(即砂土液化过程中的“软化”现象),以土单 元残余有效应力为参考指标计算场地动力反应的一种计算方法
基于ABAQUS 的材料本构 子程序二次 开发
考虑土体的 动力非线性 效应
建立土体材料 特性与有效 应力之间的 联系
动力有效应力本构模型介绍
–其中
∆ε v ,d =C1 (γ a − C2ε v ,d ) +
Cε
2 3 v,d
4
γ a + C ε v ,d
(5)
当
(σ v' )1− m (6) Er = ' n−m mk2 (σ v 0 ) γ a = 0 ∆ε v ,d = (C3 − C1C2 )ε v ,d < 0 时, C4
动力有效应力本构模型介绍
Martin和Finn的振动孔隙水压力模型及Byrne的相关简化模型 Martin和Finn的振动孔隙水压力模型及Byrne的相关简化模型 的振动孔隙水压力模型及Byrne • Martin-Finn的振动孔隙水压力应变模型 – 土的体积变化以压缩为正,孔隙水体积以排出为正 (1) ∆ε v ,d + ∆ε v ,r = ∆ε v , f
时间/s
NJ10波作用下左侧墙剪应力时程曲线
后续工作计划
• 有效应算法与总应力算法增加计算工况并撰写论文 • 两侧带商业街(结构竖向不规则)地铁车站地震反 应论文撰写 • 地铁车站对邻近地面高层结构地震反应影响论文撰 写
The End
谢谢,请批评指正!
分析方法流程及验证
计算结果分析
正弦波作用下土单元滞回曲线图
模型小结
1.模型对于场地振动孔压计算效果良好
2.分析方法能正确的反应有效应力衰减产生的 砂土软化现象
有效应力方法与总应力方法的比较
车站模型建立详解
有效应力方法与总应力方法的比较
液化及变形规律
NJ10波作用下场地变形图(放大10倍) NJ10波作用下场地振动孔压比分布
