2012年北京市高考数学试卷文科教师版
(2021年整理)2012北京卷高考数学(文科)试题及答案解析

(完整)2012北京卷高考数学(文科)试题及答案解析编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整)2012北京卷高考数学(文科)试题及答案解析)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整)2012北京卷高考数学(文科)试题及答案解析的全部内容。
数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一 、选择题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项。
1、已知集合A={x ∈R|3x+2>0} B={x ∈R|(x+1)(x-3)>0} 则A ∩B=A (-∞,-1)B (-1,-23)C (—23,3)D (3,+∞)2 在复平面内,复数103ii+对应的点的坐标为A (1 ,3)B (3,1) C(—1,3) D (3 ,—1)(3)设不等式组,表示平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是 (A )4π (B )22π- (C )6π(D )44π-(4)执行如图所示的程序框图,输出S 值为 (A )2 (B)4 (C )8 (D )16(5)函数f(x)=x121x2⎛⎫- ⎪⎝⎭的零点个数为(A)0 (B)1(C)2 (D)3(6)已知为等比数列,下面结论种正确的是(A)a1+a3≥2a2(B)(C)若a1=a3,则a1=a2(D)若a3>a1,则a4>a2(7)某三棱锥的三视图如图所示,该三棱锥的表面积是(A)28+5B)30+65C)56+5)60+5(8)某棵果树前n年的总产量S n与n之间的关系如图所示,从目前记录的结果看,前m年的年平均产量最高,m的值为(A)5(B)7(C)9(D)11第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分。
2012年北京市高考文科数学试卷真题及参考答案(文科)

20XX 年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效,考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷(选择题共40分)一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合{}320A x x =∈+>R ,()(){}130B x x x =∈+->R ,则A B =( ).A.(),1-∞-B.21,3⎛⎫-- ⎪⎝⎭C.2,33⎛⎫- ⎪⎝⎭D.()3,+∞ 2.在复平面内,复数10i3i+对应的点的坐标为(). A.()1,3B.()3,1C.()1,3- D.()3,1- 3. 设不等式组0202x y⎧⎨⎩剟剟,表示的平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是(). A.π4B.π22- C.π6D.4π4- 4. 执行如图所示的程序框图,输出的S 值为().A.2B.4C.8D.165. 函数121()2xf x x ⎛⎫=- ⎪⎝⎭的零点个数为().A.0B.1C.2D.36. 已知{}n a 为等比数列. 下面结论中正确的是().A.1322a a a +…B.2221322a a a +…C.若13a a =,则12a a =D.若31a a >,则42a a > 7. 某三棱锥的三视图如图所所示,该三棱锥的表面积是().A.28+30+C.56+60+8. 某棵果树前n 年的总产量n S 与n 之间的关系如图所示.从目前记录的结果看,前m 年的年平均产量最高,m 的值为().A.5B.7C.9D.11第II 卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分.09.直线y x =被圆()2224x y +-=截得的弦长为. 10. 已知{}n a 为等差数列,n S 为其前n 项和,若112a =,23S a =,则2a =; n S =.11.在△ABC 中,若3a =,b =π3A ∠=,则C ∠的大小为. 12.已知函数()lg f x x =,若()1f ab =,则()()22f a f b +=.13.已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE CB ⋅的值为;DE DC ⋅的最大值为.14.已知()()()23f x m x m x m =-++,()22xg x =-,若x ∀∈R ,()0f x <或()0g x <,则m的取值范围是.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分)已知函数()sin cos sin 2()sin x x x f x x-=.(1)求()f x 的定义域及最小正周期; (2)求()f x 的单调递减区间.16.(本小题共14分)如图1,在Rt △ABC 中,90C ∠=,D ,E 分别是AC ,AB 的中点,点F 为线段CD 上的一点. 将△ADE 沿DE折起到△1A DE 的位置,使1A F CD ⊥. 如图2. (1)求证:DE ∥平面1A CB ; (2)求证:1A F BE ⊥;(3)线段1A B 上是否存在点Q ,使1A C ⊥平面DEQ17.(本小题共13分)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物与其他垃圾 三类分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类 (1)试估计厨余垃圾投放正确的概率; (2)试估计生活垃圾投放错误的概率; (3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a ,b ,c ,其中0a >,600a b c ++=,当数据a ,b ,c 的方差2s 最大时,写出a ,b ,c 的值(结论不要求证明). 并求此时2s 的值.(求:()()()2222121n s x x x x x x n ⎡⎤=-+-+⋅⋅⋅+-⎣⎦, 其中x 为数据1x ,2x ,…,n x 的平均数).18.(本小题共13分)已知函数()2()10f x ax a =+>,3()g x x bx =+.(1)若曲线()y f x =与曲线()y g x =在它们的交点()1,c 处具有公共切线,求a ,b 的值; (2)当3a =,9b =-时,求函数()()f x g x +在区间[],2k 上的最大值为28.求k 的取值范围.19.(本小题共14分)已知椭圆C :()222210x y a b a b+=>>的一个顶点为()2,0A ,离心率为. 直线()1y k x =-与椭圆C 交于不同的两点M ,N .(1)求椭圆C 的方程; (2)当△AMN的面积为3时,求k 的值. .20.(本小题共13分)设A 是如下形式的2行3列的数表,满足性质P :a ,b ,c ,d ,e ,f []1,1∈-,且0a b c d e f +++++=.记()i r A 为A 的第i 行各数之和(1,2i =),()j c A 为A 的第j 列各数之和(1,2,3j =);记()k A 为1()r A ,2()r A ,1()c A ,2()c A ,3()c A 中的最小值.(1)对如下数表A ,求()k A 的值;(2)设数表形如其中10d -剟. 求()k A 的最大值;(3)对所有满足性质P 的2行3列的数表A ,求()k A 的最大值.。
高考文科数学试卷北京卷附答案

2012年高考文科数学试卷(北京卷)附答案2012年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项。
1、已知集合A={x∈R|3x+2>0}B={x∈R|(x+1)(x-3)>0}则A∩B=A(-,-1)B(-1,-)C(-,3)D(3,+)2在复平面内,复数对应的点的坐标为A(1,3)B(3,1)C(-1,3)D(3,-1)(3)设不等式组,表示平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是(A)(B)(C)(D)(4)执行如图所示的程序框图,输出S值为(A)2(B)4(C)8(D)16(5)函数f(x)=的零点个数为(A)0(B)1(C)2(D)3(6)已知为等比数列,下面结论种正确的是(A)a1+a3≥2a2(B)(C)若a1=a3,则a1=a2(D)若a3>a1,则a4>a2(7)某三棱锥的三视图如图所示,该三棱锥的表面积是(A)28+(B)30+(C)56+(D)60+(8)某棵果树前n年的总产量Sn与n之间的关系如图所示,从目前记录的结果看,前m年的年平均产量最高,m 的值为(A)5(B)7(C)9(D)11第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分。
(9)直线y=x被圆x2+(y-2)2=4截得弦长为__________。
(10)已知为等差数列,Sn为其前n项和,若a1=,S2=a3,则a2=____________,Sn=_________________。
(11)在△ABC中,若a=3,b=,,则的大小为_________。
(12)已知函数f(x)=lgx,若f(ab)=1,则f(a2)+f(b2)=_____________。
2012年高考真题——文数(北京卷)word版(附答案)

2012年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一 、选择题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项。
(1)已知集合{|320}A x R x =∈+>,{|(1)(3)0}B x R x x =∈+->,则A B =I (A )(,1)-∞- (B )2(1,)3-- (C )2(,3)3- (D )(3,)+∞ (2)在复平面内,复数103ii+对应的点的坐标为 (A )(1,3) (B )(3,1) (C )(1,3)- (D )(3,1)- (3)设不等式组02,02x y ≤≤⎧⎨≤≤⎩表示的平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是 (A )4π(B )22π-(C )6π(D )44π-(4)执行如图所示的程序框图,输出的S 值为 (A )2 (B )4 (C )8 (D )16(5)函数121()()2xf x x =-的零点个数为(A )0 (B )1 (C )2 (D )3 (6)已知{}n a 为等比数列,下面结论中正确的是(A )1322a a a +≥ (B )2221322a a a +≥(C )若13a a =,则12a a = (D )若31a a >,则42a a > (7)某三棱锥的三视图如图所示,该三棱锥的表面积是 (A )2865+ (B )3065+ (C )56125+ (D )60125+(8)某棵果树前n 年的总产量n S 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为 (A )5 (B )7 (C )9 (D )11第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2012高考真题——文科数学(北京卷)解析版

2012年北京高考数学(文)逐题详解2012年的北京数学高考是高中新课改后的第三次高考,试卷延续了近几年高考数学命题的风格,题干大气,内容丰富,难度客观讲适中,和以往一样,其中8,14,20三个题技巧性较高,侧重考查学生的数学思维和探索精神。
一、试题体现数学的人文教育功能拿到试卷的第一感觉是亲切,大部分试题均注重考查基础知识、基本技能和基本方法,考查数学传统的主干知识,较好把握了传统知识的继承点和新增知识的起步点,但是有几个试题还是非常具有心意,难度不小,重点考察能力,给笔者留下了较深的印象:例如选择第3题,在不等式背景下考查了一个概率问题,还是非常具有综合性的。
选择第7题,常见的三视图问题,但是计算几何体的表面积,对空间想象力要求还是很高的。
填空题第13小题,难度虽然不大,但是综合性以及对于函数思想的要求都很高。
第16题,立体几何考查了一个折纸的问题,难度虽然不大,但是形式还是比较有亮点的,第三问又设计为探索型问题,体现了能力立意的考试要求,要求学生有较好的空间想象力和逻辑推理能力才能顺利解答. 再比如17题以生活背景为模型考查了一个概率统计的知识,题目难度仍然不大,但是第三问非常有创新思维的让学生大胆猜想方差最大的情况,还是非常考查能力的,另外,从生活的角度命题,让学生体验数学的建模思想和应用价值,激发学生学习数学的兴趣,拓展视野,开展研究性学习,实现数学的人文教育功能。
二、试题解析(一)、选择题:【解析】第(1)题和往年一样,依然是集合(交集)运算,本次考察的是一次和二次不等式的解法。
因为,利用二次不等式的解法可得,画出数轴图易得:,答案:D【解析】第(2)题考查的是复数除法的化简运算以及复平面,实部虚部的概念。
,实部为1,虚部为3,对应复平面上的点为,答案:A【解析】第(3)题是一道微综合题,它涉及到的知识包括:线性规划,圆的概念和面积公式,概率。
题目中表示的区域如右图正方形所示,而动点D可以存在的位置为正方型面积减去四分之一圆的面积部分,因此,答案:D【解析】第(4)题考查程序框图,涉及到判断循环结束的时刻,以及简单整数指数幂的计算。
2012年普通高等学校招生统一考试(北京卷)数学文 word版含答案

2012年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一 、选择题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项。
1、已知集合A={x ∈R|3x+2>0} B={x ∈R|(x+1)(x-3)>0} 则A ∩B=A (-∞,-1)B (-1,-23) C (-23,3)D (3,+∞) 2 在复平面内,复数103i i +对应的点的坐标为 A (1 ,3) B (3,1) C(-1,3) D (3 ,-1)(3)设不等式组,表示平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是(A )4π (B )22π- (C )6π (D )44π- (4)执行如图所示的程序框图,输出S 值为(A )2(B )4(C )8(D )16(5)函数f(x)=x121x2⎛⎫- ⎪⎝⎭的零点个数为(A)0 (B)1(C)2 (D)3(6)已知为等比数列,下面结论种正确的是(A)a1+a3≥2a2(B)(C)若a1=a3,则a1=a2(D)若a3>a1,则a4>a2(7)某三棱锥的三视图如图所示,该三棱锥的表面积是(A)28+B)30+C)56+D)60+(8)某棵果树前n年的总产量S n与n之间的关系如图所示,从目前记录的结果看,前m年的年平均产量最高,m的值为。
2012年北京高考数学文科试卷(带答案)

r2012年普通高等学校招生全国统一考试(北京卷)数学(文科)第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.已知集合{}{}320,(1)(3)0A x x B x x x =∈+>=∈+->R R ,则A B I=( )A.(,1)-∞-B.2(1,)3--C.2(,3)3-D.(3,)+∞ 【测量目标】集合的含义与表示、集合的基本运算. 【考查方式】给出两个集合,求交集.【参考答案】C 【试题解析】23A x x ⎧⎫=>-⎨⎬⎭⎩,利用二次不等式的解法可得{3B x x =>或}1x <,画出数轴易得}{3A B x x =>I . 2.在复平面内,复数10i3i+对应的点坐标为 ( ) A. (1,3) B.(3,1) C.(1,3)- D.(3,1-)【测量目标】复数的运算法则及复数的几何意义. 【考查方式】给出复数,求对应的点坐标. 【参考答案】A 【试题解析】10i 10i(3i)13i 3i (3i)(3i)-==++++,实部是1,虚部是3,对应复平面上的点为(1,3),故选A. 3.设0202x x ⎧⎫⎨⎬⎭⎩剟剟不等式组表示的平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是 ( )A.π4 B. π22- C. π6 D.4π4-【测量目标】判断不等式组表示的平面区域、几何概型.【考查方式】给出不等式组,求不等式组所表示的区域中点到直线距离的概率. 【参考答案】D【试题解析】题目中0202x x ⎧⎫⎨⎬⎭⎩剟剟表示的区域表示正方形区域,而动点D 可以存在的位置为正方形面积减去四分之一的圆的面积部分,因此2122π24π4224p ⨯-⨯-==⨯,故选D4. 执行如图所示的程序框图,输出的S 值为 ( )A.2B.4 C .8 D.16 【测量目标】循环结构的程序图框.【考查方式】给出程序图,求最后的输出值. 【参考答案】C 【试题解析】0,11,12,23,8,k s k s k s k s ==⇒==⇒==⇒==循环结束,输出的S 为8,故选C.5.函数121()()2xf x x =-的零点个数为 ( )A. 0B. 1C. 2D. 3【测量目标】导函数的定义与应用.【考查方式】已知复合函数,求零点个数. 【参考答案】B【试题解析】函数121()()2x f x x =-的零点,即令()0f x =,根据此题可得121()2xx =,在平面直角坐标系中分别画出这两个函数的图像,可得交点只有一个,所以零点只有一个,故选答案B .6. 已知}{n a 为等比数列.下面结论中正确的是 ( )A.1222a a a +…B.2221322a a a +…C.若则12a a = ,则132a a a +…D.若31a a >,则42a a >【测量目标】等比数列的公式与性质.【考查方式】给出等比数列,判断选项中那些符合等比数列的性质. 【参考答案】B【试题解析】当10,0a q <<时,可知1320,0,0,a a a <<>,所以A 选项错误;当1q =-时,C 选项错误;当0q <时,323142a a a q a q a a >⇒<⇒<,与D 选项矛盾。
2012年高考文科数学北京卷及答案

数学试卷 第1页(共18页)数学试卷 第2页(共18页)数学试卷 第3页(共18页)绝密★启用前2012年普通高等学校招生全国统一考试(北京卷)数学(文科)本试卷共6页,150分.考试时长120分钟.考试生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合{320}A x x =∈+>R |,{|(1)(3)0}B x x x =∈+->R ,则A B =( )A . (,1)-∞-B . 2(1,)3-- C . 2(,3)3-D . (3,)+∞2. 在复平面内,复数10i3i+对应的点的坐标为 ( )A . (1,3)B . (3,1)C .(1,3)-D . (3,1)-3. 设不等式组02,02x y ⎧⎨⎩≤≤≤≤表示的平面区域为D .在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是( )A . π4 B . π22-C .π6D .4π4- 4. 执行如图所示的程序框图,输出的S 值为 ( )A . 2B . 4C . 8D . 16 5. 函数121()()2x f x x =-的零点个数为( )A . 0B . 1C . 2D . 3 6. 已知{}n a 为等比数列.下面结论中正确的是( )A . 1322a a a +≥B . 2221322a a a +≥C . 若13a a =,则12a a =D . 若31a a >,则42a a >7. 某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .28+ B .30+C .56+D .60+8. 某棵果树前n 年的总产量n S 与n 之间的关系如图所示.从目前记录的结果看,前m 年的年平均产量最高,m 的值为( )A . 5B . 7C . 9D . 11第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分.9. 直线y x =被圆22(2)4x y +-=截得的弦长为________. 10. 已知{}n a 为等差数列,n S 为其前n 项和.若112a =,23S a =,则2a =________;=n S ________.11. 在ABC △中,若3a =,b =,π3A ∠=,则C ∠的大小为________. 12. 已知函数()lg f x x =,若()1f ab =,则22()()f a f b +=________.13. 已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则 DE CB 的值为________;DE DC 的最大值为________.14. 已知()(2)(3)f x m x m x m =-++,()22x g x =-.若x ∀∈R ,()0f x <或()0g x <,则m的取值范围是________.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题共13分) 已知函数(sin cos )sin 2()sin x x xf x x-=.(Ⅰ)求()f x 的定义域及最小正周期; (Ⅱ)求()f x 的单调递减区间.16.(本小题共14分)俯视图侧(左)视图正(主)视图434姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效--------数学试卷 第4页(共18页)数学试卷 第5页(共18页) 数学试卷 第6页(共18页)如图1,在Rt ABC △中,90C ∠=,D ,E 分别为AC ,AB 的中点,点F 为线段CD 上的一点.将ADE △沿DE 折起到1A DE △的位置,使1A F CD ⊥,如图2.(Ⅰ)求证:DE ∥平面1ACB ; (Ⅱ)求证:1A F BE ⊥;(Ⅲ)线段1A B 上是否存在点Q ,使1A C ⊥平面DEQ ?说明理由.17.(本小题共13分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1 000吨生活垃圾,数据统计如下(单位:吨):(Ⅰ)试估计厨余垃圾投放正确的概率; (Ⅱ)试估计生活垃圾投放错误的概率;(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a ,b ,c ,其中0a >,600a b c ++=.当数据a ,b ,c 的方差2s 最大时,写出a ,b ,c 的值 (结论不要求证明),并求此时2s 的值.(求:2222121[()()()]n s x x x x x x n=-+-++-,其中x 为数据1x ,2x ,,n x 的平均数)18.(本小题共13分)已知函数2()1(0)f x ax a =+>,3()g x x bx =+.(Ⅰ)若曲线()y f x =与曲线()y g x =在它们的交点(1,)c 处具有公共切线,求a ,b 的值; (Ⅱ)当3a =,9b =-时,若函数()()f x g x +在区间[,2]k 上的最大值为28,求k 的取值范围.19.(本小题共14分)已知椭圆C :22221(0)x y a b a b+=>>的一个顶点为(2,0)A ,直线(1)y k x =-与椭圆C 交于不同的两点M,N . (Ⅰ)求椭圆C 的方程; (Ⅱ)当AMN ∆时,求k 的值.20.(本小题共13分)设A 是如下形式的2行3列的数表,满足性质P :,,,,,[1,1]a b c d e f ∈-,且0a b c d e f +++++=.记()i r A 为A 的第i 行各数之和(1,2)i =,()j c A 为A 的第j 列各数之和(1,2,3)j =;记()k A 为1|()|r A ,2|()|r A ,1|()|c A ,2|()|c A ,3|()|c A 中的最小值.(Ⅰ)对如下数表A ,求()k A 的值;(Ⅱ)设数表A 形如其中10d -≤≤.求()k A 的最大值;(Ⅲ)对所有满足性质P 的2行3列的数表A ,求()k A 的最大值.D FDE BCA 1F CB 图2图1数学试卷 第7页(共18页)数学试卷 第8页(共18页) 数学试卷 第9页(共18页)2012年普通高等学校招生全国统一考试(北京卷)数学(文科)答案解析{|1A B x x x x ⎧⎫=<-⎨⎬⎩⎭【提示】求出集合,然后直接求解AB 。
2012年全国高考文科数学试题及答案-北京卷

2012年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一 、选择题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项。
(1)已知集合{|320}A x R x =∈+>,{|(1)(3)0}B x R x x =∈+->,则A B = (A )(,1)-∞- (B )2(1,)3-- (C )2(,3)3- (D )(3,)+∞ (2)在复平面内,复数103ii+对应的点的坐标为 (A )(1,3) (B )(3,1) (C )(1,3)- (D )(3,1)-(3)设不等式组02,02x y ≤≤⎧⎨≤≤⎩表示的平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是(A )4π(B )22π-(C )6π(D )44π-(4)执行如图所示的程序框图,输出的S 值为 (A )2 (B )4 (C )8 (D )16(5)函数121()()2xf x x =-的零点个数为(A )0 (B )1 (C )2 (D )3 (6)已知{}n a 为等比数列,下面结论中正确的是(A )1322a a a +≥ (B )2221322a a a +≥ (C )若13a a =,则12a a = (D )若31a a >,则42a a > (7)某三棱锥的三视图如图所示,该三棱锥的表面积是(A )28+ (B )30+(C )56+ (D )60+(8)某棵果树前n 年的总产量n S 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为 (A )5 (B )7 (C )9 (D )11第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2012年高考文科数学北京卷
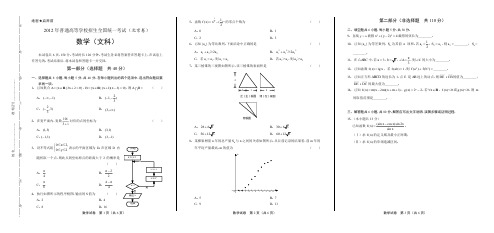
4. 执行如图所示的程序框图,输出的 S 值为 A. 2 C. 8 B. 4
O
1
2
3
4
5
6
7
8
9 10 11 n
A. 5 C. 9
B. 7 D. 11 数学试卷 第 2 页(共 6 页) 数学试卷 第 3 页(共 6 页)
效
D. 16 数学试卷 第 1 页(共 6 页)
16.(本小题共 14 分) 如图 1,在 Rt△ABC 中, C 90 ,D,E 分别为 AC , AB 的中点,点 F 为线段 CD 上的 一点.将 △ADE 沿 DE 折起到 △A1 DE 的位置,使 A1 F⊥CD ,如图 2.
1
(
)
第二部分(非选择题 共 110 分)
二、填空题共 6 小题,每小题 5 分,共 30 分. 9. 直线 y x 被圆 x2 ( y 2)2 4 截得的弦长为________.
2012 年普通高等学校招生全国统一考试(北京卷)
数学(文科)
本试卷共 6 页,150 分.考试时长 120 分钟.考试生务必将答案答在答题卡上,在试卷上 作答无效.考试结束后,将本试卷和答题卡一并交回.
4
CB 的值为________;
DE
DC 的最大值为________.
B
(
)
2
3
4 侧(左)视图
14. 已知 f ( x) m( x 2m)( x m 3) , g ( x) 2 x 2 .若 x R , f ( x)<0 或 g ( x)<0 ,则 m 的取值范围是________.
满足性质 P: a, b, c, d , e, f [1,1] ,且 a b c d e f 0 . 记 ri ( A) 为 A 的第 i 行各数之和 (i 1,2) , c j ( A) 为 A 的第 j 列各数之和 ( j 1,2,3) ;记
2012年6月8日全国各地高考文科数学试题及参考答案北京卷

2012年全国各地高考数学试题普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一 、选择题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项。
(1)已知集合{|320}A x R x =∈+>,{|(1)(3)0}B x R x x =∈+->,则A B = (A)(,1)-∞- (B)2(1,)3-- (C)2(,3)3- (D)(3,)+∞ (2)在复平面内,复数103ii+对应的点的坐标为 (A)(1,3) (B)(3,1) (C)(1,3)- (D)(3,1)- (3)设不等式组02,02x y ≤≤⎧⎨≤≤⎩表示的平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是(A)4π(B)22π-(C)6π(D)44π-(4)执行如图所示的程序框图,输出的S 值为(A)2 (B)4 (C)8 (D)16(5)函数121()()2xf x x =-的零点个数为(A)0 (B)1 (C)2 (D)3 (6)已知{}n a 为等比数列,下面结论中正确的是(A)1322a a a +≥ (B)2221322a a a +≥(C)若13a a =,则12a a = (D)若31a a >,则42a a > (7)某三棱锥的三视图如图所示,该三棱锥的表面积是(A)28+ (B)30+(C)56+ (D)60+(8)某棵果树前n 年的总产量n S 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为 (A)5 (B)7 (C)9 (D)11第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
(9)直线y x =被圆22(2)4x y +-=截得的弦长为__________。
2012年高考试题及解析:文科数学(北京卷)

2012年普通高等学校招生全国统一考试数学(文)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一 、选择题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项。
(1).已知集合A={x ∈R|3x+2>0} B={x ∈R|(x+1)(x-3)>0} 则A∩B=(A ) (﹣∞,﹣1) (B ) (﹣1,﹣23) (C )(﹣23,3) (D ) (3,+∞) 【考点】集合【难度】容易【点评】本题考查集合之间的运算关系,即包含关系。
在高一数学强化提高班上学期课程讲座1,第一章《集合》中有详细讲解,其中第02节中有完全相同类型题目的计算。
在高考精品班数学(文)强化提高班中有对复数相关知识的总结讲解。
(2).在复平面内,复数103i i+对应的点的坐标为 (A ) (1 ,3) (B ) (3,1) (C )(-1,3) (D ) (3 ,-1)【考点】复数的计算【难度】容易【点评】本题考查复数的计算。
在高二数学(文)强化提高班下学期,第四章《复数》中有详细讲解,其中第02节中有完全相同类型题目的计算。
在高考精品班数学(文)强化提高班中有对复数相关知识的总结讲解。
(3)设不等式组0202x y ≤≤⎧⎨≤≤⎩,表示平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是(A )4π (B )22π- (C )6π (D )44π- 【考点】概率【难度】容易【点评】本题考查几何概率的计算方法。
在高二数学(文)强化提高班,第三章《概率》有详细讲解,在高考精品班数学(文)强化提高班中有对概率相关知识的总结讲解。
(4)执行如图所示的程序框图,输出S 值为(A )2 (B ) (C )8 (D )16【考点】算法初步【难度】中等【点评】本题考查几何概率的计算方法。
2012年北京市高考文科数学试卷真题及参考答案(文科)

2012年普通高等学校招生全国统一考试数学〔文〕〔卷〕本试卷共5页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效,考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷〔选择题共40分〕一、本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知集合{}320A x x =∈+>R ,()(){}130B x x x =∈+->R ,则A B =〔 〕.A.(),1-∞-B.21,3⎛⎫-- ⎪⎝⎭C.2,33⎛⎫- ⎪⎝⎭D.()3,+∞ 2.在复平面内,复数10i3i+对应的点的坐标为〔〕. A.()1,3 B.()3,1C.()1,3- D.()3,1- 3. 设不等式组0202x y⎧⎨⎩,表示的平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是〔〕. A.π4B.π22- C.π6D.4π4- 4. 执行如图所示的程序框图,输出的S 值为〔〕.A.2B.4C.8D.165. 函数121()2xf x x ⎛⎫=- ⎪⎝⎭的零点个数为〔〕.A.0B.1C.2D.36. 已知{}n a 为等比数列. 下面结论中正确的是〔〕.A.1322a a a +B.2221322a a a +C.若13a a =,则12a a =D.若31a a >,则42a a > 7. 某三棱锥的三视图如图所所示,该三棱锥的表面积是〔〕.A.2865+3065+ C.565+60125+8. 某棵果树前n 年的总产量n S 与n 之间的关系如图所示.从目前记录的结果看,前m 年的年平均产量最高,m 的值为〔〕.A.5B.7C.9D.11第II 卷〔共110分〕二、填空题:本大题共6小题,每小题5分,共30分.09.直线y x =被圆()2224x y +-=截得的弦长为. 10. 已知{}n a 为等差数列,n S 为其前n 项和,若112a =,23S a =,则2a =; n S =.11.在△ABC 中,若3a =,3b =π3A ∠=,则C ∠的大小为. 12.已知函数()lg f x x =,若()1f ab =,则()()22f a f b +=.13.已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE CB ⋅的值为;DE DC ⋅的最大值为.14.已知()()()23f x m x m x m =-++,()22xg x =-,若x ∀∈R ,()0f x <或()0g x <,则m的取值范围是.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.〔本小题共13分〕已知函数()sin cos sin 2()sin x x x f x x-=.〔1〕求()f x 的定义域与最小正周期; 〔2〕求()f x 的单调递减区间.16.〔本小题共14分〕如图1,在Rt △ABC 中,90C ∠=,D ,E 分别是AC ,AB 的中点,点F 为线段CD 上的一点. 将△ADE 沿DE折起到△1A DE 的位置,使1A F CD ⊥. 如图2. 〔1〕求证:DE ∥平面1A CB ; 〔2〕求证:1A F BE ⊥;〔3〕线段1A B 上是否存在点Q ,使1A C ⊥平面DEQ ?说明理由.17.〔本小题共13分〕近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物与其他垃圾 三类分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类“厨余垃圾〞箱 “可回收物〞箱 “其他垃圾〞箱 厨余垃圾 400100 100 可回收物 30 240 30 其他垃圾20 20 60〔1〕试估计厨余垃圾投放正确的概率; 〔2〕试估计生活垃圾投放错误的概率; 〔3〕假设厨余垃圾在“厨余垃圾〞箱、“可回收物〞箱、“其他垃圾〞箱的投放量分别为a ,b ,c ,其中0a >,600a b c ++=,当数据a ,b ,c 的方差2s 最大时,写出a ,b ,c 的图1图2值〔结论不要求证明〕. 并求此时2s 的值.〔求:()()()2222121n s x x x x x x n ⎡⎤=-+-+⋅⋅⋅+-⎣⎦, 其中x 为数据1x ,2x ,…,n x 的平均数〕.18.〔本小题共13分〕已知函数()2()10f x ax a =+>,3()g x x bx =+.〔1〕若曲线()y f x =与曲线()y g x =在它们的交点()1,c 处具有公共切线,求a ,b 的值; 〔2〕当3a =,9b =-时,求函数()()f x g x +在区间[],2k 上的最大值为28.求k 的取值范围.19.〔本小题共14分〕已知椭圆C :()222210x y a b a b+=>>的一个顶点为()2,0A ,离心率为2. 直线()1y k x =-与椭圆C 交于不同的两点M ,N .〔1〕求椭圆C 的方程; 〔2〕当△AMN的面积为3时,求k 的值. .20.〔本小题共13分〕设A 是如下形式的2行3列的数表,满足性质P :a ,b ,c ,d ,e ,f []1,1∈-,且0a b c d e f +++++=.记()i r A 为A 的第i 行各数之和〔1,2i =〕,()j c A 为A 的第j 列各数之和〔1,2,3j =〕;记()k A 为1()r A ,2()r A ,1()c A ,2()c A ,3()c A 中的最小值.〔1〕对如下数表A ,求()k A 的值;〔2〕设数表形如其中10d -. 求()k A 的最大值;〔3〕对所有满足性质P 的2行3列的数表A ,求()k A 的最大值.。
2012年高考数学北京文解析版

2012年普通高等学校招生全国统一考试数学(文)(北京卷)解析本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一 、选择题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项。
1、已知集合A={x ∈R|3x+2>0} B={x ∈R|(x+1)(x-3)>0} 则A ∩B= A (-∞,-1)B (-1,-23) C (-23,3)D (3,+∞) [答案]D[解析]和往年一样,依然是集合(交集)运算,本题考查的是一次和二次不等式的解法.因为A={x ∈R|3x+2>0}32->⇒x ,利用二次不等式的解法可得{}31>-<=x x x B 或,画出数轴易得:A ∩B={x|x >3}.[点评]集合的运算往往与解不等式联系在一起考查,属低档题. 2 在复平面内,复数103ii+对应的点的坐标为 A (1 ,3) B (3,1) C(-1,3) D (3 ,-1) [答案]A [解析]i i ii i i i i i i i 3110301091030)3)(3()3(1031022+=+=--=-+-=+,实部为1,虚部为3,对应点为(1,3).[点评]复数的除法原则是分子分母同时乘以分母的共轭复数,即分母实数化,这一过程要熟练掌握.(3)设不等式组,表示平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是 (A )4π (B )22π- (C )6π (D )44π-[答案]D[解析]这是道微综合题,它涉及到的知识包括:线性规划,圆的概念和面积公式,概率.题目中表示区域如下图正方形所示,而动点D 可以存在的位置为正方形面积减去四分之一圆的面积,因此P=4422241222ππ-=⨯-⨯[点评]与面积、体积、长度有关的概率问题属于几何概型.(4)执行如图所示的程序框图,输出S值为(A)2 (B)4 (C)8 (D)16[答案]C[解析]本题考查程序框图,设计到判断循环结束的时刻,以及简单整数指数幂的计算,k=o,s=1⇒k=1,s=1⇒k=2,s=2⇒k=3,s=8,结束[点评]读懂程序,做好循环结束的判断.本题属低档题.(5)函数f(x)=x121x2⎛⎫- ⎪⎝⎭的零点个数为(A)0 (B)1(C)2 (D)3[答案]B[解析]该题表面上看考查的是零点问题,实质上是函数图像问题(单调性)的变式,所涉及的函数为幂函数和指数函数. 函数f(x)=x121x2⎛⎫- ⎪⎝⎭的零点,即令f(x)=0,可得xx)21(21=,在坐标系中分别画出这两个函数的图像,可得交点只有一个,所以零点只有一个. [点评]函数的基本性质在每年的高考中是重点,要予以重视.(6)已知{n a }为等比数列,下面结论中正确的是(A )a 1+a 3≥2a 2(B )2223212a a a ≥+(C )若a 1=a 3,则a 1=a 2(D )若a 3>a 1,则a 4>a 2 [答案]B[解析]该题考查的等比数列的基本概念,鉴于是选择题,可以选择排除法解决.当0,0,00,02311><<<<a a a q a 时,可知,故A 错;当q=-1时,C 选项错误;当q<0时,241313a a q a q a a a <⇒<⇒>,与D 选项矛盾.正确答案为B.[点评]等差、等比数列的基本性质,要多用特例去验证. (7)某三棱锥的三视图如图所示,该三棱锥的表面积是(A )28+B )30+C )56+D )60+[答案]B[解析]本题考查的是三棱锥的三视图问题,问题变化为求表面积,因此对学生的计算基本功以及空间想象能力都存在着综合性的考查.从所给的三视图可以得到该几何体的直观图,如下图所示,结合图中的数据,利用勾股定理计算出各边的长度,进而求出面积.563056101010+=+++=+++=左右后底表S S S S S[点评]把三视图正确地转化为直观图是解决问题的关键.(8)某棵果树前n 年的总产量S n 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为(A )5(B )7(C )9(D )11 [答案]C[解析]该题考查知识点很灵活,要根据图像看出变化趋势,由于目的是看年平均产量最高,就需要随着n 的增大,总年产量变化超过平均值的加入,随着n 的增大,由图可知6,7,8,9这几年增长最快,超过平均值,所以应该加入,因此选C.[点评]考察阅读理解能力,这也对数学的学习平时要求不能过于僵化,要灵活. 第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
北京市高考数学试题及答案文科Word版

适用精选文件资料分享2012 年北京市高考数学试题及答案( 文科 Word版)2012 年一般高等学校招生全国一致考试数学(文)(北京卷)本试卷共 5 页,150 分。
考试时长 120 分钟。
考生务势必答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共 40 分)一、选择题共 8 小题,每题 5 分,共 40 分,在每题给出的四个选项中,选出吻合题目要求的一项。
1 、已知会集 A={x∈R|3x+2>0} B={x∈R|(x+1) (x-3) >0} 则 A∩B= A(- ,-1 )B (-1 ,- ) C (- ,3 )D (3,+ ) 2 在复平面内,复数对应的点的坐标为 A (1 ,3) B (3,1) C(-1,3) D (3 ,-1)(3)设不等式组,表示平面地域为 D,在地域 D内随机取一个点,则此点到坐标原点的距离大于 2 的概率是(A)( B)(C)(D)(4)履行以下列图的程序框图,输出 S 值为(A)2 (B)4 (C)8(D)16 (5) 函数 f (x)=的零点个数为(A)0 (B)1(C)2 (D)3 (6)已知为等比数列,下边结论种正确的选项是(A)a1+a3≥2a2(B)(C)若 a1=a3,则 a1=a2(D)若 a3> a1,则 a4>a2 (7)某三棱锥的三视图以下列图,该三棱锥的表面积是(A) 28+ (B)30+ (C)56+ (D)60+ (8)某棵果树前 n 年的总产量 Sn 与 n 之间的关系以下列图,从目前记录的结果看,前m年的年均匀产量最高,m的值为(A)5(B)7(C)9(D)11 第二部分(非选择题共 110 分)二、填空题共 6 小题,每题 5 分,共 30 分。
(9)直线 y=x 被圆 x2+(y-2 )2=4 截得弦长为 __________。
(10)已知 {an} 为等差数列,Sn 为其前 n 项和,若 a1= ,S2=a3,则 a2=____________,Sn=_________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年北京市高考数学试卷(文科)一、选择题共8小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项.1.(5分)(2012?北京)已知集合A={x∈R|3x+2>0},B={x∈R|(x+1)(x﹣3)>0},则A∩B=()C.﹙,3﹚D.(.(﹣1,)3,+∞)(﹣∞,﹣A.1)B【分析】求出集合B,然后直接求解A∩B.【解答】解:因为B={x∈R|(x+1)(x﹣3)>0﹜={x|x<﹣1或x>3},>},{x|x3x+2>0﹜=∈又集合A={xR|>}∩{x|x<﹣1或x>3x|x}={x|x>3},∩所以AB={故选:D.对应的点的坐标为(北京)在复平面内,复数).(5分)(2012?2 D.(3,﹣1)B.(3,1,A.(13))C.(﹣1,3)==1+3i,能求出在复平面内,【分析】由复数对应的点的坐标.【解答】解:∵===1+3i,∴在复平面内,复数对应的点的坐标为(1,3),故选:A.3.(5分)(2012?北京)设不等式组,表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是()B.A.C.D.【分析】本题属于几何概型,利用“测度”求概率,本例的测度即为区域的面积,故只要求出题中两个区域:由不等式组表示的区域和到原点的距离大于2的点构成的区域的面积后再求它们的比值即可.【解答】解:其构成的区域D如图所示的边长为2的正方形,面积为S=4,1.满足到原点的距离大于2所表示的平面区域是以原点为圆心,以2为半径的圆外部,,π面积为=4﹣P=2的概率∴在区域D内随机取一个点,则此点到坐标原点的距离大于故选:D.)2012?北京)执行如图所示的程序框图,输出的S值为(4.(5分)(16D..2B.4C8.A的数值,不满足判断框的条件即可结束循环.K列出循环过程中【分析】S与,S=1,k=11【解答】解:第次判断后,k=22第次判断后S=2,,S=83第次判断后,k=3第4次判断后3<3,不满足判断框的条件,结束循环,输出结果:8.故选:C.x的零点个数为(﹣(北京)函数f(x)=x))5.(5分)(2012?C.A.0B.12D.3【分析】先判断函数的单调性,由于在定义域上两个增函数的和仍为增函数,故函数f(x)为单调增函数,而f(0)<0,f()>0由零点存在性定理可判断此函数仅有一个零点【解答】解:函数f(x)的定义域为[0,+∞)在定义域上为增函数﹣在定义域上为增函数,y=∵y=在定义域上为增函数=f(x∴函数)而f(0)=﹣1<0,f(1)=>0的零点个数为1个f(故函数x)=故选:B.6.(5分)(2012?北京)已知{a}为等比数列,下面结论中正确的是()n2222aaB.a ≥+≥A.a+a2a231213C.若a=a,则a=aD.若a>a,则a>a24131231,当且仅当a,q同为正时,a+a=+a≥2a成立;【分析】a2132132;若a=a,则a=aq,从,所以131122﹣1),其q﹣a=a(,则;若a>aaqq>a,而aa=a而可知a或a=﹣12311421121正负由q的符确定,故可得结论.,当且仅当a,qa【解答】解:设等比数列的公比为q,则+a=同为213不正确;成立,故A+正时,aa≥2a213正确;,∴,故B22=1,∴q=±1,∴a=a或a=﹣a,故=a=a若a,则aq,∴qC不正确;2112131122﹣1),其正负由q(q=a﹣a,∴qa,则>a若a>aaq的符确定,故D不1411312正确故选:B.7.(5分)(2012?北京)某三棱锥的三视图如图所示,该三棱锥的表面积是()+1212D.60.30+6C.56+A.28+6B利用三视图的数据求出几何体的表面【分析】通过三视图复原的几何体的形状,积即可.的三角形,和5【解答】解:三视图复原的几何体是底面为直角边长为4,如图,,底边长为5一个侧面垂直底面的等腰三角形,高为4,=10=S所以底,=S后,=10=S右.=S=6左.6S++S=SSS+=30+几何体的表面积为:左后右底.B故选:8.(5分)(2012?北京)某棵果树前n年的总产量S与n之间的关系如图所示.从n目前记录的结果看,前m年的年平均产量最高,则m的值为()11D.7C.9A.5B.可分析n之间的关系,年的总产量S与【分析】由已知中图象表示某棵果树前n出平均产量的几何意义为原点与该点边线的斜率,结合图象可得答案.)点,nP(Sn年的总产量S与n在图中对应【解答】解:若果树前的斜率OP则前n年的年平均产量即为直线的斜率最大OP由图易得当n=9时,直线年的年平均产量最高,9即前.C故选:分.30小题,每小题5分,共二、填空题共622.=4截得的弦长为y=x被圆x)+(y﹣2.9(5分)(2012?北京)直线的距离,利用垂径定理y=x【分析】确定圆的圆心坐标与半径,求得圆心到直线构造直角三角形,即可求得弦长.222),半径为0,2(y﹣2)的圆心坐标为(=4【解答】解:圆x+的距离为∵圆心到直线y=x22截得的弦长为2=∴直线y=x被圆x+(y﹣2)=4故答案为:,=a,S若S为其前n项和,a=}北京)510.(分)(2012?已知{a为等差数列,3n1n2.=S,1=则a n2以及等差数列的从而可求出第二项,根据等差数列的性质可求出公差,【分析】.前n项和.【解答】解:根据{a}为等差数列,S=a+a=a=+a;2322n1∴d=a﹣a=23∴a=+=12=S=n,1故答案为:,,则∠C的大小为,(2012?北京)在△ABC中,若a=3b=11.(5分).,可求得∠B,从而可得∠利用正弦定理=C的大小.【分析】【解答】解:∵△ABC中,a=3,b=,,,=得:=∴由正弦定理∴sin∠B=.又b<a,∴∠B<∠A=.∴∠B=.∴∠C=π﹣﹣=.故答案为:.22)(b)+)ab=1,则f(af(.12(5分)(2012?北京)已知函数fx)=lgx,若f (=2.2222=2lg+b)=lga(=1,知falgb)+f()),(【分析】由函数fx)=lgxf(ab=lg(ab(ab).由此能求出结果.【解答】解:∵函数f(x)=lgx,f(ab)=lg(ab)=1,2222lgb)=lgabf(a)+f(+2=2lg(ab)=2)(=lgab.故答案为:2.13.(5分)(2012?北京)已知正方形ABCD的边长为1,点E是AB边上的动点.则.1的值为直接利用向量转化,求出数量积即可.【分析】<>.===1【解答】解:因为=1故答案为:x.若=22﹣,3)g(x)x)=m(x﹣2m)(x+m+(.14(5分)(2012?北京)已知f,m的取值范围(4(fx)<0或g(x)<0,则?x∈R,x)+3(x+m﹣(x)=m(x2m)根据题意有由于【分析】g(x)=22﹣≥0时,x ≥1,f时成立,根据二次函数的性质可求>1<0在xx,0(x)≥时,2,当x≥1=2【解答】解:∵g(x)g﹣0)<(xx()<0或g又∵?x∈R,f时恒成立≥10在xm2m)(x++3)<((∴此时fx)=mx﹣)的0轴交点都在(1,则由二次函数的性质可知开口只能向下,且二次函数与x左面<<则<0m<<∴﹣4),40(﹣故答案为:三、解答题共6小题,共80分,解答应写出文字说明,演算步骤或证明过程..)=f(x(13分)(2012?北京)已知函数15.)的定义域及最小正周期;(1)求f(x)的单调递减区间.(2)求f(x即可2x﹣)﹣1x)化为(fx)=sin(∈【分析】(1)由sinx≠0可得x≠kπ(kZ),将(f求其最小正周期;x﹣≤2kπ+,2x﹣)﹣1,再由2kπ+≤2x(2)由(1)得f(x)=(sin)的单调递减区间.kπ(k∈Z)即可求f(x≠,x≠kπ(k∈Z)【解答】解:(1)由sinx≠0得.Z}∈≠kπ,k故求f(x)的定义域为{x|x=)∵f(x=2cosx(sinx﹣cosx)=sin2x﹣cos2x﹣1=sin(2x﹣)﹣1=π.x)的最小正周期T=∴f((2)∵函数y=sinx的单调递减区间为[2kπ+,2kπ+](k∈Z)∴由2kπ+≤2x﹣≤2kπ+,x≠kπ(k∈Z)得kπ+≤x≤kπ+,(k∈Z)∴f(x)的单调递减区间为:[kπ+,kπ+](k∈Z)16.(14分)(2012?北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△ADE的位置,1使AF⊥CD,如图2.1(1)求证:DE∥平面ACB;1(2)求证:AF⊥BE;1(3)线段AB上是否存在点Q,使AC⊥平面DEQ?说明理由.11.;ACBAB的中点,易证DE∥平面,(1)DE分别为AC,【分析】1⊥平AFF⊥CD,可证,从而有DE⊥AF,又A)由题意可证(2DE⊥平面ADC1111,问题解决;面BCDE⊥DEDEPDEQ即为平面,由Q,则PQ∥BC,平面C(3)取A,AB的中点P,11CA ⊥平面DEP,从而底边AC的中点,可证AC平面,P是等腰三角形DAC1111.DEQ ⊥平面的中点,ABAC,)∵1D,E分别为【解答】解:(,CB平面A∥BC,又DE?∴DE1.CB∥平面A∴DE1,∥BC⊥BC且DE(2)由已知得AC,⊥AC∴DE,⊥CDD,又DE∴DE⊥A1,DC?平面A⊥平面DEADC,而AF∴111,CDF⊥⊥AF,又ADE∴11,⊥平面BCDEF∴A1.⊥BE∴AF1,C.理由如下:如图,分别取ACQ,使A⊥平面DEQ上存在点)线段(3AB111.BC,则QPQ∥的中点ABP,1,∥DEBC∵.PQ∴DE∥.即为平面∴平面DEQDEP由(Ⅱ)知DE⊥平面ADC,1∴DE⊥AC,1又∵P是等腰三角形DAC底边AC的中点,11∴AC⊥DP,1∴AC⊥平面DEP,从而AC⊥平面DEQ,11故线段AB上存在点Q,使AC⊥平面DEQ.11北京)近年来,某市为促进生活垃圾的分类处理,将生活垃2012?13分)(17.(圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,1000为调查居民生活垃圾分类投放情况,先随机抽取了该市三类垃圾箱总计;吨生活)试估计厨余垃圾投放正确的概率;1()试估计生活垃圾投放错误的概率;(2箱的投放量分别其他垃圾”可回收物”箱、“3)假设厨余垃圾在“厨余垃圾”箱、“(2最大时,写出s,c的方差+c=600.当数据a,ba为ab,,c,其中a>0,+b2的值.s的值(结论不要求证明),并求此时,ab,c2的平x,x…,=(求:S[,+…++],其中为数据xn21均数)吨,故可求厨余垃圾投”600(1)厨余垃圾吨,投放到“厨余垃圾箱400【分析】放正确的概率;故可求生活垃圾投放错误的概率;60200)(2生活垃圾投放错误有++20=30020+,=(3)计算方差可得2sc=0时,有,b=0,,因此有当a=600=80000.【解答】解:(1)由题意可知:厨余垃圾600吨,投放到“厨余垃圾”箱400吨,;故厨余垃圾投放正确的概率为(2)由题意可知:生活垃圾投放错误有200+60+20+20=300,故生活垃圾投放错;误的概率为(3)由题意可知:∵a+b+c=600,∴a,b,c的平均数为200,=∴2222222,因此有当a=600,b=0+c,2bc+2ac≥ac=0∵(a+b+c)+=ab+b时,+c+2ab+2=80000.有s23+bx.(x)=x)+1(a>0,分)18.(13(2012?北京)已知函数f(x)=axg (1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处有公共切线,求a,b的值;(2)当a=3,b=﹣9时,函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.【分析】(1)根据曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,可知切点处的函数值相等,切点处的斜率相等,故可求a、b的值;32﹣9x+=x1+3x,求导函数,确=fx)(x)+g(x)b=(2)当a=3,﹣9时,设h(定函数的极值点,进而可得k≤﹣3时,函数h(x)在区间[k,2]上的最大值为h (﹣3)=28;﹣3<k<2时,函数h(x)在区间[k,2]上的最大值小于28,由此可得结论.2+1(a>0),则f′(x)1f(x)=ax)=2ax,k=2a,【解答】解:(132+b,k=3+bbx,则g′(x)=3x,xg()=x+2由(1,c)为公共切点,可得:2a=3+b ①又f(1)=a+1,g(1)=1+b,∴a+1=1+b,即a=b,代入①式,可得:a=3,b=3.32﹣9x3x+(x)=x1+=f﹣9时,设h(x)(x)+g(2)当a=3,b=2+6x﹣9,则h′(x)=3x令h'(x)=0,解得:x=﹣3,x=1;21∴k≤﹣3时,函数h(x)在(﹣∞,﹣3)上单调增,在(﹣3,1]上单调减,(1,2)上单调增,所以在区间[k,2]上的最大值为h(﹣3)=28﹣3<k<2时,函数h(x)在区间[k,2]上的最大值小于28所以k的取值范围是(﹣∞,﹣3]19.(14分)(2012?北京)已知椭圆C:+=1(a>b>0)的一个长轴顶点为A(2,0),离心率为,直线y=k(x﹣1)与椭圆C交于不同的两点M,N,(Ⅰ)求椭圆C的方程;时,求的面积为k的值.(Ⅱ)当△AMN,可建立方程组,【分析】(Ⅰ)根据椭圆一个顶点为A (2,0),离心率为从而可求椭圆C的方程;22222k+)xx﹣消元可得﹣1)与椭圆C联立(1+2k4ky=k,(Ⅱ)直线(x ﹣4=0,从而可求|MN|,A(2,0)到直线y=k(x﹣1)的距离,利用△AMN的面积为,可求k的值.【解答】解:(Ⅰ)∵椭圆一个顶点为A (2,0),离心率为,∴∴b=;的方程为C∴椭圆22222k+﹣4kxx+(消元可得12k)C)﹣(直线,(Ⅱ)y=kx1与椭圆联立﹣4=0,则x+x=,)M(x,y,N(x,y)设212211=MN|=∴|∵A(2,0)到直线y=k(x﹣1)的距离为S=的面积∴△AMN∵△AMN的面积为,∴∴k=±1.20.(13分)(2012?北京)设A是如下形式的2行3列的数表,满足性质P:a,b,c,d,e,f∈[﹣1,1],且a+b+c+d+e+f=0.记r(A)为A的第i行各数之和(i=1,2),C(A)为A的第j列各数之和(j=1,ji2,3);记k(A)为|r(A)|,|r(A)|,|c(A)|,|c(A)|,|c(A)32211|中的最小值.)的最大值;A.求≤≤其中﹣1d0k()的最大值.(kA,求列的数表行的(Ⅲ)对所有满足性质P23Aj【分析】(),i=1行各数之和(的第A)为(Ar1)根据i2的第AC,)为A(ji列各数之和(j=1,2,3);记k(A)为|r(A)|,|r(A)|,|c(A)|,121|c(A)|,|c(A)|中的最小值可求出所求;32(2)k(A)的定义可求出k(A)=1+d,然后根据d的取值范围可求出所求;(III)任意改变A三维行次序或列次序,或把A中的每个数换成它的相反数,所**)(A(A)得数表A=k仍满足性质P,并且k因此,不防设r(A)≥0,c(A)≥0,c(A)≥0,然后利用不等式的性质可211知3k(A)≤r(A)+c(A)+c(A),从而求出k(A)的最大值.211【解答】解:(1)因为r(A)=1.2,r(A)=﹣1.2,c(A)=1.1,c(A)=0.7,2211c(A)=﹣1.8,3所以k(A)=0.7(2)r(A)=1﹣2d,r(A)=﹣1+2d,c(A)=c(A)=1+d,c(A)=﹣2﹣322112d 因为﹣1≤d≤0,所以|r(A)|=|r(A)|≥1+d≥0,|c(A)|≥1+d≥0321所以k(A)=1+d≤1当d=0时,k(A)取得最大值1(III)任给满足性质P的数表A(如下所示)abcdef任意改变A三维行次序或列次序,或把A中的每个数换成它的相反数,所得数**)A)=k(P,并且k(表AA仍满足性质因此,不防设r(A)≥0,c(A)≥0,c(A)≥0,211由k(A)的定义知,k (A)≤r(A),k(A)≤c(A),k(A)≤c(A),211从而3k(A)≤r(A)+c (A)+c(A)=(a+b+c)+(a+d)+(b+e)=(a+b+c+d+e+f)211+(a+b﹣f)=a+b ﹣f≤3所以k(A)≤1由(2)可知,存在满足性质P的数表A使k(A)=1,故k(A)的最大值为1.。
