D算法求最短路径
D算法,F算法,爱尔兰B,爱尔兰C公式的matlab例程

实验一:路径选择实验D算法:%D算法—求V1点到其他各点的最短路径function yy_ddisp('D算法:输入图G的全值矩阵W');d=input('w=');n=length(d);for i=1:nd(i,i)=inf;endtemp=[1];path=zeros(n);path(:,1)=ones(n,1);w=d(1,:);w(1)=0;wgt=w;x=1;y=1;for i=1:na(i)=i;enddisp('置定端集Gp:');for k=1:n-1min=inf;p=length(temp);q=length(wgt);for i=1:nin1=find(temp==i);for j=1:nin2=find(temp==j);if isempty(in1)&~isempty(in2)if wgt(i)>wgt(j)+d(j,i) wgt(i)=wgt(j)+d(j,i);endif min>wgt(i);x=i;min=wgt(i);endendendendw(x)=wgt(x);temp(p+1)=a(x);for i=1:nif w(x)==w(i)+d(i,x)y=i;endendl=1;while path(y,l)~=0l=l+1;endfor i=1:l-1path(x,i)=path(y,i);endpath(x,l)=a(x);disp('运算次数k=');disp(k);disp('此次运算得到的Gp:');disp(temp);enddisp('V1到其他各点的最短路径及径长:') for i=1:ndisp('目的节点i=');disp(i);disp('最短路径:')disp(path(i,:));disp('径长:')disp(w(i));endfigure(1);%hold off;clf;axis([1,10,0,5]);for k=1:10b(1,k)=k;endb(2,:)=rand(1,10)*5;text(1.05,b(2,1)+0.1,'v1');text(2,b(2,2)+0.1,'v2');text(3,b(2,3)+0.1,'v3');text(4,b(2,4)+0.1,'v4');text(5,b(2,5)+0.1,'v5');text(6,b(2,6)+0.1,'v6');text(7,b(2,7)+0.1,'v7');%text(8,b(2,8)+0.1,'v8');%text(9,b(2,9)+0.1,'v9');%text(10,b(2,10)+0.1,'v10');hold on;for i=2:nidage=path(i,:);c=1;while c<n&idage(c)~=0&idage(c+1)~=0 f=idage(c);g=idage(c+1);s=[b(1,f),b(1,g)];t=[b(2,f),b(2,g)];plot(s,t);hold on;c=c+1;endendfor e=1:nplot(b(1,e)-0.01,b(2,e),'bd');endtitle('D算法')%end%F算法—求解各端点之间的最短路径function yy_fdisp('F算法:输入图G的权值矩阵W0'); w0=input('w0=');n=length(w0);r0=zeros(n);for i=1:nfor j=1:nif w0(i,j)~=inf&i~=jr0(i,j)=j;elser0(i,j)=0;endendenddisp(w0);disp(r0);for k=1:nfor i=1:nfor j=1:nif i~=j&w0(i,j)>w0(i,k)+w0(k,j)w0(i,j)=w0(i,k)+w0(k,j);r0(i,j)=k;endendendfor x=1:nr0(x,x)=0;enddisp('节点k=');disp(k);disp('作为中间转接点时得到的W和R:')disp(w0);disp(r0);end实验二:通信业务量分析实验算法:function ErlangBpn=[];s=[];x=0.1:0.1:100;m=[1 2 3 4 5 6 7 8 9 10 15 20 30 35 40 50 60 70 80 90 100]; L=length(m);for i=1:Lfor a=0.1:0.1:100for k=0:m(i)s=[s,a.^k/factorial(k)];add=sum(s);endpn0=(a.^m(i)/factorial(m(i)))./add;pn=[pn,pn0];s=[];endloglog(x,pn);set(gca,'Xlim',[0.1 100]);set(gca,'XGrid','on');set(gca,'XMinorTick','off');set(gca,'XTick',[0.1 1.0 10.0 100]);%set(gca,'XMinorGrid','off');set(gca,'Ylim',[0.001 0.1]);set(gca,'YGrid','on');set(gca,'YMinorTick','off');%set(gca,'YTick',[0.001 0.002 0.005 0.01 0.02 0.05 0.1]);%set(gca,'YMinorGrid','off');hold onpn=[];endxlabel('话务量强度a(erl)','fontsize',8);ylabel('呼损率Pc','fontsize',8);hold offgtext('0.002');gtext('0.005');gtext('0.02');gtext('0.05');gtext('m=1','fontsize',15);for i=2:Lgtext('m=','fontsize',15);gtext(int2str(m(i)),'fontsize',15);endfunction ErlangCpc=[];s=[];m=[1 2 3 4 5 6 7 8 9 10 15 20 30 35 40 50 60 70 80 90 100];L=length(m);for i=1:Lfor a=1:100if a<=m(i)for k=0:(m(i)-1)s=[s,a.^k/factorial(k)];add=sum(s);endpc0=a.^m(i)/(a.^m(i)+factorial(m(i))*(1-a/m(i))*add);pc=[pc,pc0];s=[];endendx=1:length(pc);loglog(x,pc);set(gca,'XGrid','on');set(gca,'XMinorTick','off');set(gca,'Xlim',[1 100]);%set(gca,'XTick',[0.1 0.2 0.5 1 2 5 10 20 50 100]);%set(gca,'XMinorGrid','off');set(gca,'Ylim',[0.01 1]);set(gca,'YGrid','on');%set(gca,'YMinorTick','off');hold onpc=[];endxlabel('话务量强度a(erl)','fontsize',8);ylabel('呼叫等待概率Pw','fontsize',8);gtext('0.02');gtext('0.05');gtext('0.2');gtext('0.5');gtext('m=1','fontsize',15);for i=2:Lgtext('m=','fontsize',15);gtext(int2str(m(i)),'fontsize',15); end。
迪杰斯特拉算法步骤

迪杰斯特拉算法步骤简介迪杰斯特拉算法(Dijkstra’s algorithm)是一种用于在加权图中找到最短路径的算法。
它由荷兰计算机科学家艾兹赫尔·迪杰斯特拉于1956年提出,并被广泛应用于网络路由和地图导航等领域。
迪杰斯特拉算法的基本思想是从一个起点到其他所有顶点的最短路径逐步扩展,直到找到目标顶点的最短路径为止。
算法步骤迪杰斯特拉算法的步骤如下:步骤一:初始化1.创建一个空的最短路径表,用于保存每个顶点到起点的最短路径长度。
2.将起点的最短路径长度设置为0,将其他顶点的最短路径长度设置为无穷大(表示尚未计算出最短路径)。
3.创建一个空的已访问集合,用于保存已经计算过最短路径的顶点。
步骤二:选择最短路径顶点1.从起点开始,选择一个未访问的顶点,其最短路径长度最小。
2.将该顶点标记为已访问。
步骤三:更新最短路径1.对于当前选择的顶点,遍历其所有邻接顶点。
2.如果通过当前选择的顶点到达邻接顶点的路径长度小于该邻接顶点的最短路径长度,则更新该邻接顶点的最短路径长度。
步骤四:重复步骤二和步骤三1.重复步骤二和步骤三,直到所有顶点都被访问过或者找到目标顶点的最短路径。
步骤五:输出最短路径1.根据最短路径表,可以得到起点到每个顶点的最短路径长度。
2.根据最短路径表和邻接矩阵,可以还原出起点到每个顶点的最短路径。
实例演示为了更好地理解迪杰斯特拉算法的步骤,我们以一个简单的示例来进行演示。
假设有以下加权无向图:A/ \2 3/ \B---4----C\ 2 /\ /1 5\ /D我们的目标是求取顶点A到其他所有顶点的最短路径。
1.初始化最短路径表和已访问集合:–最短路径表:A(0), B(∞), C(∞), D(∞)–已访问集合:空2.选择最短路径顶点:起始顶点A的最短路径长度为0,因此选择A作为当前最短路径顶点。
3.更新最短路径:–从A出发,到达B的路径长度为2,小于B当前的最短路径长度(正无穷),因此更新B的最短路径长度为2。
弗洛伊德算法求解最短路径

弗洛伊德算法求解最短路径算法的基本思想是采用动态规划的方式,逐步地计算图中所有顶点对之间的最短路径长度。
算法首先初始化一个二维数组D,其中D[i][j]表示从顶点i到顶点j的最短路径长度。
初始时,D[i][j]的值为无穷大,表示顶点i到顶点j没有直接路径。
然后,算法通过逐步更新D数组的值,不断地优化顶点对之间的最短路径。
算法的具体步骤如下:1.初始化D数组:对于图中的每一对顶点i和j,如果i等于j,则置D[i][j]=0,表示顶点到自身的距离为0;否则,如果i和j之间有边存在,则置D[i][j]为边的权重,否则置为无穷大。
2.对于图中的每一个顶点k,依次考虑顶点对(i,j),其中i和j分别表示图中的任意两个顶点。
如果从顶点i先经过顶点k再到达顶点j的路径长度小于当前D[i][j]的值,则更新D[i][j]为新的较短路径长度。
3.对于每一对顶点i和j,以每一个顶点k为中间节点,重复步骤2、这样,在每一次迭代中,D数组会根据当前的顶点k得到更短的路径。
4.根据更新后的D数组,可以得到任意两个顶点之间的最短路径长度。
如果需要获取最短路径上的具体路径,则可以使用一个辅助数组P,其中P[i][j]表示从顶点i到顶点j的最短路径上,从顶点i到顶点j前一个顶点的编号。
通过回溯P数组,可以得到最短路径上的所有顶点。
弗洛伊德算法的时间复杂度为O(n^3),其中n表示图中顶点的个数。
由于要对所有顶点对之间的路径长度进行计算,因此算法的运行时间较长。
然而,该算法适用于复杂图中的最短路径计算,可以得到任意两个顶点之间的最短路径及其长度。
弗洛伊德算法在实际应用中有广泛的应用。
例如,在路由算法中,可以使用弗洛伊德算法来计算网络中所有节点之间的最短路径,并根据计算结果进行路由选择。
此外,弗洛伊德算法也可以应用于交通规划、航空航线优化等领域。
总之,弗洛伊德算法是一种用于求解图中所有顶点对之间最短路径的动态规划算法。
通过逐步更新路径长度的方式,可以得到任意两个顶点之间的最短路径及其长度。
D算法

最短路径--------------------------------------------------------------------------------从某源点到其余顶点之间的最短路径设有向网G=(V,E),以某指定顶点为源点v0,求从v0出发到图中所有其余各项点的最短路径。
以图5-5-1所示的有向网络为例,若指定v0为源点,通过分析可以得到从v0出发到其余各项点的最短路径和路径长度为:v0 → v1 :无路径v0 → v2 :10v0 → v3 :50 (经v4)v0 → v4 :30v0 → v5 :60 (经v4、v3)图5-5-1 带权有向图如何在计算机中求得从v0到其余各项点的最短路径呢?迪杰斯特拉(Dijkstra)于1959年提出了一个按路径长度递增的次序产生最短路径的算法。
其基本思想是:把图中所有顶点分成两组,第一组包括已确定最短路径的顶点(初始只包括顶点v0),第二组包括尚未确定最短路径的顶点,然后按最短路径长度递增的次序逐个把第二组的顶点加到第一组中去,直至从v0出发可以到达的所有顶点都包括到第一组中。
在这过程中,总保持从v0到第一组各顶点的最短路程长度都不大于从v0到第二组的任何顶点的最短路径长度。
另外,每一个顶点对应一个距离值,第一组的顶点对应的距离值就是从v0到此顶点的只包括第一组的顶点为中间顶点的最短路径长度。
设有向图G有n个顶点(v0为源点),其存储结构用邻接矩阵表示。
算法实现时需要设置三个数组s[n]、dist[n]和path[n]。
s用以标记那些已经找到最短路径的顶点,若s[i]=1,则表示已经找到源点到顶点vi的最短路径,若s[i]=0,则表示从源点到顶点vi的最短路径尚未求得,数组的初态只包括顶点v0,即s[0]=1。
数组dist记录源点到其他各顶点当前的最短距离,其初值为:dist[i]=G.arcs[0][i] i=1,2,…,n-1path是最短路径的路径数组,其中path[i]表示从源点v0到顶点vi之间的最短路径上该顶点的前驱顶点,若从源点到顶点vi无路径,则path[i]=-1。
dijkstra算法最短路径

《求解最短路径:应用迪杰斯特拉算法》一、介绍Dijkstra算法的概念和基本原理Dijkstra算法是一种用于解决最短路径问题的算法,它由荷兰计算机科学家Edsger Dijkstra在1959年发明,用于求解从源点到其他所有结点的最短路径。
它的基本原理是:在一张图中,从源点到每一个结点的最短路径是从源点开始,经过最少的边到达每一个结点的路径。
Dijkstra算法的实现过程中,首先要建立一个有向图,该图由顶点和边组成,每条边都有一个权值,表示从一个顶点到另一个顶点的距离。
然后,从源点开始,每次选择最小权值的边,继续查找下一个顶点,直到找到终点。
最后,将所有路径之和求出,即为源点到目标点的最短路径。
举例来说,假如有一张有向图,其中有A,B,C,D四个结点,以及AB,AC,BD,CD四条边,其中AB,AC,BD边的权值分别为2,3,1,CD边的权值为4。
如果要求求出从A到D的最短路径,则可以使用Dijkstra算法,首先从A出发,选择权值最小的边,即BD,则A-B-D的路径长度为3,接着从B出发,选择权值最小的边,即CD,则A-B-D-C的路径长度为7,因此,从A到D的最短路径为A-B-D,路径长度为3。
Dijkstra算法的优点是算法简单,实现方便,时间复杂度低,它可以用于解决路径规划,车辆调度,网络路由等问题,同时,它也可以用于解决复杂的最短路径问题。
因此,Dijkstra算法在计算机科学中有着重要的应用价值。
二、讨论Dijkstra算法的应用及其优势Dijkstra算法是一种用于解决最短路径问题的算法,它的应用和优势非常广泛。
首先,Dijkstra算法可以用于解决交通路网中的最短路径问题。
例如,在一个城市的交通路网中,如果一个乘客要从一个地方到另一个地方,那么他可以使用Dijkstra算法来查找最短的路径。
这样可以节省乘客的时间和金钱,也可以减少拥堵。
此外,Dijkstra算法还可以用于解决计算机网络中的最短路径问题。
迪杰斯特拉算法求最短路径表格

迪杰斯特拉算法求最短路径表格迪杰斯特拉算法(Dijkstra's algorithm)是一种用于寻找加权图中从单个源节点到所有其他节点的最短路径的算法。
它采用一种贪婪的策略,通过逐步扩展起点到终点的路径来找到最短路径。
本文将详细介绍迪杰斯特拉算法,并给出一个完整的最短路径表格。
算法描述:1.创建一个包含所有节点的集合,并初始化所有节点的距离为无穷大(除了起点为0)。
2.按照起点到各个节点的距离逐步更新节点的距离,直到找到所有节点的最短路径为止。
具体步骤如下:a.选取一个未加入集合的距离最小的节点,将其加入集合。
b.对于与该节点相邻的所有节点,更新它们的距离。
c.如果更新后的距离小于原来的距离,则更新节点的距离。
3.重复步骤2,直到所有节点都加入集合为止。
下面我们通过一个具体的例子来演示迪杰斯特拉算法求最短路径表格。
假设有如下的有向图:```+--++--+2+--+A,---->,B,--4->,D+--++--+,+--+v+--+3,+--+C,--->,+--++--+```图中每条边上的数字表示该边的权重。
首先,我们创建一个包含所有节点的集合,并初始化所有节点的距离为无穷大,起点A的距离为0。
节点,距离---,---A,0B ,infC ,infD ,infE ,inf然后选择起点A的邻居节点B和C中距离最小的节点B,将其加入集合。
节点,距离A,0B,2C ,infD ,infE ,inf接下来,更新节点B的邻居节点D和E的距离。
由于A到B的距离是2,加上B到D的距离为4,得到A到D的距离为6、同理,A到E的距离为5节点,距离---,---A,0B,2C ,infD,6E,5再次选择集合中距离最小的节点B,更新其邻居节点D和E的距离。
节点,距离---,---B,2C,11D,6E,5继续重复上述步骤,直到所有节点都加入集合。
节点,距离---,---A,0B,2C,11D,6E,5通过上述步骤,我们得到了从起点A到所有其他节点的最短路径距离。
多点最短路径算法

多点最短路径算法多点最短路径算法是一种用于计算多个起点到多个终点之间最短路径的算法。
在实际应用中,我们经常需要计算多个起点到多个终点之间的最短路径,例如在城市规划中,我们需要计算多个地点之间的最短路径,以便规划出最优的交通路线。
多点最短路径算法有多种实现方式,其中比较常用的有Floyd算法和Johnson算法。
Floyd算法是一种基于动态规划的算法,它通过逐步扩展中间节点的方式来计算最短路径。
具体来说,Floyd算法维护一个二维数组D,其中D[i][j]表示从i到j的最短路径长度。
算法的核心思想是:对于每个中间节点k,如果从i到j的路径经过k 比不经过k更短,则更新D[i][j]的值为D[i][k]+D[k][j]。
Johnson算法是一种基于Bellman-Ford算法的改进算法,它通过对图进行一次变换,将图中的负权边转化为非负权边,然后再使用Dijkstra算法来计算最短路径。
具体来说,Johnson算法首先使用Bellman-Ford算法计算出每个节点到其他节点的最短路径长度的下界,然后对图进行一次变换,将每条边的权值加上对应的下界值,从而将负权边转化为非负权边。
最后,使用Dijkstra算法来计算每个起点到每个终点的最短路径。
无论是Floyd算法还是Johnson算法,它们都可以有效地计算多个起点到多个终点之间的最短路径。
但是,由于算法的时间复杂度较高,因此在实际应用中需要根据具体情况选择合适的算法,并进行优化。
例如,在稠密图中,Floyd算法的时间复杂度为O(n^3),而Johnson算法的时间复杂度为O(n^2logn),因此在稠密图中,Floyd 算法更为适用。
而在稀疏图中,Johnson算法的时间复杂度更低,因此更为适用。
多点最短路径算法是一种非常重要的算法,它可以帮助我们计算多个起点到多个终点之间的最短路径,从而优化交通路线、网络通信等方面的应用。
在实际应用中,我们需要根据具体情况选择合适的算法,并进行优化,以提高算法的效率和准确性。
信号与系统毕业设计

2、设计方案论证
2.1最短路径的概念及算法介绍
最短路径问题是图论研究中的一个经典算法问题,旨在寻找图中两结点之间的最短路径。算法具体的形式包括:确定起点的最短路径问题即已知起始结点,求最短路径的问题。确定终点的最短路径问题与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题。在无向图中该问题与确定起点的问题完全等同,在有向图中该问题等同于把所有路径方向反转的确定起点的问题。确定起点终点的最短路径问题即已知起点和终点求两结点之间的最短路径。全局最短路径问题求图中所有的最短路径。用于解决最短路径问题的算法被称做“最短路径算法
沈阳大学
课程设计说明书NO.5
经S中顶点到Vk的路径权值之和初使时令S={V0},T={其余顶点},T中顶点对应的距离值ƒ若存在<V0,Vi>,为<V0,Vi>弧上的权值ƒ若不存在<V0,Vi>,为∝从T中选取一个其距离值为最小的顶点W,加入S对T中顶点的距离值进行修改:若加进W作中间顶点,从V0到Vi的距离值比不加W的路径要短,则修改此距离值重复上述步骤,直到S中包含所有顶点,即S=V为止。
3.3设计结果输出
图4节点0到各个节点得最短距离输出图
图Hale Waihona Puke 最小生成树图3.4设计结果与分析
沈阳大学
通信网作业答案
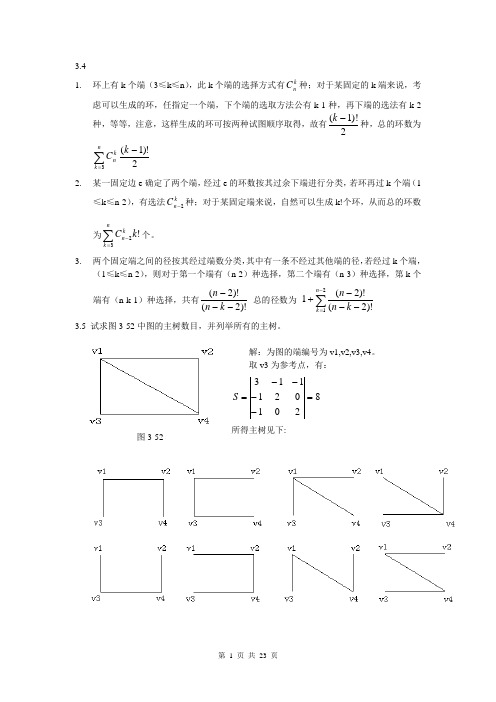
解:首先作出图形:
经计算:
因而有
其余有向径长均为∞,或不存在。
3.8 图有六个端,其无向距离矩阵如下:
1.用P算法,求出最短树。
2.用K算法,求出最短树。
3.限制条件为两端间通信的转接次数不超过2的最短树。
解:
1.P算法求解:
2.K算法求解:
按最小边长顺序取得: 此结果意味着最短树不唯一。
1)稳定条件为: 2b/c<1。
2)网络的平均时延:
对v1v2和v2v3间的业务:
对v1v3间的业务:
3)系统稳定时,总的通过量为:3b/c。
4)线路的平均利用率==2b/c。
一般来说,通过率与利用率均有增加,这是以稳定性和时延为代价换来的。
4.12在分组交换系统中,设信息包以泊松率到达,平均到达率为,但信息包的长度为固定b比特,信道容量为c比特/秒。由于端内存储量的限制,设除了在传送的包外,只允许有两个信息包等待传送,试:
解:
由于是D/D/1问题,故子系统运行情况完全确定,第一个顾客到达后,系统无顾客,经过b后,服务完毕,顾客离去,再经过a-b后,下一个顾客到达。
此时有:
顾客不等待时
G/G/1上界公式
当a<b时系统将不稳定,以恒定的速率增加顾客,即每隔 时间后,系统队列长度增长1。
4.7求M/E2/1即时拒绝系统的呼损,其中E2是二阶爱尔兰分布,
3.原图有一个边长全为1的基本子图G1,要求转接次数小于等于2,若选取G1的任何4个连续顶点, ,作为基础,然后再按要求增加边,例如以 为基础,增加 ,得到一个树长为7转接次数小于等于2的树T1,事实上,以任何4个连续顶点均可得到树长为7的转接次数小于等于2的树
最短路径算法——Dijkstra算法

最短路径算法——Dijkstra算法摘要:数据结构作为计算机科学的核心,已经成为人们必须掌握的一切信息知识。
作为经典的最短路径算法,Dijkstra算法数据结构被在生活中的各方面都有所体现。
本文从数据结构和最短路径算法的定义入手,介绍了Dijkstra算法的算法优缺点和算法实例,最后阐述了最短路径算法在现实生活中的作用,说明该算法的重要意义。
关键词:最短路径;Dijkstra算法;应用一、数据结构与算法1.1 数据结构数据结构是解释数据之间关系的科学。
典型的数据结构包括数组、链表、树和图[1]。
如何准确地使用各种数据结构至关重要。
这种数据结构就是图表,它是“树型”数据结构的扩展。
节点是一个节点(单独的节点),不能连接或连接到另一个节点。
结果,图中节点之间的关系变得更加复杂,并且通过计算机从一个节点到另一个节点的路径变得更加困难。
数据结构彼此具有一个或多个某种联系的元素数据汇总。
一般情况下,经过筛选的数据结构可以让用户感受到良好的体验或使用效率。
数据逻辑结构、数据存储结构和数据操作三部分是数据结构研究的主要内容。
线性结构和非线性结构一起组成了数据结构中的逻辑结构。
对线性结构的解释是:简单的一个表就是一种线性结构,这个表中所有的节点都符合线性关系。
除此之外,线性表是一种典型的线性结构,栈、队列、字符串都是线性结构。
对非线性结构的解释是:在一个简单表中的节点之间存在若干个对应关系是非线性结构。
在现实应用中,非线性结构主要包括了数组、树结构、图结构等数据结构。
1.2最短路径算法最短路径在图论中定义为在有向图中两结点间找一条权值最小的路径。
最短路径算法是对图状结构进行分析,找到需要的、合适的结点及路径,在交通、路径规划、城市建设、灾难逃生等领域广泛应用[2]。
最短路径法是一种机器学习技术,用于搜索连通图中结点之间的最短路径,是计算复杂系统中发现最优路径的有效方法。
最短路径法可以应用于许多不同类型的问题,包括路由算法、资源分配问题、最优布线、交通规划等,还可以被用于搜索引擎中搜索优化的相关工作。
Dijkstra算法

Dijkstra算法(重定向自Dijkstra 法)Dijkstra算法(狄克斯特拉算法)Dijkstra算法概述Dijkstra算法是由荷兰计算机科学家狄克斯特拉(Dijkstra)于1959 年提出的,因此又叫狄克斯特拉算法。
是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。
其基本原理是:每次新扩展一个距离最短的点,更新与其相邻的点的距离。
当所有边权都为正时,由于不会存在一个距离更短的没扩展过的点,所以这个点的距离永远不会再被改变,因而保证了算法的正确性。
不过根据这个原理,用Dijkstra求最短路的图不能有负权边,因为扩展到负权边的时候会产生更短的距离,有可能就破坏了已经更新的点距离不会改变的性质。
举例来说,如果图中的顶点表示城市,而边上的权重表示著城市间开车行经的距离。
Dijkstra 算法可以用来找到两个城市之间的最短路径。
Dijkstra算法的输入包含了一个有权重的有向图G,以及G中的一个来源顶点S。
我们以V表示G中所有顶点的集合。
每一个图中的边,都是两个顶点所形成的有序元素对。
(u,v)表示从顶点u到v有路径相连。
我们以E所有边的集合,而边的权重则由权重函数w: E → [0, ∞]定义。
因此,w(u,v)就是从顶点u到顶点v的非负花费值(cost)。
边的花费可以想像成两个顶点之间的距离。
任两点间路径的花费值,就是该路径上所有边的花费值总和。
已知有V中有顶点s及t,Dijkstra算法可以找到s到t的最低花费路径(i.e. 最短路径)。
这个算法也可以在一个图中,找到从一个顶点s到任何其他顶点的最短路径。
算法描述这个算法是通过为每个顶点v保留目前为止所找到的从s到v的最短路径来工作的。
初始时,源点s的路径长度值被赋为0(d[s]=0),同时把所有其他顶点的路径长度设为无穷大,即表示我们不知道任何通向这些顶点的路径(对于V中所有顶点v除s外d[v]= ∞)。
当算法结束时,d[v]中储存的便是从s到v的最短路径,或者如果路径不存在的话是无穷大。
最短路径算法——Dijkstra 算法

最短路径算法——Dijkstra算法一、最短路径问题最短路问题是图论理论的一个经典问题。
寻找最短路径就是在指定网络中两结点间找一条距离最小的路。
最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。
最短路径算法的选择与实现是通道路线设计的基础,最短路径算法是计算机科学与地理信息科学等领域的研究热点,很多网络相关问题均可纳入最短路径问题的范畴之中。
经典的图论与不断发展完善的计算机数据结构及算法的有效结合使得新的最短路径算法不断涌现。
在带权图(即网络)G=(V,E)中,若顶点v i,v j是图G的两个顶点,从顶点v i到v j 的路径长度定义为路径上各条边的权值之和。
从顶点v i到v j可能有多条路径,其中路径长度最小的一条路径称为顶点v i到v j的最短路径。
求最短路径具有很高的实用价值,在各类竞赛中经常遇到。
一般有两类最短路径问题:一类是求从某个顶点(即源点)到其他顶点(即终点)的最短路径;另一类是求图中每一对顶点间的最短路径。
本讲主要讲述一种单源最短路径(Single source shortest path)算法——Dijkstra 算法,用于解决非负权有向图的单源最短路径问题。
二、Dijkstra算法2.1 Dijkstra算法Dijkstra算法是典型最短路算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率偏低。
Dijkstra算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
2.2 Dijkstra算法思想对于图G=(V,E),假设(u,v)是E中的边,c u,v是边的长度(即边权)。
如果把顶点集合V划分为两个集合S和T:S中所包含的顶点,他们到u的距离已经确定;T中所包含的顶点,他们到u的距离尚未确定。
数学建模最短路径问题

数学建模最短路径问题
在数学建模中,求解最短路径问题是一个经典的问题。
在一个有向、加权图中,最短路径指的是从起点到终点路径上的各边权值之和最小的路径。
下面介绍两种常用的最短路径求解方法:
Dijkstra算法
Dijkstra算法是一种基于贪心策略的单源最短路径算法。
它的基本思想是从起点开始,不断扩展到其他结点,每次选择当前路径中距离最小的结点进行扩展。
具体步骤如下:
初始化距离数组dist[]为正无穷,起点距离设为0;
将起点加入集合S;
重复以下过程,直到所有结点都被加入集合S:
在非S中的结点中选择距离起点最近的结点w,并将它加入集合S;
对S中结点可以直接到达的结点v,更新它们的距离dist[v]为min{dist[v], dist[w]+边(w,v)的权值}。
Floyd算法
Floyd算法是一种多源最短路径算法,它通过动态规划的方式求解任意两个结点之间的最短路径。
具体步骤如下:
初始化距离矩阵D,如果结点i和结点j有边相连,则D[i,j]为边的权值,否则为正无穷;
三重循环求解任意两个结点之间的最短路径:
对于每对结点i和结点j,考虑是否经过中间结点k可以获得更短的路径。
即D[i,j] = min{D[i,j], D[i,k]+D[k,j]}。
最后得到的距离矩阵D即为任意两个结点之间的最短路径长度。
D算法

D*算法D*是动态A*(D-Star,Dynamic A*)卡内及梅隆机器人中心的Stentz在1994和1995年两篇文章提出,主要用于机器人探路。
是火星探测器采用的寻路算法。
主要方法:1.先用Dijstra算法从目标节点G向起始节点搜索。
储存路网中目标点到各个节点的最短路和该位置到目标点的实际值h,k(k为所有变化h之中最小的值,当前为k=h。
每个节点包含上一节点到目标点的最短路信息1(2),2(5),5(4),4(7)。
则1到4的最短路为1-2-5-4。
原OPEN和CLOSE中节点信息保存。
2.机器人沿最短路开始移动,在移动的下一节点没有变化时,无需计算,利用上一步Dijstra 计算出的最短路信息从出发点向后追述即可,当在Y点探测到下一节点X状态发生改变,如堵塞。
机器人首先调整自己在当前位置Y到目标点G的实际值h(Y),h(Y)=X到Y的新权值c(X,Y)+X 的原实际值h(X).X为下一节点(到目标点方向Y->X->G),Y是当前点。
k值取h值变化前后的最小。
3.用A*或其它算法计算,这里假设用A*算法,遍历Y的子节点,点放入CLOSE,调整Y的子节点a的h值,h(a)=h(Y)+Y到子节点a的权重C(Y,a),比较a点是否存在于OPEN和CLOSE 中,方法如下:while(){从OPEN表中取k值最小的节点Y;遍历Y的子节点a,计算a的h值h(a)=h(Y)+Y到子节点a的权重C(Y,a){if(a in OPEN) 比较两个a的h值if( a的h值小于OPEN表a的h值){更新OPEN表中a的h值;k值取最小的h值有未受影响的最短路经存在break;}if(a in CLOSE) 比较两个a的h值//注意是同一个节点的两个不同路径的估价值if( a的h值小于CLOSE表的h值){更新CLOSE表中a的h值; k值取最小的h值;将a节点放入OPEN表有未受影响的最短路经存在break;}if(a not in both)将a插入OPEN表中;//还没有排序}放Y到CLOSE表;OPEN表比较k值大小进行排序;}机器人利用第一步Dijstra计算出的最短路信息从a点到目标点的最短路经进行。
floyed算法 例题

floyed算法例题
弗洛伊德算法(Floyd's Algorithm),也称为弗洛伊德-沃舍尔算法(Floyd-Warshall Algorithm),是一种用于求解所有顶点对最短路径的动态规划算法。
它可以在有向图或带权图中计算出任意两个顶点之间的最短路径。
下面是一个使用弗洛伊德算法求解最短路径的简单例题:
假设有一个带权有向图如下所示:
图中的边上显示了权重,表示从一个顶点到另一个顶点的距离或代价。
我们要使用弗洛伊德算法计算出所有顶点之间的最短路径。
1.初始化距离矩阵,对于图中的边,用实际的权重赋值;对
于不可达的边,用一个很大的数(例如9999)表示。
2.使用弗洛伊德算法更新距离矩阵。
逐个顶点遍历,以k作
为中介顶点,在i、j两个顶点之间比较是否有更短的路径,
如果有则更新距离矩阵。
o k = A:
o k = B:
o k = C:
o k = D:
3.根据最终的距离矩阵,我们可以得到所有顶点之间的最短
路径。
使用矩阵的对角线元素,可以看出最短路径为:
o A到A的最短路径长度为0;
o A到B的最短路径长度为2,最短路径为A -> B;
o A到C的最短路径长度为1,最短路径为A -> C;
o A到D的最短路径长度为3,最短路径为A -> C -> D。
同样的,我们可以得到其他顶点之间的最短路径。
弗洛伊德算法通过动态规划的方式,逐步优化所有顶点之间的最短路径,时间复杂度为O(V^3),其中V为顶点的数量。
这使得它非常适用于解决小规模的图的最短路径问题。
最短路径算法与应用中的问题分析(史上最全路径算法总结)

二,任意权值的单源最短路径算法,解决上述问题 2.
1, 问题的描述: 给定一个有向带权图 D 与源点 v,各边上的权值为任意实数,要求找出从 v 出 发到 D 中其它各顶点的最短路径。 2, 算法的主要思想: 此种情况下我们可以用 Bellman-ford 算法。 当图中没有由带负权值的边组成的回 路时,有 n 个顶点的图中任意两个顶点之间如果存在最短路径,此路径最多有 n-1 条边。 Bellman-Ford 方法构造一个最短路径长度数组序列 dist1[u], dist2[u], …, distn-1[u],其中,dist n-1[u]是从源点 v 出发最多经过不构成带负长度边回路的 n-1 条边到达终点 u 的最短路径长度。算法的最终目的是计算出 dist
六,如果权值非负,求其总长最短的一条过全部节点的初级回路。解 决问题 7。
1,问题的描述: 给定一个正权完全图, 求其总长最短的哈密顿回路。 所谓的哈密顿回路便是无向 图中一条经过全部节点的初级回路。这个便是图论中非常经典的旅行商问题。 2,算法的主要思想: 解决旅行商问题的一种比较精确的求解方法是分支与界法。 分支与界法的基本思路是: 1, 首先将边权由小到大排序,初始界 d0 。 2, 在边权序列中依次选边进行深探,直到选取 n 条边,判断是否构成 H 回路, 若是, d0 d (s1) ,结束。 3, 继续深探, 依次删除当前 si 中的最长边, 加入后面第一条待选边, 进行深探, 如果它是 H 回路且 d( si ) d 0 ,则 d0 d ( si ) 作为界。 4, 退栈过程,不能再深探时需要退栈。如果栈空,结束,其最佳值为 d0。否则 如果新分支的 d( si ) d 0 ,继续退栈;若 d(si)<d0,转 3. 这种搜索过程是在不断的构造分支与确定界值。一旦确定了界值,则对大于等于 界值的分支不在搜索, 而且最后得到的界值就是问题的最佳解。但是在最坏的情 况下,该算法的时间复杂度是 O(n!)。因此在实际问题中,我们经常采用近似算 法求解问题的近似最优解,近似算法中比较好的是“便宜”算法。 便宜算法的基本思路: 初始化时 T=(1,1); S ={2,3, · · · ,n} T 是一个不断扩充的初级回路,最初是一个自环。首先我们选取 S 中与 T 距离最 近的节点 j。设(j,t)是相应的边,这时节点 j 或插入到回路 T 中 t 的前面或者 插入到其后面,这根据 j 插入后回路 T 长度增量的大小而定。即如果 ,则插入到 t 与 t1 之间,否则 w ( j ,t ) w ( j ,t 1) w( t ,t 1) w (j t , ) w (j t , 2 ) w t ( t, 2 ) 插入在 t 与 t2 之间。
最短路问题__D算法

5
2
3
4
6
7
8
4
8
p6=3
p7=3
min {d23,d53,d58,d78}=min {2+6,6+9,6+4,3+8}=min {8,15,10,11}=8
X={1,2,3,4,5,6,7}, p3=8
X={1,2,3,4,6,7}
p1=0 1
3
p2=2 2
2
1
10
p4=1
4
7
6
5
9
p5=6
5
p3=8 3
6
5
2
3
4
6 p6=3
7 4
p7=3
8 8
p8=10
min {d38,d58,d78}=min {8+6,6+4,3+7}=min {14,10,11}=10
X={1,2,3,4,5,6,7,8}, p8=10
X={1,2,3,4,6,7,8}
p1=0 1
3
p2=2 2
2
1
10
p4=1
m vj s{ T i(v nj) }mT i(v n 3)T { ,(v4)T ,(v5)T ,(v6)} T(v3)4, 所以 p(v3)有 4 ,
v2 2
3
v1
1
2
v4
4
2
T ( v 5 ) , P i ( v 3 ) n l 3 ] 5 m [5 , 4 4 ] i 5 n[
3
4
7
5
6
5
2
3
4
6
7
4
8 8
min {d12,d14,d16}=min {0+2,0+1,0+3}=min {2,1,3}=1 X={1,4}, p4=1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Dijkstra算法是典型的算法。Dijkstra算法是很有代表性的算法。Dijkstra一般的表述通常有两种方式,一种用永久和临时标号方式,一种是用OPEN, CLOSE表的方式,这里均采用永久和临时标号的方式。注意该算法要求图中不存在负权边。
首先,引进一个辅助向量D,它的每个分量D[i]表示当前所找到的从始点v到每个终点vi的的长度:如D[3]=2表示从始点v到终点3的路径相对最小长度为2。这里强调相对就是说在算法过程中D的值是在不断逼近最终结果但在过程中不一定就等于长度。它的初始状态为:若从v到vi有弧,则D为弧上的权值;否则置D为∞。显然,长度为 D[j]=Min{D | vi∈V} 的路径就是从v出发的长度最短的一条。此路径为(v,vj)。 那么,下一条长度次短的是哪一条呢?假设该次短路径的终点是vk,则可想而知,这条路径或者是(v,vk),或者是(v,vj,vk)。它的长度或者是从v到vk的弧上的权值,或者是D[j]和从vj到vk的弧上的权值之和。 一般情况下,假设S为已求得的终点的集合,则可证明:下一条最短路径(设其终点为X)或者是弧(v,x),或者是中间只经过S中的顶点而最后到达顶点X的路径。因此,下一条长度次短的的长度必是D[j]=Min{D | vi∈V-S} 其中,D或者是弧(v,vi)上的权值,或者是D[k](vk∈S)和弧(vk,vi)上的权值之和。算法描述如下: 1)arcs表示弧上的权值。若不存在,则置arcs为∞(在本程序中为MAXCOST)。S为已找到从v出发的的终点的集合,初始状态为空集。那么,从v出发到图上其余各顶点vi可能达到的度的初值为D=arcs[Locate Vex(G,v),i] vi∈V 2)选择vj,使得D[j]=Min{D | vi∈V-S} 3)修改从v出发到集合V-S上任一顶点vk可达的最短路径长度。
题目:设计一个运用改进的D算法进行物流系统路径优化的仿真程序,要求可随机或由用户操控产生物流网络示意图,并给出仿真结果。
引言
最短路径问题是图论中的一个重要问题,在交通运输、物流配送、网络分析等方面都有着广泛的应用,求解最短路径的方法也有很多,诸如动态规划法、启发式算法、迭代法等,本文就最经典的Dijkstra算法给出C语言程序并进行分析,提出一种改进的算法,并对改进算法进行算法分析。
if (newdist < dist[j])
{
dist[j] = newdist;
prev[j] = u;
}
}
}
}
}
//展示最佳路径函数
void ShowPath(int v,int u,int dist[MAXSIZE],int prev[MAXSIZE])
{
int j = 0;
int w = u;
改进算法实例分析:设有向带权图如图I所示,
应用改进的Dijkstra算法,其迭代过程如表1所示。
图一
三.改进的Dijkstra算法的C语言程序及仿真结果
改进的Dijkstra算法的C语言程序实现如下:
#include<stdio.h>
#include <stdlib.h>
#define MAXSIZE 20 //顶点最大个数
s[v] = 1;//源节点作为最初的s子集
for (i = 1; i < n; i++)
{
int temp = maxint;
int u = v;
//加入具有最小代价的邻居节点到s子集
for (j = 1; j <= n; j++)
{
if ((!s[j]) && (dist[j] < temp))
int count = 0;
int way[MAXSIZE] ;
//way=(int *)malloc(sizeof(int)*(n+1));
//回溯路径
while (w != v)
{
count++;
way[count] = prev[w];
w = prev[w];
}
//输出路径
printf("最佳路径是:\n");
printf("到达点%d的前一点是%d \n",i,prev[i]);
ShowPath(v,i, dist, prev);
}
}
}
仿真结果如图二所示:
图二
四.课设小结
本次我的课设内容是改进Dijkstra算法,通过自己动手设计的过程,更加深入地学习了解了各种GIS的最短路径搜索算法,尤其是Dijkstra算法的各种优化算法。程序化地解决问题是我们学工科的最基本的技能,对于D算法的改进,使我不仅深入学习到了课本中的知识,更加对于生活中的各种问题的优化有了新的见地。算法的用处十分广泛,他不仅能解决工程问题,更是能应用到生活生产的方方面面,研究算法能够极大地培养人的思维逻辑能力及做事的严谨性。一个算法你要将它转化成程序语言,是一个并不轻松的过程,当中有任何的细小失误都可能使程序运行失败。
// for (i = 1; i <= n; i++)
//{
// cost[i]=(int *)malloc(sizeof(int)*(n+1));
// }
//输入代价矩阵
for (j = 1; j <= n; j++)
{
for (t = 1; t <= n; t++)
{
scanf("%d",&cost[j][t]);
在本次课设的过程中,我学到了很多课本中学不到的知识技能பைடு நூலகம்并且由于是独立完成所以极大地培养了我独自完成一项任务的各方面综合能力,为以后走上工作岗位奠定了扎实的基础。
//Dijkstra算法实现函数
void dijkstra(int n,int v,int dist[MAXSIZE],int prev[MAXSIZE],int cost[MAXSIZE][MAXSIZE])
{
int i;
int j;
int maxint = 65535;//定义一个最大的数值,作为不相连的两个节点的代价权值
{
u = j;
temp = dist[j];
}
}
s[u] = 1;
//计算加入新的节点后,更新路径使得其产生代价最短
for (j = 1; j <= n; j++)
{
if ((!s[j]) && (cost[u][j] < maxint))
{
int newdist = dist[u] + cost[u][j];
int dist[MAXSIZE];//最短路径代价
int prev[MAXSIZE];//前一跳节点空间
printf("请输入顶点数: ");
scanf("%d",&n);
printf("请输入邻接矩阵:\n");
// cost=(int **)malloc(sizeof(int)*(n+1));
二.改进后的Dijkstra算法
改进算法如下:为了判断顶点之间的邻接关系方便,使用邻接链表的形式来存储有向带权图,邻接链表使用一维数组存储每个顶点的信息及指向单链表的指针,单链表用来存储与相应顶点邻接的顶点的信息以及每条边上的权值,集合s存储那些已经找到最短路径的顶点,初始只包含源点v。;数组dist记录从源点到其余各顶点当前的最短路径,初始时,数组dist存储从源点到其邻接顶点的权值,而对于其它非邻接顶点,则存储一个无穷大的数;数组pre存储最短路径上终点y之前的那个顶点,初始时pre[i]=Vo;数组heap用来进行堆排序,将数组heap的数据元素类型设为结构体类型,包括顶点信息及最短路径信息,初始时heap存储与v。邻接的顶点及这些顶点的当前路径最小值;数组m用来记录每个结点在堆中的位置,初始时只记录与vo邻接的顶点在堆中的位置,其余存储单元为0;算法利用堆排序算法按路径长度大小将heap调整成小头堆,取堆顶元素W,加入集合S,在堆中删除堆顶元素,并调整数组m中各顶点的位置值,然后比较以w作为中间结点.和w邻接的顶点集和S的差集中任意顶点v;的当前路径的大小,用小的值取代dist数组中的值,然后将修改了dist值的那些结点放人heap数组,并设置计数器k记录结点个数;最后将数组中的前k个元索按最短路径值调整成小头堆,取堆顶元素放入集合s,如此反复迭代,直到所有顶点都加入到集合S中为止。
printf("*****************************\n");
printf("路径展示\n");
printf("*****************************\n");
for(i = 1; i <= n ; i++)
{
if(i!=v)
{
printf("从点%d到点%d的最短距离为%d\n",v,i,dist[i]);
for (j = count; j >= 1; j--)
{
printf("%d -> ",way[j]);
}
printf("%d\n",u);
}
//主函数,主要做输入输出工作
void main()
{
int i,j,t;
int n,v;
int cost[MAXSIZE][MAXSIZE];//代价矩阵
}
}
//dist = (int *)malloc(sizeof(int)*n);
