哈工大材料力学试卷及答案
哈工大材料力学试卷及答案

一、填空题:请将正确答案写在划线内(每空1分,计16分) ⒈ 工程构件正常工作的条件是 ――――――――――――、、――――――――――――、―――――――――――――。
⒉ 工程上将延伸律------- δ的材料称为脆性材料。
⒊ 矩形截面梁横截面上最大剪应力max τ出现在―――――――――――各点,其值=τmax -------------。
4.平面弯曲梁的q 、F s 、M 微分关系的表达式分别为--------------、、-------------、、 ----------------。
5.四个常用的古典强度理论的表达式分别为―――――――――――――――――、―――――――――――――――――――――、 ――――――――――――――、―――――――――――――――――――――――――――――――――。
6.用主应力表示的广义虎克定律为 ――――――――――――――――――――― ;――――――――――――――――――――――;-―――――――――――――――――――――――。
二、单项选择题⒈ 没有明显屈服平台的塑性材料,其破坏应力取材料的――――――――――――。
⑴ 比例极限p σ; ⑵ 名义屈服极限2.0σ; ⑶ 强度极限b σ; ⑷ 根据需要确定。
2. 矩形截面的核心形状为----------------------------------------------。
⑴ 矩形; ⑵ 菱形; ⑶ 正方形; ⑷三角形。
3. 杆件的刚度是指――――――――――――――-。
⑴ 杆件的软硬程度; ⑵ 杆件的承载能力; ⑶ 杆件对弯曲变形的抵抗能力; ⑷ 杆件对弹性变形的抵抗能力;4. 图示二向应力单元体,如剪应力改变方向,则―――――――――――――。
⑴ 主应力的大小和主平面的方位都将改变;⑵ 主应力的大小和主平面的方位都不会改变; ⑶ 主应力的大小不变,主平面的方位改变; ⑷ 主应力的大小改变,主平面的方位不变。
材料力学习题答案 哈工业大材料力学本科生试卷和课后题目

材料力学习题答案2-4 a)MPa 15MPa,10-=='''y x x τσb)MPa 3.7MPa,3.47=='''y x x τσ c)MPa 65MPa,5.12-=-='''y x x τσd)MPa 6.60MPa,35-=='''y x x τσ e)MPa 5.20MPa,49.0=='''y x x τσf)MPa 0MPa,2.38=-='''y x x τσ2-6 a) MPa 32,0219MPa,7MPa,57max 21='=-==τασσσb)MPa 32,0219MPa,7MPa,57max 21='-=-==τασσσ c)MPa 25,45MPa,25MPa,25max 21==-==τασσσ d)MPa 2.41,9537MPa,2.71MPa,2.11max 21='=-==τασσσe) MPa 7.44,7113MPa,7.84MPa,7.4max 21='=-==τασσσ f)MPa 32,0219MPa,27MPa,37max 21='-=-==τασσσ 2-8 a) 略略;;))cos ),cos 1(,0),cos 1(0max 0320c b x στθσσσθσσ=-==+=2-10 1071=σMPa ,02=σ,203-=σMPa2-11 3.43-=xy τMPa ,3.43-''y x τMPa ,50='y σMPa2-137.841=σ MPa ,202=σMPa ,7.43-=σMPa ,1001=I MPa ,8002=I (MPa )2,240003=I (MPa )32-14 a)701=σ MPa ,602=σMPa ,303=σMPa ,70max =σMPa ,20max =τMPab) 501=σ MPa ,502=σMPa ,303=σMPa ,50max =σMPa ,10max =τMPa3-1 εx =0,εy =c ,εz =kx +iy +2gz ,γxy =b ,γyz =ix +2fy +jz +d ,γzx =2ex +iy +kz 。
材料力学习题(7)第十二章 哈工业大材料力学本科生试卷和课后题目

材料力学习题(7)第十二章哈工业大材料力学本科生试卷和课后题目材料力学习题第12章12-1 一桅杆起重机,起重杆AB的横截面积如图所示。
钢丝绳的横截面面积为10mm2。
起重杆与钢丝的许用力均为[?]?120MPa,试校核二者的强度。
习题2-1图习题12-2图12-2 重物F=130kN悬挂在由两根圆杆组成的吊架上。
AC是钢杆,直径d1=30mm,许用应力[?]st=160MPa。
BC是铝杆,直径d2= 40mm, 许用应力[?]al= 60MPa。
已知ABC为正三角形,试校核吊架的强度。
12-3 图示结构中,钢索BC由一组直径d =2mm的钢丝组成。
若钢丝的许用应力[?]=160MPa,横梁AC单位长度上受均匀分布载荷q =30kN/m作用,试求所需钢丝的根数n。
若将AC改用由两根等边角钢形成的组合杆,角钢的许用应力为[?] =160MPa,试选定所需角钢的型号。
12-4 图示结构中AC为钢杆,横截面面积A1=2cm2;BC杆为铜杆,横截面面积A2=3cm2。
[?]st = 160MPa,[?]cop = 100MPa,试求许用载荷[F]。
习题12-3图习题12-4图12-5 图示结构,杆AB为5号槽钢,许用应力[?] = 160MPa,杆BC为hb= 2的矩形截面木杆,其截面尺寸为b = 5cm, h = 10cm,许用应力[?] = 8MPa,承受载荷F = 128kN,试求:(1)校核结构强度;(2)若要求两杆的应力同时达到各自的许用应力,两杆的截面应取多大?习题12-5图习题12-6图12-6 图示螺栓,拧紧时产生?l = 0.10mm的轴向变形,试求预紧力F,并校核螺栓强度。
已知d1=8mm, d2=6.8mm, d3=7mm, l1=6mm, l2=29mm, l3=8mm; E=210GPa,[?]=500MPa。
12-7 图示传动轴的转速为n=500r/min,主动轮1输入功率P1=368kW,从动轮2和3分别输出功率P2=147kW和P3=221kW。
哈工程《材料力学实验》题库及答案

好像不可以,无法保证将应变片贴在材料内部又不改变材料的性能 79. 在应变计电测技术中,什么叫电桥平衡? 电桥输出电压为零 80. 在光弹性演示实验中,采用的光源是单色光吗? 是,也可以用白光 81. 什么是全桥测量? P119 电桥的四个桥臂上都接工作应变计 82. 请说出下列力学量的单位:弹性模量;屈服极限;应变。 E:GP :Pa με 83. 电子万能试验机的紧急制动按钮有什么作用?做试验时应该按下该按钮吗? 紧急关闭试验机,以防止发生危险或损坏试验机。不应该按下 84. 可以用电子万能试验机做矩形截面梁的纯弯曲试验吗? P144 好像可以 85. 画出铸铁拉伸过程的应力-应变曲线。 86. 光弹性演示试验中,什么是明场,什么是暗场? 两偏振片偏振轴互相平行为亮场,互相垂直为暗场 87. 本学期机测法的试验中,测定的是哪两种金属材料的力学性能? 低碳钢和铸铁 88. 工程实际中可以把铸铁材料作为抗压构件吗? P24 可以 = (4~8) 89. 相同尺寸的铸铁和低碳钢试件,哪个扭转性能更好些? 低碳钢 90. 在压缩试验中可以得到低碳钢的强度极限吗?为什么? 不可以。因为变形强化阶段后期,试件严重变形,但不会被压断,所以不能 91. 电测法中,电桥的基本特性是什么? P118 两相邻桥臂电阻所感受的应变代数值相减,而两相对桥臂电阻所感受的应变代数值相加 92. 请说出应变片的粘贴步骤。 ① 检查、分选应变计
② 表面清理 ③ 粘贴应变计 ④ 黏结层的固化 ⑤ 粘贴质量检查 ⑥ 连接线的焊接与固定 93. 写出拉压胡克定律和剪切胡克定律。 σ=Eε τ=Gγ 94. 若圆形截面试件的直径为 d,写出其抗扭截面模量的表达式。 = 95. 在测 G 试验中百分表转过 1 周,测得的相对位移是 0.5mm 还是 1.0mm? 1.0mm 96. 在电测法中,温度补偿片为什么可以消除工作应变片的温度效应? P118 因为二者粘贴部位温度始终相同,因此由温度引起的阻值改变相同,而二者又相邻,应变要做差,因 而可以消除影响 97. 能否用一片应变计测定薄壁压力容器的内压? 不清楚 98. 什么是半桥测量? P120 电桥的两个桥臂 AB 和 BC 上均接工作应变计 99. 光弹性演示实验中,所用的试件是什么材料制成的? 环氧树脂和聚碳酸酯 100. 谈谈你对《材料力学实验》课程的体会和建议。
哈工大材料力学试卷及答案

一、填空题:请将正确答案写在划线内(每空1分,计16分)⒈ 工程构件正常工作的条件是 ――――――――――――、、――――――――――――、―――――――――――――。
⒉ 工程上将延伸律------- δ的材料称为脆性材料。
⒊ 矩形截面梁横截面上最大剪应力max τ出现在―――――――――――各点,其值=τmax -------------。
4.平面弯曲梁的q 、F s 、M 微分关系的表达式分别为--------------、、-------------、、----------------。
5.四个常用的古典强度理论的表达式分别为―――――――――――――――――、―――――――――――――――――――――、――――――――――――――、―――――――――――――――――――――――――――――――――。
6.用主应力表示的广义虎克定律为 ――――――――――――――――――――― ;――――――――――――――――――――――;-―――――――――――――――――――――――。
二、单项选择题⒈ 没有明显屈服平台的塑性材料,其破坏应力取材料的――――――――――――。
⑴ 比例极限p σ; ⑵ 名义屈服极限2.0σ;⑶ 强度极限b σ; ⑷ 根据需要确定。
2. 矩形截面的核心形状为----------------------------------------------。
⑴ 矩形; ⑵ 菱形; ⑶ 正方形; ⑷三角形。
3. 杆件的刚度是指――――――――――――――-。
⑴ 杆件的软硬程度; ⑵ 杆件的承载能力;⑶ 杆件对弯曲变形的抵抗能力; ⑷ 杆件对弹性变形的抵抗能力; 4. 图示二向应力单元体,如剪应力改变方向,则―――――――――――――。
⑴ 主应力的大小和主平面的方位都将改变;⑵ 主应力的大小和主平面的方位都不会改变;⑶ 主应力的大小不变,主平面的方位改变;⑷ 主应力的大小改变,主平面的方位不变。
哈尔滨工业大学期末考试试题(B卷)

哈工大2002年春季学期题号-一--二二三四五六七八九附加分总分得分班级姓名一、单选或多选题(每小题3分,共8小题24分)1.某点为平面应力状态(如图所示),该点的主应力分别为A = 50MPa、二2 =0 、3=° -B二50MPa、二2=50 MPa、匚3= 0;C -1 =0、匚 2 二50 MPa、■T 3 = 0 -D -1 =0、二2 = 0、-3 : "50MPa。
正确答案是___________50er (MPtL)2.关于弹性体受力后某一方向的应力与应变关系有如下论述: 正确的是。
A 有应力一定有应变,有应变不一定有应力;B 有应力不一定有应变,有应变不一定有应力;C 有应力不一定有应变,有应变一定有应力;D 有应力一定有应变,有应变一定有应力。
3•下面有关体积应变的几个论述,正确的是________________A 与平均应力成正比;B与平均应力成反比;C与三个相垂直面上的正应力之和有关;D与平均应力无关。
4.下面有关应变能的几个论述,正确的是A与载荷的加载次序有关,与载荷的最终值无关;B与载荷的加载次序无关,与载荷的最终值无关;C与载荷的加载次序有关,与载荷的最终值有关;D 与载荷的加载次序无关,与载荷的最终值有关。
5•关于斜弯曲变形的下述说法,正确的是_________________A中性层与挠曲线所在的面正交;B中性轴过横截面的形心;C挠曲线在载荷作用面内;D挠曲线不在载荷作用面内。
A 单位力(广义)只能加在载荷作用点处;B单位力(广义)只能加在欲求位移的点处;C只能加单位集中力;D 只能加单位集中力偶。
正确的是_____________ 。
7 •压杆的稳定性,A 与压杆所承受的轴向压力大小有关;B与压杆的临界力大小有关;C 与压杆所承受的轴向压力大小无关;D 与压杆的临界力大小无关。
正确答案是___________& 自由落体冲击时的动荷系数,A 与被冲击物的刚度有关;B与自由落体下落的高度有关;C 与被冲击物的刚度无关;D 与冲击刚发生时,自由落体下落的速度有关。
材料力学试题及答案哈尔滨工业大学
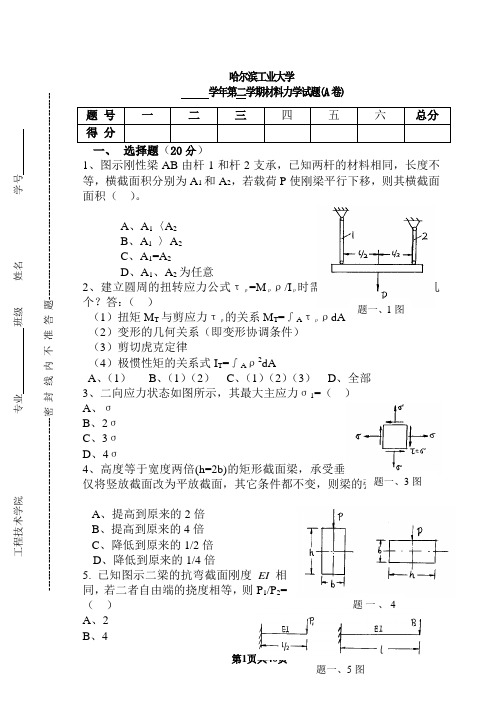
哈尔滨工业大学学年第二学期材料力学试题(A 卷)一、 选择题(20分)1、图示刚性梁AB 由杆1和杆2支承,已知两杆的材料相同,长度不等,横截面积分别为A 1和A 2,若载荷P 使刚梁平行下移,则其横截面面积( )。
A 、A 1〈A 2B 、A 1 〉A 2C 、A 1=A 2D 、A 1、A 2为任意2、建立圆周的扭转应力公式τρ=M ρρ/I ρ时需考虑下列因素中的哪几个?答:( )(1)扭矩M T 与剪应力τρ的关系M T =∫A τρρdA (2)变形的几何关系(即变形协调条件) (3)剪切虎克定律(4)极惯性矩的关系式I T =∫A ρ2dA A 、(1) B 、(1)(2) C 、(1)(2)(3) D 、全部 3、二向应力状态如图所示,其最大主应力σ1=( ) A 、σ B 、2σ C 、3σ D 、4σ4、高度等于宽度两倍(h=2b)的矩形截面梁,承受垂直方向的载荷,若仅将竖放截面改为平放截面,其它条件都不变,则梁的强度()A 、提高到原来的2倍B 、提高到原来的4倍C 、降低到原来的1/2倍D 、降低到原来的1/4倍5. 已知图示二梁的抗弯截面刚度EI 相同,若二者自由端的挠度相等,则P 1/P 2=( )A 、2B 、4题 号 一 二 三 四 五 六 总分 得 分题一、3图 工程技术学院 _______________专业 班级 姓名____________ 学号---------------------------------------------------密 封 线 内 不 准 答 题-------------------------------------------------------------题一、4题一、1图C 、8D 、16二、作图示梁的剪力图、弯矩图。
(15分)三、如图所示直径为d 的圆截面轴,其两端承受扭转力偶矩m 的作用。
设由实验测的轴表面上与轴线成450方向的正应变,试求力偶矩m 之值、材料的弹性常数E 、μ均为已知。
哈尔滨工业大学期末材料力学本科试题(B)

哈工大2004年春季学期期末材料力学试题(B)题号-一- -二二三四五六七八九十总分分数8 12 10 8 8 4(注意:本试题满分分)、(8分)单项选择题(共4个小题,每小题2分,合计8分)1材料的失效模式_________ 。
A只与材料本身有关,而与应力状态无关;B与材料本身、应力状态均有关;C 只与应力状态有关,而与材料本身无关;D与材料本身、应力状态均无关。
2 •关于偏心拉伸(压缩)变形的下述说法,正确的是____________A 只发生平面弯曲这一种变形;B中性轴通过横截面的形心;C中性轴不通过横截面的形心;D 只发生拉伸(压缩)这一种变形。
3.对莫尔积分(单位载荷法)的下述讨论,正确的是_____________A仅仅适用于弯曲变形;B 等式两端具有不相同的量纲;C 等式两端具有相同的量纲;D仅仅适用于曲杆。
r、平均应力m、应力幅值'-a分别为A 40、20、10;B 20、10、20 ;C 0、20、10;D 0、20、20。
正确答案是(应力单位为、(12分)直径d =100mm的横梁CD,由直径d l =35mm的支杆AB支承,尺寸如图所示。
AB杆材料为Q235钢,其材料常数见下表。
若横梁CD材料许用应力[刁=160 MPa, AB支杆许用稳定安全系数[n]st=3.0。
试求该结构所能承受的最大载荷q max。
(忽略截面剪力与轴力)E a P a S a bGPa MPa200 200 240 310 1.144.图示交变应力的循环特征三、(10分)平面刚架如图所示。
其各部分的抗弯刚度均为常量 试求点D 在铅垂方向的位移 V D 。
(忽略截面剪力与轴力)B亠.■4四、(8分)直径d =60mm 的圆截面折杆, A 端固定,受力与其他尺寸如图所示。
若材料的许用应力[二]^OOMPa ,试按最大切(剪)应力强度理论(第三强度理论)校核 A端外表面点b 的强度(忽略剪切)。
五、(8分)图示为某构件内危险点的应力状态(图中应力单位为 MPa ),试分别求其第、第四强度理论的相当应力Cr2、二r4 ( " =0.3 )。
材料力学习题哈工业大材料力学本科生试卷和课后题目
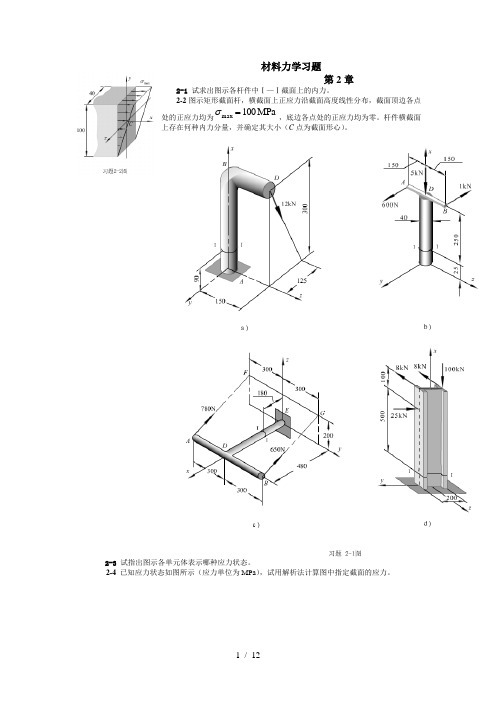
材料力学习题第2章2-1 试求出图示各杆件中Ⅰ—Ⅰ截面上的内力。
2-2图示矩形截面杆,横截面上正应力沿截面高度线性分布,截面顶边各点处的正应力均为MPa100max=σ,底边各点处的正应力均为零。
杆件横截面上存在何种内力分量,并确定其大小(C点为截面形心)。
2-3 试指出图示各单元体表示哪种应力状态。
2-4 已知应力状态如图所示(应力单位为MPa),试用解析法计算图中指定截面的应力。
2-5 试作应力圆来确定习题2-4图中指定截面的应力。
2-6已知应力状态如图所示(应力单位为MPa ),试用解析法求:(1)主应力及主方向;(2)主切应力及主切平面;(3)最大切应力。
2-7 已知应力状态如习题2-6图所示,试作应力圆来确定:(1)主应力及主方向; (2)主切应力及主切平面;(3)最大切应力。
2-8已知构件内某点处的应力状态为两种应力状态的叠加结果,试求叠加后所得 应力状态的主应力、主切应力。
2-9图示双向拉应力状态,σσσ==y x 。
试证明任一斜截面上的正应力均等于σ,而切应力为零。
2-10 已知K 点处为二向应力状态,过K 点两个截面上的应力如图所示(应力单位为MPa )。
试分别用解析法与图解法确定该点的主应力。
2-11 一点处的应力状态在两种坐标系中的表示方法分别如图 a)和b)所示。
试确定未知的应力分量y y x xy '''σττ、、的大小与方向。
2-12 图示受力板件,试证明尖角A 处各截面的正应力与切应力均为零。
2-13 已知应力状态如图所示(单位为MPa ),试求其主应力及第一、第二、第三不变量321II I 、、。
2-14 已知应力状态如图所示(单位为MPa ),试画三向应力圆,并求主应力、最大正应力与最大切应力。
第3章3-1 已知某点的位移分量u = A , v = Bx +Cy +Dz , w = Ex 2+Fy 2+Gz 2+Ixy +Jyz +Kzx 。
哈工大2007年材料力学期末考试A卷附有答案资料

哈工大2007年材料力学期末考试A卷附有答案1. 单项选择题: (共8小题,每小题3分,总分24分) 1-1. 以下关于虚功和虚位移的论述中正确的是( b ).A. 力F在其虚位移d上所作的功为/2Fd B. 虚位移必须满足位移约束条件C. 虚位移引起的系统能量变化比真实位移引起的小 D.虚功只能由外力引起1-2. 以下( a ) 不是疲劳的特征.A. 破坏时名义应力值等于材料的静强度值B. 构件需要经过一定的应力循环才破坏C. 破坏断面明显划分为光亮区域与颗粒状的粗糙区域D. 破坏是脆性断裂1-3. 关于面积相同的圆形和正方形截面(如图1-3所示),对各自主轴x的抗弯能力,以下描述正确的是( a ).A. ()()>.a bb a>. B. ()()C. ()()=. D. 两者相差超过50%a b图1-3 图1-41-4. 图1-4所示结构的静不定次数是( c )A. 1 次B. 2 次C. 3次D.4次1-5. 如图1-5所示,梁在其中点处受一集中载荷F。
假设梁的横截面宽度保持不变,若按等强度观点设计梁的横截面高度,那么梁的大致形状是( c )图1-51-6. 直径为d的圆形截面和边长为a的正方形截面对其各自形心轴的惯性半径分别是( a ).A. /4d和/(23)aB. /(22)ad和/6C. /4ad和/2D. /(22)d和/(23)a1-7. 以下关于第三和第四强度理论的论述中正确的是(a )A. 满足第三强度理论必然满足第四强度理论B. 满足第四强度理论必然满足第三强度理论C. 有时(A)成立,有时(B)成立D. 两强度理论并无必然联系1-8. 关于梁的弯曲,以下不正确的是( c )A. 各类挠曲线方程都是分段成立的B. 在各段上分布外载、剪力和弯矩函数依次越来越光滑C. 应用22=时可以用剪力匹配条件来确定未知参数d v dx M x/()D. 挠度函数()dv x dx总是连续的v x及()/2. 图2所示梁AC刚度为EI。
哈尔滨工程大学材料力学试卷
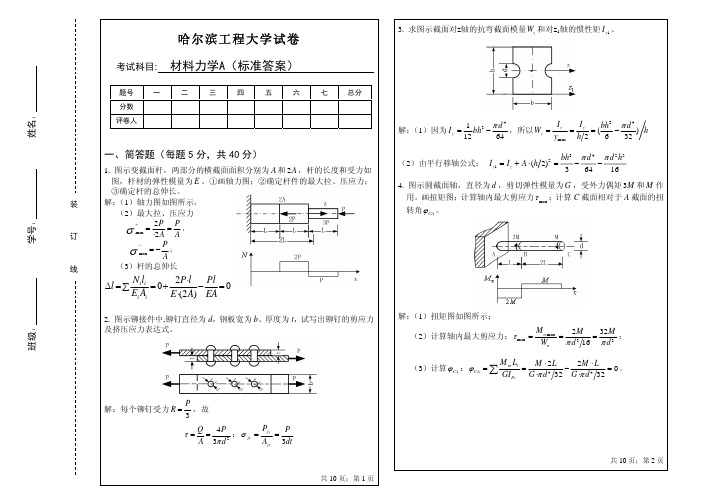
最大动应力:
32M ,平均应力 σ m = 0 π d3
σ d max = kd
⎛ Q 2hEπ d 2 = ⎜1 + 1 + 5Ql πd2 / 4 ⎜ ⎝
⎞ 4Q ⎟ 2 ⎟πd ⎠
共 10 页;第 4 页 共 10 页;第 3 页
二、画图示外伸梁的剪力图、弯矩图,并确定 Q max 、 M
max
fE =
1 ∂M ( x) M ( x) dx = 0 ∫ EI ∂M
将各内力代入后可得: yc =
fE =
2a 1 ⎡ a M dx + ∫ [ M − P( x − a)]dx ⎤ ⎥ a ⎣ ⎦ EI ⎢ ∫0 1 = 2 Ma − Pa 2 = 0 2
1 Pa 4 3 由平衡方程,RA=P, M A = Pa 。由对称性知A与B处的反力相等, 4 3 即 M B = M A = Pa ,且有RB=RA=P。 4
M ni Li M ⋅ 2L 2M ⋅ L = − = 0。 4 GI Pi G ⋅π d 32 G ⋅π d 4 32
解:每个铆钉受力 R =
P ,故 3
τ=
Pjy P Q 4P ; σ jy = = = 2 A 3π d Ajy 3dt
共 10 页;第 2 页 共 10 页;第 1 页
5. 空心圆轴横截面上扭矩为 M n ,方向如图,内、外径分别为 d 和 D,在图 上画出扭转剪应力分布规律,并写出内壁上点 A 的扭转剪应力表达式。
将 E = 200GPa , µ = 0.3 , D = 1m , t = 1cm 代入上式得
姓名:
解: 1)求约束反力 ( 线
RA =
7 3 qa (方向向上) RB = qa (方向向下) , 4 4
哈工大材料力学期末考卷

哈工大2007年春季学期 材料力学期中考试试题Mechanics of Materials Midterm Exam Spring 2007(NOTE: This midterm exam, 100 marks in total, is worth 25 percent of your final score.) 1. S INGLE C HOICE Q UESTIONS : (7 questions, 3 marks each, 21 marks in total) 1-1. After cold-work hardening processing,which of the following properties of steel will remain approximately the same?( )A. modulus of elasticityB. proportional limitC. percent elongationD. percent reduction in area1-2. On the mechanical properties of cast iron, the following two statements are made: (1). its shear resisting capability is weaker than that of tension resisting;(2). its compressive strength is higher than its tensile strength. Among them, ( ) A. (1) is true, (2) is false . B. (1) is false, (2) is true . C. (1) is true, (2) is true . D. (1) is false, (2) is false .1-3. In Fig. 1-3, two prismatic bars are shown, one with a circular cross-section, the other one with a square cross-section. If both bars are made of the same material and they have the same cross-sectional area, but with different length, when subjected to the same axial force F , their ( ) are NOT the same.A. axial normal stress sB. axial strain eC. axial elongation l DD. lateral strain e ¢Fig. 1-3 Fig. 1-41-4. In Fig. 1-4, among the three strain gauges bonded to the surface of a circular shaft subjected to torsion, the reading of strain from gauges ( ) will almost be zero. A. 1 and 2 B. 2 and 3 C. 1 and 3 D. 1, 2 and 31-5. For an arbitrary shape shown in Fig. 1-5, when the z axis moves downward away from the centroid C in a parallel fashion, then ( )(Note: z S is the first moment of the area about the z axis)A. z S increases , z I decreases .B. z S decreases , z I increases .C. z S increases , z I increases .D. z S decreases , z I decreases .Fig. 1-5 Fig. 1-61-6. The two bars (a) and (b) shown in Fig. 1-6 are made of the same material and have identical cross-sectional area. After deformation, their longitudinal axes become two concentric arcs. If a s and b s are the maximum normal stress in beam (a) and (b), respectively, then ( )A. a b s s <.B. a b s s =.C. a b s s >.D. it is uncertain about a s and b s ’s relation .1-7. A cantilevered beam is made from two channel sections laid back to back without any bonding in between, as shown in Fig. 1-7. A concentrated force F is applied at its right end. Which of the following plots describes the correct normal stress distribution on the cross-section? ( )Fig. 1-72. Shown in Fig. 2 is a differential element from a structural member. AC is a free surface (traction free). Determine: (1) all the three principal stresses; (2) the distortion strain energy density f u . Take 200GPa E = and 0.3n =. (12 marks)Fig. 23. For a material with two elastic constants E and n , if x e and y e are obtained from experiment, show that for a general plane stress state, the following statements are true,22,1,1().1x yx y xy z x y EE e ne s n e ne s n ne e e n +=-+=-=-+- (12 marks)4. Shown in Fig. 4 are two prismatic bars connected by a rigid triangular plate. Bar 1 (the horizontalone) is made of steel and has a cross-sectional area of 2110cm A =. Bar 2 (the vertical one) is made of copper and has a cross-sectional area of 2220cm A =. All members are pin-supported or pin-connected. Determine the average normal stress acting on the cross sections in bars 1 and 2 when a load of 200kN F = is applied. Take 1200GP a E = and 2100GP a E = for the modulus of elasticity for steel and copper, respectively. (15 marks)Fig. 45. The cross-section of a solid circular shaft is shown in Fig. 5. The shaft has a diameter of 50mm d = and is subjected to a torque of 1kN m T = applied at its two ends. Determine (1) the shear stress and shear strain on the cross-section at a radius of /4A d r =; (2) the maximum shear stress and the angle of twist per unit length.Take the shear modulus of elasticity 80GPa G =. (15 marks)Fig. 56. Draw the shear and moment diagrams for the beam shown in Fig. 6. (12 marks)Fig. 67. For the cantilevered beam shown in Fig. 7, draw the state of stress of elements located at pointsA B C D E. Also, present the formulas for the calculation of all the stress components at each point. ,,,,(13 marks)Fig. 7。
哈工大材料力学2010年春期中考试试题及答案

剪力 和 弯矩 问 的微 分 关 系 鼻 考虑此
•B 兰 k N 6
( 竖 直向上 )
'
我
处 的跳 跃
可 得 如儗
剪
6
注意
此 为 英 文教 材作 法
中文慧佳囟符号 倒转
剪 力 图 需上 下 翻 转
或者 用 截 面 法
求得 僕下 分 段 表达 式
(X
1
) kN
m
,
o
[
×
S 4
目丅
丅为 达 成 目 的
再同
行 制成
为
十偛
的立 方 体
¬
如图
1
所示
有 沿
科 学 家 先 将材 料
向 两表面 始终被因
x
和 傾方 向 分 别 施 加
( 此处
) 和
的正 应 变
在 加 载过 程 中
E
立方体
规
范
定住
实 验 仪 器记 录 到 了 应 变 能 u 同
U •B
的
系列 对应 值
G
并按 抛 物 线 拟 合成
·
.
E, A
E, A .
只储 E, A ,
.
·
s(
琴 辱)
,, .
°
. •B
(压 应 力)
多 2o 由 于 第2 4 号 齿 轮 输 入 功 率 其 上 输 入 扭 矩 即 沿 旋 转 方 向 其余 齿 轮 输 出 功 事 砬 ÃÖ 所 虿 扭 矩 抵 抗 旋 转 故 与 旋 转 方 向相 反 现 计 算各 输 出 齿轮 上 所 受 扭 矩
z
°
此为英文教材作法
+
生 熬材 因 符号 倒转 剪应 变需上 下 翻 转 旋 转 亦 相应 调 整 少
哈工程材料力学考题整理

哈尔滨工程大学试卷考试科目:材料力学B一简答题(每题5分,共40分)1、等截面圆杆受力如图,弹性模量200E GPa =,若杆的总伸长不允许超过1mm ,试求杆的直径的最小值。
60kN20kN200mm200mm2、空心圆轴横截面上扭矩为n M ,方向如图,内、外径分别为d 和D ,在图上画出扭转剪应力分布规律图,并写出内壁上点A 的扭转剪应力表达式。
dDAonM 共9页;第1页3、螺栓联接结构受力如图,两板宽均为b 、厚均为t 。
若材料的拉(压)、剪切、挤压许用应力分别为[]σ、[]τ、jy σ⎡⎤⎣⎦。
写出该联接件的强度条件。
dtt PP4、求图示图形的形心位置及对形心轴c y 轴的惯性矩yc I 。
(图中尺寸单位为mm )30cy C cz 3030909030共9页;第2页班级:学号:姓名:装订线题号一二三四五六总分分数评卷人5、圆轴扭转时,测得与轴线呈45 角方向上的线应变45εε=-,拉压弹性模量E 和泊松比 已知。
试求横截面上的剪应力τ。
eM eM 456、写出弯曲对称循环情况下构件的持久极限计算表达式,并说明各量的含义。
共9页;第3页7、重量为Q 的重物自由下落在图示刚架的C 点,设材料的抗弯刚度EI 和抗弯截面模量W 均已知,且已知C 点的静变形343j Qa EI ∆=。
试求冲击时刚架内的最大正应力(轴力影响不考虑)。
CBAaaHQ8、试绘制某塑性材料的临界应力总图(中长杆用直线型经验公式),并标出各段计算临界应力的公式。
共9页;第4页班级:学号:姓名:装订线二、画出图示梁的剪力图、弯矩图,并确定max Q 和maxM。
(12分)BAa aCq2qaqa212qa 212qa max Q qa=2max12Mpa =QMxx共9页;第5页三、如图圆截面轴。
已知2.n M kN m =,11P kN =,2 1.5P kN =,[]150MPa =,横截面直径80d mm =。
材料力学 哈工大2018期末试题及答案
哈工大2018年春季学期材料力学期末考试参考答案一、(20分)参考答案方法1:BC 段均布载荷导致:θ1A =−q (2l )324EI =−ql 33EI ;v 1D =−5q (2l )4384EI =−80ql 4384EI 。
AB 段悬臂梁,BC 段刚化导致:θ2A =ql 36EI ;v 2D =0。
AB 段刚化,其上均布载荷等效至B 点,由弯矩ql 22导致:θ3A =ql 222l 3EI =ql 33EI ;v 3D =ql 22(2l )216EI =ql 48EI叠加后得到:θA =θ1A +θ2A +θ3A =ql 36EI(逆时针);此项合10分v D =v 1D +v 2D +v 3D =−ql 412EI (向下)。
此项合10分方法2:叠加法θq B =q (2l )324EI =ql 33EI (↻);θM B =q2l 2⋅2l 3EI =ql 33EI(↺)因此θB =0,θA =θB +ql 36EI =ql 36EI (↺,逆时针)此项合10分v D =5q (2l )4384EI −12ql 2⋅(2l )216EI =5ql 424EI −ql 48EI =ql 412EI (↓,向下)此项合10分**若有用其它方法求解的,均按θA (10分),v D (10分)处理。
二、(24分)参考答案此为一次静不定问题,取HJFl l 1(a)(b)(c)(d)J(1)力法方程:X 1δ11+∆1F =0中与静不定判定一起合为4分图(c)自乘:δ11=1⋅1⋅l EA +1EI (12l ⋅l ⋅23l +l ⋅l ⋅l )=l 38EI +4l 33EI =35l 324EI 5分图(a+b 与c)图乘:∆1F =−1EI 12l ⋅l 2⋅Fl 2+1EI (l ⋅l ⋅Fl +l 2⋅Fl ⋅34l )=−Fl 38EI +11Fl 38EI =5Fl 34EI 5分求解得X 1=−5Fl 34EI 35l 324EI =−67F (压)2分(2)为求C 截面转角,在C 施加逆时针单位弯矩(见图(d))θC =−12l 2⋅Fl 2⋅1EI +l ⋅Fl ⋅1EI +l ⋅l ⋅1EI X 1=−Fl 28EI +Fl 27EI =Fl 256EI(逆时针↺)8分三、(20分)参考答案解:1)利用扭矩平衡求出F 值:F cos (α)D 2=m x F =2m x D cos (α)=2×20×1030.4cos (20o )=106.4kN 4分2)F sin (α)导致弯矩:M z =Fl sin (α)4=106.4×103×1×sin (20o )4=9.098kN ⋅m ;4分3)F cos (α)导致弯矩:M y =Fl cos (α)4=106.4×103×1×cos (20o )4=25.0kN ⋅m ;4分导致扭矩:T =−F cos (α)D 2=−106.4×103×cos (20o )×0.42=−20.0kN ⋅m 2分4)利用第四强度理论:σr 4=1W z √M 2z +M 2y +0.75T 2=1πd 3/32√(9.098)2+(25.0)2+0.75202=31.75kN ⋅m πd 3/32≤[σ]d 3≥31.75kN ⋅m π[σ]/32=32×31.75×103π200×1065分d ≥11.74cm取轴的直径为11.74cm 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题:请将正确答案写在划线内(每空1分,计16分) ⒈ 工程构件正常工作的条件是――――――――――――、、――――――――――――、―――――――――――――。
⒉ 工程上将延伸律------- δ的材料称为脆性材料。
⒊ 矩形截面梁横截面上最大剪应力max τ出现在―――――――――――各点,其值=τmax -------------。
4.平面弯曲梁的q 、F s 、M 微分关系的表达式分别为--------------、、-------------、、----------------。
5.四个常用的古典强度理论的表达式分别为―――――――――――――――――、―――――――――――――――――――――、――――――――――――――、―――――――――――――――――――――――――――――――――。
6.用主应力表示的广义虎克定律为 ――――――――――――――――――――― ;――――――――――――――――――――――;-―――――――――――――――――――――――。
二、单项选择题⒈ 没有明显屈服平台的塑性材料,其破坏应力取材料的――――――――――――。
⑴ 比例极限p σ; ⑵ 名义屈服极限2.0σ; ⑶ 强度极限b σ; ⑷ 根据需要确定。
2. 矩形截面的核心形状为----------------------------------------------。
⑴ 矩形; ⑵ 菱形; ⑶ 正方形; ⑷三角形。
3. 杆件的刚度是指――――――――――――――-。
⑴ 杆件的软硬程度; ⑵ 杆件的承载能力; ⑶ 杆件对弯曲变形的抵抗能力; ⑷ 杆件对弹性变形的抵抗能力;4. 图示二向应力单元体,如剪应力改变方向,则―――――――――――――。
⑴ 主应力的大小和主平面的方位都将改变;⑵ 主应力的大小和主平面的方位都不会改变; ⑶ 主应力的大小不变,主平面的方位改变;⑷ 主应力的大小改变,主平面的方位不变。
5、图示拉杆头和拉杆的横截面均为圆形,拉杆头的剪切面积A =――――――――――――。
A.Dh πB.dh πC.4/2d πD.4/)(22d D -π6、当系统的温度升高时,下列结构中的――――――――――不会产生温度应力.A BC D三、简答题(每小题6分,计12分) 1.支承情况不同的圆截面压杆如图所示,已知各杆的直径和材料均相同且都为大柔度杆。
①若只考虑纸平面内的稳定,问:那个杆的临界力最大?②若在保持截面的面积不变的条件下将各压杆的截面改成正方形,试问各压杆的稳定性是提高了还是降了?2.分别按第三和第四强度理论设计弯扭组合变形杆件的截面,按第三强度论设 计的杆件截面比按第四强度理论设计的截面那个大?为什麽?四、(12分)某形截面的外伸梁如图所示,已知:mm 600=l ,截面对中性轴的惯性矩46mm 1073.5⨯=z I ,m m 721=y ,m m 382=y 。
梁上的荷载kN 9,kN 2421==F F 。
材料的许用拉应力[]a MP 30=t σ,许用压应力[]a MP 90=c σ,试校核梁的强度。
五、(14分)荷载F作用在梁AB 及CD 的联接处,试求每根梁在连接处所受的力。
已知其跨长比和刚度比分别为54232121==EI EI l l 和六、(14分)承受均布荷载的矩形截面简支梁如图所示,F 的作用线通过截面形心且与y 轴成15角,已知m 4=l ,mm 80=b ,mm 120=h ,材料的容许应力MPa 10=σ,试求梁容许承受的最大荷载max F七、(14分)矩形截面受压柱如图所示,其中1F 的作用线与柱轴线重合,2F 的作用点位于y轴上,kN 8021==F F ,mm 240=b ,2F 的偏心距mm 100=e 。
求 (1)柱的横截面上不出现拉应力时的h 最小尺寸;(2)当h 确定后求柱横截面上的最大压应力。
一、填空题:请将正确答案写在划线内(每空1分,计16分) 1. 足够的强度,足够的刚度,足够的稳定性; 2.000052- ;3.中性轴上各点,AF τsmax 23=; 4. q xMF x M q x F ===22s s d d ,d d ,d d ; 5.()313321211,,σσσσσνσσσσr r t r -=+-==()()()[]213232221421σσσσσσσr -+-+-=; 6.()[]32111σσνσE ε+-=,()[]13221σσνσE ε+-=,()[]21331σσνσEε+-=。
二、单项选择题:请将正确答案的序号填入划线内(每小题3分,计18分) 1.(2);2.(2);3.(4);4.(3).5.(2) 6.(1) 三、简答题(每小题6分,计12分) 1.(d),提高了;2.按第三强度理论设计的轴径大,因为按第三强度理论 []3122)32(T M σπd +≥按第四强度理论 []3122)75.032(T M σπd +≥四、(12分)(步骤(1)正确,3分;步骤(2)4分、(3)正确,5分)(a )(b)解:⑴画梁的弯矩图,如图b 示.⑵校核最大拉应力。
由图可知B C M M 5.1= ,21895.1y y =,所以12y M y M B C ,故知最大拉应力在B 截面的上边缘各点[]t 661max ,MPa 6.221073.572108.1σσ =⨯⨯⨯==Z B t I y M即拉应力强度满足。
⑶校核最大压应力。
由于21y M y M B C ,故知最大压应力C 截面上边缘点[]c 661max ,MPa 8.331073.572107.2σσ =⨯⨯⨯==z C c I y M即压应力强度也满足。
五、(14分)解:一次超静定问题,基本静定系如图b所示。
(4分)变形协调条件为 C B w w = (2分) 变形协调方程()23213133EI Xl EI l X F =- (6分) 由此解得F X 167135=(2分) 六、(14分) (z y z y W W M M ,,,写出正确,各得2分)Nmm 1018.5259.044mkN 20sin 46⨯=⨯⨯==φFl M y Nmm 103.19966.044m kN 20cos 43⨯=⨯⨯==Fl M z332m m 101286⨯==hb W y 332mm 101926⨯==bh W Z []σW M W M σz z y yMPa 141mm 10192Nmm103.19mm 10128Nmm 1018.5336336max =⨯⨯+⨯⨯=+=(5分)该梁强度足够 (1分)七(14分) 解:偏心压缩问题,移2F 至1F 作用线处kNm m 200452⨯==e F M e (2分)(1) 若使截面上不出现拉应力,则有 (6分)062221=-+bh eF bh F F解得 mm 372=h(2)柱截面上的最大压应力 (6分) MPa 34.417.217.262221max =+=++=bheF bh F F σ一、判断题:正确的划√,错误的划×(每小题2分,计10分)1、对于没有屈服极限的塑性材料,通常将总应变为0.2%时的应力值,定为屈服强度,表示。
()并以2.0P2、空心截面与实心截面比较,由于充分发挥了截面各点的承载能力,因此是扭转变形的合理截面形状。
()3、不论荷载怎样变化,简支梁的最大挠度可用梁跨中截面的挠度来代表。
()4、若压力作用点离截面核心越远,则中性轴离截面越远。
()5、塑性铰单向自由转动,形成塑性铰处弯矩为零。
()二、单项选择题:请将正确答案的序号填入划线内(每小题2分,共12分)1、塑性材料冷作硬化后,材料的力学性能发生了变化。
试判断以下结论哪一个是正确的():A.屈服应力提高,弹性模量降低;B.屈服应力提高,塑性降低;C.屈服应力不变,弹性模量不变;D.屈服应力不变,塑性不变。
2、在图所示状态中,按剪应力互等定理,相等的是______。
A.τ1=-τ2;B.τ2=-τ3;C.τ3=-τ4;D.τ4=-τ2;3、等直梁受载如图所示.若从截面C截开选取基本结构,则_____.A.多余约束力为F C,变形协调条件为ωC=0;B.多余约束力为F C,变形协调条件为θC=0;C.多余约束力为M C,变形协调条件为ωC=0;D.多余约束力为M C ,变形协调条件为θC =0;4、图示三根压杆,横截面面积及材料各不相同,但它们的 相同。
A.长度因数; B.相当长度; C.柔度; D.临界压力5、构件由突加荷载引起的应力,是相应静载引起应力的 。
A .一倍(1=d K ) B .二倍(2=d K ) C .三倍(3=d K ) D .四倍(4=d K )6、图示拉杆头和拉杆的横截面均为圆形,拉杆头的剪切面积和挤压面积 分别为( )。
A.Dh π ,4/2d π B.dh π ,4/)(22d D -π C.4/2d π, 4/2D π D.4/)(22d D -π,dh π三、填空题(每空2分,共10)1、 直径为D 的实心圆轴,最大的容许扭矩为T ,若将轴的横截面积增加一倍,则其最大容许扭矩为____ __。
2、图示为某点的应力状态,其最大切应力τmax=__ ___MPa。
3、若构件内的应力随时间作交替变化,则该应力称为,构件长期在此应力作用下,会发生无明显塑性变形的骤然断裂,这种破坏现象称为。
4、杆件的刚度代表杆件的能力。
5、图示低碳钢拉杆的外表面上有斜线,当杆件变形时,请将杆上斜线新的位置画在图上,低碳钢的破坏是由应力引起的。
四、作图题(13分)画出所示梁的剪力图和弯矩图,在图上注明控制截面的F s和M的值,并指出剪力和弯矩绝对值的最大值。
五、计算题(17分)1图示为一矩形截面铸铁梁,受两个横向力作用。
(1)从梁表面的A、B、C三点处取出的单元体上,用箭头表示出各个面上的应力。
(2)定性地绘出A、B、C三点的应力圆。
(3)在各点的单元体上,大致地画出主平面的位置和主应力的方向。
(4)试根据第一强度理论,说明(画图表示)梁破坏时裂缝在B、C两点处的走向。
六、计算题(12分)铸铁梁受荷载情况如图示。
已知截面对形心轴的惯性矩Iz=403×10-7m 4,铸铁抗拉强度[σ+]=50MPa ,抗压强度[σ-]=125MPa 。
试按正应力强度条件校核梁的强度。
七、计算题(13分)图示结构中,AC 为刚杆,CD 杆的材料为Q235钢,C 、D 两处均为 球铰,已知d =20mm,材料的E =200Gpa,MPa s 235=σ,稳定安全因数0.3=st n .试确定该结构的许可荷载。
八、计算题(10分)作等直杆的轴力图一、填空题(每空2分计10分)1、⨯2、 √3、×4、×5、×二、单项选择题:请将正确答案的序号填入划线内(每小题2分,共12分)1、B2、C3、A4、B5、B6、B 三、填空题:(14分)1、22;2、30;3、交变应力,疲劳破坏;4、抵抗变形 5、切四、简答题:(13分)求支座约束反力 KN F KNF B A 210== (3分)剪力图 (3分) 弯矩图 (3分)m KN M KN F S .37max max == (4分)五、计算题(17分)A 、B 、C 三点的应力状态每个2分, (共6分)A 、B 、C 三点的应力圆每个2分, (共6分) A 、B 、C 三点的主应力圆每个1分, (共3分) 梁破坏时裂缝在B 、C 两点处的走向 (2分) 六、计算题(12分) 作弯矩图B 截面C 截面七、计算题(12分)压杆所受外力 4PF F =(1分) 压杆临界力的计算 1=μ l=1m (1分)mm di 54==(1分) 200510001=⨯=μ=λi l (2分) 6.91=σπ=λsp Ep λ≥λ大柔度 (2分) (3分)由稳定性条件:kN EI F cr 5.1510642014.31020014.31000643222=⨯⨯⨯⨯=π=st cr Pn F F≤4kNn F F st cr P 67.200.351544=⋅⋅=⋅=2475.12mkN ⋅MPa3.36=733max1040310611024--+⨯⨯⨯⨯=B σ733max10403101391024---⨯⨯⨯⨯=B σMPa8.82=733max10403101391075.12--+⨯⨯⨯⨯=C σMPa 44=求反力1分作图2分(3(3(3(2分)八、计算题(10分)02021=+---=∑R P P R X(1分)EAaR EA a N L 111==∆(1分)EAaP R EA a N L 2)(2122+==∆ (1分)EAaR EA a N L 233==∆ (1分)0321=∆+∆+∆L L L (2分)P R P R 4/74/521=-=(2分)(2分)一、判断题:正确的划√,错误的划×(每小题2分,计10分)1、对于没有屈服极限的塑性材料,通常将弹性应变为0.2%时的应力值,定为屈服强表示。
