中南大学电路理论基础电路
合集下载
中南大学电路理论第10章一阶电路分析
第10章 10.1
§10-1电路中的过渡过程及换路定律
一. 动态电路及方程 描述含有储能元件(电容或电感)时电路的方程
为微分方程. ------动态方程 含有电容或电感元件的电路, 称为动态电路.
二. 一阶电路
能用一阶微分方程描述的电路称为一阶电路. 按储能元件的性质,一阶电路可分为:
RC电路 R L电路
放电过程。
一. RC放电电路
上图中，若开关S合于a，电容上电压充电到U0时， 将S由a合向b， 即 uC(0–)= U0 ，
根据KVL uR + uC=0
RC
—d —uC
dt
+ uC =0
15
2020年10月1日
S t=0
a
+
U-
uR
R
bi
U0
uC
o
i
U0
uR
R
–U0 变化曲线
16
RC
—d —uC
)
1 L
t
t 0
u(
)d
令t0 0 , t 0
iL (0
)
iL (0
)
1 L
0
u(
0
)d
由于u(t)为有限值, 则
iL(0 ) iL(0 ) ------电感里的电流不会发生突变
当iL(0 ) iL(0 ) 0时, 电感在换路的瞬间电感相当于开路
11
2020年10月1日
三. 其他非独立初始条件的计算
dt
+ uC =0
第10章 10.2
上式的通解为指数函数，即
uc uC = Ae pt
C
由特征方程 RCp +1=0
中南大学电工学第2章正弦交流电路_02
例3 电路如图所示，图中各仪表均为交流电流表，其读数是 电路如图所示，图中各仪表均为交流电流表， 电流表的有效值。已知A 的读数为8A 8A， 的读数为60A 60A， 电流表的有效值。已知A1的读数为8A，A2的读数为60A，A3的 读数为66A 求电流表A 66A。 的读数，并画出相量图。 读数为66A。求电流表A和A4的读数，并画出相量图。 I4 I 解：由于电路为并联电 A A4 A3 路，则可设 I3 + A1 A2 US= US 0 V 1 US I1 I j L ω R j L 2 ω 则由已知条件得 I1= 8 0 A， 2= 60 -90 A，I3= 66 90 A ， I ， 根据KCL有 有 根据 I4= I2+I3= 60 -90 +66 90 =6 90 A I= I1+I4= 8 0 +6 90 =10 36.9 A 故表A的读数为 的读数为6A。 故表 的读数为10A，表A4的读数为 。 的读数为 ， 的读数为 相量图如图。 相量图如图。 I2 I2 I4 I I1 US I3
▲额定视在功率 额定视在功率 SN = UN IN —— 额定容量 ▲有功功率守恒 有功功率守恒: 有功功率守恒 P = ∑Pi =∑ Ui Ii cosϕ i ▲无功功率守恒 无功功率守恒: 无功功率守恒 Q = ∑Q i = ∑ Ui Ii sinϕ i ▲视在功率不守恒 视在功率不守恒: 视在功率不守恒 S ≠∑S i =∑ Ui Ii
& I 1 = 10 90 ° A = j10 A & & & I = I 1 + I 2 = 10 0 ° A
& & U L = I ( j10 )V = j100 V
中南大学 电路理论基础 电路第9章1PPT课件
2、根据相量模型列出相量方程式或画相量图
3、用复数运算或相量图求解 4、将结果变换成要求的时域形式
各种方
法
11
例1
i2 i1
i3 + _u
R 1 10 ,R 0 2 1 0 0 ,L 5m 0,0 C H 1F 0 ,
U 1V 0 , 0 3r 1a /s 4 ,求d :各支路电流。
说明：Z 是一个复数，但并不是正弦交流量，上面不能加点。
Z在方程式中只是一个运算工具。
4
二. 复导纳 正弦激励下
I +
U -
无源 线性
I
+
U
Y
-
复导 Yd e Z 1f 纳 U I U I i uY Y
单 纯电阻 YR G
个 元 件
纯电感
YL1jLjBL
感纳
BL
1
L
时 纯电容 YCjCjBC 容纳 BC C
I
ZZ3
11 1
•
IS 1.13/82oA
Z1 Z2 ZZ3
16
例3. 列写电路的回路电流方程 _ U S +
I1
jL R1
I 2
R4
R2
I 3
R3
1 j c
I S
?
解：
( R 1 R 2 jL ) I 1 ( R 1 jL ) I 2 R 2 I 3 U S
第9章正弦稳态电路分析
要求 ： 1. 复阻抗、复导纳 2.定性分析：相量图 3.定量计算：相量形式的各种分析计算方法 4. 功率计算：P、Q、S、cos ф 、复功率 5. 谐振分析
1
9. 1 复阻抗和复导纳
一. 复阻抗 正弦激励下
中南大学电路理论基础作业
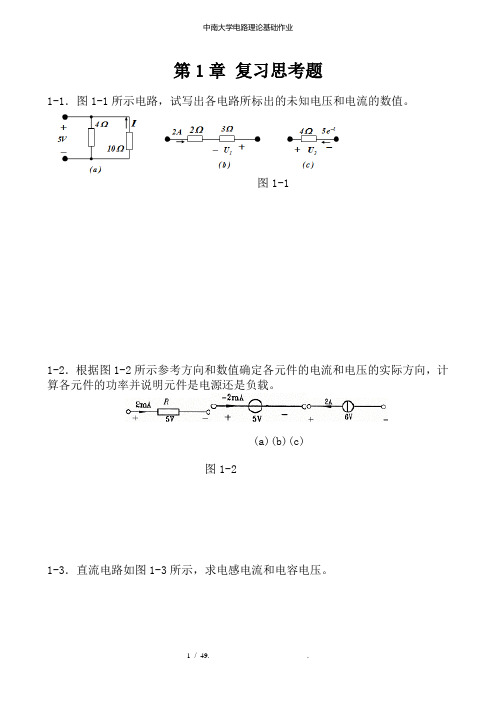
第1章复习思考题1-1．图1-1所示电路，试写出各电路所标出的未知电压和电流的数值。
图1-11-2．根据图1-2所示参考方向和数值确定各元件的电流和电压的实际方向，计算各元件的功率并说明元件是电源还是负载。
(a)(b)(c)图1-21-3．直流电路如图1-3所示，求电感电流和电容电压。
图1-31-4．如图1-4所示，电路中包含的各个元件的电压和电流参考方向如图所示，其中100P 1=W ，10P 2-=W ，50P 3=W ，20P 4=W ，求5P ，元件5是电源还是负载？图1-41-5．求图1-5所示电路中的电压1u 和1i 。
图1-51-6．求图1-6所示电路中的电压u 。
3Ω2Ω4Ωi10 V图1-61-7．求图1-7所示电路中的电压U 。
2ΩU4Ω+ -+ -+- +- 5V2V 5V 1Aa bde图1-71-8．图1-8所示电路中，已知5u ab -=V ，求电压源电压s u 。
图1-81-9．电路如图1-9所示，试求电压U X。
图1-91-10．如图1-10所示的图，如果选1、2、3、4、8支路为树，则其基本回路组是什么？如果选择自然网孔为基本回路组，则其对应的树由哪些支路组成？②⑤123 4 6 10 ④ 8 9 ⑥57 ③图1-10第2章 复习思考题2-1．写出题21图所示各电路的端口电压电流的伏安特性方程。
(a) (b)图2-12-2．电路如图2-2(a)、(b)、(c)、(d)、(e)和(f)所示，试计算a 、b 两端的电阻，其中电阻R =8。
(a) (b)(c)(d)(e) (f)图2-22-3．利用电源等效变换，化简图2-3(a)和(b)的一端口网络。
(a) (b)图2-32-4．利用电源的等效变换求图示2-4电路中的电流I 。
图2-42-5．求图2-5电路中的受控电流源的功率。
2Ω6V+I2Ω 2A7Ω6A2Ω图2-52-6．求图2-6各电路的输入电阻R in。
图2-6第3章复习思考题3-1．用支路电流法求图3-1所示电路中各支路电流及各电阻上吸收的功率。
中南大学电路第10章
返 回 上 页 下 页
解 ①先求 iL (0 ) 1 4
小结 求初始值的步骤:
1.由换路前电路（稳定状态）求uC(0－)和iL(0－)。 2.由换路定律得 uC(0+) 和 iL(0+)。
3.画0+等效电路。
(1)换路后的电路; (2)电容（电感）用电压源（电流源）替代。 （取0+时刻值，方向与原假定的电容电压、电 感电流方向相同）。 4.由0+电路求所需各变量的0+值。
返 回
上 页
下 页
uC (0+) = uC (0－)
q =C uC
结论
q (0+) = q (0－)
电荷 守恒
换路瞬间，若电容电流保持为有限值， 则电容电压（电荷）换路前、后保持不变。
返 回
上 页
下 页
③电感的初始条件
iL
+
1 t iL (t ) u L ( )d L ∞ 1 0 1 t uL ( )d uL ( )d L ∞ L 0
代入初始值
uC (0+)=uC(0－)=U0
A=U0
返 回 上 页 下 页
uC U 0e
uC U 0 i e R R
或
t RC
t 0
t RC
t RC
I 0e
t 0
t t duC 1 U 0 RC i C CU 0e RC ( ) e dt RC R
f (0 ) f (0 )
0－ O 0＋ t
注意 初始条件为 t = 0＋时，u 、i 及其各阶导
数的值。
返 回 上 页 下 页
△例1-1 图示为电容放电电路，电容原先带有电压Uo， 求开关闭合后电容电压随时间的变化。 (t=0) Ri uC 0 (t 0) 解 + C uC duC R RC uC 0 i －
解 ①先求 iL (0 ) 1 4
小结 求初始值的步骤:
1.由换路前电路（稳定状态）求uC(0－)和iL(0－)。 2.由换路定律得 uC(0+) 和 iL(0+)。
3.画0+等效电路。
(1)换路后的电路; (2)电容（电感）用电压源（电流源）替代。 （取0+时刻值，方向与原假定的电容电压、电 感电流方向相同）。 4.由0+电路求所需各变量的0+值。
返 回
上 页
下 页
uC (0+) = uC (0－)
q =C uC
结论
q (0+) = q (0－)
电荷 守恒
换路瞬间，若电容电流保持为有限值， 则电容电压（电荷）换路前、后保持不变。
返 回
上 页
下 页
③电感的初始条件
iL
+
1 t iL (t ) u L ( )d L ∞ 1 0 1 t uL ( )d uL ( )d L ∞ L 0
代入初始值
uC (0+)=uC(0－)=U0
A=U0
返 回 上 页 下 页
uC U 0e
uC U 0 i e R R
或
t RC
t 0
t RC
t RC
I 0e
t 0
t t duC 1 U 0 RC i C CU 0e RC ( ) e dt RC R
f (0 ) f (0 )
0－ O 0＋ t
注意 初始条件为 t = 0＋时，u 、i 及其各阶导
数的值。
返 回 上 页 下 页
△例1-1 图示为电容放电电路，电容原先带有电压Uo， 求开关闭合后电容电压随时间的变化。 (t=0) Ri uC 0 (t 0) 解 + C uC duC R RC uC 0 i －
中南大学电路理论基础课件电路第章
–us2
R3
+
–us3
us11
ia
us 22 R11
R21
R11ia+R12ib=us11 R21ia+R22ib=us22
R12
us1-us2
us2-us3
R22 R12
R22 Δ
us11
R12 Δ
us 22
R22
R22 Δ
us1
R12 Δ
R22
us 2
R12 Δ
us 3
证得
ia = ia1 + ia2 + ia3
A
A
A
1A
++
1V -
_1V
1A
+
1A +
1V 1
?
-
-
1A
B
满足
B
不满足
B
2) 被替代的支路和电路其它部分应无耦合关系。 （控制量或受控源）
20
第20页，共58页。
§4-3. 戴维南定理 和 诺顿定理
在有些情况下，只需计算电路中某一支路中的电流， 如计算右图中电流 I3，若用前面的方法需列方程组， 必然出现一些不需要的变量。
源去掉，使电路开路。
13
第13页，共58页。
例3 求电压Us 。
注意受控源
I1 6
+ 10 I1 –
+ 10V
–
+
4
Us 4A
–
解: (1) 10V电压源单独作用：
I1' 6
+ 10 I1'–
+
10V –
+
+
R3
+
–us3
us11
ia
us 22 R11
R21
R11ia+R12ib=us11 R21ia+R22ib=us22
R12
us1-us2
us2-us3
R22 R12
R22 Δ
us11
R12 Δ
us 22
R22
R22 Δ
us1
R12 Δ
R22
us 2
R12 Δ
us 3
证得
ia = ia1 + ia2 + ia3
A
A
A
1A
++
1V -
_1V
1A
+
1A +
1V 1
?
-
-
1A
B
满足
B
不满足
B
2) 被替代的支路和电路其它部分应无耦合关系。 （控制量或受控源）
20
第20页，共58页。
§4-3. 戴维南定理 和 诺顿定理
在有些情况下，只需计算电路中某一支路中的电流， 如计算右图中电流 I3，若用前面的方法需列方程组， 必然出现一些不需要的变量。
源去掉，使电路开路。
13
第13页，共58页。
例3 求电压Us 。
注意受控源
I1 6
+ 10 I1 –
+ 10V
–
+
4
Us 4A
–
解: (1) 10V电压源单独作用：
I1' 6
+ 10 I1'–
+
10V –
+
+
中南大学电工学第2章正弦交流电路_03
三、线电压与相电压的关系 1、Y接法
A +
IA
A
UA
– Y X Z
C UC
UA B UCA
设 U AN U A U0o UBN UB U 120o UCN UC U120o
B
IB I C U BC
N B C
UB
U AB U AN U BN U0o U 120 o 3U30 o U BC U BN U CN U 120 o U120 o 3U 90 o U CA U CN U AN U120 o U0o 3U150 o
(2) 三相负载不对称（RA=5 、RB=10 、RC=20 ） 分别计算各线电流 U 220 0 A IA A 44 0A RA 5
U 220 120 B IB A 22 120 A RB 10
U 220 120 C IC A 11 120 A RC 20
Δ 接 : U l U p , I l 3I p 1 P 3U l I l cosφ 3U l I l cosφ 3
注意： (1) 为相电压与相电流的相位差角(阻抗角)，不要误以为 是线电压与线电流的相位差。
(2) cos为每相的功率因数，在对称三相制中即三相功率因数： cos A= cos B = cos C = cos 。
U A U0 U B U 120o U C U120o Z | Z | φ
UA UC
中南大学 电路理论基础课件 电路第6章3
(t-t0)
（1） 0 t0
9
t
3. 函数的筛分性（或采样特性）
f ( t ) ( t ) d t f ( 0 ) ( t ) d t f ( 0 )
f(0)(t)
(1)
(t)
f(0)
0
f(t)
t
* f(t)在 t0 处连续 同理有：
f ( t ) ( t t 0 ) d t f ( t 0 )
（1）加4ε的阶跃输入时：
iL (t )
4 2 .4
(1 e
24 t
) ( t )
（2）加4δ的冲激输入时： i ( t ) 40 e 24 t ( t ) L
u L (t ) L di L dt
22
96 e
24 t
(t )
1 RC
t RC
e
(t )
uC
R 阶跃响应 0
1 C
iC
1 t 0 t iC (1) t t
1 RC
21
uC
冲激响应 0
例6-7：求冲激响应 uL(t)和 iL(t)
R1 6 Req iL + uL – 等效 R2 4 4δ
2.4
+
10δ L –
0.1H
+
L –
0.1H
iL + uL –
iL ( 0
) 0
L
iL不可能是冲激
dt
0 0
Ri L dt
0
0 0
L
di L dt
中南大学电工学第1章直流电路01.ppt
注：理想电容不消耗量，只存储电场能
23
第1章 直流电路
3、电感元件
电路符号
实际电感元件
原理:用导线绕成的线圈, 通以变化电流，将在线圈两端产生感应电压。
• 伏安特性(VAR):
u L di dt
单位：亨(利)(H) 1mH 103 H
• 微分关系:
i(t)
i(t0 )
1 L
t
u( )d
t0
“记忆”元件
电容器由中间隔以绝缘介质的两块金属极板组成
C
+q
-q
iu
• 伏安特性（VAR):
i C du dt
单位：法拉(F) 1F 106 F,
1pF 10 12 F
• 微分关系:
u(t
)
u
(t0
)
1 C
t
i( )d
t0
“记忆”元件
{ • 功率:关联参考方向下 P ui Cu du dt
>0 吸收能量 <0 发出能量
已设定。已知：I1=2A, I2=-1A, I3=-1A, U1=7V, U2=3V,
U3=4V, U4=8V, U5=4V, 求各元件消耗或向外发出的功率。
解：元件4：为关联参考方向
U2 _ +2
U4 _ +4
P4=U4I3=8×(－1)=－8w, 发出功率,电源
元件5：为非关联参考方向
I1 +
U1 1 _
• 功率:关联参考方向下
{ P ui Li di dt
>0 吸收 <0 发出
注：理想电感不消耗量，只存储磁场能
24
第1章 直流电路
1.4.2 理想有源元件
中南大学电子电工课件8三相电路讲解
《电工技术B》课程
8三相电路
中南大学 姜霞
8 三相电路
重点内容 对称三相电路变为一相的计算方法，对称三相电路的电流
和电压的线值与相值之间的关系以及对称三相电路的计算。 注意：对称三相电路一般按正序给出。另外，对称三相电路
的电流和电压的线值与相值之间的关系不能混淆。
8.1 三相电路的基本概念
一、对称三相电源
8.1 三相电路的基本概念
A IA
B
IB
ቤተ መጻሕፍቲ ባይዱ
C
IC
Z
IAB
Z
ICA
Z IBC
ICA
IC IA
IC IB
IAB
IBC
IB
IA IAB ICA IB IBC IAB IC ICA IBC IA 3IAB 30
IB 3IBC 30 IC 3ICA 30
30
IA
8.1 三相电路的基本概念
1 ZN
)U NN
Z
1 Z1
(U A
U B
U C )
U NN 0
IA
U A U NN Z Z1
U A Z Z1
IN IA IB IC 0
IB
U B Z Z1
2IA
IC
U C Z Z1
IA
8.2 对称三相电路
U A
IA
A
Z 1
A
Z
U B
IB
B
Z 1
B
Z
N
U C
IC
C
8.1 三相电路的基本概念
<二> 三相电源的三角形连接方式
A(Z)
A
uA B(X)
uC
uB C(Y)
8三相电路
中南大学 姜霞
8 三相电路
重点内容 对称三相电路变为一相的计算方法，对称三相电路的电流
和电压的线值与相值之间的关系以及对称三相电路的计算。 注意：对称三相电路一般按正序给出。另外，对称三相电路
的电流和电压的线值与相值之间的关系不能混淆。
8.1 三相电路的基本概念
一、对称三相电源
8.1 三相电路的基本概念
A IA
B
IB
ቤተ መጻሕፍቲ ባይዱ
C
IC
Z
IAB
Z
ICA
Z IBC
ICA
IC IA
IC IB
IAB
IBC
IB
IA IAB ICA IB IBC IAB IC ICA IBC IA 3IAB 30
IB 3IBC 30 IC 3ICA 30
30
IA
8.1 三相电路的基本概念
1 ZN
)U NN
Z
1 Z1
(U A
U B
U C )
U NN 0
IA
U A U NN Z Z1
U A Z Z1
IN IA IB IC 0
IB
U B Z Z1
2IA
IC
U C Z Z1
IA
8.2 对称三相电路
U A
IA
A
Z 1
A
Z
U B
IB
B
Z 1
B
Z
N
U C
IC
C
8.1 三相电路的基本概念
<二> 三相电源的三角形连接方式
A(Z)
A
uA B(X)
uC
uB C(Y)
中南大学电工学ppt第1讲电路的基本概念
（实际方向与参考方向一致）
U 1V
IR
（实际方向与参考方向相反）
二、电压和电压的参考方向
<一> 电压 单位正电荷在电场力的作用下从A点到B点电场力所做的 dw 功为AB两点之间的电压，即： u dq 若电压的大小和方向不随时间变化，则这种电压叫做恒定电 压，也称为直流电压，常用大写字母U表示。 若电流的大小和方向都随时间变化，则称为交流电压，用 小写字母u表示 电压的单位是伏特！ 电压的实际方向：高电位指向低电位。 1V = 1000 mV 1mV = 1000μV <二> 电压的参考方向表示 <1> 用箭头表示； <2> 用双下标，如 uAB；<3>用正负符号。
I
+
(２)当U和I参考方向选择不一致的前提下
若 P = UI 0
a b + U _ R
“吸收功率” I （负载）
“ 发出功率” U （电源） - _ b
+
例： 已知：方框代表电源或负载，U = 220V，I = -1A 试问：哪些方框是电源，哪些是负载？
+ U I (a) + U I U +
-
I (c)
-
-
(b)
U +
-
I (d)
解： (a) 电压、电流实际方向非关联，故为电源； (b)电压、电流实际方向关联，故为负载； (c)电压、电流实际方向关联，故为负载 ； (d)电压、电流实际方向非关联，故为电源。
1-3 电路元件
1.3.1 电阻元件 一、线性电阻（简称电阻） 电阻符号为：
A B R u i
1 5A b a 点电位： Va = 5V
中南大学 电路理论基础课件 电路第11章
23
结论：对称三相电路（Y-Y)
1. UnN=0，电源中点与负载中点等电位。 2. 中线电流为零。 3. 有无中线对电路没有影响。 没有中线(Y–Y接，三相三线制)，可加中线
中线有阻抗时可短路掉
4. 对称情况下，各相电压、电流都是对称的。只要算出一 相的电压、电流，则其它两相的电压、电流可按对称关 系直接写出。
13:25
u BC uCA
C
注意规定的 正方向
10
三相三线制与三相四线制：
IA
IA
A +
– X Y Z
A
A +
– X Y Z
A
UA
UA B UCA
UA
UA B UCA
C
U
C
U
B
B
IB
N
B C
IC
UBC
C
U
C
U
B
B
IB
B C
IC
UBC
三相四线制（有中线）
第十一章 三相电路
§11.1 §11.2 §11.3 §11.4 §11.5 三相电路 线/相电压（电流）的关系 对称三相电路的计算 不对称三相电路的概念 三相电路的功率
学习方法： 复杂交流电路的一种特殊形式。 1.交流电路的分析方法 2.特殊性：对称电路的简化（抽单相计算）
13:25 1
§11.1 三相电路
求线电流。
B
I
C
解： 连接中线Nn，取A相为例计算 +
U
AN
IA
设
o U AB 380 30 V o U AN 220 0 V
中南大学 电路理论基础课件 电路第7章
(4)
u C ( 0 ) 25 由 du C C dt 5
K 358 ， 176
25 t
u C 358 e
sin( 139 t 176 ) V
t 0
uC 358 25 0
t
19
§7. 2 二阶电路的零状态响应和全响应
一. 零状态响应
2 2
y1=0
y1=c
4a 0 b 4a 0
2
二个不等负实根
p1t
二个相等负实根
二个共轭复根
通解y2
A1e
A 2e
p2t
(A1 A 2t) e
pt
Ke
t
sin( t )
解y(t)
待定系数：
y ( t ) y1 y 2
p1,2 b b 4a
U 0e
t
U0
uc uC i
0
U 0e
t
衰减振荡 欠阻尼
2-
0
-
+
0
2
t
t
uL
U 0e
13
能量转换关系 0<t<
uC减小，i 增大
< t < -
uC减小，i 减小
- < t <
|uC |增大，i 减小
+
C -
R L C
+ -
求 y(t)
解: 数学知：方程的解由特解y1及通解y2组成 y ( t ) y1 y 2 (1)特解按C是否为0（齐次/非齐次）分析 (2)通解按特征根P1, P2的不同取值分析
P1 , 2 b b 2a
中南大学电路理论第三版第一单元课件
电路理论分析
例 图中方框代表电源或电阻, 若各电压、电流的 参考方向如图所示，并已测得(或计算得知)：I1 =2A, I2 =1A, I3 = -1A, U1 =1V, U2 = -3V, U3 =8V, U4 = -4V, U5 =7V, U6 = -3V。试标出电流、电压实际 方向并求各方框的功率。
规定正电荷的运动方向为电流的实际方向 元件(导线)中电流流动的实际方向只有两种可能:
实际方向
A
B B
A
实际方向
问题 对于复杂电路或电路中的电流随时间变化时，
电流的实际方向往往很难事先判断。
中南大学 信息科学与工程学院电路理来自分析参考方向i A
任意假设电路中元件的电流方 向即为电流的参考方向。
欧姆公式必须与参考方向配套使用
B.线性电阻元件功率 线性电阻元件在任何时刻吸收的功率为: (u,i取关联参考方向) Ri2 = Gu2 0 p = ui = (u,i取非关联参考方向) -Ri2 = -Gu2 0 电阻元件对电流呈现阻力，消耗功率
中南大学 信息科学与工程学院
电路理论分析
线性电阻元件
•是耗能元件 •是双方向性元件 •其伏安特性曲线 (Volt-ampere Characteristic) 是一条通过原点的直线 斜率确定电阻值 不带“记忆” 0 u
i
中南大学 信息科学与工程学院
电路理论分析
C.线性电阻元件的两种特殊情况： ① 不论端电压为何值,只要电流恒为零,则称为 “开路”,相当于 R = 或 G =0 ② 不论电流为何值,只要端电压恒为零,则称为 “短路”,相当于 R =0 或 G =
中南大学 信息科学与工程学院
电路理论分析
中南大学 电路理论基础 电路第6章1PPT课件
iL(0 )
结论 换路瞬间，若电感电压保持为有限值，
则电感电流（磁链）换路前后保持不变。
14
换路定理: 在换路瞬间，电容上的电压、 电感中的电流不能突变。
设：t=0 时换路 0 --- 换路前瞬间
0 --- 换路后瞬间
则： uC(0)uC(0)
iL(0)iL(0)
15
三、初始值的确定
在t=0+时电路中电压电流的瞬态值及各阶导数称为暂 态电路的初始值。初始值的确定要依据换路定则及电路性 质来分析，也受电路约束方程的制约。步骤如下：
8
电容电路 K R
uC
+
U
_U
uC C
t
电容为储能元件，它储存的能量为电场能量 ，其
大小为：
WC
tuidt 1cu2
0
2
因为能量的存储和释放需要一个过程，所以有
电容的电路存在过渡过程。
9
电感电路
KR
+ t=0
U
iL
U _
iL
R
t
电感为储能元件，它储存的能量为磁场能量，
其大小为：
WL
tudi t1L2i
1、换路前的瞬间，电路处于旧稳态——电容开路、电感
短路 求出uC(0-) 和 iL(0-)
2、由换路定律得 独立初始值uC(0+) 和 iL(0+)
3 、 画 0+ 等 值 电 路 。 换 路 后 的 瞬 间 ， 将 电 容 用 定 值 电 压 uC(0+) 或电感用 iL(0+) 定值电流代替。若电路无储能， 则视电容C为短路，电感L为开路。
0
2
因为能量的存储和释放需要一个过程，所以有 电感的电路存在过渡过程。
中南大学 电路理论基础课件 电路第17章
二. 折线法 折线法：将非线性电阻近似地用折线来表示，也即分段线性化 特点：求解过程分为几个线性段，应用线性电路的计算方法 例： i 折线化 u 理想化 uR u i
+º
uS _ º D R
+ uR _
0
2
3
例二
i
u Ua U0 u O
A
B
Ia
i
当 i<Ia , u<Ua OA段
当 i>Ia, u>Ua AB段 等 效 电 路 +º OA段 i
US= RS i + u(t)
RS
US
i R
i=g(u)
P
P
U0 US u
小 信 号 范 围
I0 U0 同时满足 U = R i+ u S S
i=g(u)
即
I0=g(U0) US= RS I0 + U0
P点称为静态工作点 , 表示电路没有信号时的工作情况。
第二步： US 0 ， uS(t) 0
u3 = 500 + 500 = 1000V
i3=10A i4=0.010A
u4 = 50 0.01+ 0.5 (0.01)3 50 i4
①非线性电阻能产生与输入信号不同的频率（变频作用）。 ②非线性电阻工作范围充分小时，可用工作点处的线性 电阻来近似。 ③齐次性和叠加性不适用于非线性。
第三步：求小信号下产生的电压和电流
I1 2
+ Emsinw_t
I2 + 7 _U2 5
I3
+ U3ቤተ መጻሕፍቲ ባይዱ_
I1=Emsinw t /(2+5//7)= 0.2033 Emsinw t I2= I1 5/12 =0.0847 Emsinw t I3= I1 7/12 =0.1186 Emsinw t
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
R6
1 R2
R1 i1
+
US1
_
i2 2 i3 i4
R4 3
i5
IS5
R3 4
R5
(2) 标注节点，列独立KCL方程 节点 1： – i1 +i2 + i6 =0
对n个节点的电路， 可以证明：独立的 KCL方程只有n-1个 。
节点 2：– i2 + i3 + i4 =0 (1) 节点 3：– i4 + i5 – i6 =0
#1
+
#2
R3 R4
#1
+
uS5 _
uS5 _
_ uS1
R6 #2 R3
平面电路：可以画在平面上,不出现支路交叉的电路。
非平面电路：在平面上无论将电路怎样画，总有支 路相互交叉。
02:05:07
∴ 是平面电路
总有支路相互交叉 ∴是非平面电路
9
独立回路的选取：
可以证明: 用KVL只能列出b–n+1个独立回路电压方程， 对平面电路，b–n+1个网孔即是一组独立回路。
i6
R6
平面电路
1 R2
i2 2 3
R4 3
R1 i1
i3 i4
i5
IS5
+
US1
_ 1 R3
4 2 R5
i5 +
R5 +
R5IS5_
—
(3) 选定b-n+1个独立回路，列写独立KVL电压方程。
要弄清支路电压与电流关系 u5 = R5（ i5 + is5）
回路1：R1 i1 + R2 i2 + R3 i3 = uS1
目的：找出求解线性电路的一般分析方法 。
对象：含独立源、受控源的电阻网络的直流稳态解。
(可推广应用于其他类型电路的稳态分析中）
应用：主要用于复杂的线性电路的求解。
基础： 电路的连接关系—KCL，KVL定律
元件特性(约束)(对电阻电路，即欧姆定律)
相互独立
复杂电路的分析法就是根据KCL、KVL及元件VCR 列方程、 解方程。根据列方程时所选变量的不同可分为支路电流法、 网孔电流法、回路电流法、节点电压法。
2
n=8，
1 4 3 b=12
5
对非平面电路，要使用树的概念来找到独立回路
02:05:07
10
3.3 支路电流法 (branch current method )
支路电流法：以各支路电流为未知量列写电路方程分析电 路的方法。支路电流法是最基本的方法，在 方程数目不多的情况下可以使用
支路电流法的一般步骤：
有 向 图3
1. 连通图 图分：连通图与不连通图。 图G的任意两节点间至少有一条路经时称G为连通图。
+
抽象
-
不连通图
+
抽象
-
连通图
2. 路经
从图G的一个节点出发沿着一些支路连续移动到达 另一节点所经过的支路构成路经。
3. 回路
回路L是连通图G的一个子图。 具有下述性质 (1)连通； (2)每个节点关联支路数恰好为2。
123 75 6 84
02:05:06
23 5
回路
12 5
7 84
不是回路
5
4 . 树 (Tree)
树T是连通图G的一个子图，具有下述性质：
(1)连通； (2)包含G的所有节点； (3)不包含回路。
16个
树支：属于树T 的支路
树不唯一
连支：属于G而不属于T的支路
02:05:06
6
显然，有n结点和b条支路的连通图，任取一个树 则：树支数 bt= n-1、连支数 bl=b-(n-1)
2i1 0i2 4i2 5
0i1 3i2 7i3 9
02:05:06
2
§3-1/2 电路的图
+
抽象
-
支路
i1 i2 i3
抽象 i1
i2 i3
电路图
抽象图
பைடு நூலகம்
i1 i2 i3
一. 图的基本概念 G={支路，节点}
L
uS
R2
+
R1
R3
抽象 C
抽象
无 箭头为支路电压 向 和电流的参考方 图 向（关联）
02:05:07
14
例1. US1=130V, US2=117V, R1=1, R2=0.6, R3=24.
a
I1
I2
R1
R2
+ 1+ 2
US1
US2
–
–
I3
求各支路电流及电压源 各自发出的功率。
KCL
R1 i1 + R2 i2 + R3 i3 = +uS1 –R3 i3 + R4 i4 + R5 i5 = – R5 iS5 – R2 i2 – R4 i4 + R6 i6 = 0
i1,i2….i6
KVL
对一般形式：1、等式左边为电阻压降的代数和；2、等 式右边是回路经过的所有电压源及电流源（电流源与电 阻的并→电压源与电阻的串）；3、在等式右边时，电压 源极性与回路绕行方向一致，取—，反之取 + 。
一、先确定树：树T是连通图G的一个子图，具有下述性质： (1)连通； (2)包含G的所有节点； (3)不包含回路。
二、每加一条连支，得到一个单连支回路，共一组b-n+1 个单连支回路，就是一组基本独立回路（？）
图中，粗红线即被选为树支，细线即为连支
R1
+
_
R1
+
R2 #3
uS1
#3
R2
R5
R6
R5
R4
02:05:06
1
关于多变量线性代数方程的标准形式
a11x1 a12x2 a1n xn b1
a21x1
a22x2
a2n xn
b2
an1x1 an2x2 ann xn bn
例如： i1 i2 i3 0
(1) 标定各支路电流（电压）的参考方向； (2) 选定(n–1)个节点，列写其KCL方程； (3) 选定b–(n–1)个独立回路，列写其KVL方程；
(元件特性代入)
(4) 求解上述方程，得到b个支路电流；
(5) 进一步计算支路电压和进行其它任何分析。
02:05:07
11
举例说明原理：b=6， n=4 ： （ R5、 IS5为一条支路） (1) 标定各支路电流的参考方向 i6
回路2：–R3 i3 + R4 i4 + R5 i5 = – R5 iS5
（2）
回路3：– R2 i2 – R4 i4 + R6 i6 = 0
02:05:07
在此：元件特性已直接代入
13
（4）联立求解，求出各支路电流，进一步求出各支路电压。
– i1 +i2 + i6 =0 – i2 + i3 + i4 =0 – i4 + i5 – i6 =0
4 1
3 56 2
7
树支数 4：
（2、3、6、7）
树
连支数 3：
（1、4、5）
单连支回路（在树的基础上，每加一连支，即得一回路。 共b-(n-1)个单连支回路，必为一组独立基本回路）
4
1 5
特点：1、所有的支路 都出现了；2、两两之
间必有不同的支路。
02:05:07
7
归纳：列KVL方程时，如何得基本独立回路组？
1 R2
R1 i1
+
US1
_
i2 2 i3 i4
R4 3
i5
IS5
R3 4
R5
(2) 标注节点，列独立KCL方程 节点 1： – i1 +i2 + i6 =0
对n个节点的电路， 可以证明：独立的 KCL方程只有n-1个 。
节点 2：– i2 + i3 + i4 =0 (1) 节点 3：– i4 + i5 – i6 =0
#1
+
#2
R3 R4
#1
+
uS5 _
uS5 _
_ uS1
R6 #2 R3
平面电路：可以画在平面上,不出现支路交叉的电路。
非平面电路：在平面上无论将电路怎样画，总有支 路相互交叉。
02:05:07
∴ 是平面电路
总有支路相互交叉 ∴是非平面电路
9
独立回路的选取：
可以证明: 用KVL只能列出b–n+1个独立回路电压方程， 对平面电路，b–n+1个网孔即是一组独立回路。
i6
R6
平面电路
1 R2
i2 2 3
R4 3
R1 i1
i3 i4
i5
IS5
+
US1
_ 1 R3
4 2 R5
i5 +
R5 +
R5IS5_
—
(3) 选定b-n+1个独立回路，列写独立KVL电压方程。
要弄清支路电压与电流关系 u5 = R5（ i5 + is5）
回路1：R1 i1 + R2 i2 + R3 i3 = uS1
目的：找出求解线性电路的一般分析方法 。
对象：含独立源、受控源的电阻网络的直流稳态解。
(可推广应用于其他类型电路的稳态分析中）
应用：主要用于复杂的线性电路的求解。
基础： 电路的连接关系—KCL，KVL定律
元件特性(约束)(对电阻电路，即欧姆定律)
相互独立
复杂电路的分析法就是根据KCL、KVL及元件VCR 列方程、 解方程。根据列方程时所选变量的不同可分为支路电流法、 网孔电流法、回路电流法、节点电压法。
2
n=8，
1 4 3 b=12
5
对非平面电路，要使用树的概念来找到独立回路
02:05:07
10
3.3 支路电流法 (branch current method )
支路电流法：以各支路电流为未知量列写电路方程分析电 路的方法。支路电流法是最基本的方法，在 方程数目不多的情况下可以使用
支路电流法的一般步骤：
有 向 图3
1. 连通图 图分：连通图与不连通图。 图G的任意两节点间至少有一条路经时称G为连通图。
+
抽象
-
不连通图
+
抽象
-
连通图
2. 路经
从图G的一个节点出发沿着一些支路连续移动到达 另一节点所经过的支路构成路经。
3. 回路
回路L是连通图G的一个子图。 具有下述性质 (1)连通； (2)每个节点关联支路数恰好为2。
123 75 6 84
02:05:06
23 5
回路
12 5
7 84
不是回路
5
4 . 树 (Tree)
树T是连通图G的一个子图，具有下述性质：
(1)连通； (2)包含G的所有节点； (3)不包含回路。
16个
树支：属于树T 的支路
树不唯一
连支：属于G而不属于T的支路
02:05:06
6
显然，有n结点和b条支路的连通图，任取一个树 则：树支数 bt= n-1、连支数 bl=b-(n-1)
2i1 0i2 4i2 5
0i1 3i2 7i3 9
02:05:06
2
§3-1/2 电路的图
+
抽象
-
支路
i1 i2 i3
抽象 i1
i2 i3
电路图
抽象图
பைடு நூலகம்
i1 i2 i3
一. 图的基本概念 G={支路，节点}
L
uS
R2
+
R1
R3
抽象 C
抽象
无 箭头为支路电压 向 和电流的参考方 图 向（关联）
02:05:07
14
例1. US1=130V, US2=117V, R1=1, R2=0.6, R3=24.
a
I1
I2
R1
R2
+ 1+ 2
US1
US2
–
–
I3
求各支路电流及电压源 各自发出的功率。
KCL
R1 i1 + R2 i2 + R3 i3 = +uS1 –R3 i3 + R4 i4 + R5 i5 = – R5 iS5 – R2 i2 – R4 i4 + R6 i6 = 0
i1,i2….i6
KVL
对一般形式：1、等式左边为电阻压降的代数和；2、等 式右边是回路经过的所有电压源及电流源（电流源与电 阻的并→电压源与电阻的串）；3、在等式右边时，电压 源极性与回路绕行方向一致，取—，反之取 + 。
一、先确定树：树T是连通图G的一个子图，具有下述性质： (1)连通； (2)包含G的所有节点； (3)不包含回路。
二、每加一条连支，得到一个单连支回路，共一组b-n+1 个单连支回路，就是一组基本独立回路（？）
图中，粗红线即被选为树支，细线即为连支
R1
+
_
R1
+
R2 #3
uS1
#3
R2
R5
R6
R5
R4
02:05:06
1
关于多变量线性代数方程的标准形式
a11x1 a12x2 a1n xn b1
a21x1
a22x2
a2n xn
b2
an1x1 an2x2 ann xn bn
例如： i1 i2 i3 0
(1) 标定各支路电流（电压）的参考方向； (2) 选定(n–1)个节点，列写其KCL方程； (3) 选定b–(n–1)个独立回路，列写其KVL方程；
(元件特性代入)
(4) 求解上述方程，得到b个支路电流；
(5) 进一步计算支路电压和进行其它任何分析。
02:05:07
11
举例说明原理：b=6， n=4 ： （ R5、 IS5为一条支路） (1) 标定各支路电流的参考方向 i6
回路2：–R3 i3 + R4 i4 + R5 i5 = – R5 iS5
（2）
回路3：– R2 i2 – R4 i4 + R6 i6 = 0
02:05:07
在此：元件特性已直接代入
13
（4）联立求解，求出各支路电流，进一步求出各支路电压。
– i1 +i2 + i6 =0 – i2 + i3 + i4 =0 – i4 + i5 – i6 =0
4 1
3 56 2
7
树支数 4：
（2、3、6、7）
树
连支数 3：
（1、4、5）
单连支回路（在树的基础上，每加一连支，即得一回路。 共b-(n-1)个单连支回路，必为一组独立基本回路）
4
1 5
特点：1、所有的支路 都出现了；2、两两之
间必有不同的支路。
02:05:07
7
归纳：列KVL方程时，如何得基本独立回路组？