实验作业2----MATLAB作图
实验二MATLAB绘制图形

grid on %在所画出的图形坐标中加入栅格
绘制图形如下
50
10
1
0.8
40
10
0.6
0.4
30
10
0.2
0
1020
-0.2
-0.4
1010
-0.6
-0.8
0
10
-1
-2
0
2
-2
0
2
10
10
10
10
10
10
如果在图中不加栅格
程序如下:
clear x=logspace(-1,2);%在10^(-1)到10^2之间产生50个 对数等分的行向量 subplot(121); loglog(x,10*exp(x),'-p') subplot(122); semilogx(x,cos(10.^x))
(2)plot(x,y): 基本格式,x和y可为向量或矩阵. 1. 如果x,y是同维向量,以x元素为横坐标,以y元素 为纵坐标绘图. 2. 如果x是向量,y是有一维与x元素数量相等的矩阵, 则以x为共同横坐标, y元素为纵坐标绘图,曲线数目 为y的另一维数. 3. 如果x,y是同维矩阵,则按列以x,y对应列元素为 横、纵坐标绘图,曲线数目等于矩阵列数.
y=2*exp(-0.5*x).*cos(4*pi*x);
2
plot(x,y)
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
1
2
3
4
5
6
7
例4 绘制曲线
t=(0:0.1:2*pi);
x=t.*sin(3*t);
y=t.*sin(t).*sin(t);
实验二MATLAB绘图11页word文档

实验二MATLAB绘图一.实验目的掌握matlab二维图形和三维图形的绘制方法,并会对图形进行处理,掌握符号函数(显函数、隐函数和参数方程)的画图,掌握空间曲线和空间曲面的绘图,会对所绘图形进行加格栅,图例和标注等一些简单的处理.二.实验原理与方法(一).曲线图:Matlab作图是通过描点、连线来实现的,故在画一个曲线图形之前,必须先取得该图形上的一系列的点的坐标(即横坐标和纵坐标),然后将该点集的坐标传给Matlab函数画图.命令格式为:plot(x,y,s)其中x,y分别表示所取点集的横纵坐标,s指定线型及颜色.缺省时表示画的是蓝色实线.Plot(X,Y1,S1,X,Y2,S2,……,X,Yn,Sn)表示将多条线画在一起.例在[0,2*pi]用红线画sin(x),用绿圈画cos(x).解:x=linspace(0,2*pi,30);y=sin(x);z=cos(x);plot(x,y,’r’,x,z,’g o’)所得图形如下图所示(二)符号函数(显函数、隐函数和参数方程)画图(1) ezplotezplot(‘f(x)’,[a,b])表示在a<x<b绘制显函数f=f(x)的函数图ezplot(‘f(x,y)’,[xmin,xmax,ymin,ymax])表示在区间xmin<x<xmax和 ymin<y<ymax绘制隐函数f(x,y)=0的函数图ezplot(‘x(t)’,’y(t)’,[tmin,tmax])表示在区间tmin<t<tmax绘制参数方程x=x(t),y=y(t)的函数图.例在[0,pi]上画y=cos(x)的图形解输入命令:ezplot(‘sin(x)’,[0,pi])例在[0,2*pi]上画t=,tx3cos=星形图siny3解输入命令:ezplot(‘cos(t).^3’,’sin(t).^3’,[0,2*pi])例在[-2,0.5],[0,2]上画隐函数0e x的图)+xysin(=解输入命令:ezplot('exp(x)+sin(x.*y)',[-2,0.5,0,2])(2) fplot格式:fplot(‘fun’,lims)表示绘制字符串fun 指定的函数在lims=[xmin,xmax]的图形注意:[1] fun 必须是M 文件的函数名或是独立变量为x 的字符串.[2] fplot 函数不能画参数方程和隐函数图形,但在一个图上可以画多个图形。
实验2 Matlab绘图操作

实验2 Matlab 绘图操作实验目的:1、 掌握绘制二维图形的常用函数;2、 掌握绘制三维图形的常用函数;3、 掌握绘制图形的辅助操作。
实验内容:1. 设sin .cos x y x x ⎡⎤=+⎢⎥+⎣⎦23051,在x=0~2π区间取101点,绘制函数的曲线。
2. 已知: y x =21,cos()y x =22,y y y =⨯312,完成下列操作:(1) 在同一坐标系下用不同的颜色和线性绘制三条曲线; (2) 以子图形式绘制三条曲线;(3) 分别用条形图、阶梯图、杆图和填充图绘制三条曲线。
3.已知:ln(x x e y x x ⎧+≤⎪⎪=⎨⎪+>⎪⎩20102,在x -≤≤55区间绘制函数曲线。
4. 绘制极坐标曲线sin()a b n ρθ=+,并分析参数a 、b 、n 对曲线形状的影响。
5.在xy 平面内选择区域[][],,-⨯-8888,绘制函数z =6. 用plot 函数绘制下面分段函数的曲线。
,(),,x x f x x x x ⎧++>⎪==⎨⎪+<⎩235000507. 某工厂2005年度各季度产值(单位:万元)分别为:450.6、395.9、410.2、450.9,试绘制柱形图和饼图,并说明图形的实际意义。
8. 在同一坐标轴中绘制下列两条曲线并标注两曲线交叉点。
(1).y x =-205(2)sin()cos ,sin()sin x t tt y t tπ=⎧≤≤⎨=⎩303详细实验内容:1.设sin .cos x y x x ⎡⎤=+⎢⎥+⎣⎦23051,在x=0~2π区间取101点,绘制函数的曲线。
>> x=(0:2*pi/100:2*pi);>> y=(0.5+3*sin(x)/(1+x.^2))*cos(x); >> plot(x,y)2.已知: y x =21,cos()y x =22,y y y =⨯312,完成下列操作: (1)在同一坐标系下用不同的颜色和线性绘制三条曲线; >> x= linspace(0, 2*pi, 101);>> y1=x.*x; >> y2=cos(2x); >> y3=y1.*y2;plot(x,y1,'r:',x,y2,'b',x,y3, 'ko')(2)以子图形式绘制三条曲线;>> subplot(2,2,1),plot(x,y1)subplot(2,2,2),plot(x,y2)subplot(2,2,3),plot(x,y3)(3)分别用条形图、阶梯图、杆图和填充图绘制三条曲线。
matlab实验2
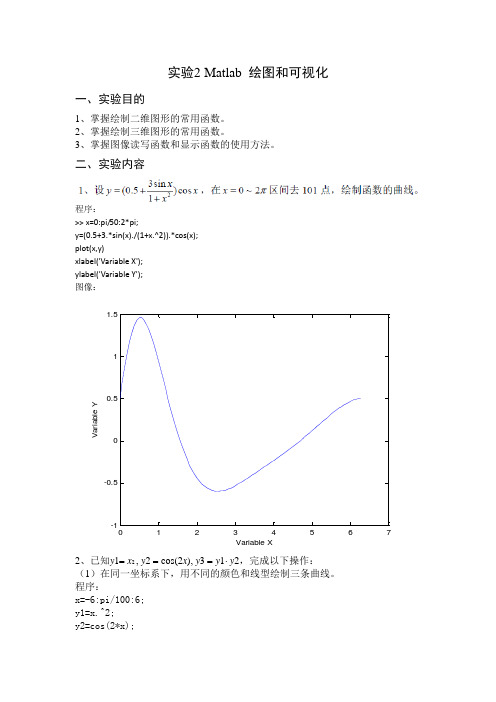
实验2 Matlab 绘图和可视化一、实验目的1、掌握绘制二维图形的常用函数。
2、掌握绘制三维图形的常用函数。
3、掌握图像读写函数和显示函数的使用方法。
二、实验内容程序:>> x=0:pi/50:2*pi;y=(0.5+3.*sin(x)./(1+x.^2)).*cos(x); plot(x,y)xlabel('Variable X'); ylabel('Variable Y'); 图像:01234567-1-0.50.511.5Variable XV a r i a b l e Y2、已知y 1= x 2 , y 2 = cos(2x ), y 3 = y 1⋅ y 2,完成以下操作:(1)在同一坐标系下,用不同的颜色和线型绘制三条曲线。
程序:x=-6:pi/100:6; y1=x.^2;y2=cos(2*x);y3=y1.*y2;plot(x,y1,'b',x,y2,'g-.',x,y3,'r:') xlabel('Variable X'); ylabel('Variable Y'); 图像:-6-4-20246-30-20-1010203040Variable XV a r i a b l e Y(2)在同一个图形窗口中,以子图的形式绘制三条曲线。
程序:x=-6:pi/100:6; y1=x.^2;y2=cos(2*x); y3=y1.*y2;subplot(3,1,1);plot(x,y1); xlabel('Variable X'); ylabel('Variable Y');subplot(3,1,2);plot(x,y2); xlabel('Variable X'); ylabel('Variable Y');subplot(3,1,3);plot(x,y3); xlabel('Variable X'); ylabel('Variable Y');-6-4-2024602040Variable XV a r i a b l e Y-6-4-20246-101Variable XV a r i a b l e Y-6-4-20246-50050Variable XV a r i a b l e Y(3)在同一个图形窗口中,以子图的形式,分别用条形图、阶梯图、杆图和填 充图绘制三条曲线。
实验二(2) MATLAB绘图

实验二(2)MATLAB绘图一.实验目的1、掌握matlab二维图形的绘制方法, 会对所绘图形进行加格栅,图例和标注等一些简单的处理;2、了解对数坐标图的绘制方法;3、了解符号函数(显函数、隐函数和参数方程)的绘制方法;二.实验原理与方法(一)二维绘图:Matlab作图是通过描点、连线来实现的,故在画一个曲线图形之前,必须先取得该图形上的一系列的点的坐标(即横坐标和纵坐标),然后将该点集的坐标传给Matlab函数画图.命令格式为:plot(x,y,s)其中x,y分别表示所取点集的横纵坐标,s指定线型及颜色.缺省时表示画的是蓝色实线.Plot(X,Y1,S1,X,Y2,S2,……,X,Yn,Sn)表示将多条线画在一起.例1:在[0,2*pi]用红线画sin(x),用绿圈画cos(x).解:x=linspace(0,2*pi,30);y=sin(x);z=cos(x);plot(x,y,‟r‟,x,z,‟go')(二) 符号函数(显函数、隐函数和参数方程)画图(1) ezplotezplot(…f(x)‟,[a,b])表示在a<x<b绘制显函数f=f(x)的函数图ezplot(…f(x,y)‟,[xmin,xmax,ymin,ymax])表示在区间xmin<x<xmax和ymin<y<ymax绘制隐函数f(x,y)=0的函数图ezplot(…x(t)‟,‟y(t)‟,[tmin,tmax])表示在区间tmin<t<tmax绘制参数方程x=x(t),y=y(t)的函数图.例2: 在[0,pi]上画y=sin(x)的图形解 输入命令:ezplot(…sin(x)‟,[0,pi])例3: 在[-2,0.5],[0,2]上画隐函数0)sin(=+xy e x 的图解 输入命令:ezplot('exp(x)+sin(x*y)',[-2,0.5,0,2])(2) fplot格式:fplot(…fun‟,lims)表示绘制字符串fun 指定的函数在lims=[xmin,xmax]的图形注意:[1] fun 必须是M 文件的函数名或是独立变量为x 的字符串.[2] fplot 函数不能画参数方程和隐函数图形,但在一个图上可以画多个图形。
2.实验二MATLAB绘图一答案

2.实验⼆MATLAB绘图⼀答案实验⼆ MATLAB 绘图⼀1. 编程绘制y=sin(t)/t 的曲线,t 的定义域是[-10Π,10Π],绘图时加⽹格解:t=[-10*pi:0.2:10*pi];y=sin(t)./t;plot(t,y),grid on-40-30-20-10010203040-0.4-0.20.20.40.60.812. 在[0,10]之间⽤⼀张图画出y=sin(t),y1=cos(t)的曲线,y ⽤红⾊实线绘制,y1⽤蓝⾊长划线绘制,绘图时加⽹格,横纵坐标⽐例相同,横轴标明“时间”,纵轴标明“正弦、余弦”,图题“正弦和余弦曲线”,要有图例说明,且⽤⿏标拖动来标注“sin(t)”、“cos(t)”。
解: t=0:0.1:10;y1=sin(t);y2=cos(t);plot(t,y1,'r',t,y2,'b--'); title('正弦和余弦曲线'); legend('正弦','余弦')xlabel('时间t'),ylabel('正弦、余弦') grid axis squaregtext('sin(t)'),gtext('cos(t)')246810-1-0.8-0.6-0.4-0.200.20.40.60.81正弦和余弦曲线时间t正弦、余弦3. ⽤三种⽅法编程,同时在⼀张图上观察常⽤对数、⾃然对数函数在[0,10]之间的曲线,其中在两种⽅法中,常⽤对数曲线⽤⿊⾊实线绘制,⾃然对数曲线⽤红⾊“+”绘制,绘图时,MATLAB 不要提⽰“W arning ” 解⼀: t=[0.1:0.1:10]; y1=log10(t); y2=log(t);plot(t,y1,'-k'),hold on plot(t,y2,'+r'),hold off246810-2.5-2-1.5-1-0.500.511.522.5解⼆: t=[0.1:0.1:10]; y1=log10(t); y2=log(t); plot(t,[y1;y2])246810-2.5-2-1.5-1-0.500.511.522.5解三: t=[0.1:0.1:10]; y1=log10(t); y2=log(t); plot(t,y1,'-k',t,y2,'+r')246810-2.5-2-1.5-1-0.500.511.522.54.曲线y=x+2x2+3x3,x的定义域为[-3,3],在⼀张图上⽤排成⼀⾏的三幅⼦图分别显⽰该曲线:⿊⾊实线图、脉冲图、条形图,每幅图均有图题及横纵坐标轴说明解:x=[-3:0.1:3];y=x+2*x.^2+3*x.^3;subplot(1,3,1),plot(x,y,'k')title('plot(x,y)')xlabel('x'),ylabel('y')subplot(1,3,2),stem(x,y)title(' stem(x,y)')xlabel('x'),ylabel('y')subplot(1,3,3),bar(x,y)title(' bar(x,y)')xlabel('x'),ylabel('y')5.通过MATLAB的help功能⾃学如何绘制饼图,在⼀张图上分上下两幅分别绘制“通信08-1”、“通信08-2”、“电⼦08-1”、“电⼦08-2”的“MATLAB ⼤侠”⽐例为3:3:2:2的饼图和⽴体饼图,其中,“通信08-1”的饼被抽出。
MATLAB实验二

3. 三维图形
• 三、视点
➢view(az,el)-------------设置观察点方向
az为方位角,el为仰角。 • 方位角为视点位置在XY平面上的投影与X轴形成的角度,
正值表示逆时针,负值表示顺时针。 • 仰角为XY平面的上仰或下俯角,正值表示视点在XY平
面上方,负值表示视点在XY平面下方。
figure grid gtext hold subplot text title xlabel ylabel
创建图形窗口 放置坐标网格线 用鼠标放置文本 保持当前图形窗口内容 创建子图 放置文本 放置图形标题 放置X轴坐标标记 放置Y轴坐标标记
3. 三维图形 • 一、 plot3函数
• 将二维函数plot的功能扩展到三维空间,绘制三维图形。 • 函数格式:plot3(x1,y1,z1,c1,x2,y2,z2,c2,…)
theta=[0:0.01:2*pi];
rho=sin(2*theta).*cos(2*theta);
polar(theta,rho); 绘制极坐标图命令
title('polar plot');
例9、程序:
theta=linspace(0, 2*pi);
r=cos(4*theta);
polar(theta, r);
所组成的画面。
4. 动画设计
• 【例14】 播放一个不断变化的眼球程序段。
• m=moviein(20); 建立一个20个列向量组成的矩阵
• for j=1:20
•
plot(fft(eye(j+10))) %绘制出每一幅眼球图并保存到m矩阵中
• m(:,j)=getframe;
实验2:MATLAB作图

数学实验
例4
x 画出函数 y e 的曲线(用ezplot和fplot).
(1) 输入:
syms x y=‘exp(x)’ ezplot(y)
输出结果:
数学实验
(2) 输入:
syms x y='exp(x)'
fplot(y,[-5,7],'r*')
输出结果:
数学实验
例5 绘制函数 y sin
线型、颜色和数据点可以选择,不选则用MATLAB设定的默认值.
数学实验
3. 常用绘图函数
(1)绘图常用命令
plot(x,y,‘r+-’) 离散数据画函数曲线图 fplot(y,[a,b]) 连续函数y在区间[a,b]上做曲线图 ezplot(y,[a,b]) 连续函数y在区间[a,b]上做曲线图 hold on 保持图形 hold off 取消保持图形 subplot(m,n,p) 分块绘图,分割成m行n列,p为编号 plot(x1,y1,x2,y2) 同一图中绘制多条曲线 axis([xmin,xmax,ymin,ymax]) 确定坐标系的范围 axis(‘equal’) 各坐标轴刻度增量相同 axis(‘on’) 返回(缺省的)坐标轴显现状态 [x,y,z]=meshgrid(x,y,z) 三维网格坐标的生成
输出结果:
数学实验
y3 x 2 ,y4 e x分块绘制在同一窗口. y 2 cos x , 例8 将函数 y1 sin x ,
输入:
subplot(2, 2, 1) fplot('sin(x)', [-pi, pi], 'r') title('sin(x)') subplot(2,2,2) fplot('cos(x)',[-pi, pi], 'm:')
MATLAB作图

MATLAB 作图实验目的:熟悉MA TLAB 作图功能,了解MA TLAB 的作图方法,掌握MA TLAB 一些常用的作图命令。
实验要求:先阅读实验内容后,完成相应的练习,并将操作过程及结果记录下来。
实验内容:1.二维图形1)曲线图plot(X ,Y ,S),X ,Y 是向量,表示点集的横坐标和纵坐标,S 是线型plot(X ,Y)plot(X1,Y1,S1,...,Xn ,Yn ,Sn)将多条线画在一起2)符号函数(显函数、隐函数和参数方程)画图ezplot(f) 表示在默认区间-2*pi<x<2*pi 绘制f=f(x)的函数图形ezplot(f ,[a,b]) 表示在a<x<b 绘制显函数f=f(x)的函数图形ezplot(f,[xmin,xmax,ymin,ymax) 表示在区间xmin<x<xmax 和ymin<y<ymax 绘制隐函数f(x,y)=0图形 ezplot(X,Y ,[tmin,tmax]) 表示在区间tmin<t<tmax 绘制参数方程x=x(t),y=y(t)的函数图fplot(fun,lims) 表示绘制字符串fun 指定的函数在lims=[xmin,xmax]的图形,fun 必须是M 文件的函数名或是独立变量为X 的字符串,此字符串被送入函数eval ,函数fun(x)必须对向量中的每个元素x 返一行向量。
Fplot 不能画参数方程和隐函数图形,但在一个图上可以画多个图形。
3)对数坐标图loglog(Y):表示x,y 坐标都是对数坐标系semilogx(Y):表示x 坐标轴是对数坐标系semilogy(...):表示y 坐标轴是对数坐标系plotyy :有两个y 坐标轴,一个在左边,一个在右边练习11) 在区间[0,2*pi]画sin(x);在[0,2*pi]用红线画sin(x),用绿圈画cos(x),给出操作过程及结果。
实验作业2 MATLAB作图

实验作业2 MATLAB作图1、用plot,fplot 绘制函数y=cos(tan( x))的图形。
解:代码如下:x=linspace(-0.5,0.5,30);y=cos(tan(pi*x));plot(x,y)结果:fplot('[cos(tan(pi*x))]',[-0.5,0.5])结果:注意事项: fplot('[cos(tan(pi*x))]',[-0.5,0.5])不能写成fplot('[cos(tan(pi*x))]',(-0.5,0.5))否则是错误程序。
2. 用ezplot绘制函数exy-sin(x+y)=0 在[-3, 3]上的图形。
解:代码如下:ezplot('exp(x*y)-sin(x+y)=0',[-3,3])3.用matlab以动画的方式绘制出摆线x=a(t-sint) y=a(1-cost) (a自己赋值)的渐屈线clear;clc;close;a=1;syms tx=a*(t-sin(t));y=a*(1-cos(t));ezplot(x,y,[0,2*pi]),grid on ;hold on;dy=diff(y)/diff(x);dyy=diff(dy)/diff(x);xx=x-(1+dy^2)*dy/dyy;%渐屈线的坐标yy=y+(1+dy^2)/dyy;M=50;t=0;xxx=subs(xx);yyy=subs(yy);H1=plot(xxx,yyy,'r');hold on;grid on ;axis([0,7,-2.5,2.5]);x1=subs(x);y1=subs(y);H2=plot([x1,xxx],[y1,yyy],'k--');H3=plot(x1,y1,'ko');H4=plot(xxx,yyy,'ro');tt=linspace(0,2*pi,M);for i=1:Mpause(0.2);t=tt(1:i);xxx=subs(xx);yyy=subs(yy);x1=subs(x);y1=subs(y);set(H1,'xdata',xxx,'ydata',yyy);set(H2,'xdata',[x1(i),xxx(i)],'ydata',[y1(i),yyy(i)]);set(H3,'xdata',x1(i),'ydata',y1(i));set(H4,'xdata',xxx(i),'ydata',yyy(i));end绘制函数⎩⎨⎧-=-=)cos 1()sin (t a y t t a x 在]2,0[π∈t 上的图形。
北科大MATLAB实验报告第二次作业MATLAB绘图

《数学实验》报告实验名称第二堂课MATLAB绘图练习学院东凌经济管理学院专业班级管信112姓名杨忠璟学号********2013年5 月一、【实验目的】1. 掌握MATLAB二维曲线绘图2. 掌握MATLAB二维特殊图形的绘制3. 掌握MATLAB三维曲线绘图4. 掌握MATLAB三维特殊图形绘制5. 掌握MATLAB绘图的控制命令二、【实验任务】练习:课本4.1,4.3,4.5,4.9三、【实验程序】1) 4.1程序:绘制的图像,要求用蓝色的星号画图,并且画出其包络线的图像,用红色的点划线画图。
x=0:pi/50:4*pi;y=exp(x/3).*sin(3*x);plot(x,y,'b*'),hold ony1=exp(x/3);plot(x,y1,'r.')y2=-exp(x/3);plot(x,y2,'r.')grid on2) 4.3程序:在同一个图形窗口画三个子图,要求使用指令gtext 、axis 、legend 、title、xlabel 、ylabel:①②③x1=-pi:pi/50:pi;x2=pi:pi/100:4*pi;x3=1:0.01:8;y1=x1.*cos(x1);y2=x2.*tan(1./x2).*sin(x2.^3);y3=exp(1./x3).*sin(x3);subplot(1,3,1),plot(x1,y1,'m.'),grid on,title('曲线y=xcos(x)')gtext('y1=xcos(x)'),legend('y1=xcosx'),xlabel('x轴'),ylabel('y轴')subplot(1,3,2),plot(x2,y2,'r-'),grid on,title('曲线y=xtan(1/x)sin(x^3)')gtext('y2=xtan(1/x)sin(x^3)'),legend('y2=xtan(1/x)sin(x^3)'),xlabel('x轴'),ylabel('y轴')subplot(1,3,3),plot(x3,y3,'b*'),grid on,title('曲线y=exp(1/x)sin(x)')gtext('y3=exp(1/x)sin(x)'),legend('y3=exp(1/x)sinx')xlabel('x轴'),ylabel('y轴')3) 4.5程序:绘制圆锥螺线的图像并加各种标注,圆锥螺线的参数方程为:t=0:pi/50:20*pi;x=t.*cos(pi/6.*t);y=t.*sin(pi/6.*t);z=2*t;plot3(x,y,z),grid onxlabel('x轴 x=tcos(pi/6t)')ylabel('y轴 y=tsin(pi/6t)')zlabel('z轴 z=2t')title('圆锥螺线')legend('圆锥螺线')4) 4.9程序:画三维曲面与平面z=3的交线t=-2:0.01:2;[x,y]=meshgrid(t);z1=5-x.^2-y.^2;subplot(131),mesh(x,y,z1),title('三维曲面')z2=3*ones(size(x));subplot(1,3,2),mesh(x,y,z2),title('平面')r0=abs(z1-z2)<=1;zz=r0.*z2;yy=r0.*y;xx=r0.*x;subplot(1,3,3),plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'m-');title('交线')四、【实验结果】1) 4.1程序:2) 4.3程序:3) 4.5程序:4) 4.9程序五、【实验总结】初步了解学习了MATLAB绘图的功能,通过MATLAB的强大绘图功能,我们可以把很多数学上抽象的图像问题展现在计算机上进行分析。
MATLAB实验报告绘图

68 54 35;
45 25 12;
48 68 45;
68 54 69];
x=sum(t);
h=pie(x);
textobjs=findobj(h,'type','text');
str1=get(textobjs,{'string'});
val1=get(textobjs,{'extent'});
输出图像:
3.画出所表示的三维曲面(图1.3-4)。的取值范围是。
输入程序: x=-8:0.5:8;
y=x';
X=ones(size(y))*x;
Y=y*ones(size(x));
R=sqrt(X.^2+Y.^2)+eps;
Z=sin(R)./R;
surf(X,Y,Z);
colormap(cool)
实验名称
MATLAB绘图
1、实验目的和要求:
2、了解MATLAB的绘图指令。
3、掌握绘图函数的用法、简单的图形标注,简单颜色设定。
4、掌握MATLAB二维曲线绘图、三维曲线绘图,以及一些特殊图形的绘制。
5、掌握MATLAB二维曲线绘图、三维曲线绘图,以及一些特殊图形的绘制。
实验内容和步骤:
1.作多条曲线
plot3(y1,y2,t);
title('helix'),text(0,0,0,'origin');
xlable('sin(t)'),ylable('cos(t)'),zlable('t');
gridon;
实验二MATLAB绘制图形

4
5
6
7
hold on;
%后续图形叠加显示
plot(t,y2);
hold on;
plot(t,y3);
二、三维图形
1、 基本的三维绘图命令
三维曲线图
plot3函数可以绘制三维曲线:
plot3(x1, y1, z1, 's1', x2, y2, z2, 's2'…)
例13 函数plot3绘制的三维曲线图
theta = (-pi:0.01:pi);
rho(1,:) = 2*sin(5*theta).^2;
rho(2,:) = cos(10*theta).^3;
rho(3,:) = sin(theta).^2;
rho(4,:) = 5*cos(3.5*theta).^3;
120
for i = 1:4
% 极坐标图形输出函数 150
实验二 MATLAB绘制图形
(一) 实验类型:验证性 (二) 实验类别:基础实验 (三) 实验学时数:2学时
.
实验内容
一、二维图形 二、三维图形
一、二维图形 1、 基本二维绘图命令
(1) plot函数
plot(x):缺省自变量的绘图格式,x可为向量或矩阵. 当x为向量时,以x元素值为纵坐标,以相应元素下标为
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0
1
2
3
4
5
6
7
例6 分析下列程序绘制的曲线. x1=linspace(0,2*pi); x2=linspace(0,3*pi); x3=linspace(0,4*pi); y1=sin(x1); y2=1+sin(x2); y3=2+sin(x3); x=[x1;x2;x3]'; y=[y1;y2;y3]'; plot(x,y,x1,y1-1)
实验二MATLAB的基本绘图方法

实验二MATLAB的基本绘图方法一、实验目的1.二维平面图形的绘制2.三维立体图形的绘制3.隐函数作图二、实验地点:A204三、实验日期:四、实验内容(一)二维平面图形的绘制1、Plot的使用方法介绍plot 是绘制二维图形的最基本函数,它是针对向量或矩阵的列来绘制曲线的。
也就是说,使用plot 函数之前,必须首先定义好曲线上每一点的x 及y 坐标,常用格式为:(1)plot(x) 当x 为一向量时,以x 元素的值为纵坐标,x 的序号为横坐标值绘制曲线。
当x 为一实矩阵时,则以其序号为横坐标,按列绘制每列元素值相对于其序号的曲线,当x 为m×n 矩阵时,绘制成n 条曲线。
请自设向量进行绘图。
(2)plot(x,y) 以x 元素为横坐标值,y 元素为纵坐标值绘制曲线。
(3)plot(x,y1,x,y2,…) 以公共的x 元素为横坐标值,以y1,y2,…元素为纵坐标值绘制多条曲线。
例1:画出一条正弦曲线和一条余弦曲线。
x=0:pi/10:2*pi;y1=sin(x);y2=cos(x);plot(x,y1,x,y2)请尝试给plot()加上标记符参数,如:plot(x,y1,'*',x,y2,'^')。
注:在绘制曲线图形时,常常采用多种颜色或线型来区分不同的数据组,MA TLAB 软件专门提供了这方面的参数选项,我们只要在每个坐标后加上相关字符串,就可实现它们的功能。
具体参见课件。
2、图形修饰MATLAB 软件为用户提供了一些特殊的图形函数,用于修饰已经绘制好的图形。
图形修饰函数表如下:函数含义grid on (/off) 给当前图形标记添加(取消)网络xlable(‘string’) 标记横坐标ylabel(‘string’) 标记纵坐标title(‘string’) 给图形添加标题text(x,y,’string’) 在图形的任意位置增加说明性文本信息gtext(‘string’) 利用鼠标添加说明性文本信息axis([xmin xmax ymin ymax]) 设置坐标轴的最小最大值例2、给例1的图形中加入网络和标记。
实验二 matlab图形绘制

实验二matlab图形绘制一、实验目的1、学习MATLAB图形绘制的基本方法;2、熟悉和了解MATLAB图形绘制程序编辑的基本指令;3、熟悉掌握利用MATLAB图形编辑窗口编辑和修改图形界面,并添加图形的各种标注;二、实验原理1.二维数据曲线图(1)绘制单根二维曲线plot(x,y);(2)绘制多根二维曲线plot(x,y) 当x是向量,y是有一维与x同维的矩阵时,则绘制多根不同颜色的曲线。
当x,y是同维矩阵时,则以x,y对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
(3)含有多个输入参数的plot函数plot(x1,y1,x2,y2,…,xn,yn)(4)具有两个纵坐标标度的图形plotyy(x1,y1,x2,y2)2.图形标注与坐标控制1)title (图形名称)2)xlabel(x轴说明)3)ylabel(y轴说明)4)text(x,y图形说明)5)legend(图例1,图例2,…)6)axis ([xmin xmax ymin ymax zmin zmax])3.图形窗口的分割subplot(m,n,p)4.三维曲线plot3(x1,y1,z1,选项1,x2,y2,选项2,…,xn,yn,zn,选项n)5.三维曲面mesh(x,y,z,c) 与surf(x,y,z,c)。
一般情况下,x ,y ,z 是维数相同的矩阵。
X ,y 是网格坐标矩阵,z 是网格点上的高度矩阵,c 用于指定在不同高度下的颜色范围。
三、实验内容及步骤1.绘制下列曲线: (1) 21100x y +=x=0:0.02:10; y=100./(1+x.^2); plot(x,y)title('my first plot'); xlabel('x'); ylabel('y'); grid on截图:(2) 2221x e y -=πx=0:0.02:10;y=1./(2*pi).*exp(-(x.^2)./2); plot(x,y)title('my first plot'); xlabel('x'); ylabel('y'); grid on截图:(3) 122=+y x 6t=-4:0.02:4; y=4*sin(t); x=4*cos(t);plot(x,y)title('my first plot'); xlabel('x'); ylabel('y'); grid on截图:(4) ⎩⎨⎧==325t y t x t=0:0.02:10; x=t.^2; y=5.*t.^3; plot(x,y)title('my first plot'); xlabel('x');ylabel('y');grid on截图:2.在一个图形窗口绘制正弦和余弦曲线,要求给图形加标题“正弦和余弦曲线”,X轴Y轴分别标注为“时间t”和“正弦、余弦”,添加图例,在图形的某个位置标注“sin(t)”“cos(t)”,显示网格。
实验二MATLAB的绘图功能
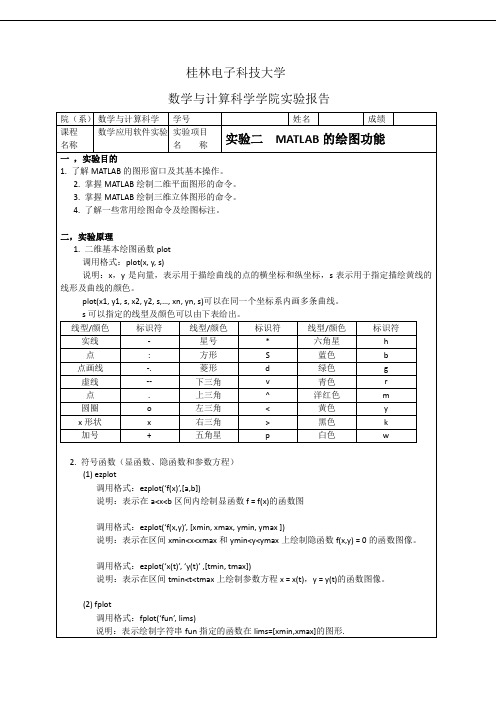
>> t = 0:pi/100:10*pi;
x=2*cos(t).^3;
>> y=2*sin(t).^3;
>> plot(x,y)
6.画出双纽线 的图形;
ezplot('(x^2+y^2)^2=3*(x^2-y^2)',[-3 3 -3 3])
7.画出三维曲线图:
>> t=0:pi/100:2*pi;
说明:x,y, z是向量,表示用于描绘曲线的点的在x上的坐标、y轴上的坐标及z上的坐标,s表示用于指定描绘黄线的线形及曲线的颜色。
plot3(x1, y1, z1, s, x2, y2, z2, s,…, xn, yn, zn, s)可以在同一个坐标系内画多条曲线。
5.空间曲面
(1)空间网线图mesh
4.在极坐标系下画出三叶形曲线 ,并尝试不同的线形和颜色;
theta = 0:pi/100:2*pi;
>> r=3*sin(3*theta);
>> polar(theta,r,'r')
theta = 0:pi/100:2*pi;
r=3*sin(3*theta);
polar(theta,r,'g+')
二,实验原理
1.二维基本绘图函数plot
调用格式:plot(x, y, s)
说明:x,y是向量,表示用于描绘曲线的点的横坐标和纵坐标,s表示用于指定描绘黄线的线形及曲线的颜色。
plot(x1, y1, s, x2, y2, s,…, xn, yn, s)可以在同一个坐标系内画多条曲线。
s可以指定的线型及颜色可以由下表给出。
Matlab实验报告(三)-MATLAB绘图

实验目的1.掌握MATLAB的基本绘图命令。
2.掌握运用MATLAB绘制一维、二维、三维图形的方法.3.给图形加以修饰。
一、预备知识1.基本绘图命令plotplot绘图命令一共有三种形式:⑴plot(y)是plot命令中最为简单的形式,当y为向量时,以y的元素为纵坐标,元素相应的序列号为横坐标,绘制出连线;若y为实矩阵,则按照列绘出每列元素和其序列号的对应关系,曲线数等于矩阵的列数;当y为复矩阵时,则按列以每列元素的实部为横坐标,以虚部为纵坐标,绘出曲线,曲线数等于列数。
⑵ plot(x,y,[linspec])其中linspec是可选的,用它来说明线型。
当x和y为同维向量时,以x为横坐标,y为纵坐标绘制曲线;当x是向量,y是每行元素数目和x维数相同的矩阵时,将绘出以x为横坐标,以y中每行元素为纵坐标的多条曲线,曲线数等于矩阵行数;当x为矩阵,y为相应向量时,使用该命令也能绘出相应图形。
⑶ plot(x1,y1,x2,y2,x3,y3……)能够绘制多条曲线,每条曲线分别以x和y为横纵坐标,各条曲线互不影响。
线型和颜色MATLAB可以对线型和颜色进行设定,线型和颜色种类如下:线:—实线:点线 -.虚点线——折线点:.圆点 +加号 *星号 x x型 o 空心小圆颜色:y 黄 r 红 g 绿 b 蓝 w 白 k 黑 m 紫 c 青特殊的二维图形函数表5 特殊2维绘图函数[1] 直方图在实际中,常会遇到离散数据,当需要比较数据、分析数据在总量中的比例时,直方图就是一种理想的选择,但要注意该方法适用于数据较少的情况。
直方图的绘图函数有以下两种基本形式。
·bar(x,y) 绘制m*n 矩阵的直方图.其中y 为m *n 矩阵或向量,x 必须单向递增。
·bar(y) 绘制y 向量的直方图,x 向量默认为x=1:m close all; %关闭所有的图形视窗。
x=1:10;y=rand (size(x )); bar(x,y ); %绘制直方图.123456789100.51Bar()函数还有barh ()和errorbar ()两种形式,barh()用来绘制水平方向的直方图,其参数与bar()相同,当知道资料的误差值时,可用errorbar ()绘制出误差范围,其一般语法形式为:errorbar (x,y,l,u)其中x,y 是其绘制曲线的坐标,l ,u 是曲线误差的最小值和最大值,制图时,l 向量在曲线下方,u 向量在曲线上方。
MATLAB实验二-绘图-参考答案-仅供参考

实验二:MATLAB 的绘图
实验目的:
1、掌握 MATLAB 的各种二维绘图; 2、掌握 MABLAB 的三维绘图; 3、了解 MABLAB 的 MATLAB 的绘图修饰。
实验内容
1、 2、 3、 1. 基本二维绘图函数 2. 颜色,线条的设置,绘制多图 3. 三维绘图 4. 图形标注,坐标,修饰等处理
0.1 x
sin(0.5 x) 和 y 0.2e 0.1x cos(0.5 x) 在区间
[0,2] 上的曲线图,添上图例、题头、坐标轴。
x=0:pi/20:2*pi; plot(x,0.2*exp(0.1*x)+sin(0.5*x),x,0.2*exp(0.1*x)+cos(0.5*x)) legend('0.2*exp(0.1*x)+sin(0.5*x)','0.2*exp(0.1*x)+cos(0.5*x)') xlabel('x'); ylabel('y'); title('两曲线示意图') 6、1)数据如下表所示: 数学系毕业学生去向 国家单位 私营企业 出国 读研 待业 比例(%) 10 40 5 20 25
实验要求
1、学生在实验操作过程中自己动手独立完成,1 人为 1 组。 2、完成实验报告:按照试验的每个题目的具体要求完成
实验数据记录及分析(命令与结果)
1、 运行该端程序,注释程序。 v=[‘-1’;’+1’]; t=[0:0.05:2*pi]; % t 的取值范围是 0 到 2pi,其步长为 0.05 plot(t,sin(t)); xlabel(‘time(0—2\pi)’); % 在坐标轴 x 上标注 time(0-2\pi) ylabel(‘value’); % 在坐标轴 y 标注 value text(pi/2,0.9,[‘\uparrowsin(\pi/2)=’,v(2,:)]); % 在 (pi/2, 0.9) 处用向上的箭头标注 sin(pi/2)=+1 text(pi*3/2,-0.9,[‘\downarrowsin(\pi*3/2)=’,v(1,:)]); text(0,0.6,[‘Date:’,date]); % 在(0,0.6)处显示 Date 当前日期 gtext( [‘Date:’,date]); % 通过鼠标箭头标注 Date 日期 2、运行该端程序(掌握 subplot,pause) ,注释程序 t=0:0.1:4*pi; y=exp(-0.1*t).*sin(t); clf % 清空绘图窗口 figure(1) % 新建一个绘图窗口, 标号为 1 subplot(2,2,1) % 将一个绘图窗口划分成一个 2*2 的子区域, 并按行从左至右 依次排号,1 表示第一个绘图子区域 stem(t,y) % 绘制火柴杆图 title('stem(t,y)') % 加标题为 stem(t,y) pause % 在当前完成的图像上停留,按任意键显示后面的命令 subplot(2,2,2) stairs(t,y) % 绘制阶梯图 title('stairs (t,y)') pause subplot(2,2,3)
实验二MATLAB绘制图形

实验二MATLAB绘制图形(一)实验类型:验证性(二)实验类别:基础实验(三)实验学时数:2学时(四)实验目的1、熟悉MATLAB基本命令与操作;2、熟悉MATLAB的矩阵运算;3、掌握MATLAB的绘图功能.(五)实验内容MATLAB基本命令与实际操作、矩阵运算、多项式运算以及绘图功能(六)实验要求1、学生在实验操作过程中自己动手独立完成,1人为1组。
2、完成实验报告:按照试验的每个题目的具体要求完成(七)实验仪器、设备计算机(安装Windows98 、Windows2000 或Windows XP或以上)(八)实验课承担单位:数学实验室1、基本的绘图命令plot(x1,y1,option1,x2,y2,option2,…)x1,y1给出的数据分别为x,y轴坐标值,option1为选项参数,以逐点连折线的方式绘制1个二维图形;同时类似地绘制第二个二维图形,……等。
这是plot命令的完全格式,在实际应用中可以根据需要进行简化。
比如:plot(x,y);plot(x,y,option)选项参数option定义了图形曲线的颜色、线型及标示符号,它由一对单引号括起来。
2、选择图像figure(1);figure(2);…;figure(n)打开不同的图形窗口,以便绘制不同的图形。
3、grid on:在所画出的图形坐标中加入栅格grid off:除去图形坐标中的栅格4、hold on:把当前图形保持在屏幕上不变,同时允许在这个坐标内绘制另外一个图形。
hold off:使新图覆盖旧的图形5、设定轴的范围axis([xmin xmax ymin ymax])6、文字标示text(x,y,’字符串’)在图形的指定坐标位置(x,y)处,标示单引号括起来的字符串。
gtext(‘字符串’)利用鼠标在图形的某一位置标示字符串。
title(‘字符串’)在所画图形的最上端显示说明该图形标题的字符串。
xlabel(‘字符串’),ylabel(‘字符串’)设置x,y坐标轴的名称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验作业2----MATLAB作图
实验作业2 MATLAB作图1、用plot,fplot 绘制函数y=cos(tan( x))的图形。
解:
代码如下:
x=linspace(-0.5,0.5,30);
y=cos(tan(pi*x));
plot(x,y)
结果:
fplot('[cos(tan(pi*x))]',[-0.5,0.5])
结果:
注意事项: fplot('[cos(tan(pi*x))]',[-0.5,0.5])不能写成fplot('[cos(tan(pi*x))]',(-0.5,0.5))否则是错误程序。
2. 用ezplot绘制函数exy-sin(x+y)=0 在[-3, 3]上的图形。
解:
代码如下:
ezplot('exp(x*y)-sin(x+y)=0',[-3,3])
3.用matlab以动画的方式绘制出摆线x=a(t-sint) y=a(1-cost) (a自己赋值)的渐屈线
clear;
clc;
close;
a=1;
syms t
x=a*(t-sin(t));
y=a*(1-cos(t));
ezplot(x,y,[0,2*pi]),grid on;hold on;
dy=diff(y)/diff(x);
dyy=diff(dy)/diff(x);
xx=x-(1+dy^2)*dy/dyy;%渐屈线的坐标
yy=y+(1+dy^2)/dyy;
M=50;
t=0;
xxx=subs(xx);
yyy=subs(yy);
H1=plot(xxx,yyy,'r');hold on;grid on;axis([0,7,-2.5,2.5]);
x1=subs(x);
y1=subs(y);
H2=plot([x1,xxx],[y1,yyy],'k--');
H3=plot(x1,y1,'ko');
H4=plot(xxx,yyy,'ro');
tt=linspace(0,2*pi,M);
for i=1:M
pause(0.2);
t=tt(1:i);
xxx=subs(xx);
yyy=subs(yy);
x1=subs(x);
y1=subs(y);
set(H1,'xdata',xxx,'ydata',yyy);
set(H2,'xdata',[x1(i),xxx(i)],'ydata',[y1(i),yyy(i)]);
set(H3,'xdata',x1(i),'ydata',y1(i));
set(H4,'xdata',xxx(i),'ydata',yyy(i));
end
绘制函数⎩⎨⎧-=-=)
cos 1()sin (t a y t t a x 在]2,0[π∈t 上的图形。
程序:a=input('please input a=');
t=linspace(0,2*pi,100);
x=a*(sin(t));
y=a*(t-cos(t));
plot(x,y);
please input a=10
4.
5. 在同一平面中的两个窗口分别画出心形线和马鞍面。
要求:1)在图形上加格栅、图例和标注;
2)定制坐标;
3)以不同角度观察马鞍面。
解:
心型线代码如下:
clear;
clc;
i=-pi:0.1:pi;
x=2.*(sin(i)-sin(2*i)./2);
y=2.*(cos(i)-cos(i).^2);
plot(x,y);
axis([-3 3 -4.2 1]);%制定图形坐标title('心形线');%当前图顶端加图例xlabel('x');%当前图x轴加图例
ylabel('y');%当前图y轴加图例
grid on;%加格栅到当前图上
心型线运行结果显示如下图:
图3.1(心型线)
马鞍线代码如下:
clear;
clc;
a=10;
b=10;
x=-1.5:0.1:1.5;
y=-1.5:0.1:1.5;
[X,Y]=meshgrid(x,y);%x行y列的矩阵
Z=X.^2/a-Y.^2/b;
figure(2);%新建窗口
subplot(221);%分割当前窗口,作图显示在该分割块上
surf (X,Y,Z);
title('马鞍面');
xlabel('x');
ylabel('y');
subplot(222);
surf (X,Y,Z);
title('马鞍面');
xlabel('x');
ylabel('y');
view(20,30);%改变视角到(20,30) subplot(223);
surf (X,Y,Z);
title('马鞍面');
xlabel('x');
ylabel('y');
view(50,20);%改变视角到(50,20)subplot(224);
surf (X,Y,Z);
title('马鞍面');
xlabel('x');
ylabel('y');
view(60,10);%改变视角到(60,10)
马鞍线运行结果显示如下图:
图3.2(马鞍面)
7.以不同的视角观察球面x2+y2+z2=r2和圆柱面x2+y2=rx所围区域.
解:
代码如下:
clear;
clc;
r=2;
[x0,y0,z0]=sphere(50);
x=r*x0;y=r*y0;z=r*z0;
surf(x,y,z);hold on;
f=@(x,y)x.^2+y.^2-r*x;
ezsurf(f,[-1.5,2.5],[-2,1.5]);
axis equal;
view(30,20);
运行结果显示如下图:
图3.3。
