现代结构分析方法-4a
我国初次分配的原则和结构分析

我国初次分配的原则和结构分析作者:郑志国来源:《江汉论坛》2022年第06期摘要:我國初次分配实行按劳分配为主体的多种分配方式,分配依据是人们的劳动贡献和提供生产要素的贡献,一般通行同等贡献获得同等收入的分配原则。
在社会主义市场经济中,按劳分配是通过商品交换来实现的,主要以价值或货币形态分配劳动者创造的增加值,由人们根据自己的需要到市场购买消费品,因此,按劳分配一般是由企业或用人单位来组织实施,同质同量劳动获得同量报酬原则在企业层面就是同等业绩获得同等工资。
我国按劳分配的主体地位体现在劳动贡献是消费品分配的主要依据,国民总收入大部分用于实行按劳分配。
如果把劳动者报酬和工资性收入全部视为按劳分配所得,那么它们分别占初次分配总收入和居民可支配收入的大部分,这都可以视为以按劳分配为主体在分配结构上的表现。
在全面建设社会主义现代化国家新征程中,应当改进国民总收入和初次分配收入项目核算方法,防止资本侵蚀劳动报酬,抑制国际资本对中方收入的挤压,进一步提高企业生产一线工人的工资水平。
关键词:按劳分配原则;初次分配;国民经济核算体系;生产要素;国际资本中图分类号:F047 文献标识码:A 文章编号:1003-854X(2022)06-0005-07我国初次分配实行按劳分配为主体的多种分配方式,分配依据是人们的劳动贡献和提供生产要素的贡献,通行同等贡献获得同等收入的原则。
如何更好实行按劳分配为主体的多种分配方式,调动广大劳动者和社会各方面的积极性,通过高质量发展来增加财富总量和促进共同富裕,这是值得深入研究的问题。
①一、初次分配的同等贡献获得同等收入原则一个国家的初次分配对象用现行指标核算是国内生产总值或国民总收入,从企业层次看则是一定时期创造的增加值。
依据人们的劳动贡献和提供生产要素的贡献来分配,必须使收入和贡献相称:对劳动者实行同质同量劳动获得同量报酬原则,对生产要素实行同质同量要素获得同量收入原则。
因为劳动贡献和一般生产要素贡献通常不能用同一标准来考核,所以这两类贡献与各自收入的关系有差异。
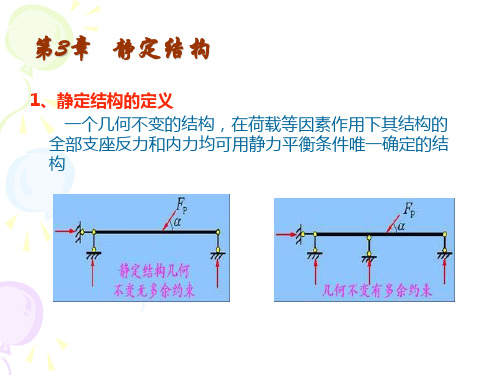
第03章: 结构力学 静定结构内力分析
2
2qa 2
2qa2
4qa
2
2
4qa2
14qa2
2qa2 q
14qa
弯矩图
10
也可直接从悬臂端开始计算杆件 8 2qa2
8qa 2
B
10qa 2
6qa 2q
2
2qa 2
4qa2
14qa
2
M图
(4)绘制结构Q图和N图 2qa2 2qa2 C 6qa q E
D
2q A 2a 2a 4a B
3a
6qa
FN2=0
FN=0
FN=0
FN1=0
判断结构中的零杆
FP FP FP/2
FP/ 2
FP
截
面
法
截取桁架的某一局部作为隔离体, 由平面任意力系的平衡方程即可求得未知 的轴力。 对于平面桁架,由于平面任意力系的 独立平衡方程数为3,因此所截断的杆件数 一般不宜超过3
试用截面法求图示桁架指定杆件的内力。
5、三铰拱的合理轴线 拱的合理轴线:在固定荷载作用下使拱处于无弯距状态 的轴线。 求解公式:在竖向荷载作用下,三铰拱的合理轴线使拱 的各截面处于无弯距状态,即
M M FH y 0
0
M y FH
0
结论: (1)三铰拱在沿水平线均匀分布的竖向荷载作用下,合理轴 线为一抛物线。
y
M AD
1 qL x2 8
M BD
q(l x) 1 x qx 2 2 2
Mx1max
1 qL x2 8
由以上三处的弯矩得到:
q(L x) 1 2 1 2 x qx qL x 2 2 8
整理得:
x 0.172L
外文翻译--结构分析的矩阵方法

南京理工大学毕业设计(论文)外文资料翻译学院(系):机械工程学院专姓学业:名:号:机械工程及自动化徐峰010*******外文出处:(用外文写)Theory of structuresPublisher:McGraw Hill 附件: 1.外文资料翻译译文;2.外文原文。
指导教师评语:翻译内容符合毕业设计内容的要求,翻译工作量较大,翻译基本正确、符合科技外语的翻译习惯和用法,较好的完成了翻译工作。
签名:年月日附件1:外文资料翻译译文结构分析的矩阵方法1. 力法和应变方法在前述的章节已经介绍解决静不定系统的各种各样的方法。
它们可分为两大类。
例如,在分析拱门和框架结构时,分析步骤如下。
首先,所有的冗余的约束被对应的冗余的力(或力矩)取代,这些力的大小可通过基于应变能的最小势能原理解得。
类似的过程也被用于解静不定桁架的分析,这些方法统称为力法。
在连续梁和框架分析中,另一种不同的方法曾被使用。
在这个情况下,我们首先计算了结点的旋转的角度(变形)而冗余力是后来才求的。
在连续梁的分析中使用了的3角度方程代表另一种方法。
这样的方法称为应变方法。
我们用一个例子来说明这两种方法之间的区别,如图10.1的平面静不定桁架,一力P 分解为Px和PY,作用在的5根悬于刚性基础的等截面杆交点A处。
因为杆数量大于A 点平衡方程的数目,很明显这是一个静不定问题。
一般来说,如果绞点A由n根杆铰接而成,那么冗余的杆将是(n-2)。
因此,为了根据力法解出对应的冗余的力X1,X2,X3,……Xn-2,我们根据这些力的作用,通过最小势能原理获得应变能表达式,进而获得所需的方程:эU/эX1=0эU/эX2=0 ……(a)其中每个方程都包含所有冗余力,因此随着杆数目的增加,方程(a)的求解将变得越来越麻烦。
解决相同的问题,Navier 建议使用的移置方法。
在图10.1的系统中,如果知道在力P 作用下A点的各自的水平位移u、垂直位移v,那么系统变形将完全确定下来。
建筑结构静力弹塑性分析方法及其减震控制

二、静力弹塑性分析方法的实施 步骤
二、静力弹塑性分析方法的实施步骤
1、定义材料属性:静力弹塑性分析需要输入材料的弹性模量、泊松比、剪切 模量、密度等参数,以及材料的非线性应力-应变关系。
二、静力弹塑性分析方法的实施步骤
2、建立结构模型:使用有限元方法建立结构模型,包括几何形状、边界条件 和载荷条件。
建筑结构静力弹塑性分析方法
建筑结构静力弹塑性分析方法
建筑结构静力弹塑性分析方法的基本原理是在荷载作用下,结构产生变形, 并导致应力和应变的产生。通过考虑材料的弹性和塑性性能,可以得出结构的弹 塑性响应。具体的计算步骤包括以下几个步骤:
建筑结构静力弹塑性分析方法
1、建立结构的计算模型,并确定结构的材料参数和边界条件; 2、对结构进行静力荷载作用下的弹性分析,得出结构的弹性响应;
内容摘要
在进行静力弹塑性分析时,需要考虑多种荷载工况,例如自重、风载、地震 作用等。通过在MIDASGEN中设置相应的荷载工况,可以模拟高层建筑结构在不同 荷载作用下的响应。同时,还需要根据建筑结构的特点,选择合适的分析方法和 计算参数,例如静力弹塑性分析方法、屈服准则等。
内容摘要
在MIDASGEN中,可以通过输出位移、应力、应变等结果,对高层建筑结构的 静力弹塑性进行分析。通过与其他方法(如有限元方法、实验方法等)的比较, 可以发现MIDASGEN在分析高层建筑结构的静力弹塑性方面具有较高的对高层建筑结构进行静力弹塑性分析是可行的,并且能 够得出可靠的结果。在实际工程中,MIDASGEN可以为高层建筑结构的安全性和稳 定性评估提供有力的支持。在进行高层建筑结构的静力弹塑性分析时,需要注意 建模的准确性、参数设置的合理性、荷载工况的全面性以及结果分析的可靠性等 问题。通过不断改进和完善分析过程,可以进一步提高MIDASGEN在高层建筑结构 分析中的精度和效率。
现代汉语 第四节 短语及层次分析法

(三)短语的结构分类
• • • • • • • • • • • • 偏正词组 述宾词组(动宾) 述补词组(动补) 主谓词组 联合词组(并列) 连谓词组(连动) 兼语词组(递系) 同位词组 量词结构 (数量) 方位结构 介词结构 “的”字结构
词组
短语
结构
二、词组的基本结构类型
• (一)偏正词组 • 前面的成分修饰、限定、说明后面的成分。 • 修饰语+中心语 •中国的崛起 • 干净衣服 漂亮的姑娘 •文艺演出 • 白衬衣 木头桌子 •科技进步 • 学校的房子 我的书 •他们的猜测 • 绿油油的麦苗 红红的脸 •动人的笑 • 三本书 两位老师 •别人的精明 • 昨天的故事 北京的气候 •分析的精确 • (名词性词组) • 定语——中心语
• • • • • •
刻苦学习 积极工作 赶快走 慢慢思考 才回来 正在吃饭 格外努力 更加认真 忽然电话响了 渐渐地他走远了 悄悄地来了 一声不响地坐着
• (动词性、形容词性词组) • 状语——中心语
• • • • • • • • • • •
状中间的语义关系: 1、修饰语表方式 仔细研究 赶快走 渐渐消失 大力发展 2、表程度 非常便宜 特别高兴 极其可悲 那么可爱 3、表时间 正在进行 即将开始 马上结束 常常迟到 4、表处所 在家休息 在操场上集合 在会议室开会 5、表否定 不去 没有参加
• • • • • • • • • • • • •
述宾之间的语义关系: 1、受事(客体) 穿大衣 买本子 喝水 讨论问题 观察地形 2、结果 做大衣 写文章 盖房子 想办法 3、工具 浇水 捆绳子 打吊瓶 裹绷带 4、处所 去北京 睡地板 住旅馆 回娘家 逛公园 5、与事 给妈妈 告诉他 教孩子 6、施事 来人 坐着主席团 躺着一个人
材料现代分析方法习题及答案优选全文

下载温馨提示:该文档是学者精心编制而成, 希望能够帮助大家解决实际的问题。
文档下载后可定制随意修改, 请根据实际需要进行相应的调整和使用, 谢谢!并且, 我们为大家提供各种各样类型的实用资料, 如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等, 如想了解不同资料格式和写法, 敬请关注!下列哪些晶面属于[11]晶带?(1)、(1)、(231)、(211)、(101)、(01)、(13), (0), (12), (12), (01), (212), 为什么?答:(0)(1)、(211)、(12)、(01)、(01)晶面属于[11]晶带, 因为它们符合晶带定律:hu+kv+lw=0。
产生X射线需具备什么条件?答:实验证实:在高真空中, 凡高速运动的电子碰到任何障碍物时, 均能产生X射线, 对于其他带电的基本粒子也有类似现象发生。
电子式X射线管中产生X射线的条件可归纳为:1, 以某种方式得到一定量的自由电子;2, 在高真空中, 在高压电场的作用下迫使这些电子作定向高速运动;3, 在电子运动路径上设障碍物以急剧改变电子的运动速度。
分析下列荧光辐射产生的可能性, 为什么?(1)用CuKαX射线激发CuKα荧光辐射;(2)用CuKβX射线激发CuKα荧光辐射;(3)用CuKαX射线激发CuLα荧光辐射。
答: 根据经典原子模型, 原子内的电子分布在一系列量子化的壳层上, 在稳定状态下, 每个壳层有一定数量的电子, 他们有一定的能量。
最内层能量最低, 向外能量依次增加。
根据能量关系, M、K层之间的能量差大于L、K成之间的能量差, K、L层之间的能量差大于M、L层能量差。
由于释放的特征谱线的能量等于壳层间的能量差, 所以Kß的能量大于Ka的能量, Ka能量大于La的能量。
(1)因此在不考虑能量损失的情况下:(2)CuKa能激发CuKa荧光辐射;(能量相同)(3)CuKß能激发CuKa荧光辐射;(Kß>Ka)(4)CuKa能激发CuLa荧光辐射;(Ka>la)F的物理意义。
4A分子筛性能表征方法及其应用

4A分子筛性能表征方法及其应用孟玉堂;刘俊;汤光平【摘要】采用热重-质谱联用法、扫描电镜形貌观察、物相分析、孔径及比表面积分析、热重和静态吸附分析等方法,对4A 分子筛从微观结构到宏观性能进行了系统地表征,为全面掌握4A 分子筛的性能特点、合理设置其使用条件提供了重要的数据参考。
还讨论了相应的分析方法在分子筛性能表征中的应用,也为其他类型的分子筛表征提供了可行的试验方法。
%Analytical methods such as thermogravimetry-mass spectrum united technique,SEM morphology observation,phase analysis,pore size and specific surface area analysis,thermogravimetric analysis and static adsorption analysis were utilized to characterize 4A molecular sieve systematically,from which the properties from micro to macro were gained.Through the research,not only the comprehensive parameters of 4A molecular sieve were obtained,but also the important reference to reasonably set the service condition of 4A molecular sieve were introduced.In addition,the application of each characterization method was discussed,which could offer feasible ways to study other kinds of molecular sieves.【期刊名称】《理化检验-物理分册》【年(卷),期】2016(000)003【总页数】5页(P151-155)【关键词】4A分子筛;联用;物相;吸附性能【作者】孟玉堂;刘俊;汤光平【作者单位】中国工程物理研究院机械制造工艺研究所,绵阳 621900;中国工程物理研究院机械制造工艺研究所,绵阳 621900;中国工程物理研究院机械制造工艺研究所,绵阳 621900【正文语种】中文【中图分类】TQ4244A分子筛作为一种无机功能材料,具有微孔分布均匀、比表面积巨大、内表面高度极化等特性,晶穴内有较高的静电场,可通过静电场诱导使分子极化,使其对极性分子如水分子有很强的亲和力,可作为除湿剂或干燥剂对含湿空气进行深度除湿处理,在武器产品储存环境控制方面有较多应用[1-4]。
材料现代分析方法

1000 1
100
10
0.1 0.01
整理课件
1 0.001
0.1 nm 0.0001 μm
13
OM
Ni-Cr合金的铸造组织
整理课件
14
SEM
整理课件
15
人类血细胞SEM照片
酵母
人类精子
整理课件
16
图为IBM公司的Eigler博士用扫描探针显微镜(SPM)搬动 35个氙原子绘制的“IBM”字样。如果这种原子搬动技术 被巧妙使用的话,就完全可以绘制成美妙的原子艺术画。
结构层次 物体尺寸
研究对象
研究方法
宏观结构 > 100 m 大晶粒、颗粒集 团
显微结构 0.2-100m 多晶集团
肉眼、放大 镜
显微镜
亚显微结 构
微观结构
10-200 nm
< 10 nm
微晶集团 晶格点阵
整理课件
扫描电镜
扫描隧道电 镜
8
2.材料分析的内容
表面和内部组织形貌。包括材料的外观形貌(如纳米 线、断口、裂纹等)、晶粒大小与形态、各种相的尺 寸与形态、含量与分布、界面(表面、相界、晶界)、 位向关系(新相与母相、孪生相)、晶体缺陷(点缺 陷、位错、层错)、夹杂物、内应力。
通过电磁性质变化研究分子运动——介电松弛与核磁共 振;
通过体积变化研究分子运动——热膨胀计
整理课件
34
课程说明
教材与参考书 《材料研究方法》——王培铭,许乾慰主编,科学出版社 《材料现代分析方法》——左演声,陈文哲,梁伟主编,北京工业大学
出版社 《聚合物材料表征与测试》 》——杨万泰主编,中国轻工业出版社
基于其它物理性质或电化学性质与材料的特征 关系建立的色谱分析、质谱分析、电化学分析 及热分析等方法也是材料现代分析的重要方法。 相对而言,上述四大类方法在材料研究中应用 得更加频繁。
钢结构中的杨氏模量和弯曲刚度分析

钢结构中的杨氏模量和弯曲刚度分析钢结构在现代建筑中扮演着重要的角色,其高强度和优良的可塑性使其成为许多大型建筑项目的首选材料。
而钢结构的设计和分析则需要考虑材料的力学性质,其中杨氏模量和弯曲刚度是两个重要的参数。
杨氏模量是描述材料刚度的物理量,它反映了材料在受力时的变形程度。
对于钢结构而言,杨氏模量可以用来衡量材料在受力时的弹性变形程度。
杨氏模量越大,材料的刚度越高,抗弯能力也就越强。
因此,在钢结构设计中,了解和准确计算杨氏模量是至关重要的。
钢材的杨氏模量通常可以通过实验测量得到,但对于不同类型的钢材和不同的应力状态,其杨氏模量可能会有所不同。
一般来说,钢材的杨氏模量在200 GPa至210 GPa之间。
然而,在实际设计中,为了更准确地计算钢结构的弯曲刚度,需要考虑到材料的非线性行为和应力-应变关系。
钢结构的弯曲刚度是指在受到弯曲力矩作用下,结构的抵抗变形的能力。
弯曲刚度的计算需要考虑结构的几何形状、截面尺寸和材料的力学性质等因素。
一般来说,弯曲刚度与截面的惯性矩成正比,与杨氏模量成反比。
也就是说,当杨氏模量增大时,弯曲刚度也会增大。
在实际的钢结构设计中,为了准确计算弯曲刚度,可以采用有限元分析等数值方法。
有限元分析是一种常用的结构分析方法,通过将结构离散化为有限个单元,利用数值计算的方法求解结构的力学行为。
在有限元分析中,可以考虑材料的非线性行为和应力-应变关系,从而更准确地计算弯曲刚度。
除了杨氏模量和弯曲刚度,钢结构的设计还需要考虑其他因素,如荷载、变形、稳定性等。
荷载是指结构所承受的外部力和力矩,包括静荷载和动荷载。
变形是指结构在受力下发生的形变,包括弹性变形和塑性变形。
稳定性是指结构在受力下不发生失稳现象,保持平衡和安全。
综上所述,钢结构中的杨氏模量和弯曲刚度是设计和分析中需要考虑的重要参数。
了解和准确计算这些参数可以帮助工程师设计出更安全和可靠的钢结构。
通过采用数值方法如有限元分析,可以更准确地计算弯曲刚度。
分子生物学中的动态学和结构分析方法

分子生物学中的动态学和结构分析方法分子生物学是一门研究生命活动基本单位分子及其相互作用的学科,涉及到很多分子结构和动态学分析的方法。
这些方法在近年来的技术进步中得到了极大的发展,为我们深入了解生命科学奠定了重要的基础。
一、动态学分析方法1. 电子显微镜技术电子显微镜技术已经成为分子生物学中最常用的方法之一。
通过利用电子束直接照射样品,可以得到物质内部的高分辨率图像,使我们能够观察到细胞和分子的三维结构。
近年来,随着样品制备技术和图像处理算法的不断改进,电子显微镜技术已经能够解析非常小的生物分子,如蛋白质和核酸,甚至能够直接拍摄到生物分子的动态变化过程。
2. 核磁共振技术核磁共振技术是一种利用物质内部核子间相互作用的技术,可以对分子结构和动态进行精确地探测。
核磁共振技术可通过核磁共振光谱法、核磁共振成像法等多种方法进行应用。
利用核磁共振技术,可以分析分子结构和构象、分子的动态过程以及分子与分子之间的相互作用。
这项技术在细胞和分子生物学领域中的应用非常广泛,例如,可以用核磁共振光谱法来确定蛋白质的三维结构,通过核磁共振成像法实现对分子运动轨迹的实时监测。
3. 荧光显微镜技术荧光显微镜技术是利用荧光物质发出的荧光信号来研究分子动态的一种技术。
现在,荧光显微镜技术已经非常发达,可以利用荧光标记蛋白质、核酸等生物大分子,以便在细胞内观察它们的运动和相互作用。
在染色体、细胞质骨架等细胞结构显微解剖研究中,荧光显微镜技术也是非常重要的工具。
二、结构分析方法1. X射线衍射技术X射线衍射技术是一种基于布拉格衍射的方法,是对许多大分子的结构和构象进行分析的最重要方法之一。
这种技术通过将样品中的大分子进行晶体生长,再利用射线对晶体进行照射,进而通过分析被散射的X光的图像信息得出晶体中分子的结构。
现在已经可以对许多大分子,如蛋白质、核酸、病毒等进行结构分析。
这种技术可以被认为是分子生物学的一项里程碑式的技术,它改变了我们对生命的基本概念,带领我们进入了新时代的生命科学。
作文结构分析与构思方法

作文结构分析与构思方法作文是语文学习中一项重要的能力训练,而作文的结构和构思方法对于一篇优秀的作文来说至关重要。
本文将从分析作文结构和构思方法两个方面进行探讨。
首先,作文结构是指整篇文章的组织框架。
一篇合理的作文结构能够让读者清晰地了解文章的逻辑关系,使文章具有条理性和可读性。
一般来说,作文结构包括引子、正文和结尾三个部分。
引子是作文的开端,需要吸引读者的注意力。
可以运用一些引人入胜的话题、事例或引用名人名言,使读者对文章产生兴趣。
正文是文章的核心部分,需要承载主要观点和论述内容。
在正文中,可以采用并列、递进或对比等不同的组织方式,将观点层层展开,使文章更具说服力。
结尾是作文的总结和结束,需要给读者留下深刻的印象。
可以通过提出问题、发表观点或给出建议等方式,使文章具有思考与启发的作用。
其次,构思方法是指在写作前对主题进行思考和准备的过程。
良好的构思方法可以帮助我们清晰地理解主题,并有序地进行写作。
以下是几种常用的构思方法:1. 定位主题:要先确定作文的主题是什么,从而明确写作的方向。
可以通过阅读题目、材料或进行头脑风暴,挖掘主题的内涵和要点。
2. 划分框架:将主题划分为几个有关联的小点,然后按照逻辑顺序展开,形成作文的纲要。
可以使用思维导图等工具帮助整理思路。
3. 寻找素材:根据划分的小点,寻找与之相关的素材和例子。
可以通过阅读、观察、调研等方式搜集信息,使文章有实际的支撑和论证。
4. 建立逻辑关系:在构思过程中,要注意各个小点之间的逻辑关系,避免内容重复或脱节。
可以运用因果关系、递进关系、对比关系等方法,使文章的逻辑更加紧密。
5. 注重文采:在构思过程中,可以思考如何通过修辞手法、修辞语言等方式使作文更加生动有趣。
可以尝试使用比喻、拟人、夸张等手法,以提升作文的艺术性。
综上所述,作文的结构分析和构思方法是写好一篇作文的基础。
通过合理的结构组织和巧妙的构思方法,可以使作文更具说服力和可读性。
因此,在进行写作时,我们应该充分认识到结构的重要性,有计划地进行结构分析和构思,以提升作文的质量。
化合物的结构鉴定与表征

DEPT谱中,CH3显正峰,CH2显负峰,CH显正峰。通过谱图编辑,我们可以很容 易辨认碳的级数。
O 7 2 3 4 16 5 8范围
δ(ppm) 类型 SP3杂化碳 (饱和碳) -CH3 -CH2 -CH -C-O-CHn(n=0-3) -N-CHn(n=0-3) 8-30 15-55 20-60 35-70 在上列数据基础之上+15-30 在上列数据基础之上+10-25 65-85 100-150 110-160 160-210
3已知化合物的结构推断在实际工作中并不需要测定完一个化合物的所有波谱数据才能判断化合物的结构有些化合物特别是已知化合物在化合物结构类型初步判断的基础之上结合文献调研通过与标准品的理化常数性质及薄层对照检查或一些简单的波谱如红外光谱紫外光谱数据对照比较即可作出判断
化合物的结构鉴定与表征
(硕士研究生学位课)
SP杂化碳(炔碳) ≡CH SP2杂化碳 烯碳 芳环及芳杂环碳 羰基碳 =CH C6H6 C=O
5、二维核磁共振谱
1.二维J分解谱(2D J-resolved Spectroscopy, 2DJ) 2.二维化学位移相关谱(Two-Dimesional Chemical Shift Correlation Spectroscopy)
1H,1H化学位移相关谱(1H,1H COSY) Heteronuclear multiple-quantum correlation (HMQC)
Heteronuclear multibond correlations: HMBC
2D NMR – homonuclear through space correlations: ROESY, NOESY
1. 图谱提供的信息
化学分子结构分析方法

化学分子结构分析方法化学分子结构分析是化学学科中非常关键和基本的一个领域。
通过分析化学分子的基本结构,可以更深入地研究化学反应和化学物质的特性,对于新材料的开发以及医药业也具有重要的应用价值。
本文将着重介绍化学分子结构分析的方法。
一、元素分析法元素分析法是一种通过分析元素的含量来确定分子结构的方法。
这种方法通常用于有机化合物的结构分析,可以确定化合物中各种元素的含量,并推断化合物的基本结构。
元素分析法的原理是利用分析化学中的定量分析方法,为各种元素设定准确的定量方法,从而确定样品中的各种元素的含量。
基于这些数据,可以进一步确定样品的分子式和分子结构。
二、紫外-可见分光光度法紫外-可见分光光度法是一种测定化合物的电子能级和电磁波长的方法,常用于分析含有共轭体系的物质的分子结构。
这种方法可以通过分析物质的分子结构和化学键的能量来确定物质的吸收和反射光谱,从而得到物质的荧光和光谱数据。
紫外-可见分光光度法的原理是利用物质对于某些波长范围内的光的吸收特性来确定物质的分子结构和基本特性。
这种方法可以通过分析物质的吸收光谱和反射光谱来推断物质的分子结构。
三、样品制备和NMR分析法样品制备和NMR分析法通常用于分析含有核磁共振信号的复杂化学物质的分子结构。
这种方法可以通过NMR技术对样品进行分析,从而确定样品的分子结构和基本特性。
样品制备和NMR分析法的原理是制备样品,并将其添加到核磁共振谱仪器中进行分析。
这种方法通常涉及到样品的制备、样品的处理、样品的转换和样品的输入到核磁共振谱仪器中等多个步骤。
四、拉曼分析法拉曼分析法是一种分析物质分子的振动能量的方法,可以通过测量分子的拉曼散射信号来确定分子的结构和基本特性。
这种方法通常用于分析含有非常小的化学分子的化学物质的结构。
拉曼分析法的原理是利用光密度和拉曼散射信号之间的差异来确定物质的分子结构。
这种方法可以通过分析样品的拉曼散射信号和分子振动数据来推断物质的分子结构。
系统分析方法范文

系统分析方法范文系统分析方法是指对复杂系统进行分析和研究的一种方法论体系,旨在提供有效的问题解决方案和决策支持。
系统分析方法的应用领域广泛,包括企业管理、信息系统开发、工程项目管理等。
在系统分析中,需要对系统的组成、功能、流程、结构等关键要素进行深入的研究和分析,以掌握系统的内在规律和运行机制。
本文将介绍几种常用的系统分析方法。
一、数据流图法(Data Flow Diagram,简称DFD)数据流图法是一种图形化的分析工具,主要用于描述和分析系统内部的数据流动关系。
数据流图通过绘制不同层次的图形,将系统的输入、输出、处理和存储等关键元素直观地展现出来,以帮助分析师深入理解和把握系统的功能和流程。
通过数据流图的分析,可以发现系统中的瓶颈、问题和改进点,并进行相应的优化方案设计。
二、结构化分析方法(Structured Analysis,简称SA)结构化分析方法是一种将系统拆分为多个模块,通过分析每个模块的功能和关系,来理解和解决系统问题的方法。
结构化分析方法主要关注系统模块之间的层次结构和信息流动,并通过流程图、层次图等方式进行描述。
通过结构化分析方法,可以清晰地了解系统的组成和功能,有助于分析师识别问题的根源和优化路径。
三、数据建模方法(Data Modeling)数据建模方法是一种通过抽象和建模的方式,描述和分析系统的数据和数据之间的关系。
数据建模方法主要包括实体关系模型(Entity-Relationship Model,简称ER模型)和统一建模语言(Unified Modeling Language,简称UML)等。
通过数据建模方法,可以清晰地描述系统的数据结构和数据处理过程,有助于分析师理解系统的逻辑和运行机制。
四、面向对象分析方法(Object-Oriented Analysis,简称OOA)面向对象分析方法是一种以对象为中心,从面向对象的视角来分析系统的方法。
面向对象分析方法主要关注系统中的对象、类和关系,通过类图、对象图等方式进行表示和分析。
结构有限元教程

结构有限元教程结构有限元分析是一种常用的工程分析方法,用于模拟和预测结构的行为和性能。
本教程将介绍结构有限元分析的基本原理和步骤,帮助读者快速上手并掌握这一技术。
1. 什么是结构有限元分析?结构有限元分析是一种数值计算方法,通过将结构划分为小块,建立离散的数学模型,然后使用有限元方法对模型进行求解,从而得到结构的应力、位移、变形等信息。
这种分析方法广泛应用于工程领域,如航空航天、土木工程、机械设计等。
2. 结构有限元分析的基本原理结构有限元分析的基本原理是将结构划分为有限个单元,每个单元内部的行为可以用简单的数学模型来描述,然后将这些单元通过节点连接起来,形成整个结构的模型。
通过对单元的位移、应变和应力进行求解,可以获得结构的整体行为。
3. 结构有限元分析的步骤进行结构有限元分析通常需要经过以下步骤:- 建立几何模型:使用专业的建模软件绘制结构的几何模型,包括结构的尺寸、形状等信息。
- 离散化:将结构划分为有限个单元,通常是三角形或四边形单元,每个单元内部的行为可以用简单的数学模型来描述。
- 建立数学模型:对每个单元进行数学建模,定义单元的材料特性、边界条件等信息。
- 求解:使用有限元方法对整个结构进行求解,通过迭代计算得到结构的应力、位移等结果。
- 分析结果:对求解结果进行分析和后处理,评估结构的性能和稳定性。
4. 结构有限元分析的应用结构有限元分析广泛应用于各个工程领域,例如:- 建筑工程:用于分析建筑的结构稳定性、抗震性能等。
- 桥梁工程:用于评估桥梁的承载能力和疲劳寿命。
- 航空航天工程:用于模拟飞机、火箭等结构的受力和变形。
- 汽车工程:用于分析汽车的碰撞安全性和刚度。
- 机械设计:用于优化机械结构的刚度、强度等性能。
5. 结构有限元分析的优势和局限性结构有限元分析具有以下优势:- 能够模拟和预测复杂结构的行为和性能。
- 可以在设计阶段发现和解决潜在的问题,减少后期修正的成本。
- 可以进行参数化分析,评估不同设计方案的优劣。
化学结构分析

化学结构分析化学结构分析是一项关键的化学技术,用于研究和理解物质的分子构成和性质。
它通过分析物质的分子结构来解释其化学性质、反应机理和相互作用。
本文将介绍常用的化学结构分析方法及其在实际应用中的重要性。
一、质谱分析(Mass Spectrometry)质谱分析是一种通过电离样品的分子或离子,并根据其质量-荷质比(m/z)比进行分离和检测的技术。
它可以用来确定化合物的分子量以及分析复杂混合物中的成分。
质谱分析在有机化学、生物化学、药物研发等领域中得到广泛应用。
二、核磁共振(nuclear magnetic resonance, NMR)核磁共振是利用核自旋与外加磁场的相互作用进行分析的一种方法。
通过测量核磁共振信号的强度和频率,可以了解化合物的分子结构、立体化学和官能团的存在。
核磁共振广泛应用于有机化学、药学和材料科学领域。
三、红外光谱(Infrared Spectroscopy)红外光谱是通过测量物质对不同波长红外光的吸收和散射来分析化合物结构的方法。
它可以用来确定化合物的官能团、分子结构和化学键的类型。
红外光谱在有机化学、聚合物科学和药物研发中具有广泛的应用价值。
四、质子磁共振成像(Proton magnetic resonance imaging, MRI)质子磁共振成像利用核磁共振技术对人体组织进行成像,提供了高分辨率的内部结构信息。
它在医学诊断、神经科学和生物医学研究中被广泛应用,可以用来检测疾病、观察脑活动和研究生物分子的代谢。
五、X射线晶体学(X-ray crystallography)X射线晶体学通过测量晶体对X射线的衍射图案来确定分子的三维结构。
它被广泛应用于化学、材料科学和生物学领域,可以用来解析蛋白质、有机化合物和无机材料的结构,帮助科学家理解物质的性质和功能。
结论化学结构分析是研究和理解物质分子构成和性质的关键技术。
质谱分析、核磁共振、红外光谱、质子磁共振成像和X射线晶体学等方法在化学、医学和材料科学等领域发挥着重要作用,推动了科学研究和技术创新的进展。
现代材料分析方法习题汇总及答案

现代材料分析⽅法习题汇总及答案材料分析测试⽅法复习题简答题:1. X射线产⽣的基本条件答:①产⽣⾃由电⼦;②使电⼦做定向⾼速运动;③在电⼦运动的路径上设置使其突然减速的障碍物。
2. 连续X射线产⽣实质答:假设管电流为10mA,则每秒到达阳极靶上的电⼦数可达6.25x10(16)个,如此之多的电⼦到达靶上的时间和条件不会相同,并且绝⼤多数达到靶上的电⼦要经过多次碰撞,逐步把能量释放到零,同时产⽣⼀系列能量为hv(i)的光⼦序列,这样就形成了连续X射线。
3. 特征X射线产⽣的物理机制答:原⼦系统中的电⼦遵从刨利不相容原理不连续的分布在K、L、M、N等不同能级的壳层上,⽽且按能量最低原理从⾥到外逐层填充。
当外来的⾼速度的粒⼦动能⾜够⼤时,可以将壳层中某个电⼦击出去,于是在原来的位置出现空位,原⼦系统的能量升⾼,处于激发态,这时原⼦系统就要向低能态转化,即向低能级上的空位跃迁,在跃迁时会有⼀能量产⽣,这⼀能量以光⼦的形式辐射出来,即特征X射线。
4. 短波限、吸收限答:短波限:X射线管不同管电压下的连续谱存在的⼀个最短波长值。
吸收限:把⼀特定壳层的电⼦击出所需要的⼊射光最长波长。
5. X 射线相⼲散射与⾮相⼲散射现象答:相⼲散射:当X 射线与原⼦中束缚较紧的内层电⼦相撞时,电⼦振动时向四周发射电磁波的散射过程。
⾮相⼲散射:当X 射线光⼦与束缚不⼤的外层电⼦或价电⼦或⾦属晶体中的⾃由电⼦相撞时的散射过程。
6. 光电⼦、荧光X 射线以及俄歇电⼦的含义答:光电⼦:光电效应中由光⼦激发所产⽣的电⼦(或⼊射光量⼦与物质原⼦中电⼦相互碰撞时被激发的电⼦)。
荧光X 射线:由X 射线激发所产⽣的特征X 射线。
俄歇电⼦:原⼦外层电⼦跃迁填补内层空位后释放能量并产⽣新的空位,这些能量被包括空位层在内的临近原⼦或较外层电⼦吸收,受激发逸出原⼦的电⼦叫做俄歇电⼦。
8. 晶⾯及晶⾯间距答:晶⾯:在空间点阵中可以作出相互平⾏且间距相等的⼀组平⾯,使所有的节点均位于这组平⾯上,各平⾯的节点分布情况完全相同,这样的节点平⾯成为晶⾯。
名词化

名词化结构分析编辑名词化,作为用某一语法类别或语法结构去代替另一语法类别或语法结构的形式,在本质上涉及到一系列的变化过程。
下面几个小节将分别描述名词化过程中级的变化、语义功能的变化和部分语义成分的变化。
名词化结构的级变化如表二所示,韩礼德把语义分成三级,分别为“言辞列”(sequence)、“言辞”(figure)和“成分”(element)。
言辞是对事件的语义表达,因为人类经验主要由发生的事构成,语法通过小句的构建把这些发生的事件转换为语义。
若干表示事件的言辞构成言辞列,由小句组体现。
级阶理论容许向下移动的“级转移”(rank shift),即一个已知单位可移至下一级,但下级单位不能上移。
名词化结构用名词或名词词组代替了一致式中的小句或句组,因此“级转移”是名词化的重要内容。
例如,在下面的两个句子中:(4a) The driver drove the bus too fast down the hill, so the brakes failed.(4b) The driver’s overrapid downhill driving of the bus caused brake failure.(4a)是一致式,(4b)通过语法隐喻把(4a)的两个小句向下转移为两个名词性词组结构。
名词化的语义功能变化伴随着级向下转移,名词化结构产生了有别于一致式结构的功能意义变化(changes in status)。
韩礼德(1995a)指出,我们在进行语义分析时,要看语义功能、语法功能和语法类别三个方面的变化。
就上例而言,动词drive转化成driving时,语义功能由process 转化为entity,语法功能由transitivity转化为thing ,语法类别则由动词转化为名词。
而too fast转化为overrapid后,语义功能由circumstance转化为quality,语法功能由manner转化为epithet,语法类别则由副词转化为形容词。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Y • 立方晶系中,晶面族{111}表示正八面体的面; Z • 立方晶系中,晶面族{110}表示正十二面体的面;
Y
X
画出晶面 (321)
cr
ar
r b
(200)、(333)等是否存在? 具有公因子的晶面不存在
在体心点阵上画出晶面 (200)
cr
ar
r b
这些阵点在空间呈周期性规则排列并具有完全相同的周围 环境,这种由它们在三维空间规则排列的阵列称为空间点 阵,简称点阵。
具有代表性的基本单元(最小平行六 面体)作为点阵的组成单元,称为 晶胞。将晶胞作三维的重复堆砌就 构成了空间点阵。
晶胞选取的原则
同一空间点阵可因选取方式不同而得到不相同的晶胞
晶胞选取的原则
c
a
b zx y
1 晶体学基础
晶体结构的基本特征:原子(或分子)在三维 空间呈周期性重复排列,即存在长程有序
1.1 空间点阵和晶胞
阵点 为了便于分析研究晶体中质点的排列规律性,可先将实际
晶体结构看成完整无缺的理想晶体并简化,将其中每个质 点抽象为规则排列于空间的几何点,称之为阵点。
空间点阵 晶胞
晶体结构和空间点阵的区别
γ-Fe, fcc
c
b a
Cu3Au, simple cubic
1.2 晶向指数和晶面指数
晶向:晶体中原子的位置、原子列 的方向 晶面:阵点构成的平面 Miller(密勒)指数统一标定晶向指数和晶面指数
•晶向指数
任意阵点P的位置可以
用示O矢。P量= 或uar者+坐v标br来+ w表cr
r b
C
I
F
单胞体积=用来定义单胞的基础矢量的行列式值
为什么不存在 六方晶系的底 心点阵?
a2 a1
晶体结构和空间点阵的区别
空间点阵是晶体中质点排列的几何学抽象,用以描 述和分析晶体结构的周期性和对称性,由于各阵点 的周围环境相同,它只能有14种类型
晶体结构则是晶体中实际质点(原子、离子或分子) 的具体排列情况,它们能组成各种类型的排列,因 此,实际存在的晶体结构是无限的。
简单菱方和简单六方的关系
初基六角点阵
菱方体点阵作为非初基六角点阵
四方:简单四方 体心四方
a = b ≠ c,
FÆI
α = β = γ = 90o
立方:简单立方
体心立方 a = b = c,
面心立方
α = β = γ = 90o
cr
ar
r b
简单单胞
复合单胞
cr
ar
r b
cr
ar
r b
cr
ar
+
k
2
⎞2 ⎟ ⎠
+
⎛ ⎜⎝
l c
⎞2 ⎟⎠
晶 带 所有平行或相交于同一直线的晶面构成一
个晶带,此直线称为晶带轴。属此晶带的 晶面称为晶带面(共带面)。
[u v w]
hu + kv + lw = 0
晶面1 (h1 k1 l1) 晶面2 (h2 k2 l2)
晶带轴 [u v w]
h1k1l1
u : v : w = k1 l1 : l1 h1 : h1 k1 k2 l2 l2 h2 h2 k2
(102)
Y
(111)
(321)
X
正交点阵中一些晶面的面指数
晶面指数的意义
Z XZ X
晶面指数所代表的不仅是某一晶面,而是代表着 一组相互 平行的晶面。 在晶体内凡晶面间距和晶面上原子的分布完全相同, Y只是空间位向不同的晶面可以归并为同一晶面族,以 {h k l}表示,它代表由对称性相联系的若干组等效晶面 的总和。
晶向指数:[ u v w]
晶向指数的例子
正交晶系一些重要晶向的晶向指数
晶向指数的意义
晶向指数表示着所有相互平行、方向一致的晶向; 所指方向相反,则晶向指数的数字相同,但符号相反;
晶体中因对称关系而等同的各组晶向可归并为一个晶向 族,用<u v w>表示
晶面指数
晶面指数标定步骤:
1)在点阵中设定参考坐标系,设置方法与确定晶向指数时相 同;
单斜:简单单斜 底心单斜
a ≠ b ≠ c,
α = γ = 90o ≠ β
正交:简单正交 底心正交 体心正交 面心正交
a ≠ b ≠ c,
α = β = γ = 90o
六方:简单六方
a1 = a2 = a3 ≠ c, α = β = 90o ,γ = 120o
菱方:简单菱方
a = b = c, α = β = γ ≠ 90o
晶体学基础
物质:气态,液态,固态 固态物质:晶体,非晶体
晶体:原子在空间呈有规则地周期性重复排列; 非晶体:原子无规则排列。
晶体中原子排列的作用
原子排列
组织
性能
研究固态物质的内部结构,即原子排列和分布规律是 了解掌握材料性能的基础,才能从内部找到改善和发 展新材料的途径。
1 晶体学基础
晶体结构的基本特征:原子(或分子)在空间 呈周期性重复排列,即存在长程有序
晶面间距愈大,该晶面 上的原子排列愈密集; 晶面间距愈小,该晶面 上的原子排列愈稀疏。
晶面间距
正交晶系 立方晶系 六方晶系
dhkl =
1
⎛ ⎜⎝
h a
⎞2 ⎟⎠
+
⎛ ⎜⎝
k b
⎞2 ⎟⎠
+
⎛ ⎜⎝
l c
⎞2 ⎟⎠
dhkl =
a h2 + k2 + l2
dhkl =
1
4 3
⎛ ⎜ ⎝
h2
+
hk a2
(h3 k3 l3)
(h2 k2 l2)
cr
ar
r b
020 (130)
r
ar b
[0 0 1]
(110) (200)
选取的平行六面体应反映出点阵的最高对称性;
平行六面体内的棱和角相等的数目应最多;
当平行六面体的棱边夹角存在直角时,直角数目应最 多;
当满足上述条件的情况下,晶胞应具有最小的体积。
晶胞、晶轴和点阵矢量
abcr, ,
r r r 点阵常数:a, b, c 棱边夹角α, β, γ a c b 220)晶面是否存在? 要求指数和为偶数; 选最低指数
在面心点阵上画出晶面 (111),(200),(220)
cr
ar
r b
(100),(110), (222)晶面是否存在? 同奇同偶
晶面指数确定了晶面的位向和间距。
由晶面指数求面间距dhkl
通常,低指数的面间距 较大,而高指数的晶面 间距则较小
2)求得待定晶面在三个晶轴上的截距,若该晶面与某轴平行, 则在此轴上截距为无穷大;若该晶面与某轴负方向相截,则在 此轴上截距为一负值;
3)取各截距的倒数;
4)将三倒数化为互质的整数比,并加上圆括号,即表示该晶面 的指数,记为( h k l )。
晶面指数的例子
Z
(010)
(100)
(120)
14种布拉菲点阵
根据6个点阵参数间的相互关系,可将全部空间点阵归属 于7种类型,即7个晶系。按照“每个阵点的周围环境相同 “的要求,布拉菲(Bravais A.)用数学方法推导出能够 反映空间点阵全部特征的单位平行六面体只有14种,这 14种空间点阵也称布拉菲点阵。
三斜:简单三斜 a ≠ b ≠ c, α ≠ β ≠ γ ≠ 90o
