湘教版9上数学练习题 与方位角有关的应用问题
最新湘教版九年级数学(初三)上册4.4 第2课时 与坡度、方位角有关的应用问题 课件

约等于 293 .
如图,一铁路路基的横断面为等腰梯形,路基 的顶宽(即等腰梯形的上底长)为10.2m,路基的坡度 i=1:1.6,等腰梯形的高为6.2m.求路基的底宽(精确到 0.1m)和坡角α(精确到1′).
答:路基底宽为30.0m, 坡角 α = 32.
例2 如图,海岛A四周20海里周围内为暗礁区,一 艘货轮由东向西航行,在B处见岛A在北偏西60˚,航 行24海里到C,见岛A在北偏西30˚,货轮继续向西航 行,有无触礁的危险?
i hl
坡度通常写成 1 : m 的形式. 如图中的∠MPN叫作坡角(即山坡与地平面的夹角).
显然,坡度等于坡角的正切. 坡度越大,山坡越陡.
例1 如图,一山坡的坡度 i = 1:1.8,小刚从
山坡脚下点P上坡走了24m到达点N,他上升 了多少米(精确到0.1m)?这座山坡的坡角是多 少度(精确到1′)?
July 12, 2020
039、:0少成57年功.1易都2.学永20老远20难不09成会:0,言57一弃.1寸 ,2.光放20阴弃20不者09可永:0轻远50。不9。会:05成:0功37。.12.202009:057.12.2020
盛开的春地去方春,又在回这,醉新人桃芬换芳旧的符季。节在,那愿桃你花 409、:0桃57花.1潭2.水20深20千09尺:0,57不.1及2.汪20伦20送09我:0情50。9:05:037.12.202009:057.12.2020 盛开的地方,在这醉人芬芳的季节,愿你 74.、12敏不.2而要02好为07学它.1,的2.不结20耻束20下而09问哭:0。 ,50。应9当7:0.15为20.9它2:0的250:开073始.1029而.:20笑052:。00309:0509:0509:05:0309:05:03
湘教九年级数学上册《 与坡度、方向角有关的解直角三角形的实际应用练习》课件

13.(2014·南宁)如图,一渔船由西往东航行,在 A 点测得海岛 C 位于 北偏东 60°的方向,前进 20 海里到达 B 点,此时,测得海岛 C 位于北 偏东 30°的方向,则海岛 C 到航线 AB 的距离 CD 等于_1_0___3__海里.
14.(14 分)(2014·镇江)如图,小明从点 A 处出发,沿着坡角为α的斜坡 向上走了 0.65 千米到达点 B,sin α=153,然后又沿着坡度为 i=1∶4
A.4 3米 B.6 5米 C.12 5米
D.24 米
3.(4 分)如图是某水库大坝横断面示意图.其中 AB,CD 分别表示水库
上、下底面的水平线,∠ABC=120°,BC 的长是 50 m,则水库大坝的
高度 h 是( A )
A.25 3 m B.25 m
C.25 2 m
50 3 D. 3 m
4.(4 分)(2014·衡阳)如图,一河坝的横断面为等腰梯形 ABCD,坝顶宽
9.(2014·临沂)如图,在某监测点 B 处望见一艘正在作业的渔船在南偏
西 15°方向的 A 处,若渔船沿北偏西 75°方向以 40 海里/小时的速度航
行,航行半小时后到达 C 处,在 C 处观测到 B 在 C 的北偏东 60°方向
上,则 B,C 之间的距离为( C )
A.20 海里
B.10 3海里
(2)加宽部分的体积 V=S 梯形 AFED×坝长=12×(2+10)×8×400=19 200(立方米).故完成这项工程需要土石 19 200 立方米.
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年4月22日星期五2022/4/222022/4/222022/4/22 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年4月2022/4/222022/4/222022/4/224/22/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/4/222022/4/22April 22, 2022
湘教版九年级上册数学4.4 第1课时 仰角、俯角问题2同步练习

4.4 解直角三角形的应用第1课时 仰角、俯角问题 1(绵阳中考)如图,一艘海轮位于灯塔P 的北偏东30°方向,距离灯塔80海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东45°方向上的B 处,这时,海轮所在的B 处与灯塔P 的距离为( )A . 海里B .海里 C .80海里D . 海里2. 在某次海上搜救工作中,A 船发现在它的南偏西30°方向有一漂浮物,同时在A 船正东10km 处的B 船发现该漂浮物在它的南偏西60°方向,此时,B 船到该漂浮物的距离是()A ...10km D .20km 3.(苏州中考)如图,港口A 在观测站O 的正东方向,OA=4km ,某船从港口A 出发,沿北偏东15°方向航行一段距离后到达B 处,此时从观测站O 处测得该船位于北偏东60°的方向,则该船航行的距离(即AB 的长)为()A .4km B.kmC . kmD .+1)km4. (邵阳中考)一艘观光游船从港口A 处以北偏东60°的方向出港观光,航行80海里至C 处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B 处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/小时的速度前往救援,求海警船到达事故船C 处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)5. 如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30︒,再往大树的方向前进4 m,测得仰角为60︒,已知小敏同学身高(AB)为1.6m,则这棵树的高度为()(结果精确到0.1m,3≈1.73).A. 3.5mB. 3.6 m C. 4.3m D.5.1m6.(百色中考)从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是()A.(B. ()米 C. (D. 12米7(嘉兴中考)如图,在地面上的点A处测得树顶B的仰角为α,AC=7米,则树高BC为___________米.8.(哈尔滨中考)如图,AB、CD为两个建筑物,建筑物AB的高度为60m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.(1)求两建筑物两底部之间的水平距离BD的长度;(2)求建筑物CD的高度(结果保留根号).。
湘教版九年级数学上册《锐角三角函数》4.4.2用解直角三角形解坡角(坡度)、方位角的应用

A.15 米
B.20 3米
C.20 2米
D.10 3米
阶段核心归类专训
【点拨】由题意可得∠APB=60°-15°=45°,∠PBH =60°,则可由锐角三角函数求得 PB 的长, 又由山坡的坡度 i 为 1: 3,可求得∠ABC 的度数, 从而得出△ ABP 是等腰直角三角形,则可求得答案. 【答案】B
此页为防盗标记页(下载后可删)
1、谢谢大家听得这么专心。 2、大家对这些内容这么感兴趣,真让我高兴。 3、你们专注听讲的表情,使我快乐,给我鼓励。 4、我从你们的姿态上感觉到,你们听明白了。 5、我不知道我这样说是否合适。 6、不知我说清了没有,说明白了没有。 7、我的解释不知是否令你们满意,课后让我们大家再去找有关的书来读读。 8、你们的眼神告诉我,你们还是没有明白,想不想让我再讲一遍? 9、会“听”也是会学习的表现。我希望大家认真听好我下面要说的一段话。 10、从听课的情况反映出,我们是一个素质良好的集体。 1、谢谢你,你说的很正确,很清楚。 2、虽然你说的不完全正确,但我还是要感谢你的勇气。 3、你很有创见,这非常可贵。请再响亮地说一遍。 4、××说得还不完全,请哪一位再补充。 5、老师知道你心里已经明白,但是嘴上说不出,我把你的意思转述出来,然后再请你学说一遍。 6、说,是用嘴来写,无论是一句话,还是一段话,首先要说清楚,想好了再说,把自己要说的话在心里整理一下就能说清楚。 7、对!说得很好,我很高兴你有这样的认识,很高兴你能说得这么好! 8、我们今天的讨论很热烈,参与的人数也多,说得很有质量,我为你们感到骄傲。 9、说话,是把自己心里的想法表达出来,与别人交流。说时要想想,别人听得明白吗? 10、说话,是与别人交流,所以要注意仪态,身要正,不扭动,眼要正视对方。对!就是这样!人在小时候容易纠正不良习惯,经常 注意哦。
湘教版2020年初三上册数学4.4 第2课时 与坡度、方位角有关的应用问题 课件

AE 69m. AB 692 232 72.7(m).
∵斜坡CD的坡度i=1∶2.5,CF=23m.
CF 23 1 . FD FD 2.5
FD 57.5m.
由题意易得BC=EF=6m, ∴AD=AE+EF+FD=132.5(m).
用解直角三角形的知识解决实际问题的一般步骤: (1)审题,通过图形(题目没画出图形的,可自己画出示 意图),弄清已知和未知; (2)找出有关的直角三角形,或通过作辅助线产生有关的 直角三角形,把问题转化为解直角三角形的问题; (3)根据直角三角形元素(边、角)之间关系解有关的直角 三角形.
i hl
坡度通常写成 1 : m 的形式. 如图中的∠MPN叫作坡角(即山坡与地平面的夹角).
显然,坡度等于坡角的正切. 坡度越大,山坡越陡.
例1 如图,一山坡的坡度 i = 1:1.8,小刚从
山坡脚下点P上坡走了24m到达点N,他上升 了多少米(精确到0.1m)?这座山坡的坡角是多 少度(精确到1′)?
420、:2千敏87淘而.1万好4.浪学20虽,20辛不20苦耻:2,下87吹问.1尽。4.黄。20沙72.10始42.0到2:02金2802。707.:12.1484.:23.2002720.102470..:2120482.220002:2008:22807:2.1842:3.020:0228002:208:2:380:3020:28:30
4.4 解直角三角形的应用 第2课时 与坡度、方位角有关的应用问题
观察
图中的(1)和(2),哪个山坡比较陡?
(2)中的山坡比较陡.
(1)
(2)
动脑筋
如何用数量来反映哪个山坡陡呢?
湘教版九年级数学上册课后练习题-仰角、俯角问题2

4.4 解直角三角形的应用第1课时仰角、俯角问题1(绵阳中考)如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为()A.402海里B.403海里C.80海里D.406海里2.在某次海上搜救工作中,A船发现在它的南偏西30°方向有一漂浮物,同时在A船正东10km处的B船发现该漂浮物在它的南偏西60°方向,此时,B船到该漂浮物的距离是()A.53km B.103km C.10km D.20km3.(苏州中考)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为()A.4km B.23kmC.22km D.(3+1)km4. (邵阳中考)一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)5. 如图,小敏同学想测量一棵大树的高度.她站在B 处仰望树顶,测得仰角为30︒,再往大树的方向前进4 m ,测得仰角为60︒,已知小敏同学身高(AB )为1.6m ,则这棵树的高度为( )(结果精确到0.1m ,3≈1.73).A . 3.5mB . 3.6 mC . 4.3mD .5.1m6. (百色中考)从一栋二层楼的楼顶点A 处看对面的教学楼,探测器显示,看到教学楼底部点C 处的俯角为45°,看到楼顶部点D 处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD 是( )A.(6+63)米B. (6+33)米C. (6+23)米D. 12米 C A BD7 (嘉兴中考)如图,在地面上的点A 处测得树顶B 的仰角为α,AC =7米,则树高BC 为___________米.8.(哈尔滨中考)如图,AB 、CD 为两个建筑物,建筑物AB 的高度为60m ,从建筑物AB 的顶部A 点测得建筑物CD 的顶部C 点的俯角∠EAC 为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.(1)求两建筑物两底部之间的水平距离BD的长度;(2)求建筑物CD的高度(结果保留根号).。
【湘教版】九年级数学上册:4.4.2 与坡度、方位角有关的应用问题 同步练习(含答案)

第2课时 与坡度.方位角有关的应用问题要点感知1 山坡的坡面与地平面的夹角叫作坡角,如图所示,角α为斜面的坡角.如图所示,通常把坡面的铅直高度h 和水平宽度l 的比叫作坡度,通常用字母i 表示,即i =l h (坡度通常写成1∶m 的形式).坡度i 与坡角α的关系是i =lh =tanα.坡度越大,山坡越陡.预习练习1-1 如图,修建抽水站时,沿着坡度为i =1∶6的斜坡铺设管道,下列等式成立的是( )A.sinα=61B.cosα=61C.tanα=61D.以上都不对要点感知2 从正北方向或正南方向到目标方向所形成的小于90°的角叫作方位角.如图中点A 的方向角为北偏东60°.预习练习2-1 如图,C .D 是两个村庄,分别位于一个湖的南.北两端A 和B 的正东方向上,且D 位于C 的北偏东30°方向上,且CD =6 km ,则AB =_____km .知识点1 与坡度.坡角有关的应用问题1.某堤的横断面如图.堤高BC是5米,迎水斜坡AB的长是13米,那么斜坡AB的坡度是( )A.1∶3B.1∶2.6C.1∶2.4D.1∶22.拦水坝横断面如图所示,迎水坡AB的坡比是1∶3,坝高BC=10 m,则坡面AB的长度是( )A.15 mB.203mC.103mD.20 m知识点2 与方位角有关的应用问题3.如图,某海监船和一渔船同时从点A出发,海监船沿正北方向MN 航行,渔船往北偏东60°方向以40海里/小时的速度航行,渔船半小时后到达B处,此时渔船恰好在海监船的正东方向,则此时渔船与海监船的距离为( )A.20海里B.103海里C.202海里D.30海里4.(昭通中考)小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,2≈1.41,3≈1.73)5.钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B处,发现此时钓鱼岛C与该船距离最短.(1)请在图中作出该船在点B处的位置;(2)求钓鱼岛C到B处的距离.(结果保留根号)6.一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到达事故船C 处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)7.某商场为方便顾客使用购物车,准备将滚动电梯的坡面坡度由1∶1.8改为1∶2.4(如图).如果改动后电梯的坡面长为13米,求改动后电梯水平宽度增加部分BC的长.挑战自我8.如图,在东西方向的海岸线MN上有A.B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.(参考数据:sin32°≈0.53,cos32°≈0.85,sin55°≈0.82,cos55°≈0.57) (1)求船P到海岸线MN的距离(精确到0.1海里);(2)若船A.船B分别以20海里/小时.15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.参考答案预习练习1-1 C要点感知2 331.C2.D3.B4.过P作PC⊥AB于C.在Rt△APC中,AP=200 m,∠ACP=90°,∠PAC=60°,∴PC=200×sin60°=200×3/2=1003.∵在Rt△PBC中,sin37°=PC/PB,∴PB=PC/sin37°=100×1.73/0.6≈288(m).答:小亮与妈妈相距约288米.5.AB=30×0.5=15(海里),由题意知CB⊥AB,在Rt△ABC中,∠BAC=30°,tan∠BAC=BC/AB,所以BC=ABtan∠BAC=ABtan30°=15×33=53(海里).答:钓鱼岛C到B处的距离为53海里.6.过点C作CD⊥AB交AB延长线于D.在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,∴CD=1/2AC=40海里.在Rt△CBD中,∵∠CDB=90°,∠CBD=90°-37°=53°,∴BC=CD/sin∠CBD≈400.8=50(海里),∴海警船到达事故船C处所需的时间大约为:50÷40=54(小时).答:海警船到达事故船C处所需时间约为54小时.7.在Rt△ADC中,∵AD∶DC=1∶2.4,AC=13,由AD2+DC2=AC2,得AD2+(2.4AD)2=132.∴AD=±5(负值不合题意,舍去).∴DC=12.在Rt△ABD中,∵AD∶BD=1∶1.8,∴BD=5×1.8=9.∴BC=DC-BD=12-9=3.答:改动后电梯水平宽度增加部分BC的长为3米.8.(1)过点P作PD⊥AB于点D.由题意,得∠PAB=90°-58°=32°,∠PBD=90°-35°=55°,AP=30,在Rt△ADP中,sin∠PAD=PD/AP,得PD=AP·sin∠PAD,即PD=30·sin32°≈15.9.答:船P到海岸线MN的距离约为15.9海里.(2)在Rt△BDP中,sin∠PBD=PD/BP,∴BP=PD/sin∠PBD=15.9/sin55°≈19.4,A船需要时间为30/20=1.5(小时),B船需要时间为19.4/15≈1.3(小时),∵1.5>1.3,∴B船先到达P处.答:B船先到达P处.。
2021年湘教版数学九年级上册4 解直角三角形的应用 与坡度、方位角有关的应用问题 专题练习题

湘教版数学九年级上册第4章锐角三角形 4.4 解直角三角形的应用物以类聚,人以群分。
《易经》如海学校陈泽学与坡度、方位角有关的应用问题专题练习题1. 某铁路路基的横截面是等腰梯形,已知路基高5 m,坡长10 m,则坡面的坡度为( )A.1∶2 B.1∶12 C.1∶3 D.1∶332.如图,一河坝的横断面为四边形ABCD,其中AD∥BC,AB=CD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1∶1.5,则坡底AD的长度为( )A.26米 B.28米 C.30米 D.46米3.如图,小明爬一土坡,他从A处爬到B处所走的直线距离AB=4米,此时,他离地面高度为h=2米,则这个土坡的坡角为____________.4.某商场为方便顾客使用购物车,准备将滚动电梯的坡面坡度由1∶1.8改为1∶2.4(如图).如果改动后电梯的坡面长为13米,求改动后电梯水平宽度增加部分BC的长.5.如图,C,D是两个村庄,分别位于一个湖的南、北两端A和B的正东方向上,且D位于C的北偏东30°方向上,且CD=6 km,则AB=____km.6.如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M 在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行____分钟可使渔船到达离灯塔距离最近位置.7.一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)8.如图,我渔政船在南海海面上沿正东方向匀速航行,在A点观测到我渔船C在北偏东60°方向的我国某传统渔场捕鱼作业,若渔政船航向不变,航行半小时后到达B点,观测到我渔船C在东北方向上.问:渔政船再按原航向航行多长时间,离渔船C的距离最近?(渔船C捕鱼时移动距离忽略不计,结果不取近似值)9.钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和政部门对钓鱼岛海域实行了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A,B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少(结果保留根号)10.如图,一楼房AB后有一假山,其坡度为i=1∶3,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.注:坡度i是指坡面的铅直高度与水平宽度的比)11.如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB=3米.台阶AC坡度为1∶3(即AB∶BC=1∶3),且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度.(测倾器的高度忽略不计)12.如图,从正北方向或正南方向到目标方向所形成的小于90°的角叫作__________.图中点A的方位角为______________________.答案:1. C2. D3. 30°4. 解:在Rt△ADC中,∵AD∶DC=1∶2.4,AC=13,由AD2+DC2=AC2,得AD2+(2.4AD)2=132.∴AD=5(负值不合题意,舍去).∴DC=12.在Rt△ABD中,∵AD∶BD=1∶1.8,∴BD=5×1.8=9.∴BC=DC-BD=12-9=3.答:改动后电梯水平宽度增加部分BC的长为3米5. 36. 157. 解:过点C作CD⊥AB交AB于点D,CD=AC·sin∠CAB=80×sin30°=40(海里),CDBC=sin∠CBD,∴BC=CDsin∠CBD=40sin53°=50(海里),50÷40=1.25(小时),即大约需1.25小时8. 解:过点C 作CD ⊥AB 交AB 于点D ,则CD =AC ·sin30°=12AC ,AD =AC2-CD2=32AC ,易知BD =CD =12AC ,又AB =AD -BD =32AC -12AC =(32-12)AC ,AB ∶BD =(3-1)∶1,即BD =3+12AB ,∴再航行3+12·12小时,即:3+14小时 9. 解:作BD ⊥AC 于点D.由题意可知,∠BAC =45°,∠ABC =105°,∴∠ACB =180°-∠BAC -∠ABC =30°.在Rt △ABD 中,BD =AB ·sin ∠BAD=20×22=102(海里).在Rt △BCD 中,BC =BD sin ∠BCD =10212=202(海里).答:此时船C 与船B 的距离是202海里10. 解:过点E 作EG ⊥BC 交BC 于点G ,过点E 作EH ⊥AB 交AG 于点H.易知EG =10米,CG =103米,EH =(25+103)米,△AEH 为等腰直角三角形,∴AH =HE =(25+103)米,AB =AH +HB =(25+103+10)米,即楼房AB 高(35+103)米11. 解:过点A 作AF ⊥DE 于点F.∴AF =BE ,EF =AB =3,设DE =x ,在Rt △CDE 中,CE =DE tan ∠DCE =DE tan60°=33x.在Rt △ABC 中,∵AB BC =13,AB =3,∴BC =3 3.在Rt △AFD 中,DF =DE -EF =x -3,∴AF =DF tan ∠DAF=x -3tan30°=3(x -3).∵AF =BE =BC +CE ,∴3(x -3)=33+33x ,解得x =9.答:树DE 的高度为9米12. 方位角北偏东60°【素材积累】每个人对未来都有所希望和计划,立志是成功的起点,有了壮志和不懈的努力,就能向成功迈进。
2023年湘教版九年级数学上册第3课时 与方位角有关的实际问题
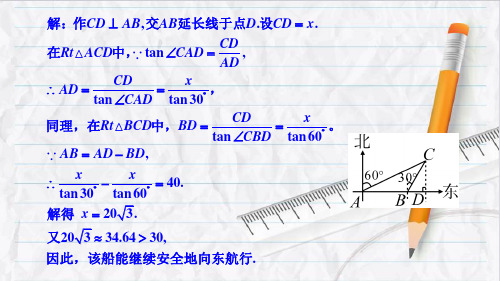
又 20 3 34.64>30,因此,该船能继续安全地向东航行.
方向角
从某点的指北方向线起,依顺时针方向到目标 方向线之间的水平夹角.
练习
1.某次军事演习中,有三艘船在同一时刻向指挥所报告:A 船说B船在它的正东方向,C船在它的北偏东55°方向;B 船说C船在它的北偏西35°方向;C船说它到A船的距离比 它到B船的距离远40km. 求A,B两船的距离(结果精确到 0.1km).
►走进颐和园,眼前是繁华的苏州街,现在依稀可以想象到当年的热闹场 面,苏州街围着一片湖,沿着河岸有许多小绿盘子里装着美丽的荷花。这 里是仿照江南水乡--苏州而建的买卖街。当年有古玩店、绸缎店、点心铺 等,店铺中的店员都是太监、宫女妆扮的,皇帝游览的时候才营业。我正 享受着皇帝的待遇,店里的小贩都在卖力的吆喝着。 ►走近一看,我立刻被这美丽的荷花吸引住了,一片片绿油油的荷叶层层 叠叠地挤在水面上,是我不由得想起杨万里接天莲叶无穷碧这一句诗。荷 叶上滚动着几颗水珠,真像一粒粒珍珠,亮晶希望对您有帮助,谢谢 晶的 。它们有时聚成一颗大水珠,骨碌一下滑进水里,真像一个顽皮的孩子!
∴ MB BN = 7 =7 2 海里.
cos 45 2 2
故选A.
3.日本福岛发生核电站事故后,我国国家海洋
局高度关注事态发展,紧急调集海上巡逻的海
监船,在相关海域进行现场监测与海水采样,
针对核泄漏在极端情况下对海洋环境的影响及
时开展分析评估.如图,上午9时,海监船位于
A处,观测到某港口城市P位因此,该船能继续安全地向东航行.
探究新知
例3:如图,一艘船以40km/h的速度向正东航行,在A处测得 灯塔C在北偏东60°方向上,继续航行1h到达B处,这时测得 灯塔C在北偏东30°方向上. 已知在灯塔C的四周30km内有暗 礁.问这艘船继续向东航行是否安全?
湘教版九上数学第3课时 与方位角有关的实际问题

∴MB=
(海里).故选A.
随堂演练
一艘帆船航行到 B处时,灯塔A在船的北偏东71º34'的方向,
帆船从B处继续向正东方向航行2400m到达C处,此时
灯塔A在船的正北方向.求C处和灯塔A的距离(精确到
1m). 北
分析
东 A
由题意,△ABC是直角三角形,
其中∠C =90º,∠A= 71º34', 71º34'
tan 7134
答:C处与灯塔A的距离约为 800 m.
课堂小结
能根据题意准确理解方位图,并 画出简单的示意图,解决实际问题。
课后作业
• 1.从课后习题中选取; • 2.完成练习册本课时的习题。
4.4 解直角三角形的应用
第3课时 与方位角有关的实际问题
湘教版·九年级上册
新课导入
例1、如图,一艘船以40km/h的速度向正东航行,在A 处测得灯塔C在北偏东60°方向上,继续航行1h到达B 处,这时测得灯塔C在北偏东30°方向上,已知在灯塔 C的四周30km内有暗礁.问这艘船继续向东航行是否安 全?
∠A所对的边BC=2400m,求
AC=?
tan A
BC
AC AC
B
BC tan A
即可.
C
解 在 Rt△ABC 中,∠C= 90º, ∠A =71º34', BC=2400m,
A
由于BC是∠A的对边,AC是邻边,
tan 7134 BC 2400 .
AC AC B
C
AC 2400 800m.
x。 tan 60°
AB AD BD,
x tan 30°
x tan 60°
=40.
解得 x 20 3.
2019秋湘教版九年级数学上册:4.4.2 第2课时 与坡度、方位角有关的应用问题

8. 如图,某山坡的坡面 AB=200 米,坡角∠BAC= 30°,则该山坡的高 BC 的长为 100 米.
9. (2018·潍坊)如图,一艘渔船正以 60 海里/小时的速 度向正东方向航行,在 A 处测得岛礁 P 在东北方向上, 继续航行 1.5 小时后到达 B 处此时测得岛礁 P 在北偏东 30°方向,同时测得岛礁 P 正东方向上的避风港 M 在北 偏东 60°方向.为了在台风到来之前用最短时间到达 M 处,渔船立刻加速以 75 海里/小时的速度继续航行
A. 2ndF sin 0 · 1 5 = B. sin 0 · 1 5 2ndF = C. 2ndF cos 0 · 1 5 = D. tan 0 · 1 5 2ndF =
5. 如图所示,在坡度为 1∶2 的山坡上种树,要求
株距(相邻两树间的水平距离)是 6 米,则斜坡上相邻两树
间的坡面距离是( B )
解:作 BH⊥AC 于点 H, 由题意得, ∠CBH=45°,∠BAH=60°, 在 Rt△BAH 中, BH=AB×sin∠BAH=6 3, 在 Rt△BCH 中,∠CBH=45°, ∴BC=cos∠BHCBH=6 6(千米). 答:B,C 两地的距离为 6 6千米.
11. (2018·邵阳)某商场为方便消费者购物,准备将原 来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示, 已知原阶梯式自动扶梯 AB 长为 10 m,坡角∠ABD 为 为 15°,请 你计算改造后的斜坡式自动扶梯 AC 的长度.(结果精确 到 0.1 m.温馨提示:sin15°≈0.26,cos15°≈0.97,tan15 °≈0.27)
解:在 Rt△ABD 中,∠ABD=30°,AB=10 m, ∴AD=ABsin∠ABD=10×sin30°=5, 在 Rt△ACD 中,∠ACD=15°,sin∠ACD=AADC, ∴AC=sin∠AADCD =sin155°≈0.526≈19.2 m. 即改造后的斜坡式自动扶梯 AC 的长度约为 19.2 米.
湘教版九年级上册数学仰角、俯角问题同步测试题

4.4 解直角三角形的应用第1课时仰角、俯角问题1(2014•绵阳中考)如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P 的距离为()A.402海里B.403海里C.80海里D.406海里2. 在某次海上搜救工作中,A船发现在它的南偏西30°方向有一漂浮物,同时在A船正东10km处的B船发现该漂浮物在它的南偏西60°方向,此时,B船到该漂浮物的距离是()A.53km B.103km C.10km D.20km3. (2014•苏州中考)如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为()A.4km B.3C.2 km D.3 +1)km4. (2014邵阳中考)一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里/小时的速度前往救援,求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)5. 如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30︒,再往大树的方向前进4 m,测得仰角为60︒,已知小敏同学身高(AB)为1.6m,则这棵树的高度为()(结果精确到0.1m,3≈1.73).A. 3.5mB. 3.6 m C. 4.3m D. 5.1m6.(2014百色中考)从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D 处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是()A.(3米B. (3)米C. (3)米D. 12米C A BD7 (2014嘉兴中考)如图,在地面上的点A 处测得树顶B 的仰角为α,AC =7米,则树高BC 为___________米.8.(2014哈尔滨中考)如图,AB 、CD 为两个建筑物,建筑物AB 的高度为60m ,从建筑物AB 的顶部A 点测得建筑物CD 的顶部C 点的俯角∠EAC 为30°,测得建筑物CD 的底部D 点的俯角∠EAD 为45°.(1)求两建筑物两底部之间的水平距离BD 的长度;(2)求建筑物CD 的高度(结果保留根号).初中生提高做题效率的方法厚薄读书法:复习课本要厚薄结合著名数学家华罗庚先生说:“书要能从薄读到厚,还要能从厚读到薄。
