河南省第四届ACM程序设计大赛原题
2021年河南省鹤壁市全国计算机等级考试C语言程序设计真题(含答案)

2021年河南省鹤壁市全国计算机等级考试C语言程序设计真题(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、单选题(12题)1. C语言中逻辑表达式的值为( )A.0或1B.非零值或者零值C.ture或falseD.'ture'或者'false'2.3.设一个广义表中结点的个数为n,则求广义表深度算法的时间复杂度为____。
A.O(1)B.O(n)C.O(n2)D.O(log2n)4. 以下说法正确的是( )。
A.C程序总是从第一个函数开始执行B.在C程序中,被调用的函数必须在main函数中定义C.C程序总是从main函数开始执行D.C程序中的main函数必须放在程序的开始部分5.6.在C++中,一个函数带有参数说明时,则参数的默认值应该在()中给出。
A.函数定义B.函数声明C.函数定义或声明D.函数调用7. 以下叙述中错误的是( )。
A.C程序中的#include和#define行均不是C语句B.除逗号运算符外,赋值运算符的优先级最低C.C程序中,j++;是赋值语句D.C程序中,+、-、*、/、%是算术运算符,可用于整型和实型数的运算8. 有以下程序main( ){ int k=5,n=0;do{ switch(k){ case 1: case 3:n+=1;k--;break;default:n=0;k--;case 2: case 4:n+=2;k--;break;}printf("%d",n);}while(k>0&&n<5);}程序运行后的输出结果是A.235B.0235C.02356D.23569.下面不能正确表示a*b/(c*d)的表达式是()。
A.(a*b)/c*dB.a*b/(c*d)C.a/c/d*bD.a*b/c/d10.11. 设有以下语句:char str1[]="string",str2[8],*str3,*str4=="string;则______不是对库函数的正确调用。
ACM软件大赛之编程大赛题目(附部分答案)

ACM 软件大赛之编程大赛比赛注意事项:l 比赛时间为3小时(小时(180180分钟);比赛分两个阶段:第一阶段限时30分钟,完成公示的3题,第二阶段限时150分钟(事先完成第一阶段题目的小组可提前进入第二阶段); l 比赛第一阶段的3道题目将在前期宣传中告知参赛选手,比赛第二阶段的题目将由赛事主席当场公布竞赛题目;主席当场公布竞赛题目;l 前两阶段题目分为三个分值(前两阶段题目分为三个分值(55分、分、1010分、分、1515分),第一阶段3道公示题都为5分;第二阶段总共15道题,根据不同的难度分值不同,分别为5道5分题,分题,55道10分题,分题,55道15分题;第一阶段参赛队员不可参考任何相关资料;第二阶段参赛队员可以携带诸如书,如书,手册,程序清单等参考资料。
手册,程序清单等参考资料。
手册,程序清单等参考资料。
比赛过程中队员不得携带任何电子媒质的资料;参比赛过程中队员不得携带任何电子媒质的资料;参赛者可以选择自己擅长的语言(赛者可以选择自己擅长的语言(C,C++,JAVA C,C++,JAVA 等等)进行编写等等)进行编写l 考虑到大一和大二学生的知识掌握程度,大一参加选手一开始就会有10分的分数,最后总分是由所做题目及初始的10分相加得到。
分相加得到。
l 每组队员根据安排使用电脑,小组人数为两人的使用一台电脑,超过两人的使用两台电脑,每台的电脑配置完全相同;脑,每台的电脑配置完全相同;l 各小组每做完一题或几题,必须交予评委老师运行,评委老师当场给分;各小组每做完一题或几题,必须交予评委老师运行,评委老师当场给分; l 如在比赛中发现作弊等行为,将取消比赛资格。
如在比赛中发现作弊等行为,将取消比赛资格。
第一阶段公示题目:题目一:(5分) 打印以下图形,纵遵从字母顺序,行字符数遵从斐波那契数列ABCCDDD EEEEEFFFFFFFFGGGGGGGGGGGGG#include<iostream>int f(int x){int a = 1 , b = 0;int max_ = x;int sum = 0; for(int i = 0; i < max_ ; i++){sum = a + b;a = b;b = sum;}return sum;}void loop_print(int num,char chr){for(int i = 0; i < num ;i++)std::cout<<chr;std::cout<<"\n";}int main(){int line_max = 7;char chr = 'A';for(int line = 0; line < line_max; line++){loop_print(f(line+1),chr);chr++;}return 0;}题目二:(5分)有个电子钟,12点显示为12:00(即12小时制),那么请问一天24时间内,出现连续3个相同数字的钟点有几个?#include<iostream>using namespace std;bool check(int me){int h= me/100;int m= me-100*h;return h<=12&&m<=59&&h>0?true:false;//12小时制小时制}int main(){int me=0;int j(0);//总计数器总计数器while( me<1270){//max 12:59int t= me;int n[4];for(int i=0;i<4;i++){n[i]=t%10;t /= 10;}if(n[1]==n[2]&&(n[0]==n[1]||n[3]==n[1])&&check( me)){//cout<<n[3]<<n[2]<<":"<<n[1]<<n[0]<<"\n";//testj++;me++;}cout<<"total: "<<j*2<<endl;}题目三:(5分)10进制的四位数中有几个符合如下特征:将其分别表示为16进制、10进制、12进制,在每种状态下,分别将各个位上的数相加,能得到3个相等10进制数。
河南省第四届ACM程序设计大赛原题

所有题目时间限制:1秒【T1】序号互换Dr.Kong 设计了一个聪明的机器人卡多,卡多会对电子表格中的单元格坐标快速计算出来。
单元格的行坐标是由数字编号的数字序号,而列坐标使用字符序号。
观察字母序号,发现第1列到第26列的字母序号分别为A,B,……,Z,接着,第27列序号为AA,第28列为AB,以此类推。
若给Dr.Kong的机器人卡多一个数字序号(比如32),它能很快算出等价的字母序号(即AF),若给机器人一个字母序号(比如AA),它也能很快算出等价的数字序号(27),你能不能与卡多比试比试,看谁能算得更快更准。
【标准输入】第一行:N 表示有多少组测试数据。
接下来N行,每行或者是一个正整数,或者是一个仅由大写字母组成的字符串。
【标准输出】对于每一行测试数据,输出一行。
如果输入为一个正整数序号,则输出等价的字母序号;如果输入为字符串,则输出等价的数字序号。
【约束条件】输入保证,所有数字序号和字母序号对应的数字序号均<=2*10^9【样例】【T2】节能Dr.kong 设计的机器人卡多越来越聪明。
最近市政府公司交给卡多一项任务,每天早晨5:00开始,它负责关掉ZK大道右侧上的所有路灯。
卡多每到早晨5:00准会在ZK大道上某盏灯的旁边,然后他开始关灯。
每盏灯都有一定的功率,机器人卡多有自觉的节能意识,它希望在关灯期间,ZK大道右侧上所有的路灯的耗电总量数是最少的。
机器人卡多以1m/s的速度行走。
假设关灯动作不需要花费额外的时间,因为当它通过某盏路灯时就顺手将灯关掉。
请编写程序,计算在给定路灯设置,灯泡功率以及机器人卡多的起始位置的情况下,卡多关灯期间,Zk大道上所有灯耗费的最小能量。
【标准输入】第一行N 表示ZK大道右侧路灯的数量(2<=N<=1000)第二行V 表示机器人卡多开始关灯的路灯号。
(1<=V<=N)接下来的N行中,每行包含两个空格隔开的整数D和W,用来描述每盏灯的参数D表示该路灯与ZK大道起点的距离(用米为单位来表示)W表示灯泡的功率,即每秒该灯泡所消耗的能量数。
ACM试题及参考答案
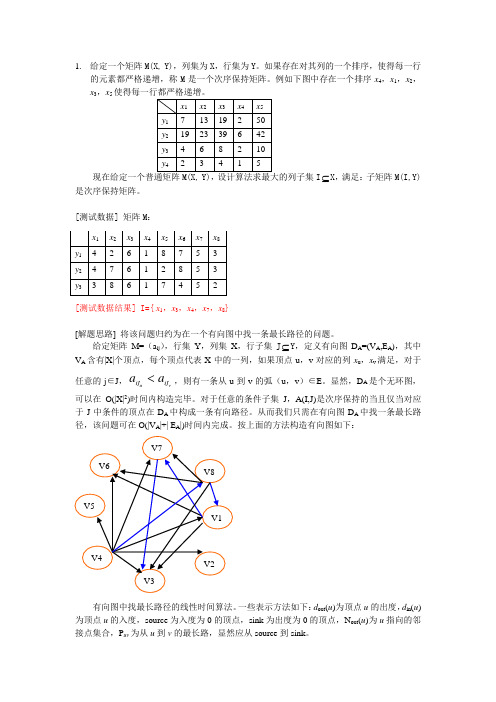
1. 给定一个矩阵M(X, Y),列集为X ,行集为Y 。
如果存在对其列的一个排序,使得每一行的元素都严格递增,称M 是一个次序保持矩阵。
例如下图中存在一个排序x 4,x 1,x 2,x 3,x 5I ⊆X ,满足:子矩阵M(I,Y)是次序保持矩阵。
[测试数据] 矩阵M :[测试数据结果] I={ x 1,x 3,x 4,x 7,x 8}[解题思路] 将该问题归约为在一个有向图中找一条最长路径的问题。
给定矩阵M=(a ij ),行集Y ,列集X ,行子集J ⊆Y ,定义有向图D A =(V A ,E A ),其中V A 含有|X|个顶点,每个顶点代表X 中的一列,如果顶点u ,v 对应的列x u ,x v 满足,对于任意的j ∈J ,u v ij ij a a <,则有一条从u 到v 的弧(u ,v )∈E 。
显然,D A 是个无环图,可以在O(|X|2)时间内构造完毕。
对于任意的条件子集J ,A(I,J)是次序保持的当且仅当对应于J 中条件的顶点在D A 中构成一条有向路径。
从而我们只需在有向图D A 中找一条最长路径,该问题可在O(|V A |+| E A |)时间内完成。
按上面的方法构造有向图如下:有向图中找最长路径的线性时间算法。
一些表示方法如下:d out (u )为顶点u 的出度,d in (u )为顶点u 的入度,source 为入度为0的顶点,sink 为出度为0的顶点,N out (u )为u 指向的邻接点集合,P uv 为从u 到v 的最长路,显然应从source 到sink 。
在每一步为每个顶点关联一个永久的或临时的标签。
v被赋了一个临时标签(v’,i v)表明在当前步,算法找出的最长的从source到v的有向路长度为i v,且经由v’而来。
v被赋了一个永久标签[v’,i v]表明从source到v的最长有向路长度为i v,且经由v’而来,通过回溯每个顶点的永久标签就可以找出最长有向路。
第一届河南省ACM竞赛(正式赛)

第一届河南省大学生程序设计竞赛(正式比赛试题)主办:河南省计算机学会承办:郑州大学信息工程学院协办:YOCSEF郑州分论坛地点:郑州大学南校区软件学院时间:2008年5月18日文件命名:程序文件名为:T题号。
例如:若用C语言,第二题应提交:T2.C【试题一】灾区已经非常困难,灾民需要帐篷、衣物、食品和血浆。
可通往灾区的道路到处都是塌方,70%以上的路面损坏,桥梁全部被毁。
中国空军立即启动应急预案,展开史上最大强度非作战空运行动,准备向灾区空投急需物资。
由于余震不断,天气恶劣,怎样知道空投的物资是否落在某灾区的区域内?经过空中观测,多数灾区为一圆形,空投的物资落在P(X,Y)点。
你能否给出一个正确判断?【标准输入】第1行:N ( N为灾区数)接下有N行:Ri Xi Yi(Ri为圆半径(Xi ,Yi)为空投物资的坐标i=1, 2, …., N )【标准输出】输出有N行,每行为YES (若物资落在灾区所在的圆上或圆内,输出YES或NO否则输出NO)【约束条件】(1) 3 ≤N≤ 10(2)Ri是一个正整数Ri <=100 i=1, 2, …., N(3)Xi Yi均为整数 -100≤ Xi ,Yi ≤100 i=1, 2, …., N(4)假设所有圆的圆心坐标均为(0,0)(5)时间限制:1000MS【样例】据不完全统计,受地震影响,四川大部分灾区通信陷入瘫痪,数千个基站因断电、传输中断等原因退出服务,目前总公司已紧急部署对受灾地区进行通信抢修。
按照应急通信保障预案,必须尽快、付出代价最小,效率更高来全力恢复通信。
由于四川大部分灾区都处于山区,有很多基站之间不能直接建立通信。
现已知建立各基站之间直接通信的代价,问如何建立总代价最小的通信网,使得任意两个基站之间都能通信?【标准输入】第1行:N M(N为基站数M为能直接建立通信关系数)接下有M行:I J P(每行有三个数。
I J 为基站的编号P为基站I与基站之间直接通信的代价)【标准输出】T(建立通信网的最小代价数)【约束条件】(1)2 ≤N ≤100 10 ≤M≤1000(2) 0 < P ≤ 1000 P为正整数(3)时间限制:1000MS【样例】密码破译某组织欲破获一个外星人的密码,密码由一定长度的字串组成。
acm大赛试题及答案

acm大赛试题及答案ACM大赛试题及答案1. 题目一:字符串反转问题描述:编写一个程序,输入一个字符串,输出其反转后的字符串。
输入格式:输入包含一个字符串,字符串长度不超过100。
输出格式:输出反转后的字符串。
示例:输入:hello输出:olleh答案:```pythondef reverse_string(s):return s[::-1]input_string = input().strip()print(reverse_string(input_string))```2. 题目二:计算阶乘问题描述:编写一个程序,输入一个非负整数n,输出n的阶乘。
输入格式:输入包含一个非负整数n,n不超过20。
输出格式:输出n的阶乘。
示例:输入:5输出:120答案:```pythondef factorial(n):if n == 0:return 1else:return n * factorial(n - 1)n = int(input())print(factorial(n))```3. 题目三:寻找最大数问题描述:给定一个包含n个整数的数组,找出数组中的最大数。
输入格式:输入包含一个整数n,表示数组的大小,随后是n个整数。
输出格式:输出数组中的最大数。
示例:输入:5 1 2 3 4 5输出:5答案:```pythonn = int(input())numbers = list(map(int, input().split()))max_number = max(numbers)print(max_number)```4. 题目四:判断闰年问题描述:编写一个程序,输入一个年份,判断该年份是否为闰年。
输入格式:输入包含一个整数,表示年份。
输出格式:如果输入的年份是闰年,则输出"Yes",否则输出"No"。
示例:输入:2000输出:Yes答案:```pythonyear = int(input())if (year % 4 == 0 and year % 100 != 0) or (year % 400 == 0):print("Yes")else:print("No")```5. 题目五:斐波那契数列问题描述:编写一个程序,输入一个非负整数n,输出斐波那契数列的第n项。
郑州大学第四届程序设计竞赛试题

Programming Contest of Zhengzhou Univercity In honor of JacmY,one of the best programers in ZZUACM lab.1.数数我们平时数数都是喜欢从左向右数的,但是我们的小白同学最近听说德国人数数和我们有些不同,他们正好和我们相反,是从右向左数的。
因此当他看到123时会说“321”。
现在有一位德国来的教授在郑州大学进行关于ACM的讲座。
现在他聘请你来担任他的助理,他给你一些资料让你找到这些资料在书中的页数。
现在你已经找到了对应的页码,要用英文把页码告诉他。
为了简化我们的问题,你只需要返回单词的大写的首字母。
(“数字0”读成“字母O”)注意:每个数字式单独读取的,因此不会出现11读成double one的情况。
Input输入分两部分:第一部分:一个整数T(1<=T<=1000)第二部分:一共T行,每行为一个数字。
每个数的长度不超过10位。
O u tput每组输出单独占一行,输出对应的返回给德国教授的页码缩写。
SampleInput Output212 1234TO FTTO2.无线网络覆盖我们的乐乐同学对于网络可算得上是情有独钟,他有一个计划,那就是用无线网覆盖郑州大学。
现在学校给了他一个机会,因此他要购买很多的无线路由。
现在他正在部署某条大道的网络,而学校只允许把他的无线路由器放在路的正中间。
我们默认这条大道是笔直的并且它在任何地方的宽度都一样。
并且所有的路由器的覆盖面积是相同的。
现在乐乐计算出这条大道的长和宽,以及路由器的覆盖半径,想起你帮忙帮他计算出他最少要购买的路由器的数量。
注意:为了防止某种干扰,两台无限路由之间的最小距离不能小于1米。
图1中为一条矩形的道路,中间的虚线代表中线。
图2为最小覆盖的示意图。
I nput输入包括多组测试数据:第一部分:一个整数T(1<=T<=500)。
ACM校赛比赛题目及分析

Problem A -- 超级难题Time Limit:1000ms Memory Limit:65535KBDescriptionACM程序设计大赛是大学级别最高的脑力竞赛,素来被冠以"程序设计的奥林匹克"的尊称。
大赛自1970年开始至今已有30年历史,是世界范围内历史最悠久、规模最大的程序设计竞赛。
比赛形式是:经过校级和地区级选拔的参赛组,于指定的时间、地点参加世界级的决赛,由3个成员组成的小组应用一台计算机解决6到8个生活中的实际问题。
参赛队员必须在5小时内编完程序并进行测试和调试。
此种大赛对参赛学生的逻辑分析能力、策略制定和脑力方面具有极大的挑战性。
大赛提倡在压力较大的情况下,培养学生的创造力、团队合作精神以解决竞赛的问题,从而挑选和发掘世界上最优秀的程序设计人才竞赛的历史可以上溯到1970年,当时在美国德克萨斯A&M大学举办了首届比赛。
当时的主办方是the Alpha Chapter of the UPE Computer Science Honor Society。
作为一种全新的发现和培养计算机科学顶尖学生的方式,竞赛很快得到美国和加拿大各大学的积极响应。
1977年,在ACM计算机科学会议期间举办了首次总决赛,并演变成为目前的一年一届的多国参与的国际性比赛。
迄今已经举办了29届ACM/ICPC以团队的形式代表各学校参赛,每队由3名队员组成。
每位队员必须是入校5年内的在校学生。
比赛期间,每队使用1台电脑需要在5个小时内使用C、C++、Pascal或Java中的一种编写程序解决8或10个问题。
程序完成之后提交裁判运行,并把运行结果及时通知参赛队。
而且有趣的是每队在正确完成一题后,组织者将在其位置上升起一只代表该题颜色的气球2009年的时候队伍A参加了ACM的区域赛,那次区域赛比赛总共有N个题,队伍A做了N个题中的M个。
队伍A 做第一题所用的时间为T1分钟,做第一题所用的时间为T2分钟,.......做第M题所用的时间为Tm分钟。
2022-2023学年河南省郑州市全国计算机等级考试C语言程序设计测试卷(含答案)

2022-2023学年河南省郑州市全国计算机等级考试C语言程序设计测试卷(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、单选题(12题)1.数据独立性是数据库技术的重要特点之一。
所谓数据独立性是指()A.数据与程序独立存放B.不同的数据被存放在不同的文件中C.不同的数据只能被对应的应用程序所使用D.以上三种说法都不对2.具有n个结点的连通图至少有()条边。
A.n-1B.nC.n(n-1)/2D.2n3.考虑一个特殊的hash函数h,能将任一字符串hash成一个整数k,其概率P(k)=2^(-k),k=1,2,…,∞。
对一个未知大小的字符串集合S中的每一个元素取hash值所组成的集合为h(S)。
若h(S)中最大的元素Maxh(S)=10,那么S的大小的期望是()A.1024B.512C.5D.104.下列叙述中正确的是( )。
A.算法就是程序B.设计算法时只需要考虑数据结构的设计C.设计算法时只需要考虑结果的可靠性D.以上三种说法都不对5. 下列二维数组初始化语句中,不正确的是( )。
A.intb[][2]={1,2,3,4,5,6,7};B.intb[3][5]={0,0,0};C.intb[][4]={{1,2},{3,4,5},{6}};D.intb[3][2]={(1,2),(3,4),(5,6)};6. C语言中最简单的数据类型包括( )。
A.整型、实型、逻辑型B.整型、实型、字符型C.整型、字符型、逻辑型D.字符型、实型、逻辑型7.设有如下定义:intx=10,y=3,z; 则语句printf("%d\n",z=(x%y,x/y));的输出结果是()。
A.1B.0C.4D.38.下列哪个算法是对一个list排序的最快方法()A.快速排序B.冒泡排序C.二分插入排序D.线性排序9.已知二叉树后序遍历序列是CDABE,中序遍历序列是CADEB,它的前序遍历序列是()A.ABCDEB.ECABDC.EACDBD.CDEAB10.标准库函数fgets(s,n,file)的功能是( )。
河南acm试题及答案

河南acm试题及答案河南ACM试题及答案1. 问题描述编写一个程序,计算给定整数序列中,满足条件的子序列数量。
条件为:子序列中任意两个相邻元素的差的绝对值不超过1。
2. 输入格式第一行包含一个整数N,表示序列的长度,1 <= N <= 100000。
第二行包含N个整数,表示序列中的元素,-1000000 <= 数字 <= 1000000。
3. 输出格式输出满足条件的子序列数量。
4. 样例输入```51 2 3 2 1```5. 样例输出```5```6. 问题分析本题需要对给定的整数序列进行遍历,使用动态规划的方法来计算满足条件的子序列数量。
设dp[i]表示以第i个元素结尾的满足条件的子序列数量,那么dp[i]的值可以通过dp[i-1](当前元素与前一个元素相等或相邻)和dp[i-2](当前元素与前两个元素相邻)计算得出。
7. 算法实现```pythondef countSubsequences(nums):dp = [0] * (len(nums) + 1)dp[0] = 1for i in range(1, len(nums) + 1):for j in range(i):if abs(nums[i-1] - nums[j-1]) <= 1:dp[i] += dp[j]return sum(dp)```8. 测试用例对于样例输入,程序应输出5,表示有5个满足条件的子序列。
9. 注意事项- 确保输入数据的格式正确。
- 考虑边界条件,如序列长度为1时的情况。
- 动态规划数组的大小应根据序列长度动态调整。
2022-2023学年河南省郑州市全国计算机等级考试C语言程序设计真题二卷(含答案)

2022-2023学年河南省郑州市全国计算机等级考试C语言程序设计真题二卷(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、单选题(12题)1.以下说法错误的是()。
A.由3种基本结构组成的结构化程序不能解决过于复杂的问题B.由3种基本结构组成的结构化程序能解决一些简单的问题C.由3种基本结构组成的结构化程序能解决递归问题D.由3种基本结构组成的结构化程序能解决数学上有解析解的问题2.有以下程序:A.CDEFB.ABEFC.ABCDD.CDAB3.面向对象方法中,继承是指( )。
A.一组对象所具有的相似性质B.一个对象具有另一个对象的性质C.各对象之间的共同性质D.类之间共享属性和操作的机制4.以下关于C语言的叙述中正确的是()。
A.C语言中的注释不可以夹在变量名或关键字的中间B.C语言中的变量可以在使用之前的任何位置进行定义C.在C语言算术表达式的书写中,运算符两侧的运算数类型必须一致D.C语言的数值常量中夹带空格不影响常量值的正确表示5. 以下叙述中错误的是()。
A.C语句必须以分号结束B.复合语句在语法上被看作一条语句C.空语句出现在任何位置都不会影响程序运行D.赋值表达式末尾加分号就构成赋值语句6.以下叙述正确的是()。
A.“char c1, *c2, *c3[10];”是合法的变量定义语句B.数组说明符的方括号中不能使用表达式C.数组元素下标可以是非整数D.若有定义“char array[4];”,则语句“printf( “%c”, array[“3”]);”是合法的7. 若二维数组a有m列,则在a[i][j]刚前的元素个数为( )。
A.i*m+j-1B.i*m+jC.j*m+iD.i*m+j+18.若有定义“int a=1,b=2,c=3,d=4,m=2,n=2;”,则执行“(m = a>b) && (n=c>d)”后n 的值是()。
2021-2022学年河南省焦作市全国计算机等级考试C语言程序设计真题(含答案)

2021-2022学年河南省焦作市全国计算机等级考试C语言程序设计真题(含答案)学校:________ 班级:________ 姓名:________ 考号:________一、单选题(12题)1.有以下程序:#include <stdio.h>void f1(char *a, char b ) {char c; c=*a; *a=b; b=c;}void f2(char a, char b ) {char c; c=a; a=b; b=c;}void f3(char *a, char *b ) {char c; c=*a; *a=* b; *b=c;}main(){char t1, t2 ;t1=‘A’; t2=‘B’;f3(&t1, &t2); putchar(t1); putchar(t2);t1=‘A’; t2=‘B’; f2(t1, t2); putchar(t1); putchar(t2);t1=‘A’; t2=‘B’; f1(&t1, t2); putchar(t1); putchar(t2);printf(“\n”);}程序运行后的输出结果是()。
A.ABBABBB.BAABBBC.BABABAD.BABAAB2.3.4.5.6.结构化程序所规定的三种最基本控制结构是A.A.输入、处理、输出B.树形、网形、环形C.顺序、选择、循环D.主程序、子程序、函数7.下列叙述中错误的是( )。
A.线性表是由n个元素组成的一个有限序列B.线性表是一种线性结构C.线性表的所有结点有且仅有一个前件和后件D.线性表可以是空表8.在下列给出的表达式中,与while(E)中的(E)不等价的表达式是( )。
A.(!E==0)B.(E>0||E<0)C.(E==0)D.(E!=0)9.在C语言中,要求运算数必须是整型的运算符是()。
A./B.++C.!=D.%10.若某表最常用的操作是在最后一个结点之后插入一个结点或删除最后一个结点,则采用()存储方式最节省运算时间。
ACM程序设计竞赛例题[1]
![ACM程序设计竞赛例题[1]](https://img.taocdn.com/s3/m/4595c6dd7cd184254a353550.png)
备战ACM资料习题1.0-1背包问题在0 / 1背包问题中,需对容量为c 的背包进行装载。
从n 个物品中选取装入背包的物品,每件物品i 的重量为wi ,价值为pi 。
对于可行的背包装载,背包中物品的总重量不能超过背包的容量,最佳装载是指所装入的物品价值最高。
程序如下:#include <stdio.h>void readdata();void search(int);void checkmax();void printresult();int c=35, n=10; //c:背包容量;n:物品数int w[10], v[10]; //w[i]、v[i]:第i件物品的重量和价值int a[10], max; //a数组存放当前解各物品选取情况;max:记录最大价值//a[i]=0表示不选第i件物品,a[i]=1表示选第i件物品int main(){readdata(); //读入数据search(0); //递归搜索printresult();}void search(int m){if(m>=n)checkmax(); //检查当前解是否是可行解,若是则把它的价值与max比较{a[m]=0; //不选第m件物品search(m+1); //递归搜索下一件物品a[m]=1; //不选第m件物品search(m+1); //递归搜索下一件物品}}void checkmax(){int i, weight=0, value=0;for(i=0;i<n;i++){if(a[i]==1) //如果选取了该物品{weight = weight + w[i]; //累加重量value = value + v[i]; //累加价值}}if(weight<=c) //若为可行解if(value>max) //且价值大于max max=value; //替换max}void readdata(){for(i=0;i<n;i++)scanf("%d%d",&w[i],&v[i]); //读入第i件物品重量和价值}void printresult(){printf("%d",max);}2.装载问题有两艘船,载重量分别是c1、c2,n个集装箱,重量是wi (i=1…n),且所有集装箱的总重量不超过c1+c2。
ACM程序设计竞赛例题[1]
![ACM程序设计竞赛例题[1]](https://img.taocdn.com/s3/m/8e8360ed84868762cbaed565.png)
A C M程序设计竞赛例题[1]-CAL-FENGHAI.-(YICAI)-Company One1备战ACM资料习题1.0-1背包问题在0 / 1背包问题中,需对容量为c 的背包进行装载。
从n 个物品中选取装入背包的物品,每件物品i 的重量为wi ,价值为pi 。
对于可行的背包装载,背包中物品的总重量不能超过背包的容量,最佳装载是指所装入的物品价值最高。
程序如下:#include <>void readdata();void search(int);void checkmax();void printresult();int c=35, n=10; ");printf("\n");}printf("\n");}6.素数环问题把从1到20这20个数摆成一个环,要求相邻的两个数的和是一个素数。
分析:用回溯算法,考察所有可能的排列。
程序如下:#include <>#include <>void search(int);void init(); 表示空格;’X’表示墙。
程序如下:#include <>#include <>void search(int,int);int canplace(int,int);void readdata(); Floodfill给一个20×20的迷宫和一个起点坐标,用广度优先搜索填充所有的可到达的格子。
提示:参考第2题。
2. 电子老鼠闯迷宫如下图12×12方格图,找出一条自入口(2,9)到出口(11,8)的最短路本题给出完整的程序和一组测试数据。
状态:老鼠所在的行、列。
程序如下:#include<>void readdata();a[i][j]=0; ....注:测试数据可在运行时粘贴上去(点击窗口最左上角按钮,在菜单中选则“编辑”/“粘贴”即可)。
2021年河南省郑州市全国计算机等级考试C语言程序设计预测试题(含答案)

2021年河南省郑州市全国计算机等级考试C语言程序设计预测试题(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、2.填空题(10题)1. 最简单的交换排序方法是______。
2. 数据结构分为线性数据结构和非线性数据结构,带链的队列属于( )。
3. 面向对象的模型中,最基本概念是对象和【】。
4. 下列程序段的运行结果是______。
char str[]="ABCD",*p=str;printf("%d\n",*(p+3));5. 阅读下列程序,则程序的输出结果为【】。
#include"stdio.h"struct ty{ int data;char c;};main(){ struct ty a={30,'x'};fun(a);printf("%d%c",a.data,a.c);}fun(struct ty b){ b.data=20;b.c='y';}6. 以下程序的输出结果是【】。
#include <string.h>main(){printf("%d\n",strlen("IBM\n012\1\\"));}7. 函数fun的返回值是【】。
fun(char *a,char *b){ int num=0,n=0;while(*(a+num)!='\0')num++;while(b[n]){ *(a+num)=b[n];num++;n++;} return num;}8. 以下程序运行后的输出结果是【】。
main(){ int x,a=1,b=2,c=3,d=4;x=(a<b)?a:b; x=(x<c)?x:c; x=(d>x)?x:d;printf("%d\n",x);}9. 若有以下函数定义,函数返回值的类型是【】。
ACM程序设计试题及参考答案

ACM程序设计试题及参考答案猪的安家Andy和Mary养了很多猪。
他们想要给猪安家。
但是Andy没有足够的猪圈,很多猪只能够在一个猪圈安家。
举个例子,假如有16头猪,Andy建了3个猪圈,为了保证公平,剩下1头猪就没有地方安家了。
Mary生气了,骂Andy没有脑子,并让他重新建立猪圈。
这回Andy建造了5个猪圈,但是仍然有1头猪没有地方去,然后Andy又建造了7个猪圈,但是还有2头没有地方去。
Andy都快疯了。
你对这个事情感兴趣起来,你想通过Andy建造猪圈的过程,知道Andy家至少养了多少头猪。
输入输入包含多组测试数据。
每组数据第一行包含一个整数n (n <= 10) – Andy 建立猪圈的次数,解下来n行,每行两个整数ai, bi( bi <= ai <= 1000), 表示Andy建立了ai个猪圈,有bi头猪没有去处。
你可以假定(ai, aj) = 1.输出输出包含一个正整数,即为Andy家至少养猪的数目。
样例输入33 15 17 2样例输出16答案:// 猪的安家.cpp : Defines the entry point for the console application.//#include "stdafx.h"#include "iostream.h"void main(){int n;int s[10][2];bool r[10];char ch;cout<<"请输入次数:"<<endl;cin>>n;for (int i=0;i<n;i++){cout<<"请输入第"<<i+1<<"次的猪圈个数和剩下的猪:,用--分开,"<<endl;cin>>s[i][0]>>ch>>ch>>s[i][1];}for (i=0;i<10;i++)r[i]=true;for (int sum=1;;sum++){for (i=0;i<n;i++)r[i]=(sum%s[i][0]==s[i][1]);for (i=0;i<n;i++){if (r[i]==0)break;}if (i==n)break;}cout<<"猪至少有"<<sum<<"只。
程序设计大赛试题及答案

试题1、数学黑洞(程序文件名maths.c/maths.cpp)【问题描述】任给一个4位正整数,其各位数位上的数字不全相同,将数字重新组合成一个最大的数与最小的数相减,重复这个过程,最多7步,必得6174。
对任给的4位正整数(各位数位上的数字不全相同),编程输出掉进黑洞的步数。
【输入】一行,一个4位正整数n(1000< n<9999)【输出】掉进黑洞的步数输入1234输出32、进制转换(程序文件名conver.c/conver.cpp)【问题描述】任给一个十进制整数n,及正整数m(m<=16且m≠10), 将n转换成m进制并输出。
【输入】一行,两个整数n,m(0 ≤ n ≤ 500000,2 ≤ m ≤ 16,且m≠10),中间用一个空格隔开,其中n 表示十进制数。
【输出】转换后的数【输入输出样例】输入255 8输出3773、分数线划定(程序文件名score.c/score.cpp)【问题描述】公务员选拔工作正在 A 市如火如荼的进行。
为了选拔优秀人才,A 市对所有报名的选手进行了笔试,笔试分数达到面试分数线的选手方可进入面试。
面试分数线根据计划录取人数的150%划定,即如果计划录取m名公务员,则面试分数线为排名第m*150%(向下取整)名的选手的分数,而最终进入面试的选手为笔试成绩不低于面试分数线的所有选手。
现在就请你编写程序划定面试分数线,并输出所有进入面试的选手的报名号和笔试成绩。
【输入】第一行,两个整数n,m(5 ≤ n ≤ 5000,3 ≤ m ≤ n),中间用一个空格隔开,其中n 表示报名参加笔试的选手总数,m 表示计划录取的人数。
输入数据保证m*150%向下取整后小于等于n。
第二行到第 n+1 行,每行包括两个整数,中间用一个空格隔开,分别是选手的报名号k(1000 ≤ k ≤ 9999)和该选手的笔试成绩s(1 ≤ s ≤ 100)。
数据保证选手的报名号各不相同。
河南省第四届大学生程序设计竞赛规则

河南省第四届大学生程序设计竞赛规则●竞赛宗旨ACM国际大学生程序设计竞赛(ACM/ICPC)是大学生们展示和提高编程技能与应用计算机解决问题能力的机会。
河南省第四届程序设计竞赛邀请河南省大学生参加,开展编程方面的公平竞赛,增进彼此间的交流和友谊。
●参赛队组成1.教练是参赛队伍所代表高校的正式教师,教练必须保证所有队员符合本规则的规定。
教练作为参赛队伍的代表,负责竞赛活动中的联系工作。
2.只有当竞赛组委会从教练处获得所有保证队伍合格的材料后,一支队伍才能获得参赛的资格。
3.每支队伍最多由三名参赛队员组成。
4.每支队伍中至少有两名参赛队员必须是未取得学士学位或者同等学历的学生。
5.取得学士学位超过两年,或进行研究生学习超过两年的学生不符合参赛队员的资格。
●比赛规则1.比赛形式为场地赛。
比赛时间均为5小时,命题6-10题(部分英文题目).2.参赛队员可以携带诸如书、手册、笔记和程序清单等参考资料。
但不得携带任何电子媒质的资料。
3.试题的解答提交裁判称为运行,每一次运行会被判为正确或者错误,判决结果会及时通知参赛队伍。
4.名次统计:首先按照正确题目数量排名,如果正确数相同的,将按照完成题目所花费的总时间从小到大的顺序进行排名。
每道试题用时将从竞赛开始到试题解答被判定为正确为止,其间每一次错误的运行将被加罚20分钟时间,未正确解答的试题不计时。
5.参赛者可以使用自己熟悉的任何编程环境完成比赛题目,但是,必须保证自己提交的C/C++代码可以在GCC和(或)G++3.4.1版本以上编译器中正常编译执行。
推荐的集成开发环境是DEV-CPP 4.9.9.2beta。
Dev-C++ 5.0 beta 9 (4.9.9.2) 下载主页:/projects/dev-cpp/6.每支队伍使用一台计算机,所有队伍使用计算机的规格配置完全相同。
7.参赛者禁止作弊。
一经发现,不仅会被清除出本次比赛,也将被禁止参加今后的程序设计竞赛,同时将情况通报所属院校。
河南省第四届ACM程序设计大赛部分答案

´ð°¸½ö¹©²Î¿¼¡¾T1¡¿ÐòºÅ»¥»»#include<stdio.h>#include<stdlib.h>#include<math.h>int Pow(int n,int x){int i,sum=1;for(i=1;i<=x;i++)sum*=n;return sum;}int main(){char **p,c;int i,j,k,sum,n,l,*q;scanf("%d",&n);p=(char**)malloc(n*sizeof(char*));for(i=0;i<n;i++){*(p+i)=(char*)malloc(Pow(10,4)*sizeof(char));scanf("%s",*(p+i));}for(i=0;i<n;i++){sum=0;l=0;while(*(*(p+i)+l)!='\0')l++;if(*(*(p+i))>='A'&&*(*(p+i))<='Z'){for(j=0;j<l;j++)sum+=(*(*(p+i)+j)-'A'+1)*Pow(26,l-1-j);printf("%d\n",sum);}else{sum=0;j=0;while(*(*(p+i)+j)!='\0'){sum+=(*(*(p+i)+j)-'0')*Pow(10,l-1-j);j++;}q=(int*)malloc(l*sizeof(int));j=0;while(sum!=0){q[j]=sum%26;sum=sum/26;if(q[j]==0){q[j]=26;sum--;}j++;}for(k=0;k<j;k++)printf("%c",(q[j-1-k]-1+'A'));putchar('\n');}}free(p);system("psuse");return 0;}¡¾T2¡¿½ÚÄÜ#include<stdio.h>#include<stdlib.h>int N,**P;int main(){long digui(int now,long sum,int time);int i,v;long Wmin;scanf("%d",&N);scanf("%d",&v);P=(int **)malloc(N*sizeof(int *));for(i=0;i<N;i++){*(P+i)=(int *)malloc(3*sizeof(int));scanf("%d%d",*(P+i),*(P+i)+1);*(*(P+i)+2)=1;}Wmin=digui(v-1,0,0);printf("%ld\n",Wmin);return 0;}long digui(int now,long sum,int time) {int i;long w1=0,w2=0,sum1,sum2,time1,time2;P[now][2]=0;for(i=now-1;i>=0;i--){if(P[i][2]==1){time1=time+P[now][0]-P[i][0];sum1=sum+time1*P[i][1];w1=digui(i,sum1,time1);break;}}for(i=now+1;i<N;i++){if(P[i][2]==1){time2=time+P[i][0]-P[now][0];sum2=sum+time2*P[i][1];w2=digui(i,sum2,time2);break;}}P[now][2]=1;if(w1==0&&w2==0)return sum;elseif(w1!=0&&w2!=0)return w1<w2 ? w1 : w2;elseif(w1!=0)return w1;elsereturn w2;}¡¾T3¡¿±í´ïʽÇóÖµ¡¾·½·¨Ò»¡¿#include<stdio.h>#include<string.h>#include<stdlib.h>int i,j;char **p;int Pow(int x,int y){int k,sum=1;for(k=0;k<y;k++)sum*=x;return sum;}int main(){int N,sum;int digui();scanf("%d",&N);p=(char**)malloc(N*sizeof(char*));for(i=0;i<N;i++){*(p+i)=(char*)malloc(300*sizeof(char));scanf("%s",*(p+i));}for(i=0;i<N;i++){j=0;sum=digui();printf("%d\n",sum);}return 0;}int digui(){int k=0,l,sum=0,num1,num2;char *s,c;c=*(*(p+i)+j++);if('0'<=c&&c<='9'){s=(char*)malloc(4*sizeof(char));s[0]=c;k=1;while('0'<=(c=*(*(p+i)+j++))&&c<='9'){s[k]=c;k++;}j--;l=k;for(k=0;k<l;k++)sum+=(s[k]-'0')*Pow(10,l-1-k);return sum;}else{s=(char*)malloc(3*sizeof(char));s[0]=c;s[1]=*(*(p+i)+j++);s[2]=*(*(p+i)+j++);j++;num1=digui();j++;num2=digui();j++;if(s[0]=='a')return num1+num2;elseif(s[2]=='n')return num1<num2 ? num1 : num2;elsereturn num1>num2 ? num1 : num2;}}¡¾·½·¨¶þ¡¿#include<stdio.h>#include<string.h>#include<stdlib.h>int Pow(int x,int y){int i,sum=1;for(i=0;i<y;i++)sum*=x;return sum;}int main(){int i,n,j,m,k,l,N,sum,z1[100],num;char **p,z2[100][3],s[4],c;scanf("%d",&N);p=(char**)malloc(N*sizeof(char*));for(i=0;i<N;i++){*(p+i)=(char*)malloc(300*sizeof(char));scanf("%s",*(p+i));}for(i=0;i<N;i++){j=k=l=0;do{c=*(*(p+i)+j++);if('0'<=c&&c<='9'){s[0]=c;m=1;while('0'<=(c=*(*(p+i)+j++))&&c<='9'){s[m]=c;m++;}j--;n=m;for(num=0,m=0;m<n;m++)num+=(s[m]-'0')*Pow(10,n-1-m);z1[k]=num;k++;while(z2[l-1][0]==','){k--;if(z2[l-2][0]=='a')z1[k-1]=z1[k-1]+z1[k];elseif(z2[l-2][2]=='n')z1[k-1]=z1[k-1]<z1[k] ? z1[k-1] : z1[k];elsez1[k-1]=z1[k-1]>z1[k] ? z1[k-1] : z1[k];l=l-2;if(l==0)sum=z1[0];}}elseif(c==','){z2[l][0]=c;l++;}elseif(c!=')'){z2[l][0]=c;z2[l][1]=*(*(p+i)+j++);z2[l][2]=*(*(p+i)+j++);j++;l++;}}while(l!=0);printf("%d\n",sum);}return 0;}¡¾T4¡¿×ßÃÔ¹¬#include<stdio.h>#include<stdlib.h>int N,**a,**b;int main(){int i,j,max,min,cha;int digui(int r,int c,int max,int min);scanf("%d",&N);a=(int **)malloc(N*sizeof(int *));b=(int **)malloc(N*sizeof(int *));for(i=0;i<N;i++){*(a+i)=(int *)malloc(N*sizeof(int));*(b+i)=(int *)malloc(N*sizeof(int));}for(i=0;i<N;i++)for(j=0;j<N;j++){scanf("%d",&a[i][j]);b[i][j]=0;}max=min=a[0][0];cha=digui(0,0,max,min);printf("%d\n",cha);return 0£»}int digui(int r,int c,int max,int min){int k,ch,cha[4];b[r][c]=1;if(a[r][c]>max)max=a[r][c];elseif(a[r][c]<min)min=a[r][c];ch=cha[0]=cha[1]=cha[2]=cha[3]=-1;if(r==N-1&&c==N-1){b[r][c]=0;return max-min;}else{if(r-1>=0&&b[r-1][c]==0)cha[0]=digui(r-1,c,max,min);。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
所有题目时间限制:1秒【T1】序号互换Dr.Kong 设计了一个聪明的机器人卡多,卡多会对电子表格中的单元格坐标快速计算出来。
单元格的行坐标是由数字编号的数字序号,而列坐标使用字符序号。
观察字母序号,发现第1列到第26列的字母序号分别为A,B,……,Z,接着,第27列序号为AA,第28列为AB,以此类推。
若给Dr.Kong的机器人卡多一个数字序号(比如32),它能很快算出等价的字母序号(即AF),若给机器人一个字母序号(比如AA),它也能很快算出等价的数字序号(27),你能不能与卡多比试比试,看谁能算得更快更准。
【标准输入】第一行:N 表示有多少组测试数据。
接下来N行,每行或者是一个正整数,或者是一个仅由大写字母组成的字符串。
【标准输出】对于每一行测试数据,输出一行。
如果输入为一个正整数序号,则输出等价的字母序号;如果输入为字符串,则输出等价的数字序号。
【约束条件】输入保证,所有数字序号和字母序号对应的数字序号均<=2*10^9【样例】【T2】节能Dr.kong 设计的机器人卡多越来越聪明。
最近市政府公司交给卡多一项任务,每天早晨5:00开始,它负责关掉ZK大道右侧上的所有路灯。
卡多每到早晨5:00准会在ZK大道上某盏灯的旁边,然后他开始关灯。
每盏灯都有一定的功率,机器人卡多有自觉的节能意识,它希望在关灯期间,ZK大道右侧上所有的路灯的耗电总量数是最少的。
机器人卡多以1m/s的速度行走。
假设关灯动作不需要花费额外的时间,因为当它通过某盏路灯时就顺手将灯关掉。
请编写程序,计算在给定路灯设置,灯泡功率以及机器人卡多的起始位置的情况下,卡多关灯期间,Zk大道上所有灯耗费的最小能量。
【标准输入】第一行N 表示ZK大道右侧路灯的数量(2<=N<=1000)第二行V 表示机器人卡多开始关灯的路灯号。
(1<=V<=N)接下来的N行中,每行包含两个空格隔开的整数D和W,用来描述每盏灯的参数D表示该路灯与ZK大道起点的距离(用米为单位来表示)W表示灯泡的功率,即每秒该灯泡所消耗的能量数。
路灯是按顺序给定的。
(0<=D<=1000,0<=W<=1000)【标准输出】输出一个整数,即消耗总能量之和的最小值。
注意结果小于200,000,000【样例】【T3】表达式求值Dr.Kong 设计的机器人卡多掌握了加减运算以后,最近又学会了一些简单的函数求值,比如,它知道函数min(20,23)的值是20,add(10,98)的值是108等等。
经过训练,Dr.Kong设计的机器人卡多甚至会计算一种嵌套的更复杂的表达式。
假设表达式可以简单定义为:1.一个正的十进制数x是一个表达式。
2.如果x和y是表达式,则函数min(x.y)也是表达式,其值为x,y中最小的数。
3.如果x和y是表达式,则函数max(x,y)也是表达式,其值为x,y中最大数。
4.如果x和y是表达式,则函数add(x,y)也是表达式,其值为x,y之和。
例如,表达式max(add(1,2),7)的值为7.请编写程序,对给定的一组表达式,帮助DrKong算出正确答案,以便校队卡多计算的正误。
【标准输入】第一行:N 表示要计算的表达式的个数(1<=N<=10)接下来有N行,每行是一个字符串,表示待求值的表达式(表达式中不会有多余的空格,每行不超过300个字符,表达式中出现的十进制数都不超过1000.)【标准输出】输出有N行,每行对应一个表达的值。
【样例】【T4】走迷宫DrKong设计的机器人卡多非常爱玩,它常常偷偷跑出实验室,在某个游乐场玩之不疲。
这天卡多又跑出来了,在SJTL游乐场玩个不停,坐完碰碰车,又玩滑滑梯,这时卡多又走入了一个迷宫。
整个迷宫是用一个N*N的方阵给出,方阵中单元格中填充了一个整数,表示走到这个位置的难度。
这个迷宫可以向上,向下,向左,向右走,但不能穿越对角线。
走迷宫的取胜规则很有意思,看谁能更快地找一条路径,其路径上的单元格最大难度与最小难度之差是最小的。
当然了,或许这样的路径不是最短的。
机器人卡多现在在迷宫的左上角(第一行,第一列)而出口在迷宫的右下角(第N行,第N列)。
卡多很聪明,很快就找到了这样的一条路径。
你能找到吗?【标准输入】第一行:N 表示迷宫是N*N的方阵(2<=N<=100)接下来N行,每行包含N个整数,用来表示每个单元格中的难度(0<=任意难度<=120)【标准输出】输出为一行整数,表示路径上的难度与最低难度的差。
【样例】提示:样例中粗斜体数字为机器人卡多选择的路径。
【T5】宝物传说HMH大沙漠中有一个迷宫,里面藏有许多宝物。
迷宫里可能有N个藏宝地点,用1到N标记。
藏宝地点之间最多有一条通路相连。
标记为1为迷宫的进出口。
某天,DrKong找到了迷宫的地图,他已经知道其中K(1<=K<=N)个不同的地点真的藏有宝物。
Drkong 决定让他的机器人卡多去探险。
卡多在经过某个藏宝地点时可能会拿走宝物。
但它每拿走一个藏宝地点的宝物后,它的载重量会增加W。
迷宫中的通路是不平坦到处是陷阱。
假设每条通路都有一个危险度,其值与通过此路的载重量成正比。
当机器人卡多进入迷宫时,它的载重量为0,。
只有当卡多携带宝物的载重量不大于某个通路的危险度时,它才能顺利通过此路,否则就会掉下陷阱,不能出来。
Drkong希望他的机器人卡多尽量多带出宝物,当然他更希望卡多最后能从标记1的地点出来。
请编写程序,帮助Drkong计算一下,卡多最多能带出多少个藏宝地点的宝物。
【标准输入】第一行:NMKW接下来K行,每行一个整数,表示有藏有宝物的地点标号。
在接下来M行,每行三个整数X,Y,Z,表示地点X与地点Y之间有一条危险度为Z的通路。
【标准输出】输出一个整数,表示卡多最多能带出的宝物的堆数。
【约束条件】1<=N<=8000 1<=K<=N 1<=M<=15000 1<=W,Z<=10000数据保证所有的地点之间都是有道路可以到达的。
提示:机器人卡多经过一个宝藏地点是可以不拿走宝物,而且同一宝藏的点可以经过多次。
【样例】SUBSTRINGYou are given a string input. You are to find the longestsubstring of input such that the reversal of the substring is also a substring of input . In case of a tie , return the string that occurs earliest in input.Note well: The substring and its reversal may overlap partially or completely. The entire original string is itself a valid substring. The best we can do is find a one character substring , so we implement the tie-breaker rule of taking the earliest one first.[Standard ouput]The first line of input gives a single integer, 1<=N<=10, the number of test case. Then follow ,for each test case , a line containing between 1 and 50 characters, inclusive .Each character of input will be an uppercase letter(‘A’-‘Z’). [Standard output]Output for each test case the longest substring of input such that the reversal of the substring is also a substring of input.[Sample input]3ABCABAXYZXCVCX[Sample Output]ABAXXCVCX[ T7 ]BOBSLEDDINGDr.kong has entered a bobsled competition because he hefty weight wil give his an advantage over the L meter course(2<=L<=1000).Dr.kong will push off the starting line at 1 meter per second ,but his speed can change while he rides along the course. Near the middle of every meter per second or by braking to stay at the same speed or decrease his speed by one meter per second .Naturally, Dr.kong must negotiate N(1<=N<=500) turns on the way down the hill. Turn i is located T_i meters from the course start (1<=T_i<=L-1),and he must beenter the corner meter at a peed of at most S_i meters per second (1<=S_i<=1000). Dr.kong can cross the finish line at any speed he likes.Help Dr.kong learn the fastest speed he can attain without exceeding the speed limits on the turns .Consider this course with the meter markers as integers and the turn speed limits in brackets(e.g,’[3]’):0 1 2 3 4 5 6 7[3]8 9 10 11[1] 12 13[8]14(start)|-------------------------------------------------------------------------------|(finish)Below is a chart of Dr.kong’s speeds at the beginning of each meter length of the course:Max: [ 3 ] [ 1 ] [ 8 ]Mtrs: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14Spd: 1 2 3 4 4 5 4 3 4 3 2 1 2 3 4His maxinun speed was 5 near the beginning of meter 4.[Standard input ]Line 1: Two space-separated integers : L and NLine 2—N+1: Line i+1 describes turn i with two space-separated integer: T-i and S-i[Standard output ]Line 1:A single integer, representing the maximum speed which Dr.kong can attain between the start and the finish line , inclusive.[Sample input] [Sample output]14 3 57 111 113 8[ T8 ]SECRETDr.kong is constructing a new machine and wishes to keep it secret as long as possible .He has hidden in it deep within some forest and needs to be the machine during its construction . He has a secret tunnel that he uses only for the return trips .The forest comprises N(2<=N<=200) landmarks (numbered 1…N) connected by P (1<=P<=40000) bidirectional trails (numbered 1…P) and with a positive length that does not exceed 1000,000. Multiple trails might join a pair of landmarks/To minimize his chances of detection , Dr.kong knows he cannot use any trail on the forest more than once and that he should try to use the shorest trails.Help Dr.kong get from the entrance ( landmark 1) to the secret machine (landmark N) a total of T times . Find the minimum possible length of the longest single trail that he will have to use , subject to the constraint that he use no trail more than once .(Note well: The foal is to minimize the length of the longest trail ,not the trail lengths.)It is guaranteed that Dr.kong can make all T trips without reusing a trail. [Standard input ]Line 1:Three space-separated integers: N, P,and TLine 2:Line i+1 contains three space-separated integers, A_i, B_i, and L_i. [Standard ouuput]Line 1: A single integer that is the minimum possible length of the longest segment of Dr,kong’s route[Sample input] [Sample output]7 9 2 51 2 22 3 53 7 51 4 1 4 3 14 5 75 7 1 16 3 67 3。
