NOIP2007 提高组 复赛试题
2007年noip提高组题目解析

[解题思想2 by peterche1990/2wsx2wsx2wsx/czp] 容易求出所有最长路,以及所有最长路上的点。依 次枚举,复杂度是O(KN^3),其中K是最长路的条数。 该算法易于实现,但是写得不好会TLE1个点,部分 大牛就是这样没有得400的。
[解题思想3] 引理:如果树有多条直径,则每条直径上都存在一个core。 明:首先,如图,如果ABCD和FBCE都是直径的话,则AB=FB, CD=CE(如果不然,可设AB>FB,则FBCE<ABCE,矛盾!)。 这样,ABCE,FBCD也都是直径。我们给BC起个名字叫“公共 段”。题目中说过,公共段必然存在。 考虑ecc的定义,路径的ecc是指所有的点到路径的距离的最大值。 核指的是直径上长度满足约束的ECC最小的子路经。假如根据直径 ABCE算得的core是GHBI,路径GHBI的ecc就是max{BF,AG,DI,EI}, 这个最大值取到了最小。由于DC=EC,也就是说,如果路径和公 共段有交集,公共段的一端上,不包含CORE的直径是可以任选的。 换言之,此时max{BF,AG,ID}有最小值,此时用AB替换BF,发现必 然有BF=AB>AG,ecc=max{BF,ID}。也就是说,如果路径和公共段 有交集,实际计算max时,只需要计算路径在公共段上的部分的 ecc,然后和公共段两端的路径长取一遍MAX就行了。
第四个题目 core [题目转述] 给出一棵无根树,边上有权。称最长路径为直径, 定义路径的偏心距为:点到路径的上的点的最小值 的距离的最大值,给出一个s,找出直径上的某段长 度不超过s的路径,使得偏心距最小。
[解题思想] 算法是严格立方的。中心理念是不要做重复的工作。算法比较笨 拙。考虑到树的性质,对于任意两点,最短路=联通路=最长路。 首先求出多源最短路,该步可以由类似Tarjan的算法,在O(N^2) 内解决。实际上由于下一步的复杂度高达三次方,这里就直接 floyd了。同时可以求出最长路径上都有哪些点。在NOI2007中, 记录最短路的中间结点是很有用的。设mid[a,b]是a,b之间的联通 路上的一个中间点,。 由于这是一棵树,最短路必然唯一。考虑问题的解,构造一个函 数F(k,a,b)为K到ab间的最短路的长度。则 f(k,a,b)=min{d[k,mid[a,b],f[k,a,mid[a,b]],f[k,mid[a,b],b]} 写出了这 个方程,便不难得出一个三次方的算法。 在实际coding的时候,把k放在最外层枚举,这样内层实际上只 用到了f的后面2维,用2维数组记录即可。
NOIP2007提高组复赛试题

全国信息学奥林匹克联赛(NOIP2007)复赛提高组题目一览(2007年11月17日 3小时完成)说明:1.文件名(程序名和输入输出文件名)必须使用小写2.C/C++中函数main()的返回值必须是int,程序正常结束时返回值必须是0。
3.全国统一评测时采用的机器参考配置为:CPU 2.0GHz,内存256M。
1.统计数字(count.pas/c/cpp)【问题描述】某次科研调查时得到了n个自然数,每个数均不超过1500000000(1.5*109)。
已知不相同的数不超过10000个,现在需要统计这些自然数各自出现的次数,并按照自然数从小到大的顺序输出统计结果。
【输入】输入文件count.in包含n+1行;第一行是整数n,表示自然数的个数;第2~n+1每行一个自然数。
【输出】输出文件count.out包含m行(m为n个自然数中不相同数的个数),按照自然数从小到大的顺序输出。
每行输出两个整数,分别是自然数和该数出现的次数,其间用一个空格隔开。
【输入输出样例】【限制】40%的数据满足:1<=n<=100080%的数据满足:1<=n<=50000100%的数据满足:1<=n<=200000,每个数均不超过1500 000 000(1.5*109)2.字符串的展开(expand.pas/c/cpp)【问题描述】在初赛普及组的“阅读程序写结果”的问题中,我们曾给出一个字符串展开的例子:如果在输入的字符串中,含有类似于“d-h”或者“4-8”的字串,我们就把它当作一种简写,输出时,用连续递增的字母H 或数字串替代其中的减号,即,将上面两个子串分别输出为“defgh”和“45678”。
在本题中,我们通过增加一些参数的设置,使字符串的展开更为灵活。
具体约定如下:(1) 遇到下面的情况需要做字符串的展开:在输入的字符串中,出现了减号“-”,减号两侧同为小写字母或同为数字,且按照ASCII码的顺序,减号右边的字符严格大于左边的字符。
2007-2011年noip初赛提高组试题及答案

第十七届全国青少年信息学奥林匹克联赛初赛试题(提高组 Pascal语言两小时完成)●● 全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●一、单项选择题(共20题,每题1.5分。
共计30分。
每题有且仅有一个正确选项。
)1.在二进制下,1100011 +()= 1110000。
A.1011 B.1101 C.1010 D.11112.字符“A”的ASCII码为十六进制41,则字符“Z”的ASCII码为十六进制的()。
A.66 B.5A C.50 D.视具体的计算机而定3.右图是一棵二叉树,它的先序遍历是()。
A.ABDEFC B.DBEFAC C.DFEBCA D.ABCDEF4.寄存器是()的重要组成部分。
A.硬盘B.高速缓存C.内存D.中央处理器(CPU)5.广度优先搜索时,需要用到的数据结构是()。
A.链表B.队列C.栈D.散列表6.在使用高级语言编写程序时,一般提到的“空间复杂度”中的“空间”是指()。
A.程序运行时理论上所占的内存空间B.程序运行时理论上所占的数组空间C.程序运行时理论上所占的硬盘空间D.程序源文件理论上所占的硬盘空间7.应用快速排序的分治思想,可以实现一个求第K大数的程序。
假定不考虑极端的最坏情况,理论上可以实现的最低的算法时间复杂度为()。
A.O(n2)B.O(n log n)C.O(n) D.O(1)8.为解决Web应用中的不兼容问题,保障信息的顺利流通,()制定了一系列标准,涉及HTML、XML、CSS等,并建议开发者遵循。
A.微软 B.美国计算机协会(ACM) C.联台国教科文组织D.万维网联盟(W3C)9.体育课的铃声响了,同学们都陆续地奔向操场,按老师的要求从高到矮站成一排。
每个同学按顺序来到操场时,都从排尾走向排头,找到第一个比自己高的同学,并站在他的后面。
这种站队的方法类似于()算法。
A.快速排序B.插入排序C.冒泡排序D.归并排序10.1956年()授予肖克利(William Shockley)、巴丁(John Bardeen)和布拉顿(Walter Brattain),以表彰他们对半导体的研究和晶体管效应的发现。
历年NOIP提高组试题难度列表

NOIP2008-D
NOIP2009-A
NOIP2009-B
火柴棒等式 模拟
传纸条 双栈排序
动态 规划
构造
潜伏者 模拟
Hankson的 趣味题
数学
枚举,优化/开表 0.8
历届搜索
题一般都比较
多维状态DP 0.7 难,搜索算法
本身简单,于
枚举,贪心/二分 图
0.4
是题目会提高
选手对其他方
模拟
【构造】
动态 规划
构 造, 贪心
多维DP
BFS/贪心,并查 集
平均难度系 数:0.27
构造类题 目一般没有明 确的算法,需
NOIP2010-D
引水入城
搜索 BFS
要选手仔细分 析题目的实
质,并得出解法。
这个解法通常不是唯一的。有时一个好的贪心可以得相当
多的分。有时搜索剪枝可以很大的提高效率。同样以多得分为
需要掌握
模拟,字符串
质数及其性 0.8 质,基础的实
子序列DP,贪心 优化
0.2
数操作,加法 原理和乘法原
置换群,贪心 0.2 理。此类题需
字符串,抽样检 测,表达式
区间环DP
要选手对数学 0.3 规律的灵感。
【图论】 0.6 平均难度系
资源分配DP,构 造
0.6
数:0.50 历届考察
模拟
动态规划/组合 数学,高精度
金明的预算 动态
方案
规划
作业调度方 案
模拟
2^k进制数
动态 规划
统计数字 模拟
字符串的展 开
模拟
矩阵取数游 动态
戏
规划
树网的核 图论
历届noip提高组复赛试题

NOI’ 95“同创杯”全国青少年信息学(计算机)奥林匹克竞赛分区联赛复赛试题(高中组)(上机编程,完成时间:210 分钟)<1>编码问题:设有一个数组A:ARRAY[0..N-1] OF INTEGER;数组中存放的元素为0~N-1 之间的整数,且A[i]≠ A[j](当i≠ j时)。
例如: N=6 时,有:此时,数组 A 的编码定义如下:A[0] 的编码为0;A[i] 的编码为:在A[0] ,A[1]∴上面数组 A 的编码为:A= ( 4,3, 0, 5,1, 2),, A[i-1] 中比 A[i] 的值小的个数(B= (0, 0,0,3,1, 2)i=1 ,2,, N-1 )程序要求解决以下问题:①给出数组 A 后,求出其编码。
②给出数组 A 的编码后,求出 A 中的原数据。
<2> 灯的排列问题:设在一排上有 N 个格子( N≤ 20),若在格子中放置有不同颜色的灯,每种灯的个数记为 N 1, N2, N k( k 表示不同颜色灯的个数)。
放灯时要遵守下列规则:①同一种颜色的灯不能分开;②不同颜色的灯之间至少要有一个空位置。
例如: N=8 (格子数)R=2 (红灯数)B=3 (蓝灯数)放置的方法有:R-B 顺序R R B B BR R B B BR R B B BR R B B BR R B B BR R B B BB-R顺序B B B BBBBBBBBBBBBBBR RRRBRRRRRRRR放置的总数为12 种。
数据输入的方式为:NP1(颜色,为一个字母)P2N1(灯的数量)N2Q(结束标记, Q 本身不是灯的颜色)程序要求:求出一种顺序的排列方案及排列总数。
<3> 设有一个四层的积木块,1~ 4 层积木块的数量依次为:5, 6,7, 8如下图所示放置:815851691423414326其中,给出第三层与第四层所标示的数字,并已知第三层的数据是由第四层的数据计算出来的。
NOIP2007复赛普及组试题
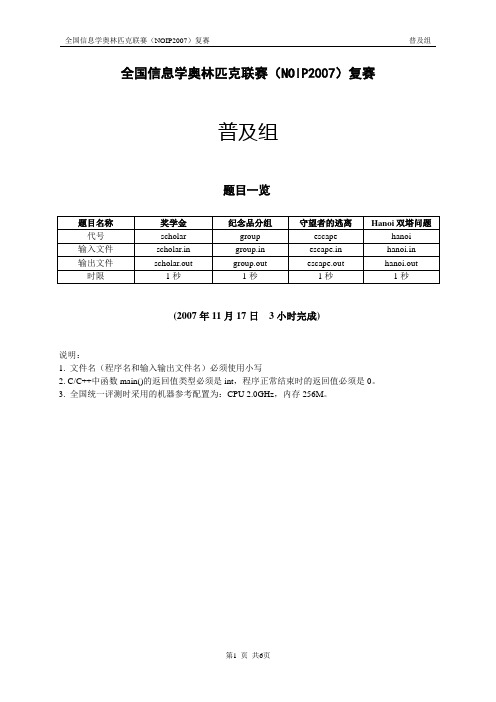
全国信息学奥林匹克联赛(NOIP2007)复赛普及组题目一览(2007年11月17日3小时完成)说明:1. 文件名(程序名和输入输出文件名)必须使用小写2. C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3. 全国统一评测时采用的机器参考配置为:CPU 2.0GHz,内存256M。
1.奖学金(scholar.pas/c/cpp)【问题描述】某小学最近得到了一笔赞助,打算拿出其中一部分为学习成绩优秀的前5名学生发奖学金。
期末,每个学生都有3门课的成绩:语文、数学、英语。
先按总分从高到低排序,如果两个同学总分相同,再按语文成绩从高到低排序,如果两个同学总分和语文成绩都相同,那么规定学号小的同学排在前面,这样,每个学生的排序是唯一确定的。
任务:先根据输入的3门课的成绩计算总分,然后按上述规则排序,最后按排名顺序输出前5名学生的学号和总分。
注意,在前5名同学中,每个人的奖学金都不相同,因此,你必须严格按上述规则排序。
例如,在某个正确答案中,如果前两行的输出数据(每行输出两个数:学号、总分)是:7 2795 279这两行数据的含义是:总分最高的两个同学的学号依次是7号、5号。
这两名同学的总分都是279(总分等于输入的语文、数学、英语三科成绩之和),但学号为7的学生语文成绩更高一些。
如果你的前两名的输出数据是:5 2797 279则按输出错误处理,不能得分。
【输入】输入文件scholar.in包含n+1行:第1行为一个正整数n,表示该校参加评选的学生人数。
第2到n+1行,每行有3个用空格隔开的数字,每个数字都在0到100之间。
第j行的3个数字依次表示学号为j-1的学生的语文、数学、英语的成绩。
每个学生的学号按照输入顺序编号为1~n (恰好是输入数据的行号减1)。
所给的数据都是正确的,不必检验。
【输出】输出文件scholar.out共有5行,每行是两个用空格隔开的正整数, 依次表示前5名学生的学号和总分。
【精选资料】NOIP提高组复赛试题与简解转载

Day1铺地毯【问题描述】为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域(可看做是平面直角坐标系的第一象限)铺上一些矩形地毯。
一共有n 张地毯,编号从1 到n。
现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地毯覆盖在前面已经铺好的地毯之上。
地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的那张地毯的编号。
注意:在矩形地毯边界和四个顶点上的点也算被地毯覆盖。
【输入】输入文件名为 carpet.in。
输入共 n+2 行。
第一行,一个整数 n,表示总共有n 张地毯。
接下来的 n 行中,第i+1 行表示编号i 的地毯的信息,包含四个正整数a,b,g,k,每两个整数之间用一个空格隔开,分别表示铺设地毯的左下角的坐标(a,b)以及地毯在x轴和y 轴方向的长度。
第 n+2 行包含两个正整数x 和y,表示所求的地面的点的坐标(x,y)。
【输出】输出文件名为 carpet.out。
输出共 1 行,一个整数,表示所求的地毯的编号;若此处没有被地毯覆盖则输出-1。
【输入输出样例 1】【输入输出样例说明】如下图,1 号地毯用实线表示,2 号地毯用虚线表示,3 号用双实线表示,覆盖点(2,2)的最上面一张地毯是3 号地毯。
【输入输出样例 2】【输入输出样例说明】如上图,1 号地毯用实线表示,2 号地毯用虚线表示,3 号用双实线表示,点(4,5)没有被地毯覆盖,所以输出-1。
【数据范围】对于 30%的数据,有n≤2;对于 50%的数据,0≤a, b, g, k≤100;对于 100%的数据,有0≤n≤10,000,0≤a, b, g, k≤100,000。
【一句话题意】给定n个按顺序覆盖的矩形,求某个点最上方的矩形编号。
【考察知识点】枚举【思路】好吧我承认看到图片的一瞬间想到过二维树状数组和二维线段树。
置答案ans=-1,按顺序枚举所有矩形,如果点在矩形内则更新ans。
注意题中给出的不是对角坐标,实际上是(a,b)与(a+g,b+k)。
noip2007初赛提高组精彩试题(卷)和问题详解

第十三届全国青少年信息学奥林匹克联赛初赛试题(提高组Pascal 语言二小时完成)●●全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●一、单项选择题(共 10 题,每题 1.5 分,共计 15 分。
每题有且仅有一个正确答案.)。
1. 在以下各项中。
()不是 CPU 的组成部分。
A. 控制器B. 运算器C. 寄存器D. 主板E. 算术逻辑单元(ALU)2. 在关系数据库中, 存放在数据库中的数据的逻辑结构以( )为主。
A. 二叉树B. 多叉树C. 哈希表D. B+树E. 二维表3.在下列各项中,只有()不是计算机存储容量的常用单位。
A. ByteB. KBC. MBD. UBE. TB4.ASCII码的含义是()。
A. 二—十进制转换码B. 美国信息交换标准代码C. 数字的二进制数码D. 计算机可处理字符的唯一编码E. 常用字符的二进制编码5.在 Pascal 语言中,表达式 (23 or 2 xor 5)的值是()A. 18B.1 C.23 D.32 E.246.在 Pascal 语言中,判断整数a 等于 0 或b等于 0或c等于0 的正确的条件表达式是()A. not ((a<>0) or (b<>0) or (c<>0))B. not ((a<>0) and (b<>0) and (c<>0))C. not ((a=0) and (b=0)) or (c=0)D.(a=0) and (b=0) and (c=0)E. not ((a=0) or (b=0) or (c=0))7. 地面上有标号为A、B、C的3根细柱, 在A柱上放有10个直径相同中间有孔的圆盘, 从上到下次依次编号为1, 2, 3, ……,将A柱上的部分盘子经过B柱移入C柱, 也可以在B 柱上暂存。
如果B柱上的操作记录为:“进,进,出,进,进,出,出,进,进,出,进,出,出”。
NOIP2001-2011提高组复赛试题合集

神经元〔编号为 1) 图中,X1—X3 是信息输入渠道,Y1-Y2 是信息输出渠道,C1 表示神经元目前的状态, Ui 是阈值,可视为神经元的一个内在参数。 神经元按一定的顺序排列,构成整个神经网络。在兰兰的模型之中,神经网络中的神 经无分为几层;称为输入层、输出层,和若干个中间层。每层神经元只向下一层的神经元 输出信息,只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。
第九届全国青少年信息学奥林匹克联赛(N0IP2003)
2003 年 11 月 29 日 提高组试题 三小时完成
题一
神经网络
【问题背景】 人工神经网络(Artificial Neural Network)是一种新兴的具有自我学习能力的计算 系统,在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究 一直是当今的热门方向, 兰兰同学在自学了一本神经网络的入门书籍后, 提出了一个简化模 型,他希望你能帮助他用程序检验这个神经网络模型的实用性。 【问题描述】 在兰兰的模型中,神经网络就是一张有向图,图中的节点称为神经元,而且两个神经 元之间至多有一条边相连,下图是一个神经元的例子:
题三 统计单词个数(30 分) 问题描述 给出一个长度不超过 200 的由小写英文字母组成的字母串(约定;该字串以每行 20 个字母的方式输入,且 保证每行一定为 20 个)。要求将此字母串分成 k 份(1<k<=40),且每份中包含的单词个数加起来总数最大 (每份中包含的单词可以部分重叠。当选用一个单词之后,其第一个字母不能再用。例如字符串 this 中 可包含 this 和 is,选用 this 之后就不能包含 th)。 单词在给出的一个不超过 6 个单词的字典中。 要求输出最大的个数。 输入格式 去部输入数据放在文本文件 input3.dat 中,其格式如下: 第一行为一个正整数(0<n<=5)表示有 n 组测试数据 每组的第一行有二个正整数(p,k) p 表示字串的行数; k 表示分为 k 个部分。 接下来的 p 行,每行均有 20 个字符。
NOIP2007提高组解题报告

第一题:count 统计数字输入一个数n(n<=200000)和n个自然数(每个数都不超过1.5*10^9),请统计出这些自然数各自出现的次数,按顺序从小到大输出。
输入数据保证不相同的数不超过10000个。
样例输入:8242451002100样例输出:2 34 25 1100 2第一题program scholar(input,output);var a,b,c,id,s:array[1..300]of integer;v:array[0..0]of boolean;i,j,k,t,m,n,x,y:integer;beginassign(input,'scholar.in');assign(output,'scholar.out');reset(input);rewrite(output);readln(n);for i:=1 to n dobegin readln(a[i],b[i],c[i]);id[i]:=i;end;for i:=1 to n dos[i]:=a[i]+b[i]+c[i];for i:=1 to n-1 dofor j:=i to n dobeginif s[i]<s[j]thenbegint:=s[i];s[i]:=s[j];s[j]:=t;t:=a[i];a[i]:=a[j];a[j]:=t;t:=b[i];b[i]:=b[j];b[j]:=t;t:=c[i];c[i]:=c[j];c[j]:=t;t:=id[i];id[i]:=id[j];id[j]:=t;end;if s[i]=s[j]thenif a[i]<a[j] thenbegint:=s[i];s[i]:=s[j];s[j]:=t;t:=a[i];a[i]:=a[j];a[j]:=t;t:=b[i];b[i]:=b[j];b[j]:=t;t:=c[i];c[i]:=c[j];c[j]:=t;t:=id[i];id[i]:=id[j];id[j]:=t;endend;for i:=1 to 5 dowriteln(id[i],' ',a[i]+b[i]+c[i]);close(input);close(output);end.第二题:expand 字符串的展开我们可以用减号对连续字母或数字进行缩写,于是字符串a-dha3-68就可以展开为abcdha34568。
NOIP2007提高组题解

NOIP2007提高组题解1.count一切直接nlogn的算法,在常数不大的时候都能过。
我采用的是接近O(n+klogk)的算法,这里k=10000,即不同的数的个数:先把数存放到Hash表中,读完以后再取出Hash表内的数据排序。
Hash函数采用mod 99991的方式。
发生冲突采用类似开散列的解决办法:如果Hash(n)的位置已经被占用,但关键字不匹配,那接下来考虑Hash(n+1)的位置,直到找到一个空位,或者关键字相同。
提一句:直至今年,C的stdlib.h库中qsort函数仍然可以使用。
2.expand这题考查的是字符串处理的技巧。
注意一定要满足以下全部条件:非头非尾,两边均字母或均数字,左边字符比右边字符小。
这时候才按要求进行填充工作。
另:C/C++选手在熟练掌握for语句的情况下可以把顺序、逆序、大小写放在同一个过程里实现,降低编程复杂度。
3.game注意到每一行都是独立的一个结构,因此可以把每一行的答案全部加起来就是最后答案。
对于每一行,有状态转移方程:f(i,j) = 2*max(a(i)+f(i+1,j),a(j)+f(i,j-1)),边界f(i,i)=2*a(i),其中f(i,j)表示从i到j这一子段单独操作可以达到的最大权值。
最后答案就把每一行的f(0,m-1)加起来即可。
这里可以算得答案不超过30位10进制数,所以高精度的digit数组开到30足够了。
乘法也不用写,用两次加法即可。
4.core以下是我在比赛时的做法:可以证明的是,如果图中存在多条路径,则在任何一条直径上都存在一条core(反证法,用到直径的距离最大性)。
因此只需讨论一条直径上的core的情况即可。
接着,如果一条路径包括了一条子路径的所有边,那么子路径的解不会比父路径更优。
这一点后面将用到。
下面是算法:先寻找一条直径:任取一点u',遍历得到到它的最远点u,再对u寻找一个到它的最远点v,则路径u-v一定是一条直径(想想为什么),在刚才遍历u-v的时候记录遍历到每一个点的时候的前继,那么从v出发一直寻找前继到u,就能记录下这一条直径。
NOIP历年复赛提高组试题

全国信息学奥林匹克分区联赛(NOIP)复赛提高组试题第一届全国信息学奥林匹克分区联赛(NOIP1995)复赛试题(提高组竞赛用时:3.5小时)1、编码问题设有一个数组A:ARRAY[0..N-1]OFINTEGER;数组中存放的元素为0~N-1之间的整数,且A[i]≠A[j](当i≠j时)。
例如:N=6时,有:A=(4,3,0,5,1,2)此时,数组A的编码定义如下:A[0]的编码为0;A[i]的编码为:在A[0],A[1],…,A[i-1]中比A[i]的值小的个数(i=1,2,…,N-1)∴上面数组A的编码为:B=(0,0,0,3,1,2)程序要求解决以下问题:①给出数组A后,求出其编码。
②给出数组A的编码后,求出A中的原数据。
2、灯的排列问题设在一排上有N个格子(N≤20),若在格子中放置有不同颜色的灯,每种灯的个数记为N1,N2,……N k(k表示不同颜色灯的个数)。
放灯时要遵守下列规则:①同一种颜色的灯不能分开;②不同颜色的灯之间至少要有一个空位置。
例如:N=8(格子数);R=2(红灯数);B=3(蓝灯数),放置的方法有:R-B顺序B-R顺序放置的方法总数为12种。
数据输入的方式为:NP1(颜色,为一个字母)N1(灯的数量)P2 N2……Q(结束标记,Q本身不是灯的颜色)程序要求:求出一种顺序的放置(排列)方案及放置(排列)方案总数。
3、积木块上的数字设有一个四层的积木块,1~4层积木块的数量依次为:5,6,7,8,如下图所示放置:其中,给出第三层与第四层所标示的数字,并已知第三层的数据是由第四层的数据计算出来的。
计算的方法是:第三层的某个数据A是由第四层相邻的两个数据B,C经过某种计算后产生的:计算所用到的计算符为:+,-,⨯,且无优先级之分(自左向右计算),运算符最多为2个。
如:3+4⨯5=35 5⨯4+3=23可以看出,上图中的第三层的数据是由第四层的数据用以下计算公式计算出来的:A=B⨯C+B也就是:8=2⨯3+2,15=3⨯4+3,……14=2⨯6+2程序要求:给出第四层与第三层的数据后,将第一、二层的每块积木标上相应的数据,并输出整个完整的积木图及计算公式。
NOIP2007提高组复赛试题解题报告

NOIP2007提高组复赛试题解题报告我小菜也来发题解了,不过现在都已经过去那么长时间再来发题解未免太迟,但是写题解可以让自己对题目始终抱有需要深刻理解的态度,所以我还是坚持写题解。
NOIP2007的题目并不十分难,我们浙江省有1个满分,不知道2008年题目会怎么样。
首先我这里题目就省略了,因为这年头题目网上满天飞,所以直接开始写题解。
一、统计数字。
这题其实是道送分题,而且还十分弱智,不知道是考排序还是数据结构,这题解法有很多,可以快排,BST,HASH。
这些方法都很容易AC,而且据说写裸BST(不严格平衡的BST)都能满分,可见这题简单的程度。
记得当时我是用先读入数据,然后一趟快排,最后去重输出,简单吧,这题我就不费话,直接帖上程序:[参考程序]program count(input,output);constmaxn=200000;maxn1=10000;typearr=array[1..maxn] of longint;nums=recordnumb,time:longint;end;varnum:arr;ans:array[1..maxn1] of nums;i,j,k,n:longint;f1,f2:text;procedure ranqsort(var num:arr; low,high:longint);vari,j,k,tmp,x:longint;beginwhile low<high do begini:=low-1;k:=random(high-low+1)+low;tmp:=num[k]; num[k]:=num[high]; num[high]:=tmp;x:=num[high];for j:=low to high-1 do if num[j]<=x thenbegininc(i);tmp:=num[i]; num[i]:=num[j]; num[j]:=tmp;end;tmp:=num[i+1]; num[i+1]:=num[high]; num[high]:=tmp; ranqsort(num,low,i);low:=i+2;end;end;beginfillchar(num,sizeof(num),0);fillchar(ans,sizeof(ans),0);assign(f1,'count.in'); reset(f1);assign(f2,'count.out'); rewrite(f2);readln(f1,n);for i:=1 to n do readln(f1,num[i]);close(f1);randomize;ranqsort(num,1,n);j:=1; ans[1].numb:=num[1]; ans[1].time:=1;for i:=2 to n do if num[i]=ans[j].numb then inc(ans[j].time) else begin inc(j); ans[j].numb:=num[i]; ans[j].time:=1; end; for i:=1 to j do writeln(f2,ans[i].numb,' ',ans[i].time);close(f2);end.二、字符串的展开这道题是全卷思路最简单的一道题,简单模拟即可,但是这一点恰恰是这道题目的难点,因为字符串处理的题目对编程熟练程度要求比较高,而且这题还要考虑好多种因素,比如说有可能字符串开头出现了“-”号,结果不少人当时就因此有一个点WA的WA,崩溃的崩溃。
NOIP历年复赛提高组试题.

第十届全国信息学奥林匹克分区联赛(NOIP2004)复赛试题(提高组竞赛用时:3小时)1、津津的储蓄计划(Save.pas/dpr/c/cpp)【问题描述】津津的零花钱一直都是自己管理。
每个月的月初妈妈给津津300元钱,津津会预算这个月的花销,并且总能做到实际花销和预算的相同。
为了让津津学习如何储蓄,妈妈提出,津津可以随时把整百的钱存在她那里,到了年末她会加上20%还给津津。
因此津津制定了一个储蓄计划:每个月的月初,在得到妈妈给的零花钱后,如果她预计到这个月的月末手中还会有多于100元或恰好100元,她就会把整百的钱存在妈妈那里,剩余的钱留在自己手中。
例如11月初津津手中还有83元,妈妈给了津津300元。
津津预计11月的花销是180元,那么她就会在妈妈那里存200元,自己留下183元。
到了11月月末,津津手中会剩下3元钱。
津津发现这个储蓄计划的主要风险是,存在妈妈那里的钱在年末之前不能取出。
有可能在某个月的月初,津津手中的钱加上这个月妈妈给的钱,不够这个月的原定预算。
如果出现这种情况,津津将不得不在这个月省吃俭用,压缩预算。
现在请你根据2004年1月到12月每个月津津的预算,判断会不会出现这种情况。
如果不会,计算到2004年年末,妈妈将津津平常存的钱加上20%还给津津之后,津津手中会有多少钱。
【输入文件】输入文件save.in包括12行数据,每行包含一个小于350的非负整数,分别表示1月到12月津津的预算。
【输出文件】输出文件save.out包括一行,这一行只包含一个整数。
如果储蓄计划实施过程中出现某个月钱不够用的情况,输出-X,X表示出现这种情况的第一个月;否则输出到2004年年末津津手中会有多少钱。
【样例输入1】29023028020030017034050908020060【样例输出1】-7【样例输入2】29023028020030017033050908020060【样例输出2】1580【问题描述】在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。
NOIP2007 初赛试题及答案提高组C

NOIP2007 初赛试题(提高组C)2008-08-03 15:09分类:默认分类字号:大中小信息学奥赛试题NOIP2007 初赛试题(提高组C)© 中国计算机学会20071第十三届全国青少年信息学奥林匹克联赛初赛试题(提高组C 语言二小时完成)●●全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●一、单项选择题(共10 题,每题1.5 分,共计15 分。
每题有且仅有一个正确答案)。
1. 在以下各项中,()不是CPU 的组成部分。
A. 控制器B. 运算器C. 寄存器D. 主板E. 算术逻辑单元(ALU)2.在关系数据库中,存放在数据库中的数据的逻辑结构以()为主。
A. 二叉树B. 多叉树C.哈希表D. B+树E.二维表3.在下列各项中,只有()不是计算机存储容量的常用单位。
A. ByteB. KBC.MBD.UBE.TB4.ASCII 码的含义是()。
A. 二—十进制转换码B. 美国信息交换标准代码C. 数字的二进制编码D. 计算机可处理字符的唯一编码E. 常用字符的二进制编码5.在C 语言中,表达式23|2^5 的值是()A. 23B. 1C.18D.32E.246.在C 语言中,判断a 等于0 或b 等于0 或c 等于0 的正确的条件表达式是()A. !((a!=0)||(b!=0)||(c!=0))B. !((a!=0)&&(b!=0)&&(c!=0))C. !(a==0&&b==0)||(c!=0)D. (a=0)&&(b=0)&&(c=0)E. !((a=0)||(b=0)||(c=0))7.地面上有标号为A、B、C 的3 根细柱,在A 柱上放有10 个直径相同中间有孔的圆盘,从上到下依次编号为1,2,3,……,将A 柱上的部分盘子经过B 柱移入C 柱,也可以在B 柱上暂存。
如果B 柱上的操作记录为:“进,进,出,进,进,出,出,进,进,出,进,出,出”。
NOIP2007提高组初赛试题与答案

y+=20+(q[2]*100-q[3])/(p[p[4]%3]*5); printf("%d,%d\n", x,y); return 0;
© 中国计算机学会 2007
4
NOIP2007 初赛试题(提高组 C)
} /*注:本例中,给定的输入数据可以避免分母为 0 或数组元素下标越界。 */ 输入:6 6 5 5 3 输出:_______________
NOIP2007 初赛试题(提高组 C)
第十三届全国青少年信息学奥林匹克联赛初赛试题
( 提高组 C 语言 二小时完成 )
●● 全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效 ●●
一、 单项选择题 (共 10 题,每题 1.5 分,共计 15 分。每题有且仅有一个正确答案)。
1. 在以下各项中,( )不是 CPU 的组成部分。
B.有些编译系统可以检测出死循环 C. 死循环属于语法错误,既然编译系统能检查各种语法错误,当然也应该能检查出死循环 D. 死循环与多进程中出现的“死锁”差不多,而死锁是可以检测的,因而,死循环也是可以检测 的 E. 对于死循环,只能等到发生时做现场处理,没有什么更积极的手段
二、 不定项选择题 (共 10 题,每题 1.5 分,共计 15 分。每题正确答案的个数大于或等于 1。多选 或少选均不得分)。
但这一点还没有得到理论上的证实,也没有被否定 D. 一个问题如果是NP类的,与C有相同的结论
20. 近20年来,许多计算机专家都大力推崇递归算法,认为它是解决较复杂问题的强有力的工具。在下 列关于递归算法的说法中,正确的是( )。
© 中国计算机学会 2007
NOIP完善程序真题(07-10)

NOIP2007提高组第一题格雷码 (Gray Code)Gray Code是一种二进制编码,编码顺序与相应的十进制数的大小不一致。
其特点是,对于两个相邻的十进制数,对应的两个格雷码只有一个二进制位不同。
另外,最大数与最小数间也仅有一个二进制位不同,以4位二进制数为例,编码如下:十进制数格雷码十进制数格雷码0 0000 8 11001 0001 9 11012 0011 10 11113 0010 11 11104 0110 12 10105 0111 13 10116 0101 14 10017 0100 15 1000如果把每个二进制的位看做一个开关,则将一个数变为相邻的另一个数,只须改动一个开关。
因此,格雷码广泛用于信号处理、数-模转换等领域。
下面程序的任务是:由键盘输入二进制的位数n(n<16),再输入一个十进制数m(0≤m<2n),然后输出对应于m的格雷码(共n位,用数组gr[ ]存放)program s501;varbound,m,n,i,j,b,p:integer;gr:array[0..14]of integer;beginbound:=1; writeln('input n,m'); readln(n,m);for i:=1 to n do bound:=[ ① ];if (m<0)or(m>=bound)then beginwriteln('Data error!');[ ② ];end;b:=1;for i:=1 to n dobeginp:=0; b:=b*2;for[ ③ ] to m doif ([ ④ ]) then p:=1-p;gr:=p;end;for i:=n[ ⑤ ] do write(gr); writeln;end.NOIP2007提高组第二题连续邮资问题某国发行了n种不同面值的邮票,并规定每封信上最多允许贴m张邮票。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【输出】
输出文件 core.out 只有一个非负整数,为指定意义下的最小偏心距。
【输入输出样例 1】
core.in 5 2 1 2 5 2 3 2 2 4 4 2 5 3 core.out 5
【输入输出样例 2】
core.in 8 6 1 3 2 2 3 2 3 4 6 4 5 3 4 6 4 4 7 2 7 8 3 core.out 5
对于 Pascal 语言 对于 C 语言 对于 C++语言 fpc count.pas gcc –o count count.c g++ -o count count.cpp fpc expand.pas gcc –o expand expand.c g++-o expand expand.cpp fpc game.pas gcc –o game game.c g++ -o game game.cpp fpc core.pas gcc –o core core.c g++ -o core core.cpp
ECC( F ) max{d (v, F ), v V } 。
任务:对于给定的树网 T=(V, E,W)和非负整数 s,求一个路径 F,它是某直径上的一段路径 (该路径两端均为树网中的结点) ,其长度不超过 s(可以等于 s) ,使偏心距 ECC(F)最小。我们 称这个路径为树网 T=(V,E,W)的核(Core) 。必要时,F 可以退化为某个结点。一般来说,在上 述定义下,核不一定只有一个,但最小偏心距是唯一的。 下面的图给出了树网的一个实例。图中,A-B 与 A-C 是两条直径,长度均为 20。点 W 是树网 的中心,EF 边的长度为 5。如果指定 s=11,则树网的核为路径 DEFG(也可以取为路径 DEF) ,偏 心距为 8。如果指定 s=0(或 s=1、s=2) ,则树网的核为结点 F,偏心距为 12。
【输入输出样例 2】
expand.in 2 3 2 a-d-d expand.out aCCCBBBd-d
【输入输出样例 3】
expand.in 3 4 2 di-jkstra2-6 expand.out dijkstra2************6
【限制】
40%的数据满足:字符串长度不超过 5 100%的数据满足:1<=p1<=3, 1<=p2<=8, 1<=p3<=2。字符串长度不超过 100
第2页 共6页
全国信息学奥林匹克联赛(NOIP2007)复赛
提高组
(1)遇到下面的情况需要做字符串的展开:在输入的字符串中,出现了减号“-” ,减号两侧 同为小写字母或同为数字,且按照 ASCII 码的顺序,减号右边的字符严格大于左边的字符。 (2)参数 p1:展开方式。p1=1 时,对于字母子串,填充小写字母;p1=2 时,对于字母子串, 填充大写字母。这两种情况下数字子串的填充方式相同。p1=3 时,不论是字母子串还是数字子串, 都用与要填充的字母个数相同的星号“*”来填充。 (3)参数 p2:填充字符的重复个数。p2=k 表示同一个字符要连续填充 k 个。例如,当 p2=3 时,子串“d-h”应扩展为“deeefffgggh” 。减号两侧的字符不变。 (4)参数 p3:是否改为逆序:p3=1 表示维持原有顺序,p3=2 表示采用逆序输出,注意这时 仍然不包括减号两端的字符。例如当 p1=1、p2=2、p3=2 时,子串“d-h”应扩展为“dggffeeh” 。 (5)如果减号右边的字符恰好是左边字符的后继,只删除中间的减号,例如: “d-e”应输出 为“de” , “3-4”应输出为“34” 。如果减号右边的字符按照 ASCII 码的顺序小于或等于左边字符, 输出时,要保留中间的减号,例如: “d-d”应输出为“d-d” , “3-1”应输出为“3-1” 。
【限制】
40%的数据满足:5<=n<=15 70%的数据满足:5<=n<=80 100%的数据满足:5<=n<=300, 0<=s<=1000。边长度为不超过 1000 的正整数
第6页 共6页
【输入】
输入文件 count.in 包含 n+1 行: 第 1 行是整数 n,表示自然数的个数。 第 2~n+1 行每行一个自然数。
【输出】
输出文件 count.out 包含 m 行(m 为 n 个自然数中不相同数的个数) ,按照自然数从小到大 的顺序输出。每行输出两个整数,分别是自然数和该数出现的次数,其间用一个空格隔开。
四、运行内存限制
运行内存上限 128M 128M 128M 128M
注意事项:
1. 文件名(程序名和输入输出文件名)必须使用大写。 2. C/C++中函数 main()的返回值类型必须是 int,程序正常结束时的返回值必须是 0。 3. 全国统一评测时采用的机器配置为:CPU 1.9GHz,内存 512M,上述时限以此配置为准。各省 在自测时可根据具体配置调整时限。
【输入输出样例 1 解释】
第 1 次:第 1 行取行首元素,第 2 行取行尾元素,本次得分为 1*21+2*21= 第 3 次:得分为 3*23+4*23=56。总得分为 6+20+56=82
【输入输出样例 2】
game.in 1 4 4 5 0 5 game.out 122
【输入输出样例 3】
game.in 2 10 96 56 54 46 86 12 23 88 80 43 16 95 18 29 30 53 88 83 64 67 game.out 316994
第4页 共6页
全国信息学奥林匹克联赛(NOIP2007)复赛
提高组
【限制】
60%的数据满足:1<=n, m<=30, 答案不超过 1016 100%的数据满足:1<=n, m<=80, 0<=aij<=1000
全国信息学奥林匹克联赛(NOIP2007)复赛
提高组
全国信息学奥林匹克联赛(NOIP2007)复赛
提高组
(请选手务必仔细阅读本页内容)
一、题目概况
中文题目名称 英文题目名称 可执行文件名 输入文件名 输出文件名 每个测试点时限 测试点数目 每个测试点分值 比较方式 题目类型 统计数字 count count count,in count.out 1秒 10 10 全文比较 传统 字符串的展开 expand expand expand.in expand.out 1秒 10 10 全文比较 传统 矩阵取数游戏 game game game.in game.out 1秒 10 10 全文比较 传统 树网的核 core core core.in core.out 1秒 10 10 全文比较 传统
4. 树网的核
(core.pas/c/cpp) 【问题描述】
设 T=(V, E, W) 是一个无圈且连通的无向图(也称为无根树) ,每条边带有正整数的权,我 们称 T 为树网(treenetwork) ,其中 V, E 分别表示结点与边的集合,W 表示各边长度的集合, 并设 T 有 n 个结点。 路径:树网中任何两结点 a,b 都存在唯一的一条简单路径,用 d(a,b)表示以 a,b 为端点的 路径的长度,它是该路径上各边长度之和。我们称 d(a,b)为 a,b 两结点间的距离。 一点 v 到一条路径 P 的距离为该点与 P 上的最近的结点的距离: d(v,P)=min{d(v,u),u 为路径 P 上的结点}。 树网的直径:树网中最长的路径称为树网的直径。对于给定的树网 T,直径不一定是唯一的, 但可以证明:各直径的中点(不一定恰好是某个结点,可能在某条边的内部)是唯一的,我们称该 点为树网的中心。 偏心距 ECC(F):树网 T 中距路径 F 最远的结点到路径 F 的距离,即
第5页 共6页
全国信息学奥林匹克联赛(NOIP2007)复赛
提高组
【输入】
输入文件 core.in 包含 n 行: 第 1 行,两个正整数 n 和 s,中间用一个空格隔开。其中 n 为树网结点的个数,s 为树网的核 的长度的上界。设结点编号依次为 1, 2, ..., n。 从第 2 行到第 n 行,每行给出 3 个用空格隔开的正整数,依次表示每一条边的两个端点编号和 长度。例如,“2 4 7”表示连接结点 2 与 4 的边的长度为 7。 所给的数据都是正确的,不必检验。
第3页 共6页
全国信息学奥林匹克联赛(NOIP2007)复赛
提高组
3. 矩阵取数游戏
(game.pas/c/cpp) 【问题描述】
帅帅经常跟同学玩一个矩阵取数游戏:对于一个给定的 n*m 的矩阵,矩阵中的每个元素 aij 均 为非负整数。游戏规则如下: 1. 每次取数时须从每行各取走一个元素,共 n 个。m 次后取完矩阵所有元素; 2. 每次取走的各个元素只能是该元素所在行的行首或行尾; 3. 每次取数都有一个得分值,为每行取数的得分之和,每行取数的得分 = 被取走的元素值*2i, 其中 i 表示第 i 次取数(从 1 开始编号) ; 4. 游戏结束总得分为 m 次取数得分之和。 帅帅想请你帮忙写一个程序,对于任意矩阵,可以求出取数后的最大得分。
【输入输出样例】
count.in 8 2 4 2 4 5 100 2 100 count.out 2 3 4 2 5 1 100 2
【限制】
40%的数据满足:1<=n<=1000 80%的数据满足:1<=n<=50000 100%的数据满足:1<=n<=200000,每个数均不超过 1 500 000 000(1.5*109)
第1页 共6页
全国信息学奥林匹克联赛(NOIP2007)复赛
提高组
1.统计数字
(count.pas/c/cpp) 【问题描述】
