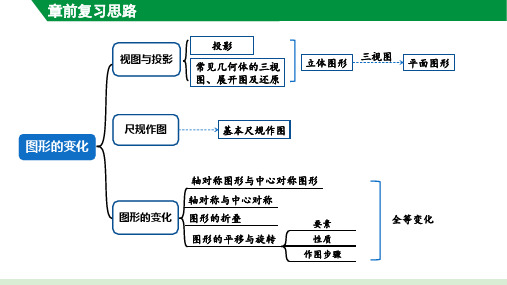
中考数学总复习 第七章 空间与图形 7.5 尺规作图 命题与证明
2024年中考数学总复习考点梳理第七章第一节尺规作图
第一节 尺规作图
返回目录
3. 如图,在等腰△ABC中,AB=AC,BC=8. (1)请用尺规作图法,作∠BAC的平分线,交BC边于点N;(不写 作法,保留作图痕迹) 解:(1)如解图,AN即为所求(作法不唯一);
第3题图
第3题解图
第一节 尺规作图
返回目录
(2)若AN=3,求△ABC的周长.
(2)∵AB=AC,AN是∠BAC的平分线, ∴N是BC的中点,AN⊥BC. ∵BC=8,∴BN=4, ∵AN=3,在Rt△ABN中,AB2=AN2+BN2, ∴AB= AN 2 BN 2 = 32 42 =5, ∴AC=5, ∴△ABC的周长为5+5+8=18.
第1题图 第1题解图
返回目录
第一节 尺规作图
返回目录
二、作一个角等于已知角
作图步骤
1. 在∠α上以点O为圆心,适当长为半径作弧,交∠α的两边于 点P,Q; 2. 作射线O′A; 3. 以点O′为圆心,OP(或OQ) 长为半径作弧,交O′A于点M;
第一节 尺规作图
返回目录
4. 以点M为圆心,PQ长为半径作弧,交步骤3中的弧于点N; 5. 过点N作射线O′B,∠AO′B即为所求角 原理:三边分别相等的两个三角形全等;全等三角形对应角相 等;两点确定一条直线
过直线外一点 (1)作高;(2)求线 高线的性质,锐角三
2023 19
9 平行四边形
(二)
作直线的垂线 段长
角函数
(1)求三角形周长
解答题
勾股定理,锐角三角
2021 20
6 直角三角形 作垂直平分线 ;(2)求三角函数
(一)
函数
值
解答题
作一个角等于 (1)作等角;(2)求 平行线的判定,平行
人教版数学中考复习课件第七章第一节 尺规作图

尺规作图题常见考查类型 1.直接作图,如作角平分线,线段的垂直平分线,作一个角等于已 知角等,直接利用五种基本的尺规作图来解答. 2.给出作图痕迹或步骤,判断结论正误或进行相关计算,对于此种 类型的题目,平时要对五种基本尺规作图了熟于心,从而判断是哪种基 本作图,再根据作图依据进行结论判断或计算.
5.★(2020·郴州)如图,在矩形 ABCD 中,AD=4,AB=8.分别以点 B,D 为圆心,以大于12BD 的长为半径画弧,两弧相交于点 E 和 F.作直线 EF 分别与 DC,DB,AB 交于点 M,O,N,则 MN= 2 5 .
6.(2020·扬州)如图,在△ABC 中,按以下步骤作图: ①以点 B 为圆心,任意长为半径作弧,分别交 AB,BC 于点 D,E. ②分别以点 D,E 为圆心,大于12DE 的长为半径作弧,两弧交于点 F. ③作射线 BF 交 AC 于点 G. 如果 AB=8,BC=12,△ABG 的面积为 18,则△CBG 的面积为 27 .
∴∠DBA=∠ACD=45°, ∵AC=6,BC=8,∴AB=10, ∴AD=BD=AB·sin 45°=10× 22=5 2.
7.(2020·青海)如图,在 Rt△ABC 中,∠C=90°.
(1)尺规作图:作 Rt△ABC 的外接圆⊙O;作∠ACB 的角平分线交⊙O 于点 D,连接 AD;(不写作法,保留作图痕迹)
解:如图,Rt△ABC 的外接圆⊙O,线段 CD 即为所求.
(2)若 AC=6,BC=8,求 AD 的长. 解:连接 BD, ∵∠C=90°. ∴AB 是⊙O 的直径, ∴∠BDA=90°, ∵CD 平分∠ACB, ∴∠ACD=∠BCD=45°,
命题点:尺规作图及相关的证明与计算(2020 年考查 2 次,2019 年考 查 2 次,2018 年考查 2 次,2017 年考查 1 次)
中考数学一轮复习课件:第7章 第1节 尺规作图

● 1.如图,在△ABC中,根据尺规作图痕迹,下列说法不一定正确的是 ● A.AF=BF
●
C.∠BAF=∠EBC
● BD..A∠ED=BF12+A∠CDFB=90°
()
B
●
2.在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为
等腰三角形.下列作法不正确的是
图2
ABD 的面积是__3_0___.
③如图 3,若 AC=BC,按以下步骤作
图:a.以点 A 为圆心,以任意长为半径作
弧,分别交 AC,AB 于点 M,N;b.分别
以 M,N 为圆心,以大于12MN 长为半径作
图3
弧,两弧在∠BAC 内交于点 O;c.作射线 AO,交 BC 于点 D,若 BD
=2,则 CD 的长为___2___.
()
A
A
B
CDBiblioteka ●3.如图,在△ABC中,∠B=40°,∠C=50°.
● (1)通过观察尺规作图的痕迹,可以发现直线DF是线段AB的______________,射线AE是 ∠DAC的____________.
●
(2)∠DAE的度数为________.
垂直平分线
角平分线
25°
中考考点“链”教材
●
例 典例精讲 已知△ABC.
长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,
则点G的坐标为
(A )
A.( 5-1,2)
B.( 5,2)
C.(3- 5,2)
D.( 5-2,2)
AD 于点 F,交 AC 于点 O.若点 O 是 AC 的中点,则
CD 的长为
A.2 2
2021年广东省深圳市数学中考专题复习 命题、证明和尺规作图课件

对点练习 1 1.下列命题,其中是真命题的为( D ) A.一组对边平行,另一组对边相等的四边形是平行四边形 B.对角线互相垂直的四边形是菱形 C.对角线相等的四边形是矩形 D.一组邻边相等的矩形是正方形
2.用反证法证明“a≥b”,对于第一步的假设,下列正确的
是( C )
A.a≤b
B.a≠b
C.a<b
六年深圳 2015 年 2016 年 2017 年 2018 年 2019 年 2020 年
中考
第8题 第9题
第 10 题 第 9 题
1.(2019·深圳)下面命题正确的是( D ) A.矩形的对角线互相垂直 B.方程 x2=14x 的解为 x=14 C.六边形的内角和为 540° D.一条斜边和一条直角边分别相等的两个直角三角形全等
D.a=b
知识点 2:尺规作图 基本作图
作一条线段等于已知线段
作角的平分线
图示
作线段的垂直平分线 作一个角等于已知角
过直线上一点作已知直线的垂线 过直线外一点作已知直线的垂线
对点练习 2 1.用尺规在一个平行四边形内作菱形 ABCD,下列作法中错 误的是( C )
A.
B.
C.
D.
2.已知:线段 a,∠α.求作:△ABC,使 AB=AC=a,∠B =∠α.
过点 A 作 AH⊥CD 于点 H(图略), 在 Rt△ACH 中,∠ACH=45°, ∴sin∠ACH=AAHC,∴AH=4× 22=2 2, ∴四边形 ACDB 的面积为:4×2 2=8 2.
——基于全国中考的13道过关强化题
基础训练 1.(2020 秋·福田区校级月考)下列命题正确的是( C ) A.一组对边平行,另一组对边相等的四边形是平行四边形 B.对角线相等的矩形是正方形 C.16 的平方根是±4 D.有一组邻边相等的四边形是菱形
2023版山西数学中考总复习第七章圆提分小专题十六-尺规作图的探究与应用

一题多解
解:方法一,作图依据Байду номын сангаас直径所对的圆周 角是直角. 如答图1,连接OP,以OP为直径作圆交 ⊙O于点A,连接PA,直线PA即为所求.
一题多解
方法二,作图依据是证明两个三角形全等(SAS). 如答图2,连接PO交⊙O于B,过点B作PO的垂线, 在PO的垂线上取一点C,使OC = OP,连接OC交 ⊙O于点A,连接PA,直线PA即为所求.
∴四边形ABCD是矩形(依据:
).
又∵AB = BC,∴矩形ABCD是正方形.
解:(2)45 45 ∠BAC 90 90 有三个角是直角的四边形为矩形
3. 如图,已知P是⊙O外一点.用两种不同的方法过点P作⊙O的一条切 线. 要求:(1)用无刻度直尺和圆规作图 .(2)保留作图的痕迹,写出 必要的文字说明.
提分训练 方法触类旁通
1. 如图,已知直线AB及AB外一点P. 求作:直线PQ,使PQ⊥AB于点 Q.甲、乙两名同学的作法如下图所示:
请判断以上两种作法是否正确,请说明理由.
解:甲、乙两名同学的作法都正确. 理由如下: 甲同学作图的依据是直径所对的圆 周角等于90°. ∵C,Q,P在⊙O上,CP是⊙O的 直径,∴∠PQC = 90°, 即PQ⊥AB.
解:(1)如答图 1 所示,连接 BE 交AC于点F, 线段BF即为所求.
3. 已知△ABC 和△CDE 都为正三角形,点 B,C,D 在同一直线上,请 仅用无刻度的直尺完成下列作图,简述作法,保留作图痕迹. (2)如图2,当BC ≠ CD时,作△ABC的中线BG.
解:(2)如答图 2 所示,延长 BA 交 DE 的延长线于 F,连接 AD,CF 交于 点 O,连接 OB 交 AC 于点 G,线段BG 即为所求.
浙教版初中数学中考复习:尺规作图及命题、证明 (共38张PPT)【优秀课件】

解析:
20
考点四:尺规作图的综合应用
21
解析:
22
考点四:尺规作图的综合应用
• 【例】(2018·湖州)尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作 图考他的大臣:
• ①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点; • ②分别以点A、D为圆心,AC长为半径画弧,G是两弧的一个交点; • ③连结OG. • 问:OG的长是多少? • 大臣给出的正确答案应是( )
尺规作图及命题、证明
命题趋势:
• 主要是考查利用尺规作图解决实际问题的能力,中考试题题型主要以设计 、探究形式的解答题为主.
2
考点一:基本尺规作图 • 尺规作图:在几何作图里,我们把用没有刻度的直尺和圆规作图,简称为尺规
作图.
• 基本作图:
• (1)作一条线段等于已知线段; (2)作一个角等于已知角; (3)作一个角的平分线;
C. ③
D. ④
5
解析:
• 【解析】①是作一个角等于已知角的正确方法;
•
②是作一个角的平分线的正确作法;
•
③是作一条线段的垂直平分线,但缺少另一个交点,作法错误;
•
④是过直线外一点P作已知直线的垂线的正确作法.
• 【思维提升】尺规作图的关键:①先分析题目,读懂题意,判断题目要求作什么;
•
②读懂题意后,再运用几种基本作图方法解决问题;
23
解析:
24
考点四:尺规作图的综合应用
25
解析:
26
解析:
27
考点五:命题、定理、证明 • 定义与命题:
• (1)能清楚地规定某一名词或术语的意义的句子叫做该名称或术语的定义. • (2)判断某一件事情的句子叫做命题.正确的命题称为真命题;不正确的命题称为
2025年中考数学考点分类专题归纳之尺规作图

2025年中考数学考点分类专题归纳尺规作图1、定义(1)尺规作图是指用没有刻度的直尺和圆规作图.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.(2)基本要求它使用的直尺和圆规带有想像性质,跟现实中的并非完全相同.直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上画刻度.圆规可以开至无限宽,但上面亦不能有刻度.它只可以拉开成你之前构造过的长度.2、基本作图有:(1)作一条线段等于已知线段.(2)作一个角等于已知角.(3)作已知线段的垂直平分线.(4)作已知角的角平分线.(5)过一点作已知直线的垂线.3、复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.4、应用与设计作图主要把简单作图放入实际问题中.首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.1.(2024•鄂尔多斯)如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于CD为半径作弧,两弧交于点M,N;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是()A.∠ABC=60°B.S△ABE=2S△ADEC.若AB=4,则BE D.sin∠CBE2.(2024•河南)如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为()A.(1,2)B.(,2)C.(3,2)D.(2,2)3.(2024•郴州)如图,∠AOB=60°,以点O为圆心,以任意长为半径作弧交OA,OB于C,D两点;分别以C,D为圆心,以大于CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上截取线段OM=6,则M点到OB的距离为()A.6 B.2 C.3 D.4.(2024•宜昌)尺规作图:经过已知直线外一点作这条直线的垂线,下列作图中正确的是()A.B.C.D.5.(2024•襄阳)如图,在△ABC中,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为()A.16cm B.19cm C.22cm D.25cm6.(2024•潍坊)如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:(1)作线段AB,分别以A,B为圆心,以AB长为半径作弧,两弧的交点为C;(2)以C为圆心,仍以AB长为半径作弧交AC的延长线于点D;(3)连接BD,BC.下列说法不正确的是()A.∠CBD=30°B.S△BDC AB2C.点C是△ABD的外心D.sin2A+cos2D=17.(2024•台州)如图,在▱ABCD中,AB=2,BC=3.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是()A.B.1 C.D.8.(2024•巴中)如图,在Rt△ABC中,∠C=90°,按下列步骤作图:①以点B为圆心,适当长为半径画弧,与AB,BC分别交于点D,E;②分别以D,E为圆心,大于DE的长为半径画弧,两弧交于点P;③作射线BP交AC于点F;④过点F作FG⊥AB于点G.下列结论正确的是()A.CF=FG B.AF=AG C.AF=CF D.AG=FG9.(2024•昆明)如图,点A在双曲线y═(x>0)上,过点A作AB⊥x轴,垂足为点B,分别以点O和点A为圆心,大于OA的长为半径作弧,两弧相交于D,E两点,作直线DE交x轴于点C,交y轴于点F (0,2),连接AC.若AC=1,则k的值为()A.2 B.C.D.10.(2024•安顺)已知△ABC(AC<BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是()A.B.C.D.11.(2024•湖州)尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连结OG.问:OG的长是多少?大臣给出的正确答案应是()A.r B.(1)r C.(1)r D.r12.(2024•益阳)如图,在△ABC中,AB=5,AC=4,BC=3.按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AC于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,两弧相交于点E;③作射线AE;④以同样的方法作射线BF.AE交BF于点O,连接OC,则OC=_______.13.(2024•抚顺)如图,▱ABCD中,AB=7,BC=3,连接AC,分别以点A和点C为圆心,大于AC的长为半径作弧,两弧相交于点M,N,作直线MN,交CD于点E,连接AE,则△AED的周长是____.14.(2024•葫芦岛)如图,OP平分∠MON,A是边OM上一点,以点A为圆心、大于点A到ON的距离为半径作弧,交ON于点B、C,再分别以点B、C为圆心,大于BC的长为半径作弧,两弧交于点D、作直线AD分别交OP、ON于点E、F.若∠MON=60°,EF=1,则OA=_______.15.(2024•山西)如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_______.16.(2024•东营)如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=3,AC=10,则△ACD的面积是____.17.(2024•淮安)如图,在Rt△ABC中,∠C=90°,AC=3,BC=5,分别以点A、B为圆心,大于AB的长为半径画弧,两弧交点分别为点P、Q,过P、Q两点作直线交BC于点D,则CD的长是__.18.(2024•南京)如图,在△ABC中,用直尺和圆规作AB、AC的垂直平分线,分别交AB、AC于点D、E,连接DE.若BC=10cm,则DE=___cm.19.(2024•赤峰)如图,D是△ABC中BC边上一点,∠C=∠DAC.(1)尺规作图:作∠ADB的平分线,交AB于点E(保留作图痕迹,不写作法);(2)在(1)的条件下,求证:DE∥AC.20.(2024•攀枝花)已知△ABC中,∠A=90°.(1)请在图1中作出BC边上的中线(保留作图痕迹,不写作法);(2)如图2,设BC边上的中线为AD,求证:BC=2AD.21.(2024•牡丹江)在四边形ABCD中,∠B=∠C=90°,AB=3,BC=4,CD=1.以AD为腰作等腰△ADE,使∠ADE=90°,过点E作EF⊥DC交直线CD于点F.请画出图形,并直接写出AF的长.22.(2024•贵港)尺规作图(只保留作图痕迹,不要求写出作法).如图,已知∠α和线段a,求作△ABC,使∠A=∠α,∠C=90°,AB=a.23.(2024•北京)下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.已知:直线l及直线l外一点P.求作:直线PQ,使得PQ∥l.作法:如图,①在直线l上取一点A,作射线PA,以点A为圆心,AP长为半径画弧,交PA的延长线于点B;②在直线l上取一点C(不与点A重合),作射线BC,以点C为圆心,CB长为半径画弧,交BC的延长线于点Q;③作直线PQ.所以直线PQ就是所求作的直线.根据小东设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明.证明:∵AB=____,CB=____,∴PQ∥l(__________)(填推理的依据).24.(2024•孝感)如图,△ABC中,AB=AC,小聪同学利用直尺和圆规完成了如下操作:①作∠BAC的平分线AM交BC于点D;②作边AB的垂直平分线EF,EF与AM相交于点P;③连接PB,PC.请你观察图形解答下列问题:(1)线段PA,PB,PC之间的数量关系是__________;(2)若∠ABC=70°,求∠BPC的度数.25.(2024•陇南)如图,在△ABC中,∠ABC=90°.(1)作∠ACB的平分线交AB边于点O,再以点O为圆心,OB的长为半径作⊙O;(要求:不写做法,保留作图痕迹)(2)判断(1)中AC与⊙O的位置关系,直接写出结果.26.(2024•青岛)已知:如图,∠ABC,射线BC上一点D.求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P到∠ABC两边的距离相等.27.(2024•广安)下面有4张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:(1)画一个直角边长为4,面积为6的直角三角形.(2)画一个底边长为4,面积为8的等腰三角形.(3)画一个面积为5的等腰直角三角形.(4)画一个一边长为2,面积为6的等腰三角形.28.(2024•河南)如图,反比例函数y(x>0)的图象过格点(网格线的交点)P.(1)求反比例函数的解析式;(2)在图中用直尺和2B铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:①四个顶点均在格点上,且其中两个顶点分别是点O,点P;②矩形的面积等于k的值.29.(2024•湖北)图①、图②都是由边长为1的小菱形构成的网格,每个小菱形的顶点称为格点.点O,M,N,A,B均在格点上,请仅用无刻度直尺在网格中完成下列画图.(1)在图①中,画出∠MON的平分线OP;(2)在图②中,画一个Rt△ABC,使点C在格点上.30.(2024•宁波)在5×3的方格纸中,△ABC的三个顶点都在格点上.(1)在图1中画出线段BD,使BD∥AC,其中D是格点;(2)在图2中画出线段BE,使BE⊥AC,其中E是格点.31.(2024•济宁)在一次数学活动课中,某数学小组探究求环形花坛(如图所示)面积的方法,现有以下工具;①卷尺;②直棒EF;③T型尺(CD所在的直线垂直平分线段AB).(1)在图1中,请你画出用T形尺找大圆圆心的示意图(保留画图痕迹,不写画法);(2)如图2,小华说:“我只用一根直棒和一个卷尺就可以求出环形花坛的面积,具体做法如下:将直棒放置到与小圆相切,用卷尺量出此时直棒与大圆两交点M,N之间的距离,就可求出环形花坛的面积.”如果测得MN=10m,请你求出这个环形花坛的面积.32.(2024•金华)如图,在6×6的网格中,每个小正方形的边长为1,点A在格点(小正方形的顶点)上.试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形.。
课标中考数学总复习第七单元图形与变换投影与视图含尺规作图课件

影
物体视图称为 左视图
主视图的长与俯视图的长对正
主视图的高与左视图的高平齐 三视图 左视图的宽与俯视图的宽相等 的画法 以上规律简述为 :长对正 ,高平齐 ,宽相等 ; 与规律 注意:画三视图时看得见的轮廓线画成 实线 ,看不见的轮
廓线画成虚线
考点必备梳理
考点一
考点二
考点三
考点四
考点五
考点三常见几何体的三视图 (高频)
考点必备梳理
考题初做诊断
考法必研突破
考法1
考法2
考法3
考法4
考法5
解析:由这个几何体的三视图可知 ,这个几何体是底面半径为 2、
高为4的圆柱轴剖面的一半 ,其表面积为上、下两个相等的半径为 2
的半圆、底面半径为 2、高为4的圆柱侧面的一半以及边长为 4的
正方形组成 ,因此,其面积分别为 4π、8π和16,则该几何体的表面
考点必备梳理
考题初做诊断
考法必研突破
考法1
考法2
考法3
考法4
考法5
对应练8(2017·湖北荆门 )如图是由若干个大小相同的小正方体
所搭成的几何体的三视图 ,则搭成这个几何体的小正方体的个数是
(B )
A.6个 B.7个 C.8个D.9个 解析: 如图,以俯视图为基础 ,将另两个视图中小正方形的个数填 写在俯视图的相应位置 ,即可得小正方体的个数是 7.故选B.
解析:左视图看到中间的横线是实线 ,且以矩形竖直一对边的中 点为端点 .
考法1
考法2
考法3
考法4
考点必备梳理
考法5
考题初做诊断
考法必研突破
考法 3根据三视图还原几何体 例3(2020·山东济宁 )一个几何体的三视图如图所示 ,则该几何体 的表面积是 ( )
【人教版】2017届中考复习:第19讲《尺规作图与命题、证明》ppt课件

2.以下命题是真命题的是 ( A.等腰梯形是轴对称图形
A
)
B.对角线相等的四边形是矩形 C.四边相等的四边形是正方形 D.有两条相互垂直的对称轴的四边形是菱形
3.下列选项中,可以用来证明命题“若 a2> 1, 则 a> 1”是假命题的反例是 ( A. a=- 2 C. a= 1 A )
B. a=- 1 D. a= 2
4.与圆有关的尺规作图 (1) 过不在同一直线上的三点作圆 (即三角形的外 接圆); (2)作三角形的外接圆、内切圆; (3)作圆的内接正方形和正六边形.
5.作图题的一般步骤 (1)已知;(2)求作;(3)分析;(4)作法;(5)证明.其 中步骤 (3)(4)(5)一般不作要求,所作图中要保留作图痕 迹. 6.有关中心对称或轴对称的作图以及设计图案是 中考中常见的类型.
解: (1)如图,点 D 为所作;
(2)∵ DA = DB , ∴∠ DAB = ∠ B = 37° , ∴∠ ADC= 37° + 37° = 74° , ∴∠ CAD= 90° - 74° = 16° .
7. (2016· 盐城 )如图,已知△ ABC 中,∠ ABC= 90° .
(1) 尺规作图:按下列要求完成作图 (保留作图痕 迹,请标明字母 ), ①作线段 AC 的垂直平分线 l,交 AC 于点 O;
为半径作弧, 两弧相交于点 M 和 N, 作直线 MN 交 AB 于点 D,交 BC 于点 E,连接 CD,下列 结论错误的是 ( A. AD= BD C.∠ A=∠ BED ) B. BD= CD D.∠ ECD=∠ EDC
【解析】根据作法与作图痕迹可知 MN 为 AB 的 垂直平分线,∴ AD= BD,∠ BDE= 90° ;∵∠ ACB= 90° ,∴ CD= BD.∵∠ A+∠ B=∠ B+∠ BED= 90° , ∴∠ A = ∠ BED ; 由 已 知 条 件 无 法 证 得 ∠ECD = ∠ EDC.故选 D. 【答案】 D
中考数学第7章 图形的变化第一节 尺规作图

俯视图 可以分清几何体的长和宽,提供底面的形状.
考点3 几何体的展开与折叠
1.常见几何体的展开图 几何体
展开图的特点
图示(选其中一种)
6个大小相同的正方形
2个大小相同的圆和1 个矩形
考点3 几何体的展开与折叠
几何体
展开图的特点
1个圆和1个扇形
图示(选其中一种)
《安徽·中考》数学
安徽中考考点过关
第七章 图形的变化
第二节 投影与视图
目录(安徽·中考)
考点
• 考点1 投影 • 考点2 三视图 • 考点3 几何体的展开与折叠
方法
• 命题角度1 常见几何体的三视图 • 命题角度2 由三视图还原几何体
考点
考点1 投影 一个物体放在阳光下或者灯光前,就会在地面上或者墙面上留下它的影子, 这个影子称为物体的投影.
,BD =⑦ CD .
对应线段相等 (2)如果对应线段或其延长线相交,那么交点
AC =⑨ A'C' , BC =⑩ B'C' .
在对称轴上.
(2)如果两个图形的对应线段或其延长线相
性
交,那么交点在对称轴上.
质
∠B =⑪ ∠C ,
对应角相等 ∠BAD =⑫ ∠CAD ,
∠A =⑭ ∠A' , ∠B =⑮ ∠B' ,
考点2 三视图
4.常见几何体的三视图
几何体
主视图
左视图
俯视图
考点2
三视图
几何体
主视图
左视图
俯视图
考点2 三视图 5.由三视图确定几何体 由三视图想象几何体时,首先分别根据主视图、左视图、俯视图想象几何体 的正面、左侧和底面,然后综合起来考虑整体.
中考数学复习第七章图形与变换第26讲尺规作图

步骤
(1)以点 O 为圆心,任意长为半径作弧,交直线于
作直 过直线上 A,B 两点;
线l 的垂
一点 O 作 直线 l 的
(2)分别以点 A,B 为圆心,以大于12AB 的长为半径
线 垂线 MN 向直线两侧作弧,两弧分别交于点 M,N,作直线
MN,则直线 MN 即为所求垂线
(1)在直线异于点 P 的一侧取点 M;
第一部分 教材同步复习
17
【解答】 (1)如下图;(画法有多种,正确画出一种即可,以下几种画法仅供参
考)
四边形 ABCH 即为所求
四边形 ABDH 即为所求
四边形 ABHJ 即为所求
四边形 ABFH 即为所求
第一部分 教材同步复习
18
(2)如下图.(画法有两种,正确画出其中一种即可)四边形ANDF和四边形ACNF 均为所画的菱形.
∠α 的两边于点 P,Q;
(2)作射线 O′A′;
作一个角∠
(3)以 O′为圆心,OP 长为半径作弧,交 O′A′于
A′O′B′等
于∠α
点 M; (4)以点 M 为圆心,PQ 长为半径作弧交前弧于点 N;
(5)过点 N 作射线 O′B′,∠A′O′B′即为所求
角
图示
第一部分 教材同步复习
9
五种尺规作图
第一部分 教材同步复习
5
(4)如图,以AB为直径的⊙O交△ABC的BC,AC边于D,E两点, 在图中仅以没有刻度的直尺画出三角形的三条高.(简单叙述你的画 法)
解 : 如 图 , 连 接 AD , BE 交 于 点 G , 连 接 CG 并 延 长 交 AB 于 F.AD,BE,CF即为△ABC的高.
第一部分 教材同步复习
最新中考数学总复习第七章尺规作图及图形变换 数学思维 分类讨论思想

于 A,B 两点(xA>xB),动点 P 在 x 轴上移动,过点 P 作 y 轴的平行线, 交直线 y=2x 于点 M,交函数 y=2的图象于点 N,若 PM>PN,点 P
x
的坐标为(a,0),则实数 a 的取值范围是 a>1或a<-1 .
点拨:易得A(1,2),B(-1,-2),当点P位于点A的右侧或点B的左
x
(2)把 y=0 代入 y=-x+3 得 x=3,∴B(3,0).
∵C(4,-1),∴BC= (4-3)2 + 12= 2. 当 BC=BD 时,D(3- 2,0)或 D(3+ 2,0);
返回
数学
当 BC=DC 时,如图,过点 C 作 CH⊥x 轴于点 H, ∵CH⊥BD,∴BH=HD=4-3=1, ∴OD=OH+HD=4+1=5,∴D(5,0). 综上所述,点 D 的坐标为(3+ 2,0)或(3- 2,0)或(5,0).
a= 3
4 b=-
15 4
,
∴抛物线的解析式为 y= 3 x2- 15x+3.
44
返回
数学
(2)如图.
∵A(1,0),B(4,0),C(0,3),
∴OB=4,AB=3,BC=5,
直线 BC:y=-3 x+3,
4
由二次函数,可得对称轴为直线 x= 5 , 2
∴P 5 , 9 ,∴由勾股定理,可得 BP= 15.
返回
数学
点拨:相似的分类讨论重点也是对应关系,但是一般我们都要 先确定两点:①相似的三角形形状是否有特点(如是否是等腰 三角形、是否是直角三角形、是否有135°);②每类讨论分 支中可能会多解,也可能无解.
