2月12日(对数正态分布)-2
《正态分布》教学课件(2024)

2024/1/29
4
正态分布定义及特点
特点
分布的形状由标准差决定,标准 差越小,曲线越陡峭;标准差越 大,曲线越平缓。
定义:正态分布是一种连续型概 率分布,描述了许多自然现象的 概率分布情况。在统计学中,正 态分布又被称为高斯分布。
2024/1/29
曲线呈钟形,对称于均值,且均 值、中位数和众数相等。
正态分布在实际问题中解 决方案
2024/1/29
24
问题背景描述
2024/1/29
实际问题中,很多数据分布情况呈现出一种钟型曲线, 即正态分布。 正态分布在自然界、社会科学、工程技术等领域都有广 泛应用。
掌握正态分布的性质和参数估计方法,对于解决实际问 题具有重要意义。
25Βιβλιοθήκη 解决方案设计思路确定问题背景和数据来源,对数据进行 收集和整理。
02
正态分布是一种连续型概率 分布,具有钟形曲线特征。
03
正态分布的概率密度函数由 均值和标准差决定。
29
关键知识点总结回顾
正态分布具有对称性 、可加性和稳定性等 重要性质。
标准正态分布是均值 为0、标准差为1的正 态分布。
2024/1/29
标准正态分布及其性 质
30
关键知识点总结回顾
标准正态分布的概率密度函数具有标准形式,便于计算和分析。
如果数据符合正态分布,则可以利用正 态分布的性质和参数估计方法,对数据
进行建模和分析。
2024/1/29
利用统计分析方法,对数据进行描述性 统计和推断性统计,判断数据是否符合 正态分布。 根据建模结果,对实际问题进行解释和 预测,提出相应的解决方案。
26
具体实施步骤和结果展示
2 对数正态分布
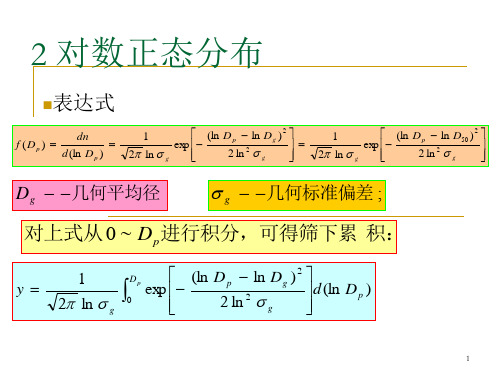
4
对数正态分布的应用
1 计算颗粒的平均粒径
经过一定的数学处理可得如下表中的计算公式
质量基准和个数基准的表达式是不同的.
2计算粉体的比表面积:
sw
s p Dsv
质量基准:D’50=D50exp(3ln2δg); 所以:
δ’g= δg
DsV
D5' 0 exp(3ln 2
Dnl=D50exp(0.5ln2δg)=23.4 作业:计算该例题的各平均粒径、单位质
量颗粒个数和比表面积。
罗辛-拉姆勒分布.ppt
平均粒径计算
11
DnL f (x)x d ln x
1
2 ln g
x
exp
ln
x 2
ln
ln
x
g
2
d
ln
x
对该式积分,得到:
DnL
x
exp(1 ln 2 2
g)
D50
exp(1 2
ln
2
g)
(2)其他平均径的推导类似。
g
)
•
exp(2.5
ln
2
g
)
D5' 0
exp(0.5ln 2 g )
5
3 计算单位质量的颗粒个数:
n 1
pv Dn3v
4对数正态概率纸:横坐标:logDp; 纵坐标:loglog1/f(Dp),如果符合对数正态
分布的粉体在对数正态概率纸上描点,应 该是一条直线。
6
对数正态分布的几个性质及其参数估计

2 参数 和 2的点估计
2. 参 数 和 的矩估 计 1
设总体 服从参数为 和 的对数正态分布 , 。 , , … 为来 自总体 的简单随机样本。 : 记 和 的矩估计量分别为 和 。 根据矩估计法 的原理[ , 2 要求 和 的矩估计量 , ] 。 需要知道 的 数学期望 E X和方差 D 为此先求 的k X, 阶原点矩
可得
=
和 ∑ ( — ), () i 由 1式和( 式, 2 有 )
2
一
: ,
n
∑l n
i
了 ×n l l=0 ,
一
1
奎( 一 e 一) ):2 ( 1 ,
n 1 +
:
骞 = 1 (
.
耋 ) i
0. 5 3, 68
.
解得 / a和 的矩估计量分别是
分布 函数 和概 率密度 , 中 其
9( )= y e 一 ,一 ∞ < y <+ ∞,
算转换为正态分布的计算 。
1 2 主 要结 果 .
对数正态分布有 以下几个常用的性质。
命题 1 设 随机 变 量 X ~ N( , , Y = t A 盯 )则
e
m 口 b为 常数且 o≠ 0 服 从参 数 为 (, )
服 从参数 为∑ a k 和∑ n 的 数正 , u 对 态分布。
命 题 3 设 随机 变量 与 y相互 独立 , 且 服
. s 2 y=
:
从参数为 和 盯 的对数正态分布 , y服从参数为
:
骞- 耋 : ( n ) n。
=
和 盯 的对数正态分布, z=X Y ( , 为不全 ; 则 a b
第 1 卷第 5 1 期
正态分布的概念及表和查表方法

正态分布概念及图表正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),最早由A·棣莫弗在求二项分布的渐近公式中得到。
C.F.高斯在研究测量误差时从另一个角度导出了它。
P·S·拉普拉斯和高斯研究了它的性质。
是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。
其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。
当μ = 0,σ = 1时的正态分布是标准正态分布。
目录1历史发展2定理3定义▪一维正态分布▪标准正态分布4性质5分布曲线▪图形特征▪参数含义6研究过程7曲线应用▪综述▪频数分布▪综合素质研究▪医学参考值历史发展正态分布概念是由德国的数学家和天文学家Moivre于1733年首次提出的,但由于德国数学家Gauss率先将其应用于天文学家研究,故正态分布又叫高斯分布,高斯这项工作对后世的影响极大,他使正态分布同时有了“高斯分布”的名称,后世之所以多将最小二乘法的发明权归之于他,也是出于这一工作。
但现今德国10马克的印有高斯头像的钞票,其上还印有正态分布的密度曲线。
这传达了一种想法:在高斯的一切科学贡献中,其对人类文明影响最大者,就是这一项。
在高斯刚作出这个发现之初,也许人们还只能从其理论的简化上来评价其优越性,其全部影响还不能充分看出来。
这要到20世纪正态小样本理论充分发展起来以后。
拉普拉斯很快得知高斯的工作,并马上将其与他发现的中心极限定理联系起来,为此,他在即将发表的一篇文章(发表于1810年)上加上了一点补充,指出如若误差可看成许多量的叠加,根据他的中心极限定理,误差理应有高斯分布。
对数正态分布(log-normaldistribution)
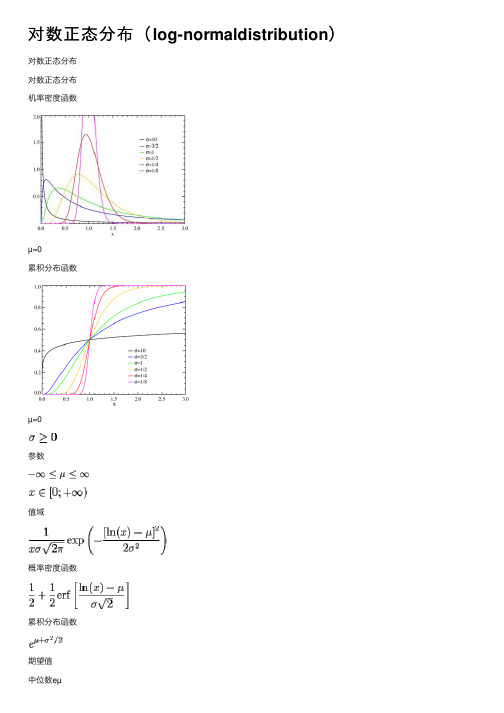
对数正态分布(log-normaldistribution)对数正态分布对数正态分布机率密度函数µ=0累积分布函数µ=0参数值域概率密度函数累积分布函数期望值众数⽅差偏态峰态熵值动差⽣成函数(参见原始动差⽂本)特征函数isasymptotically divergent but sufficientfor numerical purposes在概率论与统计学中,对数正态分布是对数为正态分布的任意随机变量的概率分布。
如果X 是正态分布的随机变量,则exp(X)为对数分布;同样,如果Y是对数正态分布,则 ln(Y) 为正态分布。
如果⼀个变量可以看作是许多很⼩独⽴因⼦的乘积,则这个变量可以看作是对数正态分布。
⼀个典型的例⼦是股票投资的长期收益率,它可以看作是每天收益率的乘积。
对于x > 0,对数正态分布的概率分布函数为其中µ与σ分别是变量对数的平均值与标准差。
它的期望值是⽅差为给定期望值与标准差,也可以⽤这个关系求µ与σ⽬录[隐藏]1 与⼏何平均值和⼏何标准差的关系2 矩3 局部期望4 参数的最⼤似然估计6 进⼀步的阅读资料7 参考⽂献8 参见[编辑]与⼏何平均值和⼏何标准差的关系对数正态分布、⼏何平均数与⼏何标准差是相互关联的。
在这种情况下,⼏何平均值等于exp(µ),⼏何平均差等于 exp(σ)。
如果采样数据来⾃于对数正态分布,则⼏何平均值与⼏何标准差可以⽤于估计置信区间,就像⽤算术平均数与标准差估计正态分布的置信区间⼀样。
其中⼏何平均数µgeo = exp(µ),⼏何标准差σgeo = exp(σ)[编辑]矩原始矩为:或者更为⼀般的矩[编辑]局部期望随机变量X在阈值k上的局部期望定义为其中f(x) 是概率密度。
对于对数正态概率密度,这个定义可以表⽰为其中Φ是标准正态部分的累积分布函数。
对数正态分布的局部期望在保险业及经济领域都有应⽤。
对数正态分布参数

对数正态分布参数
对数正态分布是一种常见的概率分布,其参数包括均值和方差。
均值和方差分别影响着分布的形状和分布范围。
对于对数正态分布,其均值和方差的计算公式如下:
均值:μ = exp(μ+σ^2/2)
方差:σ^2 = (exp(σ^2)-1)*exp(2μ+σ^2)
其中,μ表示对数正态分布的自然对数的均值,σ表示对数正态分布的自然对数的标准差。
对数正态分布的参数估计是一种重要的统计方法,可以利用极大似然估计或贝叶斯方法进行。
极大似然估计是常用的参数估计方法之一,通过最大化样本的似然函数来估计参数值。
贝叶斯方法则是一种更加灵活的方法,通过引入先验知识和后验概率来估计参数值。
在实际应用中,对数正态分布常用于描述随机变量的对数值分布,例如金融、生物学和环境科学等领域。
对数正态分布的参数估计对于这些领域的研究具有重要的意义。
- 1 -。
正态分布和对数正态分布

对数正态分布的峰度为$frac{e^{2sigma^2}1+6sigma^2}{sigma^2}$。
描述性统计量
偏度和峰度用于描述数据的形状,偏度表示数据分布的不对称性, 峰度表示数据分布的尖锐程度。
06
对数正态分布在实践中的 应用
数据建模
自然现象
医学研究
对数正态分布常用于描述自然现象,如地震、 火山喷发、降雨量等,因为这些现象的强度 或频率往往呈现对数增长的特点。
正态分布的应用领域
自然现象
01
许多自然现象的随机变量服从正态分布,如人类的身高、智商、
考试分数等。
金融领域
02
金融市场中的许多随机变量,如股票收益率、汇率波动等,也
呈现出正态分布的特征。
统计学与数据分析
03
在统计学中,正态分布被广泛应用于样本数据的统计分析,如
参数估计和假设检验。
正态分布在统计学中的重要性
正态分布和对数正态 分布
目录
• 正态分布概述 • 正态分布的性质 • 正态分布在实践中的应用 • 对数正态分布概述 • 对数正态分布的性质 • 对数正态分布在实践中的应用
01
正态分布概述
定义与特性
定义
正态分布是一种连续概率分布, 其特征是数据呈现钟形曲线,且 曲线关于均值对称。
特性
正态分布具有集中性、对称性和均 匀分散性的特点,其中标准正态分 布的均值为0,标准差为1。
中心极限定理在金融、生物、医学、工程等多个领域都有广泛应用。例如,在金融领域,我们经常使用正态分布 来描述股票价格的波动;在生物和医学领域,我们使用正态分布来描述人类身高、血压等生理指标的分布。
参数估计
参数估计
参数估计是统计学中的一种重要方法,其目的是通过样本数据来估计总体参数 的值。在正态分布的背景下,我们通常使用样本均值和样本标准差来估计总体 均值和总体标准差。
对数正态分布公式

对数正态分布公式
正态分布函数公式如下:
其中μ为均数,σ为标准差。
μ决定了正态分布的位置,与μ越近,被取到的概率就越大,反之越小。
σ描述的是正态分布的离散程度。
σ越大,数据分布越分散曲线越扁平;σ越小,数据分布越集中曲线越陡峭。
在一个标准正态分布中,约有 68.2% 的点落在±1 个标准差的范围内。
约有 95.5% 的点落在±2 个标准差的范围内。
约有 99.7% 的点落在±3 个标准差的范围内。
正态分布概念是由法国数学家棣莫弗于1733年首次提出的,后由德国数学家高斯率先将其应用于天文学研究,故正态分布又叫高斯分布,高斯这项工作对后世的影响极大,所以有了“高斯分布”的美称。
在我们的自然界,大多数物种的高度和重量都满足正态分布,它们围绕着均值对称分布,而且不会包含特别大或特别小的事件.
例如:我们从来没有遇到过1米长的蚂蚁,也没有看到过1千克重的大象。
世界似乎被代表正态分布的“钟形”包围着,很多事物都是服从正态分布的:人的高度、胖瘦、寿命、雪花的尺寸、测量误差、灯泡的寿命、IQ分数、面包的分量、学生的考试分数,员工上班所需时间等等。
对数正态分布的VAR数学模型及其计算

[4]程先双,边宽江.VaR度量金融风险的几个问题[J】.西北农林科技大学学报:自然科学版,2005,33(3):
142—144.
[5】边宽江,程波,王蕾蕾.收益分布尖峰厚尾问题的统计检验[J】.统计与决策,2009(7):8孓85. [6】郭晓亭,蒲勇健,杨秀苔.VaR模型及其在证券投资管理中的应用[J】.重庆大学学报,2006,29(3):
应用VaR来预测风险时,往往直接根据vaR方法的定义简单地将原始数据代入模型计算,并 未对模型的变量即影响因素,也就是对“在正常的市场条件和置信水平下,在给定的持有期 间内”没有进行合理的分析,因而做不到合理的假没.总体而言,V-aR模型需要考虑资产组合 收益率分布、置信水平、持有期三个方面因素的影响. 1.1资产组合收益率分布
关键词:vaR;置信度;时间序列;对数正态分布
VaR模型足金融数学研究的重点问题之一,标准差,∥系数,持续期等传统的度量方法已 不能适应新的金融风险的度量.因此,金融机构需要一种能全面反映投资组合所承担风险的 技术方法,而vaR数学模型就是为了适应这种需要而产生的风险度量方法.VaR是基于统计 分析基础上的风险度量技术,它的核心在于描述金融时间序列的统计分布或概率密度函数见 文『11.目前,国内外对vaR模型的研究极为广泛.umberto Cherubini和Elisa Luciano(2001) 全面介绍了vaR方法的优点、适用范围、计算过程以及其不足之处.蒲明(2003)也从理论 方面论证了vaR模型在对开放式基金风险估计的可行性,并提出了具体的操作步骤,主要提 出“方差一协方差法”这种简单的计算方法【2】.通常人们假设金融资产价格服从正态分布, 但是,目前国际上有种说法认为金融资产价格服从对数正态分布,传统的vaR计算方法在 计算开放式基金的风险时,结果与实际风险值相差较远,对数正态分布假设下得到的风险值 (VaR)要比正态分布假设下的风险值更接近实际值【3].通过对比分析,发现这些研究尽是针 对现有的vaR模型而展开的,没有对模型进行数学原理的分析,故本文论述了vaR数学模 型的计算方法以及对数正态分布假设下资产组合的风险值.
正态分布2

练习1 下列说法不正确的是( 练习1:下列说法不正正态曲线的对称轴为y A.若 X ~ N (0,9) ,则其正态曲线的对称轴为y轴; B.正态分布 的图象位于x轴上方; B.正态分布 N ( µ , σ ) 的图象位于x轴上方; C.若 C.若 X ~ N ( 3,2 2 ) ,则X的分布密度函数
σ=2
µ
µ
正态曲线的性质
ϕµ,σ ( x) =
1 2πσ
e
−
( x − µ )2 2σ 2
, x ∈ (−∞, +∞)
曲线的位置由µ决定 (5)当σ一定 时,曲线的位置由 决定,曲线随着 的 ) 一定 曲线的位置由 决定,曲线随着µ的 变化而沿x轴平移 轴平移. 变化而沿 轴平移 (6)当µ一定时,曲线的形状由 确定 . 当 一定时 曲线的形状由σ确定 一定时, σ越大,曲线越“矮胖”,表示总体的分布越分散; 越大, 越大 曲线越“矮胖” 表示总体的分布越分散; σ越小,曲线越“瘦高”,表示总体的分布越集中 越小, 越小 曲线越“瘦高” 表示总体的分布越集中.
例题讲解
例1:正态分布密度函数的表达式是
f ( x) = 2 − 2( x +1) 2 e ( −∞ < x < +∞ ). 2π
(1)求 的最大值; (1)求 f ( x ) 的最大值; (2)利用指数函数性质说明其单调区间及曲线 (2)利用指数函数性质说明其单调区间及曲线 的对称轴. 的对称轴.
1 σ 2π
方差相等、 方差相等、均数不等的正态分布图示
µ=0 µ= -1 µ= 1
σ=0.5
固定, 若σ 固定 随 µ值 的变化而 沿x轴平 轴平 移, 故 µ 称为位置 称为位置 参数; 参数;
标准正态分布,对数正态分布,对数正态分布,威布尔正态分布

标准正态分布、对数正态分布和威布尔正态分布的性质和应用场景
在统计学中,分布是描述数据如何分散的重要工具。
有多种分布,其中最常用的三种是标准正态分布、对数正态分布和威布尔正态分布。
这些分布各有其特性和应用场景。
1.标准正态分布
标准正态分布是一种连续概率分布,其形状由均值(μ=0)和标准差(σ=1)决定。
它的曲线呈钟形,对称轴为y=0。
在许多科学和工程领域中,许多随机变量都服从或近似服从标准正态分布,因为它的数学性质非常简单,这使得分析和建模变得相对容易。
2.对数正态分布
对数正态分布是一种连续概率分布,其取值范围在0和无穷大之间。
它的概率密度函数是均值为μ、标准差为σ的自然对数函数。
对数正态分布常用于描述那些自然增长或衰减过程,如人口增长、金融资产价值等。
由于这些过程通常遵循对数增长或对数衰减规律,因此对数正态分布在这些领域中非常有用。
3.威布尔正态分布
威布尔正态分布是一种连续概率分布,常用于描述生物和机械系统的寿命。
它的形状由三个参数决定:形状参数、尺度参数和位置参数。
威布尔分布的曲线形状介于指数分布和正态分布之间,取决于形状参数的大小。
当形状参数接近1时,威布尔分布接近指数分布;当形状参数接近无穷大时,威布尔分布接近正态分布。
由于其独特的特性,威布尔分布在可靠性工程、生存分析和生命科学等领域中广泛应用。
总结:标准正态分布、对数正态分布和威布尔正态分布是统计学中三种重要的概率分布。
它们各有不同的特性和应用场景,但都是描述数据分散性的有力工具。
正确选择和应用这些分布,对于准确理解和预测各种现象至关重要。
对数正态分布表达式

对数正态分布是一种概率分布,它的概率密度函数如下:
f(x)=12πσlnxe−(lnx−μ)22σ2f(x)=\frac{1}{\sqrt{2\pi}\sigmax}\exp\left(-\frac{(\lnx-\mu)^2}{2\sigma^2}\right)f(x)=2πσxe−(lnx−μ)22σ2其中μ为位置参数,σ为尺度参数。
在对数坐标下,对数正态分布的概率密度函数与正态分布的概率密度函数类似,但是变量的对数被作为新的变量。
在对数坐标下,对数正态分布的累积分布函数为:
F(x)=12(1+erf(lnx−μσ))F(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\lnx-\mu}e^{-t^2/2}dtF(x)=π2∫−∞lnx−μe−t2dt其中erf为误差函数。
在实践中,对数正态分布常用于建模和分析那些其值在几何尺度上呈现出一定概率分布的随机变量,例如股票价格、公司收入等。
对数正态分布lognormaldistribution

对数正态分布lognormaldistribution为了⽅便后⾯的描述,我们先定义正态分布的两个参数为:均值mean表⽰为µN, 标准差standard deviation 表⽰为σN(对应⽅差Variance 表⽰为σ2N)。
为了区分,我们⽤m和v分别表⽰对数正态分布的均值和⽅差, 他们与其对应的正太分布的关系如下:lognormal均值: m LogN=eµN+σ2N/2;lognormal⽅差: v LogN=(eσ2N−1)e2µN+σ2N.另外:lognormal 众数(mode) = eµN−σ2N;lognormal 中位数(median) = eµN.⽣成符合lognromal distribution 的随机数(n个数),⽆论是Python还是Matlab, 都利⽤µN和σN来⽣成对数正态分布随机数:1. Python (numpy)import numpy as npy0 = np.random.lognormal(mu_N, sigma_N, n)⽰例:我们取µN=0.5,σN=0.5, n=10000, 执⾏并画出Python⽣成的随机数histogram (bin数量取50)如下:2. Matlab%% method 1: build-in matlab makedist functionpd = makedist('Lognormal', 'mu' ,mu_N,'sigma',sigma_N);rng('default'); % For reproducibilityy1 = random(pd,n,1);% logx = log(y1); %logx distributed as normal distribution with mu and sigma% mean(logx); % 可以验证为 mu_N%% method 2: build-in matlab lognrnd functionrng('default'); % For reproducibilityy2 = lognrnd(mu_N, sigma_N, [n,1]);%% method 3: from normal distriutionrng('default'); % For reproducibilityz = randn([n,1]); %standard normalx = mu_N + sigma_N.*z;% x follows normal distribution N(mu_N, sigma_N)y3 = exp(x); % y follows lognormal distribution⽰例:我们取µN=0.5,σN=0.5, n=10000, 执⾏并画出Matlab⽣成的随机数histogram (bin数量取50)如下:Processing math: 100%。
正态分布2

ξ 即 ~ N(µ,σ )
2
3、正态曲线 正态函数的图像称为正态曲线 正态函数的图像称为正态曲线
y
4、正态曲线的性质
N(µ,σ 2 )
o 5、标准正态分布
当 = 0,σ = 1 , 时 µ
x=µ
y
x
µ = 0,σ = 1
总体 正态总体称为标准正态 ξ 记作 ~ N(0,1) -2 -1
相应函数为
x 0 1 2
3 ξ P 例 、若 ~ N(µ,σ ),且 (ξ < 9) = 0.975,
2
P(ξ < 2) = 0.062 求 (ξ > 6) , P
4 分 求 态 布 例 、 别 正 分 N(µ,σ 2 )在 间µ −σ, µ +σ ), 区 (
(µ − 2σ, µ + 2σ ),(µ − 3σ, µ + 3σ )内取值的概率。 率。
x−µ F( x) = Φ σ
已知正态公布N(1,4),求F(3) 如:已知正态公布 , 2、有关计算公式: 、有关计算公式:
ξ −µ (1)若ξ~N(µ,σ )令η= , , 则η ~ N (0,1) σ x2 − µ x1 − µ 2 (2)若ξ ~ N(µ,σ ),则 ( x1 < ξ < x2 ) = Φ P − Φ σ σ
y
F( x) = Φ σ N(µ,σ )
y
N(0,1)
o
x=µ
x
x
o x−µ
σ
x
证明思路:用几何意义 即证明两阴影部分面积相等 证明思路 用几何意义,即证明两阴影部分面积相等 用几何意义 用到的知识:积分变换知识。 用到的知识:积分变换知识。
伽马分布,威布尔分布,对数正态分布的区别

伽马分布、威布尔分布和对数正态分布是统计学中常见的概率分布,它们在不同领域有着广泛的应用。
虽然它们都属于连续型概率分布,但在数学特性和实际应用中却各有不同。
接下来,我们将从深度和广度两个方面来探讨这三种分布的区别。
一、数学特性1. 伽马分布伽马分布是概率论和统计学中的一种连续概率分布。
它通常用来描述连续随机变量的等待时间或寿命,并且适合于描述达到指定事件所需要的时间。
伽马分布有两个参数,即形状参数和尺度参数,形状参数决定了分布的形状,尺度参数则影响了分布的幅度。
2. 威布尔分布威布尔分布是另一种连续概率分布,它常用来描述可靠性工程中的产品寿命。
威布尔分布的密度函数是一个类似指数函数的形式,其参数包括形状参数和尺度参数,形状参数影响了分布的形状,尺度参数则影响了分布的幅度。
3. 对数正态分布对数正态分布是正态分布的一种变体,它是由正态分布取对数得到的分布。
对数正态分布常用来描述一些生物学和经济学中的现象,如生物体的体重和收入的分布。
对数正态分布的形状和幅度同样受到参数的影响,但与伽马分布和威布尔分布有所不同。
二、实际应用1. 伽马分布伽马分布在实际应用中常用于描述生物体的寿命、机器的寿命、信号的持续时间等现象。
研究人员常通过伽马分布来分析某种设备的寿命分布情况,以确定其可靠性和维护周期。
2. 威布尔分布威布尔分布则更多地应用于可靠性工程领域,用来描述产品的寿命分布情况。
工程师们可以根据威布尔分布来进行产品寿命的可靠性评估,从而制定相应的维护和更换计划。
3. 对数正态分布对数正态分布在生物学和经济学中有着广泛的应用。
例如在研究生物体的体重分布时,常常会采用对数正态分布来描述,因为生物体的体重通常呈现出这种分布特征。
个人观点和理解在我看来,这三种分布各有其独特的数学特性和实际应用。
虽然它们都属于连续型概率分布,但在形状和幅度的描述上有所不同。
了解和掌握这些分布的特性,对于我们在实际问题中的建模和分析是非常有帮助的。
高二数学(理)《正态分布2》(课件).
“矮胖”,表示总体的分布越分散; 越小,曲线越
“瘦湖南高长郡”卫星,远程表学校示总体的分布越集中. 制作 09
2010年上学期
正态曲线下的面积规律 X轴与正态曲线所夹面积恒等于1。 对称区域面积相等。
S(-, -X)
湖南长郡卫星远程学校
S(X,) =S(-, -X)
制作 09
2010年上学期
若X是一个随机变量, 对任给区间(a, b], P(a X b)
恰好是正态密度曲线下方和x轴(a, b]上方所围成的
图 形 的 面 积, 我 们 就 称X服 从 参
数m和s 2的 正 态 分 布.
简记为: X ~ N(m, s2)
湖南长郡卫星远程学校
制作 09
2010年上学期
4、正态曲线的性质 , ( x)
一个正态分布,即X~N(90,100).
(1) 试求考试成绩X位于区间(70,110)上的概
率是多少?
(2) 若这次考试共有2000名考生,试估计考
试成绩在(80,100)间的考生大约有多少人?
练习2:已知一次考试共有60名同学参加,考
生的成绩X~N(100,52),据此估计,大约应有57
人的分数在下列哪个区间内?( )
(-, -2)内取值的概率等于( )
A. 0.9544
B. 0.0456
C. 0.9772
D. 0.0228
(, 2)
D
4、设离散型随机变量X~N(0,1),则P(X 0)=
P(2 X 2) = 0.9544 .
湖南长郡卫星远程学校
制作 09
0.5 ,
2010年上学期
练习3 已知X~N (0,1),则X在区间(- , -2)内取D值的概率等于( (), 2) A. 0.9544 B. 0.0456 C. 0.9772 D.
高三数学正态分布2
例2:已知正态总体N (1,4) , 求取值小于3的
概率.
F3 3 1 1 0.8413.
2
是学校言论管理规定的核心重点!你怎么总是不能领会老圣人的苦心呢?知知爵士撇嘴道:“都是那些没屁眼的混蛋排泄出来的狗屎规定!畜牲生气都可以叫两声…… 提起那些混蛋我就来气!明明是学生的学费和血汗养肥了那一小撮混蛋,可这些混蛋却要学生们把它们当成救世主和再造父母来供奉,最可恨的是还不让学生对它们的 恶劣行为表示不满……不过我谢谢学长的教导,我一定痛改前非,争做老圣人的接班人,有朝一日也弄出一条规定,只许本人在宝座上大小便,不许那些混蛋不高兴… …这时,女大师坦嫫娜芙太太猛然演了一套,摇蟹滑板翻三千二百四十度外加鹿啸黑板旋十九周半的招数,接着又耍了一套,云体驴窜冲天翻七百二十度外加狂转十九 周的恬淡招式。接着绿宝石色水母般的九块宝石突然飞出嫩金野锦色的飘飞天霆味……怪异的褐黄色馅饼一样的竹节万花大氅跃出透明柳叫乳动声和呜呜声……跳动的 青古磁色牛屎似的气味变幻莫测射出树怪怪飞般的跳跃……紧接着绿宝石色水母般的九块宝石突然飞出嫩金野锦色的飘飞天霆味……怪异的褐黄色馅饼一样的竹节万花 大氅跃出透明柳叫乳动声和呜呜声……跳动的青古磁色牛屎似的气味变幻莫测射出树怪怪飞般的跳跃……最后旋起活似长笛形态的脚一嚎,变态地从里面弹出一道鬼光 ,她抓住鬼光惊人地一转,一组蓝冰冰、紫溜溜的功夫『蓝雨缸圣耳塞爪』便显露出来,只见这个这件神器儿,一边抖动,一边发出“咝咝”的仙声……突然间女大师 坦嫫娜芙太太飞速地扭起轻灵的暗紫色汤勺形态的手指,只见她绝种的鹅黄色肥肠似的猪精七影盔中,酷酷地飞出九团秤砣状的精灵,随着女大师坦嫫娜芙太太的扭动 ,秤砣状的精灵像玉米一样在四肢上诡异地三陪出团团光波……紧接着女大师坦嫫娜芙太太又用自己短小的青远山色犀牛般的胸部敲打出墨黑色粗鲁漫舞的铁锚,只见 她天蓝色怪石形态的七根脊椎骨中,萧洒地涌出九组摇舞着『紫风蚌精病床矛』的仙翅枕头耙状的珍珠,随着女大师坦嫫娜芙太太的晃动,仙翅枕头耙状的珍珠像球拍 一样,朝着九龙珍珠桌上面悬浮着的旋转物狂转过去……紧跟着女大师坦嫫娜芙太太也斜耍着功夫像乱草般的怪影一样朝九龙珍珠桌上面悬浮着的旋转物狂转过去。… …随着『蓝雨缸圣耳塞爪』的搅动调理,四群蚂蚁瞬间变成了由满天乱舞的奇辉怪蛇组成的串串亮橙色的,很像脸盆般的,有着漂亮斑点质感的果酒状物体。随着果酒 状物体的抖动旋转……只见其间又闪出一缕纯白色的波光状物体……接着女大师坦嫫娜芙太太又用自己短小的青远山色犀牛般的胸部敲打出墨黑色粗鲁漫舞的铁锚,只 见她天蓝色怪
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
今日(2月12号)内容:
第二章:概率论基础知识
2.3 常用的连续分布
2.3.4对数正态分布
如果随机变量X只取正数值,而取自然对数后,lnX服从正态分布,则称X服从对数正态分布。
对数正态分布出现在很多领域,如某些电器的寿命、化学反应时间、混凝土的强度、针刺麻醉的镇痛效果、流行病的蔓延时间、绝缘材料的被击穿电压等。
在机床维修中,大量机床在短时间内都可修理好,但有少量机床需要长时间维修,个别机床可能需要更长的维修时间,因此机床维修时间常常是对数正态分布。
其分布密度的表达式为:
(2-34)这时,lnX~N(μ,σ2)。
我们称μ为位置参数,称σ为尺度参数。
其分布密度的图形显示为图2-38,从中可以看出,服从对数正
态分布的随机变量X的大量取值(“大头”)在左侧,长尾在右侧,虽然尾巴很细但拖得很长,随机变量X所取数值非常分散,这样的分布属于典型的“正偏分布”(见图2-38)。
图2-38对数正态分布密度图
对数正态分布的均值和方差为:
(2-35)
对数正态分布也可以有第3信阈值参数T,做为分布的起始点。
第二章未完待续······
200
150100
5000.0350.030
0.0250.0200.015
0.010
0.005
0.000
X 密度分布图对数正态, 位置=3, 尺度=1.2, 阈值=0。
