2008年上海中考数学试卷及答案
2008年上海中考数学

2008年上海中考数学一、绪论2008年是上海中考中一年,数学是考试科目之一。
数学作为一门基础学科,在中考中占据着重要的位置。
本文将以2008年上海中考数学为主题,对该年度的数学考试进行分析和总结。
二、考试概要1. 考试时间和形式2008年上海中考数学考试于6月举行。
考试形式为闭卷考试,学生需要在规定时间内完成试卷上的各项要求。
2. 考试内容数学考试内容包含了以下几个方面:•数的性质与运算•一次函数与一元一次方程•平面图形•平面图形的性质和计算•数据的收集整理与表示三、试题分析1. 数的性质与运算在数的性质与运算部分的试题中,涉及到了整数、分数和小数的加减乘除运算。
同时也考察了学生对数学基本概念的掌握和应用能力。
2. 一次函数与一元一次方程一次函数与一元一次方程是数学中重要的内容之一。
在2008年的数学中考中,这部分试题主要考查了学生对一次函数图像的理解和方程解的求解能力。
3. 平面图形平面图形是中学数学中的基础内容,包括了点、线、面等概念。
在数学考试中,平面图形部分的试题主要考察了学生对平面图形的辨认和计算能力。
4. 数据的收集整理与表示数据分析是现代社会中重要的技能之一。
在2008年的数学中考中,数据的收集整理与表示部分试题主要考察了学生对数据表格、图表等形式的理解和分析能力。
四、总结与展望2008年上海中考数学试题的难易程度适中,整体考查了学生对数学基本概念和运算能力的掌握情况。
同时,还通过一些应用题考查了学生的综合运用能力。
未来,数学教育应继续注重培养学生的数学思维和解决问题的能力,提高学生对数学的兴趣和学习动力。
同时,结合实际应用,将数学与其他学科进行有机结合,培养学生跨学科的综合能力。
以上是对2008年上海中考数学的简要分析和总结。
希望对读者有所帮助。
谢谢!。
上海市2008年初中毕业生统一学业考试含答案

2008年上海市初中毕业生统一学业考试物 理 试 卷一、填空题1、教室里的日光灯正常工作电压为________V ,消耗的是________能,家用电器之间是__________连接的。
(选填“串联”或“并联”)2、 图1(a)、(b)中的情景表示了力的作用效果,其中图1_______主要表示力能使物体的运动状态发生改变;图1_________主要表示力能使物体发生形变。
[均选填“(a)”或“(b)”]3、如图2所示,灭火器放在烈日下温度会_______(选填“升高”或“降低”),这是通过_______的方法使其内能增加,具有一定的危险性,为了安全,灭火器应存放在阴凉干燥处。
4、如图3所示,小朋友从滑梯上滑下,其重力势能__________(选填“增大”或“减小”),他与滑梯接触面间的摩擦是__________摩擦(选填“滚动”可“滑动”)。
当他滑至水平面进,还会继续向前运动,是由于他具有______ ___。
5、2008年北京奥运火炬传递的主题是“传递激情,传递梦想”。
若火炬手以1m/s 的速度沿直线匀速通过60m ,需________s ,以路旁的树木为参照物,火炬手是________的。
(选填“静止”或“运动”)。
6、木块在大小为2N 的水平拉力作用下,10s 内在水平面上沿拉力方向前进1m ,拉力功为________J ,功率为_______w ;若木块重5N ,在此过程中重力对木块做功为________J 。
7、若10s 内通过某导体横截面的电量为2库,通过导体的电流为________A ,此时导体两端的电压为6V ,其电阻为______Ω。
当该导体两端的电压为3V 时,该导体电阻为_____Ω。
图1图2图38、重为9.8N 的木块漂浮在水面是且保持静止,木块所受浮力的大小为_______N ,浸在水中的体积为___________m 3。
9、在图4的示所示的电路中,电源电压保持不变。
2005-2008年(上海市中考考试数学试卷(含详细答案)

2005年上海市初中毕业生统一学业考试数学试卷一、填空题(本大题共14题,满分42分) 1、 计算:()22x=2、 分解因式:22a a -= 3、计算:)11=4、函数y =的定义域是5、 如果函数()1f x x =+,那么()1f =6、 点A(2,4)在正比例函数的图象上,这个正比例函数的解析式是7、 如果将二次函数22y x =的图象沿y 轴向上平移1个单位,那么所得图象的函数解析式是8、 已知一元二次方程有一个根为1,那么这个方程可以是 (只需写出一个方程) 9、 如果关于x 的方程240x x a ++=有两个相等的实数根,那么a = 10、 一个梯形的两底长分别为6和8,这个梯形的中位线长为 11、 在△ABC 中,点D 、E 分别在边AB 和AC 上,且DE ∥BC ,如果AD =2,DB =4,AE =3,那么EC =12、 如图1,自动扶梯AB 段的长度为20米,倾斜角A为α,高度BC 为 米(结果用含α的三角比表示). 13、 如果半径分别为2和3的两个圆外切,那么这两个圆的圆心距是14、 在三角形纸片ABC 中,∠C =90°,∠A =30°,AC =3,折叠该纸片,使点A 与点B 重合,折痕与AB 、AC 分别相交于点D 和点E (如图2),折痕DE 的长为二、选择题:(本大题共4题,满分12分)15、 在下列实数中,是无理数的为 ( ) A 、0 B 、-3.5 CD16、 六个学生进行投篮比赛,投进的个数分别为2、3、3、5、10、13,这六个数的中位数为 ( )A 、3B 、4C 、5D 、617、 已知Rt △ABC 中,∠C =90°,AC =2,BC =3,那么下列各式中,正确的是( )图1图2A 、2sin 3B =B 、2cos 3B =C 、23tgB =D 、23ctgB =18、 在下列命题中,真命题是 ( )A 、两个钝角三角形一定相似B 、两个等腰三角形一定相似C 、两个直角三角形一定相似D 、两个等边三角形一定相似 三、(本大题共3题,满分24分) 19、 (本题满分8分) 解不等式组:()315216x xx x+>-⎧⎨+-<⎩,并把解集在数轴上表示出来.20、 (本题满分8分) 解方程:228124x x x x x +-=+--x-5-4-3-2-15432O 121、 (本题满分8分,每小题满分各为4分)(1)在图3所示编号为①、②、③、④的四个三角形中,关于y 轴对称的两个三角形的编号为 ;关于坐标原点O 对称的两个三角形的编号为 ; (2)在图4中,画出与△ABC 关于x 轴对称的△A 1B 1C 1四、(本大题共4题,满分42分)22、 (本题满分10分,每小题满分各为5分)在直角坐标平面中,O 为坐标原点,二次函数2y x bx c =++的图象与x 轴的负半轴相交于点C (如图5),点C 的坐标为(0,-3),且BO =CO (1) 求这个二次函数的解析式; (2) 设这个二次函数的图象的顶点为M ,求AM 的长.23、(本题满分10分)已知:如图6,圆O是△ABC的外接圆,圆心O在这个三角形的高CD上,E、F分别是边AC和BC的中点,求证:四边形CEDF是菱形.24、 (本题满分10分,第(1)、(2)、(3)小题满分各为2分,第(4)小题满分4分) 小明家使用的是分时电表,按平时段(6:00-22:00)和谷时段(22:00-次日6:00)分别计费,平时段每度电价为0.61元,谷时段每度电价为0.30元,小明将家里2005年1月至5月的平时段和谷时段的用电量分别用折线图表示(如图7),同时将前4个月的用电量和相应电费制成表格(如表1) 根据上述信息,解答下列问题:(1) 计算5月份的用电量和相应电费,将所得结果填入表1中; (2) 小明家这5个月的月平均用电量为 度;(3) 小明家这5个月的月平均用电量呈 趋势(选择“上升”或“下降”);这5个月每月电费呈 趋势(选择“上升”或“下降”);(4) 小明预计7月份家中用电量很大,估计7月份用电量可达500度,相应电费将达243元,请你根据小明的估计,计算出7月份小明家平时段用电量和谷时段用电量.用电量(度)54月3月2月1月25、 (本题满分12分,每小题满分各为4分)在△ABC 中,∠ABC =90°,AB =4,BC =3,O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D ,交线段OC 于点E ,作EP ⊥ED ,交射线AB 于点P ,交射线CB 于点F 。
上海十年中考数学压轴题及答案解析

上海十年中考数学压轴题解析2001年上海市数学中考27.已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD =5,AB =DC =2. (1)如图8,P 为AD 上的一点,满足∠BPC =∠A .图8①求证;△ABP ∽△DPC ②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域; ②当CE =1时,写出AP 的长(不必写出解题过程).27.(1)①证明:∵∠ABP =180°-∠A -∠APB ,∠DPC =180°-∠BPC -∠APB ,∠BPC =∠A ,∴∠ABP =∠DPC .∵在梯形ABCD 中,AD ∥BC ,AB =CD ,∴∠A =∠D .∴△ABP ∽△DPC .②解:设AP =x ,则DP =5-x ,由△ABP ∽△DPC ,得DCPD AP AB =,即252xx -=,解得x 1=1,x 2=4,则AP 的长为1或4.(2)①解:类似(1)①,易得△ABP ∽△DPQ ,∴DQ AP PD AB =.即y xx +=-252,得225212-+-=x x y ,1<x <4. ②AP =2或AP =3-5.(题27是一道涉及动量与变量的考题,其中(1)可看作(2)的特例,故(2)的推断与证明均可借鉴(1)的思路.这是一种从模仿到创造的过程,模仿即借鉴、套用,创造即灵活变化,这是中学生学数学应具备的一种基本素质,世上的万事万物总有着千丝万缕的联系,也有着质的区别,模仿的关键是发现联系,创造的关键是发现区别,并找到应付新问题的途径.)上海市2002年中等学校高中阶段招生文化考试27.操作:将一把三角尺放在边长为1的正方形ABCD 上,并使它的直角顶点P 在对角线AC 上滑动,直角的一边始终经过点B ,另一边与射线DC 相交于点Q .图1 图2 图3探究:设A 、P 两点间的距离为x .(1)当点Q 在边CD 上时,线段PQ 与线段PB 之间有怎样的大小关系?试证明你观察得到结论;(2)当点Q 在边CD 上时,设四边形PBCQ 的面积为y ,求y 与x 之间的函数解析式,并写出函数的定义域; (3)当点P 在线段AC 上滑动时,△PCQ 是否可能成为等腰三角形?如果可能,指出所有能使△PCQ 成为等腰三角形的点Q 的位置,并求出相应的x 的值;如果不可能,试说明理由. 五、(本大题只有1题,满分12分,(1)、(2)、(3)题均为4分) 27.图1 图2 图3(1)解:PQ =PB ……………………(1分)证明如下:过点P 作MN ∥BC ,分别交AB 于点M ,交CD 于点N ,那么四边形AMND 和四边形BCNM 都是矩形,△AMP 和△CNP 都是等腰直角三角形(如图1).∴ NP =NC =MB . ……………………(1分) ∵ ∠BPQ =90°,∴ ∠QPN +∠BPM =90°.而∠BPM +∠PBM =90°,∴ ∠QPN =∠PBM . ……………………(1分) 又∵ ∠QNP =∠PMB =90°,∴ △QNP ≌△PMB . ……………………(1分) ∴ PQ =PB . (2)解法一由(1)△QNP ≌△PMB .得NQ =MP . ∵ AP =x ,∴ AM =MP =NQ =DN =x 22,BM =PN =CN =1-x 22, ∴ CQ =CD -DQ =1-2·x 22=1-x 2.得S △PBC =21BC ·BM =21×1×(1-x 22)=21-42x . ………………(1分) S △PCQ =21CQ ·PN =21×(1-x 2)(1-x 22)=21-x 423+21x 2 (1分) S 四边形PBCQ =S △PBC +S △PCQ =21x 2-x 2+1. 即 y =21x 2-x 2+1(0≤x <22). ……………………(1分,1分)解法二作PT ⊥BC ,T 为垂足(如图2),那么四边形PTCN 为正方形. ∴ PT =CB =PN .又∠PNQ =∠PTB =90°,PB =PQ ,∴△PBT ≌△PQN .S 四边形PBCQ =S △四边形PBT +S 四边形PTCQ =S 四边形PTCQ +S △PQN =S 正方形PTCN …(2分)=CN 2=(1-x 22)2=21x 2-x 2+1∴ y =21x 2-x 2+1(0≤x <22). ……………………(1分)(3)△PCQ 可能成为等腰三角形①当点P 与点A 重合,点Q 与点D 重合,这时PQ =QC ,△PCQ 是等腰三角形, 此时x =0 ……………………(1分) ②当点Q 在边DC 的延长线上,且CP =CQ 时,△PCQ 是等腰三角形(如图3) ……………………(1分) 解法一 此时,QN =PM =x 22,CP =2-x ,CN =22CP =1-x 22. ∴CQ =QN -CN =x 22-(1-x 22)=x 2-1. 当2-x =x 2-1时,得x =1. ……………………(1分) 解法二 此时∠CPQ =21∠PCN =22.5°,∠APB =90°-22.5°=67.5°, ∠ABP =180°-(45°+67.5°)=67.5°,得∠APB =∠ABP ,∴ AP =AB =1,∴ x =1. ……………………(1分)上海市2003年初中毕业高中招生统一考试27.如图,在正方形ABCD中,AB=1,弧AC是点B为圆心,AB长为半径的圆的一段弧。
2008年上海数学中考试卷分析

2008年上海数学中考试卷分析崇明县实验中学郭洪星各内容板块占分统计表各年级教材相关的知识点占分统计表我从两个不同的板块进行了分值的统计:1、根据《数学课程标准(试行稿)》把六、七、八、九四个年级的教学内容划分成数与运算、方程与代数、图形与几何、函数与分析、数据整理与概率统计共五块。
其中代数分值88分,几何分值62分,代数知识与几何知识的分值接近6∶4,这个比值跟前两年类似,都是控制在6∶4左右。
2、根据以往从重点知识的角度出发,着重统计了一元二次方程、函数、统计、相似形、锐角三角比和圆六个板块。
这六个板块分值89分,占整卷分值的五分之三左右,以往这六块内容的分值基本在整卷分值的三分之二左右。
占比的下降可能与“二期课改”教材内容的增减有关。
下面我谈几点对2008年上海数学中考试卷的认识:1、注重“双基”的考查基本知识、基本技能是学生继续学习和进一步发展的基石。
今年的数学中考试卷中118分为基础题,有些基础题就来源于课本,往往是把课本例题、习题改变知识的呈现方式,进行适当地调换和引申。
为此,在平时的教学中我们要立足课本,注重“双基”训练。
2、注重数学思想、数学方法的考查《数学课程标准(试行稿)》中对数学思想方法有这样一段描述:知道数学思想方法在进行数学思考和解决问题中的作用,通过有关数学知识和技能的学习,逐步领会字母表示数的思想、化归思想、方程思想、函数思想、数形结合思想、分类讨论思想、分解与组合思想等基本数学思想,掌握待定系数法、消元法、换元法、配方法等基本数学方法。
那么,在今年的中考试卷中考查了哪些数学思想方法呢?在数学思想上,第2题、第24题的第(1)小题体现了字母表示数的数学思想;第9题、第20题体现了化归思想即把分式方程转化为整式方程;第21题的第(2)小题、第22题的第(2)小题体现了方程思想;第25题的第(1)小题体现了函数思想;第24题的第(2)小题及第25题的第(3)小题都体现了与相似三角形有关的分类讨论思想;第13题函数图像的平移、第21题的第(1)题体现了图形运动的思想;至于数形结合思想更是在试卷中多处出现。
上海中考10年2008-2018真题分类

考点梳理 第一单元 数与运算一、数的整除:数的整除性、奇数和偶数、因数和倍数、素数和合数,公因数和最大公因数、公倍数和最小公倍数、分解素因数;能被2和5整除的正整数的特征。
二、实数:考点1、实数的有关概念1.(2005)在下列实数中,是无理数的为 ( ).A. 0B. -3.5C.D. 2 (2010)下列实数中,是无理数的为( )A. 3.14B. 13 C. 3 D. 93.(2011)下列分数中,能化为有限小数的是( )A .B .C .D .4.(2015)下列实数中,是有理数的为( )A 、2;B 、34;C 、π;D 、0. 5.(2016)如果a 与3互为倒数,那么a 是( ) A .﹣3 B .3 C .﹣D .6.(2017)下列实数中,无理数是 ( )A .0;BC .2-;D .277.(2018) -8的立方根是 考点2、近似计算、科学记数法1.(2014)据统计,2013年上海市全社会用于环境保护的资金约为60 800 000 000元,这个数用科学记数法表示为( )考点3、实数的运算 1.(2012)计算112-= . 2.(2015)计算:=+-22_______.3.(2014)计算的结果是( ) ..D4.(20130111()2π--+ .5.(2014)计算:﹣﹣+||.6.(2016)计算:|﹣1|﹣﹣+. 7.(2017)11221192-⎛⎫-+ ⎪⎝⎭11.(2018 )A. 4B.3C.D.第二单元 方程与代数一、整式与分式: 考点4、整式及其运算1.(2008)计算a a 32⋅的结果是( )A .5aB .6aC .25a D .26a 2.(2009)计算32()a 的结果是( )A .5a B .6a C .8a D .9a3.(2009)某商品的原价为100元,如果经过两次降价,且每次降价的百分率都是m ,那么该商品现在的价格是 元(结果用含m 的代数式表示). 4.(2010)计算:a 3 ÷ a 2 = __________.5.(2010)计算:( x + 1 ) ( x ─ 1 ) = ____________.6. (2011)计算:a 2•a 3= _________ .7. (2012)在下列代数式中,次数为3的单项式是( )A .2xy ;B . 33+x y ;C .3x y ;D .3xy .8.(2014)计算:a (a+1)= _________ .9.(2015)当a >0时,下列关于幂的运算正确的是( )A. a 0=1;B. a -1=-a ; C. (-a )2=-a 2; D. 2211aa =. 10.(2016)下列单项式中,与a 2b 是同类项的是( )A .2a 2bB .a 2b 2C .ab 2D .3ab 11.(2016)计算:a 3÷a= .12.(2016)如果a=,b=﹣3,那么代数式2a+b 的值为 . 13.(2017)计算:22a a ⋅=________14.(2018)计算:22(1)a a +-= . 考点5、因式分解:1.(2008)分解因式:24x -= 2.(2010)分解因式:a 2 ─ a b = ______________. 3.(2011)因式分解:x 2﹣9y 2= _________ . 4.(2012)因式分解=xy x - . 5.(2013)因式分解:21a - = _____________. 考点6、分式的意义与性质 1.(2015)如果分式32+x x有意义,那么x 的取值范围是____________. 考点7、分式的运算 1.(2007)化简:111x x -=+ . 2.(2009)计算:22221(1)121a a a a a a +-÷+---+.3.(2013)计算:23b aa b⨯= ___________. 4.(2015)先化简,再求值:2124422+--+÷++x x x x x x x ,其中12-=x5.(2018)先化简,再求值:2221211aa a a a a+⎛⎫-÷ ⎪-+-⎝⎭,其中a =二、二次根式: 考点8、二次根式的概念1.(2007 ).A B C D 2.(2009= . 3. (2011)下列二次根式中,最简二次根式是( ) A .B .C .D .4.(2012 )A B C ; D .5.(2013)下列式子中,属于最简二次根式的是( ) (A ) 9; (B )7 ; (C ) 20 ; (D )13. 考点9、二次根式的运算1.(2008+ 2. (2010)计算:12131271)()2-+-3. (2011)计算:.4.(2012))1122112-⨯-⎝⎭考点10、方程解的概念 1.(2008)如果2x =是方程112x a +=-的根,那么a 的值是 ( ) A .0 B .2 C .2- D .6- 考点11、一元二次方程的根的判别式1.(2009)如果关于x 的方程20x x k -+=(k 为常数)有两个相等的实数根,那么k = .2.(2010)已知一元二次方程 x + x ─ 1 = 0,下列判断正确的是( )A.该方程有两个相等的实数根B.该方程有两个不相等的实数根C.该方程无实数根D.该方程根的情况不确定3. (2011)如果关于x 的方程x 2﹣2x+m=0(m 为常数)有两个相等实数根,那么m= _________ .4.(2012)如果关于x 的一元二次方程26+=0x x c -(c 是常数)没有实根,则c 的取值范围是 . 5.(2013)下列关于x 的一元二次方程有实数根的是( )(A )210x +=;(B )210x x ++=;(C )210x x -+= ;(D )210x x --=.6.(2014)如果关于x 的方程x 2﹣2x+k=0(k 为常数)有两个不相等的实数根,则k 的取值范围是 _ . 7.(2015)如果关于x 的一元二次方程x 2+4x -m =0没有实数根,那么m 的取值范围是________. 8.(2016)如果关于x 的方程x 2﹣3x+k=0有两个相等的实数根,那么实数k 的值是 . 9.(2017)下列方程中,没有实数根的是( )A .220x x -=; B .2210x x --=; C .2210x x -+=; D .2220x x -+=. 10.(2018)下列对一元二次方程230x x +-=根的情况的判断,正确的是( )A.有两个不相等的实数根B.有两个相等的实数根C.有且只一个实数根D.没有实数根 考点12、分式方程1.(2008)用换元法解分式方程21221x x x x --=-时,如果设21x y x-=,并将原方程化为关于y 的整式方程,那么这个整式方程是 .2.(2007)解方程:22321011x x x x x --+=--. 3.(2008)解方程:2654111x x x x x ++=--+4.(2009)用换元法解分式方程13101x x x x --+=-时,如果设1x y x-=,将原方程化为关于y 的整式方程,那么这个整式方程是( )A .230y y +-=B .2310y y -+=C .2310y y -+=D .2310y y --=5.(2010)解方程:x x ─ 1 - 2 x ─ 2x ─ 1 = 0 6.(2012)解方程:261393x x x x +=+--7.(2014)解方程:﹣=. 8.(2016)解方程:﹣=1.9.(2017)解方程:231133x x x -=--考点13、无理方程1.(20082=的根是2.(20091=的根是 .3.(2010)方程 x + 6 = x 的根是____________.4.(2012的根是 . 5.(2015)方程223=-x 的解是_______________. 6.(2016)方程=2的解是 .7.(20171=的根是________. 考点14、方程组的解法 1.(2009)解方程组:21220y x x xy -=⎧⎨--=⎩,①.②2. (2011)解方程组:.3.(2013)解方程组: 22220x y x xy y -=-⎧⎨--=⎩4.(2018)方程组202x y x y -=⎧⎨+=⎩的解是考点15、方程的应用1.(2011)某小区2010年屋顶绿化面积为2000平方米,计划2012年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是 _________ .2.(2014)某文具店二月份销售各种水笔320支,三月份销售各种水笔的支数比二月份增长了10%,那么该文具店三月份销售各种水笔 _________ 支.3.(2017)某市前年PM2.5的年均浓度为50微克/立方米,去年比前年下降了10%.如果今年PM2.5的年均浓度比去年也下降10%,那么今年PM2.5的年均浓度将是________微克/立方米.4.(2017)某企业今年第一季度各月份产值占这个季度总产值的百分比如图所示,又知二月份产值是72万元,那么该企业第一季度月产值的平均数是_____万元. 5.(2018)某商品原价为a 元,如果按原价的八折销售,那么售价是 元(用含字母a 的代数式表示)考点16、不等式的解法 1.(2009)不等式组1021x x +>⎧⎨-<⎩,的解集是( )A .1x >-B .3x <C .13x -<<D .31x -<< 2.(2010)不等式 3 x ─ 2 > 0 的解集是____________. 3.(2011)如果a >b ,c <0,那么下列不等式成立的是( )A .a+c >b+cB .c ﹣a >c ﹣bC .ac >bcD .4.(2012)不等式组2<62>0x x ⎧⎨⎩--的解集是( )A .>3x -;B .<3x -;C .>2x ;D .<2x .5.(2013)不等式组1023x x x->⎧⎨+>⎩ 的解集是____________.6.(2014)不等式组的解集是_______________.7.(2015)解不等式组:⎪⎩⎪⎨⎧+≤-->9131624x x x x ,并把解集在数轴上表示出来.8.(2016)不等式组的解集是 .9.(2017)不等式组2620x x >⎧⎨->⎩的解集是_______________.10.(2018)解不等式组:21512x xx x +>⎧⎪⎨+-≥⎪⎩,并把解集在数轴上表示出来.第三单元 图形与几何一、长方体的再认识:长方体,长方体的画法,直线与直线、直线与平面、平面与平面的基本位置关系。
2008年上海市初中毕业生统一学业考试数学

上海市2008年初中毕业生统一学业考试数学(满分150分,考试时间100分钟)一、选择题(本大题含Ⅰ、Ⅱ两组,每组各6题,每题4分,满分24分)考生注意:1.请从下列Ⅰ、Ⅱ两组中选择一组,完成相应的1~6题。
2.下列各题的四个选项中,有且只有一个选项是正确的是。
Ⅰ组:供使用一期课改教材的考生完成1.计算2a·3a的结果是()A.5a B.6a C.5a2D.6a22.如果x=2是方程112x a+=-的根,那么a的值是()A.0 B.2 C.-2 D.-63.在平面直角坐标系中,直线y=x+1经过()A.第一、二、三象限B.第一、二、四象限C.第一、三、四象限D.第二、三、四象限4.在平面直角坐标系中,抛物线y=x2-1与x轴的交点的个数是()A.3 B.2 C.1 D.05.如果x1、x2是一元二次方程x2-6x-2=0的两个实数根,那么x1+x2的值是()A.-6 B.-2 C.6 D.26.如图,从圆O外一点P引圆O的两条切线P A、PB,切点分别为A、B。
如果∠APB=60°,P A=8,那么弦AB 的长是()A.4 B.8 C.D.Ⅱ组:供使用二期课改教材的考生完成1.计算2a·3a的结果是()A.5a B.6a C.5a2D.6a22.如果x=2是方程112x a+=-的根,那么a的值是()A.0 B.2 C.-2 D.-63.在平面直角坐标系中,直线y=x+1经过()A .第一、二、三象限B .第一、二、四象限C .第一、三、四象限D .第二、三、四象限4.计算3a -2a 的结果是( )A .aB .aC .-aD .-a5.从一副未曾启封的扑克牌中取出1张红桃、2张黑桃的牌共3张,洗匀后,从这3张牌中任取1张牌恰好是黑桃的概率是( )A .12 B .13 C .23D .16.如图,在平行四边形ABCD 中,如果AB =a ,AD =b ,那么a +b 等于( )A .BDB .AC C .DBD .CA二、填空题(本大题共12题,每题4分,满分48分)7.不等式x -3<0的解集是________。
003——上海市2008年初中毕业生统一学业考试(答案部分)

3 上海市2008年初中毕业生统一学业考试I 组1.D 【解析】本题重点考查了单项式乘以单项式的法则,单项式和单项式相乘时,将系数和同底数幂分别相乘.本题是一道较为简单的题目.2.C 【解析】本题重点考查了方程的解和一元一次方程的解法.因为x=2是方程1a x 21-=+的根,所以将x=2代入求关于a 的一元一次方程即可.本题是一道较为简单的题目.3.A 【解析】本题考查了一次函数图象的性质.一次函数y=kx +b 的图象由k 、b 的符号决定,k >0,b >0,图象过一、二、三象限;k >0,b <0,图象过一、三、四象限;k <0,b >0,图象过一、二、四象限;k <0,b <0,图象过二、三、四象限.本题较简单.4.B 【解析】本题重点考查二次函数图象的性质及根的判别式.抛物线与x 轴有几个交点,要看△,△>0,则图象与x 轴有两个交点;△=0,则图象与x 轴有一个交点;△<0,则图象与x 轴无交点.本题也可以这样考虑:二次函数常数项为-1,与y 轴交于负半轴,抛物线开口向上,所以必有2个交点.5.C 【解析】本题重点考查了一元二次方程根与系数的关系.在一元二次方程 0)0(a c bx ax 2≠=++中,ac x x ,a b -x x 2121==+,在本题中,因为21x ,x 是一元二次方程02-6x -x 2=的两个实数根,所以6ab -x x 21==+,本题是一道较为简单的题目.6.B 【解析】本题重点考查了切线长定理及等边三角形的性质.从圆外一点引圆的两条切线,它们的切线长相等.所以PA=PB ,又因为∠APB=60°,所以△PAB 为等边三角形,所以PA=AB= PB=8.本题是一道较为简单的题目.Ⅱ组1.D 【解析】本题重点考查了单项式乘以单项式的法则,单项式和单项式相乘时,将系数和同底数幂分别相乘.本题是一道较为简单的题目.2.C 【解析】本题重点考查了方程的解和一元一次方程的解法.因为x=2是方程1a x 21-=+的根,所以将x=2代入求关于a 的一元一次方程即可.本题是一道较为简单的题目.3.A 【解析】本题考查了一次函数图象的性质.一次函数y=kx +b 的图象由k 、b 的符号决定,k >0,b >0,图象过一、二、三象限;k >0,b <0,图象过一、三、四象限;k <0,b >0,图象过一、二、四象限;k <0,b <0,图象过二、三、四象限.本题较简单.4.B 【解析】本题主要考查向量的基础知识,本题是一道较为简单的题目.5.C 【解析】本题利用摸扑克牌这个情境,重点考查了概率,因为2张黑桃占总数的32,所以本题应选C .本题是一道较为简单的题目. 6.B 【解析】本题重点考查了向量的知识及平行四边形的性质.由题意知b a =+.本题是一道较为简单的题目.7.x <3 【解析】本题重点考查一元一次不等式的解法.在解一元一次不等式把未知数的系数化为1时,如果左右两边同乘以或除以一个负数,不等号的方向应改变.本题较简单.8.(x +2)(x -2) 【解析】本题重点考查了用平方差公式分解因式.分解因式要注意有公因式的,先提取公因式,然后再考虑利用公式,若是二项,一般考虑平方差公式,三项则考虑完全平方公式,四项或四项以上应利用分组分解法.本题较简单.9.01-2y -y 2=【解析】本题重点考查了用换元法解分式方程.将y 代入原方程得2y1-y =,即2y 1-y 2=,移项得01-2y -y 2=,本题是一道难度中等的题目.10.x=-1 【解析】本题重点考查了无理方程的解法.2x -3=,所以3-x=4,即x=-1.本题是一道较为简单的题目.11.3【解析】本题考查了函数值的运算方法.易知312f(2)=+=,本题是一道较简单的题目.12.-2【解析】本题重点考查了反比例函数的图象的性质.点在图象上,则可将(2,-1)代入0)(k xk y ≠=求得k=-2.本题是一道较为简单的题目.13.y=2x +1【解析】本题重点考查了用待定系数法求一次函数解析式及一次函数图象的平移规律.由图象可知直线OA 的解析式为y=2x ,据平移规律上加下减,则所得新函数解析式为y=2x +1.14.30【解析】本题利用“限塑令”这个新情境考查了样本估计总体及概率的知识.既考查了数学知识,又增强学生的环保意识.因为80名学生有两名不知道,则不知道的占401,所以全体学生约有304011200=⨯人.本题是一道较为简单的题目.15.40°【解析】本题重点考查平行线的性质及对顶角相等的知识点.由图知∠1的对顶角∠3也为40°,根据平行线的性质∠2=∠3=40°.本题是一道较为简单的题目.16.1∶9【解析】本题重点考查了相似比和面积比的关系.两个相似三角形面积的比应等于相似比的平方.本题是一道较为简单的题目.17.32【解析】本题重点考查了相似三角形的性质及平行四边形的性质.由平行四边形的性质可知AD=BC ,由题意知△AFD ∽△EFB ,则根据相似三角形的性质可得32BC BE AD BE FD BF ===. 18.3或5【解析】本题重点考查了等腰三角形的性质,勾股定理,利用锐角三角函数解直角三角形等知识点.本题是一道综合性较强的题目,也是一道难度中等的题目.本题存在两种情况,如图①②所示,①过点A 作AD 垂直BC ,连结OB ,根据垂径定理可得BD=CD ,又因为53cosB =,AB=AC=5,所以BD=CD=3,在Rt △ABD 中,根据勾股定理可得AD=4,在Rt △OBD 中,根据勾股定理可得OD=1,所以AO=AD +OD=4+1=5;同理在如图②中,可以求出AO=AD -OD=4-1=3.故答案为3或5.19.本题重点考查了二次根式的化简及混合运算,本题是一道较为简单的题目.解:原式=42223-312=+++20.本题考查了分式方程、一元二次方程的解法及验根的方法等知识,难度不大.解:方程左右两边同乘以(x +1)(x -1)得6x +5(x +1)=(x +4)(x -1)整理得09-8x -x 2=解之得:1x ,9x 21-==经检验:9x 1=是原方程的根,-1x 2=是原方程的增根.所以原方程的根是x=921.本题是一道创新型题目,重点考查轴对称图形和利用勾股定理解直角三角形等知识点,可以提高学生运用数学知识解决实际问题的能力.本题是一道较简单的题目.解:(1)图略(2)因为i=1∶0.75,所以CH ∶EH=1∶0.75,设CH=x ,则EH=0.75x ,在Rt △ECH 中25x 43x 22=⎪⎭⎫ ⎝⎛+,解之得x=4或x=-4(不合题意,舍去),所以CH=4,EH=3,在Rt △DOH 中222OH DH -OD =即222r)(47-r)(7+=+所以38r = 22.本题重点考查了利用统计图和一元二次方程解决实际问题的知识.考查学生解决问题的能力和动手操作能力.本题是一道难度中等的题目.解:(1)45(2)设2006年的年增长率为x 242x )x 200(12=+则解之得x=10%所以2006年的人数为200(1+10%)=220万人.(3)图略.23.本题重点考查了平行四边形的性质及菱形、正方形的识别等重要知识点.是一道综合性的题目,也是一道难度中等的题目.证明:(1)∵四边形ABCD 为平行四边形∴OA=OC .∴△ACE 是等边三角形.∴AC=CE=AE ∴EO ⊥AC(等腰三角形三线合一)∴四边形ABCD 为菱形.(2)∵△ACE 是等边三角形.∴∠AEO=∠OEC=30°∵∠AED=2∠EAD∴∠EAD=15°∴∠DAO=45°又∵四边形ABCD 是菱形,∴∠DAO=∠BAO=45°∴∠DAB=90°∴菱形ABCD 为正方形.24.本题重点考查利用待定系数法求二次函数解析式及一次函数的性质,三角形相似等重要知识点,本题是一道综合性的题目,能较全面考查学生的能力,本题是一道难度较大的题目.解:(1) 3bx x y 2++-=的图象经过点A(-1,0),所以0=-1-b +3,则 b=2所以函数解析式为32x x y 2++-=顶点坐标为(1,4)(2) ⎪⎭⎫ ⎝⎛59,57或(3,3) 过E 作EF 垂直x 轴于F ,作H D 1垂直x 轴于H ,N D 2垂直x 轴于N ,过B 作BM 垂直x 轴于M则 Rt △BMC ∽Rt △AFE ∽Rt △AEC ∽2AND Rt ∆∴34N D AN H D AH EC AE CM BM 21==== 又∵在Rt △ACE 中,AC=5,∴AE=4又∵1E D 1=所以3AD 1=∵在H AD Rt 1∆中,34H D AH 1= ∴512AH ,59H D 1== ∴)59,57(D 1 同理3),(3D 2∴D 为)59,57(或(3,3) 25.本题属于现在中考常见的动点问题,利用动点问题重点考查了三角形相似、两圆相切、勾股定理、一元二次方程等知识点,是一个综合性极强的题目,可以培养考生灵活运用知识的能力,本题是一个较难的题目.解:(1)作ML ∥AD 交AB 于点L 则ML 是三角形的中位线所以x 212x)(421BE)(AD 21ML +=+=+= 所以0)x(x 212x)21(2221y >+=+⨯⨯= (2)作DH 垂直BC ,H 为垂足由题意知,M ,L 为外切两圆的圆心 所以2DE 1ML +=;即2DE 1x)(421+=+; 所以DE -x=2在Rt △DHE 中,HE=x -4,DH=AB=2所以224)-(x 4DE +=所以⎪⎪⎩⎪⎪⎨⎧-+==-224)(x 4DE 2x DE解之得34x =,310DE = 所以34BE = (3)如果以A ,N ,D 为顶点的三角形与△BME 相似,所以∠MBE=∠MAD ,则∠ADB=∠E因为∠ADB=∠DBE所以∠3=∠DBE 所以522024DE B D 22==+==所以84-2022BH BE ===综评:试卷重点考查学生的数学基础知识和基本运算能力.大部分填空题和选择题只考查一个知识点,一个概念或一次运算,难度基本与课本练习题难度持平,第18题的计算和推理结合简洁、合理,第19题二次根式的运算,第20题解分式方程,第21题画出轴对称图形和解直角三角形,第22题统计知识的应用,第23题的几何论证难度也不大,第24题的函数型综合题以及第25题几何型综合题难度能稍大一些.试题也出现几个考查实际应用能力的试题:如填空题第14题关于“限塑令”知晓问题的随机抽样调查问题,第21题有关图纸画轴对称图形和有关直角三角形的计算问题和第22题有关旅游收入和入境旅游人数的图象信息问题,它们突出了运用数学知识、方法解决问题的能力要求,创设的情景结合了学生的实际,但在技巧、方法的要求上又不过高,没有人为地将问题复杂化.本次考试增加了识图、读图、画图等考查日常生活中学生运用数学知识解决实际问题的能力.纵观试卷题目的实际背景都告诉学生一个事实,数学是源自生活又高于生活的.(李军刚)。
2008年上海市中考数学真题及答案

2008年上海市中考数学真题及答案(满分150分,考试时间100分钟)考生注意:1.本试卷含三个大题,共25题:第一大题选择题含Ⅰ、Ⅱ两组选做题,Ⅰ组供使用一期课改教材的考生完成,Ⅱ组供使用二期课改教材的考生完成;其余大题为共做题;一、选择题:(本大题含Ⅰ、Ⅱ两组,每组各6题,每题4分,满分24分) 考生注意:1.请从下列Ⅰ、Ⅱ两组中选择一组,并在答题纸的相应位置填涂选定的组号,完成相应的1—6题.若考生没有填涂任何组号或将两个组号全部填涂,默认考生选择了Ⅰ组;2.下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.Ⅰ组:供使用一期课改教材的考生完成1.计算23a a 的结果是( ) A .5aB .6aC .25aD .26a2.如果2x =是方程112x a +=-的根,那么a 的值是( ) A .0B .2C .2-D .6-3.在平面直角坐标系中,直线1y x =+经过( ) A .第一、二、三象限 B .第一、二、四象限 C .第一、三、四象限D .第二、三、四象限4.在平面直角坐标系中,抛物线21y x =-与x 轴的交点的个数是( ) A .3B .2C .1D .05.如果12x x ,是一元二次方程2620x x --=的两个实数根,那么12x x +的值是( ) A .6- B .2- C .6 D .26.如图1,从圆O 外一点P 引圆O 的两条切线PA PB ,,切点分别为A B ,.如果60APB ∠=,8PA =,那么弦AB 的长是( )A .4B .8C.D.Ⅱ组:供使用二期课改教材的考生完成 1.计算23a a 的结果是( ) A .5aB .6aC .25aD .26a2.如果2x =是方程112x a +=-的根,那么a 的值是( ) P图1A .0B .2C .2-D .6-3.在平面直角坐标系中,直线1y x =+经过( ) A .第一、二、三象限 B .第一、二、四象限 C .第一、三、四象限D .第二、三、四象限4.计算32a a -的结果是( ) A .aB .aC .a -D .a -5.从一副未曾启封的扑克牌中取出1张红桃,2张黑桃的牌共3张,洗匀后,从这3张牌中任取1张牌恰好是黑桃的概率是( ) A .12B .13C .23D .16.如图2,在平行四边形ABCD 中,如果AB a =,AD b =, 那么a b +等于( ) A .BD B .ACC .DBD .CA二、填空题:(本大题共12题,每题4分,满分48分) [请将结果直接填入答题纸的相应位置]7.不等式30x -<的解集是 . 8.分解因式:24x -= . 9.用换元法解分式方程21221x x x x --=-时,如果设21x y x-=,并将原方程化为关于y 的整式方程,那么这个整式方程是 . 102=的根是 . 11.已知函数()f x =(2)f = .12.在平面直角坐标系中,如果双曲线(0)ky k x=≠经过点(21)-,,那么k = .13.在图3中,将直线OA 向上平移1个单位,得到一个一次函数的图像,那么这个一次函数的解析式是 .14.为了了解某所初级中学学生对2008年6月1日起实施的“限塑令”是否知道,从该校全体学生1200名中,随机抽查了80名学生,结果显示有2名学生“不知道”.由此,估计该校全体学生中对“限塑令”约有 名学生“不知道”.图2x15.如图4,已知a b ∥,140∠=,那么2∠的度数等于 .16.如果两个相似三角形的相似比是1:3,那么这两个三角形面积的比是 .17.如图5,平行四边形ABCD 中,E 是边BC 上的点,AE 交BD 于点F ,如果23BE BC =,那么BFFD= .18.在ABC △中,5AB AC ==,3cos 5B =(如图6).如果圆O 的半径为10,且经过点B C ,,那么线段AO 的长等于 .三、解答题(本大题共7题,满分78分) 19.(本题满分10分) 计算:3(36)821+-+-. 20.(本题满分10分) 解方程:2654111x x x x x ++=--+ 21.(本题满分10分,第(1)小题满分3分,第(2)小题满分7分) “创意设计”公司员工小王不慎将墨水泼在一张设计图纸上,导致其中部分图形和数据看不清楚(如图7所示).已知图纸上的图形是某建筑物横断面的示意图,它是以圆O 的半径OC 所在的直线为对称轴的轴对称图形,A 是OD 与圆O 的交点.(1)请你帮助小王在图8中把图形补画完整;12a b图4 E DAF图5ABC图6图7 OC A 图8(2)由于图纸中圆O 的半径r 的值已看不清楚,根据上述信息(图纸中1:0.75i =是坡面CE 的坡度),求r 的值. 22.(本题满分10分,第(1)小题满分3分,第(2)小题满分4分,第(3)小题满分3分)某人为了了解他所在地区的旅游情况,收集了该地区2004至2007年每年的旅游收入及入境旅游人数(其中缺少2006年入境旅游人数)的有关数据,整理并分别绘成图9,图10.根据上述信息,回答下列问题:(1)该地区2004至2007年四年的年旅游收入的平均数是 亿元;(2)据了解,该地区2006年、2007年入境旅游人数的年增长率相同,那么2006年入境旅游人数是 万;(3)根据第(2)小题中的信息,把图10补画完整. 23.(本题满分12分,每小题满分各6分)如图11,已知平行四边形ABCD 中,对角线AC BD ,交于点O ,E 是BD 延长线上的点,且ACE △是等边三角形.(1)求证:四边形ABCD 是菱形;(2)若2AED EAD ∠=∠,求证:四边形ABCD 是正方形.2004 2005 2006 2007 年旅游收入 (亿元) 90 7050 3010 图9 旅游收入图 图10 EDB AO 图1124.(本题满分12分,第(1)小题满分5分,第(2)小题满分7分)如图12,在平面直角坐标系中,O 为坐标原点.二次函数23y x bx =-++的图像经过点(10)A -,,顶点为B .(1)求这个二次函数的解析式,并写出顶点B 的坐标;(2)如果点C 的坐标为(40),,AE BC ⊥,垂足为点E ,点D 在直线AE 上,1DE =,求点D 的坐标.25.(本题满分14分,第(1)小题满分5分,第(2)小题满分4分,第(3)小题满分5分)已知24AB AD ==,,90DAB ∠=,AD BC ∥(如图13).E 是射线BC 上的动点(点E 与点B 不重合),M 是线段DE 的中点.(1)设BE x =,ABM △的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域; (2)如果以线段AB 为直径的圆与以线段DE 为直径的圆外切,求线段BE 的长;(3)联结BD ,交线段AM 于点N ,如果以A N D ,,为顶点的三角形与BME △相似,求线段BE 的长.B A D M E C图13 B A D C 备用图x 图12参考答案一、选择题:(本大题含Ⅰ,Ⅱ两组,每组各6题,满分24分) 1.D ; 2.C ; 3.A ; 4.B ; 5.C ; 6.B . 二、填空题:(本大题共12题,满分48分) 7.3x <; 8.(2)(2)x x -+; 9.2210y y --=;10.1x =-;12.2-; 13.21y x =+; 14.30;15.40;16.1:9;17.23; 18.3或5.三、解答题:(本大题共7题,满分78分)19.解:原式13=+-················· (8分) 4=. ································ (2分)20.解:去分母,得65(1)(4)(1)x x x x ++=+-. ····················· (3分)整理,得2890x x --=. ······················· (2分) 11x ∴=-,29x =.·························· (4分) 经检验,11x =-是增根,29x =是原方程的根. ·············· (1分) 所以,原方程的根是9x =. 21.(1)(图形正确); ························· (3分) (2)解:由已知OC DE ⊥,垂足为点H ,则90CHE ∠=.1:0.75i =,43CH EH ∴=. ······················ (1分) 在Rt HEC △中,222EH CH EC +=.设4CH k =,3(0)EH k k =>,又5CE =,得222(3)(4)5k k +=,解得1k =.3EH ∴=,4CH =. ········· (3分)7DH DE EH ∴=+=,7OD OA AD r =+=+,4OH OC CH r =+=+.在Rt ODH △中,222OH DH OD +=,222(4)7(7)r r ∴++=+.解得83r =. ····························· (3分) 22.(1)45; ····························· (3分) (2)220; ······························ (4分) (3)(图正确). ···························· (3分) 23.证明:(1)四边形ABCD 是平行四边形,AO CO ∴=. ······· (2分) 又ACE △是等边三角形,EO AC ∴⊥,即DB AC ⊥. ········· (2分)∴平行四边形ABCD 是菱形;······················ (2分) (2)ACE △是等边三角形,60AEC ∴∠=. ············· (1分)EO AC ⊥,1302AEO AEC ∴∠=∠=. ··············· (1分) 2AED EAD ∠=∠,15EAD ∴∠=.45ADO EAD AED ∴∠=∠+∠=. · (1分)四边形ABCD 是菱形,290ADC ADO ∴∠=∠=. ··········· (2分) ∴四边形ABCD 是正方形. ······················· (1分) 24.解:(1)二次函数23y x bx =-++的图像经过点(10)A -,,013b ∴=--+,得2b =, ······················ (2分)所求二次函数的解析式为223y x x =-++. ··············· (1分)则这个二次函数图像顶点B 的坐标为(14),; ················ (2分)(2)过点B 作BF x ⊥轴,垂足为点F .在Rt BCF △中,4BF =,3CF =,5BC =,4sin 5BCF ∴∠=.在Rt ACE △中,sin AEACE AC∠=,又5AC =, 可得455AE =.4AE ∴=. ······················ (2分) 过点D 作DH x ⊥轴,垂足为点H .由题意知,点H 在点A 的右侧,易证ADH ACE △∽△.AH DH ADAE CE AC∴==. 其中3CE =,4AE =.设点D 的坐标为()x y ,,则1AH x =+,DH y =, ①若点D 在AE 的延长线上,则5AD =.得15435x y +==,3x ∴=,3y =,所以点D 的坐标为(33),; ②若点D 在线段AE 上,则3AD =.得13435x y +==,75x ∴=,95y =,所以点D 的坐标为7955⎛⎫⎪⎝⎭,. 综上所述,点D 的坐标为(33),或7955⎛⎫⎪⎝⎭,. ················ (5分) 25.解:(1)取AB 中点H ,联结MH ,M 为DE 的中点,MH BE ∴∥,1()2MH BE AD =+. ········ (1分) 又AB BE ⊥,MH AB ∴⊥. ····················· (1分)12ABM S AB MH ∴=△,得12(0)2y x x =+>; ··········· (2分)(1分)(2)由已知得DE =. ·················· (1分)以线段AB 为直径的圆与以线段DE 为直径的圆外切,1122MH AB DE ∴=+,即11(4)222x ⎡+=+⎣. ······· (2分)解得43x =,即线段BE 的长为43; ··················· (1分)(3)由已知,以A N D ,,为顶点的三角形与BME △相似, 又易证得DAM EBM ∠=∠. ······················ (1分) 由此可知,另一对对应角相等有两种情况:①ADN BEM ∠=∠;②ADB BME ∠=∠. ①当ADN BEM ∠=∠时,AD BE ∥,ADN DBE ∴∠=∠.DBE BEM ∴∠=∠. DB DE ∴=,易得2BE AD =.得8BE =; ··············· (2分) ②当ADB BME ∠=∠时,AD BE ∥,ADB DBE ∴∠=∠. DBE BME ∴∠=∠.又BED MEB ∠=∠,BED M EB ∴△∽△. DE BEBE EM ∴=,即2BE EM DE =,得2x =解得12x =,210x =-(舍去).即线段BE 的长为2. ··········· (2分) 综上所述,所求线段BE 的长为8或2.。
2008年中考数学试题及答案解析
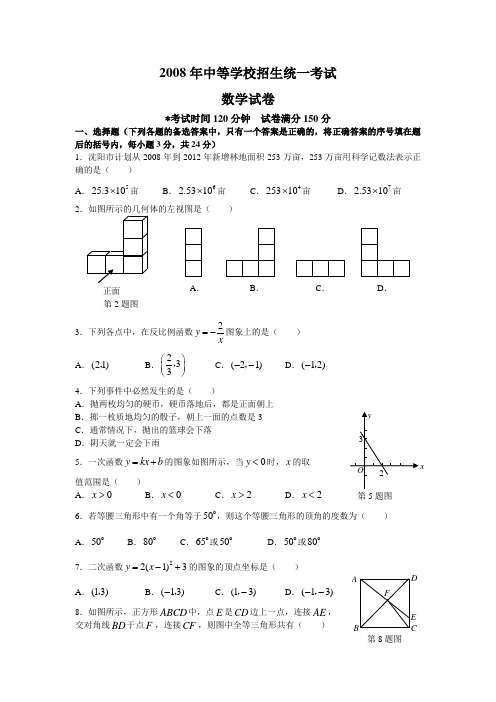
2008年中等学校招生统一考试数学试卷*考试时间120分钟 试卷满分150分一、选择题(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号填在题后的括号内,每小题3分,共24分)1.沈阳市计划从2008年到2012年新增林地面积253万亩,253万亩用科学记数法表示正确的是( ) A .525.310⨯亩B .62.5310⨯亩C .425310⨯亩D .72.5310⨯亩2)3.下列各点中,在反比例函数2y x=-图象上的是()A .(21),B .233⎛⎫⎪⎝⎭,C .(21)--,D .(12)-,4.下列事件中必然发生的是( )A .抛两枚均匀的硬币,硬币落地后,都是正面朝上B .掷一枚质地均匀的骰子,朝上一面的点数是3C .通常情况下,抛出的篮球会下落D .阴天就一定会下雨5.一次函数y kx b =+的图象如图所示,当0y <时,x 的取 值范围是( ) A .0x > B .0x <C .2x >D .2x <6.若等腰三角形中有一个角等于50,则这个等腰三角形的顶角的度数为( ) A .50B .80C .65或50D .50或807.二次函数22(1)3y x =-+的图象的顶点坐标是( )A .(13),B .(13)-,C .(13)-,D .(13)--, 8.如图所示,正方形ABCD 中,点E 是CD 边上一点,连接AE , 交对角线BD 于点F ,连接CF ,则图中全等三角形共有( )正面第2题图A .B .C .D .第5题图xADCEFB第8题图A .1对B .2对C .3对D .4对二、填空题(每小题3分,共24分)9.已知A ∠与B ∠互余,若70A ∠=,则B ∠的度数为 . 10.分解因式:328m m -= .11.已知ABC △中,60A ∠=,ABC ∠,ACB ∠的平分线交于点O ,则BOC ∠的度数为 .12.如图所示,菱形ABCD 中,对角线AC BD ,相交于点O ,若再补 充一个条件能使菱形ABCD 成为正方形,则这个条件是 (只填一个条件即可). 13.不等式26x x -<-的解集为 .14.如图所示,某河堤的横断面是梯形ABCD ,BC AD ∥,迎水坡AB 长13米,且12tan 5BAE ∠=,则河堤的高BE 为 米.15.观察下列图形的构成规律,根据此规律,第8第15题图16.在平面直角坐标系中,点A 的坐标为(11),,点B 的坐标为(111),,点C 到直线AB 的距离为4,且ABC △是直角三角形,则满足条件的点C 有 个.三、(第17小题6分,第18,19小题各8分,第20小题10分,共32分)17.计算:101(1)52-⎛⎫π-+-+- ⎪⎝⎭18.解分式方程:1233xx x=+--.19.先化简,再求值:222()()2y x y x y x y ++---,其中13x =-,3y =.第1个 ……第2个 第3个 第4个ADC BO 第12题图 B C DA 第14题图20.如图所示,在66⨯的方格纸中,每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形,如图①中的三角形是格点三角形. (1)请你在图①中画一条直线将格点三角形分割成两部分,将这两部分重新拼成两个不同的格点四边形,并将这两个格点四边形分别画在图②,图③中; (2)直接写出这两个格点四边形的周长.四、(每小题10分,共20分)21.如图所示,AB 是O 的一条弦,OD AB ⊥,垂足为C ,交O 于点D ,点E 在O 上.(1)若52AOD ∠=,求DEB ∠的度数;(2)若3OC =,5OA =,求AB 的长.22.小刚和小明两位同学玩一种游戏.游戏规则为:两人各执“象、虎、鼠”三张牌,同时各出一张牌定胜负,其中象胜虎、虎胜鼠、鼠胜象,若两人所出牌相同,则为平局.例如,小刚出象牌,小明出虎牌,则小刚胜;又如,两人同时出象牌,则两人平局. (1)一次出牌小刚出“象”牌的概率是多少?(2)如果用A B C ,,分别表示小刚的象、虎、鼠三张牌,用1A ,1B ,1C 分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少?用列表法或画树状图(树形图)法加以说明.图① 第20题图图②图③第21题图 小刚 小明A 1B 1C 1A B C 第22题图23.在学校组织的“喜迎奥运,知荣明耻,文明出行”的知识竞赛中,每班参加比赛的人数相同,成绩分为A B C D ,,,四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:请你根据以上提供的信息解答下列问题:(1)此次竞赛中二班成绩在C 级以上(包括C 级)的人数为 ; (2)请你将表格补充完整:(3)请从下列不同角度对这次竞赛成绩的结果进行分析:①从平均数和中位数的角度来比较一班和二班的成绩; ②从平均数和众数的角度来比较一班和二班的成绩;③从B 级以上(包括B 级)的人数的角度来比较一班和二班的成绩. 六、(本题12分)24.一辆经营长途运输的货车在高速公路的A 处加满油后,以每小时80千米的速度匀速行驶,前往与A 处相距636千米的B 地,下表记录的是货车一次加满油后油箱内余油量y (升)与行驶时间x (1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示y 与x 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)(2)按照(1)中的变化规律,货车从A 处出发行驶4.2小时到达C 处,求此时油箱内余油多少升?(3)在(2)的前提下,C 处前方18千米的D 处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在D处至少加多少升油,才能使货车到达B 地.(货车在D 处加油过程中的时间和路程忽略不计)第23题图 一班竞赛成绩统计图 二班竞赛成绩统计图25.已知:如图①所示,在ABC △和ADE △中,AB AC =,AD AE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD ,的中点. (1)求证:①BE CD =;②AMN △是等腰三角形.(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立; (3)在(2)的条件下,请你在图②中延长ED 交线段BC 于点P .求证:PBD AMN △∽△.八、(本题14分) 26.如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,OB =ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD .点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,. (1)判断点E 是否在y 轴上,并说明理由; (2)求抛物线的函数表达式;(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.2008年沈阳市中等学校招生统一考试C E ND A BM图① C A EM B D N图② 第25题图第26题图数学试题参考答案及评分标准一、选择题(每小题3分,共24分) 1.B 2.A 3.D 4.C 5.C 6.D7.A8.C二、填空题(每小题3分,共24分) 9.2010.2(2)(2)m m m +-11.12012.90BAD ∠=(或AD AB ⊥,AC BD =等)13.4x >14.1215.65 16.8 三、(第17小题6分,第18,19小题各8分,第20小题10分,共32分)17.解:原式1(2)5=+-+- ···························································· 4分125=-+- ··················································································· 5分6= ······································································································ 6分18.解:12(3)x x =-- ·················································································· 2分126x x =--7x = ··········································································································· 5分 检验:将7x =代入原方程,左边14==右边 ························································ 7分所以7x =是原方程的根 ·················································································· 8分 (将7x =代入最简公分母检验同样给分)19.解:原式2222222xy y x xy y x y =++-+-- ················································ 4分 xy =- ········································································································· 6分 当13x =-,3y =时,原式1313⎛⎫=--⨯= ⎪⎝⎭······················································································ 8分 20.解:(1)答案不唯一,如分割线为三角形的三条中位线中任意一条所在的直线等.································· 2分拼接的图形不唯一,例如下面给出的三种情况:图① 图② 图③ 图④图①~图④,图⑤~图⑦,图⑧~图⑨,画出其中一组图中的两个图形. ······················ 6分 (2)对应(1)中所给图①~图④的周长分别为4+8,4+4+ 图⑤~图⑦的周长分别为10,8+8+图⑧~图⑨的周长分别为2+4+ ···································· 10分 四、(每小题10分,共20分) 21.解:(1)OD AB ⊥,AD DB ∴= ··························································· 3分 11522622DEB AOD ∴∠=∠=⨯= ································································· 5分 (2)OD AB ⊥,AC BC ∴=,AOC △为直角三角形, 3OC =,5OA =,由勾股定理可得4AC == ·············································· 8分 28AB AC ∴== ························································································· 10分 22.解:(1)1()3P =一次出牌小刚出象牌“” ··················································· 4分(2)树状图(树形图):·············································································· 8分图⑤ 图⑥图⑦图⑧ 图⑨A 1B 1C 1 AA 1B 1C 1 BA 1B 1C 1C开始小刚 小明或列表···························································· 8分 由树状图(树形图)或列表可知,可能出现的结果有9种,而且每种结果出现的可能性相同,其中小刚胜小明的结果有3种. ········································································ 9分1()3P ∴=一次出牌小刚胜小明. ····································································· 10分 五、(本题12分) 23.解:(1)21······························································································ 2分 (2)一班众数为90,二班中位数为80 ······························································· 6分 (3)①从平均数的角度看两班成绩一样,从中位数的角度看一班比二班的成绩好,所以一班成绩好; ···································································································· 8分 ②从平均数的角度看两班成绩一样,从众数的角度看二班比一班的成绩好,所以二班成绩好; ················································································································· 10分 ③从B 级以上(包括B 级)的人数的角度看,一班人数是18人,二班人数是12人,所以一班成绩好. ······························································································· 12分 六、(本题12分) 24.解:(1)设y 与x 之间的关系为一次函数,其函数表达式为y kx b =+ ················ 1分将(0100),,(180),代入上式得, 10080b k b =⎧⎨+=⎩ 解得20100k b =-⎧⎨=⎩20100y x ∴=-+ ·························································································· 4分验证:当2x =时,20210060y =-⨯+=,符合一次函数; 当 2.5x =时,20 2.510050y =-⨯+=,也符合一次函数.∴可用一次函数20100y x =-+表示其变化规律,而不用反比例函数、二次函数表示其变化规律. ··················································· 5分 y ∴与x 之间的关系是一次函数,其函数表达式为20100y x =-+ ··························· 6分 (2)当 4.2x =时,由20100y x =-+可得16y =即货车行驶到C 处时油箱内余油16升. ····························································· 8分 (3)方法不唯一,如:方法一:由(1)得,货车行驶中每小时耗油20升, ············································· 9分 设在D 处至少加油a 升,货车才能到达B 地.依题意得,63680 4.220101680a -⨯⨯+=+, ··················································· 11分 解得,69a =(升) ····················································································· 12分方法二:由(1)得,货车行驶中每小时耗油20升, ············································· 9分 汽车行驶18千米的耗油量:1820 4.580⨯=(升) D B ,之间路程为:63680 4.218282-⨯-=(千米)汽车行驶282千米的耗油量:2822070.580⨯=(升) ················································································· 11分 70.510(16 4.5)69+--=(升) ···································································· 12分 方法三:由(1)得,货车行驶中每小时耗油20升, ············································· 9分设在D 处加油a 升,货车才能到达B 地.依题意得,63680 4.220101680a -⨯⨯++≤,解得,69a ≥ ····························································································· 11分 ∴在D 处至少加油69升,货车才能到达B 地. ················································· 12分七、(本题12分) 25.证明:(1)①BAC DAE ∠=∠ BAE CAD ∴∠=∠AB AC =,AD AE = ABE ACD ∴△≌△BE CD ∴= ·································································································· 3分 ②由ABE ACD △≌△得ABE ACD ∠=∠,BE CD =M N ,分别是BE CD ,的中点,BM CN ∴= ················································· 4分 又AB AC = ABM ACN ∴△≌△AM AN ∴=,即AMN △为等腰三角形 ···························································· 6分 (2)(1)中的两个结论仍然成立. ···································································· 8分 (3)在图②中正确画出线段PD由(1)同理可证ABM ACN △≌△ CAN BAM ∴∠=∠ BAC MAN ∴∠=∠ 又BAC DAE ∠=∠MAN DAE BAC ∴∠=∠=∠AMN ∴△,ADE △和ABC △都是顶角相等的等腰三角形 ································· 10分 PBD AMN ∴∠=∠,PDB ADE ANM ∠=∠=∠PBD AMN ∴△∽△ ···················································································· 12分 八、(本题14分)26.解:(1)点E 在y 轴上 ·············································································· 1分 理由如下:连接AO ,如图所示,在Rt ABO △中,1AB =,BO =2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠= 由题意可知:60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上,∴点E 在y 轴上. ································································· 3分 (2)过点D 作DM x ⊥轴于点M1OD =,30DOM ∠=∴在Rt DOM △中,12DM =,2OM =点D 在第一象限,∴点D 的坐标为12⎫⎪⎪⎝⎭, ················································································ 5分 由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),∴点A的坐标为( ·················································································· 6分抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将(A ,12D ⎫⎪⎪⎝⎭,代入22y ax bx =++中得32131242a a ⎧+=⎪⎨+=⎪⎩解得89a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为:2829y x x =--+ ·················································· 9分(3)存在符合条件的点P ,点Q . ································································· 10分。
2008年中考数学三角形解答题选编(含答案)

2008 年中考数学几何解答题 三角形1.(08市卷15题)15.(本小题满分5分)已知:如图,C 为BE 上一点,点A D ,分别在BE 两侧.AB ED ∥,AB CE =,BC ED =. 求证:AC CD =. 证明: 证明:AB ED ∥,B E ∴∠=∠.……2分在ABC △和CED △中,AB CE B E BC ED =⎧⎪∠=∠⎨⎪=⎩,,, ABC CED ∴△≌△. ·············································································· 4分 AC CD ∴=. ························································································· 5分2.(08某某某某)24.(本小题满分6分) 如图,在ABC △中,2BAC C ∠=∠.(1)在图中作出ABC △的内角平分线AD .(要求:尺规作图,保留作图痕迹,不写证明)(2)在已作出的图形中,写出一对相似三角形,并说明理由.24.解:(1)如图,AD 即为所求. ···················· 2分 (2)ABD CBA △∽△,理由如下. ················· 3分AD 平分2BAC BAC C ∠∠=∠,,BAD BCA ∴∠=∠. ······································· 5分 又B B ∠=∠,ABD CBA ∴△∽△. ··············· 6分3.(08年某某某某)(本小题满分7分)已知:如图,AB=AD,AC=AE,∠BAD=∠CAE.求证:AC=DE.(第22题)ABCDABCDACEDB(第21题图)DCBA4.(08年某某某某)(A 类)已知如图,四边形ABCD 中,AB =BC ,AD =CD ,求证:∠A =∠C. (B 类)已知如图,四边形ABCD 中,AB =BC ,∠A =∠C ,求证:AD =CD.证明:(A )连结AC ,因为AB =AC ,所以∠BAC =∠BCA ,同理AD =CD 得∠DAC =∠DCA所以∠A =∠BAC +∠DAC =∠BCA +∠DCA =∠C (B )如(A )只须反过来即可.5. (08某某某某)20.(10分)如图,∠A =36°,∠DBC =36°,∠C =72°,找出图中的一个等腰三角形,并给予证明.我找的等腰三角形是:. 证明:我所找的等腰三角形是:△ABC (或△BDC 或△DAB )…4分 证明:在△ABC 中,∵∠A =36°,∠C =72°,∴∠ABC =180°-(72°+36°)=72°. ………………………………… 7分∵∠C =∠ABC , ∴AB =AC ,∴△ABC 是等腰三角形. …………………………………………………………… 10分DC BA[注]若找△BDC 或△DAB 参照给分.6. (08某某某某)21、(8分)已知:如图,E 、C 两点在线段BF 上,BE=CF ,AB=DE ,AC=DF 。
上海市浦东新区2007—2008学年中考数学预测卷

上海市浦东新区2007—2008学年中考数学预测卷(满分150分,考试时间100分钟)考生注意:1.本试卷含三个大题,共25题;第一、二大题分别含I 、II 两组选做题,I 组供使用一期课改教材的考生完成,II 组供使用二期课改教材的考生完成;其余大题为共做题;2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题含I 、II 两组试题,每组各6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.下列实数中,无理数是…………………………………………………………………( ).(A )0 (B )3.14 (C )22 (D )722 2.(I 组)方程0352=+-x x 两根的倒数和是…………………………………………( ).(A )5 (B )3 (C )53 (D )35 (II 组)投掷一枚硬币两次,第一次正面朝上,第二次正面朝下的概率是……( ).(A )21 (B )31 (C )32 (D )41 3.在函数y =2x 、x y 2=、22x y =的图像中,具有沿某条直线翻折,直线两旁的部分能够互相重合的性质的图像有………………………………………………………………( ).(A )0个 (B )1个 (C )2个 (D )3个4.某校修建一条400米长的跑道,开工后每天比原计划多修10米,结果提前2天完成了任务.设原计划每天修x 米,那么根据题意可列出方程…………………………………( ).(A )210400400=+-x x (B )240010400=-+xx (C )210400400=--x x (D )240010400=--x x 5.在A 处观察B 处时的仰角为α,那么在B 处观察A 处时的俯角为………………( ).(A )α (B )α-︒90 (C )α+︒90 (D )α-︒1806.如果两圆的半径分别为3和4,圆心距为3,那么这两个圆的位置关系是…………( ).(A )外离 (B )外切 (C )相交 (D )内切二、填空题:(本大题含I 、II 两组试题,每组各12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置上】7.“a 的立方与b 的平方的差”用代数式表示为 .8.不等式组⎪⎩⎪⎨⎧<-≥+321,23x x 的解集为 . 9.已知522=+n m ,那么)()(n m n n m m --+的值是 .10.如果等式4)4(2-=-x x 成立,那么x 应满足的条件是 .11.如果函数5)(+=x x f ,那么)4(f = .12.如果直线y =kx +3与直线y =−2x 互相平行,那么k = .13.抛物线4322+-=x x y 与y 轴的交点坐标是 .14.在同一平面内,已知直线a 、b 、c ,且a ∥b ,b ⊥c ,那么直线a 和c 的位置关系是 .15.如果正多边形的中心角是36°,那么这个正多边形的边数是 .16.(I 组)已知⊙O 的半径为5cm ,点P 到点O 的距离为13cm ,P A 切⊙O 于点A ,那么P A = cm .(II 组)已知向量与向量== .17.已知在△ABC 中,点D 、E 分别在边AB 和AC 上,DE ∥BC ,31=AB AD ,那么△ADE 与△CDE 的面积之比是 .18.如图,已知⊙A 和⊙B 的半径相等,那么在这两个圆所在的平面内可以作为旋转中心将⊙A 旋转至⊙B 的点有 个.三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)计算:012112)12(22142)(-+++-+--.20.(本题满分10分)解方程:21221442+--+=-x x x x .21.(本题满分10分)已知:如图,在⊙O 中,弦CD 与直径AB 相交于点E ,∠BED =60°,DE =OE =2.求:(1)CD 的长;(2)⊙O 的半径.B22.(本题满分10分)为了解某地区14000名初三学生学习数学的情况,从一次数学考试的成绩中,随机抽取了部分学生的数学成绩作为一个样本,整理成如下的分数段表:说明:1.每个分数段可含最低值,不含最高值;2.分数不小于60分的为及格,分数不小于80分的为优良.根据分数段表提供的信息回答:(1)这次抽查到的学生人数为 名;(2)抽查样本的中位数所在的分数段是 ;(3)这个样本的优良率为 ;(4)这个样本的及格率为 ;(5)根据这个样本提供的数据可以估计这个地区初三学生这次数学考试的及格人数约为名.23.(本题满分12分)已知:如图,AM 是△ABC 的中线,∠DAM =∠BAM ,CD ∥AB . 求证:AB =AD +CD .24.(本题满分12分)如图,已知点A 在第一象限内,点B 和点C 在x 轴上,且关于原点O 对称,AO =AB .如果关于x 的方程07)4(22=+-++-BO BO x BO x 有实数根,△ABO 的面积为2,反比例函数的图像经过点A .(1)求BO 的长.(2)求反比例函数的解析式.(3)如果P 是这个反比例函数图像上的一点,且∠BPC =90°,求点P 的坐标.25.(本题满分14分)如图,已知在梯形ABCD 中,AD ∥BC ,AB =CD =5,52=BC AD ,53cos =B ,P 是边BC 上的一个动点,∠APQ =∠B,PQ 交射线AD 于点Q .设点P 到点B 的距离为x ,点Q 到点D 的距离为y .(1)用含x 的代数式表示AP 的长. (2)求y 关于x 的函数解析式,并写出它的定义域.(3)△CPQ 与△ABP 能否相似?如果能,请求出BP的长;如果不能,请说明理由.P Q浦东新区2007—2008学年中考数学预测卷参考答案及评分说明一、选择题:(本大题共6题,每题4分,满分24分)1.C ; 2.I 组D (II 组D ); 3.D ; 4.A ; 5.A ; 6.C .二、填空题:(本大题共12题,每题4分,满分48分)7.23b a -; 8.71<≤-x ; 9.5; 10.4≥x ; 11.3; 12.2-; 13.(0,4);14.互相垂直; 15.10; 16.I 组12(II 组3-); 17.21; 18.无数. 三、解答题:(本大题共7题,满分78分)19.解:原式=11212292+++-+………………………………………………(5分) =11222232+-+-+……………………………………………(3分) =225.……………………………………………………………………(2分) 20.解:()()21221224+--+=+-x x x x x .………………………………………………(1分) ()()222442--++-=x x x x .………………………………………………(2分) 242442+-++-=x x x x .…………………………………………………(2分)0232=+-x x .………………………………………………………………(2分) 解得 21=x ,12=x .…………………………………………………………(2分) 经检验:21=x 是增根,12=x 是原方程的根.………………………………(1分) ∴原方程的根是1=x .21.解:(1)过点O 作OF ⊥CD 于点F .∴DF =CF .……………………………………………………………………(2分)在△OEF 中,∵∠OFE =90°,∠OEF =60°,OE =2,∴EF =1.……………………(2分) ∴CF =DF =DE +EF =3.∴CD =6.………………………………………………………………………(2分)(2)联结OC .在△OEF 中,∵∠OFE =90°,∠OEF =60°,OE =2,∴OF =3.…………………(2分) 在△OFC 中,∵∠OFC =90°,CF =3,OF =3,∴OC =32.……………………(2分)22.(1)500;(2)80~100;(3)50.6%;(4)85.2%;(5)11928.………………(各2分)23.证明:延长AM ,与CD 的延长线相交于点N .∵CD ∥AB ,∴∠BAM =∠N .………………………………………………(2分)又∵∠BMA =∠CMN ,BM =CM ,∴△ABM ≌△NCM .……………………(2分)∴AB =CN . ……………………………………………………………………(2分)∵∠BAM =∠N ,∠DAM =∠BAM ,∴∠DAM =∠N .……………………(2分)∴AD =ND .……………………………………………………………………(2分)∴AB =CN =AD +CD .…………………………………………………………(2分)24.解:(1)∵关于x 的方程07)4(22=+-++-BO BO x BO x 有实数根,∴()()074422≥+--+=∆BO BO BO .…………………………………(2分) ∴()0232≥--BO .∴()022≤-BO . 又∵()022≥-BO ,∴()022=-BO .…………………………………(1分) ∴2=BO .…………………………………………………………………(1分)(2)设A (x ,y ),其中y >0.∵S △ABO =2,∴221=⋅⨯y OB .∴y =2.…………………………………(1分) 又∵AO =AB ,即点A 在OB 中垂线上,∴x =1.…………………………(1分) ∴A (1,2).设反比例函数的解析式为)0(≠=k xk y .代入A (1,2),得k =2. ∴所求反比例函数的解析式为xy 2=.……………………………………(1分) (3)设点P 的坐标为(x ,x 2). ∵点C 、B 关于原点O 对称,B (2,0),∴C (–2,0).………………(1分)∴BC =4.当∠BPC =90°时,222PC BP BC +=, 即2222242(4)2(4x x x x ++++-=).……………………………………(1分) 化简整理,得04422=+-xx .……………………………………………(1分) ∴0)2(2=-x x .∴02=-x x .整理,得22=x . 解得 2±=x .……………………………………………………………(1分) 经检验:2±=x 都是原方程的根.∴点P 的坐标为(2,2)或(2,2--).…………………………(1分)25.解:(1)作AH ⊥BC 于点H .∵53cos =B ,5=AB ,∴BH =3,AH =4.…………………………………(2分) ∴224)3(+-=x AP 2562+-=x x . …………………………………(1分)(2)∵52=BC AD ,∴526=+AD AD . ∴4=AD ,10=BC . ……………………………………………………(1分) ∵AD ∥BC ,∴∠P AQ =∠APB .∵∠APQ =∠B .∴△APQ ∽△PBA .…………………………………………………………(1分) ∴BPAP AP AQ =.………………………………………………………………(1分) ∴xx x x x y 256256422+-=+-+. ∴xx x y 25102+-=. ……………………………………………………(1分) 定义域为0<x ≤10.…………………………………………………………(1分)(3)要使△CPQ 与△ABP 相似,必须有∠PQC =∠B 或∠PCQ =∠B .(i )如果∠PQC =∠B ,那么∠APQ =∠PQC .∴AP ∥CQ .∵AQ ∥PC ,∴四边形APCQ 是平行四边形.………………………(1分) ∴AQ =PC ,即x y -=+104. ∴x xx x -=++-10425102.………………………………………(1分) 整理,得 0251622=+-x x .∴2148456164252416162±=±=⨯⨯-±=x .………………(1分) (ⅱ)如果∠PCQ =∠B 时,那么点Q 与点D 重合.………………………(1分)∴y =0,即025102=+-xx x .…………………………………………(1分) ∴x =5.……………………………………………………………………(1分) 综上所述,△CPQ 与△ABP 能相似,此时2148±=BP 或5.。
上海市08年中考试卷

上海市08年中考试卷Part 2 Vocabulary and Grammar(第二部分词汇和语法)V. Choose the best answer(选择最恰当的答案)( ) 31. Linda always takes ___ active part in sports after school.A. /B. aC. anD. the( ) 32. Betty, let's make a cake ________ some flour, sugar, butter and milk.A. atB. ofC. inD. with( ) 33. David talked with a friend of ______ on the Internet for a long time yesterday.A. heB. hisC. himD. himself( ) 34. _______engineers and workers are helping to rebuild the damaged city.A. ManyB. MuchC. A littleD. A lot( ) 35. Steven and William are keen ________ playing computer games.A. toB. withC. onD. at( ) 36. I knocked on the door several times but _________answered, so I left.A. somebodyB. nobodyC. anybodyD. everybody( ) 37. Plastic bags have caused serious environmental pollution, ________?A. haven’t theyB. have theyC. don’t theyD. do they( ) 38. The snow storm which hit this area last night was _________ in recent years.A. heavyB. heavierC. heaviestD. the heaviest ( ) 39. We should leave early tomorrow morning, ______ we won't get there on time.A. soB. orC. butD. and( ) 40. Bill won’t make any progress ______ he studies harder than before.A. ifB. whenC. becauseD. unless( ) 41. George was frightened to see a snake in the grass. His face turned ___________.A. paleB. cleanC. sadlyD. happily ( ) 42. After a long journey, the eight pandas from Wolong safely _________ in Beijing.A. arrivedB. reachedC. gotD. came ( ) 43. Look! Jane's grandmother ________ with some aged people in the park.A. dancesB. dancedC. is dancingD. was dancing ( ) 44. Kevin ________ to work in his hometown after he graduated from university.A. goesB. wentC. will goD. had gone ( ) 45. — Must I return the magazine to you right now, Sandy?— No, you _________. You may keep it until next Wednesday.A. needn’tB. can’tC. mustD. may( ) 46. Our headmaster asked us __________ a report on how to protect wild animals.A. writeB. writingC. to writeD. wrote( ) 47. The plane from Shanghai to Paris will _________ in an hour.A. take upB. take awayC. take outD. take off( ) 48. Our monitor has won the first prize in the competition. We’re very ____________ him.A. busy withB. famous forC. good atD. proud of( ) 49. Do you know ___________?A. when will the Beijing Olympic Games endB. when the Beijing Olympic Games will endC. when would the Beijing Olympic games endD. when the Beijing Olympic Games would end( ) 50. —Would you like me to bring you a cup of coffee? ---____________A. Yes, I’d like to.B. It’s a pleasure.C. Yes, please.D. It doesn’t matter.VI. Choose the word or expression which is closest in meaning to the underlined part in each sentence.(选择与下列各句中划线部分内容意思相近的单词或短语):( ) 51. Please raise your hands if you agree to the summer holiday plan.( ) 52. Most people prefer sending messages by mobile to making phone calls.( ) 53. Although the officers met with a lot of difficulties, they found a solution finally. ( ) 54. We all clapped our hands when Jin Jing, the brave Shanghai girl, entered the hall.( ) 55. Jerry hasn’t heard from Mary up till now. He is worried about her.( ) 56. I saw the young couple watering the flowers in the garden at the moment.( ) 57. Lucy got everything ready before going abroad for her further study in arts.( ) 58. Too much sweet food is bad for your health. You’d better have more vegetables and fruits.VII. Complete the sentences with the given words in their proper forms(用括号中所给单词的适当形式完成下列句子。
浦东新区2008年中考数学预测卷参考答案及评分说明

浦东新区2008年中考数学预测卷参考答案及评分说明一、选择题:(本大题共6题,每题4分,满分24分)1.C ; 2.I 组D (II 组D ); 3.D ; 4.A ; 5.A ; 6.C .二、填空题:(本大题共12题,每题4分,满分48分)7.23b a -; 8.71<≤-x ; 9.5; 10.4≥x ; 11.3; 12.2-; 13.(0,4);14.互相垂直; 15.10; 16.I 组12(II 组3-); 17.21; 18.无数. 三、解答题:(本大题共7题,满分78分)19.解:原式=11212292+++-+………………………………………………(5分) =11222232+-+-+……………………………………………(3分) =225.……………………………………………………………………(2分) 20.解:()()21221224+--+=+-x x x x x .………………………………………………(1分) ()()222442--++-=x x x x .………………………………………………(2分) 242442+-++-=x x x x .…………………………………………………(2分)0232=+-x x .………………………………………………………………(2分) 解得 21=x ,12=x .…………………………………………………………(2分) 经检验:21=x 是增根,12=x 是原方程的根.………………………………(1分) ∴原方程的根是1=x .21.解:(1)过点O 作OF ⊥CD 于点F .∴DF =CF .……………………………………………………………………(2分)在△OEF 中,∵∠OFE =90°,∠OEF =60°,OE =2,∴EF =1.……………………(2分) ∴CF =DF =DE +EF =3.∴CD =6.………………………………………………………………………(2分)(2)联结OC .在△OEF 中,∵∠OFE =90°,∠OEF =60°,OE =2,∴OF =3.…………………(2分) 在△OFC 中,∵∠OFC =90°,CF =3,OF =3,∴OC =32.……………………(2分)22.(1)500;(2)80~100;(3)50.6%;(4)85.2%;(5)11928.………………(各2分)23.证明:延长AM ,与CD 的延长线相交于点N .∵CD ∥AB ,∴∠BAM =∠N .………………………………………………(2分)又∵∠BMA =∠CMN ,BM =CM ,∴△ABM ≌△NCM .……………………(2分)∴AB =CN . ……………………………………………………………………(2分)∵∠BAM =∠N ,∠DAM =∠BAM ,∴∠DAM =∠N .……………………(2分)∴AD =ND .……………………………………………………………………(2分)∴AB =CN =AD +CD .…………………………………………………………(2分)24.解:(1)∵关于x 的方程07)4(22=+-++-BO BO x BO x 有实数根,∴()()074422≥+--+=∆BO BO BO .…………………………………(2分) ∴()0232≥--BO .∴()022≤-BO . 又∵()022≥-BO ,∴()022=-BO .…………………………………(1分) ∴2=BO .…………………………………………………………………(1分)(2)设A (x ,y ),其中y >0.∵S △ABO =2,∴221=⋅⨯y OB .∴y =2.…………………………………(1分) 又∵AO =AB ,即点A 在OB 中垂线上,∴x =1.…………………………(1分) ∴A (1,2).设反比例函数的解析式为)0(≠=k xk y .代入A (1,2),得k =2. ∴所求反比例函数的解析式为xy 2=.……………………………………(1分) (3)设点P 的坐标为(x ,x 2). ∵点C 、B 关于原点O 对称,B (2,0),∴C (–2,0).………………(1分)∴BC =4.当∠BPC =90°时,222PC BP BC +=, 即2222242(4)2(4x x x x ++++-=).……………………………………(1分) 化简整理,得04422=+-xx .……………………………………………(1分) ∴0)2(2=-x x .∴02=-x x .整理,得22=x . 解得 2±=x .……………………………………………………………(1分) 经检验:2±=x 都是原方程的根.∴点P 的坐标为(2,2)或(2,2--).…………………………(1分)25.解:(1)作AH ⊥BC 于点H .∵53cos =B ,5=AB ,∴BH =3,AH =4.…………………………………(2分) ∴224)3(+-=x AP 2562+-=x x . …………………………………(1分)(2)∵52=BC AD ,∴526=+AD AD . ∴4=AD ,10=BC . ……………………………………………………(1分) ∵AD ∥BC ,∴∠P AQ =∠APB .∵∠APQ =∠B .∴△APQ ∽△PBA .…………………………………………………………(1分) ∴BPAP AP AQ =.………………………………………………………………(1分) ∴xx x x x y 256256422+-=+-+. ∴xx x y 25102+-=. ……………………………………………………(1分) 定义域为0<x ≤10.…………………………………………………………(1分)(3)要使△CPQ 与△ABP 相似,必须有∠PQC =∠B 或∠PCQ =∠B .(i )如果∠PQC =∠B ,那么∠APQ =∠PQC .∴AP ∥CQ .∵AQ ∥PC ,∴四边形APCQ 是平行四边形.………………………(1分) ∴AQ =PC ,即x y -=+104. ∴x xx x -=++-10425102.………………………………………(1分) 整理,得 0251622=+-x x .∴2148456164252416162±=±=⨯⨯-±=x .………………(1分) (ⅱ)如果∠PCQ =∠B 时,那么点Q 与点D 重合.………………………(1分)∴y =0,即025102=+-xx x .…………………………………………(1分) ∴x =5.……………………………………………………………………(1分) 综上所述,△CPQ 与△ABP 能相似,此时2148±=BP 或5.。
08年上海中考数学答案

2008年上海市中考数学试卷答案Ⅰ组:供使用一期课改教材的考生完成1.D 分析:此题是单项式的乘法,把系数与系数相乘,字母与字母相乘,计算即可.2a•3a=2×3×a1+1=6a 2.故选D. 2.C 分析:把x═2代入方程21x+a=﹣1得出一个关于a 的方程,求出方程的解即可.∵x=2是方程21x+a=﹣1的根,∴代入得:21×2+a=﹣1,∴a=﹣2,故选C.本题考查了一元一次方程的解和解一元一次方程,解此题的关键是得出一个关于a 的方程.3.A 分析:根据一次函数图象与系数的关系,由k ,b 的符号直接判断直线所经过的象限.直线y=x+1,∵k=1>0,∴直线图象经过第一、三象限,∵b=1,∴直线与y 轴正半轴相交,∴直线y=x+1经过一、二、三象限.故选A .本题主要考查一次函数图象在坐标平面内的位置与k 、b 的关系.解答本题注意理解:直线y=kx+b 所在的位置与k 、b 的符号有直接的关系.k >0时,直线必经过一、三象限;k <0时,直线必经过二、四象限.b >0时,直线与y 轴正半轴相交;b=0时,直线过原点;b <0时,直线与y 轴负半轴相交.4.B 分析:根据b 2﹣4ac 与零的关系即可判断出二次函数y=x 2﹣1的图象与x 轴交点的个数.∵b 2﹣4ac=0﹣4×1×(﹣1)=4>0,∴二次函数y=x 2﹣1的图象与x 轴有两个交点.本题考查二次函数y=ax 2+bx+c 的图象与x 轴交点的个数的判断.5.C 分析:由一元二次方程根与系数的关系,得x 1+x 2=6.本题考查了一元二次方程根与系数的关系,方程ax 2+bx+c=0的两根为x 1,x 2,则x 1+x 2=﹣a b ,x 1•x 2=ac .6.B 分析:根据切线长定理知PA=PB ,而∠P=60°,所以△PAB 是等边三角形,由此求得弦AB 的长.∵PA 、PB 都是⊙O 的切线,∴PA=PB ,又∵∠P=60°,∴△PAB 是等边三角形,即AB=PA=8,故选B.此题主要考查的是切线长定理以及等边三角形的判定.Ⅱ组:供使用二期课改教材的考生完成1.D 分析:根据单项式与单项式相乘的运算法则:把他们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式,计算即可.2a•3a=(2×3)•(a•a )=6a 2.故选D.本题考查了单项式与单项式相乘,熟练掌握运算法则是解题的关键.2.C 分析:此题可将x=2代入方程,然后得出关于a 的一元一次方程,解方程即可得出a 的值.将x=2代入方程21x+a=﹣1得1+a=﹣1,解得:a=﹣2.故选C.此题考查的是一元一次方程的解法,方程两边可同时减去1,即可解出a 的值.3.A 分析:∵直线y=x+1∴k=1>0,b=1∴直线经过第一、二、三象限,故选A.一次函数图象的四种情况:①当k >0,b >0,函数y=kx+b 的图象经过第一、二、三象限,y 的值随x 的值增大而增大;②当k >0,b <0,函数y=kx+b 的图象经过第一、三、四象限,y 的值随x 的值增大而增大;③当k <0,b >0时,函数y=kx+b 的图象经过第一、二、四象限,y 的值随x 的值增大而减小;④当k <0,b <0时,函数y=kx+b 的图象经过第二、三、四象限,y 的值随x 的值增大而减小.4.B 分析:根据平面向量的加减运算的知识求解,即可求得答案.3a -2a =a .故选B.此题考查了平面向量的知识.此题比较简单,注意掌握平面向量的加减运算法则是解此题的关键.5.C 分析:让黑桃张数除以总张数3即可求得从这3张牌中任取1张牌恰好是黑桃的概率.∵1红桃,2黑桃的牌共3,∴这3牌中任取1张牌恰好是黑桃的概率是32.故选C. 6.B 分析:∵四边形ABCD 是平行四边形,∴AD=BC ,AD ∥BC ,∵AD =b ,∴BC =b , ∵AB =a ,∴a +b =AB +BC =AC .故选B.此题考查了平面向量的知识与平行四边形的性质.此题难度不大,注意掌握三角形法则的应用,注意数形结合思想的应用.7.x <3 分析:利用不等式的基本性质,将两边不等式同时加上3,不等号的方向不变.解不等式x ﹣3<0得,x <3.本题考查了同学们解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.解不等式要依据不等式的基本性质,在不等式的两边同时加上或减去同一个数整式不等号的方向不变;在不等式的两边同时乘以或除以同一个正数不等号的方向不变;在不等式的两边同时乘以或除以同一个负数不等号的方向改变.8.(x+2)(x ﹣2) 分析:直接利用平方差公式进行因式分解即可.x 2﹣4=(x+2)(x ﹣2).本题考查了平方差公式因式分解.能用平方差公式进行因式分解的式子的特点是:两项平方项,符号相反.9.y 2﹣2y ﹣1=0 分析:由x x 12-=y 可得y x x 112=-.所以原方程可化为y ﹣y 1=2,整理得y 2﹣2y ﹣1=0.用换元法解分式方程是一种常用的方法之一,通过换元法解分式方程可化繁为简,化难为易,因此对注意总结能用该种方法的方程特点.10.x=-1 分析:此题需把方程两边平方去根号后求解,然后把求得的值进行检验即可.两边平方得:3﹣x=4,x=﹣1.检验:当x=﹣1时,原方程的左边=2,右边=2,∴x=﹣1是原方程的根.故答案为x=﹣1.本题主要考查解无理方程,在解无理方程是最常用的方法是两边平方法及换元法,本题用了平方法.注意要把求得的x 的值代入原方程进行检验.11.3 分析:把自变量x=2代入函数关系式进行计算即可得解.()3122=+=f .本题考查了函数值的求解,比较简单,把自变量的值代入函数关系式计算即可.12.-2 分析:把点(2,﹣1)代入反比例函数y=x k 即可求出k 的值.∵反比例函数y=x k (k≠0)经过点(2,﹣1),∴﹣1=2k ,解得k=﹣2.本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定适合此函数的解析式.13.y=2x+1 分析:寻找寻找原直线解析式上的向上平移1个单位得到的点.可从直线OA 上找两点:(0,0)、(2,4)这两个点向上平移1个单位得到的点是(0,1)(2,5),那么这两个点在将直线OA 向上平移1个单位,得到一个一次函数的图象y=kx+b 上,则b=1,2k+b=5,解得:k=2.∴解析式为y=2x+1.解决本题的关键是找到所求直线解析式中的两个点.14.30 分析:用随机抽查的80名学生中有2名学生对“限塑令”不知道,即可求得不知道的所占的比例是802=401,即可估计该校全体学生中对“限塑令”约有多少名学生“不知道”.1200×401=30.本题考查统计中用样本估计总体的思想.15.40 分析:根据两条直线平行,同位角相等可以得∠1的同位角是40,再根据对顶角相等可以求出∠2.如图,∵∠1=40°,∴∠3=40°,∵a ∥b ,∴∠2=∠3=40°.故答案为40.此题主要运用了平行线的性质以及对顶角相等的性质.16.1:9 分析:根据相似三角形的面积比等于相似比的平方求出即可.∵两个相似三角形的相似比是1:3,又∵相似三角形的面积比等于相似比的平方,∴这两个三角形面积的比是1:9.本题考查了相似三角形的性质,注意:相似三角形的面积比等于相似比的平方. 17.32 分析:由平行四边形的性质可证△BEF ∽△DAF ,再根据相似三角形的性质得BE :DA=BF :DF 即可解.ABCD 是平行四边形,∴BC ∥AD ,BC=AD ∴△BEF ∽△DAF ∴BE :DA=BF :DF ∵BC=AD ∴BF :DF=BE :BC=2:3.本题考查了平行四边形的性质及相似三角形的判定定理和性质.18.3或5 分析:分两种情况考虑:(i )如图1所示,∵AB=AC ,OB=OC ,∴AO 垂直平分BC ,∴OA ⊥BC ,D 为BC 的中点,在Rt △ABD 中,AB=5,cos ∠ABC=53,∴BD=3,根据勾股定理得:AD=22BD AB -=4,在Rt △BDO 中,OB=10,BD=3,根据勾股定理得:OD=22BD OB -=1,则AO=AD+OD=4+1=5;(ii )如图2所示,∵AB=AC ,OB=OC ,∴AO 垂直平分BC ,∴OD ⊥BC ,D 为BC 的中点,在Rt △ABD 中,AB=5,cos ∠ABC=53, ∴BD=3,根据勾股定理得:AD=22BD AB -=4,在Rt △BDO 中,OB=10,BD=3,根据勾股定理得:OD=22BD OB -=1,则OA=AD ﹣OD=4﹣1=3,综上,OA 的长为3或5. 分析:分两种情况考虑:(i )如图1所示,由AB=AC ,OB=OC ,利用线段垂直平分线逆定理得到AO 垂直平分BC ,在直角三角形ABD 中,由AB 及cos ∠ABC 的值,利用锐角三角函数定义求出BD 的长,再利用勾股定理求出AD 的长,在直角三角形OBD 中,由OB 与BD 的长,利用勾股定理求出OD 的长,由AD+DO 即可求出AO 的长;(ii )同理由AD ﹣OD 即可求出AO 的长,综上,得到所有满足题意的AO 的长.此题考查了垂径定理,勾股定理,等腰三角形的性质,以及直角三角形的性质,熟练掌握定理及性质是解本题的关键.19. 原式=2+1+3-23+22=4. 分析:先分母有理化,再根据二次根式乘除法进行计算即可.本题考查了二次根式的混合运算,是基础知识要熟练掌握.20.方程两边都乘以(x+1)(x ﹣1),得6x+5(x+1)=(x+4)(x ﹣1),整理得x 2﹣8x ﹣9=0, 解得x=9或﹣1.检验:当x=﹣1时,(x+1)(x ﹣1)=0,∴x=﹣1是增根,舍去.当x=9时,(x+1)(x ﹣1)≠0,∴x=9是原方程的解. 分析:由于x 2﹣1=(x+1)(x ﹣1),所以本题的最简公分母是(x+1)(x ﹣1).方程两边都乘最简公分母,可把分式方程转换为整式方程求解.解分式方程的基本思想是“转化思想”,方程两边都乘最简公分母,把分式方程转化为整式方程求解.解分式方程一定注意要代入最简公分母验根.需注意:当分母是多项式,又能进行因式分解时,应先进行因式分解,再确定最简公分母.21.(1)补全图形如图所示;(2)由已知OC ⊥DE ,垂足为点H ,则∠CHE=90°.∵i=1:0.75,∴EH CH =34.在Rt △HEC 中,EH 2+CH 2=EC 2.设CH=4k ,EH=3k (k >0),又∵CE=5,得(3k )2+(4k )2=25,解得k=1.∴EH=3,CH=4.∴DH=DE+EH=7,OD=OA+AD=r+7,OH=OC+CH=r+4.在Rt △ODH 中,OH 2+DH 2=OD 2,∴(r+4)2+72=(r+7)2.解得r=38. 分析:(1)由图形是关于半径OC 所在直线为对称轴的轴对称图形,将图形补画完整.(2)由坡面CE 的坡度求得CH 、EH 的长,再在△DOH 中,运用勾股定理求得圆O 的半径r .此题主要考查学生对坡度坡角的掌握及三角函数、勾股定理的运用能力.22.(1)该地区2004至2007年四年的年旅游收入的平均数=(10+30+50+90)÷4=45(亿元);(2)由于该地区2006年、2007年入境旅游人数的年增长率相同,设年增长率为x ,则得:200(1+x )2=242,解得,x=10%,或x=﹣2.1(舍去),所以2006年入境旅游人数=200×(1+10%)=220万人;(3)如图所示. 分析:(1)折线图中得出2004至2007年四年的年旅游收入分别为:10,30,50,90亿元,根据平均数的概念计算平均数;(2)由于该地区2006年、2007年入境旅游人数的年增长率相同,可设年增长率为x ,根据题意,列出方程,进而即可求出答案;(3)补充统计图即可.解决有关统计图的问题关键在于读图,理解图象中所蕴含的信息,运用所学知识去解决问题.此题考查学生识别图象,并能获取信息和解决问题的能力.23.证明:(1)∵四边形ABCD 是平行四边形,∴AO=CO .又∵△ACE 是等边三角形,∴EO ⊥AC (三线合一),即AC ⊥BD ,∴四边形ABCD 是菱形(对角线互相垂直的平行四边形是菱形).(2)∵四边形ABCD 是平行四边形,∴AO=CO .又∵△ACE 是等边三角形,∴EO 平分∠AEC (三线合一),∴∠AED=21∠AEC=21×60°=30°,又∵∠AED=2∠EAD ∴∠EAD=15°,∴∠ADO=∠DAE+∠DEA=15°+30°=45°(三角形的一个外角等于和它外角不相邻的两内角之和),∵四边形ABCD 是菱形,∴∠ADC=2∠ADO=90°,∴平行四边形ABCD 是正方形. 分析:(1)根据对角线互相垂直的平行四边形是菱形.由题意易得△AOE ≌△COE ,∴∠AOE=∠COE=90°,∴BE ⊥AC ,∴四边形ABCD 是菱形;(2)根据有一个角是90°的菱形是正方形.由题意易得∠ADO=∠DAE+∠DEA=15°+30°=45°,∵四边形ABCD 是菱形,∴∠ADC=2∠ADO=90°∴四边形ABCD 是正方形.此题主要考查菱形和正方形的判定,要灵活应用判定定理及等腰三角形的性质、外角的性质定理.24.(1)∵二次函数y=﹣x 2+bx+3的图象经过点A (﹣1,0),∴0=﹣1﹣b+3,解得b=2,所求二次函数的解析式为y=﹣x 2+2x+3,则这个二次函数图象顶点B 的坐标为(1,4);(2)过点B 作BF ⊥x 轴,垂足为点F ,在Rt △BCF 中,BF=4,CF=3,BC=5,∴sin ∠BCF=54,在Rt △ACE 中,sin ∠ACE=AC AE ,又∵AC=5,可得5AE =54,∴AE=4,过点D 作DH ⊥x 轴,垂足为点H .由题意知,点H 在点A 的右侧,易证△ADH ∽△ACE ,∴ACAD CE DH AE AH ==,其中CE=3,AE=4,设点D 的坐标为(x ,y ),则AH=x+1,DH=y ,①若点D 在AE 的延长线上,则AD=5,得41+x =3y =55,∴x=3,y=3,所以点D 的坐标为(3,3);②若点D 在线段AE 上,则AD=3.得41+x =3y =53,∴57=x ,59=y ,所以点D 的坐标为(57,59).综上所述,点D 的坐标为(3,3)或(57,59). 分析:(1)将点A 的坐标代入,可得出b 的值,从而求出函数解析式,然后可得出顶点坐标;(2)过点B 作BF ⊥x 轴,垂足为点F ,过点D 作DH ⊥x 轴,垂足为点H .由题意知,点H 在点A 的右侧,则可得出△ADH ∽△ACE ,从而有ACAD CE DH AE AH ==,然后分别讨论,①若点D 在AE 的延长线上,则AD=5,解出x 和y 的值,若点D 在线段AE 上,则AD=3,同理也可求出点D 的坐标.此题属于二次函数综合题,涉及了待定系数法求函数解析式、相似三角形的判定与性质,解答本题的难点是第二问,关键是分类讨论,注意不要漏解,难度一般.25.(1)取AB 的中点H ,连接MH ,∵M 是线段DE 的中点∴MH=21(BE+AD ),MH ∥AD ,∵∠DAB=90°,∴AD ⊥AB ,∴MH ⊥AB ,∴S △ABM =21AB•MH 得y=21x+2;(x >0)(2)过点D 作DF ⊥BC 交于F ,由图形可得DE=()2224+-x ,又∵MH=21AD+21BE=21(AD+BE ),即21(x+4)=21[2+()2224+-x ].解得x=34.即线段BE 的长为34.(3)因为如果三角形ADN 和BME 相似,一定不相等的角是∠ADN 和∠MBE ,因为AD ∥BC ,如果两角相等,那么M 与D 重合,显然不合题意,故应分两种情况进行讨论.①当∠ADN=∠BEM 时,那么∠ADB=∠BEM ,作DF ⊥BE ,垂足为F ,tan ∠ADB=tan ∠BEM .AB :AD=DF :FE=AB :(BE ﹣AD ).即2:4=2:(x ﹣4).解得x=8.即BE=8.②∠ADB=∠BME ,而∠ADB=∠DBE ,∴∠DBE=∠BME ,∵∠E 是公共角,∴△BED ∽△MEB ,∵EM BE BE DE =,即BE 2=DE•EM ,∴BE 2=21DE 2,∴x 2=21[22+(x ﹣4)2],∴x 1=2,x 2=﹣10(舍去),∴BE=2.综上所述线段BE 为8或2. 分析:(1)在△ABM 中,已知了AB 的长,要求面积就必须求出M 到AB 的距离,如果连接AB 的中点和M ,那么这条线就是直角梯形的中位线也是三角形ABM 的高,那么AB 边上的高就是(AD+BE )的一半,然后根据三角形的面积公式即可得出y ,x 的函数关系式;(2)根据以AB ,DE 为直径的圆外切,那么可得出的是AD+BC=AB+DE ,那么可根据BE ,AD 的差和AB 的长,用勾股定理来表示出DE ,然后根据上面分析的等量关系得出关于x 的方程,即可求出x 的值,即BE 的长;(3)如果三角形ADN 和BME 相似,一定不相等的角是∠ADN 和∠MBE ,因为AD ∥BC ,如果两角相等,那么M 与D 重合,显然不合题意.因此本题分两种情况进行讨论:①当∠ADN=∠BME 时,∠DBE=∠BME ,因此三角形BDE 和MBE 相似,可得出关于DE ,BE ,EM 的比例关系式,即可求出x 的值.②当∠AND=∠BEM 时,∠ADB=∠BEM ,可根据这两个角的正切值求出x 的值.本题主要考查了直角梯形的性质,中位线定理以及相似三角形的性质等知识点,(3)中要根据不同的对应角相等来分情况讨论,不要漏解.。
上海市2008年—2014年中考数学压轴题图文解析

满分解答
(1)如图 2,过点 A 作 AH⊥BC,垂足为 H.
4 ,所以 BH=4,AH=3. 5 又已知 BC=8,由于 BH=4,所以点 A 在 BC 的垂直平分线上. 所以 CA=BA=5 . 如图 3,当圆 C 经过点 A 时,CP=CA =5.
在 Rt△ABH 中,AB=5 ,cosB=
图2 图3 (2)如图 4,当 AP//CG 时,由于 AE//BC,CP=CE ,所以四边形 AECP 是菱形,边长 为圆的半径 r. 过点 C 作 CQ⊥AD,垂足为 Q. 在 Rt△CEQ 中, CQ=3 ,CE= r, EQ=4-r,由勾股定理,
1 1 8 4 S△BDP= BP DE (t 3) (t 3) , 2 2 3 3
如图 6,过点 D 作 x 轴的平行线交 y 轴于 M,过点 P 作 y 轴的平行线,设两条直线交于 点 N.
8 1 4 由于 S 矩形 OMNP= t ,S△OCP=t,S△OCP= ,S△PND= (t 1) , 3 3 3 8 1 4 4 所以 S△CDP= t t (t 1) t 1 . 3 3 3 3 4 1 解方程 (t 3) t 1 ,得 t=5. 3 3
华东师大出版社荣誉出品 《挑战中考数学压轴题》系列产品·2
上海市 2008 年—2014 年中考数学压轴题图文解析
例1 例2 例3 例4 例5 例6 例7 例8 例9 例 10 例 11 例 12 例 12 2014 年上海市中考第 24 题 / 2 2014 年上海市中考第 25 题 / 4 2013 年上海市中考第 24 题 / 6 2013 年上海市中考第 25 题 / 8 2012 年上海市中考第 24 题 / 10 2012 年上海市中考第 25 题 / 12 2011 年上海市中考第 24 题 / 14 2011 年上海市中考第 25 题 / 16 2010 年上海市中考第 24 题 / 18 2010 年上海市中考第 25 题 / 19 2009 年上海市中考第 24 题 / 21 2009 年上海市中考第 25 题 / 23 2008 年上海市中考第 25 题 / 25
2008-2011年上海市中考数学试题汇编 2

统计图表专题要点:1、扇形图:即用圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分占总体的百分比的大小,这样的统计图叫做扇形图。
2、条形图:用一个单位长度表示一定的数量关系,根据数量的多少画成长短不同的条形,条形的宽度必须保持一致,然后把这些条形排列起来,这样的统计图叫做条形图。
3、折线图:折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后用线段顺次把各点连接起来,这样的统计图叫做折线图。
4、频数分布直方图:在统计数据时,我们经常把数据按照不同的范围分成几个组,分成的组的个数称为组数,每一组两个端点的差称为组距。
一般我们称落在不同小组中的数据个数为该组的频数,在平面直角坐标系中,横轴标出每个组的端点,纵轴表示频数,每个矩形的高代表对应的频数,我们称这样的统计图为频数分布直方图,直方图中各矩形之间没有空隙。
5、频率分布直方图:在平面直角坐标系中,横轴标出每个组的端点,纵轴表示“频率/组距”,每个矩形的面积表示这一组数据的频率。
我们称这样的统计图为频率分布直方图,直方图中各矩形之间没有空隙。
举例:1、如图所示的是某粮店的大米、面粉、小米、玉米面的销售情况统计图,观察图形,你能从中得到哪些信息?如果你是这家粮店的老板,你会怎么做?分析:这个问题是一道开放性问题。
其目的是想通过这个统计图得到很多有用的信息,其中的有些信息可以帮助老板了解民众的需求量大小,如:(1)大米的销售量最大,需多进货;(2)小米的销售量最小,需少进货;(3)面粉的需求量仅次于大米的需求量,也应多进货,等等。
2、政府为了更好地加强城市建设,就社会热点问题广泛征求市民意见,方式是发调查表,要求每位被调查人员只写一个你最关心的有关城市建设的问题,经统计整理,发现对环境保护问题提出的最多,共700人,同时作出相应的条形统计图,如图所示,请回答下列问题.(1)共收回调查表多少张?(2)提道路交通问题的有多少人?(3)请你把这个条形统计图用扇形统计图表示出来.分析:(1)700÷35%=2000(张),∴共收回调查表2000张.(2)2000×20%=400(人),∴提道路交通问题的有400人.(3)表示各问题的扇形的圆心角度数为:其他:360°×5%=18°.房屋建设:360°×15%=54°.环境保护:360°×35%=126°.绿化:360°×25%=90°.道路交通:360°×20%=72°.3、美化城市,改善人们的居住环境已成为城市建设的一项重要内容,某市城区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿化面积不断增加,如图所示,根据图中所提供的信息,回答下列问题.(1)2004年底的绿地面积为多少公顷?比2003年底增加了多少公顷?(2)在2002年、2003年、2004年这三年中,增加绿地面积最多的是哪年?(3)为满足城市发展的需要,计划在2005年底使城市绿地面积达到70.2公顷,试求2005年底绿地面积的增长率.分析:(1)2004年底的绿地面积为60公顷,比2003年底增加了60-56=4(公顷). (2)51-48=3(公顷),56-51=5(公顷),60-56=4(公顷),∴绿地面积增加最多的是2003年.(3)设2005年绿地面积的年增长率为x,依题意得60(1+x)=70.2,解得x=17%。
2008年南汇区中考数学模拟卷参考答案及评分标准

2008年南汇区中考数学模拟卷参考答案及评分标准一、选择题(Ⅰ、Ⅱ组)1.B 2.C 3.A 4.B 5.D 6.C.二、填空题7.22b a - 8.()n m m 327+ 9. a a 22 10.02=+y x 11.10 12.二、三、四 13.左 下 14.50 15.5 16.120 17.222- 18.21cm 或9cm.三、解答题19.去分母,得()()x x -≤-7223, …………………………2′去括号,得x x 21463-≤-,……………………………2′移项、合并同类项,得 205≤x , ……………………2′两边都除以5,得 4≤x .………………………………2′所以不等式的正整数解是:1,2,3,4. ………………2′20.解:(1) 将点A 的坐标(-2,1)代入2,-==m x m y 得………2′ ∴ xy 2-= …………………………1′ 将点B 的坐标(1,n )代入2,2-=-=n xy 得…………………1′ 故点B 的坐标为(1,-2) …………………………1′将(-2,1)和(1,-2)分别代入b kx y +=,得⎩⎨⎧-=-=⇒⎩⎨⎧-=+=+-.1,12,12b k b k b k …………………………2′ ∴反比例函数解析式为xy 2-=,一次函数解析式为1--=x y . …………………………1′(2) 02<<-x , 1>x . …………………………2′21.证明:∵∠ABC =∠ACB =60°…………………………1′∴∠ABD =∠ECD =120°…………………………2′又∵∠ADB +∠DAB =∠ABC =60°…………………2′∠ADB +∠EDC =60°…………………………1′∴∠DAB =∠EDC …………………………2′ ∴⊿ABD ∽⊿DCE …………………………2′22.解:(1)04年至08年甲校学生参加课外活动的人数比乙校增长得快(答案合理即可). …………………………3′(2)比较大小(填 >、=、<):08年甲校参加科技活动的学生数 > 08年乙校参加科技活动的学生数.…………………………3′(3)804%30680%501200=⨯+⨯(人) …………………………4′23.解:(1)设商品的单价为(60+x )元,则每个商品的利润是()[]5060-+x 元,销售量是(500-10x )个. …………………………1′依题意,有 ()[]()8000105005060=--+x x .………………………2′ 整理,得 0300402=+-x x , …………………………1′ 解方程,得 30,1021==x x , …………………………1′ 商品的单价可定为60+10=70元,或60+30=90元. …………………………1′当商品单价为70元时,其进货量为500-10×10=400个;当商品单价为90元时,其进货量为500-10×30=200个. …………………………1′答:售价为70元时,进货是400个;售价为90元时,进货是200个. …………………………1′(2)由 ()[]()10000105005060=--+x x , …………………………1′ 整理,得 0500402=+-x x , …………………………1′ ∵ 020001600<-=∆, …………………………1′ 方程无实根.即赚10000元不可能. …………………………1′…………………………1′24. (1) ⎪⎭⎪⎬⎫=∠=∠=CN BM BCN ABM BCAB (1′) (SAS) ∠BAM =∠CBN (1′)∠BAQ +∠ABQ ∠ABQ +∠QBM ……(1′) 60……(1′)(2) ∵ABCD 为正方形,∴∠ABC =∠BCD =90°,AB=BC . ……(1′)在⊿ABM 和⊿BCN 中, BCN ABM CN BM BCN ABM BC AB ∆≅∆⇒⎪⎭⎪⎬⎫=∠=∠=. …………………………2′∴ ∠BAQ = ∠QBM ,∴ ∠BQM = ∠BAQ +∠ABQ =∠ABQ +∠QBM =90°. ……………………2′(3)108°,120°,180°-n︒360或()n n ︒-1802……………………1′+1′+1′ 25.解:(1) 过点P 作P E ⊥BC 于E ,在R t ⊿ABC 中,10862222=+=+=BC AB AC 米. …………1′ 依题意有 t PC t CQ t AP 210,,2-===.由 AB ⊥BC,PE ⊥BC ,得PE ∥AB ,∴ACPC AB PE =.即()65621053102106+-=-=⇒-=t t PE t PE ………………………2′ ∴⎪⎭⎫ ⎝⎛+-⋅⋅-⨯⨯=-=∆∆656218621t t S S S PQC ABC 243532+-=t t . 即 243532+-=t t S . (0<t<5) …………………………3′+1′ (2) ①当QC PC =时,有 )(310210秒=⇒-=t t t . …………………………2′ ②当QC PQ =时,有 ()9255421021=⇒=-t t t (秒) …………………………2′ ③当PC PQ =时,有 21805421021=⇒=-t t t (秒) …………………………2′ 所以,当t 为秒秒、秒、2180925310时,⊿PQC 为等腰三角形. ……1′。
