各章计算题及答案
初中数学各章试题及答案

初中数学各章试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项是正数?A. -3B. 0C. 5D. -1答案:C2. 以下哪个图形是轴对称图形?A. 平行四边形B. 矩形C. 梯形D. 非等腰三角形答案:B3. 计算 \(3x + 5 = 14\) 的解,正确的是?A. \(x = 3\)B. \(x = 1\)C. \(x = 4\)D. \(x = 2\)答案:A4. 一个圆的半径是5厘米,那么它的面积是多少平方厘米?A. 78.5B. 25πC. 100πD. 50π答案:C5. 以下哪个是二次方程?A. \(x + 2 = 0\)B. \(x^2 + 2x + 1 = 0\)C. \(x^2 - 4x + 4 = 0\)D. \(x^3 - 2x^2 + 3 = 0\)答案:B二、填空题(每题3分,共15分)6. 一个数的相反数是-7,这个数是______。
答案:77. 计算 \((2x - 3) + (x + 4)\) 的结果,合并同类项后得到______。
答案:3x + 18. 一个等腰三角形的底角是45°,那么顶角的度数是______。
答案:90°9. 已知一个长方体的长、宽、高分别是5cm、3cm、2cm,那么它的体积是______立方厘米。
答案:3010. 一个数的平方根是4,那么这个数是______。
答案:16三、解答题(每题10分,共20分)11. 解方程 \(2x - 3 = 7\),并说明解法。
答案:首先移项,得到 \(2x = 7 + 3\),即 \(2x = 10\),然后两边同时除以2,得到 \(x = 5\)。
12. 证明三角形内角和为180°。
答案:设三角形的三个内角分别为A、B、C。
根据三角形的外角定理,一个外角等于两个不相邻内角的和。
因此,角A的外角等于角B加角C。
同理,角B的外角等于角A加角C,角C的外角等于角A加角B。
管理会计计算题及答案
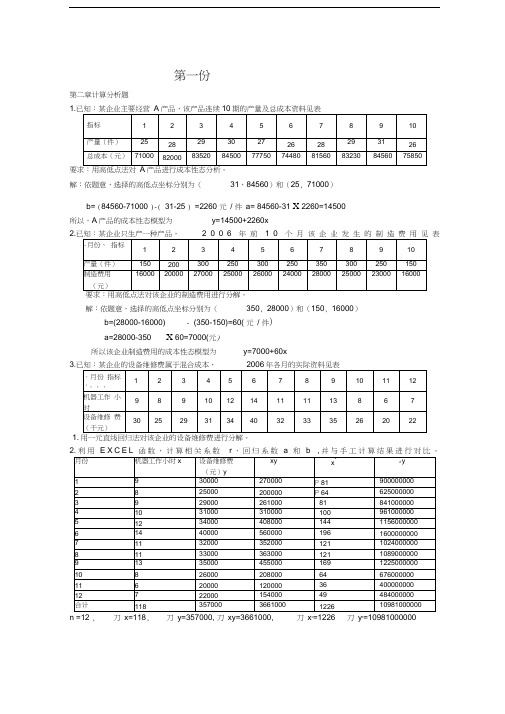
第一份第二章计算分析题1.要求:用高低点法对产品进行成本性态分析。
解:依题意,选择的高低点坐标分别为(31,84560)和(25, 71000)b= (84560-71000 )-( 31-25 ) =2260 元/ 件a= 84560-31 X 2260=14500所以,A产品的成本性态模型为y=14500+2260x2.表解:依题意,选择的高低点坐标分别为(350, 28000)和(150, 16000)b=(28000-16000) - (350-150)=60( 元/ 件)a=28000-350 X 60=7000(元)所以该企业制造费用的成本性态模型为y=7000+60x3.1. 用一元直线回归法对该企业的设备维修费进行分解。
n =12 , 刀x=118, 刀y=357000, 刀xy=3661000, 刀x2=1226 刀y2=109810000002 2r=(12 X 3661000-118 X 357000)十 (12X 1226-118 )x( 12X 10981000000-357000 )〜0.9785 T + 1 (x 与y 基本正相关)b=(12 X 3661000-118 X 357000) - (12 X 1226-118 2)=2292 元/ 小时a=(357000-2292 X 118) - 12=7212 元因此,该企业的成本性态模型为: y=7212+2292x第三章变动成本法计算成本题(注:计算变动非生产成本的业务量用销售量)1.已知:某公司从事单一产品生产, 连续三年销售量均为 1000件,而三年的产量分别为 1000件、1200件和800件。
单位产品售价为 200元,管理费用与销售费用均为固定成本,两项 费用各年总额均为50000元,单位产品变动生产成本为90元,固定性制造费用为 20000元,第一年的期初存货量为零。
(1) 分别采用变动成本法和完全成本法计算第一年的营业利润。
生产运作管理课后计算机题及实践题(部分)答案
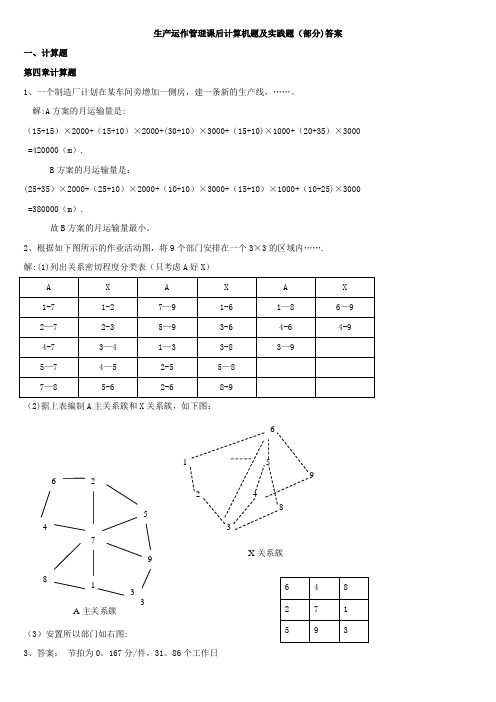
生产运作管理课后计算机题及实践题(部分)答案一、计算题 第四章计算题1、一个制造厂计划在某车间旁增加一侧房,建一条新的生产线,……。
解:A 方案的月运输量是:(15+15)×2000+(15+10)×2000+(30+10)×3000+(15+10)×1000+(20+35)×3000 =420000(m ).B 方案的月运输量是:(25+35)×2000+(25+10)×2000+(10+10)×3000+(15+10)×1000+(10+25)×3000 =380000(m ).故B 方案的月运输量最小。
2、根据如下图所示的作业活动图,将9个部门安排在一个3×3的区域内……. 解:(1)列出关系密切程度分类表(只考虑A 好X )(2)据上表编制A 主关系簇和X 关系簇,如下图:(3)安置所以部门如右图:3、答案: 节拍为0。
167分/件,31。
86个工作日X 关系簇4、答案:(2)节拍为0。
25分/件,(3)最小工作地数为5 (4)重新组合的工作地为:(A,B),(C,D,E),(F,G),(H,I),(J),(K,L),效率为83.3%5、答案:为A第五章计算题:1、一个工作人员欲制定一个金属切削作业的时间定额……解:正常时间为:10。
4×125%=13(分)标准时间为:13×(1+16%)=15。
08(分)2、观测一项作业,共60次……解:(1)观测到的时间:1.2分钟(2)正常时间:1。
2×95%=1。
14分钟(3)标准时间:1。
2×95%×(1+10%)=1。
27分钟3、答案:377分钟.4、答案:5.85分钟。
5、一新达成的工会合同允许……解:正常工作时间:(分)标准作业时间:6、答案:57次观察。
7、答案:37个周期.8、在一个对航空特快货运飞机……解:(1)闲置时间百分数的估计值是:6/60=10%(2)大约需要的观测次数为:第六章计算题:1、答案:(1)依题意以∝=0。
本科管理会计各章计算习题和答案

第二章习题1.某公司2004年下半年各月设备维修费资料如下:月份 7 8 9 10 11 12业务量(千小时) 40 32 52 48 56 44维修费(元)580 500 700 660 740 625要求:⑴根据上述资料采用高低点法将维修费分解为固定成本和变动成本,并写出成本公式;⑵2005年1月该公司计划使用机器55千小时,则预计的机器设备维修费为多少?2.新华化工厂今年只产销一种产品A,其产销量及有关成本资料如下:产销资料成本资料0件单位直接材料10元期初存货本期2000件单位直接人工8元产量本期1500件单位变动制造费6元销量期末500件固定制造费20000元存货单价50元固定推销管理费4000元要求:分别采用变动成本计算法和完全成本计算法,⑴计算本年度的单位产品生产成本和期末存货成本;⑵计算本年度的税前利润3.甲工厂只生产一种产品,2005年有关的业务量、售价与成本资料如下:期初存货量0,本年投产完工量2000件,本年销售量1000件,单价200元/件,直接材料元,直接人工80000元,变动制造费用8000元。
固定制造费用20000元,变动销售费用2000元,固定销售费用2500元,变动管理费用1000元,固定管理费用5000元。
要求:分别用变动成本法和完全成本法计算该企业的单位产品成本和期间成本。
4.某公司只生产一种产品,全年产量为1200件,每件直接材料6元,直接人工3元,变动制造费用2元,全年固定制造费用6000元。
该公司本年销售产品1000件,该产品单价20元,每件变动销售及管理费用1元,固定销售及管理费用为1000元。
要求:用两种成本计算法:⑴计算单位产品成本和总成本;⑵计算该公司的收益。
5.某企业只产销一种产品,第一、第二年的销售量均为6000件,而产量分别为6000件、8000件。
第一年期初存货为0,每件产品的售价10元,单位变动成本为4元,固定制造费用总额每年24000元,各年的固定推销与管理费用为5000元。
中职数学各章习题含答案

中职数学各章习题含答案中职数学各章习题含答案数学是一门重要的学科,它不仅是科学研究的基础,也是我们日常生活中必不可少的一部分。
对于中职学生来说,数学的学习更加注重实用性和应用性。
为了帮助中职学生更好地掌握数学知识,本文将为大家提供中职数学各章习题含答案。
第一章:整数与有理数1. 计算:(-3) + 5 - (-2) + (-4) = ?答案:-42. 计算:(-2) × (-3) × 4 = ?答案:243. 计算:(-5) ÷ 2 = ?答案:-2.54. 计算:(-2) ÷ (-4) = ?答案:0.5第二章:代数式与多项式1. 计算:(3x + 4y) - (2x - 5y) = ?答案:5x + 9y2. 计算:(2x + 3y) × (4x - 5y) = ?答案:8x² + 7xy - 15y²3. 计算:(3x - 2y) ÷ (x + y) = ?答案:3 - 5/(x + y)4. 计算:(2x + 3y)² = ?答案:4x² + 12xy + 9y²第三章:一次函数与一元一次方程1. 计算:解方程2x + 5 = 15答案:x = 52. 计算:解方程3(x + 2) = 15答案:x = 33. 计算:解方程2x - 3 = 5x + 2答案:x = -14. 计算:解方程2(3x - 1) = 4(2x + 3) - 4x 答案:x = -5第四章:二次函数与一元二次方程1. 计算:解方程x² - 6x + 8 = 0答案:x = 2, x = 42. 计算:解方程2x² + 3x - 2 = 0答案:x = -2, x = 0.53. 计算:解方程3x² - 4x + 1 = 0答案:x = 1/3, x = 14. 计算:解方程x² + 5x + 6 = 0答案:x = -2, x = -3第五章:函数与方程组1. 计算:解方程组2x + y = 53x - y = 1答案:x = 2, y = 12. 计算:解方程组x + y = 32x - y = 4答案:x = 2, y = 13. 计算:解方程组3x + y = 72x - 2y = 2答案:x = 2, y = 14. 计算:解方程组x + y = 22x + 3y = 7答案:x = 1, y = 1通过以上习题的训练,我们可以更好地掌握中职数学各章的知识点。
管理会计计算题及答案

第一份:第二章计算分析题1.已知:某企业主要经营A产品,该产品连续10期的产量及总成本资料见表要求:用高低点法对A产品进行成本性态分析。
解:依题意,选择的高低点坐标分别为(31,84560)和(25,71000)b=(84560-71000)÷(31-25)=2260 元/件a= 84560-31×2260=14500所以,A产品的成本性态模型为y=14500+2260x2.已知:某企业只生产一种产品,2006年前10个月该企业发生的制造费用见表要求:用高低点法对该企业的制造费用进行分解。
解:依题意,选择的高低点坐标分别为(350,28000)和(150,16000)b=(28000-16000)÷(350-150)=60(元/件)a=28000-350×60=7000(元)所以该企业制造费用的成本性态模型为y=7000+60x3.已知:某企业的设备维修费属于混合成本,2006年各月的实际资料见表1.用一元直线回归法对该企业的设备维修费进行分解。
2.利用EXCEL函数,计算相关系数r,回归系数a和b ,并与手工计算结果进行对比。
r=(12×3661000-118×357000)÷(12×1226-1182)×(12×10981000000-3570002)≈0.9785→+1 (x与y基本正相关)b=(12×3661000-118×357000)÷(12×1226-1182)=2292 元/小时a=(357000-2292×118)÷12=7212 元因此,该企业的成本性态模型为:y=7212+2292x第三章变动成本法计算成本题(注:计算变动非生产成本的业务量用销售量)1.已知:某公司从事单一产品生产,连续三年销售量均为1000件,而三年的产量分别为1000件、1200件和800件。
十三章内能、十四章内能的利用 计算题集及答案

十三章、十四章计算题集1.新农村建设中正在大力推广使用瓶装液化气.如果每瓶装10kg液化气,液化气的热值取4.2×107J/kg,则每瓶液化气全部完全燃烧放出的热量是J,若放出的热量有40%被水吸收,在标准大气压下可把kg的水从20℃加热至沸腾.[c水=4.2×103J/ (kg•℃)].2.某市建立的垃圾焚烧电厂,年处理垃圾可达2.0×105t.生活垃圾的平均热值约为63(1)发动机在做功冲程里,高温、高压的燃气推动活塞向下运动,对外做功,同时将(24到人们的重视,大多数家用汽车的发动机均为汽油机,它把汽油燃烧产生的内能部分转化成机械能,再通过传动机构将动力传给车轮使汽车行驶,小明的爸爸新买了一辆小汽车,如图所示,小明坐着这辆汽车匀速行驶144km,用时2h,消耗汽油9kg,其发动机的功率为23kW.请运用所学的知识解答下列问题.(汽油的热值为4.6×107J/kg)(1)汽车效率比较低,原因是什么?指出两点即可.(2)汽车匀速行驶时所受的牵引力是多大?(3)汽车发动机的效率是多少?(4)观察小汽车的外型,判断小汽车在水平路面高速行驶和静止时,对地面压力哪一个大?为什么?5.阅读短文,回答问题:在我国随着人民生活水平的不断提高,汽车已经走进了很多普通的家庭,最近小王家也购买了一辆小汽车.小王十分高兴,将汽车里里外外看了个遍,并且进行了认真的考,发现汽车上许多地方都用到了物理知识,下面就是他思考的问题,请你帮他补充完整.(1 )汽车上很多地方都用到了物理知识,下列现象所对应的解释不合理的是.A、打开油箱盖会闻到汽油的味道﹣﹣﹣﹣扩散现象B、环保汽车使用气体燃料﹣﹣﹣﹣减少对大气的污染C、空调车车窗玻璃设计为双层﹣﹣﹣﹣减少车内外热量的传递D、小排量的车一般经济省油﹣﹣﹣﹣发动机的效率低(2)如图所示是汽油机工作过程中的四个冲程,其中属于压缩冲程的是.(3)一台单缸四冲程汽油机,若飞轮转速是1200 r/min,该汽油机每秒钟内完成个冲程,做功次.(4)若汽车油箱的容积为60dm3,油箱内装的是密度为0.71×103kg/m3、热值为4.6×107J/kg 的汽油,当该车以20m/s 的速度匀速行驶100km 时所消耗的汽油为5kg,汽车发动机的输出的功率为12kW,则汽车发动机的效率为.6.一辆总重为1.6×104N的汽车在高速公路上匀速行驶了10km.所受的平均阻力是汽车总重的0.05倍,求:(1)汽车发动机的牵引力;(2)汽车发动机的牵引力在这段路程内所做的功;(3)若在这段路程内,若小汽车消耗汽油是0.4kg,已知汽油的热值q=4.6×107J/kg.求小汽车发动机的效率.7.小汽车的百公里油耗是衡量汽车性能的一个重要的理论指标,某品牌小汽车百公里耗油量为8L,已知汽油的热值为4.6×107J/kg,汽油的密度为0.75×103kg/m3.汽车发动机的效率为30%.请计算:(1)8L汽油完全燃烧放出的热量;(2)汽车行驶过程中受到的阻力.8.位于海林市的林海雪原,是英雄杨子荣战斗过的地方,解放战争时期,著名的“智取威虎山”就发生在这里.在牡丹江通往威虎山的公路中,公路从山底到最高点的高度差约800 米,一辆满载货物的卡车总质量为23吨,汽油机效率为25%,汽车爬坡的机械效率为80%,问卡车到达山顶需多少千克汽油?(汽油热值为4.6×107J/Kg,g=10N/kg)910辆轿车,小华利用所学的物理知识对骄车进行了一系列探索与研究活动:(1)小华同学阅读了轿车发动机的说明书后,将内燃机的能量流向制成如图甲所示的图表,请根据给出的信息:计算完全燃烧0.21kg的汽油能够使12kg、15℃的冷却水温度升高多少摄氏度?(c水=4.2×103J/(kg•℃),汽油的热值为4.6×107J/kg)(写出计算过程)(2)若轿车以60kW的恒定功率启动做直线运动,运动过程中受到的阻力不变,运动的速度υ与时间t的关系如图乙所示.则在0~5s时间内,轿车发动机对外做功多少J?轿车在运动过程中受到的阻力是多少?(写出计算过程)11.一台汽油机工作时,排出的废气带走的能量占总能量的35%,气缸向周围散热损失的能量占总能量的30%,克服机械运行的摩擦损失的能量占总能量的5%,其他能量损耗不计.求:(1)这台汽油机的效率是多少?(2)如果每分钟需做有用功3×103 J,这台汽油机每分钟至少需要消耗汽油多少克?(汽油的热值是4.6×107J/kg)12.一辆使用汽油为燃料的小汽车,以20m/s的速度在水平路面上匀速行驶时,发动机的实际功率为20kW.若小汽车行驶的距离为100km,汽油的热值q=4.6×107J/kg,小汽车发动机的效率为25%.求小汽车在这段路程中:(1)运动的时间;(2)发动机所做的功;(3)消耗汽油的质量(保留一位小数).13.某学校小组想研究酒精灯烧水时的热效率.他们用酒精灯给100g初温为20℃的水加热,经过一段时间测得水温升高了60℃、消耗了4.2g酒精.已知:水的比热容为4.2×103J/ (kg℃),酒精的热值为3×107J/kg.求:(1)此过程中水吸收的热量;(2)4.2g酒精完全燃烧放出的热量;(3)酒精灯烧水时的热效率.14.用煤气灶把2kg、初温为20℃的水烧到100℃,消耗了0.03kg煤气.已知水的比热容是4.2×103J/(kg•℃),煤气的热值为4.48×l07J/kg.计算:(1)水吸收的热量为多少J?(2)煤气完全燃烧放出的热量为多少J?(3)煤气灶烧水的效率为多少?15.一辆小轿车以某一速度在平直路面上匀速行驶100km,消耗汽油10L.若这些汽油完全燃烧放出的热量有30%用来驱动汽车做有用功,已知:所用汽油的热值为4.6×107J/kg,密度为0.7×103kg/m3,求:(1)这些汽油完全燃烧放出的热量;(2)这辆轿车以该速度匀速行驶时受到的阻力.十三章、十四章计算题集参考答案与试题解析一.选择题(共2小题)1.新农村建设中正在大力推广使用瓶装液化气.如果每瓶装10kg液化气,液化78 JQ放(2Q吸由m水==500kg21tQ=mq=1000kg×6.3×106J/kg=6.3×109J,燃烧1t垃圾可获得的电能:W=7.56×108J,生活垃圾燃烧发电的效率:η==×100%=12%.故答案为:6.3×109;12%.二.选择题(共10小题)3.图1为四缸发动机工作原理:内燃机通过连杆把四个汽缸的活塞连在一根曲轴上,并使各汽缸的做功过程错开,在飞轮转动的每半周里,都有一个汽缸在做功,其他三个汽缸分别在做吸气、压缩和排气工作.p=,∴燃气对活塞所做的功:W=Fl=pSl=pV.故答案为:(1)内;机械;(2)pS;pSl;Sl.4.目前,“节能减排”已引起全球的关注.如何减少能耗,提高汽车发动机的效率越来越受到人们的重视,大多数家用汽车的发动机均为汽油机,它把汽油燃烧产生的内能部分转化成机械能,再通过传动机构将动力传给车轮使汽车行驶,小明的爸爸新买了一辆小汽车,如图所示,小明坐着这辆汽车匀速行驶144km,用时2h,消耗汽油9kg,其发动机的功率为23kW.请运用所学的知识解答下列问题.(汽油的热值为4.6×107J/kg)(1)汽车效率比较低,原因是什么?指出两点即可.(2)汽车匀速行驶时所受的牵引力是多大?(3)汽车发动机的效率是多少?(4)观察小汽车的外型,判断小汽车在水平路面高速行驶和静止时,对地面压力哪一个大?为什么?【解答】解:(1)汽油机工作时的能量损失:①燃料在气缸内燃烧时,有一部分燃料没有完全燃烧,就随着废气被排到空气中,带走一部分能量;②排气冲程中排出的废气温度很高,带去一部分热能;③热机工作时,气缸机件散热,消耗一部分内能;④热机内相对运动的机件间摩擦做功消耗能量.由于以上能量的损失,导致了汽油机的效率比较低.(2)汽车的速度:v===72km/h=20m/s,∵P=Fv,∴牵引力大小:F===1150N;(3)汽车行驶两小时做的有用功:W=Fs=1150N×144000m=1.656×108J,9kg汽油完全燃烧放出的热量:Q放=mq=9kg×4.6×107J/kg=4.14×108J,汽油机的效率:η===40%;(4)静止时对路面的压力大,因为高速行驶时,汽车上表面的空气流速大,对汽车的压强小,使汽车有一个向上托的力.答:(1)汽车效率比较低,原因是①燃料在气缸内燃烧时,有一部分燃料没有完全燃烧,就随着废气被排到空气中,带走一部分能量;②排气冲程中排出的废气温度很高,带去一部分热能.(2)汽车匀速行驶时所受的牵引力是150N;(3)汽车发动机的效率是40%;(4)静止时对路面的压力大,因为高速行驶时,汽车上表面的空气流速大,对汽车的压强小,使汽车有一个向上托的力.5.阅读短文,回答问题:在我国随着人民生活水平的不断提高,汽车已经走进了很多普通的家庭,最近小王家也购买了一辆小汽车.小王十分高兴,将汽车里里外外看了个遍,并且进行了认真的思考,发现汽车上许多地方都用到了物理知识,下面就是他思考的问题,请你帮他补充完整.(1 )汽车上很多地方都用到了物理知识,下列现象所对应的解释不合理的是D.A、打开油箱盖会闻到汽油的味道﹣﹣﹣﹣扩散现象B、环保汽车使用气体燃料﹣﹣﹣﹣减少对大气的污染C、空调车车窗玻璃设计为双层﹣﹣﹣﹣减少车内外热量的传递D、小排量的车一般经济省油﹣﹣﹣﹣发动机的效率低(2)如图所示是汽油机工作过程中的四个冲程,其中属于压缩冲程的是A.(3)一台单缸四冲程汽油机,若飞轮转速是1200 r/min,该汽油机每秒钟内完成40个冲程,做功10次.(4)若汽车油箱的容积为60dm3,油箱内装的是密度为0.71×103kg/m3、热值为4.6×107J/kg 的汽油,当该车以20m/s 的速度匀速行驶100km 时所消耗的汽油为5kg,汽车发动机的输出的功率为12kW,则汽车发动机的效率为26%.【解答】解:A、打开油箱盖会闻到汽油的味道,表明汽油分子在不停地做无规则运动,属于扩散现象,故A正确;B、气体燃料中碳元素的含量低于液化石油气中碳元素的含量,燃烧相同质量的气体燃料和液化石油气时,燃烧天然气排放的二氧化碳比燃烧液化石油气排放的二氧化碳少,所以相同条件下,减少对大气的污染,故B正确;C、车窗为双层玻璃会大大减少因为热传导而发生的车内外热量的传递,故C正确;D、完成一样的有用功时由于小排量汽车消耗的能源比大排量的车消耗的能源少,所以发动机的效率高,故D错误.(2)A、两气门都关闭,活塞上行,汽缸容积变小,是压缩冲程;B、排气门开启,气体流出汽缸,是排气冲程;C、两气门都关闭,活塞下行,汽缸容积变大,是做功冲程;D、进气门开启,气体流入汽缸,是吸气冲程;(3)若飞轮转速是1200r/min=20r/s,表示每秒飞轮转动20圈,由于热机完成一个工作循环,飞轮转动2周,经过4个冲程,燃气对外做功1次,所以转动20圈经过40个冲程,对外做功10次.(4)由v=得行驶时间:t===5000s;汽车的有用功W=Pt=12×103W×5000s=6×107J;有释放的能量Q=qm′=4.6×107J/kg×5kg=2.3×108J;发动机的效率η=×100%=×100%=26%.故答案为:(1)D;(2)A;(3)40;10;(4)26%.6.一辆总重为1.6×104N的汽车在高速公路上匀速行驶了10km.所受的平均阻力是汽车总重的0.05倍,求:(1)汽车发动机的牵引力;(2)汽车发动机的牵引力在这段路程内所做的功;(3)若在这段路程内,若小汽车消耗汽油是0.4kg,已知汽油的热值q=4.6×107J/kg.求小汽车发动机的效率.【解答】解:(1)因为汽车匀速行驶,所以牵引力F=f=0.05×1.6×104N=800N;(2)牵引力做的功:W=Fs=800N×10000m=8×106J;(3)汽油完全燃烧放出的热量:Q=mq=0.4kg×4.6×107J/kg=1.86×107J,放小汽车发动机的机械效率:η=×100%=×100%≈43%.答:(1)汽车发动机的牵引力为800N;(2)汽车发动机的牵引力在这段路程内所做的功为8×106J;(3)汽车发动机的机械效率43%.7.小汽车的百公里油耗是衡量汽车性能的一个重要的理论指标,某品牌小汽车百公里耗油量为8L,已知汽油的热值为 4.6×107J/kg,汽油的密度为0.75×103kg/m3.汽车发动机的效率为30%.请计算:(1)8L汽油完全燃烧放出的热量;(2)汽车行驶过程中受到的阻力.【解答】解:(1)汽油的体积V=8L=0.008m3汽油的质量m=ρV=0.75×103kg/m3×0.008m3=6kg;8L汽油完全燃烧放出的热量Q=mq=6kg×4.6×107J/kg=2.76×108J;(2)根据η=可知,车发动机做的机械功为:W=ηQ=30%×2.76×108J=8.28×107J,s=100km=105m所以F===828N,因为轿车做匀速直线运动,所以轿车受到的阻力f=828N.答:(1)8L汽油完全燃烧放出的热量为2.76×108J;(2)汽车行驶过程中受到的阻力为828N.8.位于海林市的林海雪原,是英雄杨子荣战斗过的地方,解放战争时期,著名的“智取威虎山”就发生在这里.在牡丹江通往威虎山的公路中,公路从山底到最高点的高度差约800米,一辆满载货物的卡车总质量为23吨,汽油机效率为25%,汽车爬坡的机械效率为80%,问卡车到达山顶需多少千克汽油?(汽油热值为4.6×107J/Kg,g=10N/kg)【解答】解:因为G=mg,=Gh=mgh=2.3×104kg×10N/kg×800m=1.84×108J;所以卡车做的有用功为W有用因为η=,所以发动机做的总功为W===2.3×108J;总因为η=,====9.2×108J;所以汽油燃烧放出的热量为Q总因为Q=mq,所以需要汽油的质量为m===20kg.答:卡车到达山顶需要20kg的汽油.9.一台四冲程汽油机,已知其飞轮的转速为1200r/min,则该汽油机每秒内做功的次数是10次,完成40个冲程数,在做功冲程中,它把燃料燃烧放出的内能部分转化为机械能,当完全燃烧1kg汽油,则能够获得 4.6×107J的内能,用来做有用功的能量为 1.38×107J(汽油的热值为4.6×107J/kg,效率为30%).【解答】解:一台单缸四冲程柴油机的飞轮转速为1200r/min,说明1min曲轴(飞轮)转1200r;则每秒钟,曲轴(飞轮)转=20转,完成=10个工作循环,做功10次,完成40个冲程.在做功冲程中,它通过燃料燃烧,将内能部分转化为机械能;汽油完全燃烧时放出的热量:Q放=mq=1kg×4.6×107J/kg=4.6×107J;∵η=,∴该汽油机转化的能对外做有用功:W有用=ηQ=30%×4.6×107J=1.38×107J.故答案为:10;40;内能;4.6×107;1.38×107.10.随着人民生活水平的不断提高,汽车已经走进我们的家庭,小华的爸爸最近也购买了一辆轿车,小华利用所学的物理知识对骄车进行了一系列探索与研究活动:(1)小华同学阅读了轿车发动机的说明书后,将内燃机的能量流向制成如图甲×106J;水吸收的热量为:Q吸=30%Q放=30%×9.66×106J=2.898×106J;Q吸=cm△t可知;水温度升高值:△t===57.5℃;(2)因轿车以60kW的恒定功率启动做直线运动,所以轿车发动机做功W=Pt=6×104W×5s=3×105J;由图示知轿车匀速直线运动时的速度是v=30m/s;由P=Fv得:F===2000N;由于做匀速直线运动,因此受到的阻力等于牵引力,即f=F=2000N.(3)汽油的热值为4.6×107J/kg,完全燃烧10kg的汽油产生的热量:Q放'=m'q=10kg×4.6×107J/kg=4.6×108J;由图可知,有用功的能量:η=100%﹣30%﹣30%﹣5%=35%;'=35%×4.6×108J=1.61×108J;因此产生的有用功:W=ηQ放根据W=Fs可知,汽车行驶的距离为:s===6.44×104m;(4)通过对1、2、3、4的分析可知速度越大制动距离越大,即制动距离一定与速度有关,但明显不是正比关系.故可以想到可能与速度的平方成正比,通过计算可知制动距离的确与速度的平方成正比:则由=,解得:120km/h的制动距离为72m.答:(1)水升高的温度为57.5℃;(2)轿车在运动过程中受到的阻力是2000N;(3)锡到宜兴距离为6.44×104m;(4)72.11.一台汽油机工作时,排出的废气带走的能量占总能量的35%,气缸向周围散热损失的能量占总能量的30%,克服机械运行的摩擦损失的能量占总能量的5%,其他能量损耗不计.求:(1)这台汽油机的效率是多少?(2)如果每分钟需做有用功3×103J,这台汽油机每分钟至少需要消耗汽油多少克?(汽油的热值是4.6×107J/kg)【解答】解:(1)汽油机的效率:η=100%﹣35%﹣30%﹣5%=30%答:汽油机的效率为30%.=3×103 J,(2)汽油机每分钟需做有用功W有燃料完全燃烧放出的总能量Q总===1×104J汽油机每分钟至少需要消耗汽油m===0.22×10﹣3kg=0.22g答:这台汽油机每分钟至少需要消耗汽油0.22g.12.一辆使用汽油为燃料的小汽车,以20m/s的速度在水平路面上匀速行驶时,发动机的实际功率为20kW.若小汽车行驶的距离为100km,汽油的热值q=4.6×107J/kg,小汽车发动机的效率为25%.求小汽车在这段路程中:(1)运动的时间;(2)发动机所做的功;(3)消耗汽油的质量(保留一位小数).【解答】解:(1)由v=可知,运动的时间:t===5000s;(2)发动机所做的功:W=Pt=20000W×5000s=1×108J;(3)由η=可得,燃烧汽油得到的总能量:Q===4×108J;由Q=mq可得,消耗汽油的质量:m==≈8.7kg.答:(1)运动的时间为5000s;(2)发动机所做的功为1×108J;(3)消耗汽油的质量为8.7kg.三.解答题(共4小题)13.某学校小组想研究酒精灯烧水时的热效率.他们用酒精灯给100g初温为20℃的水加热,经过一段时间测得水温升高了60℃、消耗了4.2g酒精.已知:水的比热容为4.2×103J/(kg℃),酒精的热值为3×107J/kg.求:(1)此过程中水吸收的热量;(2)4.2g酒精完全燃烧放出的热量;(3)酒精灯烧水时的热效率.【解答】解:(1)100g=0.1kg,水吸收的热量:Q吸=cm△t=4.2×103J/(kg•℃)×0.1kg×60℃=2.52×104J;(2)酒精完全燃烧产生的热量:Q放=mq=0.0042kg×3×107J/kg=1.26×105J;(3)酒精灯烧水时的热效率:η==×100%=20%.答:(1)水吸收的热量是2.52×104J;(2)4.2g酒精完全燃烧放出的热量是1.26×105J;(3)酒精灯烧水时的热效率是20%.14.用煤气灶把2kg、初温为20℃的水烧到100℃,消耗了0.03kg煤气.已知水的比热容是4.2×103J/(kg•℃),煤气的热值为4.48×l07J/kg.计算:(1)水吸收的热量为多少J?(2)煤气完全燃烧放出的热量为多少J?(3)煤气灶烧水的效率为多少?=cm△t=4.2×103J/(kg•℃)×2kg×(100℃【解答】解:(1)水吸收的热量:Q吸﹣20℃)=6.72×105J;=mq=0.03kg×4.48×107J/kg=1.344×(2)0.03kg煤气完全燃烧放出的热量:Q放106J;煤气灶烧水的效率:η=×100%=×100%=50%.答:(1)水吸收的热量为6.72×105J;(2)煤气完全燃烧放出的热量为1.344×106J;(3)煤气灶烧水的效率为50%.15.一辆小轿车以某一速度在平直路面上匀速行驶100km,消耗汽油10L.若这些汽油完全燃烧放出的热量有30%用来驱动汽车做有用功,已知:所用汽油的热值为4.6×107J/kg,密度为0.7×103kg/m3,求:(1)这些汽油完全燃烧放出的热量;(2)这辆轿车以该速度匀速行驶时受到的阻力.【解答】解:(1)∵ρ=,V=10L=10×10﹣3m3,∴m=ρV=0.7×103kg/m3×10×10﹣3m3=7kg,汽油完全燃烧放出的热量:Q放=mq=7kg×4.6×107J/kg=3.22×108J;(2)由题知,用来驱动汽车做的有用功:W有=Q放×30%=3.22×l08J×30%=9.66×107J=Fs,∵W有轿车牵引力:F===966N,又∵轿车匀速行驶,∴轿车受到的阻力:f=F=966N.答:(1)这些汽油完全燃烧放出的热量为3.22×l08J;(2)这辆轿车以该速度匀速行驶时受到的阻力为966N.。
《初等数论》各章习题参考解答

《初等数论》各章习题参考解答第一章习题参考解答1.解:因为25的最小倍数是100,9的最小倍数是,所以满足条件的最小正整数11111111100a =。
2.解:3在100!的分解式中的指数()1001001001003100!33113148392781⎡⎤⎡⎤⎡⎤⎡⎤=+++=+++=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦, 在100!的分解式中的指数()1001001001001002100!50251261942481664⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=++++=++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,∴ ()9448474847100!2343123,,61k k k k =⋅⋅=⋅⋅=⋅=。
故 max 47n =,min 3M k =,(),61k =。
故 当M 最小值是3的倍数,但不是2的倍数。
3.解:112121n n n n x x ++++++等价于()()21221n n n x x x ++-+-,从而3x ³(n 就不会太大,存在反向关系)。
由()()22121n nn x x x -+-?+,得()()2212n n n x x -+?,即()()()121122nn x x -+?。
若2n ³,则()()()()251221114242nn x xx x-?+??,导致25140x x -+?,无解。
所以,只有1n =,335314x x x +-?,只能是37,14x +=,从而4,11x =。
综上所述,所求正整数对()()(),4,111,1x n =、。
4.解:按题意,2m n >>,记*,m n k k N =+?;则()222211111n n k nk n k k a a a a a a a a a a a a +++-+-?-+--++-22211111n k k n k k a a a a a a a a a ++?---+?-+-,故 存在无穷多个正整数a 满足2111n k k a a a a ++-+-。
第十章计算题参考答案

(2) 设P=1则:
(3)
P=0.995
17.工业上为了合成具有一定分子量的聚酰胺-1010,一般先将癸二胺(M1=172)和癸二酸(M2=202)制备成“1010盐”,然后再进行缩聚。现已知该“1010盐”为中性,因此另加1.0%(以单体总数计)mol的苯甲酸(M’=122)作为官能团封锁剂控制聚酰胺-1010的分子量,若反应程度P=0.998。⑴写出合成聚酰胺-1010有关的聚合反应方程式。⑵计算该聚酰胺-1010的数均相对分子质量。
答案:(1)合成聚酰胺-1010有关的聚合反应方程式:
“1010盐”为中性,意味着[-NH2]=[-COOH],则加入单官能团化合物苯甲酸做分子量稳定剂,控制尼龙1010的分子量:
(2)计算该聚酰胺-1010的数均分子量
11.制造尼龙-66时,为了保持己二酸和己二胺的等摩尔比,通常先使二者成盐,然后于254℃(K=300)进行缩聚。若反应在密闭容器中进行,当反应进行t小时后,测得体系中残留水为0.25mol/L。试写出成盐方程式,并计算所得缩聚物的平均聚合度。
答案:尼龙-66盐的形成:
假设起始氨基、羧基的摩尔浓度均为1mol/L,成盐后在密闭容器中缩聚,达平衡时,氨基及羧基的量为cmol/L则生成聚合物为(1-c)mol/L,与残留水的量na相同,均为0.25mol/L,则依照平衡反应式得到:,
16.由已二胺和已二酸合成聚酰胺(K=365)。(1)如果已二胺和已二酸等mol反应,估算封闭体系的Xn最大可达多少?(2)如果已二胺和已二酸等mol(已二胺和已二酸均为2mol)反应,要达到Xn=100的聚合物,体系中水应控制在多少?(3)如果已二胺和已二酸非等mol反应,要求当反应程度为0.995时分子量(Mn)控制为16000,试计算两单体的当量系数r和过量分率q。
各章计算题及答案(2)

第二章 课后作业 书59页2. 以下是某银行的资金来源与成本状况,试计算以下银行的加权平均成本和可用资金加权平均成本率。
表2-4 某银行的资金与成本结构表利息成本=20×2%+40×4%+30×6%+10×12%=5(万元)营业成本=20×5%+40×1%+30×0.5%+10×0.25%=1.575(万元)可用资金总额=20×78%+40×94%+30×94%+10×97%=91.1(万元)资金成本率=(5+1.575)/(20+40+30+10)=6.575%可用资金成本率=(5+1.575)/91.1=7.22%第三章 课后作业 书100~101页 1.某客户向银行申请一年期3000万美元的贷款。
由于该客户是银行的重点客户,虽然银行资金不足,银行还是通过了这个申请。
为了筹集这笔资金,该银行出售了年利率为9%,金额为2000万美元的大额存单,并且按10%的年利率向其他银行借款1000万美元。
与此贷款申请有关的信用调查和其他费用估计为20000美元。
银行的信用分析部门建议,对此贷款至少收取0.25%的风险溢价和0.5%的利润。
要求:如果银行采用成本加成定价法,那么该笔贷款的价格是多少。
贷款价格=资金成本率+经营成本率+风险溢价+目标利润率%15.10%5.0%25.030002300010100092000=+⨯⨯++%%+贷款价格=2.某客户借入一笔1年期的8000元的贷款。
要求:(1)如果采用月等额分期偿还方式,年利率为14%,试用年百分比法计算该笔贷款的真实利率。
(2) 如果采用按季偿还方式,年利率为12%,试用单一利率法计算该笔贷款的真实利率。
(3)如果采用利息首付的方式,年利率为10%,试用贴现法计算该笔贷款的真实利率。
解: (1)客户实际使用的资金平均余额为:实际利率为:(2)客户实际使用的资金平均余额为:实际利率为:(3)3. 某客户得到一笔25年期,450000元,年利率为12.5%的固定利率住宅抵押贷款,约定还款方式为按月等额支付本息。
土力学地基基础章节计算题及答案

土力学地基基础章节计算题及答案本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March章节习题及答案第一章 土的物理性质1 有一块体积为60 cm 3的原状土样,重 N, 烘干后 N 。
已只土粒比重(相对密度)s G =。
求土的天然重度、天然含水量w 、干重度d 、饱和重度sat 、浮重度’、孔隙比e 及饱和度S r解:分析:由W 和V 可算得,由W s 和V 可算得d ,加上G s ,共已知3个指标,故题目可解。
363kN/m 5.1710601005.1=⨯⨯==--V W γ 363s d kN/m 2.1410601085.0=⨯⨯==--V W γ3w sws kN/m 7.261067.2=⨯===∴γγγγs s G G%5.2385.085.005.1s w =-==W W w 884.015.17)235.01(7.261)1(s =-+=-+=γγw e (1-12) %71884.06.2235.0s =⨯=⋅=e G w S r (1-14) 注意:1.使用国际单位制; 2.w 为已知条件,w =10kN/m3;3.注意求解顺序,条件具备这先做; 4.注意各的取值范围。
2 某工地在填土施工中所用土料的含水量为5%,为便于夯实需在土料中加水,使其含水量增至15%,试问每1000 kg 质量的土料应加多少水 解:分析:加水前后M s 不变。
于是:加水前: 1000%5s s =⨯+M M (1) 加水后: w s s 1000%15M M M ∆+=⨯+ (2) 由(1)得:kg 952s =M ,代入(2)得: kg 2.95w =∆M 注意:土料中包含了水和土颗粒,共为1000kg ,另外,swM M w =。
3 用某种土筑堤,土的含水量w =15%,土粒比重G s =。
分层夯实,每层先填0.5m ,其重度等=16kN/ m 3,夯实达到饱和度r S =85%后再填下一层,如夯实时水没有流失,求每层夯实后的厚度。
计算机应用基础各章习题参考答案

计算机应用基础各章习题参考答案第一章计算机基础知识一、单选题1、世界上第一台电子计算机诞生于()A 1946 年B 1956 年C 1966 年D 1976 年答案:A解析:世界上第一台电子计算机名为 ENIAC,于 1946 年在美国宾夕法尼亚大学诞生。
2、计算机能够直接识别和执行的语言是()A 机器语言B 汇编语言C 高级语言D 数据库语言答案:A解析:机器语言是计算机能够直接识别和执行的语言,由二进制代码组成。
3、一个完整的计算机系统包括()A 计算机及其外部设备B 主机、键盘、显示器C 系统软件和应用软件D 硬件系统和软件系统答案:D解析:计算机系统由硬件系统和软件系统两大部分组成。
硬件是计算机的物理设备,软件则是使硬件能正常工作的程序和相关数据。
4、以下不属于输入设备的是()A 鼠标B 键盘C 打印机D 扫描仪答案:C解析:打印机属于输出设备,用于将计算机处理的结果输出到纸张等介质上。
5、计算机的内存储器比外存储器()A 速度快B 存储量大C 便宜D 以上说法都不对答案:A解析:内存储器的读写速度比外存储器快,但存储容量通常较小。
二、多选题1、计算机的特点包括()A 运算速度快B 计算精度高C 具有记忆和逻辑判断能力D 自动化程度高答案:ABCD解析:这些都是计算机的显著特点,使其在各个领域得到广泛应用。
2、计算机的性能指标主要有()A 字长B 主频C 内存容量D 运算速度答案:ABCD解析:字长决定了计算机的处理能力,主频影响计算机的运行速度,内存容量和运算速度也是衡量计算机性能的重要指标。
3、以下属于计算机应用软件的有()A WordB ExcelC WindowsD Photoshop答案:ABD解析:Word 和 Excel 是办公软件,Photoshop 是图像处理软件,都属于应用软件。
Windows 是操作系统,属于系统软件。
三、判断题1、计算机只能处理数字信息。
(×)解析:计算机不仅能处理数字信息,还能处理文字、图像、声音等多种形式的信息。
《微积分》各章习题及详细答案

第一单元 函数与极限一、填空题1、已知x x f cos 1)2(sin +=,则=)(cos x f 。
2、=-+→∞)1()34(lim22x x x x 。
3、0→x 时,x x sin tan -是x 的 阶无穷小。
4、01sinlim 0=→xx kx 成立的k 为 。
5、=-∞→x e xx arctan lim 。
6、⎩⎨⎧≤+>+=0,0,1)(x b x x e x f x 在0=x 处连续,则=b 。
7、=+→xx x 6)13ln(lim0 。
8、设)(x f 的定义域是]1,0[,则)(ln x f 的定义域是__________。
9、函数)2ln(1++=x y 的反函数为_________。
10、设a 是非零常数,则________)(lim =-+∞→xx ax a x 。
11、已知当0→x 时,1)1(312-+ax 与1cos -x 是等价无穷小,则常数________=a 。
12、函数xxx f +=13arcsin )(的定义域是__________。
13、____________22lim22=--++∞→x x n 。
14、设8)2(lim =-+∞→xx ax a x ,则=a ________。
15、)2)(1(lim n n n n n -++++∞→=____________。
二、选择题1、设)(),(x g x f 是],[l l -上的偶函数,)(x h 是],[l l -上的奇函数,则 中所给的函数必为奇函数。
(A))()(x g x f +;(B))()(x h x f +;(C ))]()()[(x h x g x f +;(D ))()()(x h x g x f 。
2、xxx +-=11)(α,31)(x x -=β,则当1→x 时有 。
(A)α是比β高阶的无穷小; (B)α是比β低阶的无穷小; (C )α与β是同阶无穷小; (D )βα~。
《微积分》各章习题及详细答案

第一章 函数极限与连续一、填空题1、已知x x f cos 1)2(sin +=,则=)(cos x f 。
2、=-+→∞)1()34(lim22x x x x 。
3、0→x 时,x x sin tan -就是x 的 阶无穷小。
4、01sin lim 0=→xx kx 成立的k 为 。
5、=-∞→x e xx arctan lim 。
6、⎩⎨⎧≤+>+=0,0,1)(x b x x e x f x 在0=x 处连续,则=b 。
7、=+→xx x 6)13ln(lim 0 。
8、设)(x f 的定义域就是]1,0[,则)(ln x f 的定义域就是__________。
9、函数)2ln(1++=x y 的反函数为_________。
10、设a 就是非零常数,则________)(lim =-+∞→xx ax a x 。
11、已知当0→x 时,1)1(312-+ax 与1cos -x 就是等价无穷小,则常数________=a 。
12、函数xxx f +=13arcsin )(的定义域就是__________。
13、lim ____________x →+∞=。
14、设8)2(lim =-+∞→xx ax a x ,则=a ________。
15、)2)(1(lim n n n n n -++++∞→=____________。
二、选择题1、设)(),(x g x f 就是],[l l -上的偶函数,)(x h 就是],[l l -上的奇函数,则 中所给的函数必为奇函数。
(A))()(x g x f +;(B))()(x h x f +;(C))]()()[(x h x g x f +;(D))()()(x h x g x f 。
2、xxx +-=11)(α,31)(x x -=β,则当1→x 时有 。
(A)α就是比β高阶的无穷小; (B)α就是比β低阶的无穷小; (C)α与β就是同阶无穷小; (D)βα~。
计算方法各章作业答案

计算方法作业第二章插值1.(1(2)用二次Lagrange插值多项式求当X=0.15时Y的近似值。
(3)写出余项R(x)=f(x)-Pn(x)的表达式。
解:(1)Pn (x) =knknkjj jkj yxxxx)(00∑∏=≠=--n=3P 3(x)=321321))()(())()((yxxxxxxxxxxxx------+13121132))()(())()((yxxxxxxxxxxxx------+23212231))()(())()((yxxxxxxxxxxxx------+32313321))()(())()((yxxxxxxxxxxxx------x 0=0.0 x1=0.1 x2=0.2 x3=0.3y 0=0.0000 y1=0.0998 y2=0.1987 y3=0.2955P 3(x)=0000.0)3.00.0)(2.00.0)(1.00.0()3.0)(2.0)(1.0(⨯------xxx+0998.0)3.01.0)(2.01.0)(0.01.0()3.0)(2.0)(0.0(⨯------xxx+1987.0)3.02.0)(1.02.0)(0.02.0()3.0)(1.0)(0.0(⨯------xxx+2955.0)2.03.0)(1.03.0)(0.03.0()2.0)(1.0)(0.0(⨯------xxx(2) y(0.15) = P2(0.15) = 0.1494(3)R(x) = f(x)-Pn (x)=)!1()()1(++nf nξnk0=∏(x - x k)=!4)(4ξf(x – 0.0) (x – 0.1)(x – 0.2)(x – 0.3)第三章 方程求根5.求解方程12-3x+2cosx=0的迭代法n n x x cos 3241+=+(1)证明对于任意的x 0€R 均有*lim x x n x =∞→ (x *为方程的根)(2)取x 0=4,用此迭代法求方程根的近似值,误差不超过10-3,列出各次的迭代值。
理论力学(第2版)习题答案

各章习题(计算题)部分答案第1章 略 第2章2-1 R 3284kN F .=,R cos()2063,.=︒F i ,R cos()1163,.=︒F j 2-2 3162kN T .=,30β=︒ 2-3 482.α=︒,R 496kN x F .= 2-4 11866N 50N x y F .F ==,2230N 40N x y F F ==-, 330N 60N x y F F ==, 44566N 566N x y F .F .==, 2-5 R 0F =2-6(a) 707kN 354kN 354kN Ax Ay B F .F .F .===,,(b) 05kN 5kN Ax Ay B F F F ===,,(c) 933kN 433kN 612kN Ax Ay B F .F .F .===,,(垂直于支撑面,指向简支梁) 2-7 min 15kN F =,N 25kN F =2-8 0866kN 05kN 1kN Ax Ay BD F .F .T ===,, 2-9 N N 1732kN 3464kN 15m A C F .F .AC .===,, 2-10 03436kN AB AC F F .==,2-11 BC F =,Ax F =,Ay F G = 2-12 N 65EF G F =+2-13 N N C D F F =2-14 231N 1155N 231N 845N AB AE BC BD F F .F F .====,,,2-15 (a) 33PF P F B Ay =-=,(b) P F F B A 32== (A F ,B F 方向相反,组成一力偶) (c) 0==B A F F2-16 1F,AB F,OA F =,7kN BC F =- 2-17 1905N 1905N 1905N 1905N Ax Ay Cx Cy F F F F =-===-,,, 2-18 3571N 3571N 3571N 3571N Ax Ay Cx Cy F F F F ==-=-=,,,·312··312·2-19 24kN m M =⋅,1155kN A B F F .== 第3章3-1 2400N Ax F =,1200N Ay F =,8485N BC F .= 3-2 R 0F'=,260N m O M =⋅ 3-3 (a) R F'qa =,221qa M O = (b) R12F'ql =,21ql q M O = 3-4(a) Ax F =,40kN Ay F =,120kN m A M =⋅,N C F = (b) 0=AxF ,25kN Ay F .=-,15kN By F =,D 25kN y F .=3-5 当60α=︒时,min 4AB PrF L= 3-6 0=Ax F ,qa F Ay2=,2qa M A =3-7 (a)2400N Ax F =,1000N Ay F =-,2400N Dx F =-,2000N Dy F = (b)2400N Ax F =-,1000N Ay F =-,2400N Dx F =,2000N Dy F =3-8 Ax F =,Ay F =,Bx F =,By F =3-9 rPLF Ax 2-=,P F Ay =,r PL F Bx 2=,P F By =,r PL F D 2=,P F C 2=3-10 R 32E F qa =-,qa F BD 22= 3-11 23kN Ax Cx F F .=-=-,1kN Ay Cy F F == 3-12 3PF AC -=,0=EF F ,32P F BD -= 3-13 2F F BC=,2F F DE = 第4章4-1 T 20kN F =,104kN OA F .=-,139kN OB F .=- 4-2 254kN m x M .=⋅,146kN m y M .=⋅,0=z M 4-3 0)(=P z M4-4 θαsin sin )(Pa M AB =P 4-5 3C A B WT T T ===4-6 1kN T =,0=Ax F ,750N Ay F =-,500N Az F =-,433N Bx F =,500N BZ F = 4-7 F F F -==61,F F =3,0542===F F F·313··313·4-8 321M a cM a b M +=,a M F Ay 3=,a M F Az 2=,0=Dx F ,a M F Dy 3-=,aM F Dz 2-= 4-9 4kN Ax F =,146kN Az F .=-,79kN Bx F .=,29kN Bz F .=-4-10 5kN Ox F =-,4kN Oy F =-,8kN Oz F =,32kN m Ox M =⋅,30kN m Oy M =-⋅,20kN m Oz M =⋅4-11 (a ) 10412kN N F .=,20213kN N F .=,30375kN N F .= 4-12 )(22221221r r r r x C --=,0=C y4-13 (a ) 589mm C x .=-,0=C y (b ) 797mm C x .=,349mm C y .= 4-14 )(22221221r r r r x C --=,0=C y4-15 0Ax F =,121(P )2Ay F P =-+,21P 2Az P F =+,0Cx F =,0Cy F =,22Cz P F =第5章5-1 min F =,s arctan f α= 5-2 )()m m sin +cos -P F αϕθϕ=,m θϕ=5-3 (1) A 先滑动,(2) A 、B 一起滑动 5-4 能保持平衡,S 201N F = 5-5 223.0=f5-6 3πarcsin 43πff α=+5-7 1s sin cos P F f αα=-,2s sin cos PF f αα=+,故21F F >5-8 min 845kN Q .= 5-9 435N P .=5-10 θ≤9926.︒5-11 120cm x >5-12 s 2(sin cos )Q R f L αα⋅+≤P ≤s 2(sin cos )Q Rf L αα⋅-5-13 min 1475N P .=5-14 4961N m .⋅≤C M ≤7039N m .⋅ 5-15 11cm b <5-16s s sin cos cos sin f Q f αααα-+≤P ≤s s sin cos cos sin f Q f αααα+- 5-17 arc ϕ=·314··314·5-18 500N P = 5-19 s f ≥15.0 5-20 75mm b .< 第6章6-1 (cos sin )x v lk kt kt =-,(cos sin )y v lk kt kt =-+; )sin (cos 2kt kt lk a x +-=,)sin (cos 2kt kt lk a y --= 6-2 (1) 0=s ;v R ω=;0a τ=,2n a R ω=(2) R s 23=;12v R ω=;2a ωτ=,2n 14a R ω= (3) R s =;0v =;2a R ωτ=-,n 0a =6-3 直角坐标法:t R x ω2cos =,t R y ω2sin =;2sin2x v R t ωω=-,2cos2y v R t ωω=; t R a x ωω2cos 42-=,t R a y ωω2sin 42-=自然坐标法:t R s ω2=;2v R ω=;0a τ=,2n 4a R ω= 6-4 ()sin M x l b t ω=+,()cos M y l b t ω=-;22221()()M M x y l b l b +=+-6.52222()1()x a y b l l-+=+6-6 22)sin (cos h t r l t r x B +-+=ωω,h y B -=6-7v =322xb u a -= 6-8 )cos sin arctan(00tr h tr ωωθ-=6-9 当0s t =时,157cm s M v ./=;0M a τ=,n2617cm s M a ./=当2s t =时,0M v =;2123cm s M a ./τ=-,n0M a =6-10 C x =C y =2C avv l=6-11 t e R t e y ωω222cos sin -+=;[cos v e t ωω=6-12 02cos4m x .t =;0566m s v ./=-;22263m s a ./=-6-13 0arctan rad v tbϕ=;02220rad s bv /b v t ω=+6-14 225t =ϕ;120m s v /=;236000m s n a /= 6-15 8rad s /ω=;2384rad s ./ε=-6-16 转轴O 的位置位于正方形的中心;1rad s /ω=,21rad s /ε=6-17 12C v r ω=;n 214C a r ω=,12C a r ετ=·315··315·6-18 12m s M v ./=;n 272m s M a ./=,206m s M a ./τ= 6-19 0377m s C v ./=6-20 2225000rad s /dεπ=;25922m s a ./= 6-21 32rad .ϕ=6-22 12mm h =6-23 02=ω,222r lb ωε-=6-24 02m s AB v ./=,2005m s AB a ./=;02m s C v ./=,n 20267m s C a ./=,2005m s C a ./τ=6-25 2012ωr a =,方向沿1AO ;2024ωr a =,指向轮心第7章7-1 x'vt =,cos()a kt y'ϕ=+,轨迹方程为cos()ky'a x'vϕ=+ 7-2 2cos M v R ωϕ=,方向水平向左 7-3 (a )2309rad s ./ω=; (b )2182rad s ./ω=7-4 (1)34OC v b ω=,34C lv v b=;(2)234K v a b = 7-5 当0ϕ︒=时,0v =;当30ϕ=︒时,100cm s v /=,向右;当90ϕ︒=时,200cm s v /=,向右7-6 126m s BC v ./=;2274m s BC a ./= 7-7 10cm s CD v /=;2346cm s CD a ./= 7-8 a a =7-9 3v ω=,方向向上7-10 1.732rad /s ω=,28.66rad /s ε=- 7-11 0.173m /s v =,20.05m /s a = 7-12 0.173m /s M v =,20.35m/s M a =7-13 πcos 15sin BC nr v αβ=7-14 23CD r v ω=;29310ωr a C D =7-15 a 3465mm s v ./=;21400mm s CD a /=第8章8-1 122v v r ω-=,122O v v v +=8-2 156cm s C v ./=,17cm s D v /=·316··316·8-3 877cm s C v ./=8-4 375rad s OB ./ω=,I 6rad s /ω=8-5 600mm s A v /=,200mm s B v /=,s C v /=;4rad s 3ABC /ω=,05rad s BD ./ω= 8-6 2rad s AB /ω=,2578rad s AB ./ε=-;667rad s BC ./ω=-,21926rad s BC ./ε=8-7 2()C A Rv a R r r=-,2Bx C a a τ=,2(2)()C By R r v a R r r -=- 8-8 2022ωr a B =,20211ωε=B O 8-9 032C v r ω=,20123ωr a C =8-10 01.15v l ω=8-11 16186rad s O C ./ω=,127817rad s O C ./ε=-8-12 s CD v /=,22m s 3CD a /= 8-13 n 2400cm s B a /=,21705cm s B a ./τ=-,21705cm s C a ./=-8-14 34e OC v v OB b ω==,OC ε=;12E v v =,E a = 8-15 21960mm s B a /=,298rad s AB ./ε=8-160C v ω,方向向左;rR B O 01ωω=,逆时针转向8-17 22()C Rv a R r =-,B a =8-18 n 202B a a ω=,2002)B a a ετ=-8-19 330ωω=B ;209)349(10ω+-=B a 8-20 2m s B v /=,2828m s C v ./=,28m s B a /=,21131m s C a ./= 第9章9-1 rgf=max ω 9-2 min 67r min n /=9-3 1v =9-4 0cos cos sin v x b kt kt k α=+,0sin sin vy kt kα=9-5 0cos x v t α=,201sin 2y v t gt α=+·317··317·9-6 0(1e )kt v s k-=- 9-7 202s t .=,707m s .= 9-8 172N F .=9-9 )(22g a amL F AC +=ω,)(22g a a mL F BC -=ω9-10 max 584kN F .=,min 536kN F .=9-11 g f f a ααααsin cos cos sin -+=,N cos sin W F f αα=- 9-12 )cos 1(200t m F t x ωωυ-+=第10章10-1 (a ) 12p mL ω=,方向水平向右;(b ) p mR ω=,方向水平向右;(c ) p me ω=,方向垂直于OC 的连线;(d ) C p mv =,方向水平向右10-2 30N x F =10-3 11221022a gP P P P F -++= 10-4 11r 12m v v v m m =++10-5 0(sin cos )v t g f'αα=-10-6 12(54)2l p m m ω=+,方向与曲柄垂直且向上 10-7 t m m l m x m m kx ωωsin 1211+=++10-8 2R s =10-9 (1) 3123123(22)cos ,2()C P L P P P L tx P P P ω+++=++ (2) 12123(2)sin ;2()C P P L t y P P P ω+=++2321max 222ωL gP P P F Ox ++=10-10 椭圆 2224l y x =+10-11 (1) 2sin G Wx l t P W Gω+=++ (2) 2m a x 2x G W F l g ω+=10-12 向右移377cm . 10-13 33(sin )cos ox R F m g m a r θθ=+,1233()(sin )sin oy RF m g m g a m g m a rθθ=+-++ 10-14 21212)(m m gm m f b m a ++-=·318··318·10-15 17cm A s =,向左移动;9cm B s =,向右移动 10-16 2max12(2)2ox r F F G G gω=++10-17 24(cos sin )3Ox mR F ωϕεϕπ=-+,24(sin cos )3Oy mR F mg ωϕεϕπ=+- 第11章11-1 (a ) ω2031ml L =,(b ) ω2021mR L =,(a ) ω2023mR L =11-2 208m s a ./=,2862kN T F .=,4626kN Oy F .=11-3 (1) ωωω22231ml mR Ml L O ---=,(2) ωω2231ml Ml L O --=11-4 θω22sin )312(l M m L O +=11-5 480r min n /=11-6 022ωωmr J ma J z z ++=11-7 0N 0Pr F fgt ω= 11-8 211212122()()R M R M'm m R R ε-=+11-9 )()(2212J i J gPR R PR Mi a ++-=11-10 t P P gkl)3(3cos210+=δϕ11-11 gR RW g J R W M a 2101sin +-=α,1T 1sin W F W a g α=+ 11-12 g J r m r m r m r m O++-=2222111122ε11-13 g R m r R m r R m a )()()(2222121ρ++++=,)()()(22221212ρρ+++-=R m r R m g m m Rr F11-14 v =T 13F mg =11-15 θsin 74g a =,θsin 71mg F -= 11-16 g a C 355.0=11-17 3)(2121m m gm m f F a ++-=·319··319·11-18 gr M R m r m R fm r m a 2222121ρ++-=,T 11A F m g m a =-,2T 2B m RF fm g a r=+11-19 2N 22sin 12D QL F a Lα=+,αcos g a Cx =,22212sin 12L a g a a Cy +=α 11-20 N 3633N B F .=11-21 P F F x O x O 516.021==,P F y O 434.11=,P F y O 164.12=第12章12-1 )cos 1(0ϕ+=mgr W AB ,)sin (cos 0θϕ-=mgr W AC 12-2 129904J F W .=,10500J f W =- 12-3 12206J W .=-,23206J W .=,031=W 12-4 (a) 2216T ml ω=,(b) 2234T mR ω=,(c) 2214T mR ω=,(d) 234C T mv =,12-5 10J W =重,503J W .=重12-6 θω222sin 61ml T = 12-7 21s s hf += 12-8 2122)cos (sin 2m m f gr m M r++-=ααϕϕω12-9 v=12-10 A v =12-11 A v =12-12 v =11/sin M R W a g W Wα-=+12-13 C v =45C a g =12-14 98N F .= 12-15 θωsin 3632121l g m m m m ++=,θεcos 23632121lgm m m m ++=12-16 C v =321321843)43(m m m gm m m F +++=12-17 (1) 2211)3()sin (2Rm m gR m M +-=αε, (2) R m m gR m M m F Ox )3(2)2sin cos 6(2121++=αα; ααsin )3()sin 3(21212⋅+++=Rm m gR m M m g m F Oy·320··320·12-18 v =m khmg a 34-=,41s 36F kh mg =+ 第13章13-1 αsin 32g a =13-2 g a 32=,T 3WF =13-3 Q P Pg a 322+=,QP PQF 32+=13-4 g P T a 3cos 2α=,N sin F P T α=-,s 1cos 3F T α= 13-5 22233cos sin 3()sin 2b a g b a ϕϕωϕ-=-13-6 445N ADF .=,54N BE F =13-7 2222(sin )cos sin J mr mr M ϕϕϕϕϕ++= 13-8 2222143)2(43ωr m gr m m M -+=,2143ωr m F Ox -=,4)2()(22121ωr m m g m m F Oy +-+= 13-9 0β=︒时,2329N Ax F =-,1382N Bx F =,1962N Ay By F F .==180β=︒时,12238N Ax F .=,592N Bx F =-,1962N Ay By F F .==13-10 2023ωmr F Ax -=,mgr F Ay =,20221ωmr F Bx =,mgr F By =13-11 g a a C x C 1712==,mg F 175= 13-12 l g 791=ε,lg 732-=ε,0=Ox F ,mg F Oy 72=第14章14-1 ctg 2P /Q /ϕ= 14-2 (3ctg 2)Ax F /P θ=14-3 A F P /=14-4 ctg Q P θ= 14-5 450N Q P /==14-6 12F F l =/2(cos )a ϕ14-7 05kN 21kN m Ax Ay A F F m ===⋅,,14-8 1866kN P .=14-9 2()F lx a k b=+14-10 2(kN)Ax F =, 3.804(kN)Ay F =,24(kN m)A M =-⋅,18.588(kN)B F =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
各章计算题及答案文件管理序列号:[K8UY-K9IO69-O6M243-OL889-F88688]
第二章课后作业书59页2. 以下是某银行的资金来源与成本状况,试计算以下银行的加权平均成本和可用资金加权平均成本率。
表2-4 某银行的资金与成本结构表
利息成本=20×2%+40×4%+30×6%+10×12%=5(万元)
营业成本=20×5%+40×1%+30×0.5%+10×0.25%=1.575(万元)
可用资金总额=20×78%+40×94%+30×94%+10×97%=91.1(万元)
资金成本率=(5+1.575)/(20+40+30+10)=6.575%
可用资金成本率=(5+1.575)/91.1=7.22%
第三章课后作业书100~101页
1.某客户向银行申请一年期3000万美元的贷款。
由于该客户是银行的重点客户,虽然银行资金不足,银行还是通过了这个申请。
为了筹集这笔资金,该银行出售了年利率为9%,金额为2000万美元的大额存单,并且按10%的年利率向其他银行借款1000万美元。
与此贷款申请有关的信用调查和其他费用估计为20000美元。
银行的信用分析部门建议,对此贷款至少收取0.25%的风险溢价和0.5%的利润。
要求:如果银行采用成本加成定价法,那么该笔贷款的价格是多少。
贷款价格=资金成本率+经营成本率+风险溢价+目标利润率
2.某客户借入一笔1年期的8000元的贷款。
要求:
(1)如果采用月等额分期偿还方式,年利率为14%,试用年百分比法计算该笔贷款的真实利率。
(2) 如果采用按季偿还方式,年利率为12%,试用单一利率法计算该笔贷款的真实利率。
(3)如果采用利息首付的方式,年利率为10%,试用贴现法计算该笔贷款的真实利率。
解: (1)
客户实际使用的资金平均余额为: 实际利率为:
(2)
客户实际使用的资金平均余额为: 实际利率为:
(3)
3. 某客户得到一笔25年期,450000元,年利率为12.5%的固定利率住宅抵押贷款,约定还款方式为按月等额支付本息。
要求:该客户的每月支付额、利息总额。
利息总额=4906.59×25×12-450000=1021977(元) 第七章 商业银行资本管理 248~249页
3.
(1)求资产收益率 ()()()()
%
56.112.0145.0108
.012.011111
1=+⨯-⨯=+-⋅
=
SG DR TA EC SG ROA
(2)求外源资本量△EK=5.76万元
4.。
