第3讲数学建模的插值法(免费阅读)
第3讲 数学建模的插值法

8
分段线性插值
y o
Ln ( x ) y j l j ( x )
j 0 n
xj-1 xj xj+1 xn x
x0
x x j 1 , x j 1 x x j n越大,误差越小. x j x j 1 x x j 1 l j ( x) , x j x x j 1 lim Ln ( x) g ( x), x0 x x j x j 1 n 0, 其它 9
f (x, y) (ax b)(cy d)
其中有四个待定系数,利用该函数在矩形的四个顶 点(插值节点)的函数值,得到四个代数方程,正 好确定四个系数。 返回
23
用MATLAB作网格节点数据的插值
z=interp2(x0,y0,z0,x,y,’method’)
被插值点 的函数值
插值 节点
计算量与n无关;
xn
例
1 g ( x) , 6 x 6 2 1 x
用分段线性插值法求插值,并观察插值误差.
1.在[-6,6]中平均选取5个点作插值(xch11)
2.在[-6,6]中平均选取11个点作插值(xch12)
3.在[-6,6]中平均选取21个点作插值(xch13)
4.在[-6,6]中平均选取41个点作插值(xch14) To MATLAB xch11,xch12, xch13,xch14
被插值点
插值方法
要求x0,y0单调; x,y可取为矩阵, 或x取行向量,y取 为列向量,x,y的值 分别不能超出x0,y0 的范围。
‘nearest’ 最邻近插值 ‘linear’ 双线性插值 ‘cubic’ 双三次插值 缺省时, 双线性插值
数学建模插值及拟合详解Word版

数学建模插值及拟合详解Word版插值和拟合实验⽬的:了解数值分析建模的⽅法,掌握⽤Matlab进⾏曲线拟合的⽅法,理解⽤插值法建模的思想,运⽤Matlab⼀些命令及编程实现插值建模。
实验要求:理解曲线拟合和插值⽅法的思想,熟悉Matlab相关的命令,完成相应的练习,并将操作过程、程序及结果记录下来。
实验内容:⼀、插值1.插值的基本思想·已知有n +1个节点(xj,yj),j = 0,1,…, n,其中xj互不相同,节点(xj, yj)可看成由某个函数 y= f(x)产⽣;·构造⼀个相对简单的函数 y=P(x);·使P通过全部节点,即 P (xk) = yk,k=0,1,…, n ;·⽤P (x)作为函数f ( x )的近似。
2.⽤MATLAB作⼀维插值计算yi=interp1(x,y,xi,'method')注:yi—xi处的插值结果;x,y—插值节点;xi—被插值点;method—插值⽅法(‘nearest’:最邻近插值;‘linear’:线性插值;‘spline’:三次样条插值;‘cubic’:⽴⽅插值;缺省时:线性插值)。
注意:所有的插值⽅法都要求x是单调的,并且xi不能够超过x的范围。
练习1:机床加⼯问题x035791112131415y0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6⽤程控铣床加⼯机翼断⾯的下轮廓线时每⼀⼑只能沿x⽅向和y⽅向⾛⾮常⼩的⼀步。
表3-1给出了下轮廓线上的部分数据但⼯艺要求铣床沿x⽅向每次只能移动0.1单位.这时需求出当x坐标每改变0.1单位时的y坐标。
试完成加⼯所需的数据,画出曲线.步骤1:⽤x0,y0两向量表⽰插值节点;步骤2:被插值点x=0:0.1:15; y=y=interp1(x0,y0,x,'spline');步骤3:plot(x0,y0,'k+',x,y,'r')grid on答:x0=[0 3 5 7 9 11 12 13 14 15 ];y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6 ];x=0:0.1:15;y=interp1(x0,y0,x,'spline');plot(x0,y0,'k+',x,y,'r')grid on0510150.511.522.53.⽤MATLAB 作⽹格节点数据的插值(⼆维) z=inte rp2(x0,y0,z0,x,y,’method’) 注:z —被插点值的函数值;x0,y0,z0—插值节点;x ,y —被插值点;method —插值⽅法(‘nearest’ :最邻近插值;‘linear’ :双线性插值; ‘cubic’ :双三次插值;缺省时:双线性插值)。
插值算法的介绍及其在数学建模中的应用

插值算法的介绍及其在数学建模中的应⽤⽬录插值算法的介绍及其在数学建模中的应⽤%本⽂根据清风数学建模课程插值算法及相关资料总结⽽成,仅供学习使⽤%本⽂参考了(),对介绍的顺序及内容进⾏了改进%由于本⽂仅仅是简要介绍插值算法在建模中的应⽤,因此样条插值的可微性证明等各种复杂繁琐的部分在本⽂中不再引⼊%本⽂仅介绍⼀维数据的插值,多维数据的插值⽅法与⼀维插值类似⼀、插值的介绍及其作⽤数模⽐赛中,常常需要根据已知的样本点进⾏数据的处理和分析,⽽有时候现有数据较少或数据不全,不⾜以⽀撑分析的进⾏,这时就需要使⽤插值法“模拟产⽣”⼀些新的但⼜⽐较靠谱的值来满⾜需求,这就是插值的作⽤。
%在直观上,插值就是找到⼀个连续函数使其经过每个样本点%插值法还可⽤于短期的预测问题(插值与拟合经常会被弄混,为了区分,这⾥简要介绍⼀下拟合:即找到⼀个函数,使得该函数在最⼩⼆乘的意义下与已知样本点的总体差别最⼩,该函数不⼀定要经过样本点。
通常情况下,拟合要求已知样本点的数据较多,当数据较少时不适⽤)⼆、插值法原理三、插值法的分类%注:下⾯的1、2、3、4 并⾮是并列关系,⼏个部分之间也有交叉,⽬的在于逐渐引出数学建模中最常⽤的两种插值⽅法:三次样条插值与三次埃尔⽶特插值。
1、普通多项式插值多项式插值中,拉格朗⽇插值与⽜顿插值是经典的插值⽅法,但它们存在明显的龙格现象(下⾯会解释龙格现象),且不能全⾯反映插值函数的特性(仅仅保证了插值多项式在插值节点处与被插函数有相等的函数值)。
然⽽在许多实际问题中,不仅要求插值函数与被插值函数在所有节点处有相同的函数值,它也需要在⼀个或全部节点上插值多项式与被插函数有相同的低阶甚⾄⾼阶的导数值。
对于这些情况,拉格朗⽇插值和⽜顿插值都不能满⾜。
因此,数学建模中⼀般不使⽤这两种⽅法进⾏插值,这⾥也不再介绍这两种⽅法。
龙格现象(Runge phenomenon): 1901年,Carl Runge 在他的关于⾼次多项式插值风险的研究中,发现⾼次插值函数可能会在两端处波动极⼤,产⽣明显的震荡,这种现象因此被称为龙格现象。
数学建模插值及拟合详解之欧阳地创编

插值和拟合实验目的:了解数值分析建模的方法,掌握用Matlab进行曲线拟合的方法,理解用插值法建模的思想,运用Matlab一些命令及编程实现插值建模。
实验要求:理解曲线拟合和插值方法的思想,熟悉Matlab相关的命令,完成相应的练习,并将操作过程、程序及结果记录下来。
实验内容:一、插值1.插值的基本思想·已知有n +1个节点(xj,yj),j = 0,1,…, n,其中xj互不相同,节点(xj, yj)可看成由某个函数 y= f (x)产生;·构造一个相对简单的函数y=P(x);·使P通过全部节点,即 P (xk) = yk,k=0,1,…, n ;·用P (x)作为函数f ( x )的近似。
2.用MATLAB作一维插值计算yi=interp1(x,y,xi,'method')注:yi—xi处的插值结果;x,y—插值节点;xi—被插值点;method—插值方法(‘nearest’:最邻近插值;‘linear’:线性插值;‘spline’:三次样条插值;‘cubic’:立方插值;缺省时:线性插值)。
注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
练习1:机床加工问题机翼断面下的轮廓线上的数据如下表:x 0 3 5 7 9 11 12 13 14 15y 0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6 用程控铣床加工机翼断面的下轮廓线时每一刀只能沿x方向和y方向走非常小的一步。
表3-1给出了下轮廓线上的部分数据但工艺要求铣床沿x方向每次只能移动0.1单位.这时需求出当x坐标每改变0.1单位时的y坐标。
试完成加工所需的数据,画出曲线.步骤1:用x0,y0两向量表示插值节点;步骤2:被插值点x=0:0.1:15; y=y=interp1(x0,y0,x,'spline');步骤3:plot(x0,y0,'k+',x,y,'r')grid on答:x0=[0 3 5 7 9 11 12 13 14 15 ];y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.01.6 ];x=0:0.1:15;y=interp1(x0,y0,x,'spline');plot(x0,y0,'k+',x,y,'r')grid on3.用MATLAB作网格节点数据的插值(二维)z=interp2(x0,y0,z0,x,y,’method’)注:z—被插点值的函数值;x0,y0,z0—插值节点;x,y—被插值点;method—插值方法(‘nearest’:最邻近插值;‘linear’:双线性插值;‘cubic’:双三次插值;缺省时:双线性插值)。
3-插值余项

Ln (x )
n
x j k l j (x )
j 0
n
又∵ f (n+1) (x) ≡0,所以其插值余项E(x)=0,
x j k l j (x ) x k
i 0
第一章——插值方法
n
19
练习:课本55页12题
第一章——插值方法
20
取c
(t k
0
n
xk )
f (x ) p n (x ) , 则有g (x ) f (x ) (x )
所以,误差函数R(t)=f(t)-g(t)至少有n+2个零点
罗尔定理:若函数f(x)满足下列条件:
1、 在闭区间[a,b]内连续;2、在开区间(a,b)内可导;
3、f(a)=f(b) 则至少存在一点ξ∈(a,b),使得f`(ξ)=0
第一章——插值方法
f
( n 1)
9
插值区间: 由插值节点所界定的范围[min xi,max xi] 内插: 插值点x位于插值区间内 外推: 插值点x位于插值区间外
第一章——插值方法
10
2、误差的事后估计
考察拉格朗日余项公式:
f (n 1) ( ) n f (x ) p n (x ) (x x k ) (n 1) k 0
先用x0与x1,x2进行线性插值,求出y=f(x)的一个 近似值y1;同样取x0与 x2,求出y2。 按余项定理得:
y y1 f (1 )
数学建模之Newton 插值法

计算方法
第二章
插值法
—— Newton 插值法
1
Newton 插值
为什么 Newton 插值
Lagrange 插值简单易用,但若要增加一个节点时,全部基函 数 lk(x) 都需重新计算,不太方便。
13
插值举例
可以看出,当增加一个节点时,牛顿插值公式只 需在原来的基础上增加一项,前面的计算结果仍 然可以使用。与拉格朗日插值相比,牛顿插值具 有灵活增加节点的优点!
注:增加插值节点时,须加在已有插值节点的后面!
14
向前差分
在实际应用中,通常采用等距节点: xi = x0 + i h ,i = 1, 2, …, n h>0,称为步长
Nn(x)
f [ x, x0 , ... , xn ]( x x0 )...(x xn1 )( x xn )
Rn(x)
10
Newton 插值公式
f (x) = Nn(x) + Rn(x)
N n ( x ) a0 a1 ( x x0 ) a2 ( x x0 )( x x1 ) an ( x xi )
f ( k ) ( ) f [ x0 , x1 , , xk ] k!
差商的等价定义:(教材上的所采用的定义) f [ x0 , , xk 2 , xk ] f [ x0 , , xk 1 ] f [ x0 , x1 , , xk ] xk xk 2 若 h(x) = c f(x),则 h[ x0 , x1 ,, xk ] c f [ x0 , x1 ,, xk ] 若 h(x) = f(x) + g(x),则 h[ x0 , x1 ,, xk ] f [ x0 , x1 ,, xk ] g[ x0 , x1 ,, xk ]
数学建模_插值与拟合总结

y0 y1
⎪⎩a0 + a1xn + a2 xn2 + L + an xnn = yn
记此方程组的系数矩阵为 A ,则
(3)
1 x0 x02 L x0n det( A) = 1 x1 x12 L x1n
LLLLLLL
1 xn xn2 L xnn 是范德蒙特(Vandermonde)行列式。当 x0 , x1,L, xn 互不相同时,此行列式值不为零。因 此方程组(3)有唯一解。这表明,只要 n + 1 个节点互不相同,满足插值要求(2)的
z=x(i); s=0.0; for k=1:n
p=1.0; for j=1:n
if j~=k p=p*(z-x0(j))/(x0(k)-x0(j));
end end s=p*y0(k)+s; end y(i)=s; end
-176-
1.2 牛顿(Newton)插值 在导出 Newton 公式前,先介绍公式表示中所需要用到的差商、差分的概念及性质。 1.2.1 差商
=
f0
+
Δf 0 h
(x − x0 ) + L +
Δn f0 n! h n
( x − x0 )( x − x1)L( x − xn−1)
若令 x = x0 + th ,则上式又可变形为
Nn (x0
+ th)
=
f0
+ tΔf0
+L +
t(t
− 1)L(t n!
−n
+ 1) Δn
f0
上式称为 Newton 向前插值公式。
f [x, x0 , x1] = f [x0 , x1, x2 ] + ( x − x2 ) f [x, x0 , x1, x2 ] LL
插值法内插与外插

插值法内插与外插插值法(内插与外插)Interpolation and Extrapolation数学问题探讨当我们在表现资料时,常常会有需要比实际量测点上的值更细密的情况,或者是有需要在范围外预测其值。
比方说天气图的绘制,不论是气压或是雨量,都不可能做到处处都有测量站,又例如我们关心一天之中温度随时间的变化,但是实际上记录气温的动作可能只是每小时一次,则我们要作一个连续的图时,就会用到插值法。
插值法的中心议题是:在我们己具备一组表列数(tabulated value)的情况下,如何得出没被定到之区域的值。
什么样的函数才能被插值,这是数学上讨论的间问题,参见课文p.99第四段。
然而,我们会要用到插值法的场合往往都不知道描述对象背后的函数是什么形式(但相信其有连续的本质),因此我们也只能尽力求真实。
使用插值法所建立的函数,在表列点上一定要重现原本给定的表列值,否则就不是插值法而是函数近似或曲线拟合的间问题了,它们是不一样的。
插值的作法,很直观地来讲,就是,(1)先从表列值来获得函数f(x),再(2)用函数f(x)求出我们所要的任何特定x之f(x)函数值。
然而,比较精密且系统化的数值方法却不是用这两个步骤来进行插值,原因是前述两阶段方法对于插值的精密度并没有控制,效率较差,也比较会有进位误差。
一般在做插值法,是从欲插值点x附近的几个表列点xi开始,建立插值函数f(x),并且也试著网罗更多表列点来插值,看随著项数变多误差会不会变小,如此找出最适合的函数f(x)。
我们会比较希望演算法在从表列值建立插值用函数时,也能提供误差分析以供我们或程式来判断。
毕竟可用的插值函数f(x)并非唯一,而即便是己设定了采用一种方法,如多项式法,也会有该使用多少项才最恰当的问题。
建立插值函数所需之邻近表列值个数,我们称之为插值法的order(阶),较高阶未必保证得到较合理的插值,这点在多项式插值法尤其如此,要小心注意。
详见课文中之例图上两图实线都是原现象背后的真正值,短虚线代表低阶多项式插值结果,长虚线代表高阶多项式插值结果。
数学建模插值与拟合课件
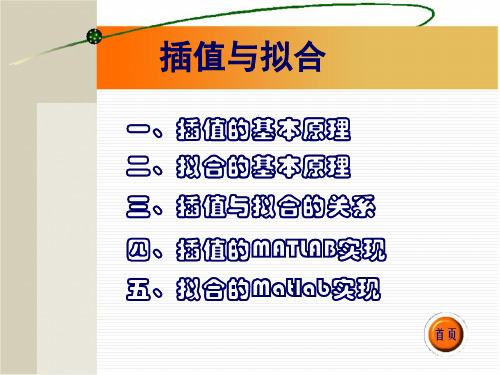
设函数 y f (x) 在 n 1个相异点 x0 , x1, x2 , , xn 上的值为 y 0 , y1, y2 , , yn ,要求一个次数≤n 的代数多
项式
Pn (x) a0 a1x a2 x 2 an x n
使在节点 xi 上成立 Pn (xi ) yi (i 0,1,2, , n) ,称此为 n 次代数插值问题,Pn (x) 称为插值多项式。可以证明 n
如果不要求近似函数通过所有数据点, 而是要求它能较好地反映数据变化规律的近 似函数的方法称为数据拟合。(必须有函数 表达式)
近似函数不一定(曲线或曲面)通过所 有的数据点。
三、插值与拟合的区别和联系
1、联系 都是根据实际中一组已知数据来构造一个能够 反映数据变化规律的近似函数的方法。 2、区别 插值问题不一定得到近似函数的表达形式,仅 通过插值方法找到未知点对应的值。数据拟合 要求得到一个具体的近似函数的表达式。
图所示,当n 增大时,pn x在两端会发出激烈
的振荡,这就是所谓龙格现象。
龙格现象
2
y=1/(1+x2) y=p4(x) y=p10(x) 1.5
1
0.5
0
-0.5
-5 -4 -3 -2 -1
0
1
2
3
4
5
x
To MATLAB lch(larg1)
分段插值的概念
所谓分段插值,就是将被插值函数逐段 多项式化。一般来说,分段插值方法的处理 过程分两步,先将所考察的区间作一分划
y1
lj(x)
当n =2 时,有三点二次(抛物线)插值多项式:
P2
(x)
(x (x0
x1)(x x2 ) x1)(x0 x2 )
数学建模插值和拟合问题的总结

插值和数据拟合一、 插值方法问题:已知n+1个节点(x j ,y j )(j=0,1,…,n),a=x 0<x 1<…< x n =b ,求任一插值点x*处的插值y*方法:构造一个相对简单的函数y=f(x),使得f 通过所有节点,即f(x j )= y j ,再用y=f(x)计算x*的值。
1. 拉格朗日多项式插值设f(x)是n 次多项式,记作1110()n n n n n L x a x a x a x a --=++++要求对于节点(,)j j x y 有(),0,1,,n j j L x y j n ==将n+1个条件带入多项式,就可以解出多项式的n+1个系数。
实际上,我们有n 次多项式011011()()()()()()()()()i i n i i i i i i i n x x x x x x x x l x x x x x x x x x -+-+----=----满足1,()0,,,0,1,,i j i jl x i j i j n =⎧=⎨≠=⎩则0()()nn i i i L x y l x ==∑就是所要的n 次多项式,称为拉格朗日多项式。
由拉格朗日多项式计算的插值称为拉格朗日插值。
一般来讲,并不是多项式的阶数越高就越精确,一般采用三阶、二阶或一阶(线性)多项式,对相邻点进行分段插值。
2. 样条插值在分段插值时,会造成分段点处不光滑,如果要求在分段点处光滑,即不仅函数值相同,还要一阶导数和二阶导数相同,则构成三阶样条插值。
一般用于曲线绘制,数据估计等。
例 对21,[5,5](1)y x x =∈-+,用n=11个等分节点做插值运算,用m=21个等分插值点作图比较结果。
见inter.m 程序二、 曲线拟合 三、 给药方案 1. 问题一种新药用于临床必须设计给药方案,在快速静脉注射的给药方式下,就是要确定每次注射剂量多大,间隔时间多长.我们考虑最简单的一室模型,即整个机体看作一个房室,称为中心室,室内血液浓度是均匀的.注射后浓度上升,然后逐渐下降,要求有一个最小浓度1c 和一个最大浓度2c .设计给药浓度时,要使血药浓度保持在1c ~2c 之间.2. 假设(1)药物排向体外的速度与中心室的血药浓度成正比,比例系数是k(>0),称为排出速度.(2)中心室血液容积为常数V ,t=0的瞬间注入药物的剂量为d ,血药浓度立即为dV. 3. 建模设中心室血药浓度为c(t),满足微分方程(0)dckc dtd c V=-=用分离变量法解微分方程,有()ktd c te V-=(*) 4. 方案设计每隔一段时间τ,重复注入固定剂量D ,使血药浓度c(t)呈周期变化,并保持在1c ~2c 之间.如图:设初次剂量加大到D 0,易知0221,D Vc D Vc Vc ==-,2121()11ln[],()()ln c Vc t t t c t c k d k c τ=-=-= 那么,当12,c c 确定后,要确定给药方案0{,,}D D τ,就要知道参数V 和k .5. 由实验数据做曲线拟合确定参数值已知1210,25(/)c c g ml μ==,一次注入300mg 药物后,间隔一定ln lndc kt V=- 记12ln ,,lndy c a k a V==-=,则有 12y a t a =+求解过程见medicine_1.m得120.2347, 2.9943a a =-=,由d=300(mg)代入算出k=0.2347,V=15.02(L) 从而有0375.5(),225.3(), 3.9()D mg D mg τ===小时四、 口服给药方案 1. 问题口服给药相当于先有一个将药物从肠胃吸收入血液的过程,可简化为一个吸收室,一个中心室,记t 时刻,中心室和吸收室的血液浓度分别是1()()c t c t 和,容积分别是V ,V1,中心室的排除速度为k ,吸收速度为k1,且k,k1分别是中心室和吸收室血液浓度变化率与浓度的比例系数,t=0口服药物的剂量为d ,则有11111,(0)dc dk c c dt V =-= (1) 111,(0)0V dckc k c c dt V=-+= (2) 解方程(1)有111()k td c te V -=代入方程(2)有111()()k t kt k d c t e e V k k--=--其中三个参数1,,dk k b V=,可由下列数据拟合得到:(非线性拟合)。
数值分析第三章 插值法

+ (0.3367 − 0.32)(0.3367 − 0.36) × 0.333487 (0.34 − 0.32)(0.34 − 0.36)
+ (0.3367 − 0.32)(0.3367 − 0.34) × 0.352274 = 0.330374
(0.36 − 0.32)(0.36 − 02.36 4)
x x0 x1 y 01
一次插值多项式y = P1 (x)可以由两个基本插值多项 式 l0 (x)、l1 (x) 与函数值y0、y1的线性组合来表示
6
6
线性插值
例3.2.1:已知y = f (x)的函数表
x13 y12
求线性插值多项式,并计算x=1.5的函数值
解:已知两点的线性插值多项式
Rn (x) = f (x) − Pn (x)
定理3.2:设f (n)(x)在区间[a, b]上连续,f (n + 1)(x) 在[a, b]上存在,x0, x1,…, xn是[a, b]上互异的节 点,记插值问题的余项为 Rn (x) = f (x) − Pn (x) , 那么,当x ∈ [a, b]时,有如下估计
≈
P2 (115)
=
(115 (100
− 121)(115 − 144) − 121)(100 − 144)
× 10
+ (115 − 100)(115 − 144) ×11 (121 − 100)(121 − 144)
+ (115 − 100)(115 − 121) ×12 (144 − 100)(144 − 121)
P1 ( x)
=
x−3 1−3
×1+
x −1× 3−1
2
数学建模 插值与拟合共103页

56、极端的法规,就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要,人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益, 而是为 了公共 的利益 ;一部 分靠有 害的强 制,一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ,那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
60、人民的幸福是至高无个的法。— —西塞 罗
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
(完整版)数学建模 插值和拟合

x
xn
x
4.2 MATLAB实现插值
Matlab 实现:实现插值不需要编制函 数程序,它自身提供了内部的功能函数 interp1(一维分段插值) interp2(二维) interp3(三维) intern(n维)
4.3.1一维插值
用MATLAB作插值计算
一维插值函数: yi=interp1(x,y,xi,'method')
h=1:0.1:12;
t=interp1(hours,temps,h,'spline');
plot(hours,temps,'+',h,t,'r:')
xlabel('Hour'),ylabel('Degrees Celsius’)
例1:从1点12点的11小时内,每隔1小时测量一次温度, 测得的温度的数值依次为:5,8,9,15,25,29, 31,30,22,25,27,24.试估计(1)每隔1/10小时 的温度值;(2)估计1点30分和13的温度值。
例1:从1点到12点的11小时内,每隔1小时测量一次温 度,测得的温度的数值依次为:5,8,9,15,25, 29,31,30,22,25,27,24.试估计(1)每隔 1/10小时的温度值;(2)估计1点30分和13的温度值。
hours=1:12;
temps=[5 8 9 15 25 29 31 30 22 25 27 24];
x x0 y y0
x1 … xn y1 … yn
其中x0,x1, …xn是n+1个互不相同的点,求一个 近似函数 (x) ,使得
( xi ) f ( xi ) i 0,1 …n
数学建模插值法
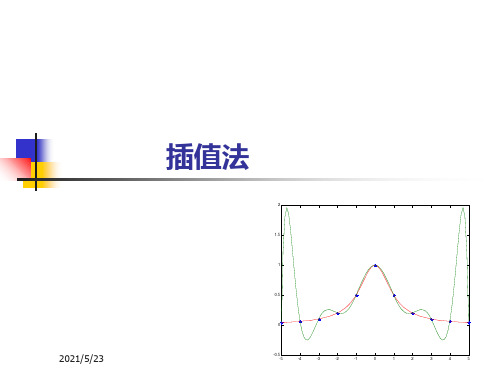
给定数据表:
x
0.4
0.5
0.6
0.7
0.8
lnx
-0.916291 -0.693147 -0.510826 -0.356675 -0.223144
用lagrange插值公式计算 clear x0=0.4:0.1:0.8; y0=log(x0); x=0.54; lagrange(x0,y0,x)
ln(0.54)的函数值
function Y=newpoly(x,y,X) %牛顿插值 n=length(x); D=zeros(n); D(:,1)=y'; for j=2:n %计算差商矩阵 for k=j:n D(k,j)=(D(k,j-1)-D(k-1,j-1))/(x(k)-x(k-j+1)); end end C=D(n,n); for k=(n-1):-1:1 %构造插值多项式 C=conv(C,poly(x(k))); m=length(C); C(m)=C(m)+D(k,k); end Y=polyval(C,X);
2021/5/23
13
龙格现象
Runge在上个世纪初发现:
在[-5,5]上用n+1个等距节点作n次插值多项式Pn(x), 当在n→∞时,插值多项式Pn(x)在区间中部趋于
f(x)=1/(1+x2) , 但对于3.63≤∣x∣≤5的x,Pn(x)严重发散。 用图形分析问题。
2021/5/23
14
for n=10:2:20
-0.916291 -0.693147 -0.510826 -0.356675 -0.223144
计算ln(0.54)的值.
2021/5/23
3
一、问题的提出
(数学建模课件)10.1数据插值方法及应用

2、多项式插值
设有 m 次多项式
P(x) a0 x m a1x m1 am1x am
通过所有 n 1个点 (x0 , y0 ), (x1, y1),, (xn , yn ) ,那么就有
a0 xi m a1xi m1 am1xi am yi , i 0,1,, n
2 vi
vi2 4vi1 3vi 2(ti1 ti )
向后差商公式
2 vi
3vi 4vi1 vi2 2(ti ti1 )
估算出水塔中水的流速(单位:立方米/小时)
见下表。
时刻
0 0.921 1.843 2.949 3.871 4.978 5.900
流速 54.516 42.320 38.085 41.679 33.297 37.814 30.748
用二阶差商来估算 ti 时刻的水流速度,即 f (ti ) 2vi 。
具体地,因为所有数据被水泵两次工作分割成三
组数据,对每组数据的中间数据采用中心差商,前后
两个数据不能够采用中心差商,改用向前或向后差
商。
中心差商公式
2 vi
vi2
8vi1 8vi1 12(ti1 ti )
vi2
向前差商公式
先用 MATLAB 画出水流速散点图。
t=[0 0.921 1.843 2.949 3.871 4.978 5.9 7.006 7.982 8.967 10.954 12.032 12.954 13.875 14.982 15.903 16.826 17.931 19.037 19.959 20.839 22.958 23.88 24.986 25.908]; r=[54.516 42.320 38.085 41.679 33.297 37.814 30.748 38.455 32.122 41.718 73.686 76.434 71.686 60.19 68.333 59.217 52.011 56.626 63.023 54.859 55.439 57.602 57.766 51.891 36.464];
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s i ( x i ) s i 1 ( x i ) s i ( x i ) , s i 1 ( x i ) s i ( x i ) , s i 1 ( x i ) ( i 1 , , n 1 )
4)S(x0)S(xn)0 (自然边界条 2 ) 3 ) 4 ) a i,b i,c i,d i S ( x )
称为拉格朗日插值基函数。 7
拉格朗日(Lagrange)插值
特别地: 两点一次(线性)插值多项式:
L1xxx0 xx11y0xx1 xx00y1
三点二次(抛物)插值多项式:
L 2 x x x 0 x x 1 1 x x 0 x x 2 2 y 0 x x 1 x x 0 0 x x 1 x x 2 2 y 1 x x 2 x x 0 0 x x 2 x 1 x 1 y 2
To MATLAB
xch11,xch12 ,xch13, xch14
返回
11
三次样条插值
比分段线性插值更光滑。
y
a
xi-1 xi
bx
在数学上,光滑程度的定量描述是:函数 ( 曲 线 ) 的 k 阶导数存在且连续,则称该曲线具有 k 阶光 滑性。
光滑性的阶次越高,则越光滑。是否存在较低
次的分段多项式达到较高阶光滑性的方法?三次 样条插值就是一个很好的例子。
12
三次样条插值
S ( x ) { s i( x )x ,[ x i 1 ,x i] i , 1 , n }
1)si(x)aix3bix2cixdi (i1, n) 2)S(xi)yi (i0,1, n) 3)S(x)C2[x0,xn]
被插值点
插值方法
‘nearest’ :最邻近插值
‘linear’ : 线性插值;
注意:所有的插值方法 ‘spline’ : 三次样条插值
都要求x是单调的,并且xi ;
不能够超过x的范围。
‘cubic’ : 立方插值。
缺省时: 分段线性插值。
15
例:在1-12的12小时内,每隔1小时测量一次温 度,测得的温度依次为:5,8,9,15,25,29, 31,30,22,25,27,24。试估计每隔1/10小 时的温度值。
三、用Matlab解插值问题 网格节点数据的插值 散点数据的插值
返回
4
一维插值的定义
已知 n+1个节点 (xj,yj)(j 0 ,1 , n ,其中 x j
互不相同,不妨设 a x 0 x 1 x n b ),
求任一插值点 x*( xj )处的插值 y * .
y*
y1
y0
ln i m S(x)g(x)
g(x)为被插值函数。 13
例
g(x)1 1x2, 6x6
用三次样条插值选取11个基点计算插值(ych)
To MATLAB ych(larg1)
返回
14
用MATLAB作插值计算
一维插值函数:
yi=interp1(x,y,xi,'method')
xi处的插 插值节点 值结果
x
计算量与n无关; n越大,误差越小.
ln i L m n(x)g(x)x ,0xxn
10
例
g(x)1 1x2, 6x6
用分段线性插值法求插值,并观察插值误差.
1.在[-6,6]中平均选取5个点作插值(xch11)
2.在[-6,6]中平均选取11个点作插值(xch12) 3.在[-6,6]中平均选取21个点作插值(xch13) 4.在[-6,6]中平均选取41个点作插值(xch14)
其中Li(x) 为n次多项式:
L i( x ) ( x ( ix x x 0 ) 0 ) x x i( ( x x 1 1 ) ) ( ( x x i x x i i 1 1 ) ) x x i ( ( x x i 1 i ) 1 ) ( x ( x ix n x ) n )
数学建模与数学实验
插值
1
实验目的
1、了解插值的基本内容。 2、掌握用数学软件包求解插值问题。
实验内容
[1]一维插值 [2]二维插值 [3]实验作业
2
一维插值
一、插值的定义 二、插值的方法
拉格朗日插值
分段线性插值
三次样条插值 三、用Matlab解插值问题
返回
3
二维插值
一、二维插值定义
二、网格节点插值法 最邻近插值 分片线性插值 双线性插值
x0 x1 x *
xn
返回
6
拉格朗日(Lagrange)插值
已知函数f(x)在n+1个点x0,x1,…,xn处的函数值为 y0,y1,…,yn 。求一n次多项式函数Pn(x),使其满足:
Pn(xi)=yi,i=0,1,…,n. 解决此问题的拉格朗日插值多项式公式如下
n
Pn(x) Li(x)yi i0
返回
9
分段线性插值
y
o x0
xj-1
n
L n ( x )
y jl j ( x )
j 0
x x j1 x j x j1
,
x
j1
x
xj
lj(x)
x xj
x j1 x j1
,
x
j
x
x j1
0
,
其它
xj xj+1 xn
x0 x1 x *
xn
节点可视为由
yg(x)产生g表达式Leabharlann 杂,或无封闭形式, 或未知.。
5
构造一个(相对简单的)函数 yf(x),通过全部节点, 即
f(x j) y j (j 0 ,1 , n ) 再用 f (x) 计算插值,即 y* f (x*).
y*
y1
y0
直接验,L 证 nx满 可足 知插. 值条件
8
1
例
g(x)1x2, 5x5
采用拉格朗日多项式插值:选取不同插值 节点个数n+1,其中n为插值多项式的次数,当n 分别取2,4,6,8,10时,绘出插值结果图形.
To Matlab lch(larg1)
拉格朗日多项式插值的 这种振荡现象叫 Runge现象
