多因素分析 案例
多因素案例分析

表18-13不同体质指数高血压患病率
体质指数 (X)
调查人数 患病
未患病
患病率
( Y=1 病 例 )( Y=0 对 照 )(%)
超重或肥胖 (X=1暴露) 正常 (X=0非暴露) 合计
4148
1656(a)
2492(b)
39.92
6792
1331(c)
5461(d)
19.6
10940 2987
7953
甲医师以生存结局为观察指标,整理得A、B两 组死亡情况(表19-2)。考虑到例数较少, 采用Fisher确切概率法,得P=0.097,说明 两种治疗方法疗效差别无统计学意义。
乙医师以生存时间为观察指标,考虑到肾功能是否异 常为可能混杂因素,采用多重线性回归进行校正混杂 因素后的组间生存时间比较,结果见表19-3。说明校 正肾功能是否异常后,两种治疗方法疗效差别无统计 学意义,与甲医师的结论一致。
延续到两周内=2,慢性病持续到两周 内=3
1.该赋值方式是否恰当?
发病时间的设置不恰当,虽然‘发病时间’为有序 多分类资料,但是不能确定数据中的数值可以真实 反映其测度,故以最高值为参照水平,产生两个哑 变量。
X 7
“发病时X 间71 ”哑变量X:72
1
1
0
2
0
1
3
0
0
2.并说明各种变量赋值方法主要的利弊。
(2)针对原始数据和分析目的,指出正确的分析 方法并说明理由。
➢ 由原始数据可知,共有group、kidney、time、 status四个变量,其中time、status 为因变量;
➢ 本题的目的在于评价A、B两种治疗方案对某病 的治疗效果,所以因变量应包含生存结局变量 (是否死亡)和生存时间变量;
统计应用spss大作业-多因素分析
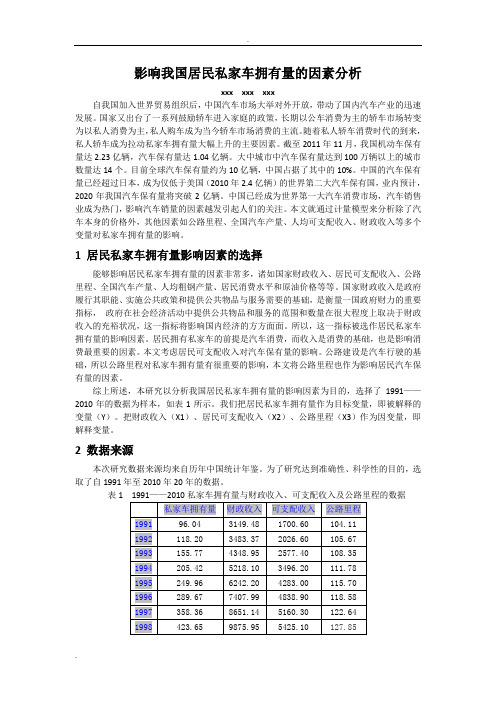
影响我国居民私家车拥有量的因素分析xxx xxx xxx自我国加入世界贸易组织后,中国汽车市场大举对外开放,带动了国内汽车产业的迅速发展。
国家又出台了一系列鼓励轿车进入家庭的政策,长期以公车消费为主的轿车市场转变为以私人消费为主,私人购车成为当今轿车市场消费的主流。
随着私人轿车消费时代的到来,私人轿车成为拉动私家车拥有量大幅上升的主要因素。
截至2011年11月,我国机动车保有量达2.23亿辆,汽车保有量达1.04亿辆。
大中城市中汽车保有量达到100万辆以上的城市数量达14个。
目前全球汽车保有量约为10亿辆,中国占据了其中的10%。
中国的汽车保有量已经超过日本,成为仅低于美国(2010年2.4亿辆)的世界第二大汽车保有国,业内预计,2020年我国汽车保有量将突破2亿辆。
中国已经成为世界第一大汽车消费市场,汽车销售业成为热门,影响汽车销量的因素越发引起人们的关注。
本文就通过计量模型来分析除了汽车本身的价格外,其他因素如公路里程、全国汽车产量、人均可支配收入、财政收入等多个变量对私家车拥有量的影响。
1 居民私家车拥有量影响因素的选择能够影响居民私家车拥有量的因素非常多,诸如国家财政收入、居民可支配收入、公路里程、全国汽车产量、人均粗钢产量、居民消费水平和原油价格等等。
国家财政收入是政府履行其职能、实施公共政策和提供公共物品与服务需要的基础,是衡量一国政府财力的重要指标,政府在社会经济活动中提供公共物品和服务的范围和数量在很大程度上取决于财政收入的充裕状况,这一指标将影响国内经济的方方面面。
所以,这一指标被选作居民私家车拥有量的影响因素。
居民拥有私家车的前提是汽车消费,而收入是消费的基础,也是影响消费最重要的因素。
本文考虑居民可支配收入对汽车保有量的影响。
公路建设是汽车行驶的基础,所以公路里程对私家车拥有量有很重要的影响,本文将公路里程也作为影响居民汽车保有量的因素。
综上所述,本研究以分析我国居民私家车拥有量的影响因素为目的,选择了1991——2010年的数据为样本,如表1所示。
多因素案例分析

PART 03
案例分析方法
定性分析方法
描述性分析
通过详细描述案例背景、过程和结果,对案例进行全面深入的理 解。
归纳推理
从案例中归纳出一般性规律或结论,用于解释和预测类似情境。
因果分析
探究案例中各种因素之间的因果关系,以解释事件发生的原因。
定量分析方法
统计分析
运用统计学方法对案例数据进行分析,以揭示数据背后的规律。
建议3
强调解决方案和实施建议的重要性和必要性,以引起相关人员的重 视和关注。
PART 06
案例总结与展望
案例总结
案例背景
介绍案例发生的背景,包括时间、地点、涉 及的主要人物和事件等。
案例描述
详细描述案例的具体情况,包括问题的提出、 解决方案的制定和实施等。
案例分析
对案例进行深入分析,包括对问题的识别、 解决方案的有效性评估等。
https://
2023 WORK SUMMARY
多因素案例分析
REPORTING
目录
• 案例背景介绍 • 影响因素分析 • 案例分析方法 • 案例分析过程 • 案例分析结果 • 案例总结与展望
https://
PART 01
案例背景介绍
https://
2023 WORK SUMMARY
THANKS
感谢观看
REPORTING
ABCD
政策法规
政府政策和法规的变化,可能影响组织的合法性和运营 方式。
技术发展
新技术的出现和应用,可能带来组织变革和竞争优势。
直接因素
市场需求
市场需求的变化,直接影响组织的销售和盈 利能力。
客户需求
客户需求的多样性和变化,直接影响产品或 服务的改进和创新。
多因素实验设计案例

结果与分析
4.不同情境以及年龄对幼儿坚持性行为的影响
幼儿的4种典型行为的年龄差异均显著 随着年龄的增长,幼儿的溜号行为、求助行为、自言自语及
拾取方法的表现均有所变化。
结果与分析
4. 不同情境以及年龄对幼儿坚持性行为的影响
溜号行为的情境差异非常显著 其他典型行为受情境的影响不明显。
结果与分析
1.教师态度、言语指导和年龄对3~6岁幼儿坚持时间的影响
幼儿年龄主效应极为显著 教师态度主效应极为显著 教师言语指导主效应极为显著 年龄 × 言语指导方式的交互作用极为显著 言语指导 × 教师态度的交互作用极为显著 年龄 × 教师态度的交互作用不显著 年龄 × 言语指导 × 教师态度的交互作用不显著
2.被试同质性检验——《幼儿自我控制能力发展教师评定问卷》 3.实验材料——红豆、绿豆,两个盒子 4.实验设计与程序 4.1实验设计
3 × 2 × 2
(年龄×教师态度×言语指导方式)
研究方法
4.2实验程序
主试的选择——12名教师(工作年限2年以上) 记录员的选择——4名研究生
预实验——10人
发现不利因素,控制无关变量
恐惧型:重要他人启动&无重要他人启动——目标承诺得分 差异不显著(F(1,187)=0.57,p>0.05);
讨论
重要他人对目标追求的影响 依恋类型在重要他人影响目标追求过程中的调节作用
结论
1. 重要他人能显著地影响个体的目标追求; 2. 依恋关系在重要他人影响目标追求过程中起到调节作用;
控制组:自我信息回忆、描述 依恋类型量表 & 目标承诺量表
6.数据收集与统计分析
结果与分析——描述性统计结果
财务报告_多因素分析法(3篇)

第1篇摘要随着我国市场经济的发展,企业之间的竞争日益激烈,财务报告作为企业对外展示经营状况的重要窗口,其准确性和可靠性越来越受到重视。
多因素分析法作为一种综合性的财务分析方法,能够帮助企业深入挖掘财务数据背后的影响因素,为决策提供有力支持。
本文以某上市公司为例,运用多因素分析法对其财务报告进行分析,旨在揭示企业财务状况的内在规律,为投资者和企业管理层提供参考。
关键词:财务报告;多因素分析法;上市公司;案例分析一、引言财务报告是企业对外展示经营状况的重要窗口,其质量直接关系到投资者、债权人等利益相关者的决策。
多因素分析法作为一种综合性的财务分析方法,通过分析影响企业财务状况的多个因素,揭示其内在规律,为企业决策提供有力支持。
本文以某上市公司为例,运用多因素分析法对其财务报告进行分析,以期为投资者和企业管理层提供参考。
二、案例背景某上市公司成立于2000年,主要从事房地产开发业务。
经过多年的发展,公司已发展成为我国房地产行业的领军企业之一。
近年来,随着国家宏观调控政策的实施,房地产市场出现波动,该公司也面临着一定的经营压力。
为了深入了解公司财务状况,本文对其财务报告进行多因素分析。
三、多因素分析法概述多因素分析法是一种综合性的财务分析方法,其基本原理是将影响企业财务状况的因素分解为多个相互独立的因素,并分析这些因素对企业财务状况的影响程度。
具体步骤如下:1. 确定分析指标:根据分析目的,选择合适的财务指标,如营业收入、净利润、资产负债率等。
2. 构建因素模型:将影响企业财务状况的因素分解为多个相互独立的因素,并建立因素模型。
3. 数据收集与处理:收集相关数据,对数据进行处理,确保数据的准确性和可靠性。
4. 因素分析:运用统计分析方法,分析各因素对企业财务状况的影响程度。
5. 结果解读:根据分析结果,揭示企业财务状况的内在规律,为企业决策提供参考。
四、案例分析1. 确定分析指标本文选取以下指标进行分析:(1)营业收入:反映企业经营活动产生的收入。
5M因素法(鱼骨图)分析案例
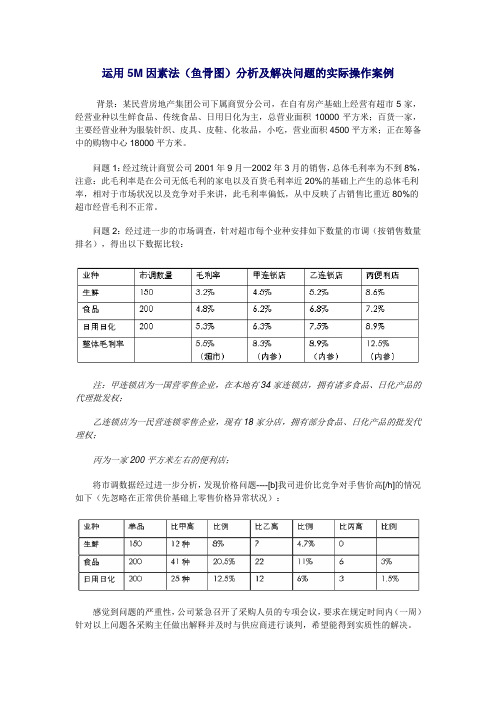
运用5M因素法(鱼骨图)分析及解决问题的实际操作案例背景:某民营房地产集团公司下属商贸分公司,在自有房产基础上经营有超市5家,经营业种以生鲜食品、传统食品、日用日化为主,总营业面积10000平方米;百货一家,主要经营业种为服装针织、皮具、皮鞋、化妆品,小吃,营业面积4500平方米;正在筹备中的购物中心18000平方米。
问题1:经过统计商贸公司2001年9月—2002年3月的销售,总体毛利率为不到8%,注意:此毛利率是在公司无低毛利的家电以及百货毛利率近20%的基础上产生的总体毛利率,相对于市场状况以及竞争对手来讲,此毛利率偏低,从中反映了占销售比重近80%的超市经营毛利不正常。
问题2:经过进一步的市场调查,针对超市每个业种安排如下数量的市调(按销售数量排名),得出以下数据比较:注:甲连锁店为一国营零售企业,在本地有34家连锁店,拥有诸多食品、日化产品的代理批发权;乙连锁店为一民营连锁零售企业,现有18家分店,拥有部分食品、日化产品的批发代理权;丙为一家200平方米左右的便利店;将市调数据经过进一步分析,发现价格问题----[b]我司进价比竞争对手售价高[/h]的情况如下(先忽略在正常供价基础上零售价格异常状况):感觉到问题的严重性,公司紧急召开了采购人员的专项会议,要求在规定时间内(一周)针对以上问题各采购主任做出解释并及时与供应商进行谈判,希望能得到实质性的解决。
一周过去了,供价问题依然没有得到明显的改善,高出比例依然居高不下。
总结各采购主任的解释,主要如下:1、甲、乙对手拥有诸多敏感商品的控制权,近水楼台先得月,人家有权利及有实力去进行降价;2、公司政策对于供应商的通道利润要求过高,厂商在无奈情况下,只有提高供价,保持其基本利润,如果要求供应商降价,只有舍弃部分通道利润才可行;3、公司要求的经营方式过于呆板,竞争对手部分商品是从批发市场上进行铲货来冲击市场,而公司没有此先例,都是以正常方式进行经营;4、公司的付款方式问题:由于现金进货与押款进货的供价有区别,但是公司最低的付款要求为7天付款,因此在价格上没有办法降低;5、竞争对手的恶意竞争行为:牺牲利润,亏本赚吆喝;6、人手不够,杂事多,没有办法集中时间与精力与供应商谈判。
因素分析案例

• 分析过程
• 1.昌荣面粉厂近两年经营情况
• 报告年度比上年度的利润减少71万元, 主要是由于销售收入减少使利润减少61 万元,由于总成本增加使利润减少14万 元。销售收入为什么会出现骤减呢?
• 2.销售收入变动的影响因素 • 由于报告年度面粉销售量比上年度减少1760
吨,使销售收入减少197万元,由于面粉出 厂价格上涨28.67%,使销售收入增加136万 元。两个因素增减相抵,销售收入减少61万 元。总成本为什么增加呢?
• 电单耗全国最低320度/吨,全国平均水平为430度/ 吨,而该厂的电单耗达 570度/吨,比全国平均水 平高32.56%。如果电单耗降至全国平均水平,仍 以年产量 6500吨计算,可节约电91万度,可节约 电费23万元。
• 3.总成本变动的影响因素
• 报告年度的单位成本达到 1400元,比上年 度967元上升433元,由于单位成本上升使 总成本增加184万元,由于产量减少使总 成本减少170万元,增减相抵,总成本增 加14万元。单位成本为什么增加呢?
• 4.单位成本的影响因素
• 单位变动成本报告年度为1063.3元,比上 年度的738.6元增加324.7元,由于单位变 动成本的增加,使总成本增加138万元。 单位固定成本报告年度为336.7元,比上 年度的228.4元增加108.3元,由于单位固 定成本的增加,使总成本增加46万元。 单位变动成本为什么大幅度上升呢?
• 钢材消耗总量=产量×单位产品材料消耗量
=产量×(单位产品净重量+单位产品工艺 损耗量+单位产品非工艺损耗量)
• 第二层,将单耗提高而多消耗的钢材分解为 如下三个因素,用连环替代法分析:
由于单位产品净重增加而多耗钢材84吨: 420×(1344/420-1200/400)=84吨; 由于单位产品工艺损耗量增加而多耗钢材 63吨: 420×(273/420-200/400)=63吨; 由于单位产品非工艺损耗量增加而多耗钢 材210吨: 420×(420/420-200/400)=210吨;
心理学多因素实验设计案例

心理学多因素实验设计案例案例:不同音乐类型和学习环境对记忆效果的影响。
一、实验目的。
咱就想知道啊,听着不同类型的音乐,然后在不同的学习环境里,到底对记忆东西有啥不一样的影响呢?是能让我们像超级学霸一样过目不忘,还是变得像金鱼一样只有七秒记忆呢 。
二、实验因素和水平。
1. 音乐类型(因素A)水平一:古典音乐,就像莫扎特、贝多芬那些高大上的曲子,感觉一听就很有文化气息 。
水平二:流行音乐,周杰伦啊、泰勒·斯威夫特之类的,超级抓耳,大街小巷都在放的那种。
水平三:摇滚音乐,比如崔健、AC/DC,充满激情,让你听了就忍不住想摇头晃脑的那种。
2. 学习环境(因素B)水平一:安静的图书馆环境,超安静,只有翻书的沙沙声和偶尔的咳嗽声。
水平二:稍微有点嘈杂的咖啡店环境,有咖啡机的嗡嗡声,人们的低声交谈声。
水平三:家庭环境,可能会有电视的背景音,家人偶尔走动的声音。
三、实验设计类型。
我们采用3×3的完全随机多因素实验设计。
也就是说,我们要把这音乐类型的三个水平和学习环境的三个水平进行各种组合,然后随机分配给不同的参与者。
四、实验对象。
找了90个大学生,为啥是大学生呢?因为他们学习任务多,而且好忽悠……不是,是因为他们比较容易找到,而且处于经常需要记忆知识的阶段 。
五、实验过程。
1. 先把这90个大学生随机分成9组,每组10个人。
2. 对于第一组,让他们戴着耳机听古典音乐,然后坐在模拟图书馆的安静环境里,给他们一篇文章看15分钟,然后把文章拿走,让他们尽可能地回忆文章里的内容,记录下他们能回忆起来的字数。
3. 第二组呢,同样听古典音乐,但是是在模拟咖啡店的嘈杂环境里做同样的事情,记录回忆字数。
4. 第三组听古典音乐,在模拟家庭环境里进行,然后记录。
5. 第四组换成流行音乐,按照上面三种环境分别进行实验,记录回忆字数。
6. 第五组听摇滚音乐,也在三种环境下依次做实验,记录结果。
六、可能的结果和解释。
应用5M因素法鱼骨图分析解决问题案例
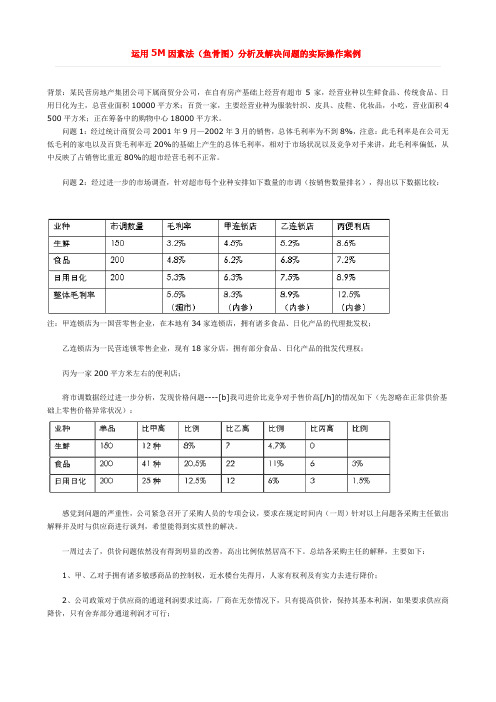
运用5M因素法(鱼骨图)分析及解决问题的实际操作案例背景:某民营房地产集团公司下属商贸分公司,在自有房产基础上经营有超市5家,经营业种以生鲜食品、传统食品、日用日化为主,总营业面积10000平方米;百货一家,主要经营业种为服装针织、皮具、皮鞋、化妆品,小吃,营业面积4 500平方米;正在筹备中的购物中心18000平方米。
问题1:经过统计商贸公司2001年9月—2002年3月的销售,总体毛利率为不到8%,注意:此毛利率是在公司无低毛利的家电以及百货毛利率近20%的基础上产生的总体毛利率,相对于市场状况以及竞争对手来讲,此毛利率偏低,从中反映了占销售比重近80%的超市经营毛利不正常。
问题2:经过进一步的市场调查,针对超市每个业种安排如下数量的市调(按销售数量排名),得出以下数据比较:注:甲连锁店为一国营零售企业,在本地有34家连锁店,拥有诸多食品、日化产品的代理批发权;乙连锁店为一民营连锁零售企业,现有18家分店,拥有部分食品、日化产品的批发代理权;丙为一家200平方米左右的便利店;将市调数据经过进一步分析,发现价格问题----[b]我司进价比竞争对手售价高[/h]的情况如下(先忽略在正常供价基础上零售价格异常状况):感觉到问题的严重性,公司紧急召开了采购人员的专项会议,要求在规定时间内(一周)针对以上问题各采购主任做出解释并及时与供应商进行谈判,希望能得到实质性的解决。
一周过去了,供价问题依然没有得到明显的改善,高出比例依然居高不下。
总结各采购主任的解释,主要如下:1、甲、乙对手拥有诸多敏感商品的控制权,近水楼台先得月,人家有权利及有实力去进行降价;2、公司政策对于供应商的通道利润要求过高,厂商在无奈情况下,只有提高供价,保持其基本利润,如果要求供应商降价,只有舍弃部分通道利润才可行;3、公司要求的经营方式过于呆板,竞争对手部分商品是从批发市场上进行铲货来冲击市场,而公司没有此先例,都是以正常方式进行经营;4、公司的付款方式问题:由于现金进货与押款进货的供价有区别,但是公司最低的付款要求为7天付款,因此在价格上没有办法降低;5、竞争对手的恶意竞争行为:牺牲利润,亏本赚吆喝;6、人手不够,杂事多,没有办法集中时间与精力与供应商谈判。
spss相关分析案例多因素方差分析【范本模板】

本次实验采用2005年东部、中部和西部各地区省份城镇居民月平均消费类型划分的数据(课本139页),将东部、中部和西部看作三个不同总体,31个数据分别来自于这三个总体。
本人对这三个不同地区的城镇居民月平均消费水平进行比较,并选取人均粮食支出、副食支出、烟酒及饮料支出、其他副食支出、衣着支出、日用杂品支出、水电燃料支出和其他非商品支出八个指标来衡量城镇居民月平均消费情况.在进行比较分析之前,首先对个数据是否服从多元正态分布进行检验,输出结果为:表一如表一,因为该例中样本数n=31〈2000,所以此处选用Shapiro-Wilk统计量。
由正态性检验结果的sig。
值可以看到,人均粮食支出、烟酒及饮料支出、其他副食支出、水电燃料支出和其他非商品支出均明显不遵从正态分布(Sig.值小于0.05,拒绝服从正态分布的原假设),因此,在下面分析中,只对人均副食支出、衣着支出和日用杂品支出三项指标进行比较,并认为这三个变量组成的向量都遵从正态分布,并对城镇居民月平均消费状况做出近似的度量.另外,正态性的检验还可以通过Q-Q图来实现,此时应判别数据点是否与已知直线拟合得好。
如果数据点均落在直线附近,说明拟合得好,服从正态分布,反之,不服从。
具体情况这里不再赘述。
下面进行多因素方差分析:一、多变量检验表二由地区一栏的(即第二栏)所列几个统计量的Sig.值可以看到,无论从那个统计量来看,三个地区的城镇居民月平均消费水平都是有显著差别的(Sig。
值小于0。
05,拒绝地区取值不同,对Y,即城镇居民月平均消费水平的取值没有显著影响的原假设)。
二、主体间效应检验表三Tests of Between—Subjects EffectsSource Dependent Variable Type III Sum ofSquares df Mean Square F Sig。
Corrected Model 人均副食支出(元/人) 11612.395a 2 5806.198 8.880 .001 人均日用杂品支出(元/人)66.367b 2 33.183 4.732 .017人均衣着支出(元/人) 107。
双因素和三因素分析例子

例1.某省三种出口商品的统计资料如表7—6所示,要求据此分析出口价、出口量的变动对出口额的影响。
出口商品因素分析表这是总量指标的两因素分析,先写出分析的指数体系:∑q1p1 ∑q1p0 ∑q1p1———=———×———∑q0p0 ∑q0p0 ∑q1p0依指数体系系列计算栏q1p1、q1p0、q0p0 有:∑q1p1 25 480 000(1)出口额指数:———=————— =124.96%∑q0p0 20 390 000∑q1p1—∑q0p0=25 480 000—20 390 000=5 090 000(美元)∑q1p0 24 410 000(2)出口量指数:——— =——————=119.72%∑q0p0 20 390 000∑q1p0 —∑q0p0=24 410 000—20 390 000=4 020 000(美元)∑q1p1 25 480 000(3)出口价指数:———=——————=104.38%∑q1p0 24 410 000∑q1p1 —∑q1p0=25 480 000 — 24 410 000 = 1 070 000(美元)分析:由于出口价格上升4.38%,出口额增加了107万美元,由于出口量上升19.72%出口额增加了402万美元,两者共同影响,三种商品的出口额上涨了24.96%,即增加509万美元。
例2.假设某厂生产产品的有关资料如表,要求运用指数体系,分析产品产量,单位产品原材料消耗量及单位原材料价格对原材料费用总额的影响。
某厂产品产量及其原材料单耗情况表原材料费用总额因素分析计算表故有:(1)产品产量指数∑q1m0p0 17 000= = 87.18%∑q0m0p0 19 500∑q1m0p0 —∑q0m0p0 =17 000—19 500=-2 500(元)(2)原材料单耗指数:∑q1m1p0 15 300= = 90.00%∑q1m0p0 17 000∑q1m1p0-∑q1m0p0=15 300-17 000=-1 700(元)(3)原材料价格指数∑q1m1p1 14 400= = 94.12%∑q1m1p0 15 300∑q1m1p1-∑q1m1p0=14 400-15 300=-900(元)(4)原材料费用总额指数:∑q1m1p1 14 400= = 73.85%∑q0m0p0 19 500∑q1m1p1-∑q0m0p0=14 400-19 500=-5 100(元)(5)综合影响:各因素指数连乘积=原材料费用总指数87.18%× 90.00%×94.12% = 73.85%各因素影响绝对额之和=原材料费用减少额(-2 500)+(-1 700)+(-900)=-5 100(元)分析,由于生产量减少12.82%,少支出的费用为2 500元;由于单位产品原材料消耗降低10%,少支出费用1 700元;又由于原材料价格下降5.88%,少支出费用900原。
spss 多因素方差分析例子
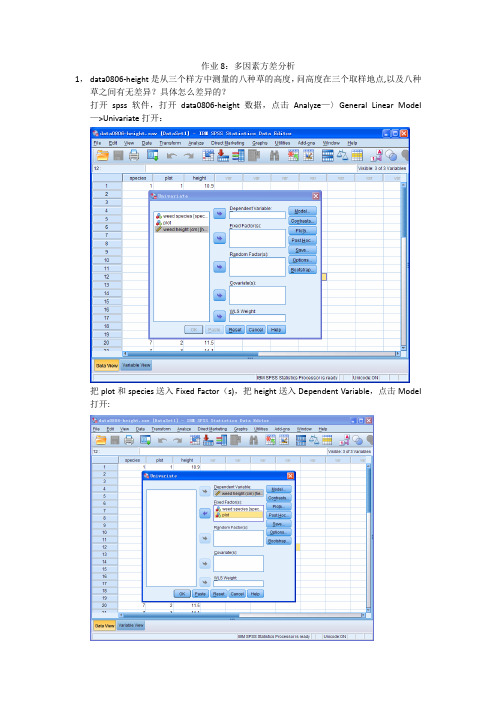
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze—〉General Linear Model —>Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model 打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM e rror,即无法分开MM intercept和MM error,无法检测interaction的影响,无法进行方差分析,重新Analyze—〉General Linear Model-〉Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21。
【因素分析法的计算例题】多因素分析法研究

【因素分析法的计算例题】多因素分析法研究多因素分析法研究小编为大家整理的相关的多因素分析法研究资料,供大家参考选择。
多因素分析研究多个因素间关系及具有这些因素的个体之间的一系列统计分析方法称为多元(因素)分析。
主要包括:多元线性回归(multiple linear regression) 判别分析(disoriminant analysis) 聚类分析(cluster analysis)主成分分析(principal component analysis) 因子分析(factor analysis) 典型相关(canonical correlation) logistic 回归(logistic regression) Cox 回归(COX regression)1、多元回归分析(multiple linear regression)回归分析是定量研究因变量对自变量的依赖程度、分析变量之间的关联性并进行预测、预报的基本方法。
研究一个因变量对几个自变量的线性依存关系时,其模型称为多元线性回归。
函数方程建立有四种方法:全模型法、向前选择法、向后选择法、逐步选择法。
全模型法其数学模型为:ebbbb++++=ppxxxyL22110式中 y 为因变量, pxxxL21, 为p个自变量,0b为常数项,pbbbL21,为待定参数,称为偏回归系数(partial regression coefficient)。
pbbbL21,表示在其它自变量固定不变的情况下,自变量Xi 每改变一个单位时,单独引起因变量Y的平均改变量。
多因素分析法研究e为随机误差,又称残差(residual), 它是在Y的变化中不能为自变量所解释的部分例如:1、现有20名糖尿病病人的血糖(Lmmoly/,)、胰岛素(LmUx/,1)及生长素(Lgx/,2m)的数据,讨论血糖浓度与胰岛素、生长素的依存关系,建立其多元回归方程。
逐步回归分析(stepwise regression analysis)在预先选定的几个自变量与一个因变量关系拟合的回归中,每个自变量对因变量变化所起的作用进行显著性检验的结果,可能有些有统计学意义,有些没有统计学意义。
多因素分析课程设计案例

多因素分析课程设计案例一、课程目标知识目标:1. 让学生理解多因素分析的概念,掌握其主要原理和应用场景。
2. 使学生掌握多因素分析的基本步骤,包括数据收集、数据处理、因素提取和因素旋转等。
3. 帮助学生掌握多因素分析结果的解释方法,并能够将其应用于实际问题。
技能目标:1. 培养学生运用统计软件进行多因素分析的操作能力。
2. 培养学生独立分析问题、解决问题,将多因素分析应用于实际案例的能力。
3. 提高学生的团队协作能力和沟通能力,能够就多因素分析结果进行有效讨论和展示。
情感态度价值观目标:1. 激发学生对数据分析的兴趣,培养其主动探索科学问题的精神。
2. 培养学生严谨的科学态度,注重数据的真实性和分析结果的客观性。
3. 增强学生的社会责任感,使其认识到多因素分析在解决实际问题中的价值。
本课程针对高年级学生,结合学科特点,以实际案例为载体,注重培养学生的数据分析能力和实际问题解决能力。
在教学过程中,关注学生的个体差异,充分调动学生的主观能动性,提高其团队协作和沟通能力。
通过本课程的学习,使学生能够掌握多因素分析的基本原理和方法,并在实际问题中运用所学知识,达到学以致用的目的。
二、教学内容1. 多因素分析基本概念:因素分析的定义、类型和适用条件。
2. 多因素分析原理:主成分分析、因子分析的基本原理和数学模型。
3. 多因素分析步骤:数据收集、数据预处理、因素提取、因素旋转和结果解释。
4. 多因素分析应用案例:选择与学科相关的实际案例,分析案例背景、数据来源和因素分析过程。
5. 软件操作:使用统计软件(如SPSS、R等)进行多因素分析的具体操作步骤和技巧。
6. 结果解释与应用:多因素分析结果的解释方法,如何将分析结果应用于实际问题解决。
教学内容安排与进度:第一课时:多因素分析基本概念及原理介绍。
第二课时:多因素分析步骤及案例讲解。
第三课时:软件操作教学与实践。
第四课时:结果解释与应用,案例分析讨论。
教学内容参考教材相关章节,结合课程目标进行整合,确保学生能够系统、全面地掌握多因素分析的知识点,为实际应用打下坚实基础。
多因素分析 案例

多因素分析案例案例1 某医生为研究乳腺癌彩超血流显像的相关因素,检测了121例乳腺癌患者,其中血流丰富者68个,中等血流者48个,无血流者5个。
选择患者的年龄、乳腺癌的大小、组织学分类、导管内癌和浸润性导管癌组织学分级及雌激素受体,孕酮受体等因素,进行了多因素logistic回归分析。
结果显示,对血流程度有影响的因子,其作用从大到小依次为:肿块大小(OR=5.931),肿块分好程度(低分化OR=4.318,中分化OR=1.681),患者年龄(OR=0.949)。
其余因素对血流程度无影响。
问题:本案例中的涉及到了哪些变量?分别属于什么类型?因变量自变量分别是什么?本案例可否用直线相关或者回归分析?为什么?在进行多因素logistic回归前,是否应该先进行单因素分析?如何分析?单因素logistic回归分析与多因素logistic回归分析有何区别?能否直接做多因素logistic回归分析?得到logistic回归分析结果后,如何解释?如何应用这个结果?案例2 某研究者观察了确诊后采取同样方案进行化疗的26例急性混合型白血病患者,欲了解某种不良染色体是否会影响患者病情的缓解,于是将治疗后120天内症状是否缓解作为结果变量y(缓解=0,未缓解=1),有无不良染色体chr(有=1,无)作为研究因素,数据收集后(详细数据见表19-5)进行一系列统计分析,请结合以下问题,对分析结果进行恰当的评价。
表19-5 急性混合型白血病患者化疗后观察数据age bl cd chr sex t y age bl cd chr sex t y 28 0 0 1 0 3 0 48 1 0 1 1 15 0 33 1 1 1 1 120 1 48 1 0 1 0 120 1 35 0 0 1 0 7 0 48 1 0 1 0 120 139 0 0 1 0 5 0 49 1 0 0 0 120 140 0 0 1 0 16 0 54 1 1 0 0 120 0 42 0 0 1 0 2 0 55 0 1 0 1 12 042 1 1 0 1 120 1 57 1 1 0 1 116 043 0 1 1 1 120 1 60 1 1 0 1 109 044 0 0 1 0 4 0 61 0 1 1 0 40 0 44 0 0 1 0 19 0 62 0 0 1 0 16 044 0 1 1 0 120 1 62 0 1 1 0 118 045 1 0 0 0 108 0 63 1 1 0 0 120 1 47 0 0 1 0 18 0 74 0 0 1 0 7 0(1)按照有无不良染色体分组比较缓解率,考虑到例数较小,采用Fisher精确概率法,得到P值为0.667,此时的结论如何?(2)考虑到有无不良染色体并非研究人员可以随机分配的处理,所以比较组之间其它影响患乾缓解的因素不一定均衡,因而需要考虑平衡其他可能的影响因素的作用。
多因素实验设计案例

多因素实验设计案例实验设计是科学研究中非常重要的一部分,通过设计合理的实验,可以解决研究中的问题,并得出科学的结论。
多因素实验设计是一种考虑多个因素影响的实验设计方法。
下面将介绍一个多因素实验设计的案例。
假设我们想要研究不同养殖环境对鸡蛋孵化率的影响。
我们认为孵化率可能受到环境温度、湿度和光照强度等多个因素的影响。
我们选择了温度、湿度和光照强度作为研究因素,并设计了一个三因素二水平的实验。
首先,我们需要确定温度、湿度和光照强度的两个水平。
根据之前的研究和经验,我们选择了25°C和30°C作为温度的两个水平,60%和70%作为湿度的两个水平,5000 lx和7000 lx作为光照强度的两个水平。
接下来,我们需要确定实验的处理组合。
因为是一个三因素二水平的实验,所以总共有2^3=8个处理组合。
我们列出所有的处理组合如下:温度(A)湿度(B)光照强度(C)25°C 60% 5000 lx25°C 60% 7000 lx25°C 70% 5000 lx25°C 70% 7000 lx30°C 60% 5000 lx30°C 60% 7000 lx30°C 70% 5000 lx30°C 70% 7000 lx然后,我们需要随机分配实验单元到不同的处理组合中。
为了消除可能的混杂效应,我们可以采用随机化的方法。
将每个处理组合写在一张卡片上,然后将这些卡片放入一个袋子中,并在实验开始前适当搅拌袋子,然后取出一张卡片,即为一个处理组合。
在实验开始前,我们需要确定每个处理组合的重复次数。
根据实验资源的限制和统计学原则,我们选择每个处理组合的重复次数为3次。
也就是说,我们需要在每个处理组合中重复实验3次。
在实验进行过程中,我们需要记录每个处理组合的孵化率。
我们可以通过统计每个处理组合中鸡蛋的成功孵化数量并除以总的鸡蛋数量来得到孵化率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多因素分析案例案例1 某医生为研究乳腺癌彩超血流显像的相关因素,检测了121例乳腺癌患者,其中血流丰富者68个,中等血流者48个,无血流者5个。
选择患者的年龄、乳腺癌的大小、组织学分类、导管内癌和浸润性导管癌组织学分级及雌激素受体,孕酮受体等因素,进行了多因素logistic回归分析。
结果显示,对血流程度有影响的因子,其作用从大到小依次为:肿块大小(OR=5.931),肿块分好程度(低分化OR=4.318,中分化OR=1.681),患者年龄(OR=0.949)。
其余因素对血流程度无影响。
问题:本案例中的涉及到了哪些变量?分别属于什么类型?因变量自变量分别是什么?本案例可否用直线相关或者回归分析?为什么?在进行多因素logistic回归前,是否应该先进行单因素分析?如何分析?单因素logistic回归分析与多因素logistic回归分析有何区别?能否直接做多因素logistic回归分析?得到logistic回归分析结果后,如何解释?如何应用这个结果?案例2 某研究者观察了确诊后采取同样方案进行化疗的26例急性混合型白血病患者,欲了解某种不良染色体是否会影响患者病情的缓解,于是将治疗后120天内症状是否缓解作为结果变量y(缓解=0,未缓解=1),有无不良染色体chr(有=1,无)作为研究因素,数据收集后(详细数据见表19-5)进行一系列统计分析,请结合以下问题,对分析结果进行恰当的评价。
表19-5 急性混合型白血病患者化疗后观察数据age bl cd chr sex t y age bl cd chr sex t y 28 0 0 1 0 3 0 48 1 0 1 1 15 0 33 1 1 1 1 120 1 48 1 0 1 0 120 1 35 0 0 1 0 7 0 48 1 0 1 0 120 139 0 0 1 0 5 0 49 1 0 0 0 120 140 0 0 1 0 16 0 54 1 1 0 0 120 0 42 0 0 1 0 2 0 55 0 1 0 1 12 042 1 1 0 1 120 1 57 1 1 0 1 116 043 0 1 1 1 120 1 60 1 1 0 1 109 044 0 0 1 0 4 0 61 0 1 1 0 40 0 44 0 0 1 0 19 0 62 0 0 1 0 16 044 0 1 1 0 120 1 62 0 1 1 0 118 045 1 0 0 0 108 0 63 1 1 0 0 120 1 47 0 0 1 0 18 0 74 0 0 1 0 7 0(1)按照有无不良染色体分组比较缓解率,考虑到例数较小,采用Fisher精确概率法,得到P值为0.667,此时的结论如何?(2)考虑到有无不良染色体并非研究人员可以随机分配的处理,所以比较组之间其它影响患乾缓解的因素不一定均衡,因而需要考虑平衡其他可能的影响因素的作用。
于是该研究者进一步查阅了相关文献,追加记录了患者的年龄age(岁)、骨髓原幼细胞数分组bl (大于等于50%=1,小于50%=0)、CD34表达式cd(阳性=1,阴性=0)、性别sex(男=1,女=0)这几个变量(数据见表19-5),采用多因素logistic模型分析,经逐步法近α=0.10水准得到表19-6中的结果。
此时的结论又如何?表19-6 急性混合型白血病患者化疗后观察数据的逐步logistic回归分析结果回归系数标准误X2 自由度P值RRBl -2.054 0.971 4.472 1 0.034 7.800常数项-1.872 0.760 6.073 1 0.014 0.154综合上述分析过程,你对此项研究的设计、资料收集及统计分析方法的选择有何评论?案例3 某研究者为探讨帕金森病(PD)与吸烟的关系,采用以人群为基础的病例-对照研究,调查某市PD病例共114例,以及对照205例(性别、民族及居住于与病例相匹配)。
采用非条件logistic回归分析,结果见表18-12。
请根据所提供信息,分析该研究中存在的主要统计学缺陷。
表18-12 PD 与吸烟关系的非条件logisti 回归分析变量 回归系数 标准误 W a l d X 2 P 值 OR OR 的95%CI 性别 0.936 0.0298 9.821 0.009 2.549 1.420,4.579 年龄0.030 0.299 4.612 0.032 1.031 0.573,1.852 吸烟年限 -0.619 0.315 3.866 0.049 0.538 0.290,0.346 喝茶 -1.616 0.283 32.619 0.000 0.199 0.114,0.346 饮酒-0.0310.3390.0090.9260.9690.499,1.884案例4 为探讨超重和肥胖对高血压病的影响,2004年,某研究者采用整群抽样的方法,对某地6个镇35周岁以上的常住人口进行高血压普查,同时收集了身高、体重等相关信息。
体质指数BMI ≥25判为“超重或肥胖”,BMI <5为“正常”;收缩压≥140mmHg 和(或)舒张压≥90mmHg 判为“高血压”。
整理后资料见表18-13。
自变量X 为体质指数,X=1表示“超重或肥胖”,X=0表示“正常”;因变量Y 为是否患病, Y=1表示“患病”,Y=0表示“未患病”。
X 对Y 影响的单因素logistic 回归结果见表18-14。
请问该二分类单因素logistic 回归所得OR 值与采用2*2表所计算的OR 有何关系?表18-3 不同体质指数高血压患病率表18-4 非条件logistic 回归分析结果案例5 某医生在河南平顶山煤矿区人群糖尿病(DM )现况调查基础上,对筛选出的174例糖尿病病例和3066例糖耐量正常者进行以人群为基础的病例-对照研究。
调查内容包括性别、年龄、糖尿病史、肥胖、体力劳动、饮酒和饮食等因素,分析目的主要是糖尿病者是否与肥胖有关。
该医生应用单因素的分析方法,分别估计暴露于各危险因素的糖尿病患病优势比,对优势比假设检验和区间估计。
分析结果表明糖尿病患病与年龄、糖尿病史、体质指数 (X )调查人数患病 (Y=1 病例) 未患病 (Y=0 对照) 患病率 (%) 超重或肥胖 (X=1暴露) 4148 1656(a) 2492(b) 39.92 正常(X=0非暴露) 6792 1331(c) 5461(d) 19.60 合计109402987795327.30体质指数(BMI)、腰臀比值(WHR)、舒张压、多食高粱豆类、职业体力劳动等的关联有统计意义。
该医生应用非条件logistic回归分析糖尿病发生与各种危险因素的关联性,先做糖尿病患病与逐个因素的单因素logistic回归结果摘要在表18-6中。
然后将单因素分析有统计学意义的危险因素引入多因素logistic回归模型进行逐步筛选,筛选结果列在表18-7中,结果表明,年龄大、母亲有糖尿病史、同胞有糖尿病史、最重时体质指数(BMI)高、腰臀比值(WHR)高、舒张压高、多食高粱和豆类可能是糖尿病的独立危险因子;职业性体力活动强度高和多食浅色蔬菜可能是糖尿病患病的独立保护因子。
讨论:(1)该研究在设计方面存在什么问题?(2)该资料的统计分析存在什么问题?(3)什么因素可能影响糖尿病与肥胖的关系,在该研究设计中存在哪些可能的混杂因素?(4)如何校正混杂因素的影响?(5)目前的统计分析程序存在什么问题?(6)如何应用logistic回归校正混杂因素的影响?(7)如何根据研究目的估计校正混杂因素后糖尿病与肥胖的关联?表18-6 非条件logistic回归单因素分析结果变量OR OR的95%CI 变量OR OR的95%CI性别0.52 0.38-0.71 年龄 2.44 2.08-2.87居住年限 1.58 1.24-2.03 母亲DM史 5.93 3.25-10.82子女有DM 8.95 2.22-36.08 同胞DM史 4.99 2.44-10.21现进BMI 3.35 2.41-4.65 最重时BMI 4.44 3.01-6.56现时WHR 5.91 4.05-8.63 饮酒指数0.67 0.47-0.960.71 0.63-0.80 收缩压 3.89 2.39-6.33职业性体力活动舒张压 3.28 2.27-4.48 大米0.11 0.03-0.45小米 1.64 1.24-2.18 高粱 2.96 1.35-6.52豆类 1.47 1.19-1.82 禽肉 1.30 1.02-1.66鲜奶 1.52 1.10-2.10 豆制品 1.27 1.03-1.06浅色蔬菜0.51 0.37-2.74 动物油0.78 0.66-0.910.78 0.97-0.91 月经 1.80 1.38-2.36两年前动物油表18-7 非条件logistic回归多因素分析结果及各危险因子的PAR%值变量回归系数标准误标准回归系数OR OR的95%CI PAR% 年龄0.7134 0.0900 0.4242 2.04 1.71-2.44 80.04母亲DM史 1.7984 0.3613 0.1369 6.04 2.98-12.26 7.19同胞DM史0.8069 0.4349 0.0532 2.24 0.96-5.26 3.18 -0.1191 0.0689 -0.0909 0.89 0.78-1.02 -19.20 职业性体力活动最重时BMI 0.6135 0.2255 0.1691 1.85 1.19-2.87 37.35现进BMI 0.9437 0.2207 0.2571 2.57 1.67-3.96 48.80舒张压0.4111 0.2507 0.0670 1.51 1.01-2.26 8.15高粱0.7988 0.2951 0.0709 2.22 1.25-3.96 3.20豆类0.2211 0.1187 0.0774 1.25 0.99-1.57 10.63浅色蔬菜-0.6935 0.1974 -0.1202 0.50 0.34-0.74 -269.54。
