区域填充算法区域填充算法
实验三 区域填充算法的实现

实验三区域填充算法的实现一、实验目的和要求:1、掌握区域填充算法基本知识2、理解区域的表示和类型,能正确区分四连通和八连通的区域3、了解区域填充的实现原理,利用Microsoft Visual C++ 6.0或win-TC实现区域种子填充的递归算法。
二、实验内容:1、编程完成区域填色2、利用画线函数,在屏幕上定义一个封闭区域。
3、利用以下两种种子填充算法,填充上述步骤中定义的区域(1)边界表示的四连通区域种子填充的实现(2)内点表示的四连通区域种子填充的实现4、将上述算法作部分改动应用于八连通区域,构成八连通区域种子填充算法,并编程实现。
三、实验结果分析四连通图的实现:程序代码:#include<graphics.h>#include <conio.h>#include<math.h>#include<time.h>void BoundaryFill4(int x,int y,int Boundarycolor,int newcolor){if(getpixel(x,y) != newcolor && getpixel(x,y) !=Boundarycolor){putpixel(x,y,newcolor);Sleep(1);BoundaryFill4(x-1,y,Boundarycolor,newcolor);BoundaryFill4(x,y+1,Boundarycolor,newcolor);BoundaryFill4(x+1,y,Boundarycolor,newcolor);BoundaryFill4(x,y-1,Boundarycolor,newcolor);}}void polygon(int x0,int y0,int a,int n,float af){int x,y,i;double dtheta,theta;if(n<3)return;dtheta=6.28318/n;theta=af*0.0174533;moveto(x0,y0);x=x0;y=y0;for(i=1;i<n;i++){x=x+a*cos(theta);y=y+a*sin(theta);lineto(x,y);theta=theta+dtheta;}lineto(x0,y0);}void main(){int x=50,y=75;int a,b,c,d,i,j;int graphdriver=DETECT;int graphmode=0;initgraph(&graphdriver,&graphmode," ");cleardevice();setcolor(RGB(0,255,0));setfillstyle(WHITE);polygon(x,y,60,5,0.);a=100;b=100;c=RGB(0,255,0);d=RGB(255,0,255);BoundaryFill4(a,b,c,d);getch();closegraph();}实验结果八连通的实现程序代码:#include<graphics.h>#include<conio.h>#include<time.h>#include <malloc.h>#include <windows.h>#define MaxSize 100typedef struct{int x;int y;}Seed,ElemType;typedef struct{ElemType data[MaxSize];int top; //栈顶指针} SqStack;void InitStack(SqStack *&s){s=(SqStack *)malloc(sizeof(SqStack));s->top=-1;}int StackEmpty(SqStack *s){return(s->top==-1);}int Push(SqStack *&s,ElemType e){if (s->top==MaxSize-1)return 0;s->top++;s->data[s->top]=e;return 1;}int Pop(SqStack *&s,ElemType &e){if (s->top==-1)return 0;e=s->data[s->top];s->top--;return 1;}void floodfill8(int x,int y,int oldcolor,int newcolor) {if(getpixel(x,y)==oldcolor){putpixel(x,y,newcolor);Sleep(2);floodfill8(x,y+1,oldcolor,newcolor);floodfill8(x,y-1,oldcolor,newcolor);floodfill8(x-1,y,oldcolor,newcolor);floodfill8(x+1,y,oldcolor,newcolor);floodfill8(x+1,y+1,oldcolor,newcolor);floodfill8(x+1,y-1,oldcolor,newcolor);floodfill8(x-1,y+1,oldcolor,newcolor);floodfill8(x-1,y-1,oldcolor,newcolor);}}void main(){int a,b,c,d,i,j;int graphdriver=DETECT;int graphmode=0;initgraph(&graphdriver,&graphmode," "); cleardevice();setfillstyle(RGB(255,255,255));setcolor(GREEN);int points[]={320,200,270,290,370,290}; fillpoly(3,points);rectangle(500,420,100,100);a=RGB(255,255,255);b=RGB(255,0,0);floodfill8(320,240,a,b);c=RGB(0,0,0);d=RGB(0,0,255);floodfill8(320,180,c,d);getch();closegraph();}实验结果:2、结果分析:通过以上各算法运行结果分析与对比可知:1.四连通算法的缺点是有时不能通过狭窄区域,因而不能填满多边形。
c语言多边形区域填充算法

c语言多边形区域填充算法C语言多边形区域填充算法一、介绍多边形区域填充算法是计算机图形学中的一项重要技术,用于将给定的多边形区域进行填充,使其呈现出丰富的颜色或纹理,增强图形的效果和表现力。
本文将介绍一种常用的C语言多边形区域填充算法——扫描线填充算法。
二、扫描线填充算法原理扫描线填充算法是一种基于扫描线的填充方法,其基本思想是将多边形区域按照水平扫描线的顺序,从上到下逐行扫描,通过判断扫描线与多边形边界的交点个数来确定是否进入多边形区域。
具体步骤如下:1. 首先,确定多边形的边界,将其存储为一个边表。
边表中的每个边都包含起点和终点的坐标。
2. 创建一个活性边表(AET),用于存储当前扫描线与多边形边界的交点。
初始时,AET为空。
3. 从上到下逐行扫描多边形区域,对每一条扫描线,从边表中找出与该扫描线相交的边,并将其加入AET中。
4. 对于AET中的每一对交点,按照从左到右的顺序两两配对,形成水平线段,将其填充为指定的颜色或纹理。
5. 在扫描线的下一行,更新AET中的交点的坐标,然后重复步骤4,直到扫描到多边形区域的底部。
三、代码实现下面是一个简单的C语言实现扫描线填充算法的示例代码:```#include <stdio.h>#include <stdlib.h>#include <stdbool.h>typedef struct {int x;int y;} Point;typedef struct {int yMax;float x;float dx;int next;} Edge;void fillPolygon(int n, Point* points, int color) {// 获取多边形的边界int yMin = points[0].y;int yMax = points[0].y;for (int i = 1; i < n; i++) {if (points[i].y < yMin) {yMin = points[i].y;}if (points[i].y > yMax) {yMax = points[i].y;}}// 创建边表Edge* edges = (Edge*)malloc(sizeof(Edge) * n);int k = n - 1;for (int i = 0; i < n; i++) {if (points[i].y < points[k].y) {edges[i].yMax = points[k].y;edges[i].x = points[i].x;edges[i].dx = (float)(points[k].x - points[i].x) / (points[k].y - points[i].y);edges[i].next = k;} else {edges[i].yMax = points[i].y;edges[i].x = points[k].x;edges[i].dx = (float)(points[i].x - points[k].x) / (points[i].y - points[k].y);edges[i].next = i;}k = i;}// 扫描线填充for (int y = yMin; y < yMax; y++) {int xMin = INT_MAX;int xMax = INT_MIN;for (int i = 0; i < n; i++) {if (y >= edges[i].yMax) {continue;}edges[i].x += edges[i].dx;if (edges[i].x < xMin) {xMin = edges[i].x;}if (edges[i].x > xMax) {xMax = edges[i].x;}int j = edges[i].next;while (j != i) {edges[j].x += edges[j].dx; if (edges[j].x < xMin) {xMin = edges[j].x;}if (edges[j].x > xMax) {xMax = edges[j].x;}j = edges[j].next;}}for (int x = xMin; x < xMax; x++) { drawPixel(x, y, color);}}free(edges);}int main() {// 定义多边形的顶点坐标Point points[] = {{100, 100},{200, 200},{300, 150},{250, 100}};// 填充多边形区域为红色fillPolygon(4, points, RED);return 0;}```四、总结通过扫描线填充算法,我们可以实现对多边形区域的填充,从而提升图形的表现效果。
区域填充算法范文

区域填充算法范文
常见的区域填充算法有种子填充算法和扫描线填充算法。
种子填充算法是一种递归算法,从指定的种子点开始,将其颜色设为
目标颜色,并继续填充其相邻的像素点,直到所有相邻的像素点都被填充
为目标颜色。
这个过程可以通过递归或者使用栈进行实现。
种子填充算法
的优点是简单易懂,但对于复杂的区域存在堆栈溢出的风险。
扫描线填充算法利用了图形中连续的扫描线和区域的边界特性。
首先,确定区域的上下边界,然后对每一条扫描线从左往右进行遍历。
当扫描线
与区域的边界相交时,根据交点的颜色决定当前像素点的填充颜色。
该算
法可以通过判断相邻像素点的颜色是否相同来确定区域的边界。
为了提高算法的效率,可以使用填充算法的优化技术。
例如,使用堆
栈数据结构来存储需要填充的像素点,避免了递归过程中的堆栈溢出问题。
另外,可以使用四邻域或八邻域填充算法来决定像素点的相邻关系,减少
算法的时间复杂度。
总之,区域填充算法是图形学和图像处理中的重要算法之一,通过将
指定的区域填充为指定的颜色,实现了各种复杂任务的自动化处理和可视
化展示。
随着计算机技术的发展,区域填充算法的应用前景将会更加广泛,并且不断出现新的算法和优化技术,提高填充效率和质量。
区域填充算法

区域填充算法⼀、区域填充概念区域:指已经表⽰成点阵形式的填充图形,是象素的集合。
区域填充:将区域内的⼀点(常称种⼦点)赋予给定颜⾊,然后将这种颜⾊扩展到整个区域内的过程。
区域填充算法要求区域是连通的,因为只有在连通区域中,才可能将种⼦点的颜⾊扩展到区域内的其它点。
1、区域有两种表⽰形式1. 内点表⽰:枚举出区域内部的所有象素内部所有象素着同⼀个颜⾊边界像素着与内部象素不同的颜⾊。
2. 边界表⽰:枚举出区域外部的所有象素边界上的所有象素着同⼀个颜⾊内部像素着与边界象素不同的颜⾊。
2、区域连通1. 四向连通区域:从区域上⼀点出发可通过上、下、左、右四个⽅向移动的组合,在不越出区域的前提下,到达区域内的任意象素。
2. ⼋向连通区域:从区域上⼀点出发可通过上、下、左、右、左上、右上、左下、右下⼋个⽅向移动的组合,在不越出区域的前提下,到达区域内的任意象素。
3. 四连通与⼋连通区域的区别连通性:四连通可以看作⼋连通的⾃⼰,但是对边界有要求⼆、简单种⼦填充算法1、基本思想给定区域G⼀种⼦点(x, y),⾸先判断该点是否是区域内的⼀点,如果是,则将该点填充为新的颜⾊,然后将该点周围的四个点(四连通)或⼋个点(⼋连通)作为新的种⼦点进⾏同样的处理,通过这种扩散完成对整个区域的填充。
这⾥给出⼀个四连通的种⼦填充算法(区域填充递归算法),使⽤【栈结构】来实现原理算法原理如下:种⼦像素⼊栈,当【栈⾮空】时重复如下三步:2、算法代码这⾥给出⼋连通的种⼦填充算法的代码:void flood_fill_8(int[] pixels, int x, int y, int old_color, int new_color) { if (x < w && x > 0 && y < h && y > 0) {// 如果是旧的颜⾊⽽且还没有给他填充过if (pixels[y * w + x] == old_color) {// 填充为新的颜⾊pixels[y * w + x]== new_color);// 递归flood_fill_8(pixels, x, y + 1, old_color, new_color);flood_fill_8(pixels, x, y - 1, old_color, new_color);flood_fill_8(pixels, x - 1, y, old_color, new_color);flood_fill_8(pixels, x + 1, y, old_color, new_color);flood_fill_8(pixels, x + 1, y + 1, old_color, new_color);flood_fill_8(pixels, x + 1, y - 1, old_color, new_color);flood_fill_8(pixels, x - 1, y + 1, old_color, new_color);flood_fill_8(pixels, x - 1, y - 1, old_color, new_color);}}}3、OpenCV实现import cv2def seed_fill(img):ret, img = cv2.threshold(img, 128, 255, cv2.THRESH_BINARY_INV) label = 100stack_list = []h, w = img.shapefor i in range(1, h-1, 1):for j in range(1, w-1, 1):if (img[i][j] == 255):img[i][j] = labelstack_list.append((i, j))while len(stack_list) != 0:cur_i = stack_list[-1][0]cur_j = stack_list[-1][1]img[cur_i][cur_j] = labelstack_list.remove(stack_list[-1])# 四邻域,可改为⼋邻域if (img[cur_i-1][cur_j] == 255):stack_list.append((cur_i-1, cur_j))if (img[cur_i][cur_j-1] == 255):stack_list.append((cur_i, cur_j-1))if (img[cur_i+1][cur_j] == 255):stack_list.append((cur_i+1, cur_j))if (img[cur_i][cur_j+1] == 255):stack_list.append((cur_i, cur_j+1))cv2.imwrite('./result.jpg', img)cv2.imshow('img', img)cv2.waitKey()if __name__ == '__main__':img = cv2.imread('./test.jpeg', 0)seed_fill(img)4、简单种⼦填充算法的优点和缺点优点:1. 该算法也可以填充有孔区域缺点:1. 有些像素会多次⼊栈,降低算法效率,栈结构占空间2. 递归执⾏,算法简单,但效率不⾼,区域内每⼀像素都要进/出栈,费时费内存3. 改进算法,减少递归次数,提⾼效率三、扫描线种⼦填充算法⽬标:减少递归层次适⽤于边界表⽰的4连通区间1、基本思想在任意不间断区间中只取⼀个种⼦像素(不间断区间指在⼀条扫描线上⼀组相邻元素),填充当前扫描线上的该段区间;然后确定与这⼀区段相邻的上下两条扫描线上位于区域内的区段,并依次把它们保存起来,反复进⾏这个过程,直到所保存的各个区段都填充完毕。
cad 区域填充的算法

cad 区域填充的算法
CAD区域填充是一种用于计算机辅助设计软件中的算法,用于在指定区域内填充颜色。
这个算法基于扫描线填充方法,它从图形的顶部开始
扫描,逐行地将颜色填充到区域中。
具体而言,CAD区域填充算法可以通过以下步骤来实现:
1. 选择一个起始点,并确保该点位于待填充区域内。
2. 在当前扫描线上,从起始点开始向左和向右移动,找到左和右边界。
这可以通过检测不同颜色或图形边界来确定。
3. 填充当前扫描线的像素点,从左边界到右边界之间的像素。
4. 移动到下一行,通过向下移动一行并在新的扫描线上重复步骤2和
步骤3,直到所有行都被处理完毕或者遇到边界。
5. 当遇到边界或结束时,停止填充过程。
需要注意的是,在实际应用中,为了提高效率和减少计算量,可以使
用一些优化策略来加速CAD区域填充算法的执行,例如边界框剪裁和
扫描线段合并。
总之,CAD区域填充算法是一种实现图形填充的重要方法,它可以在计算机辅助设计软件中帮助用户快速填充指定区域并实现更好的可视化
效果。
区域填充算法的实现

区域填充算法的实现实现区域填充算法的一种常见方法是使用递归。
以下是一个使用递归实现的区域填充算法的伪代码:1. 定义函数fillPixel(x, y, targetColor, fillColor):-如果像素点(x,y)的颜色与目标颜色相同,将其颜色修改为填充颜色。
-否则,返回。
2. 定义函数regionFill(x, y, targetColor, fillColor):-如果像素点(x,y)的颜色与目标颜色相同,返回。
- 否则,调用fillPixel(x, y, targetColor, fillColor)。
- 递归调用regionFill(x-1, y, targetColor, fillColor)。
- 递归调用regionFill(x+1, y, targetColor, fillColor)。
- 递归调用regionFill(x, y-1, targetColor, fillColor)。
- 递归调用regionFill(x, y+1, targetColor, fillColor)。
3. 调用regionFill(seedX, seedY, targetColor, fillColor)。
在上述算法中,fillPixel函数用于将特定颜色填充到像素点(x, y)。
regionFill函数使用递归的方式遍历相邻的像素点,并对目标颜色的像素点调用fillPixel函数。
seedX和seedY表示种子像素点的坐标,targetColor表示目标颜色,fillColor表示填充颜色。
实现区域填充算法时还需要考虑以下几个问题:1.像素点的表示:图像可以由二维数组表示,其中每个元素表示一个像素点的颜色。
2.填充颜色选择:填充颜色可以由RGB值表示,或者在预定义的颜色集合中选择。
3.边界处理:对于位于图像边界上的种子像素点,需要特殊处理以防止数组越界错误。
4.递归终止条件:填充算法使用递归,需要定义递归终止的条件,以防止无限递归。
第3章 填充
3.5.2 多边形域填充 常用的填充方法是按扫描线顺序,计算扫描线 与多边形的相交区间,再用要求的颜色显示这些区 间的像素,即完成填充工作,简称为扫描线填充算 法。区间的端点可以通过计算扫描线与多边形边界 线的交点获得,该方法适用于自动填充。
1.多边形域的填充步骤 一般多边形的填充过程,对于一条扫描线,可以分为 4个步骤: (1) 求交:计算扫描线与多边形各边的交点。 (2) 排序:把所有交点按x递增顺序进行排序。 (3) 交点配对:第1个与第2个,第3个与第4个等两两配对, 每对交点就代表扫描线与多边形的一个相交区间。 (4) 区间填色:把这些相交区间内的像素置成多边形颜色。
对例3.4重新使用改进后的简单种子填充算法步骤如下。 解: (1) 种子像素(3, 2)入栈并着色。 (2) 出栈(3, 2)。入栈(2, 2)、(3, 3)、(4, 2)、(3, 1)并着色。 (3) 出栈(3, 1)。入栈(2, 1)、(4, 1)并着色。 (4) 出栈(4, 1)。 (5) 出栈(2, 1)。 (6) 出栈(4, 2)。 (7) 出栈(3, 3)。入栈(2, 3)并着色。 (8) 出栈(2, 3)。 (9) 出栈(2, 2)。入栈(1, 2)并着色。 (10) 出栈(1, 2),栈空结束。
3.5 区域填充
3.5.1 种子填充算法
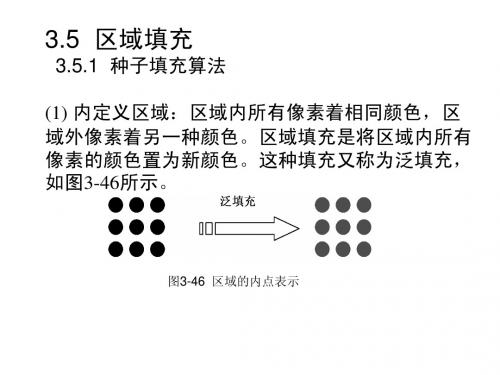
(1) 内定义区域:区域内所有像素着相同颜色,区 域外像素着另一种颜色。区域填充是将区域内所有 像素的颜色置为新颜色。这种填充又称为泛填充, 如图3-46所示。
图3-46 区域的内点表示
(2) 边界定义区域:区域边界像素着特定颜色,区 域内像素不取特定颜色。区域填充是将区域内所有 像素的颜色置为边界像素颜色或新颜色。这种填充 称为边界填充,如图3-47所示。
区域填充算法

7
9 9
9
对边界和内点表示的八连通区域的填充,只要将上述算法的对四 个像素点填充改为八个像素点即可。 四连通区域种子填充算法的缺点是有时不能通过狭窄区域区域, 因而不能填满多边形。八连通算法的缺点是有时会填出多边形的 边界。由于填不满比涂出更容易补救,因此四连通算法比八连通 算法用得更多。
(3)扫描线种子填充算法
(2)内点表示的四连通区域种子填充算法
基本思想:从多边形内部任一点(像素)出发,按照“右 上左下”的顺序判断相邻像素,若是区域内的像素,则对 其填充,并重复上述过程,直至所有像素填充完毕。 可以使用栈结构来实现该算法,种子像素入栈,档栈非空, 重复执行下面操作: 1)栈顶像素出栈; 2)将出栈像素置成多边形填充的颜色;
基本思想:从多边形内部任一点(像素)出发,按照 “右上左下”的顺序判断相邻像素,若不是边界像素 且没被填充过,则对其填充,并重复上述过程,直至 所有像素填充完毕。 可以使用栈结构来实现该算法,种子像素入栈,档栈 非空,重复执行下面操作: 1)栈顶像素出栈; 2)将出栈像素置成多边形填充的颜色; 3)按“右上左下”的顺序检查与出栈像素相邻的四个 像素,若其中某个像素不在边界上且未置成多边形色, 则把该像素入栈。
扫描线算法分析(举例分析)
基本思想:在任意不间断的区间中只取一个像素(不 间断区间指一条扫描线上的一组相邻元素),填充当 前扫描线上的该段区间,然后确定与这一段相邻的上 下两条扫描线位于区域内的区段,并依次把它们保存 起来,反复进行这个过程,指导所有保存的每个区段 都填充完毕。
(3)扫描线种子填充算法
种子像素入栈,当栈非空时,重复以下步骤: (1)栈顶像素出栈 (2)沿扫描线对出栈像素的左右像素进行填充, 直到遇到边界像素为止 (3)将上述区间内最左、最右像素记为xl 和xr (4)在区间[xl ,xr]中检查与当前扫描线相邻的上 下两条扫描线是否全为边界像素、或已填充 的像素,若为非边界、未填充的像素,则把 每一区间的最右像素取为种子像素入栈
扫描线区域填充算法

扫描线区域填充算法
扫描线区域填充算法,又称为"扫描线填涂算法",它用于对平面中特定区域填充指定的颜色、灰度或纹理,是计算机图形学中常用的算法之一。
该算法的原理是:给定待填充的区域内的点的有限个边界,从某一顶点开始,以某一规则遍历所有的边界点,形成边界数组,接着顺次扫描边界数组,将包含在边界中的每个合理像素点标记成已填充状态,由此而达到填充区域的目的。
算法步骤如下:
(1)设置起始点A,判断是否存在右方向上有没有边界点,若有,则把下一个边界点B作为起始点;
(2)从起始点A 开始,以扫描线的形式一次扫描边界点,把有效的像素点标记为“已填充”;
(3)把已扫描的点加入边界数组,直到下一个边界点C,且C点不等于起始点A;
(4)重复步骤(2)和(3),直至再回到起始点A,完成一次区域填充;
(5)如果还有未填充的区域,则重复步骤(1)至(4),直至所有区域填充完成。
实际应用中,为了避免停滞,可以采用八方向搜索策略;此外,由于扫描线填充算法中填充空间的范围是由边界点定义的,因此,当边界未经处理的是孤立的点或直线时,将无法实现实际的填充效果。
计算机图形学--第四讲 区域填充算法

任课教师:李陶深教授tshli@12直线生成算法圆与椭圆的绘制算法5图元的概念436区域填充算法裁剪反走样技术4.4 区域填充算法4.4 区域填充算法—基础知识(3)线框多边形物体:只需扫描转换线段填充多边形物体:要扫描转换多边形本质:点阵表示。
特点:面着色,画面明暗自然、色彩丰富。
4.4 区域填充算法4.4 区域填充算法—基础知识(4)图形学中多边形的两种表示方式顶点表示:用多边形的有序顶点序列表示多边形点阵表示:用位于多边形内部的像素集合来表示多边形4.4 区域填充算法多边形边界的矢量形式数据之上,可用于程序填色,也可用于交互填色。
形边界的图像形式数据之上,并还需提供多边形边界内一点的坐标。
概括地说,该算法先画边界,然后对内定义区域填充。
所以,它一般只能用于人机交互填色,而难以用于程序填色。
4.4 区域填充算法—多边形填色算法的问题多边形填色算法面临的一个首要问题,是判断一个像素是在多边形内还是多边形外。
Question1: How to Judge…?Question2: How to improve …?图4.14 射线法图4.15 转角法4.4 区域填充算法4.4 区域填充算法4.4 区域填充算法4.4 区域填充算法4.4 区域填充算法大量的求交、乘除运算4.4 区域填充算法—扫描线填色算法(1)基本思路:扫描线算法按扫描线的顺序计算出扫描线与多边形的相交区间,然后用要求的颜色填充这些区间内的像素。
该算法利用了扫描线的连续性和边的连续性,避免对像素的逐点判断和反复求交运算,减少了计算量,提高了算法速度。
具体处理过程:先求出扫描线与多边形边的交点,利用扫描线的连续性求出多边形与扫描线相交的连续区域,然后利用多边形边的连续性,求出下一条扫描线与多边形的交点,对所有扫描线由上到下依次处理。
4.4 区域填充算法—扫描线填色算法(2) 算法实现的步骤:对每一条扫描线执行如下四步:(1) 求交:求扫描线与多边形各边的交点;(2) 排序:将求得的交点按递增顺序进行排序;(3) 交点配对:确定相交区间;(4) 区间填色:将相交区间内的像素置成多边形色, 相交区间外的像素置成背景色。
区域填充算法

3、基于曲线积分的区域填充算法
• 算法的实现: ➢对一个区域进行轮廓跟踪,求出区域的边
• 改进算法的基本思想是:每找到一个新的内部
区段时,不仅将新区段的y值(yn)和左右列值xnl, xnr压入堆栈,而且同时把当前区段的y值和左右 列值xl,xr也压入堆栈,以保存和传递有关的信息。
3、基于曲线积分的区域填充算法
基于曲线积分的区域填充算法是邓国强,孙 景鳌等(2001)提出的一种以格林公式求区域面 积为基本原理进行区域填充的特殊算法。
1、递归种子填充算法
递归种子填充算法,又称边界填色算 法。
算法的原理是:让单个像元作为填充 胚,在给定的区域范围内,通过某种方法 进行蔓延,最终填充满整个多边形区域。 为了实现填充胚的蔓延,可采用四邻法或 八邻法进行填充。
2、扫描线种子填充算法
(1)扫描线种子填充算法
扫描线种子填充算法的对象是一个个扫描 线段。扫描线段是指区域内同值相邻像素 在水平方向的组合,它的两端以具有边界 值的像素为边界,即一段扫描线段的中间 只有同一种像素。
(2)计算多边形面积
4、区域填充算法在地图制图中的应用
(2)计算多边形面积
Sa
24
1 5 2
1 13 33 2
Sb
30
1 2
5
1 2
17
41
ScΒιβλιοθήκη 1031 213
1 2
17
图形学_06_二维图形填充

⑷.对于多边形的水平边 , 则不计它与扫描线 对于多边形的水平边,
的交点。 的交点。
F H G C
E G′ D ℓ m
A
B
如图: 与扫描线ℓ 如图 : ① 边 AB与扫描线 ℓ 与扫描线 交点不计,则扫描线ℓ 交点不计 , 则扫描线ℓ与边 HA有一 ( 下方) 交点A, 有一( 下方 ) 交点 , 有一 只计一次,与边BC有一交 只计一次 , 与边 有一交 下方) , 则填充AB。 点 ( 下方 ) B, 则填充 。
Ymax Ymin中的 中的X 中的
1 m
下一结点地址
8 7 6 5 4 3 2 1 0 ∧ ∧ 3 7 ∧ 9 2 ∧ 9 7
e3 e3
−5 2
∧ ∧ e5 e2
e4 11 7
3 2
∧
11 13 0 0
−5 2
e1
e6 5 7
3 2
∧
② 有效边表(当前边表AET) 有效边表(当前边表AET) 为一动态链表, 由一系列边结点组成, 为一动态链表 , 由一系列边结点组成 , 表 示当前扫描线与所有相关的边求出的交点, 示当前扫描线与所有相关的边求出的交点, 且 按 X 从小 到大排 序 。 当 该边处 理完毕 , 则 从 AET中删除,若ET中有相关边,则加入到 中删除, 中有相关边, 中删除 中有相关边 则加入到AET, , 直至ET、 全为空。 直至 、AET全为空。 全为空 以下图为例: 以下图为例:
四连通区域
八连通区域
1、简单填充算法 基本思想: 从多边形内部任一点(象素 象素)出 基本思想 : 从多边形内部任一点 象素 出 左上右下”顺序判断相邻象素, 发,依“左上右下”顺序判断相邻象素,若其 不是边界象素,对其填充,并重复上述过程, 不是边界象素,对其填充,并重复上述过程, 直到所有象素填充完毕——称四向种子填充算 称四向种子填充算 直到所有象素填充完毕 法。
算法系列之十二:多边形区域填充算法--递归种子填充算法

算法系列之十二:多边形区域填充算法--递归种子填充算法平面区域填充算法是计算机图形学领域的一个很重要的算法,区域填充即给出一个区域的边界(也可以是没有边界,只是给出指定颜色),要求将边界范围内的所有象素单元都修改成指定的颜色(也可能是图案填充)。
区域填充中最常用的是多边形填色,本文中我们就讨论几种多边形区域填充算法。
一、种子填充算法(Seed Filling)如果要填充的区域是以图像元数据方式给出的,通常使用种子填充算法(Seed Filling)进行区域填充。
种子填充算法需要给出图像数据的区域,以及区域内的一个点,这种算法比较适合人机交互方式进行的图像填充操作,不适合计算机自动处理和判断填色。
根据对图像区域边界定义方式以及对点的颜色修改方式,种子填充又可细分为几类,比如注入填充算法(Flood Fill Algorithm)、边界填充算法(Boundary Fill Algorithm)以及为减少递归和压栈次数而改进的扫描线种子填充算法等等。
所有种子填充算法的核心其实就是一个递归算法,都是从指定的种子点开始,向各个方向上搜索,逐个像素进行处理,直到遇到边界,各种种子填充算法只是在处理颜色和边界的方式上有所不同。
在开始介绍种子填充算法之前,首先也介绍两个概念,就是“4-联通算法”和“8-联通算法”。
既然是搜索就涉及到搜索的方向问题,从区域内任意一点出发,如果只是通过上、下、左、右四个方向搜索到达区域内的任意像素,则用这种方法填充的区域就称为四连通域,这种填充方法就称为“4-联通算法”。
如果从区域内任意一点出发,通过上、下、左、右、左上、左下、右上和右下全部八个方向到达区域内的任意像素,则这种方法填充的区域就称为八连通域,这种填充方法就称为“8-联通算法”。
如图1(a)所示,假设中心的蓝色点是当前处理的点,如果是“4-联通算法”,则只搜索处理周围蓝色标识的四个点,如果是“8-联通算法”则除了处理上、下、左、右四个蓝色标识的点,还搜索处理四个红色标识的点。
区域填充算法运行代码

区域填充算法运行代码区域填充算法是一种计算机图形学算法,用于填充封闭区域。
它在渲染二维图形中起着重要作用,常用于涂色、填充多边形等操作。
下面是一个使用C语言实现的区域填充算法的运行代码示例,代码中使用了递归法实现区域填充。
```c#include <graphics.h> // 引入图形库的头文件//递归实现的区域填充算法void fillRegion(int x, int y, int fillColor, int borderColor) int currentColor = getpixel(x, y); // 获取当前像素的颜色if(currentColor != borderColor && currentColor != fillColor) putpixel(x, y, fillColor); // 填充当前像素//向上填充fillRegion(x, y - 1, fillColor, borderColor);//向下填充fillRegion(x, y + 1, fillColor, borderColor);//向左填充fillRegion(x - 1, y, fillColor, borderColor);//向右填充fillRegion(x + 1, y, fillColor, borderColor);}int mainint gd = DETECT, gm; // 图形模式和图形驱动程序检测initgraph(&gd, &gm, ""); // 初始化图形界面//绘制一个闭合多边形作为填充区域int poly[8] = {100, 100, 200, 100, 200, 200, 100, 200};drawpoly(4, poly);//设置填充颜色和边界颜色int fillColor = YELLOW;int borderColor = BLACK;//调用区域填充函数fillRegion(150, 150, fillColor, borderColor);getch(;closegraph(;return 0;```在上面的代码中,我们首先引入了图形库的头文件`graphics.h`,然后使用`initgraph`函数初始化了图形界面。
扫描线区域填充算法

扫描线区域填充算法算法步骤如下:1.找到图形区域的上下边界:-遍历图形的所有边界点,找到最大纵坐标和最小纵坐标,确定扫描线的上下边界。
2.初始化扫描线列表:-从上到下依次生成扫描线,建立一个扫描线列表。
3.计算扫描线与图形的交点:-遍历扫描线列表中的每个扫描线,与图形的所有边界进行求交。
-如果与边界有交点,将交点的横坐标存入一个集合中,集合中的数据按从小到大排序。
4.进行填充:-遍历扫描线列表中的每个扫描线,找到对应的交点集合。
-将集合中的每两个横坐标之间的像素点进行填充。
以下是对算法的详细解释:首先,我们需要遍历所有边界点,找到最大纵坐标和最小纵坐标。
这样就确定了我们需要扫描的区域范围,也就是扫描线的上下边界。
接下来,我们生成一个扫描线列表。
从上到下依次生成每一条扫描线,将其存储在扫描线列表中。
然后,对于每一条扫描线,我们需要计算该扫描线与图形的交点。
我们遍历图形的所有边界,并与当前扫描线进行求交。
如果与边界有交点,我们将交点的横坐标存入一个集合中。
这个集合中的数据按从小到大排序,以便后续的填充操作。
最后,我们对于每一条扫描线,找到对应的交点集合。
我们遍历集合中的每两个横坐标之间的像素点,将其进行填充。
这可以通过修改像素的颜色或设置像素的属性来实现。
总结一下,扫描线区域填充算法通过逐行扫描图形区域,计算每行与区域内部的交点,然后进行填充。
该算法的优点是简单、高效,适用于填充简单凸多边形等闭合图形。
然而,该算法对于非凸多边形或包含内孔的图形表现较差,可能需要额外的处理逻辑。
扫描线区域填充算法

扫描线区域填充算法算法步骤如下:1.首先需要定义一个边表(ET)和活动边表(AET)。
-边表是存储多边形所有边的一张表格,将每条边的y坐标、x坐标以及斜率存储起来。
-活动边表是指当前扫描线与多边形边的交点,它是一个按照x坐标排列的列表。
2.初始化边表(ET)和活动边表(AET)。
-通过遍历多边形的边,将边表中存储对应的边信息。
-初始时活动边表为空。
3.根据多边形的顶点,将边添加到边表中。
-对于每条边,计算出其斜率,以及y坐标的最小值和最大值。
4.进行扫描线填充:a.设置当前扫描线的y坐标,从最小的y值开始,逐行向下扫描。
b.遍历边表,将与当前扫描线相交的边添加到活动边表中。
c.按照x坐标对活动边表进行排序。
d.遍历活动边表,两两配对,填充对应的像素点。
e.过滤掉扫描线下方的边。
f.更新活动边表,将不再与当前扫描线相交的边从活动边表中删除。
5.重复步骤4,直到扫描完整个区域。
然而,扫描线区域填充算法也存在一些局限性和问题:-对于包含小尺寸多边形的大区域填充,算法的迭代次数会增加,导致填充时间变长。
-在多边形内有重叠区域时,算法无法区分内外部,可能导致填充错误。
-当多边形内有孔洞时,算法无法正确填充孔洞。
为了解决以上问题,可以采用一些优化策略来改进算法性能和填充效果。
例如,可以使用边表索引和活动边表的双向链表结构,减少查找和插入操作的时间开销。
此外,还可以使用扫描线的上下两根线段来同时填充两个相邻区域,提高填充速度。
总结起来,扫描线区域填充算法是一种常用且有效的图形填充算法,通过逐行扫描和交点判断来填充封闭区域。
它可以广泛应用于计算机图形学领域,如图形渲染、图像处理等。
算法在实际应用中需根据具体场景进行优化和改进,以满足不同需求。
第四讲 区域填充

点阵字符:存储量大,易于显示
矢量字符:存储量小,美观,变换方便; 但需 要光栅化后才能显示。
字符属性
字体 宋体 仿宋体 楷体 黑体 隶书
字高 宋体 宋体 宋体 宋体
字宽 大海 大海 大海 大海
字倾斜角
倾斜 倾斜
对齐 (左对齐、中心对齐、右对齐)
字色 红色、绿色、蓝色
条件:需提供多边形各顶点的坐标及填充色或图案
扫描线算法
扫描线算法
目标:利用相邻像素之间的连贯性,提高算 法效率 处理对象:非自交多边形 (边与边之间除 了顶点外无其它交点)
(1) 边的相关性及边记录 算法首先要求出扫描线与边界的交点
已知扫描线yi与AB边的交点是(xi,yi)则:
(1) 边的相关性及边记录 yi+1=yi+1, xi+1=xi+1/m m是这条边的斜率 m=1/dx 设ax+by+c=0 (1) 则 斜率m=-b/a 由(1)有 xi+1=-1/a(byi+1+c) 同时 yi+1=yi+1 则 xi+1=-1/a(b(yi+1)+c)=-1/a(byi +c)-b/a
条件: 要求给出边界颜色特征及区域内的一个点,并要 求区域是连通的
区域:分为4连通区域和8连通区域
四个方向运动 八个方向运动
表示内点
四连通区域 八连通区域
67 5 4S9
328
表示边界点
区域连通方式对填充结果的影响
4连通区域边界填 充算法的填充结果
8连通区域边界填 充算法的填充结果
常见的种子填充算法由边界表示的四连通区域种子填充算 法、内点表示的四连通区域种子填充算法、边界表示的八连通 区域种子填充算法、内点表示的八连通区域种子填充算法。
区域填充算法区域填充算法

区域填充算法区域填充算法
下面将介绍两种常见的区域填充算法:扫描线填充算法和种子填充算法。
1. 扫描线填充算法(Scanline Fill Algorithm):
-扫描线填充算法基于扫描线的原理,从图像的上方向下扫描,对每条扫描线上的像素进行填充。
-算法流程如下:
-选择一个初始扫描线,例如选择图像的最上面一条扫描线;
-遍历该扫描线上的每一个像素,判断是否需要填充该像素;
-如果需要填充,则向区域内部延伸扫描线,同时判断该扫描线上的相邻像素是否需要填充;
-一直延伸扫描线,直到整个区域被填充完毕。
-扫描线填充算法的优点是简单、易于实现,但是算法的效率较低,在处理大尺寸区域时耗时较长。
2. 种子填充算法(Seed Fill Algorithm):
-种子填充算法基于种子点的概念,选择一个起始点作为种子点,然后根据预设的填充规则进行填充。
-算法流程如下:
-选择一个起始点作为种子点,将该点填充上颜色;
-判断该种子点的相邻像素是否需要填充,如果需要则将其填充;
-一直延伸填充,直到整个区域被填充完毕。
-种子填充算法的优点是效率较高,能够处理较大的区域,但是需要选择合适的填充规则,否则可能会导致填充区域不准确或者出现漏填的情况。
以上两种区域填充算法在实际应用中会根据具体的场景和需求选择合适的算法进行使用。
在实际实现时,还需要考虑一些特殊情况,如图像边界处理、扫描顺序等,以确保算法的正确性和效率。
矩形区域填充算法

矩形区域填充算法
矩形区域填充算法是一种常用的计算机图形学算法。
该算法的主要作用是将一定区域内的颜色进行填充。
在计算机可视化技术中,该算法是非常重要的,特别是在制作游戏、动画和画图软件中。
该算法的实现过程较为简单,其主要原理是通过输入一个种子点,向四周扩展填充其颜色。
整个填充过程可以理解为一个递归的过程,即将当前点的颜色变更、修改并递归到四周的点。
这种递归填充算法能够保证填充区域的完整性和准确性。
矩形区域填充算法的实现通常涉及以下步骤:
(1)输入起始点:首先需要用户输入一个起始点,作为要填充的区域的起点。
该点往往是具有特殊颜色的点。
(2)确定填充颜色:用户需要指定要填充的颜色。
该颜色将被用于填充区域。
(3)填充区域:从起始点开始,进行递归填充操作。
如果当前点的颜色与起始点的颜色相同,则修改当前点的颜色为要填充的颜色,递归到当前点的四周点进行相同的操作;否则,递归结束。
(4)显示填充结果:填充完毕后,显示填充的结果图形。
在实际应用中,该算法可能存在一些问题,如内存消耗和填充速度等方面的问题。
此外,一些具有不规则形状或复杂边界的区域可能需要采用其他算法或技术来完成填充。
总之,矩形区域填充算法是一种常用的计算机图形学算法,其实现过程简单,应用广泛。
在可视化技术的应用中扮演着重要角色,可以用于制作游戏、动画和画图软件等。
但在应用时,需考虑应用环境和效率等方面的问题,选择适合的算法或技术完成填充。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单方程产生圆弧
圆的极坐标方程为:
x R cos y R sin
i 1 i (为一固定角度步长 ) xi 1 round( R cos i 1 ) yi 1 round( R sin i 1 )
30
中点Bresenham画圆
给定圆心在原点,半径为整数R的圆,其方程为
17
D 2xd 2x ( d k ) D 2y
中点Bresenham算法——算法步骤
输入直线的两端点P0(x0,y0)和P1(x1,y1)。
计算初始值△x、△y、D=△x-2△y、x=x0、y=y0。
绘制点(x,y)。判断D的符号。若D<0,则(x,y)更 新 为 ( x+1,y+1),D 更 新 为 D+2△x-2△y; 否 则 (x,y)更新为(x+1,y), D更新为D-2△y。 当直线没有画完时,重复上一步骤,否则结束。 程序演示
9
中点Bresenham算法
算法原理:根据直线的斜率确定或选择变量在 x或y方向上每次递增一个单位,而另一方向的 增量为1或0,它取决于实际直线与相邻象素点
的距离,这一距离称为误差项。
10
假定0≤k≤1, 即0≤ Δy/Δ x ≤1,x是最大位移方向
Pu(xi+1,yi+1) Q M(xi+1,yi+1/2) P(xi,yi) Pd(xi+1,yi)
(x0+1,y0+0.5) (x0,y0)
图5.9 计算初值
16
中点Bresenham算法——改进
改进:用2d△x代替d ,令D=2d△x 则:
D0 2xd0 2x (0.5 k ) x 2y d 0 D0 D 2xd 2x ( d 1 k ) 2xd 2x 2y D 2x 2y d 0 D0
图5.8 误差项递推
d 2 F ( xi 2, yi 0.5) yi 0.5 k ( xi 2) b
d1 k d 2 yi 0.5 k ( xi 1) b k
中点Bresenham算法
初始值d的计算
d 0 F ( x0 1, y0 0.5) y0 0.5 k ( x0 1) b y0 kx0 b k 0.5 0.5 k
2
2 2
( xi 2) ( yi 1.5) R
2 2 2
xi
2
xi+1 xi+2
d 2 ( xi 1 1) ( yi 0.5 1) R
2
图5.15 d>0的情况
2
( xi 1) 2 xi 3 ( yi 0.5) 2( yi 0.5) 1 R ( xi 1) ( yi 0.5) 2( xi yi ) 5 d1 2( xi yi ) 5
21
改进1:令e=d-0.5
xi 1 xi 1 y yi 1 i 1 yi (d 0.5) (d 0.5)
xi 1 xi 1 y yi 1 i 1 yi
(e 0) (e 0)
误差项的计算 • d初=0, • 每走一步:d=d+k • if (e>0) then d=d-1
8
中点Bresenham算法
直线的方程
y y1 y0 F ( x, y) y kx b 0 , 其中k x x1 x0
y F(x,y)=0 F(x,y)>0 F(x,y)<0 x F(x,y)<0 F(x,y)=0 F(x,y)>0 x y
图5.3 直线将平面分为三个区域
中点Bresenham画圆
判别式的初始值
d 0 F ( x0 1, y0 0.5) F (1, R 0.5) 1 ( R 0.5) R
2 2
1.25 R
36
改进:用d-0.25代替d
此时有:
d d 2 xi 3 d0 1 R
d 0.25 d 0.25
图5.7 误差项递推
d 2 yi 0.5 k ( xi 1) b 1 k d1 1 k
误差项的递推(d≥0)
d1 F ( xi 1, yi 0.5) yi 0.5 k ( xi
(x i+2,yi+0.5) 1) b (xi+1,yi+0.5) (xi,yi) d>=0
2
图形生成的概念
图形的生成:是在指定的
输出设备上,根据坐标描
述构造二维几何图形。
图形的扫描转换:在光栅
显示器等数字设备上确定
图5.1 用象素点集逼近直线
一个最佳逼近于图形的象
素集的过程。
3
5.1 直线的扫描转换
直线的绘制要求
(1)直线要直; (2)直线的端点要准确,无定向性无断裂; (3)直线的亮度、色泽要均匀; (4)画线的速度要快; (5)具有不同的色泽、亮度、线型等。
y y=x R
x
图5.12 1/8圆弧
27
圆的扫描转换
简单方程生成圆弧
中点Bresenham算法
28
简单方程产生圆弧
算法原理:利用其函数方程,直接离散计算。 圆的函数方程为: x
2
y R
2
2
xi1 xi 1
x 0, R
2 2 i 1
2
(5 - 7)
29
yi1 round( R x )
max(|△x|,|△y|)=|△y|,此时|k|≥1:
1 1 xi 1 xi x xi x xi y k 1 yi 1 yi y yi y yi 1 y
数值微分法(DDA法)——特点
增量算法 直观、易实现 不利于用硬件实现
第五章 基本图形生成算法
如何指定的输出设备上根据坐标描述构造基 本二维几何图形(点、直线、圆、椭圆、多边 形域、字符串及其相关属性等)。
1
第五章 基本图形生成算法
图形生成的概念 直线段的扫描转换 圆的扫描转换 多边形的扫描转换与区域填充 属性处理
反走样技术
在OpenGL中绘制图形
图5.14 d≤0的情况
2
d 2 ( xi 1 1) ( yi 0.5) R
2 2 2
( xi 1) 2 xi 3 ( yi 0.5) R d1 2 xi 3
yi
P
误差项的递推(d>0)
yi-1 yi-2
2 2
d 2 F ( xi 2, yi 1.5)
x y R
2 2
2
构造函数F(x,y)=x2+y2-R2。 对于圆上的点,有F(x,y)=0; 对于圆外的点,F(x,y)>0; 而对于圆内的点,F(x,y)<0。
31
y
Pu P M Pd
x
图5.13 中点Bresenham画圆的原理
中点Bresenham画圆
构造判别式:
d F ( xM , yM ) F ( xi 1, yi 0.5) ( xi 1)2 ( yi 0.5)2 R2
改进的Bresenham算法——算法步骤
1.输入直线的两端点P0(x0,y0)和P1(x1,y1)。 2.计算初始值△x、△y、e=-△x、x=x0、y=y0。 3.绘制点(x,y)。 4.e更新为e+2△y,判断 e的符号。若e>0,则 (x,y) 更新为(x+1,y+1),同时将e更新为e-2△x;否则 (x,y)更新为(x+1,y)。
当d≤0时,下一点取Pu(xi +1,yi); 当d>0时,下一点取Pd(xi +1,yi-1)。
33
yi
P
误差项的递推(d≤0)
yi-1 yi-2 xi
2 2
d 2 F ( xi 2, yi 0.5)
( xi 2)2 ( yi 0.5)2 R 2
xi+1 xi+2
图5.4 Brensemham算法生成直线的原理
判别式:
d F ( xM , yM ) F ( xi 1, yi 0.5) yi 0.5 k ( xi 1) b
则有:
xi1 xi 1 yi 1 yi1 y i
(d 0) (d 0)
y
yi+1 ε△y yi xi ε△x xi+1 x
xi 1 xi x yi 1 yi y
ε=1/max(|△x|,|△y|)
图5.2 DDA算法原理
6
max(|△x|,|△y|)=|△x|,即|k|≤1的情况:
1 xi 1 xi x xi x xi 1 x 1 yi 1 yi y yi y yi k x
图5.6 Brensemham算法生成直线的原理
误差项的递推(d<0)
d1 F ( xi 1, yi 0.5) yi 0.5 k ( xi 1) b
d 2 F ( xi 2, yi 1.5) yi 1.5 k ( xi 2) b
(x i+2,yi+1.5) (xi+1,yi+0.5) (xi,yi) d<0
5.当直线没有画完时,重复步骤3和4。否则结束。
