高一上学期期末考试题
江苏省连云港市2023-2024学年高一上学期期末考试语文试题(含解析)

江苏省连云港市2023-2024学年高一上学期期末语文试卷一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,19分)阅读下面的文字,完成小题。
①党的二十大报告提出,要“扎实推动乡村产业、人才、文化、生态、组织振兴”。
其中,文化振兴既是乡村振兴的重要内容,也为实现乡村全面振兴注入活力。
②中华民族五千多年历史孕育了丰富的乡土文化,如宗族文化、节庆文化、耕读文化、祭祀文化等。
这些文化元素相互交织形构了朴素的乡村价值观和认知体系,进而构建了乡村社会的行为规范。
随着社会经济的快速发展,传统乡土文化蕴含的礼俗秩序开始在乡村社会中消解,乡村出现了内核“空心”。
重塑乡土文化,建设乡村精神家园,对筑牢乡村振兴之根,确保乡村社会的持续稳定发展具有重要意义。
③乡村优秀传统文化记录了乡村历史、信仰、习俗和生活方式,成为维系乡村社会深层情感的集体记忆。
重视物质文化遗产的传承,保护好古树、古桥、古村落、古建筑等蕴含丰富历史信息和文化内涵且不可再生的文化资源,保留代表性乡村公共记忆景观。
积极推进剪纸、捏面人等非物质文化遗产保护,培育乡村文化的传承人,延续和发展历史遗留的珍贵精神财富。
鼓励年轻人学习传统技艺和表演,让更多的年轻人认识和了解地方乡村传统文化,培养他们的文化自信和认同感。
在保护和传承中寻根溯源,从而在中国传统式的“乡愁”中滋养乡土文化归属。
④涵养乡风文明可以为乡村发展提供精神动力和智力支持,有效地满足农民对美好生活精神层面的需要,提升农民的主人翁意识和社会责任意识,同时进一步增强农民的文化自信和文化认同。
加强乡风文明建设,要在传承优秀传统文化的基础上,充分发挥先进文化的引领作用,尊重乡村本位和农民主体地位。
围绕农民需要提供文化服务,组织农民开展文化活动,提升农民素质和乡风文明程度。
⑤党的领导是乡村振兴的前提和方向保证,是乡村社会的凝聚力和向心力的坚实保障。
涵养乡风文明,必须坚持和加强党对农村工作的全面领导,强化基层党组织的政治担当,推进改革创新,发挥好党建引领作用。
广东深圳中学2023-2024学年高一上学期期末考试数学试题 答案解析

深圳中学2023-2024学年度第一学期期末考试试题评分标准年级:高一 科目:数学命题人:贺险峰 审题人:邱才颙、黎建蒙单项选择题:题号 1 2 3 4 5 6 7 8 答案 CB AB CC BA多项选择题:题号 9 10 11 12 答案 ABCACDBCAB二、填空题:13. 95 . 14. 12 . 15. 43 . 16.1[4,]2−一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.【详解】依题意,“居民人数多”, “男、女使用手机扫码支付的情况差异不大”, “老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异”, 所以最合理的是按年龄段分层随机抽样. 故选:C2.【详解】因为7πrad 3154=,终边落在第四象限,且与45−角终边相同,故与7π4的终边相同的角的集合{}{}31536045360S k k αααα==+⋅==−+⋅ 即选项B 正确;选项AC 书写不规范,选项D 表示角终边在第三象限. 故选:B.3.【详解】根据三角函数定义可知3cos 5α=, 又22sin cos 1αα+=,则225cos 31sin cos ααα−===. 故选:A4.【详解】因为21cos 212sin 3αα=−=,所以3sin 3α=±,因为()0,πα∈,所以3sin 3α=. 故选:B .5.【详解】因为某人的血压满足函数式()11525sin(160π)P t t =+,又因为1sin(160π)1t −≤≤,所以11525()11525P t −≤≤+,即90()140P t ≤≤, 即此人的血压在血压计上的读数为140/90mmhg ,故①正确; 因为收缩压为140mmhg ,舒张压为90mmhg ,均超过健康范围, 即此人的血压不在健康范围内,故②错误,③正确; 对于函数()11525sin(160π)P t t =+,其最小正周期2π1160π80T ==(min ), 则此人的心跳为180T=次/分,故④正确; 故选:C6.【详解】由题图可知:2023年母亲周末陪伴孩子日均时长超过8小时的占比为138.7%3>,A 说法正确;2023年父母周末陪伴孩子日均时长超过6小时的占比为131.5%24.2%55.7%2+=>,B 说法正确;2023年母亲周末陪伴孩子日均时长的5个时段占比的极差为38.7% 2.5%36.2%−=,C 说法错误;2023年父母周末陪伴孩子日均时长的10个时段占比的中位数为21.4%19.0%20.2%2+=,D 说法正确. 故选:C .7.【详解】将函数()2sin f x x =图象上所有点的横坐标缩小为原来的12,得到2sin 2y x =的图象, 再向右平移π6个单位长度,得到()ππ2sin 22sin 263g x x x ⎛⎫⎛⎫=−=− ⎪ ⎪⎝⎭⎝⎭的图象.当π0,2x ⎡⎤∈⎢⎥⎣⎦时,ππ2π2,333x ⎡⎤−∈−⎢⎥⎣⎦,令π23x t −=,π2π,33t ⎡⎤∈−⎢⎥⎣⎦,则关于t 的方程2sin t a =在π2π,33−⎡⎤⎢⎥⎣⎦上有两个不等的实数根1t ,2t ,所以12πt t +=,即12ππ22π33x x −+−=,则125π6x x +=,所以()125π3tan tan 63x x +==−. 故选:B8.【详解】考虑三角函数的定义域,将选项代入验证可得最大“好整数”为1 故选:A二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.【详解】根据角度制和弧度制的定义可知,度与弧度是度量角的两种不同的度量单位,所以A 正确;由圆周角的定义知,1度的角是周角的1360,1弧度的角是周角的12π,所以B 正确; 根据弧度的定义知,180︒一定等于π弧度,所以C 正确;无论是用角度制还是用弧度制度量角,角的大小均与圆的半径长短无关,只与弧长与半径的比值有关,故D 不正确. 故选:ABC.10.【详解】ππc s cos sin os n 3i 3x x x x ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭ππ1cos cos 332x x ⎛⎫=−−== ⎪⎝⎭,A 正确;tan10tan 35tan10tan 35︒+︒+︒︒()()tan 10351tan10tan 35tan10tan 35=︒+︒−︒︒+︒︒tan 451=︒=,B 不对;22tan 22.512tan 22.511tan 451tan 22.521tan 22.522︒︒==︒=−︒−︒,C 正确;()2311cos 403sin502cos 2012223sin 503sin503sin502−︒−︒−︒===−︒−︒−︒,D 正确. 故选:ACD11.【详解】因为由频率分布直方图无法得出这组数据的最大值与最小值, 所以这组数据的极差可能为70,也可能为小于70的值,所以A 错误;因为(0.00820.0120.01540.030)10700.651a a a a ++++++⨯=+=,解得0.005a =, 所以B 正确;该校竞赛成绩的平均分的估计值550.00510650.00810x =⨯⨯+⨯⨯+750.01210850.01510950.03010⨯⨯+⨯⨯+⨯⨯10540.0051011520.0051090.7+⨯⨯⨯+⨯⨯⨯=分,所以C 正确.设这组数据的第30百分位数为m ,则(0.0050.0080.012)10(80)0.015100.3m ++⨯+−⨯⨯=,解得2413m =, 所以D 错误. 故选:BC .12.【详解】因为ππ31sin ,cos ,3322⎛⎫⎛⎫−=− ⎪ ⎪ ⎪⎝⎭⎝⎭,所以由三角函数的定义得1sin 2α=,3cos 2α=−,所以5π2π,6k k α∈=+Z , 则()()cos sin 2sin cos 2sin 2f x x x x ααα=−=−5π5πsin 22πsin 2,66x k x k ∈⎛⎫⎛⎫=−−=− ⎪ ⎪⎝⎭⎝⎭Z ,A: 22111cos 22sin 222αα⎛⎫−==⨯= ⎪⎝⎭,故A 正确;B :因为5π62π4ππsin sin 1332f ⎛⎫⎛⎫=−== ⎪⎪⎝⎭⎝⎭,所以2π3x =是()y f x =的图象的一条对称轴,故B 正确;C :将函数()y f x =图象上的所有点向左平移5π6个单位长度, 所得到的函数解析式为5π5πsin 2sin 2665π6y x x ⎡⎤⎛⎫⎛⎫=+−=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故C 错误;D :令()0f x =,得5πsin 206x ⎛⎫−= ⎪⎝⎭,解得5π5ππ2π,,6122k x k k x k ∈∈−=⇒=+Z Z , 仅0k =,1,即5π11π,1212x =符合题意, 即()y f x =在4π0,3⎛⎫⎪⎝⎭内恰有两个零点,故D 错误.故选:AB三、填空题:本题共4小题,每小题5分,共20分. 13.【详解】设所求平均成绩为x ,由题意得5092309020x ⨯=⨯+⨯,∴95x =. 故答案为:9514.【详解】因为π02α<<且11cos c 2πos 73α=<=,则ππ32α<<, 又02βπ<<,所以π3παβ<+<,且()533sin 142αβ+=<, 所以π2π3αβ<+<,则()()211cos 1sin 14αβαβ+=−−+=−,243sin 1cos 7αα=−=, 所以()()()cos cos cos cos sin sin βαβααβααβα=+−=+++⎡⎤⎣⎦111534311471472=−⨯+⨯=. 故答案为:12 15.【详解】因为函数()()sin 0,02f x x πωϕωϕ⎛⎫=+>≤≤ ⎪⎝⎭是R 上的奇函数,则()()f x f x −=−,即sin cos cos sin x x ϕωωϕ=−, 又因为0ω>,所以sin 0ϕ=,因为π02ϕ≤≤,所以0ϕ=;故()sin f x x ω=; 又因为图象关于点3π,04A ⎛⎫⎪⎝⎭对称,则3ππ4k ω=,Z k ∈,所以43k ω=,Z k ∈,因为函数在区间π0,4⎡⎤⎢⎥⎣⎦上是单调函数,则12ππ24ω⨯≥,得04ω<≤;所以43ω=, 故答案为:43.16.【详解】cos cos sin sin cos cos 1y αβαβαβ=−+−−(cos 1)cos (sin )sin (cos 1)βαβαβ=+−−+22(cos 1)sin sin()(cos 1)ββαϕβ=+++−+22cos sin()(cos 1)βαϕβ=++−+由sin()[1,1]αϕ+∈−,得22cos (cos 1)22cos (cos 1)y ββββ−+−+≤≤+−+, 令1cos t β=+,则[0,2]t ∈,则2222t t y t t ≤≤−−−, 所以22212()422y t t t ≥−−=−++≥−,当且仅当2t =,即cos 1β=时取等号,且222112()222y t t t ≤−=−−+≤,当且仅当22t =,即1cos 2β=−时取等号, 所以y 的取值范围为1[4,]2−.故答案为:1[4,]2−四、解答题:本题共6小题,共20分.解答应写出文字说明、证明过程或演算步骤.17(本题满分10分)已知()()()()3πsin πcos 2πcos 2.πcos sin π2f αααααα⎛⎫−−− ⎪⎝⎭=⎛⎫−−− ⎪⎝⎭(1)化简()f α;(2)若α是第三象限角,且()1sin π5α−=,求()f α的值.【详解】(1)()f α=()sin cos sin cos sin sin αααααα⋅⋅−==−⋅ --------------5分(2)由诱导公式可知()1sin πsin 5αα−=−=,即1sin 5α=−--------7分又α是第三象限角,所以22126cos 1sin 155αα⎛⎫=−−=−−=− ⎪⎝⎭------------9分 所以()26cos 5f αα=−=.-----------------------10分18(本题满分12分)据调查,某市政府为了鼓励居民节约用水,减少水资源的浪费,计划在本市试行居民生活用水定额管理,即确定一个合理的居民用水量标准x (单位:吨),月用水量不超过x 的部分按平价收费,超出x 的部分按议价收费.为了了解全市居民用水量分布情况,通过抽样,获得了n 户居民某年的月均用水量(单位:吨),其中月均用水量在(]9,12内的居民人数为39人,并将数据制成了如图所示的频率分布直方图.(1)求a 和n 的值;(2)若该市政府希望使80%的居民月用水量不超过标准x 吨,试估计x 的值;(3)在(2)的条件下,若实施阶梯水价,月用水量不超过x 吨时,按3元/吨计算,超出x 吨的部分,按5元/吨计算.现市政府考核指标要求所有居民的月用水费均不超过70元,则该市居民月用水量最多为多少吨? 【详解】(1)()0.0150.0250.0500.0650.0850.0500.0200.0150.00531a +++++++++⨯=,1.300a ∴=--------------------2分 用水量在(]9,12的频率为0.06530.195⨯=,392000.195n ∴==(户)---------------4分 (2)()0.0150.0250.0500.0650.08530.720.8++++⨯=<,()0.0150.0250.0500.0650.0850.05030.870.8+++++⨯=>,0.800.7215316.60.870.72−∴+⨯=−(吨)-------------------------8分(3)设该市居民月用水量最多为m 吨,因为16.6349.870⨯=<,所以m 16.6>, 则()16.6316.6570w m =⨯+−⨯≤,解得20.64m ≤,答:该市居民月用水量最多为20.64吨.------------------------12分19(本题满分12分)已知函数()()223sin πcos 2cos f x x x x =−+.(1)若ππ,63x ⎡⎤∈−⎢⎥⎣⎦,求函数()f x 的值域;(2)若函数()()1g x f x =−在区间π,6m ⎡⎤−⎢⎥⎣⎦上有且仅有两个零点,求m 的取值范围.【详解】(1)由题意得()()223sin πcos 2cos f x x x x=−+π3sin2cos 212sin 216x x x ⎛⎫=++=++ ⎪⎝⎭,-----------------4分当ππ,63x ⎡⎤∈−⎢⎥⎣⎦,则ππ5π2[,]666x +∈−,则1πsin 2126x ⎛⎫−≤+≤ ⎪⎝⎭,则π02sin 2136x ⎛⎫≤++≤ ⎪⎝⎭,即函数()f x 的值域为[]0,3;---------------------6分(2)由题()()π2sin 216g x x f x ⎛⎫+ ⎪⎝=−⎭=在区间π,6m ⎡⎤−⎢⎥⎣⎦上有且仅有两个零点,--------7分当π,6x m ⎡⎤∈−⎢⎥⎣⎦时,πππ2[,2]666u x m =+∈−+,原问题转化为sin y u =在ππ[,2]66m −+有且仅有2个零点,-----------------9分故π5π11ππ22π,61212 m m ≤+<≤<解得,即5π11π,1212m ⎡⎫⎪⎢⎣⎭的取值范围是.-------------12分20(本题满分12分)某生物研究者于元旦在湖中放入一些凤眼莲(其覆盖面积为k ),这些凤眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲的覆盖面积为224m ,三月底测得凤眼莲的覆盖面积为236m ,凤眼莲的覆盖面积y (单位:2m )与月份x (单位:月)的关系有两个函数模型()0,1xy ka k a =>>与()120,0y px k p k =+>>可供选择.(1)试判断哪个函数模型更合适并求出该模型的解析式;(2)求凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份. (参考数据:lg 20.3010,lg 30.4711≈≈).【详解】(1)函数()0,1x y ka k a =>>与()120,0y px k p k =+>>在()0,∞+上都是增函数, 随着x 的增加,函数()0,1xy ka k a =>>的值增加的越来越快,而函数()120,0y px k p k =+>>的值增加的越来越慢,由于凤眼莲在湖中的蔓延速度越来越快,因此选择模型()0,1xy ka k a =>>符合要求,------2分根据题意可知2x =时,24y =;3x =时,36y =,所以232436ka ka ⎧=⎨=⎩,解得32323a k ⎧=⎪⎪⎨⎪=⎪⎩,故该函数模型的解析式为*32323N 2,11,x y x x ⎛⎫=⋅ ⎪⎝≤≤∈⎭;---6分(2)当0x =时,323y =,元旦放入凤眼莲的覆盖面积是232m 3,---------8分 由3233210323x⎛⎫⋅>⨯ ⎪⎝⎭,得3102x⎛⎫> ⎪⎝⎭,-------------9分 所以32lg1011log 10 5.93lg3lg 20.47110.3010lg 2x >==≈≈−−,----------------11分 又*N x ∈,所以6x ≥,即凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份是六月份.-----------12分21(本题满分12分)已知函数()()sin (0,0π)f x x ωϕωϕ=+><<的最小正周期为π,且直线2x π=−是其图象的一条对称轴.(1)求函数()f x 的解析式;(2)将函数()y f x =的图象向右平移π4个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图象对应的函数记作()y g x =,已知常数*R,N n λ∈∈,且函数()()()F x f x g x λ=+在()0,πn 内恰有2023个零点,求常数λ与n 的值.【详解】(1)由三角函数的周期公式可得2π2πω==,()()sin 2f x x ϕ∴=+,--------2分 令()π2πZ 2x k k ϕ+=+∈,得()ππZ 422k x k ϕ=−+∈, 由于直线2x π=−为函数()y f x =的一条对称轴,所以,()πππZ 2422k k ϕ−=−+∈, 得()3ππZ 2k k ϕ=+∈,由于0πϕ<<,1k ∴=−,则2ϕπ=, 因此,()πsin 2cos 22f x x x ⎛⎫=+= ⎪⎝⎭;-------------------4分(2)将函数()y f x =的图象向右平移π4个单位,得到函数ππcos 2cos 2sin 242y x x x ⎡⎤⎛⎫⎛⎫=−=−= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图象对应的函数为()sin g x x =,-----------------6分()()()2cos 2sin 2sin sin 1F x f x g x x x x x λλλ=+=+=−++,令()0F x =,可得22sin sin 10x x λ−−=,令[]sin 1,1t x =∈−,得2210t t λ−−=,280λ∆=+>,则关于t 的二次方程2210t t λ−−=必有两不等实根1t 、2t ,则1212t t =−,则1t 、2t 异号,(i )当101t <<且201t <<时,则方程1sin x t =和2sin x t =在区间()()0,πN n n *∈均有偶数个根,从而方程22sin sin 10x x λ−−=在()()0,πN n n *∈也有偶数个根,不合乎题意;-----------8分(ii )当11t =−时,则2102t <<,当()0,2πx ∈时,1sin x t =只有一根,2sin x t =有两根, 所以,关于x 的方程22sin sin 10x x λ−−=在()0,2π上有三个根,由于202336741=⨯+,则方程22sin sin 10x x λ−−=在()0,1348π上有36742022⨯=个根, 由于方程1sin x t =在区间()1348π,1349π上无实数根,方程2sin x t =在区间()1348π,1349π上有两个实数解, 因此,关于x 的方程22sin sin 10x x λ−−=在区间()0,1349π上有2024个根,不合乎题意,-------------------10分 (iii )当11t =,则2102t −<<,当()0,2πx ∈时,1sin x t =只有一根,2sin x t =有两根,所以,关于x 的方程22sin sin 10x x λ−−=在()0,2π上有三个根,由于202336741=⨯+,则方程22sin sin 10x x λ−−=在()0,1348π上有36742022⨯=个根, 由于方程1sin x t =在区间()1348π,1349π上只有一个根,方程2sin x t =在区间()1348π,1349π上无实数解,因此,关于x 的方程22sin sin 10x x λ−−=在区间()0,1349π上有2023个根,合乎题意; 此时,2211110λλ⨯−⨯−=−=,得1λ=,综上所述:1λ=,1349n =.---------------------------12分22(本题满分12分)已知二次函数()f x 满足:()2132f x x x +=++.()24log 231xg x ⎛⎫=+ ⎪−⎝⎭(1)求()f x 的解析式;(2)求()g x 的单调性与值域(不必证明); (3)设()2cos cos 2h x x m x =+(,2ππ2x ⎡⎤∈−⎢⎥⎣⎦),若()()f h x g h x ≥⎡⎤⎡⎤⎣⎦⎣⎦,求实数m 的值. 【详解】(1)由题意()2132f x x x +=++,令1t x =+,则1x t =−,有()22(1)3(1)2f t t t t t =−+−+=+,故()2f x x x =+ ------------2分(2)函数()24log 231x g x ⎛⎫=+ ⎪−⎝⎭,由420031x x +>⇒>−,即定义域为()0,+∞, 且4231xu =+−在()0,+∞上单调递减及2log y u =单调递增 所以()24log 231xg x ⎛⎫=+⎪−⎝⎭在()0,+∞上单调递减.---------------4分 且()g x 的值域是()1,+∞------------------6分(3)结合(2)结论知()24log 231xg x ⎛⎫=+⎪−⎝⎭在()0,+∞上单调递减且()12g =, 又()2f x x x =+在()0,+∞上单调递增且()12f =故当1x ≥时,()()2,01f x g x x ≥≥<<时,()()2f x g x <<, 由()()()1f h x g h x h x ≥⇒≥⎡⎤⎡⎤⎣⎦⎣⎦恒成立,-----------------8分 即()22cos 2cos 11x m x +−≥在,22x ππ⎡⎤∈−⎢⎥⎣⎦上恒成立,设[]cos 0,1x t =∈, 则不等式()22210mt t m +−+≥在[]0,1t ∈上恒成立,-----------9分 ①当0m =时,不等式化为210t −≥,显然不满足恒成立; ②当0m >时,将0t =代入得()10m −+≥,与0m >矛盾; ③当0m <时,只需()()10,1,12210,1,m m m m m m −+≥⎧≤−⎧⎪⇒⇒=−⎨⎨+−+≥≥−⎪⎩⎩,综上,实数m 的值为1−.---------------------12分。
山东省潍坊市2023-2024学年高一上学期期末考试英语试题

山东省潍坊市2023-2024学年高一上学期期末考试英语试题学校:___________姓名:___________班级:___________考号:___________一、阅读理解Why waste time and money booking a hotel when you can enjoy the beautiful British countryside at these wonderful motorhome and caravan (旅行拖车) destinations in the UK.Ferneley’s Ice Cream and CafeLocated between the coast and the countryside, this beautiful location offers a bit of everything for families, and their dogs. What makes Ferneley’s stand out is their family farm that creates fresh local produce using milk from their own cows. It’s also a great chance for kids to learn more about what goes on at a farm and how they raise their cattle.Halfpenny Green VineyardProducing prize-winning English wines for over 30 years, Halfpenny Green Vineyard, is a wine-lover’s favourite in the green Staffordshire countryside. You can park up your campervan for free and take a guided tour around the site while tasting the produce. On top of all this, there is a wild Zoological Park, which is home to a wide variety of animals, providing an educational experience for the whole family.Fur and Feather InnThe beautiful Woodfordes Brewery in Norwich is situated right next to the inn, offering bookable tours and prize-winning beer. Park up and have some real beer before lying down for the night in the van. The building itself is of British style, a country pub in the heart of the Norfolk Broads. This is a must-visit for beer lovers.Rectory FarmWith a mass of parking space, a large pick-your-own farm with large fields and a wide variety of fruits and vegetables and a children’s woodland play area, the Rectory Farm offers the perfect family day out. It’s even got a lovely farm shop with an outdoor cafe, so you can sit and relax with a coffee while the kids eat their fruits.1.What can visitors do in Halfpenny Green Vineyard?A.Make wines.B.Win some prizes.C.Learn knowledge about animals.D.Visit the site at will.2.Which destination is the least likely choice for families with kids?A.Ferneley’s Ice Cream and Cafe.B.Halfpenny Green Vineyard.C.Fur and Feather Inn.D.Rectory Farm.3.Where is the text probably taken from?A.A tourist review.B.A geography book.C.A novel.D.A travel brochure.In 1943, Roman Totenberg, a violinist, bought a rare (稀有的) and special violin called a Stradivarius. It was made in 1734, in Italy, by Antonio Stradivari. Only about 600 of his violins are believed to still exist. They were regarded as the rarest and best instruments in the world.Roman’s Stradivarius was his musical partner for 38 years. Then bad luck struck; the violin was stolen from his office after a concert while he greeted well-wishers. He was shocked and upset by its loss. “Yes, it’s a bit like losing your arm,” he told his daughter, Jill.It took Roman a year to find and buy a new violin as the size and tones (音质) of each were different from his. He had to learn his musical pieces all over again! Roman kept playing into his 90s and taught at Boston University until he died in 2012, aged 101.His daughter says, “We wondered from time to time if the violin would surface, but... Our mother and father taught us to keep moving forward and not think over what life throws at you.”In 2015, the wife of the man who stole the violin wanted to know if it was really a Stradivarius. She had looked after him when he was dying from cancer and now it belonged to her. She took it to master violin maker and dealer Phillip Injeia. He recognized it immediately and contacted the FBI. Jill, who received the call from FBI, said in an interview, “I said, ‘I have to call my sisters. I’ll tell them not to get their hopes up,’ but Phillip Injeian said, ‘You don’t have to do that. This is the violin.’”Jill said they would sell the violin, not to a collector but someone who would play it. She said it would finally be in the hands of another great artist and its amazing voice would be heard in concert halls around the country.4.Why did Roman feel like he had lost an arm after the violin was stolen?A.It cost him a lot of money.B.It had served as a useful arm.C.It had been his musical partner.D.It was created by a famous maker.5.What is the turning point of this story?A.The FBI got in touch with Jill.B.The Stradivarius was found missing.C.Roman Totenberg died in 2012, aged 101.D.The violin was taken to a master violin maker and dealer.6.Why would the family like the violin to be owned by a violinist?A.They intended to become well-known.B.They wanted to sell it at a higher price.C.They hoped to remember Roman Totenberg.D.They wished to make the most of the Stradivarius.7.Which words can best describe Phillip Injeian?A.Expert and confident.B.Creative and careful.C.Learned and proud.D.Strong-willed and friendly.It’s reported that about 20 percent of the Amazon rainforest has disappeared during thespecies native to the Amazon River area, it’s affecting humans worldwide. When it comes to the protection of the Amazon, it’s hard for many people to relate because they don’t feel connected to the area. There are actually a lot of direct connections, no matter how far away we are.A connection that affects everyone on the planet is climate (气候) change. Planting new trees in the forest is basically a way of removing CO2 from the air. Rain forests have a carbon (碳) reduction nearly equal to half of what is in the air. About half of that is in the Amazon. Another case in point is a big snake called the bushmaster that lives in the Amazon. Today, millions of people use medicines made from its venom (毒液) to treat high blood pressure. So they have longer, fuller, and more productive lives.In the 1960s, there was only one highway in the entire Amazon. That’s an area as large as the continental United States with one highway and three million people. Today, there are between 30 million to 40 million people, countless roads, and about 20 percent forests have been cut down. But on the plus side, 50 years ago there were only two national parks and a national forest and a reserve in Brazil. Today, more than 50 percent of the Amazon is under some form of protection.“There’s been a lot of damage done and forest lost, but nothing is gone until it’s gone”, noted National Geographic explorer Dr. Thomas Lovejoy. “We want to see more shared planning between the departments of transportation, energy, agriculture, and the other industries in the area. We think Amazon cities can have higher quality of life and keep people in existing cities so there’s less reason to deforest.”8.Which can replace the underlined word “Deforestation” in paragraph 1?A.Planting more trees.B.Destroying the forests.C.Protecting the species.D.Polluting the rivers.9.What might the partial loss of the Amazon rainforest lead to?A.The increase of extreme weather.B.The removal of CO2.C.More people with high blood pressure.D.The overgrowth of the bushmaster. 10.How does paragraph 3 mainly develop?A.By making comparisons.B.By listing reasons.C.By explaining a definition.D.By making a summary.11.What is Dr. Thomas’ attitude towards the future of the Amazon rainforest?A.Doubtful.B.Worried.C.Positive.D.Uncaring.While screen time is known to affect sleep, new research suggests that interactive (互动的) activities, such as texting friends or playing video games, put off and reduce the time spent asleep to a greater degree than passive (被动的) screen time like watching television, especially for teens.The team studied the daytime screen-based activities of 475 teenagers using daily surveys. They asked the teens how many hours they had spent that day communicating with friends through social media and how many hours they spent playing video games, surfing the internet and watching television or videos. Finally, the researchers asked if they had joined in any of these activities in the hour before bed.Next, the team measured their sleep time for one week. The researchers found that the teens spent an average of two hours per day communicating with friends via social media, about 1.3 hours playing video games, less than an hour surfing the internet and about 1.7 hours watching television or videos. For every hour throughout the day that they used screens to communicate with friends, they fell asleep about 11 minutes later averagely. For every hour to play video games, they fell asleep about 9 minutes later. Those who talked, texted orplayed games in the hour before bed lost the most sleep: about 30 minutes later.Interestingly, David, lead author of the study, said the team found no obvious relations between passive screen-based activities and sleep. “It could be that passive activities are less mentally exciting than interactive activities,” said Anne, co-author of the study. “It’s a tricky situation,” she said. “These screen tools are really important to everyone nowadays, so it’s hard to put a limit on them, but if you’re really looking out for a teenager’s health and well-being, you might consider limiting the more interactive activities, especially in the hour before bed.”12.Which of the following belongs to interactive screen activities?A.Seeing movies.B.Watching videos.C.Texting friends.D.Surfing the internet.13.Who might lose the most sleep according to the text?A.Lucy who watched a three-hour movie before going to bed.B.Jack who had a 30-minute video chat with his brother before bed.C.Sam who played computer games for two hours throughout the day.D.Amy who chatted with her friends on WeChat for one hour in the morning. 14.What does the underlined word “tricky” mean in paragraph 4?A.Frightening.B.Awkward.C.Hopeless.D.Encouraging. 15.What can be a suitable title for the text?A.Screen time activities cut down our sleep hoursB.Interactive screen use reduces sleep time in teenagersC.Passive screen use is better than interactive screen useD.Parents should prevent children from using social mediaReading is a healthy habit that everyone should develop from childhood because of theThe following will discuss the effects of not reading books, so you can basically consider and judge where you are and understand how reading can be beneficial.17 People who don’t read and don’t like to read find it harder to learn than people who actually read. For example, most students who fail to develop a reading habit find it difficult to get through school. This then leads to students dropping out, which is bad for society. Reading is a habit that strengthens the brain and develops your inborn love ofwanting to learn more. Therefore, not being addicted to books closes you off from this.Narrow mindedness. Reading a variety of books broadens the readers’ mind. Most people who don’t read have a certain narrow mindedness to them that can easily be noticed.18 When you don’t read, you’re forced to take everything at face value and then create and shape your views in this way.Low brain power. One advantage of reading is its ability to improve brain function. Reading can help people become better thinkers and use brains more effectively. People who don’t read usually have low brain power because they don’t exercise the brain as much as readers do. 19Poor imagination. Reading books allows you to tap into your imaginative power. 20 This is important because it expands (拓展) your thought process as well as the ability to understand. People who don’t read books usually are short of the inspiration necessary to create imagination. This makes it difficult to be creative.A.Learning difficulty.B.The reason for this is simple.C.Such exercise strengthens the brain.D.Inability to fully understand the world.E.It then makes you picture what you read.F.It is developed slowly just as any habit would.G.The ability to read is important in today’s world.二、完形填空As Hallee gets to the finish line of the 800-metre run for kids, the crowd is cheeringWhen the twins were five, Jada decided that she wanted to be a(n) 27 . Her parents signed her up for Little Athletics, a track-and-field organisation for children. After watching Jada’s first training period, Hallee 28 her parents and said, “I can do that, too. Sign me up.” “Would she even be able to 29 ? Hallee doesn’t have feeling in her waist (腰) and lower legs,” thought her Dad, Gavin. 30 , Hallee’s parents had such strong belief in her that they signed her up.Hallee’s running wasn’t without its challenges. Her legs ached badly during and after races, and she 31 people would laugh at her. Her parents helped her work through her 32 by attending all her events.In fact, nobody laughed; people were shocked at her 33 . When asked what she would 34 to other children, Hallee offered two powerful suggestions: “Don’t 35 when people say you can’t do something. And try your best.”21.A.amazing B.funny C.embarrassing D.natural 22.A.melted B.broke C.stopped D.opened 23.A.waiting B.changing C.going D.thinking 24.A.aware B.eager C.afraid D.unable 25.A.suffered B.searched C.spoke D.read 26.A.harder B.better C.stronger D.heavier 27.A.designer B.engineer C.boxer D.runner 28.A.calmed down B.turned down C.referred to D.turned to 29.A.run B.walk C.jump D.dance 30.A.Instead B.However C.So D.Besides 31.A.feared B.learned C.accepted D.forgot 32.A.confusion B.curiosity C.confidence D.anxiety 33.A.determination B.creativity C.hobby D.imagination 34.A.bring B.say C.write D.add 35.A.compete B.cheat C.listen D.improve三、语法填空阅读下面短文,在空白处填入1个适当的单词或括号内单词的正确形式。
内蒙古呼和浩特市回民中学2024_2025学年高一语文上学期期末考试试题A卷

内蒙古呼和浩特市回民中学2024-2025学年高一语文上学期期末考试试题(A卷)(卷面分值:150分,考试时长:150分钟)一、现代文阅读(24分)(一)论述类文本阅读(本题共3小题,6分)阅读下面的文字,完成1-3题。
陶渊明——魏晋风流的杰出代表安贫乐道与崇尚自然,是陶渊明思索人生得出的两个主要结论,也是他人生的两大支柱和艺术化人生的详细表现。
“安贫乐道”是陶渊明的为人准则。
他所谓的“道”,偏重于个人的品德节操方面,体现了儒家思想。
他特殊推崇颜回、黔娄、袁安、荣启期等安贫乐道的贫士,要像他们那样努力保持品德节操的纯净,决不为追求高官厚禄而玷污自己。
他并不一般地鄙视出仕,而是不愿同流合污。
他希望建功立业,又要功成身退。
他也考虑贫富的问题,安贫和求富在他心中常常发生冲突,但是他能用“道”来求得平衡:“贫富常交战,道胜无戚颜。
”(《咏贫士》其五)而那些安贫乐道的古代贤人,也就成为他的榜样:“何以慰吾怀,赖古多此贤。
”。
(《咏贫士》其二)他的晚年很贫困,到了挨饿的程度,但是并没有丢失其为人的准则。
“崇尚自然”是陶渊明对人生更深刻的哲学思索。
“自然”一词不见于《论语》、《孟子》,而是老庄哲学特有的范畴。
老庄所谓“自然”不同于近代与人类社会相对而言的客观的物质性的“自然界”,它是一种状态,非人为的、原来如此的、自然而然的。
世间万物皆按其原来的面貌而存在,依其自身固有的规律而变更,无须任何外在的条件和力气。
人应当顺应自然的状态和变更,抱朴而含真。
陶渊明希望返归和保持自己原来的、未经世俗异化的、天真的性情。
所谓“质性自然、非矫厉所得。
”(《归去来兮辞序》),说明自己的质性自然如此,受不了绳墨的约束。
所谓“久在樊笼里,复得返自然”(《归园田居》其一),表达了返回自然得到自由的喜悦。
在《形影神》里,他让“神”辨自然以释“形”、“影”之苦。
“形”指代人企求长生的愿望,“影”指代人求善立名的愿望,“神”以自然之义化解它们的苦恼。
完整版)高一第一学期数学期末考试试卷(含答案)

完整版)高一第一学期数学期末考试试卷(含答案)高一第一学期期末考试试卷考试时间:120分钟注:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集U=R,集合A={x|3≤x<7},B={x|x^2-7x+10<0},则(A∩B)的取值为A。
(−∞,3)∪(5,+∞)B。
(−∞,3)∪[5,+∞)C。
(−∞,3]∪[5,+∞)D。
(−∞,3]∪(5,+∞)2.已知a⋅3^a⋅a的分数指数幂表示为A。
a^3B。
a^3/2C。
a^3/4D。
都不对3.下列指数式与对数式互化不正确的一组是A。
e=1与ln1=0B。
8^(1/3)=2与log2^8=3C。
log3^9=2与9=3D。
log7^1=0与7^1=74.下列函数f(x)中,满足“对任意的x1,x2∈(−∞,0),当x1f(x2)”的是A。
x^2B。
x^3C。
e^xD。
1/x5.已知函数y=f(x)是奇函数,当x>0时,f(x)=logx,则f(f(100))的值等于A。
log2B。
−1/lg2C。
lg2D。
−lg26.对于任意的a>0且a≠1,函数f(x)=ax^−1+3的图像必经过点(1,4/5)7.设a=log0.7(0.8),b=log1.1(0.9),c=1.10.9,则a<b<c8.下列函数中哪个是幂函数A。
y=−3x^−2B。
y=3^xC。
y=log_3xD。
y=x^2+1是否有模型能够完全符合公司的要求?原因是公司的要求只需要满足以下条件:当x在[10,1000]范围内时,函数为增函数且函数的最大值不超过5.参考数据为e=2.L,e的8次方约为2981.已知函数f(x)=1-2a-a(a>1),求函数f(x)的值域和当x 在[-2,1]范围内时,函数f(x)的最小值为-7.然后求出a的值和函数的最大值。
2023-2024学年广东省深圳中学高一学期期末数学试题及答案

深圳中学2023-2024学年度第一学期期末考试试题年级:高一 科目:数学参考:以10为底的对数叫常用对数,把10log N 记为lg N ;以()e e 2.718281828=⋯为底的对数叫自然对数,把e log N 记为ln N .一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 为了解某地区居民使用手机扫码支付的情况,拟从该地区的居民中抽取部分人员进行调查,事先已了解到该地区老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异,而男、女使用手机扫码支付的情况差异不大.在下面的抽样方法中,最合理的是( )A. 抽签法B. 按性别分层随机抽样C. 按年龄段分层随机抽样D. 随机数法2. 下列与7π4的终边相同的角的表达式中,正确的是( )A. ()2π315Z k k +∈B. ()36045Z k k ⋅-∈C ()7π360Z 4k k ⋅+∈D. ()5π2πZ 4k k +∈3. 角α的终边与单位圆O 相交于点P ,且点P 的横坐标为35的值为( )A.35B. 35-C.45 D. 45-4. 已知角()0,πα∈,且1cos 23α=,则sin α的值为( )A.B.C.D. 5. 健康成年人的收缩压和舒张压一般为90~139mmhg 和60~89mmhg ,心脏跳动时,血压在增加或减小,血压的最大值、最小值分别为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数为120/80mmhg 为标准值.设某人的血压满足函数式()11525sin(160π)P t t =+,其中()P t 为血压(mmhg ),t 为时间(min ).给出以下结论:①此人血压在血压计上的读数为140/90mmhg ②此人的血压在健康范围内③此人的血压已超过标准值④此人的心跳为80次/分.的其中正确结论的个数为( )A. 1B. 2C. 3D. 46. 孩子在成长期间最需要父母的关爱与陪伴,下表为2023年中国父母周末陪孩子日均时长统计图.根据该图,下列说法错误的是( )A. 2023年母亲周末陪伴孩子日均时长超过8小时的占比大于13B. 2023年父亲周末陪伴孩子日均时长超过6小时占比大于12C. 2023年母亲周末陪伴孩子日均时长的5个时段占比的极差为28.8%D. 2023父母周末陪伴孩子日均时长10个时段占比的中位数为20.2%7. 将函数()2sin f x x =图象上所有点横坐标缩小为原来的12,再向右平移π6个单位长度,得到函数()g x 的图象,若()0g x a -=在π0,2⎡⎤⎢⎥⎣⎦上有两个不同的零点1x ,2x ,则()12tan x x +=( )A.B.C.D. 8. 如果对于任意整数πππ,sin,cos ,tan n n n n k k k都是有理数,我们称正整数k 是“好整数”,下面的整数中哪个是最大的“好整数”( )A. 1B. 2C. 3D. 4二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.的的的9. 下列说法中正确的是( )A. 度与弧度是度量角的两种不同的度量单位B. 1度的角是周角的1360,1弧度的角是周角的12πC. 根据弧度的定义,180︒一定等于π弧度D. 不论是用角度制还是用弧度制度量角,角的大小均与圆的半径长短有关10. 下列各式中,值是12的是( )A. ππc s cos sin os n 3i 3x x x x ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭ B. tan10tan 35tan10tan 35︒+︒+︒︒C.2tan 22.51tan 22.5︒-︒D.22cos 203sin 50-︒-︒11. 2023年是共建“一带一路”倡议提出十周年.某校组织了“一带一路”知识竞赛,将学生的成绩(单位:分,满分:120分)整理成如图的频率分布直方图(同一组中的数据用该组区间的中点值为代表),则( )A. 该校竞赛成绩的极差为70分B. a 的值为0.005C. 该校竞赛成绩的平均分的估计值为90.7分D. 这组数据的第30百分位数为8112. 在平面直角坐标系中,已知角α的顶点与坐标原点重合,始边与x 轴的非负半轴重合,终边经过点ππsin ,cos 33⎛⎫- ⎪⎝⎭,()cos sin 2sin cos 2f x x x αα=-则下列结论正确的是( )A. 11cos 22α-=B. 2π3x =是()y f x =的图象的一条对称轴C. 将函数()y f x =图象上的所有点向左平移5π6个单位长度,所得到的函数解析式为sin 2y x=D. ()y f x =在4π0,3⎛⎫⎪⎝⎭内恰有3个零点三、填空题:本题共4小题,每小题5分,共20分.13. 某班级有50名同学,一次数学测试平均成绩是92分,如果30名男生的平均成绩为90分,那么20名女生的平均成绩为____分.14. 已知1cos 7α=,()sin αβ+=,π02α<<,π02β<<,则cos β=________.15. 已知函数()()πsin 0,02f x x ωϕωϕ⎛⎫=+>≤≤⎪⎝⎭是R 上的奇函数,其图象关于点3,04A π⎛⎫⎪⎝⎭对称,且在区间0,4⎡⎤⎢⎥⎣⎦π上是单调函数,则ω的值为______.16. cos()cos cos 1y αβαβ=++--的取值范围是_________.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 已知()()()()3πsin πcos 2πcos 2.πcos sin π2f αααααα⎛⎫--- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭(1)化简()f α;(2)若α是第三象限角,且()1sin π5α-=,求()f α的值.18. 据调查,某市政府为了鼓励居民节约用水,减少水资源的浪费,计划在本市试行居民生活用水定额管理,即确定一个合理的居民用水量标准x (单位:吨),月用水量不超过x 的部分按平价收费,超出x 的部分按议价收费.为了了解全市居民用水量分布情况,通过抽样,获得了n 户居民某年的月均用水量(单位:吨),其中月均用水量在(]9,12内的居民人数为39人,并将数据制成了如图所示的频率分布直方图.(1)求a 和n 的值;(2)若该市政府希望使80%的居民月用水量不超过标准x 吨,试估计x 的值;(3)在(2)的条件下,若实施阶梯水价,月用水量不超过x 吨时,按3元/吨计算,超出x 吨的部分,按5元/吨计算.现市政府考核指标要求所有居民的月用水费均不超过70元,则该市居民月用水量最多为多少吨?19. 已知函数()()2πcos 2cos f x x x x =-+.(1)若ππ,63x ⎡⎤∈-⎢⎥⎣⎦,求函数()f x 的值域;(2)若函数()()1g x f x =-在区间π,6m ⎡⎤-⎢⎥⎣⎦上有且仅有两个零点,求m 的取值范围.20. 某生物研究者于元旦在湖中放入一些凤眼莲(其覆盖面积为k ),这些凤眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲的覆盖面积为224m ,三月底测得凤眼莲的覆盖面积为236m ,凤眼莲的覆盖面积y (单位:2m )与月份x (单位:月)的关系有两个函数模型()0,1xy ka k a =>>与()120,0y px k p k =+>>可供选择.(1)试判断哪个函数模型更合适并求出该模型的解析式;(2)求凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份.(参考数据:lg 20.3010,lg 30.4711≈≈).21. 已知函数()()sin (0,0π)f x x ωϕωϕ=+><<的最小正周期为π,且直线π2x =-是其图象的一条对称轴.(1)求函数()f x 的解析式;(2)将函数()y f x =的图象向右平移π4个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图象对应的函数记作()y g x =,已知常数*,n λ∈∈R N ,且函数()()()F x f x g x λ=+在()0,πn 内恰有2023个零点,求常数λ与n 的值.22. 已知二次函数()f x 满足:()()224132,log 231x f x x x g x ⎛⎫+=++=+⎪-⎝⎭(1)求()f x 的解析式;(2)求()g x 的单调性与值域(不必证明);(3)设()ππ2cos cos2,22h x x m x x ⎛⎫⎡⎤=+∈-⎪⎢⎥⎣⎦⎝⎭,若()()f h x g h x ⎡⎤⎡⎤≥⎣⎦⎣⎦,求实数m 的值.深圳中学2023-2024学年度第一学期期末考试试题年级:高一 科目:数学参考:以10为底的对数叫常用对数,把10log N 记为lg N ;以()e e 2.718281828=⋯为底的对数叫自然对数,把e log N 记为ln N .一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 为了解某地区居民使用手机扫码支付的情况,拟从该地区的居民中抽取部分人员进行调查,事先已了解到该地区老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异,而男、女使用手机扫码支付的情况差异不大.在下面的抽样方法中,最合理的是( )A 抽签法B. 按性别分层随机抽样C. 按年龄段分层随机抽样D. 随机数法【答案】C 【解析】【分析】根据抽样方法确定正确答案.【详解】依题意,“居民人数多”, “男、女使用手机扫码支付的情况差异不大”,“老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异”,所以最合理的是按年龄段分层随机抽样.故选:C 2. 下列与7π4的终边相同的角的表达式中,正确的是( )A. ()2π315Z k k +∈B. ()36045Z k k ⋅-∈C. ()7π360Z 4k k ⋅+∈D. ()5π2πZ 4k k +∈【答案】B 【解析】【分析】AC 项角度与弧度混用,排除AC ;D 项终边在第三象限,排除D.【详解】因为7πrad 3154= ,终边落在第四象限,且与45- 角终边相同,故与7π4终边相同的角的集合.的{}{}31536045360S k k αααα==+⋅==-+⋅即选项B 正确;选项AC 书写不规范,选项D 表示角终边在第三象限.故选:B.3. 角α的终边与单位圆O 相交于点P ,且点P 的横坐标为35的值为( )A.35B. 35-C.45 D. 45-【答案】A 【解析】【分析】利用三角函数定义以及同角三角函数之间的平方关系即可得出结果.【详解】根据三角函数定义可知3cos 5α=,又22sin cos 1αα+=53cos α===.故选:A4. 已知角()0,πα∈,且1cos 23α=,则sin α的值为( )A.B.C. D. 【答案】B 【解析】【分析】根据余弦的二倍角公式即可求解.【详解】因为21cos 212sin3αα=-=,所以sin α=,因为()0,πα∈,所以sin α=.故选:B .5. 健康成年人的收缩压和舒张压一般为90~139mmhg 和60~89mmhg ,心脏跳动时,血压在增加或减小,血压的最大值、最小值分别为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数为120/80mmhg为标准值.设某人的血压满足函数式()11525sin(160π)P t t =+,其中()P t 为血压(mmhg ),t 为时间(min ).给出以下结论:①此人的血压在血压计上的读数为140/90mmhg ②此人的血压在健康范围内③此人的血压已超过标准值 ④此人的心跳为80次/分其中正确结论的个数为( )A. 1 B. 2 C. 3 D. 4【答案】C 【解析】【分析】根据所给函数解析式及正弦函数的性质求出()P t 的取值范围,即可得到此人的血压在血压计上的读数,从而判断①②③,再计算出最小正周期,即可判断④.【详解】因为某人的血压满足函数式()11525sin(160π)P t t =+,又因为1sin(160π)1t -≤≤,所以11525()11525P t -≤≤+,即90()140P t ≤≤,即此人的血压在血压计上的读数为140/90mmhg ,故①正确;因为收缩压为140mmhg ,舒张压为90mmhg ,均超过健康范围,即此人的血压不在健康范围内,故②错误,③正确;对于函数()11525sin(160π)P t t =+,其最小正周期2π1160π80T ==(min ),则此人的心跳为180T=次/分,故④正确;故选:C6. 孩子在成长期间最需要父母的关爱与陪伴,下表为2023年中国父母周末陪孩子日均时长统计图.根据该图,下列说法错误的是( )A. 2023年母亲周末陪伴孩子日均时长超过8小时的占比大于13B. 2023年父亲周末陪伴孩子日均时长超过6小时的占比大于12C. 2023年母亲周末陪伴孩子日均时长的5个时段占比的极差为28.8%D. 2023父母周末陪伴孩子日均时长的10个时段占比的中位数为20.2%【答案】C 【解析】【分析】根据题意结合统计相关知识逐项分析判断.【详解】由题图可知:2023年母亲周末陪伴孩子日均时长超过8小时的占比为138.7%3>,A 说法正确;2023年父母周末陪伴孩子日均时长超过6小时的占比为131.5%24.2%55.7%2+=>,B 说法正确;2023年母亲周末陪伴孩子日均时长的5个时段占比的极差为38.7% 2.5%36.2%-=,C 说法错误;2023年父母周末陪伴孩子日均时长的10个时段占比的中位数为21.4%19.0%20.2%2+=,D 说法正确.故选:C .7. 将函数()2sin f x x =图象上所有点的横坐标缩小为原来的12,再向右平移π6个单位长度,得到函数()g x 的图象,若()0g x a -=在π0,2⎡⎤⎢⎥⎣⎦上有两个不同的零点1x ,2x ,则()12tan x x +=( )A.B. C.D. 【答案】B 【解析】【分析】根据函数图象的变换可得()π2sin 23g x x ⎛⎫=-⎪⎝⎭,即可结合正弦函数的对称性得12πt t +=,进而125π6x x +=,即可求解.【详解】将函数()2sin f x x =图象上所有点的横坐标缩小为原来的12,得到2sin 2y x =的图象,再向右平移π6个单位长度,得到()ππ2sin 22sin 263g x x x ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭的图象.当π0,2x ⎡⎤∈⎢⎥⎣⎦时,ππ2π2,333x ⎡⎤-∈-⎢⎥⎣⎦,令π23x t -=,π2π,33t ⎡⎤∈-⎢⎥⎣⎦,则关于t 的方程2sin t a =在π2π,33-⎡⎤⎢⎥⎣⎦上有两个不等的实数根1t ,2t ,所以12πt t +=,即12ππ22π33x x -+-=,则125π6x x +=,所以()125πtan tan 6x x +==.故选:B8. 如果对于任意整数πππ,sin,cos ,tan n n n n k k k都是有理数,我们称正整数k 是“好整数”,下面的整数中哪个是最大的“好整数”( )A. 1 B. 2C. 3D. 4【答案】A 【解析】【分析】利用三角函数定义域代入选项逐个验证即可得出结论.【详解】考虑三角函数的定义域,对于选项A ,当1k =时,sin π,cos π,tan πn n n 对于任意整数n ,都是整数,满足题意;对于B ,当2k =时,2ππtantan n n k =对于整数1,没有意义,不满足题意;同理可得对于C 和D ,当3ππtantan n n k =或4ππtan tan n n k =时,代入验证可知不满足题意;所以可知最大“好整数”为1故选:A二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9. 下列说法中正确的是( )A. 度与弧度是度量角的两种不同的度量单位B. 1度的角是周角的1360,1弧度的角是周角的12πC. 根据弧度的定义,180︒一定等于π弧度D. 不论是用角度制还是用弧度制度量角,角的大小均与圆的半径长短有关【答案】ABC 【解析】【分析】根据角度制与弧度制的定义,以及角度制和弧度制的换算公式,以及角的定义,逐项判定,即可求解.【详解】根据角度制和弧度制的定义可知,度与弧度是度量角的两种不同的度量单位,所以A 正确;由圆周角的定义知,1度的角是周角的1360,1弧度的角是周角的12π,所以B 正确;根据弧度的定义知,180︒一定等于π弧度,所以C 正确;无论是用角度制还是用弧度制度量角,角的大小均与圆的半径长短无关,只与弧长与半径的比值有关,故D 不正确.故选:ABC.10. 下列各式中,值是12的是( )A. ππc s cos sin os n 3i 3x x x x ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭ B. tan10tan 35tan10tan 35︒+︒+︒︒C.2tan 22.51tan 22.5︒-︒D.22cos 203sin 50-︒-︒【答案】ACD 【解析】【分析】利用两角差的余弦公式,诱导公式,二倍角公式即可逐个选项判断.【详解】ππc s cos sin os n 3i 3x x x x ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭ππ1cos cos 332x x ⎛⎫=--== ⎪⎝⎭,A 正确;tan10tan 35tan10tan 35︒+︒+︒︒()()tan 10351tan10tan 35tan10tan 35=︒+︒-︒︒+︒︒tan 451=︒=,B 不对;22tan 22.512tan 22.511tan 451tan 22.521tan 22.522︒︒==︒=-︒-︒,C 正确;()2311cos 403sin502cos 2012223sin 503sin503sin502-︒-︒-︒===-︒-︒-︒,D 正确.故选:ACD11. 2023年是共建“一带一路”倡议提出十周年.某校组织了“一带一路”知识竞赛,将学生的成绩(单位:分,满分:120分)整理成如图的频率分布直方图(同一组中的数据用该组区间的中点值为代表),则( )A. 该校竞赛成绩的极差为70分B. a 的值为0.005C. 该校竞赛成绩的平均分的估计值为90.7分D. 这组数据的第30百分位数为81【答案】BC【解析】【分析】利用频率分布直方图,用样本估计总体,样本的极差、平均值、百分位数相关知识计算即可.【详解】因为由频率分布直方图无法得出这组数据的最大值与最小值,所以这组数据的极差可能为70,也可能为小于70的值,所以A 错误;因为(0.00820.0120.01540.030)10700.651a a a a ++++++⨯=+=,解得0.005a =,所以B 正确;该校竞赛成绩的平均分的估计值550.00510650.00810x =⨯⨯+⨯⨯+750.01210850.01510950.03010⨯⨯+⨯⨯+⨯⨯10540.0051011520.0051090.7+⨯⨯⨯+⨯⨯⨯=分,所以C 正确.设这组数据的第30百分位数为m ,则(0.0050.0080.012)10(80)0.015100.3m ++⨯+-⨯⨯=,解得2413m =,所以D 错误.故选:BC .12. 在平面直角坐标系中,已知角α的顶点与坐标原点重合,始边与x 轴的非负半轴重合,终边经过点ππsin ,cos 33⎛⎫- ⎪⎝⎭,()cos sin 2sin cos 2f x x x αα=-则下列结论正确的是( )A. 11cos 22α-=B. 2π3x =是()y f x =的图象的一条对称轴C. 将函数()y f x =图象上的所有点向左平移5π6个单位长度,所得到的函数解析式为sin 2y x=D. ()y f x =在4π0,3⎛⎫⎪⎝⎭内恰有3个零点【答案】AB 【解析】【分析】利用三角函数的定义求得α,从而得到()f x 的解析式,进而利用三角函数的性质与平移的结论,逐一分析各选项即可得解.【详解】因为ππ1sin ,cos 332⎛⎫⎛⎫-= ⎪ ⎪ ⎪⎝⎭⎝⎭,所以由三角函数的定义得1sin 2α=,cos α=,所以5π2π,6k k α∈=+Z ,则()()cos sin 2sin cos 2sin 2f x x x x ααα=-=-5π5πsin 22πsin 2,66x k x k ∈⎛⎫⎛⎫=--=- ⎪ ⎪⎝⎭⎝⎭Z ,A : 22111cos 22sin 222αα⎛⎫-==⨯= ⎪⎝⎭,故A 正确;B :因为5π62π4ππsin sin 1332f ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭,所以2π3x =是()y f x =的图象的一条对称轴,故B 正确;C :将函数()y f x =图象上的所有点向左平移5π6个单位长度,所得到的函数解析式为5π5πsin 2sin 2665π6y x x ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故C 错误;D :令()0f x =,得5πsin 206x ⎛⎫-= ⎪⎝⎭,解得5π5ππ2π,,6122k x k k x k ∈∈-=⇒=+Z Z ,仅0k =,1,即5π11π,1212x =符合题意,即()y f x =在4π0,3⎛⎫⎪⎝⎭内恰有两个零点,故D 错误.故选:AB三、填空题:本题共4小题,每小题5分,共20分.13. 某班级有50名同学,一次数学测试平均成绩是92分,如果30名男生的平均成绩为90分,那么20名女生的平均成绩为____分.【答案】95【解析】【分析】利用平均数的求法计算即可.【详解】设所求平均成绩为x ,由题意得5092309020x ⨯=⨯+⨯,∴95x =.故答案为:9514. 已知1cos 7α=,()sin αβ+=,π02α<<,π02β<<,则cos β=________.【答案】12##0.5【解析】【分析】根据题意,分别求得()sin ,cos ααβ+,再由余弦的差角公式,代入计算,即可得到结果.【详解】因为π02α<<且11cos c 2πos 73α=<=,则ππ32α<<,又02βπ<<,所以π3παβ<+<,且()sin αβ+=<,所以π2π3αβ<+<,则()11cos 14αβ+==-,sin α==,所以()()()cos cos cos cos sin sin βαβααβααβα=+-=+++⎡⎤⎣⎦11111472=-⨯+=.故答案为:1215. 已知函数()()πsin 0,02f x x ωϕωϕ⎛⎫=+>≤≤⎪⎝⎭是R 上的奇函数,其图象关于点3,04A π⎛⎫⎪⎝⎭对称,且在区间0,4⎡⎤⎢⎥⎣⎦π上是单调函数,则ω的值为______.【答案】43【解析】【分析】由函数为奇函数,得0ϕ=,再根据函数图像关于点3,04A π⎛⎫⎪⎝⎭对称,可知43kω=,根据函数的单调性可得04ω<≤,进而得解.【详解】因为函数()()sin 0,02f x x πωϕωϕ⎛⎫=+>≤≤ ⎪⎝⎭是R 上的奇函数,则()()f x f x -=-,即sin cos cos sin x x ϕωωϕ=-,又因为0ω>,所以sin 0ϕ=,因为π02ϕ≤≤,所以0ϕ=;故()sin f x x ω=;又因为图象关于点3π,04A ⎛⎫⎪⎝⎭对称,则3ππ4k ω=,Z k ∈,所以43k ω=,Z k ∈,因为函数在区间π0,4⎡⎤⎢⎥⎣⎦上是单调函数,则12ππ24ω⨯≥,得04ω<≤;所以43ω=,故答案为:43.16. cos()cos cos 1y αβαβ=++--取值范围是_________.【答案】1[4,]2-【解析】【分析】由和角的余弦公式变形给定函数,再利用辅助角公式变形,结合正弦函数的性质用含cos β的关系式表示y ,再借助二次函数最值求解即得.【详解】cos cos sin sin cos cos 1y αβαβαβ=-+--(cos 1)cos (sin )sin (cos 1)βαβαβ=+--+)(cos 1)αϕβ=+-+)(cos 1)αϕβ=+-+由sin()[1,1]αϕ+∈-,得(cos 1)(cos 1)y ββ-+≤≤+,令t =,则t ∈,则22t y t ≤≤--,所以221(42y t t ≥-=-+≥-,当且仅当t =,即cos 1β=时取等号,且2211(22y t t ≤-=-+≤,当且仅当t =,即1cos 2β=-时取等号,的所以y 的取值范围为1[4,]2-.故答案为:1[4,]2-四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17. 已知()()()()3πsin πcos 2πcos 2.πcos sin π2f αααααα⎛⎫--- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭(1)化简()f α;(2)若α是第三象限角,且()1sin π5α-=,求()f α的值.【答案】(1)()cos f αα=-(2【解析】【分析】(1)利用诱导公式化简即可;(2)利用诱导公式及同角三角函数的关系计算即可.【小问1详解】因为()()()()3πsin πcos 2πcos 2πcos sin π2f αααααα⎛⎫--- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭()sin cos sin cos sin sin αααααα⋅⋅-==-⋅,所以()cos fαα=-.【小问2详解】由诱导公式可知()1sin πsin 5αα-=-=,即1sin 5α=-,又α是第三象限角,所以cos α===所以()cos fαα=-=.18. 据调查,某市政府为了鼓励居民节约用水,减少水资源的浪费,计划在本市试行居民生活用水定额管理,即确定一个合理的居民用水量标准x (单位:吨),月用水量不超过x 的部分按平价收费,超出x 的部分按议价收费.为了了解全市居民用水量分布情况,通过抽样,获得了n 户居民某年的月均用水量(单位:吨),其中月均用水量在(]9,12内的居民人数为39人,并将数据制成了如图所示的频率分布直方图.(1)求a 和n 的值;(2)若该市政府希望使80%的居民月用水量不超过标准x 吨,试估计x 的值;(3)在(2)的条件下,若实施阶梯水价,月用水量不超过x 吨时,按3元/吨计算,超出x 吨的部分,按5元/吨计算.现市政府考核指标要求所有居民的月用水费均不超过70元,则该市居民月用水量最多为多少吨?【答案】(1)1300a =,200n = (2)16.6吨 (3)20.64吨【解析】【分析】(1)频率分布直方图总面积为1,由此即可求解.(2)先判断所求值所在的区间,再按比例即可求解.(3)按题意列不等式即可求解.【小问1详解】()0.0150.0250.0500.0650.0850.0500.0200.0150.00531a +++++++++⨯= ,1.300a ∴=用水量在(]9,12频率为0.06530.195⨯=,392000.195n ∴==(户)【小问2详解】()0.0150.0250.0500.0650.08530.720.8++++⨯=< ,()0.0150.0250.0500.0650.0850.05030.870.8+++++⨯=>,0.800.7215316.60.870.72-∴+⨯=-(吨)【小问3详解】设该市居民月用水量最多为m 吨,因为16.6349.870⨯=<,所以m 16.6>,则()16.6316.6570w m =⨯+-⨯≤,解得20.64m ≤,答:该市居民月用水量最多为20.64吨.19. 已知函数()()2πcos 2cos f x x x x =-+.(1)若ππ,63x ⎡⎤∈-⎢⎥⎣⎦,求函数()f x 的值域;(2)若函数()()1g x f x =-在区间π,6m ⎡⎤-⎢⎥⎣⎦上有且仅有两个零点,求m 的取值范围.【答案】(1)[]0,3(2)5π11π,1212⎡⎫⎪⎢⎣⎭【解析】【分析】(1)利用诱导公式以及二倍角公式化简可得()f x 的表达式,结合ππ,63x ⎡⎤∈-⎢⎥⎣⎦,确定π26x +的范围,即可求得答案;(2)由π,6x m ⎡⎤∈-⎢⎥⎣⎦,确定πππ2[,2666x m +∈-+,根据()g x 在区间π,6m ⎡⎤-⎢⎥⎣⎦上有且仅有两个零点,结合正弦函数的零点,列出相应不等式,即求得答案.【小问1详解】由题意得()()2πcos 2cos f x x x x=-+的πcos 212sin 216x x x ⎛⎫=++=++ ⎪⎝⎭,当ππ,63x ⎡⎤∈-⎢⎥⎣⎦,则ππ5π2[,666x +∈-,则1πsin 2126x ⎛⎫-≤+≤ ⎪⎝⎭,则π02sin 2136x ⎛⎫≤++≤ ⎪⎝⎭,即函数()f x 的值域为[]0,3;【小问2详解】由题可得π6m >-,当π,6x m ⎡⎤∈-⎢⎥⎣⎦时,πππ2[,2666x m +∈-+,()()π2sin 216g x x f x ⎛⎫+ ⎪⎝=-⎭=,且()g x 在区间π,6m ⎡⎤-⎢⎥⎣⎦上有且仅有两个零点,而sin y x =在π[,2π)6-有且仅有2个零点,分别为0,π,故π5π11ππ22π,61212m m ≤+<∴≤<,即5π11π,1212m ⎡⎫∈⎪⎢⎣⎭.20. 某生物研究者于元旦在湖中放入一些凤眼莲(其覆盖面积为k ),这些凤眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲的覆盖面积为224m ,三月底测得凤眼莲的覆盖面积为236m ,凤眼莲的覆盖面积y (单位:2m )与月份x (单位:月)的关系有两个函数模型()0,1x y ka k a =>>与()120,0y px k p k =+>>可供选择.(1)试判断哪个函数模型更合适并求出该模型的解析式;(2)求凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份.(参考数据:lg 20.3010,lg 30.4711≈≈).【答案】(1)选择模型()0,1x y ka k a =>>符合要求,*32323N 2,11,xy x x ⎛⎫=⋅ ⎪⎝≤≤∈⎭ (2)六月份【解析】【分析】(1)根据指数函数与幂函数的增长速度即可选得哪一个模型,再利用待定系数法即可求出该模型的解析式;(2)由(1)结合已知可得3233210323x ⎛⎫⋅>⨯ ⎪⎝⎭,再结合已知数据即可得出答案.【小问1详解】函数()0,1x y ka k a =>>与()120,0y pxk p k =+>>在()0,∞+上都是增函数,随着x 的增加,函数()0,1x y kak a =>>的值增加的越来越快,而函数()120,0y px k p k =+>>的值增加的越来越慢,由于凤眼莲在湖中的蔓延速度越来越快,因此选择模型()0,1x y kak a =>>符合要求,根据题意可知2x =时,24y =;3x =时,36y =,所以232436ka ka ⎧=⎨=⎩,解得32323a k ⎧=⎪⎪⎨⎪=⎪⎩,故该函数模型的解析式为*32323N 2,11,x y x x ⎛⎫=⋅ ⎪⎝≤≤∈⎭;【小问2详解】当0x =时,323y =,元旦放入凤眼莲的覆盖面积是232m 3,由3233210323x ⎛⎫⋅>⨯ ⎪⎝⎭,得3102x ⎛⎫> ⎪⎝⎭,所以32lg1011log 10 5.93lg 3lg 20.47110.3010lg 2x >==≈≈--,又*N x ∈,所以6x ≥,即凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份是六月份.21. 已知函数()()sin (0,0π)f x x ωϕωϕ=+><<的最小正周期为π,且直线π2x =-是其图象的一条对称轴.(1)求函数()f x 的解析式;(2)将函数()y f x =的图象向右平移π4个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图象对应的函数记作()y g x =,已知常数*,n λ∈∈R N ,且函数()()()F x f x g x λ=+在()0,πn 内恰有2023个零点,求常数λ与n 的值.【答案】(1)()cos2f x x =(2)1,1349n λ==【解析】【分析】(1)由周期求得ω,再由对称性求得ϕ得解析式;(2)由图象变换求得()g x ,然后可得()F x 的表达式,令[]sin 1,1t x =∈-,()0F x =化为22210,Δ80t t λλ--==+>,则关于t 的二次方程2210t t λ--=必有两不等实根12t t 、,则1212t t =-,则12t t 、异号,然后分类讨论()0F x =在(0,π)n 上解的个数后得出结论.【小问1详解】由三角函数的周期公式可得()()2π2,sin 2πf x x ωϕ==∴=+,令()π2π2x k k Z ϕ+=+∈,得()ππ422k x k Z ϕ=-+∈,由于直线π2x =-为函数()y f x =的一条对称轴,所以,()πππZ 2422k k ϕ-=-+∈,得()3ππZ 2k k ϕ=+∈,由于0π,1k ϕ<<∴=-,则π2ϕ=,因此,()πsin 2cos22f x x x ⎛⎫=+= ⎪⎝⎭;小问2详解】将函数()y f x =的图象向右平移π4个单位,得到函数ππcos 2cos 2sin242y x x x ⎡⎤⎛⎫⎛⎫=-=-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍后所得到的图象对应的函数为()sin g x x =,()()()2cos2sin 2sin sin 1F x f x g x x x x x λλλ=+=+=-++ ,令()0F x =,可得22sin sin 10x x λ--=,令[]sin 1,1t x =∈-,得22210,Δ80t t λλ--==+>,【则关于t 的二次方程2210t t λ--=必有两不等实根12t t 、,则1212t t =-,则12t t 、异号,(i )当101t <<且201t <<时,则方程1sin x t =和2sin x t =在区间()()*0,πNn n ∈均有偶数个根,从而方程22sin sin 10x x λ--=在()()*0,πNn n ∈也有偶数个根,不合乎题意;(ii )当11t =-时,则212t =,当()0,2πx ∈时,1sin x t =只有一根,2sin x t =有两根,所以,关于x 的方程22sin sin 10x x λ--=在()0,2π上有三个根,由于202336741=⨯+,则方程22sin sin 10x x λ--=在()0,1348π上有36742022⨯=个根,由于方程1sin x t =在区间()1348π,1349π上无实数根,方程2sin x t =在区间()1348π,1349π上有两个实数解,因此,关于x 的方程22sin sin 10x x λ--=在区间()0,1349π上有2024个根,不合乎题意,(iii )当11t =,则212t =-,当()0,2πx ∈时,1sin x t =只有一根,2sin x t =有两根,所以,关于x 的方程22sin sin 10x x λ--=在()0,2π上有三个根,由于202336741=⨯+,则方程22sin sin 10x x λ--=在()0,1348π上有36742022⨯=个根,由于方程1sin x t =在区间()1348π,1349π上只有一个根,方程2sin x t =在区间()1348π,1349π上无实数解,因此,关于x 的方程22sin sin 10x x λ--=在区间()0,1349π上有2023个根,合乎题意;此时,1122λ-+=,1λ=,综上所述:1,1349n λ==.22. 已知二次函数()f x 满足:()()224132,log 231x f x x x g x ⎛⎫+=++=+ ⎪-⎝⎭(1)求()f x 的解析式;(2)求()g x 的单调性与值域(不必证明);(3)设()ππ2cos cos2,22h x x m x x ⎛⎫⎡⎤=+∈- ⎪⎢⎥⎣⎦⎝⎭,若()()f h x g h x ⎡⎤⎡⎤≥⎣⎦⎣⎦,求实数m 的值.【答案】(1)()2f x x x =+ (2)在()0,∞+上单调递减,值域是()1,+∞.(3)1-【解析】【分析】(1)利用换元法,令1t x =+,代入化简即可求出函数的解析式;(2)可设4231x u =+-,利用复合函数的单调性,即可判定函数的单调性,进而求得值域;(3)由(2)知,()12g =,()12f =,结合()(),f x g x 的单调性可知当1x ≥时,()()2,01f x g x x ≥≥<<时,()()2f x g x <<,由()()f h x g h x ⎡⎤⎡⎤≥⎣⎦⎣⎦恒成立,即为()1h x ≥恒成立,设[]cos 0,1x t =∈,只需不等式()22210mt t m +-+≥在[]0,1t ∈上恒成立,讨论m 的取值范围即可求解.【小问1详解】由题意()2132f x x x +=++,令1t x =+,则1x t =-,有()()22(1)312f t t t t t =-+-+=+,故()2f x x x =+【小问2详解】函数()24log 231x g x ⎛⎫=+⎪-⎝⎭,由420031x x +>⇒>-,即定义域为()0,∞+,且4231x u =+-在()0,∞+上单调递减及2log y u =单调递增所以()24log 231x g x ⎛⎫=+ ⎪-⎝⎭在()0,∞+上单调递减.因为()0,x ∞∈+,42231x u =+>-,所以()g x 的值域是()1,∞+【小问3详解】结合(2)结论知()24log 231x g x ⎛⎫=+⎪-⎝⎭在()0,∞+上单调递减且()12g =,又()2f x x x =+在()0,∞+上单调递增且()12f =故当1x ≥时,()()2,01f xg x x ≥≥<<时,()()2f x g x <<,由()()()1f h x g h x h x ⎡⎤⎡⎤≥⇒≥⎣⎦⎣⎦恒成立,即()22cos 2cos 11x m x +-≥在ππ,22x ⎡⎤∈-⎢⎥⎣⎦上恒成立,设[]cos 0,1x t =∈,则不等式()22210mt t m +-+≥在[]0,1t ∈上恒成立,①当0m =时,不等式化为210t -≥,显然不满足恒成立;②当0m >时,将0=t 代入得()10m -+≥,与0m >矛盾;③当0m <时,只需()()10,1,12210,1,m m m m m m ⎧-+≥≤-⎧⎪⇒⇒=-⎨⎨+-+≥≥-⎪⎩⎩,综上,实数m 的值为-1.【点睛】关键点点睛:本题考查了换元法求函数的解析式,函数的单调性,解题的关键是根据函数的单调性得出()1h x ≥,转化为二次不等式恒成立,考查了分类讨论的思想.。
北京市海淀区2023-2024学年高一上学期期末考试 数学 Word版含答案

海淀区高一年级练习数 学考生须知:1.本试卷共6页,共三道大题,26道小题,满分150分,考试时间120分钟.2.在试卷上准确填写学校名称、班级名称、姓名.3.答案一律填涂或书写在答题卡上,用黑色字迹签字笔作答.4.考试结束,请将本试卷交回.一、选择题:共14小题,每小题4分,共56分.在每小题列出的四个选项中,选出符合题目要求的一项1.已知全集{}2,1,0,1,2U =--,集合{}2,1,0A =--,则U A = ( )A .{}1,2,3B .{}1,2C .()0,2D .()1,22.某学校有高中学生1500人,初中学生1000人.学生社团创办文创店,想了解初高中学生对学校吉祥物设计的需求,用分层抽样的方式随机抽取若干人进行问卷调查,已知在初中学生中随机抽取了100人,则在高中学生中抽取了( )A .150人B .200人C .250人D .300人3.命题“,20x x ∃∈+≤R ”的否定是( )A .,20x x ∃∈+>RB .,20x x ∃∈+<RC .,20x x ∀∈+>RD .,20x x ∀∈+<R 4.方程组202x y x x +=⎧⎨+=⎩解集是( )A .()(){}1,1,1,1--B .()(){}1,1,2,2-C .()(){}1,1,2,2--D .()(){}2,2,2,2-- 5.某部门调查了200名学生每周的课外活动时间(单位:h ),制成了如图所示的频率分布直方图,其中课外活动时间的范围是[]10,20,并分成[)[)[)[)[]10,12,12,14,14,16,16,18,18,20五组.根据直方图,判断这200名学生中每周的课外活动时间不少于14h 的人数是( )A .56B .80C .144D .1846.若实数a ,b 满足a b >,则下列不等式成立的是( )A .a b >B .a c b c +>+C .22a b >D .22ac bc >7.函数()22x f x x =+的零点所在的区间为( )A .()2,1--B .()1,0-C .()0,1D .()1,28.在同一个坐标系中,函数()()()log ,,x a a f x x g x a h x x -===的部分图象可能是( )A .B .C .D .9.下列函数中,既是奇函数,又在()0,+∞上单调递减的是( )A .()f x x =B .()f x x x =-C .()11f x x 2=+ D .()3f x x = 10.已知0.1232,log 3,log 2a b c ===,则实数a ,b ,c 的大小关系是( )A .c a b >>B .c b a >>C .a c b >>D .a b c >>11.已知函数()1212x f x a =-+,则“1a =”是()f x 为奇函数的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件12.已知函数()()2log 12f x x x =++-,则不等式()0f x <的解集为A .(),1-∞B .()1,1-C .()0,1D .()1,+∞13.科赫(Koch )曲线是几何中最简单的分形,科赫曲线的产生方式如下:如图,将一条线段三等分后,以中间一段为边作正三角形并去掉原线段生成1级科赫曲线“”,将1级科赫曲线上每一线段重复上述步骤得到2级科赫曲线,同理可得3级科赫曲线……在分形中,一个图形通常由N 个与它的上一级图形相似,且相似比为r 的部分组成.若1D r N=,则称D 为该图形的分形维数.那么科赫曲线的分形气维数是( )A .2log 3B .3log 2C .1D .32log 2 14.已知函数()2,,x a x a f x x x a +≤⎧=⎨>⎩,若存在非零实数0x ,使得()()00f x f x -=-成立,则实数a 的取值范围是( )A .(],0-∞B .1,4⎛-∞⎤ ⎥⎝⎦ C .[]4,0 D .12,4⎡-⎤⎢⎥⎣⎦ 二、填空题:共6小题,每小题5分,共30分15.函数()()lg 1f x x =-的定义域是__________.16.已知幂函数()f x 经过点()2,8,则函数()f x =___________.17.农科院作物所为了解某种农作物的幼苗质量,分别从该农作物在甲、乙两个不同环境下培育的幼苗中各随机抽取了15株幼苗进行检测,量出它们的高度如下图(单位:cm ):记该样本中甲、乙两种环境下幼苗高度的中位数分别为a ,b ,则a b -=___________.若以样本估计总体,记甲、乙两种环境下幼苗高度的标准差分别为12,s s ,则1s ____2s (用“<,>或=”连接).18.已知函数()4f x x a x=+-没有零点,则a 的一个取值为_______;a 的取值范围是___________.19.已知函数()22,0,0x x x f x x ⎧≥⎪=⎨-<⎪⎩,则()f x 的单调递增区间为________;满足()4410f x <⨯的整数解的个数为____________(参考数据:lg 20.30≈)20.共享单车已经逐渐成为人们在日常生活中必不可少的交通工具.通过调查发现人们在单车选择时,可以使用“Tullock 竞争函数”进行近似估计,其解析式为()()[],0,1,01aa a x S x x a x x =∈>+-(其中参数a 表示市场外部性强度,a 越大表示外部性越强).给出下列四个结论:①()S x 过定点11,22⎛⎫ ⎪⎝⎭; ②()S x 在[]0,1上单调递增;③()S x 关于12x =对称; ④取定x ,外部性强度a 越大,()S x 越小.其中所有正确结论的序号是______________.三、解答题:共64分,解答应写出文字说明,演算步骤或证明过程.21.(本小题12分)化简求值:(I )()10.530.204640.13π927-⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭ (II )5log 333325log 2log 59-+ 22.(本小题12分)已知一元二次方程22320x x +-=的两个实数根为12,x x求值:(I )2212x x +;(II )1211x x + 23.(本小题9分)国务院正式公布的《第一批全国重点文物保护单位名单》中把重点文物保护单位(下述简称为“第一批文保单位”)分为六大类.其中“A :革命遗址及革命纪念建筑物”、“B :石窟寺”、“C :古建筑及历史纪念建筑物”、“D :石刻及其他”、“E :古遗址”、“F :古墓葬”,北京的18个“第一批文保单位”所在区分布如下表:(I )某个研学小组随机选择北京市“第一批文保单位”中的一个进行参观,求选中的参观单位恰好为“C :古建筑及历史纪念建筑物”的概率;(II )小王同学随机选择北京市“第一批文保单位”中的“A :革命遗址及革命纪念建筑物”中的一个进行参观:小张同学随机选择北京市“第一批文保单位”中的“C :古建筑及历史纪念建筑物”中的一个进行参观.两人选择参观单位互不影响,求两人选择的参观单位恰好在同一个区的概率;(III )现在拟从北京市“第一批文保单位”中的“C :古建筑及历史纪念建筑物”中随机抽取2个单位进行常规检查,记抽到海淀区的概率为1P ,抽不到海淀区的概率记为2P ,试判断1P 和2P 的大小(直接写出结论).24.(本小题9分)已知集合{}25320,22|A x x x B x x ⎧⎫=--<=-≥⎨⎬⎩⎭(I )求,R A B A B ;(II )记关于x 的不等式()222440x m x m m -+++≤的解集为M ,若B M R =,求实数m 的取值范围.25.(本小题11分)已知函数()()()ln 1ln 1f x x k x =-++,请从条件①、条件②这两个条件中选择一个作为已知,解答下面的问题:条件①:()()0f x f x +-=条件②:()()0f x f x --=注:如果选择条件①和条件②分别解答,按第一个解答记分.(I )求实数k 的值;(II )设函数()()()11k F x x x =-+,判断函数()F x 在区间上()0,1的单调性,并给出证明;(III )设函数()()2k g x f x x k =++,指出函数()g x 在区间()1,0-上的零点的个数,并说明理由.26.(本小题11分)已知函数()()(),,f x g x h x 的定义域均为R ,给出下面两个定义:①若存在唯一的x ∈R ,使得()()()()f g x h f x =,则称()g x 与()h x 关于()f x 唯一交换;②若对任意的x ∈R ,均有()()()()f g x h f x =,则称()g x 与()h x 关于()f x 任意交换.(I )请判断函数()1g x x =+与()1h x x =-关于()2f x x =是唯一交换还是任意交换,并说明理由;(II )设()()()22()20,1f x a x a g x x bx =+≠=+-,若存在函数()h x ,使得()g x 与()h x 关于()f x 任意交换,求b 的值;(III )在(II )的条件下,若()g x 与()f x 关于()11x x e x e ω-=+唯一交换,求a 的值.。
河北省邯郸市2023-2024学年高一上学期期末质量检测试题 语文(含答案)

绝密★启用前邯郸市2023—2024学年第一学期期末质量检测高一语文(答案在最后)班级____________姓名____________注意事项:1.答卷前.考生务必将自己的姓名、班级和考号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,19分)阅读下面的文字,完成1~5题。
表面上,种子拥有致命毒素似乎是很合理的,这是一种自然的适应性改变。
毕竟,为了保护种子。
有什么办法比杀死任何想要吃掉它们的东西更好呢?但实际上,从令人讨厌到真正致命的这个进化步骤要复杂得多。
当一粒种子受到攻击时,植物的当务之急就是让攻击者停下来,这也是苦味、辣味和灼烧感很常见的原因。
直接的生理不适赶走了种子掠食者,并告诫它们不要再来。
它们甚至可以将这个教训传递给其他同类。
相反,毒素可能需要过几个小时或几天才能发挥效力,这样就无法阻止正在掠食种子的攻击者了。
理论上说,像蓖麻毒蛋白这样无味的毒素可能会让一只动物吃光一棵蓖麻植株的所有种子,然后离开,并在不知道原因的情况下死去。
因此,引发不适感的化学物质可以阻止各类种子掠食者,而致命的毒素只能消灭单独的掠食者,这是一场持久战。
这引发了一个问题,是什么进化诱因促使一些毒素不断变强,导致像蓖麻毒蛋白这样的化合物具有几乎令人难以理解的强大效力?“似乎没有明显的答案。
”当我提出这个问题的时候,德里克·比利告诉我。
我有段时间没联系他了,但当我遇到无法解决的难题时,这位种子研究方面的“神”总是慷慨地帮助我。
他解释说.种子的毒素往往以不同的方式影响不同的攻击者。
为了使一只动物感到轻微胃痛,并警告它不要再吃这种种子,而进化出来的物质,也许对另一只动物来说是完全致命的。
2024北京朝阳区高一上学期期末物理试题及答案

2024北京朝阳高一(上)期末物理2024.1(考试时间90分钟满分100分)一、本题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.下列物理量属于标量的是A.速度 B.加速度 C.力 D.路程2.小郑同学对田径比赛中的一些运动进行了思考,其中正确的是A.原地投掷实心球的成绩,其依据是实心球的位移大小B.跳远比赛中研究运动员起跳是否犯规时,可以将其看成质点C.跳高比赛中运动员以“背越式”飞越横杆时,其重心可能低于横杆D.在标准跑道上的400米跑比赛中小红获得冠军,是由于她全程的平均速度最大3.如图甲、乙所示,分别表示物体运动的位移x、速度v随时间t的变化图像。
下列说法正确的是A.甲图中物体在0~t1时间内沿x轴正向做匀加速直线运动B.甲图中物体在t1~t2时间内沿x轴正向做匀速直线运动C.乙图中物体在0~t1时间内速度的变化率保持恒定D.乙图中物体在t1~t2时间内处于静止状态4.如图所示,台秤放置在水平地面上,物块静止在水平秤盘上。
下列说法正确的是A.地面受到的压力是由于台秤底座发生微小形变产生的B.物块所受支持力的反作用力是地面受到的压力C.物块的重力与秤盘对物块的支持力是一对相互作用力D.台秤对地面的压力与地面对台秤的支持力是一对平衡力5.在太空舱内可采用动力学方法测物体质量。
先对质量为m0的标准物体施加一水平推力,测得其加速度大小为2m/s2;然后将该标准物体与待测物体紧靠在一起施加相同的水平推力,测得其共同加速度大小为1m/s2。
若m0=2kg,则待测物体的质量为A.1kg B.2kg C.3kg D.4kg6.无人快递车可以完成短途物流配送。
在一条东西方向的平直公路上进行实验测试,确定某交通岗亭为位置零点,以向西方向为正方向,如图所示。
快递车某段时间在此公路上运动的位置坐标x随时间t的变化规律为x = 2t 2 -4t + 9(x 、t 均取国际单位)。
高一数学上册期末考试试卷及答案解析(经典,通用)

高一数学上册期末考试试卷及答案解析一、单选题 1.设全集2,1,0,1,2U,集合{}{}0,1,21,2A =-,B=,则()U A B =( )A .{}01, B .{}0,1,2 C .{}1,1,2- D .{}0,1,1,2-2.“5x >”是“3x >”的( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分又不必要条件3.下列命题中正确的( ) ①0与{0}表示同一个集合;②由1,2,3组成的集合可表示为{1,2,3}或{3,2,1}; ③方程(x -1)2(x -2)=0的所有解的集合可表示为{1,1,2}; ④集合{x |4<x <5}可以用列举法表示. A .只有①和④ B .只有②和③ C .只有②D .以上语句都不对 4.下列命题中,既是全称量词命题又是真命题的是( ) A .矩形的两条对角线垂直 B .对任意a ,b ∈R ,都有a 2 + b 2≥ 2(a ﹣b ﹣1) C .∃x ∈R , |x | + x = 0 D .至少有一个x ∈Z ,使得x 2 ≤2成立5.已知02x <<,则y = )A .2B .4C .5D .66.若110a b <<,则下列结论不正确的是( ) A .22a b <B .1ba <C .2b aa b +>D .2ab b <7.命题p :“2R,240x ax ax ∃∈+-≥”为假命题的一个充分不必要条件是( ) A .40aB .40a -≤<C .30a -≤≤D .40a -≤≤8.集合{1,2,4}A =,{}2B x x A =∈,将集合A ,B 分别用如图中的两个圆表示,则圆中阴影部分表示的集合中元素个数恰好为4的是( ) A .B .C .D .二、多选题9.已知集合222{2,1,4},{0,2}A a a a B a a =+-=--,5A ∈,则a 为( ) A .2B .2-C .5D .1-10.若正实数,a b 满足1a b +=,则下列说法正确的是( ) A .ab 有最小值14 B C .1122a b a b +++有最小值43D .22a b +有最小值1211.下列命题为真命题的是( ). A .若a b >,则11b a >B .若0a b >>,0c d <<,则abd c < C .若0a b >>,且0c <,则22cc a b > D .若a b >,且11a b>,则0ab < 12.若“x M x x ∀∈>,”为真命题,“3x M x ∃∈>,”为假命题,则集合M 可以是( )A .()5-∞-,B .(]31--,C .()3+∞,D .[]03,三、填空题13.若命题2:0,30p x x ax ∀≥-+>,则其否定为p ⌝:__________________.14.已知:282p x -≤-≤,:1q x >,:2r a x a <<.若r 是p 的必要不充分条件,且r 是q 的充分不必要条件,则实数a 的取值范围为______. 15.设集合{}{}21,2,R (1)0A B x x a x a ==∈-++=,若集合C = A B ,且C 的子集有4个,则实数a 的取值集合为______________. 16.若a ∈R ,0b >,3a b +=,则当=a ______时,1||3||a a b +取得最小值.四、解答题17.求解下列问题:(1)已知0b a <<,比较1a 与1b 的大小; (2)比较()()37x x ++和()()46x x ++的大小.18.已知集合{|15}A x x =<≤,{}|04B x x =<<,{}|121C x m x m =+<<-. (1)求A B ,R ()A B ⋃: (2)若BC C =,求实数m 的取值范围.19.已知不等式20x ax b -+<的解集为{}17x x <<. (1)求实数,a b 的值.(2)求不等式101ax bx +>-的解集.20.已知0,0x y >>,且280x y xy +-=,求(1)xy 的最小值; (2)x y +的最小值. 21.22.“绿水青山就是金山银山”,为了保护环境,某工厂在政府部门的鼓励下进行技术改进,把二氧化碳化为某种化工产品,经测算,该处理成本y (单位:万元)与处理量x (单位:吨)之间的函数关系可近似表示为2401600y x x =-+,3050x ≤≤,已知每处理一吨二氧化碳可获得价值20万元的某种化工产品.(1)当处理量为多少吨时,每吨的平均处理成本最少?(2)判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元该工厂才不会亏损?参考答案:1.A 【分析】先求出UB ,再根据交集的定义可求()U A B ∩.【详解】{}2,0,1UB =-,故(){}0,1UAB =,故选:A.2.A 【分析】根据集合与充分必要条件的关系,判断选项. 【详解】{}5x x > {}3x x >,所以“5x >”是“3x >”的充分不必要条件. 故选:A3.C 【分析】由集合的表示方法判断①,④;由集合中元素的特点判断②,③.【详解】①{0}表示元素为0的集合,而0只表示一个元素,故①错误;②符合集合中元素的无序性,正确; ③不符合集合中元素的互异性,错误;④中元素有无穷多个,不能一一列举,故不能用列举法表示. 故选:C .4.B 【分析】根据全称量词和特称量词命题的定义判断,全称量词命题要为真命题必须对所以的成立,对选项逐一判断即可.【详解】A 选项为全称量词命题,却是假命题,矩形的两条对角线相等,并不垂直,故A 错误.C,D 选项是特称量词命题,故错误. B 选项是全称量词命题,用反证法证明, 因为()()2222222110a b a b a b +-++=-++≥所以对,a b ∀∈R ,()2221a b a b +--≥,故B 正确.故选:B. 5.【答案】A 【分析】设直角三角形的两个直角边为x ,y ,由此可得2225x y +=,又面积1=2S xy ,利用基本不等式可求面积的最大值. 【详解】设直角三角形的两个直角边为x ,y ,则2225x y +=, 又1=2S xy由基本不等式可得221125=2224x y S xy ⎛⎫+≤= ⎪⎝⎭(当且仅当x =y 立) 故选:A.6.B 【分析】由110a b <<得出0b a <<,再利用不等式的基本性质和基本不等式来判断各选项中不等式的正误. 【详解】110a b<<,0b a ∴<<,0b a ∴->->,22a b ∴<,A 选项正确;1b b a a-=>-,B 选项错误;由基本不等式可得2baa b +≥=,当且仅当1b a =时等号成立,1b a >,则等号不成立,所以2baa b +>,C 选项正确;0b a <<,2b ab ∴>,D选项正确.故选:B.【点睛】本题考查不等式正误的判断,涉及不等式的基本性质和基本不等式,考查推理能力,属于基础题.7.C 【分析】由题意,p ⌝为真命题,进而可得p ⌝为真命题时的充要条件,再根据充分与必要条件的性质判断选项即可. 【详解】命题2:R,240p x ax ax ∃∈+-≥为假命题,即命题2:R,240p x ax ax ⌝∀∈+-<为真命题.首先,0a =时,40-<恒成立,符合题意; 其次0a ≠时,则0a <且2(2)160a a ∆=+<,即40a ,综上可知,40a .结合选项可得,{}{}3040a a a a -≤≤⊆-<≤,即:30a -≤≤是40a 的一个充分不必要条件. 故选:C8.C 【分析】记U A B =⋃,然后分析每个选项对应的集合的运算并求解出结果进行判断即可.【详解】因为{}1,2,4A =,{}2B x x A=∈,所以{}2,B =--,记{}2,U AB ==--,对于A 选项,其表示(){}4U A B =,不满足;对于B 选项,其表示(){}2,U A B =--,不满足;对于C 选项,其表示(){2,U A B =--,满足;对于D 选项,其表示{}1,2A B =,不满足;故选:C.9.BC 【分析】结合元素与集合的关系,集合元素的互异性来求得a 的值.【详解】依题意5A ∈,当215a+=时,2a =或2a =-,若2a =-,则{}{}2,5,12,0,4A B ==,符合题意;若2a =,则220a a --=,对于集合B ,不满足集合元素的互异性,所以2a =不符合.当245a a -=时,1a =-或5a =,若1a =-,则212a +=,对于集合A ,不满足集合元素的互异性,所以1a =-不符合.若5a =,则{}{}2,26,5,0,18A B ==,符合题意. 综上所述,a 的值为2-或5. 故选:BC10.BCD 【分析】由已知结合基本不等式及其变形形式分别检验各选项即可判断.【详解】由正实数,a b 满足1a b +=,则2124a b ab +⎛⎫≤= ⎪⎝⎭,当且仅当12a b ==时,等号成立,所以ab 的最大值为14,故A 选项错误;由()222a b a b =+++=12a b ==时,,故B 选项正确;由11111(33)22322a b a b a b a b a b ⎛⎫+=++ ⎪++++⎝⎭111[(2)(2)]3221222322a b a b a b a b a b a b a b a b ⎛⎫=++++ ⎪++⎝⎭++⎛⎫=++ ⎪++⎝⎭14233⎛≥+= ⎝,当且仅当12a b ==时,等号成立,所以1122a b a b +++有最小值43,故C 选项正确;由222222()1()2()2222a b a b a b a b ab a b ++⎛⎫+=+-≥+-⨯== ⎪⎝⎭,当且仅当12a b ==时,等号成立,所以22a b +有最小值12,故D 选项正确. 故选:BCD.11.BCD 【解析】举反例说明选项A 错误;利用不等式的性质证明出选项B ,C 正确;利用作差法证明出选项D 正确.【详解】选项A :当取1a =,1b =-时,11b a <,∴本命题是假命题. 选项B :已知0a b >>,0cd <<,所以110dc->->,∴abd c ->-,故abd c <,∴本命题是真命题. 选项C :222211000a b a b a b >>⇒>>⇒<<,∵0c <,∴22cca b >,∴本命题是真命题. 选项D :111100b aa b a b ab->⇒->⇒>, ∵a b >,∴0b a -<,∴0ab <,∴本命题是真命题. 故选:BCD【点睛】本题考查不等式的性质,考查命题的真假,属于基础题. 12.AB 【解析】根据假命题的否定为真命题可知3x M x ∀∈≤,,又x M x x ∀∈>,,求出命题成立的条件,求交集即可知M 满足的条件.【详解】3x M x ∃∈>,为假命题,3x M x ∴∀∈≤,为真命题,可得(,3]M ⊆-∞,又x M x x ∀∈>,为真命题, 可得(,0)M ⊆-∞, 所以(,0)M ⊆-∞,故选:AB【点睛】本题主要考查了含量词命题的真假,集合的包含关系,属于中档题.13.20,30x x ax ∃≥-+≤【分析】直接利用存在量词写出其否定即可. 【详解】因为命题2:0,30p x x ax ∀≥-+>, 所以其否定p ⌝:20,30x x ax ∃≥-+≤.故答案为:20,30x x ax ∃≥-+≤.14.()5,6【分析】根据充分与必要条件,可得p ,q ,r 中集合的包含关系,再根据区间端点列式求解即可.【详解】易得:610p x ≤≤.记p ,q ,r 中x 的取值构成的集合分别为A ,B ,C ,由于r 是p 的必要不充分条件,r 是q 的充分不必要条件,则AC ,CB ,则016210a a a >⎧⎪≤<⎨⎪>⎩,解得56a <<,即实数a 的取值范围是()5,6.故答案为:()5,615.{}1,2【分析】先求出集合B 中的元素,再由C 的子集有4个,可知集合C 中只有2个元素,然后分1,2a a ==和1a ≠且2a ≠三种情况求解即可.【详解】由2(1)0x a x a -++=,得1x =或x a =, 因为集合C = A B ,且C 的子集有4个, 所以集合C 中只有2个元素, ①当1a =时,{}1B =,因为{}1,2A =,所以{}1,2A B ⋃=,即{}1,2C =,所以1a =满足题意,②当2a =时,{}1,2B =,因为{}1,2A =,所以{}1,2A B ⋃=,即{}1,2C =,所以2a =满足题意, ③当1a ≠且2a ≠时,{}1,B a =, 因为{}1,2A =,所以{}1,2,A B a =,即{}1,2,C a =,不合题意,综上,1a =或2a =,所以实数a 的取值集合为{}1,2, 故答案为:{}1,216.32-【分析】由题知3a <,进而分0<<3a 和0a <两种情况,结合基本不等式求解即可.【详解】解:因为3a b +=,0b >,所以30b a =->,即3a <.当0<<3a 时,11173||99999a ab a b a a b a b a b ++=+=++≥+, 当且仅当34a =时取等号,所以当34a =时,13a a b+取得最小值79;当0a <时,11139999a a b a b a a ba b a b ++=--=---≥-+59=, 当且仅当32a =-时取等号,所以当32a =-时,13a a b+取得最小值59.综上所述,当32a =-时,13a a b+取得最小值.故答案为:32-17.(1)11a b <(2)()()()()3746x x x x ++<++【分析】(1)利用差比较法比较大小. (2)利用差比较法比较大小.(1)11110,0,0,0,b a b a ab b a a b ab a b-<<>-<-=<<.(2)()()()()()()()()4630,737634x x x x x x x x ++=-<-+<+++++.18.(1){|05}A B x x ⋃=<≤;R(){05}A B x x x ⋃=≤>∣或;(2)52m ≤. 【分析】(1)由并集的定义及补集的定义进行计算即可; (2)BC C =等价于C B ⊆,按B =∅和B ≠∅讨论,分别列出不等式,解出实数m 的取值范围. (1)∵集合{|15}A x x =<≤,{}|04B x x =<<, ∴{|05}A B x x ⋃=<≤;R(){05}A B x x x ⋃=≤>∣或.(2) 因为BC C =,所以C B ⊆,当B =∅时,则121m m +≥-,即2m ≤;当B ≠∅时,则12110214m m m m +<-⎧⎪+≥⎨⎪-≤⎩,解得522m <≤;综上,实数m 的取值范围为52m ≤.19.(1)8,7a b ==;(2)11(,)(,)87-∞-⋃+∞【分析】(1)由解集得到方程20x ax b -+=的根,利用韦达定理可求,a b .(2)利用(1)中的结果并把分式不等式转化为一元二次不等式可求解集.【详解】(1)因为不等式20x ax b -+<的解集是{}17x x <<. 所以20x ax b -+=的解是1和7.故1771ab +=⎧⎨⨯=⎩,解得 87a b =⎧⎨=⎩. (2)由101ax bx +>-得81071x x +>-,即()()81710x x +->, 解得18x <-或17x >,故原不等式的解集为11(,)(,)87-∞-⋃+∞. 20.(1)64;(2)18.【解析】(1)由280x y xy +-=,得到821x y +=,利用基本不等式,即可求解. (2)由280x y xy +-=,得821x y +=,根据8282()()10y xx y x y x y x y +=++=++,结合不等式,即可求解.【详解】(1)由280x y xy +-=,可得821x y +=,又由0,0x y >>,可得821x y =+≥,当且仅当82x y =,即4x y =时,等号成立,即64xy ≥, 所以xy 的最小值为64. (2)由280x y xy +-=,得821x y +=,因为0,0x y >>,可得8282()()101018y x x y x y x y x y +=++=++≥+, 当且仅当82y xx y =,即12,6x y ==时等号成立,所以x y +的最小值为18.【点睛】利用基本不等式求最值时,要注意其满足的三个条件:“一正、二定、三相等”:(1)“一正”:就是各项必须为正数;(2)“二定”:就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”:利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方. 21.(1)[0,254] (2){}|2a a <【分析】(1)首先求解集合A ,再求二次函数的值域;(2)首先将不等式,参变分离得2452x x a x -+-<-,转化为求函数的最值,即可求解. (1)2230x x --≤等价于()()2310x x -⋅+≤,.解得312x -≤≤所以3|12A x x ⎧⎫=-≤≤⎨⎬⎩⎭. ∴二次函数223253424y x x x ⎛⎫=-++=--+ ⎪⎝⎭, 函数在区间31,2⎡⎤-⎢⎥⎣⎦单调递增,所以当32x =时,y 取最大值为254, 当1x =-时,y 取最小值为0,所以二次函数234y x x =-++.x A ∈的值域是[0,254]. (2)由(1)知3|12A x x ⎧⎫=-≤≤⎨⎬⎩⎭ ∵()24520x a x a +-+->恒成立. 即24520x ax x a +-+->恒成立.∴()2245x a x x -⋅>-+-恒成立. .∵312x -≤≤.∴20x -<.()()222214545122222x x x x x a x x x x x-+-+--+∴<===-+----∵20x ->,∴()1222x x-+≥-.. 当且仅当122x x -=-且312x -≤≤时,即1x =时,等号成立,. ∴2a <,故a 的取值范围为{}|2a a < 22.(1)31a b ==, (2)32a -≤<-或45a <≤ (3)53a ≥-【分析】(1)根据二次函数与对应不等式和方程的关系,利用根与系数的关系,即可求出a 、b 的值;(2)由()1f x b <-得()23220x a x a -+++<,令()()2322h x x a x a =-+++,求出()0h x <解集中恰有3个整数时a 的取值范围即可.(3)由()f x b ≥在[]31x ∈--,上恒成立,知()23210x a x a -+++在[]31x ∈--,上恒成立,化简得()()222213122x x x x a x x -+---+=--,设[]253t x =-∈--,,()2111t t g t t t t+-==-+,求出()g t 的最大值,进一步求出实数a 的取值范围;(1)解:因为函数()()2321f x x a x a b =-++++,a ,b R ∈,又()0f x >的解集为{2|x x <或4}x >,所以2,4方程()23210x a x a b -++++=的两根,由()2432421a a b ⎧+=+⎨⨯=++⎩, 解得31;a b ==, (2)由()1f x b <-得()23220x a x a -+++<, 令()()2322h x x a x a =-+++,则()()()()12h x x a x =-+-,知()20h =,故()0h x <解集中的3个整数只能是3,4,5或1-,0,1;①若解集中的3个整数是3,4,5,则516a <+≤,得45a <≤;②解集中的3个整数是1-,0,1;则211a -≤+<-,得32a -≤<-;综上,由①②知,实数a 的取值范围为32a -≤<-或45a <≤. (3)因为函数()()2321f x x a x a b =-++++,a ,b R ∈,由()f x b 在[]31x ∈--,上恒成立,知()23210x a x a -+++在[]31x ∈--,上恒成立, 化简得()()222213122x x x x a x x -+---+=--,设[]253t x =-∈--,, 设()2111t t g t t t t +-==-+,因为在()g t 在[]53--,上单调递增, 即()153133g t --+=--,所以53a ≥-. 23.(1)40吨(2)不会获利,700万元【分析】(1)根据已知条件,结合基本不等式的公式,即可求解.(2)当3050x ≤≤时,该工厂获利S ,则()2220401600(30)700S x x x x =--+=---,再结合二次函数的性质,即可求解. (1)由题意可得,二氧化碳的平均处理成本1600()40yP x x x x==+-,3050x ≤≤,当3050x ≤≤时,1600()404040P x x x =+-≥=, 当且仅当1600x x=,即40x =等号成立, 故()P x 取得最小值为(40)40P =,故当处理量为40吨时,每吨的平均处理成本最少. (2)当3050x ≤≤时,该工厂获利S , 则()2220401600(30)700S x xx x =--+=---,当3050x ≤≤时,max 7000S =-<,故该工厂不会获利,国家至少需要补贴700万元,该工厂不会亏损.。
2023-2024学年山东省滨州市高一上学期期末考试地理试题
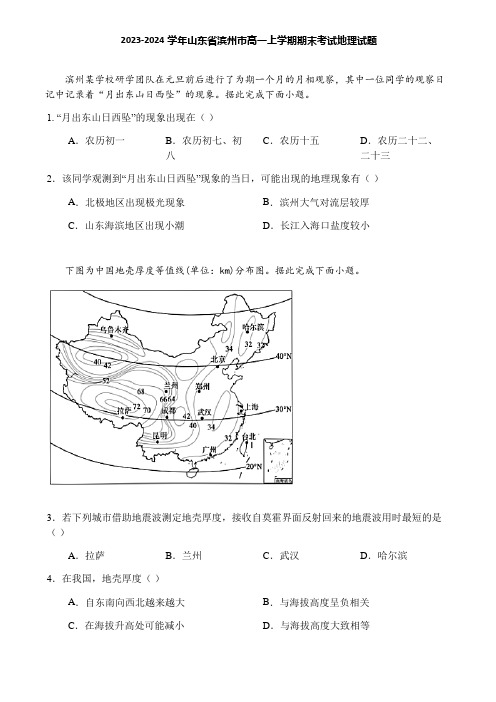
2023-2024学年山东省滨州市高一上学期期末考试地理试题滨州某学校研学团队在元旦前后进行了为期一个月的月相观察,其中一位同学的观察日记中记录着“月出东山日西坠”的现象。
据此完成下面小题。
1. “月出东山日西坠”的现象出现在()A.农历初一B.农历初七、初八C.农历十五D.农历二十二、二十三2.该同学观测到“月出东山日西坠”现象的当日,可能出现的地理现象有()A.北极地区出现极光现象B.滨州大气对流层较厚C.山东海滨地区出现小潮D.长江入海口盐度较小下图为中国地壳厚度等值线(单位:km)分布图。
据此完成下面小题。
3.若下列城市借助地震波测定地壳厚度,接收自莫霍界面反射回来的地震波用时最短的是()A.拉萨B.兰州C.武汉D.哈尔滨4.在我国,地壳厚度()A.自东南向西北越来越大B.与海拔高度呈负相关C.在海拔升高处可能减小D.与海拔高度大致相等太阳辐射、地面辐射、大气逆辐射和净辐射(由天空向下投射和由地表向上投射的所有辐射量之差)能影响森林生态系统。
下图为2003—2016年我国某热带季雨林地区不同季节(干热季、雨季和雾凉季)某辐射值的日变化分布图。
据此完成下面小题。
5.推测图中曲线示意的辐射类型是()A.净辐射B.地面辐射C.太阳辐射D.大气逆辐射6.图中①②③三条曲线对应的季节分别为()A.雾凉季、干热季、雨季B.雨季、干热季、雾凉季C.雾凉季、雨季、干热季D.干热季、雾凉季、雨季7.曲线③在8:40左右出现高值,其主要影响因素是()A.雾B.风速C.云量D.太阳辐射城市近地面O₃的形成与工业和交通排放的废气有关,能严重影响一个城市的空气质量。
内蒙古巴彦浩特镇的山谷风是影响当地污染物扩散的关键因子之一。
下左图为巴彦浩特镇山谷风变化图,右图为同期巴彦浩特不同观测站O₃平均浓度日变化图。
据此完成下面小题。
8.山脉位于巴彦浩特镇的()A.东部B.西部C.南部D.北部9.监测时段内,巴彦浩特O₃浓度升降速度明显存在差异,主要原因可能是()A.夜间工厂下班后,排放的O₃减少,城市O₃浓度下降快B.白天山区气温回升,山风风力较强,城市O₃浓度上升快C.夜间山风影响小,不利于O₃生成,城市O₃浓度上升慢D.夜间时,残留山区的O₃回流城市,城市O₃浓度下降慢下图为世界某区域海平面等压线(单位:hpa)分布图。
河南省郑州市2023-2024学年高一上学期期末考试 生物含答案

郑州市2023—2024学年上期期末考试高一生物试题卷(答案在最后)注意事项:本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。
考试时间90分钟,满分100分。
考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效。
交卷时只交答题卡。
第I卷(选择题,共50分)一、选择题(本题包括25个小题,每小题2分,共50分。
每小题只有一个选项符合题意。
)1.细胞是最基本的生命系统,下列说法错误..的是()A.施莱登观察到植物的花粉、胚珠、柱头等的细胞都有细胞核,得出植物细胞都有细胞核这一结论,运用的是不完全归纳法B.箭竹和大熊猫都具有细胞、组织、器官、系统等生命系统的结构层次C.细胞学说认为,新细胞是由老细胞分裂产生的D.细胞学说阐明了生物界的统一性2.下列哪种细胞在结构上与其他三种细胞的差异最大()A.蓝细菌B.酵母菌C.叶肉细胞D.口腔上皮细胞3.下表是组成玉米细胞和人体细胞的部分元素及含量(干重,质量分数),下列有关说法正确的是()元素玉米细胞人体细胞C43.5755.99H 6.247.46O44.4314.62N 1.469.33K0.92 1.09Ca0.23 4.67P0.20 3.11Mg0.180.16S0.170.78A.不仅表中的元素,生物体内的所有元素,在无机自然界中都能找到B.Mg在玉米和人体细胞中含量均较少,所以它并不重要C.人体细胞中N的含量高于玉米,这可能与人体细胞中糖类含量较高有关D.表中列举的元素中Ca和K是微量元素4.水和无机盐是细胞中重要的两类无机物,下列说法错误..的是()A.自由水可以运送养料和废物B.越冬期的小麦细胞中自由水与结合水的比例上升C.细胞中大多数无机盐以离子的形式存在D.人体内Na+缺乏会引起神经、肌肉细胞的兴奋性降低5.下列对细胞中糖类和脂质的认识正确的是()A.磷脂是所有细胞必不可少的脂质B.植物细胞和动物细胞的组成成分中都有纤维素C.脂肪、淀粉和糖原都是人体细胞内的储能物质D.糖类可以大量转化为脂肪,脂肪也可以大量转化为糖类6.洋葱根尖细胞的核酸中含有的碱基和五碳糖种类分别是()A.12B.41C.52D.817.下列关于人体中蛋白质功能的叙述,错误..的是()A.蛋白质是生命活动的主要承担者B.抗体可帮助人体抵御病原体的侵害C.红细胞中血红蛋白能运输氧D.一些激素是蛋白质,如胰岛素、性激素等8.细胞膜是细胞的边界,下列关于细胞膜的结构和功能,说法错误..的是()A.细胞膜具有控制物质进出细胞的功能B.精子和卵细胞之间的结合和识别与细胞膜上信号分子、受体有关C.功能越复杂的细胞膜,蛋白质的种类与数量就越多D.对细胞有害的物质不能通过细胞膜进人细胞9.对细胞膜成分和结构的探索涉及科学史上许多经典的实验,下列实验和结论的对应关系错误..的是()实验结论A溶于脂质的物质,容易穿过细胞膜;不溶于脂质的物质,不容易穿过细胞膜细胞膜是由脂质组成的B用丙酮从人的红细胞中提取脂质,在空气—水界面上铺展为单分子层,测得单层分子的面积恰为红细胞表面积的2倍细胞膜中的脂质排列为连续的两层C细胞的表面张力明显低于油—水界面的表面张力细胞膜除含脂质分子外,可能还附有蛋白质D电子显微镜下看到了细胞膜清晰的暗—亮—暗的三层结构细胞膜是由脂质—蛋白质—脂质三层结构构成10.下图表示细胞的生物膜系统的部分组成在结构和功能上的联系,下列说法错误..的是()A.图中的甲是内质网B.分泌蛋白是在图中的乙内合成和加工的C.从图中可以看出,溶酶体可以吞噬并杀死侵入细胞的病毒D.图中显示的膜都属于生物膜系统,它们在结构和功能上紧密联系11.下列关于细胞核的说法错误..的是()A.核膜具有双层膜,把核内物质与细胞质分开B.细胞核是细胞代谢和遗传的中心C.控制细胞器进行物质合成、能量转化的指令,主要通过核孔从细胞核进入细胞质D.核仁与某种RNA的合成以及核糖体的形成有关12.下列物质通过细胞膜时,需要消耗ATP的是()A.水分子进入根毛细胞B.二氧化碳被排出细胞C.葡萄糖被肾小管上皮细胞重吸收D.小肠上皮细胞吸收维生素D13.某生物兴趣小组做了淀粉酶对淀粉和蔗糖的水解作用的实验,有关说法错误..的是()序号项目试管1试管21注入可溶性淀粉溶液2ml-2注入蔗糖溶液-2ml3注入新鲜的淀粉酶溶液2ml2mlA.淀粉和蔗糖都是非还原糖,它们的水解产物中都有还原糖B.实验自变量是底物的不同C.保温一段时间后,用斐林试剂检测都会出现砖红色的沉淀D.本实验说明了酶具有专一性14.细胞代谢离不开酶,下列关于酶的说法错误..的是()A.与无机催化剂相比,酶的催化效率更高B.无机催化剂催化的化学反应范围比较广,而酶具有专一性C.与无机催化剂相比,酶所催化的化学反应一般是在比较温和的条件下进行的D.酶制剂适宜在低温和低pH下保存15.ATP是细胞的能量货币,下列说法错误..的是()A.有氧呼吸的三个阶段都有ATP的生成B.一个人在剧烈运动的状态下,每分钟约有0.5kg的ATP转化为ADP,此时细胞中的ATP含量会显著下降C.许多吸能反应与ATP水解的反应相联系,如蛋白质的合成D.形成ATP所需要的能量可以来自光能,也可以来自有机物分解所释放的能量16.下图是ATP为主动运输供能示意图,下列说法错误..的是()A.图中蛋白质既可以做载体蛋白,也可以催化ATP水解B.载体蛋白磷酸化后空间结构发生改变,使Ca2+的结合位点转向膜外侧,将Ca2+释放到膜外C.载体蛋白磷酸化伴随着能量的转移D.载体蛋白空间结构发生变化是不可逆的变性17.下图是探究酵母菌细胞呼吸方式的实验装置,有关说法错误..的是()A.装置甲中NaOH溶液的作用是排除空气中的CO2对实验结果的干扰B.装置乙中的Ⅱ应先封口放置一段时间再与Ⅲ连接,是为了保证无氧条件C.若装置甲和乙中澄清石灰水换成溴麝香草酚蓝溶液,颜色变化是由蓝变绿再变黄D.能明显检测到有酒精生成的是I和Ⅱ18.下列对绿叶中色素的提取和分离实验的叙述错误..的是()A.研磨过程中加人二氧化硅有助于研磨充分B.研磨过程中加入碳酸钙是为了防止色素遭破坏C.色素提取液要使用95%的乙醇D.滤纸条上扩散最快的色素带颜色是橙黄色19.光合作用中能量的转化过程是()A.光能→ATP中的化学能→热能B.光能→ATP和NADPH中的化学能→糖类中的化学能C.光能→ATP和NADPH中的化学能→C。
高一数学上学期期末考试试卷含答案(共3套)

高一级第一学期期末考试数学试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 下列四组函数,表示同一函数的是()A. B.C. D.2. 平行于同一平面的两条直线的位置关系是()A. 平行B. 相交C. 异面D. 平行、相交或异面3. 已知集合,,则()A. B. C. D.4. 图中的直线的斜率分别是,则有()A. B. C. D.5. 设,,则()A. B. C. D.6. 方程在下面哪个区间内有实根()A. B. C. D.7. 一个几何体的三视图如图所示,则该几何体的体积为()A. B. C. D.8. 一圆锥的侧面展开图是一个半圆,则这个圆锥的母线与底面所成角是()A. B. C. D.9. 若函数的值域为,则实数的取值范围是()A. B. C. D.10. 如图,二面角的大小是,线段,,与所成的角为,则与平面所成的角的余弦值是()A. B. C. D.11. 正四面体中,是棱的中点,是点在底面内的射影,则异面直线与所成角的余弦值为()A. B. C. D.12. 已知函数在闭区间上的值域为,则满足题意的有序实数对在坐标平面内所对应点组成图形为()A. B.C. D.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知,则__________.14. 已知两条平行直线分别过点,,且的距离为5,则直线的斜率是__________.15. 已知函数,若函数有3个零点,则实数的取值范围是__________.16. 如图,将一边为1的正方体沿相邻三个面的对角线截出一个棱锥,则三棱锥的内切球半径是__________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 求值或化简:(1);(2).18. 如图,正三角形的边长为6,,,点分别在边上,且,,相交于.(1)求点的坐标;(2)判断和是否垂直,并证明.19. 已知函数.(1)求函数的定义域;(2)判断函数的奇偶性,并证明你的结论;(3)在函数图像上是否存在两个不同的点,使直线垂直轴,若存在,求出两点坐标;若不存在,说明理由.20. 如图,在四棱锥中,底面,,,,为棱的中点.(1)求证:;(2)试判断与平面是否平行?并说明理由.21. 《中华人民共和国个人所得税法》规定,公民全月工资、薪金(扣除三险一金后)所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额个人所得税计算公式:应纳税额=工资-三险一金=起征点. 其中,三险一金标准是养老保险8%、医疗保险2%、失业保险1%、住房公积金8%,此项税款按下表分段累计计算:(1)某人月收入15000元(未扣三险一金),他应交个人所得税多少元?(2)某人一月份已交此项税款为1094元,那么他当月的工资(未扣三险一金)所得是多少元?22. 设,函数,其中.(1)求的最小值;(2)求使得等式成立的的取值范围.参考答案1【答案】D【解析】试题分析:A.,对应法则不同;B.,定义域不同;C.,定义域不同;故选D。
高一数学第一学期期末考试试卷(共5套,含参考答案)

高一第一学期期末考试数学试卷 满分:150分 时间: 120分钟一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}{}|27,|1,A x x B x x x N =-<<=>∈,则AB 的元素的个数为( )A.3B.4C.5D.62.两条直线a ,b 满足a ∥b ,b α⊂,则a 与平面α的关系是( ) A.a ∥α B.a 与α相交 C.a 与α不相交 D.a α⊂3.方程的1xe x =的根所在的区间是( ). A.)21,0( B.)1,21( C.)23,1( D.)2,23(4.函数y=x (x 2-1)的大致图象是( )5.如图所示,已知正四棱锥S —ABCD 侧棱长为2,底面边长为3,E 是SA 的中点,则异面直线BE 与SC 所成角的大小为( ) A.90°B.60°C.45°D.30°6.长方体1111ABCD A B C D -中,2AB =,1AA =3AD =,则 长方体1111ABCD A B C D - 的外接球的直径为 ( ) A.2 B.3 C.4 D.57.圆锥的表面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为( ) A.120° B.150° C.180° D.240°8.如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错误..的是( ) A.BD ∥平面CB 1D 1 B.AC 1⊥BDC.AC 1⊥平面CB 1D 1D.异面直线AD 与CB 1角为60°9.若方程1ln 02xx a ⎛⎫-+= ⎪⎝⎭有两个不等的实数根,则a 的取值范围是( )A.1,2⎛⎫+∞ ⎪⎝⎭B.()1,+∞C.1,2⎛⎫-∞ ⎪⎝⎭D.(),1-∞10.某几何体的三视图如图所示(单位: cm ),则该几何体的表面积是( )A.65B.6C.2D.511.已知函数()22log f x x x =+,则不等式()()120f x f +-<的解集为( )A. ()(),13,-∞-⋃+∞B. ()(),31,-∞-⋃+∞C. ()()3,11,1--⋃-D. ()()1,11,3-⋃12.已知()()()2,log 0,1x a f x ag x x a a -==>≠,若()()440f g ⋅-<,则y=()f x ,y=()g x 在同一坐标系内的大致图象是( )二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知不等式062<-+px x 的解集为{|32}x x -<<,则p = .14.2lg 2= _________15.函数()lg 21y x =+的定义域是______________________. 16.函数x21f x =-log x+23⎛⎫⎪⎝⎭()()在区间[-1,1]上的最大值为________. 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分10分)全集R U =,函数()lg(3)f x x =+-的定义域为集合A ,集合{}02<-=a x x B .(1)求U A ð; (2)若A B A = ,求实数a 的取值范围.18.(本题满分12分)已知函数⎪⎩⎪⎨⎧>-+≤-=)0(,1)1(log )0(,2)21()(2x x x x f x(1)求)(x f 的零点; (2)求不等式()0f x >的解集.19.(12分)如图,在直角梯形ABCD 中,AD ∥BC ,AD =AB ,∠A =90°,BD ⊥DC ,将△ABD 沿BD 折起到△EBD 的位置,使平面EBD ⊥平面BDC. (1) 求证:平面EBD ⊥平面EDC ; (2) 求ED 与BC 所成的角.20.(12分)一块边长为10 cm 的正方形铁块按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器.(1)试把容器的容积V 表示为x 的函数; (2)若x =6,求图2的正视图的面积.21.(本小题满分12分)在三棱柱111C B A ABC -中,侧面11A ABB 为矩形,1AB =,1AA ,D 为1AA 的中点,BD 与1AB 交于点O ,⊥CO 侧面11A ABB .(Ⅰ)证明:1AB BC ⊥; (Ⅱ)若OA OC =,求点1B 到平面ABC 的距离.1A A1B B1C COD22.(本小题满分12分)已知函数4()log (41)x f x kx =++(k ∈R ),且满足(1)(1)f f -=. (1)求k 的值;(2)若函数()y f x =的图象与直线12y x a =+没有交点,求a 的取值范围; (3)若函数1()2()421f x xx h x m +=+⋅-,[]20,log 3x ∈,是否存在实数m 使得()h x 最小值为0,若存在,求出m 的值;若不存在,请说明理由.高一第一学期期末考试 数学试卷参考答案一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 1 14. 2 15. 16. 316.解析:∵y =⎝ ⎛⎭⎪⎫13x 和y =-log 2(x +2)都是[-1,1]上的减函数,∴f(x)=⎝ ⎛⎭⎪⎫13x-log 2(x +2)在区间[-1,1]上是减函数,∴函数f(x)在区间[-1,1]上的最大值为f(-1)=3.答案:3三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.解:(1)∵⎩⎨⎧>->+0302x x ∴23x -<<…………………………………3分∴A=(-2,3) ∴(][)23u C A =-∞-+∞,,……………………………5分 (2)当0≤a 时,φ=B 满足A B A = ……………………………6分当0>a 时,)(a a B ,-= ∵AB A = ∴A B ⊆[]∴⎪⎩⎪⎨⎧≤-≥-32a a , ∴40≤<a ……………………………9分 综上所述:实数a 的范围是4≤a ……………………………………10分18.解:(1)由0)(=x f 得,⎪⎩⎪⎨⎧=-≤02)21(0x x 或⎩⎨⎧=-+>01)1(log 02x x ,解得1-=x 或1=x .所以,函数)(x f 的零点是—1,1..................................6分(2)由()0f x >得,01()202xx ≤⎧⎪⎨->⎪⎩或20log (1)10x x >⎧⎨+->⎩,解得1x <-或1x >.所以,不等式1)(>x f 的解集是{x |1x <-或1x >}.................................12分19.(1) 证明:∵平面EBD ⊥平面BDC ,且平面EBD ∩平面BDC =BD ,CD ⊥BD , ∴CD ⊥平面EBD , ∵CD 平面EDC ,∴平面EBD ⊥平面EDC.……………………………6分 (2) 解:如答图,连接EA ,取BD 的中点M ,连接AM ,EM , ∵AD ∥BC ,∴∠EDA 即为ED 与BC 所成的角. 又∵AD =AB ,∴ED =EB. ∴EM ⊥BD ,∴EM ⊥平面ABCD.设AB =a ,则ED =AD =a ,EM =MA , ∴AE =a ,∴∠EDA =60°.即ED 与BC 所成的角为60°……………………………12分20.(12分)解 (1)设所截等腰三角形的底边边长为x cm. 在Rt △EOF 中,EF =5 cm ,OF =12x cm ,所以EO =25-14x 2.于是V =13x225-14x 2(cm 3).依题意函数的定义域为{x|0<x<10}.……………………………6分(2)正视图为等腰三角形,腰长为斜高,底边长=AB =6, 底边上的高为四棱锥的高=EO =25-14x 2=4,S =4×62=12(cm 2).……………………………12分21.解:(1),由 得又即又又BD 与CO 交于O 点,又……………………………6分(2),,又AB=1,可得,由得……………………………12分22.解析:(1)(1)(1)f f -=,即144log (41)log (41)k k -+-=++444512log log 5log 144k ∴=-==- ∴12k =- ………………………………………………………………………… ………5分(2)由题意知方程411log (41)22x x x a +-=+即方程4=log (41)x a x +-无解, 令4()log (41)x g x x =+-,则函数()y g x =的图象与直线y a =无交点444411()log 41)log log (1)44x x x xg x x +=+-==+( 任取1x 、2x ∈R ,且12x x <,则12044x x <<,121144x x ∴>. 12124411()()log 1log 1044x x g x g x ⎛⎫⎛⎫∴-=+-+> ⎪ ⎪⎝⎭⎝⎭,()g x ∴在(),-∞+∞上是单调减函数.1114x +>, 41()log 104xg x ⎛⎫∴=+> ⎪⎝⎭. ∴a 的取值范围是(],0.-∞ ……………………………………………………………… 9分注意:如果从复合函数角度分析出单调性,给全分。
2023-2024学年山东省临沂高一上学期期末数学质量测试题(含答案)

2023-2024学年山东省临沂高一上册期末数学质量测试题一、单选题1.已知1sin3α=,,2παπ⎛⎫∈ ⎪⎝⎭,则tanα的值为()A.4BC.-D.【正确答案】A根据同角三角函数的基本关系求出cosα,tanα;【详解】解:因为1sin3α=,22sin cos1αα+=,所以cos3α=±,因为,2παπ⎛⎫∈ ⎪⎝⎭,所以cos3α=-,所以1sin3tancos43ααα==-故选:A2.已知命题:0p x∀>,2log2x x>,则命题p的否定为()A.0x∀>,2log2x x≤B.00x∃>,002log2x x≤C.00x∃>,002log2x x<D.00x∃≤,002log2x x≤【正确答案】B根据全称命题的否定是特称命题,可得选项.【详解】因为全称命题的否定是特称命题,所以命题:0p x∀>,2log2x x>,则命题p的否定为“00x∃>,002log2x x≤”,故选:B.3.已知函数()xf x a=(0a>且1a≠)在(0,2)内的值域是2(1,)a,则函数()y f x=的函数大致是()A .B.C .D .【正确答案】B【详解】试题分析:由题意可知21a>,所以1a>,所以()f x是指数型的增函数.故选B.指数函数的图象与性质.4.若正实数a ,b ,c 满足1b a c c c <<<,则a ,b 的大小关系为()A .01a b <<<B .01b a <<<C .1b a <<D .1a b<<【正确答案】A【分析】根据已知可得01c <<,根据指数函数的单调性,即可得出答案.【详解】因为c 是正实数,且1c <,所以01c <<,则函数x y c =单调递减.由1b a c c c <<<,可得10b a c c c c <<<,所以01a b <<<.故选:A.5.若0a >且1a ≠,函数()(),140.52,1x a x f x a x x ⎧≥⎪=⎨-+<⎪⎩,满足对任意的实数12x x ≠都有11222112()()()()x f x x f x x f x x f x +>+成立,则实数a 的取值范围是()A .(1,)+∞B .(1,8)C .(4,8)D .[4,8)【正确答案】D【分析】由已知可得函数()f x 在R 上单调递增,根据分段函数的单调性列出不等式组,即可求得实数a 的取值范围.【详解】解:11222112()()()()x f x x f x x f x x f x +>+ ,∴对任意的实数12x x ≠都有1212()[()()]0x x f x f x -->成立,可知函数()f x 在R 上单调递增,1140.50(40.5)12a a a a >⎧⎪∴->⎨⎪≥-⨯+⎩,解得[4,8)a ∈,故选:D.6.已知1:12p x ≥-,:2q x a -<,若p 是q 的充分不必要条件,则实数a 的取值范围为()A .(],4-∞B .[]1,4C .(]1,4D .()1,4【正确答案】C【分析】求出p 、q 中的不等式,根据p 是q 的充分不必要条件可得出关于实数a 的不等式组,由此可解得实数a 的取值范围.【详解】解不等式112x ≥-,即131022x x x --=≤--,解得23x <≤,解不等式2x a -<,即22x a -<-<,解得22a x a -<<+,由于p 是q 的充分不必要条件,则(]2,3()2,2a a -+,所以2223a a -≤⎧⎨+>⎩,解得14a <≤.因此,实数a 的取值范围是(]1,4.故选:C.本题考查利用充分不必要条件求参数,同时也考查了分式不等式和绝对值不等式的求解,考查计算能力,属于中等题.7.已知函数π()cos()0,||2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的最小正周期为π,且当π3x =时,函数()f x 取最小值,若函数()f x 在[,0]a 上单调递减,则a 的最小值是()A .π6-B .5π6-C .2π3-D .π3-【正确答案】A【分析】根据最小正周期求出2ω=,根据当π3x =时,函数取最小值,求出π3ϕ=,从而π()cos 23f x x ⎛⎫=+ ⎪⎝⎭,由[,0]x a ∈得到22,33πππ3x a ⎡⎤+∈+⎢⎥⎣⎦,由单调性列出不等式,求出06π,a ⎡⎫∈-⎪⎢⎣⎭,得到答案.【详解】因为0ω>,所以2π2π2πT ω===,故13πcos(2)ϕ⨯+=-,所以2ππ2π,Z 3k k ϕ+=+∈,解得:ππ,Z k k ϕ=+∈23,因为π||2ϕ<,所以只有当0k =时,π3ϕ=满足要求,故π()cos 23f x x ⎛⎫=+ ⎪⎝⎭,因为[,0]x a ∈,所以22,33πππ3x a ⎡⎤+∈+⎢⎥⎣⎦,故π2,33π0a ⎡⎫∈⎪⎢⎣⎭+,解得:06π,a ⎡⎫∈-⎪⎢⎣⎭,故a 的最小值为π6-.故选:A8.质数也叫素数,17世纪法国数学家马林·梅森曾对“21p -”(p 是素数)型素数作过较为系统而深入的研究,因此数学界将“21p -”(p 是素数)形式的素数称为梅森素数.已知第6个梅森素数为1721M =-,第14个梅森素数为60721N =-,则下列各数中与NM最接近的数为()(参考数据:lg 20.3010≈)A .18010B .17710C .14110D .14610【正确答案】B【分析】根据题意,得到6076075901717212==2212N M -≈-,再结合对数的运算公式,即可求解.【详解】由第6个梅森素数为1721M =-,第14个梅森素数为60721N =-,,可得6076075901717212=212N M -≈-,令5902k =,两边同时取对数,则590lg 2lg k =,可得lg 590lg 2k =,又lg 20.3010≈,所以lg 5900.3010177.59k ≈⨯=,17710k ≈与NM最接近的数为17710.故选:B.二、多选题9.下列结论正确的是()A .若,a b 为正实数,a b ¹,则3223+a b a b b a +>B .若,,a b m 为正实数,a b <,则a m ab m b+<+C .若,a b R ∈,则“0a b >>”是“11a b <”的充分不必要条件D .当0,2x π⎛⎫∈ ⎪⎝⎭时,2sin sin x x +的最小值是【正确答案】AC利用作差法可考查选项A 是否正确;利用作差法结合不等式的性质可考查选项B 是否正确;利用不等式的性质可考查选项C 是否正确;利用均值不等式的结论可考查选项D 是否正确.【详解】对于A ,若a ,b 为正实数,a b ¹,()()()233220a b a b ab a b a b +-+=-+>,3322a b a b ab ∴+>+,故A 正确;对于B ,若a ,b ,m 为正实数,a b <,()()0m b a a m a b m b b b m -+-=>++,则a m ab m b+>+,故B 错误;对于C ,若11a b <,则110b aa b ab--=<,不能推出0a b >>,而当0a b >>时,有0>0b a ab -<,,所以0b aab -<成立,即11a b<,所以“0a b >>”是“11a b<”的充分不必要条件,故C 正确;对于D ,当0,2x π⎛⎫∈ ⎪⎝⎭时,0sin 1x <<,2sin sin x x +≥=,当且仅当()sin 0,1x =时取等号,故D 不正确.故选:AC.易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:(1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.10.已知关于x 的方程23xm -=有两个不等实根,则实数m 的取值可能是()A .2B .3C .4D .5【正确答案】CD【分析】化简方程得23x m =±,利用指数函数的值域,列式求解得出答案.【详解】23xm -= ,23x m ∴-=±,23x m -= 有两个不等实根,即23x m =±有两个不等实根,则3030m m +>⎧⎨->⎩,解得3m >,显然选项A ,B 不满足,选项C ,D 满足.故选:CD.11.定义在R 上的函数()f x 满足()(2)f x f x =+,当[3,5]x ∈时,()2|4|f x x =--,则下列说法正确的是()A .ππsin cos 66f f⎛⎫⎛⎫< ⎪ ⎝⎭⎝⎭B .(sin1)(cos1)f f <C .2π2πcos sin 33f f ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭D .(cos 2)(sin 2)f f >【正确答案】BD【分析】根据函数的周期性可得()f x 在[]1,1-上的解析式以及函数在[0,1]上的单调性.比较自变量的大小,即可根据单调性判断A 、B 项;又易知()f x 在[1,1]-上为偶函数,则根据()()f x f x =,可将[1,0]-上的自变量转化为[0,1]上,进而根据单调性,即可判断C 、D 项.【详解】当[1,1]x ∈-时,则[45]3,x +∈,于是()(2)(4)2||f x f x f x x =+=+=-,当01x ≤≤时,()2f x x =-,所以函数()f x 在[0,1]上单调递减;当10x -≤<时,()2f x x =+,所以函数()f x 在[1,0]-上是增函数.()f x 的定义域[1,1]-关于原点对称,且此时()()22-=--=-=f x x x f x则()f x 在[1,1]-上为偶函数.对于A 项,因为ππ0sincos 166<<<,所以ππsin cos 66f f ⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭,故A 错误;对于B 项,因为0cos1sin11<<<,所以(cos1)(sin1)f f >,故B 正确;对于C项,因为2π12π0cossin 1323<==<,所以2π2πcossin 33f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭>,所以2π2πcos sin 33f f ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,故C 错误;因为ππ0|cos 2|cos sin |sin 2|144<<=<<,所以(|cos2|)(|sin 2|)f f >,所以(cos 2)(sin 2)f f >,故D 正确.故选:BD.12.已知定义域为R 的奇函数()f x ,当0x >时,21,01()1,121x x x f x x x ⎧-+<≤⎪=⎨>⎪-⎩,下列说法中错误的是()A .当121122x x -<<<时,恒有()()12f x f x >B .若当(0,]x m ∈时,()f x 的最小值为34,则m 的取值范围为17,26⎡⎤⎢⎥⎣⎦C .存在实数k ,使函数()()F x f x kx =-有5个不相等的零点D .若关于x 的方程3()[()]04f x f x a ⎡⎤--=⎢⎥⎣⎦所有实数根之和为0,则34a =-【正确答案】ACD【分析】根据奇函数的定义确定()f x 在(1,0)-上单调性与性质,然后由函数值大小可判断A ,由函数解析式分段求函数值的范围后可判断B ,由直线y kx =与函数()f x 的图象交点个数判断C ,求出3()4f x =的根是17,26,然后确定a 值使()f x a =根的和为53-即可判断D .【详解】选项A ,()f x 是奇函数,10x -≤<时,22()()[()()1]1f x f x x x x x =--=----+=---213()24x =-+-,在1(,0)2-上递减,且()0f x <,()f x 是奇函数,则(0)0f =,01x <≤时,2213()1()24f x x x x =-+=-+,在1(0,)2上递减,但()0f x >,因此()f x 在11(,)22-上不是增函数,A 错;选项B ,当01x <≤时,2213()1()24f x x x x =-+=-+,13()24f =,因此12m ≥,当1m >时,1()21f x x =-是减函数,由13214x =-得76x =,因此76m ≤,综上有1726m ≤≤,B 正确;选项C ,易知0x =是()F x 的一个零点,由于(1)1f =,y kx =过点(1,1)时,1k =,此时由21y xy x x =⎧⎨=-+⎩得21x x x -+=,2(1)0x -=,121x x ==,即直线y x =与21y x x =-+在点(1,1)处相切,因此1k >时,直线y kx =与21(01)y x x x =-+<<的图象只有一交点,在01k <<时,直线y kx =与1(1)21y x x =>-只有一个交点,从而0k >时,直线y kx =与()F x 的图象有三个交点,而0x >时,()0f x >,因此0k ≤,直线y kx =与()F x 的图象无交点,所以直线y kx =与()F x 的图象不可能是5个交点,即函数()()F x f x kx =-不可能有5个不相等的零点,C 错;选项D ,由上讨论知3()4f x =的解为12x =和76x =,因此若关于x 的方程3()[()]04f x f x a ⎡⎤--=⎢⎥⎣⎦所有实数根之和为0,由()f x 是奇函数知若34a =-,则()f x a =的解是12x =-和76x =-,符合题意,但513(537213f ==⨯-(由此讨论知3()7f x =只有一解),即53()37f -=-,即37a =-时,关于x 的方程3()[()]04f x f x a ⎡⎤--=⎢⎥⎣⎦所有实数根之和也为0,D 错.故选:ACD .方法点睛:解决分段函数的零点与交点问题,把零点问题转化为直线与函数图象交点问题进行处理,从而利用函数的性质确定出函数解析式,作出函数图象,观察出结论并找到解题思路.三、填空题13.已知弧长为πcm 3的弧所对圆周角为6π,则这条弧所在圆的半径为____________cm .【正确答案】1【分析】由弧度制公式lrα=求解即可得出答案.【详解】已知弧长为πcm 3的弧所对圆周角为6π,则所对的圆心角为π3,lrα=,313l r ππα∴===,故1.14.已知函数()()22,1log 1,1x ax f x x x ⎧+≤⎪=⎨->⎪⎩,若()02f f ⎡⎤=⎣⎦,则实数a 的值为_________.先求()03f =,再代入求()3f ,求实数a 的值.【详解】()00223f =+=,()()03log 22a f f f ⎡⎤===⎣⎦,即22a =,又0a >,且1a ≠,所以a =15.若函数()log a f x x =(0a >且1a ≠)在1,42⎡⎤⎢⎥⎣⎦上的最大值为2,最小值为m,函数()(32g x m =+[0,)+∞上是增函数,则a m -的值是____________.【正确答案】3【分析】根据对数函数的单调性,分类讨论,再结合已知进行求解得出a 和m 的值,最后根据()g x 的单调性检验即可得到.【详解】当1a >时,函数()log a f x x =是正实数集上的增函数,而函数()log a f x x =在1,42⎡⎤⎢⎥⎣⎦上的最大值为2,因此有(4)log 42a f ==,解得2a =,所以21log 12m ==-,此时()g x =[)0,∞+上是增函数,符合题意,因此()213a m -=--=;当01a <<时,函数()log a f x x =是正实数集上的减函数,而函数()log a f x x =在1,42⎡⎤⎢⎥⎣⎦上的最大值为2,因此有11log 222a f ⎛⎫== ⎪⎝⎭,a =44m ==-,此时()g x =-在[)0,∞+上是减函数,不符合题意.综上所述,2a =,1m =-,3a m -=.故3.16.若函数()()()sin cos 0f x x x ϕϕ<π=++<的最大值为2,则常数ϕ的值为_______.【正确答案】2π根据两角和的正弦公式以及辅助角公式即可求得()()f x x θ=+,可得2=,即可解出.【详解】因为()()()cos sin sin 1cos f x x x x ϕϕθ=++=+,2=,解得sin 1ϕ=,因为0ϕπ<<,所以2ϕπ=.故答案为.2π四、解答题17.在①22{|1}1x A x x -=<+,②{||1|2}A x x =-<,③23{|log }1xA x y x -==+这三个条件中任选一个,补充在下面的横线上,并回答下列问题.设全集U =R ,______,22{|0}.B x x x a a =++-<(1)若2a =,求()()U UC A C B ;(2)若“x A ∈”是“x B ∈”的充分不必要条件,求实数a 的取值范围.【正确答案】(1)1{}1|x x x ≤-≥或(2)(][),34,-∞-⋃+∞【分析】(1)根据除法不等式,绝对值不等式,对数函数的定义域即可分别求出三种情形下的集合A ;(2)对集合B 中不等式进行因式分解,再根据充分必要条件和集合包含关系即可求解.【详解】(1)若选①:222213{|1}{|0}{|0}{|13}1111x x x x A x x x x x x x x x --+-=<=-<=<=-<<++++,()22{|0}{|()10}{|(2)(1)0}B x x x a a x x a x a x x x ⎡⎤=++-<=++-<=+-<⎣⎦,所以{|2<1}B x x =-<,{|13}U C A x x x =≤-≥或,{|21}U C B x x x =≤-≥或,故()()U U C A C B ⋃=1{}1|x x x ≤-≥或.若选②:{|12}{|212}{|13}A x x x x x x =-<=-<-<=-<<()22{|0}{|()10}{|(2)(1)0}B x x x a a x x a x a x x x ⎡⎤=++-<=++-<=+-<⎣⎦,所以{|2<1}B x x =-<,{|13}U C A x x x =≤-≥或,{|21}U C B x x x =≤-≥或,故()()U U C A C B ⋃=1{}1|x x x ≤-≥或.若选③:()(){}233{|log }031011x x A x y x x x x x x ⎧⎫--====-+=⎨⎬++⎩⎭{|13}x x -<<,()22{|0}{|()10}{|(2)(1)0}B x x x a a x x a x a x x x ⎡⎤=++-<=++-<=+-<⎣⎦,所以{|2<1}B x x =-<,{|13}U C A x x x =≤-≥或,{|21}U C B x x x =≤-≥或,故()()U U C A C B ⋃=1{}1|x x x ≤-≥或.(2)由(1)知{|13}A x x =-<<,()22{|0}{|()10}B x x x a a x x a x a ⎡⎤=++-<=++-<⎣⎦,因为“x A ∈”是“x B ∈”的充分不必要条件,(i )若(1)a a -<--,即12a >,此时{|(1)}B x a x a =-<<--,所以1,3(1)aa -≥-⎧⎨≤--⎩等号不同时取得,解得4a ≥.故4a ≥.(ii )若(1)a a -=--,则B =∅,不合题意舍去;(iii )若(1)a a ->--,即12a <,此时{|(1)}B x a x a =--<<-,1(1),3a a -≥--⎧⎨≤-⎩等号不同时取得,解得3a ≤-.综上所述,a 的取值范围是(][),34,-∞-⋃+∞.18.(1)已知sin 2cos 0αα-=,求22sin cos sin 3sin cos 2cos αααααα--的值;(2)已知4sin()5απ+=,且sin cos 0αα<,求()()()2sin 3tan 34cos παπααπ----的值.【正确答案】(1)12-;(2)73.【分析】(1)先求出tan 2α=,再进行弦化切代入即可求解;(2)先求出4sin 5α=-,3cos 5α=,得到4tan 3α=-,再进行诱导公式和弦化切变换,代入即可求解.【详解】(1)由sin 2cos 0αα-=知tan 2α=∴原式=2tan 21tan 3tan 24622ααα==-----(2) 4sin()5απ+=∴4sin 05α=-<又sin cos 0αα<∴cos 0α>∴3cos 5α==∴4tan 3α=-原式=()()2sin 3tan 4cos απαπα---=2sin 3tan 4cos ααα+-=44237533345⎛⎫⎛⎫⨯-+⨯- ⎪ ⎪⎝⎭⎝⎭=-⨯19.已知函数()323log 1x f x x -=-.(1)求函数()f x 的解析式及定义域;(2)求函数()f x 在()(),00,2x ∈-∞⋃时的值域.【正确答案】(1)()()12031xf x x =-≠-,()f x 的定义域为()(),00,∞-+∞U (2)()15,3,8⎛⎫-∞⋃+∞ ⎪⎝⎭【分析】(1)利用换元法求得函数的解析式,根据函数定义域的求法,求得函数的定义域.(2)结合3x 的取值范围来求得()f x 在()(),00,2x ∈-∞⋃时的值域.【详解】(1)对于3log x ,需0x >;对231x x --,需1x ≠;则()()3log ,00,x ∈-∞⋃+∞,令3log t x =,则0t ≠,3t x =,()()231123312313131tt t t t f t ⋅--⋅-===----,所以()()12031x f x x =-≠-,即()f x 的定义域为()(),00,∞-+∞U .(2)当0x <时,11031,1310,1,13131x xxx <<-<-<<-->--,12331x ->-.当02x <<时,1111139,0318,,318318x xx x <<<-<>-<---,1115223188x-<-=-.所以()f x 在()(),00,2x ∈-∞⋃时的值域为()15,3,8⎛⎫-∞⋃+∞ ⎪⎝⎭.20.已知函数()24f x x π⎛⎫=- ⎪⎝⎭,x R ∈.(1)求函数()f x 的最小正周期和单调递减区间;(2)求函数()f x 在区间,82ππ⎡⎤-⎢⎣⎦上的最小值和最大值,并求出取得最值时x 的值.【正确答案】(1)最小正周期为π,单调减区间是5,88k k ππππ⎡⎤++⎢⎥⎣⎦,Z k ∈;(2)max ()f x =,此时8x π=,min ()1f x =-,此时2x π=.【分析】(1)直接利用周期公式计算周期,再利用整体代入法求余弦型函数的单调减区间即可;(2)先求出24x π-的取值范围,再利用余弦函数的性质求最值及取最值的条件即可.【详解】解:(1)()f x 的最小正周期22||2T πππω===.令2224k x k ππππ≤-≤+,解得588k x k ππππ+≤≤+,Z k ∈,此时时,()f x 单调递减,()f x ∴的单调递减区间是5,88k k ππππ⎡⎤++⎢⎥⎣⎦,Z k ∈;(2),82x ππ⎡⎤∈-⎢⎥⎣⎦,则32,424x πππ⎡⎤-∈-⎢⎥⎣⎦,故cos 2,142x π⎡⎤⎛⎫-∈⎢⎥ ⎪⎝⎭⎣⎦,()24f x x π⎛⎫⎡=-∈- ⎪⎣⎝⎭,max ()f x ∴=cos 214x π⎛⎫-= ⎪⎝⎭,即204x π-=,即8x π=;min ()1f x =-,此时cos 242x π⎛⎫-=- ⎪⎝⎭,即3244x ππ-=,即2x π=.方法点睛:解决三角函数()cos y A x ωϕ=+的图象性质,通常利用余弦函数的图象性质,采用整体代入法进行求解,或者带入验证.21.2022年冬天新冠疫情卷土重来,我国大量城市和地区遭受了奥密克戎新冠病毒的袭击,为了控制疫情,某单位购入了一种新型的空气消毒剂用于环境消毒,已知在一定范围内,每喷洒1个单位的消毒剂,空气中释放的浓度(y 单位:毫克/立方米)随着时间(x 单位:小时)变化的关系如下:当04x 时,1618y x =--;当410x <时,15.2y x =-若多次喷洒,则某一时刻空气中的消毒剂浓度为每次投放的消毒剂在相应时刻所释放的浓度之和.由实验知,当空气中消毒剂的浓度不低于4(毫克/立方米)时,它才能起到杀灭空气中的病毒的作用.(1)若一次喷洒4个单位的消毒剂,则有效杀灭时间可达几小时?(2)若第一次喷洒2个单位的消毒剂,6小时后再喷洒(14)a a 个单位的消毒剂,要使接下来的4小时中能够持续有效消毒,试求a 的最小值.(精确到0.1取1.4)【正确答案】(1)8(2)1.6【分析】(1)根据喷洒4个单位的净化剂后浓度为()644,048202,410x f x x x x ⎧-≤≤⎪=-⎨⎪-<≤⎩,由()4f x ≥求解;(2)得到从第一次喷洒起,经()610x x ≤≤小时后,浓度为()()116251286g x x a x ⎛⎫⎛⎫=-+- ⎪ ⎪ ⎪--⎝⎭⎝⎭,化简利用基本不等式求解.【详解】(1)解:因为一次喷洒4个单位的净化剂,所以其浓度为()644,0448202,410x f x y x x x ⎧-≤≤⎪==-⎨⎪-<≤⎩,当04x ≤≤时,64448x-≥-,解得0x ≥,此时04x ≤≤,当410x <≤时,2024x -≥,解得8x ≤,此时48x <≤,综上08x ≤≤,所以若一次喷洒4个单位的消毒剂,则有效杀灭时间可达8小时;(2)设从第一次喷洒起,经()610x x ≤≤小时后,其浓度为()()116251286g x x a x ⎛⎫⎛⎫=-+- ⎪ ⎪ ⎪--⎝⎭⎝⎭,1616101441414a ax a x a x x=-+-=-+----,因为[][]144,8,1,4x a -∈∈,所以161444414a x a a a x -+--≥--=---,当且仅当161414ax x-=-,即14x =-时,等号成立;所以其最小值为4a --,由44a -≥,解得244a -≤,所以a 的最小值为24 1.6-≈.22.我们知道,指数函数()xf x a =(0a >,且1a ≠)与对数函数()log a g x x =(0a >,且1a ≠)互为反函数.已知函数()2xf x =,其反函数为()g x .(1)求函数()()()223F x g x tg x =-+⎡⎤⎣⎦,[]2,8x ∈的最小值;(2)对于函数()x ϕ,若定义域内存在实数0x ,满足()()00x x ϕϕ-=-,则称()x ϕ为“L 函数”.已知函数()()()223,1,3,1f x mf x x h x x ⎧⎡⎤--≥-⎪⎣⎦=⎨-<-⎪⎩为其定义域上的“L 函数”,求实数m 的取值范围.【正确答案】(1)答案见解析(2)[)1,∞-+【分析】(1)利用换元法令2log ,[1,3]p x p =∈,可得所求为关于p 的二次函数,根据二次函数的性质,分析讨论,即可得答案.(2)根据题意,分别讨论在[1,1]-、(,1)-∞-和(1,)+∞上存在实数0x ,满足题意,根据所给方程,代入计算,结合函数单调性,分析即可得答案.【详解】(1)由题意得2()log g x x=所以()()()()222223log 2log 3F x g x tg x xt x =-+=-+⎡⎤⎣⎦,[]2,8x ∈,令2log ,[1,3]p x p =∈,设2()23,[1,3]M p p tp p =-+∈则()M p 为开口向上,对称轴为p t =的抛物线,当1t ≤时,()M p 在[1,3]上为单调递增函数,所以()M p 的最小值为(1)42M t =-;当13t <<时,()M p 在(1,)t 上单调递减,在(,3)t 上单调递增,所以()M p 的最小值为2()3M t t =-;当3t ≥时,()M p 在[1,3]上为单调递减函数,所以()M p 的最小值为(3)126M t =-;综上,当1t ≤时,()F x 的最小值为42t -,当13t <<时,()F x 的最小值为23t -,当3t ≥时,()F x 的最小值为126t-(2)①设在[1,1]-上存在0x ,满足()()00x x ϕϕ-=-,则0000114234230x x x x m m +--+-⋅-+-⋅-=,令0022x x t -=+,则2t ≥=,当且仅当00x =时取等号,又0[1,1]x ∈-,所以115222t -≤+=,即52,2t ⎡⎤∈⎢⎥⎣⎦,所以00001124234232260x x x x m m t mt +--+-⋅-+-⋅-=---=,所以28471,2220t t m t t -⎡⎤==---⎢⎥⎣⎦所以71,20m ⎡⎤∈--⎢⎥⎣⎦②设在(,1)-∞-存在0x ,满足()()00x x ϕϕ-=-,则00134230x x m --+-+-⋅-=,即001232x x m --=-⋅有解,因为1232x x y --=-⋅在(,1)-∞-上单调递减,所以12m >-,同理当在(1,)+∞存在0x ,满足()()00x x ϕϕ-=-时,解得12m >-,所以实数m 的取值范围[)1,∞-+解题的关键是理解新定义,并根据所给定义,代入计算,结合函数单调性及函数存在性思想,进行求解,属难题。
海南省2023-2024学年高一上学期期末考试 物理含解析

2023-2024学年度第一学期高一年级期末考试物理试题(答案在最后)(考试时间:90分钟)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,本试卷由考生自己保留,将答题卡交回。
一、单项选择题(本题共8小题,每小题3分,共24分。
在每个小题给出的四个选项中,只有一个选项符合题意)1.公元前4世纪末,我国的《墨经》中提到“力,形之所以奋也”,意为力是使有形之物突进或加速运动的原因。
力的单位用国际单位制的基本单位符号来表示,正确的是()A.1kg m s -⋅⋅ B.2kg m s -⋅⋅ C.2Pa m ⋅ D.1J m -⋅2.如图是一皮带传动装置的示意图,右轮半径为r ,A 是它边缘上的一点。
左侧是一轮轴,大轮半径为4r ,小轮半径为2r 。
B 点在小轮上,到小轮中心的距离为r 。
C 点和D 点分别位于小轮和大轮的边缘上。
如果传动过程中皮带不打滑,则()A.A 和B 的线速度大小相等B.C 和D 的线速度大小相等C.A 和C 的角速度大小相等D.B 和D 的角速度大小相等3.如图所示能正确描述质点运动到P 点时的速度v 和加速度a 的方向关系的是()A. B.C. D.4.如图所示,粗糙的水平地面上放置一质量m=10kg的物块,物块与地面之间的动摩擦因数μ=0.2,物块右端连接有一根劲度系数k=100N/m的轻质弹簧。
现在弹簧的右端施加一水平向右的拉力F=10N,设最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2。
以下说法中正确的是()A.物块受到的弹力只有一个B.物块将向右运动C.水平地面受到的摩擦力方向向右,大小为10ND.弹簧的伸长量为20cm5.如图所示,轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小铁球,在电梯运行时,乘客发现弹簧的伸长量比电梯静止时的伸长量大了,这一现象表明()A.电梯的加速度方向一定是向上B.乘客处于失重状态C.电梯一定是在下降D.电梯的加速度方向一定是向下6.如图所示,质量分别为m和2m的A,B两物块,用一轻弹簧相连,将A用轻绳悬挂于天花板上,用一木板托住物块B.调整木板的位置,当系统处于静止状态时,悬挂A物块的悬绳恰好伸直且没有拉力,此时轻弹簧的形变量为x突然撤去木板,重力加速度为g,物体运动过程中,弹簧始终在弹性限度内,则下列说法正确的是()A.撤去木板瞬间,B 物块的加速度大小为gB.撤去木板瞬间,B 物块的加速度大小为0.5gC.撤去木板后,B 物块向下运动3x 时速度最大D.撤去木板后,B 物块向下运动2x 时速度最大7.一艘船的船头始终正对河岸方向行驶,如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 集合{}{}R x y y B R x x y y A x ∈==∈+==,2,,1,则A B ⋂等于
A. ()+∞,0
B. {}1,0
C. {}1,2
D. {})2,1(),1,0(
2.函数23212---=x x x y 的定义域 A. ]1,(-∞ B. ]2,(-∞ C. ]1,21()21
,(-⋂--∞ D. ]1,2
1()21,(-⋃--∞ 3.若直线10mx y +-=与直线230x y -+=平行,则m 的值为
A. 2
B. 2-
C. 12
D. 12
- 4.直线0ax by c ++=经过第一、第二、第四象限,则,,a b c 应满足
A .ab >0,bc >0
B .ab >0,bc <0
C .ab <0,bc >0
D .ab <0,bc <0
5.已知两条不同的直线n m ,,两个不同的平面βα,,则下列命题中正确的是
A.若,,//,βαβα⊥⊥n m 则n m ⊥
B.若,,,//βαβα⊥⊥n m 则n m //
C.若,,,βαβα⊥⊥⊥n m 则n m ⊥
D.若,//,//,//βαβαn m 则n m //
6. 已知圆锥的表面积为6π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径为
A .21+
B .2
C .3
D .2
7. 两条平行线1l :3x -4y -1=0,与2l :6x -8y -7=0间的距离为
A.12
B. 35
C. 65 D .1
8.在梯形ABCD 中,o ABC 90=∠,//,222AD BC BC AD AB === .将梯形ABCD 绕
AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为
A.23π
B.43π
C.53
π D.2π 9.设c b a ,,均为正数,且a a
21log 2=,b b 21log 21=⎪⎭⎫ ⎝⎛,c c 2log 21=⎪⎭⎫ ⎝⎛.则 A .c b a << B .a b c << C . b a c << D . c a b <<
10.某三棱锥的三视图如右图所示,该三棱锥的表面积是
A .56125+
B . 60125+
C .3065+
D . 2865+
11.已知函数2
)(|,|23)(x x g x x f =-=,构造函数⎩⎨⎧>≥=)()(),()()(),()(x f x g x f x g x f x g x F ,那么函数)(x F y =
A. 有最大值1,最小值1-
B. 有最大值1,无最小值
C. 有最小值1-,无最大值 D .有最大值3,最小值1
12. 已知球的直径4SC =,B A ,是球面上的两点2AB =, 045BSC ASC ∠=∠=,则棱锥S ABC -的体积是
A. 335
B. 334
C. 332
D. 3
3 二.填空题: 本大题共4小题,每小题5分,共20分.
13.过点)2,1(且与直线3450x y +-=垂直的直线方程_______________.
14.长方体的一个顶点上三条棱长分别是3、4、5,且它的八个顶点都在同一球面上,这个球的表面积是_______________.
15.函数log (1)8a y x =-+(0a >且1)a ≠的图象恒过定点P ,P 在幂函数()f x 的图象上, 则(3)f =___________.
16.如图,已知四棱锥ABCD P -,底面ABCD 为正方形,⊥PA 平面ABCD .给出下列
命题:
①AC PB ⊥;②平面PAB 与平面PCD 的交线与AB 平行;
③平面⊥PBD 平面PAC ;④PCD ∆为锐角三角形.
其中正确命题的序号是_______________. (写出所有正确命题的序号)
三.解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17. (本小题满分10分)
A B D
C P
已知点)1,2(-P ,求:
(Ⅰ)过点P 且与直线032=+-y x 平行的直线方程;
(Ⅱ)过点P 且与原点距离为2的直线方程.
18. (本小题满分12分)
设U R =,}{}{13
,24A x x B x x =≤≤=<<,}{1C x a x a =≤≤+(a 为实数) (Ⅰ)分别求A
B ,()U A
C B ; (Ⅱ)若B C C =,求a 的取值范围.
19. (本小题满分12分)
如下的三个图中,分别是一个长方体截去一个角所得多面体的直观图以及它的主视图和左(侧)视图(单位:cm )
(Ⅰ)按照给出的尺寸,求该多面体的体积;
(Ⅱ)在所给直观图中连结'BC ,证明:'BC ∥面EFG .
20. (本小题满分12分)
如图,在三棱锥V ABC -中,平面VAB ⊥平面ABC ,VAB ∆为等边三角形,AC BC ⊥且2AC BC ==,,O M 分别为AB ,VA 的中点.
(Ⅰ)求证:平面MOC ⊥平面VAB ;
(Ⅱ)求三棱锥A MOC -的体积.
21.(本小题满分12分)
已知函数)32(log )(2
21+-=ax x x f .
(Ⅰ)若函数的定义域为R ,求实数a 的取值范围; (Ⅱ)若函数的值域为]1,(--∞,求实数a 的值;
(Ⅲ)若函数在区间)1,21(上为增函数,求实数a 的取值范围.
22.(本小题满分12分)
如图甲,⊙O 的直径2AB =,圆上两点,C D 在直径AB 的两侧,使o o DAB CAB 60,45=∠=∠,沿直径AB 折起,使两个半圆所在的平面互相垂直(如图乙),F 为BC 的中点,E 为AO 的中点.P 为AC 上的动点,根据图乙解答下列各题:
(Ⅰ)求三棱锥ABC D -的体积.
(Ⅱ)求证:不论点P 在何位置,都有DE ⊥BP ;
(Ⅲ)在BD 弧上是否存在一点G ,使得FG ∥平面ACD 若存在,试确定点G 的位置,并给出证明;若不存在,请说明理由.
|。
