材料力学 截面几何特性
合集下载
材料力学 截面的几何性质

附
录
附录Ⅰ
§Ⅰ-1 §Ⅰ-2 §Ⅰ-3 §Ⅰ-4
截面的几何性质
截面的静矩和形心位置 惯性矩、惯性积和惯性半径 平行移轴公式 转轴公式 主惯性矩
静矩与形心
一、静矩的定义(与力矩类似)(也称面积矩或一次矩) 截面对z轴的静矩: y 截面对y轴的静矩:
Sz Sy
dS
A A
z
ydA
A
3
z 100
I
C
CI
a1 a2
I y I yI I yII 443 10 768 10
4
4
y
1211 104 mm 4
由于z轴是对称轴 ,故图形对两轴的惯性积为
140 103.3
CII
II
y
I yz 0
20
I z y 2 dA 2h y 2 bdy
3
附
录
组合截面形心
组合截面:如果截面的图形是由几个简单图形(如矩形、圆形 等)组成的,这种截面称为组合截面。 组合截面对X、Y轴静矩的计算:
S x Ai yci Ayc
i
n
S y Ai xci Axc
i
n
Ai——任一简单图形的面积; xci,yci——任一简单图形的形心坐标; n——全部简单图形的个数。 确定组合截面形心位置的公式:
C H/2
X
1 h 1 h yc 1 y1 ( y1 ) ( y1 ) 2 2 2 2
h 1 h S x Ayc 1 b( y 1 ) ( y 1 ) 2 2 2
b
b 2 2 (h 4y1 ) 8
例2、图形对 x 轴的静矩为
录
附录Ⅰ
§Ⅰ-1 §Ⅰ-2 §Ⅰ-3 §Ⅰ-4
截面的几何性质
截面的静矩和形心位置 惯性矩、惯性积和惯性半径 平行移轴公式 转轴公式 主惯性矩
静矩与形心
一、静矩的定义(与力矩类似)(也称面积矩或一次矩) 截面对z轴的静矩: y 截面对y轴的静矩:
Sz Sy
dS
A A
z
ydA
A
3
z 100
I
C
CI
a1 a2
I y I yI I yII 443 10 768 10
4
4
y
1211 104 mm 4
由于z轴是对称轴 ,故图形对两轴的惯性积为
140 103.3
CII
II
y
I yz 0
20
I z y 2 dA 2h y 2 bdy
3
附
录
组合截面形心
组合截面:如果截面的图形是由几个简单图形(如矩形、圆形 等)组成的,这种截面称为组合截面。 组合截面对X、Y轴静矩的计算:
S x Ai yci Ayc
i
n
S y Ai xci Axc
i
n
Ai——任一简单图形的面积; xci,yci——任一简单图形的形心坐标; n——全部简单图形的个数。 确定组合截面形心位置的公式:
C H/2
X
1 h 1 h yc 1 y1 ( y1 ) ( y1 ) 2 2 2 2
h 1 h S x Ayc 1 b( y 1 ) ( y 1 ) 2 2 2
b
b 2 2 (h 4y1 ) 8
例2、图形对 x 轴的静矩为
材料力学截面的几何性质

I z I zi
i
,I y I yi,
i
2 I y dA , 元面积对z轴的惯性矩就等于将各元 因 z
面积对z轴的惯性矩求和,因质量连续分布,求和则为积 分。
应用于圆环的情形,可看成两个圆形截面,
I I 1 I 2 I z I y 2I z 2I y,
定义:I A 2 dA
I zy A zydA ——平面图形对z,y轴的惯性积;
极惯性矩.
• 二、性质
1、 I z、I y 恒为正, I zy 可正、可负、也可以为零,其正 负值与坐标轴的位置有关。 2、单位:(长度)4;
例4-4 : 计算直径为d的圆截面对形心轴z,y的惯性矩 和惯性积。 解:用平面极坐标 (r , ).
y
dy
R
o
y
sz A ydA y z dy
z
z
0 2 R sin cos d
3 2
dz
R3 3
y R
o
z
z
sz 4R 3 yc 2 A R 3 4
R3
z R cos y R sin dy R cosd
sz A zdA z y dz
270 50
S y zci Ai 0,( z1 z2 0);
i
y
s z yci Ai y1 A1 y2 A2 15 300 30
i
270 30 270 50 23.625 105 (mm) 2 , 2
• 4-2 惯性矩和惯性积
1 d 4 64
因坐标轴是对称轴,如对左右的 dA (如上图),
i
,I y I yi,
i
2 I y dA , 元面积对z轴的惯性矩就等于将各元 因 z
面积对z轴的惯性矩求和,因质量连续分布,求和则为积 分。
应用于圆环的情形,可看成两个圆形截面,
I I 1 I 2 I z I y 2I z 2I y,
定义:I A 2 dA
I zy A zydA ——平面图形对z,y轴的惯性积;
极惯性矩.
• 二、性质
1、 I z、I y 恒为正, I zy 可正、可负、也可以为零,其正 负值与坐标轴的位置有关。 2、单位:(长度)4;
例4-4 : 计算直径为d的圆截面对形心轴z,y的惯性矩 和惯性积。 解:用平面极坐标 (r , ).
y
dy
R
o
y
sz A ydA y z dy
z
z
0 2 R sin cos d
3 2
dz
R3 3
y R
o
z
z
sz 4R 3 yc 2 A R 3 4
R3
z R cos y R sin dy R cosd
sz A zdA z y dz
270 50
S y zci Ai 0,( z1 z2 0);
i
y
s z yci Ai y1 A1 y2 A2 15 300 30
i
270 30 270 50 23.625 105 (mm) 2 , 2
• 4-2 惯性矩和惯性积
1 d 4 64
因坐标轴是对称轴,如对左右的 dA (如上图),
截面几何性质(材料力学)
§-4 惯性矩和惯性积的转轴公式 截面的主惯性轴和主惯性矩
1.惯性矩和惯性积的转轴公式
y
bh3 Iz 12
C z
bh3 Iz' 12
h
b
y
注意: 1. 两个座标系的原点 必须重合; 2. 两轴惯性矩之和为常量
z
O
I y1 I
z1
I y I I p z
I z1 I y1
4)解法四 y1 I z I z1
I z0 I z0 1 I z0 2 I z0 3 I z0 4
A3 y
d 4
64
2 I y 2 I z0 3 I z0 3
d4
64 Iy
2
A2 z0
d
4
128
I z I z1 I z0 3 OC
d
2
d4 Iy 128 18
1) 极惯性矩、惯性矩和惯性积均与所取的坐标系有关, 2) 惯性积可正可负 3) 单位m4 或 mm4
y dA
4. 惯性半径
Iy iy A
Iz iz A
y
(单位m 或 mm)
O
z z
例
试计算图示矩形截面对于其对称轴x和y的惯性矩。
y dy
解: 取平行于x轴的狭长条, 则 dA=b dy
h
1 2
I zc I yc
2
4 I 2c zc 321104 mm4 y
I yc 0 I min
I zc I yc 2
1 2
I zc I yc
2
4 I 2c zc 57.4 104 mm 4 y
材料力学截面的几何性质课件

材料力学截面的几何 性质课件
目录
• 截面的基本性质 • 截面的二次矩 • 截面的抗弯截面系数 • 截面的抗扭截面系数 • 材料力学截面的应用
01 截面的基本性质
截面的面积
面积
截面面积是二维平面图形被截后,与 原图形相比增加的面积。对于矩形、 圆形、三角形等简单形状,截面面积 可以通过几何公式直接计算。
的刚度和稳定性。
截面惯性矩
截面惯性矩是衡量截面抗弯刚度 的指标,对于承受弯矩的构件, 选择具有较大惯性矩的截面可以
减少挠度和转角。
截面抵抗矩
截面抵抗矩是衡量截面抗剪切能 力的指标,对于承受剪力的构件 ,选择具有较大抵抗矩的截面可
以增加构件的承载能力。
工程设计中的应用
桥梁设计
在桥梁设计中,需要考虑梁的截面尺寸、材料类型和截面形式等 因素,以确保桥梁具有足够的强度和刚、单位等因素,以确保数 据处理结果的准确性和可靠性。
1.谢谢聆 听
根据微面积和其对应的主 轴方向余弦,计算出截面 二次矩。
主轴的确定
根据计算出的惯性矩,找 出三个主轴的方向余弦和 角度。
实例分析
圆截面
圆截面的二次矩为常数, 且各主轴与截面垂直,说 明圆截面在弯曲时没有翘 曲的趋势。
矩形截面
矩形截面的二次矩与宽度 的平方成正比,说明矩形 截面有较好的抗弯能力。
工字形截面
工字形截面的二次矩比同 样面积的矩形截面小,但 抗弯能力仍高于同样重量 的实心杆件。
03 截面的抗弯截面系数
定义与性质
01
抗弯截面系数是截面对其轴线的惯性矩除以截面的面积 得到的数值,用来度量截面在弯矩作用下抵抗变形的能 力。
02
不同形状的截面有不同的抗弯截面系数,如圆截面为1 ,矩形截面为1.13,工字形截面为1.44等。
目录
• 截面的基本性质 • 截面的二次矩 • 截面的抗弯截面系数 • 截面的抗扭截面系数 • 材料力学截面的应用
01 截面的基本性质
截面的面积
面积
截面面积是二维平面图形被截后,与 原图形相比增加的面积。对于矩形、 圆形、三角形等简单形状,截面面积 可以通过几何公式直接计算。
的刚度和稳定性。
截面惯性矩
截面惯性矩是衡量截面抗弯刚度 的指标,对于承受弯矩的构件, 选择具有较大惯性矩的截面可以
减少挠度和转角。
截面抵抗矩
截面抵抗矩是衡量截面抗剪切能 力的指标,对于承受剪力的构件 ,选择具有较大抵抗矩的截面可
以增加构件的承载能力。
工程设计中的应用
桥梁设计
在桥梁设计中,需要考虑梁的截面尺寸、材料类型和截面形式等 因素,以确保桥梁具有足够的强度和刚、单位等因素,以确保数 据处理结果的准确性和可靠性。
1.谢谢聆 听
根据微面积和其对应的主 轴方向余弦,计算出截面 二次矩。
主轴的确定
根据计算出的惯性矩,找 出三个主轴的方向余弦和 角度。
实例分析
圆截面
圆截面的二次矩为常数, 且各主轴与截面垂直,说 明圆截面在弯曲时没有翘 曲的趋势。
矩形截面
矩形截面的二次矩与宽度 的平方成正比,说明矩形 截面有较好的抗弯能力。
工字形截面
工字形截面的二次矩比同 样面积的矩形截面小,但 抗弯能力仍高于同样重量 的实心杆件。
03 截面的抗弯截面系数
定义与性质
01
抗弯截面系数是截面对其轴线的惯性矩除以截面的面积 得到的数值,用来度量截面在弯矩作用下抵抗变形的能 力。
02
不同形状的截面有不同的抗弯截面系数,如圆截面为1 ,矩形截面为1.13,工字形截面为1.44等。
材料力学截面的几何性质课件

截面的对称性
截面可以是对称的或非对称的。
对称截面是指沿中心线对称的截面,如圆形、正 方形等。
非对称截面是指不沿中心线对称的截面,如椭圆 形、三角形等。
截面的重心
重心是物体质量的集中点,对于规则形状的物体,重心位置可以通过几何计算得 到。
对于截面,重心是截面质量的集中点,其位置可以通过计算截面的面积和质量得 到。
材料力学的发展历程
总结词
材料力学的发展经历了多个阶段,从最早的实验观察到现代的理论建模和计算机模拟。
详细描述
最初的材料力学研究主要基于实验观察和经验总结,随着数学和物理学的发展,人们开始建立更精确 的理论模型,并使用计算机进行模拟和分析。这些理论模型和方法在解决复杂工程问题方面发挥了重 要作用。
02
意义
主惯性矩是衡量截面抗弯和抗扭能力的一个重要参数,其 值越大,抗弯和抗扭能力越强。
04
材料力学截面的弯曲性质
弯曲的定义
弯曲是指物体在力的作用下发 生形变,其中物体的一部分相 对于另一部分发生转动。
弯曲变形通常发生在梁、柱等 细长结构中,其中截面上的应 力分布不均匀。
弯曲变形可以通过施加外力或 重力等作用力引起,也可以由 热膨胀、收缩等因素引起。
扭转的变形能
1 2
变形能
物体在受到外力作用时,由于发生变形而储存的 能量称为变形能。
扭转变形能
物体在扭转变形时,由于变形而储存的能量称为 扭转变形能。
3
扭转变形能的计算
扭转变形能可以通过计算截面上的剪切应变和剪 切胡克常数来计算。
扭转的稳定性
01
稳定性
在材料力学中,稳定性是指物体在外力作用下保持其平衡状态的能力。
剪切变形能
材料力学 3 截面的几何性质

大小:正,负,0。
y
量纲:[长度]3
二、截面的形心 几何形心=等厚均质薄片重心 z 形心坐标公式:
yc
C
zc
yc zc
y dA A z dA
A
A
Sz A Sy A
O
A
y
S y A zc
S z A yc
结论: 若 S z 0 yc 0 z 轴通过形心。反之,亦成立。
转轴公式
sin 2 I yz cos2
I y1 I z1 I y I z
二、形心主轴和形心主惯性矩 1、主轴和主惯性矩:坐标旋转到= 0 时,
Ix y
0 0
Ix I y 2
sin20 I xy cos 20 0
tan 2 0
2 I xy Ix Iy
z1
I yzc y1 z1 dA
A
a
O
z
yc
I z A y 2dA A (b y1 )2 dA
2 A ( y1 2by1 b 2 )dA
y
zc 为形心轴, S zc Ayc 0
I zc 2bS zc b 2 A
I zc b 2 A
2
a
2677710 .52 cm 4
平 衡 项 惯 性 矩 6686481 . 857.8 单 个 形 心 惯 性 矩 779.53
组合截面可以大大提高截面惯性矩。
I y Iz 2 cos2 I yz sin 2 cos2 I yz sin 2
I y Iz 2
I y Iz 2
当=0时,
dI y1 d
材料力学截面图形的几何性质

y dA C
y yC
S y zdA
A
O
zC z
z
图形对 z 轴的静矩
S z ydA
A
静矩的单位:m3,cm3,mm3
2
4.1 截面的静矩与形心
2.形心的位置
yC
ydA
A
A
Sz zC A ,
zdA
A
A
Sy A
静矩的性质 (1)静矩与轴有关,可正可负可为零。 (2)若yC,zC坐标轴过形心,则有
S yC 0
S zC 0
A1 c1 A2 c2
Sy
(3)组合图形静矩可分块计算求代数和
S z S z1 S z 2 A1 yC1 A2 yC 2
(4)求形心
S z A1 yC1 A2 yC 2 yC A A
A1 zC1 A2 zC 2 zC A A
3
4.1 截面的静矩与形心
O
dy
z
I y z 2dA
b 2 b 2
3 b h 2 hz dz 12
b
因为z轴(或y轴)为对称轴,故惯性积 惯性矩与惯性积
例4 试计算图示圆形截面对O点的极惯性矩IP和对于其形心 轴(即直径轴)的惯性矩Iy和Iz。 解:建立如图所示坐标系,取图示微元dA,
y
I yz yzdA
A
dA
(1)惯性积与轴有关,可正可负可 为零。
(2)若 y , z 轴有一为图形的对称轴, 则 Iyz = 0。
y
性质
O
z
z
11
4.3 平行移轴公式 1.平行移轴公式
已知任意形状的截面(如图)的面积A以及对于形心轴xC 和yC的惯性矩 I xC,I yC 及惯性积 I x y ,现需导出该截面对于 C C 与形心轴xC , yC平行的x轴和y轴的惯性矩Ix,Iy和惯性积Ixy。
y yC
S y zdA
A
O
zC z
z
图形对 z 轴的静矩
S z ydA
A
静矩的单位:m3,cm3,mm3
2
4.1 截面的静矩与形心
2.形心的位置
yC
ydA
A
A
Sz zC A ,
zdA
A
A
Sy A
静矩的性质 (1)静矩与轴有关,可正可负可为零。 (2)若yC,zC坐标轴过形心,则有
S yC 0
S zC 0
A1 c1 A2 c2
Sy
(3)组合图形静矩可分块计算求代数和
S z S z1 S z 2 A1 yC1 A2 yC 2
(4)求形心
S z A1 yC1 A2 yC 2 yC A A
A1 zC1 A2 zC 2 zC A A
3
4.1 截面的静矩与形心
O
dy
z
I y z 2dA
b 2 b 2
3 b h 2 hz dz 12
b
因为z轴(或y轴)为对称轴,故惯性积 惯性矩与惯性积
例4 试计算图示圆形截面对O点的极惯性矩IP和对于其形心 轴(即直径轴)的惯性矩Iy和Iz。 解:建立如图所示坐标系,取图示微元dA,
y
I yz yzdA
A
dA
(1)惯性积与轴有关,可正可负可 为零。
(2)若 y , z 轴有一为图形的对称轴, 则 Iyz = 0。
y
性质
O
z
z
11
4.3 平行移轴公式 1.平行移轴公式
已知任意形状的截面(如图)的面积A以及对于形心轴xC 和yC的惯性矩 I xC,I yC 及惯性积 I x y ,现需导出该截面对于 C C 与形心轴xC , yC平行的x轴和y轴的惯性矩Ix,Iy和惯性积Ixy。
材料力学第四章截面的几何性质

确定截面的剪切中心
在材料力学中,剪切中心是剪切应力作用下截面 发生剪切变形的点。通过计算截面的形心,可以 近似确定剪切中心的位置。
确定截面的质心
质心是截面质量的中心点,通过计算截面的形心, 可以近似确定质心的位置,这对于动力学分析和 稳定性分析非常重要。
03 主轴和主惯性矩
主轴的定义与计算
主轴
截面上的各点处到截面形心距离最大的方向。
预测物体的变形和破坏
通过分析截面的几何性质,可以预测 物体在不同受力条件下的变形和破坏 行为,为工程实践提供指导。
02 截面的面积和形心
截面面积的定义与计算
截面面积的定义
截面面积是指通过截面边界轮廓 线围成的区域面积。
截面面积的计算
可以通过测量截面轮廓线的长度 ,然后使用公式计算面积。对于 不规则形状,可以使用微元法或 积分法计算。
截面几何性质的应用前景
随着科技的发展和工程需求的提高,截面几何性质在材料力学中的重要性将更加凸 显,其在航空航天、交通运输、建筑等领域的应用将更加广泛。
随着新型材料的不断涌现,截面几何性质的研究将有助于深入了解这些材料的力学 行为,为新型材料的优化和应用提供理论支持。
随着数值模拟和计算机技术的发展,截面几何性质的研究将更加精确和深入,有助 于提高工程结构的分析和设计水平。
在实际工程中,主轴和主惯性矩也是 进行有限元分析时的重要输入参数, 用于模拟结构的力学行为并优化设计。
在结构设计时,根据主轴和主惯性矩 可以合理地选择材料的类型和截面的 形状,以提高结构的刚度和稳定性。
04 极惯性矩和惯性积
极惯性矩的定义与计算
极惯性矩
截面对任意直径的极惯性矩等于截面 面积与该直径的平方的乘积。
截面是确定物体受力分布和变形程度 的关键因素,通过研究截面的几何性 质,可以深入了解物体的力学性能, 为工程设计和安全评估提供依据。
在材料力学中,剪切中心是剪切应力作用下截面 发生剪切变形的点。通过计算截面的形心,可以 近似确定剪切中心的位置。
确定截面的质心
质心是截面质量的中心点,通过计算截面的形心, 可以近似确定质心的位置,这对于动力学分析和 稳定性分析非常重要。
03 主轴和主惯性矩
主轴的定义与计算
主轴
截面上的各点处到截面形心距离最大的方向。
预测物体的变形和破坏
通过分析截面的几何性质,可以预测 物体在不同受力条件下的变形和破坏 行为,为工程实践提供指导。
02 截面的面积和形心
截面面积的定义与计算
截面面积的定义
截面面积是指通过截面边界轮廓 线围成的区域面积。
截面面积的计算
可以通过测量截面轮廓线的长度 ,然后使用公式计算面积。对于 不规则形状,可以使用微元法或 积分法计算。
截面几何性质的应用前景
随着科技的发展和工程需求的提高,截面几何性质在材料力学中的重要性将更加凸 显,其在航空航天、交通运输、建筑等领域的应用将更加广泛。
随着新型材料的不断涌现,截面几何性质的研究将有助于深入了解这些材料的力学 行为,为新型材料的优化和应用提供理论支持。
随着数值模拟和计算机技术的发展,截面几何性质的研究将更加精确和深入,有助 于提高工程结构的分析和设计水平。
在实际工程中,主轴和主惯性矩也是 进行有限元分析时的重要输入参数, 用于模拟结构的力学行为并优化设计。
在结构设计时,根据主轴和主惯性矩 可以合理地选择材料的类型和截面的 形状,以提高结构的刚度和稳定性。
04 极惯性矩和惯性积
极惯性矩的定义与计算
极惯性矩
截面对任意直径的极惯性矩等于截面 面积与该直径的平方的乘积。
截面是确定物体受力分布和变形程度 的关键因素,通过研究截面的几何性 质,可以深入了解物体的力学性能, 为工程设计和安全评估提供依据。
材料力学第四章截面的几何性质
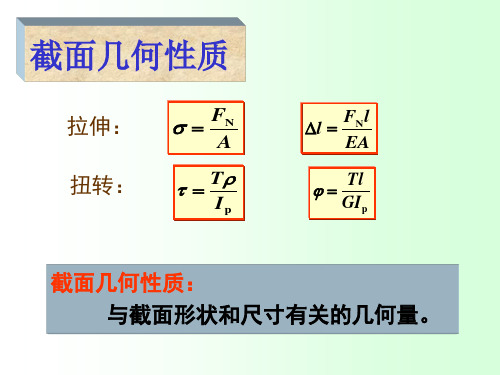
I y A z 2dA I z A y2dA
n
I y
I yi
i 1
n
I z
I zi
i 1
n
I p
I pi
i 1
z
I p A2dA
y
A1 A2
…
dA
An
z
y o
【例题 4】试计算图示圆环对其形心轴的惯性 矩和极惯性矩。
z
Iy
Iz
D4 64
d 4 64
y
C
D4 d 4
I p 32 32
0 23.7 0 23.7 90
zo z zc
1 cm
Iyc = 279 cm4
Izc = 100 cm4
Iyczc = -97 cm4
yo
12 cm
0
yc
c
o
8 cm
1 cm y
Imax
m in
I yc
I zc 2
I yc
2
I zc
2
I2 yc zc
Iyc = 279 cm4 Izc = 100 cm4 Iyczc = -97 cm4
0
o
y1
u
y
证明:设通过截面 O 点的y、z 轴为主轴,u、v 为另一对 主轴,其中o不是 /2 的整数倍,由转轴公式:
I uv
Iy
Iz 2
sin 20
I yz cos 20
0
而:I yz 0 sin 20 0 I y Iz
从而:
I y1z1
Iy
2
Iz
sin
2
I yz
cos 2
0
故过O点的任何一对正 交轴都是主轴,定理得证。
材料力学课件第六章截面图形的几何性质

例6-1 求图示半径为r的半圆形对其直径轴x的静矩及其形心坐 标yC。 解:过圆心O作与x轴垂直的y轴,在距x任意高度y处取一个与x 轴平行的窄条, d A 2 r2 - y2 d y
所以 S x A y d A 0
r
2 3 y( 2 r - y ) d y r 3
2 2
y dA yC O C r
第6章 截面的几何性质
惯性矩与惯性积的移轴定理
y z1
z
已知: Iy,Iz,Iyz A dA
y
求: Iy1,Iz1,Iy1z1
I y 1 z1 d A
2 A
O a
y1
O´ b
z
I z1 y1 dA
2 A
I y1z1 y1 z1dA
A
y1=y+a z1=z+b
第6章 截面的几何性质
2 A
b 2 b 2
hb3 z hdz 12
2
惯性矩与惯性积的移轴定理
第6章 截面的几何性质
惯性矩与惯性积的移轴定理
惯性矩与惯性积的移轴定理
移轴定理(parallel-axis theorem)是指图形对于 互相平行轴的惯性矩、惯性积之间的关系。即通过已 知图形对于一对坐标的惯性矩、惯性积,求图形对另 一对坐标的惯性矩与惯性积。
Δ Pi y i P
于是有 同理有
yC
x xC
xi
§6-1 截面的静距与形心位置
工程中常遇到由基本图形构成的组合截面,例如下面 例题中所示的两种横截面。当对组合截面杆件计算在外力 作用下的应力和变形时需要求出它们对于形心轴x,y (本 节中的x轴就是以前我们所用的z轴) 的一些几何性质,例
材料力学 截面的几何性质

O1 O 2
O
x
O3
x 1
C
课堂练习
I.
&
任意图形,若对某一对正交坐标轴的惯性积为零, 则这一对坐标轴一定是该图形的( )。
B
A. 形心轴; B. 主轴 C. 主形心轴 D. 对称轴 在图示开口薄壁截面图形中,当( 为一对主轴。
y
)时,y-z轴始终保持
A. y轴不动,x轴平移; B. x轴不动,y轴平移; C. x轴不动,y轴任意移动;
y b C 1x C 2x O a x
æ 1 öæ 2 ö æ 1 öæ h ö = ç bh ÷ç h ÷ + ç ah ÷ç ÷ è 2 øè 3 ø è 2 øè 3 ø
h 2 = (a + 2 b ) 6
形心位置
h
x = 0
h 2 (a + 2 b ) h a + 2 b S x y = = பைடு நூலகம்· = 6 A h 3 a + b (a + b ) 2
主惯性矩:
图形对主轴的惯性矩,称主惯性矩
形心主轴:
过形心的主轴称为形心主轴
形心主矩:
图形对形心主轴的惯性矩称为形心主矩
课堂练习
I.
&
在下列关于平面图形的结论中,(
)是错误的。
A.图形的对称轴必定通过形心; B.图形两个对称轴的交点必为形心; C.图形对对称轴的静矩为零; D.使静矩为零的轴必为对称轴。 在平面图形的几何性质中,(
y
dA y
ü2、惯性矩和极惯矩永远为正,
惯性积可能为正、为负、为零。
x 1
ü3、任何平面图形对于通过其形
材料力学——7截面的几何性质

y1
x1
x y
dA y1
x1
x
I x I y I x I y I x1 cos2 I xy sin 2 2 2
I x I y I x I y I y1 cos2 I xy sin 2 2 2 I x I y I x1 y1 2 sin 2 I xy cos2
A
等于形心坐标
t A
A
A
A
x
dA
y
x
xi Ai x A (正负面积法公式) 累加式 : y yi Ai A
y
x
S y Ax Ai xi
S x Ay Ai yi
例1 试确定下图的形心。
10
y
120 C2 C1(0,0) C2(-35,60)
解 : 组合图形,用正负面积法解之。 1.用正面积法求解,图形分割及坐标
y 2d d yC O x1
解: ①建立坐标系如图。
②求形心位置。
x xC
b
xi Ai 0 0 x A A 2 d d y A i i y 2 4 2 0.177d A 2 d 3 d 4
③ 建立形心坐标系;求:IyC , IxC , I xCy
负面积 C2 C1
x A x A x x
i i
1
1
2
A2
A
A1 A2
x
5(70110 ) 20.3 1208070110
图(b)
2 惯性矩、惯性积、极惯性矩 一、惯性矩:(与转动惯量类似) 是面积与它到轴的距离的平方之积。
I x y dA
截面图形的几何性质-材料力学

yC
Sz A
558000 9000
62
Sz Sz1 Sz2 120 40 20 140 30110 558000
A A1 A2 120 40 140 30 9000
120
I
CI
C
CII
II
y 30
参考轴
z 40
yC
zC 140
注意
① 由两块组成组合图形,其复合图形形心一定位于两个子图的形心连线上。 ② 组合图形形心计算公式也适用于负面积情况, 但要记住面积为负号。
z
I
C1 C
s
C2
II
b
y1 h
y
y2
t
典型例题
例3 已知组合截面尺寸t=20mm,h=140mm,b=100mm。试求截面图
形对形心轴 y 的惯性矩。
t
解: 由平行移轴定理
矩形1对y轴的惯性矩:
I (1) y
I y1
b12 A1
矩形2对y轴的惯性矩:
I (2) y
I y2
b22 A2
整个截面的惯性矩:
Iz
y 2 dA
A
h y2bdy 0
b
y3 3
/
h 0
bh3 3
y
h b
dy y
z
典型例题
例2 试求图示截面对形心轴zC轴的惯性矩。
IzC
y 2 dA
A
h
2 h
y2bdy
2
b
y3 3
h
/
2
h
2
bh3
12
I yC
z 2dA
A
y
yC
hb3 =
材料力学 07截面几何性质

描述截面的转动性能。
第7章 截面的几何性质
§7–1 静矩和形心 §7–2 惯性矩、惯性积、惯性半径 §7–3 惯性矩和惯性积的平行移轴定理 §7–4 惯性矩和惯性积的转轴公式、
主惯性矩和主惯性积
§7-3 惯性矩和惯性积的平行移轴定理 1、平行移轴定理:(与转动惯量的平行移轴定理类似)
y
yC
x
dA
(3)惯性积的数值可正可负,也可能等于零。若一对坐标轴中有 一轴为图形的对称轴,则图形对这一对称轴的惯性积必等于零 。但图形对某一对坐标轴的惯性积为零,这一对坐标轴中并不 一定有图形的对称轴。
(4)组合图形对某一对坐标轴的惯性积,等于各组合图形对同一 坐标轴的惯性积之和,即
∑ I xy = I xyi
4、惯性半径:
I x = ix2 A
Iy
=
i
2 y
A
惯性半径的特征
⇒ ix = Ix A iy = Iy A
(1)、惯性半径是对某一坐标轴定义的。 (2)、惯性半径的单位为m。 (3)、惯性半径的数值恒为正值。
惯性半径是衡量截面图形对某一轴惯性矩大小的参照值。
• 静矩 • 极惯性矩 • 惯性矩
几何关系
(2) 惯性矩的单位为m4。
(3)极惯性矩和轴惯性矩的数值均为大于零的正值 。
(4)图形对某一点的极惯性矩的数值,恒等于图形对以该点为坐 标原点的任意一对正交坐标轴的轴惯性矩之和,即
∫ Iρ = ρ2dA=Ix+Iy A
(5)组合图形对某一点的极惯性矩或某一轴的轴惯性矩,分别等 于各组合图形对同一点的极惯性矩或同一轴惯性矩之和,即
圆轴扭转 弯曲梁
τ = Tρ IP
ϕ = Tl GI P
σ
第7章 截面的几何性质
§7–1 静矩和形心 §7–2 惯性矩、惯性积、惯性半径 §7–3 惯性矩和惯性积的平行移轴定理 §7–4 惯性矩和惯性积的转轴公式、
主惯性矩和主惯性积
§7-3 惯性矩和惯性积的平行移轴定理 1、平行移轴定理:(与转动惯量的平行移轴定理类似)
y
yC
x
dA
(3)惯性积的数值可正可负,也可能等于零。若一对坐标轴中有 一轴为图形的对称轴,则图形对这一对称轴的惯性积必等于零 。但图形对某一对坐标轴的惯性积为零,这一对坐标轴中并不 一定有图形的对称轴。
(4)组合图形对某一对坐标轴的惯性积,等于各组合图形对同一 坐标轴的惯性积之和,即
∑ I xy = I xyi
4、惯性半径:
I x = ix2 A
Iy
=
i
2 y
A
惯性半径的特征
⇒ ix = Ix A iy = Iy A
(1)、惯性半径是对某一坐标轴定义的。 (2)、惯性半径的单位为m。 (3)、惯性半径的数值恒为正值。
惯性半径是衡量截面图形对某一轴惯性矩大小的参照值。
• 静矩 • 极惯性矩 • 惯性矩
几何关系
(2) 惯性矩的单位为m4。
(3)极惯性矩和轴惯性矩的数值均为大于零的正值 。
(4)图形对某一点的极惯性矩的数值,恒等于图形对以该点为坐 标原点的任意一对正交坐标轴的轴惯性矩之和,即
∫ Iρ = ρ2dA=Ix+Iy A
(5)组合图形对某一点的极惯性矩或某一轴的轴惯性矩,分别等 于各组合图形对同一点的极惯性矩或同一轴惯性矩之和,即
圆轴扭转 弯曲梁
τ = Tρ IP
ϕ = Tl GI P
σ
材料力学-截面几何特性

IxC1 (70mm)3 10mm/12 28.58104 mm4 I yC1 70mm(10mm)3 /12 0.58104 mm4
I 0 xC 2 yC 2
IxC IxC1 A1 yc21 IxC2 A2 yc22 1104 mm4 1200mm2 (15mm)2 28.58mm4 700mm2 (25mm)2 100.33mm4
64
9 /2
Ix2 Ix2C A2 (a xc2 )2 28mm 4 (80mm )2 (100 17)2 8 3467mm4
组合截面对x轴的惯性矩为
I x I x1 2I x2 5333mm4 23467mm4 12270mm4
§I-4 惯性矩和惯性积的转轴公式 ·截面 的主惯性轴和主惯性矩
A
A ( yC b)2 dA
A ( yC2 2byC b2 )dA
I xC 2bSxC b2 A
Ix IxC 2bSxC b2 A
因为C为形心
SxC AyC 0
y
yC
x
dA
a
r
bC y
xC
x
I x I xC b2 A 同理:
I y I yC a2 A I xy I xC yC abA I p I pC (a2 b2 ) A
C1
80
x
图(b)
x
xi
Ai
x 1
A1x
2
A2
A
A1A2
409600 45 7700 19.7mm 9600 7700
y
yi Ai
y 1
A1
y
2
A2
A
A1 A2
609600 65 7700 39.7mm 9600 7700
I 0 xC 2 yC 2
IxC IxC1 A1 yc21 IxC2 A2 yc22 1104 mm4 1200mm2 (15mm)2 28.58mm4 700mm2 (25mm)2 100.33mm4
64
9 /2
Ix2 Ix2C A2 (a xc2 )2 28mm 4 (80mm )2 (100 17)2 8 3467mm4
组合截面对x轴的惯性矩为
I x I x1 2I x2 5333mm4 23467mm4 12270mm4
§I-4 惯性矩和惯性积的转轴公式 ·截面 的主惯性轴和主惯性矩
A
A ( yC b)2 dA
A ( yC2 2byC b2 )dA
I xC 2bSxC b2 A
Ix IxC 2bSxC b2 A
因为C为形心
SxC AyC 0
y
yC
x
dA
a
r
bC y
xC
x
I x I xC b2 A 同理:
I y I yC a2 A I xy I xC yC abA I p I pC (a2 b2 ) A
C1
80
x
图(b)
x
xi
Ai
x 1
A1x
2
A2
A
A1A2
409600 45 7700 19.7mm 9600 7700
y
yi Ai
y 1
A1
y
2
A2
A
A1 A2
609600 65 7700 39.7mm 9600 7700
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
iy = Iy A
ix =
Ix A
2 I x = ix A
2 I y = iy A
§I-3 惯性矩与惯性积的平行移轴公 式 组合截面的惯性矩和惯性积
一,平行移轴公式 平行移轴公式
y yC x a dA xC C b y x
x = a + xC y = b + yC
I x = ∫ y 2 dA
d (2a ) I x1 = 12 (80 mm )(200 mm )3 = 5 333 ×104 mm 4 = 12
3
对于半圆形
d sin(π / 2) 80mm xc 2 = = = 17.0mm 3×π / 2 3×π / 2
d4 16 I x2 = π / 2 64 9×π / 2
I x = I x1 + 2 I x2 = 5333mm 4 + 2 × 3467 mm 4 = 12270mm 4
§I-4 惯性矩和惯性积的转轴公式 截 面的主惯性轴和主惯性矩
一, 惯性矩和惯性积的转轴公式
y y1 x1
x y
dA y1 x1 x
坐标的旋转变换: 坐标的旋转变换: x1 =xcosα + ysinα y1 = xsinα + ycosα 轴的惯性矩: 对x1轴的惯性矩:
同理: 同理:
I y1 = Ix + Iy 2 Ix Iy 2 cos 2α + I xy sin 2α
I x1 y1 =
Ix Iy 2
sin 2α + I xy cos 2α
I x1 + I y1 = I x + I y = I p
图形对通过同一坐 标原点任意一对相 互垂直坐标轴的两 个轴惯性矩之和为 常量, 常量,等于图形对原 点的极惯性矩
3 3
2
I xC 1 = 120mm × (10mm) / 12 = 1×10 mm
4 4
4 4
I yC 1 = (120mm) ×10mm / 12 = 144 ×10 mm
I xC 1 y C 1 = 0
A2 = 70mm × 10mm = 700mm 2
I xC 1 = (70mm)3 ×10mm / 12 = 28.58 ×10 4 mm 4 I yC 1 = 70mm × (10mm)3 / 12 = 0.58 ×10 4 mm 4 I xC 2 yC 2 = 0
(3)计算形心主惯性矩
I x0 =
Ix + Iy 2
1 2 + ( I x I y ) 2 + 4 I xy 2
4 4Leabharlann = 321.4× 10 mm
I y0 =
Ix + Iy 2
1 2 2 ( I x I y ) + 4 I xy 2
4 4
= 57.4 × 10 mm
�
I x1 = ∫ y12 dA
α
= ∫ ( x sin α + y cos α ) dA
2
= I x cos 2 α 2 I xy sin α cos α + I y sin 2 α
I x1 = I x cos 2 α 2 I xy sin α cos α + I y sin 2 α
I x1 = Ix + Iy 2 + Ix Iy 2 cos 2α I xy sin 2α
y
I x = ∫ y 2 dA
A
x
I y = ∫ x 2 dA
dA y x
A
ρ
I p = ∫ ρ 2 dA = I x + I y
A
I xy = ∫ xydA
A
惯性矩和极惯矩永远为正,惯性积可能为正,为 惯性矩和极惯矩永远为正,惯性积可能为正, 为零(主惯性轴), ),任何平面图形对于通过 负,为零(主惯性轴),任何平面图形对于通过 其形心的对称轴和与此对称轴垂直的轴的惯性积 为零 惯性半径 任意形状的截面图形的面积为A,则图形对 轴 任意形状的截面图形的面积为 ,则图形对y轴 和x轴的惯性半径分别定义为 轴的惯性半径分别定义为
A
ρ
= ∫ ( yC + b) 2 dA
A 2 = ∫ ( yC + 2byC + b 2 )dA A
= I xC + 2bS xC + b 2 A
I x = I xC + 2bS xC + b 2 A
因为C为形心 因为 为形心
S xC = AyC = 0
Ix = IxC + b2 A
同理: 同理:
I xC = I xC 1 + A y + I xC 2 + A2 y
2 1 c1
2 c2
= 1×10 4 mm 4 + 1200mm 2 × (15mm) 2 + 28.58mm 4 + 700mm 2 × (25mm) 2 = 100.33mm
4
I yC = I yC 1 + A1 xc21 + I yC 2 + A2 xc22
形心主轴的确定
如果截面有一根对称轴, 如果截面有一根对称轴,则该轴及与之正交的 形心轴即为形心主轴
y y c x y x c x y x
c
c
如果截面具有三根以上的对称轴, 如果截面具有三根以上的对称轴,过形心的任 意轴及与之正交的形心轴均为形心主轴
y x y x
c
c
如果截面没有对称轴,形心主轴的确定: 如果截面没有对称轴,形心主轴的确定: 1,确定形心位置; 确定形心位置; 过形心取一对正交轴x,y, 2,过形心取一对正交轴 ,利用平行移轴公式计 算截面对这对轴的惯性矩Ix,Iy和惯性积Ixy. 算截面对这对轴的惯性矩 惯性积 3,利用下面的公式计算主轴位置
I x0 y0 =( I x I y 2 sin2α 0 + I xy cos2α 0 )=0
tan 2α 0 =
Ix + Iy
2 I xy Ix Iy
4,利用下面的公式计算主惯性矩
1 2 I x0 = + ( I x I y ) 2 + 4 I xy 2 2 Ix + Iy 1 2 I y0 = ( I x I y ) 2 + 4 I xy 2 2
I x = ∑ I xi
i =1 =1
n
n
I y = ∑ I yi
i =1
I xy = ∑ I xyi
i =1
n
例题Ⅰ 例题Ⅰ- 5 试求图a所 示截面对于x轴的惯性矩Ix , 对于y轴的惯性矩Iy ,以及 y I 对于x,y轴的惯性积Ixy .
(a)
解:将截面看作由一个矩形和两个 半圆形组成, 半圆形组成,对于矩形
= 144 ×10 4 mm 4 + 1200mm 2 × (20mm) 2 + 0.58 ×10 mm + 700mm × (35mm)
4 4 2 2
= 278.33mm
4
I xC yC = A1 xc1 yc1 + A2 xc 2 yc 2
= 1200mm × (15mm) × (20mm)
2
y yC x a dA xC C b y x
I y = I yC + a2 A
I xy = I xC yC + abA
I p = I pC + (a2 + b2 ) A
注意: 点必须为形心 注意: C点必须为形心
ρ
组合截面的惯性矩( 二,组合截面的惯性矩(积): 组合截面对某坐标轴的惯性矩( 组合截面对某坐标轴的惯性矩(积), 等于其中 各部分对同一坐标轴惯性矩 (积)之和. 之和.
材料力学
附录I 附录I 截面的几何性质
§I–1 截面的面积矩和形心 1
截面的面积矩(静矩,一次矩) 一,截面的面积矩(静矩,一次矩)
y
面积矩:是面积与它到轴的距离之积( 面积矩:是面积与它到轴的距离之积(用S表 示).
S y = ∫ xdA
A A
S x = ∫ ydA
x y x dA
同一截面对于不同的坐标 轴面积矩不同 面积矩可正, 面积矩可正,可负也可为 零
∑x A = x A + x x=
i i
1
1
2
A2
A
A1 + A2
40 × 9600 45 × 7700 = = 19.7 mm 9600 7700
∑y A y=
i
i
A
=
y 1 A1 + y 2 A2 A1 + A2
80
x
60 × 9600 65 × 7700 = 39.7 mm = 9600 7700
二,截面的形心
y
∫ xdA x=
A
A
x
dA
∫ ydA y=
A
x
C y
A
y
x
Sy = Ax
Sx = Ay
如果截面对某一轴的面积矩等于零, ①如果截面对某一轴的面积矩等于零,则该轴必过 截面的形心; 截面的形心; 截面对于通过形心的轴的面积矩必等于零. ②截面对于通过形心的轴的面积矩必等于零.
组合截面的静矩与形心: 三,组合截面的静矩与形心:
+ 700mm × (25mm) × (35mm)
2
= 97.25 ×10 4 mm 4
(2)计算主轴位置
tan 2α 0 =
2 I xy Ix Iy
2 × 97.25 ×10 4 mm 4 = 100.33 ×10 4 mm 4 278.33 ×10 4 mm 4 = 1.093
ix =
Ix A
2 I x = ix A
2 I y = iy A
§I-3 惯性矩与惯性积的平行移轴公 式 组合截面的惯性矩和惯性积
一,平行移轴公式 平行移轴公式
y yC x a dA xC C b y x
x = a + xC y = b + yC
I x = ∫ y 2 dA
d (2a ) I x1 = 12 (80 mm )(200 mm )3 = 5 333 ×104 mm 4 = 12
3
对于半圆形
d sin(π / 2) 80mm xc 2 = = = 17.0mm 3×π / 2 3×π / 2
d4 16 I x2 = π / 2 64 9×π / 2
I x = I x1 + 2 I x2 = 5333mm 4 + 2 × 3467 mm 4 = 12270mm 4
§I-4 惯性矩和惯性积的转轴公式 截 面的主惯性轴和主惯性矩
一, 惯性矩和惯性积的转轴公式
y y1 x1
x y
dA y1 x1 x
坐标的旋转变换: 坐标的旋转变换: x1 =xcosα + ysinα y1 = xsinα + ycosα 轴的惯性矩: 对x1轴的惯性矩:
同理: 同理:
I y1 = Ix + Iy 2 Ix Iy 2 cos 2α + I xy sin 2α
I x1 y1 =
Ix Iy 2
sin 2α + I xy cos 2α
I x1 + I y1 = I x + I y = I p
图形对通过同一坐 标原点任意一对相 互垂直坐标轴的两 个轴惯性矩之和为 常量, 常量,等于图形对原 点的极惯性矩
3 3
2
I xC 1 = 120mm × (10mm) / 12 = 1×10 mm
4 4
4 4
I yC 1 = (120mm) ×10mm / 12 = 144 ×10 mm
I xC 1 y C 1 = 0
A2 = 70mm × 10mm = 700mm 2
I xC 1 = (70mm)3 ×10mm / 12 = 28.58 ×10 4 mm 4 I yC 1 = 70mm × (10mm)3 / 12 = 0.58 ×10 4 mm 4 I xC 2 yC 2 = 0
(3)计算形心主惯性矩
I x0 =
Ix + Iy 2
1 2 + ( I x I y ) 2 + 4 I xy 2
4 4Leabharlann = 321.4× 10 mm
I y0 =
Ix + Iy 2
1 2 2 ( I x I y ) + 4 I xy 2
4 4
= 57.4 × 10 mm
�
I x1 = ∫ y12 dA
α
= ∫ ( x sin α + y cos α ) dA
2
= I x cos 2 α 2 I xy sin α cos α + I y sin 2 α
I x1 = I x cos 2 α 2 I xy sin α cos α + I y sin 2 α
I x1 = Ix + Iy 2 + Ix Iy 2 cos 2α I xy sin 2α
y
I x = ∫ y 2 dA
A
x
I y = ∫ x 2 dA
dA y x
A
ρ
I p = ∫ ρ 2 dA = I x + I y
A
I xy = ∫ xydA
A
惯性矩和极惯矩永远为正,惯性积可能为正,为 惯性矩和极惯矩永远为正,惯性积可能为正, 为零(主惯性轴), ),任何平面图形对于通过 负,为零(主惯性轴),任何平面图形对于通过 其形心的对称轴和与此对称轴垂直的轴的惯性积 为零 惯性半径 任意形状的截面图形的面积为A,则图形对 轴 任意形状的截面图形的面积为 ,则图形对y轴 和x轴的惯性半径分别定义为 轴的惯性半径分别定义为
A
ρ
= ∫ ( yC + b) 2 dA
A 2 = ∫ ( yC + 2byC + b 2 )dA A
= I xC + 2bS xC + b 2 A
I x = I xC + 2bS xC + b 2 A
因为C为形心 因为 为形心
S xC = AyC = 0
Ix = IxC + b2 A
同理: 同理:
I xC = I xC 1 + A y + I xC 2 + A2 y
2 1 c1
2 c2
= 1×10 4 mm 4 + 1200mm 2 × (15mm) 2 + 28.58mm 4 + 700mm 2 × (25mm) 2 = 100.33mm
4
I yC = I yC 1 + A1 xc21 + I yC 2 + A2 xc22
形心主轴的确定
如果截面有一根对称轴, 如果截面有一根对称轴,则该轴及与之正交的 形心轴即为形心主轴
y y c x y x c x y x
c
c
如果截面具有三根以上的对称轴, 如果截面具有三根以上的对称轴,过形心的任 意轴及与之正交的形心轴均为形心主轴
y x y x
c
c
如果截面没有对称轴,形心主轴的确定: 如果截面没有对称轴,形心主轴的确定: 1,确定形心位置; 确定形心位置; 过形心取一对正交轴x,y, 2,过形心取一对正交轴 ,利用平行移轴公式计 算截面对这对轴的惯性矩Ix,Iy和惯性积Ixy. 算截面对这对轴的惯性矩 惯性积 3,利用下面的公式计算主轴位置
I x0 y0 =( I x I y 2 sin2α 0 + I xy cos2α 0 )=0
tan 2α 0 =
Ix + Iy
2 I xy Ix Iy
4,利用下面的公式计算主惯性矩
1 2 I x0 = + ( I x I y ) 2 + 4 I xy 2 2 Ix + Iy 1 2 I y0 = ( I x I y ) 2 + 4 I xy 2 2
I x = ∑ I xi
i =1 =1
n
n
I y = ∑ I yi
i =1
I xy = ∑ I xyi
i =1
n
例题Ⅰ 例题Ⅰ- 5 试求图a所 示截面对于x轴的惯性矩Ix , 对于y轴的惯性矩Iy ,以及 y I 对于x,y轴的惯性积Ixy .
(a)
解:将截面看作由一个矩形和两个 半圆形组成, 半圆形组成,对于矩形
= 144 ×10 4 mm 4 + 1200mm 2 × (20mm) 2 + 0.58 ×10 mm + 700mm × (35mm)
4 4 2 2
= 278.33mm
4
I xC yC = A1 xc1 yc1 + A2 xc 2 yc 2
= 1200mm × (15mm) × (20mm)
2
y yC x a dA xC C b y x
I y = I yC + a2 A
I xy = I xC yC + abA
I p = I pC + (a2 + b2 ) A
注意: 点必须为形心 注意: C点必须为形心
ρ
组合截面的惯性矩( 二,组合截面的惯性矩(积): 组合截面对某坐标轴的惯性矩( 组合截面对某坐标轴的惯性矩(积), 等于其中 各部分对同一坐标轴惯性矩 (积)之和. 之和.
材料力学
附录I 附录I 截面的几何性质
§I–1 截面的面积矩和形心 1
截面的面积矩(静矩,一次矩) 一,截面的面积矩(静矩,一次矩)
y
面积矩:是面积与它到轴的距离之积( 面积矩:是面积与它到轴的距离之积(用S表 示).
S y = ∫ xdA
A A
S x = ∫ ydA
x y x dA
同一截面对于不同的坐标 轴面积矩不同 面积矩可正, 面积矩可正,可负也可为 零
∑x A = x A + x x=
i i
1
1
2
A2
A
A1 + A2
40 × 9600 45 × 7700 = = 19.7 mm 9600 7700
∑y A y=
i
i
A
=
y 1 A1 + y 2 A2 A1 + A2
80
x
60 × 9600 65 × 7700 = 39.7 mm = 9600 7700
二,截面的形心
y
∫ xdA x=
A
A
x
dA
∫ ydA y=
A
x
C y
A
y
x
Sy = Ax
Sx = Ay
如果截面对某一轴的面积矩等于零, ①如果截面对某一轴的面积矩等于零,则该轴必过 截面的形心; 截面的形心; 截面对于通过形心的轴的面积矩必等于零. ②截面对于通过形心的轴的面积矩必等于零.
组合截面的静矩与形心: 三,组合截面的静矩与形心:
+ 700mm × (25mm) × (35mm)
2
= 97.25 ×10 4 mm 4
(2)计算主轴位置
tan 2α 0 =
2 I xy Ix Iy
2 × 97.25 ×10 4 mm 4 = 100.33 ×10 4 mm 4 278.33 ×10 4 mm 4 = 1.093
