《机械设计基础》试题库_轮系
杨可桢《机械设计基础》(第5版)笔记和课后习题(轮系)

图 5-3 解:这是一个定轴轮系,由题意可得:
1 / 14
圣才电子书 十万种考研考证电子书、题库视频学习平台
反转原理:给周转轮系施以附加的公共角速度 H 后,不改变轮系中各构件之间的相
对运动,原轮系将转化成为一假想的定轴轮系,由此可按定轴轮系的公式计算该新轮系的传
动比。
设周转轮系中两个太阳轮分别为 G、K,行星架为 H,则其转化轮系的传动比:
圣才电子书 十万种考研考证电子书、题库视频学习平台
第5章 轮 系
5.1 复习笔记
一、轮系的类型 轮系是指由一系列齿轮组成的传动系统。 根据轮系运转时各个齿轮轴线相对于机架位置是否固定,分为三类: 1.定轴轮系:轮系中各齿轮轴线相对于机架均为固定,又分为平面定轴轮系和空间定 轴轮系。 2.周转轮系:轮系中至少有一个齿轮轴线位置不固定,而是绕着其他齿轮的固定轴线 回转。周转轮系由太阳轮、行星轮、系杆及机架组成,又可分为差动轮系(自由度为 2)和 行星轮系(自由度为 1)。 3.复合轮系:既包含定轴轮系,又包含周转轮系,或者是由几部分周转轮系组成。 根据轮系中各轮几何轴线在空间的相对位置,分为两类:平面轮系和空间轮系。
图 5-2
5-2 在图 5-3 所示轮系中,已知 z1=15,z2=25, z2' =15,z3=30, z3' =15z4=30, z4' =2(右 旋),z5=60, z5' =20(m=4 mm),若 n1=500 r/min,求齿条 6 线速度 v 的大小和方向。
3 / 14
圣才电子书 十万种考研考证电子书、题库视频学习平台
(5)空间周转轮系中,由于角速度矢量与系杆的角速度矢量不平行,所以不能用代数 法相加减。但是不影响基本构件之间传动比的计算。
机械设计基础试题库填空题1

填空题
1.由一系列相互啮合的齿轮组成的传动系统称为(
)。
【代码】21711139
【答案】轮系
2. 轮系根据齿轮轴线的位置是否固定,可分为(
)和行星轮
系两大类。
【代码】21711148
【答案】定轴轮系
3. 轮 系 中 , 惰 轮 不 会 影 响 轮 系 传 动 比 的 大 小 , 而 只 是 改 变 齿 轮 的
23. 简单行星轮系是行星轮系的一种,其自由度数目为 (
)。
【代码】22211138
【答案】1
24.国家标准中,V 带的基准长度是在其(
)面上所测得的长度。
【代码】23311146
【答案】中性层(或节面)
25. 根据工作原理不同,带传动可分为(
)带传动和啮合带传动两
类。
【代码】22811099
【答案】摩擦
26. 普通 V 带传动的主要失效形式有:带在带轮上产生上(
)
和带发生疲劳破坏。
【代码】23711143
【答案】打滑
27. 带 传 动 常 用 的 张 紧 方 法 有 两 种 : 安 装 (
) 和调整
(
)。
【代码】24411148
【答案】张紧轮 中心距
28. 带传动通常是由主动带轮、从动带轮和(
)所组成。
)
Hale Waihona Puke 结构承载能力较高,应用广泛。
【代码】23111105
【答案】帘布芯
(
)。
【代码】21911119
【答案】相同
14. 若轮系中所有齿轮轴线的位置都是固定不变的,这样的轮系称为
(
)。
【代码】21711155
《机械设计基础》题库 计算 轮系 自由度

试题题型:计算题一、计算图示机构的自由度,并判断机构是否具有确定的运动。
(如有复合铰链、虚约束、局部自由度须指出)DEDEHKCDDE二、轮系的计算 1.在图示轮系中,已知各轮齿数为Z 1=Z 3=30,Z 2=90,Z 2’=40,Z 3’=40,Z 4=30,试求传动比i 1H ,并说明I、H轴的转向是否相同?2.在图示轮系中,已知各轮齿数为Z 1 =15,Z 2=20, Z 2’ = Z 3’= Z 4=30, Z 3=40,Z 5= 90,试求传动比I ⅠⅡ,并说明I、Ⅱ轴的转向是否相同?3.在图示轮系中,已知各轮的齿数为Z 1= 20,Z 2=30,Z 3=80, Z 4=25,Z 5=50,试求传动比i 15。
’ Ⅱ4.在图示轮系中,已知各轮齿数为Z1= 55, Z2=11,Z3=77,Z3’=49,Z4=12,Z5=73,试求传动比i1H。
5.在图示轮系中,已知各轮齿数为Z1= Z2= 30,Z3= 40,Z4=20,Z5=18,Z6=38,试求传动比i1H。
6.在图示轮系中,已知各轮齿数为Z1= Z2’= 20,Z2=40,Z3= 80,试求传动比i1H。
7.在图示轮系中,已知各轮齿数为Z 1=19,Z 2=76, Z 2’= 40,Z 3=20,Z 4= 80,试求传动比i 1H 。
8.在图示轮系中,已知各轮齿数为Z 1= 20,Z 2’= 25,Z 2= Z 3=30,Z 3’= 20,Z 4=75,试求1、轮系的传动比i 1H 。
2、若n 1=1000r/min ,转臂H的转速n H =?9.在图示轮系中,已知各轮齿数为Z 1= Z 3=15 ,Z 2’= 60,Z 2= Z ,3=20,Z 4= 65,试求轮系的传动比i 1H 。
210.在图示轮系中,已知各轮齿数为Z 1=101, Z 2=100,Z 3=99,Z 4= 100,轮1的转速n 1=1r/min ,(顺时针),且n 4=n 1,n 4的方向与n 1相反,求n H 的大小及转向。
机械设计基础考试试题及答案

《机械设计基础》试题一一、单项选择题(本大题共20小题,每小题2分,共40分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内。
1.在如图所示的齿轮—凸轮轴系中,轴4称为( A ) A 零件 B.机构 C.构件 D.部件2.若组成运动副的两构件间的相对运动是移动,则称这种运动副为( B )A.转动副B.移动副C.球面副D.螺旋副3.渐开线齿轮的齿廓曲线形状取决于( D )A.分度圆B.齿顶圆C.齿根圆D.基圆 4.机构具有确定相对运动的条件是( A )A.机构的自由度数目等于主动件数目B.机构的自由度数目大于主动件数目C.机构的自由度数目小于主动件数目D.机构的自由度数目大于等于主动件数目 5.一般转速的滚动轴承计算准则为( C )A.进行静强度计算B.进行极限转速计算C.进行疲劳寿命计算D.进行热平衡计算 6.柴油机曲轴中部的轴承应采用( B )A.整体式滑动轴承B. 剖分式滑动轴承C.深沟球轴承D.圆锥滚子轴承 7.螺纹联接的自锁条件为( A )A.螺纹升角≤当量摩擦角B.螺纹升角>摩擦角C.螺纹升角≥摩擦角D.螺纹升角≥当量摩擦角 8.机械运转不均匀系数是用来描述机械运转不均匀程度的重要参数,其表达式为( C ) A.σωω=-max min B. σωω=+max min2C. σωωω=-max min mD. σωωωω=-+max min max min9.铰链四杆机构的死点位置发生在( A )A.从动件与连杆共线位置B.从动件与机架共线位置C.主动件与连杆共线位置D.主动件与机架共线位置 10.当轴的转速较低,且只承受较大的径向载荷时,宜选用( C )A.深沟球轴承B.推力球轴承C.圆柱滚子轴承D.圆锥滚子轴承 11.作单向运转的转轴,其弯曲应力的变化特征是( A )A.对称循环B.脉动循环C.恒定不变D.非对称循环 12.在一般机械传动中,若需要采用带传动时,应优先选用( C )A.圆型带传动B.同步带传动C.V 型带传动D.平型带传动13.铰链四杆机构中,若最短杆与最长杆长度之和小于其余两杆长度之和,则为了获得曲柄摇杆机构,其机架应取( B )A.最短杆B.最短杆的相邻杆C.最短杆的相对杆D.任何一杆14.若被联接件之一厚度较大、材料较软、强度较低、需要经常装拆时,宜采用( B ) A.螺栓联接 B.双头螺柱联接 C.螺钉联接 D.紧定螺钉联接 15.在凸轮机构的从动件选用等速运动规律时,其从动件的运动( A )A.将产生刚性冲击B.将产生柔性冲击C.没有冲击D.既有刚性冲击又有柔性冲击 16.与标准直齿圆柱齿轮的复合齿轮形系数Y FS 值有关的参数是( C ) A.工作齿宽b B.模数m C.齿数z D.压力角α 17.齿轮传动中,轮齿齿面的疲劳点蚀经常发生在( B )A.齿根部分B.靠近节线处的齿根部分C.齿顶部分D.靠近节线处的齿顶部分18.普通圆柱蜗杆传动的正确啮合条件是( B ) (注:下标t 表示端面,a 表示轴向,1表示蜗杆、2表示蜗轮) A.m t1=m a2, αt1=αa2,γ=β B.m a1=m t2, αa1=αt2,γ=β C.m t1=m a2, αt1=αa2,γ=-β D.m a1=m a2, αa1=αt2,γ=-β19.下列联轴器中,能补偿两轴的相对位移并可缓冲、吸振的是( D )A.凸缘联轴器B.齿式联轴器C.万向联轴器D.弹性柱销联轴器 20.带传动的主要失效形式是带的( A )A.疲劳拉断和打滑B.磨损和胶合C.胶合和打滑D.磨损和疲劳点蚀二、填空题(本大题共10小题,每小题1分,共10分)21.在机构中采用虚约束的目的是为了改善机构的运动状况和受力情况。
《华中科技大学《机械设计基础》试题库》

5
3
4
Ⅰ1
Ⅱ 3’
2
2’
3.在图示轮系中,已知各轮的齿数为 Z1= 20, Z2=30,Z3=80, Z4=25,Z5=50,试求传动 比 i15。
3
H 2
4
24 H
1 5
1
3’
4.在图示轮系中,已知各轮齿数为 Z1= 55, Z2=11,Z3=77,Z3’=49,Z4=12,Z5=73,试 求传动比 i1H。
教材名称及版本:《机械设计基础》第三版 编者及出版社: 黄华梁、彭文生 主编
高等教育出版社
试题题型:作图题(按作图规则作图,图线清晰)
1.在下图所示的偏置直动从动件盘形凸轮机构中已 知凸轮为一偏心圆盘。圆盘半径R=25mm,凸轮回 转中心到圆盘中心的距离 lAB=10mm。 (1)绘出凸轮的理论廓线; (2)确定凸轮的基圆半径 r0; (3)凸轮 1 以匀角速ω回转,使推杆 2 上下运动, 求图示位置凸轮已转过的角度φ、推杆的位移 s(φ,s 算出数值。图中ω=1rad/s,尺寸单位 为 mm)。 (4)求图示位置机构的压力角α; (5)若在杆端处加一滚子,其他条件不变,杆 2 的 运动规律与原来的是否相同,为什么?
G
D
H C
I
A
B O
D E
F
E A B
C D
1
《机械设计基础》试题库
F
B
E
C A
D
C
B
D
FE
O
A G
GC D
A E
F
B
H
G
K
E
A
DB
O
F C
O
B A
C O
D E F
杨可桢《机械设计基础》章节题库(轮系)【圣才出品】

三、计算题 1.在如图 5-1 所示轮系中,已知蜗杆为单头且右旋,转速 n1=1440r/min,转动方 向如图 5-1 所示,其余各轮齿数为:z2=40,z2’=20,z2=30,z3’=18,z4=54, 试: (1)说明轮系属于何种类型; (2)计算齿轮 4 的转速 n4; (3)在图中标出齿轮 4 的转动方向。
来判定。
4.在定轴轮系中,每个齿轮的轴线都是 【答案】固定
的。
5.惰轮对轮系的
并无影响,但却可以改变
【答案】传动比;从动轮
的转动方向。
6.如果在齿轮传动中,一个齿轮的
绕另一个齿轮的
1 / 17
旋转,这个轮系称周
圣才电子书
转轮系。
十万种考研考证电子书、题库视频学习平台
(1)机构自由度 F; (2)搅拌轴的角速度 ωF 及转向。
图 5-8 解:(1)机构自由度:F=3n-2PL-PH=3×2-2×2-1=1 (2)轮 1 为固定轮,即 1=0 ,则得:
有 又 得搅拌轴的角速度:
,方向与ωR 相同。
10.计算行星轮系的传动比时,可把行星轮系转化为一假想的定轴轮系,用定轴轮系 的方法解决行星轮系的问题。( )
3 / 17
圣才电子书
【答案】√
十万种考研考证电子书、题库视频学习平台
11.定轴轮系和行星轮系的主要区别在于系杆是否转动。( ) 【答案】√
12.渐开线标准直齿圆柱齿轮传动,由于安装不准确,产生了中心距误差,但其传动 比的大小仍保持不变。( )
6.在周转轮系中,凡具有固定几何轴线的齿轮就称为行星轮。( ) 【答案】×
7.定轴轮系可以把旋转运动转变成直线运动。( ) 【答案】√
8.轮系的传动比计算,不但要确定其数值,还要确定其转向关系。( ) 【答案】√
机械设计基础试题库(四川农业大学)

《机械设计基础》试题库试题库汇总表序号题型题目数量备注一单项选择题440二判断题569三填空题389四分析题27五计算题209六综合题12汇总1646一、单项选择题1.轮系运动时,各齿轮轴线位置固定不动的称为()。
A. 差动轮系B. 定轴轮系C. 行星轮系D. 简单行星轮系【代码】21711019【答案】B2.在行星轮系中,凡具有固定几何轴线的齿轮被称为()。
A. 行星轮B. 太阳轮C. 惰轮D. 系杆【代码】22111016【答案】B3.在行星轮系中,轴线位置会发生改变的齿轮被称为()。
A. 行星轮B. 太阳轮C. 惰轮D. 系杆【代码】22111022【答案】A4.轮系的传动比等于组成该轮系的各对啮合齿轮中()之比。
A. 主动轮齿数的连乘积与从动轮齿数的连乘积B. 主动轮齿数的连加与从动轮齿数的连加C. 从动轮齿数的连乘积与主动轮齿数的连乘积D. 从动轮齿数的连加与主动轮齿数的连加【代码】21811015【答案】C5.至少有一个齿轮的轴线的位置会发生改变的轮系被称为()。
A. 行星轮系B. 定轴轮系C. 复合轮系D. 都不是【代码】21711025【答案】A6.按齿轮轴线的位置是否固定,轮系可以分为()两种类型。
A.定轴轮系和差动轮系(自由度)B.差动轮系和行星轮系C.定轴轮系和复合轮系 D.定轴轮系和行星轮系(周转轮系) 【代码】21711037【答案】D7.行星轮系中的差动轮系,其自由度为()个。
A.1 B.2 C.3 D.4【代码】22211015【答案】B8.下列四项功能中,哪几项()可以通过轮系的运用得以实现。
①两轴的较远距离传动②变速传动③获得大的传动比④实现合成和分解运动A.①② B.①②③C.②③④ D.①②③④【代码】22311017【答案】D9.轮系下列功用中,哪一功用必须依靠行星轮系实现?()。
A.实现变速 B.实现变向C.实现远距离传动 D.实现运动的分解【代码】22311022【答案】D10. 在轮系中,只改变齿轮转向而不影响轮系传动比的齿轮,通常称为()。
《机械设计基础》试题库_轮系

第 5 章 轮系习题与参考答案一、复习思考题1.为什么要应用轮系?试举出几个应用轮系的实例?2.何谓定轴轮系?何谓周转轮系?行星轮系与差动轮系有何区别? 3.什么叫惰轮?它在轮系中有什么作用?4.定轴轮系的传动比如何计算?式中( - 1) m 有什么意义? 5.定轴轮系末端的转向怎样判别?6.如果轮系的末端轴是螺旋传动,应如何计算螺母的移动量?二、填空题1.由若干对齿轮组成的齿轮机构称为 。
轮系三种。
3.对平面定轴轮系, 始末两齿轮转向关系可用传动比计算公式中 的符号来判定。
4.行星轮系由 、 和 三种基本构件组成。
5.在定轴轮系中,每一个齿轮的回转轴线都是 的。
7.如果在齿轮传动中,其中有一个齿轮和它的绕另一个旋转,则这轮系就叫周转轮系。
8.旋转齿轮的几何轴线位置均 的轮系,称为定轴轮系。
9.轮系中 两轮 之比,称为轮系的传动比。
10.加惰轮的轮系只能改变 的旋转方向,不能改变轮系的 。
n11.一对齿轮的传动比,若考虑两轮旋转方向的同异,可写成 i = 1 = 士 ——。
n212.定轴轮系的传动比, 等于组成该轮系的所有 轮齿数连乘积与所有轮 齿数连乘积之比。
13.在周转转系中,凡具有几何轴线的齿轮,称中心轮,凡具有几何轴线的齿轮,称为行星轮,支持行星轮并和它一起绕固定几何轴线旋转的构件,称为 。
14.周转轮系中,只有一个 时的轮系称为行星轮系。
15.转系可获得 的传动比,并可作距离的传动。
16.转系可以实现要求和 要求。
2.根据轮系中齿轮的几何轴线是否固定,可将轮系分 轮系、 轮系和6.惰轮对 并无映响,但却能改变从动轮的 方向。
17.转系可以运动,也可以运动。
18.采用周转轮系可将两个独立运动为一个运动,或将一个独立的运动成两个独立的运动。
19.差动轮系的主要结构特点,是有两个。
20.周转轮系结构尺寸,重量较。
21.周转轮系可获得的传动比和的功率传递。
三、判断题1 .转系可分为定轴轮系和周转轮系两种。
机械设计基础_孙立鹏_习题第五章轮系
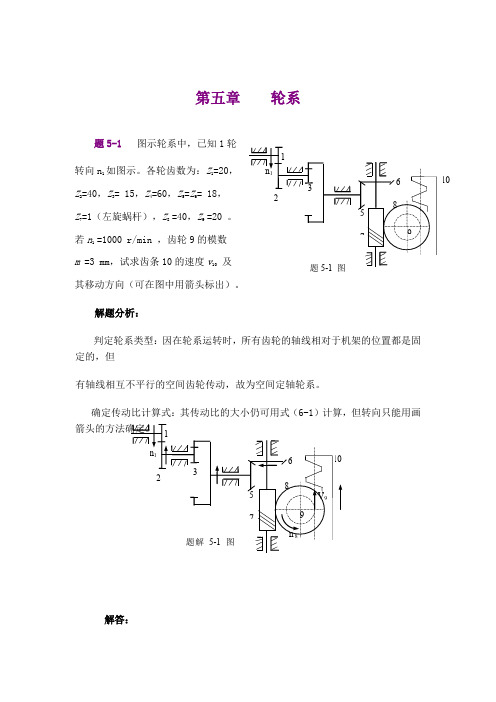
第五章轮系题5-1图示轮系中,已知1轮Array如图示。
各轮齿数为:Z1=20,转向n1Z=40,Z3= 15,Z4=60,Z5=Z6= 18,2Z=1(左旋蜗杆),Z8=40,Z9 =20 。
7若n1 =1000 r/min ,齿轮9的模数m =3 mm,试求齿条10的速度v及10其移动方向(可在图中用箭头标出)。
解题分析:判定轮系类型:因在轮系运转时,所有齿轮的轴线相对于机架的位置都是固定的,但有轴线相互不平行的空间齿轮传动,故为空间定轴轮系。
确定传动比计算式:其传动比的大小仍可用式(6-1)计算,但转向只能用画解答:1.确定齿条10的速度v 10 大小∵ 320118152040186040753186428118=⨯⨯⨯⨯⨯⨯===z z z z z z z z n n i∴min /125.3min /320100018189r r i n n n ====s /mm .s /mm .n mz n d v v 82960125320360609999910=⨯⨯⨯π=π=π==2.确定齿条10移动方向根据圆柱齿轮传动、锥齿轮传动及蜗杆传动的转向关系,可定出蜗轮转向n 8为逆时针方向,齿轮9与蜗轮8同轴,n 9 = n 8,齿条10线速度v 10与9轮线速度v 9方向一致,故齿条10的移动方向应朝上(↑)题5-2 图示轮系中,已知蜗杆1的齿数为Z 2= 50 ;蜗杆2′为单头右旋蜗杆, 蜗轮3的齿数为Z 3=40;其余各轮齿 数为;Z 3′=30,Z 4 = 20 ,Z 4′ = 26 , Z 5 =18,Z 5′=28,Z 6=16,Z 7=18。
要求:(1) 分别确定蜗轮2、蜗轮3的 轮齿螺旋线方向及转向n 2、n 3 ;(2) 计算传动比i 17 ,并确定齿 轮7的转向n 7。
解题分析:判定轮系类型:因在轮系运转时,所有齿轮的轴线相对于机架的 位置都是固定的,但有轴线相互不 平行的空间齿轮传动,故为空间定 轴轮系。
机械设计基础期末试题及答案

机械设计基础期末试题及答案一、填空题(每空1分,共30分)1、构件是机器的_运动___单元体;零件是机器的__制造___单元体;部件是机器的__装配___单元体。
2、平面运动副可分为______低副__和____高副___,低副又可分为__转动副_____和___移动副____。
3、轮系运动时,所有齿轮几何轴线都固定不动的,称___定轴轮系____轮系,至少有一个齿轮几何轴线不固定的,称___行星轮系______轮系。
4、为保证带传动的工作能力,一般规定小带轮的包角α≥___120°_______。
5、若键的标记为键B20×70GB1096-79,则该键为__B____平键,b=___20___,L=_____70___。
6、轴的作用是_____支承轴上的旋转零件________________________。
按轴的承载情况不同,可以分为___传递运动和转矩____、___心轴_____、__转轴、传动轴_______。
7、凸轮机构是由_____机架_______、________凸轮____、______从动件______三个基本构件组成的。
8、在曲柄摇杆机构中,当曲柄等速转动时,摇杆往复摆动的平均速度不同的运动特性称为___急回特性_________。
9、在蜗轮齿数不变的情况下,蜗杆的头数越少,则传动比就越_______大_____。
10、齿轮啮合时,当主动齿轮的____齿根__推动从动齿轮的___齿顶___,一对轮齿开始进入啮合,所以开始啮合点应为______从动轮齿顶圆______与啮合线的交点;当主动齿轮的___齿顶___推动从动齿轮的___齿根___,两轮齿即将脱离啮合,所以终止啮合点为________主动轮齿顶圆____与啮合线的交点。
11、滚动轴承内圈与轴颈的配合采用____基孔制__制,外圈与轴承孔的配合采用基轴制_______制。
二、判断题(每题1分,共10分)1、基圆以内有渐开线。
《机械设计基础》复习题答案(带齿轮轴轮系联接及液压等)解读

一、选择题1、渐开线齿轮的齿廓曲线形状取决于【D】A、分度圆B、齿顶圆C、齿根圆D、基圆2、在液压传动中,油泵属于【A】A、动力元件B、执行元件C、控制元件D、辅助元件3、在一皮带传动中,若主动带轮的直径为10cm,从动带轮的直径为30cm则其传动比为: 【B】A、0.33B、3C、4D、53、带传动是依靠来传递运动和功率的。
【B】A、带与带轮接触面之间的正压力B、带与带轮接触面之间的摩擦力C、带的紧边拉力D、齿轮之间的啮合4、在一般机械传动中,若需要带传动时,应优先选用【V】A、圆形带传动B、同步带传动C、V型带传动D、平型带传动5、在一齿轮系中,若各齿轮和传动件的几何轴线都是固定的,则此轮系为【A】A、定轴轮系B、动轴轮系C、周转轮系D、行星轮系6、一轮系有3对齿轮参加传动,经传动后,则输入轴与输出轴的旋转方向【D】A、相同B、相反C、不变D、不定7、下列哪一种齿轮传动能改变两轴间的传动方向【D】A、直齿圆柱齿轮B、斜齿圆柱齿轮C、内啮合齿轮D、圆锥齿轮8、轴承代号3312B中,其轴承内径为 : 【B】A.33mm B、60mm C、312mm D、12mm9、普通平键联接所能传递的最大转矩为T,现要传递的转矩为1.5T,则应:【D】(A)把键长增大到1.5倍,(B)把键高增大到1.5倍,(C)把键宽增大到1.5倍,(D)安装一对平键。
10、三角带横截面为等腰梯形,夹角为40度,在设计三角带轮时,轮槽夹角一般确定为:【C】(A)大于40度(B)等于40度(C)小于40度二、判断题:1.(×)普通平键联接是依靠键的上下两面的摩擦力来传递扭距的。
2.(×)m,d,ha* c*都是标准值的齿轮是标准齿轮。
5.(√)渐开线标准直齿圆柱齿轮传动,由于安装不准确,产生了中心距误差,但其传动比的大小仍保持不变。
6、()分度圆上压力角的变化,对齿廓的形状有影响。
?-#7、(√)速比公式i12=n1/n2=Z2/Z1不论对齿轮传动还是蜗杆传动都成立。
机械设计基础试题库完整

《机械设计基础》试题库试题库汇总表一、单项选择题1.轮系运动时,各齿轮轴线位置固定不动的称为()。
C. 行星轮系D. 简单行星轮系【代码】21711019【答案】B2.在行星轮系中,凡具有固定几何轴线的齿轮被称为()。
A. 行星轮B. 太阳轮C. 惰轮D. 系杆【代码】22111016【答案】B3.在行星轮系中,轴线位置会发生改变的齿轮被称为()。
A. 行星轮B. 太阳轮C. 惰轮D. 系杆【代码】22111022【答案】A4.轮系的传动比等于组成该轮系的各对啮合齿轮中()之比。
A. 主动轮齿数的连乘积与从动轮齿数的连乘积B. 主动轮齿数的连加与从动轮齿数的连加C. 从动轮齿数的连乘积与主动轮齿数的连乘积D. 从动轮齿数的连加与主动轮齿数的连加【代码】21811015【答案】C5.至少有一个齿轮的轴线的位置会发生改变的轮系被称为()。
C. 复合轮系D. 都不是【代码】21711025【答案】A6.按齿轮轴线的位置是否固定,轮系可以分为()两种类型。
A.定轴轮系和差动轮系(自由度)B.差动轮系和行星轮系C.定轴轮系和复合轮系D.定轴轮系和行星轮系(周转轮系) 【代码】21711037【答案】D7.行星轮系中的差动轮系,其自由度为()个。
A.1 B.2 C.3 D.4【代码】22211015【答案】B8.下列四项功能中,哪几项()可以通过轮系的运用得以实现。
①两轴的较远距离传动②变速传动③获得大的传动比④实现合成和分解运动A.①②B.①②③C.②③④D.①②③④【代码】22311017【答案】D9.轮系下列功用中,哪一功用必须依靠行星轮系实现?()。
A.实现变速B.实现变向C.实现远距离传动D.实现运动的分解【代码】22311022【答案】D10. 在轮系中,只改变齿轮转向而不影响轮系传动比的齿轮,通常称为()。
A. 行星轮B. 太阳轮C. 惰轮D. 中心轮【代码】22011016【答案】C11. 定轴轮系传动比计算式中的(-1)m,m表示()。
《机械设计基础》第七章 轮系及减速器

(2) 找出所有的单一周转轮系后余下的就是定轴轮系 (3) 分别列出计算各基本轮系传动比的方程式。 (4) 找出各基本轮系之间的联系。 (5) 将各基本轮系传动比方程式联立求解,即可求得混合轮系的传动比。
例7-5:已知各轮齿数为:z1=20, z2=40, z2 ′=20, z3=30,z4=80, 求传动比i1H。
i12 i23 i34
n1 z 2, n2 z1 z3 n2 , n3 z 2 n3 z4 , n4 z3
z5 n4 i45 , n5 z4
其中n2=n2′,n3=n3′。将以上各式两边连乘可得,
n3 n4 n1n2 3 z2 z3 z4 z5 i12 i23 i34 i45 (1) z3 z4 n2 n3 n4 n5 z1 z2
50 nH 30 80 0 nH 20 50
nH≈14.7r/min
正号表示nH转向和n1的转向相同 本例中行星齿轮2和2′的轴线和齿轮1(或齿轮3)及系杆H的 轴线不平行,所以不能直接利用公式。
§7—4 复合轮系传动比的计算
在计算混合轮系传动比时,既不能将整个轮系作为定轴轮系来处理, 也不能对整个机构采用转化机构的办法。 计算混合轮系传动比的正确方法是: (1) 找出各个单一周转轮系
§5-5 轮系的应用
一、实现分路传动
Ⅳ
二、实现相距较远的两轴之间的传动
三、获得较大传动比 四、实现换向传动 五、用作运动的分解
Ⅲ Ⅴ Ⅵ 主轴
六、在尺寸及重量较小的条件下,实现大功率传动 七、用作运动的合成
图9-20
Ⅱ
杨可桢《机械设计基础》课后习题及详解(轮系)【圣才出品】

5-2 在图 5-3 所示轮系中,已知 z1=15,z2=25, z2' =15,z3=30, z3' =15z4 =30, z4' =2(右旋),z5=60, z5' =20(m=4 mm),若 n1=500 r/min,求齿条 6
1 / 12
圣才电子书
图 5-11
① 齿轮 4、5、6、7、H 构成周转轮系,有
②
又有:nH=n3,nP=n7,联立式①②可得: np
1 4
n1Βιβλιοθήκη n4 ③(1)将已知代入式③,可得 np
1 4
n1
n4
1 1000110000
4
0.25r
/
min
P 和轮 1 的转向相同。
(2) np 0 。
(3)将已知代入式③,可得
,且与
z2 无关。
5-8 在 图 5-9 所 示 锥 齿 轮 组 成 的 行 星 轮 系 中 , 已 知 各 轮 的 齿 数 为
,求 nh 的大小和方向。
图 5-9
解:由题意可得: i1H3
n1H n3H
n1 nH n3 nH
z2 z3 z1z2
,又 n3 0
则有:
5 / 12
圣才电子书
解得:
十万种考研考证电子书、题库视频学习平台
负号表示方向与 n1 相反。
5-9 在图 5-10 所示差动轮系中,已知各轮的齿数
齿轮
1 的转速为 200 r/min(箭头向上),齿轮 3 的转速为 50 r/min(箭头向下),求行星架
转速 nH 的大小和方向。
图 5-10 解:这是一个周转轮系,其中齿轮 1、3 为中心轮,齿轮 2、2′为行星轮,H 为行星架, 则有:
机械设计基础试题4

《机械设计基础》试题4一.填空题(每空1分,共20分)1.所谓定轴轮系是指,而周转轮系是指2.在周转轮系中,轴线固定的齿轮称为;兼有自转和公转的齿轮称为;而这种齿轮的动轴线所在的构件称为。
时,可采用变位的办法来避免3.当直齿圆柱齿轮的齿数少于zmin根切。
4.齿条刀具与普通齿条的区别是。
5.当两外啮合直齿圆柱标准齿轮啮合时,小齿轮轮齿根部的磨损要比大齿轮轮齿根部的磨损。
6.渐开线的形状取决于__________大小。
7.中心距的可分性是指_______________________________________________________。
8.一对平行轴斜齿圆柱齿轮的正确啮合条件为_________________________,____________________________,______________ ___________,____________________________。
9.从加工原理来分,齿轮的加工方法有_______________和_______________________。
10.变位齿轮指的是_____________________________________________________。
11.齿轮的标准安装指的是______________________________________________。
12.按轴与轴承间的摩擦形式,轴承分为________________,_________________。
二.判断题(每题0.5分,共5分)1.渐开线标准齿轮的齿根圆 恒大于基圆。
---------------( )2.对于单个齿轮来说,节圆半径就等于分度圆半径。
--------------( )3.用范成法切制渐开线直齿圆柱齿轮发生根切的原因是齿轮太小了,大的齿轮就不会根切。
------------------------------( )4.范成法切削渐开线齿轮时,一把模数为m 、压力角为α的刀具可以切削相同模数和压力角的任何齿数的 齿轮。
机械设计基础知识点与试题库 下

第六章 轮系简答题1. 定轴齿轮与周转轮系的主要区别是什么样?2. 齿轮系的转向如何确定,(-1)”适用于何种类型的齿轮系?3. 周转轮系由哪几种基本构件组成?一. 填空题.1. 在定轴轮系中,每一个齿轮的回转轴线都是 的.2. 定轴系中的惰轮对_无影响,主要用于改变从动轮的 。
3. 周转轮系中,i H AK 表示 ,iAK 表示 。
4. 平面定轴轮系中,主、,从动轮的转向取决于 ;当 时,主、动轮转向相同:当 时,主,从动轮转向相反 。
5. 一个单一的周转轮系由 、和 组成,一般——不超过两个: 和 的几何轴线必须重合。
6. 一对平行轴外啮全轮传动,两轮转向 ;一对平行轴内啮全轮传动,两轮转向 。
三.选择题。
1,周转轮第的转化轮系为 、。
A.定轴轮系 B.行星轮系 C.差动轮系2.如图1所示轮系,若z1=z2=z3,则传动比i1H=3.在主轴转系的转化轮系中,若轮a 、b 的传动比 为正,则轮a 、b 的绝对速度方向A .相同 B.相反 C.不能确定四.计算题1.图示的轮系中,已知各齿轮的齿数z1=20,z2=40,z’=18,z4=18,z7=20,齿轮7的模数m=3mm,蜗杆头数为1(左旋), 蜗轮齿数z6=40,齿轮1为主动轮,转向如图所示,转速n1=100r/min,试示齿条8的速度和移动方向。
i1H。
3.已知图4.图5所示为输送带行星轮系中,已知各齿轮的齿数分别z1=12,z2=33,z2’=30,z3=78,z4=75,电动机的转速n1=1450r/min,试求输出轴转速nr的大小与方向。
七、其他常用机构1、掌握槽轮机构的工作原理与应用、2、棘轮机构的工作原理与应用,3、螺旋机构的应用及方向判断与移动距离的计算一、填空题1.所谓间歇运动机构,就是在主动件作运动时,从动件能够产生周期性的、、运动机构。
2.欲将一匀速回转运动转变成单向间歇回转运动,采用的机构有、、等,其中间歇时间可调的机构是机构。
《机械设计基础》试题库
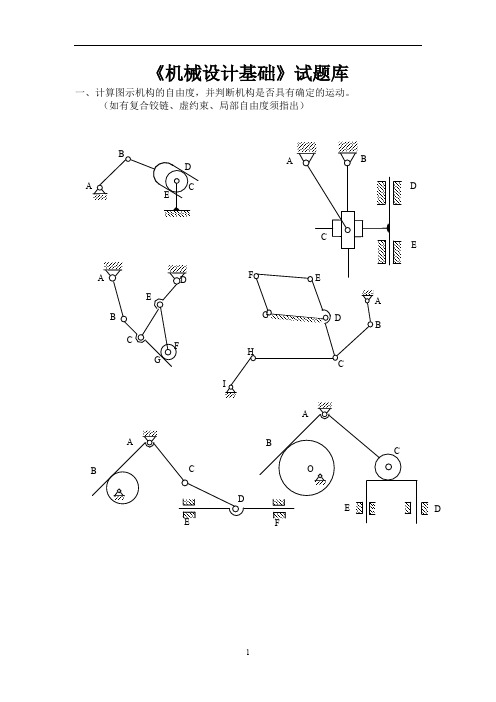
《机械设计基础》试题库一、计算图示机构的自由度,并判断机构是否具有确定的运动。
(如有复合铰链、虚约束、局部自由度须指出)DEDCDDE二、轮系的计算1.在图示轮系中,已知各轮齿数为Z1=Z3=30,Z2=90,Z2’=40,Z3’=40,Z4=30,试求传动比i1H,并说明I、H轴的转向是否相同?2.在图示轮系中,已知各轮齿数为Z1 =15,Z2=20, Z2’ = Z3’= Z4=30, Z3=40,Z 5= 90,试求传动比IⅠⅡ,并说明I、Ⅱ轴的转向是否相同?3.在图示轮系中,已知各轮齿数为Z1=1(右旋蜗杆), Z2=40 ,Z2’= 24,Z3=72,Z,3=18,Z4= 114.1、该轮系属于何种轮系2、求轮系的传动比i1H,并在图中标出系杆H的转向。
4.在图示轮系中,已知各轮齿数为Z1= 20,Z2=30,Z 2’= 50, Z3=80, n1=50r/min,方向如图所示,试求nH的大小和方向。
5.在图示轮系中,已知各轮齿数为Z1= Z4=20,Z 2= Z5=30,Z3= Z6=100,试求传动比i1H。
ⅠⅠⅡ6.在图示轮系中,已知各轮齿数为Z 1=100, Z 2=40,Z 2’=30, Z 3=90, Z ,3=50, Z 4=2(右旋), n 1=200r/min ,n 4=1250r/min ,转向如图所示,试求n H的大小及方向。
7.在图示轮系中,已知各轮齿数为Z 1=15, Z 2=25,Z 2’=20, Z 3=20, Z 4=60,Z 4’= 55, n 1=110r/min ,转向如图所示,试求n h 的大小及转向。
8.某起重装置,其运动简图所图所示,已知各轮齿数为Z 1=Z 2=20,Z 3=60,Z 4=2(蜗杆), Z 5=40,n 1的转向如图所示,试求 1、该轮系属于何种轮系? 2、i 15的大小;3、此时重物W是上升还是下落?三、作图题(按作图规则作图,图线清晰) 1.凸轮为一偏心圆盘。
机械设计基础第5章 轮系习题解答2
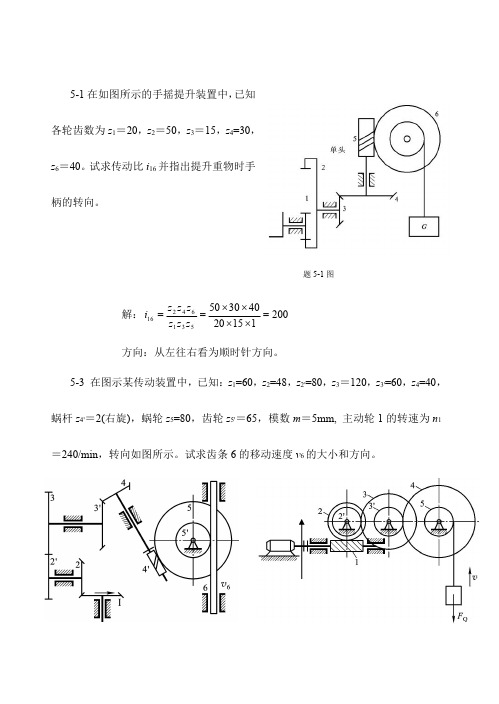
5-1在如图所示的手摇提升装置中,已知各轮齿数为z 1=20,z 2=50,z 3=15,z 4=30,z 6=40。
试求传动比i 16并指出提升重物时手柄的转向。
题5-1图解:2001152040305053164216=⨯⨯⨯⨯==z z z z z z i 方向:从左往右看为顺时针方向。
5-3在图示某传动装置中,已知:z 1=60,z 2=48,z 2'=80,z 3=120,z 3'=60,z 4=40,蜗杆z 4'=2(右旋),蜗轮z 5=80,齿轮z 5'=65,模数m =5mm,主动轮1的转速为n 1=240/min ,转向如图所示。
试求齿条6的移动速度v 6的大小和方向。
题5-3图题5-4图解:齿条的移动方向如图所示,其轮系传动比为:322608060804012048'4'3'2154325115=⨯⨯⨯⨯⨯⨯===z z z z z z z z n n i 则齿轮5’的转速为:min /5.7322401515r i n n ===又齿轮5’分度圆直径为:mm m z d 325565'5'5=⨯==所以齿条的移动速度为:s m n d v /128.0600005.73251000605'56=⨯⨯=⨯=ππ5-4如图所示为一电动卷扬机的传动简图。
已知蜗杆1为单头右旋蜗杆,蜗轮2的齿数z 2=42,其余各轮齿数为z 2'=18,z 3=78,z 3'=18,z 4=55;卷筒5与齿轮4固联,其直径D 5=400mm ,电动机转速。
n 1=1500r/min ,试求:(1)转筒5的转速n 5的人小和重物的移动速度v 。
(2)提升重物时,电动机应该以什么方向旋转?解:1.其轮系传动比为:11.5569500518181557842'3'214324114==⨯⨯⨯⨯===z z z z z z n n i 则齿轮4的转速(即转筒5的转速)为:min /70.211.556150014145r i n n n ====所以重物的移动速度为:s m n D v /057.0600007.2400100060556=⨯⨯=⨯=ππ5-5在如图所示周转轮系中,已知各轮齿数为z 1=60,z 2=20,z 2'=20,z 3=20,z 4=20,z 5=100,试求传动比i 41。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章 轮系
习题与参考答案
一、复习思考题
1.为什么要应用轮系试举出几个应用轮系的实例
2.何谓定轴轮系何谓周转轮系行星轮系与差动轮系有何区别 3.什么叫惰轮它在轮系中有什么作用
4.定轴轮系的传动比如何计算式中(-1)m
有什么意义 5.定轴轮系末端的转向怎样判别
6.如果轮系的末端轴是螺旋传动,应如何计算螺母的移动量
二、填空题
1.由若干对齿轮组成的齿轮机构称为 。
2.根据轮系中齿轮的几何轴线是否固定,可将轮系分 轮系、 轮系和 轮系三种。
3.对平面定轴轮系,始末两齿轮转向关系可用传动比计算公式中 的符号来判定。
4.行星轮系由 、 和 三种基本构件组成。
5.在定轴轮系中,每一个齿轮的回转轴线都是 的。
6.惰轮对 并无映响,但却能改变从动轮的 方向。
7.如果在齿轮传动中,其中有一个齿轮和它的 绕另一个 旋转,则这轮系就叫周转轮系。
8.旋转齿轮的几何轴线位置均 的轮系,称为定轴轮系。
9.轮系中 两轮 之比,称为轮系的传动比。
10.加惰轮的轮系只能改变 的旋转方向,不能改变轮系的 。
11.一对齿轮的传动比,若考虑两轮旋转方向的同异,可写成±==
2
1
n n i ——。
12.定轴轮系的传动比,等于组成该轮系的所有 轮齿数连乘积与所有 轮齿数连乘积之比。
13.在周转转系中,凡具有 几何轴线的齿轮,称中心轮,凡具有 几何轴线的齿轮,称为行星轮,支持行星轮并和它一起绕固定几何轴线旋转的构件,称为 。
14.周转轮系中,只有一个 时的轮系称为行星轮系。
15.转系可获得 的传动比,并可作 距离的传动。
16.转系可以实现 要求和 要求。
17.转系可以运动,也可以运动。
18.采用周转轮系可将两个独立运动为一个运动,或将一个独立的运动成两个独立的运动。
19.差动轮系的主要结构特点,是有两个。
20.周转轮系结构尺寸,重量较。
21.周转轮系可获得的传动比和的功率传递。
三、判断题
1.转系可分为定轴轮系和周转轮系两种。
()
2.旋转齿轮的几何轴线位置均不能固定的轮系,称之为周转轮系。
()
3.至少有一个齿轮和它的几何轴线绕另一个齿轮旋转的轮系,称为定轴轮系。
()4.定轴轮系首末两轮转速之比,等于组成该轮系的所有从动齿轮齿数连乘积与所有主动齿轮齿数连乘积之比。
()
5.在周转轮系中,凡具有旋转几何轴线的齿轮,就称为中心轮。
()
6.在周转轮系中,凡具有固定几何轴线的齿轮,就称为行星轮。
()
7.定轴轮系可以把旋转运动转变成直线运动。
()
8.轮系传动比的计算,不但要确定其数值,还要确定输入输出轴之间的运动关系,表示出它们的转向关系。
()
9.对空间定轴轮系,其始末两齿轮转向关系可用传动比计算方式中的(-1)m的符号来判定。
()
10.计算行星轮系的传动比时,把行星轮系转化为一假想的定轴轮系,即可用定轴轮系的方法解决行星轮系的问题。
()
11.定轴轮系和行星轮系的主要区别,在于系杆是否转动。
()
例解
1. 所谓定轴轮系是指在轮系运转时,所有齿轮的轴经相对于机架的位置都是固定的轮系;周转轮系是指轮系中至少有一个齿轮的轴线绕另一个齿轮轴线转动的轮系。
2. 一个基本的周转轮系是由一个系杆,若干个行星轮和不超过二个与行星轮啮合的中心组成的。
3. 自由度为2的周转轮系称为差动轮系,而自由度为1的周转轮系称为行星轮系。
4. 复合轮系是指既包含定轴轮系部分,又包含周转轮系部分或由几个基本周转轮系组成的复杂轮系。
复合轮系传动比的正确计算方法是:1)正确区分各基本轮系;2)列出各基本轮系传动比计算方程式;3)建立各基本轮系之间的联系;4)将各基本轮系传动比计算方程式联立求解,得到复合轮系的传动比。
5. 图示为锥齿轮组成的周转轮系。
已知Z 1=Z 2=17,Z 2′=30,Z 3=45,若1轮转速n 1=200r/min ,试求系杆转速n H 。
解答:
1.判定轮系类型,确定传动比计算式 轮系类型—因在一轮系运转时,齿轮2和2′的轴线相对于机架的位置不固
定,且齿轮3固定不转动,故为行星轮系;
传动比公式—系杆转速n H 须通过行星轮系的转化轮系(假想定轴轮系)传动比公式求得。
2.确定系杆转速n H
1)转化轮系传动比公式:5.130
174517021321313113
=⨯⨯==--=--=='z z z z n n n n n n n n n i H H H H H H H
2)min /4005
.02005.11200113111r i n i n n H H H -=-=-=-==
n H 与n 1的转向相反。
6. 分析与思考:1)何谓原周转轮系的转化轮系i 13H 与i 13是否相等2)能否用i 12H 计算式中的转向关系,求上题解图所示周转轮纱中行星轮2的转速n 2为什么
答:1)给整个周转轮系加上一绕系杆的固定轴线转动的公共角速度(-ωH ),转化而得的假想定轴轮系称为原周转轮系的转化轮系。
i 13H
与i 13不相等,因为i 13H =n 1H /n 3H ≠i 13=n 1/n 3。
2)不能用i 12H 计算式求解n 2。
因轮2的轴线与中心轮和系杆的轴线不平行,它们的角速度不能按代数量进行加减,即:ω2H ≠ω2–ωH ,故不能用i 12H 的计算式求解n 2。
7. 图示轮系中,已知蜗杆1为双头左旋蜗杆,转向如图示,蜗轮2的齿数为Z 2=50;蜗杆2′为单头右旋蜗杆,蜗轮3的齿数为Z 3=40;其余各轮齿数为:
Z 3′=30,Z 4=20,Z 4′=26,Z 5=18,Z 5′=28, Z 6=16,Z 7=18。
试求传动比i 17及n 7的方向。
解答:1.判定轮系类型,确定传动比计算式
轮系类型—因在轮系运转时,所有齿轮的轴线相对于机架的位置都是固定的,但有轴线相互不平行的空间齿轮传动,故为空间定轴轮系。
因此其转向只能用画箭头的方法确定。
8. 图示轮系中,已知1轮转向n 1如图示。
各轮齿数为:Z 1=20,Z 2=40,Z 3=15,Z 4=60,Z 5=Z 6=18,Z 7=1(左旋蜗杆)Z 8=40,Z 9=20。
若n 1=1000r/min ,齿轮9的模数m=3mm ,试求齿条10的速度V 10及其移动方向(可在图中用箭头标出)。
填空题答案: 1.轮系
2.定轴 行星 混合
3.(-1)m
4.行星轮 中心轮 系杆 5.固定的
6.传动比 转动 7.几何轴线 齿轮 8.固定
9.首末 转速
10.从动轮 传动比 11.
1
2
z z 12.从动轮 主动轮
13.固定 运动 系杆(或转臂) 14.主动件 15.较大 较远 16.变速 变向 17.合成 分解 18.合成 分解 19.主动件 20.紧凑 轻 21.较大 较大
判断题答案:
1.√
2.√
3.×
4.√
5.×
6.×
7.√
8.√
9.× 10.√ 11.√。
