容斥问题公式及运用
容斥原理的基本应用

容斥原理的基本应用什么是容斥原理容斥原理,又称为容错原理、排容原理,是组合数学中一种常用的计数原理。
容斥原理用于解决计数问题,特别是解决两个或多个集合的并、交、差等计数问题。
它通过将复杂的集合拆分成简单的部分,并根据不同情况逐步计算得到最终的结果。
容斥原理有助于简化计数问题的解决过程,使得问题的求解更加简洁明了。
容斥原理的应用场景容斥原理在组合数学、概率论、计算机科学等领域有广泛的应用。
它可以解决一些复杂的计数问题,包括排列组合问题、概率计算问题、鸽巢原理问题等。
容斥原理在解决这些问题时,可以极大地简化计算的复杂度,提高解题效率。
以下是容斥原理的基本应用场景:1.列表中元素的多重选择问题2.集合的并、交、差运算问题3.满足多个条件的计数问题4.重复计算问题容斥原理的基本原理容斥原理的基本原理可以通过一个简单的示例来说明。
假设有A、B两个集合,记其元素个数分别为|A|和|B|。
那么A和B的并集的元素个数可以通过以下公式计算得到:|A∪B| = |A| + |B| - |A∩B|其中,|A∩B|表示A和B集合的交集中的元素个数。
上述公式中的两次求并集都将交集的元素计算了两次,所以需要将交集的元素个数减去一次,以避免重复计算。
这就是容斥原理的基本思想。
容斥原理的基本应用举例列表中元素的多重选择问题假设有一个列表,其中有苹果、橙子、香蕉、草莓这四种水果。
现在需要从这个列表中选择1种、2种、3种甚至全部4种水果的可能性有多少种?根据容斥原理,我们可以通过以下步骤进行计算:1.计算只选择1种水果的情况,共有4种可能性。
2.计算只选择2种水果的情况,共有C(4,2) = 6种可能性。
3.计算只选择3种水果的情况,共有C(4,3) = 4种可能性。
4.计算选择全部4种水果的情况,共有1种可能性。
根据容斥原理,计算总的可能性的公式为:总可能性 = 只选择1种水果的数量 - 只选择2种水果的数量 + 只选择3种水果的数量 - 选择全部4种水果的数量带入上述计算结果,得到总可能性为4 - 6 + 4 - 1 = 1种。
三者容斥问题3个公式

一、容斥问题的3个公式容斥原理是指一种计数方法。
先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复。
1.两个集合的容斥原理:n(A∪B)=n(A)+n(B) -n(A∩B)2.三个集合的容斥原理:|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|3.n个集合的容斥原理:要计算几个集合并集的大小,我们要先将所有单个集合的大小计算出来,然后减去所有两个集合相交的部分,再加回所有三个集合相交的部分,再减去所有四个集合相交的部分,依此类推,一直计算到所有集合相交的部分。
二、容斥问题的应用:对于容斥问题,解题关键做到不重不漏,各个集合相加,理清各集合间的关系,扣掉重复补上遗漏的。
用于理解的主要方法是画文氏图,但考试中应尽量避免画图,这样速度偏慢些。
【例1】:某调查公司对甲、乙、丙三部电影的收看情况向135人进行调查,有89人看过甲片,有47人看过乙片,有63人看过丙片,既看过甲、乙片为30人,既看过乙、丙片为31人,既看过甲、丙片为32人,其中有24人三部电影都看过,问多少人一部也没有看过呢?【解析】:既看过甲、乙片为30人是包含只看过甲乙还有甲乙丙三人两个部分,以M、N、W为既看过甲、乙片的人,N既看过乙、丙片的人,既看过甲、丙片的人,X为三部都看过的人数,这里面W、N、X都是有包含三者这个区域,根据把重复数的次数变为1次,或者说把重叠的面积变为一层,做到不重不漏的原则,则公式转化为I=A+B+C-(M+N+W)+X+Y,135=89+47+63-(30+31+32)+ 24+Y,Y=5人。
结论:三者容斥问题,画图之后可知,三个圆相交的地方有1层、2层、3层三种情况,当将三个集合相加的时候,2层和3层区域分别多计算一次和两次,故若想求全集,需要将重叠区域减掉,故三者容斥问题的公式为:A∪B∪C=A+B+C -A∩B-B∩C-C∩A+A∩B ∩C。
容斥原理的应用举例

容斥原理的应用举例什么是容斥原理容斥原理是概率论、组合数学中常用的一种计数方法,它用于求解多个事件的并或交的概率或数量。
容斥原理是以集合论为基础的一种推理思想,通过排除重复计数,从而得到准确的计数结果。
容斥原理的公式容斥原理的公式可以表示为:|A1 ∪ A2 ∪ ... ∪ An| = |A1| + |A2| + ... + |An| - |A1 ∩ A2| - |A1∩ A3| - ... - |An-1 ∩ An| + |A1 ∩ A2 ∩ A3| + ... + (-1)^(n-1) * |A1 ∩ A2 ∩ ... ∩ An|其中,|A1 ∪ A2 ∪ … ∪ An| 表示事件 A1、A2、…、An 的并的概率或数量,|A1| 表示事件 A1 的概率或数量,|A1 ∩ A2| 表示事件 A1 和 A2 的交的概率或数量,以此类推。
容斥原理的应用举例容斥原理在组合数学和概率论中有广泛的应用,下面举几个例子来说明容斥原理的具体应用。
例子1:求解有限集合的元素个数假设有三个集合 A、B、C,它们分别有 |A|、|B|、|C| 个元素,求这三个集合的并集的元素个数。
根据容斥原理的公式,有:|A ∪ B ∪ C| = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |D|其中,|A ∩ B| 表示集合 A 和 B 的交的元素个数,以此类推。
例子2:求解排列组合中不满足条件的情况假设有两个集合 A 和 B,它们分别有 |A|、|B| 个元素,要求从 A 和 B 中选择指定数量的元素排列组合,但要满足某个特定的条件,那么可以使用容斥原理来计算不满足条件的情况。
Count = |A| * |B| - |A ∩ B|其中,|A ∩ B| 表示满足条件的情况。
例子3:求解事件的概率假设有三个事件 A、B、C,它们分别发生的概率分别为 P(A)、P(B)、P(C),求这三个事件的并的概率。
容斥问题应用题解题技巧及公式

容斥问题应用题解题技巧及公式容斥原理是一种组合数学中常用的计数方法,用于解决包含重叠部分的计数问题。
常见的应用有如下几种情况:
1.求集合的并:当求两个集合的并集大小时,可以使用容斥原理来避免重复计数。
公式为|A∪B| = |A| + |B| - |A∩B|,其中|A∪B|表示A和B的并集大小,|A|表示集合A的大小,|B|表示集合B的大小,|A∩B|表示A和B的交集大小。
2.求集合的交:当求两个集合的交集大小时,可以使用容斥原理来避免重复计数。
公式为|A∩B| = |A| + |B| - |A∪B|,其中|A∩B|表示A和B的交集大小,|A|表示集合A的大小,|B|表示集合B的大小,|A∪B|表示A和B的并集大小。
3.求不满足某个条件的情况:当求满足某个条件的情况时,可以使用容斥原理来求不满足该条件的情况。
假设有n个事件,A1到An,分别表示这些事件,那么不满足任何一个事件的情况数目为S =
∑|Ai| - ∑|Ai∩Aj| + ∑|Ai∩Aj∩Ak| - ... +/-
|A1∩A2∩...∩An|。
其中|Ai|表示事件Ai发生的情况数目,
|Ai∩Aj|表示事件Ai和Aj同时发生的情况数目,依此类推。
在应用容斥原理解题时,需要注意对问题进行合理的划分,避免出现重复计数或者漏计的情况。
同时,需要对问题进行适当的拓展和转化,以便更好地利用容斥原理解决更复杂的计数问题。
容斥原理公式大全

容斥原理公式大全容斥原理是组合数学中常用的一种计数方法,可以用于解决涉及多个集合的计数问题。
它的基本思想是通过求解包含或排除一些元素的方式来计算所需的数量。
1. 容斥原理的基本形式:如果A₁,A₂,...,Aₙ是有限集合,并且S表示它们的并集,则有:|S| = |A₁∪A₂∪...∪Aₙ| = Σ|Aᵢ| - Σ|Aᵢ∩Aₙ| + Σ|Aᵢ∩Aₙ∩Aₙ| - ... + (-1)ⁿ⁻¹|A₁∩A₂∩...∩Aₙ|,其中|X|表示集合X中元素的个数。
2. 两个集合的容斥原理:如果A和B是两个有限集合,则有:|A∪B| = |A| + |B| - |A∩B|。
3. 三个集合的容斥原理:如果A,B和C是三个有限集合,则有:|A∪B∪C| = |A| + |B| + |C| - |A∩B| - |A∩C| - |B∩C| + |A∩B∩C|。
4. 四个集合的容斥原理:如果A,B,C和D是四个有限集合,则有:|A∪B∪C∪D| = |A| + |B| + |C| + |D| - |A∩B| - |A∩C| - |A∩D| -|B∩C| - |B∩D| - |C∩D| + |A∩B∩C| + |A∩B∩D| + |A∩C∩D| +|B∩C∩D| - |A∩B∩C∩D|。
5. n个集合的容斥原理:如果A₁,A₂,...,Aₙ是n个有限集合,则有:|A₁∪A₂∪...∪Aₙ| = Σ|Aᵢ| - Σ|Aᵢ∩Aₙ| + Σ|Aᵢ∩Aₙ∩Aₙ| - ... + (-1)ⁿ⁻¹|A₁∩A₂∩...∩Aₙ|。
容斥原理的思想可以扩展到更多个集合的情况,通过求解交集和补集的方式来计算复杂集合的数量。
它在组合数学中具有广泛的应用,特别是在计数问题中常常能够提供简洁有效的解决方案。
容斥原理的三大公式应用题

容斥原理的三大公式应用题一、引言容斥原理是概率论中常用的一种计数方法,用来解决排除法不能解决的问题。
它通过巧妙地计算多个事件的交集与并集的关系,帮助我们更加灵活地计算概率。
本文将介绍容斥原理的三大公式的应用题,并通过列点的方式进行详细解析。
在解题过程中,我们将通过具体案例来帮助读者理解和掌握容斥原理的运用方法。
二、容斥原理的三大公式容斥原理的三大公式分别是:1.二事件容斥公式2.三事件容斥公式3.n事件容斥公式接下来,我们将分别利用这三个公式来解决几个具体的问题。
三、二事件容斥公式应用题假设有两个事件A和事件B,现在要计算同时发生事件A和事件B的概率。
具体问题如下:某班级有50个学生,其中35个学生会玩篮球,30个学生会踢足球,有20个学生既会玩篮球又会踢足球。
现在从班级中随机选择一个学生,求该学生既会玩篮球又会踢足球的概率。
解题思路如下:首先,我们需要知道事件A和事件B的概率,即分别计算玩篮球的学生和踢足球的学生在班级中的比例。
•玩篮球的概率:35/50•踢足球的概率:30/50然后,我们需要计算同时发生事件A和事件B的概率。
•既会玩篮球又会踢足球的概率:20/50最后,我们可以使用二事件容斥公式来计算既会玩篮球又会踢足球的概率:P(A ∩ B) = P(A) + P(B) - 2P(A ∩ B)= (35/50) + (30/50) - 2(20/50)= 45/50= 9/10所以,该学生既会玩篮球又会踢足球的概率为9/10。
四、三事件容斥公式应用题假设有三个事件A、B和C,现在要计算同时发生事件A、B和C的概率。
具体问题如下:某班级有50个学生,其中30个学生会玩篮球,25个学生会踢足球,20个学生会打乒乓球,有10个学生既会玩篮球又会踢足球,有5个学生既会踢足球又会打乒乓球,有3个学生既会玩篮球又会打乒乓球。
现在从班级中随机选择一个学生,求该学生既会玩篮球又会踢足球又会打乒乓球的概率。
重叠问题(容斥问题)
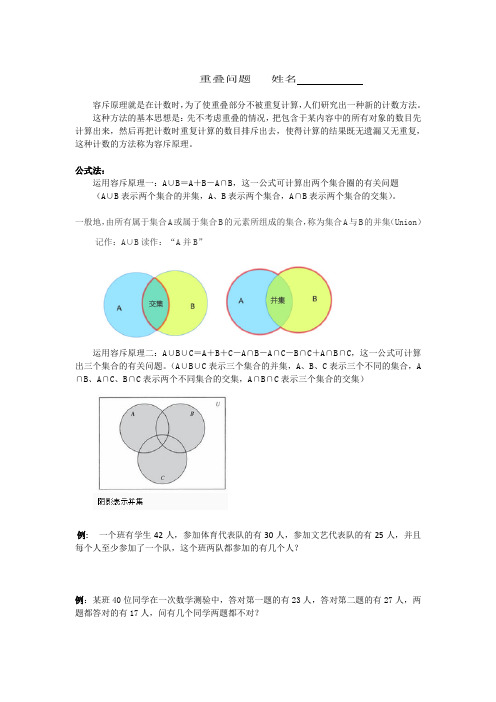
重叠问题姓名容斥原理就是在计数时,为了使重叠部分不被重复计算,人们研究出一种新的计数方法。
这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
公式法:运用容斥原理一:A∪B=A+B-A∩B,这一公式可计算出两个集合圈的有关问题(A∪B表示两个集合的并集,A、B表示两个集合,A∩B表示两个集合的交集)。
一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集(Union)记作:A∪B读作:“A并B”运用容斥原理二:A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C,这一公式可计算出三个集合的有关问题。
(A∪B∪C表示三个集合的并集,A、B、C表示三个不同的集合,A ∩B、A∩C、B∩C表示两个不同集合的交集,A∩B∩C表示三个集合的交集)例:一个班有学生42人,参加体育代表队的有30人,参加文艺代表队的有25人,并且每个人至少参加了一个队,这个班两队都参加的有几个人?例:某班40位同学在一次数学测验中,答对第一题的有23人,答对第二题的有27人,两题都答对的有17人,问有几个同学两题都不对?练习: 有100位旅客,其中10人既不懂英语,又不懂俄语,有75人懂英语,有83人懂俄语。
那么这100位旅客中既懂英语又懂俄语的有多少人?例:某校有三个兴趣小组,体育、书法和美术。
已知参加这三个兴趣小组的学生人数分别是25人、24人和30人。
同时参加体育、书法兴趣小组的有5人,同时参加体育、美术兴趣小组的有2人,同时参加书法、美术兴趣小组的有4人,有1人同时参加了这三个兴趣小组,问:共有多少人参加兴趣小组?练习:某校对五年级100名同学进行学习兴趣调查,结果有58人喜欢语文,有38人喜欢数学,有52人喜欢外语。
而且喜欢语文和数学(但不喜欢外语)的有6人,喜欢数学和外语(但不喜欢语文)的有4人,三科都喜欢的有12人,而且每人至少喜欢一科。
容斥原理的三个公式

容斥原理的三个公式容斥原理是数学中一个挺有意思的概念,它有三个重要的公式,今天咱们就来好好聊聊这三个公式。
我先跟您说啊,这容斥原理在解决集合相关的问题时,那可真是大显身手。
就拿咱们生活中的例子来说吧,比如说学校组织活动,有参加书法比赛的同学,有参加绘画比赛的同学,还有既参加书法又参加绘画比赛的同学。
那怎么算总共有多少同学参加了这两类比赛呢?这时候容斥原理就派上用场啦!咱们先来说说容斥原理的第一个公式。
这个公式可以表述为:两个集合 A 和 B 的并集的元素个数,等于 A 的元素个数加上 B 的元素个数,再减去 A 和 B 的交集的元素个数。
简单来说就是:|A∪B| = |A| + |B| -|A∩B| 。
举个例子哈,一个班级里,喜欢语文的有 20 个同学,喜欢数学的有 30 个同学,既喜欢语文又喜欢数学的有 10 个同学。
那喜欢语文或者喜欢数学的同学一共有多少个呢?咱们就可以用这个公式来算。
|A|就是喜欢语文的 20 个同学,|B|就是喜欢数学的 30 个同学,|A∩B|就是既喜欢语文又喜欢数学的 10 个同学。
把数字带进去,那就是 |A∪B| = 20 + 30 - 10 = 40 个同学。
您瞧,是不是很清楚明了?再来说说第二个公式。
如果是三个集合 A、B、C ,那它们的并集的元素个数就是:|A∪B∪C| = |A| + |B| + |C| - |A∩B| - |B∩C| - |C∩A| +|A∩B∩C| 。
咱们还是拿例子来说事儿。
比如说在一个班级里,喜欢体育的有 25 个同学,喜欢音乐的有 15 个同学,喜欢美术的有 20 个同学,既喜欢体育又喜欢音乐的有8 个同学,既喜欢音乐又喜欢美术的有6 个同学,既喜欢体育又喜欢美术的有 9 个同学,三个都喜欢的有 3 个同学。
那喜欢体育或者音乐或者美术的同学一共有多少个呢?咱们就把数字往公式里带:|A|是 25 ,|B|是 15 ,|C|是 20 ,|A∩B|是 8 ,|B∩C|是 6 ,|C∩A|是 9 ,|A∩B∩C|是 3 。
容斥原理三个公式小学

容斥原理三个公式小学
三集合容斥问题公式:
(1)A+B+C-A∩B-A∩C-B∩C+A∩B∩C=总数-三者都不满足的个数
解释:把ABC想象成三个圆形纸片,ABC叠加在一起的面积等于ABC 面积之和减去两两重叠的部分,但是中间三者重叠的部分减去了三次,相当于被挖空了,所以还得加上它。
(2)A+B+C-只满足两个条件的个数-2倍满足三个条件的个数=总数-三者都不满足的个数
解释:把ABC想象成三个圆形纸片,ABC叠加在一起的面积等于ABC 面积之和减去重叠两层的面积,再减去重叠三层的面积的两倍。
重叠2层,只用减去1层,重叠3层,得减掉2层。
(3)只满足一个条件的个数+只满足两个条件的个数+满足三个条件的个数=总数-三者都不满足的个数。
解释:把ABC想象成三个圆形纸片,ABC叠加在一起的面积等于只有一层的面积+重叠两层的面积+重叠三层的面积。
容斥问题

一、两集合容斥问题两集合容斥问题根据能否直接套用公式,又可以细分为标准型(直接套公式)和非标准型(不能直接套公式)。
(一)标准型两集合容斥问题的公式:满足条件A的情况数+满足条件B的情况数-两者都满足的情况数=总的情况数-两者都不满足的情况数。
对于两集合的容斥问题,如果能用公式我们直接套公式。
解题技巧:两集合容斥问题关键是匹配题型,这也是很多同学头疼的地方。
如果出现了两者都或者两者都不,就考虑两集合的容斥问题;如果两者都,两者都不同时出现,则往往能直接套公式(满足标准型)。
【例1】某班有60人,参加物理竞赛的有30人,参加数学竞赛的有32人,两科都没有参加的有20人。
同时参加物理、数学两科竞赛的有多少人( )A.28人B.26人C.24人D.22人【答案】D【解析】题干中出现了同时参加两科竞赛,即出现了两者都,又出现了两科都没有参加,即出现了两者都不,综合考虑满足两集合标准型公式。
参加物理竞赛30人,数学竞赛32人,都未参加20人,总人数60人,设两个竞赛都参加的有x人,参加数学+参加物理-都参加的人数=总人数-都未参加,30+32-x=60-20,x=22。
选择D。
两集合标准型题型特征非常明显,难度不大。
为了增加难度,有时题目特征不明显,这就需要我们发现特征,解决问题。
【例2】一名外国游客到北京旅游,他要么上午出去游玩,下午在旅馆休息,要么上午休息,下午出去游玩,而下雨天他只能一天都待在屋里。
期间,不下雨的天数是12天,他上午待在旅馆的天数为8天,下午待在旅馆的天数为12天,他在北京共待了( )A.16天B.20天C.22天D.24天【答案】A【解析】此题咋一看,没有出现两者都,两者都不这样的字眼,不符合两集合容斥问题的特征。
但细想此题出现了上午待在旅馆,下午待在旅馆,即出现了满足条件A,B,想到容斥问题。
同时题干中出现了不下雨,有不下雨自然就有下雨,下雨其实就是上下午都在旅馆,即出现了两者都,从而判断出是两集合的容斥问题。
容斥原理的三大公式

容斥原理(Inclusion-Exclusion Principle)是概率论和组合数学中常用的一种技巧,用于解决计数问题。
它通过对各种情况的交集和并集进行适当的计算,避免了重复计数或漏计的问题。
容斥原理的三大公式是指在应用容斥原理时常用的三个公式:
1.二项式容斥原理:
对于给定的事件A和B,二项式容斥原理可以表示为:P(A∪B) = P(A) + P(B) - P(A∩B)。
这个公式表示,两个事件的联合概率等于它们各自的概率之和减去它们的交集概率。
2.三个事件的容斥原理:
对于给定的事件A、B和C,三个事件的容斥原理可以表示为:P(A∪B∪C) = P(A) + P(B) + P(C) - P(A∩B) - P(A∩C) - P(B∩C) + P(A∩B∩C)。
这个公式表示,三个事件的联合概率等于它们各自的概率之和减去它们两两交集的概率之和,再加上它们的三个事件的交集概率。
3.n个事件的容斥原理:
对于给定的n个事件Ai(1≤i≤n),n个事件的容斥原理可以表示为:
P(A1∪A2∪...∪An) = ΣP(Ai) -ΣP(Ai∩Aj) + ΣP(Ai∩Aj∩Ak) - ... + (-1)^(n-1) * P(A1∩A2∩...∩An)。
这个公式表示,n个事件的联合概率等于它们各自的概率之和减去它们两两交集的概率之和,再加上它们三个事件的交集概率之和,依此类推,最后加上或减去n 个事件的交集概率。
这些容斥原理的公式可以帮助我们在计算概率或解决组合数学问题时进行正确的计数,避免了重复计数或漏计的错误。
容斥原理常识型公式

容斥原理常识型公式
摘要:
1.容斥原理的定义与概念
2.容斥原理的公式表示
3.容斥原理的应用示例
4.容斥原理的扩展与深化
正文:
【1.容斥原理的定义与概念】
容斥原理,是概率论中的一个基本原理,用于解决离散事件的概率计算问题。
它是基于集合的概念,通过研究事件之间的关系,给出了求解复杂事件发生概率的一种方法。
【2.容斥原理的公式表示】
容斥原理的公式表示为:P(A∪B) = P(A) + P(B) - P(A∩B)。
其中,
P(A∪B) 表示事件A 和事件B 的并集发生的概率,P(A) 和P(B) 分别表示事件A 和事件B 发生的概率,P(A∩B) 表示事件A 和事件B 的交集发生的概率。
【3.容斥原理的应用示例】
假设有一个袋子,里面有3 个红球和2 个绿球。
从袋子中随机抽取一个球,求抽到红球的概率。
根据容斥原理,抽到红球的概率为:P(红球) = P(红球) + P(绿球) - P(红球∩绿球)。
因为绿球和红球是互斥事件,即抽到一个球后,就不能再抽到另一个
球,所以P(红球∩绿球) = 0。
所以,P(红球) = P(红球) + P(绿球) = 3/5。
【4.容斥原理的扩展与深化】
容斥原理不仅适用于离散事件,还可以扩展到连续事件的概率计算。
在连续事件的概率计算中,需要用到积分的概念,此时的容斥原理公式为:
P(A∪B) = ∫[P(A|x)dx + P(B|x)dx - P(A∩B|x)dx]。
容斥原理及其应用

容斥原理及其应用容斥原理是组合数学中的一种重要方法,用来计算多个事件的概率或计数。
容斥原理的核心思想是通过逐步剔除重复计数的方式得到准确的计数结果。
下面将详细介绍容斥原理及其应用。
一、容斥原理的基本概念:设集合U为一个样本空间,A₁,A₂,...,Aₙ为U的n个子集,容斥原理给出了如下关于这些集合的计数或概率的公式:```P(A₁∪A₂∪...∪Aₙ)=Σ[P(A₁)-P(A₁∩A₂)+P(A₁∩A₂∩A₃)-...+(-1)ⁿ⁻¹P(A₁∩A₂∩...∩Aₙ)]```其中P(A₁)表示事件A₁的概率,P(A₁∩A₂)表示事件A₁与A₂同时发生的概率,依此类推。
二、容斥原理的证明:容斥原理的核心思路是通过排除重复计数的方法得到准确的计数结果。
可以用一个数轴来表示样本空间U,集合A₁,A₂,...,Aₙ所对应的子集分别在数轴上画出,然后逐步排除交集的部分。
具体证明过程如下:1.先考虑只有两个集合A₁和A₂的情况,根据概率的加法原理可得:```P(A₁∪A₂)=P(A₁)+P(A₂)-P(A₁∩A₂)```这里P(A₁∩A₂)表示事件A₁和A₂同时发生的概率,由于在P(A₁)和P(A₂)中分别计算了P(A₁∩A₂),所以要减去一次P(A₁∩A₂)去除重复计数。
2.推广到三个集合A₁、A₂、A₃的情况,根据加法原理得:```P(A₁∪A₂∪A₃)=P(A₁)+P(A₂)+P(A₃)-P(A₁∩A₂)-P(A₁∩A₃)-P(A₂∩A₃)+P(A₁∩A₂∩A₃)```这里减去了P(A₁∩A₃)和P(A₂∩A₃)是因为它们在P(A₁)、P(A₂)和P(A₃)中分别计算了两次,要减去一次去除重复计数。
加上P(A₁∩A₂∩A₃)是因为它在前面的计算中被减去了两次,要加回来。
3.对于n个集合的情况,以此类推可以得到容斥原理的一般形式。
三、容斥原理的应用:容斥原理在组合数学和概率论中具有广泛的应用1.计数问题:利用容斥原理可以解决一些与集合计数相关的问题,如给定集合A₁,A₂,...,Aₙ,求它们的并集的元素个数。
三集合容斥两个公式的用法

三集合容斥两个公式的用法三集合容斥是概率论和组合数学中的一种常用方法,用于求解三个集合的交集的元素个数或概率。
下面将详细介绍三集合容斥的两种公式及其应用。
1. 三集合容斥公式(加法公式):如果A,B,C是三个集合,那么它们的交集元素个数(或概率)可以通过以下公式计算:|A ∩ B ∩ C| = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C|其中,|X|表示集合X的元素个数或概率。
这个公式可以通过对三个集合的元素个数逐个相加,再依次减去两个集合的交集和三个集合的交集来计算三个集合的交集元素个数。
这个公式的本质是通过排除多次计算交集的情况,将交集的元素加回去,从而得到准确的交集元素个数。
2. 三集合容斥公式(乘法公式):如果A,B,C是三个集合,那么它们的交集元素个数可以通过另一个公式计算:|A ∩ B ∩ C| = |A| + |B| + |C| - 2|A ∩ B| - 2|A ∩ C| - 2|B ∩ C| + 3|A ∩ B ∩ C|这个公式的计算过程与加法公式类似,只是在计算交集的元素个数时,交集的元素所在的集合会被减去多次,而交集的元素所在的集合之间的交集会被加回去多次。
应用:三集合容斥公式在概率论和组合数学中有广泛的应用,下面举几个例子说明它的用法:1) 生日悖论:假设有n个人,在这些人中随机选取若干个人的生日,三集合容斥可以用来计算至少两人生日相同的概率。
可以令A为至少两人生日相同,B为至少三人生日相同,C为至少四人生日相同。
根据三集合容斥公式,可以计算出|A ∩ B ∩ C|,从而计算出至少两人生日相同的概率。
2) 排列组合问题:在排列组合问题中,三集合容斥可以用来计算满足一定条件的排列组合个数。
例如,求由A、B、C三个字母组成的长度为n的字符串中,既不包含“A”,也不包含“B”的字符串个数。
可以将A视为包含“A”的字符串集合,B 视为包含“B”的字符串集合,C视为包含“A”和“B”的字符串集合,然后根据三集合容斥公式计算出符合条件的字符串个数。
容斥原理公式大全

容斥原理公式大全容斥原理是一种基本的计数原理,用于解决组合数学中的计数问题。
它的核心思想是通过相互排斥的事件之间的关系来计算它们的交集的大小。
在集合论中,容斥原理可以通过以下公式来表达:\[|A_1 \cup A_2 \cup \dots \cup A_n| = \sum_{i=1}^{n} |A_i| -\sum_{1 \leq i < j \leq n} |A_i \cap A_j| + \sum_{1 \leq i < j < k\leq n} |A_i \cap A_j \cap A_k| - \dots + (-1)^{n-1} |A_1 \cap A_2 \cap \dots \cap A_n|\]其中,\(A_1, A_2, \dots, A_n\) 是 n 个事件,\(A_i\) 代表第 i 个事件,\(|A|\) 代表事件 A 的大小。
以二个事件为例,容斥原理可以简化为以下公式:\[|A_1 \cup A_2| = |A_1| + |A_2| - |A_1 \cap A_2|\]这个公式表示两个事件 A1 和 A2 的并集的大小等于它们各自的大小之和减去它们的交集的大小。
容斥原理还可以推广到多个事件的情况。
通过反复使用这个公式,可以计算多个事件的并集的大小。
容斥原理在组合数学、概率论、统计学等领域具有广泛的应用。
它可以用于解决组合数学中的排列组合问题,计算事件的概率,估计事件的期望值等等。
除了上述公式,容斥原理还有一些等价的形式,如包含减法形式、指示函数形式等。
这些形式可以根据具体的问题选择使用。
在解决问题时,需要注意事件之间的相互排斥关系,避免重复计算。
通过合理地应用容斥原理,可以简化问题的复杂度,提高计算效率。
行测容斥原理三个公式

行测容斥原理三个公式容斥原理是概率论和组合数学中一个重要的计数方法,用于解决求交集、并集等问题。
下面将介绍容斥原理的三个公式:互斥事件的加法原理、重叠事件的减法原理和容斥原理。
一、互斥事件的加法原理:在概率论中,如果A和B是两个互斥事件,那么它们的并集的概率等于它们的概率之和。
数学上可以表达为:P(A∪B)=P(A)+P(B)其中P(A∪B)表示事件A和事件B的并集的概率,P(A)和P(B)分别表示事件A和事件B的概率。
二、重叠事件的减法原理:在概率论中,如果A和B是两个事件,那么它们的交集的概率等于它们的和减去它们的并集。
数学上可以表达为:P(A∩B)=P(A)+P(B)-P(A∪B)其中P(A∩B)表示事件A和事件B的交集的概率,P(A)和P(B)分别表示事件A和事件B的概率,P(A∪B)表示事件A和事件B的并集的概率。
三、容斥原理:容斥原理是一种组合数学中的计数方法,用于求多个集合的交集和并集的元素个数。
如果有n个集合A1,A2,...,An,那么它们的交集的元素个数可以用容斥原理表示为:A1∩A2∩...∩An,=∑,Ai,-∑,Ai∩Aj,+∑,Ai∩Aj∩Ak,-...+(-1)^(n+1),A1∩A2∩...∩An其中,X,表示集合X中元素的个数,∑表示求和,Ai表示第i个集合。
容斥原理的应用:1.求多个集合的并集的元素个数:A1∪A2∪...∪An,=∑,Ai,-∑,Ai∩Aj,+∑,Ai∩Aj∩Ak,-...+(-1)^n,A1∩A2∩...∩An2.求多个集合的交集的元素个数:A1∩A2∩...∩An,=∑(-1)^(i+1)(,Ai,-∑(-1)^(j+1)(,Ai∩Aj,-∑(-1)^(k+1)(...)))容斥原理的推广:容斥原理可以推广到更多的事件,不仅限于两个或三个事件。
总结:容斥原理是概率论和组合数学中重要的计数方法,通过互斥事件的加法原理、重叠事件的减法原理和容斥原理可以求解事件的概率和集合的元素个数。
容斥原理三大公式

容斥原理三大公式容斥原理是数学中一个非常实用的工具,它能帮助我们在解决一些集合问题时更加得心应手。
容斥原理主要有三大公式,接下来咱们就好好唠唠这三个公式。
咱们先来说说这第一个公式。
假设咱们有两个集合 A 和 B,那么 A 和 B 的并集元素个数就等于 A 的元素个数加上 B 的元素个数,再减去A 和B 的交集元素个数。
用数学式子表示就是:|A∪B| = |A| + |B| -|A∩B| 。
我给您举个例子哈,就说咱们班同学,喜欢数学的有 20 人,喜欢语文的有 15 人,既喜欢数学又喜欢语文的有 5 人。
那喜欢数学或者语文的同学一共有多少人呢?咱们就用这个公式来算算。
|A| 就是喜欢数学的 20 人,|B| 是喜欢语文的 15 人,|A∩B| 是既喜欢数学又喜欢语文的 5 人。
所以喜欢数学或者语文的同学一共有 20 + 15 - 5 = 30 人。
再来说说第二个公式。
要是有三个集合 A、B、C,那么它们的并集元素个数就是 A 的元素个数加上 B 的元素个数加上 C 的元素个数,然后减去 A 和 B 的交集元素个数,减去 A 和 C 的交集元素个数,减去 B 和 C 的交集元素个数,最后再加上 A、B、C 三个集合的交集元素个数。
式子就是:|A∪B∪C| = |A| + |B| + |C| - |A∩B| - |A∩C| - |B∩C| +|A∩B∩C| 。
比如说,咱们学校组织兴趣小组,参加绘画小组的有 12 人,参加音乐小组的有 8 人,参加体育小组的有 10 人。
参加绘画和音乐小组的有 3 人,参加绘画和体育小组的有 4 人,参加音乐和体育小组的有 2 人,三个小组都参加的有 1 人。
那参加兴趣小组的一共有多少人呢?咱们照样用公式来算,|A| 是绘画小组的 12 人,|B| 是音乐小组的 8 人,|C| 是体育小组的 10 人,|A∩B| 是 3 人,|A∩C| 是 4 人,|B∩C| 是 2 人,|A∩B∩C| 是 1 人。
容斥原理题再也不用怕,两个万能公式

容斥原理题再也不用怕,两个万能公式容斥原理题再也不用怕,两个万能公式1.关键提示:容斥原理是2004年、2005年中央国家公务员考试的一个难点,很多考生都觉得无从下手,其实,容斥原理关键内容就是两个公式,考生只要把这两个公式灵活掌握就可全面应对此类题型。
另外在练习及真考的过程中,请借助图例将更有助于解题。
2.核心公式:(1)两个集合的容斥关系公式:A +B=A∪B+A∩B(2)三个集合的容斥关系公式:A +B+C=A∪B∪C+A∩B+B∩C+C∩A-A∩B∩C例题1:2004年中央A类真题某大学某班学生总数为32人,在第一次考试中有26人及格,在第二次考试中有24人及格,若两次考试中,都没有及格的有4人,那么两次考试都及格的人数是( )。
A.22 B.18 C.28 D.26解析:设A=第一次考试中及格的人(26),B=第二次考试中及格的人(24)显然,A+B=26+24=50;A∪B=32-4=28,则根据公式A∩B=A+B-A∪B=50-28=22所以,答案为A。
例题2:2004年山东真题某单位有青年员工85人,其中68人会骑自行车,62人会游泳,既不会骑车又不会游泳的有12人,则既会骑车又会游泳的有()人 A.57 B.73 C.130 D.69解析:设A=会骑自行车的人(68),B=会游泳的人(62)显然,A+B=68+62=130;A∪B=85-12=73,则根据公式A∩B=A+B-A∪B=130-73=57所以,答案为A。
例题3:电视台向100人调查前一天收看电视的情况,有62人看过2频道,34人看过8频道,11人两个频道都看过。
两个频道都没看过的有多少人?解析:设A=看过2频道的人(62),B=看过8频道的人(34)显然,A+B=62+34=96;A∩B=两个频道都看过的人(11)则根据公式A∪B=A+B-A∩B=96-11=85所以,两个频道都没有看过的人数=100-85=15所以,答案为15。
容斥问题466

容斥问题466摘要:1.容斥问题的基本概念2.容斥问题的解决方法3.容斥问题的实际应用正文:一、容斥问题的基本概念容斥问题是组合数学中的一个重要问题,主要研究从一组数集中选取元素组成集合的方法。
它涉及到两个基本的集合运算:并集和交集。
在容斥问题中,给定一组数集,要求通过并集和交集的运算,得到所有可能的子集。
二、容斥问题的解决方法解决容斥问题的方法主要是利用容斥原理。
容斥原理是组合数学中的一个基本原理,它给出了求解容斥问题的一般方法。
容斥原理的公式表达式为:|A ∪B| = |A| + |B| - |A ∩B|其中,|A ∪B| 表示A 和B 的并集的元素个数,|A| 和|B| 分别表示A 和B 的元素个数,|A ∩B| 表示A 和B 的交集的元素个数。
利用容斥原理,我们可以通过计算并集、交集的元素个数,来求解容斥问题。
具体步骤如下:1.计算每个数集的元素个数;2.利用容斥原理公式,计算并集的元素个数;3.根据并集的元素个数,求解交集的元素个数;4.根据交集的元素个数,求解所有可能的子集。
三、容斥问题的实际应用容斥问题在实际生活中有着广泛的应用,例如在计算机科学中的集合运算、数据结构等。
在计算机程序设计中,解决容斥问题的方法可以有效地优化算法,提高程序的运行效率。
此外,容斥问题在组合数学、离散数学、概率论等领域也有着广泛的应用。
通过学习容斥问题,我们可以更好地理解这些领域的基本概念和方法,提高自己的学术素养和实际能力。
总之,容斥问题是组合数学中的一个基本问题,它涉及到并集、交集等集合运算。
通过利用容斥原理,我们可以解决容斥问题,求解所有可能的子集。
容斥原理4个集合公式

容斥原理4个集合公式
容斥原理是组合数学中的一种常用原理,用于计算多个集合的并、交和差的元
素个数。
下面我将为您介绍容斥原理的4个集合公式。
1. 两个集合的容斥原理公式:
设集合 A 和集合 B 分别有 m 和 n 个元素,集合 A 与集合 B 的交集有 k 个元素,则 A 和 B 的并集中的元素个数为 m+n-k。
2. 三个集合的容斥原理公式:
设集合 A、B 和 C 分别有 m、n 和 p 个元素,集合 A、B 和 C 的交集分别为 x、y 和 z 个元素,集合 A、B 和 C 的并集中的元素个数为 m+n+p-x-y-z+(x∩y∩z)。
3. 四个集合的容斥原理公式:
设集合 A、B、C 和 D 分别有 m、n、p 和 q 个元素,集合 A、B、C 和 D 的交
集分别为 x、y、z 和 w 个元素,集合 A、B、C 和 D 的并集中的元素个数为
m+n+p+q-x-y-z-w+(x∩y∩z∩w)。
4. 一般情况下的容斥原理公式:
容斥原理可以推广到任意个集合上。
当有 k 个集合 A1、A2、...、Ak,分别有
m1、m2、...、mk 个元素,并且这些集合的交集为空集时,这 k 个集合的并集中的
元素个数为 m1+m2+...+mk。
这些容斥原理的公式可以帮助我们计算集合的元素个数,特别在计算排列组合
中常常使用到。
通过准确应用这些公式,我们可以简化问题的计算过程,并得到准确的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
容斥问题公式及运用
在计数时,必须注意无一重复,无一遗漏。
为了使重叠部分不被重复计算,研究出一种新的计数方法。
这种方法的基本思路是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
一、容斥原理1:两个集合的容斥原理
如果被计数的事物有A、B两类,那么,先把A、B两个集合的元素个数相加,发现既是A类又是B类的部分重复计算了一次,所以要减去。
如下图所示。
【示例1】一次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4人语、数都是满分,那么这个班至少有一门得满分的同学有多少人?
解:数学得满分人数→A,语文得满分人数→B,数学、语文都是满分人数→A∩B,至少有一门得满分人数→A∪B。
A∪B=15+12-4=23,共有23人至少有一门得满分。
二、容斥原理2:三个集合的容斥原理
如果被计数的事物有A、B、C三类,那么,将A、B、C三个集合的元素个数相加后发现两两重叠的部分重复计算了1次,三个集合公共部分被重复计算了2次。
如下图所示,灰色部分A∩B-A∩B∩C、B∩C-A∩B∩C、C∩A-A∩B ∩C都被重复计算了1次,黑色部分A∩B∩C被重复计算了2次,因此总数A∪B∪C=A+B+C-(A∩B-A∩B∩C)-(B∩C-A∩B∩C)-(C∩A-A ∩B∩C)-2A∩B∩C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C。
即得到:
【示例2】某班有学生45人,每人都参加体育训练队,其中参加足球队的有25人,参加排球队的有22人,参加游泳队的有24人,足球、排球都参加的有12人,足球、游泳都参加的有9人,排球、游泳都参加的有8人,问:三项都参加的有多少人?
解:参加足球队→A,参加排球队→B,参加游泳队→C,足球、排球都参加的→A∩B,足球、游泳都参加的→C∩A,排球、游泳都参加的→B ∩C,三项都参加的→A∩B∩C。
三项都参加的有A∩B∩C=A∪B∪C-A-B-C+A∩B+B∩C+C∩A=45-25-22-24+12+9+8=3人。
例1 在1到1000的自然数中,能被3或5整除的数共有多少个?不能被3或5整除的数共有多少个?
分析:显然,这是一个重复计数问题(当然,如果不怕麻烦你可以分别去数3的倍数,5的倍数)。
我们可以把“能被3或5整除的数”分别看成A类元素和B类元素,能“同时被3或5整除的数(15的倍数)”就是被重复计算的数,即“既是A类又是B类的元素”。
求的是“A类或B类元素个数”。
我们还不能直接计算,必须先求出所需条件。
1000÷3=333……1,能被3整除的数有333个(想一想,这是为什么?)同理,可以求出其他的条件。
例2 某个班的全体学生在进行了短跑、游泳、投掷三个项目的测试后,有4名学生在这三个项目上都没有达到优秀,其余每人至少有一项达到了优秀,达到了优秀的这部分学生情况如下表:
求这个班的学生共有多少人?
分析:这个班的学生数,应包括达到优秀和没有达到优秀的。
4+17+18+15-6-6-5+2=39(人)
例 3 在一根长的木棍上有三种刻度线,第一种刻度线将木棍分成10等份,第二种将木棍分成12等份,第三种将木棍分成15等份。
如果沿每条刻度线将木棍锯断,木棍总共被锯成多少段?
分析:很显然,要计算木棍被锯成多少段,只需要计算出木棍上共有多少条不同的刻度线,在此基础上加1就是段数了。
若按将木棍分成10等份的刻度线锯开,木棍有9条刻度线。
在此木棍上加上将木棍分成12等份的11条刻度线,显然刻度线有重复的,如5/10和6/12都是1/2。
同样再加上将木棍分成15等份的刻度线,也是如此。
所以,我们应该按容斥原理的方法来解决此问题。
用容斥原理的那一个呢?想一想,被计数的事物有那几类?每一类的元素个数是多少?
解答:
解一:[10,12,15]=60,设木棍60厘米
60÷10=6厘米,60÷12=5厘米,60÷15=4(厘米
10等分的为第一种刻度线,共10-1=9(条)
12等分的为第二种刻度线,共12-1=11(条)
15等分的为第三种刻度线,过15-1=14(条)
第一种与第二种刻度线重合的[6,5]=30,60÷30-1=2-1=1(条)
第一种与第三种刻度线重合的[6,4]=12,60÷12-1=5-1=4(条)
第二种与第三种刻度线重合的[5,4]=20,60÷20-1=3-1=2(条)
三种刻度线重合的没有,[6、5、4]=60
因此,共有刻度线9+11+14-1-4-2=27条,木棍总共被锯成
27+1=28段。
解二:总长看成单位1分别分成10、12、15段。
1/10与1/12的最小公倍数1/2,1/10与1/15的最小公倍数1/5,1/12与1/15的最小公倍数1/3,1/10,1/12和1/15的最小公倍数为1,有10+12+15-(2+5+3)+1=28
解三:10、12、15的最小公倍数是60,假设木棍就是长60,
1、那么,分成10等份的每份6,刻度就是
0,6,12,18,24,30,36,42,48,54,60
2、分成12等分的每份就是5,
0,5,10,15,20,25,30,35,40,45,50,55,60
3、分成15等分的每份就是4,
0,4,8,12,16,20,24,28,32,36,40,44,48,52,
56,60
4、把相同刻度的合并,就是有刻度如下:
0,4,5,6,8,10,12,15,16,18,20,24,25,28,30,
32,35,36,40,42,44,45,48,50,52,54,55,56,60。
