2018年丰台区高三一模试题及答案

合集下载

2018丰台一模理综试题及答案官方完美版

丰台区2018年高三年级第二学期综合练习（一）理科综合2018. 03本试卷满分共300分考试时间150分钟注意事项：1. 答题前，考生务必先将答题卡上的学校、年级、班级、姓名、准考证号用黑色字迹签字笔填写清楚，并认真核对条形码上的准考证号、姓名，在答题卡的“条形码粘贴区”贴好条形码。

2. 本次考试所有答题均在答题卡上完成。

选择题必须使用2B铅笔以正确填涂方式将各小题对应选项涂黑，如需改动，用橡皮擦除干净后再选涂其它选项。

非选择题必须使用标准黑色字迹签字笔书写，要求字体工整、字迹清楚。

3. 请严格按照答题卡上题号在相应答题区内作答，超出答题区域书写的答案无效，在试卷、草稿纸上答题无效。

4. 请保持答题卡卡面清洁，不要装订、不要折叠、不要破损。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 S 32 Na 23 Cl 35.5第一部分（选择题共120分）1．下列显微观察实验不需要．．．经过染色处理的是A．观察新鲜黑藻叶片的细胞质流动B．观察人口腔上皮细胞中的线粒体C．观察花生子叶细胞中的脂肪颗粒D．观察洋葱根尖分生区细胞的有丝分裂2．右图表示核糖体上合成蛋白质的过程。

四环素抑制tRNA与细菌核糖体的A位点结合，关叙述正确的是A．核糖体的主要成分是蛋白质和mRNAB．四环素与A位点结合促进了新肽键的形成C．图中从E位点离开的tRNA可转运甲硫氨酸D．人体细胞与细菌细胞的核糖体没有差异3．中地雀和仙人掌地雀是生活在加拉帕戈斯群岛同一区域的两种地雀，在干旱季节，蒺藜和仙人掌是两种地雀赖以生存的食物资源。

蒺藜的种子大而坚硬，外部长有尖刺。

干旱过后，中地雀的种群数量剧烈下降，雌性死亡更多。

下列推测错误．．的是A．可用标志重捕法调查两种地雀的种群数量和性别比例B．仙人掌地雀不食用蒺藜种子因而与中地雀无竞争关系C．中地雀小喙个体和雌性个体死亡率高的原因是食物组成的变化D．大粒种子的选择作用将会导致中地雀喙尺寸的平均值增加4．高原鼠兔对高原低氧环境有很强的适应性。

北京市丰台区2018届高三3月综合练习(一模)数学(文)试卷

丰台区2018年高三年级第二学期综合练习（一）数学（文科）2018. 03第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）复数21i=+ (A) 1i -+ (B) 1i -- (C) 1i + (D) 1i -(2）已知命题p ：∃x <1，21x ≤，则p ⌝为(A) ∀x ≥1, 21x (B) ∃x <1, 21x (C) ∀x <1, 21x (D) ∃x ≥1, 21x（3）已知0a b <<，则下列不等式中恒成立的是(A)11a b> (B) (C) 22a b > (D) 33a b >（4）已知抛物线C 的开口向下，其焦点是双曲线2213y x -=的一个焦点，则C 的标准方程为(A) 28y x = (B) 28x y =- (C) 2y = (D) 2x = （5）设不等式组05,05x y ≤≤⎧⎨≤≤⎩确定的平面区域为D ，在D 中任取一点(,)P x y 满足2x y +≥的概率是(A) 1112 (B) 56 (C) 2125(D)2325（6）执行如图所示的程序框图，那么输出的a 值是(A) 12-(B) 1- (C) 2 (D) 12（7）某三棱锥的三视图如图所示，则该三棱锥的体积为 (A)43(B) 4 (C) 83 (D)侧视图俯视图正视图（8）设函数π()sin(4)4f x x =+9π([0,])16x ∈，若函数()()y f x a a =+∈R 恰有三个零点1x ，2x ，3x 123()x x x <<，则1232x x x ++的值是 (A)π2(B)3π4(C)5π4(D)π第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分。

（9）已知集合{|20}A x x =-≤≤，{|03}B x x =<≤，则A B =U ．（10）圆心为(1,0)，且与直线1y x =+相切的圆的方程是．（11）在△ABC 中，2a =，4c =，且3sin 2sin A B =，则cos C =____．（12）已知点(2,0)A ，(0,1)B ，若点(,)P x y 在线段AB 上，则xy 的最大值为____．（13）已知定义域为R 的奇函数()f x ，当0x >时，2()(1)1f x x =--+．①当[1,0]x ∈-时，()f x 的取值范围是____；②当函数()f x 的图象在直线y x =的下方时，x 的取值范围是．（14）已知C 是平面ABD 上一点，AB AD ⊥，1CB CD ==．①若3AB AC =，则AB CD ⋅=____；①若AP AB AD =+，则||AP 的最大值为____．三、解答题共6小题，共80分。

2018年北京市丰台区高考数学一模试卷(理科)

2018年北京市丰台区高考数学一模试卷（理科）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1. 已知全集U ={x|x <5}，集合A ={x|x −2≤0}，则∁U A =( )A.{x|x ≤2}B.{x|x >2}C.{x|2<x <5}D.{x|2≤x <5}2. 已知命题p:∃x <1，x 2≤1，则￢p 为（）A.∀x ≥1，x 2>1B.∃x <1，x 2>1C.∀x <1，x 2>1D.∃x ≥1，x 2>13. 设不等式组{x −2y ≤0x −y +2≥0x ≥0表示的平面区域为Ω．则（）A.原点O 在Ω内B.Ω的面积是1C.Ω内的点到y 轴的距离有最大值D.若点P(x 0, y 0)∈Ω，则x 0+y 0≠04. 执行如图所示的程序框图，如果输出的a =2，那么判断框中填入的条件可以是( )A.n ≥5B.n ≥6C.n ≥7D.n ≥85. 在平面直角坐标系xOy 中，曲线C 的参数方程为{x =1+cosαy =sinα（α为参数）．若以射线Ox 为极轴建立极坐标系，则曲线C 的极坐标方程为（）A.ρ=sinθB.ρ=2sinθC.ρ=cosθD.ρ=2cosθ6. 某三棱锥的三视图如图所示，则该三棱锥的体积为（）A.23B.43C.2D.837. 某学校为了弘扬中华传统“孝”文化，共评选出2位男生和2位女生为校园“孝”之星，现将他们的照片展示在宣传栏中，要求同性别的同学不能相邻，不同的排法种数为（）A.4B.8C.12D.248. 设函数f(x)=sin(4x +π4)(x ∈[0,9π16])，若函数y =f(x)+a(a ∈R)恰有三个零点x 1，x 2，x 3 (x 1<x 2<x 3)，则x 1+x 2+x 3的取值范围是（）A.[5π8,11π16)B.(5π8,11π16]C.[7π8,15π16)D.(7π8,15π16]二、填空题共6小题，每小题5分，共30分．如图所示，在复平面内，网格中的每个小正方形的边长都为1，点A ，B 对应的复数分别是z 1，z 2，则z2z 1=________．已知数列{a n }的前n 项和S n =n 2+n ，则a 3+a 4=________．己知抛物线M 的开口向下，其焦点是双曲线y 23−x 2=1的一个焦点，则M 的标准方程为________．在△ABC 中，a =2，c =4，且3sin A =2sin B ，则cos C =________．函数y =f(x)是定义域为R 的偶函数，当x ≥0时，函数f(x)的图象是由一段抛物线和一条射线组成（如图所示）．①当x ∈[−1, 1]时，y 的取值范围是________；②如果对任意x ∈[a, b](b <0)，都有y ∈[−2, 1]，那么b 的最大值是________．已知C是平面ABD上一点，AB⊥AD，CB=CD=1．①若AB→=3AC→，则AB→∗CD→=________；②AP→=AB→+AD→，则|AP→|的最大值为________．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．+1)−1．己知函数f(x)=2cos2x(sinxcosx(Ⅰ)求f(x)的定义域及最小正周期；(Ⅱ)求f(x)的单调递减区间．如图，在四棱锥P−ABCD中，平面PAB⊥平面ABCD，AB⊥BC，AD // BC，AD=3，PA=BC=2AB=2，PB=√3．(Ⅰ)求证：BC⊥PB；(Ⅱ)求二面角P一CD一A的余弦值；(Ⅲ)若点E在棱PA上，且BE // 平面PCD，求线段BE的长．某地区工会利用“健步行APP”开展健步走积分奖励活动．会员每天走5千步可获积分30分（不足5千步不积分），每多走2千步再积20分（不足2千步不积分）．记年龄不超过40岁的会员为A类会员，年龄大于40岁的会员为B类会员．为了解会员的健步走情况，工会从A，B两类会员中各随机抽取m名会员，统计了某天他们健步走的步数，并将样本数据分为[3, 5),[5, 7),[7, 9),[9, 11),[11, 13),[13, 15),[15, 17),[17, 19),[19, 21]九组，将抽取的A类会员的样本数据绘制成频率分布直方图，B类会员的样本数据绘制成频率分布表．(Ⅱ)从该地区A 类会员中随机抽取3名，设这3名会员中健步走的步数在13千步以上（含13千步）的人数为x ，求x 的分布列和数学期望；(Ⅲ)设该地区A 类会员和B 类会员的平均积分分别为X 1和X 2，试比较X 1和X 2的大小（只需写出结论）．已知函数f(x)=e x −a(lnx +1)(a ∈R)．(Ⅰ)求曲线y =f(x)在点（1, f(1)）处的切线方程；(Ⅱ)若函数y =f(x)在(12,1)上有极值，求a 的取值范围．已知点P(1,32)在椭圆C:x 2a 2+y 2b2=1(a >b >0)上，F(1, 0)是椭圆的一个焦点． (Ⅰ)求椭圆C 的方程；(Ⅱ)椭圆C 上不与P 点重合的两点D ，E 关于原点O 对称，直线PD ，PE 分别交y 轴于M ，N 两点，求证：以MN 为直径的圆被直线y =32截得的弦长是定值．已知无穷数列{a n }(a n ∈Z)的前n 项和为S n ，记S 1，S 2，…，S n 中奇数的个数为b n ．(Ⅰ)若a n ＝n ，请写出数列{b n }的前5项；(Ⅱ)求证：“a 1为奇数，a i (i ＝2, 3, 4,…)为偶数”是“数列{b n }是单调递增数列”的充分不必要条件；(Ⅲ)若a i ＝b i ，i ＝1，2，3，…，求数列{a n }的通项公式．参考答案与试题解析2018年北京市丰台区高考数学一模试卷（理科）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1.【答案】C【考点】补集及其运算【解析】先解出集合A={x|x≤2}，然后进行补集的运算即可．【解答】A={x|x≤2}，U={x|x<5}；∴∁U A={x|2<x<5}．2.【答案】C【考点】命题的否定【解析】运用特称命题的否定为全称命题，以及量词和不等号的变化，即可得到所求命题的否定．【解答】由特称命题的否定为全称命题，可得命题p:∃x<1，x2≤1，的否定为￢p:∀x<1，x2>1，3.【答案】A【考点】简单线性规划【解析】画出约束条件的可行域，判断选项的正误即可．【解答】不等式组{x−2y≤0x−y+2≥0x≥0表示的可行域如图：显然O在可行域内部．4.【答案】C【考点】程序框图【解析】由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量a的值，模拟程序的运行过程，可得答案．【解答】解：第1次执行循环体后，a =12，n =2，不满足退出循环的条件；第2次执行循环体后，a =−1，n =3，不满足退出循环的条件；第3次执行循环体后，a =2，n =4，满足退出循环的条件；第4次执行循环体后，a =12，n =5，不满足退出循环的条件；第5次执行循环体后，a =−1，n =6，不满足退出循环的条件；第6次执行循环体后，a =2，n =7，满足退出循环的条件；……第3k 次执行循环体后，a =2，n =3k +1，满足退出循环的条件；第3k +1次执行循环体后，a =12，n =3k +2，不满足退出循环的条件；第3k +2次执行循环体后，a =−1，n =3k +3，不满足退出循环的条件； ……若输出的a =2，则最后满足条件的n 值应为3的倍数多1，故选C .5.【答案】D【考点】圆的参数方程圆的极坐标方程【解析】曲线C 的参数方程消去参数，求出曲线的直角坐标方程，由此能求出曲线C 的极坐标方程．【解答】解：∵ 曲线C 的参数方程为{x =1+cosαy =sinα（α为参数）． ∴ 曲线C 的直角坐标方程为(x −1)2+y 2=1，即x 2+y 2−2x =0，∴ 曲线C 的极坐标方程为ρ2−2ρcosθ=0，即ρ=2cosθ．故选D .6.【答案】A【考点】由三视图求体积柱体、锥体、台体的体积计算【解析】根据三视图判断三棱锥的底面形状和高，代入体积公式计算即可．【解答】由主视图和侧视图可知棱锥的高ℎ=2，结合侧视图和俯视图可知三棱锥的底面ABC 为直角三角形，BC =1，AB =2，AB ⊥BC，∴三棱锥的体积V=13×12×1×2×2=23，7.【答案】B【考点】排列、组合及简单计数问题【解析】根据题意，分2种情况讨论：①，四人按男女男女排列，②，四人按女男女男排列，分别计算每一种情况的排法数目，由加法原理计算可得答案．【解答】根据题意，分2种情况讨论：①，四人按男女男女排列，两名男生有A22=2种排法，两名女生有A22=2种排法，此时有2×2=4种排法，②，四人按女男女男排列，同理可得此时有4种排法则一共有4+4=8种排法；8.【答案】A【考点】正弦函数的图象【解析】根据函数f(x)=sin(4x+π4)(x∈[0,9π16])，求解内层函数的范围，可得f(x)的图象，函数y=f(x)+a(a∈R)恰有三个零点，转化为f(x)与函数y=−a有三个交点问题．即可求解．【解答】函数f(x)=sin(4x+π4)(x∈[0,9π16])，可得π4≤4x+π4≤5π2，令4x+π4=t，函数y=f(t)+a(a∈R)恰有三个零点，转化为f(t)与函数y=−a有三个交点问题．根据三角函数图象的性质可得：12(t1+t2)=π2，9π4≤t3<5π2．∴(t1+t2)=π，即x1+x2=π8那么9π4≤4x3+π4<5π2，可得：π2≤x3<9π16则x1+x2+x3的取值范围是[5π8, 11π16)．二、填空题共6小题，每小题5分，共30分．【答案】−1−2i【考点】复数的运算【解析】由图形可得：A点表示的复数为i，B点表示的复数为2−i，利用复数的运算法则即可得出．【解答】由图形可得：A点表示的复数为i，B点表示的复数为2−i，∴z2z1=2−ii=(2−i)(−i)i∗(−i)=−1−2i，【答案】14【考点】数列递推式【解析】n≥2时，a n=S n−S n−1，代入即可得出．【解答】n≥2时，a n=S n−S n−1=n2+n−[(n−1)2+(n−1)]=2n．∴a3+a4=2×3+2×4=(14)【答案】x2=−8y【考点】双曲线的标准方程【解析】由双曲线方程求出其焦点坐标，可得抛物线焦点坐标，则抛物线方程可求．【解答】由双曲线y23−x2=1，得a2=3，b2=1，∴c2=a2+b2=4，得c=(2)∴双曲线y23−x2=1的下焦点F(0, −2)，即抛物线M的焦点为(0, −2)，可得p2=2，p=(4)∴M的标准方程为x2=−2py=−8y．【答案】−1 4【考点】余弦定理【解析】根据题意，由正弦定理可得3a=2b，分析可得a、b的值，由余弦定理即可得答案．【解答】根据题意，在△ABC中，3sin A=2sin B，则有3a=2b，又由a=2，则b=3，则cosC=a2+b2−c22ab =4+9−162×2×3=−14；【答案】[1, 2],−2【考点】由y=Asin（ωx+φ）的部分图象确定其解析式【解析】①根据f(x)是偶函数，图象关于y轴对称，结合图象可得y的取值范围．②当x≥0时，设抛物线的方程为y=ax2+bx+c，求解解析式，根据f(x)是定义域为R的偶函数，可得x<0的解析式，令y=1，可得x对应的值，结合图象可得b的最大值．【解答】根据f(x)是偶函数，图象关于y轴对称，当x∈[−1, 1]时，值域为x∈[0, 1]时相同，可得y的取值范围是[1, 2]．（1）当x≥0时，设抛物线的方程为f(x)=ax2+bx+c，图象过(0, 1)，(1, 2)，(3, −2)，带入计算可得：a=−1，b=2，c=1，∴f(x)=−x2+2x+1，当x<0时，−x>(0)∴f(−x)=−x2−2x+1即f(x)=−x2−2x+(1)令y=1，可得1=−x2−2x+(1)解得：x=−(2)结合图象可得b的最大值为−(2)故答案为：[1, 2]；−(2)【答案】−34,2【考点】平面向量数量积的性质及其运算律【解析】根据向量的几何意义作出几何图形，得出各点的位置关系，从而得出答案．【解答】①∵AB→=3AC→，∴C为AB的靠近A的三等分点，∴AB=32BC=32，AC=12BC=12，∵AD⊥AB，CD=1，∴∠ACD=60∘，∴AB→∗CD→=32×1×cos120∘=−34．②∵CB=CD=1，∴C位于BD的中垂线上，∴当C为BD的中点时，BD取得最大值（2）∵AB⊥AD，∴|AP→|=|AB→+AD→|=|AB→−AD→|=BD≤(2)三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．【答案】(Ⅰ)由cosx≠0，即x≠π2+kπ，∴f(x)的定义域为{x|x≠π2+kπ, k∈Z}．函数f(x)=2cos2x(sinxcosx+1)−1=2sinxcosx+2cos2x−1=sin2x+cos2x=√2sin(2x+π4)．∴f(x)的最小正周期T=2πω=2π2=π．由(Ⅰ)知f(x)=√2sin(2x+π4)．由2kπ+π2≤2x+π4≤2kπ+3π2，k∈Z．可得：kπ+π8≤x≤kπ+5π8∴f(x)的单调递减区间为[kπ+π8, kπ+5π8]，k∈Z．【考点】三角函数中的恒等变换应用【解析】(Ⅰ)根据分式中分母不能为0，可得定义域，利用二倍角公式化简即可f(x)的最小正周期；(Ⅱ)根据三角函数的单调性即可求解f(x)的单调递减区间．【解答】(Ⅰ)由cosx≠0，即x≠π2+kπ，∴f(x)的定义域为{x|x≠π2+kπ, k∈Z}．函数f(x)=2cos2x(sinxcosx+1)−1=2sinxcosx+2cos2x−1=sin2x+cos2x=√2sin(2x +π4)． ∴ f(x)的最小正周期T =2πω=2π2=π．由(Ⅰ)知f(x)=√2sin(2x +π4)．由2kπ+π2≤2x +π4≤2kπ+3π2，k ∈Z ．可得：kπ+π8≤x ≤kπ+5π8∴ f(x)的单调递减区间为[kπ+π8, kπ+5π8]，k ∈Z ．【答案】证明：(Ⅰ)∵ 在四棱锥P −ABCD 中，平面PAB ⊥平面ABCD ，AB ⊥BC ，AD // BC ，AD =3，PA =BC =2AB =2，PB =√3．∴ PA 2=PB 2+AB 2，∴ PB ⊥AB ，∴ PB ⊥平面ABCD ， ∵ BC ⊂平面ABCD ，∴ BC ⊥PB ．(Ⅱ)以B 为原点，BC 为x 轴，BA 为y 轴，BP 为z 轴，建立空间直角坐标系， A(0, 1, 0)，C(2, 0, 0)，D(3, 1, 0)，P(0, 0, √3)， CD →=(1, 1, 0)，CP →=(−2, 0, √3)，CA →=(−2, 1, 0)，设平面PCD 的法向量n →=(x, y, z)，则{n →∗CD →=x +y =0n →∗CP →=−2x +√3z =0 ，取x =√3，得n →=(√3,−√3, 2)，平面CDA 的法向量m →=(0, 0, 1)，设二面角P −CD −A 的平面角为θ，则cosθ=|m →∗n →||m →|∗|n →|=√10=√105． ∴ 二面角P −CD −A 的余弦值为√105．(Ⅲ)平面PCD 的法向量n →=(√3,−√3, 2)，设E(a, b, c)，PE →=λPA →，则(a, b, c −√3)=(0, λ, −√3λ)， ∴ E(0, λ, √3−√3λ)，BE →=(0, λ,√3−√3λ)， ∵ 点E 在棱PA 上，且BE // 平面PCD ，∴ BE →⋅n →=0−√3λ+2√3−2√3λ=0，解得λ=23， ∴ E(0, 23, √33)，∴ 线段BE 的长|BE →|=(23)(√33)=√73．【考点】直线与平面平行二面角的平面角及求法【解析】(Ⅰ)推导出PB ⊥AB ，从而PB ⊥平面ABCD ，由此能证明BC ⊥PB ．(Ⅱ)以B 为原点，BC 为x 轴，BA 为y 轴，BP 为z 轴，建立空间直角坐标系，利用向量法能求出二面角P −CD −A 的余弦值．(Ⅲ)求出平面PCD 的法向量n →=(√3,−√3, 2)，由点E 在棱PA 上，且BE // 平面PCD ，求出E(0, 23, √33)，由此能求出线段BE 的长．【解答】证明：(Ⅰ)∵ 在四棱锥P −ABCD 中，平面PAB ⊥平面ABCD ，AB ⊥BC ，AD // BC ，AD =3，PA =BC =2AB =2，PB =√3．∴ PA 2=PB 2+AB 2，∴ PB ⊥AB ，∴ PB ⊥平面ABCD ， ∵ BC ⊂平面ABCD ，∴ BC ⊥PB ．(Ⅱ)以B 为原点，BC 为x 轴，BA 为y 轴，BP 为z 轴，建立空间直角坐标系， A(0, 1, 0)，C(2, 0, 0)，D(3, 1, 0)，P(0, 0, √3)， CD →=(1, 1, 0)，CP →=(−2, 0, √3)，CA →=(−2, 1, 0)，设平面PCD 的法向量n →=(x, y, z)，则{n →∗CD →=x +y =0n →∗CP →=−2x +√3z =0 ，取x =√3，得n →=(√3,−√3, 2)，平面CDA 的法向量m →=(0, 0, 1)，设二面角P −CD −A 的平面角为θ，则cosθ=|m →∗n →||m →|∗|n →|=√10=√105． ∴ 二面角P −CD −A 的余弦值为√105．(Ⅲ)平面PCD 的法向量n →=(√3,−√3, 2)，设E(a, b, c)，PE →=λPA →，则(a, b, c −√3)=(0, λ, −√3λ)， ∴ E(0, λ, √3−√3λ)，BE →=(0, λ,√3−√3λ)， ∵ 点E 在棱PA 上，且BE // 平面PCD ，∴ BE →⋅n →=0−√3λ+2√3−2√3λ=0，解得λ=23， ∴ E(0, 23, √33)，∴ 线段BE 的长|BE →|=(23)(√33)=√73．【答案】(Ⅰ)∵ 10m =0.01，∴ m =10(00) ∵ nm =0.2，∴ n =200，∴ a =400，∴ m =1000，a =4(00)(Ⅱ)由频率分布直方图得从该地区A 类会员中随机抽取1名会员，健步走的步数在13千步以上（含13千步）的概率为25， ∴ X ∼N(3, 25)，P(X =0)=C 30×(35)3(25)0=27125， P(X =1)=C 31×(35)2×(25)=54125， P(X =2)=C 32×(35)×(25)2=36125， P(X =3)=C 33×(35)0×(25)3=8125，∴ X 的分布列为：∵ X ∼N(3, 25)，∴ E(X)=3×25=65．(Ⅲ)该地区A 类会员和B 类会员的平均积分分别为X 1和X 2，则X 1<X 2．【考点】离散型随机变量及其分布列【解析】(Ⅰ)由A 类会员的样本数据绘制成的频率分布直方图和B 类会员的样本数据绘制成的频率分布表，能求出m ，a ．(Ⅱ)由频率分布直方图得从该地区A 类会员中随机抽取1名会员，健步走的步数在13千步以上（含13千步）的概率为25，X ∼N(3, 25)，由此能求出X 的分布列和数学期望． (Ⅲ)该地区A 类会员和B 类会员的平均积分分别为X 1和X 2，则X 1<X 2．【解答】(Ⅰ)∵ 10m =0.01，∴ m =10(00)∵ nm =0.2，∴ n =200，∴ a =400，∴ m =1000，a =4(00)(Ⅱ)由频率分布直方图得从该地区A 类会员中随机抽取1名会员，健步走的步数在13千步以上（含13千步）的概率为25， ∴ X ∼N(3, 25)，P(X =0)=C 30×(35)3(25)0=27125， P(X =1)=C 31×(35)2×(25)=54125， P(X =2)=C 32×(35)×(25)2=36125， P(X =3)=C 33×(35)0×(25)3=8125，∴ X 的分布列为：∵ X ∼N(3, 25)，∴ E(X)=3×25=65．(Ⅲ)该地区A 类会员和B 类会员的平均积分分别为X 1和X 2，则X 1<X 2．【答案】(Ⅰ)f′(x)=e x −ax ，故f′(1)=e −a ，f(1)=e −a ，故切线方程是：y −e +a =(e −a)(x −1)，即y =(e −a)x ；(Ⅱ)若函数y =f(x)在(12,1)上有极值，则f′(x)=e x −ax 在(12,1)上有零点，即y =e x 和y =ax 在(12, 1)有交点，画出函数即y =e x 和y =ax 的图象，如图示：显然a >0，结合图象得：f′(12)⋅f′(1)<0，解得：√e 2<a <e ．【考点】利用导数研究函数的极值【解析】(Ⅰ)求出函数的导数，计算f(1)，f′(1)的值，求出切线方程即可；(Ⅱ)问题转化为f′(x)=e x −ax 在(12,1)上有零点，结合图象得到关于a 的不等式，解出即可．【解答】(Ⅰ)f′(x)=e x −ax ，故f′(1)=e −a ，f(1)=e −a ，故切线方程是：y −e +a =(e −a)(x −1)，即y =(e −a)x ；(Ⅱ)若函数y =f(x)在(12,1)上有极值，则f′(x)=e x −ax 在(12,1)上有零点，即y =e x 和y =ax 在(12, 1)有交点，画出函数即y =e x 和y =ax 的图象，如图示：显然a >0，结合图象得：f′(12)⋅f′(1)<0，解得：√e 2<a <e ．【答案】（I ）由题意可得：1a 2+94b 2=1，c =1，a 2=b 2+c 2，联立解得a 2=4，b 2=(3) ∴ 椭圆C 的方程为：x 24+y 23=(1)(II)证明：设直线DE 的方程为：ty =x ，D(x 1, y 1)，E(x 2, y 2)．联立{ty =x x 24+y 23=1 ，可得：y 2=123t 2+4． D(√3t√3t 2+4√3√3t 2+4)，E(√3t √3t 2+4√3√3t 2+4)．直线PD 的方程为：y −32=√3−3√3t 2+44√3t−2√3t 2+4−1)，可得M(0, 32√3−3√3t 2+44√3t−2√3t 2+4)．直线PE 的方程为：y −32=√3+3√3t 2+443t+2√3t 2+4−1)，可得N(0, 32√3+3√3t 2+443t+2√3t 2+4)．以MN 为直径的圆的方程为：x 2+(y −32+√3−3√3t 2+44√3t−2√3t 2+4)(y−32√3+3√3t 2+44√3t+2√3t 2+4)=0，∴ 把y =32代入可得：x 2+48−9(3t 2+4)48t 2−4(3t 2+4)=(0)即x 2=2736．解得x =±3√34．因此被直线y =32截得的弦长=3√32是定值．【考点】椭圆的定义【解析】（I ）由题意可得：1a 2+94b 2=1，c =1，a 2=b 2+c 2，联立解出即可得出． (II)设直线DE 的方程为：ty =x ，D(x 1, y 1)，E(x 2, y 2)．联立{ty =x x 24+y 23=1，可得：y 2=123t 2+4．可得D(√3t √3t 2+4√3√3t 2+4，E(√3t √3t 2+4√3√3t 2+4．利用点斜式可得直线PD 的方程，可得M(0, 32−√3−3√3t 2+44√3t−2√3t 2+4)．利用点斜式可得直线PE 的方程，可得N(0, 32−√3+3√3t 2+44√3t+2√3t 2+4)．以MN 为直径的圆的方程为：x 2+(y −32√3−3√3t 2+44√3t−2√3t 2+4)(y−32+√3+3√3t 2+44√3t+2√3t 2+4)=0，把y =32代入即可证明．【解答】（I ）由题意可得：1a 2+94b 2=1，c =1，a 2=b 2+c 2，联立解得a 2=4，b 2=(3) ∴ 椭圆C 的方程为：x 24+y 23=(1)(II)证明：设直线DE 的方程为：ty =x ，D(x 1, y 1)，E(x 2, y 2)．联立{ty =x x 24+y 23=1 ，可得：y 2=123t 2+4． D(√3t √3t 2+4√3√3t 2+4)，E(√3t √3t 2+4√3√3t 2+4)．直线PD 的方程为：y −32=√3−3√3t 2+44√3t−2√3t 2+4−1)，可得M(0, 32√3−3√3t 2+44√3t−2√3t 2+4)．直线PE 的方程为：y −32=√3+3√3t 2+443t+2√3t 2+4−1)，可得N(0, 32√3+3√3t 2+443t+2√3t 2+4)．以MN 为直径的圆的方程为：x 2+(y −32+√3−3√3t 2+44√3t−2√3t 2+4)(y−32√3+3√3t 2+44√3t+2√3t 2+4)=0，∴ 把y =32代入可得：x 2+48−9(3t 2+4)48t 2−4(3t 2+4)=(0)即x 2=2736．解得x =±3√34．因此被直线y =32截得的弦长=3√32是定值．【答案】 (I)a n ＝n ，S n =n(n+1)2．∴ S 1＝1，S 2＝3，S 3＝6，S 4＝10，S 5＝15． ∴ b 1＝1，b 2＝2，b 3＝2，b 4＝2，b 5＝3．证明：(II)（充分性）∵ a 1是奇数，a i (i ＝2, 3, 4…)为偶数， ∴ 对于任意i ∈N ∗，S i 都是奇数， ∴ b n ＝n ，∴ 数列{b n }是单调递增数列．（不必要性）当数列{a n }中只有a 2是奇数，其余项都是偶数时，S 1为偶数，S i (i ＝2, 3, 4…)均为奇数， ∴ b n ＝n −1，数列{b n }是单调递增数列，∴ “a 1为奇数，a i (i ＝2, 3, 4,…)为偶数”是“数列{b n }是单调递增数列”的不必要条件．综上，：“a 1为奇数，a i (i ＝2, 3, 4,…)为偶数”是“数列{b n }是单调递增数列”的充分不必要条件．(Ⅲ)(1)当a k 为奇数时，若S k 为偶数，若a k+1是奇数，则S k+1为奇数，∴ b k+1＝b k +1＝a k +1为偶数，与a k+1＝b k+1矛盾；若a k+1为偶数，则S k+1为偶数，∴ b k+1＝b k ＝a k 为奇数，与a k+1＝b k+1矛盾． ∴ 当a k 为奇数时，S k 不能为偶数；（2）当a k 为偶数，若S k 为奇数，若a k+1为奇数，则S k+1为偶数，∴ b k+1＝b k ＝a k 为偶数，与a k+1＝b k+1矛盾，若a k+1为偶数，则S k+1为奇数，∴ b k+1＝b k +1＝a k +1为奇数，与a k+1＝b k+1矛盾， ∴ 当a k 为偶数时，S k 不能是奇数．综上，a k 与S k 同奇偶，∵ a 1＝b 1＝S 1为偶数，且0≤b 1≤1，∴ b 1＝a 1＝0， ∵ a 2＝b 2≤b 1+1＝1，且b 2≥0，∴ b 2＝a 2＝0，以此类推，得到a n ＝0．【考点】数列递推式【解析】（I ）推导出a n ＝n ，S n =n(n+1)2．由此能写出数列{b n }的前5项．(II)先证充分性，推导出b n ＝n ，从而数列{b n }是单调递增数列；再证不必要性，当数列{a n }中只有a 2是奇数，其余项都是偶数时，S 1为偶数，S i (i ＝2, 3, 4…)均为奇数，b n＝n−1，数列{b n}是单调递增数列，由此能证明：“a1为奇数，a i(i＝2, 3, 4,…)为偶数”是“数列{b n}是单调递增数列”的充分不必要条件．(Ⅲ)当a k为奇数时，推导出S k不能为偶数；当a k为偶数，推导出S k不能是奇数，从而a k与S k同奇偶，由此得到a n＝0．【解答】(I)a n＝n，S n=n(n+1)．2∴S1＝1，S2＝3，S3＝6，S4＝10，S5＝15．∴b1＝1，b2＝2，b3＝2，b4＝2，b5＝3．证明：(II)（充分性）∵a1是奇数，a i(i＝2, 3, 4…)为偶数，∴对于任意i∈N∗，S i都是奇数，∴b n＝n，∴数列{b n}是单调递增数列．（不必要性）当数列{a n}中只有a2是奇数，其余项都是偶数时，S1为偶数，S i(i＝2, 3, 4…)均为奇数，∴b n＝n−1，数列{b n}是单调递增数列，∴ “a1为奇数，a i(i＝2, 3, 4,…)为偶数”是“数列{b n}是单调递增数列”的不必要条件．综上，：“a1为奇数，a i(i＝2, 3, 4,…)为偶数”是“数列{b n}是单调递增数列”的充分不必要条件．(Ⅲ)(1)当a k为奇数时，若S k为偶数，若a k+1是奇数，则S k+1为奇数，∴b k+1＝b k+1＝a k+1为偶数，与a k+1＝b k+1矛盾；若a k+1为偶数，则S k+1为偶数，∴b k+1＝b k＝a k为奇数，与a k+1＝b k+1矛盾．∴当a k为奇数时，S k不能为偶数；（2）当a k为偶数，若S k为奇数，若a k+1为奇数，则S k+1为偶数，∴b k+1＝b k＝a k为偶数，与a k+1＝b k+1矛盾，若a k+1为偶数，则S k+1为奇数，∴b k+1＝b k+1＝a k+1为奇数，与a k+1＝b k+1矛盾，∴当a k为偶数时，S k不能是奇数．综上，a k与S k同奇偶，∵a1＝b1＝S1为偶数，且0≤b1≤1，∴b1＝a1＝0，∵a2＝b2≤b1+1＝1，且b2≥0，∴b2＝a2＝0，以此类推，得到a n＝0．。

北京市丰台区2018届高三下学期3月综合练习(一模)数学(文)试题Word版含解析

丰台区2018年高三年级第二学期综合练习（一）数学（文科）第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1. 复数A. B. C. D.【答案】D【解析】复数故答案为：D.2. 已知命题p：x <1，，则为A. x ≥1,B. x <1,C. x <1,D. x ≥1,【答案】C【解析】根据全称命题与存在性命题之间的关系，可知命题的否定为，故选C．3. 已知，则下列不等式中恒成立的是A. B. C. D.【答案】A【解析】构造函数是减函数，已知,则，故A正确;,故B 不正确；C构造函数是增函数，故，故选项不正确；D. ，构造函数是增函数，故，所以选项不正确.故答案为：A.4. 已知抛物线的开口向下，其焦点是双曲线的一个焦点，则的标准方程为A. B. C. D.【答案】B【解析】双曲线的一个焦点为，故抛物线的焦点坐标也是，从而得到方程为.故答案为：B.5. 设不等式组确定的平面区域为，在中任取一点满足的概率是A. B.C. D.【答案】D【解析】不等式组确定的平面区域为是正方形，满足，即在直线上方的部分，根据几何概型的计算公式得到.故答案为：D.6. 执行如图所示的程序框图，那么输出的值是A. B.C. D.【答案】D【解析】根据题意得到当a=2,n=2A=由此可看出周期为3，当n=2018时输出结果，此时a=. 故答案为：D.7. 某三棱锥的三视图如图所示，则该三棱锥的体积为A. B.C. D.【答案】A【解析】根据三视图可知原图是个三棱锥，右侧面垂直于上底面，体积为：故答案为：A.点睛：思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.8. 设函数，若函数恰有三个零点，，，则的值是A. B. C. D.【答案】B【解析】函数，故根据题意得到化简得到=.故答案为：B.点睛：函数的零点或方程的根的问题，一般以含参数的三次式、分式、以e为底的指数式或对数式及三角函数式结构的函数零点或方程根的形式出现，一般有下列两种考查形式：(1)确定函数零点、图象交点及方程根的个数问题；(2)应用函数零点、图象交点及方程解的存在情况，求参数的值或取值范围问题．研究方程根的情况，可以通过导数研究函数的单调性、最值、函数的变化趋势等，根据题目要求，通过数形结合的思想去分析问题，可以使得问题的求解有一个清晰、直观的整体展现。

2018丰台区高三一模试题及答案

2018丰台区高三年级一模物理 2018.3 13．分子间的距离减小时（）A．分子势能一定减小B．分子势能一定增大C．分子间引力和斥力郁减小D．分子间引力和斥力都增大14．光照在某金属表面上发生了光电效应。

若只减弱光的强度，而保持频率不变，则（）A．有可能不发生光电效应B．逸出的光电子的最大初动能将减小C．单位时间内从金属表面逸出的光电子数将减少D．从光照射到金属表面到有光电子逸出的时间明显增加15．P、Q是简谐横波传播方向上的两个质点．它们的平衡位置间的距离为0.2m。

此波波速为1m/s．振幅为4cm，周期为0.4s。

在t=0时刻，P点位于平衡位置上方最大位移处。

贝Q点（）A．在0.3s时的速度最大B．在0.3s时的加速度最大C．在0.3s时的位移为4cmD．在0.3s时的位移为-4cm16．2018年2月12日我同以“一箭双星”方式成功发射“北斗三号工程’的两颗组网卫星。

已知某北斗导航卫星在离地高度为21500千米的圆形轨道上运行，地球同步卫星离地的高度约为36000干米。

下列说法正确的是（）A．此北斗导航卫星绕地球运动的周期大于24小时B．此北斗导航卫星的角速度大于地球同步卫星的角速度C．此北斗导航卫星的线速度小于地球同步卫星的线速度D．此北斗导航卫星的加速度小于地球同步卫星的加速度17．两等量正点电荷相距一定距离，它们连线的中点为O。

一带负电的粒子（不考虑重力）由静止开始，从连线的中垂线上P点运动O点。

此运动过程中，关于粒子的说法，正确的是（）A．电势能逐渐增加B．电势能先变大后变小，最后为零C．先做加速运动，后做减速运动D．始终做加速运动，到达O点时加速度为零18．某粒子A衰变为另外两种粒子B和C，其中粒子A和B所带电荷量相等，C不带电。

如图所示，粒子A 沿垂直于磁场的方向射入匀强磁场中，其轨迹为圆弧MP，衰变后产生的植子B的轨迹为圆弧PN，两轨迹在P点相切，且半径之比为RA：RB=2：1，粒子C的轨迹未画出。

2018届北京市丰台区高三年级一模数学(理)试题(解析版)

2018届北京市丰台区高三年级一模数学（理）试题一、单选题1．已知全集U={x|x<5}，集合{}|20 A x x =-≤，则U C A = A. {}| 2 x x ≤ B. {}| 2 x x C. {}|2 5 x x D. {}|2 5 x x ≤【答案】C【解析】由题意，集合{}{}|20 | 2 A x x x x =-≤=≤，所以U C A = {}|2 5 x x <<，故选C ．2．已知命题p ： ∃x <1， 21x ≤，则p ⌝为 A. ∀x ≥1, 21x B. ∃x <1, 21xC. ∀x <1, 21x D. ∃x ≥1, 21x【答案】C【解析】根据全称命题与存在性命题之间的关系，可知命题2:1,1p x x ∃<≤的否定为21,1x x ∀，故选C ．3．设不等式组-20{+20 0x y x y x ≤-≥≥表示的平面区域为Ω.则A. 原点O 在Ω内B. Ω的面积是1C. Ω内的点到y 轴的距离有最大值D. 若点P(x 0,y 0) ∈Ω，则x 0+y 0≠0 【答案】A【解析】由题意，画出不等式组坐标表示的平面区域，如图所示，原点O 在Ω内是成立的；区域Ω的面积不确定，所以不成立，区域Ω到y 轴的距离无最大值．令z x y =+，即y x z =-+，当取原点()0,0O 时，目标函数z x y =+取得最小值，此时min 0z =，故选A ．4．执行如图所示的程序框图，如果输出的a=2，那么判断框中填入的条件可以是A. n≥5B. n≥6C. n≥7D. n≥8 【答案】C【解析】执行如图所示的程序框图，可得：第一循环1,22a n ==；第二循环1,3a n =-=；第三循环2,4a n ==；第四循环1,52a n ==；第五循环1,6a n =-=；第六循环2,7a n ==，此时输出2a =，所以判断框应填入7n ≥，故选C ．5．在平面直角坐标系xO y 中，曲线C 的参数方程为1{x cos y sin αα=+=（α为参数）．若以射线Ox 为极轴建立极坐标系，则曲线C 的极坐标方程为 A. ρ=sin θ B. ρ=2sin θ C. ρ=cos θ D. ρ=2cos θ 【答案】D 【解析】由1{x cos y sin αα=+=（α为参数）得曲线C 普通方程为()2211x y -+=，又由{x cos y sin ρθρθ==，可得曲线C 的极坐标方程为2cos ρθ=，故选D ．6．某三棱锥的三视图如图所示，则该三棱锥的体积为A.23 B. 43 C. 2 D. 83【答案】A【解析】由给定的三视图可知，该几何体表示一个底面为一个直角三角形，且两直角边分别为1和2，所以底面面积为11212S =⨯⨯= 高为2h =的三棱锥，所以三棱锥的体积为11212333V Sh ==⨯⨯=，故选A ．7．某学校为了弘扬中华传统“孝”文化，共评选出2位男生和2位女生为校园“孝”之星，现将他们的照片展示在宣传栏中，要求同性别的同学不能相邻，不同的排法种数为A. 4B. 8C. 12D. 24 【答案】B【解析】由题意，现对两位男生全排列，共有222A =种不同的方式，其中两个男生构成三个空隙，把两位女生排在前两个空隙或后两个空隙中，再进行全排列，共有2224A ⨯=，所以满足条件的不同的排法种数共有248⨯=种，故选B ． 8．设函数()9=sin(4x+)0,416f x x ππ⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭,若函数()()y f x a a R =+∈恰有三个零点x 1, x 2, x 3 (x 1 <x 2 <x 3)，则x 1 + x 2 + x 3的取值范围是A. 511,816ππ⎡⎫⎪⎢⎣⎭B. 511,816ππ⎛⎤⎥⎝⎦ C. 715,816ππ⎡⎫⎪⎢⎣⎭ D. 715,816ππ⎛⎤⎥⎝⎦ 【答案】A 【解析】由90,16x π⎡⎤∈⎢⎥⎣⎦，则54,442x πππ⎡⎤+∈⎢⎥⎣⎦，又由函数()y f x a =+恰有三个零点123,,x x x ，即()y f x =与y a =-的图象有三个交点，其中2344344x x πππ+++=，可得2358x x π+=，又14,442x πππ⎡⎫+∈⎪⎢⎣⎭，解得1016x π≤<，所以123511816x x x ππ≤++<，即123511,816x x x ππ⎡⎫++∈⎪⎢⎣⎭，故选A ．点睛：本题考查了三角函数的图象与性质及函数与方程的应用，属于基础题，强调基础的重要性，是高考中的常考知识点；对于三角函数解答题中，当涉及到周期，单调性，单调区间以及最值等都属于三角函数的性质，根据三角函数的基本形式即()sin y A wx ϕ=+，后利用三角函数的性质求解．二、填空题9．如图所示，在复平面内，网格中的每个小正方形的边长都为1,点A,B 对应的复数分别是12,z z ，则21z z =_______.【答案】12i --【解析】由题意，根据复数的表示可知12,2z i z i ==-，所以()()()212212i i z i i z i i i -⋅--===--⋅-． 10．已知数列{}n a 的前n 项和n S =2n +n ，则34a a +＝______.【答案】14 【解析】由题意可知，数列{}n a 满足()()221112n nna S S n n n nn-⎡⎤=-=+--+-=⎣⎦，所以34232414a a +=⨯+⨯=．11．己知抛物线M 的开口向下，其焦点是双曲线2213y x -=的一个焦点，则M 的标准方程为______.【答案】28x y =-【解析】由双曲线的方程2213y x -=，可知2c == ，所以其下焦点的坐标为()0,2F -，设抛物线的方程为22(0)x py p =->，则22p=，所以4p =，所以抛物线的方程为28x y =-．点睛：本题考查了圆锥曲线的几何性质的应用及抛物线方程的求解，其中解答中涉及到双曲线的标准方程及其简单的几何性质、抛物线的标准方程和焦点坐标的应用，其中熟记圆锥曲线的几何性质是解答的关键．12．在△ABC 中，a=2,c=4，且3sin A =2sin B,则cos C=______. 【答案】14-【解析】由题意3sin 2sin A B =，根据正弦定理可知32a b =，又2a =，所以332b a ==，在ABC ∆中，由余弦定理可得2222222341cos 22234a b c C ab +-+-===-⨯⨯．点睛：本题主要考查了利用正弦定理和三角函数的恒等变换求解三角形问题，对于解三角形问题，通常利用正弦定理进行“边转角”寻求角的关系，利用“角转边”寻求边的关系，利用余弦定理借助三边关系求角，利用两角和差公式及二倍角公式求三角函数值. 利用正、余弦定理解三角形问题是高考高频考点，经常利用三角形内角和定理，三角形面积公式，结合正、余弦定理解题.13．函数y = f(x)是定义域为R 的偶函数，当x≥0时，函数f(x)的图象是由一段抛物线和一条射线组成（如图所示）.①当[]1,1x ∈-时，y 的取值范围是______;②如果对任意[],x a b ∈ (b <0)，都有[]2,1y ∈-，那么b 的最大值是______. 【答案】 []1,2 2-【解析】由图象可知，当0x =时，函数在[]1,1-上的最小值min 1y =，当1x =±时，函数在[]1,1-上的最小值max 2y =，所以当[]1,1x ∈-，函数()y f x =的值域为[]1,2；当[]0,3x ∈时，函数()()212f x x =--+，当[)3,x ∈+∞时，函数()5f x x =-，当()1f x =时， 2x =或7x =，又因为函数为偶函数，图象关于y 轴对称，所以对于任意[],(0)x a b b ∈<，要使得[]2,1y ∈-，则a R ∈， 7b =-或2b =-，则实数b 的最大值是2b =-．点睛：本题主要考查函数的奇偶性和函数的图象的应用，意在考查考生对概念的理解能力与应用能力、数形结合能力，求解此类函数图象判断题的关键:一是从已知函数图象过特殊点,列出关于参数的方程,从而求出参数的值;二是利用特殊点法来判断图象.本题还可以利用函数的单调性来判断函数的图象.总之,有关函数的图象判断题,利用“特殊点”与“函数的性质”,即可轻松破解.14．已知C 是平面ABD 上一点， AB AD ⊥， 1CB CD ==． ①若3AB AC =，则AB CD ⋅=____；②若AP AB AD =+，则AP 的最大值为____．【答案】 34-2 【解析】由题意，（1）中，因为3AB AC =，所以C 为线段AB 的三等分点，因为1CB CD ==，所以31,22AB AC ==，如图所示，则()3130cos 224AB CD AB AD AC AB AD AB AC π⋅=⋅-=⋅-⋅=-⨯=-，（2）中，因为AP AB AD =+，所以222222AP AB AD AB AD AB AD AB AD BD BD =+=++⋅=+==，如图所示，当点C 是线段BD 的中点时，此时BD 取得最大值，此时最大值为2BD BC CB =+=，所以AP 的最大值为2．点睛：本题考查了平面向量的线性运算法则和向量的数量积的运算，对于平面向量的计算问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式，涉及几何图形的问题，先建立适当的平面直角坐标系，可起到化繁为简的妙用，利用向量夹角公式、模公式及向量垂直的充要条件，可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决．三、解答题15．己知函数()2sin =2cos 11cos x f x x x ⎛⎫+-⎪⎝⎭(Ⅰ)求f(x)的定义域及最小正周期； (Ⅱ)求f(x)的单调递减区间．【答案】(1) π{|π,}2x x k k Z ≠+∈, πT =;(2) ()f x 的单调递减区间为ππ[π,π)82k k ++， π5π(π,π]28k k ++ ()k Z ∈．【解析】试题分析：（Ⅰ）根据三角恒等变换的公式，化简()π24f x x ⎛⎫=+ ⎪⎝⎭，即可得到函数的最小正周期；（Ⅱ）根据三角函数的图象与性质，即可得到函数的单调区间．试题解析：（Ⅰ）由 cos 0x ≠得， ππ2x k ≠+， ()k Z ∈，所以()f x 的定义域为π{|π,}2x x k k Z ≠+∈．因为()2sin 21cos 1cos x f x x x ⎛⎫=+⋅-⎪⎝⎭22sin cos 2cos 1x x x =+-sin2cos2x x =+ π24x ⎛⎫=+ ⎪⎝⎭．所以()f x 的最小正周期为2ππ2T ==．（Ⅱ）由 ππ3π2π22π242k x k +≤+≤+，可得 π5πππ88k x k +≤≤+，所以()f x 的单调递减区间为ππ[π,π)82k k ++， π5π(π,π]28k k ++ ()k Z ∈． 16．如图，在四棱锥P 一ABCD 中，平面PAB⊥平面ABCD, AB⊥BC, AD//BC,AD=3,PA=BC=2AB=2,PB(Ⅰ)求证：BC⊥PB;(Ⅱ)求二面角P 一CD 一A 的余弦值；(Ⅲ)若点E 在棱PA 上，且BE//平面PCD ，求线段BE 的长．【答案】(1)见解析;(2);(3) 【解析】试题分析：（Ⅰ）根据面面垂直的性质定理，证得BC ⊥平面PAB ，进而证得所以BC ⊥PB ；（Ⅱ）建立空间直角坐标系B xyz -，得到向量,CD PC 的坐标，再得到平面ABCD 的一个法向量为()0,0,1n =，利用向量的夹角公式，即可得到二面角的余弦值；（Ⅲ）由点E 在棱PA ，所以A E A P λ=，得到所以,)AE λ=（，()BE λ=-，再根据BE 与平面PCD 的法向量的数量积等于零，即可求解λ的值．试题解析：（Ⅰ）证明：因为平面PAB ⊥平面ABCD ，且平面PAB ⋂平面ABCD AB =，因为BC ⊥AB ，且BC ⊂平面ABCD 所以BC ⊥平面PAB ．因为PB ⊂平面PAB ，所以BC ⊥PB ．（Ⅱ）解：在△PAB 中，因为2PA =， PB = 1AB =，所以222PA AB PB =+，所以PB ⊥AB ．所以，建立空间直角坐标系B xyz -，如图所示．所以()1,0,0A -， ()0,0,0B ， ()0,2,0C ，()1,3,0D -， (P ，()1,1,0CD =-， (0,2,PC =．易知平面ABCD 的一个法向量为()0,0,1n =．设平面PCD 的一个法向量为(),,m x y z =，则0{m CD m PC ⋅=⋅=，即{2x y y ==，令2z =，则)2m =．设二面角P CD A --的平面角为α，可知α为锐角，则cos cos ,5n m n m n m α⋅====⋅，即二面角P CD A --．（Ⅲ）解：因为点E 在棱PA ，所以AE AP λ=， []0,1λ∈．因为=1AP （，所以)AE λ=（，()BE BA AE λ=+=-．又因为//BE 平面PCD ，m 为平面PCD 的一个法向量，所以0BE m ⋅=)120λλ-+=，所以1=3λ．所以23BE ⎛=-⎝⎭，所以7BE BE == 17．某地区工会利用 “健步行APP ”开展健步走积分奖励活动．会员每天走5千步可获积分30分(不足5千步不积分)，每多走2千步再积20分（不足2千步不积分）．记年龄不超过40岁的会员为A 类会员，年龄大于40岁的会员为B 类会员．为了解会员的健步走情况，工会从,A B 两类会员中各随机抽取m 名会员，统计了某天他们健步走的步数，并将样本数据分为[)3,5， [)5,7， [)7,9， [)9,11， [)11,13， [)13,15，[)15,17， [)17,19， []19,21九组，将抽取的A 类会员的样本数据绘制成频率分布直方图， B 类会员的样本数据绘制成频率分布表（图、表如下所示）．（Ⅰ）求m 和a 的值；（Ⅱ）从该地区A 类会员中随机抽取3名，设这3名会员中健步走的步数在13千步以上（含13千步）的人数为X ，求X 的分布列和数学期望；（Ⅲ）设该地区A 类会员和B 类会员的平均积分分别为1X 和2X ，试比较1X 和2X 的大小（只需写出结论）．【答案】（Ⅰ）1000,400；（Ⅱ）分布列见解析，65；（Ⅲ）12X X <. 【解析】试题分析：（Ⅰ）根据题意，根据上表的数据，即可求解m 和a 的值；（Ⅱ）由题意从该地区A 类会员中随机抽取1名会员，健步走的步数在13千步以上的概率为25，根据二项分布求得各自的概率，列出分布列，即可求解数学期望；（Ⅲ）根据平均分的计算公式，即可作出比较．试题解析：（Ⅰ）因为 100.01m=，所以 1000m =．因为0.2nm=，所以 200n =，所以400a =．所以 1000m =， 400a =．（Ⅱ）由频率分布直方图可得，从该地区A 类会员中随机抽取1名会员，健步走的步数在13千步以上（含13千步）的概率为25．所以23,5X N ⎛⎫~ ⎪⎝⎭， ()3033227055125P X C ⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭； ()21133254155125P X C ⎛⎫⎛⎫==⨯⨯=⎪ ⎪⎝⎭⎝⎭； ()12233236255125P X C ⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭； ()0333328355125P X C ⎛⎫⎛⎫==⨯⨯=⎪ ⎪⎝⎭⎝⎭．所以， X 的分布列为()26355E X =⨯=. （Ⅲ）12X X <．18．已知函数()()()=e ln 1xf x a x a R -+∈.(Ⅰ)求曲线()y f x =在点()()1,1f 处的切线方程； (Ⅱ)若函数()y f x =在1,12⎛⎫⎪⎝⎭上有极值，求a 的取值范围．【答案】(1) ()e y a x =-;(2) ⎫⎪⎪⎝⎭. 【解析】试题分析：（1）由题意()e xaf x x='-，因为()1e f a =-， ()1e f a '=-，利用点斜式方程即可求解切线的方程；（Ⅱ）由()e x af x x='-，分0a ≤和0a >讨论，即可得出函数单调性，求得函数有极值的条件，求得实数a 的取值范围．试题解析：函数()f x 的定义域为()0,+∞， ()e xaf x x='-．（Ⅰ）因为()1e f a =-， ()1e f a '=-，所以曲线()y f x =在点()()1,1f 处的切线方程为()()()e e 1y a a x --=--，即()e y a x =-．（Ⅱ）()e xa f x x='-．（ⅰ）当0a ≤时，对于任意1,12x ⎛⎫∈⎪⎝⎭，都有()0f x '>，所以函数()f x 在1,12⎛⎫⎪⎝⎭上为增函数，没有极值，不合题意．（ⅱ）当0a >时，令()e xa g x x =-，则()2e 0xa g x x=+>'．所以()g x 在1,12⎛⎫⎪⎝⎭上单调递增，即()f x '在1,12⎛⎫⎪⎝⎭上单调递增，所以函数()f x 在1,12⎛⎫⎪⎝⎭上有极值，等价于()10,{ 10.2f f >⎛⎫< ⎪⎝⎭''所以e 0, 20.a a -><所以e 2a <<．所以a的取值范围是⎫⎪⎪⎝⎭．19．已知点31,2P ⎛⎫⎪⎝⎭在椭圆C ： 22221(0)x y a b a b +=>>上， ()1,0F 是椭圆的一个焦点．（Ⅰ）求椭圆C 的方程；（Ⅱ）椭圆C 上不与P 点重合的两点D ， E 关于原点O 对称，直线PD ， PE 分别交y 轴于M ， N 两点．求证：以MN 为直径的圆被直线32y =截得的弦长是定值．【答案】（Ⅰ）22143x y +=．（Ⅱ）见解析．【解析】试题分析：（Ⅰ）依题意，得到1c =，利用定义得到2a =，即可求解椭圆的标准方程；（Ⅱ）设(),D mn ，(),E m n --，根据直线方程，求解,M N 的坐标，可得GM GN ⊥，利用 0GM GN ⋅=，求得t 的值，即可得到弦长为定值．试题解析：（Ⅰ）依题意，椭圆的另一个焦点为()1,0F '-，且1c =．因为24a ==，所以2a =，b =，所以椭圆C 的方程为22143x y +=．（Ⅱ）证明：由题意可知D ， E 两点与点P 不重合．因为D ， E 两点关于原点对称，所以设(),D m n ， (),E m n --， ()1m ≠±．设以MN 为直径的圆与直线32y =交于33,,,(0)22G t H t t ⎛⎫⎛⎫-> ⎪ ⎪⎝⎭⎝⎭两点，所以GM GN ⊥．直线PD ： ()332121n y x m --=--．当0x =时， 33212n y m -=-+-，所以3320,12n M m ⎛⎫- ⎪-+ ⎪- ⎪⎝⎭．直线PE ： ()332121n y x m +-=-+．当0x =时， 33212n y m +=-++，所以3320,12n N m ⎛⎫+ ⎪-+ ⎪+ ⎪⎝⎭．所以32,1n GM t m ⎛⎫- ⎪=-- ⎪- ⎪⎝⎭， 32,1n GN t m ⎛⎫+ ⎪=-- ⎪+ ⎪⎝⎭，因为GM GN ⊥，所以0GM GN ⋅=，所以()22249041n GM GN t m -⋅=+=-．因为22143m n +=，即223412m n +=， 224933n m -=-，所以2304t -=，所以t =所以32G ⎫⎪⎪⎝⎭，32H ⎛⎫ ⎪ ⎪⎝⎭，所以GH = 所以以MN 为直径的圆被直线32y =点睛：本题主要考查椭圆的方程与性质、直线与圆锥曲线的位置关系,解答此类题目，通常利用,,a b c 的关系，确定椭圆（圆锥曲线）方程是基础，通过联立直线方程与椭圆（圆锥曲线）方程的方程组，应用一元二次方程根与系数的关系，得到“目标函数”的解析式，确定函数的性质进行求解，此类问题易错点是复杂式子的变形能力不足，导致错漏百出，本题能较好的考查考生的逻辑思维能力、运算求解能力、分析问题解决问题的能力等．20．已知无穷数列{}()n n a a Z ∈的前n 项和为n S ，记1S ， 2S ，…， n S 中奇数的个数为n b ．(Ⅰ)若n a = n ，请写出数列{}n b 的前5项；(Ⅱ)求证："1a 为奇数， i a (i = 2,3,4,...）为偶数”是“数列{}n b 是单调递增数列”的充分不必要条件；(Ⅲ)若i i a b =，i=1, 2, 3,…，求数列{}n a 的通项公式. 【答案】(1)见解析;(2)见解析;(3) 0n a =.【解析】试题分析：（Ⅰ）代入n 的值，即可求得1=1b ， 2=2b ， 3=2b ， 4=2b ， 5=3b ．（Ⅱ）根据题意，先证充分性和不必要性，分别作出证明．（Ⅲ）分当k a 为奇数和当k a 为偶数，两种情况进而推导数列的通项公式．试题解析：（Ⅰ）解： 1=1b ， 2=2b ， 3=2b ， 4=2b ， 5=3b ．（Ⅱ）证明：（充分性）因为1a 为奇数， ()2,3,4,i a i =为偶数，所以，对于任意*i N ∈， i S 都为奇数．所以n b n =．所以数列{}n b 是单调递增数列．（不必要性）当数列{}n a 中只有2a 是奇数，其余项都是偶数时， 1S 为偶数， ()2,3,4,i S i =均为奇数，所以1n b n =-，数列{}n b 是单调递增数列．所以“1a 为奇数， ()2,3,4,i a i =为偶数”不是“数列{}n b 是单调递增数列”的必要条件；综上所述，“1a 为奇数， ()2,3,4,i a i =为偶数”是“数列{}n b 是单调递增数列”的充分不必要条件．（Ⅲ）解：（1）当k a 为奇数时，如果k S 为偶数，若1k a +为奇数，则1k S +为奇数，所以111k k k b b a +=+=+为偶数，与11k k a b ++=矛盾；若1k a +为偶数，则1k S +为偶数，所以1k k k b b a +==为奇数，与11k k a b ++=矛盾．所以当k a 为奇数时， k S 不能为偶数．（2）当k a 为偶数时，如果k S 为奇数，若1k a +为奇数，则1k S +为偶数，所以1k k k b b a +==为偶数，与11k k a b ++=矛盾；若1k a +为偶数，则1k S +为奇数，所以111k k k b b a +=+=+为奇数，与11k k a b ++=矛盾．所以当k a 为偶数时， k S 不能为奇数．综上可得k a 与k S 同奇偶．所以n n S a -为偶数．因为11n n n S S a ++=-为偶数，所以n a 为偶数．因为111a b S ==为偶数，且101b ≤≤，所以110b a ==．因为22111a b b =≤+=，且20b ≥，所以220b a ==．以此类推，可得0n a =．点睛：本题考查学生对新定义的理解能力和使用能力，本题属于偏难问题，反映出学生对于新的信息的的理解和接受能力，本题考查数列的有关知识及归纳法证明方法，即考查了数列求值，又考查了归纳法证明和对数据的分析研究，考查了学生的分析问题能力和逻辑推理能力，本题属于拔高难题，特别是第二两步难度较大，适合选拔优秀学生.。

2018年北京市丰台区高考一模数学试卷(文科)【解析版】

2018年北京市丰台区高考数学一模试卷（文科）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）复数＝（）A．﹣1+i B．﹣1﹣i C．1+i D．1﹣i2．（5分）已知命题p：∃x＜1，x2≤1，则￢p为（）A．∀x≥1，x2＞1B．∃x＜1，x2＞1C．∀x＜1，x2＞1D．∃x≥1，x2＞1 3．（5分）已知a＜b＜0，则下列不等式中恒成立的是（）A．B．C．2a＞2b D．a3＞b34．（5分）已知抛物线C的开口向下，其焦点是双曲线的一个焦点，则C的标准方程为（）A．y2＝8x B．x2＝﹣8y C．D．5．（5分）设不等式组确定的平面区域为D，在D中任取一点P（x，y）满足x+y≥2的概率是（）A．B．C．D．6．（5分）执行如图所示的程序框图，那么输出的a值是（）A．B．﹣1C．2D．7．（5分）某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．B．4C．D．8．（5分）设函数，若函数y＝f（x）+a（a∈R）恰有三个零点x1，x2，x3（x1＜x2＜x3），则x1+2x2+x3的值是（）A．B．C．D．π二、填空题共6小题，每小题5分，共30分．9．（5分）已知集合A＝{x|﹣2≤x≤0}，B＝{x|0＜x≤3}，则A∪B＝．10．（5分）圆心为（1，0），且与直线y＝x+1相切的圆的方程是．11．（5分）在△ABC中，a＝2，c＝4，且3sin A＝2sin B，则cos C＝．12．（5分）已知点A（2，0），B（0，1），若点P（x，y）在线段AB上，则xy 的最大值为．13．（5分）已知定义域为R的奇函数f（x），当x＞0时，f（x）＝﹣（x﹣1）2+1．①当x∈[﹣1，0]时，f（x）的取值范围是；②当函数f（x）的图象在直线y＝x的下方时，x的取值范围是．14．（5分）已知C是平面ABD上一点，AB⊥AD，CB＝CD＝1．①若，则＝；①若，则的最大值为．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）已知函数f（x）＝2cos x（sin x+cos x）﹣1．（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）在[0，π]上的单调递增区间．16．（13分）在数列{a n}和{b n}中，a1＝1，a n+1＝a n+2，b1＝3，b2＝7，等比数列{c n}满足c n＝b n﹣a n．（Ⅰ）求数列{a n}和{c n}的通项公式；（Ⅱ）若b6＝a m，求m的值．17．（14分）如图所示，在四棱锥P﹣ABCD中，平面P AB⊥平面ABCD，AD∥BC，AD＝2BC，∠DAB＝∠ABP＝90°．（Ⅰ）求证：AD⊥平面P AB；（Ⅱ）求证：AB⊥PC；（Ⅲ）若点E在棱PD上，且CE∥平面P AB，求的值．18．（13分）某地区工会利用“健步行APP”开展健步走积分奖励活动．会员每天走5千步可获积分30分（不足5千步不积分），每多走2千步再积20分（不足2千步不积分）．为了解会员的健步走情况，工会在某天从系统中随机抽取了1000名会员，统计了当天他们的步数，并将样本数据分为[3，5），[5，7），[7，9），[9，11），[11，13），[13，15），[15，17），[17，19），[19，21]九组，整理得到如下频率分布直方图：（Ⅰ）求当天这1000名会员中步数少于11千步的人数；（Ⅱ）从当天步数在[11，13），[13，15），[15，17）的会员中按分层抽样的方式抽取6人，再从这6人中随机抽取2人，求这2人积分之和不少于200分的概率；（Ⅲ）写出该组数据的中位数（只写结果）．19．（14分）已知椭圆C：的一个焦点为，点A（﹣2，0）在椭圆C上．（Ⅰ）求椭圆C的方程与离心率；（Ⅱ）设椭圆C上不与A点重合的两点D，E关于原点O对称，直线AD，AE 分别交y轴于M，N两点．求证：以MN为直径的圆被x轴截得的弦长是定值．20．（13分）已知函数．（Ⅰ）当时，求曲线y＝f（x）在（1，f（1））处的切线方程；（Ⅱ）若函数f（x）在定义域内不单调，求a的取值范围．2018年北京市丰台区高考数学一模试卷（文科）参考答案与试题解析一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）复数＝（）A．﹣1+i B．﹣1﹣i C．1+i D．1﹣i【解答】解：＝．故选：D．2．（5分）已知命题p：∃x＜1，x2≤1，则￢p为（）A．∀x≥1，x2＞1B．∃x＜1，x2＞1C．∀x＜1，x2＞1D．∃x≥1，x2＞1【解答】解：由特称命题的否定为全称命题，可得命题p：∃x＜1，x2≤1，的否定为￢p：∀x＜1，x2＞1，故选：C．3．（5分）已知a＜b＜0，则下列不等式中恒成立的是（）A．B．C．2a＞2b D．a3＞b3【解答】解：∵a＜b＜0；∴，，2a＜2b，a3＜b3．故选：A．4．（5分）已知抛物线C的开口向下，其焦点是双曲线的一个焦点，则C的标准方程为（）A．y2＝8x B．x2＝﹣8y C．D．【解答】解：根据题意，抛物线C的开口向下，则抛物线的焦点在y轴的负半轴上，设其方程为x2＝﹣2py，其焦点坐标为（0，﹣），双曲线的焦点为（0，±2），若抛物线的焦点是双曲线的一个焦点，则有﹣＝﹣2，则有p＝4，则抛物线的方程为：x2＝﹣8y，故选：B．5．（5分）设不等式组确定的平面区域为D，在D中任取一点P（x，y）满足x+y≥2的概率是（）A．B．C．D．【解答】解：画出满足条件的平面区域，如图示：，S△ODE＝2，S四边形OABC＝25，故满足条件的概率p＝＝，故选：D．6．（5分）执行如图所示的程序框图，那么输出的a值是（）A．B．﹣1C．2D．【解答】解：第1次执行循环体后，a＝，n＝2，不满足退出循环的条件；第2次执行循环体后，a＝﹣1，n＝3，不满足退出循环的条件；第3次执行循环体后，a＝2，n＝4，不满足退出循环的条件；第4次执行循环体后，a＝，n＝5，不满足退出循环的条件；第5次执行循环体后，a＝﹣1，n＝6，不满足退出循环的条件；第6次执行循环体后，a＝2，n＝7，不满足退出循环的条件；……第3k次执行循环体后，a＝2，n＝3k+1，不满足退出循环的条件；第3k+1次执行循环体后，a＝，n＝3k+2，不满足退出循环的条件；第3k+2次执行循环体后，a＝﹣1，n＝3k+3，不满足退出循环的条件；……第2016次执行循环体后，a＝2，n＝2017，不满足退出循环的条件；第2017次执行循环体后，a＝，n＝2018，满足退出循环的条件，故输出的a＝，故选：D．7．（5分）某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．B．4C．D．【解答】解：由三视图还原原几何体如图，该几何体为三棱锥，底面三角形ABC为等腰三角形，AB＝AC，侧面PBC⊥底面ABC，且三棱锥的高为2，则该三棱锥的体积为．故选：A．8．（5分）设函数，若函数y＝f（x）+a（a∈R）恰有三个零点x1，x2，x3（x1＜x2＜x3），则x1+2x2+x3的值是（）A．B．C．D．π【解答】解：函数令4x+＝，可得：x＝，k∈Z．∵∴令k＝0，可得一条对称轴方程x＝．∴令k＝1，可得一条对称轴方程x＝．函数y＝f（x）+a（a∈R）恰有三个零点，可知x1，x2关于其中一条对称是对称的，即x1+x2＝＝x3，x2关于其中一条对称是对称的．即x3+x2＝＝那么x1+2x2+x3＝．故选：B．二、填空题共6小题，每小题5分，共30分．9．（5分）已知集合A＝{x|﹣2≤x≤0}，B＝{x|0＜x≤3}，则A∪B＝{x|﹣2≤x ≤3}．【解答】解：集合A＝{x|﹣2≤x≤0}，B＝{x|0＜x≤3}，则A∪B＝{x|﹣2≤x≤3}．故答案为：{x|﹣2≤x≤3}．10．（5分）圆心为（1，0），且与直线y＝x+1相切的圆的方程是（x﹣1）2+y2＝2．【解答】解：圆的半径为点（1，0）到直线直线y＝x+1的距离，即r＝＝，故圆的方程为（x﹣1）2+y2＝2，故答案为：（x﹣1）2+y2＝2．11．（5分）在△ABC中，a＝2，c＝4，且3sin A＝2sin B，则cos C＝﹣．【解答】解：根据题意，在△ABC中，3sin A＝2sin B，则有3a＝2b，又由a＝2，则b＝3，则cos C＝＝＝﹣；故答案为：﹣．12．（5分）已知点A（2，0），B（0，1），若点P（x，y）在线段AB上，则xy的最大值为．【解答】解：A（2，0），B（0，1），可得AB的方程为+y＝1，（0≤x≤2），由+y≥2，可得xy≤2•（+y）2＝，当且仅当x＝，y＝时，取得最大值，故答案为：．13．（5分）已知定义域为R的奇函数f（x），当x＞0时，f（x）＝﹣（x﹣1）2+1．①当x∈[﹣1，0]时，f（x）的取值范围是[﹣1，0]；②当函数f（x）的图象在直线y＝x的下方时，x的取值范围是（﹣1，0）∪（1，+∞）．【解答】解：若x∈[﹣1，0]，﹣x∈[0，1]，f（x）是奇函数，∵当x＞0时，f（x）＝﹣（x﹣1）2+1，∴当﹣x＞0时，f（﹣x）＝﹣（﹣x﹣1）2+1＝﹣f（x），即当x＜0时，f（x）＝（x+1）2﹣1，则当x∈[﹣1，0]时，最小值为f（﹣1）＝﹣1，最大值为f（0）＝0，则此时f（x）的取值范围是[﹣1，0]．②f（x）＝，若当函数f（x）的图象在直线y＝x的下方时，则满足当x≥0，﹣（x﹣1）2+1＜x，即（x﹣1）2+x﹣1＝（x﹣1）x＞0，得x＞1或x＜0，此时x＞1，当x＜0，（x+1）2﹣1＜x，即（x+1）2﹣（x+1）＝（x+1）x＜0，得﹣1＜x＜0，综上x＞1或﹣1＜x＜0，即实数x的取值范围是（﹣1，0）∪（1，+∞），故答案为：[﹣1，0]；（﹣1，0）∪（1，+∞）14．（5分）已知C是平面ABD上一点，AB⊥AD，CB＝CD＝1．①若，则＝﹣；①若，则的最大值为2．【解答】解：①∵＝3，∴C为AB的靠近A的三等分点，∴AB＝BC＝，AC＝BC＝，∵AD⊥AB，CD＝1，∴∠ACD＝60°，∴•＝•1•cos120°＝﹣．②∵CB＝CD＝1，∴C位于BD的中垂线上，∴当C为BD的中点时，BD取得最大值2．∵AB⊥AD，∴||＝|+|＝|﹣|＝BD≤2．故答案为：；2．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）已知函数f（x）＝2cos x（sin x+cos x）﹣1．（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）在[0，π]上的单调递增区间．【解答】解：（Ⅰ）f（x）＝2sin x cos x+2cos2x﹣1＝sin2x+cos2x＝．∴f（x）的最小正周期为；（Ⅱ）由（k∈Z），得（k∈Z）．当x∈[0，π]时，单调递增区间为和．16．（13分）在数列{a n}和{b n}中，a1＝1，a n+1＝a n+2，b1＝3，b2＝7，等比数列{c n}满足c n＝b n﹣a n．（Ⅰ）求数列{a n}和{c n}的通项公式；（Ⅱ）若b6＝a m，求m的值．【解答】解：（Ⅰ）因为a n+1﹣a n＝2，且a1＝1，所以数列{a n}是首项为1，公差为2的等差数列．所以a n＝1+（n﹣1）•2＝2n﹣1，即a n＝2n﹣1．因为b1＝3，b2＝7，且a1＝1，a2＝3，所以c1＝b1﹣a1＝2，c2＝b2﹣a2＝4．因为数列{c n}是等比数列，所以数列{c n}的公比，所以，即．（Ⅱ）因为，a n＝2n﹣1，所以．所以．令2m﹣1＝75，得m＝38．17．（14分）如图所示，在四棱锥P﹣ABCD中，平面P AB⊥平面ABCD，AD∥BC，AD＝2BC，∠DAB＝∠ABP＝90°．（Ⅰ）求证：AD⊥平面P AB；（Ⅱ）求证：AB⊥PC；（Ⅲ）若点E在棱PD上，且CE∥平面P AB，求的值．【解答】（Ⅰ）证明：因为∠DAB＝90°，所以AD⊥AB．……………………（1分）因为平面P AB⊥平面ABCD，……………………（2分）且平面P AB∩平面ABCD＝AB，……………………（3分）所以AD⊥平面P AB．……………………（4分）（Ⅱ）证明：由已知得AD⊥AB因为AD∥BC，所以BC⊥AB．……………………（5分）又因为∠ABP＝90°，所以PB⊥AB．……………………（6分）因为PB∩BC＝B……………………（7分）所以AB⊥平面PBC……………………（8分）所以AB⊥PC．……………………（9分）（Ⅲ）解：过E作EF∥AD交P A于F，连接BF．……………………（10分）因为AD∥BC，所以EF∥BC．所以E，F，B，C四点共面．……………………（11分）又因为CE∥平面P AB，且CE⊂平面BCEF，且平面BCEF∩平面P AB＝BF，所以CE∥BF，……………………（13分）所以四边形BCEF为平行四边形，所以EF＝BC．在△P AD中，因为EF∥AD，所以，……………………（14分）即．18．（13分）某地区工会利用“健步行APP”开展健步走积分奖励活动．会员每天走5千步可获积分30分（不足5千步不积分），每多走2千步再积20分（不足2千步不积分）．为了解会员的健步走情况，工会在某天从系统中随机抽取了1000名会员，统计了当天他们的步数，并将样本数据分为[3，5），[5，7），[7，9），[9，11），[11，13），[13，15），[15，17），[17，19），[19，21]九组，整理得到如下频率分布直方图：（Ⅰ）求当天这1000名会员中步数少于11千步的人数；（Ⅱ）从当天步数在[11，13），[13，15），[15，17）的会员中按分层抽样的方式抽取6人，再从这6人中随机抽取2人，求这2人积分之和不少于200分的概率；（Ⅲ）写出该组数据的中位数（只写结果）．【解答】（本小题共13分）解：（Ⅰ）这1000名会员中健步走的步数在[3，5）内的人数为0.02×2×1000＝40；健步走的步数在[5，7）内的人数为0.03×2×1000＝60；健步走的步数在[7，9）内的人数为0.05×2×1000＝100；健步走的步数在[9，11）内的人数为0.05×2×1000＝100；40+60+100+100＝300．所以这1000名会员中健步走的步数少于11千步的人数为300人．…………………（4分）（Ⅱ）按分层抽样的方法，在[11，13）内应抽取3人，记为a1，a2，a3，每人的积分是90分；在[13，15）内应抽取2人，记为b1，b2，每人的积分是110分；在[15，17）内应抽取1人，记为c，每人的积分是130分；……………………（5分）从6人中随机抽取2人，有：a1a2，a1a3，a1b1，a1b2，a1c，a2a3，a2b1，a2b2，a2c，a3b1，a3b2，a3c，b1b2，b1c，b2c共15种方法．……………………（7分）所以从6人中随机抽取2人，这2人的积分之和不少于200分的有：a1b1，a1b2，a1c，a2b1，a2b2，a2c，a3b1，a3b2，a3c，b1b2，b1c，b2c共12种方法．……………（9分）设从6人中随机抽取2人，这2人的积分之和不少于200分为事件A，则．……………………（11分）所以从6人中随机抽取2人，这2人的积分之和不少于200分的概率为．（Ⅲ）中位数为．……………………（13分）19．（14分）已知椭圆C：的一个焦点为，点A（﹣2，0）在椭圆C上．（Ⅰ）求椭圆C的方程与离心率；（Ⅱ）设椭圆C上不与A点重合的两点D，E关于原点O对称，直线AD，AE 分别交y轴于M，N两点．求证：以MN为直径的圆被x轴截得的弦长是定值．【解答】解：（Ⅰ）依题意，．A（﹣2，0）在椭圆C上．所以a＝2．所以b2＝a2﹣c2＝1．所以椭圆C的方程为．离心率．证明：（Ⅱ）因为D，E两点关于原点对称，所以可设D（m，n），E（﹣m，﹣n），（m≠±2），所以．直线AD：．当x＝0时，，所以．直线AE：．当x＝0时，，所以．设以MN为直径的圆与x轴交于点G（x0，0）和H（﹣x0，0），（x0＞0），所以，，，所以．因为点G在以MN为直径的圆上，所以，即．因为，即4n2＝4﹣m2，所以，所以x0＝1．所以G（1，0），H（﹣1，0）．所以|GH|＝2．所以以MN为直径的圆被x轴截得的弦长是定值2．20．（13分）已知函数．（Ⅰ）当时，求曲线y＝f（x）在（1，f（1））处的切线方程；（Ⅱ）若函数f（x）在定义域内不单调，求a的取值范围．【解答】解：函数f（x）的定义域为（0，+∞），导函数．（Ⅰ）当时，因为，，所以曲线y＝f（x）在（1，f（1））处的切线方程为；（Ⅱ），设函数f（x）在定义域内不单调，a的取值范围是集合A；函数f（x）在定义域内单调时，a的取值范围是集合B，则A＝∁R B，所以函数f（x）在定义域内单调，等价于f'（x）≤0恒成立，或f'（x）≥0恒成立，即ae x﹣x≤0恒成立，或ae x﹣x≥0恒成立，等价于恒成立或恒成立．令，则，由g'（x）＞0得0＜x＜1，所以g（x）在（0，1）上单调递增；由g'（x）＜0得x＞1，所以g（x）在（1，+∞）上单调递减．因为g（0）＝0，，且x＞0时，g（x）＞0，所以．所以，所以．。

2018年北京市丰台区高三一模文科数学含答案纯word版

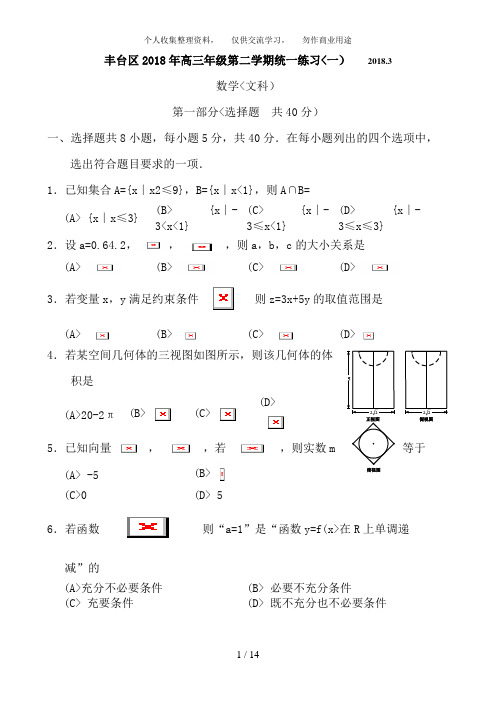
侧视图俯视图丰台区2018年高三年级第二学期统一练习<一） 2018.3数学<文科）第一部分<选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．已知集合A={x ∣x2≤9}，B={x ∣x<1}，则A ∩B= (A> {x ∣x ≤3} (B> {x ∣-3<x<1} (C> {x ∣-3≤x<1} (D> {x ∣-3≤x ≤3} 2．设a=0.64.2，，，则a ，b ，c 的大小关系是(A>(B>(C>(D>3．若变量x ，y 满足约束条件则z=3x+5y 的取值范围是(A>(B>(C>(D>4．若某空间几何体的三视图如图所示，则该几何体的体积是(A>20-2π (B> (C>(D>等于5．已知向量，，若，则实数m(A> -5 (B> (C>0 (D> 56．若函数则“a=1”是“函数y=f(x>在R 上单调递减”的(A>充分不必要条件(B> 必要不充分条件(C> 充要条件(D> 既不充分也不必要条件7．设为等比数列的前项和，若a1=1，且，，成等差数列，则数列的前5项和为(A> 341(B>(C> 1023 (D> 1024 8．已知定义在R 上的函数满足，当时，．若函数至少有6个零点，则a 的取值范围是 (A> (1，5>(B>(C>(D>第二部分<非选择题共110分）二、填空题共6小题，每小题5分，共30分． 9．在复平面内，复数对应的点的坐标为____．10．已知抛物线y2=8x 上一点P 到焦点的距离是6，则点P 的坐标是_____． 11．已知函数在x=a 时取到最小值，则a=________．12．为了了解学生的视力情况，随机抽查了一批学生的视力，将抽查结果绘制成频率分布直方图<如图所示）．若在内的学生人数是2，则根据图中数据可得被抽查的学生总数是；样本数据在内的频率是．b5E2RGbCAP13．执行如图所示的程序框图，若输出的n 的值为10，则a0=____． 14．定义在区间上的连续函数，如果，使得，则称为区间上的“中值点”．下列函数：①；②；③；④中，在区间上“中值点”多于一个的函数序号为____．<写出所有满足条件的函数的序号）p1EanqFDPw 三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15.<本小题共13分）在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且．<Ⅰ）判断△ABC 的形状； <Ⅱ）若，求的最大值．16.<本小题共13分）对某校全体教师在教学中是否经常使用信息技术实施教学的情况进行了调查，得到统计数据如下：<Ⅰ）求该校教师在教学中不经常使用信息技术实施教学的概率； <Ⅱ）在教龄10年以下，且经常使用信息技术实施教学的教师中任选2人，其中恰有一人教龄在5年以下的概率是多少？DXDiTa9E3d 17.<本小题共14分）如图，四棱锥P-ABCD 中，底面ABCD 是菱形，PA=PD ，∠BAD =60º，E 是AD 的中点，点Q 在侧棱PC 上． RTCrpUDGiT <Ⅰ）求证：AD ⊥平面PBE ；<Ⅱ）若Q 是PC 的中点，求证：PA // 平面BDQ ；<Ⅲ）若VP-BCDE =2VQ- ABCD ，试求的值．18.<本小题共13分）已知函数．<Ⅰ）若曲线y=f(x>在(1，f(1>>处的切线与直线x+y+1=0平行，求a 的值；<Ⅱ）若a>0，函数y=f(x>在区间(a ，a2-3>上存在极值，求a 的取值范围；<Ⅲ）若a>2，求证：函数y=f(x>在(0，2>上恰有一个零点． 19.<本小题共14分）已知椭圆C ：的离心率为，且经过点．<Ⅰ）求椭圆C 的标准方程；<Ⅱ）设斜率为1的直线l 与椭圆C 相交于，两点，连接MA ，MB 并延长交直线x=4于P ，Q 两点，设yP ，yQ 分别为点P ，Q 的纵坐标，且．求△ABM 的面积．5PCzVD7HxA 20.<本小题共13分）DCBQPEA设数列的前项和为，且．数列满足，．<Ⅰ）求数列的通项公式；<Ⅱ）证明：数列为等差数列，并求的通项公式；<Ⅲ）设数列的前项和为，是否存在常数，使得不等式恒成立？若存在，求出的取值范围；若不存在，请说明理由．jLBHrnAILg <考生务必将答案答在答题卡上，在试卷上作答无效）丰台区2018年高三年级第二学期数学统一练习<一）数学<文科）参考答案一、选择题：本大题共8小题，每小题5分，共40分．二、填空题：本大题共6小题，每小题5分，共30分．9．10．11．12．50，0.1213．314．①④注：第12题第一个空填对得3分，第二个空填对得2分．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．解：<Ⅰ）<法1）因为，由正弦定理可得． ……………………3分即，所以．……………………4分因为在△ABC中，，所以又，……………………5分所以，．所以△ABC为的直角三角形．……………………6分xHAQX74J0X<法2）因为，由余弦定理可得，……………………4分所以．因为，所以．……………………5分LDAYtRyKfE所以在△ABC中，．所以△ABC为的直角三角形．……………………6分Zzz6ZB2Ltk<Ⅱ）因为，……………………8分所以． (9)分因为△ABC是的直角三角形，所以，……………………10分dvzfvkwMI1所以， (1)1分rqyn14ZNXI所以． (12)分即的最大值为．……………………13分EmxvxOtOco16．解：<Ⅰ）该校教师人数为8+10+30+18=66，该校经常使用信息技术实施教学的教师人数为2+4+10+4=20．SixE2yXPq5……………………2分设“该校教师在教学中经常使用信息技术实施教学”为事件A，……………………3分则，……………………5分6ewMyirQFL．……………………6分kavU42VRUs所以该校教师在教学中不经常使用信息技术实施教学的概率是．<Ⅱ）设经常使用信息技术实施教学，教龄在5年以下的教师为<i=1，2），教龄在5至10年的教师为<j=1，2，3，4），那么任选2人的基本事件为，，，，，，，，，，，，，，共15个．……………………9分y6v3ALoS89设“任选2人中恰有一人的教龄在5年以下”为事件B，……………………10分包括的基本事件为，，，，，，，共8个，……………………11分M2ub6vSTnP则．……………………13分0YujCfmUCw所以恰有一人教龄在5年以下的概率是．17．证明：<Ⅰ）因为 E是AD的中点， PA=PD，所以AD ⊥PE ． ……………………1分eUts8ZQVRd 因为底面ABCD 是菱形，∠BAD =60º，所以 AB=BD ，又因为E 是AD的中点，所以AD ⊥BE ． ……………………2分因为 PE ∩BE=E ，……………………3分所以 AD ⊥平面PBE ． ……………………4分 <Ⅱ）连接AC 交BD 于点O ，连结OQ ．……………………5分因为O 是AC 中点， Q 是PC 的中点，所以OQ 为△PAC 中位线．所以OQ//PA ． ……………………7分sQsAEJkW5T 因为PA平面BDQ，OQ平面BDQ ． ……………………8分所以PA//平面BDQ ． ……………………9分GMsIasNXkA OD CBAQPE<Ⅲ）设四棱锥P-BCDE，Q-ABCD的高分别为，，所以VP-BCDE=SBCDE，VQ-ABCD=SABCD．……………………10分因为VP-BCDE =2VQ - ABCD，且底面积SBCDE=SABCD．……………………12分所以，……………………13分因为，所以．……………………14分18．解：<Ⅰ），……………………1分TIrRGchYzg，……………………2分7EqZcWLZNX因为曲线y=f(x>在(1，f(1>>处的切线与直线x+y+1=0平行所以，……………………3分lzq7IGf02E所以．……………………4分<Ⅱ）令，……………………5分zvpgeqJ1hk即，所以或．……………………6分因为a>0，所以不在区间(a，a2-3>内，要使函数在区间(a，a2-3>上存在极值，只需．……………………7分所以．……………………9分<Ⅲ）证明：令，所以或．因为a>2，所以2a>4，……………………10分NrpoJac3v1所以在(0，2>上恒成立，函数f(x>在(0，2>内单调递减．又因为，，……………………11分所以f(x>在(0，2>上恰有一个零点．……………………13分19．解：<Ⅰ）依题意，，所以．……………………2分因为，所以．……………………3分椭圆方程为．……………………5分<Ⅱ）因为直线l的斜率为1，可设l：，……………………6分则，消y得，……………………7分，得．因为，，所以，．……………………8分设直线MA：，则；同理．…………………9分因为，所以，即．……………………10分所以，所以，，，所以，所以．……………………12分所以，．设△ABM的面积为S，直线l与x轴交点记为N，所以．…………14分所以△ABM的面积为．20．解：<Ⅰ）当时；当时，因为适合通项公式．所以．……………………5分<Ⅱ）因为，所以，即．所以是首项为=1，公差为2的等差数列．所以，所以．……………………9分<Ⅲ）存在常数使得不等式恒成立．因为①所以②由①-②得，化简得．因为=，<1）当为奇数时，，所以，即．所以当=1时，的最大值为，所以只需；<2）当为偶数时，，所以，所以当=2时，的最小值为，所以只需；由<1）<2）可知存在，使得不等式恒成立．……………………13分<若用其他方法解题，请酌情给分）申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。

2018丰台一模文科数学试题及答案!

丰台区2018年高三年级第二学期综合练习（一）数学（文科）2018.03第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）复数21i =+ (A) 1i -+(B) 1i -- (C) 1i + (D) 1i -（2）已知命题p ：1x ∃<，21x ≤，则p ⌝为(A) 1x ∀≥，21x > (B) 1x ∃<，21x >(C) 1x ∀<，21x > (D) 1x ∃≥，21x >（3）已知0a b <<，则下列不等式中恒成立的是(A)11a b> (B)<(C) 22a b>(D) 33a b >（4）已知抛物线C 的开口向下，其焦点是双曲线2213y x -=的一个焦点，则C 的标准方程为 (A) 28y x = (B) 28x y =-(C) 2y =(D) 2x =（5）设不等式组05,05x y ≤≤⎧⎨≤≤⎩确定的平面区域为D ，在D 中任取一点(,)P x y 满足2x y +≥的概率是(A)1112 (B)56(C)2125(D)2325 （6）执行如图所示的程序框图，那么输出的a 值是(A) 12-(B) 1-(C) 2(D)12，是开始结束? 输出a侧视图俯视图正视图第6题第7题（7）某三棱锥的三视图如图所示，则该三棱锥的体积为(A)43(B) 4 (C)83(D)（8）设函数π()sin(4)4f x x =+9π([0,])16x ∈，若函数()()y f x a a =+∈R 恰有三个零点1x ，2x ，3x 123()x x x <<，则1232x x x ++的值是(A)π2(B)3π4 (C) 5π4(D) π 第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分。

丰台一模地理答案2018

丰台区2018年高三年级第二学期统一练习（一）参考答案文科综合能力测试地理部分2018.3一、选择题1. D2. C3. C4.D5.B6. B7.A8. C9.A 10. A 11. D二、综合题36.（1）（10分）以开鲁、阿鲁科尔沁旗为中心向四周逐渐增大；大部分地区降水量在345mm～555mm之间；最小值小于345mm，出现在开鲁、阿鲁科尔沁旗附近地区。

（每点2分，共6分）原因：由东南向西北，距太平洋越来越远（1分），受夏季风的影响逐渐减弱（1分），到达的海洋水汽越来越少（1分）；开鲁、阿鲁科尔沁旗附近地区为夏季风的背风坡（雨影区），降水少（1分）。

（2）（8分）时间：春、夏季流量较大，秋、冬季流量较小。

（4分）原因：春季有季节性积雪融水补给，夏季主要为大气降水补给。

（4分）空间：从上游至下游水量渐少。

（2分）原因：流经地区气候干旱，蒸发旺盛；流经沙地下渗强烈；支流汇入少；河流沿岸生产生活用水量大。

（答出3点得6分）（3）（8分）作用：防止漏水、防止跑肥（保水保肥）（2分）生态效益：防风固沙，抑制风沙危害；增加空气湿度，增加降水量，改善区域小气候；增加湿地面积，改善生态环境。

（6分）（4）（10分）传承和保护传统习俗,丰富旅游资源类型；提升旅游资源价值；提高旅游资源知名度；吸引游客,扩大客源市场（或增加旅游业的收入）；完善当地基础设施，提升接待能力和水平。

40. （2）（10分）旧金山地处亚热带大陆西岸，夏季太阳直射点北移，气温较高，受副热带高压带影响，降水少，草色枯黄。

（5分）冬季太阳直射点南移，受来自海洋的盛行西风影响，地形抬升作用明显，气候温和，降水多，绿草茵茵。

（5分）41. （1）（10分）第一产业就业比重平稳下降；第二产业就业比重变化较小；第三产业就业比重波动上升。

第二、三产业就业比重远超第一产业；1997年之后第三产业就业比重超过第二产业。

（6分）第二、第三产业是推动城市化的主要动力。

北京市丰台区2018届高三一模考试语文试题及答案

丰台区2018年高三年级第二学期综合练习（一）语文2018.03 本试卷满分共150分考试时间150分钟注意事项：1.答题前，考生务必先将答题卡上的学校、年级、班级、姓名、准考证号用黑色字迹签字笔填写清楚，并认真核对条形码上的准考证号、姓名，在答题卡的“条形码粘贴区”贴好条形码。

2.本次考试所有答题均在答题卡上完成。

选择题必须使用2B铅笔以正确填涂方式将各小题对应选项涂黑，如需改动，用橡皮擦除干净后再选涂其它选项。

非选择题必须使用标准黑色字迹签字笔书写，要求字体工整、字迹清楚。

3.请严格按照答题卡上题号在相应答题区内作答，超出答题区域书写的答案无效，在试卷、草稿纸上答题无效。

4.请保持答题卡卡面清洁，不要装订、不要折叠、不要破损。

一、本大题共8小题，共24分。

阅读下面的材料，完成1 -8题。

材料一新媒介素养的产生与新媒介的出现及快速发展密不可分。

所以，新媒介素养的内涵首先涉及的是使用者对新媒介的认知问题。

传统媒体无法摆脱的资本和权威，在新媒体时代同样存在，只是以相对民主的形态隐蔽地存在着。

表面上公众自由地操纵手中的媒介，但其注意力却常常成为两大传统权力逻辑的俘虏：资本利益驱使商家借助网络炒作大发横财，权威对信息的控制也依然存在。

此外，新传播技术产生了海量信息，一般的信息难以吸引眼球，而耸人听闻、极度反常和超级娱乐才能引起注意，造成“语不惊人死不休”的后果。

当对信息的选择成为一种“风险”和“赌注”时，公众自身能力的全面提高就显得十分重要。

新媒介需要培养这样的一批使用者，他们能够时刻警醒：所有经过媒介传播的内容都是高度选择和组织的结果；能够冷静选择，拒绝诱惑；能够超然于信息文本之外，多方求证，不盲从盲信。

“媒介即讯息”，原创媒介理论家麦克卢汉的这一命题提醒我们，对媒介形式本身的掌握也是对信息内容的掌握。

基于互联网技术的新传播革命，要求大众既要掌握这种新的信息工具的操作、使用和维护的技能，也要具备利用信息资源的技能，即能从浩瀚的信息海洋中定位自己的价值取向，通过检索、鉴别、使用信息来解决问题和创新思维的能力。

丰台高三一模物理含答案精选文档

丰台高三一模物理含答案精选文档TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-丰台区2018年高三年级第二学期综合练习（一）物理13．分子间的距离减小时（）A．分子势能一定减小B．分子势能一定增大C．分子间引力和斥力郁减小D．分子间引力和斥力都增大14．光照在某金属表面上发生了光电效应。

若只减弱光的强度，而保持频率不变，则（）A．有可能不发生光电效应B．逸出的光电子的最大初动能将减小C．单位时间内从金属表面逸出的光电子数将减少D．从光照射到金属表面到有光电子逸出的时间明显增加15．P、Q是简谐横波传播方向上的两个质点．它们的平衡位置间的距离为。

此波波速为1m/s．振幅为4cm，周期为。

在t=0时刻，P点位于平衡位置上方最大位移处。

贝Q点（）A．在时的速度最大B．在时的加速度最大C．在时的位移为4cm D．在时的位移为-4cm16．2018年2月12日我同以“一箭双星”方式成功发射“北斗三号工程’的两颗组网卫星。

已知某北斗导航卫星在离地高度为21500千米的圆形轨道上运行，地球同步卫星离地的高度约为36000干米。

一带负电的粒子（不考虑重力）由静止开始，从连线的中垂线上P点运动O点。

如图所示，粒子A沿垂直于磁场的方向射入匀强磁场中，其轨迹为圆弧MP，衰变后产生的植子B的轨迹为圆弧PN，两轨迹在P点相切，且半径之比为R A：R B=2：1，粒子C 的轨迹未画出。

2018丰台高三地理一模(word)(答案)

丰台区2018年高三年级第二学期综合练习（一）文科综合2018. 03第一部分（选择题共140分）本部分共35小题，每小题4分，共140分。

在每小题列出的四个选项中，选出最符合题目要求的一项。

2018年春晚的四大分会场（三亚、珠海、泰安和曲阜、黔东南）以众星拱月之势与北京主会场共同演绎着新春大联欢。

据此回答第1、2题。

1．四个分会场中，A．泰安市的名山属于褶皱山 B．黔东南地处我国地势的第三级阶梯C．珠海市位于珠江口的东侧 D．三亚市所在省区管辖海域面积最大2.黔东南分会场歌舞表演的主题最可能是A．南海风情，讲述春天故事 B．海晏河清，祈愿国泰民安C．展现苗侗文化，助推脱贫致富 D．铸航天强国梦，续海上丝路情2018年2月28日，北京局部有零星小雪，东北大部出现强降雪天气。

图1为该日14时亚洲部分地区海平面气压形势图（单位：hpa）。

读图,回答第3、4题。

图13．此时，A. 江西省可能会发生滑坡泥石流B. 海南岛东部沿海受风暴潮袭击C. 北京降雪规模小的原因主要是锋前暖气团较干燥D. 吉林省西部出现暴雪的原因是正处于暖锋的锋后4．图中P 锋面系统过境前后,天气变化与下图相符的是肯尼亚山位于东非高原，是距离赤道最近的雪山。

图2为非洲肯尼亚山植被的垂直分布示意图。

读图，回答第5、6题。

100020003000降水量蒸发量(mm)10002000300040005000海拔(m)可能蒸发量降水量①⑥③②④⑤⑦SE NW热带草原竹林6000森林灌丛高山沼泽冰雪图25. 图中降水量与可能蒸发量最大差值处的海拔约为A. 1500mB. 2200mC. 2700mD. 5000m 6.肯尼亚山A.①地自然带分布属于地带性规律B.②地植被为山地雨林C.③地受人类活动影响强度最大D.地处板块消亡边界A.地形复杂，气候类型多样 B ．纬度较低，水热条件充足C.政策支持，市场需求量大 D ．技术成熟，种植经验丰富 8.西南地区A.冬作马铃薯比小春马铃薯种植区的海拔高B.早春马铃薯种植区主要分布在低热河谷A B C DC.早春马铃薯比大春马铃薯种植区的海拔低D.秋作马铃薯所在种植区只能一年一熟 9.与图中大春马铃薯种植条件最接近的是Ａ. 松嫩平原Ｂ.成都平原Ｃ.太湖平原Ｄ. 珠江三角洲我国某通信设备制造商的业务涵盖了移动、宽带、IP 、光网络、电信增值业务和终端等众多领域。

【高三数学试题精选】2018年高三文科一模数学试卷(丰台区带答案)

2018年高三文科一模数学试卷（丰台区带答案）
5 c 丰台区1,0,1,2},则集合( ) 等于
(A) {-2,-1} (B) {-2,-1,0,1,2}
(c) {-2,-1,2} (D)
3 设为等比数列的前项和，，则（）
(A) 2 (B) 3 (c) 4 (D) 5
4执行右边的程序框图所得的结果是
（A）3 （B）4 （c）5 （D） 6
5 已知椭圆的一个焦点与抛物线的焦点重合，则该椭圆的离心率是
（A）（B）（c）（D）
6已知命题p ,命题q ,则下列命题为真命题的是
(A) (B)
(c) (D)
7．某四面体三视图如图所示，则该四面体的四个面中，直角三角形的面积和是
(A) 2 (B) 4 (c) (D)
8如果函数=f(x)图像上任意一点的坐标（x,）都满足方程，那么正确的选项是
(A) =f(x)是区间（0，）上的减函数，且x+
(B) =f(x)是区间（1，）上的增函数，且x+
(c) =f(x)是区间（1，）上的减函数，且x+
(D) =f(x)是区间（1，）上的减函数，且x+
二．填空题
9 若，则 = 。

10 某校从高一年级学生中随机抽取100名学生，将他们期中考试的数学成绩（均为整数）分成六段[40,50)，[50,60)，…，[90,100]后得到频率分布直方图(如图所示)．则分数在[70,80)内的人数是。

北京市丰台区2018届高三下学期3月综合练习(一模)数学(文)试题 Word版含解析

丰台区2018年高三年级第二学期综合练习（一）数学（文科）第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1. 复数A. B. C. D.【答案】D【解析】复数故答案为：D.2. 已知命题p：x <1，，则为A. x ≥1,B. x <1,C. x <1,D. x ≥1,【答案】C【解析】根据全称命题与存在性命题之间的关系，可知命题的否定为，故选C．3. 已知，则下列不等式中恒成立的是A. B. C. D.【答案】A【解析】构造函数是减函数，已知,则，故A正确;,故B 不正确；C构造函数是增函数，故，故选项不正确；D. ，构造函数是增函数，故，所以选项不正确.故答案为：A.4. 已知抛物线的开口向下，其焦点是双曲线的一个焦点，则的标准方程为A. B. C. D.【答案】B【解析】双曲线的一个焦点为，故抛物线的焦点坐标也是，从而得到方程为.故答案为：B.5. 设不等式组确定的平面区域为，在中任取一点满足的概率是A. B.C. D.【答案】D【解析】不等式组确定的平面区域为是正方形，满足，即在直线上方的部分，根据几何概型的计算公式得到.故答案为：D.6. 执行如图所示的程序框图，那么输出的值是A. B.C. D.【答案】D【解析】根据题意得到当a=2,n=2A=由此可看出周期为3，当n=2018时输出结果，此时a=.故答案为：D.7. 某三棱锥的三视图如图所示，则该三棱锥的体积为A. B.C. D.【答案】A【解析】根据三视图可知原图是个三棱锥，右侧面垂直于上底面，体积为：故答案为：A.点睛：思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.8. 设函数，若函数恰有三个零点，，，则的值是A. B. C. D.【答案】B【解析】函数，故根据题意得到化简得到=.故答案为：B.点睛：函数的零点或方程的根的问题，一般以含参数的三次式、分式、以e为底的指数式或对数式及三角函数式结构的函数零点或方程根的形式出现，一般有下列两种考查形式：(1)确定函数零点、图象交点及方程根的个数问题；(2)应用函数零点、图象交点及方程解的存在情况，求参数的值或取值范围问题．研究方程根的情况，可以通过导数研究函数的单调性、最值、函数的变化趋势等，根据题目要求，通过数形结合的思想去分析问题，可以使得问题的求解有一个清晰、直观的整体展现。

北京市丰台区2018届高中高考一模英语试卷试题一包括答案

北京市丰台区2021届高考一模英语试题(一)含答案第一局部：英语知识运用〔共两节, 总分值 45 分〕第一节：单项填空〔共15 小题，每题 1 分，总分值15 分〕从 A 、 B、 C、D 四个选项中，选出可以填入空白处的最正确选项，并在答题卡上将该项涂黑。

1．— Mr Green, can you spare me a few minutes? I still have some questions about your assignment ．—.A ． It s a pleasure B． Not at allC． Help yourself D． Sure, go ahead2．We live in _______ rapidly changing world and must learn to adapt if we are to succeed in_______ future．A ． a; 不填 B． the; the C． the; 不填 D． a; the3． The landlord wants to ______ the rent by $30 a month, which I think is unacceptable．A ． make up B． take up C． cut up D． put up 4．—Look, where are you going?— I can't ______ the map and drive at the same time, can I?A ． watch B． readC． see D． notice5． _______ the opportunity to speak at the graduation ceremony made him overjoyed ．A ． Being offered B． To offer C． Having offeredD． Offered6．All are welcome to join the Yoga Club _______ age or sex ．A ． because of B． regardless of C． in case of D． in termsof7．The locals think highly of what ______ to bring housing prices to reasonable levels in the past two years．A ． has been done B． has doneC． was being done D． was done8． The conference will be open to ______ shows interest in this research ．A ． whomeverB ． whoeverC． no matter who D ．no matter whom9． You are always throwing things about ． How ______ I know where you've left your key?A ． may B． wouldC． should D． might10．Although Hurricane Sandy has gone, it will be months ______ the damage is cleared up．A ． since B． thatC． when D． before11． ______ an effective learner, you must have good study strategies ．A ． To be B． BeingC． Having been D． To have been12．Baggage Reclaim is a place at an airport ______ you collect your baggage after arriving．A ． that B． whenC． where D． which13． It is unclear what caused the accident, but the police believe that the driver_______alcohol．A ． has drunk B． had drunk C． would drink D． drank14．— Beautiful sunshine! I hope to stay here longer ．— ______ ．Shall we put off our flight?A ． So am I B． So do IC． So is it D． So I do15．— I'm leaving for Thailand on vacation tomorrow．—.A ． So long B． CheersC． Have fun D． Best wishes第二节完型填空〔共20小题；每题1．5 分，总分值30 分〕阅读下面短文，从短文后各题所给的四个选项〔 A 、B 、 C 和D〕中，选出最正确选项，并在答题卡上涂黑。