2015基础讲义(下)
2015初中数学基础知识讲义—有理数

一、正数和负数的定义0的数叫做正数。
根据需要有时在正数前面加上正号“+”,但是正数前面的正号“+”,一般省略不写。
-”的数叫做负数。
负数前面的负号“-”不能省略。
eg :-a 不一定是负数,因为字母a 可以表示任何数,当a 是正数时,-a 是负数;当a 表示负数时,-a 则是一个正数,而不是负数;当a 表示0时,-a 就是在0前面加上一个负号,仍是0,0不分正负。
(2)具有相反意义的量正数和负数表示具有相反意义的量。
若用正数表示某种意义的量,则负数就表示与其相反的量,反之亦然。
常见的表示相反意义的量:零上和零下、前进和后退、海平面以上和海平面以下、收入和支出、向南和向北、盈利和亏损、升高和下降。
(3)0的意义(重点理解)0℃是一个确定的温度,海拔0表示海平面的平均高度。
0的意义已经不仅是表示“没有”。
1、(2013山东德州)-1, 0, 0.2,71, 3 中正数一共有 个2、(2013广西玉林市)既不是正数也不是负数的数是3、(2013浙江丽水)如果零上2℃记作+2℃,那么零下3℃记作( ) A .-3℃ B .-2℃ C .+3℃ D .+2℃4、(2014浙江宁波)杨梅开始采摘啦!每框杨梅以5千克为基准,超过的千克数记为正数,不足的千克数记为负数,记录如图,则这4框杨梅的总质量是( )(1)正整数、0 注:(1)正整数、0 (2 (3)对于小数,只有能化成分数的小数才是有理数。
初中数学基础知识讲义—有理数按数的种类分 按有理数的性质分有理数⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数正整数整数0 有理数⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数正分数正整数正有理数0注:(1)有理数的分类必须按同一标准,不漏、不重。
(2)0 (3)0(4)0 (5)01、下列个数中:1330.70125---,,,,,中负分数有 个;负整数有 个;自然数有 个2、(宁波)下列各数是正整数的是( ) A .-1 B .2 C .0.5D .133、(上海)如下列分数中,能化为有限小数的是( ) (A) 13 (B) 15; (C) 17; (D)194、(东阳县)73是( ) A.负整数 B .有理数 C .整数D .负数三、数轴的概念(1)规定了原点,正方向,单位长度的直线叫做数轴。
2015考研高数基础模块精讲讲义-汤家凤

则ak 1 1 ak 1 lim an 存在
n
1 5 1 5 2 1 5 ( ) 2 2 2 {an }单调减少且有下界
9
PartⅡ 连续与间断 一、Defs 1、连续
�f ( x)在x a处连续 若 lim f ( x) f (a ), 得f ( x)在x a处连续
x、 arctan x 任两之差位三阶无穷小
ln ln(1 ) ~
x、 sin x 、 tan x 、 arcsin
e x cos x 例1. lim x 0 x ln(1 x ) (e x 1) (1 cox) 解:I lim x 0 x2 1 x2 x2 2 lim x 0 x2 3 2
n
型三
左、右极限
�分段函数 x(xb) a �若f ( x)中含 ( x ) a b x
例1. f ( x) e
x2 x2 x 2
( x b)
, lim f ( x) ?
解:f (2 0) 0 f (2 0) lim f ( x)不存在
1
4 10 (1 2 ) 2 1 x x lim x 1 x (1 4t 10t ) 1 t a ∵ (1 x) 1 ~ ax( x 0) lim
t 1 2 2
∴ (1 4t 10t 2 ) 2 1 ~ 2t 5t 2 ~ 2t ∴I 2
xa
分类:
第一类间断点:f (a 0), f (a 0)存在 f (a 0) f (a 0)( f (a )), a为可去间断点 f (a 0) f (a 0), a为跳跃间断点 第二类间断点:f (a 0), f (a 0)至少一个不存在 例1. f ( x) x
郑晓博基础班讲义全

郑晓博基础班讲义全第⼀章财务管理基本原理知识结构与考点分析⼀、企业的组织形式(⼀)企业的三种组织形式(⼆)公司制企业的优点和缺点公司的优点:(1)有限责任制度,降低了风险;(2)⽆限存续,降低了风险;(3)所有权便于转让,提⾼了流动性。
以上三个因素,使公司容易从资本市场上筹集资⾦。
⼆、财务管理的主要内容(⼀)理解“长期投资”提⽰:个⼈/机构投资者的投资是证券投资。
(投资的对象是股票/债券等⾦融资产)投资的⽅式是直接投资:在投资后继续实际控制实物资产,直接控制投资回报提⽰:个⼈/机构投资者的投资是间接投资:通过契约或更换代理⼈间接控制投资回报投资的⽬的是获取经营活动所需的实物资源,并运⽤资源赚取营业利润。
提⽰:不是为了再出售获利。
补充知识:股权投资的判断⽆论是对⼦公司的投资、还是对合营企业、联营企业的投资,都属于经营性投资,⽬的都是从被投资⽅的经营中获得利益。
对⼦公司、合营企业、联营企业的投资,都属于经营性投资。
(⼆)理解“长期筹资”区分投资和融资直接投资是公司继续控制实物资产,直接控制投资回报。
间接投资是通过契约或者更换代理⼈间接控制投资回报。
直接融资是指不通过⾦融中介,直接在资本市场上进⾏的融资。
间接融资是指通过⾦融中介(尤其是银⾏)进⾏的融资。
(三)理解“营运资本管理”三、财务管理的基本职能财务分析和财务预测是财务决策和财务计划的基础条件,财务决策和财务计划是财务分析和财务预测的延续。
(⼀)财务分析(⼆)财务预测(三)财务决策(相当于单选题/多选题)(四)财务计划(相当于计算题)【提⽰】点击上⾯的”随堂练习”即进⼊相关的试卷。
第⼆节财务管理的⽬标与利益相关者的要求⼀、财务管理的基本⽬标1.利润最⼤化的观点2.每股收益最⼤化的观点每股收益=归属普通股股东净利润÷流通在外普通股加权平均数3.股东财富最⼤化的观点总结:财务管理⽬标的三种观点4.股东财富最⼤化的测量理解股东财富最⼤化的测量股价最⼤化的说法理解股东财富最⼤化的测量5.企业价值最⼤化理解股东财富最⼤化的测量知识总结【历年真题2009年多选题】下列有关企业财务⽬标的说法中,正确的有()。
2015届高考数学总复习 基础知识名师讲义 第三章 第六节函数y=Asin(ωx+φ)的图象及三角函数模型的应用 理

第六节 函数y =Asinx知识梳理一、三角函数图象的作法1.几何法(利用三角函数线).2.描点法:五点作图法(正、余弦曲线),三点二线作图法(正切曲线).(1)正弦函数和余弦函数的图象:正弦函数y =sin x 和余弦函数y =cos x 的图象的作图方法(用五点法):先取横坐标分别为0,π2,π,3π2,2π的五点,再用光滑的曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象.再将一个周期内的图象向左右平移2k π(k ∈N *)个单位长度,即得函数的整个图象.(2)正切函数的图象:作正切曲线常用三点二线作图法. 正弦函数、余弦函数、正切函数的图象:1.能画出y =sin x ,y =cos x ,y =tan x 的图象. 2.了解函数y =A sin(ωx +φ)的物理意义;能画出y =A sin(ωx +φ)的图象,了解参数A ,ω,φ对函数图象变化的影响.3.了解三角函数是描述周期变化现象的重要函数模型,会用三角函数解决一些简单的实际问题.图象与x 轴的交点:正弦函数为________,k ∈Z ,余弦函数为________,k ∈Z ,正切函数为________ ,k ∈Z .答案:2.(2)(k π,0) ⎝ ⎛⎭⎪⎫k π+π2,0 (k π,0)二、三角函数图象的对称轴与对称中心正弦曲线y =sin x 的对称轴为x =________(k ∈Z ),对称中心为________(k ∈Z ); 余弦曲线y =cos x 的对称轴为x =________(k ∈Z );对称中心为________,(k ∈Z ); 正切曲线y =tan x 的对称中心为________(k ∈Z ).其中,正弦函数与余弦函数在对称轴与曲线交点处有最大(小)值.答案:k π+π2 (k π,0) k π ⎝ ⎛⎭⎪⎫k π+π2,0 ⎝ ⎛⎭⎪⎫k π2,0三、函数y =A sin(ωx +φ)图象的画法1.五点法作y =A sin(ωx +φ)(A >0,ω>0)的简图.设X =ωx +φ,由X 取0,π2,π,3π2,2π来求相应的x 值及对应的y 值,再描点作图.2.正弦型函数y =A sin(ωx +φ)+B (其中A >0,ω>0)的一些结论:最大值是A +B ,最小值是B -A ,周期是T =2πω,频率是f =ω2π,相位是ωx +φ,初相是φ(即当x =0时的相位);其图象的对称轴是直线ωx +φ=k π+π2(k ∈Z ),凡是该图象与直线y =B 的交点都是该图象的对称中心.对于y =A sin(ωx +φ)和y =A cos(ωx +φ)来说,对称中心与零点相联系,对称轴与最值点相联系.3.利用图象变换作三角函数的图象.三角函数的图象变换有振幅变换、周期变换和相位变换等,重点掌握函数y =A sin(ωx +φ)+B 的作法.(1)________或叫做沿y 轴的伸缩变换:由y =sin x 的图象上的点的横坐标保持不变,纵坐标伸长(当|A |>1)或缩短(当0<|A |<1)到原来的________倍,得到y =A sin x 的图象.(2)________或叫做沿x 轴的伸缩变换:由y =sin x 的图象上的点的纵坐标保持不变,横坐标伸长(0<|ω|<1)或缩短(|ω|>1)到原来的________倍,得到y =sin ωx 的图象.(3)________或叫做左右平移:由y =sin x 的图象上所有的点向左(当φ>0)或向右(当φ<0)平行移动________个单位长度,得到y =sin(x +φ)的图象.(4)上下平移:由y =sin x 的图象上所有的点向上(当B >0)或向下(当B <0)平行移动______个单位长度,得到y =sin x +B 的图象.4.由y =A sin(ωx +φ)的图象求其解析式.给出图象确定解析式y =A sin(ωx +φ)的题型,一般从寻找“五点”中的第一零点⎝ ⎛⎭⎪⎫-φω,0作为突破口,要从图象的升降情况找准第一个零点的位置.答案:3.(1)振幅变换 |A | (2)周期变换 ⎪⎪⎪⎪⎪⎪1ω (3)相位变换 |φ| (4)|B |基础自测1.(2013·唐山模拟)函数y =sin 3x 的图象可以由函数y =cos 3x 的图象( )A .向左平移π3个单位得到B .向右平移π3个单位得到C .向左平移π6个单位得到D .向右平移π6个单位得到解析:因为sin 3x =cos ⎝ ⎛⎭⎪⎫π2-3x =cos ⎝⎛⎭⎪⎫3x -π2= cos ⎣⎢⎡⎦⎥⎤3⎝⎛⎭⎪⎫x -π6.所以函数y =cos 3x 的图象向右平移π6个单位即可得到函数y =sin 3x 的图象,故选D.答案:D2.(2013·聊城模拟)函数y =cos ⎝⎛⎭⎪⎫2x -π3的部分图象可能是( )解析:因为y =cos ⎝⎛⎭⎪⎫2x -π3,所以当2x -π3=0,即x =π6时,函数取得最大值1,结合图象看,可使函数在x =π6时取得最大值的只有D. 答案:D3.(2012·广东金山中学综合测试)如果函数y =3cos(2x +θ)的图象关于点⎝ ⎛⎭⎪⎫4π3,0成中心对称,那么|θ|的最小值是________.解析:对称中心的横坐标满足2x +θ=k π+π2(k ∈Z ),当x =4π3时,解得θ=k π-13π6,当k =2时,|θ|最小,最小值为π6. 答案:π64.函数f (x )=A sin(ωx +φ)(A ,ω,φ是常数,A >0,ω>0)的部分图象如图所示,则f (0)=______.解析:由图可知A =2,T 4=712π-π3=π4,ω=2,2×7π12+φ=2k π+3π2,φ=2k π+π3, ∴f (x )=2sin ⎝⎛⎭⎪⎫2x +2k π+π3(k ∈Z ), ∴f (0)=2sin ⎝ ⎛⎭⎪⎫2k π+π3=62. 答案:621.(2013·四川卷)函数f (x )=2sin(ωx +φ),ω>0,-π2<φ<π2的部分图象如图所示,则ω,φ的值分别是( )A .2,-π3B .2,-π6C .4,-π6D .4,π3解析:34T =5π12-⎝ ⎛⎭⎪⎫-π3,T =π,∴ω=2,∴2×5π12+φ=2k π+π2,k ∈Z ,∴φ=2k π-π3,又φ∈⎝ ⎛⎭⎪⎫-π2,π2,∴φ=-π3,选A. 答案:A2. 已知函数f (x )=sin(π-ωx )cos ωx +cos 2ωx (ω>0)的最小正周期为π. (1)求ω的值;(2)将函数y =f (x )的图象上各点的横坐标缩短到原来的12,纵坐标不变,得到函数y =g (x )的图象,求函数y =g (x )在区间⎣⎢⎡⎦⎥⎤0,π16上的最小值.解析:(1)因为f (x )=sin(π-ωx )cos ωx +cos 2ωx ,所以f (x )=sin ωx cos ωx +1+cos 2ωx2=12sin 2ωx +12cos 2ωx +12=22sin ⎝⎛⎭⎪⎫2ωx +π4+12.由于ω>0,依题意得2π2ω=π,所以ω=1.(2)由(1)知f (x )=22sin ⎝⎛⎭⎪⎫2x +π4+12,所以g (x )=f (2x )=22sin ⎝⎛⎭⎪⎫4x +π4+12.当0≤x ≤π16时,π4≤4x +π4≤π2,所以22≤sin ⎝ ⎛⎭⎪⎫4x +π4≤1⇒12≤22sin ⎝ ⎛⎭⎪⎫4x +π4≤22⇒1≤22sin ⎝ ⎛⎭⎪⎫4x +π4+12≤1+22,故g (x )在区间⎣⎢⎡⎦⎥⎤0,π16上的最小值为1.1.(2013·广州二模)若函数y =cos ⎝ ⎛⎭⎪⎫ωx +π6(ω∈N *)的一个对称中心是⎝ ⎛⎭⎪⎫π6,0,则ω的最小值为( )A .1B .2C .4D .8解析:因为函数y =cos ⎝ ⎛⎭⎪⎫ωx +π6(ω∈N *)的一个对称中心是⎝ ⎛⎭⎪⎫π6,0,所以cos ⎝⎛⎭⎪⎫ω×π6+π6=0,∴ω×π6+π6=k π+π2,k ∈Z ,即ω=6k +2,k ∈Z . 再由ω为正整数可得ω的最小值为2,故选B. 答案:B2.(2012·长春调研)函数y =sin(ωx +φ)ω>0,且|φ|<π2在区间⎣⎢⎡⎦⎥⎤π6,2π3上单调递减,且函数值从1减小到-1,那么此函数图象与y 轴交点的纵坐标为( )A.12B.22C.32D.6+24解析:因为函数的最大值为1,最小值为-1,且在区间⎣⎢⎡⎦⎥⎤π6,2π3上单调递减,又函数值从1减小到-1,可知2π3-π6=π2为半周期,则周期为π,ω=2πT =2ππ=2,此时原式为y =sin(2x +φ).又由函数过点⎝ ⎛⎭⎪⎫π6,1,代入可得φ=π6,因此函数为y =sin ⎝⎛⎭⎪⎫2x +π6,令x =0,可得y =12.答案:A。
2015一建陈印-讲义法规

第八章解决建设工程纠纷法律制度(18 分)【基本框架】【模拟题】以下属于行政纠纷的是()。
A.施工单位为文化局建设家属院被拖欠工程款B.税务局扩建办公楼挤占了某居民小区出行通道C .投标人不服招标行政监督部门对其投诉作出不予受理的决定D. 建设单位不服建设行政主管部门对工程合同争议进行的调解【答案】C (行政纠纷是因行政机关“具体行政行为”引发的纠纷)【模拟题】当事人双方在合同中约定解决争议的方法可以是调解、也可以是仲裁或诉讼。
当纠纷发生后,若一方坚决不同意调解,此时争议解决方式为()。
A.和解B. 调解C. 诉讼D. 仲裁【答案】C (调解为自愿进行的非终局解决方式。
仲裁、诉讼均为终局性解决方式。
同时约定两个终局手段的,法律规定,不能仲裁只能起诉)【2013一级真题】下列法律文书中,不具有强制执行效力的是()。
A.在仲裁程序中形成的仲裁调解书B.由行政主管部门主持达成的调解书C.人民法院在民事案件审理中制作的调解书D.经司法确认的人民调解委员会主持达成的调解协议【答案】B【2012(10 )二级真题★】根据《仲裁法》,可以进行仲裁的是()。
A.行政不作为纠纷B.工程质量纠纷C.涉外婚姻纠纷D.施工企业工资纠纷【答案】B 【解析】平等主体的公民、法人和其他组织之间发生的合同纠纷和其他财产权益纠纷,可以仲裁。
但劳动争议(伙计~老板)和农业承包合同纠纷(村民~村委会)的仲裁,不适用仲裁法。
下列纠纷不能仲裁:(一)婚姻、收养、监护、扶养、继承纠纷(家里人~家里人);(二)依法应当由行政机关处理的行政争议(民~官)。
【模拟题】下列对仲裁的理解正确的有()。
A.《仲裁法》的调整范围不包括劳动争议仲裁B.仲裁机构的审理过程和裁决结果,非经当事人同意,不得公开C.仲裁机构的审理活动独立于当地的行政机关D•仲裁庭的组织形式,由仲裁委员会主任指定E.仲裁实行一裁终局制度【答案】ABCE【模拟题】以下不属于行政复议基本特点的是()。
2015线性代数辅导讲义 答疑整理【日期更新至5.26】

学生问:2015线性代数辅导讲义,P2,评注2,第6页括号五,特征多项式公式,这两个地方没看明白,主要是不清楚行列式是怎么拆分的,以及怎么合并成特征多项式公式的,谢谢老师解答! 老师答:111213212223313233000000a a a a a a a a a λλλ--------- 行列式的性质将第1列拆开, 121322233233000000a a a a a a λλλ--=--+--1112132122233132330000a a a a a a a a a λλ--------- 这两个矩阵分别再对第2列拆开,得四个行列式,再分别对四个行列式的第3列拆开, 得8个行列式,就是第二页的所给结果,这8个三阶行列式前7个都很好计算,(主对角线性,一列只有一个非零元素展开)。
按行也可以得出一样的结果,要点就是一行(列)元素拆成两元素之和,其他行(列)元素保持不变。
学生问:老师你好,我想问一下,2015线性代数辅导讲义,P6,(3),1.10的推倒过程中前两个式子为什么相等~~~ 老师答:这三个式子是相等的, 前两式子分别等于第3个,传递性知前两个式子相等。
学生问:2015线性代数辅导讲义,P6,关于副对角线的行列式从第一不到第二步看不懂,是怎样化的能详细点吗?副对角线跟主对角线有什么区别呢?谢谢老师。
老师答:这儿的两式子没有推导关系,只是结果相等的关系。
根据行列式的定义或展开计算得出1.8的结果。
副对角线行列式的结果不只是对角线上元素乘积,还有与阶数有关的符号。
学生问:2015线性代数辅导讲义,(1)P8,图片画线处前后两个等号不理解,不知道怎么来的,以及后面那个行列式怎么的出来(2)P4,为什么D1=4老师答:这个行列式用常数12,,,n b b b , 换掉前面系数行列式中第j 列的元素得到的行列式,记为j D ,行列式按第j 列展开的计算式就是画线的式子。
4页,这就是第一行第一列一个元素的行列式。
【2015直通中考】中考物理复习讲义 物理复习基础知识归纳与题型训练 第2节 质量与密度 (含答案解析)

中考物理复习讲义之基础知识归纳与题型训练第2节 质量与密度一、物质的质量1.质量:表示物体所含物质的多少。
质量是物体本身的一种属性,它的大小与形状、状态、位置、温度等无关;物理量符号:m ;单位:kg 、t 、g 、mg 。
1t=103kg, 1kg=103g, 1g=103mg.2.常见质量数据:成年人50-70kg ,一个鸡蛋50g (5×10-2 kg ),教室空气200-300kg ,科学课本200g ,一枚硬币 (1元)6g (6×10-3 kg ),一枚大头针约80mg(8.0×10-5 kg ) 一个苹果约 150g (1.5×10-1 kg ) 一头大象约 6t 一只鸡约2kg3.质量的测量(1)测量工具:生活中:案秤、台秤、杆秤;实验室:天平,也可用弹簧测力计测出物重,再通过公式m=G/g 计算出物体质量。
(2)原理:杠杆原理(杠杆平衡条件)(3)天平测量质量的步骤: ①观察天平的称量和标尺上的分度值;把天平放在水平台上。
②把游码放到标尺左端的零刻线处(归零),调节横梁右端的平衡螺母,使天平平衡(指针指向分度盘的中线处或左右摆动幅度相等,这时横梁平衡)。
③把物体放到左盘,用镊子向右盘里加减砝码,并调节游码,使天平横梁平衡。
添加砝码从估计称量物的最大值加起,逐步减小;④读数:砝码的总质量加上游码对应的刻度值(被测物体的质量=盘中砝码总质量+ 游码在标尺上所对的刻度值)。
【提醒要点】①要正确认识天平的称量和感量。
天平的最大称量(即量程)是天平能够称的最大质量。
感量(即分度值)是指天平能分辨的最小质量,它表示天平的灵敏程度。
②天平的调节技巧:在调节天平平衡时,不管怎样,天平左、右两边的平衡螺母都向更高的托盘这边移动。
③称量时添加砝码的原则:在估计了被测物体的质量后,应先加大砝码后加小砝码,即按“先大后小”的顺序加砝码。
④天平平衡的标志分为两种情况,一种是静态平衡,一种是动态平衡。
2015考研数学基础概率习题讲义

p2 P{Y 5} ,则 (
). B. 对任何实数 都有 p1 p2 D. 对任何实数 都有 p1 p2
A. 对任何实数 都有 p1 p2 C. 仅对 的个别值有 p1 p2
8.设随机变量 X 服从标准正态分布,其密度函数为 ( x ) ,分布函数为 ( x ) ,则对任意实数 a 有 ( ). A. ( a) 1 ( x ) dx C. ( a) (a )
a 0
1 a ( x )dx 2 0 D. ( a) 2 (a) 1
B. ( a )
4x3 , 0 x 1 9.设随机变量 X 的密度函数为 f ( x) ,则使 P( X a ) P( X a ) 成立的常数 其它 0,
a (
P( A B C ) 9 / 16 ,则 P( A)
. .
4. 设 A 、 B 为事件, P( A) 0.6,P( A B) 0.3 ,则 P ( AB ) 5. 设事件 A 与 B 相互独立,已知 P ( A) 0 .5 , P ( A B ) 0.8 ,则
B. A 与 B 不互斥 D. A 与 B 互斥
B. P ( B | A ) 0 D. B A ). B. P( A) P( AB) D. P( A) P( AB) ).
9. 设 A 和 B 为任意两个事件,且 A B , P ( B) 0 ,则必有 ( A. P( A) P( A| B) C. P( A) P( A| B)
0 1/3
1 1/6
2 1/2
(2) P{ X } 、 P{1 X } 、 P{1 X } . 12. 从学校乘汽车到火车站的途中有三个交通岗,假定在各个交通岗遇到红绿信号灯的事件是相互 独立的,且概率都是 2/5.设 X 表示途中遇到红灯的次数,求 X 的分布律、分布函数. 13.已知某种型号的雷管在一定刺激下发火率为 4/5,今独立重复地作刺激试验,直到发火为止,则 消耗的雷管数 X 是一离散型随机变量,求 X 的概率分布. 14.在某公共汽车站甲、乙、丙三人分别独立地等 1,2,3 路汽车,设每个人等车时间(单位:分 钟)均服从[0,5]上的均匀分布,求三人中至少有两个人等车时间不超过 2 分钟的概率. 15. 设随机变量 X 的概率密度为 f ( x ) ,求下列随机变量 Y 的概率密度:
4-人身保险及产品基础知识(2015年5月版)讲义.

行片面比较
26
平安现有主要人寿保险产品
细分类
产品名称
普通型人寿保险
平安幸福定期寿险(A,2004)、平安附加定期寿险(2004)、 平安附加豁免保障成本定期寿险、平安平安福终身寿险
年金保险
平安保险金转换年金保险(2004)、 平安附加少儿高中教育年金 保险(分红型,2004)、平安附加少儿大学教育年金保险(分红 型,2004)
10
• 新型人寿保险
1、万能保险
万能保险保单持有人在交纳一定量的首期保费后,可以按照自己的意愿 选择任何时候交纳任何数量的保费。只要保单的现金价值足以支付保单 的相关费用,有时甚至可以不再交费。主要有以下基本特征:
• 死亡给付模式——A方式:均衡给付(给付额因定) B方式:随现金价值变化
• 保费交纳——在规定幅度内交费任意 • 结算利率——最低保证利率 • 费用收取——初始费用、风险保险费、保单管理费、手续费、 退
• 简易人寿保险
简易人寿保险是一种低保额、免体检、适应一般低工资收 入人群需要的人寿保险。简易人寿保险的交费期较短,通 常为月、半月、周。
9
• 团体人寿保险
团体人寿保险是用一张总的保险单对一个团体的成员及 其生活依赖者提供人寿保险保障的保险。主要有以下基 本特征:
• 风险选择对象——团体(性质、职工、人数、保额) • 使用团单——1张总保单,每个被保险人1张保险证 • 成本低——手续简、节约佣金、免体检、避免逆选择 • 计划灵活——条款及内容可以和保险人协商 • 采用经验费率——理赔记录决定费率
• 人身意外伤害保险的含义 • 人身意外伤害保险的特征 • 人身意外伤害保险的可保风险分析 • 人身意外伤害保险的主要种类 • 平安现有主要意外保险产品
伤寒论》讲义(下)----刘渡舟

伤寒论》讲义(下)----刘渡舟伤寒论》讲义(下)----刘渡舟清心2015-05-25 23:27 来自QQ空间日志第十讲四逆汤类方的临床应用四逆汤类方指以下两类:1.生附子、干姜同用,如四逆、通脉四逆、四逆加人参、白通加猪胆汁汤-回阳救逆。
2.炮附子为主,如附子汤、真武汤-温里祛寒。
[回阳救逆类方]:一、四逆汤:生附子、干姜、甘草。
《伤寒论》凡与干姜同用均是生附子,起回阳救逆作用。
仅乌梅丸例外,为干姜炮附子同用以温脾散寒,温里祛寒。
四逆汤适应症:1.畏寒蜷卧、冷汗自出(阳不摄阴),手足厥冷,四肢痛。
-肾阳虚衰,肌肤四末失温,阳不摄阴。
2.下利清谷,自利而渴,吐利不止,内拘急(腹痛)。
下利及清谷为两个并列的动宾词组。
清当便排拉讲。
清谷,拉不消化的食物。
……肾阳虚衰,火(命门火)不暖土,腐熟无权。
自利不渴者属太阴-寒湿下注,升降紊乱,无伤津,与热痢相区别;自利而渴者属少阴-肾阳虚衰,气化失司,津液不化,见喜热饮而不多饮。
(提示:结石并非均用利湿通淋,阳气虚衰,津液不化亦可结成结石,并郁而化热。
其根本问题是寒湿,王永炎肾结石,通阳法-附子10g肉桂20g。
用药可能会心烦气燥等的副作用)以下利为主,不是以呕吐,肾阳虚衰阴寒内凝-腰痛。
小便利-清长-阳虚不能摄阴,重则尿比重下降;小便不利-少-阳虚气化失司。
3、精神症状(1).但欲寐-精神萎靡不振,似睡非睡,睡不实,似醒非醒,醒不清。
(2).燥烦-肢体燥扰不宁。
燥烦的病机a.阴精阳气虚衰,心神精神失养。
b.真阳衰微,弱阳勉强和盛阴相争,争而不胜-肢体躁动不宁的表现,而不自知,甚则撮空理线,循衣摸床,均属阴盛则燥。
如肝性肺性脑病,休克前期躁动属阴盛则燥。
阳盛则烦,如大青龙汤阳热扰心,大承气汤实热扰心,栀子豉汤无形郁热。
4、脉象:脉沉(轻者)-脉微细,微者,薄也,浮中沉取衡量-阳气不足脉气无力;细者小也,阴血不足,脉气无力。
少阴病:阴阳虚衰,又以肾阳虚衰为主者,具有全身性正气衰微的表现。
2015年高考化学原电池和电解池讲义
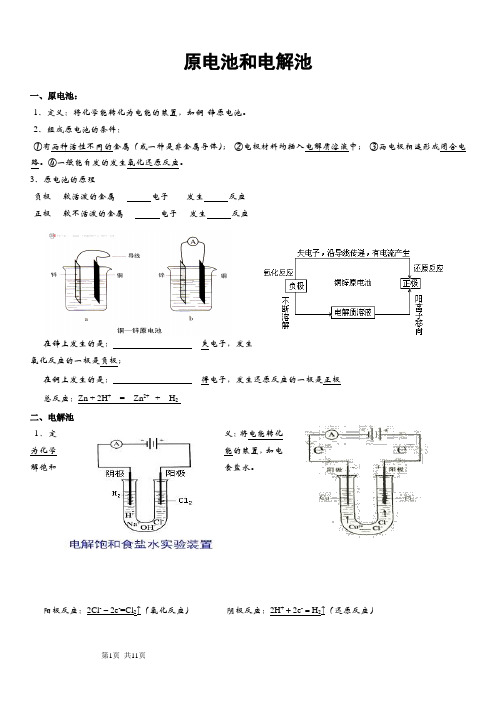
原电池和电解池一、原电池:1、定义:将化学能转化为电能的装置,如铜-锌原电池。
2、组成原电池的条件:①有两种活性不同的金属(或一种是非金属导体);②电极材料均插入电解质溶液中;③两电极相连形成闭合电路。
④一般能自发的发生氧化还原反应。
3、原电池的原理负极----较活泼的金属---- 电子------发生反应正极----较不活泼的金属---- 电子----发生反应在锌上发生的是:失电子,发生氧化反应的一极是负极;在铜上发生的是:得电子,发生还原反应的一极是正极总反应:Zn + 2H+= Zn2+ + H2二、电解池1.定义:将电能转化为化学能的装置,如电解饱和食盐水。
阳极反应:2Cl--2e-=Cl2↑(氧化反应)阴极反应:2H++2e-=H2↑(还原反应)总反应:2NaCl+2H2O2NaOH+H2↑+Cl2↑注意:①电流必须是直流②熔融态的电解质也能被电解③阴极上放电的先后顺序是:Ag+>Hg2+>Fe3+>Cu2+>(H+)>Fe2+>Zn2+;阳极上放电的先后顺序是:活泼金属电极›S2->I->Br->Cl->OH ->(F-、NO3-、SO42-等)(惰性电极)④用石墨、金、铂等还原性很弱的材料制做的电极叫做惰性电极,理由是它们在一般的通电条件下不发生化学反应。
用铁、锌、铜、银等还原性较强的材料制做的电极又叫做活性电极,它们做电解池的阳极时,先于其他物质发生氧化反应。
电解的电极反应式的书写思路与步骤:分电极(判断正负极)-----析溶液(分析电解质溶液中含有哪些离子)---判流向(判断电子流动方向、离子移动方向)-----断微粒(确定在两极上反应的是什么微粒)----写电极(书写电极反应方程式)---写方程(书写电解质电解的化学方程式或离子方程式)1)电解时溶液pH值的变化规律电解质溶液在电解过程中,有时溶液pH值会发生变化。
判断电解质溶液的pH值变化,有时可以从电解产物上去看。
①若电解时阴极上产生H2,阳极上无O2产生,电解后溶液pH值增大;②若阴极上无H2,阳极上产生O2,则电解后溶液pH值减小;③若阴极上有H2,阳极上有O2,且V(H2)=2V(O2),则有三种情况:a 如果原溶液为中性溶液,则电解后pH值不变;b 如果原溶液是酸溶液,则pH值变小;c 如果原溶液为碱溶液,则pH值变大;④若阴极上无H2,阳极上无O2产生,电解后溶液的pH可能也会发生变化。
会计从业资格《会计基础》讲义——财产清查结果的处理【应试精华会计网校】

财产清查结果的处理一、财产清查结果处理的要求对于财产清查中发现的问题,如财产物资的盘盈、盘亏、毁损或其他各种损失,应核实情况,调查分析产生的原因,按照国家有关法律法规的规定,进行相应的处理。
财产清查结果处理的具体要求有:1.分析产生差异的原因和性质,提出处理建议对于财产清查中发现的各种盘盈、盘亏以及质量问题,应核准数字,调查分析发生盈、亏的原因及性质,明确经济责任,依据有关法律、制度规定,提出处理意见和建议,同时根据企业的管理权限,将处理建议报股东大会或董事会、经理(厂长)会议或类似机构批准。
因自然原因引起的定额内盈、亏,应办理有关手续并及时转账;因企业经营管理不善造成的损失,应按规定程序报请批准后处理;因个人原因造成的损失,应由个人赔偿;因自然灾害引起的意外损失,如属投保财产,还应向保险公司索赔。
2.积极处理多余积压财产,清理往来款项对于财产清查中发现的积压、多余财产物资,应查明原因,并根据不同情况进行处理:对属于盲目采购、盲目建造或生产任务变更等原因造成的积压,除设法内部利用、改制、代用外,还应积极组织推销,以减少物资积压,加速资金周转;对于因品种不配套而造成的半成品积压,应当调整生产计划,组织均衡生产;对于利用率不高或闲置不用的固定资产,也应查明原因积极处理,做到物尽其用。
对于长期不清或有争议的债权、债务,要指定专人负责查明原因,主动与对方协商解决,按照结算纪律和结算制度的要求进行处理。
3.总结经验教训,建立和健全各项管理制度对于财产清查中发现的各种问题,应在查明问题性质和原因的基础上,认真总结经验教训,制订改进措施,建立健全财产物资管理制度,进一步落实财产管理责任制,保护单位财产的安全与完整,不断提高管理水平。
4.及时调整账簿记录,保证账实相符对于查明的各种盘盈、盘亏,应及时调整有关财产物资的账簿记录,并作为待处理财产损溢;在查明原因经批准处理后,再按批准的意见转账,进行相应的账务处理。
中级经济基础讲义--第6部分--法律(全5章)配合真题必过

第六部分法律——第三十二章法律对经济关系的调整本章重点:1.“调整经济的法律”和“经济法”2.调整社会主义市场经济的法律体系知识点一:法律调整对象法律的调整对象是社会关系。
【例题·单选题】(2015年)法律调整的对象是()。
A.宗教信仰B.自然规律C.社会关系D.道德理论『正确答案』C『答案解析』本题考查法律的含义。
法律的调整对象是社会关系。
知识点二:法律对经济关系调整经历的三个阶段1.奴隶制社会和封建社会:诸法合一阶段,刑法、民法不分。
2.自封建社会末期和自由资本主义阶段:法律进入了大分化、大发展时期。
这个时期对经济关系调整起主导作用的是民商法。
3.当代社会:民法、商法和经济法共同对经济关系进行调整,同时社会保障法、环境保护法等新兴法律部门也成为调整经济关系的辅助性法律部门。
【例题·单选题】在当代中国,法律对经济关系的调整模式是()。
A.民商法主导模式B.行政法主导模式C.经济法主导模式D.民商法、经济法主导,其他部门法辅助模式『正确答案』D『答案解析』进入当代社会,法律体系重新整合,民法、商法和经济法共同对经济关系进行调整,同时社会保障法、环境保护法等新兴法律部门也成为调整经济关系的辅助性法律部门。
知识点三、“经济法”与“调整经济的法”1.“经济法”:与民法、商法、行政法,刑法等部门法并列的一个法律部门,是现代法律体系的一个重要组成部分。
2.“调整经济的法”:是调整围绕社会物质财富的生产、交换、分配和消费过程所进行的各种经济关系的法律规范的总体,是一国所有调整经济关系的法律规范的总和。
它既包括传统法律体系中的民法、商法,也包括近代产生的经济法;既包括调整国内经济关系的法,也包括调整国际经济关系的国际私法和国际经济法。
【例题·单选题】关于“经济法”和“调整经济的法”,说法正确的是()。
A.“调整经济的法”包括了“经济法”B.两个概念内涵一致C.“经济法”的外延比“调整经济的法”的外延大D.“经济法”是与“调整经济的法”并列的法律部门『正确答案』A『答案解析』本题考查“经济法”和“调整经济的法”的区别。
2015-1-7一元一次不等式(组)基础讲义含答案

一元一次不等式(组)(讲义)一、知识点睛1. 不等式的概念:用符号>,<,≥,≤,≠连接的式子叫做不等式.“≥”叫大于或等于,也叫不小于;“≤”叫小于或等于,也叫不大于.2.不等式的基本性质:..4.①不等式的两边都加上(或减去)同一个代数式,不等号的方向不变; ②不等式的两边都乘以(或除以)同一个正数,不等号的方向不变; ③不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变.3.不等式的解与不等式的解集:使不等式成立的未知数的值;,叫做不等式的解;含有未知数的不等式的所有解,组成这个不等式的解集,通常用“xa >”或“x a <”的形式表示.不等式的解集可以在数轴上表示,需要注意实心圆点和空心圆圈的区别.4.求不等式解集的过程叫做解不等式.5. 一元一次不等式:不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.6.一元一次不等式组及其解法.一般地,关于同一未知数的几个一元一次不等式合在一起,就组成了一个一元一次不等式组.一元一次不等式组中各个不等式的解集的公共部分,叫做这个不等式组的解集.求不等式组解集的过程,叫做解不等式组. 二、精讲精练.1. a 的5倍与3的差不小于10,用不等式表示为____________.2. 某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分.已知小明在这次竞赛中的成绩超过90分,设他答对了n 道题,则根据题意可列不等式_______________.3.判断正误. (1)2≤3;( ) (2)由2x >-6,得3x <-; ( )(3)由ac bc >,且c ≠0,得a b >;( ) (4)如果0a b <<,则1ab<.( ) 4.已知ab >,c ≠0,则下列关系一定成立的是( )A .ac bc >B .a bc c> C .c a c b ->- D .c a c b +>+5. 若x a =是不等式5x +125≤0的解,则a 的取值范围是_________________.6. 不等式10x +<的解集在数轴上表示正确的是( )A .B .C .D .7.若关于x的不等式0x a -≤的解集如图所示,则a =_______.8. 若关于x 的不等式325m x -<的解集是2x >,则m =______.9. 不等式x ≤1的非负整数解是____________;不等式1x >-的最小整数解是___________. 10. 解下列不等式,并把它们的解集分别表示在数轴上.(1)2125x x --<; (2)53432x x ++-≤; (3)69251332x x x +-+-≤; (4)532122x x ++->.11. 在不等式0ax b +>中,a ,b 是常数,且a ≠0,当______时,不等式的解集是bx a>-;当_______时,不等式的解集是b xa<-. 12. 不等式84632x x x+->+的非负整数解为________________.13. 若不等式x a <只有4个正整数解,则a 的取值范围是________________. 14. 若不等式x a ≥只有2个负整数解,则a 的取值范围是________________. 15. 解下列不等式组,并把它们的解集分别表示在数轴上.(1)213821x x x +>-⎧⎨--⎩≤; (2)239253x x x x+<-⎧⎨-<⎩; (3)211132x +-<-<; (4)513(1)2151132x x x x ->+⎧⎪-+⎨-⎪⎩≥;(5)273(1)234425533x x x x x x ⎧⎪-<-⎪+⎪<⎨⎪⎪--+⎪⎩≤.16. 若不等式组420x a x >⎧⎨->⎩的解集是12x -<<,则a =________.17. 如果不等式组2123x a x b -<⎧⎨->⎩的解集是11x -<<,那么(1)(1)a b +-=_____________.18. 如果一元一次不等式组>2>x x a ⎧⎨⎩的解集是2x >,那么a 的取值范围是( )A .2a >B .2a ≥C .2a ≤D .2a <19. 如果不等式组8>41x x x m+-⎧⎨⎩≤的解集是3x <,那么m 的取值范围是( )A .3m ≥B .3m ≤C .3m =D .3m <一元一次不等式(组(随堂测试)1. 解不等式组240312123x x x +⎧⎪+-⎨<⎪⎩≥,并把它的解集表示在数轴上.2. 不等式351222x x -++≤的最小整数解为_________. 3. 如果不等式组2223x a x b ⎧--⎪⎨⎪-⎩≤≤的解集是01x ≤≤,那么a b +的值为____________.一元一次不等式(组)基础(作业)20. 下列说法中,错误的是( )A .不等式2x <的正整数解有一个B .2-是不等式210x -<的一个解C .不等式39x ->的解集是3x >-D .不等式10x <的整数解有无数个 21. 若0a b >>,c ≠0,则下列式子一定成立的是( )A .a c b c -<-B .1a b <C .22a b ->-D .22a bc c>22. 已知点M (12m -,1m -)关于x 轴的对称点在第一象限,则m 的取值范围在数轴上表示正确的是( )A .B . C, D,23. 若一组数据3,4,6,8,x 的中位数是x ,且x 是满足不等式组3050x x -⎧⎨->⎩≥的整数,则这组数据的平均数是___________.24. 若不等式22x a -+≥的解集是1x ≤,则a 的值是_________.25. 若不等式20x a -≤只有4个正整数解,则a 的取值范围是________________.26. 若不等式组2>31<1x n x m +⎧⎨+-⎩的解集是12x -<<,则m n -=____.27. 若关于x 的不等式组8236x x x a +>+⎧⎨⎩≤的解集是2x <,则a 的取值范围是_________.28. 篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队预计在2013~2014赛季全部32场比赛中至少得到48分,才有希望进入季后赛.若设这个队在将要举行的比赛中胜x 场,则x 应满足的关系式是_____________.29. 解下列不等式,并把它们的解集分别表示在数轴上.(1)521293x x --≤; (2)3221145x x --+≤; (3)321132x x -+<-;(4)326381236x x x -----≤.30. 解下列不等式组,并把它们的解集分别表示在数轴上.(1)73(1)5213122x x x x -+<-⎧⎪⎨-⎪⎩≥;(2)3(2)412>13x x x x --⎧⎪+⎨-⎪⎩≥;(3)4513777x -<--≤; (4)63315x xxx -⎧⎪-⎨<--⎪⎩≤.一元一次不等式(组)应用(讲义) 一、知识点睛1. 解一元一次不等式组的口诀:大大取大、小小取小、大小小大中间找、大大小小找不着.2.不等式应用题的三种常见类型①关键词型:不超过,至少,不低于,多于等;②不空不满型:不空也不满等;③方案设计型:原材料供应,容器容量. 二、精讲精练1.解下列不等式组.(1)42313(1)x x x x +⎧+⎪⎨⎪+<-⎩≥;(2)3(2)81213x x x x --⎧⎪+⎨>-⎪⎩≥; (3)523132x x x +⎧⎪+⎨>⎪⎩≥;(4)12(1)2235xx x x ⎧+>-⎪⎪⎨+⎪⎪⎩≥.2.如果一元一次不等式组213(1)x x x m->-⎧⎨⎩≤的解集是2x <,那么m 的取值范围是( )A .2m =B .2m >C .2m <D .2m ≥3.若关于x 的一元一次不等式组712x ax x >⎧⎨+<-⎩有解,则a 的取值范围是( )A .2a -≤B .2a >-C .12a<-D .12a -≤ 4.若关于x 的一元一次不等式组122x ax x <⎧⎨-<-⎩无解,则a 的取值范围是( )A .1a -≥B .1a >-C .1a ≤D .1a <5.若关于x 的一元一次不等式组721x mx <⎧⎨-<⎩的整数解共有3个,则m 的取值范围是( )A .67m <<B .67m <≤C .67m ≤≤D .67m <≤6.为鼓励学生参加体育锻炼,学校计划购买一批篮球和排球,已知篮球的单价为96元,排球的单价为64元,若用不超过 3 200元去购买篮球和排球共36个,且要求购买的篮球多于25个,则至少购买排球_______________个.7. 用若干辆载重量为8吨的汽车运一批货物,若每辆汽车只装4吨,则剩下20吨货物;若每辆汽车装满8吨,则最后一辆汽车不满也不空.那么汽车共有___________辆.8.“亚洲足球俱乐部冠军联赛”期间,河南球迷一行56人从旅馆乘车到天河球场为广州恒大加油.现有A ,B 两个车队,A 队比B 队少3辆车.若全部安排乘A 队的车,每辆坐5人,车不够,每辆坐6人,有的车未坐满;若全部安排乘B 队的车,每辆坐4人,车不够,每辆坐5人,有的车未坐满.则A 队有车___________辆.9.某工厂现有甲种原料360kg ,乙种原料290kg ,计划利用这两种原料生产A ,B 两种产品共50件.已知生产一件A ,B 产品所需原料如下表所示.(1)设生产x 件A 种产品,写出x 应满足的不等式组; (2)有哪几种符合题意的生产方案?请你帮助设计.10. 某工厂现有甲种布料70米,乙种布料52米,计划利用这两种布料生产A ,B 两种型号的时装共80套..利用现有布料,工厂能否完成任务?若能,请设计出所有可能的生产方案;若不能,请说明理由.11. 某仓库有甲种货物360吨,乙种货物290吨,计划用A ,B 两种货车共50辆将这批货物运往外地.若一辆A种货车能装载甲种货物9吨和乙种货物3吨;一辆B 种货车能装载甲种货物6吨和乙种货物8吨.则有哪几种运输方案?请设计出来.12. 在家电下乡活动中,某厂家计划将100台冰箱和54台电视机送到乡下.现租用甲、乙两种货车共8辆将这批家电全部运走,已知一辆甲种货车可同时装冰箱20台,电视机6台,一辆乙种货车可同时装冰箱8台,电视机8台.则将这批家电一次性运到目的地,有几种租用货车的方案?一元一次不等式(组)应用(随堂测试)4. 若关于x 的不等式组3352x x x a++⎧>⎪⎨⎪⎩≤的解集为3x <-,则a 的取值范围是( )A .3a =-B .3a >-C .3a <-D .3a -≥5. 某工厂现有甲种原料280kg ,乙种原料190kg ,计划利用这两种原料生产A ,B 两种产品50件.已知生产一件A 产品需甲种原料7kg ,乙种原料3kg ;生产一件B 产品需甲种原料3kg ,乙种原料5kg .则该工厂有哪几种生产方案?请你设计出来.一元一次不等式(组)应用(作业)31. 小美将某服饰店的促销活动内容告诉小明后,小明假设某件商品的定价为x元,并列出关系式0.3(2100) 1 000x -<,则下列哪个选项可能是小美告诉小明的内容?( )A 买两件相同价格的商品可减100元,再打3折,最后不到1 000元!B 买两件相同价格的商品可减100元,再打7折,最后不到1 000元!C 买两件相同价格的商品可打3折,再减100元,最后不到1 000元!D 买两件相同价格的商品可打7折,再减100元,最后不到1 000元!32. 把一些笔记本分给几个学生,如果每人分3本,那么余8本;如果前面的每个学生分5本,那么最后一人就分不到3本.则共有学生( ) A .4人B .5人C .6人D .5人或6人33. 若一元一次不等式组9551x x x m +<+⎧⎨>+⎩的解集是1x >,则m 的取值范围是_______________.34. 若关于x 的一元一次不等式组4132x xx m+⎧>+⎪⎨⎪>⎩有解,则m 的取值范围是_______________.35. 若关于x 的一元一次不等式组2113x x a -⎧>⎪⎨⎪<⎩无解,则化简32a a -+-的结果为_________________.36. 若关于x 的一元一次等式组0321x a x ->⎧⎨->⎩的整数解共有4个,则a 的取值范围是___________.37. “3·12”植树节,市团委组织部分中学的团员去郊区植树.某校八年级(3)班团支部领到一批树苗,若每人植4棵树,还剩37棵;若每人植6棵树,最后一人有树植,但不足3棵.则这批树苗共有___________棵.38. 解下列不等式组:(1)201211233x x x -⎧⎪--⎨-<⎪⎩≤;(2)3(2)41213x x x x --⎧⎪+⎨>-⎪⎩≥; (3)331213(1)8x x x x -⎧++⎪⎨⎪--<-⎩≥; (4)311224(1)x x x +⎧-⎪⎨⎪->+⎩≥.39. 某工厂现有甲种原料400千克,乙种原料450千克,计划利用这两种原料生产A ,B 两种产品共60件.已知生产一件A 种产品,需用甲种原料9千克、乙种原料5千克;生产一件B 种产品,需用甲种原料4千克、乙种原料10千克.则有哪几种生产方案?请你设计出来.40. 某校组织学生到外地进行社会实践活动,共有680名学生参加,并携带300件行李,学校计划租用甲、乙两种型号的汽车共20辆.经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李.则如何安排甲、乙两种汽车,可一次性地将学生和行李全部运走?请你设计方案.1、【参考答案】 知识点睛1.>,<,≥,≤,≠.大于或等于,不小于;小于或等于,不大于. 2.①代数式,不变;②正数,不变;③负数,改变.3.使不等式成立的未知数的值;含有未知数的不等式的所有解.实心圆点和空心圆圈.4.求不等式解集的过程. 5.整式,未知数.6.关于同一未知数的几个一元一次不等式合在一起.一元一次不等式组中各个不等式的解集的公共部分.求不等式组解集的过程. 精讲精练1.5310a -≥ 2.105(20)90n n --> 3.(1)√;(2)×;(3)×;(4)×. 4.D5.25a -≤6.A7.1- 8.3 9.0,1;0. 10.(1)2x <; (2)2x -≤; (3)1x -≥; (4)12x <.解集在数轴上的表示略. 11.0a>;0a <.12.0,1,2,3. 13.45a <≤ 14.32a -<-≤ 15.(1)3x ≥; (2)52x -<<;(3)514x -<<; (4)无解; (5)46x -<<. 解集在数轴上的表示略. 16.1- 17.6-18.C 19.A2、【参考答案】1.21x -<-≤,解集在数轴上的表示略.2.2- 3.3-3、【参考答案1.C2.D3.A 4.55.46.810a <≤7.1-8.2a ≥9.23248x x +-≥10.(1)13x ≥; (2)2x -≤; (3)34x >-;(4)15x -≥. 解集在数轴上的表示略.11.(1)4x ≥;(2)1x ≤;(3)2255x <≤;(4)无解.解集在数轴上的表示略. 4、【参考答案知识点睛1.大大取大、小小取小、大小小大中间找、大大小小找不着. 2.①关键词型;②不空不满型;③方案设计型. 精讲精练1.(1)2x >;(2)1x -≤;(3)12x -<≤;(4)无解. 2.D 3.C 4.C 5.D 6.8 7.6 8.109.(1)94(50)360310(50)290x x x x +-⎧⎨+-⎩≤≤;(2)共有3种生产方案.方案一,生产A 种产品30件,B 种产品20件;方案二,生产A 种产品31件,B 种产品19件;方案三,生产A 种产品32件,B 种产品18件. 10.工厂能完成任务,共有5种生产方案.方案一,生产A 型号时装36套,B 型号时装44套;方案二,生产A 型号时装37套,B 型号时装43套;方案三,生产A 型号时装38套,B 型号时装42套; 方案四,生产A 型号时装39套,B 型号时装41套;方案五,生产A 型号时装40套,B 型号时装40套. 11.共有3种运输方案.方案一,A 种货车20辆,B 种货车30辆;方案二,A 种货车21辆,B 种货车29辆;方案三,A 种货车22辆,B 种货车28辆.12.共有3种租车方案.方案一,租用甲种货车3辆,乙种货车5辆;方案二,租用甲种货车4辆,乙种货车4辆;方案三,租用甲种货车5辆,乙种货车3辆. 5、【参考答案】1.D 2.共有3种生产方案.方案一,生产A 种产品30件,B 种产品20件;方案二,生产A 种产品31件,B 种产品19件;方案三,生产A 种产品32件,B 种产品18件. 6、【参考答案】1.A 2.C 3.0m ≤ 4.2m < 5.25a -+ 6.43a -<-≤7.1218.(1)2x ≥;(2)1x ≤;(3)21x -<≤;(4)无解.9.共有3种生产方案.方案一,生产A 种产品30件,B 种产品30件;方案二,生产A 种产品31件,B 种产品29件;方案三,生产A 种产品32件,B 种产品28件.10.共有3种方案.方案一,安排甲型汽车8辆,乙型汽车12辆;方案二,安排甲型汽车9辆,乙型汽车11辆; 方案三,安排甲型汽车10辆,乙型汽车10辆.。
2015方浩概率强化讲义2

37
【例 2.13,R】设随机变量 X U 0, ,求随 机变量Y sin X 的概率密度.
38
【例 2.14】随机变量 X 的概率密度为,
1 , 1 x 0 2 1 f X x , 0 x 2 ,Y X 2 ,求Y 的概率 4 其它 0,
, k 0,1,
, n;
6
(3) 泊松分布(参数 0)
P X k
e
k
k!
, k 0,1, 2,
; X ~ P ( )
(4) 几何分布(参数为 p 0,1 )
P X k (1 p)
(5) 超几何分布
7
k 1
p, k 1,2, ; X
B p2 p1 p3 D p1 p3 p2
35
【例】设随机变量 X 概率密度为 , f x Ae , x aX b N 0,1 a 0 ,求 A,a, b
x 1 2
2
且
36
[题型三 随机变量函数的分布]
f ( x )dx 1
9
3. 分布函数的性质 (1) F x 为连续函数( f x 不一定连续) (2) P X a F a F a 0 0.
b a
(3) P{a X b} F (b) F (a ) f ( x )dx (只管积分,不管端点的开闭) (4) 若 f x 在 x 处连续,则 F x f x
G p .
(三)一维连续型随机变量 1.[ 定 义 ] : F ( x ) P{ X x }
2015初中数学基础知识讲义02—整式

①代数式、整式;②整式的加减一、代数式1、代数式:用含有数、字母及运算符号的式子,把问题中的数量关系表示出来,就是代数式。
2、代数式求值的步骤:①用数字代替字母;②按运算关系求出结果。
二、整式【______和______统称整式】(1)定义①单项式:由 与 的乘积..式子称为单项式。
单独一个数或一个字母也是单项式,如a ,5,π ·单项式的系数:单式项里的 叫做单项式的系数。
·单项式的次数:单项式中 叫做单项式的次数。
②多项式:几个 的和叫做多项式。
其中,每个单项式叫做多项式的 ,不含字母的项叫做 。
·多项式的次数:多项式里 的次数,叫做多项式的次数。
·多项式的幂:一个多项式含有几项,就叫几项式。
所以我们就根据多项式的项数和次数来命名一个多项式。
如:3n 4-2n 2+1是一个四次三项式。
(2)同类项——必须同时具备的两个条件(缺一不可):①所含的 相同;②相同 也相同。
★合并同类项,就是把多项式中的同类项合并成一项。
【合并同类项的法则:把系数相加减,字母和它的指数不变】 (3)去括号法则法则1.括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都 符号; 法则2.括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都 符号。
三、整式的运算:整式的加减实质就是 。
如遇到括号,则先 ,再 。
1、(福州市)已知22x =,则23x +的值是2、(2013苏州)按照下图所示的操作步骤,若输入x 的值为2,则输出的值为 .3、(2013山东日照)已知62=-m m ,则.____________2212=+-m m初中数学基础知识讲义—整式(一)4、多项式2235x x -+是 次 项式;单项式2-3x y的系数是 ,次数是 5、(2013济宁)如果整式xn -2-5x +2是关于x 的三次三项式,那么n 等于( )A .3 B .4 C .5 D .66、(2013佛山市)多项式2321xy xy -+的次数及最高次项的系数分别是( )A .3 3-,B .3 2-,C .3 5-,D .3 2, 7、(2013浙江湖州)计算2a-a 正确的结果是( ) A.-2a 2 B.1 C.2 D.a 8、(2013广州)下面的计算正确的是( ) A. 6a -5a=1 B. a+2a 2=3a 3 C.-(a -b)=-a+b D.2(a+b)=2a+b四、本单元需要注意的几个问题①整式(既单项式和多项式)中,分母一律不能含有字母。
2015年高考函数的图像专题讲义

2015年高考函数的图像专题讲义河南省三门峡市卢氏县第一高级中学山永峰图像是函数刻画变量之间的函数关系的一个重要途径,是研究函数性质的一种常用方法,是数形结合的基础和依据。
在今后的高考中将会加大对函数图像的考查力度。
主要以选择题、填空题的形式出现,属于中偏高档题。
主要考查形式有:知图选式、知式选图、图像变换(平移、对称、翻折、伸缩变换),以及自觉的运用图像解题。
因此要注意识图、读图能力的提高以及数形结合思想的灵活运用。
笔者以近几年高考题为载体,结合自己的教学经验整理如下,不足之处敬请斧正![备考方向要明了][归纳·知识整合]1.利用描点法作函数图象其基本步骤是列表、描点、连线.首先:①确定函数的定义域;②化简函数解析式;③讨论函数的性质(奇偶性、单调性、周期性、对称性等).其次:列表(尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等),描点,连线.2.利用图象变换法作函数的图象(1)平移变换:y =f (x )―――――――――――→a >0,右移a 个单位a <0,左移|a |个单位y =f (x -a ); y =f (x )―――――――――→b >0,上移b 个单位b <0,下移|b |个单位y =f (x )+b . (2)伸缩变换:y =f (x )1011ωωωω−−−−−−−−→<<,伸长为原来的倍>1,缩短为原来的 y =f (ωx ); y =f (x )―――――――――→A >1,伸为原来的A 倍0<A <1,缩为原来的A 倍y =Af (x ). (3)对称变换:y =f (x )―――――→关于x 轴对称 y =-f (x ); y =f (x )―――――→关于y 轴对称 y =f (-x );y =f (x )――――――→关于原点对称y =-f (-x ). (4)翻折变换:y =f (x )――――――――――――――→去掉y 轴左边图,保留y 轴右边图将y 轴右边的图象翻折到左边去y =f (|x |); y =f (x )―――――――――→留下x 轴上方图将x 轴下方图翻折上去y =|f (x )|.[探究] 1.函数y=f(x)的图象关于原点对称与函数y=f(x)与y=-f(-x)的图象关于原点对称一致吗?2.一个函数的图象关于y轴对称与两个函数的图象关于y轴对称有何区别?提示:一个函数的图象关于y轴对称与两个函数的图象关于y轴对称不是一回事.函数y=f(x)的图象关于y轴对称是自身对称,说明该函数为偶函数;而函数y=f(x)与函数y=f(-x)的图象关于y轴对称,是两个函数的图象对称.3.若函数y=f(x)的图象关于点(a,0)(a>0)对称,那么其图象如何变换才能使它变为奇函数?其解析式变为什么?提示:向左平移a个单位即可;解析式变为y=f(x+a).[自测·牛刀小试]1.(教材习题改编)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车行驶的路程s看作时间t的函数,其图象可能是()2.函数y=x|x|的图象经描点确定后的形状大致是()3.函数y=ln(1-x)的图象大致为()4.已知下图(1)中的图象对应的函数为y=f(x),则下图(2)中的图象对应的函数在下列给出的四个式子中,可能是________(填序号).①y=f(|x|);②y=|f(x)|;③y=-f(|x|);④y=f(-|x|).5.(2012·镇江模拟)函数f(x)是定义在[-4,4]上的偶函数,其在[0,4]上的图象如图所示,那么不等式f(x)cos x<0的解集为________.考点一:作函数的图象[例1]分别画出下列函数的图象:(1)y=|lg(x-1)|;(2)y=2x+1-1;(3)y=x2-|x|-2.画函数图象的一般方法(1)直接法:当函数表达式(或变形后的表达式)是熟悉的基本函数或解析几何中熟悉的曲线时,可根据这些函数或曲线的特征直接作出.(2)图象变换法:若函数图象可由某个基本函数的图象经过平移、翻折、对称得到,可利用图象变换作出,但要注意变换顺序,对不能直接找到熟悉函数的要先变形,并应注意平移变换与伸缩变换的顺序对变换单位及解析式的影响.(3)描点法:当上面两种方法都失效时,则可采用描点法.为了通过描少量点,就能得到比较准确的图象,常常需要结合函数的单调性、奇偶性等性质讨论. 强化训练: 1.分别画出下列函数的图象.(1)y =|x 2-4x +3|;(2)y =2x +1x +1;(3)y =10|lg x |. 考点二:识图与辨图[例2] (1)(2012·山东高考)函数y =cos 6x 2x -2-x的图象大致为( )(2)已知定义在区间[0,2]上的函数y =f (x )的图象如图所示,则y =-f (2-x )的图象为( )例3:[2014年福建卷] 若函数y =log a x (a >0,且a ≠1)的图像如图1-1所示,则下列函数图像正确的是( )图1-1 A BC D寻找图象与函数解析式之间的对应关系的方法(1)知图选式:①从图象的左右、上下分布,观察函数的定义域、值域;②从图象的变化趋势,观察函数的单调性;③从图象的对称性方面,观察函数的奇偶性;④从图象的循环往复,观察函数的周期性.利用上述方法,排除错误选项,筛选正确的选项.(2)知式选图:①从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;结合图像的特殊点(极值点、与坐标轴的交点等)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年考研数学基础班讲义(下)武忠祥第 七 章 微 分 方 程考 试 容 概 要 (一)常微分方程的基本概念1.微分方程 含有未知函数的导数或微分的方程称为微分方程。
简称方程。
2.微分方程的阶 微分方程中所出现的未知函数最高阶导数的阶数,称为微分方程的阶。
3.微分方程的解 满足微分方程的函数,称为该方程的解。
4.微分方程的通解 如果微分方程的解中含有任意常数,且任意常数的个数与微分方程的阶数相同,则称之为微分方程的通解。
5.微分方程的特解 微分方程的不含任意常数的解,称之为特解。
6.初始条件 确定特解的一组常数称为初始条件。
7.积分曲线 方程的一个解在平面上对应一条曲线,称为该微分方程的积分曲线。
(二)一阶微分方程 1.可分离变量的方程能表示为x x f y y g d )(d )(=的方程,称为可分离变量的方程. 求解的方法是两端积分.d )(d )(⎰⎰=x x f y y g2. 齐次方程 能化为⎪⎭⎫⎝⎛=x y dx dy ϕ的微分方程称为齐次微分方程. 求解齐次微分方程的一般方法为:令xyu =,则u x u y '+=',从而将原方程化为u u u x -=')(ϕ,此方程为可分离变量的方程。
3. 线性方程 形如)()(x Q y x p y =+'的方程称为一阶线性微分方程。
求解一阶线性微分方程的一般方法为常数变易法,或直接利用以下通解公式.d e )(e d )(d )(⎥⎦⎤⎢⎣⎡+⎰⎰=⎰-C x x Q y x x p x x p 4. 伯努利方程 (仅数学一要求)形如ny x Q y x p y )()(=+'的方程)1,0(≠n ,称为伯努利方程。
求解伯努利方程的一般方法为:令ny u -=1,将原方程化为一阶线性微分方程。
5. 全微分方程(仅数学一要求)如果方程0d ),(d ),(=+y y x Q x y x P 的左端是某个函数),(y x u 的全微分: y y x Q x y x P y x du d ),(d ),(),(+= 则称该方程为全微分方程。
此方程的通解为 C y x u =),( 求),(y x u 有以下三种方法1)偏积分 2)凑微分 3)线积分 当),(),,(y x Q y x P 在单连通域G 具有一阶连续偏导数时,方程0d ),(d ),(=+y y x Q x y x P是全微分方程的充要条件是xQ y P ∂∂=∂∂ 注 如果给定的一阶微分方程不属于上述五种标准形式,首先考虑将x ,y 对调,即认定x 为y 的函数,再判定新方程的类型;或者利用简单的变量代换将其化为上述五种类型之一而求解。
(三)可降阶的高阶方程(数学三不要求)1. )()(x f yn =型的微分方程2. ),(y x f y '=''型的方程只需令,p y =',p y '='',可将原方程化为一阶微分方程。
3. ),(y y f y '=''型的方程 只需令,p y =',ypp y d d ='',可将原方程化为一阶微分方程。
(四)常系数线性微分方程1. 线性微分方程解的结构这里只讨论二阶线性微分方程,其结论可以推广到更高阶的方程。
二阶线性微分方程的一般形式为)()()(x f y x q y x p y =+'+''这里的)(),(),(x f x q x p 均为连续函数.当方程右端的0)(≡x f 时,称为二阶线性齐次方程.否则称为二阶线性非齐次方程.齐次方程 0)()(=+'+''y x q y x p y (1) 非齐次方程 )()()(x f y x q y x p y =+'+'' (2) 定理1 如果)(1x y 和)(2x y 是齐次方程(1)的两个线性无关的特解,那么)()(2111x y C x y C y +=就是方程(1)的通解.【注】方程(1)的两个解线性无关的充要条件是它们之比不为常数.定理2 如果*y 是非齐次方程(2)的一个特解,)(1x y 和)(2x y 是齐次方程(1)的两个线性无关的特解,则)()()(2111x y x y C x y C y *++= 是非齐次微分方程(2)的通解.定理3 如果)(*1x y ,)(*2x y 是非齐次方程(2)的两个特解,则)()()(*1*2x y x y x y -=是齐次微分方程(1)的解.定理4 如果)(*1x y ,)(*2x y 分别是方程 )()()(1x f y x q y x p y =+'+'')()()(2x f y x q y x p y =+'+''的特解,则)()(*2*1x y x y +是方程)()()()(21x f x f y x q y x p y +=+'+'' 的一个特解.2. 常系数线性齐次微分方程二阶常系数线性齐次微分方程的一般形式为0=+'+''qy y p y , ③其特征方程为02=++q pr r ,设1r ,2r 为该方程的两个根。
(1)若21r r ≠,为两个不相等的实特征根,则方程③的通解为x r x r C C y 21e e 21+=(2)若21r r =为二重实特征根,则方程③的通解为x r x C C y 1e )(21+=。
(3)若βαi 1+=r ,βαi 2-=r ,为一对共轭复根,则方程③的通解为 )sin cos (e 21x C x C y xββα+=。
3. 常系数线性非齐次微分方程二阶常系数线性非齐次微分方程的一般形式为).(x f qy y p y =+'+'' ④(1)若xm x P x f λe )()(=,其中)(x P m 为x 的m 次多项式,则方程④的特解可设为,e )(*x m k x Q x y λ=其中)(x Q m 是与)(x P m 同次的多项式。
k 是特征方程含根λ的重复次数.(2)若]sin )(cos )([e )()2()1(x x P x x P x f n l x ββα+=,其中)()1(x P l ,)()2(x P n 分别为x 的l 次,n 次多项式,则方程④的特解可设为].sin )(cos )([e )2()1(*x x R x x R x y m m x k ββα+=其中)()1(x R m ,)()(x R x m 是两个m 次多项式,},max{n l m =。
当βαi +不为方程③的特征根时,取0=k ; 当βαi +为方程③的单特征根时,取1=k 。
4. 欧拉方程(仅数学一要求)形如 ),(1)1(11)(x f y p y x p yx p y x n n n n n n =+'+++--- (其中1p ,2p , ,n p 为常数)的方程称为欧拉方程。
令tx e =或x t ln =,可将上述欧拉方程化为线性常系数方程,一般地有,)1()1()(y k D D D y x k k +--=其中D 代表对t 求导数的运算。
常 考 题 型 与 典 型 例 题常考题型 1.方程求解 2.综合题 3. 应用题【例1】(2014年1)微分方程0)ln (ln =-+'y x y y x 满足条件3)1(e y =的解为.________=y【12+=x xey 】【例2】(2012年2)微分方程0)3(2=-+dy y x ydx 满足条件11==x y 的解为=y .【x y =】【例3】(2013年3)微分方程041=+'-''y y y 的通解为._________【x ex C C y 2121)(+=】【例4】(2009年1)若二阶常系数线性齐次微分方程0=+'+''by y a y 的通解为x e x C C y )(21+=,则非齐次方程x by y a y =+'+''满足条件0)0(,2)0(='=y y 的解为._________【2)1(+-=xe x y 】【例5】(2013年1,2)已知,231x xxe ey -=,22x x xe e y -=x xe y 23-=是某二阶常系数非齐次线性微分方程的3个解,则该方程的通解为._____________=y【x x xxe e C eC y 2231-+=】【例6】(2007年4)设函数)(x f 具有连续的一阶导数,且满足2022)()()(x dt t f t x x f x+'-=⎰,求)(x f 的表达式.【1)(2-=x e x f 】【例7】(2006年3)在xOy 坐标平面上,连续曲线L 过点)0,1(M ,其上任意点)0)(,(≠x y x P 处的切线斜率与直线OP 的斜率之差等于ax (常数0>a ). (I )求L 的方程;(II )当L 与直线ax y =所围成平面图形的面积为38时,确定a 的值.【2;2=-=a ax ax y 】 【例8】(2009年2)设非负函数)0()(≥=x x y y 满足微分方程02=+'-''y y x . 当曲线)(x y y =过原点时,其与直线1=x 及0=y 围成的平面区域D 的面积为2,求D 绕y 轴旋转所得旋转体的体积.【617;322π=+=V x x y 】第 八 章 多 元 函 数 微 分 学考 试 容 概 要(一)多元函数的极限、连续、偏导数与全微分1. 二元函数定义1 设D 是平面上的一个点集,若对每个点,),(D y x P ∈变量z 按照某一对应法则f 有一个确定的值与之对应,则称z 为y x ,的二元函数,记为),(y x f z =。
其中点集D 称为该函数的定义域,y x ,称为自变量,z 称为应变量。
函数值),(y x f 的全体所构成的集合称为函数f 的值域。
记为).(D f通常情况下,二元函数),(y x f z =在几何上表示一空间曲面. 2. 二元函数的极限定义2 设函数),(y x f 在区域D 上有定义,点D y x P ∈),(000或为D 的边界点,如果,0>∀ε存在0>δ,当,),(D y x P ∈且δ<-+-<2020)()(0y y x x 时,都有ε<-A x f )(成立,则称常数A 为函数),(y x f 当),(),(00y x y x →时的极限,记为A y x f y x y x =→),(lim ),(),(00或A y x f y y x x =→→),(lim 00或A P f P P =→)(lim 0注 1)这里的极限是要求点),(y x 在D 以任意方式趋近于点),(00y x 时,函数),(y x f 都趋近于同一确定的常数A ,否则该极限就不存在。
