最新结构设计大赛(桥梁)计算书培训讲学
结构设计大赛计算书

结构设计大赛计算书结构设计大赛计算书结构设计大赛是一项旨在考察参赛者对于结构设计原理和实践能力的比赛活动。
参赛者通过设计、计算和模拟结构的方法,展示自己的创造力、工程素质和解决问题的能力。
本文将从浅入深,从设计思路到实际实施,介绍结构设计大赛的相关内容。
首先,结构设计大赛的成功与否与参赛者的设计思路有着密切的关系。
设计思路是指在结构设计过程中,参赛者根据任务要求和限制条件,通过合理的分析和策略,形成一种可行的设计思想。
参赛者应该注重综合考虑结构的安全、经济和实用性,灵活运用不同的结构设计方法,如梁结构、桁架结构、柱状结构等,以满足工程要求。
其次,结构设计大赛的计算工作至关重要。
参赛者需要根据设计思路,对结构进行力学分析和计算。
力学分析包括结构的受力情况、应力分布和变形特征等。
参赛者需要熟练掌握结构力学的相关原理和计算方法,如静力学、动力学和弹性力学等。
通过准确的计算,可以充分评估结构的可靠性和安全性,为设计提供科学依据。
此外,参赛者还需要利用计算机进行结构的模拟和优化。
计算机辅助设计(CAD)和计算机辅助工程(CAE)技术的应用,能够帮助参赛者快速生成结构模型,并进行力学仿真和优化计算。
参赛者可以通过不断调整结构参数、材料选型和构件布置等,寻找最佳的设计方案。
同时,计算机模拟也可以为结构设计提供详细的结果数据,方便参赛者进行结果分析和展示。
最后,结构设计大赛还强调参赛者对于结构实施的指导意义。
结构设计不仅仅是理论上的构思和计算,更需要考虑实际的施工和使用情况。
参赛者应该重视工程实践,了解结构施工工艺和材料特性,提供合理的施工指导和建议。
只有结构设计与实际实施相结合,才能确保设计方案的可行性和有效性。
综上所述,结构设计大赛是一项需要参赛者具备全面能力和创新思维的活动。
通过设计思路、力学计算、计算机模拟和实施指导四个方面的全面考察,参赛者可以充分展现自己的结构设计才能和应对问题的能力。
希望广大参赛者能够在结构设计大赛中充分发挥自己的潜力,为工程领域的发展贡献力量。
4 白卡纸材料桥梁结构设计竞赛计算书

在整体形象给人们强烈视觉冲击和震撼的同时,理性技术的表现也不逊色。整体结构 合起来看,她就想一艘航船,在风暴中前行,展现其优良的性能,清晰地体现了力与美的 完美结合。
2.袁海庆.材料力学[M].武汉:武汉工业大学出版社,2004
-6-
3.2 内力分析
3.2.1 结构正投影简化计算分析 通过计算把结构正面投影简化,在结构上加大小为 10KG 荷载,在结点 i,l.j,k 分别作用 100N 的竖直向下的集中力,得出如下轴力图。
结构正投影简化计算轴力图 本方案结构为桁架结构,各杆件弯矩剪力为 0。 3.2.2 各杆内力分析 在正投影简化结构 i,l,j,k 结点作用 25N 的力,得出其轴力图,再利用空间力系投影原来把 轴力具体分配到各杆。通过计算得出表一,具体计算过程略。
结点处,所有杆件做圆柱体,充分发挥各构件空间协同工作性能,并与胶水连接,防止结 点破坏。
2.3 设计方案图
结构正投影图
结构概念图 红色代表受拉 绿色代表受压
-1-
3. 计算书
为了更好的了解和掌握实际模型的受力特征,我们应用结构力学求解器(SM Solver 2.0.0)对其进行了结构受力分析。
3.1 计算假定
-4-
(3-3)
Fcr=3.14^2EI/(L^2)
(3-4)
1、E 为弹性模量 1400N/mm^2
2、Iz 为极惯性距
3、a 为管壁厚度
4、R 为管得直径
桥梁工程之桥梁支座设计构造计算培训课件

7.2 桥梁支座的类型和构造
图7-4 曲线梁桥支座布置示意图
7.2 桥梁支座的类型和构造
• (4)对于悬臂梁桥,锚固跨一侧设固定支座,另 一侧设活动支座。
• 铁路桥梁固定支座、活动支座的布置应遵循以下 原则:
• ①对于桥跨结构而言,最好要使梁(支承处) 的下缘在制动力的作用下受压,从而抵消一部分 竖向荷载在下缘产生的拉力。一般固定支座设置 在坡桥较低侧以及行车方向的前方侧。在车站附 近,固定支座宜设置在车站一侧,对于坡道应设 置在高程较低一侧。
• 桥梁支座具体可根据桥梁跨径长短、支座反力大 小、支座允许的转动和位移量、选用的支座材料 以及对桥梁变形和本身建筑高度、以及满足桥梁 抗震、防震等要求选用。
• 按支座容许变形的可能性划分,通常有固定支座 和活动支座,活动支座又包括单向活动支座和双 向活动支座。
7.2 桥梁支座的类型和构造
⑴固定支座。主要承担桥跨结构支承处顺桥向、横桥向的水 平力和竖向反力,并约束相应的线变位。固定支座既要固 定主梁在墩台上的位置并传递竖向力和水平力,又要保证 主梁发生挠曲变形时在支承处能自由转动。 。
7.2 桥梁支座的类型和构造
• 桥梁支座应根据不同情况进行布置: • (1)对于简支梁桥,一端设固定支座,另一端设活动支
座。T构桥的挂孔按简支梁处理。 (2)对于多跨连续梁桥,一般每联只有一个固定支座。为
避免活动端的伸缩变形过大,一般将固定支座设在每联的 中间桥墩上。但若该处墩身较高,则应考虑避开,或采取 特殊措施,以避免该墩顶承受过大的水平力(这导致墩底 弯矩过大)。
7.1 概述
桥梁支座主要作用具体表现如下三点:
•(1)使反力明确地作用到墩台的指定位置,并 将集中反力扩散到一个足够大的面积上,以保证 墩台工作的安全可靠。
桥梁结构设计大赛计算书

桥梁结构设计大赛计算书桥梁结构设计大赛计算书大赛名称:桥梁结构设计大赛主办单位:XXX大学桥梁工程学院比赛时间:2022年X月X日比赛地点:XXX大学校园一、比赛背景桥梁是人类交通和基础设施建设中不可或缺的重要组成部分。
为了推动桥梁工程的研究和创新,促进优秀人才的培养,XXX大学桥梁工程学院决定举办桥梁结构设计大赛。
本次大赛旨在通过参赛选手的创新设计和计算能力,提升桥梁结构设计水平,促进桥梁工程的发展。
二、参赛要求与规则1.参赛对象:本次比赛开放给全国范围内的高校本科生和研究生报名参加。
2.作品要求:参赛作品需为原创桥梁结构设计方案,并附有详细的计算书。
作品形式不限,可以是CAD图纸、模型或电子文档。
3.评审标准:评审将综合考虑桥梁结构的创新性、安全性、经济性和可行性。
参赛作品需符合国家桥梁设计规范和相关标准。
4.参赛费用:参赛选手需按规定缴纳报名费用,并提交参赛申请表和相关证明材料。
三、计算书要求与内容1.计算书编写:参赛作品需附有详细的计算书,包括结构设计的计算过程、参数选择、荷载计算、受力分析、构件验算等内容。
2.计算方法:计算书应使用合理的计算方法和软件工具,确保计算准确性和可靠性。
参赛选手需在计算书中说明所采用的计算方法和工具。
3.材料选择:计算书中需详细说明所选用的材料性能参数、强度设计值、安全系数等,并合理选择材料,以确保桥梁结构的强度和稳定性。
4.荷载计算:计算书中需对桥梁结构所受的静载荷、动载荷和温度荷载进行详细计算和分析,确保桥梁结构在各种工况下的安全性能。
5.构件验算:计算书中需对桥梁结构各个构件进行验算,包括钢梁、混凝土梁、桩基等。
验算应满足设计规范的要求,确保构件的强度和稳定性。
四、奖项设置与评选方式1.奖项设置:本次大赛设一、二、三等奖各若干名,并颁发优秀组织奖、最佳创新奖等特别奖项。
2.评选方式:评审团将对参赛作品进行评审和打分,综合考虑结构设计、计算书质量、创新性等因素进行评选。
桥梁设计大赛计算书

桥梁结构设计理论方案作品名称参赛学校参赛队员、专业名称指导教师大庆市大学生结构创新设计竞赛组委会二○一一年目录1设计说明根据本次大赛要求及所提供材料,本组成员秉承“安全、节省、承载力高、美观”原则,设计此桥梁“步步精心”结构模型。
桥梁以桁架结构为主体,尽量做到受力均匀,拉杆和压杆合理分布。
其中“杆件承载力充分利用和桥身自重轻”为此设计最大亮点。
1.1设计构思在接到比赛要求最初,本组成员经过分析得出“材料本身承载力强、材质轻、只适合粘结”的结论,初步确定以“平面结构,主梁主要承力,桁架结构”为大体思路。
为减轻桥梁自重,我们决定尽量多用拉杆,但在模拟加载过程中,发现此想法难以实现。
遂改用另一种减重方式,即尽量使每根杆都受力均匀,所受最大拉(压)力和最小拉(压)力差值最小。
1.2结构选型在确定“平面结构、主梁主要承力、桁架结构”为大体思路后,设计步骤如下:①根据大赛尺寸要求,初步确定桥梁的跨度、高度和宽度;②根据以往经验和资料分析,设计出桥梁大体模型;③以实际情况为准,提取计算简图;④利用结构力学求解器软件对结构进行模拟加载,计算出各杆所承受轴力及弯矩,以确定桥梁各单元杆件截面尺寸;⑤结合杆件密度,取最优荷重比。
1.3详细计算1.3.1设计资料根据大赛要求,可以确定桥梁跨度L=1300mm,净跨L0=1200mm,桥宽B=185mm,由经验和资料初步确定桥高H=150mm,竖向腹杆间距由比赛小车车轮中心轴距离确定,选为120mm。
1.3.2桥梁形式、尺寸及支撑布置根据上述原则,最终确定桥梁如图1-1,1-2图1-1正视图图1-2俯视图1.3.3基本假定①节点粘结处按照铰接计算;②支座简支;③荷载取为竖直集中静荷载,分别作用在结点和单元上④考虑动荷载影响,计算荷载取为实际荷载1.2倍;⑤忽略桥本身自重,⑥材料材质均匀。
⑦定义杆件单元和结点码,下文提到单元和结点码皆基于此定义图1-41.3.4荷载模拟①桥面板近似为均布荷载q=mg/l0=3×10/1300=0.0125N/mm②一辆小车加砝码P’=120N,考虑动荷载影响P=1.2P’=144N③一辆小车在两榀桁架上荷载分配的原则如图1-5图1-5P1=0.25P=36NP2=0.75P=108N考虑每辆小车轮距,将一辆小车及砝码的荷载简化为两集中力Q1和Q2Q1=0.5P2=18NQ2=0.5P1=54N则桥梁计算简图如图1-6图1-6按照图1-6将计算简图输入结构力学求解器,将集中荷载依次作用在各单元中间位置,得出各杆件所受最大轴力和弯矩值,依次列在附表1-5,再将集中荷载依次作用在各结点位置,同样得出各杆件所受最大轴力和弯矩值,依次列在附表6-9,此数据作为设计最终依据。
第一组桥梁结构设计计算书

一、设计要求竞赛模型为木质单跨桥梁结构,采用木质材料制作,具体结构形式不限。
1.几何尺寸要求(1) 模型长度:模型有效长度为1200mm,两端提供竖向和侧向支撑。
对于竖向支撑,每边支撑长度为0-70mm。
(2)模型宽度:在模型有效长度范围内(中央悬空部分),模型宽度应不小于180mm,最宽不应超过300mm;在支座范围内,宽度不限,但不应超过320mm 。
(3) 模型高度:模型上下表面距离最大位置的高度不应超过400mm;为方便小车行驶,中央起拱高度不应超过40mm;端部支座位置处的高度不应超过150mm。
2.结构形式要求对于结构形式没有特定要求,桥面设置两个车道,每个车道宽不得小于90mm,车道之间不能有立柱、拉索一类的构件。
结构可以仅采用竖向支撑的方式,也可以采用竖向和侧向同时支撑的方式来实现约束。
3.材料(1)木材:用于制作结构构件。
有如下两种规格:木材规格(单位:mm)材料2 mm×2 mm×1000mm桐木2 mm×4 mm×1000m m 桐木2 mm×6 mm×1000 mm桐木4 mm×6 mm×1000mm桐木1 mm×55 mm×1000 mm桐木木材力学性能参考值:顺纹弹性模量1.0×104MPa,顺纹抗拉强度30Mpa。
(2) 502胶水:用于模型结构构件之间的连接。
二、结构选型桁架桥(truss bridge)是以桁架作为上部结构主要承重构件的桥梁。
在桥梁中被广泛应用,如大家熟知的现代诗人徐志摩脍炙人口的《再别康桥》中的桥就是一座桁架桥。
我国1993年建造的九江长江大桥,是京九铁路和合九铁路的“天堑通途”,为双层双线铁路、公路两用桥,铁路桥长7675米,公路桥长4460米,其中江上正桥长1806米,是世界最长的铁路、公路两用的钢桁梁大桥。
桁架桥(见图1)一般由主桥架、上下水平纵向联结系、桥门架和中间横撑架以及桥面系组成。
桥梁工程简支梁桥的计算讲座PPT教案

b1 2
)
(1
)
P 2a
(l0
b1 2
)
(b1 l0 ) (b1l0 )
第6页/共53页
M Ag
1 2
gl
0
2
QAg gl0
➢ 例:图示铰接悬臂板
➢ 荷载:公路Ⅰ级
➢ 桥面铺装:
➢ 8cm泥青混凝土(23KN / m3 )
➢ 9cmC30砼
(24KN / m3 )
➢ 翼板钢筋砼:(25KN / m3 )
n
i 1
Rk "
ai 2 Ii ak Ik
Rk "
ai Ii ak Ik
• l 2GIT i e 12ai EIi
Rk "
•
1 ak I
k
n
( ai 2 Ii
i 1
Gl 2
12E
n i 1
ITi ) e
第19页/共53页
Rk "
eak I k
eak I k (
1
ai 2 Ii
➢ 受荷梁承受全部荷载P
>EIH >0
受荷梁承受mP
EIH
各梁承受P/n
➢ 由此可m=见1:横向连接刚度越大m,荷载横向分m布=作1/n用越显著,各主梁 分担的荷载越趋均匀。
根据不同的横向结构简化计算模型,拟定出不同的计算方法:
杠杠原理法、偏心压力(刚性横梁)法、修正偏心压力法、铰接板 (梁)法、刚接梁法、比拟正交异性板(G-M)法等。
➢ 荷载作用位置有关:
➢ 1)单个车轮荷载作用于跨中:
➢
a
a1
l 3
(不小于23l )
➢ 对于边距为d的多个车轮:
竞赛培训之04:大跨桥梁结构选型思路解说

预应力设计/钢筋设计 力钢筋面积 力钢筋布置
参照经验数据 参照已有图纸
37
估算
布置设计
PRODUCED BY:Wenxiong Huang
3.桥梁构思实现上的控制环节
3.3PC连续梁桥设计的关键环节
桥梁布跨
选择截面形式及尺寸拟定 施工方法选择
通不过
预应力布置
恒载内力计算 结构检算 活载内力计算
OK 设计图
重庆石板坡桥,主跨 330m
诺曼底桥,钢梁伸入主跨116米。
混凝土梁
钢梁
混凝土梁
多多罗桥,边跨末端设置混凝土梁。
砼梁
钢梁
砼梁
26
PRODUCED BY:Wenxiong Huang
结合面
PC梁标准段
PC梁过渡段
钢加劲段
钢梁标准段
混凝土梁
钢混结合段
钢梁
钢混结合段立面过渡示意
27
TOC2 PRODUCED BY:Wenxiong Huang
结构的适用性 主要由其功能所决定
桥梁适用性 大赛中的体现
7
运营荷载的需求 移动加载的体现
PRODUCED BY:Wenxiong Huang
1.桥梁定义和设计原则的回顾
经济要求
在安全、适用的前提下,经济是衡量技术水平和作出方案选择的主要 因素。桥梁设计应体现出经济特性。对于重大的桥梁工程,必须进行 多方案的比较,详细研究技术上的可行性和先进性以及经济上的合理 性。这样,才能对桥梁的建造消耗、施工、技术发展和今后使用等因 素进行统筹考虑,得出合理的经济结论。
2.6“取长补短”原则
2.6.2混合梁的使用
在连续梁和斜拉桥的主梁中,部分采用混凝土主梁,部分采用钢主梁, 这种布置方式称为混合式主梁布置,简称“混合梁”。
结构设计大赛计算书

结构设计大赛计算书
我理解你的意思是希望制作一个关于结构设计大赛的计算书,以便参赛选手能够进行相关计算。
以下是一个简要的
计算书的结构设计示例:
封面:在封面上写上计算书的名称、结构设计大赛信息、
参赛选手的姓名等。
目录:列出计算书中各个章节的标题和页码,方便读者查阅。
简介:简要介绍结构设计大赛的目的、背景、参赛规则等。
章节1:设计要求和限制
- 解释参赛选手需要满足的设计要求和限制条件,包括结构类型、载荷要求、材料限制等。
章节2:设计参数和变量
- 列出设计过程中涉及到的参数和变量,如强度、位移、截面尺寸等。
章节3:理论计算方法
- 介绍常用的结构设计理论和计算方法,如梁的弯曲计算、柱的稳定计算等。
章节4:结构力学计算
- 详细说明参赛选手需要进行的结构力学计算方法,如静力分析、动力分析等。
章节5:结构设计软件使用
- 介绍常用的结构设计软件,如AutoCAD、ANSYS等,以及如何使用这些软件进行结构设计计算。
章节6:案例分析
- 给出一些结构设计的案例,包括实际结构和理论计算样例,供参赛选手进行学习和实践。
附录:补充相关信息和表格
- 包括参考文献、公式表、材料性能表、单位换算表等。
这只是一个示例,你可以根据实际情况对计算书的结构进
行调整和完善。
《桥梁结构计算》课件

悬索桥
以悬索为主要承重结构 的桥梁,包括主缆、吊
索和索塔等。
斜拉桥
以斜拉索为主要承重结 构的桥梁,包括拉索和
塔柱等。
桥梁设计要素
荷载
包括恒载、活载、风载、地震 等作用力。
稳定性
确保桥梁在各种工况下的稳定 性,防止发生失稳或倾覆。
强度
确保桥梁结构在各种荷载作用 下不会发生破坏或过大的变形 。
加强实践经验的积累
建议学生多参与实际工程项目的计算和分析 ,积累实践经验,提高解决实际问题的能力 。
THANKS 感谢观看
《桥梁结构计算》PPT课件
• 引言 • 桥梁结构基础知识 • 桥梁结构分析 • 桥梁设计计算 • 案例分析 • 课程总结与展望
01 引言
课程背景
桥梁作为交通基础设施的重要组 成部分,其安全性和稳定性至关
重要。
随着科技的发展和工程实践的积 累,桥梁结构计算理论和方法不
断完善。
为了培养具备专业知识和技能的 桥梁工程师,开展《桥梁结构计 算》课程具有重要的实际意义。
06 课ห้องสมุดไป่ตู้总结与展望
本课程主要内容回顾
桥梁结构计算的基本原理
桥梁设计中的力学问题
介绍了桥梁结构计算的基本概念、原理和 方法,包括静力学、动力学、稳定性等方 面的计算。
探讨了桥梁设计中的各种力学问题,如弯 曲、剪切、扭转等,以及如何运用计算方 法解决这些问题。
桥梁结构的稳定性分析
实际案例分析
讲解了如何进行桥梁结构的稳定性分析, 包括线性与非线性分析方法,以及如何评 估桥梁的稳定性。
某大桥设计计算
总结词:动态分析
详细描述:为了确保大桥在各种环境下的稳定性,设计团队进行了动态分析,模拟了风、雨、地震等 多种自然灾害对桥梁的影响,为后续的施工和运营提供了有力保障。
结构设计大赛计算书
结构设计计算说明书
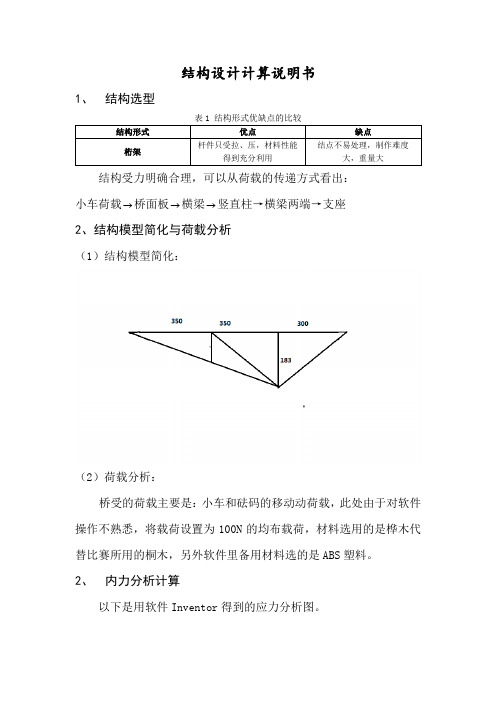
1、结构选型
结构受力明确合理,可以从荷载的传递方式看出:
小车荷载→桥面板→横梁→竖直柱→横梁两端→支座
2、结构模型简化与荷载分析
(1)结构模型简化:
(2)荷载分析:
桥受的荷载主要是:小车和砝码的移动动荷载,此处由于对软件操作不熟悉,将载荷设置为100N的均布载荷,材料选用的是桦木代替比赛所用的桐木,另外软件里备用材料选的是ABS塑料。
2、内力分析计算
以下是用软件Inventor得到的应力分析图。
3、构件的安全系数分析
4、结论
假设在该结构下梁中心处受到均布100N作用时,上面梁受到最大压应力为16.78MPa,实际条件提供为桐木,因此应该和Inventor软件分析的结果类似。
况且考虑到实际情况,不可能
一直承受100N的均布载荷,所以实际承载应该可以满足要求。
竞赛培训之02:结构设计竞赛赛题解读

Structural Design Contest
长江大学 结构设计竞赛培训课件(黄文雄)
要点解读: 失效准则:模型制作的注意点!!!
School of Urban Construction, Yangtze University PRODUCED BY:Wenxiong Huang
6 评分标准
总分100分,分如下6项:
1)计算书(10分):内容(6分)+图文(4分) 2)结构选型与制作质量(10分): 结构合理创新(6分)+模型制作美观(4分) 3)现场表现(5分):现场陈述(3分)+现场答辩(2分) 4)模型质量(25分):K MM 25 5)模型刚度(25分):K EE 25 Ed d1 2 d1 4 d3 4 6)结构线型(25分):K E 25 E 5d 4d d
一起学习、一起探讨、一起思考、共同进步!
长江大学城市建设学院:黄文雄 2014.03.30
School of Urban Construction, Yangtze University PRODUCED BY:Wenxiong Huang
尺寸要求:
加载设施:计入总重,纸质材料制作
School of Urban Construction, Yangtze University PRODUCED BY:Wenxiong Huang
2 赛题题目与模型要求
2.2 模型要求
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
桥梁结构设计理论方案作品名称蔚然水岸参赛学院建筑工程学院参赛队员吕远、李丽平、李怡潇、赵培龙专业名称土木工程一、方案构思1、设计思路对于这次的设计,我们分别考虑了斜拉桥、拱桥、梁式桥和桁架桥的设计方案。
斜拉桥可以看作是小跨径的公路桥,且对刚度有较高的要求,所以斜拉桥对材料的要求比较高,对于用桐木强度比不上其他样式的桥来得结实;拱桥最大主应力沿拱桥曲面而作用,而沿拱桥垂直方向最小主应力为零,可以很好的控制桥梁竖直方向的位移,但锁提供的支座条件较弱,且不提供水平力,显然也不是一个好的选择;梁式桥有较好的承载弯矩的能力,也可以较好的控制使用中的变形,但桥梁的稳定性是个很大的问题,控制不了桥梁的扭转变形,因此,我们也放弃了制作梁式桥的想法;而桁架桥具有比较好的刚度,腹杆即可承拉亦可承压,同时也可以较好的控制位移用料较省,所以,相比之下我们最后选择了桁架桥。
2、制作处理(1)、截杆裁杆是模型制作的第一步。
经过试验我们发现,截杆时应该根据不同的杆件,采用不同的截断方法。
对于质地较硬的杆应该用工具刀不断切磋,如同锯开;而对于较软的杆应该直接用刀刃用力按下,不宜用刀口前后切磋,易造成截面破损。
(2)、端部加工端部加工是连接的是关键所在。
为了能很好地使杆件彼此连接,我们根据不同的连接形式,对连接处进行处理,例如,切出一个斜口,增大连接的接触面积;刻出一个小槽,类似榫卯连接等。
(3)拼接拼接是本模型制作的最大难点。
由于是杆件截面较小,接触面积不够,乳胶干燥较慢等原因,连接是较为困难的。
我们采取了很多措施加以控制,如用铁夹子对连接处加强压、用蜡线进行绑扎固定等。
对于拱圈的制作,则预先将杆件置于水中浸泡并加上预应力使其不断弯曲,并按照先前划定的拱形不断调整,直至达到理想形状。
在拱脚处处理时,先粘结一个小的木块,让后用铁夹子施加很大的压力,保证连接能足够牢固。
乳胶粘接时要不断用电吹风间断性地吹风,使其尽快形成粘接力,达到强度的70%(基本固定)后即可让其自行风干。
(4)风干模型制作完成后,再次用吹风机间断性地吹粘接处,基本稳定后,让其自然风干。
(5)修饰在模型完成之后,为了增强其美观性,用砂纸小心翼翼的将杆件表明的毛刺打磨光滑,注意不要破坏结构,以免影响其稳定。
3、设计假定(1)、材质连续,均匀;(2)、梁与索之间结点为铰结;梁与塔柱(撑杆)之间的连接为刚结;撑杆与下部拉条之间为铰结;桥梁支座为连续弹性支座;(3)、桥面和桥梁本身质量以均布荷载作用在整个梁上;加载时,车辆移动荷载以集中力的形式作用在指定的梁上。
(4)、杆件计算时采用结构的计算模式;根据以上假定,通过结构力学求解器建立计算模型,所得的内力和位移作为构件设计的依据。
二、材料的力学性能1、桐木根据试验分析数据,每次试验有三到四组试验数据,剔除无效的数据,采用有效数据的平均值,根据弹性理论计算桐木的弹性模量E。
拉伸试验:(1)2×2木杆:去除第三组偏差较大的数据E1=F×L/(△L×A)=168.714×70/(2×2×2.5307)=1166.67MPaE2=F×L/(△L×A)=178.0272×70/(2×2×2.2598)=1378.65MPaE=(E1+E2)/2=1272.66MPa(2)2×5木杆:E1=F×L/(△L×A)=471.1845×70/(2×5×3.8002)=867.93MPaE2=F×L/(△L×A)=462.1775×70/(2×5×3.8319)=844.29MPaE=(E1+E2)/2=856.11MPa(3)2×10木杆:E1=F×L/(△L×A)=404.9354×110/(2×10×2.713)=820.83MPaE2=F×L/(△L×A)=694.5129×110/(2×10×2.985)=1279.33MPaE3=F×L/(△L×A)=203.97×110/(2.10×1.738)=645.47MPaE=(E1+E2+E3)/3=915.21MPa(4)3×3木杆:E1=F×L/(△L×A)=281,436×70/(3.3,3.581)=611.27MPaE2=F×L/(△L×A)=314.277×70/(3×3×6.4352)=379.84MPaE3=F×L/(△L×A)=299.169×70/(3×3×7.2362)=321.56MPaE=(E1+E2+E3)/3=437.56MPa(5)3×5木杆:去除第三组偏差较大的数据E1=F×L/(△L×A)=515.566×70/(3×5×3.6519)=658.83MPaE2=F×L(△L×A)=1085.104×70/(3×5×7.4596)=676.11MPaE=(E1+E2)/2=667.47MPa(6)4×6木杆:去除第三组偏差较大的数据E1=F×L/(△L×A)=976.335×70/(4×6×4.6522)=608.18MPaE2=F×L/(△L×A)=798.416×70/(4×6×4.7955)=485.60MPaE=(E1+E2)/2=546.89MPa由以上计算数据可以得出,截面越大,计算得到的弹性越小。
这是由于木材内部的缺陷导致的,桐木截面面积越大,截面越对称,所含的缺陷对弹性模量E的影响越小。
因此,我们取弹性模量E=60OMPa。
此外,根据木材的拉伸、压缩试验,压杆试验及弯曲试验的试验结果,我们还可以得出以下结论:①桐木的顺纹抗压强度比抗拉强度低,因此用桐木做拉杆能够更好的利用材料。
② 4×6木杆的抗弯强度比抗压强度降低很多.要充分利用材料,使之受拉较好.③ 桐木强度指标的离散性大,变异性强。
由一于内部结构不均匀份致的应力集中所致。
尤其是抗拉强度,因此受拉杆件宜采用较大的安全系数。
在计算桐木的弹性模量时,要充分考虑这个影响因素,选用有效的实验数据。
④ 木在受压时,在某个较小力值范围内会产生很大的变形;当变形到达一定数值时,桐木所能承受的压力急剧增大,但此时变形却很小。
⑤桐木为各向异性材料,顺纹方向与横纹方向受力性能差异较大。
制作中要避免横纹受力。
2、腊线根据试验数据,由公式E=F ×L/(△L ×A )计算出腊线的弹性模量,在试验数据的取值方面,由于多股腊线由单股腊线人工搓捻而成,因此多股腊线的受拉承载力受人为因素的影响,故在数据的选取中我们取保守值。
计算单股腊线的弹性模量:E=F ×L/(△L ×A)=37.2539×200/(4×20.7×14.6275)=1323.566MPa·图表资料(2)双股腊线计算双股腊线的弹性模量:E=F×L/(△L×A)=90.905×200/(4π×20.7×21.5295)=2194.309 ·图表资料(3)三股腊线计算三股腊线的弹性模量:E=F×L/(△L×A)=114.6968×200/(4π·20.7·18.7512》=3178.822MPa·图表资料(4)四股腊线计算四股腊线的弹性模量:E=F×L/(△L×A)=153.4951×200/(4×20.7×23.6309)=3375.657MPa·图表资料由于以上的计算结果及图表资料得知,由于人工搓绳的不确定性较大.不能保证多股腊线与单股腊线的弹性模量的倍数关系。
因此,腊线的弹性模量:E=1323.566 MPa三、方案立体图四、计算书1、结构选型:我们所设计的桥采用的是空间组合形式,结构以梁承受抗弯,以腹杆承受抗压抗拉。
桁架桥结构应用桐木材料和线索柔性构件抗拉强度高的腊线,结构可以做到结构自重相对较轻,体系的刚度和形状稳定性相对较大,因而可以跨越很大的空间。
同时四棱锥式的设计有避免了结构受侧向力和扭转的影响,并可以使满载时的小车可以顺利通过。
2、荷载分析桥的主要承重为:桥面板和梁本身的重量和车辆移动荷载。
(1)桥面板和梁本身的重量。
桐木材料的平均重量为0.5g/cm平方,考虑乳胶及其他因素,将其扩大至N/M。
桥梁长1660mm,经计算,桥梁自重约为g。
将其设置为均匀荷载,经计算得q=1.3N/m,考虑乳胶及其他因素,将q扩大至q=2N/m(2)车辆移动荷载。
通过做影响线确定梁、腹杆和腊线的最不利荷载位置,进而求出桥面梁和拉索的极限力和弯距。
将小车在车轮与桥面接触点简化成2个集中荷载,同时车辆通过速度可控制,所以在任意时刻可以按静载处理。
这样每条主梁同时受均布力及两个集中荷载。
小车质量=15kg。
经过计算,每个集中荷载为N=73.5N另外在加载时会存在一定的动力效应,及加载时的不均匀性等不利因素的影响,采取在制做时适当加强构件的措施,计算时不予考虑。
3、简化模型4、计算简图由于集中荷载为可动荷载,分四种最不利情况考虑,如图所示:(1)(2)(3)(4)5、荷载分析。
