matlab实习报告
MATLAB实验报告

MATLAB实验报告一、实验目的本次 MATLAB 实验旨在深入了解和掌握 MATLAB 软件的基本操作和应用,通过实际编程和数据处理,提高解决问题的能力,培养编程思维和逻辑分析能力。
二、实验环境本次实验使用的是 MATLAB R2020a 版本,运行在 Windows 10 操作系统上。
计算机配置为英特尔酷睿 i5 处理器,8GB 内存。
三、实验内容(一)矩阵运算1、矩阵的创建使用直接输入、函数生成和从外部文件导入等方式创建矩阵。
例如,通过`1 2 3; 4 5 6; 7 8 9` 直接输入创建一个 3 行 3 列的矩阵;使用`ones(3,3)`函数创建一个 3 行 3 列元素全为 1 的矩阵。
2、矩阵的基本运算包括矩阵的加减乘除、求逆、转置等。
例如,对于两个相同维度的矩阵`A` 和`B` ,可以进行加法运算`C = A + B` 。
3、矩阵的特征值和特征向量计算通过`eig` 函数计算矩阵的特征值和特征向量,加深对线性代数知识的理解和应用。
(二)函数编写1、自定义函数使用`function` 关键字定义自己的函数,例如编写一个计算两个数之和的函数`function s = add(a,b) s = a + b; end` 。
2、函数的调用在主程序中调用自定义函数,并传递参数进行计算。
3、函数的参数传递了解值传递和引用传递的区别,以及如何根据实际需求选择合适的参数传递方式。
(三)绘图功能1、二维图形绘制使用`plot` 函数绘制简单的折线图、曲线等,如`x = 0:01:2pi; y = sin(x); plot(x,y)`绘制正弦曲线。
2、图形的修饰通过设置坐标轴范围、标题、标签、线条颜色和样式等属性,使图形更加清晰和美观。
3、三维图形绘制尝试使用`mesh` 、`surf` 等函数绘制三维图形,如绘制一个球面`x,y,z = sphere(50); surf(x,y,z)`。
(四)数据处理与分析1、数据的读取和写入使用`load` 和`save` 函数从外部文件读取数据和将数据保存到文件中。
matlab实训心得体会(通用23篇)

matlab实训心得体会(通用23篇)matlab实训篇1自己刚刚接触matlab有半个学期的时间,说实话我现在对MATLAB还是摸不着头脑,一方面是自己接触的时间太短,另一方面,就是自己在上机方面投入的时间有限,实践比较少。
现在,我对MATLAB的印象仅仅在解决习题和绘制图形上,但是我很喜欢MATLAB的简单的语法,易于绘制图形,编程也非常容易, 并且具有功能强大的开放式的toolbox。
因此,尽管我一直没有这方面的应用,但是我还是对它非常感兴趣,自己正打算暑假好好研究研究MATLAB。
下面是我学习MATLAB在理论和实践方面的一点心得与体会,可能有些地方自己理解的不是很正确,但是随着学习的深入,我想我可以发现自己的错误所在。
首先我想说的是,在理论方面,在学习MATLAB过程中,我感觉到它和c语言有许多相似之处,他有c语言的特征,但是比c语言编程计算更加简单,适合于复杂的数学运算。
但是MATLAB跟其他语言也有着很大的不同。
现在用的比较多的编程语言,除了MATLAB就应该是c、c++、VHDL,VB和Delphi也接触过,如果自己抱着“把其他语言的思想运用在MATLAB里面”的话,那么我想,即使程序运行不出错,也很难把握MATLAB的精髓,也就很难发挥MATLAB的作用了。
众所周知MATLAB是一个基于矩阵运算的软件,但是,真正在运用的时候,特别是在编程的时候,许多人往往没有注意到这个问题。
在使用MATLAB时,受到了其他编程习惯的影响,特别是经常使用的C语言。
因此,在MATLAB编程时,for循环(包括while循环)到处都是。
.这不仅是没有发挥MATLAB所长,还浪费了宝贵的时间。
我这里想说的一点是,往往在初始化矩阵的时候注意到这个问题,懂得了使用矩阵而不是循环来赋值,但是,在其他环节上,就很容易疏忽,或者说,仍然没有摆脱C++、C的思想。
MATLAB博大精深,涉及的内容很多,所以,我认为不要试图掌握MATLAB的每一个功能,熟悉和你专业最相关的部分就可以了,这也是老师在课堂上经常说的。
matlab_实习报告

matlab_实习报告在大学的学习生涯中,实习是一个非常重要的环节,它能够让我们将理论知识与实际应用相结合,提升自己的专业技能和综合素质。
本次实习,我选择了使用 MATLAB 这个强大的工具进行实践操作,通过一段时间的学习和实践,我收获颇丰。
一、实习目的本次实习的主要目的是深入了解和掌握MATLAB 软件的使用方法,能够运用其解决实际问题,并提高自己的编程能力和逻辑思维能力。
同时,通过实际项目的操作,培养自己的团队协作精神和解决问题的能力,为今后的学习和工作打下坚实的基础。
二、实习单位及岗位介绍我实习的单位是_____,在实习期间,我主要负责利用 MATLAB 进行数据分析和算法实现的相关工作。
三、实习内容及过程(一)基础学习在实习的初期,我首先对 MATLAB 的基本语法和操作进行了系统的学习。
了解了变量的定义、数据类型、矩阵运算、函数的编写等基础知识。
通过大量的练习和实例,我逐渐熟悉了 MATLAB 的编程环境,能够熟练地编写简单的程序。
例如,在学习矩阵运算时,我通过编写程序实现了矩阵的加法、乘法、求逆等操作,深刻理解了矩阵运算在数学和工程中的重要应用。
(二)项目实践在掌握了基础知识后,我开始参与实际的项目。
其中一个项目是对一组数据进行分析和处理,以提取有用的信息。
首先,我使用MATLAB 读取数据文件,并对数据进行预处理,包括去除噪声、缺失值处理等。
然后,运用统计学方法对数据进行分析,计算均值、方差、相关性等统计量。
最后,通过绘图函数将分析结果以直观的图表形式展示出来,以便更好地理解数据的特征和趋势。
在这个过程中,我遇到了很多问题。
例如,数据的格式不一致导致读取错误,算法的复杂度过高导致运行时间过长等。
通过查阅资料、请教同事和不断地调试,我最终解决了这些问题,顺利完成了项目任务。
(三)算法实现除了数据分析,我还参与了算法的实现工作。
在一个图像识别的项目中,需要使用机器学习算法对图像进行分类。
MATLAB实习报告

MATLAB实习报告实习报告一、实习单位概述我在公司完成了为期两个月的MATLAB实习。
该公司是一家致力于研发和生产先进电子产品的科技型企业。
公司专注于电脑硬件和软件产品的开发,拥有一支强大的研发团队,同时与多个国内外知名大学与研究机构合作。
二、实习内容在实习期间,我主要负责开发一个基于MATLAB的图像处理算法,用于自动识别和分类图像中的目标物体。
具体而言,我的任务包括以下几个方面:1.数据预处理:对输入图片进行预处理,包括灰度化、降噪、图像增强等操作,以提高后续算法的准确性和鲁棒性。
2.特征提取:使用MATLAB内置的图像处理工具箱,提取目标物体的特征信息,如颜色、纹理、形状等。
3.目标识别:通过编写MATLAB脚本,实现目标物体的自动识别,使用机器学习算法训练分类器,并应用于测试集中的图像。
4.结果评估:对算法的准确性和性能进行评估,包括计算分类准确率、召回率等指标,并分析算法的优缺点和改进空间。
三、实习收获通过这次实习,我收获了许多宝贵的经验和知识。
首先,我深入学习了MATLAB的图像处理工具箱,了解了常用的图像处理算法和技术。
在实践中,我熟悉了MATLAB的基本语法和函数,并学会了如何利用MATLAB进行图像的读取、处理和保存。
其次,我掌握了图像特征提取和目标识别的方法和技巧。
通过对图像进行灰度化、降噪和图像增强等预处理步骤,我能够有效提取目标物体的特征信息,并通过机器学习算法实现目标的自动识别和分类。
最后,我学会了如何评估和改进算法的准确性和性能。
通过对测试集中的图像进行分类,并计算分类准确率和召回率等指标,我能够客观地评估算法的优劣,并提出针对性的改进方法。
四、实习总结通过这次实习,我不仅得到了理论知识的巩固和实践技能的提升,还培养了团队合作和解决问题的能力。
在与团队成员的合作中,我学会了如何与他人相互协作,分享经验与知识,并且通过互相帮助和配合,达到更好的工作效果。
同时,面对实习过程中遇到的问题和困难,我学会了如何利用各种资源和工具,积极主动地解决问题。
matlab实践报告

竭诚为您提供优质文档/双击可除matlab实践报告篇一:matlab实习报告mATLAb实习报告姓名:吴涛专业:电子信息工程班级学号:信息(2)班20XX1605010230指导教师:宋艳霞钱云实习时间:20XX,5,13至20XX,5,17目录:一:实习目的 (3)二:实习任务...........................三:实习要求...........................四:实习目的...........................五:实习体会...........................一:实习目的熟悉matlab的软件环境熟悉matlab的基本使用方法二:实习任务1.掌握matlab语言的基本语法规则及基本操作命令的使用。
2.熟悉运用matlab的数组,矩阵运算,数学运算的运算方法。
3.熟悉matlab的字符串,单元数组。
4.熟悉matlab的程序设计。
5.熟悉matlab的符号计算功能。
6.熟悉matlab的绘图及句柄图形。
7.6熟悉matlab的guI设计。
三:实习要求1.每次上机要签到,记录。
2.做的题目要在上机结束后以电子版和woRD文档形式交给指定负责人。
3.认真做一份实习总结报告。
四:实习内容共六题第1题:求a和b的和。
代码:a=[1,2,3]b=[4,5,6]s=a+b结果:s=579第2题:求a和b的差。
代码:a=[4,5,6]b=[1,2(:matlab实践报告),3]h=a-b结果:h=333第3题:求下列方程组的解。
6x1+3x2+4x3=3-2x1+5x2+7x3=-48x2-4x2-3x3=-7代码:A=[6,3,4;-2,5,7;8,-4,-3] b=[3;-4;-7]a=A\b结果:a=0.60007.0000-5.4000第4题:用for语句求三角函数表。
代码:forx=0:0.1:pi/4disp([x,sin(x),cos(x),tan(x)]),en d结果:00100.10000.09980.99500.10030.20000.19870.98010.20270.30000.29550.95530.30930.40000.38940.92110.4228篇二:matlab课程实践报告mATLAb实践》课程设计学生姓名:林淑真学号:110900824专业班级:通信工程四班指导教师:郑晓明二○一二年六月十五日《目录1.设计目的.........................................................22.题目分析.........................................................23.总体设计.........................................................34.具体设计.........................................................35.结果分析.........................................................226.心得体会.........................................................237.参考书目.........................................................238.附录 (24)1、设计目的综合运用mATLAb工具箱实现图像处理的guI程序设计。
matlab实习总结.(大全5篇)

matlab实习总结.(大全5篇)第一篇:matlab实习总结.MATLAB和Mathematica、Maple并称为三大数学软件。
它在数学类科技应用软件中在数值计算方面首屈一指。
MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连 matlab开发工作界面接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
MATLAB的基本数据单位是矩阵,它的指令表达式与数学、工程中常用的形式十分相似,故用MATLAB来解算问题要比用C,FORTRAN等语言完成相同的事情简捷得多,并且MATLAB也吸收了像Maple等软件的优点,使MATLAB成为一个强大的数学软件。
在新的版本中也加入了对C,FORTRAN,C++,JAVA的支持。
可以直接调用,用户也可以将自己编写的实用程序导入到MATLAB函数库中方便自己以后调用,此外许多的MATLAB爱好者都编写了一些经典的程序,用户可以直接进行下载就可以用Matlab是一个强大的数学工具,它的应用广泛,涉及到各个领域.它使用起来十分方便,不用麻烦去定义变量.它的绘图能力很强,甚至可以模拟出三维视图.矩阵是它应用的核心,许多工程繁琐的运算都需要靠矩阵来化简,这正是它的生命力所在.但是,他的函数很多,开始学时记的比较痛苦,我已经深深感觉到了.不过看多了也就熟了,感觉和学五笔差不多.它的语法简单,像我学过C语言的学起来还是蛮容易的.它的数组定义十分符合自然,是从1开始的,数组元素的调用也很接近数学的表达.此外,函数的名字也很符合英文规则,反正我用得很开心就是了.通过学习matlab,我又一次锻炼了自己的思维.它学起来得心应手也让我明白了学习一门语言(c语言对学习其他语言的帮助指导作用.同时,它也加强了我理论联系实际的能力.这是一个专业课的基础工具,学好它是必要的.在第一章中,讲的是一些matlab的入门技术,除了一些基本操作与介绍之外,还初步认识了简单指令的编制,认识了一些matlab 的特殊符号,例如运算用到的加减乘除。
matlab实验报告

(2)将上述信号左平移或右平移 得到两个新信号y2和y3,利用hold命令在同一图中显示三条曲线并通过线型和颜色加以区分。
(3)利用subplot命令将y,y2和y3以子图的形式显示。
3.
实验结果及分析
1.(1)
t1 =
0.0780
实验结果及分析
(2)
t2 =
0.0780
实验结果及分析
(3)
t3 =
0
实验结果及分析
2.
实验
名称
实验四Matlab在通信系统中的应用
实验目的
1、练习通信原理中各种调制方法及简单通信系统的Matlab编程实现;
2、学习Matlab与Simulink的混合编程。
(2)y变成虚数后,重复上述运算。
(3)创建矩阵 ,并进行如下操作,取出矩阵A的前两行元素,生成一个新矩阵B。生成一个3*3的单位矩阵B,与矩阵A进行加、减、乘、除、相等、不相等运算。
(4)随机生成2个复数x1和x2,计算x3=x1÷x2,x3的实部real_x3、虚部image_x3、模abs_x3、幅角angle_x3,并把x1,x2,x3,real_x3,image_x3,abs_x3,angle_x3保存至文件complex_学号.mat。利用save命令保存数据为mat格式文件后,用clear命令清除工作空间中的变量,再利用load命令从文件读入数据。
2、流程控制语句相关操作。
(1)使用for语句及while语句求解1至100整数中奇数的和。
(2)求连续自然数的和,当和大于等于1000时,求最后一个自然数以及自然数的和。
MATLAB_实习报告范文大全

MATLAB_实习报告范文大全第一篇:MATLAB_实习报告实习报告实习题目:专业:学号:的设计与绘图MATLAB 一.概述MATLAB 作为一种高级科学计算软件,是进行算法开发、数据可视化、数据分析以及数值计算的交互式应用开发环境。
世界上许许多多的科研工作者都在使用 MATLAB 产品来加快他们的科研进程,缩短数据分析和算法开发的时间,研发出更加先进的产品和技术。
二.实验目的1.进一步熟悉MATLAB的软件环境和基本使用方法;2.巩固运用MATLAB、矩阵运算、多项式运算、字符串、单元数组、符号计算功能、绘图及句柄图形及它们的命令语句;3.学习和巩固数字图形图像处理在MATLAB中的知识和运用;4.培养我们独立自学、设计和撰写实验报告的能力;5.通过对MATLAB的进一步学习,是我们加深所学内容的认识,理解,掌握,能把所学知识运用到实际工作中;三.实习日记1.熟悉MATLAB的软件环境和基本使用方法(第一周)MATLAB的语言的基本功能和特点:它是一种高级科学计算语言,相对于传统的C、C++ 或者FORTRAN 语言,MATLAB 提供了高效快速解决各种科学计算问题的方法。
它具有数学计算、开发工具、数据的可视化、交互式编辑创建图形、集成的算法开发编程语言和环境、图形用户界面开发环境——GUIDE、开放性、可扩展性强、专业应用工具箱等强大的功能。
具有易于学习、使用方便、支持多种操作系统、丰富的内部函数、强大的图形和符号功能等优点。
路径设置:除 MATLAB 默认的搜索路径外,用户可以设置搜索路径。
设置方法为:选择 MATLAB 窗口中的 File | Set Path 命令,进入路径搜索对话框。
MATLAB 的搜索顺序:当在命令窗口中或者一个 M 文件中输入一个元素名时,MATLAB 按照下面的顺序搜索该元素的意义,以元素foo 为例:1)查找工作区中是否存在名为 foo 的变量; 2)在当前路径中查找是否存在名 foo.m 的文件;3)按照顺序查找搜索路径中是否存在该文件。
MatLab实习心得体会3篇

MatLab实习心得体会 (2)MatLab实习心得体会 (2)精选3篇(一)在MatLab实习的期间,我学到了很多关于MatLab编程和数据分析的知识。
以下是我在实习中的心得体会:1. 学习编程基础知识:在实习开始前,我掌握了一些基础的编程知识,包括变量、数组、循环和条件语句等。
这些知识为我在MatLab实习中的编程工作打下了坚实的基础。
2. 探索MatLab的功能和工具箱:MatLab是一个非常强大的工具,它提供了许多功能和工具箱来帮助进行数据分析和建模。
在实习期间,我学会了如何使用MatLab的统计工具箱、图像处理工具箱等,这些工具使得我的数据分析工作更加高效和精确。
3. 学会解决问题的方法和技巧:在实习中,我碰到了许多编程和数据分析方面的问题。
通过解决这些问题,我学会了使用MatLab的调试工具和查找解决方案的能力。
这些经验使我在处理实际问题时变得更加自信和独立。
4. 提高编码速度和效率:MatLab是一个强大的编程语言,但在编写大型程序时,编码速度和效率非常重要。
在实习中,我意识到了编码速度和效率的重要性,并学会了一些提高编码速度和效率的技巧,如函数重用、向量化编程等。
5. 与团队合作和沟通能力:在实习期间,我有机会与其他团队成员一起工作,并参与一些团队项目。
这让我学会了与他人合作和沟通的重要性,如分享代码、交流想法和解决问题。
总的来说,MatLab实习使我获得了许多宝贵的经验和技能。
我不仅学到了关于MatLab编程和数据分析的知识,还提高了解决问题、合作和沟通的能力。
这些经验将对我未来的学习和职业发展产生积极的影响。
MatLab实习心得体会 (2)精选3篇(二)在进行MatLab实习的过程中,我学到了很多关于MatLab的知识和技巧,也锻炼了自己的解决问题的能力。
以下是我在实习过程中的一些心得体会:1. 熟练掌握基本语法:MatLab有很多基本的函数和语法,熟练掌握这些基本知识对于编写代码至关重要。
(完整word)Matlab实验报告
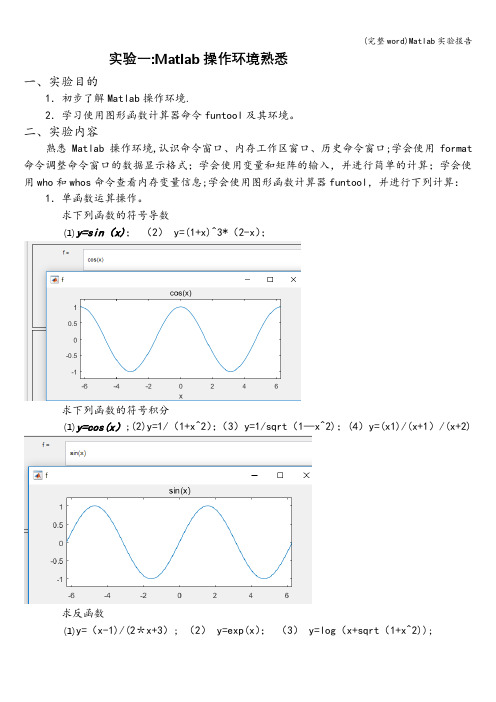
实验一:Matlab操作环境熟悉一、实验目的1.初步了解Matlab操作环境.2.学习使用图形函数计算器命令funtool及其环境。
二、实验内容熟悉Matlab操作环境,认识命令窗口、内存工作区窗口、历史命令窗口;学会使用format 命令调整命令窗口的数据显示格式;学会使用变量和矩阵的输入,并进行简单的计算;学会使用who和whos命令查看内存变量信息;学会使用图形函数计算器funtool,并进行下列计算:1.单函数运算操作。
求下列函数的符号导数(1)y=sin(x);(2) y=(1+x)^3*(2-x);求下列函数的符号积分(1)y=cos(x);(2)y=1/(1+x^2);(3)y=1/sqrt(1—x^2);(4)y=(x1)/(x+1)/(x+2)求反函数(1)y=(x-1)/(2*x+3); (2) y=exp(x);(3) y=log(x+sqrt(1+x^2));代数式的化简(1)(x+1)*(x-1)*(x-2)/(x-3)/(x—4);(2)sin(x)^2+cos(x)^2;(3)x+sin(x)+2*x—3*cos(x)+4*x*sin(x);2.函数与参数的运算操作。
从y=x^2通过参数的选择去观察下列函数的图形变化(1)y1=(x+1)^2(2)y2=(x+2)^2(3) y3=2*x^2 (4) y4=x^2+2 (5) y5=x^4 (6) y6=x^2/2 3.两个函数之间的操作求和(1)sin(x)+cos(x) (2) 1+x+x^2+x^3+x^4+x^5乘积(1)exp(—x)*sin(x) (2) sin(x)*x商(1)sin(x)/cos(x); (2) x/(1+x^2); (3) 1/(x—1)/(x—2); 求复合函数(1)y=exp(u) u=sin(x) (2) y=sqrt(u) u=1+exp(x^2)(3) y=sin(u) u=asin(x) (4) y=sinh(u) u=-x实验二:MATLAB基本操作与用法一、实验目的1.掌握用MATLAB命令窗口进行简单数学运算。
matlab实习报告二5篇

matlab实习报告二5篇第一篇:matlab实习报告二MATLAB实习报告(2)实验二 MATLAB矩阵分析与处理王夏一、实验目的1、掌握生成特殊矩阵的方法。
2、掌握矩阵分析的方法。
3、用矩阵求逆发解线性方程组。
二、实验内容1、设有分块矩阵A=[E3×3 R3×2;O2×3 S2×2],其中E、R、O、S分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证A²=[E R+RS;O S²]。
程序清单:E=eye(3);R=rand(3,2);O=zeros(2,3);S=diag([4,5]);A=[E R;O S] ;A2=A^2;C=[E R+R*S;O S^2];length(find(A2==C))==25 运行结果:ans =12、产生5阶希尔伯特矩阵H和5阶帕斯卡矩阵P,且求其行列式的值Hh和Hp以及他们的条件数Th和Tp,判断哪个矩阵的性能更好,为什么?程序清单:format rat H=hilb(5);format short P=pascal(5);Hh=det(H);Hp=det(P);Th=cond(A);Tp=cond(P);运行结果:Hh =3.7493e-012 Hp =1 Th =5.5228 Tp =8.5175e+003 实验收获:会建立希尔伯特矩阵和帕斯卡矩阵,知道怎么求矩阵行列式的值以及条件数。
希尔伯特矩阵的性能更好,条件数越接近1的矩阵性能越好。
3、建立一个5×5矩阵,求它的行列式值、迹、秩和范数。
程序清单:A=[1:5;1:0.1:1.5;2 5 7 3 9;2:6;3:0.4:4.6]Ha=det(A);Ra=rank(A);Ta=trace(A);Na=norm(A);运行结果:Ha =1.4421e-031 Ra = 3 Ta =18.7000 Na =19.49664、已知向量A,求A的特征值及特征向量,并分析其数学意义。
matlab 实验报告

matlab 实验报告Matlab实验报告引言:Matlab是一种强大的数值计算和可视化软件,广泛应用于科学、工程和经济等领域。
本实验报告将介绍我在使用Matlab进行实验过程中的一些经验和结果。
实验一:矩阵运算在这个实验中,我使用Matlab进行了矩阵运算。
首先,我创建了一个3x3的矩阵A和一个3x1的矩阵B,并进行了矩阵相乘运算。
通过Matlab的矩阵乘法运算符*,我得到了一个3x1的结果矩阵C。
接着,我对矩阵C进行了转置操作,得到了一个1x3的矩阵D。
最后,我计算了矩阵C和矩阵D的点积,并将结果输出。
实验二:数据可视化在这个实验中,我使用Matlab进行了数据可视化。
我选择了一组实验数据,包括时间和温度两个变量。
首先,我将数据存储在一个矩阵中,并使用Matlab的plot函数将时间和温度之间的关系绘制成曲线图。
接着,我使用Matlab的xlabel、ylabel和title函数添加了横轴、纵轴和标题。
最后,我使用Matlab的legend函数添加了图例,以便更好地理解图表。
实验三:数值积分在这个实验中,我使用Matlab进行了数值积分。
我选择了一个函数f(x)进行积分计算。
首先,我使用Matlab的syms函数定义了符号变量x,并定义了函数f(x)。
接着,我使用Matlab的int函数对函数f(x)进行积分计算,并将结果输出。
为了验证结果的准确性,我还使用了Matlab的diff函数对积分结果进行了求导操作,并与原函数f(x)进行了比较。
实验四:信号处理在这个实验中,我使用Matlab进行了信号处理。
我选择了一个音频文件,并使用Matlab的audioread函数读取了该文件。
接着,我使用Matlab的fft函数对音频信号进行了傅里叶变换,并将结果绘制成频谱图。
为了进一步分析信号的特征,我还使用了Matlab的spectrogram函数绘制了信号的时频图。
通过对信号的频谱和时频图的观察,我可以更好地理解信号的频率和时域特性。
matlab实习报告7

matlab实习报告7《matlab 实习报告 7》在大学的学习生涯中,我有幸参与了一次 MATLAB 的实习,这次实习让我对这一强大的数学计算和可视化工具,有了更深入的理解和掌握。
实习伊始,我对 MATLAB 的认知还停留在书本上的理论知识和简单的示例代码。
然而,随着实习的推进,我逐渐发现 MATLAB 的强大功能远远超出了我的想象。
首先,我学习了MATLAB 的基本语法和数据类型。
整数、浮点数、字符串、数组等各种数据类型在 MATLAB 中都有独特的表示和操作方式。
通过不断地练习和实践,我逐渐熟悉了如何定义变量、进行数据运算以及处理不同类型的数据。
在掌握了基本的数据操作后,我开始深入学习 MATLAB 的函数编写。
函数是 MATLAB 中实现复杂功能的重要手段。
通过自定义函数,我能够将重复使用的代码段封装起来,提高代码的可读性和可维护性。
例如,我编写了一个用于计算两个矩阵乘积的函数,通过输入两个矩阵,函数能够返回它们的乘积结果。
这个过程不仅锻炼了我的编程思维,还让我更加熟悉了矩阵运算的原理和方法。
接下来,我接触到了 MATLAB 的绘图功能。
绘图是直观展示数据和结果的重要方式。
我学会了使用 plot 函数绘制简单的折线图、使用bar 函数绘制柱状图、使用 hist 函数绘制直方图等等。
通过对数据进行可视化,我能够更清晰地理解数据的分布和趋势,从而为进一步的分析和处理提供了有力的支持。
在实习过程中,我还参与了一个实际的项目——图像去噪。
图像在采集和传输过程中往往会受到噪声的干扰,影响图像的质量和后续的处理。
利用 MATLAB 提供的图像处理工具和函数,我尝试了多种去噪算法,如均值滤波、中值滤波和高斯滤波等。
通过对不同算法的效果进行比较和分析,我最终找到了一种最适合当前图像的去噪方法。
这个过程让我深刻体会到了 MATLAB 在实际应用中的强大能力,也让我明白了理论知识与实际应用之间的紧密联系。
另外,MATLAB 的矩阵运算功能给我留下了深刻的印象。
MATLAB上机实习报告

Matlab上机实习实习报告十八周我们进行了本学期的第二次实习——Matlab上机实习。
本次实习一星期,共实习了五个部分。
分别是:一,Matlab基本操作;二,数值数组及其运算;三,Matlab图形绘制基础;四:SIMULINK仿真基础;五:句柄图形和图形用户界面制作。
下面分别介绍各部分内容:实习内容一Matlab基本操作1.实习目的:●掌握Matlab的启动和退出;●熟悉的命令窗口;●熟悉其它常用窗口和工具栏;2.输入一段程序:t=0:pi/50:4*pi;y0=exp(-t/3);y=exp(-t/3).*sin(3*t);plot(t,y,’-r’,t,y0,’:b’,t,-y0,’:b’)输出结果:3.了解文件中的一些功能和指令.例如:clear 清除当前工作区中所有变量clc 清除指令窗内容clf 清除图形窗口cd 设置当前工作目录exit,quit 退出MATLAB实习内容二数值数组及其运算1.实习目的●掌握一维数组的创建和寻访●掌握二维数组的创建和寻访●掌握MATLAB的矩阵和数组的运算●熟悉MATLAB关系操作和逻辑操作2.要求在闭区间[0,2pi]上产生50个等距采样的一维数组A,试用两种不同的指令实现。
要访问1到5元素如何实现;寻访7到最后一个元素如何实现;寻访第2.6.8个元素如何实现;寻访大于2的元素如何实现;给第3.5.9个元素赋值100如何实现:(1)>> A=linspace(0,2*pi,50);>> A=0:(50/49):50;>> AA =Columns 1 through 90 1.0204 2.0408 3.0612 4.0816 5.1020 6.1224 7.1429 8.1633Columns 10 through 189.1837 10.2041 11.2245 12.2449 13.2653 14.2857 15.3061 16.3265 17.3469Columns 19 through 2718.3673 19.3878 20.4082 21.4286 22.4490 23.4694 24.4898 25.5102 26.5306Columns 28 through 3627.5510 28.5714 29.5918 30.6122 31.6327 32.6531 33.6735 34.6939 35.7143Columns 37 through 4536.7347 37.7551 38.7755 39.7959 40.8163 41.8367 42.8571 43.8776 44.8980Columns 46 through 5045.9184 46.9388 47.9592 48.9796 50.0000(2)>> whos A>> A(1:5)ans =0 1.0204 2.0408 3.0612 4.0816(3)>> A(7:50)ans =Columns 1 through 86.12247.14298.16339.1837 10.2041 11.2245 12.2449 13.2653Columns 9 through 1614.2857 15.3061 16.3265 17.3469 18.3673 19.3878 20.4082 21.4286Columns 17 through 2422.4490 23.4694 24.4898 25.5102 26.5306 27.5510 28.5714 29.5918Columns 25 through 3230.6122 31.6327 32.6531 33.6735 34.6939 35.7143 36.7347 37.7551Columns 33 through 4038.7755 39.7959 40.8163 41.8367 42.8571 43.8776 44.8980 45.9184Columns 41 through 4446.9388 47.9592 48.9796 50.0000(4)>> A([2 6 8])ans =1.0204 5.1020 7.1429(5)>> poison=find(A>2)poison =Columns 1 through 143 4 5 6 7 8 9 10 11 12 13 14 15 16Columns 15 through 2817 18 19 20 21 22 23 24 25 26 27 28 29 30Columns 29 through 4231 32 33 34 35 36 37 38 39 40 41 42 43 44Columns 43 through 4845 46 47 48 49 50 (6)>> A([3 5 9])=100 (7)>> A=[1 2 3;4 5 6] A =1 2 3 4 5 63. 在指令窗口输入A=[1 2 3;4 5 6] 观察结果:分别用“全坐标”“单坐标”来寻访第2行第1列的元素,并说明二维数组元素的存储顺序。
matlab实验一实验报告

matlab实验一实验报告实验一:Matlab实验报告引言:Matlab是一种强大的数学软件工具,广泛应用于科学计算、数据分析和工程设计等领域。
本实验旨在通过使用Matlab解决实际问题,探索其功能和应用。
一、实验目的本次实验的主要目的是熟悉Matlab的基本操作和常用函数,了解其在科学计算中的应用。
二、实验内容1. 数值计算在Matlab中,我们可以进行各种数值计算,包括基本的加减乘除运算,以及更复杂的矩阵运算和方程求解。
通过编写相应的代码,我们可以实现这些功能。
例如,我们可以使用Matlab计算两个矩阵的乘积,并输出结果。
代码如下:```matlabA = [1 2; 3 4];B = [5 6; 7 8];C = A * B;disp(C);```2. 数据可视化Matlab还提供了强大的数据可视化功能,可以将数据以图表的形式展示出来,更直观地观察数据的规律和趋势。
例如,我们可以使用Matlab绘制一个简单的折线图,来展示某个物体在不同时间下的位置变化。
代码如下:```matlabt = 0:0.1:10;x = sin(t);plot(t, x);xlabel('Time');ylabel('Position');title('Position vs. Time');```3. 图像处理Matlab还可以进行图像处理,包括图像的读取、处理和保存等操作。
我们可以通过Matlab对图像进行增强、滤波、分割等处理,以及进行图像的压缩和重建。
例如,我们可以使用Matlab读取一张图片,并对其进行灰度化处理。
代码如下:```matlabimg = imread('image.jpg');gray_img = rgb2gray(img);imshow(gray_img);```三、实验结果与分析在本次实验中,我们成功完成了数值计算、数据可视化和图像处理等任务。
matlab专业实习报告

MATLAB专业实习报告引言本报告旨在总结我的MATLAB专业实习经历,介绍我在实习期间所学习到的知识和技能,并对实习过程中的困难和解决方案进行讨论。
实习目标在此次MATLAB专业实习中,我的主要目标是:1.掌握MATLAB编程语言的基本语法和使用方法;2.学习MATLAB在数据分析和可视化方面的应用;3.深入了解MATLAB在工程领域的应用,并学会解决实际问题;4.增强团队合作和沟通能力。
实习过程第一阶段:学习基础知识在实习开始之前,我花了一段时间系统地学习了MATLAB编程语言的基础知识。
我通过阅读MATLAB官方文档、参加在线培训课程和解决练习题来提高自己的编程能力。
第二阶段:数据分析和可视化在掌握了基础知识后,我开始学习MATLAB在数据分析和可视化方面的应用。
我学习了如何导入和处理各种类型的数据,并使用MATLAB内置函数进行统计分析和可视化展示。
第三阶段:工程实践在第二阶段的基础上,我开始将所学知识应用到实际工程问题中。
我参与了一个工程项目,该项目是开发一个用于控制系统设计的MATLAB工具。
在项目中,我与团队成员合作,负责编写代码、进行测试和提供技术支持。
第四阶段:总结与展望在实习的最后阶段,我对整个实习过程进行了总结,并对未来的学习和发展提出了展望。
通过这次实习,我不仅学到了MATLAB编程的基本知识和技能,还锻炼了自己的团队合作和沟通能力。
遇到的困难与解决方案在实习过程中,我也遇到了一些困难,例如: 1. 理解复杂的MATLAB函数和算法;2. 处理大型数据集时的内存限制问题;3. 与团队成员协调工作和解决问题。
针对这些困难,我采取了以下解决方案: 1. 通过仔细阅读MATLAB官方文档和参考书籍,结合在线资源和论坛寻求帮助,逐步理解复杂函数和算法的原理和用法; 2. 优化代码和采用分块处理的方法,以减少内存占用; 3. 主动与团队成员交流,及时沟通问题并寻求解决方案。
结论通过这次MATLAB专业实习,我不仅学到了专业知识和技能,还提高了自己的问题解决和团队合作能力。
Matlab上机实习报告

Matlab上机实习报告一、实习目的本次 Matlab 上机实习的主要目的是让我们熟悉并掌握 Matlab 软件的基本操作和应用,提高我们运用数学工具解决实际问题的能力。
通过实际的编程和计算,深入理解数学算法在计算机中的实现,培养我们的逻辑思维和创新能力。
二、实习环境实习使用的计算机操作系统为 Windows 10,安装的 Matlab 版本为R2020a。
计算机配置为:Intel Core i5 处理器,8GB 内存,512GB 固态硬盘。
三、实习内容1、矩阵运算在 Matlab 中,矩阵是最基本的数据结构。
我们首先学习了矩阵的创建、访问、修改和基本运算,如加法、减法、乘法、转置等。
通过实际的编程练习,掌握了如何利用矩阵运算解决线性方程组、求逆矩阵等问题。
例如,对于线性方程组 Ax = b,其中 A 是系数矩阵,x 是未知向量,b 是常数向量。
我们可以使用 Matlab 中的反斜杠运算符“\”来求解,即 x = A\b。
2、函数绘图Matlab 具有强大的绘图功能,能够直观地展示函数的性质和变化趋势。
我们学习了如何绘制二维和三维图形,包括折线图、散点图、柱状图、曲面图等。
通过调整绘图的参数,如线条颜色、标记形状、坐标轴范围等,可以使图形更加清晰和美观。
例如,绘制函数 y = sin(x) 在区间0, 2π 上的图像,可以使用以下代码:```matlabx = 0:001:2pi;y = sin(x);plot(x, y)```3、数值计算Matlab 提供了丰富的数值计算函数,如求积分、求导数、求解常微分方程等。
我们通过实际的案例,学会了如何运用这些函数来解决科学计算和工程中的问题。
例如,使用数值积分函数“quad”计算函数 f(x) = x^2 在区间 0, 1 上的定积分,可以使用以下代码:```matlabfunction f = myfun(x)f = x^2;endresult = quad(@myfun, 0, 1)```4、程序设计在实习过程中,我们还学习了 Matlab 的程序设计结构,包括顺序结构、选择结构(ifelse 语句)和循环结构(for 循环、while 循环)。
matlab实验一实验报告

matlab实验一实验报告一、实验目的本次实验的主要目的是熟悉 MATLAB 软件的基本操作环境和编程语法,通过实际编写和运行简单的程序,初步掌握 MATLAB 在数值计算、图形绘制和数据处理方面的基本功能。
二、实验环境本次实验使用的是 MATLAB R2020a 版本,运行在 Windows 10 操作系统上。
计算机配置为:Intel Core i5 处理器,8GB 内存。
三、实验内容及步骤1、矩阵运算创建一个 3×3 的矩阵 A,元素分别为 1 到 9。
创建一个 3×3 的零矩阵 B。
计算 A+B 和 A×B 的结果。
在 MATLAB 中,我们可以使用以下代码实现:```matlabA = 1 2 3; 4 5 6; 7 8 9;B = zeros(3);C = A + B;D = A B;disp(C);disp(D);```2、数据类型转换定义一个整数变量 x 为 5。
将 x 转换为双精度浮点数。
将 x 转换为字符串类型。
代码如下:```matlabx = 5;y = double(x);z = num2str(x);disp(y);disp(z);```3、函数调用定义一个函数 fun,输入参数为 x,返回值为 x 的平方。
调用函数 fun,计算 3 的平方。
函数定义及调用代码:```matlabfunction y = fun(x)y = x^2;endresult = fun(3);disp(result);```4、图形绘制绘制函数 y = sin(x)在区间0, 2π上的图像。
使用以下代码实现:```matlabx = 0:001:2pi;y = sin(x);plot(x, y);```四、实验结果1、矩阵运算A+B 的结果为:```matlab1 2 34 5 67 8 9```A×B 的结果为:```matlab0 0 00 0 00 0 0```2、数据类型转换将整数 5 转换为双精度浮点数,结果为 50000。
matlab实习报告总结

MATLAB实习报告总结介绍本文是对我在MATLAB实习过程中的总结与反思。
通过这次实习,我对MATLAB的使用有了更深入的了解,并且对实际问题的解决能力也有了提升。
实习目标在实习开始之前,我设定了以下几个目标: 1. 熟悉MATLAB的基本语法和常用函数; 2. 学习如何使用MATLAB解决实际问题; 3. 提升自己的编程能力和解决问题的思维能力。
实习过程第一阶段:熟悉MATLAB基本语法在实习开始之初,我花了一段时间来学习MATLAB的基本语法。
通过阅读官方文档和参考书籍,我了解了MATLAB的变量定义、矩阵运算、函数定义等基本概念和用法。
我利用空闲时间编写了一些简单的代码来巩固这些知识。
第二阶段:学习MATLAB的常用函数在熟悉基本语法之后,我开始学习MATLAB的常用函数。
我学习了MATLAB 中的统计分析函数、数据可视化函数、图像处理函数等。
通过学习这些函数,我可以更高效地处理和分析数据,同时也能够更好地展示我的结果。
第三阶段:实际问题的解决在掌握了MATLAB的基本语法和常用函数后,我开始尝试使用MATLAB解决一些实际问题。
我选择了一个与我的专业相关的问题,通过MATLAB对数据进行分析和建模。
在这个过程中,我遇到了一些困难和挑战,但通过查阅资料和请教同学,我最终成功解决了这些问题。
第四阶段:编程能力和思维能力的提升通过这次实习,我的编程能力和解决问题的思维能力得到了提升。
在实际问题的解决过程中,我学会了如何分析问题、设计算法、编写代码并调试。
通过与同学的讨论和交流,我也学会了如何思考和解决问题的不同角度。
总结与反思这次MATLAB实习让我受益匪浅。
通过实际操作,我深入了解了MATLAB的使用方法和技巧。
我学会了如何使用MATLAB解决实际问题,并且在这个过程中提升了自己的编程能力和解决问题的思维能力。
然而,我也发现了自己的不足之处。
在实习过程中,我有时会陷入“死记硬背”的状态,只注重语法和函数的使用,而不去思考问题背后的本质,这导致我在解决一些复杂问题时遇到了困难。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab实习报告实习总结报告;学校名称;实习类型学学软件MTLAB实习起止时间年月日至年;所在院(系);班级;学生姓名;学号;年月日;实习总结报告;2013年7月8日至7月26日,我们应数专业进行;这次认识实习分为两大部分:理论知识学习和上机实践;一、实习目的;这次实习的目的是使我们掌握MATLAB的基本知识;二、实习内容;(一)操作基础;MATLAB是一种用于科学计算的高实习总结报告学校名称实习类型学学软件MTLAB 实习起止时间年月日至年月日指导教师所在院(系)班级学生姓名学号年月日实习总结报告2013年7月8日至7月26日,我们应数专业进行了为期3周的实习。
这次认识实习分为两大部分:理论知识学习和上机实践学习。
这次认识实习使我对专业知识有了一定的了解,知道以后的学习重点,感受工作环节,为自己将来走向社会打下基础。
一、实习目的这次实习的目的是使我们掌握MATLAB的基本知识,能运用MATLAB来编写程序,解决一般性的问题,使得我们在完成本课程学习后,掌握MATLAB的基本知识和初步的编程能力,为以后的学习和工作提供了一个非常有用的工具。
二、实习内容(一)操作基础MATLAB是一种用于科学计算的高性能语言。
它将计算、可视化和程序设计集成在一个非常容易的环境中,使用我们熟悉的数学符号表示问题与答案。
MAT LAB系统由5个主要部分组成,包括开发环境、MATLAB数学函数库、MATLAB语言、图形、MATLAB应用程序接口。
对于MATLAB的操作基础,应该学会启动和退出MATLAB、MATLAB的桌面工具和开发环境、命令窗口、历史窗口等等。
(二)矩阵及其运算MATLAB,即“矩阵实验室”,它是以矩阵为基本运算单元。
因此,本书从最基本的运算单元出发,介绍MATLAB的命令及其用法。
1.矩阵的表示:MATLAB的强大功能之一体现在能直接处理向量或矩阵。
当然首要任务是输入待处理的向量或矩阵。
不管是任何矩阵(向量),我们可以直接按行方式输入每个元素:同一行中的元素用逗号(,)或者用空格符来分隔,且空格个数不限;不同的行用分号(;)分隔。
所有元素处于一方括号([ ])内;当矩阵是多维(三维以上),且方括号内的元素是维数较低的矩阵时,会有多重的方括号。
其中有:符号矩阵、大矩阵的生成、多维数组的创建、特殊矩阵的生成(主要有零矩阵(zero)、单位阵(eye)、全一阵(ones)、均匀分布随机矩阵(rand)、正态分布随机矩阵(randn)等)。
(三)程序设计与文件操作1.程序设计:Matlab既是一种语言,又是一种编程环境。
Matlab提供了很多方便用户的工具,用于管理变量、输入输出数据以及生成和管理M文件。
用户可在Matlab的命令窗口键入一个命令,也可以由它定义的语言在编辑器中编写应用程序,Matlab软件对此进行解释后,在Matlab环境下对它进行处理,最后返回结果 .MATLAB语言的显著特点:具有强大的矩阵运算能力:Matrix Laboratory(矩阵实验室),使得矩阵运算非常简单。
也是一种演算式语,MATLAB的基本数据单元是既不需要指定维数,也不需要说明数据类型的矩阵(向量和标量为矩阵的特例),而且数学表达式和运算规则与通常的习惯相同。
因此,MATLAB语言编程简单,使用方便。
2.文件操作:(1)指令驱动模式:即在MATLABM命令行窗口下用户输入单行指令时, M ATLAB立即处理这条指令,并显示结果,这就是MATLAB命令行方式。
缺点:命令行方式程序可读性差,而且不能存储,当处理复杂问题和大量数据时很不方便。
(2)M文件模式:将MATLAB语句构成的程序存储成以m为扩展名的文件,然后再执行该程序文件,这种工作模式称为程序文件模式。
(3)M语言文件可以分为主程序文件和函数文件, 一个M语言文件就是由若干MATLAB的命令组合在一起构成的。
M语言文件是标的纯文本格式的文件,其文件扩展名为.m。
MATLAB提供了meditor编辑器编辑M文件。
(四)数据分析与多项式计算MATLAB数据分析与多项式计算主要包括:数据统计处理、数据插值、曲线拟合、离散傅立叶变换、多项式计算等等。
在数据处理中我们要了解最大值和最小值,如果在程序中求一个矩阵的极值问题,max或min(x,[],1)代表的是每一列中最大值或最小值组合写成一个行矩阵,max或min(x,[],2)表示的是每一行中的最大值和最小值写成一个列矩阵。
在计算多项式时,了解root函数以及熟练地应用,将多项式每一项前系数都写入root中,便可以通过root函数求出根。
(五)解线性方程与函数极值线性方程:解线性方程包括:线性方程组求解、非线性方程数值求解、常微分方程初值问题的数值解法、函数极值等。
线性方程求解:(a)直接法:利用左除运算符的直接解法对于线性方程组Ax=b,可以利用左除运算符“\”求解:x=A\b。
(b)利用矩阵的分解求解线性方程组:矩阵分解是指根据一定的原理用某种算法将一个矩阵分解成若干个矩阵的乘积。
常见的矩阵分解有LU分解、QR分解、Cholesky分解,以及Schur分解、Hessenberg分解、奇异分解等。
(c)非线性方程组的求解:对于非线性方程组F(X)=0,用fsolve函数求其数值解。
fsolve函数的调用格式为:X=fsolve('fun',X0,option)其中X为返回的解,fun是用于定义需求解的非线性方程组的函数文件名,X0是求根过程的初值,option为最优化工具箱的选项设定。
最优化工具箱提供了20多个选项,用户可以使用optimset命令将它们显示出来。
如果想改变其中某个选项,则可以调用optimset()函数来完成。
例如,Display选项决定函数调用时中间结果的显示方式,其中‘off’为不显示,‘iter’表示每步都显示,‘final’只显示最终结果。
optimset(‘Display’,‘off’)将设定Display选项为‘off’。
(六)符号计算在数值计算中,计算机处理的对象和得到的结果都是数值,而在符号计算中,计算机处理的数据和得到的结果都是符号。
符号计算中首先要对符号变量进行定义。
Sym只能为单个符号变量定义,而Syms可以为多个进行定义。
定义之后,可以进行符号计算,主要用于研究符号微积分运算。
求解符号微分,可以直接采用diff()函数进行求解;符号的积分,可以使用int()函数进行计算,最后调用M文件得到正确结果。
(七)数值积分与微分MATLAB数值积分与微分主要包括:数值积分与数值微分。
求解定积分的数值方法多种多样,如简单的梯形法、辛普生(Simpson)?法、牛顿-柯特斯(Newt on-Cotes)法等都是经常采用的方法。
基本思想都是将整个积分区间[a,b]分成n 个子区间[xi,xi+1],i=1,2,?,n,其中x1=a,xn+1=b。
这样求定积分问题就分解为求和问题。
二重定积分的数值求解:使用MATLAB提供的dblquad函数就可以直接求出二重定积分的数值解。
该函数的调用格式为: I=dblquad(f,a,b,c,d,tol,trac e)该函数求f(x,y)在[a,b]×[c,d]区域上的二重定积分。
参数tol,trace的用法与函数quad完全相同。
(八)微分方程符号解法和数值解法solve函数的使用Solve(‘p*sin(x)=r’) ans=asin(r/p),dsolve函数的一般调用形式是:dsolve(‘s’,’s1’;(九)绘图操作;二维图形可以采用ezplot进行绘图,一般形式是;ezplot(f,[a,b])表示的是回执函数y;三维图形或者多维图形一般采用ezplot3进行绘;(十)图形用户界面设计图形用户和界面设计中我们要;(十一)统计方法及其应用;概率分布及其有关函数中,常用的是pdf,cdf,;(十二)图形句柄;的一般调用形式是:dsolve(‘s’,’s1’,’s2’...)(s为方程,s1,s 2,s3,为初始条件,x为自变量)。
Ode45表示的是常微分方程的数值求解。
通过此函数可以很方便快速的求出有关微分方程求解的问题。
(九)绘图操作二维图形可以采用ezplot进行绘图,一般形式是:ezplot(f,[a,b])表示的是回执函数y=f(x)在区间(a,b)上的图像。
三维图形或者多维图形一般采用ezplot3进行绘图,一般形式是: ezplot 3(x,y,z)表示的是空间曲线x=x(t),y=y(t),z=z(t),0<t<2*pi。
在输入以及输出数据时,通过改变初始数据,可以得到不同的结果。
(十)图形用户界面设计图形用户和界面设计中我们要遵循四个原则:简单性,一致性,习常性以及其他考虑因素。
如果建立主菜单条,菜单项句柄=ui menu(图形黄口句柄,属性名1,属性值1,...);子菜单句柄=uimenu(父菜单句柄,属性名1,属性值1,...)图形窗口的创建一般是窗口句柄=figure(属性名1,属性值1,属性名2,属性值2,...),对于图形用户界面设计工具-Gui de Control Panel要有简单的了解。
(十一)统计方法及其应用概率分布及其有关函数中,常用的是pdf,cdf,stat(概率密度,分布函数,均值与方差),以及样本均值mean和中值median,在描述性统计就是搜集.整理.加工和分析统计数据使之系统化。
在描述样本中心值的偏离程度中,有va r(方差),cov(协方差)等研究参数,同时还可以对参数进行估计,方差分析有anova1(单因素试验方差)和anova2(双因素试验),通过统计数据,最终进行统计图的绘制。
(十二)图形句柄图形句柄主要包括:图形对象及其句柄、图形对象属性、图形对象的创建。
我们学习了很多MATLAB高层绘图函数,这些函数都是将不同的曲线或曲面绘制在图形窗口中,而图形窗口也就是由不同图形对象(如坐标轴、曲线、曲面或文字等)组成的图形界面。
MATLAB给每个图形对象分配一个标志符,称为句柄。
以后可以通过该句柄对该图形对象的属性进行设置,也可以获取有关属性,从而能够更加自主地绘制各种图形。
直接对图形句柄进行操作的绘图方法称为低层绘图操作。
相对于高层绘图,低层绘图的操作控制和表现图形的能力更强,事实上,MATLAB的高层绘图函数都是利用低层绘图函数建立起来的。
有时单靠高层绘图不能满足要求,如,绘制特殊图形、建立图形用户界面等,这时就需要图形句柄操作。
三、实习心得这次实习我收获颇多,领会了很多东西,这次实习对于我们数学专业的学生意义重大。
可以说,这次实习完全做到了学以致用,正如陶行知先生所言:“知行合一”。
这对于我们以后的学习和将来走上工作岗位,有一定的借鉴意义。
