2017二次函数中考试题分类汇编
二次函数中考真题2017年(第1部分)
绝密★启用前二次函数中考真题--2017年第1部分一．解答题（共40小题）1．如图，抛物线y=ax2﹣x﹣2（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，已知B点坐标为（4，0）．（1）求抛物线的解析式；（2）试探究△ABC的外接圆的圆心位置，并求出圆心坐标；（3）若点M是线段BC下方的抛物线上一点，求△MBC的面积的最大值，并求出此时M点的坐标．2．如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（﹣1，0），B（4，0），C（0，﹣4）三点，点P是直线BC下方抛物线上一动点．（1）求这个二次函数的解析式；（2）是否存在点P，使△POC是以OC为底边的等腰三角形？若存在，求出P点坐标；若不存在，请说明理由；（3）动点P运动到什么位置时，△PBC面积最大，求出此时P点坐标和△PBC 的最大面积．3．如图，是将抛物线y=﹣x2平移后得到的抛物线，其对称轴为x=1，与x轴的一个交点为A（﹣1，0），另一个交点为B，与y轴的交点为C．（1）求抛物线的函数表达式；（2）若点N为抛物线上一点，且BC⊥NC，求点N的坐标；（3）点P是抛物线上一点，点Q是一次函数y=x+的图象上一点，若四边形OAPQ为平行四边形，这样的点P、Q是否存在？若存在，分别求出点P、Q的坐标；若不存在，说明理由．4．已知抛物线y=x2+bx﹣3（b是常数）经过点A（﹣1，0）．（1）求该抛物线的解析式和顶点坐标；（2）P（m，t）为抛物线上的一个动点，P关于原点的对称点为P'．①当点P'落在该抛物线上时，求m的值；②当点P'落在第二象限内，P'A2取得最小值时，求m的值．5．若三个非零实数x，y，z满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数x，y，z构成“和谐三组数”．（1）实数1，2，3可以构成“和谐三组数”吗？请说明理由；（2）若M（t，y1），N（t+1，y2），R（t+3，y3）三点均在函数y=（k为常数，k≠0）的图象上，且这三点的纵坐标y1，y2，y3构成“和谐三组数”，求实数t的值；（3）若直线y=2bx+2c（bc≠0）与x轴交于点A（x1，0），与抛物线y=ax2+3bx+3c （a≠0）交于B（x2，y2），C（x3，y3）两点．①求证：A，B，C三点的横坐标x1，x2，x3构成“和谐三组数”；②若a＞2b＞3c，x2=1，求点P（，）与原点O的距离OP的取值范围．6．在同一直角坐标系中，抛物线C1：y=ax2﹣2x﹣3与抛物线C2：y=x2+mx+n关于y轴对称，C2与x轴交于A、B两点，其中点A在点B的左侧．（1）求抛物线C1，C2的函数表达式；（2）求A、B两点的坐标；（3）在抛物线C1上是否存在一点P，在抛物线C2上是否存在一点Q，使得以AB 为边，且以A、B、P、Q四点为顶点的四边形是平行四边形？若存在，求出P、Q两点的坐标；若不存在，请说明理由．7．在平面直角坐标系中，我们定义直线y=ax﹣a为抛物线y=ax2+bx+c（a、b、c 为常数，a≠0）的“梦想直线”；有一个顶点在抛物线上，另有一个顶点在y轴上的三角形为其“梦想三角形”．已知抛物线y=﹣x2﹣x+2与其“梦想直线”交于A、B两点（点A在点B 的左侧），与x轴负半轴交于点C．（1）填空：该抛物线的“梦想直线”的解析式为，点A的坐标为，点B的坐标为；（2）如图，点M为线段CB上一动点，将△ACM以AM所在直线为对称轴翻折，点C的对称点为N，若△AMN为该抛物线的“梦想三角形”，求点N的坐标；（3）当点E在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上，是否存在点F，使得以点A、C、E、F为顶点的四边形为平行四边形？若存在，请直接写出点E、F的坐标；若不存在，请说明理由．8．如图，抛物线y=ax2+bx﹣3经过点A（2，﹣3），与x轴负半轴交于点B，与y 轴交于点C，且OC=3OB．（1）求抛物线的解析式；（2）点D在y轴上，且∠BDO=∠BAC，求点D的坐标；（3）点M在抛物线上，点N在抛物线的对称轴上，是否存在以点A，B，M，N 为顶点的四边形是平行四边形？若存在，求出所有符合条件的点M的坐标；若不存在，请说明理由．9．如图，二次函数y=x2+bx+c的图象与x轴交于A、B两点，与y轴交于点C，OB=OC．点D在函数图象上，CD∥x轴，且CD=2，直线l是抛物线的对称轴，E 是抛物线的顶点．（1）求b、c的值；（2）如图①，连接BE，线段OC上的点F关于直线l的对称点F'恰好在线段BE 上，求点F的坐标；（3）如图②，动点P在线段OB上，过点P作x轴的垂线分别与BC交于点M，与抛物线交于点N．试问：抛物线上是否存在点Q，使得△PQN与△APM的面积相等，且线段NQ的长度最小？如果存在，求出点Q的坐标；如果不存在，说明理由．10．如图，直线y=﹣x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y=﹣x2+bx+c经过点A，B．（1）求点B的坐标和抛物线的解析式；（2）M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点”．请直接写出使得M，P，N三点成为“共谐点”的m的值．11．如图，二次函数y=ax2+bx+c（a≠0）的图象交x轴于A、B两点，交y轴于点D，点B的坐标为（3，0），顶点C的坐标为（1，4）．（1）求二次函数的解析式和直线BD的解析式；（2）点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；（3）在抛物线上是否存在异于B、D的点Q，使△BDQ中BD边上的高为2？若存在求出点Q的坐标；若不存在请说明理由．12．如图，已知二次函数y=ax2+bx+4的图象与x轴交于点B（﹣2，0），点C（8，0），与y轴交于点A．（1）求二次函数y=ax2+bx+4的表达式；（2）连接AC，AB，若点N在线段BC上运动（不与点B，C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求N点的坐标；（3）连接OM，在（2）的结论下，求OM与AC的数量关系．13．如图，在平面直角坐标系中，抛物线y=x2﹣x﹣与x轴交于A、B 两点（点A在点B的左侧），与y轴交于点C，对称轴与x轴交于点D，点E（4，n）在抛物线上．（1）求直线AE的解析式；（2）点P为直线CE下方抛物线上的一点，连接PC，PE．当△PCE的面积最大时，连接CD，CB，点K是线段CB的中点，点M是CP上的一点，点N是CD上的一点，求KM+MN+NK的最小值；（3）点G是线段CE的中点，将抛物线y=x2﹣x﹣沿x轴正方向平移得到新抛物线y′，y′经过点D，y′的顶点为点F．在新抛物线y′的对称轴上，是否存在点Q，使得△FGQ为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．14．如图，抛物线y=﹣x2+x+2与x轴交于点A，B，与y轴交于点C．（1）试求A，B，C的坐标；（2）将△ABC绕AB中点M旋转180°，得到△BAD．①求点D的坐标；②判断四边形ADBC的形状，并说明理由；（3）在该抛物线对称轴上是否存在点P，使△BMP与△BAD相似？若存在，请直接写出所有满足条件的P点的坐标；若不存在，请说明理由．15．如图，抛物线y=mx2﹣16mx+48m（m＞0）与x轴交于A，B两点（点B在点A左侧），与y轴交于点C，点D是抛物线上的一个动点，且位于第四象限，连接OD、BD、AC、AD，延长AD交y轴于点E．（1）若△OAC为等腰直角三角形，求m的值；（2）若对任意m＞0，C、E两点总关于原点对称，求点D的坐标（用含m的式子表示）；（3）当点D运动到某一位置时，恰好使得∠ODB=∠OAD，且点D为线段AE的中点，此时对于该抛物线上任意一点P（x0，y0）总有n+≥﹣4my02﹣12y0﹣50成立，求实数n的最小值．16．如图，已知抛物线y=x2+bx+c的图象经过点A（l，0），B（﹣3，0），与y轴交于点C，抛物线的顶点为D，对称轴与x轴相交于点E，连接BD．（1）求抛物线的解析式．（2）若点P在直线BD上，当PE=PC时，求点P的坐标．（3）在（2）的条件下，作PF⊥x轴于F，点M为x轴上一动点，N为直线PF 上一动点，G为抛物线上一动点，当以点F，N，G，M四点为顶点的四边形为正方形时，求点M的坐标．17．如图，抛物线y=﹣x+2与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．（1）试探究△ABC的外接圆的圆心位置，求出圆心坐标；=S△ABC，求∠APB的度数；（2）点P是抛物线上一点（不与点A重合），且S△PBC（3）在（2）的条件下，点E是x轴上方抛物线上一点，点F是抛物线对称轴上一点，是否存在这样的点E和点F，使得以点B、P、E、F为顶点的四边形是平行四边形？若存在，请直接写出点F的坐标；若不存在，请说明理由．18．如图，抛物线y=ax2+bx+2经过点A（﹣1，0），B（4，0），交y轴于点C；（1）求抛物线的解析式（用一般式表示）；（2）点D为y轴右侧抛物线上一点，是否存在点D使S=S△ABD？若存在请△ABC直接给出点D坐标；若不存在请说明理由；（3）将直线BC绕点B顺时针旋转45°，与抛物线交于另一点E，求BE的长．19．如图，抛物线y=ax2+bx﹣a﹣b（a＜0，a、b为常数）与x轴交于A、C两点，与y轴交于B点，直线AB的函数关系式为y=x+．（1）求该抛物线的函数关系式与C点坐标；（2）已知点M（m，0）是线段OA上的一个动点，过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点，当m为何值时，△BDE恰好是以DE为底边的等腰三角形？（3）在（2）问条件下，当△BDE恰好是以DE为底边的等腰三角形时，动点M 相应位置记为点M′，将OM′绕原点O顺时针旋转得到ON（旋转角在0°到90°之间）；i．探究：线段OB上是否存在定点P（P不与O、B重合），无论ON如何旋转，始终保持不变．若存在，试求出P点坐标；若不存在，请说明理由；ii．试求出此旋转过程中，（NA+NB）的最小值．20．如图，抛物线y=ax2+bx﹣2的对称轴是直线x=1，与x轴交于A，B两点，与y轴交于点C，点A的坐标为（﹣2，0），点P为抛物线上的一个动点，过点P 作PD⊥x轴于点D，交直线BC于点E．（1）求抛物线解析式；（2）若点P在第一象限内，当OD=4PE时，求四边形POBE的面积；（3）在（2）的条件下，若点M为直线BC上一点，点N为平面直角坐标系内一点，是否存在这样的点M和点N，使得以点B，D，M，N为顶点的四边形是菱形？若存在，直接写出点N的坐标；若不存在，请说明理由．【温馨提示：考生可以根据题意，在备用图中补充图形，以便探究】21．如图甲，直线y=﹣x+3与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A，顶点为P．（1）求该抛物线的解析式；（2）在该抛物线的对称轴上是否存在点M，使以C，P，M为顶点的三角形为等腰三角形？若存在，请直接写出所符合条件的点M的坐标；若不存在，请说明理由；（3）当0＜x＜3时，在抛物线上求一点E，使△CBE的面积有最大值（图乙、丙供画图探究）．22．已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M（1，0），且a＜b．（Ⅰ）求抛物线顶点Q的坐标（用含a的代数式表示）；（Ⅱ）说明直线与抛物线有两个交点；（Ⅲ）直线与抛物线的另一个交点记为N．（ⅰ）若﹣1≤a≤﹣，求线段MN长度的取值范围；（ⅱ）求△QMN面积的最小值．23．如图，抛物线y=﹣x2+bx+c的图象与x轴交于A（﹣5，0），B（1，0）两点，与y轴交于点C，抛物线的对称轴与x轴交于点D．（1）求抛物线的函数表达式；（2）如图1，点E（x，y）为抛物线上一点，且﹣5＜x＜﹣2，过点E作EF∥x轴，交抛物线的对称轴于点F，作EH⊥x轴于点H，得到矩形EHDF，求矩形EHDF 周长的最大值；（3）如图2，点P为抛物线对称轴上一点，是否存在点P，使以点P，A，C为顶点的三角形是直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．24．如图所示，在平面直角坐标系xOy中，抛物线y=ax2﹣2ax﹣3a（a＜0）与x 轴交于A，B两点（点A在点B的左侧），经过点A的直线l：y=kx+b与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC．（1）求A、B两点的坐标及抛物线的对称轴；（2）求直线l的函数表达式（其中k、b用含a的式子表示）；（3）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为，求a 的值；（4）设P是抛物线对称轴上的一点，点Q在抛物线上，以点A、D、P、Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．25．如图，抛物线y=﹣x2+bx+c与x轴的两个交点分别为A（3，0），D（﹣1，0），与y轴交于点C，点B在y轴正半轴上，且OB=OD．（1）求抛物线的解析式；（2）如图1，抛物线的顶点为点E，对称轴交x轴于点M，连接BE，AB，请在抛物线的对称轴上找一点Q，使∠QBA=∠BEM，求出点Q的坐标；（3）如图2，过点C作CF∥x轴，交抛物线于点F，连接BF，点G是x轴上一点，在抛物线上是否存在点N，使以点B，F，G，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．26．如图，已知两直线l1，l2分别经过点A（1，0），点B（﹣3，0），且两条直线相交于y轴的正半轴上的点C，当点C的坐标为（0，）时，恰好有l1⊥l2，经过点A、B、C的抛物线的对称轴与l1、l2、x轴分别交于点G、E、F，D为抛物线的顶点．（1）求抛物线的函数解析式；（2）试说明DG与DE的数量关系？并说明理由；（3）若直线l2绕点C旋转时，与抛物线的另一个交点为M，当△MCG为等腰三角形时，请直接写出点M的坐标．27．如图，已知抛物线y=ax2+bx+c过点A（﹣1，0），B（3，0），C（0，3），点M、N为抛物线上的动点，过点M作MD∥y轴，交直线BC于点D，交x轴于点E．（1）求二次函数y=ax2+bx+c的表达式；（2）过点N作NF⊥x轴，垂足为点F，若四边形MNFE为正方形（此处限定点M在对称轴的右侧），求该正方形的面积；（3）若∠DMN=90°，MD=MN，求点M的横坐标．28．如图1，在平面直角坐标系xOy中，抛物线C：y=ax2+bx+c与x轴相交于A，B两点，顶点为D（0，4），AB=4，设点F（m，0）是x轴的正半轴上一点，将抛物线C绕点F旋转180°，得到新的抛物线C′．（1）求抛物线C的函数表达式；（2）若抛物线C′与抛物线C在y轴的右侧有两个不同的公共点，求m的取值范围．（3）如图2，P是第一象限内抛物线C上一点，它到两坐标轴的距离相等，点P 在抛物线C′上的对应点P′，设M是C上的动点，N是C′上的动点，试探究四边形PMP′N能否成为正方形？若能，求出m的值；若不能，请说明理由．29．如图所示，在平面直角坐标系中，⊙C经过坐标原点O，且与x轴，y轴分别相交于M（4，0），N（0，3）两点．已知抛物线开口向上，与⊙C交于N，H，P三点，P为抛物线的顶点，抛物线的对称轴经过点C且垂直x轴于点D．（1）求线段CD的长及顶点P的坐标；（2）求抛物线的函数表达式；=8S （3）设抛物线交x轴于A，B两点，在抛物线上是否存在点Q，使得S四边形OPMN，且△QAB∽△OBN成立？若存在，请求出Q点的坐标；若不存在，请说明△QAB理由．30．如图，直线y=﹣x+分别与x轴、y轴交于B、C两点，点A在x轴上，∠ACB=90°，抛物线y=ax2+bx+经过A，B两点．（1）求A、B两点的坐标；（2）求抛物线的解析式；（3）点M是直线BC上方抛物线上的一点，过点M作MH⊥BC于点H，作MD ∥y轴交BC于点D，求△DMH周长的最大值．31．如图1，经过原点O的抛物线y=ax2+bx（a≠0）与x轴交于另一点A（，0），在第一象限内与直线y=x交于点B（2，t）．（1）求这条抛物线的表达式；（2）在第四象限内的抛物线上有一点C，满足以B，O，C为顶点的三角形的面积为2，求点C的坐标；（3）如图2，若点M在这条抛物线上，且∠MBO=∠ABO，在（2）的条件下，是否存在点P，使得△POC∽△MOB？若存在，求出点P的坐标；若不存在，请说明理由．32．如图，抛物线y=﹣x2+bx+c与x轴交于点A和点B，与y轴交于点C，点B 坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点，过点D作x轴的垂线，垂足为E，连接BD．（1）求抛物线的解析式及点D的坐标；（2）点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；（3）若点M是抛物线上的动点，过点M作MN∥x轴与抛物线交于点N，点P 在x轴上，点Q在坐标平面内，以线段MN为对角线作正方形MPNQ，请写出点Q的坐标．33．抛物线y=ax2+bx+3经过点A（1，0）和点B（5，0）．（1）求该抛物线所对应的函数解析式；（2）该抛物线与直线y=x+3相交于C、D两点，点P是抛物线上的动点且位于x轴下方，直线PM∥y轴，分别与x轴和直线CD交于点M、N．①连结PC、PD，如图1，在点P运动过程中，△PCD的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；②连结PB，过点C作CQ⊥PM，垂足为点Q，如图2，是否存在点P，使得△CNQ与△PBM相似？若存在，求出满足条件的点P的坐标；若不存在，说明理由．34．如图，直线y=kx+b（k、b为常数）分别与x轴、y轴交于点A（﹣4，0）、B （0，3），抛物线y=﹣x2+2x+1与y轴交于点C．（1）求直线y=kx+b的函数解析式；（2）若点P（x，y）是抛物线y=﹣x2+2x+1上的任意一点，设点P到直线AB的距离为d，求d关于x的函数解析式，并求d取最小值时点P的坐标；（3）若点E在抛物线y=﹣x2+2x+1的对称轴上移动，点F在直线AB上移动，求CE+EF的最小值．35．已知函数y=mx2﹣（2m﹣5）x+m﹣2的图象与x轴有两个公共点．（1）求m的取值范围，并写出当m取范围内最大整数时函数的解析式；（2）题（1）中求得的函数记为C1．①当n≤x≤﹣1时，y的取值范围是1≤y≤﹣3n，求n的值；②函数C2：y=m（x﹣h）2+k的图象由函数C1的图象平移得到，其顶点P落在以原点为圆心，半径为的圆内或圆上．设函数C1的图象顶点为M，求点P与点M距离最大时函数C2的解析式．36．如图，在平面直角坐标系xOy中，抛物线y=x2﹣2x﹣3交x轴于A，B两点（点A在点B的左侧），将该抛物线位于x轴上方曲线记作M，将该抛物线位于x轴下方部分沿x轴翻折，翻折后所得曲线记作N，曲线N交y轴于点C，连接AC、BC．（1）求曲线N所在抛物线相应的函数表达式；（2）求△ABC外接圆的半径；（3）点P为曲线M或曲线N上的一动点，点Q为x轴上的一个动点，若以点B，C，P，Q为顶点的四边形是平行四边形，求点Q的坐标．37．如图，抛物线y=x2+bx+c经过B（﹣1，0），D（﹣2，5）两点，与x轴另一交点为A，点H是线段AB上一动点，过点H的直线PQ⊥x轴，分别交直线AD、抛物线于点Q，P．（1）求抛物线的解析式；（2）是否存在点P，使∠APB=90°，若存在，求出点P的横坐标，若不存在，说明理由；（3）连接BQ，一动点M从点B出发，沿线段BQ以每秒1个单位的速度运动到Q，再沿线段QD以每秒个单位的速度运动到D后停止，当点Q的坐标是多少时，点M在整个运动过程中用时t最少？38．如图，已知抛物线y=ax2+bx+1经过A（﹣1，0），B（1，1）两点．（1）求该抛物线的解析式；（2）阅读理解：在同一平面直角坐标系中，直线l1：y=k1x+b1（k1，b1为常数，且k1≠0），直线l2：y=k2x+b2（k2，b2为常数，且k2≠0），若l1⊥l2，则k1•k2=﹣1．解决问题：①若直线y=3x﹣1与直线y=mx+2互相垂直，求m的值；②抛物线上是否存在点P，使得△PAB是以AB为直角边的直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由；（3）M是抛物线上一动点，且在直线AB的上方（不与A，B重合），求点M到直线AB的距离的最大值．39．如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E的坐标分别为（3，0），（0，1）．（1）求抛物线的解析式；（2）猜想△EDB的形状并加以证明；（3）点M在对称轴右侧的抛物线上，点N在x轴上，请问是否存在以点A，F，M，N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．40．如图，在平面直角坐标系中，抛物线y=ax2+bx（a，b为常数，a≠0）经过两点A（2，4），B（4，4），交x轴正半轴于点C．（1）求抛物线y=ax2+bx的解析式．（2）过点B作BD垂直于x轴，垂足为点D，连接AB，AD，将△ABD以AD为轴翻折，点B的对应点为E，直线DE交y轴于点P，请判断点E是否在抛物线上，并说明理由．（3）在（2）的条件下，点Q是线段OC（不包含端点）上一动点，过点Q垂直于x轴的直线分别交直线DP及抛物线于点M，N，连接PN，请探究：是否存在点Q，使△PMN是以PM为腰的等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．二次函数中考真题参考答案与试题解析一．解答题（共40小题）1．如图，抛物线y=ax2﹣x﹣2（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，已知B点坐标为（4，0）．（1）求抛物线的解析式；（2）试探究△ABC的外接圆的圆心位置，并求出圆心坐标；（3）若点M是线段BC下方的抛物线上一点，求△MBC的面积的最大值，并求出此时M点的坐标．【分析】方法一：（1）该函数解析式只有一个待定系数，只需将B点坐标代入解析式中即可．（2）首先根据抛物线的解析式确定A点坐标，然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置，由此确定圆心坐标．（3）△MBC的面积可由S=BC×h表示，若要它的面积最大，需要使h取△MBC最大值，即点M到直线BC的距离最大，若设一条平行于BC的直线，那么当该直线与抛物线有且只有一个交点时，该交点就是点M．方法二：（1）略．（2）通过求出A，B，C三点坐标，利用勾股定理或利用斜率垂直公式可求出AC ⊥BC，从而求出圆心坐标．（3）利用三角形面积公式，过M点作x轴垂线，水平底与铅垂高乘积的一半，得出△MBC的面积函数，从而求出M点．【解答】方法一：解：（1）将B（4，0）代入抛物线的解析式中，得：0=16a﹣×4﹣2，即：a=；∴抛物线的解析式为：y=x2﹣x﹣2．（2）由（1）的函数解析式可求得：A（﹣1，0）、C（0，﹣2）；∴OA=1，OC=2，OB=4，即：OC2=OA•OB，又：OC⊥AB，∴△OAC∽△OCB，得：∠OCA=∠OBC；∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°，∴△ABC为直角三角形，AB为△ABC外接圆的直径；所以该外接圆的圆心为AB的中点，且坐标为：（，0）．（3）已求得：B（4，0）、C（0，﹣2），可得直线BC的解析式为：y=x﹣2；设直线l∥BC，则该直线的解析式可表示为：y=x+b，当直线l与抛物线只有一个交点时，可列方程：x+b=x2﹣x﹣2，即：x2﹣2x﹣2﹣b=0，且△=0；∴4﹣4×（﹣2﹣b）=0，即b=﹣4；∴直线l：y=x﹣4．所以点M即直线l和抛物线的唯一交点，有：，解得：即M（2，﹣3）．过M点作MN⊥x轴于N，S△BMC=S梯形OCMN+S△MNB﹣S△OCB=×2×（2+3）+×2×3﹣×2×4=4．方法二：（1）略．（2）∵y=（x﹣4）（x+1），∴A（﹣1，0），B（4，0）．C（0，﹣2），∴K AC==﹣2，K BC==，∴K AC×K BC=﹣1，∴AC⊥BC，∴△ABC是以AB为斜边的直角三角形，△ABC的外接圆的圆心是AB的中点，△ABC的外接圆的圆心坐标为（，0）．（3）过点M作x轴的垂线交BC′于H，∵B（4，0），C（0，﹣2），∴l BC：y=x﹣2，设H（t，t﹣2），M（t，t2﹣t﹣2），=×（H Y﹣M Y）（B X﹣C X）=×（t﹣2﹣t2+t+2）（4﹣0）=﹣t2+4t，∴S△MBC∴当t=2时，S有最大值4，∴M（2，﹣3）．【点评】考查了二次函数综合题，该题的难度不算太大，但用到的琐碎知识点较多，综合性很强．熟练掌握直角三角形的相关性质以及三角形的面积公式是理出思路的关键．2．如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（﹣1，0），B（4，0），C（0，﹣4）三点，点P是直线BC下方抛物线上一动点．（1）求这个二次函数的解析式；（2）是否存在点P，使△POC是以OC为底边的等腰三角形？若存在，求出P点坐标；若不存在，请说明理由；（3）动点P运动到什么位置时，△PBC面积最大，求出此时P点坐标和△PBC 的最大面积．【分析】（1）由A、B、C三点的坐标，利用待定系数法可求得抛物线解析式；（2）由题意可知点P在线段OC的垂直平分线上，则可求得P点纵坐标，代入抛物线解析式可求得P点坐标；（3）过P作PE⊥x轴，交x轴于点E，交直线BC于点F，用P点坐标可表示出PF的长，则可表示出△PBC的面积，利用二次函数的性质可求得△PBC面积的最大值及P点的坐标．【解答】解：（1）设抛物线解析式为y=ax2+bx+c，把A、B、C三点坐标代入可得，解得，∴抛物线解析式为y=x2﹣3x﹣4；（2）作OC的垂直平分线DP，交OC于点D，交BC下方抛物线于点P，如图1，∴PO=PC，此时P点即为满足条件的点，∵C（0，﹣4），∴D（0，﹣2），∴P点纵坐标为﹣2，代入抛物线解析式可得x2﹣3x﹣4=﹣2，解得x=（小于0，舍去）或x=，∴存在满足条件的P点，其坐标为（，﹣2）；（3）∵点P在抛物线上，∴可设P（t，t2﹣3t﹣4），过P作PE⊥x轴于点E，交直线BC于点F，如图2，∵B（4，0），C（0，﹣4），∴直线BC解析式为y=x﹣4，∴F（t，t﹣4），∴PF=（t﹣4）﹣（t2﹣3t﹣4）=﹣t2+4t，=S△PFC+S△PFB=PF•OE+PF•BE=PF•（OE+BE）=PF•OB=（﹣t2+4t）×∴S△PBC4=﹣2（t﹣2）2+8，∴当t=2时，S最大值为8，此时t2﹣3t﹣4=﹣6，△PBC∴当P点坐标为（2，﹣6）时，△PBC的最大面积为8．【点评】本题为二次函数的综合应用，涉及待定系数法、等腰三角形的性质、二次函数的性质、三角形的面积、方程思想等知识．在（1）中注意待定系数法的应用，在（2）中确定出P点的位置是解题的关键，在（3）中用P点坐标表示出△PBC的面积是解题的关键．本题考查知识点较多，综合性较强，难度适中．3．如图，是将抛物线y=﹣x2平移后得到的抛物线，其对称轴为x=1，与x轴的一个交点为A（﹣1，0），另一个交点为B，与y轴的交点为C．（1）求抛物线的函数表达式；（2）若点N为抛物线上一点，且BC⊥NC，求点N的坐标；（3）点P是抛物线上一点，点Q是一次函数y=x+的图象上一点，若四边形OAPQ为平行四边形，这样的点P、Q是否存在？若存在，分别求出点P、Q的坐标；若不存在，说明理由．【分析】（1）已知抛物线的对称轴，因而可以设出顶点式，利用待定系数法求函数解析式；（2）首先求得B和C的坐标，易证△OBC是等腰直角三角形，过点N作NH⊥y 轴，垂足是H，设点N纵坐标是（a，﹣a2+2a+3），根据CH=NH即可列方程求解；（3）四边形OAPQ是平行四边形，则PQ=OA=1，且PQ∥OA，设P（t，﹣t2+2t+3），代入y=x+，即可求解．【解答】解：（1）设抛物线的解析式是y=﹣（x﹣1）2+k．把（﹣1，0）代入得0=﹣（﹣1﹣1）2+k，解得k=4，则抛物线的解析式是y=﹣（x﹣1）2+4，即y=﹣x2+2x+3；（2）在y=﹣x2+2x+3中令x=0，则y=3，即C的坐标是（0，3），OC=3．∵B的坐标是（3，0），∴OB=3，∴OC=OB，则△OBC是等腰直角三角形．∴∠OCB=45°，过点N作NH⊥y轴，垂足是H．∵∠NCB=90°，∴∠NCH=45°，∴NH=CH，∴HO=OC+CH=3+CH=3+NH，设点N坐标是（a，﹣a2+2a+3）．∴a+3=﹣a2+2a+3，解得a=0（舍去）或a=1，∴N的坐标是（1，4）；（3）∵四边形OAPQ是平行四边形，则PQ=OA=1，且PQ∥OA，设P（t，﹣t2+2t+3），代入y=x+，则﹣t2+2t+3=（t+1）+，整理，得2t2﹣t=0，解得t=0或．∴﹣t2+2t+3的值为3或．∴P、Q的坐标是（0，3），（1，3）或（，）、（，）．当P在Q右边时，﹣t2+2t+3=（t﹣1）+，解得t=2或﹣，∴P（2，3），Q（1，3）（舍去）或P（﹣，﹣），Q（﹣，﹣）（舍去）．综上所述，P、Q的坐标是（0，3），（1，3）或（，）、（，）．【点评】本题考查了待定系数法求二次函数解析式，以及等腰三角形、平行四边形的性质，注意到△OBC是等腰直角三角形是解题的关键．4．已知抛物线y=x2+bx﹣3（b是常数）经过点A（﹣1，0）．（1）求该抛物线的解析式和顶点坐标；（2）P（m，t）为抛物线上的一个动点，P关于原点的对称点为P'．①当点P'落在该抛物线上时，求m的值；②当点P'落在第二象限内，P'A2取得最小值时，求m的值．【分析】（1）把A点坐标代入抛物线解析式可求得b的值，则可求得抛物线解析式，进一步可求得其顶点坐标；（2）①由对称可表示出P′点的坐标，再由P和P′都在抛物线上，可得到关于m 的方程，可求得m的值；②由点P′在第二象限，可求得t的取值范围，利用两点间距离公式可用t表示出P′A2，再由点P′在抛物线上，可以消去m，整理可得到关于t的二次函数，利用二次函数的性质可求得其取得最小值时t的值，则可求得m的值．【解答】解：（1）∵抛物线y=x2+bx﹣3经过点A（﹣1，0），∴0=1﹣b﹣3，解得b=﹣2，∴抛物线解析式为y=x2﹣2x﹣3，∵y=x2﹣2x﹣3=（x﹣1）2﹣4，∴抛物线顶点坐标为（1，﹣4）；（2）①由P（m，t）在抛物线上可得t=m2﹣2m﹣3，∵点P′与P关于原点对称，∴P′（﹣m，﹣t），∵点P′落在抛物线上，∴﹣t=（﹣m）2﹣2（﹣m）﹣3，即t=﹣m2﹣2m+3，∴m2﹣2m﹣3=﹣m2﹣2m+3，解得m=或m=﹣；②由题意可知P′（﹣m，﹣t）在第二象限，∴﹣m＜0，﹣t＞0，即m＞0，t＜0，∵抛物线的顶点坐标为（1，﹣4），∴﹣4≤t＜0，∵P在抛物线上，∴t=m2﹣2m﹣3，∴m2﹣2m=t+3，∵A（﹣1，0），P′（﹣m，﹣t），∴P′A2=（﹣m+1）2+（﹣t）2=m2﹣2m+1+t2=t2+t+4=（t+）2+；∴当t=﹣时，P′A2有最小值，∴﹣=m2﹣2m﹣3，解得m=或m=，∵m＞0，∴m=不合题意，舍去，∴m的值为．【点评】本题为二次函数的综合应用，涉及待定系数法、中心对称、二次函数的性质、勾股定理、方程思想等知识．在（1）中注意待定系数法的应用，在（2）①中求得P′点的坐标，得到关于m的方程是解题的关键，在（2）②中用t表示出P′A2是解题的关键．本题考查知识点较多，综合性较强，难度适中．5．若三个非零实数x，y，z满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数x，y，z构成“和谐三组数”．（1）实数1，2，3可以构成“和谐三组数”吗？请说明理由；（2）若M（t，y1），N（t+1，y2），R（t+3，y3）三点均在函数y=（k为常数，。
2017年全国中考数学真题分类 二次函数概念、性质和图象2017(解答题)
2017年全国中考数学真题分类 二次函数概念、性质和图象解答题三、解答题1. （2017山东滨州，24，14分）（本小题满分14分）如图，直线y ＝kx ＋b （k 、b 为常数）分别与x 轴、y 轴交于点A (－4，0)、B (0，3)，抛物线y ＝－x 2＋2x ＋1与y 轴交于点C ． （1）求直线y ＝kx ＋b 的解析式；（2）若点P (x ，y )是抛物线y ＝－x 2＋2x ＋1上的任意一点，设点P 到直线AB 的距离为d ，求d 关于x 的函数解析式，并求d 取最小值时点P 的坐标；（3）若点E 在抛物线y ＝－x 2＋2x ＋1的对称轴上移动，点F 在直线AB 上移动，求CE ＋EF 的最小值．思路分析：（1）将A 、B 两点坐标代入y ＝kx ＋b 中，求出k 、b 的值；（2）作出点P 到直线AB的距离后，由于∠AHC ＝90°，考虑构造“K 形”相似，得到△MAH 、△OBA 、△NHP 三个三角形两两相似，三边之比都是3∶4∶5．由“345NH CN CH==”可得23(3)(21)4345m x x x m d +--++-==，整理可得d 关于x 的二次函数，配方可求出d 的最小值；（3）如果点C 关于直线x ＝1的对称点C ′，根据对称性可知，CE ＝C ′E ．当C ′F ⊥AB 时，CE＋EF 最小． 解：（1）∵y ＝kx ＋b 经过A (－4，0)、B (0，3),∴403k b b -+=⎧⎨=⎩，解得k ＝34，b ＝3．∴y ＝34x ＋3．（2）过点P 作PH ⊥AB 于点H ，过点H 作x 轴的平行线MN ，分别过点A 、P 作MN 的垂线段，垂足分别为M 、N ．设H (m ，34m ＋3)，则M (－4，34m ＋3)，N (x ，34m ＋3)，P (x ，－x 2＋2x ＋1)．∵PH ⊥AB ，∴∠CHN ＋∠AHM ＝90°，∵AM ⊥MN ，∴∠MAH ＋∠AHM ＝90°．∴∠MAH ＝∠CHN ，∵∠AMH ＝∠CNH ＝90°，∴△AMH ∽△HNP ． ∵MA ∥y 轴，∴△MAH ∽△OBA ．∴△OBA ∽△NHP ． ∴345NH CN CH==． ∴23(3)(21)4345m x x x m d+--++-==． 整理得：24855d x x =-+，所以当x ＝58，即P (58，11964)．（3）作点C 关于直线x ＝1的对称点C ′，过点C ′作C ′F ⊥AB 于F ．过点F 作JK ∥x 轴，，分别过点A 、C ′作AJ ⊥JK 于点J ，C ′K ⊥JK 于点K ．则C ′(2，1)设F (m ，34m ＋3)∵C ′F ⊥AB ，∠AFJ ＋∠C ′FK ＝90°，∵CK ⊥JK ，∴∠C ′＋∠C ′FK ＝90°．∴∠C ′＝∠AFJ ，∵∠J ＝∠K ＝90°，∴△AFJ ∽△FC ′K ．∴'AJ JF FK C K =，∴33443224m m m m ++=-+，解得m ＝825或－4（不符合题意）． ∴F (825，8125)，∵C ′(2，1)，∴FC ′＝145．∴CE ＋EF 的最小值＝C ′E ＝145．2. （2017江苏徐州，26，9分）如图① ，菱形ABCD 中，5AB =cm ，动点P 从点B 出发，沿折线BC CD DA --运动到点A 停止，动点Q 从点A 出发，沿线段AB 运动到点B 停止，它们运动的速度相同.设点P 出发xs 时，BPQ ∆的面积为y 2cm .已知y 与x 之间的函数关系.如图②所示，其中,OM MN 为线段，曲线NK 为抛物线的一部分，请根据图中的信息，解答下列问题：（1）当12x <<时，BPQ ∆的面积 （填“变”或“不变”）； （2）分别求出线段OM ，曲线NK 所对应的函数表达式； （3）当x 为何值时，BPQ ∆的面积是52cm ？Ds ）图① 图②思路分析：（1）观察图象②可知，当1＜x ＜2时，y ＝10,故△BPQ 的面积不变； （2）用待定系数法求其解析式即可；（3）把y ＝5分别代入（2）中的一次函数及二次函数解析式，求出x 的值即可，对x 的值注意取舍.解：（1）不变（2）设OM所在直线的函数表达式为y＝kx，把M（1，10）代入，得k＝10. ∴线段OM的函数表达式为y＝10x（0＜x＜1）在曲线NK上取一点G，使它的横坐标52，由题意可得其纵坐标为52.∴曲线NK过三点N（2，10），G（52，52），K（3,0）∵曲线NK为抛物线的一部分，设其表达式为y＝ax2＋bx＋c，可得42102555422930a b ca b ca b c++=⎧⎪⎪++=⎨⎪++=⎪⎩解得106090abc=⎧⎪=-⎨⎪=⎩∴曲线NK的函数表达式为y＝10x2－60x＋90（2＜x＜3）（3）把y＝5代入y＝10x，解得x＝1 2，把y＝5代入y＝10x2－60x＋90，解得x1＝3－22，x2＝3＋22（舍去）∴当x＝3－22或x＝12时，BPQ∆的面积是52cm3.（2017江苏南京，26，8分）已知函数y＝－x2＋(m－1)x＋m（m为常数）（1）该函数的图像与x轴公共点的个数是（）A．0 B．1 C．2 D．1或2（2）求证∶不论m为何值，该函数的图像的顶点都在函数y＝(x＋1)2的图像上．（3）当－2≤m≤3时，求该函数的图像的顶点纵坐标的取值范围．思路分析∶（1）计算二次函数对应一元二次方程的判别式b2－4ac，判断即可；（2）先利用配方法求出（1）的函数的顶点坐标，然后代入y＝(x＋1)2，即可得证；（3）由（2）可知函数图像的顶点纵坐标，再表示为z＝，然后分类讨论即可．解∶（1）D．二次函数对应的一元二次方程为－x2＋(m－1)x＋m＝0，则b2－4ac＝(m－1)2＋4m＝(m＋1)2≥0，所以一元二次方程有两个相等或两个不相等的实数根，即对应的二次函数图像与x轴有1个或2个交点．（2）y＝－x2＋(m－1)x＋m＝－，所以该函数的图像的顶点坐标为（，）()211,24mm⎛⎫⎝+-⎪⎪⎭．把x＝代入y＝(x＋1)2，得y＝．因此，不论m为何值，该函数的图像的顶点都在函数y＝(x＋1)2的图像上．（3）设函数z＝．当m＝－1时，z有最小值0．当m＜－1时，z随m的增大而减小；当1m>-时，z随m的增大而增大．又当2m=-时，在z＝；当m＝3时，z＝＝4．因此，当－2≤m≤3时，该函数的的图像的顶点纵坐标的取值范围是0≤z≤4．4.（2017湖南衡阳，26，10分）（本小题满分10分）如图，△AOB的顶点A、B分别在x轴、y轴上，∠BAO=450，且△AOB的面积为8．（1）直接写出A、B两点的坐标；（2）过点A、B的抛物线G与x轴的另一个交点为点C．①若△ABC是以BC为腰的等腰三角形，求此时抛物线的解析式；②将抛物线G 向下平移4个单位后，恰好与直线AB只有一个交点N，求点N的坐标．思路分析：(1)因为∠BAO=450，所以OA=OB，且△AOB的面积为8，所以OA=OB=4,故直接写出点A、B的坐标为（4，0），（0,4）。
2017年浙江中考数学真题分类汇编---二次函数
2017 年浙江中考数学真题分类汇编---二次函数(解析版)2017年浙江中考真题分类汇编（数学）：专题06二次函数一、单选题（共6题；共12分）1、（2017•宁波）抛物线（m是常数）的顶点在（） A、第一象限B、第二象限C、第三象限D、第四象限2、（2017·金华）对于二次函数y=−(x−1)2+2的图象与性质，下列说法正确的是（)A、对称轴是直线x=1，最小值是2B、对称轴是直线x=1，最大值是2C、对称轴是直线x=−1，最小值是2D、对称轴是直线x=−1，最大值是23、（2017•杭州）设直线x=1是函数y=ax2+bx+c（a，b，c是实数，且a＜0）的图象的对称轴，（）A、若m＞1，则（m﹣1）a+b＞0B、若m＞1，则（m ﹣1）a+b＜0C、若m＜1，则（m﹣1）a+b＞0D、若m＜1，则（m ﹣1）a+b＜04、（2017•绍兴）矩形ABCD的两条对称轴为坐标轴，点A的坐标为（2,1）.一张透明纸上画有一个点和一条抛物线，平移透明纸，这个点与点A重合，此时抛物线的函数表达式为y=x2，再次平移透明纸，使这个点与点C重合，则该抛物线的函数表达式变为（）A、y=x 2+8x+14B、y=x2-8x+14C、y=x2+4x+3D、y=x2-4x+35、（2017·嘉兴）下列关于函数的四个命题：①当时，有最小值10；②为任意实数，时的函数值大于整数，当时的函数值；③若时，的整数值有，且是个；④若函数图象过点和，其中，，则．其中真命题的序号是（）A、①B、②C、③D、④6、（2017·丽水）将函数y=x2的图象用下列方法平移后，所得的图象不经过点A（1,4）的方法是（）A、向左平移1个单位B、向右平移3个单位C、向上平移3个单位D、向下平移1个单位二、填空题（共1题；共2分）三、解答题（共12题；共156分）8、（2017•绍兴）某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙（墙足够长），已知计划中的建筑材料可建围墙的总长为为50m.设饲养室长为x(m)，占地面积为y(m2).(1)如图1，问饲养室长x为多少时，占地面积y最大？(2)如图2，现要求在图中所示位置留2m宽的门，且仍使饲养室的占地面积最大。
(完整word版)2017中考二次函数专题(含答案),推荐文档.docx
1.如图，抛物线y=x 2+bx+c 与直线 y=x ﹣ 3 交于 A、 B 两点，其中点 A 在 y 轴上，点 B 坐标为（﹣ 4，﹣ 5），点 P为 y 轴左侧的抛物线上一动点，过点P作PC⊥x轴于点C，交AB于点D．（1）求抛物线的解析式；（2）以O，A ，P， D 为顶点的平行四边形是否存在？如存在，求点P 的坐标；若不存在，说明理由．（3）当点P运动到直线 AB 下方某一处时，过点P 作 PM⊥ AB ，垂足为 M ，连接 PA 使△PAM 为等腰直角三角形，请直接写出此时点 P 的坐标．2. 在直角坐标系xoy 中， A(0, 2) 、 B( 1,0) ，将ABO 经过旋转、平移变化后得到如图15.1所示的BCD .若直线 PC 将ABC 的面积分成 1: 3 两部分，求此时点P 的坐标；（3）现将ABO 、BCD 分别向下、向左以 1: 2 的速度同时平移，求出在此运动过程中ABO 与BCD 重叠部分面积的最大值.yACB O D x图15.13.如图，已知抛物线y＝ ax2＋ bx＋ c( a≠ 0) 的对称轴为直线 x＝－ 1，且经过A（ 1，0）， C（0， 3）两点，与x 轴对称轴 x＝－ 1 上的一个动点，求使△BPC为直角三角形的点P 的坐标．第25 题图4. 如图，在平面直角坐标系中，已知抛物线y ax2bx 8 与 x 轴交于 A，B 两点，与 y 轴交于点C，直线 l 经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接 CE，已知点 A， D 的坐标分别为否存在点F，使FOE ≌FCE ，若存在，请直接写出点 F 的坐标；若不存在，请说明理由；（3）若点P是y 轴负半轴上的一个动点，设其坐标为（0，m），直线 PB 与直线 l 交于点 Q．试探究：当m 为何值时，OPQ 是等腰三角形．5. 如图，抛物线 y=ax 2+bx﹣ 5（ a≠0）经过点 A（ 4，﹣ 5），与 x 轴的负半轴交于点 B ，与 y 轴交于点C，且 OC=5OB ，抛物线的顶点为点 D ．（ 1）求这条抛物线的表达式；（ 2）联结 AB 、BC、CD 、DA ，求四边形 ABCD 的面积；（ 3）6. 如图，已知抛物线 y=ax 2+bx+c 经过点 A （﹣ 3， 0）， B （9， 0）和 C （ 0， 4）． CD 垂直于 y 轴，交抛物线于点 D ， DE 垂直与 x 轴，垂足为 E ， l 是抛物线的对称轴，点F 是抛物线的顶点．（ 1）求出二次函数的表达式以及点 D 的坐标；（ 2）若 Rt △ AOC 沿 x 轴向右平移到其直角边OC 与对称轴 l 重合，再沿对称轴 l 向上平移到点 C 与点 F 重合，得到 Rt△ A 1O1F，求此时 Rt△ A1O1F 与矩形 OCDE 重叠部分的图形的面积；（3）若 Rt△ AOC 沿 x 轴向右平移 t 个单位长度（ 0＜ t≤6）得到 Rt△ A 2O2C2，Rt△ A 2O2C2与 Rt△ OED 重叠部分的图形面积记为S，求 S 与 t 之间的函数表达式，并写出自变量t 的取值范围．7.如图，抛物线 y=ax 2+bx+c 的图象经过点 A （﹣ 2， 0），点 B（4，0），点 D（ 2， 4），与 y 轴交于点 C，作直线BC ，连接 AC ， CD ．（ 1）求抛物线的函数表达式；（2）E是抛物线上的点，求满足∠ ECD=∠ ACO的点E的坐标；（ 3）点 M 在 y 轴上且位于点 C 上方，点 N 在直线 BC 上，点 P 为第一象限内抛物线上一点，若以点C，M ， N， P 为顶点的四边形是菱形，求菱形的边长．8.如图，在平面直角坐标系 xOy 中，抛物线 y=ax 2+bx 经过两点 A （﹣ 1， 1）， B （ 2， 2）．过点 B 作 BC∥ x存在点 M ，使得△ BCM 的面积为，求出点 M 的坐标；（ 3）连接 OA 、 OB 、OC、 AC ，在坐标平面内，求使得△ AOC 与△ OBN 相似（边 OA 与边 OB 对应）的点 N 的坐标．1.【解答】解：（ 1）∵直线y=x ﹣ 3 交于 A 、B 两点，其中点 A 在 y 轴上，∴ A （0， 3），∵ B （ 4， 5），∴，∴，∴抛物 解析式 y=x 2+x 3，（ 2）存在， P （m ，m 2+m 3），（ m ＜ 0），∴ D （ m ， m 3），∴ PD=|m 2+4m|∵ PD ∥ AO ，∴当 PD=OA=3 ，故存在以 O ，A ，P ， D 点的平行四 形，∴|m 2+4m|=3，① 当 m 2+4m=3 ，∴ m 1= 2， m 2= 2+（舍），∴ m 2+m 3= 1，∴ P （ 2， 1），21212，∴ P （ 1，），② 当 m +4m= 3 ，∴ m = 1， m = 3，Ⅰ、 m =1，∴ m +m 3=Ⅱ、 m 2= 3，∴ m 2+m 3=，∴ P （ 3，），∴点 P 的坐 （ 2，1），（ 1 ，），（ 3，）．（ 3）如 ，∵△ PAM 等腰直角三角形，∴∠ BAP=45 °，∵直 AP 可以看做是直AB 点 A 逆 旋45 °所得，直 AP 解析式 y=kx 3，∵直 AB 解析式 y=x 3，∴ k==3，∴直 AP 解析式 y=3x3， 立 ，∴ x 1=0（舍） x 2=当 x= ， y= ，∴P （ ，）．2. 解析：（ 1）∵ A(0, 2)、 B( 1,0) ，将ABO 旋 、平移 化得到如 4.1所示的 BCD ，∴ BDOA 2,CD OB 1, BDCAOB 90 . ∴ C 1,1 . ⋯⋯⋯⋯⋯⋯⋯ (1 分 )yA 、B 、C 三点的抛物 解析式y ax 2 bx c ，Aab c 0P EC3 1有 ab c 1 ，解得： a2 ., b,cx22B FOc 2D∴抛物 解析式y3 x 2 1 x2 .22图 4.1（ 2）如 4.1 所示， 直PC 与 AB 交于点 E . ∵直 PC 将ABC 的面 分成 1: 3 两部分，∴ AE1 或 AE 3， E 作 EF OB 于点 F ， EF ∥ OA .BE3 BE∴ BEF ∽BAO , ∴EFBE BF . ∴当 AE 1 ， EF 3BF ，AOBA BO BE 3 241∴EF3, BF 3，∴ E (1 324,) .4 2直 PC 解析式 ymx n ， 可求得其解析式 y2 x 7 ，31 272552 39∴2 ，∴（舍去），∴.xx 2xx 1, x 2 11) 25P ( ,2555 25当AE3 ，同理可得 P 2 ( 6 ,23) .BE7 49（ 3） ABO 平移的距离 ，A 1B 1O 1 与 B 2C 1D 1 重叠部分的面 S .可由已知求出A 1B 1 的解析式 y2 x2 t ， A 1B 1 与 x 交点坐 (t2,0) .2C 1B 2 的解析式 y1 x t 1， C 1 B 2 与 y 交点坐 (0, t1) .⋯⋯⋯ (9 分 )3 222①如 4.2 所示，当0 tA 1B 1O 1 与 B 2C 1D 1 重叠部分 四 形 .，5A 1B 1 与 x 交于点 M ，C 1B 2 与 y 交于点 N ， A 1 B 1 与 C 1B 2 交于点 Q ， OQ .y 2 x2 tx4t 3y34t3 5t由11 ，得) .⋯⋯⋯⋯⋯ (10分 )t5t ，∴ Q (3,y x2 y3A 123C 1Q∴ SSQMOSQNO1 2 t5t1 (t1)3 4tNB 2 M O D 1223 22313 t 2 t 1∴ S 的最大25B 1 O 1..12452②如 4.3所示，当34， A 1B 1O 1 与图 4.2tB 2C 1D 1 重叠部分 直角三角形 .55yA 1B 1 与 x 交于点 H ，A 1B 1 与C 1D 1 交于点 G . G (1 2t, 4 5t ) ，D 1H 2 t1 2t45t2， D 1G 4 5t .A 12C 11 D 1H gD 1G 1g 4 5tg(4 5t)1(5t 4) 2∴ S.G2 2 24H∴当341 .B 2 D 1 Ot ， S 的最大55425B 1 O 1上所述，在此运 程中ABO 与 BCD 重叠部分面 的最大.52图 4.3b1,a1,2ax 23. （ 1）依 意，得a b c 0, 解之，得 b2, ∴抛物 解析式 y2x 3 ．c 3.c3.∵ 称 x ＝－ 1，且抛物 A （ 1， 0），∴ B （－ 3， 0）． xxPC 2＝ ( － 1) 2＋ (t － 3) 2＝t 2－ 6t ＋ 10.①若 B 为直角顶点，则 22222－6t ＋ 10.解之 , 得 t ＝－ 2.BC ＋ PB ＝ PC ，即 18＋ 4＋ t ＝t ②若 C 为直角顶点，则2222＋ 10＝ 2．解之，得 t ＝ 4．BC ＋ PC ＝ PB ，即 18＋ t － 6t 4＋t③若 P 为直角顶点，则222，即 4 22＋ 10＝ 18．解之，得 t 1＝ 317 ， t 2 ＝ 3 17 ．PB ＋ PC ＝ BC ＋ t ＋ t － 6t224. 解答：（ 1）抛物线 yax 2 bx 8 经过点 A （－ 2， 0）， D （6，－ 8），4a 2b 8 0 a 11 x 23x 8 2 抛物线的函数表达式为 36a 6b8解得y8b32y1 x 23x 81 x 3 225 ， 抛物线的对称轴为直线x 3．又抛物线与 x 轴交于 A ，B 两点，点 A 的222坐标为（－ 2， 0）． 点 B 的坐标为（ 8， 0）设直线 l 的函数表达式为 y kx ． 点 D （ 6，－ 8 ）在直线 l 上，6k=－ 8，解得k4y4 x 点 E 为直线 l 和抛物线对称轴的交点．点 E 的横． 直线 l 的函数表达式为33坐标为 3，纵坐标为4 4 ，即点 E 的坐标为（ 3，－ 4 ）33（ 2）抛物线上存在点 F ，使 FOE ≌ FCE ．点 F 的坐标为（ 317, 4）或（ 3 17, 4）．（ 3）解法一：分两种情况：①当 OPOQ 时， OPQ 是等腰三角形．点 E 的坐标为（ 3，－ 4）， OE 324 25 ，过点 E 作直线 ME// PB ， 交 y 轴于点 M ，交 x 轴于点 H ，则OMOE ， OM OE5OPOQ点 M 的坐标为（ 0，－ 5）．设直线 ME 的表达式为 yk x 53k5 4，解得k11 ME 的函数表达式为15，令 y=0，， ， y x11331得 x 5 0 ，解得 x=15，点 H 的坐标为（ 15， 0）3MH//PB ，OP OB ，即 m 8 ， 8又mOMOH5153②当 QO QP 时， OPQ 是等腰三角形．当 x=0 时， y1 x 23 x88 ， 点 C 的坐标为（ 0，－ 8），2CE32(8 4)25 ， OE=CE ，12 ，又因为 QOQP ，13 ，38 4 ，解得 k 24，设直线交轴于点， 其函数表达式为，，23CE//PB CE x yk 2 x 8Nk 23CE 的函数表达式为y 4 x 8 ，令 y=0，得 4 x 8 0 ， x6，点 N 的坐标为（ 6， 0）3 3 CN//PB ，OP OB ，m8，解得 m 32OCON8 6 3m 的值为832时， OPQ 是等腰三角形．综上所述，当 或33解法二：当 x=0 时， y1 2 3x88 ， 点 C 的坐标为（ 0，－ 8）， 点 E 的坐标为x2（ 3 ，－ 4）， OE32 42 5 ， CE 32 (8 4)2 5 ，OE=CE ，12 ，设抛物线的对称轴交直线PB 于点 M ，交 x 轴于点 H ．分两种情况： ① 当 QOQP 时， OPQ 是等腰三角形．13 ，2 3 ， CE// PB又HM/ /y 轴， 四边形 PMEC 是平行四边形， EM CP 8 m ，HMHE EM4 ( 8 m) 4 mBH8 3 5 ， HM//y轴，BHM ∽ BOP ，HM BH4 m5m32OPBOm83②当 OP OQ 时， OPQ 是等腰三角形．EH // y 轴，OPQ ∽ EMQ ，EQ EM ， EQEMOQOPEM EQ OEOQ OE OP5 ( m) 5 m ， HM4 (5m) ，EH // y 轴，BHM ∽BOP ，HM BHOPBO1 m5 m8 当 m 的值为8 32 时， OPQ 是等腰三角形．或m83335. 解：（ 1） ∵ 抛物线 y=ax 2+bx ﹣ 5 与 y 轴交于点 C ， ∴C （ 0，﹣ 5）， ∴OC=5 ． ∵ OC=5OB ， ∴OB=1 ，又点 B 在 x 轴的负半轴上， ∴ B （﹣ 1， 0）．∵ 抛物线经过点 A （ 4，﹣ 5）和点 B （﹣ 1， 0），∴，解得， ∴ 这条抛物线的表达式为 y=x 2﹣ 4x ﹣ 5．（ 2）由 y=x 2﹣ 4x ﹣ 5，得顶点 D 的坐标为（ 2，﹣ 9）．连接 AC ，∵ 点 A 的坐标是（ 4，﹣ 5），点 C 的坐标是（ 0，﹣ 5）， 又S△ABC = ×4×5=10， S △ACD = ×4×4=8，∴ S 四边形 ABCD =S △ABC +S △ACD =18．（ 3）过点 C 作 CH ⊥ AB ，垂足为点 H ． ∵ S △ABC = ×AB ×CH=10 ，AB=5 ，∴ CH=2，在 RT △ BCH 中， ∠ BHC=90 °， BC=， BH==3，∴ tan ∠CBH== ．∵ 在 RT △ BOE 中， ∠ BOE=90 °， tan ∠ BEO= ，∵ ∠ BEO= ∠ ABC ， ∴，得 EO= ， ∴ 点 E 的坐标为（ 0，6. 解：（ 1） ∵ 抛物线 y=ax 2+bx+c 经过点 A （﹣ 3， 0）， B （ 9， 0）和 C （ 0，4）． ∴ 设抛物线的解析式为 y=a （x+3 ）（ x ﹣ 9）， ∵ C （ 0，4）在抛物线上， ∴4=﹣ 27a ，∴ a= ， ∴ 设抛物线的解析式为 y= ﹣ （ x+3 ）（ x 9 ） = ﹣ x 2，﹣﹣ + x+4 ∵ CD 垂直于 y 轴， C （ 0 4 ∴ ﹣ x 2 x+4=4 ， ∴ x=6， ∵ D （ 6，4），， ） + （ 2）如图 1， ∵ 点 F 是抛物线 y= ﹣ x 2+x+4 的顶点，∴ F （ 3，）， ∴ FH= ， ∵GH ∥ A 1O 1，∴，∴ ， ∴ GH=1 ，∵ Rt △ A 1O 1F 与矩形 OCDE 重叠部分是梯形 A 1O 1HG ，∴ S 重叠部分 =S △A1O1F ﹣S △FGH = A 1O 1×O 1F ﹣ GH ×FH= ×3×4 ﹣ ×1× = ．（ 3） ① 当 0＜ t ≤3 时，如图 2， ∵ C 2O 2∥ DE ， ∴，∴， ∴ O 2G=t ， ∴ S=S = OO 2×O 2G=t × t=t 2，△OO2G② 当 3＜ t ≤6 时，如图 3，∵ C 2 H ∥ OC ，∴，∴， ∴ C 2H= （ 6 ﹣ t ）， ∴ S=S 四边形 A2O2HG =S △A2O2C2﹣S△C2GH= OA ×OC ﹣ C 2H ×（ t ﹣3） = ×3×4﹣ × （ 6﹣ t ）（ t ﹣ 3）= t 2﹣ 3t+12∴ 当 0＜ t ≤3 时， S= t 2，当 3＜ t ≤6 时， S= t 2﹣ 3t+12．7. 解：（ 1） ∵ 抛物线 y=ax 2+bx+c 的图象经过点 A （﹣ 2，0），点 B （ 4，0），点 D （ 2， 4），∴ 设抛物线解析式为 y=a （ x+2）（ x ﹣ 4）， ∴ ﹣ 8a=4， ∴ a=﹣，∴ 抛物线解析式为 y=﹣（ x+2）（ x ﹣ 4）=﹣ x 2+x+4 ；（ 2）如图 1， ① 点 E 在直线 CD 上方的抛物线上，记E ′，连接 CE ′，过 E ′作 E ′F ′⊥ CD ，垂足为F ′，由（ 1）知， OC=4 ，∵ ∠ ACO= ∠ E ′CF ′，∴ tan ∠ ACO=tan ∠E ′CF ′，∴=，设线段 E ′F ′=h ，则 CF ′=2h ， ∴ 点 E ′（ 2h ，h+4 ）14∴ h=0 （舍） h= ∴ E ′（ 1，），② 点 E 在直线 CD 下方的抛物线上，记 E ，同 ① 的方法得， E （ 3，），点 E 的坐标为（ 1，），（3，）（ 3） ① CM 为菱形的边，如图 2，在第一象限内取点P ′P ′ P ′N ′∥ y 轴，交 BC于 N ′ P ′ P ′M ′∥ BC ，，过点 作，过点 作 交 y 轴于 M ′， ∴ 四边形 CM ′P ′N ′是平行四边形， ∵ 四边形 CM ′P ′N ′是菱形，∴ P ′M ′=P ′N ′，过点 P ′作 P ′Q ′⊥ y 轴，垂足为 Q ′， ∵ OC=OB ，∠ BOC=90 °，∴ ∠ OCB=45 °， ∴ ∠ P ′M ′C=45 °，设点 P ′（ m ，﹣ m 2+m+4 ），在 Rt △ P ′M ′Q ′中， P ′Q ′=m ， P ′M ′= m ， ∵ B （ 4， 0）， C （0， 4），∴ 直线 BC 的解析式为 y= ﹣ x+4 ，∵ P ′N ′∥ y 轴， ∴ N ′（ m ，﹣ m+4），∴ P ′N ′=﹣ m 2+m+4 ﹣（﹣ m+4） =﹣ m 2+2m ， ∴ m= ﹣ m 2+2m ， ∴ m=0 （舍）或 m=4 ﹣ 2 ，菱形 CM ′P ′N ′的边长为 （ 4﹣ 2 ） =4﹣ 4．② CM 为菱形的对角线，如图 3，在第一象限内抛物线上取点P ，过点 P 作 PM ∥BC ，交 y 轴于点 M ，连接 CP ，过点 M 作 MN ∥ CP ，交 BC 于 N ，∴ 四边形 CPMN 是平行四边形，连接PN 交 CM 于点 Q ，∵ 四边形 CPMN 是菱形， ∴ PQ ⊥ CM ， ∠ PCQ=∠ NCQ ， ∵ ∠OCB=45 °，∴ ∠ NCQ=45 ° ∴ ∠PCQ=45 ° ∴ ∠CPQ= ∠ PCQ=45° ∴ PQ=CQ， ， ， ， 设点 P （ n ，﹣ n 2+n+4）， ∴CQ=n ， OQ=n+2 ， ∴ n+4=﹣ n 2+n+4 ， ∴ n=0 （舍）， ∴ 此种情况不存在． ∴ 菱形的边长为4 ﹣ 4．8. 解：（ 1）把 A （﹣ 1，1）， B （ 2， 2）代入 y=ax 2+bx 得：，解得 ，故抛物线的函数表达式为y=x 2﹣ x ， ∵BC ∥x 轴，设 C （x 0， 2）． ∴ x 02﹣ x 0=2，解得： x 0=﹣或 x 0=2，∵ x 0＜ 0∴ C （﹣， 2）；（ 2）设 △BCM 边 BC 上的高为 h ， ∵BC= ， ∴ S △BCM =h=， ∴ h=2 ，点 M 即为抛物线上到 BC 的距离为2 的点， ∴ M 的纵坐标为 0 或 4，令 y=x 2﹣ x=0 ， 解得： x 1 =0，x 2=，∴ M 1（0，0）， M 2（， 0），令 y=x 2﹣x=4 ，解得： x 3=， x 4= ，∴ M 3（ ， 0）， M 4（， 4），综上所述： M 点的坐标为：（0， 0），（， 0），（， 0），（， 4）；（ 3）∵ A （﹣ 1， 1）， B（ 2， 2）， C（﹣， 2）， D（ 0， 2），∴ OB=2， OA=， OC=，∴ ∠ AOD= ∠ BOD=45 ° tan∠ COD=，①如图1，当△ AOC ∽ △ BON时，，∠ AOC= ∠ BON，，∴ ON=2OC=5 ，过 N 作 NE ⊥ x 轴于 E，∵ ∠ COD=45°﹣∠ AOC=45°﹣∠ BON=∠NOE，在 Rt△ NOE 中， tan∠ NOE=tan ∠ COD= ，∴ OE=4 ， NE=3，∴ N（4，3）同理可得N （3， 4）；②如图 2，当△ AOC ∽△ OBN 时，，∠ AOC=∠OBN，∴ BN=2OC=5，过 B 作 BG ⊥ x 轴于 G，过 N 作 x 轴的平行线交BG 的延长线于F，∴ NF⊥ BF，∵ ∠ COD=45 °﹣∠ AOC=45 °﹣∠ OBN= ∠NBF ，∴ tan∠NBF=tan ∠ COD= ，∴ BF=4，NF=3，∴ N （﹣ 1，﹣ 2），同理N （﹣ 2，﹣ 1），综上所述：使得△AOC与△ OBN相似（边OA 与边 OB 对应）的点N 的坐标是（ 4， 3），（ 3， 4），（﹣ 1，﹣ 2），（﹣ 2，﹣ 1）．。
2017年二次函数中考分类(7)
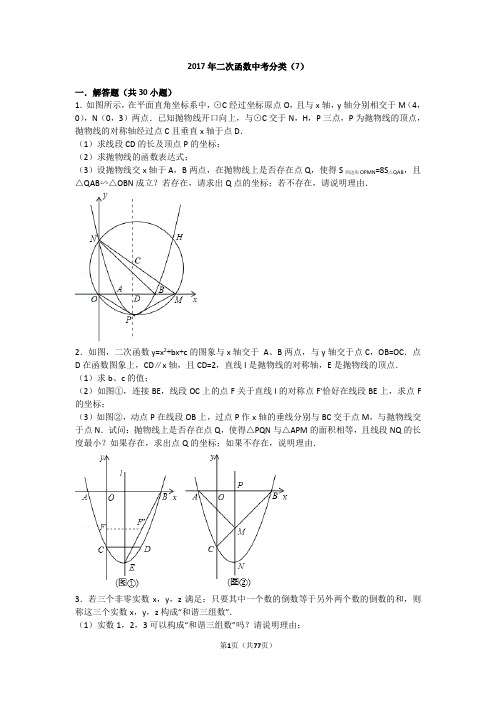
2017年二次函数中考分类（7）一．解答题（共30小题）1．如图所示，在平面直角坐标系中，⊙C经过坐标原点O，且与x轴，y轴分别相交于M（4，0），N（0，3）两点．已知抛物线开口向上，与⊙C交于N，H，P三点，P为抛物线的顶点，抛物线的对称轴经过点C且垂直x轴于点D．（1）求线段CD的长及顶点P的坐标；（2）求抛物线的函数表达式；（3）设抛物线交x轴于A，B两点，在抛物线上是否存在点Q，使得S四边形OPMN=8S△QAB，且△QAB∽△OBN成立？若存在，请求出Q点的坐标；若不存在，请说明理由．2．如图，二次函数y=x2+bx+c的图象与x轴交于A、B两点，与y轴交于点C，OB=OC．点D在函数图象上，CD∥x轴，且CD=2，直线l是抛物线的对称轴，E是抛物线的顶点．（1）求b、c的值；（2）如图①，连接BE，线段OC上的点F关于直线l的对称点F'恰好在线段BE上，求点F 的坐标；（3）如图②，动点P在线段OB上，过点P作x轴的垂线分别与BC交于点M，与抛物线交于点N．试问：抛物线上是否存在点Q，使得△PQN与△APM的面积相等，且线段NQ的长度最小？如果存在，求出点Q的坐标；如果不存在，说明理由．3．若三个非零实数x，y，z满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数x，y，z构成“和谐三组数”．（1）实数1，2，3可以构成“和谐三组数”吗？请说明理由；（2）若M（t，y1），N（t+1，y2），R（t+3，y3）三点均在函数（k为常数，k≠0）的图象上，且这三点的纵坐标y1，y2，y3构成“和谐三组数”，求实数t的值；（3）若直线y=2bx+2c（bc≠0）与x轴交于点A（x1，0），与抛物线y=ax2+3bx+3c（a≠0）交于B（x2，y2），C（x3，y3）两点．①求证：A，B，C三点的横坐标x1，x2，x3构成“和谐三组数”；②若a＞2b＞3c，x2=1，求点P（，）与原点O的距离OP的取值范围．4．已知抛物线y=x2+bx﹣3（b是常数）经过点A（﹣1，0）．（1）求该抛物线的解析式和顶点坐标；（2）P（m，t）为抛物线上的一个动点，P关于原点的对称点为P'．①当点P'落在该抛物线上时，求m的值；②当点P'落在第二象限内，P'A2取得最小值时，求m的值．5．在同一直角坐标系中，抛物线C1：y=ax2﹣2x﹣3与抛物线C2：y=x2+mx+n关于y轴对称，C2与x轴交于A、B两点，其中点A在点B的左侧．（1）求抛物线C1，C2的函数表达式；（2）求A、B两点的坐标；（3）在抛物线C1上是否存在一点P，在抛物线C2上是否存在一点Q，使得以AB为边，且以A、B、P、Q四点为顶点的四边形是平行四边形？若存在，求出P、Q两点的坐标；若不存在，请说明理由．6．如图1，已知二次函数y=ax2+bx+c（a、b、c为常数，a≠0）的图象过点O（0，0）和点A（4，0），函数图象最低点M的纵坐标为﹣，直线l的解析式为y=x．（1）求二次函数的解析式；（2）直线l沿x轴向右平移，得直线l′，l′与线段OA相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线l′折叠，当点E恰好落在抛物线上点E′时（图2），求直线l′的解析式；（3）在（2）的条件下，l′与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B′ON′，P为l′上的动点，当△PB′N′为等腰三角形时，求符合条件的点P的坐标．7．如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E 的坐标分别为（3，0），（0，1）．（1）求抛物线的解析式；（2）猜想△EDB的形状并加以证明；（3）点M在对称轴右侧的抛物线上，点N在x轴上，请问是否存在以点A，F，M，N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．8．在平面直角坐标系中，我们定义直线y=ax﹣a为抛物线y=ax2+bx+c（a、b、c为常数，a ≠0）的“梦想直线”；有一个顶点在抛物线上，另有一个顶点在y轴上的三角形为其“梦想三角形”．已知抛物线y=﹣x2﹣x+2与其“梦想直线”交于A、B两点（点A在点B的左侧），与x轴负半轴交于点C．（1）填空：该抛物线的“梦想直线”的解析式为，点A的坐标为，点B的坐标为；（2）如图，点M为线段CB上一动点，将△ACM以AM所在直线为对称轴翻折，点C的对称点为N，若△AMN为该抛物线的“梦想三角形”，求点N的坐标；（3）当点E在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上，是否存在点F，使得以点A、C、E、F为顶点的四边形为平行四边形？若存在，请直接写出点E、F的坐标；若不存在，请说明理由．9．如图，抛物线y=x2+bx+c经过点B（3，0），C（0，﹣2），直线l：y=﹣x﹣交y轴于点E，且与抛物线交于A，D两点，P为抛物线上一动点（不与A，D重合）．（1）求抛物线的解析式；（2）当点P在直线l下方时，过点P作PM∥x轴交l于点M，PN∥y轴交l于点N，求PM+PN 的最大值．（3）设F为直线l上的点，以E，C，P，F为顶点的四边形能否构成平行四边形？若能，求出点F的坐标；若不能，请说明理由．10．如图1，在平面直角坐标系中，已知抛物线y=ax2+bx﹣5与x轴交于A（﹣1，0），B（5，0）两点，与y轴交于点C．（1）求抛物线的函数表达式；（2）若点D是y轴上的一点，且以B，C，D为顶点的三角形与△ABC相似，求点D的坐标；（3）如图2，CE∥x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H 且与y轴平行的直线与BC，CE分别交于点F，G，试探究当点H运动到何处时，四边形CHEF 的面积最大，求点H的坐标及最大面积；（4）若点K为抛物线的顶点，点M（4，m）是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标．11．在平面直角坐标系xOy中，抛物线y=ax2+bx+c与y轴交于点C，其顶点记为M，自变量x=﹣1和x=5对应的函数值相等．若点M在直线l：y=﹣12x+16上，点（3，﹣4）在抛物线上．（1）求该抛物线的解析式；（2）设y=ax2+bx+c对称轴右侧x轴上方的图象上任一点为P，在x轴上有一点A（﹣，0），试比较锐角∠PCO与∠ACO的大小（不必证明），并写出相应的P点横坐标x的取值范围．（3）直线l与抛物线另一交点记为B，Q为线段BM上一动点（点Q不与M重合），设Q 点坐标为（t，n），过Q作QH⊥x轴于点H，将以点Q，H，O，C为顶点的四边形的面积S 表示为t的函数，标出自变量t的取值范围，并求出S可能取得的最大值．12．已知抛物线c1的顶点为A（﹣1，4），与y轴的交点为D（0，3）．（1）求c1的解析式；（2）若直线l1：y=x+m与c1仅有唯一的交点，求m的值；（3）若抛物线c1关于y轴对称的抛物线记作c2，平行于x轴的直线记作l2：y=n．试结合图形回答：当n为何值时，l2与c1和c2共有：①两个交点；②三个交点；③四个交点；（4）若c2与x轴正半轴交点记作B，试在x轴上求点P，使△PAB为等腰三角形．13．如图，已知抛物线y=﹣x2+bx+c与y轴相交于点A（0，3），与x正半轴相交于点B，对称轴是直线x=1（1）求此抛物线的解析式以及点B的坐标．（2）动点M从点O出发，以每秒2个单位长度的速度沿x轴正方向运动，同时动点N从点O出发，以每秒3个单位长度的速度沿y轴正方向运动，当N点到达A点时，M、N同时停止运动．过动点M作x轴的垂线交线段AB于点Q，交抛物线于点P，设运动的时间为t秒．①当t为何值时，四边形OMPN为矩形．②当t＞0时，△BOQ能否为等腰三角形？若能，求出t的值；若不能，请说明理由．14．如图，抛物线y=﹣x2+bx+c与x轴分别交于A（﹣1，0），B（5，0）两点．（1）求抛物线的解析式；（2）在第二象限内取一点C，作CD垂直X轴于点D，链接AC，且AD=5，CD=8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m的值；（3）在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请出点Q的坐标；若不存在，请说明理由．15．如图，在平面直角坐标系xOy中，已知A，B两点的坐标分别为（﹣4，0），（4，0），C （m，0）是线段A B上一点（与A，B点不重合），抛物线L1：y=ax2+b1x+c1（a＜0）经过点A，C，顶点为D，抛物线L2：y=ax2+b2x+c2（a＜0）经过点C，B，顶点为E，AD，BE的延长线相交于点F．（1）若a=﹣，m=﹣1，求抛物线L1，L2的解析式；（2）若a=﹣1，AF⊥BF，求m的值；（3）是否存在这样的实数a（a＜0），无论m取何值，直线AF与BF都不可能互相垂直？若存在，请直接写出a的两个不同的值；若不存在，请说明理由．16．如图，在平面直角坐标系xOy中，抛物线y=x2﹣2x﹣3交x轴于A，B两点（点A在点B的左侧），将该抛物线位于x轴上方曲线记作M，将该抛物线位于x轴下方部分沿x轴翻折，翻折后所得曲线记作N，曲线N交y轴于点C，连接AC、BC．（1）求曲线N所在抛物线相应的函数表达式；（2）求△ABC外接圆的半径；（3）点P为曲线M或曲线N上的一动点，点Q为x轴上的一个动点，若以点B，C，P，Q 为顶点的四边形是平行四边形，求点Q的坐标．17．已知函数y=mx2﹣（2m﹣5）x+m﹣2的图象与x轴有两个公共点．（1）求m的取值范围，并写出当m取范围内最大整数时函数的解析式；（2）题（1）中求得的函数记为C1，①当n≤x≤﹣1时，y的取值范围是1≤y≤﹣3n，求n的值；②函数C2：y=m（x﹣h）2+k的图象由函数C1的图象平移得到，其顶点P落在以原点为圆心，半径为的圆内或圆上，设函数C1的图象顶点为M，求点P与点M距离最大时函数C2的解析式．18．如图，抛物线y=ax2+bx﹣3经过点A（2，﹣3），与x轴负半轴交于点B，与y轴交于点C，且OC=3OB．（1）求抛物线的解析式；（2）点D在y轴上，且∠BDO=∠BAC，求点D的坐标；（3）点M在抛物线上，点N在抛物线的对称轴上，是否存在以点A，B，M，N为顶点的四边形是平行四边形？若存在，求出所有符合条件的点M的坐标；若不存在，请说明理由．19．如图，已知抛物线y=ax2+bx+1经过A（﹣1，0），B（1，1）两点．（1）求该抛物线的解析式；（2）阅读理解：在同一平面直角坐标系中，直线l1：y=k1x+b1（k1，b1为常数，且k1≠0），直线l2：y=k2x+b2（k2，b2为常数，且k2≠0），若l1⊥l2，则k1•k2=﹣1．解决问题：①若直线y=3x﹣1与直线y=mx+2互相垂直，求m的值；②抛物线上是否存在点P，使得△PAB是以AB为直角边的直角三角形？若存在，请求出点P 的坐标；若不存在，请说明理由；（3）M是抛物线上一动点，且在直线AB的上方（不与A，B重合），求点M到直线AB的距离的最大值．20．《函数的图象与性质》拓展学习片段展示：【问题】如图①，在平面直角坐标系中，抛物线y=a（x﹣2）2﹣经过原点O，与x轴的另一个交点为A，则a=．【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方，将这部分图象与原抛物线剩余部分的图象组成的新图象记为G，如图②．直接写出图象G对应的函数解析式．【探究】在图②中，过点B（0，1）作直线l平行于x轴，与图象G的交点从左至右依次为点C，D，E，F，如图③．求图象G在直线l上方的部分对应的函数y随x增大而增大时x 的取值范围．【应用】P是图③中图象G上一点，其横坐标为m，连接PD，PE．直接写出△PDE的面积不小于1时m的取值范围．21．在平面直角坐标系中，直线y=﹣x+1交y轴于点B，交x轴于点A，抛物线y=﹣x2+bx+c经过点B，与直线y=﹣x+1交于点C（4，﹣2）．（1）求抛物线的解析式；（2）如图，横坐标为m的点M在直线BC上方的抛物线上，过点M作ME∥y轴交直线BC 于点E，以ME为直径的圆交直线BC于另一点D，当点E在x轴上时，求△DEM的周长．（3）将△AOB绕坐标平面内的某一点按顺时针方向旋转90°，得到△A1O1B1，点A，O，B 的对应点分别是点A1，O1，B1，若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的坐标．22．如图，在平面直角坐标系中，已知抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（2，0）两点，与y轴交于点C．（1）求该抛物线的解析式；（2）直线y=﹣x+n与该抛物线在第四象限内交于点D，与线段BC交于点E，与x轴交于点F，且BE=4EC．①求n的值；②连接AC，CD，线段AC与线段DF交于点G，△AGF与△CGD是否全等？请说明理由；（3）直线y=m（m＞0）与该抛物线的交点为M，N（点M在点N的左侧），点M关于y轴的对称点为点M'，点H的坐标为（1，0）．若四边形OM'NH的面积为．求点H到OM'的距离d的值．23．如图1，点A坐标为（2，0），以OA为边在第一象限内作等边△OAB，点C为x轴上一动点，且在点A右侧，连接BC，以BC为边在第一象限内作等边△BCD，连接AD交BC于E．（1）①直接回答：△OBC与△ABD全等吗？②试说明：无论点C如何移动，AD始终与OB平行；（2）当点C运动到使AC2=AE•AD时，如图2，经过O、B、C三点的抛物线为y1．试问：y1上是否存在动点P，使△BEP为直角三角形且BE为直角边？若存在，求出点P坐标；若不存在，说明理由；（3）在（2）的条件下，将y1沿x轴翻折得y2，设y1与y2组成的图形为M，函数y=x+m 的图象l与M有公共点．试写出：l与M的公共点为3个时，m的取值．24．已知，抛物线y=ax2+bx+3（a＜0）与x轴交于A（3，0）、B两点，与y轴交于点C，抛物线的对称轴是直线x=1，D为抛物线的顶点，点E在y轴C点的上方，且CE=．（1）求抛物线的解析式及顶点D的坐标；（2）求证：直线DE是△ACD外接圆的切线；（3）在直线AC上方的抛物线上找一点P，使S△ACP=S△ACD，求点P的坐标；（4）在坐标轴上找一点M，使以点B、C、M为顶点的三角形与△ACD相似，直接写出点M 的坐标．25．已知在平面直角坐标系xOy中（如图），已知抛物线y=﹣x2+bx+c经过点A（2，2），对称轴是直线x=1，顶点为B．（1）求这条抛物线的表达式和点B的坐标；（2）点M在对称轴上，且位于顶点上方，设它的纵坐标为m，联结AM，用含m的代数式表示∠AMB的余切值；（3）将该抛物线向上或向下平移，使得新抛物线的顶点C在x轴上．原抛物线上一点P平移后的对应点为点Q，如果OP=OQ，求点Q的坐标．26．已知直线y=kx+b与抛物线y=ax2（a＞0）相交于A、B两点（点A在点B的左侧），与y 轴正半轴相交于点C，过点A作AD⊥x轴，垂足为D．（1）若∠AOB=60°，AB∥x轴，AB=2，求a的值；（2）若∠AOB=90°，点A的横坐标为﹣4，AC=4BC，求点B的坐标；（3）延长AD、BO相交于点E，求证：DE=CO．27．抛物线y=x2+bx+c与x轴交于A（1，0），B（m，0），与y轴交于C．（1）若m=﹣3，求抛物线的解析式，并写出抛物线的对称轴；（2）如图1，在（1）的条件下，设抛物线的对称轴交x轴于D，在对称轴左侧的抛物线上有一点E，使S△ACE=S△ACD，求点E的坐标；（3）如图2，设F（﹣1，﹣4），FG⊥y于G，在线段OG上是否存在点P，使∠OBP=∠FPG？若存在，求m的取值范围；若不存在，请说明理由．28．如图，⊙M的圆心M（﹣1，2），⊙M经过坐标原点O，与y轴交于点A，经过点A的一条直线l解析式为：y=﹣x+4与x轴交于点B，以M为顶点的抛物线经过x轴上点D（2，0）和点C（﹣4，0）．（1）求抛物线的解析式；（2）求证：直线l是⊙M的切线；（3）点P为抛物线上一动点，且PE与直线l垂直，垂足为E，PF∥y轴，交直线l于点F，是否存在这样的点P，使△PEF的面积最小？若存在，请求出此时点P的坐标及△PEF面积的最小值；若不存在，请说明理由．29．如图，在平面直角坐标系中，矩形OABC的边OA、OC分别在x轴、y轴上，点B坐标为（4，t）（t＞0），二次函数y=x2+bx（b＜0）的图象经过点B，顶点为点D．（1）当t=12时，顶点D到x轴的距离等于；（2）点E是二次函数y=x2+bx（b＜0）的图象与x轴的一个公共点（点E与点O不重合），求OE•EA的最大值及取得最大值时的二次函数表达式；（3）矩形OABC的对角线OB、AC交于点F，直线l平行于x轴，交二次函数y=x2+bx（b＜0）的图象于点M、N，连接DM、DN，当△DMN≌△FOC时，求t的值．30．平面直角坐标系xOy中，点A、B的横坐标分别为a、a+2，二次函数y=﹣x2+（m﹣2）x+2m的图象经过点A、B，且a、m满足2a﹣m=d（d为常数）．（1）若一次函数y1=kx+b的图象经过A、B两点．①当a=1、d=﹣1时，求k的值；②若y1随x的增大而减小，求d的取值范围；（2）当d=﹣4且a≠﹣2、a≠﹣4时，判断直线AB与x轴的位置关系，并说明理由；（3）点A、B的位置随着a的变化而变化，设点A、B运动的路线与y轴分别相交于点C、D，线段CD的长度会发生变化吗？如果不变，求出CD的长；如果变化，请说明理由．2017年二次函数中考分类（7）参考答案与试题解析一．解答题（共30小题）1．（2017•日照）如图所示，在平面直角坐标系中，⊙C经过坐标原点O，且与x轴，y轴分别相交于M（4，0），N（0，3）两点．已知抛物线开口向上，与⊙C交于N，H，P三点，P 为抛物线的顶点，抛物线的对称轴经过点C且垂直x轴于点D．（1）求线段CD的长及顶点P的坐标；（2）求抛物线的函数表达式；（3）设抛物线交x轴于A，B两点，在抛物线上是否存在点Q，使得S四边形OPMN=8S△QAB，且△QAB∽△OBN成立？若存在，请求出Q点的坐标；若不存在，请说明理由．【分析】（1）连接OC，由勾股定理可求得MN的长，则可求得OC的长，由垂径定理可求得OD的长，在Rt△OCD中，可求得CD的长，则可求得PD的长，可求得P点坐标；（2）可设抛物线的解析式为顶点式，再把N点坐标代入可求得抛物线解析式；（3）由抛物线解析式可求得A、B的坐标，由S四边形OPMN=8S△QAB可求得点Q到x轴的距离，且点Q只能在x轴的下方，则可求得Q点的坐标，再证明△QAB∽△OBN即可．【解答】解：（1）如图，连接OC，∵M（4，0），N（0，3），∴OM=4，ON=3，∴MN=5，∴OC=MN=，∵CD为抛物线对称轴，∴OD=MD=2，在Rt△OCD中，由勾股定理可得CD===，∴PD=PC﹣CD=﹣=1，∴P（2，﹣1）；（2）∵抛物线的顶点为P（2，﹣1），∴设抛物线的函数表达式为y=a（x﹣2）2﹣1，∵抛物线过N（0，3），∴3=a（0﹣2）2﹣1，解得a=1，∴抛物线的函数表达式为y=（x﹣2）2﹣1，即y=x2﹣4x+3；（3）在y=x2﹣4x+3中，令y=0可得0=x2﹣4x+3，解得x=1或x=3，∴A（1，0），B（3，0），∴AB=3﹣1=2，∵ON=3，OM=4，PD=1，∴S四边形OPMN=S△OMP+S△OMN=OM•PD+OM•ON=×4×1+×4×3=8=8S△QAB，∴S△QAB=1，设Q点纵坐标为y，则×2×|y|=1，解得y=1或y=﹣1，当y=1时，则△QAB为钝角三角形，而△OBN为直角三角形，不合题意，舍去，当y=﹣1时，可知P点即为所求的Q点，∵D为AB的中点，∴AD=BD=QD，∴△QAB为等腰直角三角形，∵ON=OB=3，∴△OBN为等腰直角三角形，∴△QAB∽△OBN，综上可知存在满足条件的点Q，其坐标为（2，﹣1）．【点评】本题为二次函数的综合应用，涉及勾股定理、垂径定理、待定系数法、相似三角形的性质和判定、二次函数的性质等知识．在（1）中利用垂径定理得到OD=2，从而求得CD 的长是解题的关键，在（2）中注意设抛物线的顶点式更容易求解，在（3）中求得Q点的纵坐标是解题的关键．本题考查知识点较多，综合性较强，难度适中．2．（2017•苏州）如图，二次函数y=x2+bx+c的图象与x轴交于A、B两点，与y轴交于点C，OB=OC．点D在函数图象上，CD∥x轴，且CD=2，直线l是抛物线的对称轴，E是抛物线的顶点．（1）求b、c的值；（2）如图①，连接BE，线段OC上的点F关于直线l的对称点F'恰好在线段BE上，求点F的坐标；（3）如图②，动点P在线段OB上，过点P作x轴的垂线分别与BC交于点M，与抛物线交于点N．试问：抛物线上是否存在点Q，使得△PQN与△APM的面积相等，且线段NQ的长度最小？如果存在，求出点Q的坐标；如果不存在，说明理由．【分析】（1）由条件可求得抛物线对称轴，则可求得b的值；由OB=OC，可用c表示出B 点坐标，代入抛物线解析式可求得c的值；（2）可设F（0，m），则可表示出F′的坐标，由B、E的坐标可求得直线BE的解析式，把F′坐标代入直线BE解析式可得到关于m的方程，可求得F点的坐标；（3）设点P坐标为（n，0），可表示出PA、PB、PN的长，作QR⊥PN，垂足为R，则可求得QR的长，用n可表示出Q、R、N的坐标，在Rt△QRN中，由勾股定理可得到关于n的二次函数，利用二次函数的性质可知其取得最小值时n的值，则可求得Q点的坐标，【解答】解：（1）∵CD∥x轴，CD=2，∴抛物线对称轴为x=1．∴．∵OB=OC，C（0，c），∴B点的坐标为（﹣c，0），∴0=c2+2c+c，解得c=﹣3或c=0（舍去），∴c=﹣3；（2）设点F的坐标为（0，m）．∵对称轴为直线x=1，∴点F关于直线l的对称点F的坐标为（2，m）．由（1）可知抛物线解析式为y=x2﹣2x﹣3=（x﹣1）2﹣4，∴E（1，﹣4），∵直线BE经过点B（3，0），E（1，﹣4），∴利用待定系数法可得直线BE的表达式为y=2x﹣6．∵点F在BE上，∴m=2×2﹣6=﹣2，即点F的坐标为（0，﹣2）；（3）存在点Q满足题意．设点P坐标为（n，0），则PA=n+1，PB=PM=3﹣n，PN=﹣n2+2n+3．作QR⊥PN，垂足为R，∵S△PQN=S△APM，∴，∴QR=1．①点Q在直线PN的左侧时，Q点的坐标为（n﹣1，n2﹣4n），R点的坐标为（n，n2﹣4n），N点的坐标为（n，n2﹣2n﹣3）．∴在Rt△QRN中，NQ2=1+（2n﹣3）2，∴时，NQ取最小值1．此时Q点的坐标为；②点Q在直线PN的右侧时，Q点的坐标为（n+11，n2﹣4）．同理，NQ2=1+（2n﹣1）2，∴时，NQ取最小值1．此时Q点的坐标为．综上可知存在满足题意的点Q，其坐标为或．【点评】本题为二次函数的综合应用，涉及待定系数法、轴对称、三角形的面积、勾股定理、二次函数的性质、方程思想及分类讨论思想等知识．在（1）中求得抛物线的对称轴是解题的关键，在（2）中用F点的坐标表示出F′的坐标是解题的关键，在（3）中求得QR的长，用勾股定理得到关于n的二次函数是解题的关键．本题考查知识点较多，综合性较强，特别是最后一问，难度很大．3．（2017•长沙）若三个非零实数x，y，z满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数x，y，z构成“和谐三组数”．（1）实数1，2，3可以构成“和谐三组数”吗？请说明理由；（2）若M（t，y1），N（t+1，y2），R（t+3，y3）三点均在函数（k为常数，k≠0）的图象上，且这三点的纵坐标y1，y2，y3构成“和谐三组数”，求实数t的值；（3）若直线y=2bx+2c（bc≠0）与x轴交于点A（x1，0），与抛物线y=ax2+3bx+3c（a≠0）交于B（x2，y2），C（x3，y3）两点．①求证：A，B，C三点的横坐标x1，x2，x3构成“和谐三组数”；②若a＞2b＞3c，x2=1，求点P（，）与原点O的距离OP的取值范围．【分析】（1）由和谐三组数的定义进行验证即可；（2）把M、N、R三点的坐标分别代入反比例函数解析式，可用t和k分别表示出y1、y2、y3，再由和谐三组数的定义可得到关于t的方程，可求得t的值；（3）①由直线解析式可求得x1=﹣，联立直线和抛物线解析式消去y，利用一元二次方程根与系数的关系可求得x2+x3=﹣，x2x3=，再利用和谐三数组的定义证明即可；②由条件可得到a+b+c=0，可得c=﹣（a+b），由a＞2b＞3c可求得的取值范围，令m=，利用两点间距离公式可得到OP2关于m的二次函数，利用二次函数的性质可求得OP2的取值范围，从而可求得OP的取值范围．【解答】解：（1）不能，理由如下：∵1、2、3的倒数分别为1、、，∴+≠1，1+≠，1+≠∴实数1，2，3不可以构成“和谐三组数”；（2）∵M（t，y1），N（t+1，y2），R（t+3，y3）三点均在函数（k为常数，k≠0）的图象上，∴y1、y2、y3均不为0，且y1=，y2=，y3=，∴=，=，=，∵y1，y2，y3构成“和谐三组数”，∴有以下三种情况：当=+时，则=+，即t=t+1+t+3，解得t=﹣4；当=+时，则=+，即t+1=t+t+3，解得t=﹣2；当=+时，则=+，即t+3=t+t+1，解得t=2；∴t的值为﹣4、﹣2或2；（3）①∵a、b、c均不为0，∴x1，x2，x3都不为0，∵直线y=2bx+2c（bc≠0）与x轴交于点A（x1，0），∴0=2bx1+2c，解得x1=﹣，联立直线与抛物线解析式，消去y可得2bx+2c=ax2+3bx+3c，即ax2+bx+c=0，∵直线与抛物线交与B（x2，y2），C（x3，y3）两点，∴x2、x3是方程ax2+bx+c=0的两根，∴x2+x3=﹣，x2x3=，∴+===﹣=，∴x1，x2，x3构成“和谐三组数”；②∵x2=1，∴a+b+c=0，∴c=﹣a﹣b，∵a＞2b＞3c，∴a＞2b＞3（﹣a﹣b），且a＞0，整理可得，解得﹣＜＜，∵P（，）∴OP2=（）2+（）2=（）2+（）2=2（）2+2+1=2（+）2+，令m=，则﹣＜m＜且m≠0，且OP2=2（m+）2+，∵2＞0，∴当﹣＜m＜﹣时，OP2随m的增大而减小，当m=﹣时，OP2有最大值，当m=﹣时，OP2有最小值，当﹣＜m＜时，OP2随m的增大而增大，当m=﹣时，OP2有最小值，当m=时，OP2有最大值，∴≤OP2＜且OP2≠1，∵P到原点的距离为非负数，∴≤OP＜且OP≠1．【点评】本题为二次函数的综合应用，涉及新定义、函数图象的交点、一元二次方程根与系数的关系、勾股定理、二次函数的性质、分类讨论思想及转化思想等知识．在（1）中注意利用和谐三数组的定义，在（2）中由和谐三数组得到关于t的方程是解题的关键，在（3）①中用a、b、c分别表示出x1，x2，x3是解题的关键，在（3）②中把OP2表示成二次函数的形式是解题的关键．本题考查知识点较多，综合性较强，特别是最后一问，难度很大．4．（2017•天津）已知抛物线y=x2+bx﹣3（b是常数）经过点A（﹣1，0）．（1）求该抛物线的解析式和顶点坐标；（2）P（m，t）为抛物线上的一个动点，P关于原点的对称点为P'．①当点P'落在该抛物线上时，求m的值；②当点P'落在第二象限内，P'A2取得最小值时，求m的值．【分析】（1）把A点坐标代入抛物线解析式可求得b的值，则可求得抛物线解析式，进一步可求得其顶点坐标；（2）①由对称可表示出P′点的坐标，再由P和P′都在抛物线上，可得到关于m的方程，可求得m的值；②由点P′在第二象限，可求得t的取值范围，利用两点间距离公式可用t表示出P′A2，再由点P′在抛物线上，可以消去m，整理可得到关于t的二次函数，利用二次函数的性质可求得其取得最小值时t的值，则可求得m的值．【解答】解：（1）∵抛物线y=x2+bx﹣3经过点A（﹣1，0），∴0=1﹣b﹣3，解得b=﹣2，∴抛物线解析式为y=x2﹣2x﹣3，∵y=x2﹣2x﹣3=（x﹣1）2﹣4，∴抛物线顶点坐标为（1，﹣4）；（2）①由P（m，t）在抛物线上可得t=m2﹣2m﹣3，∵点P′与P关于原点对称，∴P′（﹣m，﹣t），∵点P′落在抛物线上，∴﹣t=（﹣m）2﹣2（﹣m）﹣3，即t=﹣m2﹣2m+3，∴m2﹣2m﹣3=﹣m2﹣2m+3，解得m=或m=﹣；②由题意可知P′（﹣m，﹣t）在第二象限，∴﹣m＜0，﹣t＞0，即m＞0，t＜0，∵抛物线的顶点坐标为（1，﹣4），∴﹣4≤t＜0，∵P在抛物线上，∴t=m2﹣2m﹣3，∴m2﹣2m=t+3，∵A（﹣1，0），P′（﹣m，﹣t），∴P′A2=（﹣m+1）2+（﹣t）2=m2﹣2m+1+t2=t2+t+4=（t+）2+；∴当t=﹣时，P′A2有最小值，∴﹣=m2﹣2m﹣3，解得m=或m=，∵m＞0，∴m=不合题意，舍去，∴m的值为．【点评】本题为二次函数的综合应用，涉及待定系数法、中心对称、二次函数的性质、勾股定理、方程思想等知识．在（1）中注意待定系数法的应用，在（2）①中求得P′点的坐标，得到关于m的方程是解题的关键，在（2）②中用t表示出P′A2是解题的关键．本题考查知识点较多，综合性较强，难度适中．5．（2017•陕西）在同一直角坐标系中，抛物线C1：y=ax2﹣2x﹣3与抛物线C2：y=x2+mx+n 关于y轴对称，C2与x轴交于A、B两点，其中点A在点B的左侧．（1）求抛物线C1，C2的函数表达式；（2）求A、B两点的坐标；（3）在抛物线C1上是否存在一点P，在抛物线C2上是否存在一点Q，使得以AB为边，且以A、B、P、Q四点为顶点的四边形是平行四边形？若存在，求出P、Q两点的坐标；若不存在，请说明理由．【分析】（1）由对称可求得a、n的值，则可求得两函数的对称轴，可求得m的值，则可求得两抛物线的函数表达式；（2）由C2的函数表达式可求得A、B的坐标；（3）由题意可知AB只能为平行四边形的边，利用平行四边形的性质，可设出P点坐标，表示出Q点坐标，代入C2的函数表达式可求得P、Q的坐标．【解答】解：（1）∵C1、C2关于y轴对称，∴C1与C2的交点一定在y轴上，且C1与C2的形状、大小均相同，∴a=1，n=﹣3，∴C1的对称轴为x=1，∴C2的对称轴为x=﹣1，∴m=2，∴C1的函数表示式为y=x2﹣2x﹣3，C2的函数表达式为y=x2+2x﹣3；（2）在C2的函数表达式为y=x2+2x﹣3中，令y=0可得x2+2x﹣3=0，解得x=﹣3或x=1，∴A（﹣3，0），B（1，0）；（3）存在．∵AB的中点为（﹣1，0），且点P在抛物线C1上，点Q在抛物线C2上，∴AB只能为平行四边形的一边，∴PQ∥AB且PQ=AB，由（2）可知AB=1﹣（﹣3）=4，∴PQ=4，设P（t，t2﹣2t﹣3），则Q（t+4，t2﹣2t﹣3）或（t﹣4，t2﹣2t﹣3），①当Q（t+4，t2﹣2t﹣3）时，则t2﹣2t﹣3=（t+4）2+2（t+4）﹣3，解得t=﹣2，∴t2﹣2t﹣3=4+4﹣3=5，∴P（﹣2，5），Q（2，5）；②当Q（t﹣4，t2﹣2t﹣3）时，则t2﹣2t﹣3=（t﹣4）2+2（t﹣4）﹣3，解得t=2，∴t2﹣2t﹣3=4﹣4﹣3=﹣3，∴P（2，﹣3），Q（﹣2，﹣3），综上可知存在满足条件的点P、Q，其坐标为P（﹣2，5），Q（2，5）或P（2，﹣3），Q（﹣2，﹣3）．【点评】本题为二次函数的综合应用，涉及待定系数法、对称的性质、函数图象与坐标轴的交点、平行四边形的性质、方程思想及分类讨论思想等知识．在（1）中由对称性质求得a、n的值是解题的关键，在（2）中注意函数图象与坐标轴的交点的求法即可，在（3）中确定出PQ的长度，设P点坐标表示出Q点的坐标是解题的关键．本题考查知识点较多，综合性较强，难度适中．6．（2017•南充）如图1，已知二次函数y=ax2+bx+c（a、b、c为常数，a≠0）的图象过点O （0，0）和点A（4，0），函数图象最低点M的纵坐标为﹣，直线l的解析式为y=x．（1）求二次函数的解析式；（2）直线l沿x轴向右平移，得直线l′，l′与线段OA相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线l′折叠，当点E恰好落在抛物线上点E′时（图2），求直线l′的解析式；（3）在（2）的条件下，l′与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B′ON′，P为l′上的动点，当△PB′N′为等腰三角形时，求符合条件的点P的坐标．【分析】（1）由题意抛物线的顶点坐标为（2，﹣），设抛物线的解析式为y=a（x﹣2）2﹣，把（0，0）代入得到a=，即可解决问题；（2）如图1中，设E（m，0），则C（m，m2﹣m），B（﹣m2+m，0），由E、B关于对称轴对称，可得=2，由此即可解决问题；（3）分两种情形求解即可①当P1与N重合时，△P1B′N′是等腰三角形，此时P1（0，﹣3）．②当N′=N′B′时，设P（m，m﹣3），列出方程解方程即可；【解答】解：（1）由题意抛物线的顶点坐标为（2，﹣），设抛物线的解析式为y=a（x﹣2）2﹣，。
2017二次函数中考试题分类总汇编
一、选择题1、已知二次函数实用标准文案2017二次函数中考试题分类汇编y ax2bx c a 的图象如下图1所示，有下列5个结论：①abc 0；②b a c；③4a 2b c 0；④2c 3b；⑤a b m(a m b)，（m 1的实数）其中正确的结论有（）A.2个 B.3个 C.4个 D.5个2、如上图2是二次函数y＝ax2＋bx＋c图象的一部分，图象过点A（－3，0），对称轴为x＝－1．给出四个结论：①b2＞4ac；②2a＋b=0；③a－b＋c=0；④5a＜b．其中正确结论是（）．（A）②④（B）①④（C）②③（D）①③3、二次函数y x22x 1与x轴的交点个数是（）A．0 B．1 C．2 D．34、在同一坐标系中一次函数y ax b和二次函数y ax2bx的图象可能为（）y y y yO x O x O x O xA B C D5、已知二次函数y ax2bx c(a≠0)的图象开口向上，并经过点(-1，2)，(1，0). 下列结论正确的是( ) A. 当x>0时，函数值y随x的增大而增大(0)B. 当 x >0 时，函数值 y随 x 实用标准文案的增大而减小C. 存在一个负数 x ，使得当 x <x时，函数值 y 随 x 的增大而减小；当 x > x时，函数值 y随 x的增大而增大D. 存在一个正数 x ，使得当 x <x 时，函数值 y 随 x 的增大而减小；当 x >x时，函数值 y随 x的增大而增大6、已知二次函数 y =x 2-x+a (a ＞0)，当自变量 x取 m 时，其相应的函数值小于 0，那么下列结论中正确的是（）(A) m -1 的函数值小于 0 (B)m -1 的函数值大于 0(C) m -1 的函数值等于 0 (D) m -1 的函数值与 0 的大小关系不确定二、填空题1、二次函数 y =ax 2＋bx ＋c 的图象如下图 1 所示，且 P =| a －b ＋c|＋| 2a ＋b |，Q =| a ＋b ＋c|＋| 2a －b |，则 P 、Q 的大小关系为.3、如下图 2 所示的抛物线是二次函数y ax23 x a21的图象，那么 a 的值是．yyy图 1O图xO13（第 3 题）xO第 4 题x4、已知二次函数yx 2 x m 的部分图象如上图所示，则关于 x 的一元二次方程x22 x m 0 的解为．4、已知二次函数y ax2bx c 的图象如上图所示，则点 P (a ，bc ) 在第象限．三、解答题：1、知一抛物线与 x 轴的交点是 A(2,0) 、B （1，0），且经过点 C （2，8）。
2017-2021年河南中考数学真题分类汇编之二次函数
2017-2021年河南中考数学真题分类汇编之二次函数一．选择题（共2小题）1．（2019•河南）已知抛物线y＝﹣x2+bx+4经过（﹣2，n）和（4，n）两点，则n的值为（）A．﹣2B．﹣4C．2D．4 2．（2017•河南）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（1，0），对称轴为直线x＝﹣1，当y＞0时，x的取值范围是（）A．﹣1＜x＜1B．﹣3＜x＜﹣1C．x＜1D．﹣3＜x＜1二．填空题（共1小题）3．（2018•河南）已知二次函数y＝x2+bx+4顶点在x轴上，则b＝．三．解答题（共8小题）4．（2020•河南）如图，抛物线y＝﹣x2+2x+c与x轴正半轴，y轴正半轴分别交于点A，B，且OA＝OB，点G为抛物线的顶点．（1）求抛物线的解析式及点G的坐标；（2）点M，N为抛物线上两点（点M在点N的左侧），且到对称轴的距离分别为3个单位长度和5个单位长度，点Q为抛物线上点M，N之间（含点M，N）的一个动点，求点Q的纵坐标y Q的取值范围．5．（2017•河南）如图1，在平面直角坐标系中，抛物线y＝ax2+bx﹣3与直线y＝x+3交于点A（m，0）和点B（2，n），与y轴交于点C．（1）求m，n的值及抛物线的解析式；（2）在图1中，把△AOC平移，始终保持点A的对应点P在抛物线上，点C，O的对应点分别为M，N，连接OP，若点M恰好在直线y＝x+3上，求线段OP的长度；（3）如图2，在抛物线上是否存在点Q（不与点C重合），使△QAB和△ABC的面积相等？若存在，直接写出点Q的坐标；若不存在，请说明理由．6．（2021•河南）如图，抛物线y＝x2+mx与直线y＝﹣x+b相交于点A（2，0）和点B．（1）求m和b的值；（2）求点B的坐标，并结合图象写出不等式x2+mx＞﹣x+b的解集；（3）点M是直线AB上的一个动点，将点M向左平移3个单位长度得到点N，若线段MN与抛物线只有一个公共点，直接写出点M的横坐标x M的取值范围．7．（2018•河南）某公司推出一款产品，经市场调查发现，该产品的日销售量y（个）与销售单价x（元）之间满足一次函数关系关于销售单价，日销售量，日销售利润的几组对应值如表：销售单价x（元）8595105115日销售量y（个）17512575m87518751875875日销售利润w（元）（注：日销售利润＝日销售量×（销售单价﹣成本单价））（1）求y关于x的函数解析式（不要求写出x的取值范围）及m的值；（2）根据以上信息，填空：该产品的成本单价是元，当销售单价x＝元时，日销售利润w最大，最大值是元；（3）公司计划开展科技创新，以降低该产品的成本，预计在今后的销售中，日销售量与销售单价仍存在（1）中的关系．若想实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？8．（2018•河南）如图，抛物线y＝ax2+6x+c交x轴于A，B两点，交y轴于点C，直线y＝x ﹣5经过点B，C．（1）求抛物线的解析式；（2）过点A的直线交直线BC于点M．①当AM⊥BC时，过抛物线上一动点P（不与点B，C重合），作直线AM的平行线交直线BC于点Q，若以点A，M，P，Q为顶点的四边形是平行四边形，求点P的横坐标；②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，请直接写出点M的坐标．9．（2019•河南）如图，抛物线y＝ax2+x+c交x轴于A，B两点，交y轴于点C．直线y ＝﹣x﹣2经过点A，C．（1）求抛物线的解析式；（2）点P是抛物线上一动点，过点P作x轴的垂线，交直线AC于点M，设点P的横坐标为m．①当△PCM是直角三角形时，求点P的坐标；②作点B关于点C的对称点B'，则平面内存在直线l，使点M，B，B′到该直线的距离都相等．当点P在y轴右侧的抛物线上，且与点B不重合时，请直接写出直线l：y＝kx+b 的解析式．（k，b可用含m的式子表示）10．（2018•河南）如图，抛物线y＝ax2+bx+c交x轴于A、B两点，交y轴于点C（0，3），顶点F的坐标为（1，4），对称轴交x轴于点H，直线y＝x+1交x轴于点D，交y轴于点E，交抛物线的对称轴于点G．（1）求出a，b，c的值．（2）点M为抛物线对称轴上一个动点，若△DGM是以DG为腰的等腰三角形时，请求出点M的坐标．（3）点P为抛物线上一个动点，当点P关于直线y＝x+1的对称点恰好落在x轴上时，请直接写出此时点P的坐标．11．（2017•河南）如图，直线y＝﹣x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y＝﹣x2+bx+c经过点A，B．（1）求点B的坐标和抛物线的解析式；（2）M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点”．请直接写出使得M，P，N三点成为“共谐点”的m的值．2017-2021年河南中考数学真题分类汇编之二次函数参考答案与试题解析一．选择题（共2小题）1．（2019•河南）已知抛物线y＝﹣x2+bx+4经过（﹣2，n）和（4，n）两点，则n的值为（）A．﹣2B．﹣4C．2D．4【考点】二次函数图象上点的坐标特征．【专题】二次函数图象及其性质．【分析】根据（﹣2，n）和（4，n）可以确定函数的对称轴x＝1，再由对称轴的x＝即可求解；【解答】解：抛物线y＝﹣x2+bx+4经过（﹣2，n）和（4，n）两点，可知函数的对称轴x＝1，∴＝1，∴b＝2；∴y＝﹣x2+2x+4，将点（﹣2，n）代入函数解析式，可得n＝﹣4；故选：B．【点评】本题考查二次函数图象上点的坐标；熟练掌握二次函数图象上点的对称性是解题的关键．2．（2017•河南）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（1，0），对称轴为直线x＝﹣1，当y＞0时，x的取值范围是（）A．﹣1＜x＜1B．﹣3＜x＜﹣1C．x＜1D．﹣3＜x＜1【考点】二次函数图象与系数的关系；二次函数图象上点的坐标特征；抛物线与x轴的交点．【专题】数形结合；二次函数图象及其性质．【分析】根据抛物线的对称性得到抛物线与x轴的另一交点坐标，然后结合函数图象可以直接得到答案．【解答】解：∵抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（1，0），对称轴为直线x ＝﹣1，∴抛物线与x轴的另一交点坐标是（﹣3，0），∴当y＞0时，x的取值范围是﹣3＜x＜1．故选：D．【点评】本题考查了抛物线的对称性，抛物线与x轴的交点，二次函数图象上点的坐标特征．解题时，利用了“数形结合”的数学思想．二．填空题（共1小题）3．（2018•河南）已知二次函数y＝x2+bx+4顶点在x轴上，则b＝±4．【考点】二次函数的性质．【分析】根据二次函数顶点在x轴上得出Δ＝b2﹣4ac＝m2﹣4×2×2＝0，即可得出答案．【解答】解：∵二次函数y＝x2+bx+4的顶点在x轴上，∴Δ＝b2﹣4ac＝b2﹣4×1×4＝0，∴b2＝16，∴b＝±4．故答案为：±4．【点评】本题考查了二次函数的性质以及二次函数顶点在x轴上的特点，根据题意得出Δ＝b2﹣4ac＝0是解决问题的关键．三．解答题（共8小题）4．（2020•河南）如图，抛物线y＝﹣x2+2x+c与x轴正半轴，y轴正半轴分别交于点A，B，且OA＝OB，点G为抛物线的顶点．（1）求抛物线的解析式及点G的坐标；（2）点M，N为抛物线上两点（点M在点N的左侧），且到对称轴的距离分别为3个单位长度和5个单位长度，点Q为抛物线上点M，N之间（含点M，N）的一个动点，求点Q的纵坐标y Q的取值范围．【考点】待定系数法求二次函数解析式；二次函数的性质；二次函数图象上点的坐标特征．【专题】二次函数图象及其性质；应用意识．【分析】（1）先求出点B，点A坐标，利用待定系数法代入解析式求出c的值，即可求解；（2）先求出点M，点N坐标，利用函数的图象即可求解．【解答】解：（1）∵抛物线y＝﹣x2+2x+c与y轴正半轴交于点B，∴点B（0，c），c＞0．∵OA＝OB＝c，∴点A（c，0），∴0＝﹣c2+2c+c，∴c＝3或0（舍去），∴抛物线解析式为：y＝﹣x2+2x+3，∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴顶点G的坐标为（1，4）；（2）∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴对称轴为直线x＝1，顶点（1，4）．∵点M，N为抛物线上两点（点M在点N的左侧），且到对称轴的距离分别为3个单位长度和5个单位长度，∴点M的横坐标为﹣2或4，点N的横坐标为6，∴点M坐标为（﹣2，﹣5）或（4，﹣5），点N坐标为（6，﹣21），∵点Q为抛物线上点M，N之间（含点M，N）的一个动点，∴当M，N在对称轴的同侧时，﹣21≤y Q≤﹣5；当M，N在对称轴的两侧时，﹣21≤y Q≤4．∴点Q的纵坐标y Q的取值范围为﹣21≤y Q≤﹣5或﹣21≤y Q≤4．【点评】本题考查了待定系数法求二次函数解析式，二次函数的性质，二次函数图象上点的坐标特征，熟练运用二次函数的性质解决问题是本题的关键．5．（2017•河南）如图1，在平面直角坐标系中，抛物线y＝ax2+bx﹣3与直线y＝x+3交于点A（m，0）和点B（2，n），与y轴交于点C．（1）求m，n的值及抛物线的解析式；（2）在图1中，把△AOC平移，始终保持点A的对应点P在抛物线上，点C，O的对应点分别为M，N，连接OP，若点M恰好在直线y＝x+3上，求线段OP的长度；（3）如图2，在抛物线上是否存在点Q（不与点C重合），使△QAB和△ABC的面积相等？若存在，直接写出点Q的坐标；若不存在，请说明理由．【考点】二次函数综合题．【专题】开放型．【分析】（1）把点A（m，0）和点B（2，n）代入直线y＝x+3，解得：m＝﹣3，n＝5，A（﹣3，0）、B（2，5），把A、B坐标代入抛物线方程即可求解；（2）由平移得：PN＝OA＝3，NM＝OC＝3，设：平移后点P（t，t2+2t﹣3），则N（t+3，t2+2t﹣3），M（t+3，t2+2t﹣6），根据点M在直线y＝x+3上，即可求解；（3）存在．设：直线AB交y轴于D（0，3），点C关于点D的对称点为C′（0，9）按照△QAB和△Q′AB和△ABC的面积相同即可求解．【解答】解：（1）把点A（m，0）和点B（2，n）代入直线y＝x+3，解得：m＝﹣3，n ＝5，∴A（﹣3，0）、B（2，5），把A、B坐标代入抛物线方程，解得：a＝1，b＝2，∴抛物线方程为：y＝x2+2x﹣3…①，则C（0，﹣3）；（2）由平移得：PN＝OA＝3，NM＝OC＝3，设：平移后点P（t，t2+2t﹣3），则N（t+3，t2+2t﹣3），∴M（t+3，t2+2t﹣6），∵点M在直线y＝x+3上，∴t2+2t﹣6＝t+3+3，解得：t＝3或﹣4，∴P点坐标为（3，12）或（﹣4，5），则线段OP的长度为：3或；（3）存在．设：直线AB交y轴于D（0，3），点C关于点D的对称点为C′（0，9）过点C和C′分别做AB的平行线，交抛物线于点Q、Q′，则：△QAB和△Q′AB和△ABC的面积相同，直线QC和Q′C的方程分别为：y＝x﹣3和y＝x+9…②，将①、②联立，解得：x＝﹣1或x＝3或x＝﹣4，∴Q点坐标为（﹣1，﹣4）或（3，12）或（﹣4，5）．【点评】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．6．（2021•河南）如图，抛物线y＝x2+mx与直线y＝﹣x+b相交于点A（2，0）和点B．（1）求m和b的值；（2）求点B的坐标，并结合图象写出不等式x2+mx＞﹣x+b的解集；（3）点M是直线AB上的一个动点，将点M向左平移3个单位长度得到点N，若线段MN与抛物线只有一个公共点，直接写出点M的横坐标x M的取值范围．【考点】二次函数综合题．【专题】代数综合题；分类讨论；一元一次不等式（组）及应用；数据分析观念．【分析】（1）用待定系数法即可求解；（2）求出点B的坐标为（﹣1，3），再观察函数图象即可求解；（3）分类求解确定MN的位置，进而求解．【解答】解：（1）将点A的坐标代入抛物线表达式得：0＝4+2m，解得：m＝﹣2，将点A的坐标代入直线表达式得：0＝﹣2+b，解得b＝2；故m＝﹣2，b＝2；（2）由（1）得，直线和抛物线的表达式为：y＝﹣x+2，y＝x2﹣2x，联立上述两个函数表达式并解得或（不符合题意，舍去），即点B的坐标为（﹣1，3），从图象看，不等式x2+mx＞﹣x+b的解集为x＜﹣1或x＞2；（3）当点M在线段AB上时，线段MN与抛物线只有一个公共点，∵M，N的距离为3，而A、B的水平距离是3，故此时只有一个交点，即﹣1≤x M＜2；当点M在点B的左侧时，线段MN与抛物线没有公共点；当点M在点A的右侧时，当x M＝3时，抛物线和MN交于抛物线的顶点（1，﹣1），即x M＝3时，线段MN与抛物线只有一个公共点，综上所述，﹣1≤x M＜2 或x M＝3．【点评】本题考查的是二次函数综合运用，涉及到一次函数的性质、不等式的性质等，其中（3），分类求解确定MN的位置是解题的关键．7．（2018•河南）某公司推出一款产品，经市场调查发现，该产品的日销售量y（个）与销售单价x（元）之间满足一次函数关系关于销售单价，日销售量，日销售利润的几组对应值如表：销售单价x（元）8595105115日销售量y（个）17512575m87518751875875日销售利润w（元）（注：日销售利润＝日销售量×（销售单价﹣成本单价））（1）求y关于x的函数解析式（不要求写出x的取值范围）及m的值；（2）根据以上信息，填空：该产品的成本单价是80元，当销售单价x＝100元时，日销售利润w最大，最大值是2000元；（3）公司计划开展科技创新，以降低该产品的成本，预计在今后的销售中，日销售量与销售单价仍存在（1）中的关系．若想实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？【考点】二次函数的应用；一元二次方程的应用．【专题】应用题．【分析】（1）根据题意和表格中的数据可以求得y关于x的函数解析式；（2）根据题意可以列出相应的方程，从而可以求得生产成本和w的最大值；（3）根据题意可以列出相应的不等式，从而可以取得科技创新后的成本．【解答】解；（1）设y关于x的函数解析式为y＝kx+b，，得，即y关于x的函数解析式是y＝﹣5x+600，当x＝115时，y＝﹣5×115+600＝25，即m的值是25；（2）设成本为a元/个，当x＝85时，875＝175×（85﹣a），得a＝80，w＝（﹣5x+600）（x﹣80）＝﹣5x2+1000x﹣48000＝﹣5（x﹣100）2+2000，∴当x＝100时，w取得最大值，此时w＝2000，故答案为：80，100，2000；（3）设科技创新后成本为b元，当x＝90时，（﹣5×90+600）（90﹣b）≥3750，解得，b≤65，答：该产品的成本单价应不超过65元．【点评】本题考查二次函数的应用、一元二次方程的应用、不等式的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用函数和数形结合的思想解答．8．（2018•河南）如图，抛物线y＝ax2+6x+c交x轴于A，B两点，交y轴于点C，直线y＝x ﹣5经过点B，C．（1）求抛物线的解析式；（2）过点A的直线交直线BC于点M．①当AM⊥BC时，过抛物线上一动点P（不与点B，C重合），作直线AM的平行线交直线BC于点Q，若以点A，M，P，Q为顶点的四边形是平行四边形，求点P的横坐标；②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，请直接写出点M的坐标．【考点】二次函数综合题．【专题】综合题．【分析】（1）利用一次函数解析式确定C（0，﹣5），B（5，0），然后利用待定系数法求抛物线解析式；（2）①先解方程﹣x2+6x﹣5＝0得A（1，0），再判断△OCB为等腰直角三角形得到∠OBC＝∠OCB＝45°，则△AMB为等腰直角三角形，所以AM＝2，接着根据平行四边形的性质得到PQ＝AM＝2，PQ⊥BC，作PD⊥x轴交直线BC于D，如图1，利用∠PDQ＝45°得到PD＝PQ＝4，设P（m，﹣m2+6m﹣5），则D（m，m﹣5），讨论：当P点在直线BC上方时，PD＝﹣m2+6m﹣5﹣（m﹣5）＝4；当P点在直线BC下方时，PD＝m﹣5﹣（﹣m2+6m﹣5），然后分别解方程即可得到P点的横坐标；②作AN⊥BC于N，NH⊥x轴于H，作AC的垂直平分线交BC于M1，交AC于E，如图2，利用等腰三角形的性质和三角形外角性质得到∠AM1B＝2∠ACB，再确定N（3，﹣2），AC的解析式为y＝5x﹣5，E点坐标为（，﹣），利用两直线垂直的问题可设直线EM1的解析式为y＝﹣x+b，把E（，﹣）代入求出b得到直线EM1的解析式为y＝﹣x ﹣，则解方程组得M1点的坐标；作直线BC上作点M1关于N点的对称点M2，如图2，利用对称性得到∠AM2C＝∠AM1B＝2∠ACB，设M2（x，x﹣5），根据中点坐标公式得到3＝，然后求出x即可得到M2的坐标，从而得到满足条件的点M的坐标．【解答】解：（1）当x＝0时，y＝x﹣5＝﹣5，则C（0，﹣5），当y＝0时，x﹣5＝0，解得x＝5，则B（5，0），把B（5，0），C（0，﹣5）代入y＝ax2+6x+c得，解得，∴抛物线解析式为y＝﹣x2+6x﹣5；（2）①解方程﹣x2+6x﹣5＝0得x1＝1，x2＝5，则A（1，0），∵B（5，0），C（0，﹣5），∴△OCB为等腰直角三角形，∴∠OBC＝∠OCB＝45°，∵AM⊥BC，∴△AMB为等腰直角三角形，∴AM＝AB＝×4＝2，∵以点A，M，P，Q为顶点的四边形是平行四边形，AM∥PQ，∴PQ＝AM＝2，PQ⊥BC，作PD⊥x轴交直线BC于D，如图1，则∠PDQ＝45°，∴PD＝PQ＝×2＝4，设P（m，﹣m2+6m﹣5），则D（m，m﹣5），当P点在直线BC上方时，PD＝﹣m2+6m﹣5﹣（m﹣5）＝﹣m2+5m＝4，解得m1＝1（舍去），m2＝4，当P点在直线BC下方时，PD＝m﹣5﹣（﹣m2+6m﹣5）＝m2﹣5m＝4，解得m1＝，m2＝，综上所述，P点的横坐标为4或或；②作AN⊥BC于N，NH⊥x轴于H，作AC的垂直平分线交BC于M1，交AC于E，如图2，∵M1A＝M1C，∴∠ACM1＝∠CAM1，∴∠AM1B＝2∠ACB，∵△ANB为等腰直角三角形，∴AH＝BH＝NH＝2，∴N（3，﹣2），易得AC的解析式为y＝5x﹣5，E点坐标为（，﹣），设直线EM1的解析式为y＝﹣x+b，把E（，﹣）代入得﹣+b＝﹣，解得b＝﹣，∴直线EM1的解析式为y＝﹣x﹣，解方程组得，则M1（，﹣）；在直线BC上作点M1关于N点的对称点M2，如图2，则∠AM2C＝∠AM1B＝2∠ACB，设M2（x，x﹣5），∵3＝，∴x＝，∴M2（，﹣），综上所述，点M的坐标为（，﹣）或（，﹣）．【点评】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等腰直角的判定与性质和平行四边形的性质；会利用待定系数法求函数解析式；理解坐标与图形性质；会运用分类讨论的思想解决数学问题．9．（2019•河南）如图，抛物线y＝ax2+x+c交x轴于A，B两点，交y轴于点C．直线y ＝﹣x﹣2经过点A，C．（1）求抛物线的解析式；（2）点P是抛物线上一动点，过点P作x轴的垂线，交直线AC于点M，设点P的横坐标为m．①当△PCM是直角三角形时，求点P的坐标；②作点B关于点C的对称点B'，则平面内存在直线l，使点M，B，B′到该直线的距离都相等．当点P在y轴右侧的抛物线上，且与点B不重合时，请直接写出直线l：y＝kx+b 的解析式．（k，b可用含m的式子表示）【考点】二次函数综合题．【专题】函数的综合应用．【分析】（1）利用一次函数图象上点的坐标特征可求出点A，C的坐标，根据点A，C的坐标，利用待定系数法可求出二次函数解析式；（2）①由PM⊥x轴可得出∠PMC≠90°，分∠MPC＝90°及∠PCM＝90°两种情况考虑：（i）当∠MPC＝90°时，PC∥x轴，利用二次函数图象上点的坐标特征可求出点P 的坐标；（ii）当∠PCM＝90°时，设PC与x轴交于点D，易证△AOC∽△COD，利用相似三角形的性质可求出点D的坐标，根据点C，D的坐标，利用待定系数法可求出直线PC的解析式，联立直线PC和抛物线的解析式成方程组，通过解方程组可求出点P的坐标．综上，此问得解；②利用二次函数图象上点的坐标特征及一次函数图象上点的坐标特征可得出点B，M的坐标，结合点C的坐标可得出点B′的坐标，根据点M，B，B′的坐标，利用待定系数法可分别求出直线BM，B′M和BB′的解析式，利用平行线的性质可求出直线l的解析式．【解答】解：（1）当x＝0时，y＝﹣x﹣2＝﹣2，∴点C的坐标为（0，﹣2）；当y＝0时，﹣x﹣2＝0，解得：x＝﹣4，∴点A的坐标为（﹣4，0）．将A（﹣4，0），C（0，﹣2）代入y＝ax2+x+c，得：，解得：，∴抛物线的解析式为y＝x2+x﹣2．（2）①∵PM⊥x轴，∴∠PMC≠90°，∴分两种情况考虑，如图1所示．（i）当∠MPC＝90°时，PC∥x轴，∴点P的纵坐标为﹣2．当y＝﹣2时，x2+x﹣2＝﹣2，解得：x1＝﹣2，x2＝0，∴点P的坐标为（﹣2，﹣2）；（ii）当∠PCM＝90°时，设PC与x轴交于点D．∵∠OAC+∠OCA＝90°，∠OCA+∠OCD＝90°，∴∠OAC＝∠OCD．又∵∠AOC＝∠COD＝90°，∴△AOC∽△COD，∴＝，即＝，∴OD＝1，∴点D的坐标为（1，0）．设直线PC的解析式为y＝kx+b（k≠0），将C（0，﹣2），D（1，0）代入y＝kx+b，得：，解得：，∴直线PC的解析式为y＝2x﹣2．联立直线PC和抛物线的解析式成方程组，得：，解得：，，点P的坐标为（6，10）．综上所述：当△PCM是直角三角形时，点P的坐标为（﹣2，﹣2）或（6，10）．②当y＝0时，x2+x﹣2＝0，解得：x1＝﹣4，x2＝2，∴点B的坐标为（2，0）．∵点C的坐标为（0，﹣2），点B，B′关于点C对称，∴点B′的坐标为（﹣2，﹣4）．∵点P的横坐标为m（m＞0且m≠2），∴点M的坐标为（m，﹣m﹣2）．利用待定系数法可求出：直线BM的解析式为y＝﹣x+，直线B′M的解析式为y＝x﹣，直线BB′的解析式为y＝x﹣2．分三种情况考虑，如图2所示：当直线l∥BM且过点C时，直线l的解析式为y＝﹣x﹣2；当直线l∥B′M且过点C时，直线l的解析式为y＝x﹣2；当直线l∥BB′且过线段CM的中点N（m，﹣m﹣2）时，直线l的解析式为y＝x﹣m﹣2．综上所述：直线l的解析式为y＝﹣x﹣2，y＝x﹣2或y＝x﹣m﹣2．【点评】本题考查了一次函数图象上点的坐标特征、待定系数法二次函数解析式、二次函数图象上点的坐标特征、待定系数法求一次函数解析式、相似三角形的判定与性质以及平行线的性质，解题的关键是：（1）根据点的坐标，利用待定系数法求出二次函数解析式；（2）①分∠MPC＝90°及∠PCM＝90°两种情况求出点P的坐标；②利用待定系数法及平行线的性质，求出直线l的解析式．10．（2018•河南）如图，抛物线y＝ax2+bx+c交x轴于A、B两点，交y轴于点C（0，3），顶点F的坐标为（1，4），对称轴交x轴于点H，直线y＝x+1交x轴于点D，交y轴于点E，交抛物线的对称轴于点G．（1）求出a，b，c的值．（2）点M为抛物线对称轴上一个动点，若△DGM是以DG为腰的等腰三角形时，请求出点M的坐标．（3）点P为抛物线上一个动点，当点P关于直线y＝x+1的对称点恰好落在x轴上时，请直接写出此时点P的坐标．【考点】二次函数综合题．【专题】函数的综合应用．【分析】（1）由抛物线的顶点坐标可设抛物线的解析式为y＝a（x﹣1）2+4，由点C的坐标利用待定系数法可求出抛物线的解析式，进而可得出a，b，c的值；（2）利用一次函数图象上点的坐标特征可求出点D，G的坐标，进而可求出DG的长度，分DG＝DM，GD＝GM两种情况考虑：①当DG＝DM时，由等腰三角形的性质可得出HG＝HM1，进而可得出点M1的坐标；②当GD＝GM时，由等腰三角形的性质可得出GM2＝GM3＝，结合点G的坐标可得出点M2，M3的坐标．综上，此问得解；（3）过点E作EN⊥直线DE，交x轴于点N，则△DOE∽△DEN，利用相似三角形的性质可求出点N的坐标，由点E，N的坐标利用待定系数法可求出直线EN的解析式，设点P关于直线y＝x+1的对称点落在x轴上Q点处，连接PQ交DE于点R，设直线PQ 的解析式为y＝﹣2x+m，利用一次函数图象上点的坐标特征可求出点Q的坐标，联立直线PQ和直线DE的解析式成方程组，通过解方程组可得出点R的坐标，进而可得出点P 的坐标，由点P的坐标利用二次函数图象上点的坐标特征可得出关于m的一元二次方程，解之可得出m的值，再将其代入点P的坐标中即可得出结论．【解答】解：（1）∵抛物线顶点F的坐标为（1，4），∴设抛物线的解析式为y＝a（x﹣1）2+4．将C（0，3）代入y＝a（x﹣1）2+4，得：a+4＝3，解得：a＝﹣1，∴抛物线的解析式为y＝﹣（x﹣1）2+4，即y＝﹣x2+2x+3，∴a＝﹣1，b＝2，c＝3．（2）当y＝0时，x+1＝0，解得：x＝﹣2，∴点D的坐标为（﹣2，0）．当x＝1时，y＝x+1＝，∴点G的坐标为（1，），∴DH＝1﹣（﹣2）＝3，GH＝，∴DG＝＝．分两种情况考虑（如图1）：①当DG＝DM时，HG＝HM1，∴点M1的坐标为（1，﹣）；②当GD＝GM时，GM2＝GM3＝，∴点M2的坐标为（1，），点M3的坐标为（1，）．综上所述：点M的坐标为（1，﹣），（1，）或（1，）．（3）过点E作EN⊥直线DE，交x轴于点N，如图2所示．当x＝0时，y＝x+1＝1，∴点E的坐标为（0，1），∴OE＝1，DE＝＝．∵∠DOE＝∠DEN＝90°，∠ODE＝∠EDN，∴△DOE∽△DEN，∴＝，即＝，∴DN＝，∴点N的坐标为（，0）．∵点E（0，1），点N（，0），∴线段EN所在直线的解析式为y＝﹣2x+1（可利用待定系数法求出）．设点P关于直线y＝x+1的对称点落在x轴上Q点处，连接PQ交DE于点R．设直线PQ的解析式为y＝﹣2x+m，当y＝0时，﹣2x+m＝0，解得：x＝，∴点Q的坐标为（，0）．联立直线PQ和直线DE的解析式成方程组，得：，解得：，∴点R的坐标为（，）．∵点R为线段PQ的中点，∴点P的坐标为（，）．∵点P在抛物线y＝﹣x2+2x+3的图象上，∴﹣（）2+2×+3＝，整理，得：9m2﹣68m+84＝0，解得：m1＝6，m2＝，∴点P的坐标为（1，4）或（﹣，）．【点评】本题考查了待定系数法求二次函数解析式、一次函数图象上点的坐标特征、勾股定理、等腰三角形的性质、相似三角形的判定与性质、平行线的性质、中点坐标公式以及二次函数图象上点的坐标特征，解题的关键是：（1）巧设二次函数解析式，利用待定系数法求出a值；（2）分DG＝DM，GD＝GM两种情况，利用等腰三角形的性质求出点M的坐标；（3）利用二次函数图象上点的坐标特征，找出关于m的一元二次方程．11．（2017•河南）如图，直线y＝﹣x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y＝﹣x2+bx+c经过点A，B．（1）求点B的坐标和抛物线的解析式；（2）M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点”．请直接写出使得M，P，N三点成为“共谐点”的m的值．【考点】二次函数综合题．【分析】（1）把A点坐标代入直线解析式可求得c，则可求得B点坐标，由A、B的坐标，利用待定系数法可求得抛物线解析式；（2）①由M点坐标可表示P、N的坐标，从而可表示出MA、MP、PN、PB的长，分∠NBP＝90°和∠BNP＝90°两种情况，分别利用相似三角形的性质可得到关于m的方程，可求得m的值；②用m可表示出M、P、N的坐标，由题意可知有P为线段MN的中点、M为线段PN 的中点或N为线段PM的中点，可分别得到关于m的方程，可求得m的值．【解答】解：（1）∵y＝﹣x+c与x轴交于点A（3，0），与y轴交于点B，∴0＝﹣2+c，解得c＝2，∴B（0，2），∵抛物线y＝﹣x2+bx+c经过点A，B，∴，解得，∴抛物线解析式为y＝﹣x2+x+2；（2）①由（1）可知直线解析式为y＝﹣x+2，∵M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N，∴P（m，﹣m+2），N（m，﹣m2+m+2），∴PM＝﹣m+2，AM＝3﹣m，PN＝﹣m2+m+2﹣（﹣m+2）＝﹣m2+4m，∵△BPN和△APM相似，且∠BPN＝∠APM，∴∠BNP＝∠AMP＝90°或∠NBP＝∠AMP＝90°，当∠BNP＝90°时，则有BN⊥MN，∴N点的纵坐标为2，∴﹣m2+m+2＝2，解得m＝0（舍去）或m＝，∴M（，0）；当∠NBP＝90°时，过点N作NC⊥y轴于点C，则∠NBC+∠BNC＝90°，NC＝m，BC＝﹣m2+m+2﹣2＝﹣m2+m，∵∠NBP＝90°，∴∠NBC+∠ABO＝90°，∴∠ABO＝∠BNC，∴Rt△NCB∽Rt△BOA，∴＝，∴＝，解得m＝0（舍去）或m＝，∴M（，0）；综上可知当以B，P，N为顶点的三角形与△APM相似时，点M的坐标为（，0）或（，0）；②由①可知M（m，0），P（m，﹣m+2），N（m，﹣m2+m+2），∵M，P，N三点为“共谐点”，∴有P为线段MN的中点、M为线段PN的中点或N为线段PM的中点，当P为线段MN的中点时，则有2（﹣m+2）＝﹣m2+m+2，解得m＝3（舍去）或m＝0.5；当M为线段PN的中点时，则有﹣m+2+（﹣m2+m+2）＝0，解得m＝3（舍去）或m＝﹣1；当N为线段PM的中点时，则有﹣m+2＝2（﹣m2+m+2），解得m＝3（舍去）或m＝﹣；综上可知当M，P，N三点成为“共谐点”时m的值为0.5或﹣1或﹣．【点评】本题为二次函数的综合应用，涉及待定系数法、函数图象的交点、相似三角形的判定和性质、勾股定理、线段的中点、方程思想及分类讨论思想等知识．在（1）中注意待定系数法的应用，在（2）①中利用相似三角形的性质得到关于m的方程是解题的关键，注意分两种情况，在（2）②中利用“共谐点”的定义得到m的方程是解题的关键，注意分情况讨论．本题考查知识点较多，综合性较强，分情况讨论比较多，难度较大．考点卡片1．一元二次方程的应用1、列方程解决实际问题的一般步骤是：审清题意设未知数，列出方程，解所列方程求所列方程的解，检验和作答．2、列一元二次方程解应用题中常见问题：（1）数字问题：个位数为a，十位数是b，则这个两位数表示为10b+a．（2）增长率问题：增长率＝增长数量/原数量×100%．如：若原数是a，每次增长的百分率为x，则第一次增长后为a（1+x）；第二次增长后为a（1+x）2，即原数×（1+增长百分率）2＝后来数．（3）形积问题：①利用勾股定理列一元二次方程，求三角形、矩形的边长．②利用三角形、矩形、菱形、梯形和圆的面积，以及柱体体积公式建立等量关系列一元二次方程．③利用相似三角形的对应比例关系，列比例式，通过两内项之积等于两外项之积，得到一元二次方程．（4）运动点问题：物体运动将会沿着一条路线或形成一条痕迹，运行的路线与其他条件会构成直角三角形，可运用直角三角形的性质列方程求解．【规律方法】列一元二次方程解应用题的“六字诀”1．审：理解题意，明确未知量、已知量以及它们之间的数量关系．2．设：根据题意，可以直接设未知数，也可以间接设未知数．3．列：根据题中的等量关系，用含所设未知数的代数式表示其他未知量，从而列出方程．4．解：准确求出方程的解．5．验：检验所求出的根是否符合所列方程和实际问题．6．答：写出答案．2．二次函数的性质二次函数y＝ax2+bx+c（a≠0）的顶点坐标是（﹣，），对称轴直线x＝﹣，二次函数y＝ax2+bx+c（a≠0）的图象具有如下性质：①当a＞0时，抛物线y＝ax2+bx+c（a≠0）的开口向上，x＜﹣时，y随x的增大而减小；x＞﹣时，y随x的增大而增大；x＝﹣时，y取得最小值，即顶点是抛物线的最低点．。
2017年中考真题分类解析 二次函数几何方面的应用
一、选择题1. (2017江苏扬州，，3分)如图，已知△ABC 的顶点坐标分别为A （0，2）、B （1，0）、C （2，1），若二次函数21y x bx =++的图像与阴影部分（含边界）一定有公共点，则实数b 的取值范围是即1. 与（3）点G 是线段CE 的中点，将抛物线3332332--=x x y 沿x 轴正方向平移得到新抛物线y '，y '经过点D ，y '的顶点为点F ．在新抛物线y '的对称轴上，是否存在点Q ，使得∆FGQ 为等腰三角形？若存在，直接写出点Q 的坐标；若不存在，请说明理由．思路分析：（1）首先求出A 、E 点的坐标，然后设出直线AE 的解析式，并将A 、E 点的坐标代入，求得方程组的解，便可得到直线AE 的解析式；（2）由抛物线解析式求得C 点坐标，则可得出直线CE 的解析式；过点P 作PH ∥x 轴，交CE 于点H ，设出P 点坐标，可推出H 点坐标，根据斜三角形面积公式“2铅垂高水平宽⨯”可表示出∆PCE 的面积，并可计算出其面积最大时P 点的坐标；分别作K 关于CP 、CD 的对称点的对称点K 1、K 2，将KM +MN +KN 即可确定出转化成一条线段，由“两点之间，线段最短”及勾股定理计算出其最小值即可；（3）运用已知两定点时确定等腰三角形常用的方法“两圆一线”即可在抛物线y '的对称轴上找到符合条件的四个点，分别确定其坐标即可． 解：（1）∵抛物线3332332--=x x y 与x 轴交于A ，B 两点，且点E （4，n ）在抛物线上， ∴03332332=--x x ，解得：x 1＝－1，x 2＝3，∴A ，B 两点的坐标分别为（－1，0），（3，0）； 343324332-⨯-⨯=y ＝335，∴点E 坐标为（4，335）．设直线AE 的解析式的解析式为y ＝kx +b ，将A 点、E 点坐标分别代入，得：⎪⎩⎪⎨⎧+=+-=b k b k 43350，解得：⎪⎪⎩⎪⎪⎨⎧==3333b k ，∴y ＝33x +33；（2）∵令x ＝0，得y ＝ 3-，∴点C （0，3-），∵点E 坐标为（4，335），∴直线CE 的解析式为y＝3332-x ，过点P 作PH ∥x 轴，交CE 于点H ，如图，设点P 的坐标为（t，3332332--t t ），则H （t ，3332-t ），∴PH ＝3332-t －（3332332--t t ）＝t t 334332+-， ∴t t t t PH x x S C E PCE 338332334334212122+-=⎪⎪⎭⎫ ⎝⎛+-⨯⨯=⋅-=∆，∵0332<-，抛物线开口向下，40<<t ，∴当⎪⎪⎭⎫⎝⎛-⨯-=3322338t ＝2时，PCE S ∆取得最大值，此时P 为（2，3-）；∵点C （0，3-），B （3，0），由三角形中位线定理得K （23，23-），∵y C ＝y P ＝3-，∴PC ∥x 轴，作K 关于CP 的对称点K 1，则K 1（23，233-）；∵333tan ==∠OCB ，∴∠OCB ＝60゜，∵D （1，0），∴3331tan ==∠OCD ，∴∠OCD ＝ 30゜，∴∠OCD ＝∠BCD ＝30゜，∴CD 平分∠OCB ，∴点K 关于CD 的对称点K 2在y 轴上，又∵CK ＝OC ＝3，∴点K 2与点O 重合，连接OK 1，交CD 于点N ，交CP 于点M ，如图，∴KM ＝ K 1M ，KN ＝ON ，∴KM +MN +KN＝ K 1M +MN +ON ，根据“两点之间，线段最短”可得，此时KM +MN +KN 的值最小，∴K 1 K 2 ＝O K 1＝32332322=⎪⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛，∴KM +MN +KN 的最小值为3；（3）点Q 的坐标为（3，321234+-），（3，321234--），（3，32），（3，332-）．（2017浙江衢州,22，10分）（本题满分10分）定义：如图1，抛物线y ＝ax 2＋bx ＋c （a ≠0）与x 轴交于A ，两点，点P 在抛物线上（P 点与A 、B 两点不重合），如果△ABP 的三边需满足AP 2＋BP 2＝AB 2，则称点P 为抛物线y ＝ax 2＋bx ＋c （a ≠0）的勾股点．1）直接写出抛物线y ＝－x 2＋1的勾股点坐标．（2）如图2，已知抛物线C ：y ＝ax 2＋bx （a ≠0）与x 轴交于A ，B 两点，点P （1，3）是抛物线C 的勾股点，求抛物线C 的函数表达式．（3）在（2）的条件下，点Q 在抛物线C 上，求满足条件S △ABQ ＝S △ABP 的Q 点（异于点P ）的坐标．xy(第22题 图1）ABPOxy（第22题 图2）O(A )BP xy G (A )B P –11212345O思路分析：（1）所谓勾股点，即以AB 为直径的圆与抛物线的交点．y ＝－x 2＋1与x 轴交点坐标为（1，0），（－，0），故圆心为原点，半径为1，与抛物线交点为（0，1）.（2）由P 点坐标可知∠P AB ＝60°，又∠APB ＝90°，从而求得B 点坐标，利用待定系数法即可求解．（3）由S △ABQ ＝S △ABP ，故有|y Q |＝3，将y Q ＝±3分别代入抛物线解析式即可求解．解（1）勾股点的坐标（0，1）．（2）抛物线y ＝ax 2＋bx （a ≠0）过原点（0，0），即A 为（0，0）． 如图，作PG ⊥x 轴于点G ，连结P A ，PB ．∵点P 的坐标为（13， ∴AG ＝1，PG 3P A ＝2，tan ∠P AB 3 ∴∠P AB ＝60°，∴Rt △P AB 中，AB ＝cos60PAo＝4，∴点B （4，0）．设y ＝ax （x －4），当x ＝1时，y ＝3，解得a ＝－33． ∴y 3x （x －43x 243． （3）①当点Q 在x 轴上方时，由S △ABQ ＝S △ABP 易知点Q 3 3x 2433x 1＝3，x 2＝1（不合题意，舍去）．∴Q 1（33． ②当点Q 在x 轴下方时，由S △ABQ ＝S △ABP 易知点Q 的纵坐标为－3．则有－33x 2＋433x ＝－3， 解得x 1＝2＋7，x 2＝2－7．∴Q 2（2＋7，－3），Q 2（2－7，－3）．综上，满足条件的Q 点有三个：Q 1（3，3），Q 2（2＋7，－3），Q 2（2－7，－3）． 3. （2017山东济宁，21，9分）已知函数2(25)2y mx m x m =--+-的图象与x 轴有两个公共点．（1）求m 的取值范围，写出当m 取范围内最大整数时函数的解析式； （2）题（1）中求得的函数记为C 1①当1n x ≤≤-时，y 的取值范围是13y n ≤≤-，求n 的值；②函数C 2：22()y x h k =-+的图象由函数C 1的图象平移得到，其顶点P 落在以原点为圆心，半径为5的圆内或圆上．设函数C 1的图象顶点为M ，求点P 与点M 距离最大时函数C 2的解析式．思路分析：（1）根据函数2(25)2y mx m x m =--+-图象与x 轴有两个公共点，即一元二次方程2(25)20mx m x m --+-=有两个不同的实数解，即需满足m ≠0且根的判别式△＞0，解不等式组得25,12m <且0m ≠；（2）由二次函数22y x x =+性质，当14x <-时，y 随x 的增大而减小，求出n 的值为—2；（3）由图形可知当P 为射线MO 与圆的交点时，距离最大，先求出MO 的解析式，设出点P 的坐标，根据勾股定理求出点P 的坐标，继而求出PM 最大时的函数解析式为()2221y x =-+．解：（1）由题意可得：()()20,25420.m m m m ≠⎧⎪⎨---->⎡⎤⎪⎣⎦⎩解得：25,12m <且0,m ≠ 当2m =时，函数解析式为：22y x x =+．（2）函数22y x x =+图象开口向上，对称轴为1,4x =-∴当14x <-时，y 随x 的增大而减小．∵当1n x ≤≤-时，y 的取值范围是13y n ≤≤-， ∴ 223n n n +=-．∴ 2n =-或0n =（舍去）．∴2n=-．（3）∵2211 22,48 y x x x⎛⎫=+=+-⎪⎝⎭∴图象顶点M的坐标为11,48⎛⎫--⎪⎝⎭，由图形可知当P为射线MO与圆的交点时，距离最大．∴4.N（（（3）若∠DMN=90°，MD=MN，求点M的横坐标.(2∴∵∴∴∴①解当（3）设直线BC的函数表达式为y=kx+b.把点B(3,0),C(0,3)代入表达式，得30,3,k bb+=⎧⎨=⎩解得1,3.k b =-⎧⎨=⎩∴直线BC 的函数表达式为y =-x +3，设点M 的坐标为(a ,223a a -++), 则点D 的坐标为(a ,-a +3)， ∴DM =23a a -+ ，∵∴∴∴∵∴5. （2017年四川绵阳，24,11分）（本题满分12分）如图，已知抛物线y=ax2+bx+c（a≠0）的图象的顶点坐标是（2,1），并且经过点（4,2）．直线y=x+1与抛物线交于B，D两点，以BD为直径作圆，圆心为点C，圆C于直线m交于对称轴右侧的点M（t，1）．直线m上每一点的纵坐标都等于1．（1）求抛物线的解析式；（2）证明：圆C与x轴相切；（3）过点B作BE⊥m，垂足为E，再过点D作DF⊥m，垂足为F．求BE∶MF的值．解：（1）设抛物线方程为，因为抛物线的顶点坐标是（2，1），所以…………………………1分又抛物线经过点（4，2），所以，解得，………………2分所以抛物线的方程是．……………………………3分（2）联立，消去y，整理得，………………………4分解得，，…………………………5分代入直线方程，解得，，所以B（），D（），因为点C是BD的中点，所以点C的纵坐标为，………………………6分利用勾股定理，可算出BD=，即半径R=，即圆心C到x轴的距离等于半径R，所以圆C与x轴相切．…………………………7分（3）连接BM和DM，因为BD为直径，所以∠BMD=90°，所以∠BME+∠DMF=90°，又因为BE⊥m于点E，DF⊥m于点F，所以∠BME=∠MDF，所以△BME∽△MDF，所以，……………………………9分即，代入得，化简得，解得t=5或t=1，………………………………10分因为点M 在对称轴右侧，所以t =5，………………………11分所以 (12)分法2：过点C 作CH ⊥m ，垂足为H ，连接CM ，由（2）知CM =R =25，CH =R -1=23，由勾股定理，得MH =2，…………………9分又HF =，所以MF =HF -MH =-2，…………………10分 又BE =y 1-1=23-25，所以MF BE =25+1，………………………………………………12分思路分析：（1）知抛物线的顶点和其它任意一点，可设出抛物线的顶点式，代入点的坐标即可求出抛物线的解析式；（2）由抛物线与直线交于B、D，联立方程组，求出点B点D坐标，求出直径BD的长度，从而求出半径，与C的纵坐标进行比较，得出结论；（3）连接BM和DM，因为BD为直径，所以∠BMD=90°，所以∠BME+∠DMF=90°，又因为BE⊥m于点E，DF⊥m于点F，所以∠BME=∠MDF，所以△BME∽△MDF，所以，即，代入得，化简得，解得t=5或t=1，因为点M在对称轴右侧，所以t=5，所以．6.（2017四川攀枝花，24，12分）如图15，抛物线y＝x2＋bx＋c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，3）．（1）求抛物线的解析式；（2）点P在x轴下方的抛物线上，过点P的直线y＝x＋m与直线BC交于点E，与y轴交于点F，求PE＋EF 的最大值．（3）点D为抛物线对称轴上一点．①当∆BCD是以BC为直角边的直角三角形时，求点D的坐标；②若∆BCD是锐角三角形，求点D的纵坐标的取值范围．图1 备用图思路分析：（1）由点B 、C 的坐标利用待定系数法即可求出抛物线的解析式； 2）方法1：（代数法）设点的坐标转化成所求线段，找特殊角转化成所求线段，联立函数关系，代入整理成关于目标线段和的二次函数关系式，从而找到最值；方法2：（几何法）以BC 为对称轴将FCE ∆对称得到F CE '∆，作PH CF '⊥于H ，则PF +EF =PF ′= 2 PH =()()223C P P y y y -=-∴当P y 最小时，PF EF +取最大值42．3）①先设点再分类讨论，利用勾股定理得到关于所求D 点的一元方程式，解得即为D 1和D 2；②利用直径圆周角性质构造圆，利用线段距离公式建立一元方程式，解得即为D 3和D 4．结合①中D 1和D 2的坐标，当D 在D 2D 4和D 3D 1之间时候为锐角三角形，从而得到点D 的纵坐标的取值范围．解析：（1）由题意得：⎩⎪⎨⎪⎧32＋3b ＋c ＝0，c ＝3． 解得⎩⎨⎧b ＝－4，c ＝3．∴抛物线的解析式为：y ＝x 2－4x ＋3．2）方法1：如图，过P 作PG ∥CF 交CB 与G ，由题意知∠BCO ＝∠CEF ＝45°，F （0，m ）C （0，3）， ∆CFE 和∆GPE 均为等腰直角三角形， ∴EF ＝22CF ＝22（3－m ） PE ＝22PG ， 设x P ＝t （1＜t ＜3）， 则PE ＝2PG ＝2（－t ＋3－t －m ）＝2（－m －2t ＋3）， t 2－4t ＋3＝t ＋m ， ∴PE ＋EF ＝22（3－m ）＋22（－m －2t ＋3）＝ 22（－2t －2m ＋6）＝－2（t ＋m －3）＝－2（t 2－4t ）＝ －2（t －2）2＋42，∴当t ＝2时，PE ＋EF 最大值＝42．方法2：（几何法）由题易知直线BC的解析式为3y x=-+，OC=OB=3，∴∠OCB=45°．同理可知∠OFE=45°，∴△CEF为等腰直角三角形，以BC为对称轴将△FCE对称得到△F′CE，作PH⊥CF′于H点，则PF+EF=PF′= 2 PH．yxHPF'CBAOFE又PH=3C P Py y y-=-．∴当Py最小时，PF+EF取最大值，∵抛物线的顶点坐标为(2，－1)，∴当1Py=-时，(PF+EF)max= 2 ×(3+1)=4 2 ．（3）①由（1）知对称轴x＝2，设D（2，n），如图．当∆BCD是以BC为直角边的直角三角形时，D在C上方D1位置时由勾股定理得CD2＋BC2＝BD2，即（2－0）2＋（n－3）2＋（32）2＝（3－2）2＋（0－n）2 ，解得n＝5；当∆BCD是以BC为直角边的直角三角形时，D在C下方D2位置时由勾股定理得BD2＋BC2＝CD2 即（2－3）2＋（n－0）2＋（32）2＝（2－0）2＋（n－3）2 ，解得n＝－1．∴当△BCD是以BC为直角边的直角三角形时，D为（2，5）或（2，－1）．②如图：以BC的中点T（3，3），12BC为半径作⊙T，与对称轴x＝2交于D3和D4，由直径所对的圆周角是直角得∠CD3B＝∠CD2B＝90°，设D（2，m），由DT＝12BC32得（32－2）2＋（32－m）2＝232⎝⎭，解得m＝173∴D 3（2，173+）D 4（2，173-）， 又由①得D 1为（2，5），D 2（2，－1），∴若∆BCD 是锐角三角形，D 点在线段13D D 或24D D 上时（不与端点重合），则点D 的纵坐标的取值范围是－1＜D y ＜1732-或1732+＜D y ＜5．7. （2017四川内江，28，12分）如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +c （a ≠0）与y 轴交于点C （0，3），与x 轴交于A ，B 两点，点B 坐标为（4，0），抛物线的对称轴方程为x ＝1. （1）求抛物线的解析式；（2）点M 从A 点出发，在线段AB 上以每秒3个单位长度的速度向B 点运动，同时点N 从B 点出发，在线段BC 上以每秒1个单位长度的速度向C 点运动，其中一个点到达终点时，另一个点也停止运动，设△MBN 的面积为S ，点M 运动时间为t ，试求S 与t 的函数关系，并求S 的最大值；（3）在点M 运动过程中，是否存在某一时刻t ，使△MBN 为直角三角形？若存在，求出t 的值；若不存在，请说明理由．思路分析：(1) 由点B 的坐标与对称轴可求得点C 的坐标，把点A ，B ，C 的坐标分别代入抛物线的解析式，列出关于系数a ，b ，c 的方程组，求解即可；(2)设运动时间为t 秒，利用三角形的面积公式列出S △MBN 与t 的函数关系式，用配方法求的最大值；(3) 根据余弦函数，可得关于t 的方程，解方程，可得答案，注意分类讨论．解：(1)∵点B 坐标为（4，0），抛物线的对称轴方程为x ＝1，∴A （－2，0）.把点A （－2，0），B （4，0），点C （0，3），分别代入y ＝ax 2+bx+c （a≠0），得⎪⎩⎪⎨⎧==++=+-.3,0416,024ccbacba解得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=.3,43,83cba∴该抛物线的解析式为y＝348++-xx．(2) 如图1，设运动时间为t秒，则AM＝3t，BN＝t，∴MB＝6－3t．由题意得，点C的坐标为（0，3）．在Rt△BOC中，BC＝2243+＝5．如图1，过点N作NH⊥AB于点H，∴NH∥CO，∴△BHN∽△BOC，∴BCBNOCHN=，即53tHN=，∴HNt53．∴S△MBN＝21MB·HN＝21(6－3t)·t53＝=+-tt591092109)1(1092+--t．当△MBN存在时，0＜t＜2，∴当t＝1时，S△MBN最大＝109．∴S与t的函数关系为S＝109)1(1092+--t，S的最大值为109．（3）如图2，在Rt△OBC中，cos∠B＝54=BCOB，设运动时间为t秒，则AM＝3t，BN＝t．∴MB＝6－3t．当∠MNB＝90°时，cos∠B＝54=BMBN，即5436=-tt，解得t＝1724．当∠BM＇N＇＝90°时，cos∠B＝5436=-tt，解得t＝1930．综合上所述，当t＝1724或t＝1930时，△MBN为直角三角形．8. （2017江苏无锡，27，10分）如图，以原点O 为圆心，3为半径的圆与x 轴分别交于A 、B 两点（点B 在点A 的右边），P 是半径OB 上一点，过P 且垂直于AB 的直线与⊙O 分别交于C 、D 两点（点C 在点D 的上方），直线AC 、DB 交于点E ．若AC ：CE ＝1:2． （1）求点P 的坐标；（2）求过点A 和点E ，且顶点在直线CD 上的抛物线的函数表达式．xyEDCAB OP思路分析：（1）过点E 作E F ⊥x 轴于F ，设P （m ，0）.①由相似三角形的判定与性质证得AF ＝3AP ，BF ＝3PB ；②由关系式AF －BF ＝AB ，可得m ＝1．∴点P 的坐标（1，0）．（2）①由已知证得A （－3，0），E （9，62），抛物线过点（5，0）；②用待定系数法可得抛物线的函数表达式．解：（1）过点E 作E F ⊥x 轴于F ，xym FEDCABO P∵CD ⊥AB ，∴CD ∥EF ，PC ＝PD ． ∴△ACP ∽△AEF ，△BPD ∽△BEF . ∵AC ：CE ＝1:2．∴AC ：AE ＝1:3． ∴AP AF ＝CP EF ＝13，DP EF ＝PB BF ＝13． ∴AF ＝3AP ，BF ＝3PB ． ∵AF －BF ＝AB ．又∵⊙O 的半径为3，设P （m ，0）， ∴3（3＋m ）－3（3－m ）＝6∴m＝1．∴P（1，0）（2）∵P（1，0），∴OP＝1，A（－3，0）．∵OA＝3，∴AP＝4，BP＝2．∴AF＝12.连接BC．∵AB是直径，∴∠ACB＝90°．84849.（2017山东潍坊）（本小题满分13分）如图1，抛物线y=ax2+bx+c经过平行四边形ABCD的顶点A(0，3)、B(－1，0)、D(2，3)，抛物线与x轴的另一交点为E．经过点E的直线l将平行四边形ABCD分割为面积相等的两部分，与抛物线交于另一点F．点P为直线l上方抛物线上一动点，设点P的横坐标为t．（1）求抛物线的解析式；（2）当t何值时，△PFE的面积最大?并求最大值的立方根；（3）是否存在点P使△PFE为直角三角形?若存在，求出t的值；若不存在，说明理由．思路分析：（1）利用待定系数法列方程组求解抛物线的解析式；2）由平行四边形的对称性可知直线l必过其对称中心，同时利用抛物线的对称性确定E点坐标，进而可求直l的解析式，结合二次函数解析式确定点F的坐标．作PH⊥x轴，交l于点M，作FN⊥PH，列出PM关于t 的解析式，最后利用三角形的面积得S△PFE关于t的解析式，利用二次函数的最值求得t值，从而使问题得以解决；3）分两种情形讨论：①若∠P1AE=90°，作P1G⊥y轴，易得P1G=AG，由此构建一元二次方程求t的值；②若AP2E=90°，作P2K⊥x轴，AQ⊥P2K，则△P2KE∽△AQP2，由此利用对应边成比例构建一元二次方程求t的值．解：（1）将点A(0，3)、B(－1，0)、D(2，3)代入y=ax2+bx+c，得=++=+-=,324,0,3cbacba得⎪⎩⎪⎨⎧-==-=.1,2,1cba所以，抛物线解析式为：y=－x2+2x+3．2）因为直线l将平行四边形ABCD分割为面积相等的两部分，所以必过其对称中心(21，23)．由点A、D知，对称轴为x=1，∴E(3，0)，设直线l的解析式为：y=kx+m，代入点(21，23)和(3，0)得⎪⎩⎪⎧=+=+.03,2321mkmk解之得⎪⎪⎩⎪⎪⎨⎧=-=.59,53mk所以直线l的解析式为：y=53-x+59．由⎪⎩⎪⎨⎧++-=+-=,32,59532xxyxy解得x F=52-．作PH⊥x轴，交l于点M，作FN⊥PH．点P的纵坐标为y P=－t2+2t+3，点M的纵坐标为y M=53-t+59．所以PM=y P－y M=－t2+2t+3+53t－59=－t2+513t+56．则S△PFE=S△PFM+ S△PEM=21PM·FN+21PM·EH=21PM·(FN+ EH)=21·(－t2+513t+56)(3+52)=1017-·(t－1013)2+100289×1017所以当t=1013时，△PFE的面积最大，最大值的立方根为31017100289⨯=1017．（3）由图可知∠PEA≠90°．①若∠P1AE=90°，作P1G⊥y轴，因为OA=OE，所以∠OAE=∠OEA=45°，所以∠P1AG =∠AP1G=45°，所以P1G=AG．所以t=－t2+2t+3－3，即－t2+t=0，解得t=1或t=0(舍去)．②若∠AP2E=90°，作P2K⊥x轴，AQ⊥P2K，则△P2KE∽△AQP2，所以QPKEAQKP22=，所以tttttt233222+--=++-，即t2－t－1=0，解之得t =251+或t =251-＜52-(舍去)． 综上可知t =1或t =251+适合题意．10.33（2）设()224,21233P a a a a ⎛⎫---<< ⎪⎝⎭，则22,33N a a ⎛⎫-- ⎪⎝⎭∴222242133=3333222PN a a a ⎛⎫=-++--+≤ ⎪⎝⎭∵M ，N 在直线l ：2233y x =--上，PM x ∥，PN y ∥∴23PN PM = ∴51524PM PN PN +=≤即：PM PN +的最大值为：154；（3）能11. （1）求抛物线的解析式及顶点N 的坐标； （2）求证：四边形PMDA 是平行四边形；（3）求证：△DPE ∽△P AM 时点P 的坐标.∴四边形PMDA 是平行四边形；（3）由（2）得四边形PMDA 是平行四边形，PC =x ，CM =14x 2+1－2=14x 2－1；∵在Rt △PCM 中，PM 2114x ==+=P A∴四边形PMDA 是菱形，△P AM 是等腰三角形； ∴∠APM =∠ADM ；∠MDP =12∠ADM ； 根据抛物线的对称性，PD =ED ，∴△DPE 是等腰三角形，DC 平分∠PDE ， ∴∠MDP =12∠PDE ， ∴∠PDE =∠APM ；又∵∠PDE ，∠APM 分别为等腰△DPE 和△P AM 的顶角； ∴△DPE ∽△P AM PE =2x ，AM =222x +∵PE ：AM =3时，解得：x =23±； ∴相似比为3时P 点坐标为：（23±，4）12. 24.(2017湖北咸宁，24，12分)如图，抛物线c bx x y ++=221与x 轴交于A 、B 两点，与y 轴交于点C ，其对称轴交抛物线于点D ，交x 轴于点E ，已知OB=OC=6.⑴求抛物线的解析式及点D 的坐标；⑵连接BD ，F 为抛物线上一动点，当∠FAB=∠EDB 时，求点F 的坐标；⑶平行于x 轴的直线交抛物线于M 、N 两点，以线段MN 为对角线作菱形MPNQ ，当点P 在x 轴上，且PQ=12MN 时，求菱形对角线MN 的长.思路分析：(1)利用OB=OC=6得到点B(6，0)，C(0，-6)，将其代入抛物线的解析可以求出b 、c 的值，进而得到抛物线的解析式，最后通过配方得到顶点坐标；(2)由于F为抛物线上一动点，∠FAB=∠EDB，可以分两种情况求解：一是点F在x轴上方；二是点F在x轴下方.每一种情况都可以作FG⊥x轴于点G，构造Rt△AFG与Rt△DBE相似，利用对应边成比例或三角函数的定义求点F的坐标.(3)首先根据MN与x轴的位置关系画出符合要求的两种图形：一是MN在x轴上方；二是MN在x轴下方.设菱形对角线的交点T到x轴的距离为n，利用PQ=12MN，得到MT=2n，进而得到点M的坐标为(2+2n，n)∴∴∵(2)，则∵∠FAB=∠EDB，tan∠FAG=tan∠BDE，即21261222x xx--=+，解得17x=，22x=-(舍去).当x=7时，y=92，∴点F的坐标为(7，92). ……6分当点F在x轴下方时，设同理求得点F的坐标为(5，72-).综上所述，点F的坐标为(7，92)或(5，72-). ……8分(3)∵点P在x轴上，∴根据菱形的对称性可知点P的坐标为(2，0).如图，当MN在x轴上方时，设T为菱形对角线的交点.∵PQ=12MN ， ∴MT=2PT.设TP=n ，则MT=2n. ∴M(2+2n ，n).∵点M 在抛物线上， ∴21(22)2(22)62n n n =+-+-，即∴当∴即∴13.（（（S ∆∴x1=-3，x2=1,所以函数表达式为y=ax2+2ax-3a，∵直线y= x+m与x轴、y轴分别相交于B,C,两点，则OB=OC=m所以△BOC是以∠BOC为直角的等腰三角形，这时直线y=x+m与对称轴x=-1的夹角∠BAE=45°.又因点F在对称轴左侧的抛物线上，则∠BAE>45°，这时△BOC与△ADF相似，顶点A只可能对应△BOC中的直角顶点O ，即△ADF 是以A 为直角顶点的等腰三角形，且对称轴是x =-1，设对称轴x =-1与OF 交于点G. ∵直线y=x+m 过顶点A ，所以m=1-4a ，∴直线解析式为y=x+1-4a,解方程组21423y x a y ax ax a =+-⎧⎨=+-⎩，解得1114x y a =-⎧⎨=-⎩，221114x ay a a ⎧=-⎪⎪⎨⎪=-⎪⎩， 这里的（-1，4a ）即为顶点A ，点（1a -1，1a -4a ）即为顶点D 的坐标（1a -1，1a -4a ） D 点到对称轴x=-1的距离为1a -1-（-1）=1a，AE =4a -=4a,S △ADE =12×1a×4a=2,即它的面积为定值.这时等腰直角△ADF 的面积为1，所以底边DF =2，而x=-1是它的对称轴，这时D,C 重合且在y 轴上，由1a-1=0，∴a=1，此时抛物线的解析式y=x 2+2x-314. （2017湖南邵阳，26，10分）（本小题满10分）如图（十六）所示，顶点（49-21，）的抛物线y ＝ax 2＋bx＋c 过点M （2，0）. （1）求抛物线的解析式；（2）点A 是抛物线与x 轴的交点（不与点M 重合），点B 是抛物线与y 轴的交点，点C 是直线y ＝x ＋1上一点（处于x 轴下方），点D 是反比例函数y ＝xk（k >0）图象上一点.若以点A 、B 、C 、D 为顶点的四边形是菱形，求k 的值.思路分析：（1）已知抛物线的顶点坐标，可设顶点式为 y ＝a (x －2)2－4，再把点M （2，0）代入，可求a ＝1，所以抛物线的解析式可求.（2）先分别求出A 、B 两点的坐标，及AB 线段长，再根据反比例函数y ＝xk（k >0），考虑点C 在x 轴下方，故点D 只能在第一、三象限．确定菱形有两种情形：①菱形以AB 为边，如图一。
2017二次函数中考试题分类汇编
2017二次函数中考试题分类汇编2017二次函数中考试题分类汇编ax 2 bx c （a 0）的图象如下图1所示，有下列5个结论：① abc 0;② b a c ；③ 4a 2b c 0;④ 2c 3b;⑤ a b m （am b ）, （m 1 的实数）其中正确的结论有（）A. 2个 B. 3个 C. 4 个 D. 5 个2、如上图2是二次函数y=ax 2+bx + c 图象的一部分，图象过点 A （ — 3, 0）,对称轴为 x=—1.给出四个结论：①b 2>4ac ；②2a+ b=0；③a —b+c=0；④5a< b.其中正确结论 是（ ）. （A ）②④ （B ）①④ （C ）②③（D ）①③3、二次函数y x 2 2x 1与x 轴的交点个数是（ ）A. 0 B . 1 C . 2 D . 34、在同一坐标系中一次函数y ax b 和二次函数y ax 2 bx 的图象可能为（ ）5、已知二次函数y ax 2 bx c （aw 0）的图象开口向上，并经过点（-1 ,2）, （1,0）.下歹结 论正确的是（）A. 当x>0时，函数值y 随x 的增大而增大 B.当x>0时，函数值y 随x 的增大而减小C.存在一个负数XQ ,使得当x<x °时，函数值y 随x 的增大而减小；当x> x 0时，函数值y 随 x 的增大而增大D.存在一个正数x o,使得当x<x o 时，函数值y 随x 的增大而减小；当X >X Q 时，函数值y 随x 的增大而增大、选择题1、已知二次函数y6、已知二次函数y=x 2-x+a(a>0),当自变量x 取m 时，其相应的函数值小于 0,那么下列结 论中正确的是()(A) m-1的函数值小于0(B) ml 的函数值大于01、二次函数y =ax 2+bx+ c 的图象如下图1所示，且P=| a —b + c | + | 2 a+b | , Q=| a+b+c |+| 2 a —b |,则P 、Q 的大小关系为、解答题：1、知一抛物线与x 轴的交点是A( 2,0)、B (1, 0),且经过点C (2, 8)(1)求该抛物线的解析式；(2)求该抛物线的顶点坐标2、在直角坐标平面内，二次函数图象的顶点为 A(1, 4),且过点B(3,0).(1)求该二次函数的解析式；(2)将该二次函数图象向右平移几个单位，可使平移后所得 图象经过坐标原点？并直接写出平移后所得图象与x 轴的另一个交点的坐标.(C) mi 的函数值等于0 、填空题(D) mi 的函数值与0的大小关系不确定3、4、 2x m 的部分图象如上图所示，则关于 x 的4、 x 2 2x m0的解为已知二次函数 y ax 2 bx c 的图象如上图所示，则点P(a, bc)在第 已知二次函数 y2x如下图2所示的抛物线是二次函数y ax 2 次方程儿3、已知二次函数图象的顶点是(1,2),且过点0,-.2(1)求二次函数的表达式，并在下图中画出它的图象;(2)求证：对任意实数m,点M(m, m2)都不在这个二次函数的图象上.5、如图，已知二次函数y ax2 4x c的图像经过点A和点B.(1)求该二次函数的表达式；(2)写出该抛物线的对称轴及顶点坐标;(3)点P (m, m与点Q均在该函数图像上(其中no0),且这两点关于抛物线的对称轴对称, 求m的值及点Q到x轴的距离.4、二次函数y ax 2 bx c （a 0）的图象如图所示，根据图象解答下列问题: 写出方程ax 2 bx c 0的两个根.（2）写出不等式ax 2 bx c 0的解集.6、在平面直角坐标系xOy 中，已知二次函数y ax 2 点（点A 在点B 的左边），与y 轴交于点C,其顶点的横坐标为1,且过点（2,3）和（3, 12）. （1）求此二次函数的表达式；（2）若直线1：y kx （k 0）与线段BC 交于点D （不与点B, C 重合），则是否存在这样的直线1,使得以B, O, D 为顶点的三角形与ABAC 相似？若存在, 求出该直线的函数表达式及点 D 的坐标；若不存在，请说明理由；（3）若点P 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点，试比较锐角 PCO 与 ACO 的大小（不必证明），并写出此时点 P 的横坐标xp 的取值范围.*x」11O ： 1(1) (3) 写出y 随x 的增大而减小的自变量x 的取值范围. (4)若方程ax 2 bx c k 有两个不相等的实数根，求 bx c （a 0）的图象与x 轴交于A, B 两7、如图，矩形A BC O'是夕!形OABC 边OA 在x 轴正半轴上，边 OC 在y 轴正半轴上）绕B 点逆时针旋转得到的.O 点在x 轴的正半轴上，B 点的坐标为（1 , 3）.（1）如果二次函数y=ax2+bx+c （a W0）的图象经过Q O 两点且图象顶点M 的纵坐标为一1 . 求这个二次函数的解析式；（2）在（1）中求出的二次函数图象对称轴的右支上是否存在点P,使得APOMfe 直角三角形？若存在，请求出P 点的坐标和A POM 勺面积；若不存在，请说明理 由；（3）求边C' O'所在直线的解析式.8、容积率t 是指在房地产开发中建筑面积与用地面积之比， 即t = M 建筑面积,为充分利用土地S用地面积资源，更好地解决人们的住房需求，并适当的控制建筑物的高度，一般地容积率 且不大于8.一房地产开发商在开发某小区时，结合往年开发经验知，建筑面积 M （m2）与容 积率t 的关系可近似地用如图（1）中的线段l 来表示；1 m2建筑面积上的资金投入 Q （万元） 与容积率t 的关系可近似地用如图（2）中的一段抛物线段c 来表示. （I ）试求图（1）中线段l 的函数关系式，并求出开发该小区的用地面积; （H ）求出图（2）中抛物线段c 的函数关系式.t 不小于1 09、如图10,已知抛物线P： y=ax2+bx+c（aw0）与x轴交于A、B两点（点A在x轴的正半轴上），与y轴交于点C,矩形DEFG勺一条边DE在线段AB上，顶点F、G分别在线段BC AC 上，抛物线P上部分点的横坐标对应的纵坐标如下：x…-3-212…y…5—-2-45—-20…⑴ 求A、B C三点的坐标；（2）若点D的坐标为（m, 0）,矩形DEFG勺面积为S, 的函数关系，并指出m的取值范围；（3）当矩形DEFG勺面积S取最大值时，连接至点M使FM=k- DF,若点M不在抛物线P上，求k的取值范围.求S与m DF并延长10、如图①，在平面直角坐标系中，点A的坐标为（1,2），点B的坐标为（31）,二次函数y x2的图象记为抛物线li. （1）平移抛物线li,使平移后的抛物线过点A,但不过点B,写出平移后的一个抛物线的函数表达式:（2）平移抛物线l i,使平移后的抛物线过A, B两点，记为抛物线12,如图②，求抛物线12的函数表达式.（3）设抛物线12的顶点为C , K为y轴上一点.若S A ABK S A ABC ，求点标.（4）请在图③上用尺规作图的方式探究抛物线12上是否存在点P,使4ABP为等形.若存在，请判断点P共有几个可能的位置（保留作图痕迹）；若不存在，请说明师. K的坐腰三角11、如图，抛物线y x2 2x 3与x轴交A、B两点（A点在B点左侧），直线l与抛物线交于A、C两点，其中C点的横坐标为2。
2017全国中考数学真题分类-二次函数几何方面的应用(选择题+解答题)解析版
2017全国中考数学真题分类知识点20二次函数几何方面的应用（选择题+填空题+解答题）解析版一、选择题1. 8．(2017江苏扬州，，3分)如图，已知△ABC 的顶点坐标分别为A （0，2）、B （1，0）、C （2，1），若二次函数21y x bx =++的图像与阴影部分（含边界）一定有公共点，则实数b 的取值范围是A ．2b ≤-B ．2b <-C ．2b ≥-D ．2b >-【答案】C【解析】由二次函数系数a 、b 、c 的几何意义可知该函数的开口方向和开口大小是确定不变的，与y 轴的交点（０，１）也是确定不变的。
唯一变化的是“b”，也就是说对称轴是变化的。
若抛物线经过点（０，１）和Ｃ（２，１）这组对称点，可知其对称轴是直线12bx =-=，即b ＝－２时是符合题意的，所以可以排除Ｂ、Ｄ两个选择支，如果将该抛物线向右平移，此时抛物线与阴影部分就没有公共点了，向左平移才能符合题意，所以12b-≤，即2b ≥-。
二、解答题1. （2017重庆，26，12分）（本小题满分12分）如图，在平面直角坐标系中，抛物线3332332--=x x y 与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，对称轴与x 轴交于点D ，点E （4，n ）在抛物线上．（1）求直线AE 的解析式；（2）点P 为直线CE 下方抛物线上的一点，连接PC ，PE ．当∆PCE 的面积最大时，连接CD ，CB ，点K 是线段CB 的中点，点M 是CP 上的一点，点N 是CD 上的一点，求KM +MN +NK 的最小值；（3）点G 是线段CE 的中点，将抛物线3332332--=x x y 沿x 轴正方向平移得到新抛物线y '，y '经过点D，y '的顶点为点F．在新抛物线y '的对称轴上，是否存在点Q，使得∆FGQ为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．思路分析：（1）首先求出A、E点的坐标，然后设出直线AE的解析式，并将A、E点的坐标代入，求得方程组的解，便可得到直线AE的解析式；（2）由抛物线解析式求得C点坐标，则可得出直线CE的解析式；过点P作PH∥x轴，交CE于点H，设出P点坐标，可推出H点坐标，根据斜三角形面积公式“2铅垂高水平宽⨯”可表示出∆PCE的面积，并可计算出其面积最大时P点的坐标；分别作K关于CP、CD的对称点的对称点K1、K2，将KM +MN+KN即可确定出转化成一条线段，由“两点之间，线段最短”及勾股定理计算出其最小值即可；（3）运用已知两定点时确定等腰三角形常用的方法“两圆一线”即可在抛物线y '的对称轴上找到符合条件的四个点，分别确定其坐标即可．解：（1）∵抛物线3332332--=xxy与x轴交于A，B两点，且点E（4，n）在抛物线上，∴03332332=--xx，解得：x1＝－1，x2＝3，∴A，B两点的坐标分别为（－1，0），（3，0）；343324332-⨯-⨯=y＝335，∴点E坐标为（4，335）．设直线AE的解析式的解析式为y＝kx+b，将A点、E点坐标分别代入，得：⎪⎩⎪⎨⎧+=+-=bkbk4335，解得：⎪⎪⎩⎪⎪⎨⎧==3333bk，∴y＝33x+33；（2）∵令x ＝0，得y ＝ 3-，∴点C （0，3-），∵点E 坐标为（4，335），∴直线CE 的解析式为y ＝3332-x ，过点P 作PH ∥x 轴，交CE 于点H ，如图，设点P 的坐标为（t ，3332332--t t ），则H （t ，3332-t ），∴PH ＝3332-t －（3332332--t t ）＝t t 334332+-， ∴t t t t PH x x S C E PCE 338332334334212122+-=⎪⎪⎭⎫ ⎝⎛+-⨯⨯=⋅-=∆，∵0332<-，抛物线开口向下，40<<t ，∴当⎪⎪⎭⎫⎝⎛-⨯-=3322338t ＝2时，PCE S ∆取得最大值，此时P 为（2，3-）；∵点C （0，3-），B （3，0），由三角形中位线定理得K （23，23-），∵y C ＝y P ＝3-，∴PC ∥x 轴，作K关于CP 的对称点K 1，则K 1（23，233-）；∵333tan ==∠OCB ，∴∠OCB ＝60゜，∵D （1，0），∴3331tan ==∠OCD ，∴∠OCD ＝ 30゜，∴∠OCD ＝∠BCD ＝30゜，∴CD 平分∠OCB ，∴点K 关于CD 的对称点K 2在y 轴上，又∵CK ＝OC ＝3，∴点K 2与点O 重合，连接OK 1，交CD 于点N ，交CP 于点M ，如图，∴KM ＝ K 1M ，KN ＝ON ，∴KM +MN +KN ＝K 1M +MN +ON ，根据“两点之间，线段最短”可得，此时KM +MN +KN 的值最小，∴K 1 K 2 ＝O K 1＝32332322=⎪⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛，∴KM +MN +KN 的最小值为3；（3）点Q 的坐标为（3，321234+-），（3，321234--），（3，32），（3，332-）．2. （2017浙江衢州,22，10分）（本题满分10分）定义：如图1，抛物线y ＝ax 2＋bx ＋c （a ≠0）与x 轴交于A ，B 两点，点P 在抛物线上（P 点与A 、B 两点不重合），如果△ABP 的三边需满足AP 2＋BP 2＝AB 2，则称点P 为抛物线y ＝ax 2＋bx ＋c （a ≠0）的勾股点．（1）直接写出抛物线y ＝－x 2＋1的勾股点坐标．（2）如图2，已知抛物线C ：y ＝ax 2＋bx （a ≠0）与x 轴交于A ，B 两点，点P （13C 的勾股点，求抛物线C 的函数表达式．（3）在（2）的条件下，点Q 在抛物线C 上，求满足条件S △ABQ ＝S △ABP 的Q 点（异于点P ）的坐标．思路分析：（1）所谓勾股点，即以AB为直径的圆与抛物线的交点．y＝－x2＋1与x轴交点坐标为（1，0），（－1，0），故圆心为原点，半径为1，与抛物线交点为（0，1）.（2）由P点坐标可知∠PAB＝60°，又∠APB＝90°，从而求得B点坐标，利用待定系数法即可求解．（3）由S△ABQ＝S△ABP，故有|y Q|y Q物线解析式即可求解．解（1）勾股点的坐标（0，1）．（2）抛物线y＝ax2＋bx（a≠0）过原点（0，0），即A为（0，0）．如图，作PG⊥x轴于点G，连结PA，PB．∵点P的坐标为（1，∴AG＝1，PG PA＝2，tan∠PAB∴∠PAB＝60°，∴Rt△PAB中，AB＝cos60PA＝4，∴点B（4，0）．设y＝ax（x－4），当x＝1时，ya．∴y x（x－4x2x．（3）①当点Q在x轴上方时，由S△ABQ＝S△ABP易知点Qx2x1＝3，x2＝1（不合题意，舍去）．∴Q1（3．②当点Q在x轴下方时，由S△ABQ＝S△ABP易知点Qx2解得x1＝2x2＝2Q2（2，Q2（2．综上，满足条件的Q点有三个：Q1（3，Q2（2，Q2（2．3.（2017山东济宁，21，9分）已知函数2(25)2y mx m x m=--+-的图象与x轴有两个公共点．（1）求m的取值范围，写出当m取范围内最大整数时函数的解析式；（2）题（1）中求得的函数记为C1①当1n x≤≤-时，y的取值范围是13y n≤≤-，求n的值；②函数C2：22()y x h k=-+的图象由函数C1的图象平移得到，其顶点P的圆内或圆上．设函数C1的图象顶点为M，求点P与点M距离最大时函数C2的解析式．思路分析：（1）根据函数2(25)2y mx m x m=--+-图象与x轴有两个公共点，即一元二次方程2(25)20mx m x m --+-=有两个不同的实数解，即需满足m ≠0且根的判别式△＞0，解不等式组得25,12m <且0m ≠；（2）由二次函数22y x x =+性质，当14x <-时，y 随x 的增大而减小，求出n 的值为—2；（3）由图形可知当P 为射线MO 与圆的交点时，距离最大，先求出MO 的解析式，设出点P 的坐标，根据勾股定理求出点P 的坐标，继而求出PM 最大时的函数解析式为()2221y x =-+．解：（1）由题意可得：()()20,25420.m m m m ≠⎧⎪⎨---->⎡⎤⎪⎣⎦⎩解得：25,12m <且0,m ≠ 当2m =时，函数解析式为：22y x x =+．（2）函数22y x x =+图象开口向上，对称轴为1,4x =-∴当14x <-时，y 随x 的增大而减小．∵当1n x ≤≤-时，y 的取值范围是13y n ≤≤-， ∴ 223n n n +=-．∴ 2n =-或0n =（舍去）． ∴2n =-．（3）∵221122,48y x x x ⎛⎫=+=+- ⎪⎝⎭∴图象顶点M 的坐标为11,48⎛⎫-- ⎪⎝⎭，由图形可知当P 为射线MO 与圆的交点时，距离最大．∵点P 在直线OM 上，由11(0,0),(,)48O M --可求得直线解析式为：12y x =，设P （a ，b ），则有a ＝2b ， 根据勾股定理可得()2222PO b b =+求得2,1a b ==．∴PM 最大时的函数解析式为()2221y x =-+．4. （2017山东威海，25，12分）如图，已知抛物线y =ax ²+bx +c 过点A (－1,0)，B (3,0)，C （0，3）.点M ，N 为抛物线上的动点，过点M 作MD ∥y 轴，交直线BC 于点D ，交x 轴于点E . （1）求二次函数y =ax ²+bx +c 的表达式；（2）过点N 作NF ⊥x 轴，垂足为点F .若四边形MNFE 为正方形（此处限定点M 在对称轴的右侧），求该正方形的面积；（3）若∠DMN =90°，MD =MN ，求点M 的横坐标.解：∵抛物线2y ax bx c =++的图像经过点A (-1,0),B (3,0)，∴抛物线的函数表达式为y =a (x +1)(x -3),将点C (0，3)代入上式，得3=a (0+1)(0-3)， 解得a =-1.∴所求函数表达式为y =－(x +1)(x －3)=－x 2+2x +3．(2)由(1)知，抛物线的对称轴为212(1)x ==⨯-．如图1，设M 点的坐标(m ，－m 2+2m +3),∴ME =|－m 2+2m +3|．∵M ,N 关于x =1对称，且点M 在对称轴右侧， ∴N 点横坐标为2-m . ∴MN =2m -2∵四边形MNEF 为正方形∴ME =MN . ∴22322m m m -++=- ． 分两种情况:①2m - +2m +3=2m -2.解,得12m m ==不符合题意,合去).当 m ,正方形的面积为22(2224⎡⎤+-=+⎣⎦综上所述，正方形的面积为24-或24+（3）设直线BC 的函数表达式为y =kx +b .把点B (3,0),C (0,3)代入表达式，得30,3,k b b +=⎧⎨=⎩解得1,3.k b =-⎧⎨=⎩∴直线BC 的函数表达式为y =-x +3，设点M 的坐标为(a ,223a a -++), 则点D 的坐标为(a ,-a +3)， ∴DM =23a a -+ ，∵DM //y 轴，DM ⊥MN ,∴MN //x 轴. ∴M ,N 关于x =1对称. ∴N 点的横坐标为2-a ， ∴MN =22a -， ∵DM =MN ，∴2322a a a -+=- ． 分两种情况：①如图2，2322a a a -+=- ， 解，得122,1a a ==- ．②如图3，2322a a a -+=-，解，得3455,22a a +-==．综上所述，M 点的横坐标为122,1a a ==-，34,a a ==5.（2017年四川绵阳，24,11分）（本题满分12分）如图，已知抛物线y=ax2+bx+c（a≠0）的图象的顶点坐标是（2,1），并且经过点（4,2）．直线y=x+1与抛物线交于B，D两点，以BD为直径作圆，圆心为点C，圆C于直线m交于对称轴右侧的点M（t，1）．直线m 上每一点的纵坐标都等于1．（1）求抛物线的解析式；（2）证明：圆C与x轴相切；（3）过点B作BE⊥m，垂足为E，再过点D作DF⊥m，垂足为F．求BE∶MF的值．解：（1）设抛物线方程为，因为抛物线的顶点坐标是（2，1），所以…………………………1分又抛物线经过点（4，2），所以，解得，………………2分所以抛物线的方程是．……………………………3分（2）联立，消去y，整理得，………………………4分解得，，…………………………5分代入直线方程，解得，，所以B（），D（），因为点C是BD的中点，所以点C的纵坐标为，………………………6分利用勾股定理，可算出BD=，即半径R=，即圆心C到x轴的距离等于半径R，所以圆C与x轴相切．…………………………7分（3）连接BM和DM，因为BD为直径，所以∠BMD=90°，所以∠BME+∠DMF=90°，又因为BE⊥m于点E，DF⊥m于点F，所以∠BME=∠MDF，所以△BME∽△MDF，所以，……………………………9分即，代入得，化简得，解得t =5或t =1，………………………………10分因为点M 在对称轴右侧，所以t =5，………………………11分所以…………………………………………………12分法2：过点C 作CH ⊥m ，垂足为H ，连接CM ，由（2）知CM =R =25，CH =R -1=23， 由勾股定理，得MH =2，…………………9分又HF =，所以MF =HF -MH =-2，…………………10分 又BE =y 1-1=23-25，所以MF BE =25+1，………………………………………………12分思路分析：（1）知抛物线的顶点和其它任意一点，可设出抛物线的顶点式，代入点的坐标即可求出抛物线的解析式；（2）由抛物线与直线交于B、D，联立方程组，求出点B点D坐标，求出直径BD的长度，从而求出半径，与C的纵坐标进行比较，得出结论；（3）连接BM和DM，因为BD为直径，所以∠BMD=90°，所以∠BME+∠DMF=90°，又因为BE⊥m于点E，DF⊥m于点F，所以∠BME=∠MDF，所以△BME∽△MDF，所以，即，代入得，化简得，解得t=5或t=1，因为点M在对称轴右侧，所以t=5，所以．6.（2017四川攀枝花，24，12分）如图15，抛物线y＝x2＋bx＋c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，3）．（1）求抛物线的解析式；（2）点P在x轴下方的抛物线上，过点P的直线y＝x＋m与直线BC交于点E，与y轴交于点F，求PE＋EF的最大值．（3）点D为抛物线对称轴上一点．①当∆BCD是以BC为直角边的直角三角形时，求点D的坐标；②若∆BCD是锐角三角形，求点D的纵坐标的取值范围．图1 备用图思路分析：（1）由点B 、C 的坐标利用待定系数法即可求出抛物线的解析式； （2）方法1：（代数法）设点的坐标转化成所求线段，找特殊角转化成所求线段，联立函数关系，代入整理成关于目标线段和的二次函数关系式，从而找到最值；方法2：（几何法）以BC 为对称轴将FCE ∆对称得到F CE '∆，作PH CF '⊥于H ，则PF +EF =PF ′= 2 PH =()()223C P P y y y -=-∴当P y 最小时，PF EF +取最大值42．（3）①先设点再分类讨论，利用勾股定理得到关于所求D 点的一元方程式，解得即为D 1和D 2；②利用直径圆周角性质构造圆，利用线段距离公式建立一元方程式，解得即为D 3和D 4．结合①中D 1和D 2的坐标，当D 在D 2D 4和D 3D 1之间时候为锐角三角形，从而得到点D 的纵坐标的取值范围．解析：（1）由题意得：⎩⎪⎨⎪⎧32＋3b ＋c ＝0，c ＝3． 解得⎩⎨⎧b ＝－4，c ＝3．∴抛物线的解析式为：y ＝x 2－4x ＋3．（2）方法1：如图，过P 作PG ∥CF 交CB 与G ，由题意知∠BCO ＝∠CEF ＝45°，F （0，m ）C （0，3）， ∴∆CFE 和∆GPE 均为等腰直角三角形， ∴EF ＝22CF ＝22（3－m ） PE ＝22PG ，设x P ＝t （1＜t ＜3）， 则PE ＝22PG ＝22（－t ＋3－t －m ）＝22（－m －2t ＋3）， t 2－4t ＋3＝t ＋m ，∴PE ＋EF ＝22（3－m ）＋22（－m －2t ＋3）＝ 22（－2t －2m ＋6）＝－2（t ＋m －3）＝－2（t 2－4t ）＝ －2（t －2）2＋42，∴当t ＝2时，PE ＋EF 最大值＝42．方法2：（几何法）由题易知直线BC的解析式为3y x=-+，OC=OB=3，∴∠OCB=45°．同理可知∠OFE=45°，∴△CEF为等腰直角三角形，以BC为对称轴将△FCE对称得到△F′CE，作PH⊥CF′于H点，则PF+EF=PF′= 2 PH．yxHPF'CBAOFE又PH=3C P Py y y-=-．∴当Py最小时，PF+EF取最大值，∵抛物线的顶点坐标为(2，－1)，∴当1Py=-时，(PF+EF)max= 2 ×(3+1)=4 2 ．（3）①由（1）知对称轴x＝2，设D（2，n），如图．当∆BCD是以BC为直角边的直角三角形时，D在C上方D1位置时由勾股定理得CD2＋BC2＝BD2，即（2－0）2＋（n－3）2＋（32）2＝（3－2）2＋（0－n）2 ，解得n＝5；当∆BCD是以BC为直角边的直角三角形时，D在C下方D2位置时由勾股定理得BD2＋BC2＝CD2 即（2－3）2＋（n－0）2＋（32）2＝（2－0）2＋（n－3）2 ，解得n＝－1．∴当△BCD是以BC为直角边的直角三角形时，D为（2，5）或（2，－1）．②如图：以BC的中点T（3，3），12BC为半径作⊙T，与对称轴x＝2交于D3和D4，由直径所对的圆周角是直角得∠CD3B＝∠CD2B＝90°，设D（2，m），由DT＝12BC32得（32－2）2＋（32－m）2＝2322⎛⎝⎭，解得m＝173±，∴D 3（2，173+）D 4（2，173-）， 又由①得D 1为（2，5），D 2（2，－1），∴若∆BCD 是锐角三角形，D 点在线段13D D 或24D D 上时（不与端点重合），则点D 的纵坐标的取值范围是－1＜D y ＜1732-或1732+＜D y ＜5．7. （2017四川内江，28，12分）如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +c （a ≠0）与y 轴交于点C （0，3），与x 轴交于A ，B 两点，点B 坐标为（4，0），抛物线的对称轴方程为x ＝1. （1）求抛物线的解析式；（2）点M 从A 点出发，在线段AB 上以每秒3个单位长度的速度向B 点运动，同时点N 从B 点出发，在线段BC 上以每秒1个单位长度的速度向C 点运动，其中一个点到达终点时，另一个点也停止运动，设△MBN 的面积为S ，点M 运动时间为t ，试求S 与t 的函数关系，并求S 的最大值；（3）在点M 运动过程中，是否存在某一时刻t ，使△MBN 为直角三角形？若存在，求出t 的值；若不存在，请说明理由．思路分析：(1) 由点B 的坐标与对称轴可求得点C 的坐标，把点A ，B ，C 的坐标分别代入抛物线的解析式，列出关于系数a ，b ，c 的方程组，求解即可；(2)设运动时间为t 秒，利用三角形的面积公式列出S △MBN 与t 的函数关系式，用配方法求的最大值；(3) 根据余弦函数，可得关于t 的方程，解方程，可得答案，注意分类讨论．解：(1)∵点B 坐标为（4，0），抛物线的对称轴方程为x ＝1，∴A （－2，0）.把点A （－2，0），B （4，0），点C （0，3），分别代入y ＝ax 2+bx+c （a≠0），得⎪⎩⎪⎨⎧==++=+-.3,0416,024ccbacba解得⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=.3,43,83cba∴该抛物线的解析式为y＝343832++-xx．(2) 如图1，设运动时间为t秒，则AM＝3t，BN＝t，∴MB＝6－3t．由题意得，点C的坐标为（0，3）．在Rt△BOC中，BC＝2243+＝5．如图1，过点N作NH⊥AB于点H，∴NH∥CO，∴△BHN∽△BOC，∴BCBNOCHN=，即53tHN=，∴HN＝t53．∴S△MBN＝21MB·HN＝21(6－3t)·t53＝=+-tt591092109)1(1092+--t．当△MBN存在时，0＜t＜2，∴当t＝1时，S△MBN最大＝109．∴S与t的函数关系为S＝109)1(1092+--t，S的最大值为109．（3）如图2，在Rt△OBC中，cos∠B＝54=BCOB，设运动时间为t秒，则AM＝3t，BN＝t．∴MB＝6－3t．当∠MNB＝90°时，cos∠B＝54=BMBN，即5436=-tt，解得t＝1724．当∠BM＇N＇＝90°时，cos∠B＝5436=-tt，解得t＝1930．综合上所述，当t＝1724或t＝1930时，△MBN为直角三角形．8. （2017江苏无锡，27，10分）如图，以原点O 为圆心，3为半径的圆与x 轴分别交于A 、B 两点（点B 在点A的右边），P 是半径OB 上一点，过P 且垂直于AB 的直线与⊙O 分别交于C 、D 两点（点C 在点D 的上方），直线AC 、DB 交于点E ．若AC ：CE ＝1:2． （1）求点P 的坐标；（2）求过点A 和点E ，且顶点在直线CD 上的抛物线的函数表达式．思路分析：（1）过点E 作E F ⊥x 轴于F ，设P （m ，0）.①由相似三角形的判定与性质证得AF ＝3AP ，BF ＝3PB ；②由关系式AF －BF ＝AB ，可得m ＝1．∴点P 的坐标（1，0）．（2）①由已知证得A （－3，0），E （9，），抛物线过点（5，0）；②用待定系数法可得抛物线的函数表达式．解：（1）过点E 作E F ⊥x 轴于F ，∵CD ⊥AB ，∴CD ∥EF ，PC ＝PD ． ∴△ACP ∽△AEF ，△BPD ∽△BEF . ∵AC ：CE ＝1:2．∴AC ：AE ＝1:3． ∴AP AF ＝CP EF ＝13，DP EF ＝PB BF ＝13． ∴AF ＝3AP ，BF ＝3PB ． ∵AF －BF ＝AB ．又∵⊙O 的半径为3，设P （m ，0）， ∴3（3＋m ）－3（3－m ）＝6 ∴m ＝1．∴P （1，0）（2）∵P （1，0），∴OP ＝1，A （－3，0）． ∵OA ＝3，∴AP ＝4，BP ＝2．∴AF ＝12. 连接BC ．∵AB 是直径，∴∠ACB ＝90°．∵CD ⊥AB ，∴△ACP∽△CBP ．∴AP CP ＝CPBP． ∴CP 2＝AP ·BP ＝4×2＝8. ∴CP ＝．∴EF ＝3CP ＝． ∴E （9，）.∵抛物线的顶点在直线CD 上，∴CD 是抛物线的对称轴， ∴抛物线过点（5，0）.设抛物线的函数表达式为y ＝ax 2＋bx ＋c ．根据题意得09-30255819a b ca b c a b c ⎧⎪+⎨⎪+⎩＝＋，＝＋，＋，解得8484a b c ⎧⎪⎪⎪⎪⎨⎪⎪--⎪⎪⎩＝＝-＝ ∴抛物线的函数表达式为yx 2x ．9. （2017山东潍坊）（本小题满分13分）如图1，抛物线y =ax 2+bx +c 经过平行四边形ABCD 的顶点A (0，3)、B (－1，0)、D (2，3)，抛物线与x 轴的另一交点为E ．经过点E 的直线l 将平行四边形ABCD 分割为面积相等的两部分，与抛物线交于另一点F ．点P 为直线l 上方抛物线上一动点，设点P 的横坐标为t ． （1）求抛物线的解析式；（2）当t 何值时，△PFE 的面积最大?并求最大值的立方根；（3）是否存在点P 使△PFE 为直角三角形?若存在，求出t 的值；若不存在，说明理由．思路分析：（1）利用待定系数法列方程组求解抛物线的解析式；（2）由平行四边形的对称性可知直线l 必过其对称中心，同时利用抛物线的对称性确定E 点坐标，进而可求直线l 的解析式，结合二次函数解析式确定点F 的坐标．作PH ⊥x 轴，交l 于点M ，作FN ⊥PH ，列出PM 关于t 的解析式，最后利用三角形的面积得S △PFE 关于t 的解析式，利用二次函数的最值求得t 值，从而使问题得以解决； （3）分两种情形讨论：①若∠P 1AE =90°，作P 1G ⊥y 轴，易得P 1G =AG ，由此构建一元二次方程求t 的值；②若∠AP 2E =90°，作P 2K ⊥x 轴，AQ ⊥P 2K ，则△P 2KE ∽△AQP 2，由此利用对应边成比例构建一元二次方程求t 的值． 解：（1）将点A (0，3)、B (－1，0)、D (2，3)代入y =ax 2+bx +c ，得⎪⎩⎪⎨⎧=++=+-=,324,0,3c b a c b a c 得⎪⎩⎪⎨⎧-==-=.1,2,1c b a 所以，抛物线解析式为：y=－x 2+2x +3．（2）因为直线l 将平行四边形ABCD 分割为面积相等的两部分， 所以必过其对称中心(21，23)． 由点A 、D 知，对称轴为x =1，∴E (3，0)， 设直线l 的解析式为：y =kx +m ，代入点(21，23)和(3，0)得 ⎪⎩⎪⎨⎧=+=+.03,2321m k m k 解之得⎪⎪⎩⎪⎪⎨⎧=-=.59,53m k 所以直线l 的解析式为：y =53-x +59． 由⎪⎩⎪⎨⎧++-=+-=,32,59532x x y x y 解得x F =52-． 作PH ⊥x 轴，交l 于点M ，作FN ⊥PH ．点P 的纵坐标为y P =－t 2+2t +3， 点M 的纵坐标为y M =53-t +59．所以PM =y P －y M =－t 2+2t +3+53t －59=－t 2+513t +56． 则S △PFE =S △PFM + S △PEM =21PM ·FN +21PM ·EH =21PM ·(FN + EH )=21·(－t 2+513t +56)(3+52) =1017-·(t －1013)2+100289×1017 所以当t =1013时，△PFE 的面积最大，最大值的立方根为31017100289⨯=1017． （3）由图可知∠PEA ≠90°．①若∠P 1AE =90°，作P 1G ⊥y 轴，因为OA =OE ，所以∠OAE =∠OEA =45°， 所以∠P 1AG =∠AP 1G =45°，所以P 1G =AG ． 所以t =－t 2+2t +3－3，即－t 2+t =0， 解得t =1或t =0(舍去)．②若∠AP 2E =90°，作P 2K ⊥x 轴，AQ ⊥P 2K ， 则△P 2KE ∽△AQP 2，所以QP KEAQ K P 22=， 所以tt tt t t 233222+--=++-，即t 2－t －1=0，解之得t =251+或t =251-＜52-(舍去)．综上可知t =1或t =251+适合题意．10. （2017湖南岳阳，本题满分10分）如图，抛物线223y x bx c =++经过点()3,0B ，()0,2C -，直线l ：2233y x =--交y 轴于点E ，且与抛物线交于A ，D 两点．P 为抛物线上一动点（不与A ，D 重合）． （1） 求抛物线的解析式；（2） 当点P 在直线l 下方时，过点P 作PM x ∥轴交l 于点M ，PN y ∥轴交l 于点N ．求PM PN +的最大值；（3） 设F 为直线l 上的点，以E ，C ，P ，F 为顶点的四边形能否构成平行四边形？若能，求出点F 的坐标；若不能，请说明理由．备用图解：（1）将()3,0B ，()0,2C -代入223y x bx c =++，得：6302b c c ++=⎧⎨=-⎩解得：432b c ⎧=-⎪⎨⎪=-⎩∴抛物线的解析式为：224233y x x =--；（2）设()224,21233P a a a a ⎛⎫---<< ⎪⎝⎭，则22,33N a a ⎛⎫-- ⎪⎝⎭∴222242133=3333222PN a a a ⎛⎫=-++--+≤ ⎪⎝⎭∵M ，N 在直线l ：2233y x =--上，PM x ∥，PN y ∥∴23PN PM =∴51524PM PN PN +=≤即：PM PN +的最大值为：154；（3）能设22,33F m m ⎛⎫-- ⎪⎝⎭① 当EC 为边时，有224,233P m m m ⎛⎫-- ⎪⎝⎭，EC PF =即：22244=3333m m -++解得：m =，其中0m =时不成立，舍去； ② 当EC 为对角线时，PF 中点即为EC 中点（0，43-）2,23P m m ⎛⎫-- ⎪⎝⎭在抛物线上所以，224222333m m m +-=-解得：01m =-或，其中0m =时不成立，舍去；综上所述：F 点的坐标为：41,3⎛⎫- ⎪⎝⎭、()1,0-、⎝⎭、⎝⎭．11. （2017湖南常德，25，10分）如图12，已知抛物线的对称轴是y 轴，且点(2,2)，(1,54)在抛物线上，点P 是抛物线上不与顶点N 重合的一动点，过点P 作PA ⊥x 轴于A ，PC ⊥y 轴于C ，延长PC 交抛物线于E ，设M 是O 关于抛物线顶点N 的对称点，D 是C 点关于N 的对称点. （1）求抛物线的解析式及顶点N 的坐标； （2）求证：四边形PMDA 是平行四边形；（3）求证：△DPE ∽△PAM P 的坐标.图12思路分析：（1）将点(2,2)，(1,54)坐标代入y=ax2+k中求出解析式，即可得到顶点N的坐标；（2）根据解析式设出点P坐标，从而得到点A、C的坐标，再通过N的坐标求出点M的坐标和D的坐标，即可求出MD和PA 的长度，得出长度相等，而MD∥PA，所以四边形PMDA是平行四边形；（3）在（2）证明之后继续证明PM=PA，则四边形PMDA是菱形，∠MDP=12∠PDE=12∠ADM=12∠APM，所以∠PDE=∠APM，而△DPE和△PAM都是等腰三角形，顶角相等，则两个三角形相似.解：（1）设抛物线的解析式为：y=ax2+k，∵点(2,2)，(1,54)在抛物线上，∴4254a ka k+=⎧⎪⎨+=⎪⎩，解得141ak⎧=⎪⎨⎪=⎩.∴该抛物线的解析式为：y=14x2+1，顶点N的坐标为（0,1）；（2）设点P坐标为（x, 14x2+1），∵PA⊥x轴于A，PC⊥y轴于C，M是O关于抛物线顶点N的对称点，D是C点关于N的对称点.∴A（x,0），C（0,14x2+1），M（0,2），D（0，1－14x2）；PA∥y轴；∴MD=2－（1－14x2）=14x2+1=PA且MD∥PA∴四边形PMDA是平行四边形；（3）由（2）得四边形PMDA是平行四边形，PC=x，CM=14x2+1－2=14x2－1；∵在Rt△PCM中，PM2114x==+=PA∴四边形PMDA 是菱形，△PAM 是等腰三角形； ∴∠APM =∠ADM ；∠MDP =12∠ADM ； 根据抛物线的对称性，PD =ED ， ∴△DPE 是等腰三角形，DC 平分∠PDE ， ∴∠MDP =12∠PDE ， ∴∠PDE =∠APM ；又∵∠PDE ，∠APM 分别为等腰△DPE 和△PAM 的顶角； ∴△DPE ∽△PAM PE =2x ，AM =222x +∵PE ：AM =3时，解得：x =23±； ∴相似比为3时P 点坐标为：（23±，4）12. 24.(2017湖北咸宁，24，12分)如图，抛物线c bx x y ++=221与x 轴交于A 、B 两点，与y 轴交于点C ，其对称轴交抛物线于点D ，交x 轴于点E ，已知OB=OC=6.⑴求抛物线的解析式及点D 的坐标；⑵连接BD ，F 为抛物线上一动点，当∠FAB=∠EDB 时，求点F 的坐标；⑶平行于x 轴的直线交抛物线于M 、N 两点，以线段MN 为对角线作菱形MPNQ ，当点P 在x 轴上，且PQ=12MN 时，求菱形对角线MN 的长.思路分析：(1)利用OB=OC=6得到点B(6，0)，C(0，-6)，将其代入抛物线的解析可以求出b 、c 的值，进而得到抛物线的解析式，最后通过配方得到顶点坐标；(2)由于F 为抛物线上一动点，∠FAB=∠EDB ，可以分两种情况求解：一是点F 在x 轴上方；二是点F 在x 轴下方.每一种情况都可以作FG ⊥x 轴于点G ，构造Rt △AFG 与Rt △DBE 相似，利用对应边成比例或三角函数的定义求点F 的坐标.(3)首先根据MN 与x 轴的位置关系画出符合要求的两种图形：一是MN 在x 轴上方；二是MN 在x 轴下方.设菱形对角线的交点T 到x 轴的距离为n ，利用PQ=12MN ，得到MT=2n ，进而得到点M 的坐标为(2+2n ，n)，再由点M 在抛物线上，得21(22)2(22)62n n n =+-+-， 求出n 的值，最后可以求得MN=2MT=4n 的两个值. 解：(1)∵OB=OC=6， ∴B(6，0)，C(0，-6).∴216+6026b c c ⎧⨯+=⎪⎨⎪=-⎩， 解得26b c =-⎧⎨=-⎩，∴抛物线的解析式为21262y x x =--. ……2分 ∵21262y x x =--=21(2)82x --， ∴点D 的坐标为(2，-8). ……4分 (2)如图，当点F 在x 轴上方时，设点F 的坐标为(x ，21262x x --).过点F 作FG ⊥x 轴于点G ，易求得OA=2，则AG=x+2，FG=21262x x --.∵∠FAB=∠EDB，∴tan∠FAG=tan∠BDE，即21261222x xx--=+，解得17x=，22x=-(舍去).当x=7时，y=92，∴点F的坐标为(7，92). ……6分当点F在x轴下方时，设同理求得点F的坐标为(5，72-).综上所述，点F的坐标为(7，92)或(5，72-). ……8分(3)∵点P在x轴上，∴根据菱形的对称性可知点P的坐标为(2，0).如图，当MN在x轴上方时，设T为菱形对角线的交点.∵PQ=12MN ， ∴MT=2PT.设TP=n ，则MT=2n. ∴M(2+2n ，n).∵点M 在抛物线上， ∴21(22)2(22)62n n n =+-+-， 即2280n n --=.解得1n =，2n =(舍去).∴. ……10分当MN 在x 轴下方时，设TP=n ，得M(2+2n ，-n).∵点M 在抛物线上， ∴21(22)2(22)62n n n -=+-+-， 即22+80n n -=.解得114n -+=，214n -=(舍去).∴1-.综上所述，菱形对角线MN 1-. ……12分13. 24．（2017湖北宜昌）（本小题满分12分）已知抛物线y=ax 2+bx+c ，其中2a=b>0>c ，且a+b+c=0. （1）直接写出关于x 的一元二次方程ax 2+bx+c =0的一个根； （2）证明：抛物线y=ax 2+bx+c 的顶点A 在第三象限；（3）直线y= x+m 与轴,x y 轴分别相交于B,C 两点，与抛物线y=ax 2+bx+c 相交于A,D 两点.设抛物线y=ax 2+bx+c 的对称轴与x 轴相交于E ,如果在对称轴左侧的抛物线上存在点F ,使得△ADF 与△OCB 相似.并且12ADF ADE S S ∆∆=，求此时抛物线的表达式.xyO思路分析：（1）利用抛物线的对称轴、对称性及二次函数与方程的关系数形结合得出二次方程的根；（2）确定抛物线的顶点位置一可借助数形结合，二可借助顶点坐标的正负性；（3）借助一次函数与二次函数的关系确定与求解相关点的坐标，将坐标转化为相应的线段长，进而借助题意中的相似及面积关系等构建方程求解未知系数的值.解：（1）ax 2+bx+c =0的一个根为1（或者-3） （2）证明：∵ b =2a ，∴对称轴x=2ba-=-1,将b=2a 代入a+b+c=0.得c=-3a . 方法一：∵a=b>0>c ，∴b 2-4ac>0,∴244ac b a-<0, 所以顶点A （-1，244ac b a-）在第三象限.方法二：∵b =2a ， c=-3a ，∴244ac b a -=221244a b a --=-4a <0, 所以顶点A （-1，244ac b a-）在第三象限.（3）∵b =2a ， c=-3a∴242a a a -± ∴x 1=-3，x 2=1,所以函数表达式为y=ax 2+2ax-3a ，∵直线y= x+m 与x 轴、y 轴分别相交于B,C,两点，则OB=OC=m所以△BOC 是以∠BOC 为直角的等腰三角形，这时直线y=x+m 与对称轴x=-1的夹角∠BAE=45°.又因点F 在对称轴左侧的抛物线上，则∠BAE>45°，这时△BOC 与△ADF 相似，顶点A 只可能对应△BOC 中的直角顶点O ，即△ADF是以A 为直角顶点的等腰三角形，且对称轴是x =-1，设对称轴x =-1与OF 交于点G. ∵直线y=x+m 过顶点A ，所以m=1-4a ，∴直线解析式为y=x+1-4a,解方程组21423y x a y ax ax a =+-⎧⎨=+-⎩，解得1114x y a =-⎧⎨=-⎩，221114x ay a a ⎧=-⎪⎪⎨⎪=-⎪⎩， 这里的（-1，4a ）即为顶点A ，点（1a -1，1a -4a ）即为顶点D 的坐标（1a -1，1a -4a ） D 点到对称轴x=-1的距离为1a -1-（-1）=1a，AE =4a -=4a,S △ADE =12×1a×4a=2,即它的面积为定值.这时等腰直角△ADF 的面积为1，所以底边DF =2，而x=-1是它的对称轴，这时D,C 重合且在y 轴上，由1a-1=0，∴a=1，此时抛物线的解析式y=x 2+2x-314. （2017湖南邵阳，26，10分）（本小题满10分）如图（十六）所示，顶点（49-21，）的抛物线y ＝ax 2＋bx＋c 过点M （2，0）. （1）求抛物线的解析式；（2）点A 是抛物线与x 轴的交点（不与点M 重合），点B 是抛物线与y 轴的交点，点C 是直线y ＝x ＋1上一点（处于x 轴下方），点D 是反比例函数y ＝xk（k >0）图象上一点.若以点A 、B 、C 、D 为顶点的四边形是菱形，求k 的值.思路分析：（1）已知抛物线的顶点坐标，可设顶点式为 y ＝a (x －21)2－49，再把点M （2，0）代入，可求a ＝1，所以抛物线的解析式可求.（2）先分别求出A 、B 两点的坐标，及AB 线段长，再根据反比例函数y ＝xk（k >0），考虑点C 在x 轴下方，故点D 只能在第一、三象限．确定菱形有两种情形：①菱形以AB 为边，如图一。
2017年全国中考数学真题分类二次函数代数方面的应用
2017年全国中考数学真题分类 二次函数代数方面的应用一、选择题1. （2017青海西宁，10，3分）如图3，在正方形ABCD 中，AB =3cm ，动点M 自A 点出发沿AB 方向以每秒1cm 的速度运动，同时动点N 自D 点出发沿折线DC - CB 以每秒2cm 的速度运动，到达B 点时运动同时停止，设△AMN 的面积为y （c m 2），运动时间为x （秒），则下列图象中能大致反映y 与x 之间的函数关系的是A ．B ． D ．A ．B ．C ．D ．答案：A ，解析：当M 在AB 上移动，N 在DC 上时，△AMN 的面积为y =x x 23321=⋅⋅（0≤x ≤23）． 当M 在AB 上，N 在BC 上时，y =x x x x 3)26(212+-=-⨯⨯（x >23），故选A二、解答题1. （2017浙江温州，22， 10分）如图，过抛物线y ＝错误!未找到引用源。
上一点A 作x 轴的平行线，交抛物线于另 一点B ，交y 轴于点C ，已知点A 的横坐标为－2． （1）求抛物线的对称轴和点B 的坐标.（2）在AB 上任取一点P ，连结OP ，作点C 关于直线OP 的对称点D. ①连结BD ，求BD 的最小值.②当点D 落在抛物线的对称轴上，且在x 轴上方时，求直线PD 的函数表达式.思路分析：考点二次函数与一次函数的综合应用，（1）知道抛物线的解析式，求对称轴：直线错误!未找到引用源。
＝错误!未找到引用源。
＝4，用待定系数法求出A（－2， 5），B（10， 5）（2）利用三角形三边关系可知当且仅当点O、D、B三点共线时，BD取得最小值；分类讨论点D的位置，利用待定系数法求出直线PD的函数表达式．解：（1）由抛物线的解析式y＝错误!未找到引用源。
，得对称轴：直线错误!未找到引用源。
＝错误!未找到引用源。
＝4由题意知点A的横坐标为－2，代入解析式求得y＝错误!未找到引用源。
，当错误!未找到引用源。
2017全国中考数学真题分类-二次函数概念、性质和图象(选择题+填空题+解答题)解析版
2017全国中考数学真题分类知识点18二次函数概念、性质和图象（选择题+填空题+解答题）解析版一、选择题1. ．(2017四川广安，10，3分)如图所示，抛物线y ＝ax ²+bx +c 的顶点为B (－1，3)，与x 轴的交点A 在点(－3，0)和(－2，0)之间，以下结论：①b ²－4ac ＝0 ②a +b +c >0 ③2a －b ＝0 ④c －a ＝3A ．1B ．2C ．3D ．4答案：B ，解析：由图象可知，抛物线与x 轴有两个交点，∴b ²－4ac ＞0，故结论①不正确；∵抛物线的对称轴为x ＝－1，与x 轴的一个交点A 在点（－3，0）和（－2，0）之间，∴抛物线与x 轴的另一个交点在点（0，0）和（1，0）之间，∴当x ＝1时，y ＜0，∴a +b +c ＜0，故结论②不正确．∵抛物线的对称轴x ＝－2ba＝－1，∴2a ＝b ，即2a －b ＝0，故结论③正确；∵抛物线y ＝ax ²+bx+c 的顶点为B （－1，3），∴a －b +c ＝3，∵抛物线的对称轴x ＝－1，∴2a ＝b ，∴a －2a +c ＝3，即c －a ＝3，故结论④正确；综上所述，正确的结论有2个．故选B ．2. （2017浙江丽水·8·3分）将函数y ＝x 2的图象用下列方法平移后，所得的图象不经过点A （1，4）的方法是（ ）A ．向左平移1个单位B ．向右平移3个单位C ．向上平移3个单位D ．向下平移1个单位答案：D ． 解析： 选项 知识点结果 A将函数y ＝x 2的图象向左平移1个单位得到函数y ＝(x ＋1)2，其图象经过点（1，4）.×B 将函数y ＝x 2的图象向右平移3个单位得到函数y ＝(x －3)2，其图象经过点（1，4）. ×C 将函数y ＝x 2的图象向上平移3个单位得到函数y ＝x 2＋3，其图象经过点（1，4）. ×D 将函数y ＝x 2的图象向下平移1个单位得到函数y ＝x 2－1，其图象不经过点（1，4）.√3. （2017山东枣庄12，3分）已知函数221y ax ax =--（a 是常数，0a ≠），下列结论正确的是A ．当a ＝1时，函数图象经过点（－1，0）B ．当a ＝－2时，函数图象与x 轴没有交点C ．若a <0，函数图象的顶点始终在x 轴的下方D ．若a >0，则当1x ≥时，y 随x 的增大而增大答案：D ，解析：A 、当a ＝1时，函数解析式为y ＝x 2－2x －1，当x ＝－1时，y ＝1＋2－1＝2， ∴当a ＝1时，函数图象经过点（－1，2），∴A 选项不符合题意； B 、当a ＝2时，函数解析式为y ＝－2x 2＋4x －1，令y ＝－2x 2＋4x －1＝0，则△＝42－4×（－2）×（－1）＝8＞0，∴当a ＝－2时，函数图象与x 轴有两个不同的交点，∴B 选项不符合题意；C 、∵y ＝ax 2－2ax －1＝a （x －1）2－1－a ，∴二次函数图象的顶点坐标为（1，－1－a ），当－1－a ＜0时，有a ＞－1，∴C 选项不符合题意；D 、∵y ＝ax 2－2ax －1＝a （x －1）2－1－a ，∴二次函数图象的对称轴为x ＝1．若a ＞0，则当x ≥1时，y 随x 的增大而增大，∴D 选项符合题意．故选D ．4. （2017四川成都，10，3分）在平面直角坐标系xOy 中，二次函数2y ax bx c =++的图像如图所示，下列说法正确的是 （ ）A ．20,40abc b ac <-> B ．20,40abc b ac >->C. 20,40abc b ac <-<D ．20,40abc b ac >-<答案：B ，解析：由二次函数2y ax bx c =++的图象开口向上，则a ＞0，与y 轴交点在y 轴的负半轴上，由c <0，对称轴在y 轴的左侧，则2b a->0，所以b <0，所以0abc >；图象与x 轴有两点交点，则240b ac ->，综上，故选B .5. (2017浙江金华，6，3分)对于二次函数y ＝－(x －1)2＋2的图象与性质，下列说法正确的是A ．对称轴是直线x ＝1，最小值是2B ．对称轴是直线x ＝1，最大值是2C ．对称轴是直线x ＝－1，最小值是2D ．对称轴是直线x ＝－1，最大值是2 答案：B ，解析：二次函数y ＝－(x －1)2＋2的对称轴是直线x ＝1. ∵－1<0，∴抛物线开口向下，有最大值，最大值是2.6. （2017安徽中考·9．4分）已知抛物线2y ax bx c =++与反比例函数by x=的图象在第一象限有一个公共点，其横坐标为1，则一次函数y bx ac =+的图象可能是（ ）答案：B ．解析：由公共点的横坐标为1，且在反比例函数by x=的图象上，当x ＝1时，y ＝b ，即公共点坐标为（1，b ），又点（1，b ）在抛物线2y ax bx c =++上，得a ＋b ＋c ＝b ，a ＋c ＝0，由a ≠0知ac ＜0，一次函数y bx ac =+的图象与y 轴交点在负半轴上，反比例函数by x=的图象的一支在第一象限，b ＞0，一次函数y bx ac =+的图象满足y 随x 增大而增大，选项B 符合条件，选B ．7. （2017山东德州，7，3分）下列函数中，对于任意实数x 1，x 2，当x 1＞x 2时，满足y 1＜y 2的是（ ）A ．y ＝－3x ＋2B ．y ＝2x ＋1C ．y ＝2x 2＋1D ．y ＝x1-答案：A ，解析：一次函数y ＝－3x ＋2中，由于k ＝－3＜0，所以y 随着x 的增大而减小，即对于任意实数x 1，x 2，当x 1＞x 2时，满足y 1＜y 2． 8. （2017山东威海，11，3分）．已知二次函数y =ax ²+bx +c (a ≠0)的图像如图所示．若正比例函数y =(b +c )x 与反比例函数y =a b cx-+在同一坐标系中的大致图像是（ ）答案：C，解析：由抛物线知a＞0，b＜0，c＞0，故a－b+c＞0，反比例函数过一三象限;当x=1时，y=a+b+c ＜0，即b+c＜－a, 因为a＞0，所以b+c＜0，所以正比例函数过二四象限，故选C．9.（2017山东菏泽，8,3分）一次函数y＝ax+b和反比例函数y=cx在同一平面直角坐标系中的图象如图所示，则二次函数y=ax2+bx+c的图象可能是（）答案：A，解析：根据反比例函数图象和一次函数图象经过的象限，即可得出a＜0、b＞0、c＜0，由此即可得出：二次函数y=ax2+bx+c的图象开口向下，选项D不符合题意，对称轴x=－2ba＞0，选项B不符合题意，与y轴的交点在y轴负半轴，选项C不符合题意，只有选项A符合题意．10. 10．（2017年四川绵阳，10,3分）将二次函数y=x2的图象先向下平移1个单位，再向右平移3个单位，得到的图象与一次函数y=2x+b的图象有公共点，则实数b的取值范围是A．b＞8 B．b＞－8 C．b≥8 D．b≥－8答案：D 解析：二次函数向下平移1个单位，再向右平移3个单位后，得到y=（x－3）2+1，再结合与一次函数y=2x+b有公共点，联立方程组，建立关于x的一元二次方程，利用一元二次方程有解的条件△≥0，可求出b的范围．11. (2017年四川南充，10，3分)二次函数y＝ax2＋bx＋c(a，b，c是常数，且a≠0)的图象如图5所示，下列结论错误的是( )A．4ac＜b2B．abc＜0 C．b＋c＞3a D．a＜bxOy－－图5（8题图） A. B. C. D答案：D 解析：(1)∵抛物线与横轴有两个交点，∴△＞0，即b 2－4ac ＞0．∴4ac ＜b 2．可见选项A 中的结论正确．(2)∵抛物线的开口向下，∴a ＜0；∵对称轴在y 轴左边，∴－2b a＜0．∴b ＜0；∵抛物线与y 轴的负半轴相交，∴c ＜0．∴abc ＜0．可见选项B 中的结论正确． (3)∵－2b a＞－1，a ＜0，∴b ＞2a ①．∵x ＝－1时，y ＞0，∴a －b ＋c ＞0②．①＋②，得c ＞a ③．①＋③，得b ＋c ＞3a ．可见选项C 中的结论正确． (4)∵－2b a＜－12，a ＜0，∴a ＞b ．可见选项D 中的结论错误．综上所述，选项D ．12. （2017浙江舟山，10，3分）下列关于函数y ＝x 2－6x +10的四个命题：①当x ＝0时，y 有最小值10；②n 为任意实数，x ＝3+n 时的函数值大于x ＝3－n 时的函数值；③若n >3，且n 是整数，当n ≤x ≤n +1时，y 的整数值有(2n －4)个；④若函数图象过点(a ，y 0)和(b ，y 0+1)，其中a >0，b >0，则a <b ．其中真命题的序号是（ ） A ．① B ．②C ．③D ．④答案：C ，解析：因为y ＝x 2－6x +10＝(x －3)2+1，所以当x ＝3时，y 有最小值1，故①错误；n 为任意实数，当x ＝3+n 时，y ＝(3+n －3)2+1＝ n 2+1， 当x ＝3－n 时，y ＝(3－n －3)2+1＝ n 2+1，所以两函数值相等，故②错误；若n >3，且n 是整数，当n ≤x ≤n +1时，令x ＝n ，则y 1＝(n －3)2+1＝ n 2－6n +10， 令x ＝n +1，则y 2＝(n +1－3)2+1＝ n 2－4n +5， 由于y 2－ y 1＝2n －5，所以之间的整数值的个数是2n －5+1＝2n +4个，故③正确；由二次函数的图象知④错误．令x ＝4，则y ＝(4－3)2+1＝2， 令x ＝5，则y ＝(5－3)2+1＝5，y 的整数值有2，3，4，5，2n －4＝2×4－4＝4个，令x ＝6，则y ＝(6－3)2+1＝10， y 的整数值有5，6，7，8，9，10，2n －4＝2×5－4＝6个，令x ＝7，则y ＝(7－3)2+1＝10， y 的整数值有10，11，12，13，14，15，16，17共8个，2n －4＝2×6－4＝8个， 13. （2017四川攀枝花，9，3分）二次函数y ＝ax 2＋bx ＋c （a ≠0）的图像如图所示，则下列命题中正确的是（ ）A ．a ＞b ＞cB ．一次函数y ＝ax ＋c 的图像不经过第四象限C ．m （am ＋b ）＋b ＝a （m 是任意实数）D ．3b ＋2c ＞0 答案：D解析：由题意知抛物线对称轴为12b x a =-=-，即12a b =，故A 错误；a ＞0，c ＜0∴一次函数y ＝ax ＋c 的图像不经过第二象限，故B 错误；m （am ＋b ）＋b ＝a ，2b a =可得m ＝－112a b =，故C 错误；又当1x =时，0y a b c =++>，∴102b bc ++>，即320b c +>，故选D ．14. （2017江苏盐城，6，3分）如图，将函数y ＝21(2)12x -+的图像沿y 轴向上平移得到一条新函数的图像，其中点A （1，m ）、B （4，n ）平移后的对应点分别为点A ′、B ′．若曲线段AB 扫过的面积为9（图中的阴影部分），则新图像的函数表达式是A ．y ＝21(2)22x --B ．y ＝21(2)72x -+C ．y ＝21(2)52x --D ．y ＝21(2)42x -+答案：D ，解析：连接AB 、A ′B ′，则S 阴影＝S 四边形ABB ′A ′．由平移可知，AA ′＝BB ′，AA ′∥BB ′，所以四边形ABB ′A ′是平行四边形．分别延长A ′A 、B ′B 交x 轴于点M 、N ．因为A （1，m ）、B （4，n ），所以MN ＝4－1＝3．因为ABB A S''＝AA ′·MN ，所以9＝3AA ′，解得AA ′＝3，即沿y 轴向上平移了3个单位，所以新图像的函数表达式y ＝21(2)42x -+．B 'A 'ABOyx第6题图2 的增大而增大；④方程ax 2+bx +c =0有一个根大于4．其中正确的结论有 A ．1个 B ．2个 C ．3个 D ．4个答案：B ，解析：由表格所给出的自变量与函数值变化趋势，随x 的值增大，y 值先增大后变小可知抛物线的开口向下；由对称性知其图象的对称轴为x =32，所以当x ＜1时，函数值y 随x 的增大而增大正确；由表可知，方程ax 2+bx +c =0根在-1与0和3与4之间所以正确的2个．此题也可求出解析式进行判断．16.7．（2017江苏连云港，7，3分）已知抛物线20yax a 过12,Ay ，21,B y 两点，则下列关系式一定正确的是A ．120y yB ．210y y C ．120y yD ．210y y答案：C ，解析：∵20y ax a ∴抛物线的开口向上，对称轴为y 轴，12,Ay 在对称轴的左侧，21,B y 在对称轴的右侧，点A 离开对称轴的距离大于点B 离开对称轴的距离，∴120yy 因此选择C 选项．17. （2017四川达州8，3分）已知二次函数2y ax bx c =++的图象如下，则一次函数2y ax b =-与反比例函数cy x=在同一平面直角坐标系中的图象大致是（ ）A B C D答案C，解析：由于抛物线的开口向下，∴a<0，由于抛物线与y轴的交点在y轴的正半轴，∴c>0，由于抛物线的对称轴是x=-1∴-12ba=-，∴b=2a，∴y=ax-4a，对于方程组4y ax acyx=-⎧⎪⎨=⎪⎩，消去y,可整理成：240ax ax c--=，∆=2164a ac+，∵抛物线过点(-3,0),∴9a-3b+c=0,∴c=-3a,∴2222164=161240a ac a a a+-=>,∴直线与反比例函数有交点，故本题选C．18. 11．（2017四川眉山，11，3分）若一次函数y＝(a＋1)x＋a的图象过第一、三、四象限，则二次函数y＝ax2－axA．有最大值a4B．有最大值－a4C．有最小值a4D．有最小值－a4答案：B，解析：因为一次函数y＝(a＋1)x＋a的图象过第一、三、四象限，所以⎩⎨⎧a＋1＞0，a＜0，因此－1＜a＜0，而y＝ax2－ax＝a(x－12)2－14a，所以二次函数有最大值－a4．19. 8．（2017四川宜宾，8，3分）如图，抛物线211(1)12y x=++与22(4)3y a x=--交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于B、C两点，且D、E分别为顶点．则下列结论：①23a=；②AC=AE；③△ABD是等腰直角三角形；④当x>1时，y1＞y2，其中正确结论的个数是A ．1个B ．2个C ．3个D ．4个答案：C ，解析：抛物线22(4)3y a x =--过点A （1，3），∴3＝9a －3，解得a ＝23，由题意可知E （4，﹣3），点A （1,3）、C 关于x ＝4对称，得到C （7,3），∴AC ＝6，而AE = ，故AC ≠AE ，由抛物线的对称性可知，AD ＝BD 显然．根据抛物线的对称性可知，AD ＝BD ，两个函数比较大小，首先要知道这两个函数图象的交点，则2212(1)1(4)323x x ++=--，解得x 1＝1，x 2＝37，所以当1＜x ＜37时，y 1＞y 2．20. （2017山东滨州，7，3分）将抛物线y ＝2x 2向右平移3个单位，再向下平移5个单位，得到的抛物线的表达式为（ ）A ．y ＝2(x －3)2－5B ．y ＝2(x ＋3)2＋5C ．y ＝2(x －3)2＋5D ．y ＝2(x ＋3)2－5答案：A ，解析：抛物线y ＝2x 2的顶点坐标为（0，0）， ∵向右平移3个单位，再向下平移5个单位， ∴平移后的顶点坐标为（3，﹣5），∴平移后的抛物线解析式为y ＝2(x －3)2－5.故选A.21. 8．（2017江苏苏州，8，3分）若二次函数y =ax 2+1的图象经过点（-2,0），则关于x 的方程 a (x -2)2+1=0的实数根为 A ．x 1=0，x 2=4B ．x 1=—2，x 2=6C ． x 1=32，x 2=52D ．x 1=—4，x 2=0答案：A ，解析：根据“二次函数图象上点的坐标特征”可得4a +1=0，a =-14，则21(2)104x --+=，解一元二次方程得x 1=0，x 2=4．22. 9.(2017甘肃兰州，9，4分）抛物线y =3x ²-3向右平移3个单位长度，得到新抛物线的表达式为A. y =3(x -3)²-3B. y =3x ²C. y =3(x +3)²-3D. y =3x ²-6【答案】A【解析】由题知，y =3x ²-3为顶点式，直接根据二次函数图像左加右减，上加下减的平移规律进行解答即可。
近五年(2017-2021)年浙江中考数学真题分类汇编之二次函数(含解析)
2017-2021年浙江中考数学真题分类汇编之二次函数一．选择题（共16小题）1．（2018•临安区）抛物线y＝3（x﹣1）2+1的顶点坐标是（）A．（1，1）B．（﹣1，1）C．（﹣1，﹣1）D．（1，﹣1）2．（2021•绍兴）关于二次函数y＝2（x﹣4）2+6的最大值或最小值，下列说法正确的是（）A．有最大值4B．有最小值4C．有最大值6D．有最小值6 3．（2018•宁波）如图，二次函数y＝ax2+bx的图象开口向下，且经过第三象限的点P．若点P的横坐标为﹣1，则一次函数y＝（a﹣b）x+b的图象大致是（）A．B．C．D．4．（2018•绍兴）若抛物线y＝x2+ax+b与x轴两个交点间的距离为2，称此抛物线为定弦抛物线，已知某定弦抛物线的对称轴为直线x＝1，将此抛物线向左平移2个单位，再向下平移3个单位，得到的抛物线过点（）A．（﹣3，﹣6）B．（﹣3，0）C．（﹣3，﹣5）D．（﹣3，﹣1）5．（2017•杭州）设直线x＝1是函数y＝ax2+bx+c（a，b，c是实数，且a＜0）的图象的对称轴，（）A．若m＞1，则（m﹣1）a+b＞0B．若m＞1，则（m﹣1）a+b＜0C．若m＜1，则（m+1）a+b＞0D．若m＜1，则（m+1）a+b＜0 6．（2021•杭州）在“探索函数y＝ax2+bx+c的系数a，b，c与图象的关系”活动中，老师给出了直角坐标系中的四个点：A（0，2），B（1，0），C（3，1），D（2，3）．同学们探索了经过这四个点中的三个点的二次函数图象，发现这些图象对应的函数表达式各不相同，其中a的值最大为（）A．B．C．D．7．（2019•绍兴）在平面直角坐标系中，抛物线y＝（x+5）（x﹣3）经变换后得到抛物线y ＝（x+3）（x﹣5），则这个变换可以是（）A．向左平移2个单位B．向右平移2个单位C．向左平移8个单位D．向右平移8个单位8．（2019•衢州）二次函数y＝（x﹣1）2+3图象的顶点坐标是（）A．（1，3）B．（1，﹣3）C．（﹣1，3）D．（﹣1，﹣3）9．（2020•宁波）如图，二次函数y＝ax2+bx+c（a＞0）的图象与x轴交于A，B两点，与y 轴正半轴交于点C，它的对称轴为直线x＝﹣1．则下列选项中正确的是（）A．abc＜0B．4ac﹣b2＞0C．c﹣a＞0D．当x＝﹣n2﹣2（n为实数）时，y≥c10．（2020•温州）已知（﹣3，y1），（﹣2，y2），（1，y3）是抛物线y＝﹣3x2﹣12x+m上的点，则（）A．y3＜y2＜y1B．y3＜y1＜y2C．y2＜y3＜y1D．y1＜y3＜y2 11．（2019•湖州）已知a，b是非零实数，|a|＞|b|，在同一平面直角坐标系中，二次函数y1＝ax2+bx与一次函数y2＝ax+b的大致图象不可能是（）A．B．C．D．12．（2018•湖州）在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y＝ax2﹣x+2（a≠0）与线段MN有两个不同的交点，则a的取值范围是（）A．a≤﹣1或≤a＜B．≤a＜C．a≤或a＞D．a≤﹣1或a≥13．（2017•绍兴）矩形ABCD的两条对称轴为坐标轴，点A的坐标为（2，1），一张透明纸上画有一个点和一条抛物线，平移透明纸，使这个点与点A重合，此时抛物线的函数表达式为y＝x2，再次平移透明纸，使这个点与点C重合，则该抛物线的函数表达式变为（）A．y＝x2+8x+14B．y＝x2﹣8x+14C．y＝x2+4x+3D．y＝x2﹣4x+3 14．（2021•湖州）已知抛物线y＝ax2+bx+c（a≠0）与x轴的交点为A（1，0）和B（3，0），点P1（x1，y1），P2（x2，y2）是抛物线上不同于A，B的两个点，记△P1AB的面积为S1，△P2AB的面积为S2，有下列结论：①当x1＞x2+2时，S1＞S2；②当x1＜2﹣x2时，S1＜S2；③当|x1﹣2|＞|x2﹣2|＞1时，S1＞S2；④当|x1﹣2|＞|x2+2|＞1时，S1＜S2．其中正确结论的个数是（）A．1B．2C．3D．4 15．（2020•嘉兴）已知二次函数y＝x2，当a≤x≤b时m≤y≤n，则下列说法正确的是（）A．当n﹣m＝1时，b﹣a有最小值B．当n﹣m＝1时，b﹣a有最大值C．当b﹣a＝1时，n﹣m无最小值D．当b﹣a＝1时，n﹣m有最大值16．（2019•舟山）小飞研究二次函数y＝﹣（x﹣m）2﹣m+1（m为常数）性质时得到如下结论：①这个函数图象的顶点始终在直线y＝﹣x+1上；②存在一个m的值，使得函数图象的顶点与x轴的两个交点构成等腰直角三角形；③点A（x1，y1）与点B（x2，y2）在函数图象上，若x1＜x2，x1+x2＞2m，则y1＜y2；④当﹣1＜x＜2时，y随x的增大而增大，则m的取值范围为m≥2．其中错误结论的序号是（）A．①B．②C．③D．④二．填空题（共4小题）17．（2018•湖州）如图，在平面直角坐标系xOy中，已知抛物线y＝ax2+bx（a＞0）的顶点为C，与x轴的正半轴交于点A，它的对称轴与抛物线y＝ax2（a＞0）交于点B．若四边形ABOC是正方形，则b的值是．18．（2017•金华）在一空旷场地上设计一落地为矩形ABCD的小屋，AB+BC＝10m，拴住小狗的10m长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S（m2）．（1）如图1，若BC＝4m，则S＝m2．（2）如图2，现考虑在（1）中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其他条件不变，则在BC的变化过程中，当S取得最小值时，边BC的长为m．19．（2021•台州）以初速度v（单位：m/s）从地面竖直向上抛出小球，从抛出到落地的过程中，小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系式是h＝vt ﹣4.9t2．现将某弹性小球从地面竖直向上抛出，初速度为v1，经过时间t1落回地面，运动过程中小球的最大高度为h1（如图1）；小球落地后，竖直向上弹起，初速度为v2，经过时间t2落回地面，运动过程中小球的最大高度为h2（如图2）．若h1＝2h2，则t1：t2＝．20．（2021•湖州）已知在平面直角坐标系xOy中，点A的坐标为（3，4），M是抛物线y＝ax2+bx+2（a≠0）对称轴上的一个动点．小明经探究发现：当的值确定时，抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定，若抛物线y＝ax2+bx+2（a ≠0）的对称轴上存在3个不同的点M，使△AOM为直角三角形，则的值是．三．解答题（共3小题）21．（2021•宁波）如图，二次函数y＝（x﹣1）（x﹣a）（a为常数）的图象的对称轴为直线x＝2．（1）求a的值．（2）向下平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式．22．（2021•杭州）在直角坐标系中，设函数y＝ax2+bx+1（a，b是常数，a≠0）．（1）若该函数的图象经过（1，0）和（2，1）两点，求函数的表达式，并写出函数图象的顶点坐标；（2）写出一组a，b的值，使函数y＝ax2+bx+1的图象与x轴有两个不同的交点，并说明理由．（3）已知a＝b＝1，当x＝p，q（p，q是实数，p≠q）时，该函数对应的函数值分别为P，Q．若p+q＝2，求证：P+Q＞6．23．（2020•金华）如图，在平面直角坐标系中，已知二次函数y＝﹣（x﹣m）2+4图象的顶点为A，与y轴交于点B，异于顶点A的点C（1，n）在该函数图象上．（1）当m＝5时，求n的值．（2）当n＝2时，若点A在第一象限内，结合图象，求当y≥2时，自变量x的取值范围．（3）作直线AC与y轴相交于点D．当点B在x轴上方，且在线段OD上时，求m的取值范围．2017-2021年浙江中考数学真题分类汇编之二次函数参考答案与试题解析一．选择题（共16小题）1．（2018•临安区）抛物线y＝3（x﹣1）2+1的顶点坐标是（）A．（1，1）B．（﹣1，1）C．（﹣1，﹣1）D．（1，﹣1）【考点】二次函数的性质．【分析】已知抛物线顶点式y＝a（x﹣h）2+k，顶点坐标是（h，k）．【解答】解：∵抛物线y＝3（x﹣1）2+1是顶点式，∴顶点坐标是（1，1）．故选：A．【点评】本题考查由抛物线的顶点坐标式写出抛物线顶点的坐标，比较容易．2．（2021•绍兴）关于二次函数y＝2（x﹣4）2+6的最大值或最小值，下列说法正确的是（）A．有最大值4B．有最小值4C．有最大值6D．有最小值6【考点】二次函数的性质；二次函数的最值．【专题】二次函数图象及其性质；应用意识．【分析】根据题目中的函数解析式和二次函数的性质，可以得到该函数有最小值，最小值为6，然后即可判断哪个选项是正确的．【解答】解：∵二次函数y＝2（x﹣4）2+6，a＝2＞0，∴该函数图象开口向上，有最小值，当x＝4取得最小值6，故选：D．【点评】本题考查二次函数的性质、二次函数的最值，解答本题的关键是明确二次函数的性质，会求函数的最值．3．（2018•宁波）如图，二次函数y＝ax2+bx的图象开口向下，且经过第三象限的点P．若点P的横坐标为﹣1，则一次函数y＝（a﹣b）x+b的图象大致是（）A．B．C．D．【考点】二次函数的性质；一次函数的图象．【专题】函数及其图象．【分析】根据二次函数的图象可以判断a、b、a﹣b的正负情况，从而可以得到一次函数经过哪几个象限，本题得以解决．【解答】解：由二次函数的图象可知，a＜0，b＜0，当x＝﹣1时，y＝a﹣b＜0，∴y＝（a﹣b）x+b的图象在第二、三、四象限，故选：D．【点评】本题考查二次函数的性质、一次函数的性质，解答本题的关键是明确题意，利用函数的思想解答．4．（2018•绍兴）若抛物线y＝x2+ax+b与x轴两个交点间的距离为2，称此抛物线为定弦抛物线，已知某定弦抛物线的对称轴为直线x＝1，将此抛物线向左平移2个单位，再向下平移3个单位，得到的抛物线过点（）A．（﹣3，﹣6）B．（﹣3，0）C．（﹣3，﹣5）D．（﹣3，﹣1）【考点】抛物线与x轴的交点；二次函数的性质；二次函数图象上点的坐标特征；二次函数图象与几何变换．【专题】二次函数图象及其性质．【分析】根据定弦抛物线的定义结合其对称轴，即可找出该抛物线的解析式，利用平移的“左加右减，上加下减”找出平移后新抛物线的解析式，再利用二次函数图象上点的坐标特征即可找出结论．【解答】解：∵某定弦抛物线的对称轴为直线x＝1，∴该定弦抛物线过点（0，0）、（2，0），∴该抛物线解析式为y＝x（x﹣2）＝x2﹣2x＝（x﹣1）2﹣1．将此抛物线向左平移2个单位，再向下平移3个单位，得到新抛物线的解析式为y＝（x ﹣1+2）2﹣1﹣3＝（x+1）2﹣4．当x＝﹣3时，y＝（x+1）2﹣4＝0，∴得到的新抛物线过点（﹣3，0）．故选：B．【点评】本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征、二次函数图象与几何变换以及二次函数的性质，根据定弦抛物线的定义结合其对称轴，求出原抛物线的解析式是解题的关键．5．（2017•杭州）设直线x＝1是函数y＝ax2+bx+c（a，b，c是实数，且a＜0）的图象的对称轴，（）A．若m＞1，则（m﹣1）a+b＞0B．若m＞1，则（m﹣1）a+b＜0C．若m＜1，则（m+1）a+b＞0D．若m＜1，则（m+1）a+b＜0【考点】二次函数图象与系数的关系．【分析】由对称轴x＝﹣＝1得：b＝﹣2a，根据有理数的乘法，可得答案．【解答】解：由对称轴x＝﹣＝1得：b＝﹣2a．（m+1）a+b＝ma+a﹣2a＝（m﹣1）a，当m＞1时，（m﹣1）a+b＝（m﹣1）a﹣2a＝（m﹣3）a，（m﹣1）a+b与0无法判断．当m＜1时，（m+1）a+b＝（m+1）a﹣2a＝（m﹣1）a＞0．故选：C．【点评】本题考查了二次函数图象与系数的关系，利用对称轴得出b＝﹣2a是解题关键．6．（2021•杭州）在“探索函数y＝ax2+bx+c的系数a，b，c与图象的关系”活动中，老师给出了直角坐标系中的四个点：A（0，2），B（1，0），C（3，1），D（2，3）．同学们探索了经过这四个点中的三个点的二次函数图象，发现这些图象对应的函数表达式各不相同，其中a的值最大为（）A．B．C．D．【考点】二次函数图象与系数的关系．【专题】函数思想；应用意识．【分析】比较任意三个点组成的二次函数，比较开口方向，开口向下，则a＜0，只需把开口向上的二次函数解析式求出即可．【解答】解：由图象知，A、B、D组成的二次函数图象开口向上，a＞0；A、B、C组成的二次函数开口向上，a＞0；B、C、D三点组成的二次函数开口向下，a＜0；A、D、C三点组成的二次函数开口向下，a＜0；即只需比较A、B、D组成的二次函数和A、B、C组成的二次函数即可．设A、B、C组成的二次函数为y1＝a1x2+b1x+c1，把A（0，2），B（1，0），C（3，1）代入上式得，，解得a1＝；设A、B、D组成的二次函数为y＝ax2+bx+c，把A（0，2），B（1，0），D（2，3）代入上式得，，解得a＝，即a最大的值为，也可以根据a的绝对值越大开口越小直接代入ABD三点计算，即可求求解．故选：A．【点评】本题考查待定系数法求函数解析式，解本题的关键要熟练掌握二次函数的性质和待定系数法求函数的解析式．7．（2019•绍兴）在平面直角坐标系中，抛物线y＝（x+5）（x﹣3）经变换后得到抛物线y ＝（x+3）（x﹣5），则这个变换可以是（）A．向左平移2个单位B．向右平移2个单位C．向左平移8个单位D．向右平移8个单位【考点】二次函数图象与几何变换．【专题】二次函数图象及其性质．【分析】根据变换前后的两抛物线的顶点坐标找变换规律．【解答】解：y＝（x+5）（x﹣3）＝（x+1）2﹣16，顶点坐标是（﹣1，﹣16）．y＝（x+3）（x﹣5）＝（x﹣1）2﹣16，顶点坐标是（1，﹣16）．所以将抛物线y＝（x+5）（x﹣3）向右平移2个单位长度得到抛物线y＝（x+3）（x﹣5），故选：B．【点评】此题主要考查了二次函数图象与几何变换，要求熟练掌握平移的规律：左加右减，上加下减．8．（2019•衢州）二次函数y＝（x﹣1）2+3图象的顶点坐标是（）A．（1，3）B．（1，﹣3）C．（﹣1，3）D．（﹣1，﹣3）【考点】二次函数的性质．【专题】二次函数图象及其性质．【分析】由抛物线顶点式可求得答案．【解答】解：∵y＝（x﹣1）2+3，∴顶点坐标为（1，3），故选：A．【点评】本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y ＝a（x﹣h）2+k中，对称轴为x＝h，顶点坐标为（h，k）．9．（2020•宁波）如图，二次函数y＝ax2+bx+c（a＞0）的图象与x轴交于A，B两点，与y 轴正半轴交于点C，它的对称轴为直线x＝﹣1．则下列选项中正确的是（）A．abc＜0B．4ac﹣b2＞0C．c﹣a＞0D．当x＝﹣n2﹣2（n为实数）时，y≥c【考点】二次函数图象与系数的关系；二次函数图象上点的坐标特征；抛物线与x轴的交点．【专题】二次函数图象及其性质；运算能力．【分析】由图象开口向上，可知a＞0，与y轴的交点在x轴的上方，可知c＞0，根据对称轴方程得到b＞0，于是得到abc＞0，故A错误；根据二次函数y＝ax2+bx+c（a＞0）的图象与x轴的交点，得到b2﹣4ac＞0，求得4ac﹣b2＜0，故B错误；根据对称轴方程得到b＝2a，当x＝﹣1时，y＝a﹣b+c＜0，于是得到c﹣a＜0，故C错误；当x＝﹣n2﹣2（n为实数）时，代入解析式得到y＝ax2+bx+c＝a（﹣n2﹣2）2+b（﹣n2﹣2）+c＝an2（n2+2）+c，于是得到y＝an2（n2+2）+c≥c，故D正确．【解答】解：由图象开口向上，可知a＞0，与y轴的交点在x轴的上方，可知c＞0，又对称轴方程为x＝﹣1，所以﹣＜0，所以b＞0，∴abc＞0，故A错误；∵二次函数y＝ax2+bx+c（a＞0）的图象与x轴交于A，B两点，∴b2﹣4ac＞0，∴4ac﹣b2＜0，故B错误；∵﹣＝﹣1，∴b＝2a，∵当x＝﹣1时，y＝a﹣b+c＜0，∴a﹣2a+c＜0，∴c﹣a＜0，故C错误；当x＝﹣n2﹣2（n为实数）时，y＝ax2+bx+c＝a（﹣n2﹣2）2+b（﹣n2﹣2）+c＝an2（n2+2）+c，∵a＞0，n2≥0，n2+2＞0，∴y＝an2（n2+2）+c≥c，故D正确，故选：D．【点评】本题主要考查二次函数的图象和性质．熟练掌握图象与系数的关系以及二次函数与方程的关系是解题的关键．10．（2020•温州）已知（﹣3，y1），（﹣2，y2），（1，y3）是抛物线y＝﹣3x2﹣12x+m上的点，则（）A．y3＜y2＜y1B．y3＜y1＜y2C．y2＜y3＜y1D．y1＜y3＜y2【考点】二次函数图象上点的坐标特征．【专题】二次函数图象及其性质；运算能力．【分析】求出抛物线的对称轴为直线x＝﹣2，然后根据二次函数的增减性和对称性解答即可．【解答】解：抛物线的对称轴为直线x＝﹣＝﹣2，∵a＝﹣3＜0，∴x＝﹣2时，函数值最大，又∵﹣3到﹣2的距离比1到﹣2的距离小，∴y3＜y1＜y2．故选：B．【点评】本题考查了二次函数图象上点的坐标特征，主要利用了二次函数的增减性和对称性，求出对称轴是解题的关键．11．（2019•湖州）已知a，b是非零实数，|a|＞|b|，在同一平面直角坐标系中，二次函数y1＝ax2+bx与一次函数y2＝ax+b的大致图象不可能是（）A．B．C．D．【考点】二次函数的图象；一次函数的图象．【专题】一次函数及其应用；二次函数图象及其性质．【分析】根据二次函数y＝ax2+bx与一次函数y＝ax+b（a≠0）可以求得它们的交点坐标，然后根据一次函数的性质和二次函数的性质，由函数图象可以判断a、b的正负情况，从而可以解答本题．【解答】解：解得或．故二次函数y＝ax2+bx与一次函数y＝ax+b（a≠0）在同一平面直角坐标系中的交点在x 轴上为（﹣，0）或点（1，a+b）．在A中，由一次函数图象可知a＞0，b＞0，二次函数图象可知，a＞0，b＞0，﹣＜0，a+b＞0，故选项A有可能；在B中，由一次函数图象可知a＞0，b＜0，二次函数图象可知，a＞0，b＜0，由|a|＞|b|，则a+b＞0，故选项B有可能；在C中，由一次函数图象可知a＜0，b＜0，二次函数图象可知，a＜0，b＜0，a+b＜0，故选项C有可能；在D中，由一次函数图象可知a＜0，b＞0，二次函数图象可知，a＜0，b＞0，由|a|＞|b|，则a+b＜0，故选项D不可能；故选：D．【点评】本题考查二次函数的图象、一次函数的图象，解题的关键是明确二次函数与一次函数图象的特点．12．（2018•湖州）在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y＝ax2﹣x+2（a≠0）与线段MN有两个不同的交点，则a的取值范围是（）A．a≤﹣1或≤a＜B．≤a＜C．a≤或a＞D．a≤﹣1或a≥【考点】二次函数图象与系数的关系；二次函数图象上点的坐标特征．【专题】二次函数图象及其性质．【分析】根据二次函数的性质分两种情形讨论求解即可；【解答】解：∵抛物线的解析式为y＝ax2﹣x+2．观察图象可知当a＜0时，x＝﹣1时，y≤2时，且﹣≥﹣，满足条件，可得a≤﹣1；当a＞0时，x＝2时，y≥1，且抛物线与直线MN有交点，且﹣≤2满足条件，∴a≥，∵直线MN的解析式为y＝﹣x+，由，消去y得到，3ax2﹣2x+1＝0，∵Δ＞0，∴a＜，∴≤a＜满足条件，综上所述，满足条件的a的值为a≤﹣1或≤a＜，故选：A．【点评】本题考查二次函数的应用，二次函数的图象上的点的特征等知识，解题的关键是灵活运用所学知识解决问题，学会用转化的思想思考问题，属于中考常考题型．13．（2017•绍兴）矩形ABCD的两条对称轴为坐标轴，点A的坐标为（2，1），一张透明纸上画有一个点和一条抛物线，平移透明纸，使这个点与点A重合，此时抛物线的函数表达式为y＝x2，再次平移透明纸，使这个点与点C重合，则该抛物线的函数表达式变为（）A．y＝x2+8x+14B．y＝x2﹣8x+14C．y＝x2+4x+3D．y＝x2﹣4x+3【考点】二次函数图象与几何变换．【分析】先由对称计算出C点的坐标，再根据平移规律求出新抛物线的解析式即可解题．【解答】解：∵矩形ABCD的两条对称轴为坐标轴，∴矩形ABCD关于坐标原点对称，∵A点C点是对角线上的两个点，∴A点、C点关于坐标原点对称，∴C点坐标为（﹣2，﹣1）；∴透明纸由A点平移至C点，抛物线向左平移了4个单位，向下平移了2个单位；∵透明纸经过A点时，函数表达式为y＝x2，∴透明纸经过C点时，函数表达式为y＝（x+4）2﹣2＝x2+8x+14故选：A．【点评】主要考查了函数图象的平移，抛物线与坐标轴的交点坐标的求法，要求熟练掌握平移的规律：左加右减，上加下减，并用规律求函数解析式．14．（2021•湖州）已知抛物线y＝ax2+bx+c（a≠0）与x轴的交点为A（1，0）和B（3，0），点P1（x1，y1），P2（x2，y2）是抛物线上不同于A，B的两个点，记△P1AB的面积为S1，△P2AB的面积为S2，有下列结论：①当x1＞x2+2时，S1＞S2；②当x1＜2﹣x2时，S1＜S2；③当|x1﹣2|＞|x2﹣2|＞1时，S1＞S2；④当|x1﹣2|＞|x2+2|＞1时，S1＜S2．其中正确结论的个数是（）A．1B．2C．3D．4【考点】抛物线与x轴的交点；二次函数图象上点的坐标特征．【专题】二次函数图象及其性质；推理能力．【分析】不妨假设a＞0，利用图象法一一判断即可．【解答】解：方法一：不妨假设a＞0．①如图1中，P1，P2满足x1＞x2+2，∵P1P2∥AB，∴S1＝S2，故①错误．②当x1＝﹣2，x2＝﹣1，满足x1＜2﹣x2，则S1＞S2，故②错误，③∵|x1﹣2|＞|x2﹣2|＞1，∴P1，P2在x轴的上方，且P1离x轴的距离比P2离x轴的距离大，∴S1＞S2，故③正确，④如图2中，P1，P2满足|x1﹣2|＞|x2+2|＞1，但是S1＝S2，故④错误．故选：A．方法二：解：∵抛物线y＝ax2+bx+c与x轴的交点为A（1，0）和B（3，0），∴该抛物线对称轴为x＝2，当x1＞x2+2时与当x1＜2﹣x2时无法确定P1（x1，y1），P2（x2，y2）在抛物线上的对应位置，故①和②都不正确；当|x1﹣2|＞|x2﹣2|＞1时，P1（x1，y1）比P2（x2，y2）离对称轴更远，且同在x轴上方或者下方，∴|y1|＞|y2|，∴S1＞S2，故③正确；当|x1﹣2|＞|x2+2|＞1时，即在x轴上x1到2的距离比x2到﹣2的距离大，且都大于1，可知在x轴上x1到2的距离大于1，x2到﹣2的距离大于1，但x2到2的距离不能确定，所以无法比较P1（x1，y1）比P2（x2，y2）谁离对称轴更远，故无法比较面积，故④错误；故选：A．【点评】本题考查抛物线与x轴的交点，二次函数图象上的点的特征等知识，解题的关键是学会利用图象法解决问题，属于中考选择题中的压轴题．15．（2020•嘉兴）已知二次函数y＝x2，当a≤x≤b时m≤y≤n，则下列说法正确的是（）A．当n﹣m＝1时，b﹣a有最小值B．当n﹣m＝1时，b﹣a有最大值C．当b﹣a＝1时，n﹣m无最小值D．当b﹣a＝1时，n﹣m有最大值【考点】二次函数的性质；二次函数的最值．【专题】函数的综合应用；几何直观；运算能力．【分析】方法1、①当b﹣a＝1时，当a，b同号时，先判断出四边形BCDE是矩形，得出BC＝DE＝b﹣a＝1，CD＝BE＝m，进而得出AC＝n﹣m，即tan∠ABC＝n﹣m，再判断出45°≤∠ABC＜90°，即可得出n﹣m的范围，当a，b异号时，m＝0，当a＝﹣，b＝时，n最小＝，即可得出n﹣m的范围；②当n﹣m＝1时，当a，b同号时，同①的方法得出NH＝PQ＝b﹣a，HQ＝PN＝m，进而得出MH＝n﹣m＝1，而tan∠MHN＝，再判断出45°≤∠MNH＜90°，当a，b 异号时，m＝0，则n＝1，即可求出a，b，即可得出结论．方法2、根据抛物线的性质判断，即可得出结论．【解答】解：方法1、①当b﹣a＝1时，当a，b同号时，如图1，过点B作BC⊥AD于C，∴∠BCD＝90°，∵∠ADE＝∠BED＝90°，∴∠ADE＝∠BCD＝∠BED＝90°，∴四边形BCDE是矩形，∴BC＝DE＝b﹣a＝1，CD＝BE＝m，∴AC＝AD﹣CD＝n﹣m，在Rt△ACB中，tan∠ABC＝＝n﹣m，∵点A，B在抛物线y＝x2上，且a，b同号，∴45°≤∠ABC＜90°，∴tan∠ABC≥1，∴n﹣m≥1，当a，b异号时，m＝0，当a＝﹣，b＝时，n＝，此时，n﹣m＝，∴≤n﹣m＜1，即n﹣m≥，即n﹣m无最大值，有最小值，最小值为，故选项C，D都错误；②当n﹣m＝1时，如图2，当a，b同号时，过点N作NH⊥MQ于H，同①的方法得，NH＝PQ＝b﹣a，HQ＝PN＝m，∴MH＝MQ﹣HQ＝n﹣m＝1，在Rt△MHN中，tan∠MNH＝＝，∵点M，N在抛物线y＝x2上，∴m≥0，当m＝0时，n＝1，∴点N（0，0），M（1，1），∴NH＝1，此时，∠MNH＝45°，∴45°≤∠MNH＜90°，∴tan∠MNH≥1，∴≥1，当a，b异号时，m＝0，∴n＝1，∴a＝﹣1，b＝1，即b﹣a＝2，∴b﹣a无最小值，有最大值，最大值为2，故选项A错误；故选：B．方法2、当n﹣m＝1时，当a，b在y轴同侧时，a，b都越大时，a﹣b越接近于0，但不能取0，即b﹣a没有最小值，当a，b异号时，当a＝﹣1，b＝1时，b﹣a＝2最大，当b﹣a＝1时，当a，b在y轴同侧时，a，b离y轴越远，n﹣m越大，但取不到最大，当a，b在y轴两侧时，当a＝﹣，b＝时，n﹣m取到最小，最小值为，因此，只有选项B正确，故选：B．【点评】此题主要考查了二次函数的性质，矩形的判定和性质，锐角三角函数，确定出∠MNH的范围是解本题的关键．16．（2019•舟山）小飞研究二次函数y＝﹣（x﹣m）2﹣m+1（m为常数）性质时得到如下结论：①这个函数图象的顶点始终在直线y＝﹣x+1上；②存在一个m的值，使得函数图象的顶点与x轴的两个交点构成等腰直角三角形；③点A（x1，y1）与点B（x2，y2）在函数图象上，若x1＜x2，x1+x2＞2m，则y1＜y2；④当﹣1＜x＜2时，y随x的增大而增大，则m的取值范围为m≥2．其中错误结论的序号是（）A．①B．②C．③D．④【考点】二次函数图象与系数的关系；二次函数图象上点的坐标特征；抛物线与x轴的交点；等腰直角三角形；一次函数图象上点的坐标特征．【专题】数形结合；二次函数图象及其性质．【分析】根据函数解析式，结合函数图象的顶点坐标、对称轴以及增减性依次对4个结论作出判断即可．【解答】解：二次函数y＝﹣（x﹣m）2﹣m+1（m为常数）①∵顶点坐标为（m，﹣m+1）且当x＝m时，y＝﹣m+1∴这个函数图象的顶点始终在直线y＝﹣x+1上故结论①正确；②假设存在一个m的值，使得函数图象的顶点与x轴的两个交点构成等腰直角三角形令y＝0，得﹣（x﹣m）2﹣m+1＝0，其中m≤1解得：x1＝m﹣，x2＝m+∵顶点坐标为（m，﹣m+1），且顶点与x轴的两个交点构成等腰直角三角形∴|﹣m+1|＝|m﹣（m﹣）|解得：m＝0或1，当m＝1时，二次函数y＝﹣（x﹣1）2，此时顶点为（1，0），与x轴的交点也为（1，0），不构成三角形，舍去；∴存在m＝0，使得函数图象的顶点与x轴的两个交点构成等腰直角三角形故结论②正确；③∵x1+x2＞2m∴∵二次函数y＝﹣（x﹣m）2﹣m+1（m为常数）的对称轴为直线x＝m∴点A离对称轴的距离小于点B离对称轴的距离∵x1＜x2，且a＝﹣1＜0∴y1＞y2故结论③错误；④当﹣1＜x＜2时，y随x的增大而增大，且a＝﹣1＜0∴m的取值范围为m≥2．故结论④正确．故选：C．【点评】本题主要考查了二次函数图象与二次函数的系数的关系，是一道综合性比较强的题目，需要利用数形结合思想解决本题．二．填空题（共4小题）17．（2018•湖州）如图，在平面直角坐标系xOy中，已知抛物线y＝ax2+bx（a＞0）的顶点为C，与x轴的正半轴交于点A，它的对称轴与抛物线y＝ax2（a＞0）交于点B．若四边形ABOC是正方形，则b的值是﹣2．【考点】抛物线与x轴的交点；正方形的性质；二次函数的性质；二次函数图象上点的坐标特征．【专题】二次函数图象及其性质；矩形菱形正方形．【分析】根据正方形的性质结合题意，可得出点B的坐标为（﹣，﹣），再利用二次函数图象上点的坐标特征即可得出关于b的方程，解之即可得出结论．【解答】解：∵四边形ABOC是正方形，∴点B的坐标为（﹣，﹣）．∵抛物线y＝ax2过点B，∴﹣＝a（﹣）2，解得：b1＝0（舍去），b2＝﹣2．故答案为：﹣2．【点评】本题考查了抛物线与x轴的交点、二次函数图象上点的坐特征以及正方形的性质，利用正方形的性质结合二次函数图象上点的坐标特征，找出关于b的方程是解题的关键．18．（2017•金华）在一空旷场地上设计一落地为矩形ABCD的小屋，AB+BC＝10m，拴住小狗的10m长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S（m2）．（1）如图1，若BC＝4m，则S＝88πm2．（2）如图2，现考虑在（1）中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其他条件不变，则在BC的变化过程中，当S取得最小值时，边BC的长为m．【考点】二次函数的应用；等边三角形的判定与性质；矩形的性质．【分析】（1）小狗活动的区域面积为以B为圆心、10为半径的圆，以C为圆心、6为半径的圆和以A为圆心、4为半径的圆的面积和，据此列式求解可得；（2）此时小狗活动的区域面积为以B为圆心、10为半径的圆，以A为圆心、x为半径的圆、以C为圆心、10﹣x为半径的圆的面积和，列出函数解析式，由二次函数的性质解答即可．【解答】解：（1）如图1，拴住小狗的10m长的绳子一端固定在B点处，小狗可以活动的区域如图所示：由图可知，小狗活动的区域面积为以B为圆心、10为半径的圆，以C为圆心、6为半径的圆和以A为圆心、4为半径的圆的面积和，∴S＝×π•102+•π•62+•π•42＝88π，故答案为：88π；（2）如图2，设BC＝x，则AB＝10﹣x，∴S＝•π•102+•π•x2+•π•（10﹣x）2＝（x2﹣5x+250）＝（x﹣）2+，当x＝时，S取得最小值，∴BC＝，故答案为：．【点评】本题主要考查二次函数的应用，解题的关键是根据绳子的长度结合图形得出其活动区域及利用扇形的面积公式表示出活动区域面积．19．（2021•台州）以初速度v（单位：m/s）从地面竖直向上抛出小球，从抛出到落地的过程中，小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系式是h＝vt ﹣4.9t2．现将某弹性小球从地面竖直向上抛出，初速度为v1，经过时间t1落回地面，运动过程中小球的最大高度为h1（如图1）；小球落地后，竖直向上弹起，初速度为v2，经过时间t2落回地面，运动过程中小球的最大高度为h2（如图2）．若h1＝2h2，则t1：t2＝：1．【考点】二次函数的应用；解直角三角形．【专题】二次函数的应用；推理能力．【分析】利用h＝vt﹣4.9t2，求出t1，t2，再根据h1＝2h2，求出v1＝v2，可得结论．【解答】解：由题意，t1＝，t2＝，h1＝＝，h2＝＝，∵h1＝2h2，∴v1＝v2，∴t1：t2＝v1：v2＝：1，故答案为：：1．【点评】本题考查二次函数的应用，解题的关键是求出t1，t2，证明v1＝v2即可．20．（2021•湖州）已知在平面直角坐标系xOy中，点A的坐标为（3，4），M是抛物线y＝ax2+bx+2（a≠0）对称轴上的一个动点．小明经探究发现：当的值确定时，抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定，若抛物线y＝ax2+bx+2（a ≠0）的对称轴上存在3个不同的点M，使△AOM为直角三角形，则的值是2或﹣8．【考点】二次函数的性质；二次函数图象上点的坐标特征；勾股定理的逆定理．【专题】二次函数图象及其性质；等腰三角形与直角三角形；推理能力．【分析】由题意△AOM是直角三角形，当对称轴x≠0或x≠3时，可知一定存在两个以A，O为直角顶点的直角三角形，当对称轴x＝0或x＝3时，不存在满足条件的点M，当以OA为直径的圆与抛物线的对称轴x＝﹣相切时，对称轴上存在1个以点M为直角顶点的直角三角形，此时对称轴上存在3个不同的点M，使△AOM为直角三角形，利用图象法求解即可．【解答】解：∵△AOM是直角三角形，∴当对称轴x≠0或x≠3时，一定存在两个以A，O为直角顶点的直角三角形，且点M 在对称轴上的直角三角形，当对称轴x＝0或x＝3时，不存在满足条件的点M，∴当以OA为直径的圆与抛物线的对称轴x＝﹣相切时，对称轴上存在1个以M为直角顶点的直角三角形，此时对称轴上存在3个不同的点M，使△AOM为直角三角形（如图所示）．观察图象可知，﹣＝﹣1或4，∴＝2或﹣8，故答案为：2或﹣8．【点评】本题考查二次函数的性质，直角三角形的判定，圆周角定理等知识，解题的关键是判断出对称轴的位置，属于中考填空题中的压轴题．三．解答题（共3小题）21．（2021•宁波）如图，二次函数y＝（x﹣1）（x﹣a）（a为常数）的图象的对称轴为直线x＝2．（1）求a的值．（2）向下平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式．。
2017二次函数中考试题分类汇编
2017二次函数中考试题分类汇编2017二次函数中考试题分类汇编一、选择题1、已知二次函数)0(2≠++=a c bx ax y 的图象如下图1所示，有下列5个结论：① 0>abc ；② c a b +<；③ 024>++c b a ；④ b c 32<；⑤ )(b am m b a +>+，（1≠m 的实数）其中正确的结论有（ ）A. 2个 B. 3个 C. 4个 D. 5个2、如上图2是二次函数y ＝ax 2＋bx ＋c 图象的一部分，图象过点A （－3，0），对称轴为x ＝－1．给出四个结论：①b 2＞4ac ；②2a ＋b =0；③a －b ＋c =0；④5a ＜b ．其中正确结论 是（ ）．（A ）②④（B ）①④（C ）②③（D ）①③3、二次函数221y x x =-+与x 轴的交点个数是（ ）A ．0B ．1C ．2D ．34、在同一坐标系中一次函数y ax b =+和二次函数2y ax bx =+的图象可能为（ ）5、已知二次函数2y ax bx c =++(a ≠0)的图象开口向上，并经过点(-1，2)，(1，0) . 下列结论正确的是( ) A. 当x >0时，函数值y 随x 的增大而增大 B. 当x >0时，函数值y 随x 的增大而减小C. 存在一个负数x 0，使得当x <x 0时，函数值y 随x 的增大而减小；当x > x 0时，函数值y 随x 的增大而增大D. 存在一个正数x 0，使得当x <x 0时，函数值y 随x 的增大而减小；当x >x 0时，函数值y 随x 的增大而增大Oxy O xyOxy O xy6、已知二次函数y =x 2-x+a (a ＞0)，当自变量x 取m 时，其相应的函数值小于0，那么下列结论中正确的是（ ）(A) m -1的函数值小于0 (B) m -1的函数值大于0(C) m -1的函数值等于0 (D) m -1的函数值与0的大小关系不确定二、填空题1、二次函数y =ax 2＋bx ＋c 的图象如下图1所示，且P =| a －b ＋c |＋| 2a ＋b |，Q =| a ＋b ＋c |＋| 2a －b |，则P 、Q 的大小关系为 .3、如下图2所示的抛物线是二次函数2231y ax x a =-+-的图象，那么a 的值是 ．4、已知二次函数22y x x m =-++的部分图象如上图所示，则关于x 的一元二次方程220x x m -++=的解为 ．4、已知二次函数2y ax bx c =++的图象如上图所示，则点()P a bc ，在第 象限． 三、解答题：1、知一抛物线与x 轴的交点是)0,2(-A 、B （1，0），且经过点C （2，8）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2017二次函数中考试题分类汇编一、选择题1、已知二次函数)0(2≠++=a c bx ax y 的图象如下图1所示，有下列5个结论：① 0>abc ；② c a b +<；③ 024>++c b a ；④ b c 32<；⑤ )(b am m b a +>+，（1≠m 的实数）其中正确的结论有（ ）A. 2个 B. 3个 C. 4个 D. 5个2、如上图2是二次函数y ＝ax 2＋bx ＋c 图象的一部分，图象过点A （－3，0），对称轴为x ＝－1．给出四个结论：①b 2＞4ac ；②2a ＋b =0；③a －b ＋c =0；④5a ＜b ．其中正确结论 是（ ）．（A ）②④（B ）①④（C ）②③（D ）①③3、二次函数221y x x =-+与x 轴的交点个数是（ ）A ．0B ．1C ．2D ．34、在同一坐标系中一次函数y ax b =+和二次函数2y ax bx =+的图象可能为（ ）5、已知二次函数2y ax bx c =++(a ≠0)的图象开口向上，并经过点(-1，2)，(1，0) . 下列结论正确的是( ) A. 当x >0时，函数值y 随x 的增大而增大 B. 当x >0时，函数值y 随x 的增大而减小C. 存在一个负数x 0，使得当x <x 0时，函数值y 随x 的增大而减小；当x > x 0时，函数值y 随x 的增大而增大D. 存在一个正数x 0，使得当x <x 0时，函数值y 随x 的增大而减小；当x >x 0时，函数值y 随x 的增大而增大O xyOxyOxyOxyAB C D6、已知二次函数y =x 2-x+a (a ＞0)，当自变量x 取m 时，其相应的函数值小于0，那么下列结论中正确的是（ ）(A) m -1的函数值小于0 (B) m -1的函数值大于0(C) m -1的函数值等于0 (D) m -1的函数值与0的大小关系不确定 二、填空题1、二次函数y =ax 2＋bx ＋c 的图象如下图1所示，且P =| a －b ＋c |＋| 2a ＋b |，Q =| a ＋b ＋c |＋| 2a －b |，则P 、Q 的大小关系为 .3、如下图2所示的抛物线是二次函数2231y ax x a =-+-的图象，那么a 的值是 ．4、已知二次函数22y x x m =-++的部分图象如上图所示，则关于x 的一元二次方程220x x m -++=的解为 ．4、已知二次函数2y ax bx c =++的图象如上图所示，则点()P a bc ，在第 象限． 三、解答题：1、知一抛物线与x 轴的交点是)0,2(-A 、B （1，0），且经过点C （2，8）。
（1）求该抛物线的解析式；（2）求该抛物线的顶点坐标。
2、在直角坐标平面内，二次函数图象的顶点为(14)A -，，且过点(30)B ，．（1）求该二次函数的解析式；（2）将该二次函数图象向右平移几个单位，可使平移后所得图象经过坐标原点？并直接写出平移后所得图象与x 轴的另一个交点的坐标．图1xyO 第4题O yx图yO13（第3题）3、已知二次函数图象的顶点是(12)-，，且过点302⎛⎫⎪⎝⎭，．（1）求二次函数的表达式，并在下图中画出它的图象；（2）求证：对任意实数m ，点2()M m m -，都不在这个二次函数的图象上．5、如图，已知二次函数24y ax x c =-+的图像经过点A 和点B ．（1）求该二次函数的表达式；（2）写出该抛物线的对称轴及顶点坐标；（3）点P （m ，m ）与点Q 均在该函数图像上（其中m ＞0求m 的值及点Q 到x 轴的距离．4、二次函数2(0)=++≠的图象如图所示，根据图象解答下列问题：y ax bx c a（1）写出方程20++>的解集．ax bx c++=的两个根．（2）写出不等式20ax bx c（3）写出y随x的增大而减小的自变量x的取值范围．（4）若方程2++=有两个不相等的实数根，求k的取值范围．ax bx c k Array 6、在平面直角坐标系xOy中，已知二次函数2(0)=++≠的图象与x轴交于A By ax bx c a，两点（点A在点B的左边），与y轴交于点C，其顶点的横坐标为1，且过点(23)，和(312)，．--（1）求此二次函数的表达式；（2）若直线:(0)l y kx k=≠与线段BC交于点D（不与点B C，重合），则是否存在这样的直线l，使得以B O D，，为顶点的三角形与BAC△相似？若存在，求出该直线的函数表达式及点D的坐标；若不存在，请说明理由；（3）若点P是位于该二次函数对称轴右边图象上不与顶点重合的任意一点，试比较锐角∠的大小（不必证明），并写出此时点P∠与ACOPCO7、如图，矩形A ’BC ’O ’是矩形OABC(边OA 在x 轴正半轴上，边OC 在y 轴正半轴上)绕B 点逆时针旋转得到的．O ’点在x 轴的正半轴上，B 点的坐标为(1，3)．(1)如果二次函数y ＝ax 2＋bx ＋c(a ≠0)的图象经过O 、O ’两点且图象顶点M 的纵坐标为—1． 求这个二次函数的解析式；(2)在(1)中求出的二次函数图象对称轴的右支上是否存在点P ，使得ΔPOM 为直角三角形?若存在，请求出P 点的坐标和ΔPOM 的面积；若不存在，请说明理由； (3)求边C ’O ’所在直线的解析式．8、容积率t 是指在房地产开发中建筑面积与用地面积之比，即t =用地面积建筑面积S M ，为充分利用土地资源，更好地解决人们的住房需求，并适当的控制建筑物的高度，一般地容积率t 不小于1且不大于8.一房地产开发商在开发某小区时，结合往年开发经验知，建筑面积M （m 2）与容积率t 的关系可近似地用如图（1）中的线段l 来表示；1 m 2建筑面积上的资金投入Q （万元）与容积率t 的关系可近似地用如图（2）中的一段抛物线段c 来表示． （Ⅰ）试求图（1）中线段l 的函数关系式，并求出开发该小区的用地面积； （Ⅱ）求出图（2）中抛物线段c 的函数关系式.9、如图10，已知抛物线P：y=ax2+bx+c(a≠0) 与x轴交于A、B两点(点A在x轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：x …-3 -2 1 2 …y …-52-4 -520 …(1) 求A、B、C三点的坐标；(2) 若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m 的函数关系，并指出m的取值范围；(3) 当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM=k·DF，若点M不在抛物线P上，求k的取值范围.图1010、如图①，在平面直角坐标系中，点A 的坐标为(12)，，点B 的坐标为(31)，，二次函数2y x =的图象记为抛物线1l ．（1）平移抛物线1l ，使平移后的抛物线过点A ，但不过点B ，写出平移后的一个抛物线的函数表达式： （任写一个即可）．（2）平移抛物线1l ，使平移后的抛物线过A B ，两点，记为抛物线2l ，如图②，求抛物线2l 的函数表达式．（3）设抛物线2l 的顶点为C ，K 为y 轴上一点．若ABK ABC S S =△△，求点K 的坐标．（4）请在图③上用尺规作图的方式探究抛物线2l 上是否存在点P ，使ABP △为等腰三角形．若存在，请判断点P 共有几个可能的位置（保留作图痕迹）；若不存在，请说明师．x图①x图②x图③11、如图，抛物线223=--与x轴交A、B两点（A点在B点左侧），直线l与抛物线交y x x于A、C两点，其中C点的横坐标为2。
（1）求A、B 两点的坐标及直线AC的函数表达式；（2）P是线段AC上的一个动点，过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值；（3）点G抛物线上的动点，在x轴上是否存在点F，使A、C、F、G这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F点坐标；如果不存在，请说明理由。
2017二次函数中考试题分类汇编答案6、（2）假设存在直线:(0)l y kx k =≠与线段BC 交于点D （不与点B C ，重合），使得以B O D ，，为顶点的三角形与BAC △相似．在223y x x =-++中，令0y =，则由2230x x -++=，解得1213x x =-=，(10)(30)A B ∴-，，，．令0x =，得3y =．(03)C ∴，．设过点O 的直线l 交BC 于点D ，过点D 作DE x ⊥点B 的坐标为(30)，，点C 的坐标为(03)，，点A 4345.AB OB OC OBC ∴===∠=，，BC ∴==要使BOD BAC △∽△或BDO BAC △∽△， 已有B B ∠=∠，则只需BD BO BCBA=， ①或.BO BD BCBA=② 成立．若是①，则有344BO BC BD BA ⨯===．而45OBC BE DE ∠=∴=，． ∴在Rt BDE △中，由勾股定理，得222222BE DE BE BD +===⎝⎭．解得 94BE DE ==（负值舍去）．93344OE OB BE ∴=-=-=．∴点D 的坐标为3944⎛⎫⎪⎝⎭，．将点D 的坐标代入(0)y kx k =≠中，求得3k =．∴满足条件的直线l 的函数表达式为3y x =．［或求出直线AC 的函数表达式为33y x =+，则与直线AC 平行的直线l 的函数表达式为3y x =．此时易知BOD BAC △∽△，再求出直线BC 的函数表达式为3y x =-+．联立33y x y x ==-+，求得点D 的坐标为3944⎛⎫⎪⎝⎭，．］若是②，则有332BO BA BD BC ⨯===45OBC BE DE ∠=∴=，．∴在Rt BDE △中，由勾股定理，得222222(22)BE DE BE BD +===．解得 2BE DE ==（负值舍去）．321OE OB BE ∴=-=-=．∴点D 的坐标为(12)，． 将点D 的坐标代入(0)y kx k =≠中，求得2k =．∴满足条件的直线l 的函数表达式为2y x =．∴存在直线:3l y x =或2y x =与线段BC 交于点D （不与点B C ，重合），使得以B O D ，，为顶点的三角形与BAC △相似，且点D 的坐标分别为3944⎛⎫⎪⎝⎭，或(12)，．（3）设过点(03)(10)C E ，，，的直线3(0)y kx k =+≠与该二次函数的图象交于点P ． 将点(10)E ，的坐标代入3y kx =+中，求得3k =-．∴此直线的函数表达式为33y x =-+． 设点P 的坐标为(33)x x -+，，并代入223y x x =-++，得250x x -=． 解得1250x x ==，（不合题意，舍去）．512x y ∴==-，．∴点P 的坐标为(512)-，．此时，锐角PCO ACO ∠=∠．又二次函数的对称轴为1x =，∴点C 关于对称轴对称的点C '的坐标为(23)，．∴当5p x >时，锐角PCO ACO ∠<∠；当5p x =时，锐角PCO ACO ∠=∠；当25p x <<时，锐角PCO ACO ∠>∠．7、xBEA O C1x =PC '·8、解：（Ⅰ）设线段l 函数关系式为M =kt +b ，由图象得⎩⎨⎧=+=+.800006,280002b k b k 解之，得⎩⎨⎧==.2000,13000b k∴线段l 的函数关系式为M ＝13000t +2000, 1≤t ≤8. 由t =用地面积建筑面积S M 知，当t =1时，S 用地面积=M 建筑面积，把t =1代入M ＝13000t +2000中，得M =15000 m 2.即开发该小区的用地面积是15000 m 2. （Ⅱ）根据图象特征可设抛物线段c 的函数关系式为Q ＝a ( t －4)2+k , 把点（4,0.09）,（1,0.18）代入，得 ⎩⎨⎧=+-=.18.0)41(,09.02k a k 解之，得⎪⎪⎩⎪⎪⎨⎧==.1009,1001k a ∴抛物线段c 的函数关系式为 Q ＝1001( t －4)2+1009,即Q ＝1001t 2-252t +41, 1≤t ≤8.9、解：⑴ 解法一：设2(0)y ax bx c a，任取x ,y 的三组值代入，求出解析式2142y x x，令y =0，求出124,2x x ；令x =0，得y =-4，∴ A 、B 、C 三点的坐标分别是A (2，0)，B (-4，0)，C (0，-4) . ⑵ 由题意，AD DGAOOC，而AO =2，OC =4，AD =2-m ，故DG =4-2m ， 又BEEFBOOC，EF =DG ，得BE =4-2m ，∴ DE =3m ，∴S DEFG =DG ·DE =(4-2m ) 3m =12m -6m 2 (0＜m ＜2) . ⑶ ∵S DEFG =12m -6m 2 (0＜m ＜2)，∴m =1时，矩形的面积最大，且最大面积是6 . 当矩形面积最大时，其顶点为D (1，0)，G (1，-2)，F (-2，-2)，E (-2，0)，设直线DF 的解析式为y =kx +b ，易知，k =23，b =-23，∴2233y x ， 又可求得抛物线P 的解析式为：2142y x x，令2233x=2142x x，可求出x =1613.设射线DF 与抛物线P 相交于点N ，则N 的横坐标为1613，过N 作x 轴的垂线交x 轴于H ，有FN HEDF DE=161233=5619，点M 不在抛物线P 上，即点M 不与N 重合时，此时k 的取值范围是k ≠5619且k ＞0.11、解：（1）令y=0，解得11x =-或23x = ∴A （－1，0）B （3，0）； 将C 点的横坐标x =2代入223y x x =--得y=－3，∴C （2，－3）∴直线AC 的函数解析式是y=－x －1 （2）设P 点的横坐标为x （－1≤x ≤2） 则P 、E 的坐标分别为：P （x ，－x －1），E （2(,23)x x x -- ∵P 点在E 点的上方，PE=22(1)(23)2x x x x x -----=-++；∴当12x =时，PE 的最大值=94（3）存在4个这样的点F ，分别是1234(1,0),(3,0),(4(4F F F F -。