大学物理学第三版修订版下册第11章答案
大学物理第十一章气体动理论习题详细答案

第十一章 气体动理论习题详细答案一、选择题1、答案:B解:根据速率分布函数()f v 的统计意义即可得出。
()f v 表示速率以v 为中心的单位速率区间内的气体分子数占总分子数的比例,而dv v Nf )(表示速率以v 为中心的dv 速率区间内的气体分子数,故本题答案为B 。
2、答案:A解:根据()f v 的统计意义和p v 的定义知,后面三个选项的说法都是对的,后面三个选项的说法都是对的,而只有而只有A 不正确,气体分子可能具有的最大速率不是p v ,而可能是趋于无穷大,所以答案A 正确。
正确。
3、答案: A 解:2rms 1.73RT v v M ==,据题意得222222221,16H O H H H O O O T T T M M M T M ===,所以答案A 正确。
正确。
4、 由理想气体分子的压强公式23k p n e =可得压强之比为:可得压强之比为:A p ∶B p ∶C p =n A kA e ∶n B kB e ∶n C kC e =1∶1∶1 5、 氧气和氦气均在标准状态下,二者温度和压强都相同,而氧气的自由度数为5,氦气的自由度数为3,将物态方程pV RT n =代入内能公式2iE RT n =可得2iE pV =,所以氧气和氦气的内能之比为5 : 6,故答案选C 。
6、 解:理想气体状态方程PV RTn =,内能2iU RT n =(0m M n =)。
由两式得2UiP V =,A 、B 两种容积两种气体的压强相同,A 中,3i =;B 中,5i =,所以答案A 正确。
正确。
7、 由理想气体物态方程'm pV RT M=可知正确答案选D 。
8、 由理想气体物态方程pV NkT =可得气体的分子总数可以表示为PV N kT =,故答案选C 。
9、理想气体温度公式21322k m kT e u ==给出了温度与分子平均平动动能的关系,表明温度是气体分子的平均平动动能的量度。
大学物理第十一章波动光学习题答案

第十一章 波动光学习题11-1 在杨氏双缝实验中,双缝间距d =0.20 mm ,缝屏间距D =1.0 m ,若第2级明条纹离屏中心的距离为6.0 mm ,试求:(1)入射光的波长;(2)相邻两明条纹间的距离。
解:(1)由λk d D x =明知, λ22.01010.63⨯⨯= 30.610m m 600n m λ-=⨯= (2)3106.02.010133=⨯⨯⨯==∆-λd D x mm 11-2 在双缝装置中,用一很薄的云母片(n =1.58)覆盖其中的一条缝,结果使屏幕上的第7级明条纹恰好移到屏幕中央原零级明纹的位置。
若入射光的波长为550 nm ,求此云母片的厚度。
解:设云母片厚度为e ,则由云母片引起的光程差为e n e ne )1(-=-=δ 按题意 λδ7= ∴610106.6158.1105500717--⨯=-⨯⨯=-=n e λm 6.6=m μ 11-3 在折射率n 1=1.52的镜头表面涂有一层折射率n 2=1.38的MgF 2增透膜,如果此膜适用于波长λ=550 nm 的光,问膜的最小厚度应取何值?解:设光垂直入射增透膜,欲透射增强,则膜上、下两表面反射光应满足干涉相消条件,即λ)21(22+=k e n ),2,1,0(⋅⋅⋅=k 222422)21(n n k n k e λλλ+=+=)9961993(38.14550038.125500+=⨯+⨯=k k o A令0=k ,得膜的最薄厚度为996o A 。
11-4 白光垂直照射在空气中厚度为0.4μm 的玻璃片上,玻璃的折射率为1.50。
试问在可见光范围内(λ= 400~700nm ),哪些波长的光在反射中增强?哪些波长的光在透射中增强?解:(1)222n d j λδλ=+= 24 3,480n m 21n d j j λλ===- (2)22(21) 22n d j λλδ=+=+ 22n d j λ= 2,600n m j λ==;3,400nm j λ== 11-5 白光垂直照射到空气中一厚度为380 nm 的肥皂膜上,设肥皂膜的折射率为1.33,试问该膜的正面呈现什么颜色?背面呈现什么颜色? 解:由反射干涉相长公式有42221ne ne k k λδλλ=+==-, ),2,1(⋅⋅⋅=k 得4 1.3338002674nm 2214 1.3338003404nm 231k k λλ⨯⨯===⨯-⨯⨯===⨯-,红色,紫色所以肥皂膜正面呈现紫红色。
大学物理学第三版(上海交大)下册习题答案

第十一章习题11-1.直角三角形ABC 的A 点上,有电荷C 108.191-⨯=q ,B 点上有电荷C 108.492-⨯-=q ,试求C 点的电场强度(设m 03.0m ,04.0==AC BC ).解:1q 在C 点产生的场强 20114ACq E πε=2q 在C 点产生的场强 22204q E BC πε=C 点的合场强 43.2410VE m==⨯ 方向如图11-2. 用细的塑料棒弯成半径为cm 50的圆环,两端间空隙为cm 2,电量为C 1012.39-⨯的正电荷均匀分布在棒上,求圆心处电场强度的大小和方向.解: 棒长 m d r l 12.32=-=π电荷线密度 19100.1--⋅⨯==m C lqλ若有一均匀带电闭合线圈,则圆心处的合场强为0,有一段空隙,则圆心处场强等于闭合线圈产生电场再减去m d 02.0=长的带电棒在该点产生的场强。
由于r d ,该小段可看成点电荷 C d q 11100.2-⨯=='λ圆心处场强 1211920072.0)5.0(100.2100.94--⋅=⨯⨯⨯='=m V r q E πε 方向由缝隙指向圆心处11-3. 将一“无限长”带电细线弯成图示形状,设电荷均匀分布,电荷线密度为λ,四分之一圆弧AB 的半径为R ,试求圆心O 点的场强.解:设O 为坐标原点,水平方向为x 轴,竖直方向为y 轴 半无限长导线∞A 在O 点的场强 )(40j i E 1-=Rπελ半无限长导线∞B 在O 点的场强 )(40j i E 2+-=RπελAB 圆弧在O 点的场强 )(40j i E 3+=Rπελ总场强 j)i E E E E 321+=++=(40Rπελ11-4. 带电细线弯成半径为R 的半圆形,电荷线密度为φλλsin 0=,式中0λ为一常数,φ为半径R 与x 轴所成的夹角,如图所示.试求环心O 处的电场强度. 解:R d R dldE 00204sin 4πεϕϕλπελ==ϕcos dE dE x = 考虑到对称性 0=x E ϕsin dE dE y =RR d dE E y 00002084sin sin ελπεϕϕλϕπ===⎰⎰方向沿y 轴负向11-5. 一半径为R 的半球面,均匀地带有电荷,电荷面密度为σ,求球心O 处的电场强度.解:把球面分割成许多球带,球带所带电荷 dl r dq σπ2= 2322023220)(42)(4r x dl rx r x xdq dE +=+=πεσππεθc o s R x = θs i n R r = θRd dl =21sin 2224E d i πσσθθεε==⎰11-6. 图示一厚度为d 的“无限大”均匀带电平板,电荷体密度为ρ.求板内、外的场强分布,并画出场强随坐标x 变化的图线,即x E -图线(设原点在带电平板的中央平面上,Ox 轴垂直于平板).解:在平板内作一个被平板的中间面垂直平分的闭合圆柱面1S 为高斯面S E d S ∆=∙⎰21S E S x q ∆=∑ρ20ερx E =)2(d x ≤ 同理可得板外一点场强的大小 02ερd E =()2dx >11-7. 设电荷体密度沿x 轴方向按余弦规律x cos 0ρρ=分布在整个空间,式中0ρ为恒量.求空间的场强分布.解:过坐标x ±处作与x 轴垂直的两平面S ,用与x 轴平行的侧面将之封闭,构成高斯面。
大学物理(下)十一章十二章作业与解答

大学物理(下)十一章十二章作业与解答————————————————————————————————作者:————————————————————————————————日期:第十一章恒定磁场一. 选择题1.在一平面内,有两条垂直交叉但相互绝缘的导线,流经两条导线的电流大小相等,方向如图,在哪些区域中有可能存在磁感应强度为零的点?(A) 在Ⅰ、Ⅲ象限(B) 在Ⅰ、Ⅳ象限(C) 在Ⅱ、Ⅲ象限(D) 在Ⅱ、Ⅳ象限[ ]2. 载流导线在同一平面内,形状如图,在圆心O处产生的磁感应强度大小为(A)(B)(C)(D) [ ]注意见第11章课件最后的总结的那个图,半圆载流回路在圆心处的磁感强度是多少?3. 一圆形回路1及一正方形回路2,圆的直径与正方形边长相等,二者中通有大小相同电流,则它们在各自中心处产生的磁感应强度大小之比为(A) 0.90(B) 1.00(C) 1.11(D) 1.22 [ ]注意教材page304,及课件最后总结的那个图4. 在磁感应强度为的均匀磁场中做一半径为r的半球面S,S边线所在平面的法线方向单位矢量与的夹角为θ,则通过半球面S的磁通量(取半球面向外为正)为(A)(B)(C)(D)[ ]5. 如图,无限长载流直导线附近有一正方形闭合曲面S,当S向导线靠近时,穿过S的磁通量和S上各点的磁感应强度的大小B将(A) 增大,B增强(B) 不变,B不变(C) 增大,B不变(D) 不变,B增强[ ]6. 取一闭合积分回路L,使若干根载流导线穿过它所围成的面,若改变这些导线之间的相互间隔,但不越出积分回路,则(A) 回路L内的电流的代数和不变,L上各点的不变(B) 回路L内的电流的代数和不变,L上各点的改变(C) 回路L内的电流的代数和改变,L上各点的不变(D) 回路L内的电流的代数和改变,L上各点的改变[ ]7. 如图,两根导线ab和cd沿半径方向被接到一个截面处处相等的铁环上,恒定电流I 从a端流入而从d端流出,则磁感应强度沿闭合路径L的积分等于(A)(B)(C)(D)[ ]8. 一电荷为q的粒子在均匀磁场中运动,下列说法正确的是(A) 只要速度大小相同,粒子所受的洛仑兹力就相同(B) 在速度不变的前提下,若电荷q变为 -q,则粒子受力反向,数值不变(C) 粒子进入磁场后,其动能和动量都不变(D) 洛仑兹力与速度方向垂直,所以带电粒子运动的轨迹必定是圆[ ]9. 质量为m、电量为q的粒子,以速度v垂直射入均匀磁场中,则粒子运动轨道包围范围的磁通量与磁感应强度的大小之间的关系曲线为[ b ]注意见P317,(11.30)10. 如图,长直载流导线与一圆形电流共面,并与其一直径相重合(两者间绝缘),设长直电流不动,则圆形电流将(A) 向上运动(B) 绕旋转(C) 向左运动(D) 向右运动(E) 不动[ ]11. 磁场中有一载流圆线圈,其既不受力也不受力矩作用,这说明(A) 该磁场一定均匀,且线圈的磁矩方向一定与磁场方向平行(B) 该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向平行(C) 该磁场一定均匀,且线圈的磁矩方向一定与磁场方向垂直(D) 该磁场一定不均匀,且线圈的磁矩方向一定与磁场方向垂直[ ]注意见P325 第二段表述,11.36式12. 用细导线均匀密绕成长为l、半径为a(l >>a)、总匝数为N的螺线管,管内充满相对磁导率为的均匀磁介质,线圈中载有电流I,则管中任一点(A) 磁感应强度大小为(B) 磁感应强度大小为(C) 磁场强度大小为(D) 磁场强度大小为[ ]二. 填空题13.如图,电流元在P点产生的磁感应强度的大小为___________________.14. 真空中有一载有电流I的细圆线圈,则通过包围该线圈的闭合曲面S的磁通量Φ=________________. 若通过S面上某面元的磁通为,而线圈中电流增加为2I时,通过该面元的磁通为,则_______________.0 ; 1︰215. 如图,两平行无限长载流直导线中电流均为I,两导线间距为a,则两导线连线中点P的磁感应强度大小,磁感应强度沿图中环路L的线积分_______________________.0 ;16. 恒定磁场中,磁感应强度对任意闭合曲面的积分等于零,其数学表示式是____________,这表明磁感应线的特征是_________________________. ;闭合曲线17. 一长直螺线管是由直径的导线密绕而成,通以的电流,其内部的磁感应强度大小B =_____________________.(忽略绝缘层厚度)18. 带电粒子垂直磁感应线射入匀强磁场,它做______________运动;带电粒子与磁感应线成300角射入匀强磁场,则它做__________________运动;若空间分布有方向一致的电场和磁场,带电粒子垂直于场方向入射,则它做__________________运动.圆周;螺旋线;变螺距的螺旋线19. 在霍尔效应实验中,通过导电体的电流和的方向垂直(如图).如果上表面的电势较高,则导电体中的载流子带___________电荷;如果下表面的电势较高,则导电体中的载流子带___________电荷.正;负20. 如图,一载流导线弯成半径为R的四分之一圆弧,置于磁感应强度为的均匀磁场中,导线所受磁场力大小为______________,方向为_____________.; y轴正向注意:积分IRBdθ,θ的积分上下限?21. 如图,半径为R的半圆形线圈通有电流I,线圈处在与线圈平面平行指向右的均匀磁场中,该载流线圈磁矩大小为___________,方向____________;线圈所受磁力矩的大小为_________________,方向_____________.;垂直纸面向外;;向上22. 磁场中某点,有一半径为R、载有电流I的圆形实验线圈,其所受的最大磁力矩为M,则该点磁感应强度的大小为_________________.注意见教材324页三. 计算题23. 如图,两长直导线互相垂直放置,相距为d,其中一根导线与z轴重合,另一与x轴平行且在Oxy平面内,设导线中皆通有电流I,求y轴上与两导线等距的P点处的磁感应强度.解:长直载流导线在距其r处的磁感应强度为两长直载流导线在P点产生的磁感应强度方向一沿z轴方向,一沿x轴负方向且方向平行于Oxz平面与Oxy面成45o,如图示。
大学物理3第11章习题分析与解答

习 题 解 答11-1 在双缝干涉实验中,若单色光源S 到两缝21S S 、距离相等,则观察屏上中央明纹位于图中O 处。
现将光源S 向下移动到示意图中的S '位置,则( )(A )中央明条纹也向下移动,且条纹间距不变 (B )中央明条纹向上移动,且条纹间距不变 (C )中央明条纹向下移动,且条纹间距增大 (D )中央明条纹向上移动,且条纹间距增大解 由S 发出的光到达21S S 、的光成相等,它们传到屏上中央O 处,光程差0=∆,形成明纹,当光源由S 向下移动S '时,由S '到达21S S 、的两束光产生了光程差,为了保持原中央明纹处的光程差为0,它将上移到图中O '处,使得由S '沿21S S 、传到O '处的两束光的光程差仍为0.而屏上各级明纹位置只是向上平移,因此条纹间距不变。
故选B11-2 单色平行光垂直照射在薄膜上,经上下两表面反射的两束光发生干涉,如附图所示,若薄膜厚度为e , 且n 1<n 2,n 3<n 2, λ1为入射光在n 1中的波长,则两束反射光的光程为( )(A )e n 22 (B )11222n e n λ-(C )22112λn e n - (D )22122λn e n -习题11-2图解 由于n 1〈n 2,n 3〈n 2,因此光在表面上的反射光有半波损失,下表面的反射光没有半波损失,所以他们的光程差222λ-=∆e n ,这里λ是光在真空中的波3n S S ’OO ’长,与1λ的关系是11λλn =。
故选C11-3 如图所示,两平面玻璃板构成一空气劈尖,一平面单色光垂直入射到劈尖上,当A 板与B 板的夹角θ增大时,干涉图样将发生( )变化 (A )干涉条纹间距增大,并向O 方向移动 (B )干涉条纹间距减小,并向B 方向移动 (C )干涉条纹间距减小,并向O 方向移动 (D )干涉条纹间距增大,并向B 方向移动解 空气劈尖干涉条纹间距θλsin 2n l =∆,劈尖干涉又称为等厚干涉,即k相同的同一级条纹,无论是明纹还是暗纹,都出现在厚度相同的地方. 当A 板与B 板的夹角θ增大时,△l变小. 和原厚度相同的地方向顶角方向移动,所以干涉条纹向O 方向移动。
大学物理学第三版修订版下册第11章答案

习题1111.1选择题(1)一圆形线圈在磁场中作下列运动时,那些情况会产生感应电流() (A )沿垂直磁场方向平移;(B )以直径为轴转动,轴跟磁场垂直; (C )沿平行磁场方向平移;(D )以直径为轴转动,轴跟磁场平行。
[答案:B](2)下列哪些矢量场为保守力场() (A ) 静电场;(B )稳恒磁场;(C )感生电场;(D )变化的磁场。
[答案:A](3) 用线圈的自感系数 L 来表示载流线圈磁场能量的公式221LI W m=()( A )只适用于无限长密绕线管; ( B ) 只适用于一个匝数很多,且密绕的螺线环; ( C ) 只适用于单匝圆线圈; ( D )适用于自感系数L 一定的任意线圈。
[答案:D](4)对于涡旋电场,下列说法不正确的是():(A )涡旋电场对电荷有作用力; (B )涡旋电场由变化的磁场产生; (C )涡旋场由电荷激发; (D )涡旋电场的电力线闭合的。
[答案:C]11.2 填空题(1)将金属圆环从磁极间沿与磁感应强度垂直的方向抽出时,圆环将受到 。
[答案:磁力](2)产生动生电动势的非静电场力是 ,产生感生电动势的非静电场力是 ,激发感生电场的场源是 。
[答案:洛伦兹力,涡旋电场力,变化的磁场](3)长为l 的金属直导线在垂直于均匀的平面内以角速度ω转动,如果转轴的位置在 ,这个导线上的电动势最大,数值为 ;如果转轴的位置在 ,整个导线上的电动势最小,数值为 。
[答案:端点,221l B ω;中点,0]11.3一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中.回路平面与B ϖ垂直.当回路半径以恒定速率tr d d =80cm ·s -1收缩时,求回路中感应电动势的大小. 解: 回路磁通 2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m Φε V11.4 一对互相垂直的相等的半圆形导线构成回路,半径R =5cm ,如题11.4图所示.均匀磁场B =80×10-3T ,B 的方向与两半圆的公共直径(在Oz 轴上)垂直,且与两个半圆构成相等的角α当磁场在5ms 内均匀降为零时,求回路中的感应电动势的大小及方向.解: 取半圆形cba 法向为i ϖ, 题11.4图则 αΦcos 2π21B R m =同理,半圆形adc 法向为j ϖ,则αΦcos 2π22B R m=∵ B ϖ与i ϖ夹角和B ϖ与j ϖ夹角相等,∴ ︒=45α 则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV 方向与cbadc 相反,即顺时针方向.题11.5图 11.5 如题11.5图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环内感应电动势的大小和方向及MN 两端的电压N M U U -.解: 作辅助线MN ,则在MeNM 回路中,沿v ϖ方向运动时0d =m Φ∴ 0=MeNM ε 即 MN MeN εε= 又∵ ⎰+-<+-==ba ba MN ba ba Iv l vB 0ln 2d cos 0πμπε 所以MeN ε沿NeM 方向,大小为ba ba Iv -+ln 20πμ M 点电势高于N 点电势,即b a ba Iv U U N M -+=-ln 20πμ题11.6图11.6如题11.6所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以tId d 的变化率增大,求: (1)任一时刻线圈内所通过的磁通量; (2)线圈中的感应电动势. 解: 以向外磁通为正则 (1) ]ln [lnπ2d π2d π2000dad b a b Ilr l rIr l rIab bad dm +-+=-=⎰⎰++μμμΦ (2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε11.7 如题11.7图所示,用一根硬导线弯成半径为r 的一个半圆.令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转.整个电路的电阻为R .求:感应电流的最大值.题11.7图解: )cos(2π02ϕωΦ+=⋅=t r B S B m ϖϖ ∴ Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε ∴ RBfr R I m22π==ε11.8 如题11.8图所示,长直导线通以电流I =5A ,在其右方放一长方形线圈,两者共面.线圈长b =0.06m ,宽a =0.04m ,线圈以速度v =0.03m ·s -1垂直于直线平移远离.求:d =0.05m 时线圈中感应电动势的大小和方向.题11.8图解: AB 、CD 运动速度v ϖ方向与磁力线平行,不产生感应电动势. DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεϖϖϖBC 产生电动势)(π2d )(02d a Ivbl B v CB+-=⋅⨯=⎰μεϖϖϖ∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad d Ibv μεεε V 方向沿顺时针.11.9 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动.已知导轨处于均匀磁场Bϖ中,B ϖ的方向与回路的法线成60°角(如题11.9图所示),B ϖ的大小为B =kt (k 为正常).设t =0时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向. 解: ⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m ϖϖΦ∴ klvt tm-=-=d d Φε 即沿abcd 方向顺时针方向.题11.9图11.10 一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B ϖ的方向如题11.10图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0). 解: 如图逆时针为矩形导线框正向,则进入时0d d <Φt,0>ε; 题11.10图(a)题11.10图(b)在磁场中时0d d =tΦ,0=ε; 出场时0d d >tΦ,0<ε,故t I -曲线如题10-9图(b)所示. 题11.11图11.11 导线ab 长为l ,绕过O 点的垂直轴以匀角速ω转动,aO =3l磁感应强度B 平行于转轴,如图11.11所示.试求: (1)ab 两端的电势差;(2)b a ,两端哪一点电势高? 解: (1)在Ob 上取dr r r +→一小段 则 ⎰==320292d l Ob l B r rB ωωε 同理 ⎰==302181d l Oa l B r rB ωωε ∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+= (2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高.题11.12图11.12 如题11.12图所示,长度为b 2的金属杆位于两无限长直导线所在平面的正中间,并以速度v ϖ平行于两直导线运动.两直导线通以大小相等、方向相反的电流I ,两导线相距2a .试求:金属杆两端的电势差及其方向.解:在金属杆上取r d 距左边直导线为r ,则 ba b a Iv r r a r Iv l B v b a b a BA AB-+-=-+-=⋅⨯=⎰⎰+-ln d )211(2d )(00πμπμεϖϖϖ ∵ 0<AB ε ∴实际上感应电动势方向从A B →,即从图中从右向左, ∴ ba ba Iv U AB -+=ln 0πμ题11.13图11.13 磁感应强度为B ϖ的均匀磁场充满一半径为R 的圆柱形空间,一金属杆放在题11.13图中位置,杆长为2R ,其中一半位于磁场内、另一半在磁场外.当tBd d >0时,求:杆两端的感应电动势的大小和方向.解: ∵ bc ab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε =-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=-- ∴ tB R R acd d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a →11.14 半径为R 的直螺线管中,有dtdB>0的磁场,一任意闭合导线abca ,一部分在螺线管内绷直成ab 弦,a ,b 两点与螺线管绝缘,如题10-13图所示.设ab =R ,试求:闭合导线中的感应电动势.解:如图,闭合导线abca 内磁通量)436π(22R R B S B m -=⋅=ϖϖΦ∴ tB R R i d d )436π(22--=ε ∵0d d >tB∴0<i ε,即感应电动势沿acba ,逆时针方向.题11.14图题11.15图11.15 如题11.15图所示,在垂直于直螺线管管轴的平面上放置导体ab 于直径位置,另一导体cd 在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬间管内磁场如题11.15图示方向.试求:(1)ab 两端的电势差;(2)cd 两点电势高低的情况.解: 由⎰⎰⋅-=⋅l S t B l E ϖϖϖϖd d d d 旋知,此时旋E ϖ以O 为中心沿逆时针方向. (1)∵ab 是直径,在ab 上处处旋E ϖ与ab 垂直∴ ⎰=⋅ll 0d ϖ旋∴0=ab ε,有b a U U =(2)同理, 0d >⋅=⎰l E cddc ϖϖ旋ε∴ 0<-c d U U 即d c U U >题11.16图11.16 一无限长的直导线和一正方形的线圈如题11.16图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解: 设长直电流为I ,其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2a a Iar rIaμμΦ∴ 2ln π2012aIM μΦ==11.17两线圈顺串联后总自感为1.0H ,在它们的形状和位置都不变的情况下,反串联后总自感为0.4H .试求:它们之间的互感. 解: ∵顺串时 M L L L 221++= 反串联时M L L L 221-+='∴ M L L 4='-15.04='-=L L M H题11.18图11.18 一矩形截面的螺绕环如题11.18图所示,共有N 匝.试求: (1)此螺线环的自感系数;(2)若导线内通有电流I ,环内磁能为多少? 解:如题11.18图示 (1)通过横截面的磁通为 ⎰==baab NIhr h r NIlnπ2d π200μμΦ 磁链 ab IhN N lnπ220μΦψ== ∴ ab hN IL lnπ220μψ==(2)∵ 221LI W m =∴ ab hI N W m ln π4220μ=11.19 一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I .求:导线内部单位长度上所储存的磁能. 解:在R r <时 20π2RI B rμ=∴ 4222002π82Rr I B w m μμ== 取 r r V d π2d =(∵导线长1=l ) 则 ⎰⎰===RRm I Rrr I r r w W 0204320π16π4d d 2μμπ(资料素材和资料部分来自网络,供参考。
大学物理答案第11章

第十一章 恒定磁场11-1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管,两个螺线管的长度相同,R =2r ,螺线管通过的电流相同为I ,螺线管中的磁感强度大小r R B B 、满足( )(A ) r R B B 2= (B ) r R B B = (C ) r R B B =2 (D )r R B B 4=分析与解 在两根通过电流相同的螺线管中,磁感强度大小与螺线管线圈单位长度的匝数成正比.根据题意,用两根长度相同的细导线绕成的线圈单位长度的匝数之比21==R r n n r R 因而正确答案为(C ).11-2 一个半径为r 的半球面如图放在均匀磁场中,通过半球面的磁通量 为( )(A )B r 2π2 (B ) B r 2π(C )αB r cos π22(D ) αB r cos π2题 11-2 图分析与解 作半径为r 的圆S ′与半球面构成一闭合曲面,根据磁场的高斯定理,磁感线是闭合曲线,闭合曲面的磁通量为零,即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量;S B ⋅=m Φ.因而正确答案为(D ).11-3 下列说法正确的是( )(A ) 闭合回路上各点磁感强度都为零时,回路内一定没有电流穿过 (B ) 闭合回路上各点磁感强度都为零时,回路内穿过电流的代数和必定为零 (C ) 磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度必定为零(D ) 磁感强度沿闭合回路的积分不为零时,回路上任意一点的磁感强度都不可能为零 分析与解 由磁场中的安培环路定律,磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度不一定为零;闭合回路上各点磁感强度为零时,穿过回路的电流代数和必定为零.因而正确答案为(B ).11-4 在图(a)和(b)中各有一半径相同的圆形回路L1 、L2 ,圆周内有电流I1 、I2 ,其分布相同,且均在真空中,但在(b)图中L2 回路外有电流I3 ,P 1 、P 2 为两圆形回路上的对应点,则( )(A ) ⎰⎰⋅=⋅21L L d d l B l B ,21P P B B =(B ) ⎰⎰⋅≠⋅21L L d d l B l B ,21P P B B = (C ) ⎰⎰⋅=⋅21L L d d l B l B ,21P P B B ≠ (D ) ⎰⎰⋅≠⋅21L L d d l B l B ,21P P B B≠题 11-4 图分析与解 由磁场中的安培环路定律,积分回路外的电流不会影响磁感强度沿回路的积分;但同样会改变回路上各点的磁场分布.因而正确答案为(C ).11-5 半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中,若导体中流过的恒定电流为I ,磁介质的相对磁导率为μr (μr<1),则磁介质内的磁化强度为( ) (A )()r I μr π2/1-- (B ) ()r I μr π2/1- (C ) r I μr π2/- (D ) r μI r π2/分析与解 利用安培环路定理可先求出磁介质中的磁场强度,再由M =(μr-1)H 求得磁介质内的磁化强度,因而正确答案为(B ).11-6 北京正负电子对撞机的储存环是周长为240 m 的近似圆形轨道,当环中电子流强度为8 mA 时,在整个环中有多少电子在运行? 已知电子的速率接近光速. 分析 一个电子绕存储环近似以光速运动时,对电流的贡献为c I e I /Δ=,因而由lNec I =,可解出环中的电子数.解 通过分析结果可得环中的电子数10104⨯==ecIlN 11-7 已知铜的摩尔质量M =63.75 g·mol -1,密度ρ =8.9 g · cm -3,在铜导线里,假设每一个铜原子贡献出一个自由电子,(1)为了技术上的安全,铜线内最大电流密度26.0A mm m j -=⋅ ,求此时铜线内电子的漂移速率v d ;(2) 在室温下电子热运动的平均速率是电子漂移速率v d 的多少倍?分析 一个铜原子的质量A N M m /=,其中N A 为阿伏伽德罗常数,由铜的密度ρ 可以推算出铜的原子数密度m ρn /=根据假设,每个铜原子贡献出一个自由电子,其电荷为e ,电流密度d m ne j v = .从而可解得电子的漂移速率v d .将电子气视为理想气体,根据气体动理论,电子热运动的平均速率em kTπ8=v 其中k 为玻耳兹曼常量,m e 为电子质量.从而可解得电子的平均速率与漂移速率的关系.解 (1) 铜导线单位体积的原子数为M ρN n A /=电流密度为j m 时铜线内电子的漂移速率14A s m 1046.4--⋅⨯===eN M j ne j m m d ρv (2) 室温下(T =300 K)电子热运动的平均速率与电子漂移速率之比为81042.2π81⨯≈=edd m kTv v v 室温下电子热运动的平均速率远大于电子在恒定电场中的定向漂移速率.电子实际的运动是无规热运动和沿电场相反方向的漂移运动的叠加.考虑到电子的漂移速率很小,电信号的信息载体显然不会是定向漂移的电子.实验证明电信号是通过电磁波以光速传递的. 11-8 有两个同轴导体圆柱面,它们的长度均为20 m ,内圆柱面的半径为3.0 mm ,外圆柱面的半径为9.0 mm.若两圆柱面之间有10 μA 电流沿径向流过,求通过半径为6.0 mm 的圆柱面上的电流密度.题 11-8 图分析 如图所示是同轴柱面的横截面,电流密度j 对中心轴对称分布.根据恒定电流的连续性,在两个同轴导体之间的任意一个半径为r 的同轴圆柱面上流过的电流I都相等,因此可得rlI j π2=解 由分析可知,在半径r =6.0 mm 的圆柱面上的电流密度2m A μ3.13π2-⋅==rlIj 11-9 如图所示,已知地球北极地磁场磁感强度B 的大小为6.0×10-5T .如设想此地磁场是由地球赤道上一圆电流所激发的,此电流有多大? 流向如何?解 设赤道电流为I ,则由教材第11-4节例2 知,圆电流轴线上北极点的磁感强度()RIRR IR B 24202/32220μμ=+=因此赤道上的等效圆电流为A 1073.12490⨯==μRBI 由于在地球地磁场的N 极在地理南极,根据右手螺旋法则可判断赤道圆电流应该是由东向西流,与地球自转方向相反.题 11-9 图11-10 如图所示,有两根导线沿半径方向接触铁环的a 、b 两点,并与很远处的电源相接.求环心O 的磁感强度.题 11-10 图分析 根据叠加原理,点O 的磁感强度可视作由ef 、be 、fa 三段直线以及acb 、a d b 两段圆弧电流共同激发.由于电源距环较远,0=ef B .而be 、fa 两段直线的延长线通过点O ,由于0Idl r ⨯=,由毕奥-萨伐尔定律知0be fa ==B B .流过圆弧的电流I 1 、I 2的方向如图所示,两圆弧在点O 激发的磁场分别为21101π4r l I μB =,22202π4r l I μB = 其中l 1 、l 2 分别是圆弧acb 、a d b 的弧长,由于导线电阻R 与弧长l 成正比,而圆弧acb 、a d b又构成并联电路,故有2211l I l I =将21B B 、叠加可得点O 的磁感强度B . 解 由上述分析可知,点O 的合磁感强度0π4π42220211021=-=-=r l I μr l I μB B B 11-11 如图所示,几种载流导线在平面内分布,电流均为I ,它们在点O 的磁感强度各为多少?题 11-11 图分析 应用磁场叠加原理求解.将不同形状的载流导线分解成长直部分和圆弧部分,它们各自在点O 处所激发的磁感强度较容易求得,则总的磁感强度∑=iB B 0.解 (a) 长直电流对点O 而言,有0d =⨯rl I ,因此它在点O 产生的磁场为零,则点O 处总的磁感强度为1/4 圆弧电流所激发,故有RIμB 800=B 0 的方向垂直纸面向外.(b) 将载流导线看作圆电流和长直电流,由叠加原理可得RIμR I μB π22000-=B 0 的方向垂直纸面向里.(c ) 将载流导线看作1/2 圆电流和两段半无限长直电流,由叠加原理可得RIμR I μR I μR I μR I μB 4π24π4π4000000+=++=B 0 的方向垂直纸面向外.11-12 载流导线形状如图所示(图中直线部分导线延伸到无穷远),求 点O 的磁感强度B .题 11-12 图分析 由教材11-4 节例题2的结果不难导出,圆弧载流导线在圆心激发的磁感强度RαI μB π40=,其中α为圆弧载流导线所张的圆心角,磁感强度的方向依照右手定则确定;半无限长载流导线在圆心点O 激发的磁感强度R IμB π40=,磁感强度的方向依照右手定则确定.点O 的磁感强度O B 可以视为由圆弧载流导线、半无限长载流导线等激发的磁场在空间点O 的叠加. 解 根据磁场的叠加 在图(a)中,k i k k i B RI μR I μR I μR I μR I μπ24π4π44000000--=---= 在图(b)中,k i k i i B RI μR I μR I μR I μR I μπ41π14π44π4000000-⎪⎭⎫ ⎝⎛+-=---= 在图(c )中,k j i B RIμR I μR I μπ4π4830000---= 11-13 如图(a)所示,载流长直导线的电流为I ,试求通过矩形面积的磁通量.题 11-13 图分析 由于矩形平面上各点的磁感强度不同,故磁通量Φ≠BS .为此,可在矩形平面上取一矩形面元d S =l d x ,如图(b)所示,载流长直导线的磁场穿过该面元的磁通量为x l xId π2d d 0μ=⋅=ΦS B矩形平面的总磁通量ΦΦ⎰=d解 由上述分析可得矩形平面的总磁通量⎰==Φ211200lnπ2d π2d dd d Ilx l xIμμ 11-14 已知10 mm 2裸铜线允许通过50 A 电流而不会使导线过热.电流在导线横截面上均匀分布.求导线内、外磁感强度的分布.题 11-14 图分析 可将导线视作长直圆柱体,电流沿轴向均匀流过导体,故其磁场必然呈轴对称分布,即在与导线同轴的圆柱面上的各点,B 大小相等、方向与电流成右手螺旋关系.为此,可利用安培环路定理,求出导线表面的磁感强度.解 围绕轴线取同心圆为环路L ,取其绕向与电流成右手螺旋关系,根据安培环路定理,有∑⎰=⋅=⋅I μB 0πr 2d l B在导线内r <R , 2222ππRIr r R I I ==∑,因而 202πR IrμB =在导线外r >R ,I I =∑,因而rIμB 2π0=磁感强度分布曲线如图所示.11-15 有一同轴电缆,其尺寸如图(a)所示.两导体中的电流均为I ,但电流的流向相反,导体的磁性可不考虑.试计算以下各处的磁感强度:(1) r <R 1 ;(2) R 1 <r <R 2 ;(3) R 2 <r <R 3 ;(4) r >R 3 .画出B -r 图线.题 11-15 图分析 同轴电缆导体内的电流均匀分布,其磁场呈轴对称,取半径为r 的同心圆为积分路径,πr 2d ⋅=⋅⎰B l B ,利用安培环路定理∑⎰=⋅I μ0d l B ,可解得各区域的磁感强度.解 由上述分析得r <R 122101ππ12πr R μr B =⋅ 21012πR Ir μB =R 1 <r <R 2I μr B 022π=⋅rI μB 2π02=R 2 <r <R 3()()⎥⎦⎤⎢⎣⎡---=⋅I R R R r I μr B 22232203ππ2π 2223223032πR R r R r I μB --= r >R 3()02π04=-=⋅I I μr B04=B磁感强度B (r )的分布曲线如图(b).11-16 如图所示,N 匝线圈均匀密绕在截面为长方形的中空骨架上.求通入电流I 后,环内外磁场的分布.题 11-16 图分析 根据右手螺旋法则,螺线管内磁感强度的方向与螺线管中心轴线构成同心圆,若取半径为r 的圆周为积分环路,由于磁感强度在每一环路上为常量,因而πr 2d ⋅=⋅⎰B l B依照安培环路定理∑⎰=⋅I μ0d l B ,可以解得螺线管内磁感强度的分布.解 依照上述分析,有∑=⋅I μr B 02πr <R 102π1=⋅r B01=BR 2 >r >R 1NI μr B 022π=⋅rNI μB 2π02=r >R 202π3=⋅r B 03=B在螺线管内磁感强度B 沿圆周,与电流成右手螺旋.若112R R R <<- 和R 2 ,则环内的磁场可以近似视作均匀分布,设螺线环的平均半径()1221R R R +=,则环内的磁感强度近似为 RNIμB 2π0≈11-17 电流I 均匀地流过半径为R 的圆形长直导线,试计算单位长度导线内的磁场通过图中所示剖面的磁通量.题 11-17 图分析 由题11-14 可得导线内部距轴线为r 处的磁感强度()202πR Irμr B =在剖面上磁感强度分布不均匀,因此,需从磁通量的定义()S B d ⎰=r Φ来求解.沿轴线方向在剖面上取面元dS =l dr ,考虑到面元上各点B 相同,故穿过面元的磁通量dΦ=B dS ,通过积分,可得单位长度导线内的磁通量⎰=Sr B Φd解 由分析可得单位长度导线内的磁通量4πd 2π0020Iμr R Ir μΦR==⎰11-18 已知地面上空某处地磁场的磁感强度40.410T B -=⨯,方向向北.若宇宙射线中有一速率715.010m s -=⨯v 的质子,垂直地通过该处.求:(1)洛伦兹力的方向;(2) 洛伦兹力的大小,并与该质子受到的万有引力相比较.题 11-18 图解 (1) 依照B F ⋅=v q L 可知洛伦兹力L F 的方向为B ⊥v 的方向,如图所示. (2) 因B ⊥v ,质子所受的洛伦兹力N 102.316-⨯==B F v q L在地球表面质子所受的万有引力N 1064.126p -⨯==g m G因而,有101095.1/⨯=G F L ,即质子所受的洛伦兹力远大于重力.11-19 霍尔效应可用来测量血流的速度,其原理如图所示.在动脉血管两侧分别安装电极并加以磁场.设血管直径为d =2.0 mm ,磁场为B =0.080 T ,毫伏表测出血管上下两端的电压为U H =0.10 mV ,血流的流速为多大?题 11-19 图分析 血流稳定时,有H qE B q =v由上式可以解得血流的速度. 解 依照分析m/s 63.0===dBU B E HH v 11-20 带电粒子在过饱和液体中运动,会留下一串气泡显示出粒子运动的径迹.设在气泡室有一质子垂直于磁场飞过,留下一个半径为3.5 cm 的圆弧径迹,测得磁感强度为0.20 T,求此质子的动量和动能.解 根据带电粒子回转半径与粒子运动速率的关系有m /s kg 1012.121⋅⨯===-ReB m p vkeV 35.222==mp E k11-21 从太阳射来的速度为0.80×108m/s 的电子进入地球赤道上空高层范艾伦辐射带中,该处磁场为4.0 ×10-7T,此电子回转轨道半径为多大? 若电子沿地球磁场的磁感线旋进到地磁北极附近,地磁北极附近磁场为2.0 ×10-5T,其轨道半径又为多少? 解 由带电粒子在磁场中运动的回转半径高层范艾伦辐射带中的回转半径m 101.1311⨯==eB m R v地磁北极附近的回转半径m 2322==eB m R v11-22 如图(a)所示,一根长直导线载有电流I 1 =30 A ,矩形回路载有电流I 2 =20 A .试计算作用在回路上的合力.已知d =1.0 cm ,b =8.0 cm ,l =0.12 m .题 11-22图分析 矩形上、下两段导线受安培力F 1 和F 2 的大小相等,方向相反,对不变形的矩形回路来说,两力的矢量和为零.而矩形的左右两段导线,由于载流导线所在处磁感强度不等,所受安培力F 3 和F 4 大小不同,且方向相反,因此线框所受的力为这两个力的合力.解 由分析可知,线框所受总的安培力F 为左、右两边安培力F 3 和F 4 之矢量和,如图(b)所示,它们的大小分别为d lI I μF π22103=()b d l I I μF +=π22104故合力的大小为()N 1028.1π2π2321021043-⨯=+-=-=b d lI I μd l I I μF F F 合力的方向朝左,指向直导线.11-23 一直流变电站将电压为500kV 的直流电,通过两条截面不计的平行输电线输向远方.已知两输电导线间单位长度的电容为3.0×10-11F ·m -1,若导线间的静电力与安培力正好抵消.求:(1) 通过输电线的电流;(2) 输送的功率.分析 当平行输电线中的电流相反时,它们之间存在相互排斥的安培力,其大小可由安培定律确定.若两导线间距离为d ,一导线在另一导线位置激发的磁感强度dIμB π20=,导线单位长度所受安培力的大小BI F B =.将这两条导线看作带等量异号电荷的导体,因两导线间单位长度电容C 和电压U 已知,则单位长度导线所带电荷λ=CU ,一导线在另一导线位置所激发的电场强度dελE 0π2=,两导线间单位长度所受的静电吸引力λE F E =.依照题意,导线间的静电力和安培力正好抵消,即0=+E B F F从中可解得输电线中的电流.解 (1) 由分析知单位长度导线所受的安培力和静电力分别为d I μBI F B π220==dεU C λE F E 022π2== 由0=+E BF F 可得dεU C d I μ02220π2π2=解得A 105.4300⨯==μεCUI (2) 输出功率W 1025.29⨯==IU N11-24 在氢原子中,设电子以轨道角动量π2/h L =绕质子作圆周运动,其半径为m 1029.5110-⨯=a .求质子所在处的磁感强度.h 为普朗克常量,其值为s J 1063.634⋅⨯-分析 根据电子绕核运动的角动量π20h a m L ==v 可求得电子绕核运动的速率v .如认为电子绕核作圆周运动,其等效圆电流v/π20a e T e i ==在圆心处,即质子所在处的磁感强度为02a i μB =解 由分析可得,电子绕核运动的速率π2ma h=v其等效圆电流2020π4/π2ma he v a e i ==该圆电流在圆心处产生的磁感强度T 5.12π82202000===ma heμa i μB 11-25 如图[a]所示,一根长直同轴电缆,内、外导体之间充满磁介质,磁介质的相对磁导率为μr (μr <1),导体的磁化可以忽略不计.沿轴向有恒定电流I 通过电缆,内、外导体上电流的方向相反.求:(1) 空间各区域内的磁感强度和磁化强度;*(2) 磁介质表面的磁化电流.题 11-25 图分析 电流分布呈轴对称,依照右手定则,磁感线是以电缆对称轴线为中心的一组同心圆.选取任一同心圆为积分路径,应有⎰⋅=⋅r H d π2l H ,利用安培环路定理⎰∑=⋅fI d l H求出环路内的传导电流,并由H μB =,()H μM r 1-=,可求出磁感强度和磁化强度.再由磁化电流的电流面密度与磁化强度的关系求出磁化电流.解 (1) 取与电缆轴同心的圆为积分路径,根据磁介质中的安培环路定理,有∑=fπ2I r H对r <R 1221f ππrR I I =∑ 得2112πR IrH =忽略导体的磁化(即导体相对磁导率μr =1),有01=M ,21012πR IrμB =对R 2 >r >R 1I I=∑f得rI H 2π2=填充的磁介质相对磁导率为μr ,有()r I μM r 2π12-=,rI μμB r 2π02= 对R 3 >r >R 2()()2223223ππR r R R I I I f -⋅--=∑ 得()()222322332πR R r r R I H --= 同样忽略导体的磁化,有03=M ,()()2223223032πR R r r R I μB --= 对r >R 30=-=∑I I If得04=H ,04=M ,04=B(2) 由r M I s 2π⋅=,磁介质内、外表面磁化电流的大小为()()I μR R M I r si 12π112-=⋅= ()()I μR R M I r se 12π222-=⋅=对抗磁质(1r μ<),在磁介质内表面(r =R 1 ),磁化电流与内导体传导电流方向相反;在磁介质外表面(r =R 2 ),磁化电流与外导体传导电流方向相反.顺磁质的情况与抗磁质相反.H (r )和B (r )分布曲线分别如图(b)和(c )所示.。
大学物理下册11-15章答案(修改过,红色为修正地方还有以下解释)
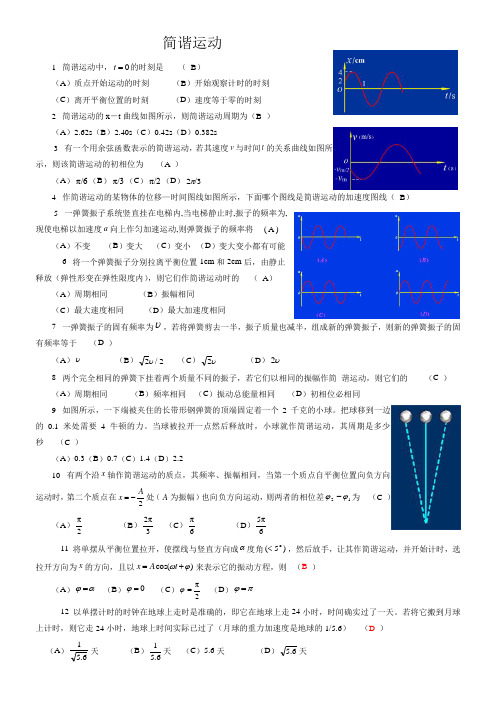
简谐运动1 简谐运动中,0=t 的时刻是 ( B )(A )质点开始运动的时刻 (B )开始观察计时的时刻(C )离开平衡位置的时刻 (D )速度等于零的时刻2 简谐运动的x -t 曲线如图所示,则简谐运动周期为(B )(A )2.62s (B )2.40s (C )0.42s (D )0.382s3 有一个用余弦函数表示的简谐运动,若其速度v 与时间t 的关系曲线如图所示,则该简谐运动的初相位为 (A )(A )π/6(B )π/3(C )π/2(D )/32π4 作简谐运动的某物体的位移—时间图线如图所示,下面哪个图线是简谐运动的加速度图线( B )5 一弹簧振子系统竖直挂在电梯内,当电梯静止时,振子的频率为,现使电梯以加速度a 向上作匀加速运动,则弹簧振子的频率将 ( A )(A )不变 (B )变大 (C )变小 (D )变大变小都有可能6 将一个弹簧振子分别拉离平衡位置1cm 和2cm 后,由静止释放(弹性形变在弹性限度内),则它们作简谐运动时的 ( A )(A )周期相同 (B )振幅相同(C )最大速度相同 (D )最大加速度相同7 一弹簧振子的固有频率为υ,若将弹簧剪去一半,振子质量也减半,组成新的弹簧振子,则新的弹簧振子的固有频率等于 (D )(A )υ (B )2/2υ (C )υ2 (D )υ28 两个完全相同的弹簧下挂着两个质量不同的振子,若它们以相同的振幅作简 谐运动,则它们的 (C ) (A )周期相同 (B )频率相同 (C )振动总能量相同 (D )初相位必相同9 如图所示,一下端被夹住的长带形钢弹簧的顶端固定着一个2千克的小球。
把球移到一边的0.1米处需要4牛顿的力。
当球被拉开一点然后释放时,小球就作简谐运动,其周期是多少秒 (C )(A )0.3(B )0.7(C )1.4(D )2.210 有两个沿x 轴作简谐运动的质点,其频率、振幅相同,当第一个质点自平衡位置向负方向运动时,第二个质点在2A x -=处(A 为振幅)也向负方向运动,则两者的相位差12ϕϕ-为 (C ) (A )2π (B )3π2 (C )6π (D )6π5 11 将单摆从平衡位置拉开,使摆线与竖直方向成α度角)5(o <,然后放手,让其作简谐运动,并开始计时,选拉开方向为x 的方向,且以)cos(ϕω+=t A x 来表示它的振动方程,则 (B )(A )αϕ= (B )0=ϕ (C )2π=ϕ (D )πϕ= 12 以单摆计时的时钟在地球上走时是准确的,即它在地球上走24小时,时间确实过了一天。
大学物理学下册答案解析第11章

第11章 稳恒磁场习 题一 选择题11-1 边长为l 的正方形线圈,分别用图11-1中所示的两种方式通以电流I (其中ab 、cd 与正方形共面),在这两种情况下,线圈在其中心产生的磁感应强度的大小分别为:[ ](A )10B =,20B =(B )10B =,02IB lπ=(C)01IB lπ=,20B =(D)01I B l π=,02IB lπ= 答案:C解析:有限长直导线在空间激发的磁感应强度大小为012(cos cos )4IB dμθθπ=-,并结合右手螺旋定则判断磁感应强度方向,按照磁场的叠加原理,可计算01IB lπ=,20B =。
故正确答案为(C )。
11-2 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,如图11-2所示,则在圆心O 处的磁感应强度大小为多少? [ ]习题11-1图习题11-2图(A )0 (B )R I 2/0μ (C )R I 2/20μ (D )R I /0μ 答案:C解析:圆线圈在圆心处的磁感应强度大小为120/2B B I R μ==,按照右手螺旋定则判断知1B 和2B 的方向相互垂直,依照磁场的矢量叠加原理,计算可得圆心O处的磁感应强度大小为0/2B I R =。
11-3 如图11-3所示,在均匀磁场B 中,有一个半径为R 的半球面S ,S 边线所在平面的单位法线矢量n 与磁感应强度B 的夹角为α,则通过该半球面的磁通量的大小为[ ](A )B R 2π (B )B R 22π (C )2cos R B πα (D )2sin R B πα 答案:C解析:通过半球面的磁感应线线必通过底面,因此2cos m B S R B παΦ=⋅=。
故正确答案为(C )。
11-4 如图11-4所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量Φ何变化?[ ](A )Φ增大,B 也增大 (B )Φ不变,B 也不变 (C )Φ增大,B 不变 (D )Φ不变,B 增大I习题11-4图习题11-3图答案:D解析:根据磁场的高斯定理0SBdS Φ==⎰,通过闭合曲面S 的磁感应强度始终为0,保持不变。
大学物理第三版第11章部分习题解答

2
(2) 如果用导线把AB两球连接起来再求以上两 点的电势
第11章部分习题解答
解: (1)
q E 2 4 0 r 1
R1 r R2
r R2
R2
q
R1
U1 q
R2
q 4 0 r
第11章 部分习题解答
第11章部分习题解答
P408题11.3.4 如图所示,两个无限大带电平板,电荷面密度 分别为 ,设P为两板间任意一点.(1)求A板上 的电荷在P点产生的场强 E A ; (2)求B板上的电 荷在P点产生的场强 E B ;(3)求A、B两板上的电 荷在P点产生的场强;(4)如果把B板拿走,A板 上的电荷如何分布?求它在P点产生的场强.
1 Q2 We 2 QU 球壳、 2 8 0 R3
Q 1 1 1 We We1 We 2 ( ) 8 0 R1 R2 R3
2
第11章部分习题解答
(2)
1 Q2 We ' QU 球 壳、 2 8 0 R3
2010.5.25
第11章部分习题解答
解: 因为A、B都是无限大带电平板,所以 (1) (2)
EA 2 0
方向向右
EB 2 0
EP E A EB 0
方向向右
(3)
方向向右
第11章部分习题解答
(4) 如果将B板拿走,A上的电荷将均匀分布在 左右两个面上,每一个面上的电荷面密度为 / 2 ,它们在P点产生的场强大小都是 2 E'A 方向向右 2 0 4 0
第11章部分习题解答
证明: 该电容器是由两个 电容分别为 C1 和 C2 的电容器并联而成 的
《大学物理学》习题解答(第11章 静电场)

1
Q L
L
2 0 r 1 4r 2 L2
2 0 r
2
【11.5】一半径为 R 的半圆细环上均匀的分布电荷 Q,求环心处的电场强度。 解取坐标 Oxy ,电荷元 d q d l R d ,由点电荷场强公式
y
d
dl
dq dE eR 4 0 R 2
由于电荷对称分布,场强也对称,则: Ex dEx 0
13
以 1.0 10 C s 的变化率失去电荷,求两球彼此趋近的瞬时相对速率(即
9
1
T q F mg x
l q
dx )是多少? dt
解 (1)如图所示,小球平衡时,
T sin F , T cos mg , F
q
2
4 0 x 2
13
q 2l x , 很小时, tan sin ,因此 x 则 mg tan 2 mg 2l 4 0 x 2 0
E d S E d S ER 2 cos ER 2
S S
z
A F C E O D B
【11.11】边长为 a 的立方体如图所示,其表面分别平行于 xy , yz 和 zx 平 面,立方体的一个顶点为坐标原点。现将立方体置于电场强度
E ( E1 kx)i E2 j 的非均匀电场中, 求立方体各表面及整个立方体表面的
Q d x ,则 L
EP
Qdx Q 1 1 1 Q [ ] 2 2 L 2 4 L ( r x ) 4 0 L r L 2 r L 2 0 4r L2 0
L2
1
(2)若点 P 在棒的垂直平分线上,因对称性, E 沿 x 轴方向的分量叠加为零,因此, E 的方向沿 y 轴, 大小为
第十一章恒定电流的磁场作业磁介质磁介质中的安培环路定理小结

作业11.1、11.211.4、11.8、11.9、11.15、11.1787磁介质90顺磁质B B >(铝、氧、锰等)弱磁质B B >>铁磁质(铁、钴、镍等)强磁性物质B B <抗磁质(铜、铋、氢等)弱磁质抗磁质顺磁质SI SI B L宏观上构成沿介质表面的等效环形电流, 称为表面束缚电流或磁化电流。
B AI 0I cbad.l113五、磁场对载流导线和运动电荷的作用(1)磁场对载流导线的作用力—安培力微分形式积分形式B l I F ⨯=d d Bl I F l⨯=⎰d 其中,是载流导线上的电流元,是所在处的磁感应强度。
l Id l I d B(2)均匀磁场对平面载流线圈的作用合力=∑F 磁力矩B p M m ⨯=式中,是载流线圈的磁矩,,其中N 是线圈匝数,I 是线圈中的电流,S 是线圈的面积,且S 的方向与电流环绕方向满足右螺旋法则。
m p S NI p m=114(3)磁力的功⎰=m1m2m d ΦΦΦI A mm1m2)(ΦI ΦΦI ∆=-=磁力的功等于电流强度I 乘以通过回路磁通量的增量∆Φm 。
(4)磁场对运动电荷的作用Bq F⨯=v 洛仑兹力:116六、磁介质(1)磁介质的分类抗磁质1<r μ顺磁质1>r μ铁磁质1>>r μ(2)磁介质的磁化在外磁场中固有磁矩沿外磁场的取向或感应磁矩的产生使磁介质的表面(或内部)出现束缚电流。
大学物理第11章习题答案

第11章 电磁感应11.1 基本要求 1理解电动势的概念。
2掌握法拉第电磁感应定律和楞次定律,能熟练地应用它们来计算感应电动势的大小,判别感应电动势的方向。
3理解动生电动势的概念及规律,会计算一些简单问题中的动生电动势。
4理解感生电场、感生电动势的概念及规律,会计算一些简单问题中的感生电动势。
5理解自感现象和自感系数的定义及物理意义,会计算简单回路中的自感系数。
6理解互感现象和互感系数的定义及物理意义,能计算简单导体回路间的互感系数。
7理解磁能(磁场能量)和磁能密度的概念,能计算一些简单情况下的磁场能量。
8了解位移电流的概念以及麦克斯韦方程组(积分形式)的物理意义。
11.2 基本概念1电动势ε:把单位正电荷从负极通过电源内部移到正极时,非静电力所作的功,即Wqε=2动生电动势:仅由导体或导体回路在磁场中的运动而产生的感应电动势。
3感生电场k E :变化的磁场在其周围所激发的电场。
与静电场不同,感生电场的电 场线是闭合的,所以感生电场也称有旋电场。
4感生电动势:仅由磁场变化而产生的感应电动势。
5自感:有使回路保持原有电流不变的性质,是回路本身的“电磁惯性”的量度。
自感系数L ://m L I N I =ψ=Φ6自感电动势L ε:当通过回路的电流发生变化时,在自身回路中所产生的感应电动势。
7互感系数M :211212M I I ψψ== 8互感电动势12ε:当线圈2的电流2I 发生变化时,在线圈1中所产生的感应电动势。
9磁场能量m W :贮存在磁场中的能量。
自感贮存磁能:212m W LI =磁能密度m w :单位体积中贮存的磁场能量22111222m B w μH HB μ===10位移电流:D d d I dt Φ=s d t∂=∂⎰DS ,位移电流并不表示有真实的电荷在空 间移动。
但是,位移电流的量纲和在激发磁场方面的作用与传导电流是一致的。
11位移电流密度:d t∂=∂D j 11.3 基本规律1电磁感应的基本定律:描述电磁感应现象的基本规律有两条。
大学物理课后习题答案(第十一章)

习题十一11-1 圆柱形电容器内、外导体截面半径分别为1R 和2R (1R <2R ),中间充满介电常数为ε的电介质.当两极板间的电压随时间的变化k t U=d d 时(k 为常数),求介质内距圆柱轴线为r 处的位移电流密度.解:圆柱形电容器电容12ln 2R R l C πε=12ln 2R R lU CU q πε==1212ln ln 22R R r U R R r lU S q D εππε===∴12lnR R r ktDj ε=∂∂=11-2 试证:平行板电容器的位移电流可写成t UCI d d d =.式中C 为电容器的电容,U 是电容器两极板的电势差.如果不是平板电容器,以上关系还适用吗? 解:∵ CU q =S CU D ==0σ∴ CU DS D ==Φ不是平板电容器时 0σ=D 仍成立∴t UCI D d d =还适用.题11-3图11-3 如题11-3图所示,电荷+q 以速度v ϖ向O 点运动,+q 到O 点的距离为x ,在O 点处作半径为a 的圆平面,圆平面与v ϖ垂直.求:通过此圆的位移电流. 解:如题11-3图所示,当q 离平面x 时,通过圆平面的电位移通量)1(222ax x q D +-=Φ[此结果见习题8-9(3)]tUC t ID D d d d d ==Φ∴23222)(2d d a x v qa tI DD +==Φ题11-4图11-4 如题11-4图所示,设平行板电容器内各点的交变电场强度E =720sin t π510V ·m -1,正方向规定如图.试求:(1)电容器中的位移电流密度;(2)电容器内距中心联线r =10-2m 的一点P ,当t =0和t =51021-⨯s 时磁场强度的大小及方向(不考虑传导电流产生的磁场).解:(1)t Dj D ∂∂=,E D 0ε= ∴tt t t E j D ππεπεε50550010cos 10720)10sin 720(⨯=∂∂=∂∂=2m A -⋅ (2)∵⎰∑⎰⋅+=⋅)(0d d S D lSj I l H ϖϖϖϖ取与极板平行且以中心连线为圆心,半径r 的圆周r l π2=,则D j r r H 22ππ=Dj r H 2=0=t 时0505106.3107202πεπε⨯=⨯⨯=rH P 1m A -⋅51021-⨯=t s 时,0=P H11-5 半径为R =0.10m 的两块圆板构成平行板电容器,放在真空中.今对电容器匀速充电,使两极板间电场的变化率为t Ed d =1.0×1013 V ·m -1·s -1.求两极板间的位移电流,并计算电容器内离两圆板中心联线r (r <R )处的磁感应强度Br 以及r =R 处的磁感应强度BR .解: (1)t E t D j D ∂∂=∂∂=0ε 8.22≈==R j S j I D D D πA(2)∵S j I l H SD lϖϖϖϖd d 0⋅+=⋅⎰∑⎰取平行于极板,以两板中心联线为圆心的圆周r l π2=,则22d d 2r t E r j r H D πεππ==∴t Er H d d 20ε=t Er H B r d d 2000εμμ==当R r =时,600106.5d d 2-⨯==t ER B R εμT *11-6 一导线,截面半径为10-2m ,单位长度的电阻为3×10-3Ω·m -1,载有电流25.1 A .试计算在距导线表面很近一点的以下各量:(1)H 的大小;(2)E 在平行于导线方向上的分量; (3)垂直于导线表面的S 分量. 解: (1)∵⎰∑=Il H ϖϖd取与导线同轴的垂直于导线的圆周r l π2=,则I r H =π2 21042⨯==rI H π1m A -⋅(2)由欧姆定律微分形式 E j σ=得21053.7/1/-⨯====IR RS SI jE σ 1m V -⋅(3)∵H E S ϖϖϖ⨯=,E ϖ沿导线轴线,H ϖ垂直于轴线 ∴S ϖ垂直导线侧面进入导线,大小1.30==EH S 2m W -⋅*11-7 有一圆柱形导体,截面半径为a ,电阻率为ρ,载有电流0I .(1)求在导体内距轴线为r 处某点的E ϖ的大小和方向;(2)该点H ϖ的大小和方向;(3)该点坡印廷矢量S ϖ的大小和方向;(4)将(3)的结果与长度为l 、半径为r 的导体内消耗的能量作比较.解:(1)电流密度S I j 00=由欧姆定律微分形式Ej σ=0得2000a I j j E πρρσ===,方向与电流方向一致(2)取以导线轴为圆心,垂直于导线的平面圆周r l π2=,则由⎰⎰=⋅SlS j l H ϖϖϖϖd d 0可得2202a r I r H =π∴202a rI H π=,方向与电流成右螺旋 (3)∵ H E S ϖϖϖ⨯=∴ S ϖ垂直于导线侧面而进入导线,大小为 42202a rI EH S πρ==(4)长为l ,半径为)(a r r <导体内单位时间消耗能量为4220222200121)(a lr I r la r I R I W πρπρ===单位时间进入长为l ,半径为r 导体内的能量422022a lr I rl S W πρπ==21W W =说明这段导线消耗的能量正是电磁场进入导线的能量.*11-8 一个很长的螺线管,每单位长度有n 匝,截面半径为a ,载有一增加的电流i ,求:(1)在螺线管内距轴线为r 处一点的感应电场; (2)在这点的坡印矢量的大小和方向.解: (1)螺线管内ni B 0μ= 由 S t B l E S l ϖϖϖϖd d ⋅∂∂-=⋅⎰⎰取以管轴线为中心,垂直于轴的平面圆周r l π2=,正绕向与B 成右螺旋关系,则22r t B r E ππ∂∂-=∴dt di nr t B r E 220μ-=∂∂-=,方向沿圆周切向,当0d d <t i时,E ϖ与B ϖ成右螺旋关系;当0d d >t i 时,E ϖ与B ϖ成左旋关系。
《大学物理教程》下册 第三版 (贾瑞皋 著)课后习题答案 科学出版社11

两层均匀电介质,它们的相对电容率 ε r1 = 6 和 ε r2 = 3。两层电介质的分界面半径 R=0.04m。 设内球壳带电量 Q= − 6 × 10 −8 C ,求: (1)D 和 E 的分布,并画出 D-r、E-r 曲线; (2)两球壳之间的电势差; (3)贴近内金属壳的电介质表面上的束缚面电荷密度。 [解] 以与球壳同心的球面为高斯面
在上板内任意点场强均为零,它是 6 个无限大均匀带电平面在该点产生的场强叠加的 结果。故有
11-2
1 (σ 1 − σ 2 − σ 3 − σ 4 − σ 5 − σ 6 ) = 0 2ε 0
考虑到(1)、(2)两式,则得到
σ1 =σ 6
(5)
上下两块导体板原来是不带电的,根据电荷守恒定律,二导体板表面出现感应电荷后, 总量仍为零。因此有
C1 = 4πε 0
R1 R2 R2 − R1
C1 C2
C3
C 2 = 4πε 0 R2
11-5
C 3 = 4πε 0 r
设小球 C 3 上电量为 q, 则 C1 上电量 Q1 -q, C 2 上电量为 Q2 + (Q1 − q ) 设三个电容上的电 压各为 U 1 、 U 2 、 U 3
U 3 = q C3
qB ⎞ ⎛ QA q B ⎜ ⎜ R + R + R ⎟ ⎟ 2 3 ⎠ ⎝ 1
⎞ ⎟V = 5.63 × 10 3 V ⎟ ⎠
⎛ 3 × 10 −8 5 × 10 −8 − 3 × 10 −8 = 9 × 10 9 × ⎜ + + ⎜ 6.0 × 10 − 2 8.0 × 10 − 2 10.0 × 10 − 2 ⎝
ε 0ε r S d
得
U=
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题11选择题(1)一圆形线圈在磁场中作下列运动时,那些情况会产生感应电流() (A )沿垂直磁场方向平移;(B )以直径为轴转动,轴跟磁场垂直; (C )沿平行磁场方向平移;(D )以直径为轴转动,轴跟磁场平行。
[答案:B](2)下列哪些矢量场为保守力场() (A ) 静电场;(B )稳恒磁场;(C )感生电场;(D )变化的磁场。
[答案:A](3) 用线圈的自感系数 L 来表示载流线圈磁场能量的公式221LI W m=()( A )只适用于无限长密绕线管; ( B ) 只适用于一个匝数很多,且密绕的螺线环; ( C ) 只适用于单匝圆线圈; ( D )适用于自感系数L 一定的任意线圈。
[答案:D](4)对于涡旋电场,下列说法不正确的是():(A )涡旋电场对电荷有作用力; (B )涡旋电场由变化的磁场产生; (C )涡旋场由电荷激发; (D )涡旋电场的电力线闭合的。
[答案:C]11.2 填空题(1)将金属圆环从磁极间沿与磁感应强度垂直的方向抽出时,圆环将受到 。
[答案:磁力](2)产生动生电动势的非静电场力是 ,产生感生电动势的非静电场力是 ,激发感生电场的场源是 。
[答案:洛伦兹力,涡旋电场力,变化的磁场](3)长为l 的金属直导线在垂直于均匀的平面内以角速度ω转动,如果转轴的位置在 ,这个导线上的电动势最大,数值为 ;如果转轴的位置在 ,整个导线上的电动势最小,数值为 。
[答案:端点,221l B ω;中点,0]一半径r =10cm 的圆形回路放在B =的均匀磁场中.回路平面与B ϖ垂直.当回路半径以恒定速率tr d d =80cm·s -1收缩时,求回路中感应电动势的大小. 解: 回路磁通 2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m Φε V一对互相垂直的相等的半圆形导线构成回路,半径R =5cm ,如题图所示.均匀磁场B =80×10-3T ,B 的方向与两半圆的公共直径(在Oz 轴上)垂直,且与两个半圆构成相等的角α当磁场在5ms 内均匀降为零时,求回路中的感应电动势的大小及方向. 解: 取半圆形cba 法向为i ϖ, 题图 则 αΦcos 2π21B R m =同理,半圆形adc 法向为j ϖ,则αΦcos 2π22B R m=∵ B ϖ与i ϖ夹角和B ϖ与j ϖ夹角相等,∴ ︒=45α 则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV 方向与cbadc 相反,即顺时针方向.题图如题图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环内感应电动势的大小和方向及MN 两端的电压N M U U -.解: 作辅助线MN ,则在MeNM 回路中,沿v ϖ方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε= 又∵ ⎰+-<+-==ba ba MN ba ba Iv l vB 0ln 2d cos 0πμπε 所以MeN ε沿NeM 方向,大小为ba ba Iv -+ln 20πμ M 点电势高于N 点电势,即b a ba Iv U U N M -+=-ln 20πμ题图如题所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以tId d 的变化率增大,求: (1)任一时刻线圈内所通过的磁通量; (2)线圈中的感应电动势. 解: 以向外磁通为正则 (1) ]ln [lnπ2d π2d π2000dad b a b Ilr l rIr l rIab bad dm +-+=-=⎰⎰++μμμΦ (2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε如题图所示,用一根硬导线弯成半径为r 的一个半圆.令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转.整个电路的电阻为R .求:感应电流的最大值.题图解: )cos(2π02ϕωΦ+=⋅=t r B S B m ϖϖ ∴ Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε ∴ RBfr R I m22π==ε如题图所示,长直导线通以电流I =5A ,在其右方放一长方形线圈,两者共面.线圈长b =0.06m ,宽a =0.04m ,线圈以速度v =0.03m·s -1垂直于直线平移远离.求:d =0.05m 时线圈中感应电动势的大小和方向. 题图解: AB 、CD 运动速度v ϖ方向与磁力线平行,不产生感应电动势. DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεϖϖϖBC 产生电动势)(π2d )(02d a Ivbl B v CB+-=⋅⨯=⎰μεϖϖϖ∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad d Ibv μεεε V 方向沿顺时针.长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动.已知导轨处于均匀磁场B ϖ中,B ϖ的方向与回路的法线成60°角(如题图所示),B ϖ的大小为B =kt (k 为正常).设t =0时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向.解: ⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m ϖϖΦ∴ klvt tm-=-=d d Φε 即沿abcd 方向顺时针方向. 题图一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B ϖ的方向如题图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0). 解: 如图逆时针为矩形导线框正向,则进入时0d d <Φt,0>ε; 题图(a)题图(b) 在磁场中时0d d =tΦ,0=ε; 出场时0d d >tΦ,0<ε,故t I -曲线如题10-9图(b)所示. 题图导线ab 长为l ,绕过O 点的垂直轴以匀角速ω转动,aO =3l磁感应强度B 平行于转轴,如图所示.试求:(1)ab 两端的电势差; (2)b a ,两端哪一点电势高? 解: (1)在Ob 上取dr r r +→一小段 则 ⎰==320292d l Ob l B r rB ωωε 同理 ⎰==302181d l Oa l B r rB ωωε ∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+= (2)∵ 0>ab ε 即0<-b a U U∴b 点电势高.题图如题图所示,长度为b 2的金属杆位于两无限长直导线所在平面的正中间,并以速度v ϖ平行于两直导线运动.两直导线通以大小相等、方向相反的电流I ,两导线相距2a .试求:金属杆两端的电势差及其方向.解:在金属杆上取r d 距左边直导线为r ,则 ba b a Iv r r a r Iv l B v b a b a BA AB-+-=-+-=⋅⨯=⎰⎰+-ln d )211(2d )(00πμπμεϖϖϖ ∵ 0<AB ε ∴实际上感应电动势方向从A B →,即从图中从右向左, ∴ ba ba Iv U AB -+=ln 0πμ题图磁感应强度为B ϖ的均匀磁场充满一半径为R 的圆柱形空间,一金属杆放在题图中位置,杆长为2R ,其中一半位于磁场内、另一半在磁场外.当tBd d >0时,求:杆两端的感应电动势的大小和方向.解: ∵ bc ab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε =-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=-- ∴ tB R R acd d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a →半径为R 的直螺线管中,有dtdB>0的磁场,一任意闭合导线abca ,一部分在螺线管内绷直成ab 弦,a ,b 两点与螺线管绝缘,如题10-13图所示.设ab =R ,试求:闭合导线中的感应电动势.解:如图,闭合导线abca 内磁通量)436π(22R R B S B m -=⋅=ϖϖΦ∴ tB R R i d d )436π(22--=ε ∵0d d >tB∴0<i ε,即感应电动势沿acba ,逆时针方向.题图题图如题图所示,在垂直于直螺线管管轴的平面上放置导体ab 于直径位置,另一导体cd 在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬间管内磁场如题图示方向.试求: (1)ab 两端的电势差;(2)cd 两点电势高低的情况.解: 由⎰⎰⋅-=⋅l S t B l E ϖϖϖϖd d d d 旋知,此时旋E ϖ以O 为中心沿逆时针方向. (1)∵ab 是直径,在ab 上处处旋E ϖ与ab 垂直∴ ⎰=⋅ll 0d ϖ旋∴0=ab ε,有b a U U =(2)同理, 0d >⋅=⎰l E cddc ϖϖ旋ε∴ 0<-c d U U 即d c U U >题图一无限长的直导线和一正方形的线圈如题图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解: 设长直电流为I ,其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2a a Iar rIaμμΦ∴ 2ln π2012aIM μΦ==两线圈顺串联后总自感为,在它们的形状和位置都不变的情况下,反串联后总自感为.试求:它们之间的互感.解: ∵顺串时 M L L L 221++= 反串联时M L L L 221-+='∴ M L L 4='-15.04='-=L L M H题图一矩形截面的螺绕环如题图所示,共有N 匝.试求: (1)此螺线环的自感系数;(2)若导线内通有电流I ,环内磁能为多少? 解:如题图示(1)通过横截面的磁通为 ⎰==baab NIhr h r NIlnπ2d π200μμΦ 磁链 ab IhN N lnπ220μΦψ== ∴ ab hN IL lnπ220μψ==(2)∵ 221LI W m =∴ ab hI N W m ln π4220μ=一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I .求:导线内部单位长度上所储存的磁能. 解:在R r <时 20π2RI B rμ=∴ 4222002π82R r I B w m μμ== 取 r r V d π2d =(∵导线长1=l ) 则 ⎰⎰===RRm I R rr I r r w W 0204320π16π4d d 2μμπ。
