可靠性习题
可靠性习题及答案

任课教师:郭进教授
-1-
系统可靠性习题
参考答案
1-1
1-2
1-3
1-4
1-5
1-6
1-7
1-8
A,B,C
C
A,C,D
B,E
A,B,C
A
B,C
B
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,通力根1保过据护管生高线产中敷工资设艺料技高试术中卷0资不配料仅置试可技卷以术要解是求决指,吊机对顶组电层在气配进设置行备不继进规电行范保空高护载中高与资中带料资负试料荷卷试下问卷高题总中2体2资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况1卷中下安,与全要过,加度并强工且看作尽护下可1都关能可于地以管缩正路小常高故工中障作资高;料中对试资于卷料继连试电接卷保管破护口坏进处范行理围整高,核中或对资者定料对值试某,卷些审弯异核扁常与度高校固中对定资图盒料纸位试,置卷编.工保写况护复进层杂行防设自腐备动跨与处接装理地置,线高尤弯中其曲资要半料避径试免标卷错高调误等试高,方中要案资求,料技编试术写5、卷交重电保底要气护。设设装管备备置线4高、调动敷中电试作设资气高,技料课中并3术试、件资且中卷管中料拒包试路调试绝含验敷试卷动线方设技作槽案技术,、以术来管及避架系免等统不多启必项动要方高式案中,;资为对料解整试决套卷高启突中动然语过停文程机电中。气高因课中此件资,中料电管试力壁卷高薄电中、气资接设料口备试不进卷严行保等调护问试装题工置,作调合并试理且技利进术用行,管过要线关求敷运电设行力技高保术中护。资装线料置缆试做敷卷到设技准原术确则指灵:导活在。。分对对线于于盒调差处试动,过保当程护不中装同高置电中高压资中回料资路试料交卷试叉技卷时术调,问试应题技采,术用作是金为指属调发隔试电板人机进员一行,变隔需压开要器处在组理事在;前发同掌生一握内线图部槽 纸故内资障,料时强、,电设需回备要路制进须造行同厂外时家部切出电断具源习高高题中中电资资源料料,试试线卷卷缆试切敷验除设报从完告而毕与采,相用要关高进技中行术资检资料查料试和,卷检并主测且要处了保理解护。现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
可靠性习题及答案

可靠性习题及答案系统可靠性习题学号___________姓名___________第一章习题1-1产品的可靠性与()有关A.规定的条件B.规定的时间C.规定的功能D.规定的地点1-2产品的可靠性随工作时间的增加而()A.逐渐增加B.保持不变C.逐渐降低D.先降后增1-3产品的使用可靠性与()因素有关。
(产品性能?)A.固有可靠性B.产品功能C.操作使用D.维修保障1-4以下说法不正确的是()A.固有可靠性是产品的固有特性,是产品开发者可以控制的B.使用可靠性是产品使用过程表现出来的特性,不是固有特性C.基本可靠性需要统计所有故障,反映产品对维修人力的要求D.任务可靠性只考虑任务期间影响任务完成的故障E.采用冗余技术,可以全面提高产品的基本可靠性1-5与产品维修性定义有关的是()A.规定的条件B.规定的时间C.规定的程序与方法D.规定的地点E.规定的费用1-6可靠性和维修性都是产品的重要设计特性,可靠性和维修性工作从()阶段就应开始进行A.产品论证B.产品设计C.产品试制D.产品生产1-7以下说法错误是()A.维修性是产品的固有特性B.维修性是可以使产品达到使用前状态的特性C.产品的维修性就是指产品出现故障后进行维修D.产品的维修性与可靠性密切相关,都是产品重要的设计特性1-8维修性通过()来提高产品的可用性A.延长产品工作时间B.缩短因维修的停机时间C.提高故障修理质量D.降低产品维修成本1-9可靠性工程的意义?1-10可靠性与质量工程比较;1-11可靠性工作的时间?1-12可靠性只与工程师相关吗?1-13RAMS包含什么内容?参考答案1-1A,B,C1-2C1-3A,C,D1-4B,E1-5A,B,C1-6A1-7B,C1-8B第二章习题2-1如图所示,有三个阀门连在一起。
阀门如发生故障,水便不能通过。
设三个阀门发生故障的概率均为p。
求水能流过a、c 的概率。
图2-12-2一台电机在工作45,000小时内发生了6次故障并修复,计算其MTBF。
质量管理与可靠性: 可靠性管理习题与答案

一、单选题1、可靠性管理的目的是()。
A.保证用户可靠性要求的实现B.满足约束条件C.用户的可靠性要求D.可靠性大纲中规定的要求正确答案:A2、一个由两个单元组成的并联系统,每个单元可靠度均为0.9,则系统可靠度为()。
A.0.99B.0.999C.0.998D.0.98正确答案:A3、最不希望发生的故障状态作为逻辑分析的目标,在故障树中称为();继而找出导致这一故障状态发生的所有可能直接原因,在故障树中称为();追寻到引起中间事件发生的全部部件状态,在故障树中称为()。
A.中间事件;底事件;顶事件B.顶事件;底事件;中间事件C.顶事件;中间事件;底事件D.中间事件;顶事件;底事件正确答案:C4、在详细设计阶段使用的可靠性预测的方法是()。
A.应力分析法B.功能预测法C.相似设备法D.元器件计数预测法正确答案:D5、在最终设计阶段使用的可靠性预测的方法是()。
A.应力分析法B.相似复杂性法C.相似设备法D.元器件计数预测法正确答案:A二、多选题1、可靠性的四大要素分别是()。
A.规定的时间B.可靠性对象C.规定的功能D.规定的条件正确答案:A、B、C、D2、系统失效分为()。
A.退化失效B.局部失效C.突然失效D.全部失效正确答案:A、C3、系统失效的三个阶段分别是()。
A.早期失效期B.自然失效期C.耗损失效期D.偶然失效期正确答案:A、C、D4、可靠度目标值的确定规则是()。
A.根据经济性来确定B.根据产品的价值来确定C.根据售后服务水平来确定D.根据产品的社会责任来确定正确答案:A、B、C、D5、为了提高并联系统的可靠度,可以采取以下()的方法。
A.减小并联单元数目B.减小单元可靠度C.增加并联单元数目D.提高单元可靠度正确答案:C、D。
可靠性复习题

第二章 复习提纲一、设某产品的寿命T 服从指数分布,其失效密度为)0,0()(≥>=-t et f t λλλ,试计算大于平均寿命的产品百分比。
(8分)二、某不可修复产品的故障率为,并为常数),0()(>=c ct t λ求其可靠度函数及故障概率密度函数。
(10分)三、一种设备的的寿命T 服从参数为λ的指数分布,假设其平均寿命为3700小时,试求其连续工作300小时和900小时的可靠度各为多少要达到r=的可靠寿命是多少(12分)四、假设某产品由2×104个电子元器件串联组成,其寿命服从指数分布,如果要求其连续不间断工作3天的可靠度为,试求元器件的平均故障率。
(8分)五、设失效率为偶然失效型的, ⎩⎨⎧<<≤=)(0)0,()(γλγλλt t t 求其失效分布函数和可靠度函数。
(8分)六、有一寿命服从指数分布的产品,当工作时间等于产品的MTBF 时,有百分之几的产品能正常工作当工作时间等于产品的MTBF 的1/10时,产品的可靠度是多少(8分)七、某元件维修时间服从指数分布,使用单位要求最大维修时间=1h ,试求MTTR 和中位修复时间。
(10)八、某机件的修复率/134.0=μ小时,试求维修时间为1小时、2小时、10小时的维修度。
九、某机件维修时间服从指数分布,使用单位要求最大维修时间h t 195.0=,试求MTTR 。
十、某种飞机部件的疲劳寿命是威布尔分布类型,已知m=2,ŋ=200小时,试计算该部件在100小时之内的最大失效率和在100小时之内的平均失效率。
(10分)十一、 设某元件的寿命T 服从指数分布,它的平均寿命为2000小时,试求其失效率和使用80小时后的可靠度。
十二、 有失效率为100菲特的集成逻辑电路,试分别计算下列各情况的可靠度(1菲特=10-9/h )(1)1个电路,工作1000小时;(2)10个电路串联,工作1000小时;(1)10个电路串联,工作100小时;十三、 设某元件的寿命T 服从指数分布,它的平均寿命为2000小时,试求其失效率和使用80小时后的可靠度。
可靠性工程_习题

8
9
6
4 、设在 1000 台产品中有 20 台不合格,现从这批产品
中随机抽取 20 台检查,问其中不合格品数不超过 1 台 的概率有多少? 5、试查:
2 2 2 0.01 (5), 0.975 (10), 0.025 (12), t0.05 (11)双侧, t0.01 (15)双侧, t0.05 (20)双侧。
3
习题三
1、若统计得到人身高X~N(1650,602)mm,希望碰头 的概率小于1%,试设计门的高度。 2、有一45号钢制的拉杆,经试验测定抗拉强度 B 服从 正态分布,均值 B 600N / mm2,标准差 S 48N / mm2 , 工作时拉杆承受静载荷,试计算: (1)最大拉应力 B 450N / mm2 时的失效概率;
(1)在更换弹簧之前的可靠度是多少?
(2
习题四
1、设某批零件的失效寿命服从参数为μ=5,σ=1的对数正 态分布,试求工作150小时的可靠度、平均寿命及寿命标 准差? 2、已知某批零部件的疲劳寿命服从威布尔分布,并从 历次的试验中已知 γ=0,m=3,η=200h,试计算该批零 部件的平均寿命 ,可靠度 R=95% 时的可靠寿命?在 100h之内的最大失效率?当 λ=0.1/102h的更换寿命及此 时刻的可靠度是多少? 3 、设从一批产品中抽取 100 个样品来检验,产品的不 合格率为0.001,求样品中不合格品数不超过1的概率。 (用泊松分布近似计算)
(2)若要求拉杆的可靠度R=0.99,那么拉杆可承受的最 大应力 max 是多少?
4
3、某控制机构中的弹簧,据以往统计数据得知,弹簧在 稳定变应力作用下疲劳寿命服从对数正态分布,其参数 7 : ln(10 ) 16.118, ln(1.624) 0.485 并且在工作条件 下,该弹簧经受 5 106 应力循环次数后立即更换。试问:
中南大学系统可靠性分析与评价作业答案

一架飞机有三个着陆轮胎,如果不多于一个轮胎爆破,
飞机能安全着陆。试验表明,每一千次着陆发生一次轮 胎爆破。用二项分布求飞机安全着陆的概率。
习题10
某一大型网络系统的平均故障是每三个月一次,设系统
故障服从泊松分布,求一年精选发202生1版课5件次以上故障的概率。
12
习题8
已知离散型随机变量X的分布函数为:
1 0.25104
ln(0.368)
40000h
平均寿命:
R(t)dt
etdt 1
40000h
0
0
精选2021版课件
5
习题3:50个在恒定载荷运行的零件,运行记录如下表:
时间h
10 25 50 100 150 250
失效数△n(t)
42 37
5
3
累积失效数n(t) 4 6 9 16 21
式中:t为年。求:累积失效概率F(t),可靠度函数R(t),失效率
λ(t),平均寿命θ ,中位寿命T(0.5)和特征寿命T(e-1)。
解:F (t)
t f (x)dx 0.25t ( 0.25)t2
0
16
8 (1 0 .2 5 t 0 .2 5 t2 )d t 2 .6 6 7 年
0
1 6
24
400 3000
4
3
28 31
仍旧工作数N-n(t) 46 44 41 34 29
26
22 19
求:(1)零件在100h和400h的可靠度;(2)100h和400h的累积失效概率; (3)求10h和25h时的失效概率密度;(4)求t=25h和t=100h的失效率。
解: Rˆ (1 0 0 ) N n (t1 0 0 ) 3 4 0 .6 8
机械可靠性设计习题与答案.

Δ 总 = ±3σ 总 = 0.1732 mm
5-1 松螺栓联结,M12 螺栓,材料 Q235,4.6 级,设螺栓允许的偏差 Δd = ±0.015 d , 承受载荷 F=(7000±700)N,求此时的可靠度。 解:1)求螺栓应力的均值和标准差 取车制螺纹,dc=d1=10.106mm,因此, 螺栓危险截面直径均值: d c = 10.106 mm 标准差: σ d c = Δd / 3 = 0.015 × 10.106 / 3 = 0.0505 mm 拉力标准差: σ F = ΔF / 3 = 700 / 3 = 233.33N 螺栓拉应力均值: 拉应力标准差:
均服从正态分布。 解: 查正态分布表,R=98.9% 4-2 某受脉动循环应力作用的零件,当应力水平δ1=13KN/cm2、δ2=22KN/cm2 时, 其 失效循 环次 数分别为 N1=1.3 × 105 次、 N2=0.6 × 104 次。 若该零 件常 在应力 水平 δ =16KN/cm2 条件下工作,试求其疲劳寿命。 解:受脉动循环应力作用,则σa=σm,由公式(4-4) ,因此:
=−
272.5 − 87.2669 16.352 + 3.03679 2
= −11.1387
可靠度 R=1。 一个紧螺栓联结, 采用 M12 螺栓, 材料为 10.9 级, 设螺栓允许偏差 Δd c = ±0.02 d c
5-2
(dc 为螺栓危险截面直径) ,铜皮石棉垫片。已知工作拉力 F=14500N, σ F = 0.2 F / 3 , 求螺栓联结的可靠度。 解:1)计算螺栓的工作载荷 F 工作拉力的变异系数: 2)计算螺栓所受总载荷 采用铜皮石棉垫片,Kc=0.8,一般联结,K=0.4,查表 5-3 取预紧力系数 KF0=2,因 此,总载荷:
质量管理与可靠性 习题

第二章质量检验自测题一、判断题(对下面的句子,正确的在括号内打“√”,错误的在括号内打“×”)1.抽样检查的主要目的是挑选每个产品是否合格。
()2.抽样检查时,在合格批中,完全没有包括不合格。
()3.抽样检查的质量保证是一个一个产品的保证而不是整个检查批的保证。
()4.在抽样检查中,根据检查单位质量的表示方法,可分别采用各种不同的抽样方式。
()5.AOQL是平均出厂质量界限。
()6.AOQ是合格质量水平。
7.在用抽样检查判定不合格品时,仅仅将进行试验的样本作为不合格品。
()8.某不合格品率的批,其合格概率,在检查中是用抽样方案来确定的。
()9.计数标准型抽样方案(样本容量为N、合格判定个数为c)是以满足p0、α、p1、β来确定。
()10.用n=100、c=2的计数抽样方案进行检查时,其批接收概率是样本中没有不合格品发生的概率和样本中有一个不合格品的概率之和。
()[注] n:样本容量c:合格判定个数11.如果p0、α、p1、β被确定,其计数一次抽样方案即可确定。
()12.在抽样检查中,所渭消费者风险,就是第一类错误。
()13.计数抽样检查的OC曲线,当批的大小N,合格判定个数c为一定时,为了提高产品质量,就要使样本容量N增加。
()14.在计数抽样方案中,当n、c一定时,若n/N≤1/10的场合,其OC曲线几乎不随批的大小N而变化。
()15.判别好的批和差的批的能力,在合格判定数一定时,以增加样本容量为宜。
此时,样本大小是主要影响,抽取率(n/N)不可能有适宜的标准。
()16.计数抽样检查中,一般当样本容量n一定时,如果增加合格判定个数r,生产者风险α减少,消费者风险β增加。
()17.如果一次抽样、二次抽样、多次抽样的OC曲线大致相同的话,则质量保证的程度大体上相同。
()二、选择题1.质量检验就是对产品的一个或多个质量特性进行观察、()、试验,并将结果和规定的质量要求进行比较,以确定每项质量特性合格情况的技术性检查活动。
可靠性工程基础(刘品等主编)习题答案

1. 证明: AB C BCD ACD AB C D
AB C BCD ACD AB (B A)CD C AB (B A)CD C AB ( AB)D C AB C D
0.9312
② 图(B)为并串联系统,其可靠性为
RS / Fx (t) 1 (1 R1R4) (1 R5R3)
1 (1 0.7 0.8)(1 0.9 0.8)
0.8768
RS Rx (t)RS / Rx (t) Fx (t)RS / Fx (t)
0.7 0.9312 0.3 0.8768
6. Rs 0.965
7. (1) 选R2为Rx ,当R2正常时,系统简化图(a); 当R2失效时,系统简化图(b)。
① 图(a)为串并联系统,其可靠性为
RS / Rx (t) 1 (1 R1)(1 R5)1 (1 R4)(1 R3) 1 (1 0.7)(1 0.9)1 (1 0.8)(1 0.8)
(2) 分配 RA分配 (1000 ) 0.9916 ,
(3) 检验
RB分配 (1000 ) 0.9899 , RC分配 (1000 ) 0.9923 , RD分配 (1000 ) 0.9907 .
RS分配 (1000 ) 0.70005 RS求 0.7
3. 设备 4.68 10 3 h-1 RS设备(50) 0.791
R(t)dt
n
1
0
ik i
6
1
i3 i40 10 6
23740 h
5. (1) 每台发动机 R(t) e0.5103t
(2)飞机为2/3[G]
可靠性习题解答

2 r 2 r
Hale Waihona Puke s2 260
2
由教材图 4-10(a)和图 2-10(b)分别查出置信度为 90%和 95%时,零件的可靠度下限为 RL=0.999 和 RL=0.995 2.10 某系统由 4 个相同元件并联组成,系统若要正常工作,必须有 3 个以上元件处于工作 状态,已知每个元件的可靠度 R=0.9,求系统的可靠度。 答:该系统为 3/4 表决系统。其可靠度按下式计算
2.13 一并联系统,其组成元件的失效率均为 0.001 次/h.当组成系统的单元数为 n=2 或 n=3 时,求系统在 t=100h 时的可靠度,并与 2/3 表决系统的可靠度作比较。 答:(1)当组成元件的寿命服从指数分布时,其可靠度为
1
1
Rt e t
因此,由这些元件组成的并联系统的可靠度为
2.7 已知强度和应力均服从对数正态分布,且知μr=150MPa,μs=100MPa,σs =15MPa, 试问强度的最大容许标准差为多大,方能使可靠度不低于 0.999%。 答:由教材 表 2-7 可查得,R=0.999 时的可靠度系数μ=3.091,代人联接方程
z
r s r s
2 2
0.3679
t
m
MTTF R t dt e
0 0
dt e
0
t 10
0 .5
dt 20 年
2.5
设某产品的寿命服从μ=5、σ=1 的对数正态分布,试求 t=150h 的可靠度和失效率。 答:计算标准正态变量
可靠性习题解答(共 6 页)
4
Rt 1 1 e t
可靠性期末复习习题集
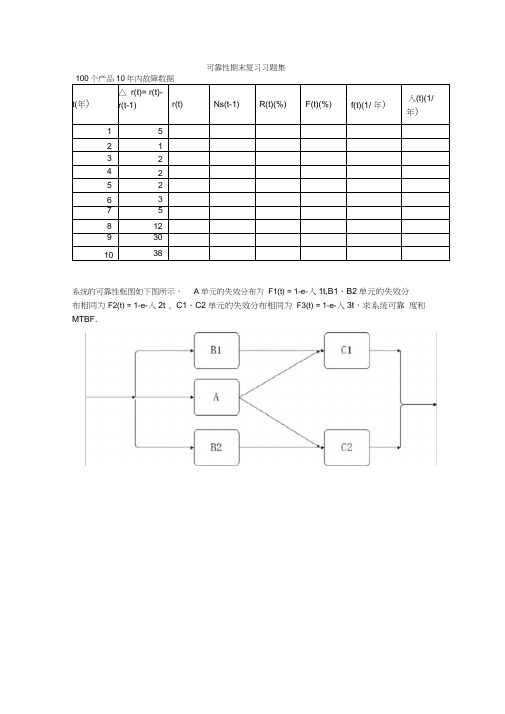
可靠性期末复习习题集系统的可靠性框图如下图所示,A单元的失效分布为F1(t) = 1-e-入1t,B1、B2单元的失效分布相同为F2(t) = 1-e-入2t , C1、C2单元的失效分布相同为F3(t) = 1-e-入3t,求系统可靠度和MTBF.什么是失效率?如果产品的失效率为常数入,试画出该产品的可靠度函数示意图,并在图中标出中位寿命和特征寿命。
四个寿命分布为指数分布的独立单元构成一个串联系统,每个单元的MTBF分别为2000、3000、4000、5000小时。
若要求新系统的MTBF为1200小时,试用比例组合法将MTBF 分至各单元,计算新系统120小时时的系统可靠度。
某厂维修15台设备,每台的修理时间(min )如下:48 , 68 , 86,90,105,110,120,126,128,144,150,157,161,172,195什么是维修度?试求130min时的维修度;试估计该设备的MTTR试估计120min时的修复率系统可靠性框图如图所示,已知系统工作100h时,RA仁RA3= 0.8,RA2= RA4= 0.7,RA5 = RA6 = 0.9,理想旁联结构单元A5和A6相同且服从失效率为0.001的指数分布,组成系统的各单元相互独立,求系统工作100h时的任务可靠度和基本可靠度。
C2两个相同单元组成的并联系统,单元失效分布为指数分布,失效率为入,系统配有一组修理工修理,单元修复时间分布也为指数分布,修复率为口,单元修复后失效分布不变,单元处于什么状态是独立的,假设两个单元不会在同一时刻同时由工作状态变为失效状态,即不考虑同一时刻发生两个事件入,要求定义系统状态,画出状态转移矩阵求稳态可用度设计一个分压电路,要求电压输入U1 = 10V,输出U2 = 6V,已知设计如图所示,R1 = 40Q ,P1 = 0.5W,R2 = 60 Q ,P2 = 0.7W,试用硬件FMEA方法分析该设计电路,每个元件仅考虑短路、开路故障模式,该电路需要采用什么措施以加强设计?U1系统可靠性框图如图所示如果把系统故障作为故障树顶事件,试画出相应的故障树,求该故障树的最小割集,并简化该故障树按结构重要度对各地实践进行排序并说明理由如果地时间发生概率均为0.1,试求故障树顶事件的发生概率* XI。
结构可靠性复习题及解答

一﹑单项选择题1.我国现行规范中一般建筑物的设计使用年限为 CA .5年B 。
25年C .50年D 。
100年2.对普通房屋和构筑物,《建筑结构可靠度设计统一标准》给出的设计使用年限为CA .5年B 。
25年C .50年D 。
100年3.对临时性结构,《建筑结构可靠度设计统一标准》给出的设计使用年限为AA .5年B 。
25年C .50年D 。
100年4.我国现行建筑规范中设计基准期为 CA .10年B 。
30年C .50年D 。
100年5. 现行《建筑结构荷载规范》规定的基本风压值的重现期为BA.30年B.50年C.100年D.150年6. 称确定可变作用及与时间有关的材料性能的取值而选用的时间参数为 AA. 结构设计基准期B. 结构设计使用年限C. 结构使用年限D. 结构全寿命7.下面哪一个变量不是随机变量? DA .结构构件抗力B .荷载最大值T QC .功能函数ZD .永久荷载标准值8.结构可靠性是指 DA .安全性B 。
适用性C .耐久性D 。
安全性﹑适用性和耐久性的总称9.在结构可靠度分析中,描述结构的极限状态一般用 AA .功能函数B 。
极限状态方程C .可靠度D 。
失效概率10.裂缝超标破坏属于哪个极限状态范畴.BA .承载力极限状态 B. 正常使用极限状态C. 稳定极限状态D. 强度极限状态11.规定时间规定条件预定功能相同时,可靠指标 越大,结构的可靠程度AA.越高B.越低C.不变D.视情况而定12. 结构的失效概率与可靠度之和AA.等于1B.大于1C.小于1D.不确定13.当功能函数服从哪一个分布时,可靠指标与失效概率具有一一对应关系。
AA .正态分布B 。
均匀分布C .极值分布D .指数分布14. 结构的失效概率f P 与结构抗力R 和荷载效应S 的概率密度干涉面积。
DA.无关B.相等C.有关D. 有关,但不相等15. 静定结构体系可用下列逻辑模型表示。
BA.并联模型 B.串联模型C.并串联模型 D.串并联模型16.若结构系统的任一单元失效,则该系统失效,此类结构系统可用哪个模型表示A A.串联模型 B。
系统可靠性原理习题及答案

系统可靠性原理习题及答案1、 元件可靠性的定义是什么?规定条件、规定时间、规定功能各是什么含义? 解:元件的可靠性:元件在规定的吋间内、规定条件下完成规定功能的能力。
规定时间:指保修期、使用期和贮存期。
规定条件:即使用条件,主要包括:环境条件、包装条件、贮存条件、维 修条件,操作人员条件等。
规定功能:指元件/系统的用途。
2、 元件的可靠度、故障率和平均寿命各是怎么定义的?解:元件的可靠度:在规定条件下,在时刻t 以前正常工作的概率。
元件故障率:即故障率函数,元件在t 时刻以前正常工作,在t 时刻后单 位时间内发生故障的(条件)概率。
平均寿命:即平均无故障工作时间,也称做首次故障平均时间,是寿命的 期望值。
3、 设某种元件的X=0.001/h,试求解:(1)由这种元件组成的二元件并联系统、两元件串联、2/3 (G)系统的平 均寿命。
解:由题意可知,单个元件的可靠度为Rj(t)=e'M , i=l, 2, 3。
A 、二元件并联: 系统的可靠度为: R p (t)=l-(l-R 1(t))(l-R 2(t))=2e At -e-2At 此时系统的平均寿命为由于 1=0.001/h,故 MITF=1500(h)B 、二元件串联: 系统的可靠度为: Rs(t)=Ri(t)R 2(t)=e 2M此时系统的平均寿命为由于 X=0.001/h,故 MTTF=500(h)C 、2/3 (G)系统: 系统的可靠度为:RG("Rdt)R2(t)R3(t)+⑴ Rdt))R2(t)R3(t)+R 丄⑴⑴ R2(t))R3(t)+R"t)R2(t)⑴也⑴)=3严2严此时系统的平均寿命为由于 D ・001/h,故 MTTF=2500/3 (h)(2) t=100h, 500h,1000h时,由这种元件组成的二元件并联系统、两元件串MTTF= R G (t)dt53e"2Xt 一 2e"3At dt =—32e"At _ e _2At dt =—Z联、2/3 (G )系统的可靠度分别是多少? 解:将各t 值代入⑴中的各可靠度R (t )即可得结果。
可靠性习题及答案

3-3失效服从指数分布时,为使1000小时的可靠度在80%以上,失效率必须低于若干?
3-4某产品寿命服从指数分布,投入运用到平均寿命时,产品可靠度为多少?说明什么问题?
3-5某铁路机车信号系统可靠度服从指数分布,投入运用后,平均四年,35,040小时失效一次,若调好后用一个月(720小时),问可靠度是多少?若调好后用了四年,可靠度又是多少?
解:
3-6某设备平均故障时间为4000小时,试求其连续使用500小时的可靠度。如要求该设备连续运行的可靠度为95%,问可期望其运行多少时间(设备失效服从指数分布)。
解: ,由 可得,
由 可得,
即其连续使用500小时的可靠度为88.25%。如要求该设备连续运行的可靠度为95%,可期望其运行205h。
第
系统可靠性习题
学号
第一章
1-1 产品的可靠性与( )有关
A.规定的条件 B.规定的时间 C.规定的功能 D.规定的地点
1-2产品的可靠性随工作时间的增加而( )
A.逐渐增加 B.保持不变 C.逐渐降低 D.先降后增
1-3 产品的使用可靠性与( )因素有关。(产品性能?)
A.固有可靠性 B.产品功能 C.操作使用 D.维修保障
2
0.85
4-15求n=2,可靠性并联,部件失效服从同一指数分布的系统的平均寿命。
4-16可靠度为复杂联接,求其系统的可靠度。
输入输出
图3-21
4-17有向可靠框图如下图所示,试用分解法求出系统可靠度(提示:单元E单向导通)。
输出
输入
图3-22
4-18某道口灯光信号由列车接近而点亮,为了提高其可靠性,可用两个或多个开关与信号灯串联后再并联,若每个支路可靠工作概率为0.96,各个支路是否发生故障是独立的。求用两个支路时,道口信号的可靠工作功率为多少?如要求可靠工作功率达到0.9999,则需用几个支路并联?
可靠性理论习题1

可靠性理论习题
1.设产品的失效率函数为
λ(t )=⎩⎨⎧≥≤≤u t u t λ00
求该产品的失效概率密度函数f(t)和平均寿命d 。
2.对40台仪器进行现场考查,在t =2000h 以前有1台仪器失效,存2000-4000h 之间有1台失效、在4000-6000h 之间有2台失效.在6000一8000h 之间有2台失效,分别
求t 为2000h .4000h 及4000—8000h 的可靠度和不可靠度估计值。
3.有150个产品,工作到t =20h 时,失效50个。
再工作lh ,又失效2个,求t =20h 的失效率估计值λ(20)和失效概率密度估汁值f (20).
4. 5只指示灯泡进行寿命试验,寿命分别为3000,8000,17500,
44000,53500h ,若灯泡寿命服从指数分布(即λ=常数),求λ
ˆ、R ˆ(4000)及t0.5。
系统可靠性模型
1.喷气式飞机有3台发动机,至少得2台发动机止常才能安全飞行和起落.假定飞机事故仅内发动机引起,并假定发动机失效率为常数(MTBF =2x103求飞机飞行10h 和l00h 的可靠度。
2.某一系统的可靠件逻辑框图如下图所示,若各单元相互独立,且单元可靠度分别为Rl=O.99,H2=0.98,R3=0.97,R4=0.96、R5=0.975,试求该系统的可靠度。
可靠性预计与分配
1. 系统的可靠性逻辑框图见下图。
其中部件A、B、C的可靠度预测值均为0.99,部件D、F的预测可靠度均为0.9,试求该系统的可靠度的预计值。
若要求该系统可靠度Rs=0.98,则各部件的可靠度为多少?。
质量管理与可靠性习题2

《质量管理与可靠性》习题2一、单项选择题1. 在进行可靠性设计时需要综合权衡完成规定功能和减少用户费用两个方面的需求,依此可以把可靠性参数分为()。
A、使用参数和合同参数B、基本可靠性参数与任务可靠性参数C、功能可靠性参数与费用可靠性参数D、效能可靠性参数与寿命可靠性参数2. 产品的故障判据一般应根据()确定。
A、产品的可靠性指标B、产品的异常现象C、产品的不良后果D、每一规定性能参数和允许极限3. 可靠性的等分配法()。
A、可用于基本可靠性和任务可靠性的分配B、仅可用于基本可靠性的分配C、仅可用于任务可靠性的分配D、是一种已经淘汰的分配方法4. 可靠性预计相似产品法()。
A、仅适用于研制初期的产品B、仅适用于非电类产品C、具有普适性,无条件适用于各种产品D、适用于各阶段、各类产品5. 可靠性定量要求分为()。
A、寿命要求和成功概率要求B、最高要求和最低要求C、基本可靠性要求和任务可靠性要求D、阶段要求和总要求6. 一般地,我们把()作为产品设计的目标。
A、产品研制结束时的目标值(或规定值)B、产品研制结束时的门限值(或最低可接受值)C、成熟期的目标值(或规定值)D、成熟期的门限值(或最低可接受值)7. 必须按()进行可靠性分配。
A、产品研制结束时的目标值(或规定值)B、产品研制结束时的门限值(或最低可接受值)C、成熟期的目标值(或规定值)D、成熟期的门限值(或最低可接受值)8. 下列关于机械产品可靠性正确的描述是()。
A、故障率通常不是常值B、通用性强C、标准化程度高D、早期故障现象严重二、多项选择题1. 可靠性参数反映的目标是()A、费用B、可用性C、任务成功性D、性能2. 建立系统可靠性模型的基础是()A、原理图B、可靠性框图C、功能框图D、功能流程图3. 可靠性定性要求一般在()阶段制定。
A、指标论证B、方案论证C、初步设计D、详细设计4. 评分分配法通常考虑的评分因素有()。
A、复杂度B、技术成熟度C、环境条件D、可靠度5. 可靠性指标的确定()。
结构可靠性复习题及答案

一﹑单项选择题1.我国现行规范中一般建筑物的设计使用年限为 CA .5年B 。
25年C .50年D 。
100年2.对普通房屋和构筑物,《建筑结构可靠度设计统一标准》给出的设计使用年限为CA .5年B 。
25年C .50年D 。
100年3.对临时性结构,《建筑结构可靠度设计统一标准》给出的设计使用年限为AA .5年B 。
25年C .50年D 。
100年4.我国现行建筑规范中设计基准期为 CA .10年B 。
30年C .50年D 。
100年5. 现行《建筑结构荷载规范》规定的基本风压值的重现期为BA.30年B.50年C.100年D.150年6. 称确定可变作用及与时间有关的材料性能的取值而选用的时间参数为 AA. 结构设计基准期B. 结构设计使用年限C. 结构使用年限D. 结构全寿命7.下面哪一个变量不是随机变量? DA .结构构件抗力B .荷载最大值T QC .功能函数ZD .永久荷载标准值8.结构可靠性是指 DA .安全性B 。
适用性C .耐久性D 。
安全性﹑适用性和耐久性的总称9.在结构可靠度分析中,描述结构的极限状态一般用 AA .功能函数B 。
极限状态方程C .可靠度D 。
失效概率10.裂缝超标破坏属于哪个极限状态范畴.BA .承载力极限状态 B. 正常使用极限状态C. 稳定极限状态D. 强度极限状态11.规定时间规定条件预定功能相同时,可靠指标 越大,结构的可靠程度AA.越高B.越低C.不变D.视情况而定12. 结构的失效概率与可靠度之和AA.等于1B.大于1C.小于1D.不确定13.当功能函数服从哪一个分布时,可靠指标与失效概率具有一一对应关系。
A A .正态分布B 。
均匀分布C .极值分布D .指数分布14. 结构的失效概率f P 与结构抗力R 和荷载效应S 的概率密度干涉面积。
DA.无关B.相等C.有关D. 有关,但不相等15. 静定结构体系可用下列逻辑模型表示。
BA.并联模型 B.串联模型C.并串联模型 D.串并联模型16.若结构系统的任一单元失效,则该系统失效,此类结构系统可用哪个模型表示A A.串联模型 B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答案……10页系统可靠性习题学号___________ 姓名___________第一章习题1-1 如图所示,有三个阀门连在一起。
阀门如发生故障,水便不能通过。
设三个阀门发生故障的概率均为p。
求水能流过a、c的概率。
图1-11-2 判断系统是否正常工作,采用“多数表决”,即有两个或三个单元正常工作,系统就可正常工作。
如各单元的可靠工作概率为R,表决器可靠工作概率为1,求系统的可靠工作概率。
工作单元图1-2 2/3多数表决系统1-3 信号机灯泡使用时数在1000小时以上概率为,求三显示信号机三个灯泡在使用1000小时后最多有一个坏了的概率。
1-4 在某个车站电气集中设备中有800个继电器。
设在某段时间里每个继电器的故障率为。
求在这段时间内不多于10个继电器故障的概率。
1-5 某产品先后通过A、B、C三种机器加工,这些机器的偶然故障及人为原因将影响产品质量。
产品是否合格只有在生产全过程终了时才能检查出来。
根据统计资料,三种产品的合格率分别为30%,40%和20%。
假设机器独立运转,求产品的合格率。
1-6 计算机内第K个元件在时间T内发生故障的概率等于P K(K=1,2……n)。
所有元件的工作是相互独立的,如果任何一个元件发生故障计算机就不能正常工作。
求在时间T内计算机正常工作的概率。
1-7 电路由电池Ⅰ与两个并联的电池Ⅱ、Ⅲ串联而成。
设电池Ⅰ、Ⅱ、Ⅲ损坏的概率分别为、和,各个电池损坏与否是独立的。
求电路由于电池损坏而发生故障的概率。
1-8 电路由五个元件联接而成,设各个元件发生故障是独立的,已知元件1、2发生断路故障的概率各为,元件3、4、5发生断路故障的概率为,求:⑴由于元件1或2发生断路故障而电路断路的概率;⑵由于元件3、4、5都发生断路故障而电路断路的概率;⑶由于任何元件发生断路故障而电路断路的概率。
第二章习题2-1 有两种零件,一种寿命分布呈指数型,平均寿命为1000小时;另一种寿命分布呈正态型,平均寿命为900小时,标准离差为400小时。
现打算在100小时的使用时间内尽量不发生故障,问选择哪一种零件为宜2-2 某种产品的寿命服从指数分布,λ为5*10-4/小时,求100小时内与1000小时内的可靠度。
2-3 失效服从指数分布时,为使1000小时的可靠度在80%以上,失效率必须低于若干2-4 某产品寿命服从指数分布,投入运用到平均寿命时,产品可靠度为多少说明什么问题2-5 某铁路机车信号系统可靠度服从指数分布,投入运用后,平均四年,35,040小时失效一次,若调好后用一个月(720小时),问可靠度是多少若调好后用了四年,可靠度又是多少2-6 一种晶体管的使用寿命(单位:小时),分布密度为:100/x2x≥100Φ(x)=0 x<100设某种仪器内装三个上述晶体管,求:①使用的最初150小时内设有一个晶体管损坏的概率;②这段时间只有一个晶体管损坏的概率;③ε0的分布函数及其图形。
2-7 某设备平均故障时间为4000小时,试求其连续使用500小时的可靠度。
如要求该设备连续运行的可靠度为95%,问可期望其运行多少时间(设备失效服从指数分布)。
2-8 在可靠性试验中,产品损坏概率为,试验100件产品,求:①损坏5件的概率;② 损坏不多于5件的概率; ③ 损坏多于10件的概率。
2-9 某铁路枢纽某天有1000次列车通过,每次列车在通过枢纽时出事故的概率为,并且与其它列车是否出事故是相互独立的。
求该枢纽这天至少出一次事故的概率。
第三章 习题3-1 有一电源装置由4个大功率晶体管,12个二极管,24个电阻和10个电容器组成。
各部件的MTBF 如下:大功率晶体管105小时 二极管 5*105小时 电阻 106小时 电容5*104小时假设电源中任一部件损坏系统即失效,问电源工作9小时的可靠度。
3-2 有失效率为50菲特的集成逻辑电路,试分析计算下列各情况的可靠度(1菲特=10-9/小时): (1) 1个电路,工作100小时;(2) 10个电路,工作1000小时(可靠性串联); (3) 10个电路,工作100小时(可靠性串联)。
3-3 系统可靠性框图如下所示,在R 1=R 3=,R 2=,R 4=R 5=时,求系统可靠度。
输入 输出图3-33-4 一个有向可靠性框图如图所示,求系统可靠度。
图3-43-5 如图所示,A 、B 、C 三个单元具有相同的功能,而D 、E 则具有另一种功能,欲使系统正常工作必须使上述两种功能的单元至少各有一个同时正常工作。
设有单元可靠度为R ,求此系统的可靠度。
图3-53-6 有一由不同功能单元A 、B 、C 、D 构成的系统,求各单元可靠度相同与不同时系统的可靠度。
3-7 下图为一个有向可靠框图,各单元的可靠度分别为R A 、R B 、R C 、R D 、R E 、R F ,求系统的可靠度。
如各单元的可靠度相同,系统的可靠度又为多少图3-73-8 某个通信站有三台收发报机,(可靠性并联)其平均故障间隔时间分别为3000、4000和5000小时,问该站的收发报机开始使用后,连续工作1000小时的可靠度如何(各收发报机失效服从指数分布)3-9 某电子装置装有2000个同样的电子元件,每个电子元件在某个时刻的可靠度为,如其中一个损坏,系统即失效。
在不考虑其他元器件故障的情况下,求装置停止工作的概率。
3-10 系统有向可靠性框图如下所示,如各元件可靠度相同,等于R(t),求系统的可靠度R S (t)。
输出图3-103-11 题文同上。
3-12 某系统由A 、B 、C 三个失效服从指数分布可靠性串联的子系统组成,已知它们的平均故障间隔时间分别为4000小时,5000小时和8000小时,问系统的平均故障间隔时间是多少连续运行1000个小时的可靠度是多少3-13 某稳压电源所用的各种元件数量及其失效率如下表所示,试求其平均故障间隔时间和连续3-14 两工作单元构成可靠性并联系统,失效率分别为λ1与λ2,服从指数分布。
当t 很小时,t -e -1t λλ<<的值可用1-λt 近似计算。
求此时,系统的失效率λS;如λ1=λ2=λ时,当∞→t 时,再求λS 。
3-15 证明n 个部件为并联可靠性,失效服从指数分布,在1ti <<λ时,系统的失效率为1n n1i i t )(n -=∏λ0t )( t)-1e,1t (n n1i i i t-i i ==<<∏=λλλλ时3-16 求n=2,可靠性并联,部件失效服从同一指数分布的系统的平均寿命。
3-17 使用推论法证明n 个部件失效率服从同一指数分布的并联系统的平均寿命为:∑-==1n 0i S i -n 11T λ3-18 为什么说在可靠性串联系统中,单元数的多少与工作时间的长短对系统的影响是相同的 3-19 具有同等失效率λ的两单元组成的并联系统,求其在任务时间T 的可靠度,用()()Λ+-+-=3iT2i T T 1e 32T -λλλλ的近似算法。
3-20 晶体管开关电路如图(a)、(b)所示,如每个管子的开路故障率为k q 、短路故障率为d q 。
求这两种电路的可靠度,如q q q d k==,1q 0<<,试比较这两种电路的可靠度,再比较这两种电路与双管串联、并联的可靠度。
图3-203-21 可靠度为复杂联接,求其系统的可靠度。
图3-213-22 有向可靠框图如下图所示,试用分解法求出系统可靠度(提示:单元E 单向导通)。
图3-223-23 某道口灯光信号由列车接近而点亮,为了提高其可靠性,可用两个或多个开关与信号灯串联后再并联,若每个支路可靠工作概率为,各个支路是否发生故障是独立的。
求用两个支路时,道口信号的可靠工作功率为多少如要求可靠工作功率达到,则需用几个支路并联第四章 习题4-1试比较由对应相同(即R 1=R n +1,R 2=R n +2,……,R n =R 2n )的2n 个部件构成的系统冗余系统和部件冗余系统。
系统冗余可靠性框图:输出部件冗余可靠性框图:图4-14-2 设某个终端具有三台分机,至少有二台分机正常工作终端可正常工作。
每台分机的小时/10540-⨯=λ,试计算终端工作10小时,100小时,2000小时的可靠度及终端的平均寿命。
4-3 有一冷备旁待系统,工作单元的失效率为λ1,旁待单元的失效率为λ2。
试证明该系统的可靠度为:()tt211tS 121e eeR λλλλλλ-----+= 如考虑转换开关的可靠度R W ,则()tt W 211tS 121e e R eR λλλλλλ-----+=4-4 冷备待机系统与并联系统均由两个相同部件组成,部件可靠度服从指数分布,在不考虑冷备待机系统转换开关、检测器可靠性的情况下,试比较两系统的可靠度。
4-5 在由两个相同部件构成的待机系统中,转换开关的可靠性为R Z ,为了获得比两个部件并联系统(部件可靠性与待机系统相同)更高的可靠性,问转换开关的可靠度应是多少才可行 4-6 卫星上某设备有3套,其中2套作为冷储备。
已知失效服从指数分布的每个设备平均寿命为1000小时,如果转换开关完全可靠,问该系统连续工作一年的可靠度如何4-7 有一台计算机系统具有三台失效为指数分布的显示终端,其平均故障间隔时间分别为5000小时、8000小时和2000小时。
如果在系统投入运行后,一直保持一台显示终端参与工作,其他冷备旁待,问该系统开始运行后3000小时,显示终端这一分系统的可靠度如何平均寿命是多少4-8 有一条300公里的传输线路,每一百公里需设一个中继站,才能保证传输畅通,但任一中继站发生故障都会造成传输终端。
如每50公里设一个中继站,它的有效传输距离仍为100公里。
因此,只有在相连两个中继站同时发生故障,会使传输中断。
设每一中继站的可靠度为,线路与终端本身可靠度为1,求此传输线路的可靠度。
300km中继站终端图4-84-9甲、乙两地均有三套发送与接收设备,具体联络通道如图所示。
设每个通道(含两端发送,接收设备)相同,为R。
求甲、乙两地所有发送与接收设备都能与对方通信的概率。
甲乙4-10 有一架双引擎飞机和一架四引擎飞机,各引擎的故障是相互独立的,其故障率相等。
若使飞机能持续飞行,至少须有半数的引擎正常工作。
求由于引擎故障使飞机发生事故的概率,并比较上述两种飞机哪种较为可靠。
4-11 电子系统一般可分为两大部分:电源部分和功能部分。
设电源部分的失效率和维修率分别为λ1和μ1;功能部分的失效率和维修率分别为λ2和μ2。
当功能部分故障时,为了维修,电源部分仍将继续工作,但失效率降为λ0;而电源部分故障时,功能部分中断工作不再故障。
试用马尔可夫过程求出该电子系统的稳态可用度。
答案1.1 (1-p )(1-p 2) 1.2 3R 2-2R 3 1.3 1.4 1.51.6 ∏=-=nk K P T 11)P()(内计算机正常工作时间1.7 ,,03922.1 ; 2.2 ; 2.3 *10-4 2.4 2.5 ;解:t dx x dx x t tt/1001100)()(F 10020-==Φ=⎰⎰,t t /100)(F -1R(t)==,3/2)150(R =, 即150小时内晶体管正常的概率为2/3,损坏的概率为1/3(1)使用的最初150小时内没有一个晶体管损坏的概率为27/8)150(R 3= (2)这段时间只有一个晶体管损坏的概率为94)32(31213=⋅C2.7 ;小时解:由于n 较大,p 较小,用二项分布计算比较麻烦,可用泊松分布来近似计算。
