MATLAB及应用-第八讲终版.ppt
合集下载
MATLAB及应用第八讲 PPT

式 中 numz,denz 与 A,B,C,D 分 别 为 系 统 得 开 环 传递函数与状态方程得参数,Ts为取样频率,w 为Bode图得频率点。
3、 显示绘制结果
可以利用下面得MATLAB命令
>>subplot(2,1,1);semilogx(w,20*log10(mag))
>>subplot(2,1,2);semilogx(w,phase)
8、lsim()函数得用法
[y,t,x]=lsim(sys,u,t); [y,t,x]=lsim(sys,u,t,x0);
9、dlsim()函数得用法
dlsim(sys,u); [y,x]=dlsim(sys,u,x0);
eg8、 求下列系统得正弦响应。其中:周期2*pi,时间 t=30s,采样周期取0、1s、
1、gensig()函数得用法
[u,t]= gensig(type,tau) [u,t]= gensig(type,tau,tf,ts)
采样时间 持续时间 信号周期 信号类型
时间序列 信号序列
eg1、 生成一个周期为2*pi,持续时间为50s,采样时间 为0、01s得正弦波与方波信号。
程序: [u1, t1]=gensig(‘sin’, 2*pi, 50, 0、01); [u2, t2]=gensig(‘square’, 2*pi, 50, 0、01); plot(t1,u1,t2,u2) axis([0 50 -1、2 1、2]) xlabel(‘time/s’) ylabel(‘c(t)’)
y=step(numc,denc,t);
plot(t,y)
title(‘Step response’)
xlabel(‘Time/s’)
3、 显示绘制结果
可以利用下面得MATLAB命令
>>subplot(2,1,1);semilogx(w,20*log10(mag))
>>subplot(2,1,2);semilogx(w,phase)
8、lsim()函数得用法
[y,t,x]=lsim(sys,u,t); [y,t,x]=lsim(sys,u,t,x0);
9、dlsim()函数得用法
dlsim(sys,u); [y,x]=dlsim(sys,u,x0);
eg8、 求下列系统得正弦响应。其中:周期2*pi,时间 t=30s,采样周期取0、1s、
1、gensig()函数得用法
[u,t]= gensig(type,tau) [u,t]= gensig(type,tau,tf,ts)
采样时间 持续时间 信号周期 信号类型
时间序列 信号序列
eg1、 生成一个周期为2*pi,持续时间为50s,采样时间 为0、01s得正弦波与方波信号。
程序: [u1, t1]=gensig(‘sin’, 2*pi, 50, 0、01); [u2, t2]=gensig(‘square’, 2*pi, 50, 0、01); plot(t1,u1,t2,u2) axis([0 50 -1、2 1、2]) xlabel(‘time/s’) ylabel(‘c(t)’)
y=step(numc,denc,t);
plot(t,y)
title(‘Step response’)
xlabel(‘Time/s’)
matlab教程ppt(完整版)

`int8()`,
`char()`, `logical()`等。
流程控制结构
顺序结构
按照代码的先后顺序执行 。
选择结构
通过条件语句实现分支选 择,包括`if`、`else`、 `elseif`等。
循环结构
通过循环语句实现重复执 行代码块,包括`for`、 `while`等。
函数编写
函数定义
使用`function`关键字定义函数, 指定输入和输出参数。
介绍MATLAB中的机器学习工具箱,包括工具箱中的函数、算 法和使用方法等。
通过实际案例演示如何使用MATLAB进行机器学习,包括数据 预处理、特征选择、模型训练和评估等。
THANKS
[ 感谢观看 ]
信号的傅里叶变换
介绍傅里叶变换的基本原理 ,以及如何使用MATLAB进 行信号的傅里叶变换和逆变 换。
滤波器设计
介绍滤波器的基本原理和设 计方法,以及如何使用 MATLAB进行滤波器的设计 和实现。
信号处理实例
通过实际案例演示如何使用 MATLAB进行信号处理,包 括信号的频谱分析、滤波、 降噪等。
数值计算基础
数值类型
介绍MATLAB中的数值类型,包括双精度、单精 度、复数等。
变量声明
解释如何声明和初始化变量,以及如何使用 MATLAB的数据类型。
运算符
介绍基本的算术运算符、关系运算符和逻辑运算 符及其用法。
方程求解
代数方程求解
介绍如何使用MATLAB求解一元和多元代数方程。
微分方程求解
介绍如何使用MATLAB求解常微分方程和偏微分方程。
MATLAB应用领域
MATLAB是一种用于算法开发、数据 可视化、数据分析和数值计算的高级 编程语言和交互式环境。
matlab教程ppt(完整版)

矩阵的数学运算
总结词
详细描述
总结词
详细描述
掌握矩阵的数学运算,如求逆 、求行列式、求特征值等。
在MATLAB中,可以使用inv() 函数来求矩阵的逆,使用det() 函数来求矩阵的行列式,使用 eig()函数来求矩阵的特征值。 例如,A的逆可以表示为 inv(A),A的行列式可以表示 为det(A),A的特征值可以表 示为eig(A)。
• 总结词:了解特征值和特征向量的概念及其在矩阵分析中的作用。 • 详细描述:特征值和特征向量是矩阵分析中的重要概念。特征值是满足Ax=λx的标量λ和向量x,特征向量是与特征值对
应的非零向量。特征值和特征向量在许多实际问题中都有应用,如振动分析、控制系统等。
04
MATLAB图像处理
图像的读取与显示
变量定义
使用赋值语句定义变量,例如 `x = 5`。
矩阵操作
学习如何创建、访问和操作矩 阵,例如使用方括号 `[]`。
函数编写
学习如何创建自定义函数来执 行特定任务。
02
MATLAB编程
变量与数据类型
01
02
03
变量命名规则
MATLAB中的变量名以字 母开头,可以包含字母、 数字和下划线,但不应与 MATLAB保留字冲突。
了解矩阵的数学运算在实际问 题中的应用。
矩阵的数学运算在许多实际问 题中都有应用,如线性方程组 的求解、矩阵的分解、信号处 理等。通过掌握这些运算,可 以更好地理解和解决这些问题 。
矩阵的分解与特征值
• 总结词:了解矩阵的分解方法,如LU分解、QR分解等。
• 详细描述:在MATLAB中,可以使用lu()函数进行LU分解,使用qr()函数进行QR分解。这些分解方法可以将一个复杂的 矩阵分解为几个简单的部分,便于计算和分析。
matlab教程ppt(完整版)

,展示数据和模型结果。
数据处理
应用MATLAB的信号处理和统计 分析函数库,进行数据预处理、
特征提取和模型训练。
机器学习与深度学习
机器学习
介绍MATLAB中的各种机器学习算法,如线性回归、决策 树、支持向量机等,以及如何应用它们进行分类、回归和 聚类。
深度学习
介绍深度学习框架和网络结构,如卷积神经网络(CNN) 、循环神经网络(RNN)等,以及如何使用MATLBiblioteka B进行 训练和部署。感谢观看
THANKS
符号微积分
进行符号微分和积分运算,如极限、导数和 积分。
符号方程求解
使用solve函数求解符号方程。
符号矩阵运算
进行符号矩阵的乘法、转置等运算。
05
MATLAB应用实例
数据分析与可视化
数据分析
使用MATLAB进行数据导入、清 洗、处理和分析,包括描述性统
计、可视化、假设检验等。
可视化
利用MATLAB的图形和可视化工 具,如散点图、柱状图、3D图等
数值求和与求积
演示如何对数值进行求和与求积 操作。
数值计算函数
介绍常用数值计算函数,如sin、 cos、tan等。
方程求解
演示如何求解线性方程和非线性方 程。
03
MATLAB编程基础
控制流
01
02
03
04
顺序结构
按照代码的先后顺序执行,是 最基本的程序结构。
选择结构
通过if语句实现,根据条件判 断执行不同的代码块。
数据分析
数值计算
MATLAB提供了强大的数据分析工具,支 持多种统计分析方法,可以帮助用户进行 数据挖掘和预测分析。
MATLAB可以进行高效的数值计算,支持 多种数值计算方法,包括线性代数、微积 分、微分方程等。
数据处理
应用MATLAB的信号处理和统计 分析函数库,进行数据预处理、
特征提取和模型训练。
机器学习与深度学习
机器学习
介绍MATLAB中的各种机器学习算法,如线性回归、决策 树、支持向量机等,以及如何应用它们进行分类、回归和 聚类。
深度学习
介绍深度学习框架和网络结构,如卷积神经网络(CNN) 、循环神经网络(RNN)等,以及如何使用MATLBiblioteka B进行 训练和部署。感谢观看
THANKS
符号微积分
进行符号微分和积分运算,如极限、导数和 积分。
符号方程求解
使用solve函数求解符号方程。
符号矩阵运算
进行符号矩阵的乘法、转置等运算。
05
MATLAB应用实例
数据分析与可视化
数据分析
使用MATLAB进行数据导入、清 洗、处理和分析,包括描述性统
计、可视化、假设检验等。
可视化
利用MATLAB的图形和可视化工 具,如散点图、柱状图、3D图等
数值求和与求积
演示如何对数值进行求和与求积 操作。
数值计算函数
介绍常用数值计算函数,如sin、 cos、tan等。
方程求解
演示如何求解线性方程和非线性方 程。
03
MATLAB编程基础
控制流
01
02
03
04
顺序结构
按照代码的先后顺序执行,是 最基本的程序结构。
选择结构
通过if语句实现,根据条件判 断执行不同的代码块。
数据分析
数值计算
MATLAB提供了强大的数据分析工具,支 持多种统计分析方法,可以帮助用户进行 数据挖掘和预测分析。
MATLAB可以进行高效的数值计算,支持 多种数值计算方法,包括线性代数、微积 分、微分方程等。
matlab教程ppt(完整版)

转置
可以使用`'`运算符对矩阵进行 转置。
矩阵高级运算
01
逆矩阵
可以使用`inv`函数求矩阵的逆矩阵 。
行列式
可以使用`det`函数求矩阵的行列式 。
03
02
特征值和特征向量
可以使用`eig`函数求矩阵的特征值 和特征向量。
秩
可以使用`rank`函数求矩阵的秩。
04
04
matlab绘图功能
绘图基本命令
控制设计
MATLAB提供了控制系统设计和分析 工具箱,可以方便地进行控制系统的 建模、分析和优化。
03
信号处理
MATLAB提供了丰富的信号处理工具 箱,可以进行信号的时域和频域分析 、滤波器设计等操作。
05
04
图像处理
MATLAB提供了图像处理工具箱,可 以进行图像的增强、分割、特征提取 等操作。
02
matlab程序调试技巧分享
01
调试模式
MATLAB提供了调试模式,可以 逐行执行代码,查看变量值,设 置断点等。
日志输出
02
03
错误处理
通过使用fprintf函数,可以在程 序运行过程中输出日志信息,帮 助定位问题。
MATLAB中的错误处理机制可以 帮助我们捕获和处理运行时错误 。
matlab程序优化方法探讨
显示结果
命令执行后,结果将在命令窗口中显示。
保存结果
可以使用`save`命令将结果保存到文件中。
matlab变量定义与赋值
定义变量
使用`varname = value`格式定义变 量,其中`varname`是变量名, `value`是变量的值。
赋值操作
使用`=`运算符将值赋给变量。例如 ,`a = 10`将值10赋给变量a。
可以使用`'`运算符对矩阵进行 转置。
矩阵高级运算
01
逆矩阵
可以使用`inv`函数求矩阵的逆矩阵 。
行列式
可以使用`det`函数求矩阵的行列式 。
03
02
特征值和特征向量
可以使用`eig`函数求矩阵的特征值 和特征向量。
秩
可以使用`rank`函数求矩阵的秩。
04
04
matlab绘图功能
绘图基本命令
控制设计
MATLAB提供了控制系统设计和分析 工具箱,可以方便地进行控制系统的 建模、分析和优化。
03
信号处理
MATLAB提供了丰富的信号处理工具 箱,可以进行信号的时域和频域分析 、滤波器设计等操作。
05
04
图像处理
MATLAB提供了图像处理工具箱,可 以进行图像的增强、分割、特征提取 等操作。
02
matlab程序调试技巧分享
01
调试模式
MATLAB提供了调试模式,可以 逐行执行代码,查看变量值,设 置断点等。
日志输出
02
03
错误处理
通过使用fprintf函数,可以在程 序运行过程中输出日志信息,帮 助定位问题。
MATLAB中的错误处理机制可以 帮助我们捕获和处理运行时错误 。
matlab程序优化方法探讨
显示结果
命令执行后,结果将在命令窗口中显示。
保存结果
可以使用`save`命令将结果保存到文件中。
matlab变量定义与赋值
定义变量
使用`varname = value`格式定义变 量,其中`varname`是变量名, `value`是变量的值。
赋值操作
使用`=`运算符将值赋给变量。例如 ,`a = 10`将值10赋给变量a。
matlab教程ppt(完整版)

控制流语句
使用条件语句(如if-else)和 循环语句(如for)来控制程序 流程。
变量定义
使用赋值语句定义变量,例如 `a = 5`。
矩阵运算
使用矩阵进行数学运算,如加 法、减法、乘法和除法等。
函数编写
创建自定义函数来执行特定任 务。
02
MATLAB编程语言基础
变量与数据类型
变量命名规则
数据类型转换
编辑器是一个文本编辑器 ,用于编写和编辑 MATLAB脚本和函数。
工具箱窗口提供了一系列 用于特定任务的工具和功 能,如数据可视化、信号 处理等。
工作空间窗口显示当前工 作区中的变量,可以查看 和修改变量的值。
MATLAB基本操作
数据类型
MATLAB支持多种数据类型, 如数值型、字符型和逻辑型等 。
04
MATLAB数值计算
数值计算基础
01
02
03
数值类型
介绍MATLAB中的数值类 型,包括双精度、单精度 、复数等。
变量赋值
讲解如何给变量赋值,包 括标量、向量和矩阵。
运算符
介绍基本的算术运算符、 关系运算符和逻辑运算符 及其优先级。
数值计算函数
数学函数
列举常用的数学函数,如 三角函数、指数函数、对 数函数等。
矩阵的函数运算
总结词:MATLAB提供了许多内置函 数,可以对矩阵进行各种复杂的运算
。
详细描述
矩阵求逆:使用 `inv` 函数求矩阵的 逆。
特征值和特征向量:使用 `eig` 函数 计算矩阵的特征值和特征向量。
行列式值:使用 `det` 函数计算矩阵 的行列式值。
矩阵分解:使用 `factor` 和 `expm` 等函数对矩阵进行分解和计算指数。
matlab编程基础与工程应用第八章课件

【 例 8.1-1】 电 阻 电 路 如 图 8-1 所 示 , 已 知 R1=R2=R3=1Ω , R4=R5=R6=2Ω,uS1=4V,uS2=-2V,求I3。
电阻电路可用回路电流法、支路电流法、节 点电压法等方法求解,本例给出回路电流法。
【解】 解法一:回路电流法。回路电流法以回路电 流为变量,根据基尔霍夫电压定律(KVL), 列写电路的独立回路组的KVL方程。如图81,将3个网孔作为选取的独立回路组,则回 路电流法的KVL方程组为
程序还调用 MATALB 信号处理工具箱中的周期 矩形脉冲的产生函数square。其调用格式为: square(T);产生一个周期为2π的矩形脉冲函数。 其最大值为 1 ,最小值为 -1. 函数自变量取值为 相量T的各元素的值。 square (T, duty);产生一个占空比duty、周期为 2π的矩形脉冲函数。 square(w*T, duty);产生一个占空比duty、周期 为2π/w的矩形脉冲函数。 由以上说明可知,square(w*t, 50)产生一个周 期为 2π/w 、占空比为 50% 、幅值为± 1 的周期 性矩形脉冲。
������ ������������ ������������ //������������ Z 1
电流表的读数即为电流������的模值。
clear clc w=1000; ZR=20; Us=160; ZL=j*w*0.04 ZC=-j*(1/(w*20*1e-6)); Z1=(ZL*ZC)/(ZL+ZC); Z=ZR+Z1; U=Us*(Z1/Z); I=U/ZL; Iy=abs(I) 程序运行结果为 Iy = 3.9801
(R1+ R6+ R2) I1- R6 I3- R2 I2=- uS1 (R2+ R4 + R5) I2- R2 I1- R5 I3=- uS2 (R3+ R5+ R6) I3- R6 I1- R5 I2= uS2
MATLAB课件-第八+十讲
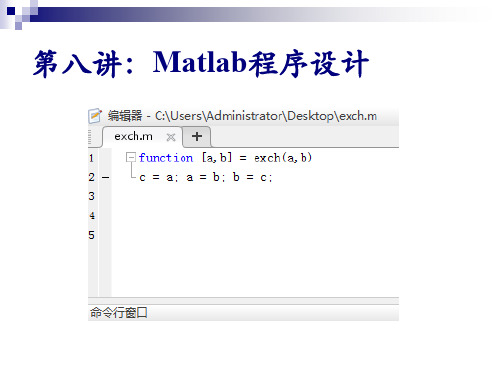
a=1 b=2 c=1 x1=-1,x2=-1
3、程序的暂停 程序执行过程中暂停,可用pause函数,其调用格 式为:
pause(延迟描述) 如果省略延迟时间,直接使用pause,则将暂停程 序,直到
用户按任一键后程序继续执行。
若要强行中止程序的运行可按Ctrl+C键。
8.2.2 选择结构
选择结构是根据给定的条件成立或不成立,分别执行不同的语句。 Matlab用于实现选择结构的语句有if语句,switch语句和try语句。 1. if 语句 在Matlab中,if语句有3种格式。 (1)单分支if语句 语句格式: if 条件
A = ‘Hello, Tom’;
disp(A) 输出为:Hello, Tom 又如:A = [1,2,3;4,5,6;7,8,9];
disp(A) 输出为:
123
456 789
%disp函数输出格式更紧凑
例 求一元二次方程 ax2 bx c 0 的根。
由于Matlab能进行复数运算,所以不需要判断方程的判别式, 可直接根据求根公式求根。 程序如下: a = input('a='); b = input('b='); c = input('c='); d = b*b-4*a*c; x = [(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)]; disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]); 程序输出为:
otherwise rate = 14/100;
%价格大于等于5000
num2cell函数是将数值 矩阵转化为单元矩阵。
3、程序的暂停 程序执行过程中暂停,可用pause函数,其调用格 式为:
pause(延迟描述) 如果省略延迟时间,直接使用pause,则将暂停程 序,直到
用户按任一键后程序继续执行。
若要强行中止程序的运行可按Ctrl+C键。
8.2.2 选择结构
选择结构是根据给定的条件成立或不成立,分别执行不同的语句。 Matlab用于实现选择结构的语句有if语句,switch语句和try语句。 1. if 语句 在Matlab中,if语句有3种格式。 (1)单分支if语句 语句格式: if 条件
A = ‘Hello, Tom’;
disp(A) 输出为:Hello, Tom 又如:A = [1,2,3;4,5,6;7,8,9];
disp(A) 输出为:
123
456 789
%disp函数输出格式更紧凑
例 求一元二次方程 ax2 bx c 0 的根。
由于Matlab能进行复数运算,所以不需要判断方程的判别式, 可直接根据求根公式求根。 程序如下: a = input('a='); b = input('b='); c = input('c='); d = b*b-4*a*c; x = [(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)]; disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]); 程序输出为:
otherwise rate = 14/100;
%价格大于等于5000
num2cell函数是将数值 矩阵转化为单元矩阵。
第8章MATLAB高级应用PPT教学课件

【例8.2】在MATLAB环境中创建一个M函数文件,用来绘制正 弦信号波形。
2020/12/10
13
4. 创建独立的外部程序EXE文件 先将M文件转换为C/C++代码文件,然后自动调
用mbuild命令对C/C++代码文件进行编译连接,得到 exe文件。
如果系统安装两个以上的编译器,第一次执行编译 时会让用户选择编译器,一旦选定以后就成为默认的编 译器。如果要改变默认的编译器,则需要使用
(3) 对于A/D、D/A卡,或其它PC硬件,可以直接用MEX文件 进行访问。
(4) 利用MEX文件,可以使用如Windows用户图形界面等资源。
2020/12/10
3
1. MEX文件系统设置
采用Microsoft Visual C/C++ 6.0编译器,在命令窗 口使用“mex -setup”命令,对MEX文件编译器进行配置 2. 测试配置
2020/12/10
7
(2) 计算功能子程序 第二部分为计算功能子程序,包含所有的实际需要完
成的功能源代码,可以是用户以前所编写的算法和程序, 以函数的形式存在。
2020/12/10
8
4. C语言MEX文件的建立 (1) 常用MATLAB API函数
在MEX文件中,常用MATLAB API函数有: mxGetM:获得矩阵的行数。 mxGetN:获得矩阵的列数。 mxGetPr:获得矩阵的实数部分的数据指针。 mexErrMsgTxt:输出错误信息,并返回到MATLAB命令 提示符下。 mxCreateString:创建一个字符串,将 MATLAB的extern\examples\mex目录设置为当前目录, 然后在命令窗口中输入:
2020/12/10
13
4. 创建独立的外部程序EXE文件 先将M文件转换为C/C++代码文件,然后自动调
用mbuild命令对C/C++代码文件进行编译连接,得到 exe文件。
如果系统安装两个以上的编译器,第一次执行编译 时会让用户选择编译器,一旦选定以后就成为默认的编 译器。如果要改变默认的编译器,则需要使用
(3) 对于A/D、D/A卡,或其它PC硬件,可以直接用MEX文件 进行访问。
(4) 利用MEX文件,可以使用如Windows用户图形界面等资源。
2020/12/10
3
1. MEX文件系统设置
采用Microsoft Visual C/C++ 6.0编译器,在命令窗 口使用“mex -setup”命令,对MEX文件编译器进行配置 2. 测试配置
2020/12/10
7
(2) 计算功能子程序 第二部分为计算功能子程序,包含所有的实际需要完
成的功能源代码,可以是用户以前所编写的算法和程序, 以函数的形式存在。
2020/12/10
8
4. C语言MEX文件的建立 (1) 常用MATLAB API函数
在MEX文件中,常用MATLAB API函数有: mxGetM:获得矩阵的行数。 mxGetN:获得矩阵的列数。 mxGetPr:获得矩阵的实数部分的数据指针。 mexErrMsgTxt:输出错误信息,并返回到MATLAB命令 提示符下。 mxCreateString:创建一个字符串,将 MATLAB的extern\examples\mex目录设置为当前目录, 然后在命令窗口中输入:
MATLAB基础及应用课件第8章

end
ห้องสมุดไป่ตู้end
第8章 MATLAB综合实训
subplot(122)
imshow(uint8(D))
%uint8(D)强制转
换D的数据格式
title('置乱后的图像')
imwrite(uint8(D),'d:\image.bmp','bmp') %
保存置乱后的图像
fid=fopen('d:\test.bin','wb')
C=zeros(65536,1);
for i=1:65536 C(i)=A(B(i));
%置乱,用密钥重新排列 图像矩阵
end
第8章 MATLAB综合实训
D=zeros(256);
k=1;
for i=1:256
%将单列矩阵转换成与原
图像同样尺寸的矩阵
for j=1:256
D(j,i)=C(k);
k=k+1;
讲解演示,评估项目的完成情况,评价内容如 下: 1)图像的视觉效果; 2)处理图像与原始图像之间的偏离程度; 3)图形用户界面是否友好。
第8章 MATLAB综合实训
8.2 数字图像增强
图像增强就是对图像进行加工,以得到对 具体应用来说视觉效果更“好”,更“有用” 的图像。 一、 项目说明
1.项目要求 (1)图像测试 (2)图像添加噪声
%读入密钥
RB=fread(fid,65536,'double');
fclose(fid)
第8章 MATLAB综合实训
RC=RD(:); RA=zeros(65536,1); for i=1:65536
matlab教程ppt(完整版)

04
MATLAB绘图与可视化
BIG DATA EMPOWERS TO CREATE A NEW
ERA
绘图基础
散点图
描述数据点在二维平面上的分 布情况。
折线图
展示数据随时间或其他变量的 变化趋势。
条形图
用于比较不同类别数据的数值 大小。
饼图
展示数据中各部分所占的比例 。
三维绘图
三维散点图
在三维空间中展示数据点的分布情况。
信号调制与解调
利用MATLAB实现信号的调制(如 FSK、PSK)与解调,以实现信号的 传输与接收。
控制系统实例
控制系统建模
01
使用MATLAB建立控制系统的数学模型,如传递函数、状态方
程等。
控制系统分析与仿真
02
基于建立的模型,进行控制系统性能分析和仿真,如稳定性分
析、时域和频域响应等。
控制策略设计
循环语句
使用`for`循环和`while`循 环实现重复执行代码块。
流程控制结构示例
演示如何使用条件语句和 循环语句实现矩阵的求和 、求积等操作。
函数编写
01
02
03
04
函数定义
使用`function`关键字定义函 数,指定输入参数和输出参数
。
函数体
在函数体内编写实现特定功能 的代码。
函数调用
通过函数名和输入参数调用函 数,获取输出结果。
通过交叉验证、性能指标等手段 评估模型的性能,并根据评估结
果对模型进行优化和调整。
THANKS
感谢观看
ห้องสมุดไป่ตู้
BIG DATA EMPOWERS TO CREATE A NEW ERA
精品课件-MATLAB 8.X程序设计及典型应用-第8章

26
第8章 MATLAB的典型应用
【例 8-6】 绘制任意匝数通电螺线管周围产生的磁感应强度 截面分布图。
建模:载流导体产生磁场的基本规律为:任一电流元 Idl 在空 间任一点 P 处产生的磁感应强度 dB 为
dB
0
4π
Idl r3
r
其中, r 为电流元到 P 点的矢径, dl 为导线元的长度矢量。P 点
图8.6 曲线拟合方法的设置及其拟合结果
12
第8章 MATLAB的典型应用
图8.7 MATALB 8.X版本的数据运行结果
13
第8章 MATLAB的典型应用
表 8-1
拟合类型 惯用方程拟合(Custom Equations) 指数方程拟合(Exponential) 傅里叶方程拟合(Fourier) 高斯方程拟合(Gaussian) 插值多项式拟合(Interpolant) 多项式拟合(Polynomial) 乘方拟合(Power) 最佳拟合(Rational) 光滑样条拟合(Smoothing Spline) 正弦函数叠加拟合 (Sum of Sin Functions) 韦伯拟合(Wiebull)
3
第8章 MATLAB的典型应用
编写文件名为exm8_1的脚本文件:
%平抛实验数据处理 clear x=[0.03 0.06 0.09 0.12 0.15]; y=[-0.004 -0.013 -0.039 -0.072 -0.13]; S=std(y,1) plot(x,y,'r*','MarkerSize',8) hold on, p=polyfit(x,y,2); px=poly2str(p,'x') X=0:0.005:0.15; Y=polyval(p,X);% plot(X,Y,'LineWidth',1.5) v0=1;g=9.8; Y1=-g*X.^2/(2*v0^2); plot(X,Y1,'k--','LineWidth',1.5) title('平抛运动实验数据二次拟合曲线和理想曲线图') xlabel('水平位移'),ylabel('竖直下落位移') legend('原始数据','二次多项式拟合曲线','理想曲线') grid on %绘制网格坐标 hold off
第8章 MATLAB的典型应用
【例 8-6】 绘制任意匝数通电螺线管周围产生的磁感应强度 截面分布图。
建模:载流导体产生磁场的基本规律为:任一电流元 Idl 在空 间任一点 P 处产生的磁感应强度 dB 为
dB
0
4π
Idl r3
r
其中, r 为电流元到 P 点的矢径, dl 为导线元的长度矢量。P 点
图8.6 曲线拟合方法的设置及其拟合结果
12
第8章 MATLAB的典型应用
图8.7 MATALB 8.X版本的数据运行结果
13
第8章 MATLAB的典型应用
表 8-1
拟合类型 惯用方程拟合(Custom Equations) 指数方程拟合(Exponential) 傅里叶方程拟合(Fourier) 高斯方程拟合(Gaussian) 插值多项式拟合(Interpolant) 多项式拟合(Polynomial) 乘方拟合(Power) 最佳拟合(Rational) 光滑样条拟合(Smoothing Spline) 正弦函数叠加拟合 (Sum of Sin Functions) 韦伯拟合(Wiebull)
3
第8章 MATLAB的典型应用
编写文件名为exm8_1的脚本文件:
%平抛实验数据处理 clear x=[0.03 0.06 0.09 0.12 0.15]; y=[-0.004 -0.013 -0.039 -0.072 -0.13]; S=std(y,1) plot(x,y,'r*','MarkerSize',8) hold on, p=polyfit(x,y,2); px=poly2str(p,'x') X=0:0.005:0.15; Y=polyval(p,X);% plot(X,Y,'LineWidth',1.5) v0=1;g=9.8; Y1=-g*X.^2/(2*v0^2); plot(X,Y1,'k--','LineWidth',1.5) title('平抛运动实验数据二次拟合曲线和理想曲线图') xlabel('水平位移'),ylabel('竖直下落位移') legend('原始数据','二次多项式拟合曲线','理想曲线') grid on %绘制网格坐标 hold off
matlab电子课件第八章

数学软件
河北理工大学理学院 阎少宏
1 shaohong@
第一章
1
第八章
SIMULINK交互式仿真集成环境 交互式仿真集成环境
SIMULINK是MATLAB最重要的组件之一,它提供了实现动态 是 最重要的组件之一, 最重要的组件之一 系统建模、 仿真的—个集成环境 它的存在使MATLAB的功能得 个集成环境。 系统建模 、 仿真的 个集成环境 。 它的存在使 的功能得 到进一步扩展。在该环境中,无须书写大量的程序. 到进一步扩展。在该环境中,无须书写大量的程序.而只要通过简 单直观的鼠标操作,就可构造出复杂的仿真模型。 单直观的鼠标操作,就可构造出复杂的仿真模型。
SIMULINK模型的三种组件: 模型的三种组件: 模型的三种组件 信源 系统 信宿
视觉上: 视觉上:方框图 文件上:扩展名为 文件上:扩展名为MDL的ASCⅡ代码 的 Ⅱ 数学上: 数学上:一组微分方程或差分方程 行为上: 行为上:实际系统的动态性状
第一章
7
二 模型文件的操作 主要操作:新建、打开、存盘、 主要操作:新建、打开、存盘、打印
第一章
4
图标或命令方式) 一、启动SIMULINK模块库窗口 (图标或命令方式) 启动 模块库窗口 二、打开source子库 打开 子库
三、打开空白模型窗口 四、在空白窗口中添加所需source模块(如:正弦波模块 模块( 在空白窗口中添加所需 模块 Sine Wave) ) 模块( 示波器Scope) 五、添加信宿库Sinks模块(如:示波器 添加信宿库 模块 ) 六、连接信号线 至此一简单模型已经建成
第一章
18
●磁滞回环模块(Backlash),和其在控制系统中的定义一致。 磁滞回环模块 ,和其在控制系统中的定义一致。 在此模块组中定义了很多分段线性的静态非线性模块, 在此模块组中定义了很多分段线性的静态非线性模块,如死区非 线性(Dead zone)、 饱和非线性 线性 、 饱和非线性(Saturation)、量化模块 、 (Quantizer)、继电模块 、继电模块(Relay)、变化率限幅模块 (Rate Limiter) 、 其实其中很多模块可以由一维查表模块实现。 等,其实其中很多模块可以由一维查表模块实现。
河北理工大学理学院 阎少宏
1 shaohong@
第一章
1
第八章
SIMULINK交互式仿真集成环境 交互式仿真集成环境
SIMULINK是MATLAB最重要的组件之一,它提供了实现动态 是 最重要的组件之一, 最重要的组件之一 系统建模、 仿真的—个集成环境 它的存在使MATLAB的功能得 个集成环境。 系统建模 、 仿真的 个集成环境 。 它的存在使 的功能得 到进一步扩展。在该环境中,无须书写大量的程序. 到进一步扩展。在该环境中,无须书写大量的程序.而只要通过简 单直观的鼠标操作,就可构造出复杂的仿真模型。 单直观的鼠标操作,就可构造出复杂的仿真模型。
SIMULINK模型的三种组件: 模型的三种组件: 模型的三种组件 信源 系统 信宿
视觉上: 视觉上:方框图 文件上:扩展名为 文件上:扩展名为MDL的ASCⅡ代码 的 Ⅱ 数学上: 数学上:一组微分方程或差分方程 行为上: 行为上:实际系统的动态性状
第一章
7
二 模型文件的操作 主要操作:新建、打开、存盘、 主要操作:新建、打开、存盘、打印
第一章
4
图标或命令方式) 一、启动SIMULINK模块库窗口 (图标或命令方式) 启动 模块库窗口 二、打开source子库 打开 子库
三、打开空白模型窗口 四、在空白窗口中添加所需source模块(如:正弦波模块 模块( 在空白窗口中添加所需 模块 Sine Wave) ) 模块( 示波器Scope) 五、添加信宿库Sinks模块(如:示波器 添加信宿库 模块 ) 六、连接信号线 至此一简单模型已经建成
第一章
18
●磁滞回环模块(Backlash),和其在控制系统中的定义一致。 磁滞回环模块 ,和其在控制系统中的定义一致。 在此模块组中定义了很多分段线性的静态非线性模块, 在此模块组中定义了很多分段线性的静态非线性模块,如死区非 线性(Dead zone)、 饱和非线性 线性 、 饱和非线性(Saturation)、量化模块 、 (Quantizer)、继电模块 、继电模块(Relay)、变化率限幅模块 (Rate Limiter) 、 其实其中很多模块可以由一维查表模块实现。 等,其实其中很多模块可以由一维查表模块实现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8、lsim()函数的用法
[y,t,x]=lsim(sys,u,t); [y,t,x]=lsim(sys,u,t,x0);
9、dlsim()函数的用法
dlsim(sys,u); [y,x]=dlsim(sys,u,x0);
eg8. 求下列系统的正弦响应。其中:周期2*pi,时间 t=30s,采样周期取0.1s.
程序:
a=[-0.5 -0.8;0.4 0.4];b=[1;-1]; c=[2 -5]; d=2; sys=ss(a,b,c,d) [u,t]=gensig(‘sin’, 2*pi, 30, 0.1) lsim(sys,u,t)
11、dcgain()函数的用法
k=dcgain(sys);
12、feedback()函数的用法
离散系统函数的调用格式为
dnyquist(a,b,c,d,Ts) dnyquist(a,b,c,d,Ts,iu) dnyquist(a,b,c,d,Ts,iu,w)
其中
TS和w分别为频率特性的取样时间和对应的频 率向量
例例5-16、5-17
例 绘制
G(s)
s2
10 1.2s
10
的nyquist图和bode图。
程序: [u1, t1]=gensig(‘sin’, 2*pi, 50, 0.01); [u2, t2]=gensig(‘square’, 2*pi, 50, 0.01); plot(t1,u1,t2,u2) axis([0 50 -1.2 1.2]) xlabel(‘time/s’) ylabel(‘c(t)’)
幅频
相频 bode(sys); bode(sys,w); [mag,phase,w]=bode(num,den) [mag,phase]=bode(num,den,w) [mag,phase,w]=bode(A,B,C,D) [mag,phase,w]=bode(A,B,C,D,iu)
式中num,den和A,B,C,D分别为系统的开环传 递函数和状态方程的参数, w为Bode图的频率 点。
>> [Gm,Pm,Wcg,Wcp]=margin(k*ng,dg)
Gm =
4.0000
Pm = 41.5340
相位裕量
Wcg =
1.4142
Wcp =
0.6118
>> G=20*log10(Gm)
G=
12.0412
幅值裕量
练习 已知二阶系统的开环传递函数为 试绘制系统的Bode图
k=10; z=[-4]; p=[0 -0.5 -50 -50]; [num,den]=zp2tf(z,p,k); Bode(num,den); title(‘Bode plot’); grid on
(二)时域响应常用的Matlab函数:
产生输入信号:gensig 求取系统单位阶跃响应:step 求取系统的冲激响应:impulse 连续系统的零输入响应: initial 连续系统对任意输入的响应: lsim 求系统稳态值:dcgain 求具有反馈结构的闭环传函:feedback
对于离散系统只需在连续系统对应函数前加d 就可以,如dstep,dimpulse,dinitial,dlsim 等。调用格式与step、impulse类似。
y=step(numc,denc,t);
plot(t,y)
title(‘Step response’)
xlabel(‘Time/s’)
dc=dcgain(numc,denc)
dc=1.
eg10. 给出如下系统的开环传递函数,试用MATLAB 求取其单位加速度响应。
Gs
3
s2 s
4
程序: num=[3];den=[1 4 3 0 0 0]; t=0:0.1:20; y=step(num,den,t); plot(t,y) title(‘Step response’) xlabel(‘Time/s’)
的调用格式为
[Gm,Pm,Wcg,Wcp]=margin(sys)
或
[Gm,Pm,Wcg,Wcp]=margin(sys)
式中 Gm和Pm分别为系统的幅值裕量和相 位裕量,而Wcg 和Wcp分别为幅值裕量和 相位裕量处相应的频率值。
例5-2 已知二阶系统的开环传递函数为 试绘制系统的开环频率特性曲线
2、step()函数的用法
时
step(sys);step(sys,t);
间
y=step(num,den,t);
向 量
[y,x,t]=step(num,den);
0
[y,x,t]=step(A,B,C,D,iu);
[ ,t]
输 状 自时 出 态 动间 矩 轨 生序 阵 迹 成列
eg2. 求下列系统在输入信号为r(t)=10*1(t)输入时,系统 在[0 20s]的响应曲线。
5、dimpulse()函数的用法
dimpulse(numz,denz); dimpulse (A,B,C,D); dimpulse (A,B,C,D,iu);
第 个 输 入
iu
eg5. 将下列连续系统离散化,并求其离散状态系统的冲 激响应曲线。
程序: 离散化: a=[-0.5 -0.8;0.4 0];b=[1;-1]; c=[2 5]; d=0; [G,H,Cd,Dd]=c2dm(a,b,c,d,0.1) 冲激响应: dimpulse(G,H,Cd,Dd)
式 中 numz,denz 和 A,B,C,D 分 别 为 系 统 的 开 环 传递函数和状态方程的参数,Ts为取样频率,w 为Bode图的频率点。
3. 显示绘制结果
可以利用下面的MATLAB命令
>>subplot(2,1,1);semilogx(w,20*log10(mag))
>>subplot(2,1,2);semilogx(w,phase)
y=impluse (num,den,t);
向 量
[y,x,t]=impluse (num,den);
0
[y,x,t]=impluse (A,B,C,D,iu);
[ ,t]
输 状 自时 出 态 动间 矩 轨 生序 阵 迹 成列
eg4. 求下列系统的脉冲响应曲线。
程序: K=1;Z=[-1];P=[-2 -3]; [num,den]=zp2tf(Z, P, K); sys=tf(num,den); t=0:0.2:20; impulse(sys,t) xlabel(‘time/s’) ylabel(‘c(t)’)
第 个 输 入
iu
eg3. 求下列系统的阶跃响应曲线。
程序: numz=[1 -1.2 0.4]; denz=[1.2 -1.5 0.9]; dstep(numz,denz) xlabel(‘time/s’) ylabel(‘c(t)’)
4、impluse()函数的用法
时
impluse(sys); impluse(sys,t); 间
离散系统的调用格式为: 相频
[mag,phase,w]=dbode(numz,denz,Ts) 幅频 [mag,phase]=dbode(numz,denz,Ts,w)
[mag,phase,w]=dbode(A,B,C,D,Ts,iu) [mag,phase,w]=dbode(A,B,C,D,Ts,iu,w)
(2) Nyquist图
连续系统函数的调用格式为
nyquist(sys) nyquist(sys,w) [Re,Im,w]=nyquist(num,den) [Re,Im,w]=nyquist(num,den,w) [Re,Im,w]=nyquist(A,B,C,D)
其中
返回值Re,Im和w分别为频率特性的实部向量、 虚部向量和对应的频率向量
6、initial()函数的用法
[y,t,x]=initial(sys,x0); [y,t,x]=initial(sys,x0,t);
7、dinitial()函数的用法
dinitial(sys,x0); [y,x,n]=dinitial(sys,x0,n);
eg6. 求下列系统在x0=[1;1]时,系统的零输入响应。
1、gensig()函数的用法
[u,t]= gensig(type,tau) [u,t]= gensig(type,tau,tf,ts)
信 号 序时 列间
序 列
信 信持采 号 号续样 类 周时时 型 期间间
eg1. 生成一个周期为2*pi,持续时间为50s,采样时间 为0.01s的正弦波和方波信号。
常用的作图方法:Bode图,奈奎斯特图
频域响应常用的Matlab函数:
画Bode图:bode 画奈奎斯特图:nyquist 画尼克尔斯图:nichols 绘制零极点位置:pzmap 计算增益和相位裕度: margin
对于离散系统只需在连续系统对应函数前加d 就可以,如dbode,dnyquist,dnichols。调用 格式类似。
程序: K=10;Z=[-1];P=[-2 -3]; [num,den]=zp2tf(Z, P, K); sys=tf(num,den); t=0:0.2:20; step(sys,t) xlabel(‘time/s’) ylabel(‘c(t)’)
3、dstep()函数的用法
dstep(numz,denz); dstep(A,B,C,D); dstep(A,B,C,D,iu);
(1)Bode图
1. 产生频率向量——横轴 频率向量可由logspace( )函数来构成。此
函数的调用格式为 ω=logspace(m,n,npts) 此命令可生成一个以10为底的指数向量
(10m∽10n ),点数由npts任意选定。
npts
10m
